Chatter suppression analysis in milling process with variable spindle speed based on the reconstructed semi-discretization method

Abstract

Milling chatter is a harmful phenomenon, which seriously affects the quality of the workpiece and limits the processing efficiency. The milling with variable spindle speed is an effective method for chatter suppression. In this paper, the reconstructed semi-discretization method (RSDM) is proposed to analyze the stability of the delay differential equations with varying delay term (VDDE) established based on the milling process with variable spindle speed. Firstly, the modulation period is discretized, and the time periodic delay term in VDDE is approximated at the discrete intervals based on the Shannon orthogonal basis. Secondly, the transition matrix is constructed, and the Floquet theory is used to build the stability boundary of milling system. The validity of the proposed method is verified by comparing with the well-accepted semi-discretization method (SDM) via a single degree of freedom milling system. Considering the limit of the acceleration of the spindle speed of machine tool, the modulation parameters RVF and RVA with sinusoidal and triangular wave modulations are optimized. Finally, the chatter frequencies and chatter types are analyzed and compared based on the reconstructed semi-discretization method.

1 Introduction

The chatter in metal cutting process is an unfavorable phenomenon, which not only reduces production efficiency, damages to machining quality, but also damages machine tool and cutting tool. The chatter is attributed to the self-excited vibration of the machining system consisted of machine tool, cutting tool, workpiece, and fixture [1,2,3,4,5,6]. The self-excited chatter may be induced by mode coupling, regenerative effect of the chip thickness, etc.; however, the regenerative chatter occurs earlier than the other types of chatter in most machining processes [7]. As a result, the regenerative effect has become the most common accepted explanation for chatter in metal cutting, which is related to the cutting force variation due to the wavy workpiece surface left during the previous revolution in cutting [7, 8].

In order to avoid chatter, the stability of the dynamics of machining system is studied from different perspectives, such as the frequency method [9,10,11], the semi-discretization method [12,13,14,15,16,17], the numerical method [18,19,20], the full-discretization method [21], the temporal finite element analysis method [22], the numerical integration method [23], and the reconstructed semi-discretization method [24, 25]. The stability analysis of machining systems can help engineers to choose cutting parameters without chatter, but it cannot improve the stability boundary of the machining system and cannot enhance machining efficiency. Chatter suppression can improve the stability boundary and enhance the machining efficiency.

In general, the means of chatter suppression are divided into the passive and active chatter suppressions. The passive chatter suppression is carried out by improving the structure dynamic of the machining system or adding auxiliary device, such as the application of variable pitch and helix angle for the milling tool and the addition of tuned vibration absorber. Active chatter suppression is carried out by controlling the parameters of dynamic model for the machining system or the cutting parameters in real time, such as the real-time control of stiffness variation for the spindle via piezoelectric stack actuators, active vibration damping controller, and active piezoelectric actuator. In addition to the above active chatter suppression, the chatter suppression based on variable spindle speed is an efficient method which does not need to add an active control device.

The ways of suppressing chatter based on variable spindle speed were first proposed by Stoferle and Grab in the 1970s [26]. The corresponding dynamic equation is delay differential equations with varying delay (VDDE). Several methods have been proposed for the stability analysis of the VDDE in the past 20 years. Pakdemirli et al. (1997) used the perturbation method to analyze the stability of varying spindle speed in turning, in which the angle of revolution is taken as the independent coordinate for maintaining a constant delay in the equations, and the amplitude of speed fluctuation is assumed to be small which are used as the perturbation parameter to construct the approximate analytical solutions [27]. Jayarma et al. (2000) used the Fourier analysis to transform the VDDE and obtained the solution of an infinite order characteristic equation, and the approximate solution of the stability of VDDE can be obtained by considering the truncated equation [28]. Sastry et al. (2001) presented a discrete time approach to the stability of the variable spindle speed in face-milling process, in which the dynamics are described by a set of differential equations with time-varying periodic coefficients and time delay. The eigenvalues of the state transition matrix of the finite dimensional system are then used to build the stability criteria [29]. Yilmaz et al. (2002) proposed a chatter suppression technique using multilevel random spindle speed variation, and the stability was assessed by the Lyapunov exponent [30]. Namachchivaya et al. (2003) adapt the perturbative method to obtain finite dimensional equations by describing the explicit time-dependent delay term as a new state variable to the original equations of motion with appropriate initial conditions [31]. Insperger and Stepan (2004) proposed the semi-discretization method to analyze the stability of turning with varying spindle speed modulated by a sinusoidal variation [14]. Long et al. (2005) used the semi-discretization method to the stability analysis for milling process with variable spindle speed [32]. Zatarain et al. (2008) presented the general theory for stability analysis in the frequency domain and for any speed variation strategies, and it was compared with the semi-discretization method for stability [33]. Seguy et al. (2010, 2011) adapt the semi-discretization method to analyze the effect of spindle speed variation (triangular and sinusoidal shape variations) in high-speed domain (corresponding to the first flip and to the first Hopf lobes), and show the period doubling chatter can effectively be suppressed by spindle speed variation, and the technique is not effective for the quasi-periodic chatter above the Hopf lobe [34, 35]. Wu et al. (2010) developed the dynamic model of the noncircular turning process. By using the spindle’s angular position as the independent variable, the dynamic model of the variable spindle speed in noncircular turning process is described by differential equation with linear periodic time-varying coefficients and a fixed delay, and the Floquet theory is applied to determine the stability boundary [36]. Long et al. (2010) made use of the semi-discretization method for stability prediction of up-milling and down-milling operations [37]. Xie et al. (2012) improved the semi-discretization method to stability predictions of milling with variable spindle speed [38]. Otto et al. (2013) developed the frozen time approach to calculate the stability lobes of machining with spindle speed variation [39]. Liang et al. (2013) proposed an improved numerical integration method to the stability analysis of VDDE [40]. Totis et al. (2014) proposed the Chebyshev collocation method to analyze the stability in milling with spindle speed variation [41]. Ding et al. (2015) proposed the numerical integration method to analyze the stability of VDDE in which the time delay is determined by the integral transcendental equation [42]. Urbikain et al. (2016) used the enhanced multistage homotopy perturbation method to the stability of turning process with spindle speed variation, and the balance between the improved stability margins and acceptable behavior of the spindle is identified by energy consumption measurement [43]. Niu et al. (2016) used the Fourier series and numerical integration method to the stability analysis of VDDE, and different spindle speed modulation schemes are compared [44].

The above researchers studied the stability of VDDE based on different methods, which play a very vital role in prompting the development of the stability analysis of VDDE. In above methods, the semi-discretization method is an efficient numerical method that provides a finite dimensional matrix approximation of the infinite dimensional monodromy matrix, while the numerical scheme is relatively simple. In the following researches, based on the semi-discrete method, we analyze the stability of the VDDE from the views of signal sampling and reconstruction, and compare the proposed method with the semi-discrete method.

This paper is organized as follows: In Section 2, the reconstructed semi-discretization method is present based on the Shannon orthogonal basis function for the stability analysis of VDDE. In Section 3, the dynamic model of milling with variable spindle speed is introduced. In Section 4, two different methods for stability analysis are compared. In Section 5, two different modulation laws of the spindle are compared, and the values of the RVA and RVF are optimized. In Section 6, the chatter types based on the reconstructed semi-discretization method are analyzed. Section 7 concludes this work.

2 Theoretical basic

2.1 Shannon sampling theorem

The sampling theorem was first proposed in 1928 by Harry Nyquist, and Claude Elwood Shannon, the founder of the information theory, described in detail the theorem in 1948. The derivation process of the theorem is not expressed here; the main contents are described as follows:

Assuming the continuous function f(t) ∈ L²(R) (where L²(R) is the square integrable function space in which the function satisfies the rule: ${\int}_{-\infty}^{+\infty }{\left|f(t)\ \right|}^2\mathrm{d}x<+\infty$), when the Fourier transform of the continuous function f(t) has the following property: F(ω) = 0, | ω | > L (where L is real that is called cutoff frequency) and the sampling interval satisfies Δ ≤ π/L, f(t) can be reconstructed without any loss of information through the following reconstruction formula:

$$ f(t)=\sum \limits_{n\in Z}f\left(n\Delta \right)\frac{\sin {\Delta}^{-1}\ \uppi \left(t-n\Delta \right)}{\Delta^{-1}\ \uppi \left(t-n\Delta \right)} $$

(1)

where the term $\frac{\sin {\Delta}^{-1}\ \uppi \left(t-n\Delta \right)}{\Delta^{-1}\ \uppi \left(t-n\Delta \right)}$ in Eq. (1) is called the Shannon interpolation function.

2.2 Shannon orthogonal basis function

According to Eq. (1), the functions f(t) can be reconstructed. When L = π, that is, the sampling frequency is equal to two times highest frequency of the sampling signal, the sampling interval Δ is equal to 1, and Eq. (1) can be transformed as:

$$ f(t)=\sum \limits_{n\in Z}f(n)\frac{\sin\ \uppi \left(t-n\right)}{\ \uppi \left(t-n\right)},\kern0.5em n\in Z $$

(2)

Denoting ${\phi}_1\left(\mu \right)=\frac{\sin \pi \mu}{\pi \mu}$, which is called the sinc function, and its curve is shown in Fig. 1. The areas of a, b, c, d, e, f, g, h, i, and j which are surrounded by the sinc function curve and the horizontal axis are respectively 0.5895, − 0.1381, 0.0817, − 0.0581, 0.0451, − 0.0369, 0.0312, − 0.0270, 0.0239, and − 0.0213. These areas can be approximated as weight coefficients in different sampling intervals. By using the Parseval theorem for sinc function ϕ₁(μ), Eq. (3) is obtained:

Fig. 1

The curve of the sinc function

$$ <{\phi}_1\left(\mu -n\right),{\phi}_1\left(\mu -m\right)>=\underset{-\infty }{\overset{+\infty }{\int }}{\phi}_1\left(\mu -n\right){\overline{\phi}}_1\left(\mu -m\right) du=\frac{1}{2\ \uppi}\underset{-\infty }{\overset{+\infty }{\int }}{\left|\ {\Phi}_1\left(\omega \right)\ \right|}^2{\mathrm{e}}^{-\mathrm{i}\omega \left(n-m\right)}\ \mathrm{d}x=\delta \left(n-m\right) $$

(3)

where the variable δ(n) is the unit impact sequence, that is,

$$ \delta (n)=\left\{\begin{array}{c}1\kern0.5em n=0\\ {}0\kern0.5em n\ne 0\end{array}\right. $$

(4)

According to Eqs. (3) and (4), it is known that the {ϕ₁(μ − n); n ∈ Z} is the standard orthogonal basis in the function space { f(x); F(ω) = 0, | ω | > π}.

2.3 The reconstructed semi-discretization method of VDDE

The dynamic equation of the cutting process with variable spindle speed can be described as the delay-differential equations (DDE) with time periodic regenerative delay term. The equation is described as:

$$ \dot{x}(t)=A(t)x(t)+B(t)x\left(t-\tau (t)\right), $$

(5)

where the variables A(t + T) = A(t), B(t + T) = B(t), τ(t + T) = τ(t), T is the principal period of the system. The first step is that the T is divided into k numbers of discrete time intervals Δt, as shown in Fig. 2a.

Fig. 2

The discretization of curves and the approximation of the delayed term. a The discretization of time period T. b The reconstruction of function based on interpolation function

The delay term τ(t) in discretization interval [t_i, t_i + 1] is approximated as

$$ {\tau}_i=\frac{1}{\Delta t}{\int}_{t_i}^{t_{i+1}}\tau (t) dt $$

(6)

The series of integers are defined as ${m}_i=\operatorname{int}\left(\frac{\tau_i+\Delta t/2}{\Delta t}\right)$, and defined $M=\underset{i=1,\dots, k}{\max}\left({m}_i\right)$. In the ith discretization interval [t_i, t_i + 1], Eq. (5) can be approximated as

$$ \dot{x}(t)={A}_ix(t)+{B}_ix\left(t-{\tau}_i\right) $$

(7)

where the variables ${A}_i=\frac{1}{\Delta t}{\int}_{t_i}^{t_{i+1}}A(t) dt$, ${B}_i=\frac{1}{\Delta t}{\int}_{t_i}^{t_{i+1}}B(t) dt$.

The solutions of Eq. (7) consist of homogenous x_ih and particular x_ip solutions. The homogenous solution is ${x}_{ih}=x\left({t}_i\right)\times {e}^{A\times \left(t-{t}_i\right)}$. Assuming that ${e}^{A\times \left(t-{t}_i\right)}\times {u}_1(t)$ is the solution of Eq. (7), and its derivatives are described as:

$$ A\times {e}^{A\times \left(t-{t}_i\right)}\times {u}_1(t)+{e}^{A\times \left(t-{t}_i\right)}\times \frac{du_1(t)}{dt},\kern0.5em t\kern0.5em \in \left[{t}_i,{t}_{i+1}\right],\kern0.5em i\kern0.5em \in \kern0.5em R $$

(8)

By substituting Eq. (8) into Eq. (7), Eq. (9) can be obtained:

$$ {e}^{A\times \left(t-{t}_i\right)}\times \frac{du_1(t)}{dt}+A\times {e}^{A\times \left(t-{t}_i\right)}\times {u}_1(t)=A\times {e}^{A\times \left(t-{t}_i\right)}\times {u}_1(t)+B\times x\left(t-{\tau}_i\right),t\in \left[{t}_i,{t}_{i+1}\right],i\in R $$

(9)

Equation 9 can be simplified as:

$$ {e}^{A\times \left(t-{t}_i\right)}\times \frac{du_1(t)}{dt}=B\times x\left(t-{\tau}_i\right),t\in \left[{t}_i,{t}_{i+1}\right],i\in R $$

(10)

$$ \frac{du_1(t)}{dt}={e}^{-\left(A\times \left(t-{t}_i\right)\right)}\times B\times x\left(t-{\tau}_i\right),t\in \left[{t}_i,{t}_{i+1}\right],i\in R $$

(11)

The variable x(t − τ_i) can be reconstructed (as shown in Fig. 2b), according to Eq. (1), as follows:

$$ x\left(t-{\tau}_i\right)=\dots +{x}_{i-m+1}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}+{x}_{i-m}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)} $$

(12)

According to Eq. (12), it can be known that it is made up of infinite items. Substituting Eq. (12) into Eq. (11) yields:

$$ \frac{du_1(t)}{dt}={e}^{-\left(A\times \left(t-{t}_i\right)\right)}\times B\times \left(\dots +{x}_{i-m+1}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}+{x}_{i-m}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)}\right) $$

(13)

To calculate the integral on both sides of Eq. (13)

$$ \underset{t_i}{\overset{t}{\int }}\frac{du_1(t)}{dt} dt=\underset{t_i}{\overset{t}{\int }}\left[\begin{array}{l}{e}^{-\left(A\times \left(t-{t}_i\right)\right)}\times B\times \Big(\dots +{x}_{i-m+1}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}\\ {}+{x}_{i-m}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)}\Big)\end{array}\right] dt $$

(14)

$$ {u}_1(t)-{u}_1\left({t}_i\right)=\underset{t_i}{\overset{t}{\int }}\left[\begin{array}{l}{e}^{-\left(A\times \left(t-{t}_i\right)\right)}\times B\times \Big(\dots +{x}_{i-m+1}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m+1\right)\times \Delta \right)}\\ {}+{x}_{i-m}\times \frac{\sin {\Delta}^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)}{\Delta^{-1}\pi \left(t-\left(i-m\right)\times \Delta \right)}\Big)\end{array}\right] dt $$

(15)

Replacing the variable t with variable η on the right side of Eq. (15) yields:

$$ \underset{t_i}{\overset{t}{\int }}\left[\begin{array}{l}{e}^{-\left(A\times \left(\tau -{t}_i\right)\right)}\times B\times \Big(\dots +{x}_{i-m+1}\times \frac{\sin {\Delta}^{-1}\pi \left(\eta -\left(i-m+1\right)\times \Delta \right)}{\Delta^{-1}\pi \left(\eta -\left(i-m+1\right)\times \Delta \right)}\\ {}+{x}_{i-m}\times \frac{\sin {\Delta}^{-1}\pi \left(\eta -\left(i-m\right)\times \Delta \right)}{\Delta^{-1}\pi \left(\eta -\left(i-m\right)\times \Delta \right)}\Big)\end{array}\right] d\eta, \eta \in \left[{t}_i,t\right] $$

(16)

$\frac{\sin {\Delta}^{-1}\pi \left(\eta -\left(i-m+1\right)\times \Delta \right)}{\Delta^{-1}\pi \left(\eta -\left(i-m+1\right)\times \Delta \right)}$ is denoted as ϕ(η − (i − m + 1)); $\frac{\sin {\Delta}^{-1}\pi \left(\eta -\left(i-m\right)\times \Delta \right)}{\Delta^{-1}\pi \left(\eta -\left(i-m\right)\times \Delta \right)}$ is denoted asϕ(η − (i − m)). The equivalent transformation of Eq. (16) is as follows:

$$ \underset{t_i}{\overset{t}{\int }}\left[\begin{array}{l}{e}^{-\left(A\times \left(\tau -{t}_i\right)\right)}\times B\times \Big(\dots +{x}_{i-m+1}\times \phi \left(\eta -\left(i-m+1\right)\right)\\ {}+{x}_{i-m}\times \phi \left(\eta -\left(i-m\right)\right)\Big)\end{array}\right] d\eta =\dots +{x}_{i-m+1}\times \underset{t_i}{\overset{t}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m+1\right)\right) d\eta +{x}_{i-m}\times \underset{t_i}{\overset{t}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m\right)\right) d\eta $$

(17)

Equation (15) is converted as:

$$ {u}_1(t)=\dots +{x}_{i-m+1}\times \underset{t_i}{\overset{t}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m+1\right)\right) d\eta +{x}_{i-m}\times \underset{t_i}{\overset{t}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m\right)\right) d\eta +C $$

(18)

where the C = u₁(t_i) = 0. x_ip is expressed as:

$$ {x}_{ip}={e}^{A\times \left(t-{t}_i\right)}\times \left[\dots +{x}_{i-m+1}\times \underset{t_i}{\overset{t}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m+1\right)\right) d\eta +{x}_{i-m}\times \underset{t_i}{\overset{t}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m\right)\right) d\eta \right] $$

(19)

The solution of Eq. (7) in the time interval [t_i, t_i + 1] can be expressed as:

$$ x(t)={x}_{ih}+{x}_{ip}=x\left({t}_i\right)\times {e}^{A\times \left(t-{t}_i\right)}+{e}^{A\times \left(t-{t}_i\right)}\times \left[\dots +{x}_{i-m+1}\times \underset{t_i}{\overset{t}{\int }}\left[\begin{array}{l}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \\ {}\phi \left(\eta -\left(i-m+1\right)\right) d\eta \end{array}\right]\kern0.5em +{x}_{i-m}\times \underset{t_i}{\overset{t}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m\right)\right) d\eta \right],t\in \left[{t}_i,{t}_{i+1}\right],i\in R $$

(20)

When t = t_i + 1, Eq. (20) is obtained:

$$ x\left({t}_{i+1}\right)={x}_{i+1}=x\left({t}_i\right)\times {e}^{A\times \left(\Delta \right)}+{e}^{A\times \left(\Delta \right)}\times \left[\dots +{x}_{i-m+1}\times \underset{t_i}{\overset{t_{i+1}}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m+1\right)\right) d\eta +{x}_{i-m}\times \underset{t_i}{\overset{t_{i+1}}{\int }}{e}^{-\left(A\times \left(\eta -{t}_i\right)\right)}\times B\times \phi \left(\eta -\left(i-m\right)\right) d\eta \right] $$

(21)

Denoting η = μ + t_i, Eq. (21) can be rearranged as follows:

$$ x\left({t}_{i+1}\right)={x}_{i+1}={x}_i\times {e}^{A\times \left(\Delta \right)}+{e}^{A\times \left(\Delta \right)}\times \left[\dots +{x}_{i-m+1}\times \underset{0}{\overset{\Delta}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times \phi \left(\mu -\left(i-m+1\right)\right) d\mu +{x}_{i-m}\times \underset{0}{\overset{\Delta}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times \phi \left(\mu -\left(i-m\right)\right) d\mu \right],\kern0.5em 0\le \mu \le \Delta $$

(22)

where $\underset{0}{\overset{\Delta}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times \phi \left(\mu -\left(i-m+1\right)\right) d\mu$ is equal to $\underset{0}{\overset{\Delta}{\int }}\left({e}^{-\left(A\times \mu \right)}\times B\times \phi \left(\mu \right)\right) d\mu$. The equivalent transformation of Eq. (22) is as follows:

$$ x\left({t}_{i+1}\right)={x}_{i+1}={x}_i\times {e}^{A\times \left(\Delta \right)}+{e}^{A\times \left(\Delta \right)}\times \left[\dots +{x}_{i-m+1}\times \underset{0}{\overset{\Delta}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times \phi \left(\mu \right) d\mu +{x}_{i-m}\times \underset{0}{\overset{\Delta}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times \phi \left(\mu \right) d\mu \right] $$

(23)

According to the normalized reconstruction formula of Eq. (2), Eq. (23) can be expressed as follows:

$$ x\left({t}_{i+1}\right)={x}_{i+1}={x}_i\times {e}^{A\times (1)}+{e}^{A\times (1)}\times \left[\dots +{x}_{i-m+1}\times \underset{0}{\overset{1}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times {\phi}_1\left(\mu \right) d\mu +{x}_{i-m}\times \underset{0}{\overset{1}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times {\phi}_1\left(\mu \right) d\mu \right] $$

(24)

In Eq. (2), the sampling interval Δ = 1 means that the principal period T is sampled by 1/(2f₀)time interval (where f₀ is the chatter frequency). “Δ = 1” is the normalized sampling interval; the actual sampling interval can be expressed as Δ₁ = 1/(2f₀) (in the actual choice, Δ₁ = 1/[(3f₀)~(5f₀)]).

In the actual sampling process, Eq. (24) is expressed as follows:

$$ x\left({t}_{i+1}\right)={x}_{i+1}={x}_i\times {e}^{A\times \left({\Delta}_1\right)}+{e}^{A\times \left({\Delta}_1\right)}\times \left[\dots +{x}_{i-m+1}\times \underset{0}{\overset{\Delta_1}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times {\phi}_1\left(\mu \right) d\mu +{x}_{i-m}\times \underset{0}{\overset{\Delta_1}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times {\phi}_1\left(\mu \right) d\mu \right] $$

(25)

Denoting

$$ N={e}^{A\times \left({\Delta}_1\right)}\times \underset{0}{\overset{\Delta_1}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times {\phi}_1\left(\mu \right) d\mu $$

(26)

N can be approximated as:

$$ \mathrm{N}={e}^{A\times \left({\Delta}_1\right)}\times \underset{0}{\overset{\Delta_1}{\int }}{e}^{-\left(A\times \mu \right)}\times B\times {\phi}_1\left(\mu \right) d\mu \approx 0.5895{e}^{A\times \left({\Delta}_1\right)}\times \left(\underset{0}{\overset{\Delta_1}{\int }}{e}^{-\left(A\times \mu \right)} d\mu \right)\times B=0.5895{e}^{A\times \left({\Delta}_1\right)}\times {e}^{-\left(A\times \mu \right)}\left.\right|{\displaystyle \begin{array}{c}{\Delta}_1\\ {}0\end{array}}\left(-{A}^{-1}\times B\right)=0.5895{e}^{A\times \left({\Delta}_1\right)}\times \left({e}^{-\left(A\times \mu \right)}-I\right)\times \left(-{A}^{-1}\times B\right)=0.5895\times \left(I-{e}^{-\left(A\times \mu \right)}\right)\times \left(-{A}^{-1}\times B\right)=0.5895\times \left({e}^{-\left(A\times \mu \right)}-I\right)\times \left({A}^{-1}B\right) $$

Denoting (e^{−(A × μ)} − I) × (A⁻¹B) = R_i. When considering the influence in other sampling intervals[t_i, t_i + 1], and the mean values of the first 10 sampling intervals of the ϕ₁(μ) (according to Fig. 1) are considered. Eq. (25) can be expressed as:

$$ x\left({t}_{i+1}\right)={x}_{i+1}={x}_i\times {e}^{A\times \left({\Delta}_1\right)}-0.0213{x}_{i-m+10}{R}_i+0.0239{x}_{i-m+9}{R}_i-0.027{x}_{i-m+8}{R}_i+0.0312{x}_{i-m+7}{R}_i-0.0369{x}_{i-m+6}{R}_i+0.0451{x}_{i-m+5}{R}_i-0.0581{x}_{i-m+4}{R}_i+0.0817{x}_{i-m+3}{R}_i-0.1381{x}_{i-m+2}{R}_i+0.5895{x}_{i-m+1}{R}_i+0.5895{x}_{i-m}{R}_i $$

(27)

According to Eq. (27), the discrete map

$$ {y}_{i+1}={C}_i{y}_i $$

(28)

$$ {y}_i= col\left({x}_i,{\dot{x}}_i,{x}_{i-1},\dots, {y}_{i-M}\right) $$

(where)

$$ {C}_i=\left[\begin{array}{ccccccccccccc}{e}^{A{\Delta}_1}& 0& 0& \dots & 0.0817{R}_i& -0.1381{R}_i& 0.5895{R}_i& 0.5895{R}_i& 0& \dots & 0& 0& 0\\ {}I& 0& 0& \dots & 0& 0& 0& 0& 0& \dots & 0& 0& 0\\ {}0& I& 0& \dots & 0& 0& 0& 0& 0& \dots & 0& 0& 0\\ {}\vdots & \vdots & \ddots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \ddots & :& :& \vdots \\ {}0& 0& 0& \dots & 0& 0& 0& 0& 0& \dots & 0& 0& 0\\ {}0& 0& 0& \dots & 0& 0& 0& 0& 0& \dots & I& 0& 0\\ {}0& 0& 0& \dots & 0& 0& 0& 0& 0& \dots & 0& I& 0\end{array}\right] $$

The connection between y₀ and y_k is described as follows:

$$ {y}_k=\Phi {y}_0 $$

(29)

Where Φ = C_k − 1C_k − 2…C₂C₁C₀, Φ is the transition matrix over the principal period. The stability lobes can be determined by scanning the spindle speed at the different axial depths (the Floquet theory). In using the Floquet theory, the ratio of the period of spindle speed variation and the tooth passing period is set to be a rational number.

$$ \max \left(\left|\lambda \right|\right)=\left\{\begin{array}{ccc}<1,& & stable\\ {}=1,& critical& stable\\ {}>1,& & unstable\end{array}\right. $$

(30)

The variable max(|λ|) indicates the biggest modulus in all modulus of eigenvalues of the transition matrix Φ_.

3 Dynamic model of turning with variable spindle speed

3.1 Milling dynamic model

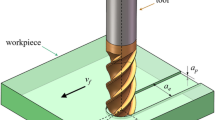
The mechanical model is show in Fig. 3, the workpiece is assumed to be flexible in x-direction, and the milling cutter is assumed to have enough rigidity compared with the workpiece.

Fig. 3

Mechanical model of the milling process with single degree of freedom

The dynamic model can be described as:

$$ m\ddot{x}(t)+c\dot{x}(t)+ kx(t)={F}_x(t) $$

(31)

where the parameter m is the modal mass, c is the damping, k is the stiffness, and F_x(t) is the cutting force in the x-direction which is expressed as [45]:

$$ {F}_x(t)=G(t)\Big(x(t)-x\left(t-\tau (t)\right) $$

(32)

$$ G(t)={a}_p\left({qf}^{q-1}\right)\sum \limits_{j=1}^N{g}_j(t){\left(\sin {\varphi}_j\right)}^q\left[\left({K}_{tc}\cos {\varphi}_j+{K}_{rc}\sin {\varphi}_j\right)\right] $$

(33)

where a_p is the axial depth of cut, q is the cutting force exponent, φ_j is the angular position of the jth cutting edge, and K_tc and K_rc denote the cutting force coefficients in tangential and radial directions, respectively. f is the feed per tooth, x(t) is the current position of the tool, and x(t − τ(t)) is the positon at the previous cut. g_j(t) is the switch function, which is applied to judge whether the tooth j is cutting or not, that is,

$$ {g}_j(t)=\left\{\begin{array}{ccc}1,& & {\varphi}_{st}\le {\varphi}_j\le {\varphi}_{ex}\\ {}0,& & otherwise\end{array}\right. $$

(34)

where the terms φ_st andφ_ex are respectively the start and exit angles of the jth cutting edge. Equation (31) is transformed into the state equation as follows:

$$ \dot{X}(t)=A(t)\dot{X}(t)+B(t)u\left(t-\tau (t)\right) $$

$$ u\left(t-\tau (t)\right)= CX\left(t-\tau (t)\right) $$

where $X(t)=\left[\begin{array}{c}x(t)\\ {}\dot{x}(t)\end{array}\right]$, $A(t)=\left[\begin{array}{cc}0& 1\\ {}\frac{H(t){a}_p}{m}& -\frac{c}{m}\end{array}\right]$, $B(t)=\left[\begin{array}{c}0\\ {}\frac{H(t){a}_p}{m}\end{array}\right]$, $u\left(t-\tau (t)\right)=\left[x\left(t-\tau (t)\right)\kern0.5em 0\right]$, $C=\left[1\kern0.5em 0\right]$,

$$ H(t)={g}_j(t)\sum \limits_{j=1}^N\left[\left({K}_{rc}\cos {\varphi}_j-{K}_{tc}\sin {\varphi}_j\right)\right]\cos {\varphi}_j $$

3.2 Approximation of the time delay term

In Fig. 3, N(t) is the time periodic spindle speed, N(t + T) = N(t); the time delay τ(t) is also time periodic, τ(t + T) = τ(t). The time delay τ(t) between the present and the previous cuts is determined by the following equation [45]:

$$ {\int}_{t-\tau (t)}^t\frac{R2\pi N(S)}{60} ds=\frac{2\pi R}{N}+x(t)-x\left(t-\tau (t)\right) $$

(35)

If the term x(t) − x(t − τ(t)) is negligible, then Eq. (35) gives

$$ {\int}_{t-\tau (t)}^t\frac{R2\pi N(S)}{60} ds=\frac{1}{N} $$

(36)

It is assumed that the spindle speed is modulated around an average values as follows:

$$ N(t)={N}_0+{N}_1S(t),S\left(t+T\right)=S(t) $$

(37)

• 1) Time delay term with sinusoidal shape

Defining S(t) as cosine modulation, S(t) is given by S(t) = sin(2πt/T).

Substituting Eq. (38) into Eq. (36) yields the implicit equation:

$$ \frac{1}{60}\left[{N}_0\tau (t)+\frac{\mathrm{T}}{2\pi }{N}_1\left(\sin \left(2\pi t/T\right)-\sin \left(2\pi \left(t-\tau (t)\right)/T\right)\right)\right]=1 $$

(38)

The ratios of modulation amplitude and modulation frequency are respectively defined:

$$ RVA=\frac{N_1}{N_0},\kern0.5em RVF=\frac{60}{\left({N}_0T\right)} $$

(39)

If the N₁ is small enough compared with the N₀, the time delay τ(t) can be approximated as:

$$ \tau (t)\approx {\tau}_0\hbox{-} {\tau}_1S(t)\kern0.5em ,\kern0.5em {\tau}_0=\frac{60}{N\times {N}_0}\kern0.5em ,\kern0.5em {\tau}_1={\tau}_0\times RVA $$

(40)

The exact and the approximate time delays τ(t) are calculated respectively based on Eqs. (36) and (40), as shown in Fig. 4 (mean spindle speed is selected as 6000 r/min, and the exact term τ(t) is computed numerically with root-finding method). When RVF = 0.01 (corresponding to T = 1 s), the ratios of the maximum deviation and exact maximum between the exact and the approximated delay terms τ(t) are equal to 0.99% for RVA = 0.1, 3.99% for RVA = 0.2, and 8.98% for RVA = 0.3. When RVF = 0.02, the ratio of maximum deviation and exact maximum has the same change laws; that is, the maximum deviation will be raise with the increase of RVA. In the following content, the small RVA is only considered for stability analysis.

Fig. 4

The exact and approximated time delay in different RVF and RVA for Ω₀ = 6000 r/min

• 2) Time delay term with triangular shape

In Eq. (37), the triangular shape function is defined as [16]:

$$ S(t)=\left\{\begin{array}{cc}1\hbox{-} 4\operatorname{mod}\left(t,T\right)/T& if0<\operatorname{mod}\left(t,T\right)\le T/2\\ {}\hbox{-} 3+4\operatorname{mod}\left(t,T\right)/T& if T/2<\operatorname{mod}\left(t,T\right)\le T\end{array}\right\} $$

(42)

where function mod (t,T) denotes the modulo function, for example, mod(13,5) = 3. The spindle speed based on triangular shape is described as follows:

$$ N(t)=\left\{\begin{array}{cc}{N}_0\left(1+ RVA\right)\hbox{-} \frac{4{N}_0 RVA}{T}\operatorname{mod}\left(t,T\right)& if0<\operatorname{mod}\left(t,T\right)\le T/2\\ {}{N}_0\left(1-3 RVA\right)+\frac{4{N}_0 RVA}{T}\operatorname{mod}\left(t,T\right)& if T/2<\operatorname{mod}\left(t,T\right)\le T\end{array}\right\} $$

(43)

According to Eq. (40), time delay τ(t) corresponding to Eq. (43) is given:

$$ \tau (t)=\left\{\begin{array}{cc}{\tau}_0\left(1\hbox{-} RVA\right)+\frac{4{\tau}_0 RVA}{T}\operatorname{mod}\left(t,T\right)& if0<\operatorname{mod}\left(t,T\right)\le T/2\\ {}{\tau}_0\left(1+3 RVA\right)\hbox{-} \frac{4{\tau}_0 RVA}{T}\operatorname{mod}\left(t,T\right)& if T/2<\operatorname{mod}\left(t,T\right)\le T\end{array}\right\} $$

(44)

4 Comparison of the stability analysis with different methods

In order to prove the effectiveness of the RSDM method (the reconstructed SDM), two cases with single degree of freedom were analyzed and compared by SDM and RSDM.

Case 1

The parameters of milling system in reference [45] are selected as follows: modal stiffness is defined as k = 20 × 10⁶ N/m, natural frequency is defined as f_n = 400 Hz, damping rate is defined as ξ = 0.02, tangential cutting force coefficient is defined as k_tc = 107 MPa, radial cutting force coefficient is defined as k_rc = 40 /107, the cutting force exponent is defined as q = 0.75, the radial immersion ratio is defined as a_e/D = 0.5 (where the term a_e denotes the radial immersion and D denotes the diameter of the milling cutter), and the number of the teeth is selected as N = 4. The stability boundaries are calculated respectively based on the RSDM and SDM under different RVF values, as shown in Fig. 5.

Fig. 5

The calculation of the stability boundaries of case 1 with sinusoidal spindle speed modulation. VSS denotes the modulation of variable spindle speed, and CSS denotes the modulation of constant spindle speed

Case 2

The parameters of milling system in reference [37] are selected as follows: modal stiffness is defined as k = 9.14 × 10⁵ N/m, natural frequency is defined as f_n = 729.07 Hz, damping rate is defined as ξ = 0.0107, tangential cutting force coefficient is defined as k_tc = 600 MPa, radial cutting force coefficient is defined as k_rc = 0.42, the cutting force exponent is defined as q = 1, the radial immersion ratio is defined as a_e/D = 0.05 (where the term a_e denotes the radial immersion and D denotes the diameter of the milling cutter), the number of the teeth denotes N = 2, and feed per tooth denotes f_z = 0.1 mm. The stability boundaries are calculated respectively based on the RSDM and SDM under different RVF values, as shown in Fig. 6.

Fig. 6

The calculation of the stability boundaries of case 2 with sinusoidal spindle speed modulation

As can be seen from Figs. 5 and 6, the stability boundaries calculated based on the reconstructed SDM are highly consistent with the stability boundaries calculated based on the SDM, but the calculation efficiencies of the stability boundaries based on RSDM are obviously improved. The calculation efficiency based on RSDM has been improved nearly three times, compared with that based on SDM.

5 Stability analysis at two different modulation waves and the optimization of modulation parameters

In order to compare the effect of triangle and sinusoidal modulation on the stability boundary, the system parameters of case 2 are selected. The stability boundary at two different modulation waves is calculated based RSDM, as shown in Fig. 7.

Fig. 7

Stability boundaries at two different modulation waves under RVA = 0.1 and RVF = 0.5 based on RSDM

As can be seen in Fig. 7, the stability boundaries constructed based on two different modulation waves are significantly improved compared with those based on constant spindle speed (VSS). Within the range of spindle speed 2000–4500 r/min, that is, the left side of the line “AB,” the stability boundary based on triangular wave is higher than that based on sinusoidal wave. However, with the range of spindle speed 4500–5000 r/min, the stability boundary based on triangular wave is lower than that based on sinusoidal wave. In general, for the system parameters of case 2 and RVA = 0.1 and RVF = 0.5, the improvement of the triangular wave to the stability boundary is better than that of the sinusoidal wave.

Under different RVA and RVF, the stability boundaries of case 2 are different; thus, the optimal RVA and RVF are analyzed. Considering the limit of acceleration of spindle speed, the RVA and RVF are also limited. For the sinusoidal wave variation, the maximum acceleration of spindle speed is identified as follows:

$$ {a}_{\mathrm{max}}=\frac{2\pi \times {N}_0^2\times RVA\times RVF}{3600} $$

(45)

For the triangular wave variation, the maximum acceleration of spindle speed is identified as follows:

$$ {a}_{\mathrm{max}}=\frac{4\times {N}_0^2\times RVA\times RVF}{3600} $$

(46)

Assuming the maximum acceleration is selected as 100rev/ s² [34], the optimal RVA and RVF are selected respectively as N₀ = 3000 r/min and N₀ = 4900 r/min based on two different modulation waves. The results are shown in Figs. 8 and 9, and the optimized parameters of RVA and RVF are calculated, as shown in Table 1.

Fig. 8

The critical axial milling depth at different RVA and RVF at spindle speed 3000 r/min

Fig. 9

The critical axial milling depth at different RVA and RVF at spindle speed 4900 r/min

Table 1 Optimization of modulation parameters considering the limit of acceleration of spindle speed

As shown in Table 1, the axial milling depth based on two modulation waves significantly increased compared with that based on constant spindle speed. In general, the improvements of the axial milling depth based on triangular wave are better than that based on sine wave.

6 Analysis of the chatter types

The chatter frequencies of the constant spindle speed are determined as follows [45]:

$$ f=\pm \frac{\omega_1}{2\pi }+\frac{j}{\tau_0}=\pm \frac{\omega_1}{2\pi }+j\frac{NN_0}{60},j=0,1,\dots, n $$

(47)

where the variable ω₁ denotes the imaginary part of critical characteristic exponent, τ₀ denotes the constant time delay term, N denotes the teeth of the tool, and N₀ denotes the spindle speed. According to the chatter frequencies of variable spindle speed in turning, the chatter frequencies of variable spindle speed in milling are described as [14]:

$$ f=\pm \frac{\omega_1}{2\pi }/T+j\frac{RVF\times N(t)}{60},j=0,1,\dots, n $$

(48)

where the term N(t) denotes variable spindle speed.

The modulation frequencies are defined as [14]

$$ {f}_m=j\frac{RVF\times {N}_0}{60},j=1,\dots, n $$

(49)

According to Eqs. (47)–(49), the chatter and modulation frequencies are calculated, as shown in Fig. 10.

Fig. 10

Chatter frequencies and modulation frequencies under different modulation waves. a Frequency analysis at CSS. b Frequency analysis at VSS—sinusoidal. c, d Frequency analysis at VSS—triangular

Figure 10d denotes the stability lobes of case 2 under different modulation laws. Figure 10a–c denote the corresponding chatter frequencies and modulation frequencies. As seen in Fig. 10, frequency bands of triangular and sinusoidal modulation waves are wider than those of constant spindle speed. In the following section, the chatter types are analyzed based on the reconstructed semi-discretization method. The critical points of the stability boundaries were selected at different modulation laws, as shown in Fig. 10.

Points A and B denote the critical points of the constant spindle speed, and the corresponding time vibration signals and Poincare section are calculated as shown in Fig. 11a–d. The time vibration displacement signals x and velocity signals $\dot{x}$ can be calculated by recursive formula of Eq. (28) using the first two elements of each y_i. The black symbols “o” in Fig. 11a–d denote the values of the variable x and $\dot{x}$ corresponding to the time interval of one revolution of the spindle.

Fig. 11

Two chatter types of the constant spindle speed. a Time vibration signals at point A. b Poincare section at point A. c Time vibration signals at point B. d Poincare section at point B

The black symbols “o” change with the law of sinusoidal function in Fig. 11a, and the black symbols “o” are converged to a circle in Poincare section in Fig. 11b. The chatter with the above properties is called secondary Hopf bifurcation which the critical characteristic multipliers are on the unit circle that are a complex conjugate pair. The black symbols “o” appear alternately in two positions in Fig. 11c, and the black symbols “o” are converged to two small areas in Poincare section in Fig. 11d. The chatter with the above properties is called period-2 or flip bifurcation that the critical characteristic multiplier is equal to − 1. Hopf and period-2 bifurcations usually exist in milling process (Fig. 12).

Fig. 12

The selection of the critical point of the case 2 under sinusoidal wave modulation

Points C, D, E, and F denote the critical points of the variable spindle speed with sinusoidal wave modulation, and the corresponding time vibration signals and Poincare section are described as shown in Fig. 13a–h. The chatters of point C and D respectively belong to Hopf and period-2 bifurcations. The black symbols “o” appear in one positions in Fig. 13e and g, and the black symbols “o” are converged to one small area in Poincare section in Fig. 13f and h. The chatter with the above properties is called period-1 bifurcation that the critical characteristic multipliers are equal to 1. The period-1 bifurcation did not appear in milling process with constant spindle speed, but it appears in milling process with sinusoidal wave modulation.

Fig. 13

Three chatter types of the variable spindle speed based on sinusoidal wave. a Time vibration signals at point C. b Poincare section at point C. c Time vibration signals at point D. d Poincare section at point D. e Time vibration signals at point E. f Poincare section at point E. g Time vibration signals at point F. h Poincare section at point F

Points H, I, J, and K denote the critical points of the variable spindle speed with triangular wave modulation, and the corresponding time vibration signals and Poincare section are described as shown in Fig. 14a–h. The chatters of points H, I, J, and K respectively belong to period-1, Hopf, period-1, and period-2 bifurcations. The period-1 bifurcation also exists in milling process with triangular wave modulation.

Fig. 14

Three chatter types of the variable spindle speed based on triangular wave. a Time vibration signals at point H. b Poincare section at point H. c Time vibration signals at point I. d Poincare section at point I. e Time vibration signals at point J. f Poincare section at point J. g Time vibration signals at point K. h Poincare section at point J

7 Conclusions

In this work, the reconstructed semi-discretization method is established to analyze the milling stability with sinusoidal and triangular modulations. The approximation of the time delay term with sinusoidal law is discussed, and results show that the approximation can be used when RVA is small, and the approximation of time delay term with triangular law is also established. In order to verify the validity of the reconstructed semi-discretization method (RSDM), the milling dynamics with single degree of freedom is used to compare the calculation efficiency, and the results show the proposed method have a higher calculation efficiency compared with the well-accepted semi-discretization method (SDM). Finally, the chatter types under constant spindle speed and sinusoidal and triangular wave modulations are analyzed based on the reconstructed semi-discretization method (RSDM), and chatter type, period-1, is observed in milling process with sinusoidal and triangular wave modulations.