Efficient identification of a flow-induced crystallization model for injection molding simulation

Abstract

Most commercial software used to simulate the injection molding process of semi-crystalline thermoplastic polymers do not explicitly take into account the polymer crystallization, which could lead to errors in the estimations of filling as well as warpage and shrinkage. This is mainly due to the common complexity of the models used to describe crystallization and the challenging respective model parameter identification under injection molding conditions. To close this gap, in this work, we use a simple thermo-mechanical crystallization model to describe the flow-induced and quiescent crystallization of an unreinforced semi-crystalline thermoplastic material during injection molding. The crystallization model is implemented in the commercial software Autodesk^® Moldflow^® Insight 2021 using the Solver API feature alongside crystallization-dependent viscosity, PVT, and solidification models. The model parameters were identified using a calibration workflow that employs surrogate models representing the simulated pressure results to perform a multi-objective optimization. The filling predictions as well as the calculated pressure fields are presented using the calibrated model parameters in comparison to those measured during the actual injection molding of a polyoxymethylene (POM) part using different process conditions. The results show major improvements in the estimations of the time-depending pressure field as well as the level of filling of the produced parts.

1 Introduction

To ensure high product quality and minimize design/pro-duction costs, injection molding simulation is broadly used in order to efficiently design molds and enable the identification of optimal process settings that mitigate common defects such as warpage, shrinkage, weldline, and short shots. The simulation of the injection molding process is a numerical implementation to solve a set of conservation equations using material models [1]. Many commercial and academic software have been developed to solve this problem, which involves flow, diverse heat transfer mechanisms in addition to a phase change as well as time-dependent boundary conditions of the polymer material domain during the various stages of the process. Taking into account all these physical phenomena in the simulation is not straightforward and necessitates some simplifying assumptions. An overview of those hypotheses with a focus on the injection molding of an unfilled semi-crystalline thermoplastic [1] is given in the following:

• Specific heat capacity: Data taken from differential scanning calorimetry (DSC) tests performed at constant cooling rates, typically quite lower than the ones encountered close to the mold wall in the actual process. The data includes the crystallization peak measured during the DSC test.

• Heat sources: Latent heat of crystallization is considered indirectly by means of the specific heat capacity data mentioned above, i.e., from a single constant cooling rate. Therefore, those solvers do not implement explicitly a heat source term related to crystallization in the energy equation.

• Solidification: This phenomenon is approximated numerically by using a single no-flow temperature (or transition temperature) below which the local melt viscosity is set to a very high value ($\sim 10^6$ Pa.s). This implementation ignores the changes in crystallization temperature induced by different local cooling rates occurring in the actual process.

• Pressure-volume-temperature (PVT): Data taken from experiments using a constant cooling rate, typically far below than the ones in the actual process, and therefore neglecting the changes in crystallization kinetics triggered by different cooling rates.

Due to the complexity of experimentally identifying crystallization parameters under injection molding conditions and the effect of crystallization on material properties during processing, many commercial software do not take it into account by default, even when dealing with the injection of semi-crystalline materials. This could lead to inaccuracies in the fill predictions as well as in the estimation of warpage and shrinkage in the simulation [1].

To overcome the assumptions mentioned above and, at the same time, to maintain the effort in material characterization as low as possible, in this work, we chose a simple crystallization model able to consider flow-induced and quiescent phenomena [2] to simulate explicitly crystallization during injection molding. From this point on, this work has two main contributions to the state-of-the-art in injection molding simulation. The first one is the numerical implementation of a flow-induced crystallization model in a commercial software for injection molding simulation. Concretely, we present the implementation of a flow-induced crystallization model coupled with melt viscosity, PVT, and solidification models in Autodesk^® Moldflow^® Insight 2021 by using its solver Application Programming Interface (known as Solver API). The second contribution is a novel material-parameter identification methodology, which uses a surrogate model-based optimization taking as reference experimental sensor data from an actual injection molding process. One innovation here is the material-parameter identification under actual processing conditions, which differs from traditional approaches where the crystallization models are calibrated based on offline experiments with thermo-mechanical conditions far away from industrial injection molding ones.

In-mold pressure signals are reliable state-of-the-art sensing equipment in industrial context. That is one of the reasons why we chose in-mold pressure sensor signals as reference data for the model calibration. Another important reason is because this physical quantity is strongly dependent on the crystallization process of the injected semi-crystalline thermoplastic material. In other words, the simulated pressure field is highly sensitive to the crystallization model parameters that we look for calibrating. A subjacent working hypothesis here is that the rest of parameters in the simulation (of material or numerical nature) are correctly calibrated and that other computed physical quantities (e.g., temperature field) are accurate.

This work looks for elucidating two research hypotheses. On the one hand, the implementation of a flow-induced crystallization model in injection molding simulation increases the robustness of the mold filling predictions. Note that this work primarily focuses on the impact of the crystallization model on the filling simulation, particularly in the estimation of pressure-field evolution and incomplete fillings (short shots) due to flow-front solidification. A discussion about the impact on shrinkage and warpage predictions falls outside the scope of this paper. The second hypothesis states that the proposed method of material parameter identification is especially advantageous for the modeling of crystallization in injection molding. In fact, we propose that the generation of a surrogate model of a high-fidelity injection molding simulation model (where the surrogate input variables are the unknown material parameters in the high-fidelity simulation model) and the subsequent identification by calibrating the generated surrogate model is more efficient than the traditional approaches based exclusively on lab experiments. In a previous work dealing with default injection molding simulation [3], this methodology performed well for a low number of training data and input parameters.

This paper is structured in four main sections. In the next section, we revisit the literature about polymer crystallization and its modeling as well as the numerical methods associated with the metamodel generation and its application in injection molding simulation. In Section 3, we show the implementation of the flow-induced crystallization model in Autodesk^® Moldflow^® Insight as well as the respective material parameter identification process by means of a pilot case using a polyoxymethylene material. In the subsequent section, we discuss the performance of the identified models at the level of the high-fidelity simulation in terms of pressure estimation and prediction of short shots. Finally, we close the paper with a conclusion.

2 Theoretical background

2.1 Polymer crystallization

2.1.1 Crystallization from the melt

There exist multiple types of crystallization such as crystallization from solution, crystallization by stretching, or crystallization from the melt. In this work, the main interest is studying polymer crystallization during the injection molding process, and therefore, only the crystallization from the melt is considered. This process involves two stages:

• 1. Nucleation or the formation of active nuclei in the liquid phase acting as starting points for the appearance of crystals [1]. Two types of nucleation can be distinguished [4, 5]:

  • Homogeneous nucleation: Caused by heat motion and starts within a few polymer chains or segments (e.g., from the bulk polymer phase).

  • Heterogeneous nucleation: Appears on foreign substrates (e.g., nucleating agents, impurities, fillers) or interfaces in multiphase systems.

• 2. Growth of the formed nuclei into semi-crystalline morphological structures. These morphologies depend on the thermo-mechanical history experienced by the polymer melt leading to the formation of two distinct microstructures having different spatial growing mechanisms [1, 6]:

  • Spherulites: Grow radially in space and form spherical structures known as spherulites, typically seen under no-flow conditions (quiescent crystallization).

  • Thread-like: Oriented semi-crystalline microstructures in which crystals mainly grow perpendicularly to flow direction, leading to deformed spherulites, shish-kebab structures, and even fibrils for high strain rates (flow-induced crystallization).

The flow conditions during injection molding affect the crystallization from the melt in several ways [7]:

• Increase the nucleation density

• Raise the crystallization kinetics

• Induce changes in the semi-crystalline morphological structures

• Increase the crystallization and melting temperature

Comprehensive research work has been done in the last few decades to better understand the physics behind polymer crystallization whether under quiescent or flow conditions. An extensive review of the various theories postulated is given by Zhang et al. [8]. The current understanding of this process under flow conditions is that there exists a Weissenberg number threshold below which no changes in crystal morphology are observed and above which the nucleation density and growth rate are altered by the intensity of flow in addition to a second threshold where thread-like (fibrillar) morphologies start appearing [9, 10].

Table 1 Overview of the literature in the field of modeling the flow-induced crystallization during polymer processing, based on [9]

2.1.2 Modeling approaches

The first modeling approaches used to describe the kinetics of quiescent crystallization are based on the Kolmogorov-Avrami-Evans (KAE) model [11,12,13] which was developed considering isothermal conditions. Such model describes the nucleation and growth of spherulites using integral equations while taking into account crystal impingement. To include a temperature dependence into the modeling, it is common to use the Hoffman-Lauritzen model which describes the temperature-dependent growth rate constant [14]. Additionally, Ozawa [15] extended the phenomenological KAE model to adhere for the non-isothermal case but it was found that it applies for a limited range of cooling rates. Nakamura et al. [16] introduced an isokinetic approach to describe the kinetic constant in the KAE model. Thereafter, Ziabicki [17] developed a generalized theory to predict non-isothermal crystallization kinetics using an empirical relation for the rate constant. As for the description of the temperature-dependent nucleation evolution, a relation based on Koscher & Fulchiron’s experimental work [18] is commonly used in literature. An alternative approach for the modeling of non-isothermal crystallization is proposed by Schneider et al. [19]. This approach uses a set of four first-order differential equations derived from the KAE model to solve for the relative crystallinity. Additionally, the solution of Schneider’s equations provides morphological information concerning the formed crystalline structures.

The pioneering work of Eder et al. [20] set the stage for the modeling of flow-induced crystallization (FIC). They based their model on the shear rate as a driving force for crystallization and proposed a model dependent on the shear rate to account for the effects of flow. Other researchers like Doufas et al. [21] took into account the effect of flow by defining a stress intensification factor. Zuidema et al. [22] proposed a strain-based model describing the spherulite evolution using the Schneider equations and a modified Eder model to account for the evolution of shish-kebabs. Guo and Narh [23] and Kim et al. [24] developed a model to describe the molecular orientation based on Nakamura’s model. Coppola et al. [25] and Titomanlio and Lamberti [26] correlated the increase of free energy to the raise of melting temperature and decrease of induction time. Zinet et al. [27] considered the first invariant of the extra stress tensor as driving force and extended the Schneider equations accordingly. A thermo-mechanical-based approach is used by Poitou et al. [2] to describe the flow-induced crystallization in the framework of generalized standard materials. Roozemond et al. [28] used the modified Schneider equations to account for the growth of both spherulites and shish-kebab crystallites. Most recently, Spina et al. [29, 30] used a multi-scale approach to model flow-induced crystallization.

To sum up, in the literature, we can find a broad range of approaches to model flow-induced crystallization. These can be clustered into two main categories according to which type of model the work is based on:

• The model family based on Nakamura’s approach: The increase of crystallization kinetics is modeled by multiplying the kinetic function by an intensification factor depending on the postulated driving force for flow-induced crystallization (stress, strain, shear rate, melting temperature increase). This approach neglects the changes in morphology.

• The family based on the KAE model and/or Schneider’s rate equations: The increase of crystallization kinetics is coupled with an enhancement of the nucleation rate and/or growth rate of the crystalline structures. In some particular cases, the increase of nucleation rate is connected to a higher volumetric free energy difference between molten and crystalline phases.

Table 1 presents an overview of the literature in the field of FIC modeling categorized according to the two above-mentioned clusters and mentions the proposed driving force describing the effect of the flow on the crystallization kinetics.

These two modeling approaches are not strictly separated as some of the functions describing the driving force in the Nakamura-based approaches can be integrated into the Schneider rate equations to obtain morphological information.

2.1.3 Effect on other material properties

During the processing and forming of semi-crystalline thermoplastics, the development of crystalline structures influences other material properties such as viscosity, specific volume, thermal capacity, and thermal conductivity. Therefore, substantial research effort has been made to develop models that describe the effect of crystallization on these material properties.

Fig. 1

Overview of the most commonly used methods during the generation of a surrogate model [62, 63]

As it is difficult to measure the viscosity and the crystallinity simultaneously, separate testing methodologies are typically performed to assess the impact of the crystallization phenomenon on the effective viscosity. Rheological measurements are done to describe the viscosity evolution as a function of temperature and shear rate, whereas DSC measurements are carried out to obtain the crystallinity evolution with temperature. Special care is taken to assure that these measurements experience the same thermal histories [50]. The experimental data obtained from the previously mentioned methods are used to obtain models describing the viscosity enhancement due to crystallization. Those coupling functions can be divided into two main classes:

• Models taken from the framework of particle suspension rheology

• Empirical equations recreating the abrupt increase in viscosity induced by crystallization

Pantani et al. [9] and Lamberti et al. [50] present concise reviews on the different developed viscosity functions found in literature that take into account the crystallinity content in relation to viscosity.

As for the specific volume, several works have been presented by Luyé et al. [51], Fulchiron et al. [52], Zheng et al. [47], and Zhao et al. [53]. They included the relative crystallinity into the calculation of the specific volume by assuming a simple mixing rule of the molten and solidified phases’ specific volumes and using Tait-based forms of equation of state. An alternative approach is to extend the classical modified 2-domain Tait PVT model by including a cooling rate dependency as proposed by Cook et al. [54], Wang et al. [55], and Hopmann et al. [56].

2.2 Surrogate modeling

Despite the advances in numerics and high-performance computing, there is still a large number of engineering problems that are difficult to solve accurately and in an acceptable time frame [57]. This is mainly due to the strong coupling and multi-dimensionality of the subjacent physical models [58]. In response to this fact, there has been a growing interest in surrogate modeling techniques to address these challenges. Such methods approximate the response of complex models using a surrogate model also known as a metamodel, which is basically a supervised machine learning model trained on a finite set of input–output data from the complex (high-fidelity) model. This makes surrogate models cheaper to run and are thus used instead of the complex model in various fields such as engineering design optimization, uncertainty quantification, and sensitivity analysis.

Table 2 Overview of the literature in the field of surrogate modeling-based optimization in injection molding simulation

Fig. 2

Sketch of the surrogate modeling-based optimization for parameter identification in injection molding simulation

2.2.1 Generation of a surrogate model

The construction of a surrogate model consists of multiple steps. The basic process can be summarized as follows [59,60,61]:

• 1. Choice of input (design) variables: Selection of input parameters, which presumably have a non-negligible impact on the model output. This choice is usually supported by preliminary experiments, whether physical or numerical ones.

• 2. Sampling in the design space: Definition of a sampling strategy also known as design of experiments and evaluation of the respective design points by means of a high-fidelity simulation or actual experiments.

• 3. Supervised learning: Selection of an emulator model in accordance with the problem at hand and model identification by fitting the input–output data obtained in the previous step.

• 4. Model validation: Assessing the performance of the surrogate model by calculating diverse statistical criteria for training and testing sets. In case of unsatisfactory results, the identification of new design points for further model enrichment is triggered.

• 5. (Optional) Model updating: Building an updated surrogate model using the additional design points along with the previous ones.

• 6. Model exploitation: Use of the generated surrogate model for further analyses such as parameter sensitivity analysis, optimization routines, or uncertainty quantification purposes.

Figure 1 provides a summary of the mathematical/nume-rical techniques most commonly used to perform the second and third steps in the surrogate model generation process presented above. After defining the design space, an additional optional step is to perform a model order reduction on the output result(s), which has to be approximated by the surrogate model. Following this, the type of emulator is chosen along with the most suitable fitting (or regression) method. In the following sections, a closer look is taken into each of the four steps shown in Fig. 1.

2.2.2 Surrogate modeling in injection molding simulation

In the last years, the use of surrogate models to approximate outputs from the injection molding simulation has been growing steadily especially in the field of process parameter optimization to enhance product quality and molding efficiency. Gao and Wang [64] employed a Kriging approximation model along with an adaptive optimization technique to minimize the warpage in produced parts by varying process parameters such as the mold and melt temperature, injection time as well as the holding pressure profile. Similar works were performed by Chen et al. [63], Wang et al. [65] and Kang et al. [66]. Other authors used radial basis function [67,68,69], artificial neural networks [70, 71], Gaussian process [72] as fast emulator to optimize process parameters for controlling shrinkage and warpage in the final part. Additional applications for surrogate models have been used for the optimization of cycle time [68] and part weight [73].

All of the previously mentioned publications use a surrogate model to find optimal process parameters. However, another interesting utilization of surrogate modeling in injection molding was recently published by Ivan et al. [74], where the surrogate model is used to identify two fiber orientation model parameters. The authors used experimental fiber orientation data obtained by micro-computed tomography to calibrate the fiber orientation model used in their high-fidelity injection molding simulation. This was done by generating an ANN-based surrogate model recreating the fiber orientation tensors across the thickness of several regions of interest in a plate as a function of two fiber orientation model parameters. In this work, we use an analogous approach to calibrate a crystallization model implemented in a high-fidelity injection molding simulation.

Table 2 provides a brief overview of the literature dealing with surrogate modeling in injection molding simulation. More comprehensive reviews can be found in [71, 75].

3 Model implementation and parameter identification

Fig. 3

DSC thermograms of the studied POM under different constant cooling rates (1, 3, 5, 10 $^{\circ }$C/min)

Table 3 Material characteristics of the studied POM homopolymer obtained from DSC measurements

A workflow of the proposed material parameter identification is sketched in Fig. 2. It includes the implementation of the crystallization model into a high-fidelity injection molding simulation software, the generation of a respective surrogate model (having as input variables the unknown material model parameters), the generation of reference data (in-mold pressure sensor signals) from actual injection molding as well as the optimization loop over the surrogate model for identifying the unknown material model parameters. In the following, we will present in detail those different blocks by using a polyoxymethylene (POM) homopolymer as a pilot case.

3.1 Experimental data generation

3.1.1 Material

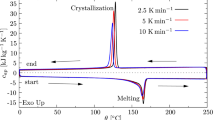
The polymer material used in this work is an injection molding grade of an unreinforced POM homopolymer. To characterize the quiescent crystallization, we carried out differential scanning calorimetry (DSC) measurements using a TA Instruments, Inc. DSC Q1000 with a heating rate of 10 $^{\circ }$C/min and several cooling rates (1, 3, 5, 10 $^{\circ }$C/min). The DSC thermograms of the different cooling rates are presented in Fig. 3. Using the DSC data, we determined the crystallization (peak) and melting (peak) temperatures along with the crystallization enthalpy for the studied POM material. Table 3 summarizes those characteristical values.

Additionally, rheological measurements are performed using an ARES rheometer from TA Instruments, Inc. with a plate-plate geometry. The test is carried out with a constant frequency of 3 rad/s and a maximal shear strain of 0.03% with a cooling rate of 3 $^{\circ }$C/min. Figure 4 presents the results of the rheological dynamic tests with temperature ramp.

3.1.2 Injection molding experiments

Injection molding experiments are performed on an electrical injection molding machine (ENGEL E-Motion 440/220 T). We used a constant cross-section cavity mold geometry, where four pressure sensors are mounted in the cavity to measure pressure signals during the injection molding process. A technical drawing of the part along with the design dimensions are shown in Fig. 5. The sensors’ location is specified by the gray circles in Fig. 5. By means of a filling study with a melt temperature of 220 $^{\circ }$C, a mold temperature of 80 $^{\circ }$C and an injection velocity of 10 cm$^{3}/$s, we determined a shot volume of 28.3 cm$^{3}$ that is used as fixed initial ram position for all subsequent injection molding experiments. On the other hand, a packing study is done with a mold temperature of 110 $^{\circ }$C and a holding pressure of 80 MPa for defining a holding time of 16 s.

A design of experiments consisting of 27 sampling points is performed where the mold temperature, the injection velocity, and the holding pressure are varied. The upper and lower bounds of these variables are presented in Table 4. All experimental runs are carried out with a melt temperature of 220 $^{\circ }$C. To import the machine and process settings along with the sensor signals during the different injection molding runs, we used the ENGEL sim link interface.

Fig. 4

Complex viscosity measured under a cooling rate of 3 $^{\circ }$C/ min with a constant frequency of 3 rad/s and a maximal shear strain of 0.03%

Fig. 5

Technical drawing of the injection-molded part including some characteristic dimensions in mm and the location of the four pressure sensors (P0, P1, P2, and P3) [3]

Table 4 Variable process settings in the injection molding experimental runs with their upper and lower bounds

Some of the experimental runs presented short shots due to the incomplete filling of the mold cavity caused by the early freezing of the gate.

3.2 Implementation of user-defined models

3.2.1 Simulation software

We selected Autodesk^® Moldflow^® Insight 2021.1 (AMI2021.1) as software to perform the high-fidelity injection molding simulations because it offers the possibility to implement user-defined functions by means of the Solver API feature.

The Solver Application Programming Interface (API) in Moldflow^® enables the user to create their own C++ functions, which are called by the solver to calculate a user-defined variable (e.g., physical property, material descriptor) during an analysis. In AMI2021.1, this feature allows user-defined models for viscosity, PVT, core shift, solidification, and fiber orientation. Additionally, due to the newly-introduced Advection API functionality, it is possible to define material derivatives that are solved in time and space by the solver while providing the user’s code access to the solution of the derivative.

3.2.2 Crystallization model

The implemented crystallization model is a thermo-mechanical-based model developed by Poitou et al. [2] in the framework of irreversible thermodynamics. The model is derived using the standard material formalism commonly used in solid mechanics to describe various coupled phenomena [2]. Such formalism necessitates two potentials, a thermodynamic potential and a pseudo-potential, to describe the behavior of a material. The first potential helps in quantifying the capability of the material to store energy whereas the second potential quantifies the capability of the material to dissipate energy [2]. More detailed information concerning this method can be found in [2, 39].

By using the standard material formalism, it is therefore possible to fully describe a coupled phenomena such as the flow-induced crystallization since the mechanical parameters are dependent on the degree of crystallinity. The coupling is taken into account by adding up the potential representing the quiescent kinetics given by the Nakamura model [16] and the potential referring to the mechanical constitutive behavior [2]. By assuming that the material is a Newtonian fluid, this mechanical dissipation potential is thus approximated using a simple relation between the strain rate tensor and the viscosity. In Poitou et al.’s model [2], the crystallization’s kinetics are modeled using a temperature-dependent function $\chi (T)$ defined by Hieber [78]. However, in this work, this relation is substituted by a rate equation described by Lauritzen and Hoffman [14], known as the Hoffman-Lauritzen equation, and related to the previous by $\chi (T)=1/K(T)^{1/n}$.

The crystallization model, which only applies for temperatures lower than the material’s melting temperature $T_m(P)$, reads as follows:

$$\begin{aligned} \begin{aligned} \dot{\alpha }(t)&= (1-\alpha )\left[ -\frac{1}{\beta }\frac{\partial \eta }{\partial \alpha }\text {tr}\textbf{D}^2 \right. \\&\quad \left. + nK(T)^{\frac{1}{n}}\left( -\ln (1-\alpha )\right) ^{1-\frac{1}{n}}\right] \end{aligned} \end{aligned}$$

(1)

$$\begin{aligned} \begin{aligned} K(T)&= K_0\exp \left( -\frac{3K_g}{T(T_m^0(P)-T)}\right) \\&\quad \times \exp \left( -\frac{3U^\star }{R(T-T_\infty (P))}\right) \end{aligned} \end{aligned}$$

(2)

where $\beta$, n, $K_0$, and $K_g$ are data-fitted parameters, $\textbf{D}$ is the strain rate tensor, $T_m^0(P)$ is the pressure-dependent equilibrium melting temperature, $U^\star$ is the activation energy for segmental jump of polymer molecules with a universal value of 6270 J/mol, R is the gas constant, and $T_\infty =T_g(P)-30$ K with $T_g(P)$ as the pressure-dependent glass transition temperature. The first term in Eq. 1 represents the contribution of the flow-induced crystallization, whereas the second term in Eq. 1 is the contribution of the quiescent one. This last term is a function of the quiescent crystal growth rate given in Eq. 2, which corresponds phenomenologically to the Avrami kinetic model parameter too.

To decrease the amount of unknown material model parameters, we determined a linear relationship between the kinetic constants of the Hoffman-Lauritzen equation, which is particular for the POM used in this work:

$$\begin{aligned} K_g=6732 \ln (K_0)+11296. \end{aligned}$$

(3)

This relationship defines the allowed couplets of $(K_g, K_0)$, which fit (2) to the values of $K_{Avrami}$ identified in the reduced range of temperatures that is typically accessible by experimental means. We determined, in turn, the Avrami kinetic constants (crystal growth rate at constant temperature) from the Ozawa kinetic constants (crystal growth rate at constant cooling rates) using the following expression:

$$\begin{aligned} K_{Avrami}=K(T)=\left[ -\frac{d}{dT}\left( K_{Ozawa}(T)^{1/n}\right) \right] ^n \end{aligned}$$

(4)

where n is the Avrami exponent and also appears in Eq. 1.

We needed this Avrami-Ozawa correlation because our DSC experiments were performed under constant cooling rates, so we identified first directly the Ozawa kinetic constants.

Fig. 6

Fitting surface relating the different pressure dependencies of the melting temperature ($b_6$), equilibrium melting temperature (a), and glass transition temperature (b)

Additionally, the pressure dependencies of the temperatures are defined by the following:

$$\begin{aligned} T_m(P)=T_m(0)+b_6P, \end{aligned}$$

(5)

$$\begin{aligned} T_m^0(P)=T_m^0(0)+aP, \end{aligned}$$

(6)

$$\begin{aligned} T_g(P)=T_g(0)+bP \end{aligned}$$

(7)

where $b_6$, a, and b are usually experimentally determined parameters. The pressure dependency of the melting temperature $b_6$ is typically obtained from PVT measurements. However, the two other dependencies are harder to determine experimentally for semi-crystalline materials. Therefore, for this work, a relation between the three parameters is proposed by computing the crystal growth curves as a function of temperature for different pressure levels using the Hoffman-Lauritzen model given in Eq. 2. For various combinations of a and b, the maximal growth rate is determined for the different pressures and the corresponding temperatures are used to calculate $b_6$. Figure 6 shows the surface representing the relation between the parameters, which seems to follow a linear relationship:

$$\begin{aligned} b_6=f\cdot a+g\cdot b \end{aligned}$$

(8)

where $f=0.629$ and $g=0.4015$ are the obtained fitted parameters. In this work, we suppose that the melting temperature and the equilibrium melting temperature have the same pressure dependency such as $b_6=a=0.175$ K/MPa (value provided by the material supplier). As a consequence, the pressure dependency of the glass transition temperature was found to be $b=0.161$ K/MPa by using (8). The crystallization model parameters are summarized in Table 5.

Table 5 The model parameters of the implemented crystallization model

3.2.3 Heat of crystallization

In the standard Moldflow^® solver, the implemented energy equation in terms of temperature T reads as follows:

$$\begin{aligned} \begin{aligned} \rho c_p \left( \frac{\partial T}{\partial t}+\textbf{v}\cdot \nabla T \right)&=\nabla \cdot (k\nabla T)+ \tau : \nabla \textbf{v} \\&\quad + \zeta T \left( \frac{\partial P}{\partial t}+\textbf{v}\cdot \nabla P \right) \end{aligned} \end{aligned}$$

(9)

where $\rho$ is the polymer density, t is the time, $\textbf{v}$ is the velocity vector, P is the pressure, $\tau$ is the viscous stress tensor, k is the polymer thermal conductivity, $c_p$ is the specific heat capacity of the melt, and $\zeta =-\frac{1}{\rho }\frac{\partial \rho }{\partial T}$ is the coefficient of volume expansion. Notice that there is no explicit term of heat source. In this work, we model however explicitly the crystallization heat release by adding a heat source term to the right of Eq. 9 as follows:

$$\begin{aligned} \dot{Q} = \rho \Delta H_c \dot{\alpha }(t) \end{aligned}$$

(10)

where $\Delta H_c$ is the latent heat of crystallization of a material sample with ultimate absolute crystallinity. The numerical implementation of the heat source term via the solver API feature is done by defining a local temperature increment $\Delta T$ as a function of the crystallization increment in a given time step:

$$\begin{aligned} \Delta T=\dot{\alpha }(t)\Delta t\dfrac{\Delta H_c}{c_p} \end{aligned}$$

(11)

where $\Delta t$ is the solver time step. This model supposes that the latent heat is released uniformly along the whole crystallization process. On the other hand, if the local temperature of the melt becomes higher than the melting temperature ($T > T_m(P)$), an instantaneous remelting of the crystals should take place. This endothermic process should lead to a local temperature reduction, modeled as follows: $\Delta T=-\alpha \dfrac{\Delta H_c}{c_p}$.

The latent heat of crystallization is given in Table 3. As here we implement explicitly the latent heat of crystallization, we have to eliminate the crystallization peak from the specific heat data as typically found in Moldflow^® material cards. In this work, we define the temperature-dependent specific heat using the values given in Table 6.

Table 6 The specific heat data used in the Moldflow^® simulations along with self-defined models

3.2.4 Viscosity model

A modified Cross-WLF model is used to describe the viscosity in this implementation. In this model, the shear viscosity depends on crystallization, temperature, shear rate, and pressure. The melt shear viscosity $\eta$ is given by the following:

$$\begin{aligned} \eta (T, P, \alpha , \dot{\gamma })=\frac{\eta _0(T,P,\alpha )}{1+(\frac{\eta _0(T,P,\alpha )\dot{\gamma }}{\tau ^\star })^{1-\lambda _v}} \end{aligned}$$

(12)

where $\dot{\gamma }$ is the shear rate, $\tau ^\star$ is the critical stress level at the transition to shear thinning, $\lambda _v$ is the power law index in the high shear rate regime, and ${\eta }_0$ is the zero shear viscosity defined as follows:

$$\begin{aligned} {\eta }_0(T, P, \alpha )=D_1 \exp \left( \frac{-A_1(T-T_{ref})}{A_2+(T-T_{ref})} \right) \vartheta (\alpha ) \end{aligned}$$

(13)

where $T_{ref}=T_g(P)$ with the pressure-dependency defined in Eq. 7, $D_1$ is theoretically the shear viscosity at $T_{ref}$, and $A_1$ and $A_2$ are data-fitted coefficients approaching the universal constant values of the WLF theory. As for $\vartheta (\alpha )$, it is a function describing the crystallization dependency of the viscosity and is an extension of Kitano et al.’s relation [81] for concentrated suspension of particles. This function is defined as follows:

$$\begin{aligned} \vartheta (\alpha )=\frac{1}{(1-\frac{\alpha }{A})^B} \end{aligned}$$

(14)

where A would represent a critical relative crystallinity at which the viscosity of the system tends to be infinite (solidification) and B is a data-fitted exponent. The coupling function $\vartheta (\alpha )={\eta }_0(T, P, \alpha )/{\eta }_0(T, P)$ is chosen to increase the effect of crystallization on viscosity at low shear rates as done by Pantani et al. [9].

Be aware that in our implementation of the Cross-WLF model, the $A_2$ coefficient does not depend on pressure. This differs from Moldflow^® implementation, which includes this pressure dependency and leads to a linear relation between ${\eta }_0$ and P for all temperatures. However, Rudolph et al. [82] showed a non-linear dependency between ${\eta }_0$ and P for low temperatures approaching the glass transition temperature of a polycarbonate material. Therefore, in this work, the main connection between shear viscosity and pressure is modeled using the glass transition temperature’s dependency.

To identify the parameters of the WLF model, the rheological measurement presented in Fig. 4 is used. The viscosity results before the onset of crystallization at 152 $^{\circ }$C are utilized to identify the temperature dependency of the shear viscosity by fitting the following linear relation:

$$\begin{aligned} \frac{1}{\ln (\eta ^{\star }/D_1) }=-\frac{A_2}{A_1}\frac{1}{(T-T_{ref})}-\frac{1}{A_1} \end{aligned}$$

(15)

where $\eta ^{\star }$ is the magnitude of the measured complex viscosity from the dynamic rheological test. On the other hand, the cross parameters describing the dependency on shear rate dependency are taken from the Moldflow^®’s material database. The model parameters for the Cross-WLF model are summarized in Table 7.

Table 7 The model parameters of the implemented viscosity model

3.2.5 PVT model

Since this work deals with a semi-crystalline thermoplastic material, the pressure-volume-temperature (PVT) relationship is defined by considering explicitly the relative crystallinity $\alpha$. We assume that the material is a simple two-phase system. In this context, we can describe the specific volume v using a mixing law of the molten and solidified phases’ specific volumes, represented respectively as $v_m$ and $v_s$. This law is written as follows:

$$\begin{aligned} v=\alpha v_s+(1-\alpha )v_m. \end{aligned}$$

(16)

The specific volumes $v_m$ and $v_s$ are defined by using the respective empirical Tait equation of state:

$$\begin{aligned} v_x(T,P)=v_0(T)\left[ 1-C\ln \left( 1+\frac{P}{B(T)}\right) \right] \end{aligned}$$

(17)

with $x=m,s$. In Eq. 17, C is a universal constant equal to 0.0894, $v_0(T)$ is the specific volume at zero gauge pressure, and B(T) describes the pressure sensitivity of the studied material. These temperature-dependent functions are defined as follows:

$$\begin{aligned} v_0(T)=b_{1x}+b_{2x}(T-b_5), \end{aligned}$$

(18)

$$\begin{aligned} B(T)=b_{3x}\exp \left( -b_{4x}(T-b_5)\right) \end{aligned}$$

(19)

where $b_{1x}$, $b_{2x}$, $b_{3x}$, $b_{4x}$, and $b_5$ are data-fitted coefficients.

In this work, the respective PVT parameters are taken from Moldflow^®’s material database and are summarized in Table 8.

Table 8 The model parameters of the implemented PVT model

3.2.6 Solidification model

A solidification criterion is used in an injection molding simulation to mimic a melt-to-solid transition in the manufacturing process. Numerically, it is treated as an abrupt increase of local viscosity to be able to solve the flow problem without shifting the system boundaries. Traditionally, the criterion is defined by a constant no-flow temperature, which should be characteristic of the material. However, the solidification of a semi-crystalline polymer is primarily dependent on its crystallization degree. Therefore, we propose a crystallization-dependent solidification model as follows:

• If $\alpha \ge A$, then polymer is treated as solid.

• If $\alpha < A$, then polymer is in melt state.

where A is the same parameter used to describe the dependency of the viscosity on crystallization given in Eq. 14.

Table 9 presents a summary of the implemented models in comparison to the ones used by the default Moldflow^® solver.

Table 9 Comparison between the implemented models and the ones used by default in a Moldflow^® simulation for the injection molding of a semi-crystalline thermoplastic material

3.3 Surrogate model generation

3.3.1 High-fidelity simulation model

The simulations are set-up to recreate the injection molding experiments presented in Section 3.1.2. The injection-molded part corresponds to the geometry shown in Fig. 5. The high-fidelity simulation emulates the in-mold cooling process of the injection-molded part, starting from the filling of the mold cavity up to the mold opening for part ejection. The thermal boundary conditions are given by a previous thermal simulation of the complete mold within a stable injection molding cycle. In Moldflow^® software, the described simulation corresponds to a Cool(FEM) + Fill + Pack analysis. The geometrical model includes cooling channels meshed as beam elements and the part as well as the feed system (nozzle and flange) meshed using tetrahedral elements with 24 layers through the thickness, where the feed system is defined as a hot runner. Lateral and top views of the meshed model are shown in Fig. 7 a and b, respectively. The computation time of a single simulation requires around 110 min in a PC with a 4.10 GHz processor and 32 GB RAM.

The process settings of the base simulation are defined according to imported data from the ENGEL sim link software tool. These include the filling and packing profiles along with the switch-over ram position and the machine settings. Since in this work multiple user-defined models are implemented, the Solver API option should be enabled and the paths of the text files containing the various model parameters should be specified accordingly.

Fig. 7

The meshed simulation model including the part (dark green), runner and sprue (light green), cooling channels (blue), and feed system (red) [3]

Table 10 Process settings of the baseline simulations for the generation of surrogate models

Table 11 Surrogate model variables with respective upper and lower bounds

3.3.2 Input variables and output

A total of three surrogate models are generated for three different processing conditions corresponding to the ones used during the experimental injection molding runs. These process settings are presented in Table 10 along with the respective labels of the experimental DOE and surrogate model. Since a cooling analysis is performed in the simulations, the inlet cooling temperature $T_{c,in}$ is varied such as $T_{c,in}=T_{mold}+4$ $^{\circ }$C of the $T_{mold}$ set experimentally. Each surrogate model is built by considering the following input variables: Crystallization model parameters $\beta$ and $K_0$, viscosity model parameters A and B, and the heat transfer coefficient during the packing phase $HTC_p$. These input variables are summarized in Table 11 along with their lower and upper limits.

Some of these ranges were determined by making some numerical tests while others were based on experimental results. For $K_0$, for example, we took as a basis the DSC measurements presented in Section 3.1.1. However, given the experimental limitations for covering a large range of cooling rates, we have to deal with an uncertain identification of $K_0$. In fact, all values within the proposed interval of variation for $K_0$ fit the available experimental data according to the Avrami-Ozawa relation given in Eq. 4. On top of that, the interval of variation is centered at $ln(K_0)=53$, which is a value determined by Plummer and Kausch [83] for POM. As for the solidification criterion A, in the case of $B=2$, the viscosity coupling is analogous to the one given by Metzner [84], where $A=0.68$ is specified for smooth spheres and $A\approx 0.44$ for rough compact crystals. As we expect the formation of spherulites and thread-like crystal morphologies during the injection molding process of POM, we propose a rough variation of $\pm 0.15$ around the value given for compact crystals. As for B in the viscosity model, Kitano [81] and Metzner [84] defined it to be equal to 2 according to suspension theory. However, in our work, B is varied between 2 and 5 to encompass larger viscosity increases with evolving crystallization, as observed experimentally for POM in Fig. 4.

$\beta$ is a parameter that controls the contribution of the flow-induced crystallization to the total relative crystallinity in the model. It turns out that the overall filling simulation is extremely sensitive to this parameter because it can trigger artificially fast solidification of the gate and therefore incomplete cavity filling. The interval of variation for $\beta$ was defined after multiple high-fidelity simulation sensitivity studies and surrogate model tests, guaranteeing a DoE that produces a representative amount of short shots and fully filled parts to efficiently calibrate the material-dependent model parameters.

The output result used to train the surrogate models is the pressure signal at a surface node corresponding to the location of the sensor P2 located directly after the gate as shown in Fig. 5.

3.3.3 Generation methodology

The training set for the generation of the different surrogate models is sampled using the Latin hypercube method. A total of 132 simulations were chosen for training and 20 simulations for testing purposes. This choice is postulated to be appropriate as five parameters are being varied in this work in comparison to the six parameters changed in our previous work [3], where an acceptable accuracy for the estimation of the pressure signal was reached using 120 training simulations.

Once the results of the high-fidelity simulation DoE are available, the generation of the surrogate models is done in MATLAB R2019b using proper orthogonal decomposition (POD) of the pressure signal and non-linear regression (NLR) of the POD basis coefficients. This methodology is partially analogous to the POD-NLR method presented in [3]. The following steps describe the process of generating the surrogate models using the POD-NLR technique used in this work:

• 1. Normalization: The pressure signal results $P_i$ ($i=1,\cdots ,S$) are normalized between 0 and 1 as follows:

  $$\begin{aligned} t_{norm}=\frac{t_{original}-t_{start}}{t_{end}} \end{aligned}$$

  (20)

  where $t_{original}$ is the imported unprocessed simulation time, $t_{start}$ represents the time at which the flow front reaches the sensor node producing a non-zero pressure value, and $t_{end}$ is the time at which the pressure signal becomes zero, i.e. the local pressure equalizes the ambient pressure. In this work, $t_{start}$ is substantially smaller than $t_{end}$, that is why we have neglected it in the denominator of the normalization equation. Subsequently, the simulated pressure is resampled using 1000 points uniformly distributed in the normalized time interval between 0 and 1.

• 2. Model order reduction: The normalized simulated pressure signal is dimensionally reduced by means of proper orthogonal decomposition (POD). To obtain the POD basis functions, the eigenvalue problem $\textbf{P}\textbf{P}^TV_k={\lambda }_k V_k$ needs to be first solved, where $\textbf{P}$ is a snapshot matrix of different pressure signals and $V_1, V_2, V_3,...$ are the eigenvectors associated to the eigenvalues ${\lambda }_1,{\lambda }_2, {\lambda }_3,...$ The POD basis functions $\phi _k$ can be then determined by normalizing the eigenvectors by $\phi _k=V_k/{\lambda }_k$. These basis functions create an orthogonal system that captures the dominant energy modes within the data and their coefficients are determined by projecting the original data onto these functions. The reconstruction of the pressure signal can be obtained by the following:

  $$\begin{aligned} P^{(s)}_{reconstructed}=\sum _{k=1}^{n}\Gamma ^{(s)}_k\phi _k \end{aligned}$$

  (21)

  where s is the high-fidelity simulation number, n is the number of modes or basis functions obtained according to a specified error value, and $\Gamma ^{(s)}_k$ is the POD basis coefficient for a specific mode k and a simulation s. The truncation criterion is done according to an error value of $\epsilon =5\times 10^{-4}$, which cuts off the number of modes once the eigenvalue condition $\frac{\lambda }{\lambda _{\max }} \ge \epsilon$ is not more satisfied.

• 3. Regression: A least-squares regression of a second-order polynomial is used to correlate the POD basis coefficients $\Gamma$, and the time shift values $t_{start}$ and $t_{end}$ with the metamodel variables. The regression equations read as follows, where the implicit Einstein summation convention is used for indexes i and j:

  $$\begin{aligned} \Gamma ^{(s)}_n=a^{(n)}+b^{(n)}_iX^{(s)}_i+c^{(n)}_{ij}X^{(s)}_iX^{(s)}_j \end{aligned}$$

  (22)
  $$\begin{aligned} t_{start}^{(s)}=d+e_iX^{(s)}_i+f_{ij}X^{(s)}_iX^{(s)}_j \end{aligned}$$

  (23)
  $$\begin{aligned} t_{end}^{(s)}=g+h_iX^{(s)}_i+z_{ij}X^{(s)}_iX^{(s)}_j \end{aligned}$$

  (24)

  where $X_i$ and $X_j$ are the surrogate model input variables and $a,b_i,c_{ij}, d,e_i, f_{ij},g,h_i,z_{ij}$ are the surrogate model parameters.

3.3.4 Performance of the surrogate models

The performance of each surrogate model is assessed by measuring its capacity to recreate the pressure signal given by the high-fidelity simulation at one sensor location. In this section, we present some predicted pressure results from both the training and testing DoE sets as well as the error metrics for the estimation of the POD basis coefficients and time shifts. In other words, we measure the quality of the fitted polynomials defined in Eqs. 22, 23, and 24 and their predictive capability.

One of the error metrics in this work is the normalized root mean squared error (RMSE) that uses the min-max normalization method to facilitate the comparison between various surrogate modeling techniques:

$$\begin{aligned} \begin{aligned} \text {Normalized RMSE}(Y, \hat{Y})&= \frac{\text {RMSE}(Y, \hat{Y})}{Y_{\text {max}}-Y_{\text {min}}} \\&= \frac{\sqrt{\frac{1}{n} \sum _{i=1}^{n} (Y^{i}-\hat{Y}^{i})^2}}{Y_{\text {max}}-Y_{\text {min}}} \end{aligned} \end{aligned}$$

(25)

where Y and $\hat{Y}$ represents the target and estimated output, respectively. In this work, the estimated output is the surrogate model response.

The second metric is the coefficient of determination also known as the $R^2$ score. It is a statistical measure that indicates how well the data fit the regression model and how well unseen samples are likely to be predicted by the model. $R^2$ ranges between $-\infty <R^2\le 1$, where 1.0 is the best score. $R^2$ is calculated as follows:

$$\begin{aligned} R^2(Y, \hat{Y}) = 1-\frac{\sum _{i=1}^{n} (Y^{i}-\hat{Y}^{i})^2}{\sum _{i=1}^{n} (Y^{i}-\bar{Y})^2} \end{aligned}$$

(26)

where $\bar{Y}=\frac{1}{n} \sum _{i=1}^{n} Y^{i}$ is the mean value of Y.

To ease the analysis of the previously mentioned metrics, the POD basis functions associated to each surrogate model are presented in Fig. 8. For the molding conditions V6 and V14, the simulation output is reduced using five basis functions. For the molding condition V27, data reduction required only three basis functions by using the same truncation error $\epsilon$. This fact means that the simulated pressure signal for the process settings V27 is less fluctuating than the ones for the other process conditions.

Fig. 8

The POD basis functions of the three generated surrogate models

Fig. 9

Comparison between the pressure predictions using the SM1 surrogate model and those obtained by four example high-fidelity simulations used for the model’s a training and b testing

Starting with the surrogate model SM1, Fig. 9a presents the pressure results of four training simulations and the approximated results given by the trained surrogate model. Even considering training data, there still exists some discrepancy between the target simulation and the surrogate model predictions, especially in the case of the green curve. These differences are somehow explainable since the metamodel is trained on a reduced form of the predicted signal and not directly on the full-resolution simulated pressure response. On the other hand, the pressure signal depicted in the green curve is more wavy than the other three curves making it more challenging to approximate using the same number of basis functions. Figure 9b shows the pressure signals of four simulations used to test the capability of the surrogate model to predict unseen data. The surrogate model is able to recreate reasonably well the form of the different pressure signals but struggles to accurately predict $t_{end}$ as seen in the case colored in dark blue.

Fig. 10

The error metrics of the calculated POD basis coefficients $\Gamma$ and time shifts $t_{start}$ and $t_{end}$ using the SM1 surrogate model when using input data from the training and testing sets

The error metrics of the surrogate model SM1 for estimating the five POD basis coefficients $\Gamma$ and the two time shift parameters are presented in Fig. 10. Figure 10 a and b show the normalized RMSE and $R^2$ score, respectively, differentiating between training and testing scenarios. As expected, error metrics for training are lower than for testing data sets. The normalized RMSE for estimating the POD basis coefficients $\Gamma _1$ and $\Gamma _4$ as well as the time shift $t_{start}$ doubles when passing from training to testing data sets. Similarly, the estimation of the POD basis coefficients $\Gamma _3$ and $\Gamma _4$ produce a negative $R^2$ score for the testing data set, which points out that the SM1 should not be used as a single regressor for those parameters. However, the overall performance of the surrogate model SM1 (normalized RMSE lower than 26%) is acceptable given that the reconstructed pressure signals (Fig. 9) are accurate enough for the calibration purposes in this work. Specifically, the reconstruction yields a mean absolute error of 3.7 MPa in the testing data set, which represents less than 7% difference with respect to the maximal injection pressure of reference.

Fig. 11

Comparison between the pressure predictions using the SM2 surrogate model and those obtained by four example high-fidelity simulations used for the model’s a training and b testing

Moving on to the surrogate model SM2, Fig. 11 shows high-fidelity simulation results in front of the surrogate model estimations for both training and testing data sets. Some minor differences between high-fidelity simulation and surrogate model are visible. In the training set, the maximum pressure of the simulation in turquoise is under-predicted whereas the end times $t_{end}$ for the simulations in green and pink are over-predicted. In the testing set, the SM2 model performs reasonably well as seen in Fig. 12b. This is confirmed by a normalized RMSE lower than 20% for all POD basis coefficients as shown in Fig. 12. Additionally, there is a relatively small difference of performance metrics between the training and testing data sets. In this case, the reconstruction of the simulated pressure signals using SM2 shows a mean absolute error of 2.3 MPa (less than 5% difference with respect to the maximal injection pressure of reference) in the testing data set.

Fig. 12

The error metrics of the calculated POD basis coefficients $\Gamma$ and time shifts $t_{start}$ and $t_{end}$ using the SM2 surrogate model when using input data from the training and testing sets

Fig. 13

Comparison between the pressure predictions using the SM3 surrogate model and those obtained by four example high-fidelity simulations used for the model’s a training and b testing

The SM3 model exhibits also a remarkable performance as observed in Fig. 13 a and b for training and testing data sets, respectively. The most noticeable deviation occurs in the training set, where the maximum pressures of the high-fidelity simulations represented in green and turquoise (Fig. 13a) are under-predicted by the metamodel. Interestingly, the model order reduction in this case required only three POD basis functions (see Fig. 8c) to satisfy the truncation error of $\epsilon =5\times 10^{-4}$. For this reason, Fig. 14 presents the error metrics for only three $\Gamma$ POD basis coefficients. In the training set, the normalized RMSE for all parameters is lower than 12%. However, the prognosis of the third POD basis coefficient $\Gamma _3$ as well as $t_{start}$ is inaccurate in the testing set (negative $R^2$), pointing out a deficiency of the chosen polynomial regressor for those parameters. Nonetheless, the reconstruction of the simulated pressure signals using SM3 is acceptable as far as it displays a mean absolute error of 4.6 MPa (less than 6% difference with respect to the maximal injection pressure of reference) in the testing data set.

Fig. 14

The error metrics of the calculated POD basis coefficients $\Gamma$ and time shifts $t_{start}$ and $t_{end}$ using the SM3 surrogate model when using input data from the training and testing sets

3.4 Surrogate model-based parameter calibration

3.4.1 Calibration algorithm

To identify the five modeling parameters presented in Table 11, a multi-objective optimization routine is performed using the lsqnonlin built-in MATLAB function from the optimization toolbox. The experimental pressure signals are used as a reference for defining the objective functions. The calibration utilizes all three surrogate models to obtain one single set of optimized parameters using the following formulation:

$$ \begin{aligned} \text {find} \quad&\textbf{V}=(\beta , K_0, A, B, HTC_{p}) \\ \text {argmin} \quad&\mid \hat{Y}_{\max }^l-Y^{\exp ,k}_{\max }\mid \quad (l=1,2,3 \\&\mid \hat{t}_{end}^l-t^{\exp ,k}_{end} \mid \quad \quad \& \; k=6,14,27) \\ \text {s.t.} \quad&{-10^{12}} \le \beta \le {-10^{10}}, \\&23 \le \ln (K_0) \le 83, \\&0.3 \le A \le 0.6, \\&2 \le B \le 5, \\&500\le HTC_{p} \le 5000 .\\ \end{aligned}$$

Fig. 15

The time intercept of a tangent straight line fitted to the pressure signal decay at the end of packing for the P2 sensor signal of the DOE level V6

Table 12 The experimentally determined parameters used to define the six objective functions used in the optimization routine to identify the modeling parameters

The optimization problem contains in total six objective functions. Three of them minimize the difference between the experiment and surrogate model for the maximal pressure value in three different processing conditions. The experimental maximal pressure is $Y^{\exp ,k}_{\max }$, where $k=6,14,27$ represents the experimental DoE labels V6, V14, and V27. On the other hand, the maximal pressure determined by the surrogate model l is $\hat{Y}_{\max }^l$. The remaining objective functions minimize the difference between predicted end time $\hat{t}_{end}^l$, calculated according to Eq. 24, and the experimentally determined end time $t^{\exp ,k}_{end}$. The experimental end time value is obtained as the time intercept of a tangent straight line fitted to the pressure signal decay at the end of packing. A visual example of the end time determination of V6 is given in Fig. 15. Table 12 summarizes the experimental reference values used to define the six objective functions.

3.4.2 Calibration results

Fig. 16

The norm of the residuals as a function of the number of iterations performed by lsqnonlin during the optimization routine

For calibrating the material models implemented in Moldflow^®, we can use now the three generated surrogate models by identifying $\beta , K_0, A, B, HTC_{p}$ according to the algorithm described in Section 3.4.1. The optimization routine necessitated 15 iterations to reach a local minimum as shown in Fig. 16. The optimization routine stopped because the function tolerance fell below 10$^{-4}$. To check if there exist other local minima in this multi-objective optimization and finally obtain the global minimum, the built-in MultiStart MATLAB function is used to find other possible local minima to the optimization problem by starting from different initial points. We did not find a different combination of optimized parameters suggesting that we found the global minimum from the first try. The optimized parameters are given in Table 13.

Table 13 Identified model parameters after multi-objective optimization

Fig. 17

The pressure signals for the V6 processing condition obtained using the simulation with the calibrated models in comparison to the ones obtained by the default Moldflow^® simulation along with the corresponding experimental results for this condition

The identified solidification criterion parameter $A=0.35$ seems reasonable since it depends theoretically on the geometry of the suspending solid crystallites. According to Kennedy and Zheng [1] and Metzner [84], A is approximately equal to 0.44 for rough compact crystals and since during injection molding fibrillar crystal structures could develop due to intense shear strain, an $A<0.44$ is plausible. The optimized value for the exponent parameter B is nearly equal to the upper bound of the searching interval (i.e., $B=5$), which underlines the strong coupling between evolving crystallization and effective shear viscosity. This correlates well with the results of the rheological test in Fig. 4, where the viscosity increases abruptly after the onset of crystallization. On the other hand, the identified value of the FIC parameter $\beta$ is not straightforward to assess but $\beta = -10^{11.37}$ translates into a lower contribution of FIC to the total relative crystallinity. The optimized value for $\ln (K_0)$ corresponds to the upper bound of the considered searching interval, which corroborates the renowned high crystallization kinetics of POM, even at quiescent conditions. The identified value is however greater than the one determined by Plummer and Kausch [83, 85] equal to 53. Finally, the heat transfer coefficient during packing was found equal to 500 W m$-{2}$ $^{\circ }\text {C}^{-1}$, which is a result prone to critic and discussion. In fact, this low value is typically used to describe the heat transfer condition under detachment between mold and part, which hardly occurs during the entire packaging phase. The heat transfer coefficient is a simulation parameter controlling the evolution of the temperature field in the polymer domain and therefore can be seen also as numerical artifact for tuning the crystallization kinetics and solidification in the simulation. For reference, in Moldflow^® the default value for the global heat transfer coefficient during packing is 2500 W m$-{2}$ $^{\circ }\text {C}^{-1}$. This result points out the need for implementing a local definition of the heat transfer coefficient, probably depending on the instantaneous local pressure, in the commercial codes of injection molding simulation.

4 Calibrated high-fidelity simulation with crystallization model

In the following, the high-fidelity simulation including the calibrated flow-induced crystallization model is compared with the default Moldflow^® simulation that does not take crystallization explicitly into account.

4.1 Pressure results

Fig. 18

The pressure signals for the V14 processing condition obtained using the simulation with the calibrated models in comparison to the ones obtained by the default Moldflow^® simulation along with the corresponding experimental results for this condition

Fig. 19

The pressure signals for the V27 processing condition obtained using the simulation with the calibrated models in comparison to the ones obtained by the default Moldflow^® simulation along with the corresponding experimental results for this condition

Fig. 20

The RMSE of the pressure predictions using the simulation with the calibrated models (optimization) and the one using the default Moldflow^® models (default) for each of the three processing conditions used to generate a surrogate model

As shown in Table 10, each surrogate model was generated using a fixing set of processing conditions and mimics one particular level of the experimental design of experiments. On the other hand, the pressure signal at the sensor located after the gate (P2) was used to identify the modeling parameters given in Table 13. Therefore, a natural way to assess the performance of the implemented models is to compare the predicted pressure signals by the standard Moldflow^® simulation (default simulation) with the high-fidelity simulation including the calibrated crystallization model (Simulation with calibrated crystallization model). Figures 17, 18, and 19 present the experimental and simulated pressure signals at the sensor locations P1, P2, and P3 (refer to Fig. 5) for the processing conditions V6, V14, and V27, respectively.

The high-fidelity simulation including the flow-induced crystallization model outperforms the default high-fidelity simulation for all processing conditions and improves particularly the pressure estimation at sensor locations P2 and P3. Interestingly, the proposed calibrated simulation is able to recreate the pressure plateau just after the switch-over as observed in Fig. 18 a and b at P1 and P2, respectively, which leads to a pressure signal delay at P3 as shown in Fig. 18c for the processing condition V14.

To quantify the improvement in pressure predictions, the normalized RMSE are calculated for the different simulation approaches and plotted in Fig. 20 a, b, and c for the processing conditions V6, V14, and V27, respectively. As expected, the prediction error decreases significantly by including the calibrated crystallization model along with the crystallization-dependent viscosity, PVT, and solidification models. Major improvements are noticeable at sensor locations P2 and P3 for the processing conditions V6 and V14, where the error decreases threefold at P2 and four times at P3. A more accurate estimation of the pressure field should in principle lead to higher accuracy when predicting part shrinkage and warpage. For the processing condition V27, the improvement of accuracy is less pronounced in comparison to the other conditions, but the error still decreased by approximately 5%.

Fig. 21

Averaged normalized RMSE of the pressure estimations at sensor location P2 using the high-fidelity simulation with the calibrated crystallization models and the default Moldflow^® simulation for all 27 experimental processing conditions used for injecting the half-length 3-mm thick part

Fig. 22

Comparison of pressure signals at position P2 for processing condition V7, V8, and V9: experimental, standard Moldflow^® simulation and Moldflow^® simulation with calibrated crystallization models

Fig. 23

The experimental fill results a in comparison to the ones predicted using the b default simulation and c simulation with the calibrated crystallization models

The previous comparison appears promising, but is biased as far as the implemented models were calibrated using the measured pressure signals for those processing conditions. Therefore, Fig. 21 presents the averaged normalized RMSE at P2 for all experimental processing conditions (all levels of the design of experiments) while using standard Moldflow^® models and Moldflow^® with the calibrated crystallization model.

According to Fig. 21, for the majority of the different DoE levels, the estimation error is decreased by more than half with respect to the default high-fidelity simulation. Some exceptions are for example the DoE levels V7, V8, and V9. To analyze the probable reasons behind this discrepancy, Fig. 22 presents the experimental pressure signal at sensor location P2 in comparison to the simulated ones (default and with calibrated crystallization models) for the mentioned DoE levels. Both simulations fail to recreate the experimental pressure signals in terms of maximum value and signal decay. In fact, all experimental signals exhibit an unusual inflection point around 10 s. This could be due to a partial remelting of the solidified material at the gate that would lead to an increased melt flux entering the cavity. Even though our proposed modeling includes the effect of remelting, our current calibrated simulation is not able to recreate such bump in pressure signal. This fact reveals that some model assumptions need to be revisited or that the models are not fully calibrated yet. Please notice however that in Fig. 22b, our proposed simulation shows an inflection point around 7 s. On the other hand, the high-fidelity simulation with calibrated crystallization models is able to predict with higher accuracy the maximal pressure before switch-over and also the pressure signal response just after changing to pressure control.

4.2 Predictions of short shots

As mentioned in Section 3.1.2, some experimental DoE levels did not produce a fully filled part, displaying what in the milieu is known as a short shot. Figure 23a summarizes the filling status of the 27 experimental DoE levels. One of the claimed advantages of implementing crystallization-dependent material models in injection molding simulation is the ability to predict if a mold cavity can be filled completely or not. The default Moldflow^® simulation is not able to predict the short shots as seen in Fig. 23b. However, our high-fidelity simulation with calibrated crystallization models makes it possible to predict most of these short shots as shown in Fig. 23c. In total, four out of the five short shots are identified along with one wrong prediction for V3 ($\approx 4$ mm of flow length not filled). For the V19 condition, the simulation showed a complete cavity filling, but experimentally, it shorted 7 mm before end of cavity. With our proposed models, the estimated flow length is accurate up to $\pm 15$ mm. For example, the actual parts produced with the processing conditions V10 shorted 10 mm before end of cavity whereas in the simulation the leftover unfilled length was around 5 mm.

5 Conclusion

We successfully implemented a flow-induced crystallization model coupled with viscosity, PVT, and solidification models in a commercial software for injection molding simulation (Autodesk^® Moldflow^® Insight). This modeling framework is applicable to any semi-crystalline thermoplastic polymer. For a given material, the identification of the material-dependent parameters requires initially standard experimental characterization of the quiescent crystallization (fundamentally based on DSC), which reduces the number of unknown parameters to 5. The lacking 5 unknown material-dependent parameters are calibrated using a surrogate model-based optimization taking as reference in-mold pressure sensor signals from an actual injection molding process. In this work, we applied the identification methodology to an industrial grade of an unreinforced polyoxymethylene (POM) homopolymer. This novel data-driven calibration method required the generation of a surrogate model (trained with 132 high-fidelity simulations) and a multi-objective optimization of the respective surrogate model. This last step needed only 15 iterations (less than 1 s) to solve the minimization problem for identifying the 5 material-dependent parameters of the flow-induced crystallization model under actual injection molding conditions. In sum, the effort of the proposed method seems quite lower in comparison with the costs (and time) associated with the extensive characterization used for identifying phenomenological crystallization models under laboratory equipment conditions.

The high-fidelity simulation with calibrated material-dependent model parameters produced a remarkable increase in the accuracy of the pressure field during injection molding. Concretely, the error in the estimation of the pressure signals at the sensor locations for a variety of processing conditions decreased by more than half when comparing the simulation including flow-induced crystallization modeling in front of the default simulation (without explicit crystallization modeling). This result highlights particularly the important role of the crystallization-viscosity coupling, which influences the pressure evolution during a mold filling. In addition, the simulation with crystallization modeling was able to predict 80% of the short shots observed in an actual injection molding DoE (5 from 27), whereas the default simulation predicted not one. This outcome underlines the importance of implementing a crystallization model in injection molding simulation as well as the use of a crystallization-dependent solidification criterion instead of today’s conventional no-flow temperature.

As an outlook into the topic of surrogate modeling, the approach presented in this work could be extended to emulate a full-time and space model of an injection molding cycle. Such emulator could be used to visualize and assess virtually an injection molding process in real time while varying input parameters, also paving the way to perform efficient uncertainty quantification. On the other hand, those models constitute an opening to the industrial deployment of digital twins in plastics processing.