Fluid Dynamic and Thermal Modeling of the Injection Molding Process in OpenFOAM$^{\textregistered }$

Abstract

For the description of the filling, packing, and cooling phases of the injection molding process, a simulation framework of a compressible two-phase fluid model with polymer-specific material models is established and validated with experimental results. With this approach, it is possible to describe the fluid dynamic, the rheological, and the thermal behavior of the material during the production process. The main focus of this work is on the description of the standard injection molding process of common thermoplastic materials for industrial application, with special focus on process relevant quantities, e.g., pressure, temperature, as these values are of utmost importance for understanding the underlying phenomena and comparing the results to experimentally measured values.

1 Introduction

Computational Fluid Dynamics (CFD) has been successfully utilized in a variety of fields in chemical and mechanical engineering, e.g., combustion simulation [1,2,3], high velocity flows [4,5,6], and the polymerization of thermoplastic polymer materials [7, 8]. For the understanding of the underlying physical phenomena, it is of great significance for the optimization of geometries and processes governed by local flow phenomena, as well as global processing conditions.

In the polymer processing industry, especially in injection molding, the reduction of the development time of tools and machines has been one of the most important issues in recent decades. A large variety of processed materials are available with varying properties. Most importantly, the material’s behavior differs from that of usual Newtonian fluids in the non-Newtonian behavior and the order of magnitude of the viscosity ($\approx$10–10000 Pas). The value can vary, depending on the shear rate, the temperature, and the pressure. With the addition of the compressibility of the liquid polymer, machines have to be able to handle considerable changes in processing conditions.

A progressive trend has been emerging during the recent years, in which computer-aided optimization has been proven to be one of the key steps in the development of machines and processes in injection molding. In simulations, the process can be visualized three-dimensionally, as opposed to experiments, in which processing conditions can only be monitored at certain locations [9, 10]. Additionally, all quantities (e.g., density, viscosity, shear rate, velocity, etc.) needed for the simulation can be evaluated, as opposed to only the pressure or temperature values in experiments.

For a serious and general optimization methodology of development, the correctness of the results has to be guaranteed for all possible geometries, processing conditions, and materials. OpenFOAM$^{\textregistered }$ offers an excellent foundation for the development of a tool for the description of polymer processing [7, 8], and especially the injection molding process [9, 10].

Due to the complexity and interdependency of quantities of fluid dynamic and thermal processes during the discontinuous process, it has to be guaranteed that a wide variety of phenomena can be modeled correctly. It is important to focus on dominant phenomena in the process in order to reduce calculation time for the industrial application.

With the proposed models, experimental validation shows promising agreement in both pressure and temperature during the entire discontinuous process of injection molding. The good agreement achieved promises the possibility of using OpenFOAM$^{\textregistered }$ as an intrinsic part of the development stage of injection molding tools and machines, as well as of a certain machine optimization simulation methodology of an intelligent, self-regulating injection molding machine.

2 Governing Equations

The physics of the injection molding process is governed by the standard compressible equations of Computational Fluid Dynamics (CFD), with the addition of material-specific models that describe the complex material behavior of polymers.

2.1 Fluid Dynamic Equations

For the description of the fluid movement, a set of coupled nonlinear partial differential equations is employed. The continuity and the momentum equations are solved in the compressible form [11].

$$\begin{aligned} \frac{\partial \rho }{\partial t}\,+\,\nabla \,\cdot \,\left( \rho \mathbf {u}\right) \,=\,0, \end{aligned}$$

(1)

(2)

In Eqs. (1) and (2), $\rho$ is the mass density of the fluid, t is the time, $\mathbf {u}$ is the vector of velocity, p is the pressure, $\tau$ is the stress tensor, and F is a certain source term (e.g., surface tension).

Equations (1) and (2) are not solved directly, but are rather transformed into a Laplacian equation of the pressure. This approach of velocity–pressure coupling is commonly used in CFD [12] and is based on the approach taken in the OpenFOAM$^{\textregistered }$ solver compressibleInterFoam [11, 13]. The discretization schemes utilized for all partial differential equations are of second-order accuracy.

2.2 Thermal Modeling

In order to describe the thermal phenomena of the process, convection, heat diffusion, and shear heating have to be considered in a certain energy equation.

$$\begin{aligned}&\frac{\partial \rho T}{\partial t}\,+\,\nabla \,\cdot \,\left( \rho \mathbf {u} T\right) \,= \nonumber \\&\,\varDelta \left( \overline{k}T\right) \,+\,\tau :\nabla \mathbf {u}\,\cdot \,\left( \frac{\alpha }{c_{\mathrm {v_l}}}\right) \,+\,\left[ \nabla \,\cdot \,\left( p\mathbf {u}\right) \right] \left( \frac{\alpha }{c_{\mathrm {v_l}}}\,+\,\frac{\left( 1\,-\,\alpha \right) }{c_{\mathrm {v_g}}}\right) , \end{aligned}$$

(3)

where T is the transported temperature, $c_v$ is the constant heat capacity, and $\overline{k}$ is the thermal conductivity of the fluid divided by the heat capacity and weighted by the phase fraction (see details in Sect. 2.3). In addition to heat convection and diffusion, two terms are included in the balance equation. The first term is a dissipation function modeling the rate of work irreversibly converted into heat. Here, the dominant contribution to injection modeling is coming from shear phenomena, and this term is commonly referred to as “shear heating.” The last term describes the rate of work for volume change [14].

Owing to the inexact surface of molds in injection molding, during processing, microscopic air entrapments can appear between the liquid polymer and the wall of the mold. Due to the heat resistance of the air, the temperature at the wall often shows a non-negligible jump [15]. Usually, the thickness of the gaseous layer is unknown. For this reason, the temperature distribution along the wall has to be modeled explicitly. This is similar to the modeling of turbulent phenomena near walls in CFD [16, 17]. Therefore, a certain heat transfer is assumed from the polymer melt into the wall with a certain heat transfer coefficient. This global “heat transfer coefficient” (HTC) models the unknown temperature distribution close to the wall, as well as the heat resistance of a possible thin gaseous layer. The coefficient is determined empirically, similar to the approach often taken in chemical engineering [18]. With this coefficient, a temperature gradient can be calculated with both a spatial distribution and a temporal evolution.

$$\begin{aligned} \nabla T = \frac{-HTC\left( T_{\mathrm {melt}}\,-\,T_{\mathrm {wall}}\right) }{k_{\mathrm {l}}}. \end{aligned}$$

(4)

Here, $T_{\text {melt}}$ represents the temperature value in the center of the first cell next to the wall, $T_{\text {wall}}$ the mold temperature, and $k_l$ the thermal conductivity of the liquid polymer.

2.3 Multiphase Modeling

Multiple phases (liquid polymer and gaseous air) are implemented using the Volume-of-Fluid (VOF) method [19,20,21], in which a scalar quantity $\alpha$ is used for the liquid phase fraction that is transported with the velocity $\mathbf {u}$. Here, $\alpha$ = 1 will denote the liquid polymer (index l) and $\alpha$ = 0 will represent the gaseous air (index g). Equation (6) describes the transport of $\alpha$.

$$\begin{aligned} \rho \,=\,\alpha \rho _{\mathrm {l}}\,\,+\,\left( 1\,-\,\alpha \right) \rho _{\mathrm {g}}, \end{aligned}$$

(5)

$$\begin{aligned} \frac{\partial \alpha }{\partial t}\,+\,\nabla \,\cdot \,\left( \alpha \mathbf {u}\right) \,+\,\nabla \,\cdot \,\left[ \alpha \left( 1\,-\,\alpha \right) \mathbf {u}_{r}\right] \,=\,S_{p}\,+\,S_{u}. \end{aligned}$$

(6)

Simple discretization schemes might create a region of a diffuse phase interface between $\alpha$ = 1 and $\alpha$ = 0. The surface compression term with the compression velocity $\mathbf {u}_{r}$ helps in maintaining a sharp liquid–gas interface (details can be found in [19, 21]). The terms $S_{u}$ and $S_{p}$ are source terms introduced by the compressibility of the material [11].

For calculation of the material properties, Eq. (7) is applied.

$$\begin{aligned} \left( \begin{array} {c} \rho \\ \nu \\ c_{\mathrm {v}} \\ \overline{k} \\ \end{array} \right) \,=\,\alpha \,\left( \begin{array} {c} \rho _{\mathrm {l}} \\ \nu _{\mathrm {l}} \\ c_{\mathrm {v_l}} \\ k_{\mathrm {l}}/c_{\mathrm {v_l}} \\ \end{array} \right) \,+\,(1-\alpha )\,\left( \begin{array} {c} \rho _{\mathrm {g}} \\ \nu _{\mathrm {g}} \\ c_{\mathrm {v_g}} \\ k_{\mathrm {g}}/c_{\mathrm {v_g}} \\ \end{array} \right) , \end{aligned}$$

(7)

where $\overline{k}$ is the weighted thermal conductivity divided by the respective specific heat capacity in Eq. (3). The dynamic viscosity of the fluid is calculated out of the density, as well as the kinematic viscosity, with $\mu \,=\,\alpha \rho _{\mathrm {l}}\nu _{\mathrm {l}}\,+\,(1-\alpha )\rho _{\mathrm {g}}\nu _{\mathrm {g}}$.

2.4 Material Models

Given the complex behavior of the material, polymer-specific models have to be employed in order to correctly describe the production process.

2.4.1 Viscosity—Cross WLF Model

The Cross WLF model combines the shear-thinning effect of polymers [22] with the William-Landel-Ferry (WLF) model [23] for the description of the temperature and pressure dependence of the viscous behavior of polymers.

$$\begin{aligned} \nu _{\mathrm {l}}(\dot{\gamma },T,p)\,=\,\frac{\nu _{\mathrm {0}}(T,p)\,}{1\,+\,\left( \frac{\nu _{\mathrm {0}}(T,p)\dot{\gamma }}{D_{\mathrm {4}}}\right) ^{1\,-\,n}}. \end{aligned}$$

(8)

Here, $D_{\mathrm {4}}$ defines the transition region from constant viscosity to the shear-thinning region, where the slope of the viscosity curve is given by the exponent n [22]. These constants are material-specific and have to be determined in rheological measurements. $\nu _{\mathrm {0}}(T,p)$ is the projected viscosity at zero shear rate ($\dot{\gamma }$ = 0) and is defined as

$$\begin{aligned} \nu _{\mathrm {0}}(T,p)\,=\,D_{\mathrm {1}}\,\text {exp}\left( \frac{\left( -A_{\mathrm {1}}\right) \,\cdot \,\left( T\,-\,D_{\mathrm {2}}\,-\,D_{\mathrm {3}}\cdot p\right) }{A_{\mathrm {2}}\,+\,T\,-\,D_{\mathrm {2}}\,-\,D_{\mathrm {3}}\cdot p}\right) . \end{aligned}$$

(9)

The constants $D_{\mathrm {1}}$, $D_{\mathrm {2}}$, $D_{\mathrm {3}}$, $A_{\mathrm {1}}$, and $A_{\mathrm {2}}$ are also material-specific and have to be determined in a manner similar to that of the constants in Eq. (8). The viscosity of air is considered to be constant.

2.4.2 Compressibility—Tait Model

The specific volume v of amorphous and semi-crystalline polymers behaves differently under the change of temperature and pressure [24]. In order to describe both material classes, the Tait model [25] is used, in which the dependence of the specific volume below a given transition temperature $T\,<T_{\mathrm {trans}}$

$$\begin{aligned} T_{\mathrm {trans}}\,=\,b_{\mathrm {5}}\,+\,b_{\mathrm {6}}\,p \end{aligned}$$

(10)

is given by

$$\begin{aligned} v_{\mathrm {polymer}}(p,T)\,=\,\left\{ v_{\mathrm {s}}(T)\,\left[ 1\,-\,C\,\text {ln}\left( 1\,+\,\frac{p}{B_{\mathrm {s}}(T)}\right) \right] \,+\,W_{\mathrm {s}}(T)\right\} , \end{aligned}$$

(11)

$$\begin{aligned} v_{\mathrm {s}}(T)\,=\,b_{\mathrm {1s}}\,+\,b_{\mathrm {2s}}\,\left( T\,-\,b_{\mathrm {5}}\right) , \end{aligned}$$

(12)

$$\begin{aligned} B_{\mathrm {s}}(T)\,=\,b_{\mathrm {3s}}\,\mathrm {exp}\left( -b_{\mathrm {4s}}\,\left( T\,-\,b_{\mathrm {5}}\right) \right) , \end{aligned}$$

(13)

$$\begin{aligned} W_{\mathrm {s}}(T)\,=\,b_{\mathrm {7}}\,\mathrm {exp}\left( b_{\mathrm {8}}\,\left( T\,-\,b_{\mathrm {5}}\right) -b_{\mathrm {9}}\,p\right) , \end{aligned}$$

(14)

and above the transition temperature, the dependence is defined by

$T\,\ge T_{\text {trans}}$

$$\begin{aligned} v_{\mathrm {polymer}}(p,T)\,=\,\left\{ v_{\mathrm {m}}(T)\,\left[ 1\,-\,C\,\text {ln}\left( 1\,+\,\frac{p}{B_{\mathrm {s}}(T)}\right) \right] \right\} , \end{aligned}$$

(15)

$$\begin{aligned} v_{\mathrm {s}}(T)\,=\,b_{\mathrm {1m}}\,+\,b_{\mathrm {2m}}\,\left( T\,-\,b_{\mathrm {5}}\right) , \end{aligned}$$

(16)

$$\begin{aligned} B_\mathrm {m}(T)\,=\,b_{\mathrm {3m}}\,\mathrm {exp}\left( -b_{\mathrm {4m}}\,\left( T\,-\,b_{\mathrm {5}}\right) \right) , \end{aligned}$$

(17)

where C = 0.0894. Here, all the constants are material-specific and have to be determined in, e.g., high-pressure-capillary experiments. With the specific volume, the density is calculated $\rho _{\mathrm {l}}$ = $1/v_{\mathrm {polymer}}(p,T)$. The air is considered to be an ideal gas.

2.5 Modeling Processing Steps of Injection Molding

Injection molding is a discontinuous process consisting of several steps. Depending on the definition of the starting point, the following main steps have to be considered [26, 27]:

• 1. Plastication: In the plasticating unit, a screw executes a rotational movement, thus moving solid polymer pellets in the direction of the mold, which has the shape of the final product. Due to friction and external heating, the polymer is melted.

• 2. Filling: The plasticating unit injects a preset amount of melt into the mold with a constant velocity. Simultaneously, the injected melt begins to cool down in the mold. Typically, a thin solid layer is formed immediately along the walls of the mold.

• 3. Packing: A constant holding pressure is applied by the screw of the plasticating unit to compensate for the volumetric shrinkage of the part during the cooling phase.

• 4. Cooling: The residual cooling time begins, the plasticating unit disconnects from the mold, and the screw prepares the next shot for the new cycle.

• 5. Part ejection: Once the part is sufficiently solidified and a predefined temperature is reached, the clamping unit opens and the mold ejects the part.

In this work, the injection process is considered, and thus the filling, packing, and cooling phases (steps 2–4) are considered as well. The processing conditions are changed between the filling and the packing phases from constant velocity to constant pressure. During the cooling phase, the thermal phenomena are dominant and fluid dynamic processes can be neglected [26, 27]. In order to model these changes within one simulation run, the boundary conditions have to be changed during the runtime.

For this, two switches are used in the simulations. The first switch from the filling phase to the packing phase is given by an integral volumetric value. Once the liquid phase fraction $\alpha$ reaches this value (typically 0.98–0.995), the simulation changes the boundary condition required by the packing phase (see Table 1). The second temporal switch gives the time of the end of the packing phase, when the simulation changes the conditions to those in the cooling phase. These switches mimic common settings of injection molding machines [26, 27].

Table 1 Boundary conditions of velocity and pressure during the phases of the process at the inlet

3 Experiments

3.1 Processing Conditions

Experiments with a standard hydraulic injection molding machine (Engel VC 200/50 tech with a screw diameter of 30 mm) are used to estimate the magnitude of errors arising due to assumptions made in the presented models (see Sect. 2). For this reason, typical processing conditions in injection molding are used.

Fig. 1

Geometry of the modeled domain with the locations of the sensors. The red region is filled with melt and is also heated to a constant processing temperature (here, 240 $^{\circ }$C)

• material: PP HD120MO,

• volume flux: 50 cm$^3$/s,

• melt and nozzle temperature: 240 $^{\circ }$C,

• tool temperature: 30 $^{\circ }$C,

• packing pressure: 338 bar,

• packing time: 26 s, and

• process time: 40 s.

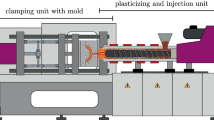
The parts considered in these analyses are two shouldered test bars, for which the mold, the distribution channel, the sprue, the nozzle, and the first part of the screw chamber are considered in the simulations (see Fig. 1). In front of the screw chamber, a sensor (Kistler 4021B) monitors the pressure in order to completely describe the pressure drop throughout the entire volume. A second pressure sensor (Kistler 6157BA) is located in the distribution channel so as to obtain the information about the pressure drop in the mold of the test bars. A symmetrically placed infrared temperature sensor (FOS MTS 408-IR-STS) measures the melt temperature.

3.2 Measurement Errors

It is important to know the experimental setup, particularly in order to quantify systematic errors. Both the pressure sensors and the infrared temperature sensors are calibrated for liquid polymers. However, a solid layer with a certain thickness arises during the injection process along the walls of the mold. This solid layer distorts and reduces both the pressure and the temperature signals. Figure 2 shows schematic sketches of the influence of the solid layer on the measurement signals. The force applied by the fluid pressure is redistributed by the solid layer in an undefined way, and similarly, the infrared radiation of the liquid polymer is modified by the solid layer distorting the temperature signal. In the experiments, a pressure reduction of up to 40 bars could be quantified at the end of the filling and the beginning of the packing phases and a temperature reduction of 15–20 $^{\circ }$C was observed during the cooling phase. These values are inaccurate and have to be analysed in more detail; however, they do give a first estimation during the evaluation of the experimental results.

Fig. 2

Schematic sketch of the influence of the solid layer on the measurement signals

4 Validation

4.1 Filling Phase

In Fig. 3, the pressure evolution at the two sensor locations in both the experiment and the simulation is shown. At the first sensor location in front of the screw chamber, the polymer is heated to a constant processing temperature. At this location, the polymer is completely in a liquid state, avoiding measurement issues given by a solid layer (see Sect. 3.2). Thus, a good quantitative agreement between simulation and experiment can be found (see Fig. 3). At the second pressure sensor, the thin solid layer distorts the experimental pressure signal, thus giving the impression of a bigger deviation between experiment and simulation. However, the deviation is given mostly by the described systematic error within the experimental setup. In order to quantify the deviations of these values, three process quantities are compared here.

Fig. 3

Time evolution of the pressure at two sensor locations in the experiment and simulation during the filling phase of the process

The first quantity is the location of the flow front. For that, the time of the first increase at the second pressure sensor is evaluated and referred to the filling phase.

$$\begin{aligned} \varDelta t_{\mathrm {fill}}\,=\,\frac{t_{\mathrm {s2,sim}}\,-\,t_{\mathrm {s2,exp}}}{t_{\mathrm {switchover}}\,-\,t_{\mathrm {start}}}\,=\,\frac{0.67\,\text {s}\,-\,0.66\,\text {s}}{1.16\,\text {s}\,-\,0.5\,\text {s}}\,=\,1.5\%. \end{aligned}$$

(18)

The second quantity is the maximum pressure in front of the screw chamber at the first sensor.

$$\begin{aligned} \varDelta p_{\mathrm {max}}\,=\,\frac{p_{\mathrm {s1,sim}}\,-\,p_{\mathrm {s1,exp}}}{p_{\mathrm {max}}\,-\,p_{\mathrm {start}}}\,=\,\frac{398.7\,\text {bar}\,-\,396.3\,\text {bar}}{396.3\,\text {bar}\,-\,1\,\text {bar}}\,=\,0.6\%. \end{aligned}$$

(19)

The last quantity in the filling phase is the maximum pressure in the cavity at the second pressure sensor.

$$\begin{aligned} \varDelta p_{\mathrm {cav}}\,=\,\frac{p_{\mathrm {s2,sim}}\,-\,p_{\mathrm {s2,exp}}}{p_{\mathrm {max}}\,-\,p_{\mathrm {start}}}\,=\,\frac{199.8\,\text {bar}\,-\,147.7\,\text {bar}}{396.3\,\text {bar}\,-\,1\,\text {bar}}\,=\,13.2\%. \end{aligned}$$

(20)

Considering this, the simulation calculates reasonable values for important values of the process (deviation $\le$15%).

4.2 Packing Phase

During the packing phase, the pressure is kept at a constant level in the screw chamber, but the pressure distribution in the mold changes, due to the cooling of the material and the change in viscosity (see Fig. 4). Here, the deviation between experiment and simulation is increasing, due to the fact that the thickness of the solid layer increases with time. The change of the pressure slope given by the freezing of the material at this point is seen in both the experiment and the simulation at approximately 20–22 s. Although the quantitative validation of the pressure in this phase cannot be done due to the previously mentioned insufficiently quantified inaccuracies in the experiments, other process parameters, like the freezing of the material, can be derived out of the change of the slope of pressure.

Fig. 4

Time evolution of the pressure at two sensor locations in the experiment and simulation during the filling and packing phases of the process

In order to quantify the deviation between experiment and simulation, the time of freezing is evaluated. For this, the point of time when the first derivative of the pressure curves changes abruptly is utilized.

$$\begin{aligned} \varDelta t_{\mathrm {freeze}}\,=\,\frac{t_{\mathrm {fr,sim}}\,-\,t_{\mathrm {fr,exp}}}{t_{\mathrm {filling+packing}}\,-\,t_{\mathrm {start}}}\,=\,\frac{20.6\,\text {s}\,-\,21.3\,\text {s}}{26\,\text {s}\,-\,0.5\,\text {s}}\,=\,-2.7\%. \end{aligned}$$

(21)

4.3 Cooling Phase

During the process, the temperature is reduced from processing temperature to values at which the part can be ejected (see Fig. 5). Here, the temporal evolution of the temperature in the simulation and the experiment is very similar. A certain deviation can be found during the cooling phase of approximately 20 $^{\circ }$C, mostly arising from the fact, that the sensor is calibrated for liquid polymers and the solid thin layer distorts the signal (see Sect. 3.2).

Fig. 5

Time evolution of the temperature in the experiment and simulation during the entire process

Here, the temperature after 40 s is evaluated in order to quantify the deviation.

$$\begin{aligned} \varDelta T_{\mathrm {end}}\,=\,\frac{T_{\mathrm {end,sim}}\,-\,T_{\mathrm {end,exp}}}{T_{\mathrm {max}}\,-\,T_{\mathrm {tool}}}\,=\,\frac{61.5\,^{\circ }\text {C}\,\,-\,43.7\,^{\circ }\text {C}}{275\,^{\circ }\text {C}\,-\,30\,^{\circ }\text {C}}\,=\,7.3\%. \end{aligned}$$

(22)

4.4 Parameter study

In order to check for consistency of the quality of the results, the volume flux is changed during the process (5, 30, 50, 70, 90 cm$^3$/s). With this, the order of magnitude of the deviation between experiment and simulation should not change.

Table 2 Deviations (in %) between experiment and simulation with different volume flux values

Table 2 shows the deviations with regard to the location of the flow front $\varDelta t_{\mathrm {fill}}$, the maximum pressure $\varDelta p_{\mathrm {max}}$, the mold pressure $\varDelta p_{\mathrm {cav}}$, the time of freezing $\varDelta t_{\mathrm {freeze}}$, and the temperature at the end of the process $T_{\mathrm {end}}$. Independently from the changes in processing conditions, the same order of error is found supporting the idea that the dominant deviations are arising systematically in the experiments. Simulation results seem to correctly describe important quantities for processing.

5 Conclusion

The suggested approach of modeling the injection molding process with the compressible form of the continuity, the Navier–Stokes and the energy equations with polymer-specific material models, as well as the dynamic change of boundary conditions during runtime, promise a good agreement between simulations and experiments. However, it is of utmost importance to understand which quantities can be compared and at which points possible systematic errors are occurring.

With this, it is possible to analyze geometries, as well as materials, and use the implemented collection of utilities for the optimization of the injection molding process.