1 Introduction

With the continuous advancement of automation manufacturing technology, high-precision and high-efficiency curve processing has become increasingly important. In conventional linear interpolation and circular arc interpolation methods, the frequent changes in motion direction and significant fluctuations in feedrate result in limited machining efficiency and precision. Non-uniform rational B-spline (NURBS) curve interpolation technology, characterized by parametrization, smoothness, and high degrees of freedom, is considered an effective approach for achieving high-precision and high-efficiency machining [1]. Furthermore, NURBS interpolation technology exhibits exceptional flexibility and compatibility, allowing for seamless integration with various computer-aided design/computer-aided manufacturing (CAD/CAM) systems and machining equipment. This technology can satisfy the processing requirements of different devices and systems [2]. In practical applications, devising an appropriate feedrate profile for the NURBS interpolation process, also known as feedrate scheduling, has become crucial to ensure highly efficient and precise interpolation for machine tools or robots.

Feedrate scheduling, also known as feedrate profiling, is a technique used to adjust the feedrate of machine tools or robotic arms based on the curvature of the interpolated curve. Its objective is to ensure optimal efficiency, smoothness, and precision of motion. Traditional methods like uniform feedrate interpolation and uniform increment interpolation often overlook curvature, leading to significant chord errors at breakpoints and regions with high curvature [3,4,5]. Chord error, referring to the distance between the interpolated curve and the parametric curve, serves as a fundamental consideration in feedrate scheduling and exhibits a positive correlation with feedrate and curvature [6].

Variable-feedrate interpolation is an effective approach to balancing efficiency and precision. It involves limiting the feedrate based on the chord error during the machining process. Two notable methods, the adaptive feedrate method proposed by Yeh et al. and the curvature-based feedrate method proposed by Xu et al., explore the relationships among chord error, curvature, and feedrate [7, 8]. These methods enable variable feedrate machining and substantially reduce chord errors.

However, these methods may fall short when applied to NURBS curves of high curvature and complexity, due to inadequate consideration for feedrate variations. Such an oversight can result in excessive and abrupt acceleration and jerk, which might exceed the machine tool’s capabilities. Consequently, this can detrimentally affect the stability of the machining process and compromise the quality of the end product [9]. Additionally, maintaining a constant low feedrate in curvature-sensitive areas can effectively limit chord errors. However, it may also affect the feedrate in adjacent regions with lower curvature [10, 11]. Thus, a careful balance must be struck to ensure optimal feedrate profiles that minimize chord errors while considering the machine’s capabilities and the complexity of the NURBS curves being interpolated [12].

Traditional point control algorithms, notably the trapezoidal and exponential models, are known for their efficiency. However, their acceleration transitions tend to be abrupt, leading to considerable vibrations and shocks [13, 14]. These issues can compromise the machining process and pose obstacles in achieving precise control.

To address these issues, various methodologies employing polynomial equations have been proposed to construct feedrate profiles. Specifically, Leng and Liu et al. have utilized cubic polynomials for this purpose. While their methods ensure a linear jerk variation, it nevertheless results in flexible impacts on machine tools due to abrupt jerk changes in specific regions [15, 16]. Li et al. utilize a quartic polynomial to construct feedrate profiles, with jerk represented as a quadratic function of time, ensuring jerk continuity [17]. However, the methods proposed by Leng, Liu, and Li do not maintain maximum acceleration and jerk, resulting in lower efficiency.

At present, the most mature and effective feedrate scheduling algorithm is the S-shaped ACC/DEC planning algorithm, which has proven successful in avoiding sudden changes in feedrate and acceleration while maintaining high efficiency. A complete S-shaped ACC/DEC planning comprises seven phases: acc-acceleration phase, uniform acceleration phase, dec-acceleration phase, uniform feedrate phase, acc-deceleration phase, uniform deceleration phase, and dec-deceleration phase [18,19,20,21]. By following these phases, S-shaped ACC/DEC planning algorithms generate smooth and continuous feedrate profiles in an S shape, while ensuring continuous trapezoidal acceleration profiles and adherence to equipment requirements regarding feedrate, acceleration, and jerk.

However, it should be noted that in these feedrate scheduling algorithms, jerk remains discontinuous and subject to sudden changes. Discontinuous jerk can result in flexible vibrations that may negatively impact machining quality and reduce the lifespan of mechanical components. Thus, despite the advantages of S-shaped ACC/DEC planning algorithms in terms of feedrate and acceleration, the issue of discontinuous jerk remains a concern.

To enhance the smoothness of feedrate and acceleration profiles, researchers have proposed jerk-continuous methods for NURBS interpolation. Two main approaches have been employed. The first approach involves adding phases to the jerk variation process to ensure jerk continuity. The second approach utilizes trigonometric functions to construct smooth and continuous jerk functions. These methods aim to mitigate the issues associated with discontinuous jerk and further improve the stability and precision of the feedrate scheduling process.

Ji et al. have introduced a constant rate of jerk change during the jerk variation phases to ensure jerk continuity [22]. Ni et al. have used trigonometric functions to control the jerk variation process, resulting in a smooth and continuous jerk profile [23]. However, these methods involve a complete acceleration-deceleration process containing 15 phases and seven variables, significantly increasing the computational complexity in feedrate scheduling.

Nie et al. have employed a sine function to construct jerk functions, while Kombarov and Sun et al. have used a double sine function for the same purpose [24,25,26]. Hu et al. employed cosine functions for the same purpose [27]. The multi-order invertibility of trigonometric functions ensures that the acceleration and feedrate functions derived from using trigonometric functions to construct jerk profiles will remain continuously invertible, thereby supporting stable processing. However, incorporating trigonometric functions in real-time interpolation can present challenges.

The direct and precise calculation of trigonometric functions is impractical, prompting the adoption of approximation methods that balance accuracy with computational efficiency. To realize this equilibrium, techniques including iterative methods, Taylor series expansions, polynomial fitting, table look-up methods, and CORDIC algorithms are applied in trigonometric function computations. Additionally, mirroring the constraints in Li et al.’s method, jerk profiles constructed using trigonometric functions encounter difficulties in preserving their maximum values. This limitation can potentially lead to diminished machining efficiency.

Although various feedrate scheduling algorithms have been developed, achieving smooth and continuous jerk profiles with high efficiency and simple calculations remains a challenge. Effective feedrate scheduling algorithms must take into account various constraints, such as limiting chord errors to achieve high-precision machining, ensuring smooth and continuous feedrate-acceleration-jerk curves for vibration reduction, enhancing feedrate curves to boost machining efficiency, and avoiding complex calculations to improve scheduling efficiency and meet the requirements of real-time interpolation.

In addition, the existing NURBS interpolation feedrate scheduling algorithms have limitations in the sub-curve splitting strategy. Current S-shaped acceleration and deceleration planning algorithms can only handle curves with at most one acceleration and one deceleration. As a result, feedrate scheduling for NURBS curve interpolation requires splitting the curve into multiple sub-curves. Critical points with high curvature are typically chosen as the basis for curve segmentation. However, this strategy may result in an excessive number of sub-curves for complex curves, leading to frequent acceleration and deceleration during machining. This can negatively impact the accuracy of the machining process.

To address these challenges, this study introduces a novel feedrate scheduling algorithm for NURBS curve interpolation. The algorithm utilizes quartic polynomials to construct jerk profiles, enabling the generation of smooth and continuous feedrate, acceleration, and jerk profiles during the machining process. Additionally, a sub-curve adaptive merging strategy is proposed to reduce the number of sub-curves in the feedrate scheduling. This strategy aims to minimize the frequency of acceleration and deceleration, thereby improving both machining efficiency and quality.

2 Feedrate scheduling algorithm

2.1 The proposed jerk function

The S-shaped ACC/DEC planning algorithm based on trigonometric functions has the potential to generate smooth and continuous jerk-acceleration-feedrate profiles. However, due to the complex calculations required and the low machining efficiency, this approach may face challenges in achieving high-precision and high-efficiency machining.

Figure 1a illustrates the jerk profile of the acc-acceleration phase generated by the trigonometric function. To avoid complex trigonometric operations and improve efficiency, this study adopts quartic polynomials to construct a superior jerk profile.

Fig. 1
figure 1

Jerk profile constructed by trigonometric function and quartic polynomials

Full size image

As illustrated in Fig. 1a, a superior jerk profile should include the following characteristics:

  1. (a)

    Jerk is 0 when t = 0;

  2. (b)

    Jerk reaches the limit when t = T/2;

  3. (c)

    Jerk is 0 when t = T.

The expression for the jerk constructed with a quartic polynomial can be expressed as:

$$J(t)={J}_{\textrm{max}}\left(\frac{a}{T^4}{t}^4+\frac{b}{T^3}{t}^3+\frac{c}{T^2}{t}^2+\frac{d}{T}t\right)$$
(1)

Based on the above-mentioned characteristics, the parameters a, b, and c can be represented by d. The variation of the jerk profile with d is illustrated in Fig. 1b. As depicted in Fig. 1b, the jerk change rate increases with d, indicating higher machine responsiveness and efficiency. When the value of d exceeds 4, the jerk profiles constructed using quartic polynomials outperform the jerk profile generated using the trigonometric function. Nonetheless, an excessively large d may result in an M-shaped jerk profile that exceeds the jerk limit, which is not acceptable. To prevent the occurrence of the M-shaped profile, the second-order derivative of jerk should not be greater than zero. Satisfying the above conditions, the optimal value of d is 8, and the corresponding expression for jerk is obtained as follows:

$$J(t)=8{J}_{\textrm{max}}\left(-\frac{2}{T^4}{t}^4+\frac{4}{T^3}{t}^3-\frac{3}{T^2}{t}^2+\frac{1}{T}t\right)$$
(2)

The segmental jerk expression constructed by quartic polynomials can be obtained based on the symmetry of the S-shaped ACC/DEC planning algorithm, as shown in Eq. (3).

The proposed S-shaped ACC/DEC planning algorithm provides smooth and continuous jerk-acceleration-feedrate-displacement profiles, as demonstrated in Fig. 2. Within a single jerk cycle, the jerk exceeds 90% of the maximum allowable jerk for more than 56% of the time, compared to 29% in the trigonometric-based jerk, indicating a high level of support for efficient machining.

Fig. 2
figure 2

The proposed jerk-continuous ACC/DEC profile

Full size image
$$J(t)=\left\{\begin{array}{cc}8{J}_{\textrm{max}}\left(-\frac{2{\tau}_1^4}{T_1^4}+\frac{4{\tau}_1^3}{T_1^3}-\frac{3{\tau}_1^2}{T_1^2}+\frac{\tau_1}{T_1}\right)& 0\le t\le {t}_1\\ {}0& {t}_1\le t\le {t}_2\\ {}8{J}_{\textrm{max}}\left(\frac{2{\tau}_3^4}{T_3^4}-\frac{4{\tau}_3^3}{T_3^3}+\frac{3{\tau}_3^2}{T_3^2}-\frac{\tau_3}{T_3}\right)& {t}_2\le t\le {t}_3\\ {}0& {t}_3\le t\le {t}_4\\ {}8{J}_{\textrm{max}}\left(\frac{2{\tau}_5^4}{T_5^4}-\frac{4{\tau}_5^3}{T_5^3}+\frac{3{\tau}_5^2}{T_5^2}-\frac{\tau_5}{T_5}\right)& {t}_4\le t\le {t}_5\\ {}0& {t}_5\le t\le {t}_6\\ {}8{J}_{\textrm{max}}\left(-\frac{2{\tau}_7^4}{T_7^4}+\frac{4{\tau}_7^3}{T_7^3}-\frac{3{\tau}_7^2}{T_7^2}+\frac{\tau_7}{T_7}\right)& {t}_6\le t\le {t}_7\end{array}\right.$$
(3)

2.2 Feedrate scheduling

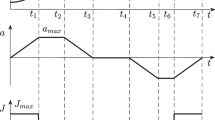
Figure 2 contains the complete seven phases in the S-shaped ACC/DEC. However, effective feedrate scheduling for a curve requires the identification of these motion phases within the actual movement and the determination of the duration of each phase. This is contingent upon the length of the curve ( S ), as well as its initial and terminal feedrates (vs and ve).

Figure 3 depicts feedrate scheduling process flow and the feedrate, acceleration, and jerk profiles for various cases. The motions are classified into eleven modes based on S, vs and ve. The motion phases inherent to each mode are presented in Table 1. Herein, the symbol “√” unequivocally confirms the existence of a phase, “×” definitively negates the presence of a phase, whereas “o” denotes the phase’s existence as indeterminable. Please refer to Table 1 for additional insights.

Fig. 3
figure 3

Feedrate scheduling flow

Full size image
Table 1 Motion phases included in different motion modes
Full size table

Drawing on the depiction of motion phases in Fig. 3 and Table 1, the subsequent sections offer a detailed description of the method for determining the included movement phases and the corresponding durations, base on S, vs and ve.

  1. 1)

    Step 1: Determine whether the machine’s maximum feedrate limit (Vmax) can be reached.

  • Assumption A: Vmax can be reached. The duration of each motion phase can be obtained from Eqs. (4) to (5). It should be noted that in the S-shaped ACC/DEC, T3 = T1, and T7 = T5. At the same time, the minimum displacement required to reach the maximum feedrate limit Vmax can be calculated by Eq. (8).

$${T}_1=\left\{\begin{array}{cc}\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}& {V}_{\textrm{max}}\ge {v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\\ {}\sqrt{\frac{5\left({V}_{\textrm{max}}-{v}_s\right)}{4{J}_{\textrm{max}}}}& {V}_{\textrm{max}}<{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\end{array}\right.$$
(4)
$${T}_2=\left\{\begin{array}{cc}\frac{V_{\textrm{max}}-{v}_s-\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}}{A_{\textrm{max}}}& {V}_{\textrm{max}}\ge {v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\\ {}0& {V}_{\textrm{max}}<{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\end{array}\right.$$
(5)
$${T}_5=\left\{\begin{array}{cc}\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}& {V}_{\textrm{max}}\ge {v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\\ {}\sqrt{\frac{5\left({V}_{\textrm{max}}-{v}_e\right)}{4{J}_{\textrm{max}}}}& {V}_{\textrm{max}}<{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\end{array}\right.$$
(6)
$${T}_6=\left\{\begin{array}{cc}\frac{V_{\textrm{max}}-{v}_e-\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}}{A_{\textrm{max}}}& {V}_{\textrm{max}}\ge {v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\\ {}0& {V}_{\textrm{max}}<{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\end{array}\right.$$
(7)
$${S}_1=\frac{1}{2}\left(\left({V}_{\textrm{max}}+{v}_s\right)\left(2{T}_1+{T}_2\right)+\left({v}_e+{V}_{\textrm{max}}\right)\left(2{T}_5+{T}_6\right)\right)$$
(8)

The feedrate scheduling can be divided into two cases based on S and S1.

  1. a.

    S ≥ S1 (M1): Vmax can be reached and there exists a uniform feedrate phase; the corresponding duration (T4) is given as following:

$${T}_4=\frac{S-{S}_1}{V_{\textrm{max}}}$$
(9)
  1. b.

    S < S1: Vmax can not be reached, and there is no uniform feedrate phase, T4 = 0. Accordingly, Vmax cannot be used to calculate the duration of each phase, and the maximum achievable feedrate and the duration of each phase need to be recalculated. The discussion can be divided into two cases based on vs and ve. When ve > vs, the overall acceleration process is presented; otherwise, the deceleration process is presented. However, the feedrate scheduling algorithms are almost identical for both cases, so only ve > vs is presented.

When ve > vs, the acceleration phase is necessarily included, and it is uncertain whether the deceleration phase is included.

  1. 2)

    Step 2: Determine whether S is sufficient for achieving acceleration.

  • Assumption B: S is sufficient for achieving acceleration and there is no deceleration phase. T1 and T2 are planned as follows:

$${T}_1=\left\{\begin{array}{cc}\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}& {v}_e\ge {v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\\ {}\sqrt{\frac{5\left({v}_e-{v}_s\right)}{4{J}_{\textrm{max}}}}& {v}_e<{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\end{array}\right.$$
(10)
$${T}_2=\left\{\begin{array}{cc}\frac{v_e-{v}_s-\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}}{A_{\textrm{max}}}& {v}_e\ge {v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\\ {}0& {v}_e<{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\end{array}\right.$$
(11)

The corresponding accelerated phase displacement can be derived as:

$${S}_2=\frac{1}{2}\left({v}_s+{v}_e\right)\left(2{T}_1+{T}_2\right)$$
(12)

The feedrate scheduling can be divided into three cases based on S and S2.

  1. a.

    S = S2 (M2): S is sufficient for achieving acceleration, and there is no deceleration phase. The obtained T1 and T2 can be adopted.

  2. b.

    S < S2 (M3): S is insufficient for achieving acceleration, and the feedrate scheduling cannot be implemented with the constructed S-shaped ACC/DEC algorithm.

  3. c.

    S > S2: The deceleration phase is included, and T1 and T2 need to be recalculated.

Case c is still uncertain and can be divided again based on whether the maximum deceleration can be achieved.

  1. 3)

    Step 3: Determine whether the maximum deceleration can be achieved.

  • Assumption C: The maximum deceleration can be obtained, but there is no uniform deceleration phase. The maximum feedrate (vf) that can be achieved is as follows:

$${v}_f={v}_e+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}$$
(13)

The uniform acceleration phase is necessarily present. The duration of each phase can be obtained by Eq. (14).

$$\left\{\begin{array}{c}{T}_1=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_2=\frac{v_e+\frac{5{A}_{\max^2}}{4{J}_{\textrm{max}}}-{v}_s}{A_{\textrm{max}}}-\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_5=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_6=0\end{array}\right.$$
(14)

The corresponding displacement is calculated by Eq. (15).

$${S}_3=\frac{1}{2}\left(\left({v}_s+{v}_f\right)\left(2{T}_1+{T}_2\right)+\left({v}_e+{v}_f\right)\left(2{T}_5+{T}_6\right)\right)$$
(15)

Based on S and S3, the feedrate scheduling can be divided into two cases.

  1. a.

    S ≥ S3 (M4): The maximum deceleration can be reached and a uniform deceleration phase may occur, and the duration of each phase needs to be calculated. The uniform acceleration phase necessarily exists when there is a uniform deceleration phase. The maximum feedrate that can be achieved is undetermined and needs to be calculated. Suppose the maximum feedrate is vf, Eq. (16) can be obtained.

$$\left\{\begin{array}{c}{T}_1=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_2=\frac{v_f-{v}_s}{A_{\textrm{max}}}-\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_5=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_6=\frac{v_f-{v}_e}{A_{\textrm{max}}}-\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\end{array}\right.$$
(16)

The maximum feedrate vf, T1, T2, T5, and T6 can be obtained by solving Eqs. (15) and (16). The solution of vf can be solved by Newton’s iterative or dichotomous method, and in this study, the dichotomous method is used to solve vf.

  1. b.

    S < S3: The maximum deceleration cannot be reached, and the feedrate profile needs to be rescheduled. Whether the maximum acceleration can be achieved needs to be determined.

  1. 4)

    Step 4: Determine whether the maximum acceleration can be achieved.

  • Assumption D: The maximum acceleration can be reached, but there is no uniform acceleration phase. The duration of each phase can be calculated by Eq. (17).

$$\left\{\begin{array}{c}{T}_1=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_2=0\\ {}{T}_5=\sqrt{\frac{5\mid {v}_s-{v}_e+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\mid }{4{J}_{\textrm{max}}}}\\ {}{T}_6=0\end{array}\right.$$
(17)

And the corresponding displacement is calculated by Eq. (18).

$${S}_4={T}_1\left(2{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\right)+{T}_5\left({v}_e+{v}_s+\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}\right)$$
(18)

Based on S and S4, the feedrate scheduling can be divided into two cases.

  1. a.

    S ≥ S4 (M5): The maximum acceleration can be reached and a uniform acceleration phase may occur, and the duration of each phase needs to be calculated. The maximum feedrate that can be achieved is undetermined and needs to be calculated. Suppose that the maximum feedrate is vf, Eq. (19) can be obtained.

$$\left\{\begin{array}{c}{T}_1=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_2=\frac{v_f-{v}_s}{A_{\textrm{max}}}-\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_5=\sqrt{\frac{5\left({v}_f-{v}_e\right)}{4{J}_{\textrm{max}}}}\\ {}{T}_6=0\end{array}\right.$$
(19)

The maximum feedrate vf, T1, T2, and T5 can be obtained by solving Eqs. (19) and (15).

  1. b.

    S < S4 (M6): The maximum acceleration and the maximum deceleration can not be reached and the duration of each phase needs to be rescheduled. Suppose that the maximum feedrate is vf, Eq. (20) can be obtained.

$$\left\{\begin{array}{c}{T}_1=\sqrt{\frac{5\left({v}_f-{v}_s\right)}{4{J}_{\textrm{max}}}}\\ {}{T}_2=0\\ {}{T}_5=\sqrt{\frac{5\left({v}_f-{v}_e\right)}{4{J}_{\textrm{max}}}}\\ {}{T}_6=0\end{array}\right.$$
(20)

The maximum feedrate vf, T1, T2, and T5 can be obtained by solving Eqs. (20) and (15).

Employing the same methodology, the identification of motion modes M7 through M11 can be accomplished. However, given the insufficient length of the curves in M3 and M8 to achieve acceleration or deceleration, adjustments to the initial or final feedrate are necessitated for the computation of each phase’s duration.

2.3 Adjustment of v e and v s

For M3, adjusting the feedrate within the specified displacement distance can be accomplished by increasing vs or decreasing ve. However, for NURBS curve feedrate scheduling, increasing the feedrate is less desirable, as it may compromise the machining quality. Therefore, it is advisable to suitably reduce ve for M3, and correspondingly, to decrease vs for M8. The feedrate adjustment process for M8 mirrors that for M3; hence, only the adjustment of ve in M3 is presented.

  • Assumption E: The maximum acceleration can be reached, but there is no uniform acceleration phase. The original ve is discarded, and the new end feedrate limit is noted as ve, c. Equation (21) needs to be satisfied.

$$\left\{\begin{array}{c}{T}_1=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_2=0\\ {}{v}_{e,c}={v}_s+\frac{5{A}_{\textrm{max}}^2}{J_{\textrm{max}}}\\ {}{S}_{21}={T}_1\left({v}_s+{v}_{e,c}\right)\end{array}\right.$$
(21)

Based on S and S21, the feedrate limit correction can be divided into two cases.

  1. a.

    S < S21: The maximum acceleration cannot be reached, and T1 needs to be recalculated. Assuming that the corrected end feedrate limit is ve, c, Eq. (22) is obtained.

$$\left\{\begin{array}{c}{T}_1=\sqrt{\frac{5\left({v}_{e,c}-{v}_s\right)}{4{J}_{\textrm{max}}}}\\ {}S={T}_1\left({v}_s+{v}_{e,c}\right)\end{array}\right.$$
(22)

Solving for Eq. (22) gives the corresponding T1, T2, and ve, c, and then ve needs to be replaced by ve, c.

  1. b.

    S ≥ S21: The maximum acceleration can be reached, and T1 and T2 need to be recalculated. Assuming that the corrected end feedrate limit is ve, c, Eq. (23) can be obtained.

Solving for Eq. (23) gives the corresponding T1, T2, and ve, c, and then ve needs to be replaced by ve, c.

$$\left\{\begin{array}{c}{T}_1=\frac{5{A}_{\textrm{max}}}{4{J}_{\textrm{max}}}\\ {}{T}_2=\frac{v_{e,c}-{v}_s-\frac{5{A}_{\textrm{max}}^2}{4{J}_{\textrm{max}}}}{A_{\textrm{max}}}\\ {}S=\frac{1}{2}\left({v}_s+{v}_{e,c}\right)\left(2{T}_1+{T}_2\right)\end{array}\right.$$
(23)

3 Feedrate scheduling of NURBS interpolation

3.1 Limitations of interpolation feedrate

3.1.1 Chord error

Machining accuracy stands as a principal constraint on the interpolation feedrate of a NURBS curve. Within the NURBS curve interpolation procedure, two predominant categories of deviations can be identified: radial error and chord error. The former is defined as the orthogonal distance between the interpolation point and the parameter curve, primarily attributed to the rounding inaccuracies of computing systems. However, given the evolution of high-precision processors, radial error has largely been mitigated and no longer presents a significant concern in modern applications.

The chord error, which signifies the Hausdorff distance between the actual and theoretical machining paths, is the main factor that affects machining accuracy. Nevertheless, accurately calculating the Hausdorff distance presents considerable challenges, rendering the circular arc approximation method a currently more widespread approach for estimating the chord height error.

Figure 4 demonstrates the computation of the chord error utilizing the circular arc approximation method [8]. Herein, the machining curve within one interpolation cycle is approximated as an arc with a radius ρi. ρi corresponds to the radius of curvature of the curve at parameter ui, which can be calculated by Eq. (24).

Fig. 4
figure 4

Calculation of chord error

Full size image
$${\rho}_i=\rho \left({u}_i\right)=\frac{1}{\kappa \left({u}_i\right)}=\frac{{\left\Vert {C}^{\prime}\left({u}_i\right)\right\Vert}^3}{\left\Vert {C}^{\prime}\left({u}_i\right)\times {C}^{\prime \prime}\left({u}_i\right)\right\Vert }$$
(24)

Construct the chord \(\overline{C\left({u}_i\right)\overline{C}\left({u}_{i+1}\right)}\) on the arc with radius ρi and make \(\left\Vert \overline{C\left({u}_i\right)\overline{C}\left({u}_{i+1}\right)}\right\Vert ={v}_i{T}_s\), where vi is the feedrate at the parameter u and Ts is the interpolation period. The chord error δi of the NURBS curve can be approximated by the chord error corresponding to the chord of length viTs on the arc, which can be expressed by Eq. (25).

$${\delta}_i={\rho}_i-\sqrt{\rho_i^2-{\left(\frac{v_i{T}_s}{2}\right)}^2}$$
(25)

As delineated by Eq. (25), a larger feedrate vi yields a significant chord error for a fixed interpolation period. Given a constraint on the maximum chord error δmax, the feedrate’s upper limit at the interpolation point C(ui) can be articulated by Eq. (26).

$${F}_c={v}_{i,\lim \delta }=\frac{2}{T_s}\sqrt{\rho_i^2-{\left({\rho}_i-{\delta}_{\textrm{max}}\right)}^2}$$
(26)

3.1.2 Dynamic performance of equipment

In addition to considering chord error, the limitation of the maximum feedrate, normal acceleration, and jerk of the machine should also be taken into account during NURBS curve interpolation.

With the maximum normal acceleration limited Ac, max, the maximum feedrate at the parameter ui can be expressed by Eq. (27) [28].

$${F}_a={V}_c\left({u}_i\right)=\sqrt{\rho_i{A}_{c,\max }}$$
(27)

In addition to changes in feedrate magnitude and direction, the centripetal acceleration also changes during NURBS curve processing, causing changes in jerk. Jerk also needs to be limited.

With the limitation of maximum jerk to Jmax, the maximum feedrate under the jerk limit can be expressed using Eq. (28) [28].

$${F}_j={V}_j\left({u}_i\right)=\sqrt[3]{\rho_i^2{J}_{\textrm{max}}}$$
(28)

In addition, it is crucial to ensure that the feedrate during machining does not exceed the predetermined maximum feedrate limit, denoted as Vmax.

In summary, the maximum feedrate achievable at the parameter ui on the NURBS curve, while considering the limitations of chord error and machine dynamics can be expressed using Eq. (29).

The feedrate limit curve ui-Flim can be constructed by calculating the maximum feedrate corresponding to any parameter ui based on Eq. (29). The feedrate limit curve is an important basis for subsequent curve splitting and feedrate scheduling.

$${F}_{\textrm{lim}}={v}_{i,\lim }=\min \left(\frac{2}{T_s}\sqrt{\rho_i^2-{\left({\rho}_i-{\delta}_{\textrm{max}}\right)}^2},\sqrt{\rho_i{A}_{c,\max }},\sqrt[3]{\rho_i^2{J}_{\textrm{max}}},{V}_{\textrm{max}}\right)$$
(29)

3.2 Splitting of sub-curves

The feedrate limit curves in NURBS curves often contain multiple feedrate minima, indicating that the machining process involves multiple acceleration and deceleration phases. However, the S-type Acc/Dec planning algorithm is typically designed for motions with a maximum of one acceleration and one deceleration phase. To enable feedrate scheduling for NURBS curves, a common approach is to split the curve into multiple sub-curves at the minima of the feedrate limit curve. Subsequently, feedrate scheduling can be performed individually for each sub-curve.

Most of the current studies have been conducted to split the NURBS curve into several sub-curves by finding the critical points, such as the maximum curvature points or the breakpoints. According to Eq. (29), it can be found that the maximum curvature points usually correspond to the minimum feedrate limit points. Therefore, in this study, the minimum feedrate points are considered the critical points and used as the basis for curve splitting.

The sub-curve splitting process can be illustrated more clearly using the trident curve depicted in Fig. 5a. Fig. 5b displays the curvature curve, and Fig. 5c presents the feedrate limit curve of the trident curve. The feedrate limit curve in Fig. 5c identifies seven minima, marked as points A–G in Fig. 5a. These points represent critical points or curvature-sensitive points since they correspond to regions of high curvature where the feedrate limits are relatively small. In the sub-curve splitting process, the trident curve will be divided into six sub-curves based on these seven critical points, and feedrate scheduling is performed for each sub-curve separately.

Fig. 5
figure 5

Sub-curve splitting of the trident curve

Full size image

The feedrate scheduling of the sub-curve was based on the initial feedrate limit vs, the terminal feedrate limit ve, and the length S of the sub-curve. vs and ve can be obtained from the feedrate limit curves; the arc length can be calculated with the adaptive quadrature method based on the Simpson rule [29, 30].

3.3 Merging of sub-curves

After obtaining the initial feedrate, terminal feedrate, and curve length of each sub-curve, feedrate scheduling for NURBS curves can be achieved by sequentially applying the algorithm described in Section 2 for each sub-curve. Most of the feedrate scheduling algorithms conclude at this stage. However, when the curve curvature is complex, there may be more sub-curves, resulting in frequent acceleration and deceleration.

In this study, an adaptive sub-curve merging strategy is employed to minimize the number of sub-curves and avoid sharp acceleration and deceleration phases. A secondary scheduling strategy is utilized in the feedrate scheduling process. In the first feedrate scheduling, feedrate scheduling is performed for each sub-curve to identify the sub-curves that can be merged. After the merging of sub-curves, a second feedrate scheduling is performed on the merged sub-curves, which have fewer sub-curves.

The merging of sub-curves can be divided into two types depending on the set sub-curve merging conditions.

3.3.1 The first type of sub-curve merging

The first type of sub-curve merging is conditioned by the fact that the feedrates at the interface of the two adjacent sub-curves have been corrected. This type of sub-curve merging typically simplifies the feedrate, acceleration, and jerk curves, improving machining efficiency and machining stability.

Figure 6 illustrates a schematic diagram of the first type of sub-curve merging. In this diagram, the feedrate limit curve is represented by Flim, the feedrate curve without curve merging are denoted as Fs1 and Fs2, and the feedrate curve after sub-curve merging is represented by Fs12.

Fig. 6
figure 6

Schematic diagram of the first type of sub-curve merging

Full size image

To aid in the description, let us designate the sub-curve located between parameters ui and uj as Ci, j, and the feedrate limit at parameter ui as Flim, i. The length of C2, 3 in Fig. 6 is not sufficient to support the feedrate decrease from Flim, 2 to Flim, 3. Therefore, Flim, 2 needs to be reduced during the feedrate scheduling process. When these two sub-curves are processed separately, the resulting feedrate curves are called Fs1 and Fs2, respectively. In this case, when machining the curve within the parameters u1 and u3, it becomes necessary to undergo one acceleration and two decelerations. Additionally, both the acceleration and deceleration at u2 need to be reduced to zero, which can negatively impact machining efficiency.

Given that the feedrate limit Flim, 2 at the interface between C1, 2 and C2, 3 is adjusted, C1, 2 and C2, 3 can be merged into a single curve, C1, 3. This merging process offers the advantage of requiring only one feedrate scheduling and disregarding the feedrate limit at u2. The resulting merged feedrate profile is denoted as Fs12, which eliminates the need for reducing acceleration and jerk to zero at u2. From Fig. 6, it is evident that Fs12 is consistently greater than both Fs1 and Fs2 at every position, indicating that machining with Fs12 will be more efficient. Furthermore, the smoother feedrate profile of Fs12 facilitates more stable machining.

Figure 7 provides a comparison of the feedrate, acceleration, and jerk profiles before and after the merging of sub-curves in the time domain. It is evident that after the sub-curves are merged, there is a reduction in machining time and an improvement in machining efficiency. Additionally, the feedrate, acceleration, and jerk curves exhibit simpler patterns after the merging process.

Fig. 7
figure 7

Feedrate, acceleration, and jerk profiles in the time domain for the first type of sub-curve merging

Full size image

3.3.2 The second type of sub-curve merging

The conditions for the merging of the second type of sub-curves can be divided into three cases, as illustrated in Fig. 8:

  1. a)

    As illustrated in Fig. 8a, the merging of two sub-curves is feasible when vf − vs ≥ k(vf − ve) and S23 ≥ kS12. Here, the parameter k is customizable and its magnitude determines the level of requirement for sub-curve merging. A larger value of k signifies a higher demand for sub-curve merging.

  2. b)

    As illustrated in Fig. 8b, the merging of two sub-curves is feasible when vf − ve ≥ k(vf − vs) and S12 ≥ kS23.

  3. c)

    As illustrated in Fig. 8c, the merging of two sub-curves is feasible when vf − vs ≥ k(vf − ve) and vf − ve ≥ k(vf − vs).

Fig. 8
figure 8

Schematic diagram of the second type of sub-curve merging

Full size image

Nevertheless, as depicted in Fig. 8, the feedrate profile resulting from sub-curve merging exceeds the feedrate limit curve in certain regions, which is unacceptable. Therefore, it becomes necessary to adjust the maximum feedrate, acceleration, and jerk to ensure that the scheduled feedrate can satisfy both the chord error and the dynamic performance requirements of the equipment.

For the second type of sub-curve merging depicted in Fig. 8a and b, three strategies can be employed to ensure that the scheduled feedrate remains within the feedrate limit. These strategies include reducing the maximum acceleration, reducing the maximum jerk, or reducing both the maximum acceleration and jerk. After conducting a comparison, it has been determined that reducing both the maximum acceleration and jerk simultaneously has the least impact on machining efficiency in the majority of cases. As a result, the strategy of simultaneously reducing the maximum acceleration and jerk is adopted in this study.

The specific implementation involves utilizing the dichotomous method in feedrate scheduling to iteratively approximate the most suitable values for Amax and Jmax. In this process, if the resulting combined feedrate profile exceeds the feedrate limit, lowering Amax and Jmax, otherwise, raising Amax and Jmax. The corrected feedrate profiles can be observed in Fig. 9a and b.

Fig. 9
figure 9

Adjusted feedrate profiles for the second type of sub-curve merging

Full size image

For the first type of curve merging shown in Fig. 7, as well as for the feedrate scheduling of a single sub-curve, there is a possibility that the resulting feedrate profile may exceed the feedrate limit. When the above situation occurs, it is also necessary to utilize the dichotomy method to reduce Amax and Jmaxto ensure that the feedrate is within the allowable range.

In the case of the second type of sub-curve merging illustrated in Fig. 8c, reducing the maximum feedrate Vmax has the least impact on the machining efficiency. In this case, it is necessary to correct Vmax to v2. The resulting corrected feedrate profile, Fs12, is depicted in Fig. 9c.

As shown in Fig. 9, when the second type of curve merging is applied and Vmax or Amax and Jmax are reduced, the resulting feedrate profile Fs12 may exhibit lower efficiency compared to the feedrate profiles Fs1 and Fs2 without curve merging. The level of efficiency reduction is also influenced by the parameter k. A larger value of k indicates a higher requirement for sub-curve merging and corresponds to a smaller reduction in efficiency for the merged feedrate profile.

Fig. 10 displays the acceleration and jerk curves after merging the sub-curves in the time domain. Upon comparison, it becomes apparent that the second type of sub-curve merging reduces the machining efficiency. However, it also simplifies the resulting feedrate, acceleration, and jerk curves, which in turn enhances the stability of the machining process. Therefore, it can be concluded that the second type of sub-curve merging achieves a more stable machining process by sacrificing some of the machining efficiency.

Fig. 10
figure 10

Feedrate, acceleration, and jerk profiles in time domain for the second type of sub-curve merging

Full size image

Once the merging of the sub-curves is finalized, the feedrate scheduling of the merged sub-curves is re-executed individually to generate superior feedrate, acceleration, and jerk profiles. Following this, the process of NURBS curve interpolation can be finalized by employing the interpolation point calculation method proposed by Xu et al [31].

4 Simulation and experimental results

4.1 Simulation and experimental environment

For the case study, the butterfly-shaped curve is chosen as it is widely recognized as a representative example of NURBS curves. Fig. 11a shows the butterfly curve, and Fig. 11b displays the curvature of the butterfly curve.

Fig. 11
figure 11

Butterfly curve and its curvature

Full size image

Figure 12 shows the experimental platform employed in this study, which is a high-precision laser machining platform. The X-axis and Y-axis of the platform are constructed using two high-performance linear motors, securely mounted on a vibration-suppressed marble platform. The controller employed is an Omron PMAC (CK3M), equipped with a 1 GHz CPU, 2 GB DDR2, and 1 GB built-in flash memory. This controller possesses excellent development capabilities, facilitating the implementation of feedrate scheduling algorithms. Due to the restricted size and weight of the experimental platform, higher feedrates and accelerations tend to induce more noticeable vibrations and equipment noise. Consequently, both the maximum machining feedrate and acceleration are constrained in both the simulation and experimentation phases. Certain parameters relevant to this experiment are outlined in Table 2.

Fig. 12
figure 12

Experimental platform

Full size image
Table 2 Test parameters of the interpolators used for the simulations
Full size table

For simulation and visualization of results, the feedrate scheduling algorithm and interpolation algorithm were implemented in MATLAB 2018b. In the experimental setup, the Power PMAC IDE was utilized to process the discrete interpolation points and interpolation feedrates, which were calculated in MATLAB, and convert them into a machining program compatible with the PMAC system. This program was then employed to drive the X-axis and Y-axis during the experiment.

For simulation and visualization of results, the feedrate scheduling algorithm and interpolation algorithm were implemented in MATLAB 2018b. In the experimental setup, the Power PMAC IDE was utilized to process the discrete interpolation points and interpolation feedrates, which were calculated in MATLAB, and convert them into a machining program compatible with the PMAC system. This program was then employed to drive the X-axis and Y-axis during the experiment.

4.2 Results of feedrate scheduling

Figure 13 illustrates the feedrate limit curves of the butterfly curve, obtained based on the parameters specified in Table 2. In this context, Fc, Fa, and Fj represent the feedrate limitations related chord error, tangential acceleration, and jerk, respectively. Flim represents the final feedrate limit curve that accounts for the combined effect of these limitations. Analysis of Fig. 13 indicates that jerk is the primary factor limiting the feedrate. This limitation is primarily attributed to the intricate curvature of the butterfly curve and the relatively small maximum jerk setup.

Fig. 13
figure 13

Feedrate limits of butterfly curve

Full size image

Figure 14 presents the results of curve splitting. In Fig. 14a, the curve is split into 32 sub-curves by utilizing curvature-sensitive points. However, by the adaptive merging of sub-curves proposed in this study, the number of sub-curves was reduced to 20, as depicted in Fig. 14b. Additionally, Fig. 14c presents the curve cut points at the parameter domain for both cases.

Fig. 14
figure 14

Splitting and merging of sub-curves

Full size image

Figure 15 displays the results of feedrate scheduling before and after curve merging. In this case, a total of 10 regions were merged, with areas labeled 4 and 7 representing Type II curve merges, while the remaining regions correspond to Type I curve merges. Regions 5 and 6 were merged with three adjacent sub-curves. By examining Fig. 15, it is evident that the merged curves exhibit improved smoothness and overall performance compared to their original counterparts.

Fig. 15
figure 15

Scheduled feedrate profiles

Full size image

The usage of a higher parameter k is the main reason for the reduction in Type II sub-curve mergers. Lowering the value of k helps alleviate the limitations associated with Type II sub-curve mergers, resulting in a decrease in the number of sub-curves and the frequency of accelerations and decelerations. However, it is important to note that reducing the value of k also leads to a decrease in machining efficiency. For this study, the value of k was set to 10 to balance the reduction in sub-curve mergers and the associated machining efficiency.

Figure 16 presents the feedrate, acceleration, and jerk profiles generated by the proposed feedrate scheduling algorithm in the time domain. Due to the curvature of the curve and the maximum feedrate limitation, the maximum acceleration is not reached throughout the machining process. Moreover, certain regions, labeled 1, 2, 5, 6, 9, and 10 in Fig. 15, experience limitations on the maximum jerk. These regions share a common characteristic: the scheduled feedrate may locally exceed the feedrate limit without constraining the maximum jerk.

Fig. 16
figure 16

Scheduled feedrate, acceleration, and jerk profiles in time domain

Full size image

Figure 17 illustrates the decomposition of displacement, feedrate, and acceleration on the X-axis and Y-axis. It is worth noting that the decomposed feedrates and accelerations do not demonstrate S-shaped variations. This is primarily attributed to the fixed processing direction at each point along the curve, which establishes a correlation between the feedrates of the X-axis and Y-axis at each point. It is impractical to independently schedule the feedrates of the axes and ensure that all final feedrates exhibit an S-shape. Hence, in most current studies, including the present one, the synthesized feedrates of the X and Y axes are scheduled. As NURBS curves inherently possess smooth and continuous characteristics, the decomposed feedrates and accelerations on the X and Y axes will also exhibit smooth and continuous behavior.

Fig. 17
figure 17

Scheduled displacements, feedrates, and accelerations in the X and Y axes

Full size image

4.3 Analysis of feedrate scheduling

Figures 18a and b show the feedrate profiles obtained using the proposed feedrate scheduling algorithm in both the parameter and time domains for the specified butterfly curves, respectively. The method proposed in this study is labeled as QP. For comparison, the curvature-based feedrate method (CBF) [7] and the S-shaped acceleration/deceleration planning algorithm with trigonometrically constructed jerk (TF) [32] are also reproduced. The obtained feedrate profiles from all three algorithms are compared and evaluated.

Fig. 18
figure 18

Comparison of feedrate profiles in parameter and time domains

Full size image

From the feedrate profile in the parameter domain, it is evident that the CBF maintains a high feedrate in most regions. However, the feedrate profile of CBF is complex and not smooth. On the other hand, QP demonstrates better efficiency compared to TF. This is primarily due to QP’s ability to maintain high levels of jerk and its sub-curve adaptive merging strategy. Furthermore, the feedrate profile of QP is the simplest and smoothest among the three methods.

Quantitatively analyzing the feedrate profiles in the time domain further compares the efficiency of the three methods. CBF exhibits the highest efficiency, followed by QP. The efficiency of QP is 8.38% higher than that of TF. The feedrate profile of QP already has a good balance between efficiency and stability. It is challenging to significantly improve the feedrate profile given the constraints of feedrate limit, maximum acceleration, and jerk. Therefore, the 8.38% efficiency improvement achieved in this study can be considered significant.

The stability of the machining process is greatly influenced by the changes in acceleration, as it can cause shocks. A smoother and more continuous acceleration profile leads to a more stable machining process. Fig. 19 illustrates the acceleration and jerk profiles obtained using the three feedrate scheduling methods. Due to the lack of consideration for the dynamic performance of the machine, the acceleration and jerk profiles of CBF are noticeably less smooth and continuous. Moreover, many areas exceed the maximum limit, which is detrimental to the stability of the machining process. On the other hand, both TF and QP yield smooth and continuous acceleration and jerk profiles that comply with the equipment limits. This contributes to a more stable machining process.

Fig. 19
figure 19

Comparison of acceleration and jerk profiles in time domain

Full size image

Figure 20 provides a visual comparison of the acceleration profiles between TF and QP within the parameter domain. QP demonstrates a more robust acceleration profile than TF in most regions. Furthermore, in the areas marked by boxes in this figure, the QP acceleration profile appears simpler, while the TF acceleration profile exhibits repeated accelerations and decelerations. In high-speed machining, the occurrence of repeated accelerations and decelerations within a short period can potentially destabilize the machine, leading to increased vibration and reduced machining quality. Hence, the smoother acceleration profile offered by QP is advantageous in maintaining stability and improving overall machining performance.

Fig. 20
figure 20

Comparison of acceleration profiles in the parameter domain

Full size image

Spectral analysis of acceleration curves can provide a quantitative assessment of acceleration stability. The main frequency of an acceleration curve with constant acceleration is 0 Hz, while the main frequency of an acceleration curve with a period of π is 0.3183 Hz. In general, a smaller main frequency indicates a relatively more stable acceleration curve.

Figure 21 displays the results of spectral analysis for the three acceleration curves. The main frequency of CBF is as high as 22.2 Hz, indicating frequent changes in acceleration during the machining process and an unstable machining process. On the other hand, the main frequencies of TF and QP are 5.3 Hz and 3.6 Hz, respectively. This suggests that the acceleration of QP is the most stable during the machining process, as it exhibits a lower main frequency.

Fig. 21
figure 21

Spectrograms of acceleration

Full size image

4.4 Experimental results

The tracking error is a crucial metric for evaluating machining accuracy. In the experiment, the tracking error is determined by collecting the actual machining positions from the X-axis and Y-axis grating scales at a frequency of 8000 Hz and comparing it with the commanded positions. The machining process is carried out based on the feedrate profile constructed using the proposed method. The resulting machining path profiles and tracking error profile are depicted in Fig. 22a and b, respectively.

Fig. 22
figure 22

Tracking error of butterfly curve

Full size image

As shown in Fig. 22, it can be observed that the tracking error exhibits a significant correlation with the curvature of the machining area. Generally, high-curvature regions exhibit larger tracking errors, while low-curvature regions demonstrate lower tracking errors. However, it is noteworthy that the region of maximum tracking error does not precisely coincide with the region of maximum curvature. Instead, the tracking error reaches its peak after crossing the maximum curvature region.

Figure 23 illustrates the commanded machining curves, actual machining curves, and tracking errors of the X-axis and Y-axis. The tracking error of the X-axis remains within 2 μm for most regions, and noticeable tracking errors only occur when there is a change in machining direction, with a maximum tracking error of 12 μm. The tracking error of the X-axis exhibits an oscillatory pattern.

Fig. 23
figure 23

Tracking error of X-axis and Y-axis

Full size image

In contrast, the tracking error of the Y-axis is more evident and accumulative. The tracking error of the Y-axis stays within 30 μm, with a maximum of 28 μm. The term “accumulative” implies that the tracking error of the Y-axis increases or decreases within a certain region. Additionally, the maximum tracking error in the Y-axis tends to occur after a change in machining direction with a certain delay, as depicted in the labeled area “a” in Fig. 23b. This phenomenon serves as the primary reason for the observed distribution of tracking errors in Fig. 22.

The significant difference in tracking errors between the X-axis and Y-axis can be attributed to the difference in load and inertia. In the experimental setup used in this study, the X-axis is mounted on the Y-axis. As a result, the Y-axis experiences a larger load and greater inertia compared to the X-axis. This disparity in dynamics leads to the inferior performance of the Y-axis in terms of tracking accuracy.

Figure 24 displays the scheduled feedrate profile, the actual feedrate profile, and the feedrate error. It is evident that the X-axis exhibits a larger feedrate error compared to the Y-axis. The tracking error of the X-axis remains nearly constant at ± 2 mm/s, while the Y-axis shows a smaller variation of ± 0.6 mm/s. One possible explanation for this difference is that the platform is driven in position mode. The X-axis, benefiting from its high performance characteristics, is capable of adjusting the feed rate more frequently in order to minimize tracking errors. In contrast, the Y-axis, due to its higher load and inertia, may not adjust the feedrate as frequently, leading to a smaller feedrate error compared to the X-axis.

Fig. 24
figure 24

Feedrate errors

Full size image

Figure 25 presents a comparison of the tracking errors obtained from the three feedrate scheduling methods. The tracking error is primarily influenced by the machining position, particularly when there is a change in the direction of motion of the Y-axis, resulting in a peak in tracking error. Consequently, the tracking errors obtained from the three feedrate scheduling methods exhibit similar patterns.

Fig. 25
figure 25

Comparison of tracking errors

Full size image

Additionally, the tracking error is also affected by the feedrate and acceleration. Generally, the tracking error increases with higher feedrates and accelerations. As a result, the CBF method yields the largest tracking error in most regions, with a mean tracking error of 17.8 μm and a maximum tracking error of 59.6 μm. One contributing factor to this large tracking error is the inability of the platform to achieve the scheduled acceleration and jerk. Moreover, the equipment displayed noticeable vibrations and abnormal noise during machining with the CBF-scheduled feedrate profiles, resulting in a significant tracking error.

The feedrate profiles scheduled using TF and QP result in smooth machining operations with no noticeable vibration or abnormal noise. The distribution of tracking errors for TF is extremely similar to that of QP, primarily due to the similarity in feedrate and acceleration profiles between the two methods. However, in regions where sub-curve merging is performed in QP, TF exhibits a more pronounced tracking error compared to QP. This can be attributed to the more frequent acceleration and deceleration experienced by TF in these regions, leading to unstable and even oscillatory feedrate profiles, thus increasing the tracking error.

The average tracking error for TF is 11.6 μm, with a maximum tracking error of 35.7 μm. The QP proposed in this study demonstrates the smallest tracking error, with an average tracking error of 10.8 μm. This is 39.89% lower than CBF and 7.14% lower than TF. The maximum tracking error for QP is 29 μm, which is 51.32% lower than CBF and 18.72% lower than TF. These results highlight the superior performance of the QP method in terms of tracking accuracy.

5 Conclusion

This study introduces an advanced S-shaped acceleration/deceleration feedrate scheduling algorithm, specifically tailored for efficient and high-precision machining of non-uniform rational B-spline curves. The algorithm employs quartic polynomials to construct the jerk function, effectively resolving the issue of jerk discontinuity found in traditional S-shaped acceleration/deceleration feedrate scheduling algorithms. This advancement significantly mitigates flexible vibrations during the machining process. Furthermore, the integration of a sub-curve merging strategy and a quadratic feedrate scheduling approach markedly diminishes frequent acceleration and deceleration in complex curve machining, thereby facilitating a more stable machining process. Comprehensive simulations and experiments demonstrate that the proposed algorithm outperforms conventional feedrate scheduling algorithms in terms of machining efficiency and accuracy. The study provides the potential to further improve the efficiency and accuracy of the non-uniform rational B-spline interpolation and supports its extension to more demanding application scenarios.