1 Introduction

Feedrate scheduling is a crucial aspect of CNC machine tool processing that significantly affects machining quality [1]. High precision, high speed and high quality are becoming the development direction of modern processing and manufacturing. In order to achieve the desired machining goals and reduce feedrate fluctuations caused by machine tool vibrations during production, appropriate feedrate scheduling can satisfy various constraints of the machine tool. However, it’s important to consider rounding errors caused by sampling interpolation time in feedrate scheduling because it can affect machining accuracy and motion stability.

The researchers investigated various feedrate scheduling methods for acceleration and deceleration. The trapezoidal feedrate scheduling method [2] is simple to implement, but compared to the jerk-limited feedrate scheduling method, interpolating along the complex tool path will lead to discontinuity of feedrate and acceleration, resulting in violent vibration. Therefore, many methods have been developed to limit acceleration, such as the sinusoidal shape method [3], time optimal method [4] and S-shape method [5], in order to schedule the feedrate, which has the advantage of improving smoothness. The acceleration and deceleration (ACC/DEC) control algorithm of sinusoidal shape method [6, 7] has continuous changes in feedrate , acceleration and acceleration, and the system runs smoothly with high flexibility, and its advantage is that it improves smoothness. Time optimal methods [8,9,10,11] solve differential equations analytically or numerically to produce minimum-time or near-minimum-time feedrate profiles. S-shaped ACC/DEC algorithm is widely used in smoothing feedrate scheduling because of its simplicity and smoothness [12,13,14]. However, these methods do not take into account the effect of interpolation period. The interpolation time is not necessarily an integral multiple of the interpolation period, which may lead to rounding errors, easy to cause velocity fluctuations, and affect the smoothness of motion and surface quality. Therefore, how to compensate or eliminate the rounding error is a problem that cannot be ignored in feedrate scheduling.

To account for rounding errors, several feedrate scheduling methodshave been proposed. Li et al. [15] proposed a variable period feedrate scheduling method to compensate for the rounding error in the linear acceleration and deceleration process. However, this feedrate scheduling method does not guarantee the continuity of acceleration and results in serious vibration and impact. The time rounding strategy given in literature [16] rounds each period of the planning result of the S-shaped ACC/DEC algorithm. A variable degree compensation strategy is proposed to compensate for the rounding error so that the feedrate is more continuous and the rounding error becomes smaller. Luo et al. [17] proposed a similar method of time rounding and error compensation, which resulted in discontinuous acceleration profile. In [18], a feedrate scheduling method based on cubic polynomial acceleration and deceleration algorithm was proposed, and the time rounding and error compensation method given in the literature [16, 17] is used.

In [19], Ni et al. proposed an optimal feedrate scheduling based on S-shaped ACC/DEC algorithm, which includes initial feedrate scheduling and rounding error compensation parameter calculation. Although interpolation time can become an integer multiple of the interpolation period, the feedrate and jerk profile will exceed the limit at some point. Ni et al. [20] proposed a time rounding scheme that round the whole time period and distribute each sub-time period according to a certain proportion. Four feedrate scheduling situations were designed for different acceleration and deceleration situations. Although rounding errors can be eliminated in most situation, rounding errors cannot be eliminated in pure deceleration situation, and the jerk profile will exceed the limit in this situation.

Aiming at these problems, this paper proposes a new feedrate scheduling method based on time rounding. Firstly, based on the typical S-shaped ACC/DEC algorithm, a new time rounding scheme is designed. Round each sub-time period separately, but different rounding methods were used for different periods to ensure that the adjusted motion parameters were limited to the system limitation. Then, the characteristics of the S-shaped addition and subtraction algorithm were analyzed, and the expression of jerk after time adjustment was derived. According to the principle of constant total displacement, the relationship between the sum of displacements of each section and the total displacement was established. The principle of velocity continuity was used to calculate the maximum achievable velocity from the start point and the end point respectively. The expression of jerk after time adjustment was deduced by using these two principles. Finally, the method of jerk, acceleration and velocity was solved again. A series of feedrate scheduling methods were designed for different acceleration and deceleration conditions. Because some acceleration and deceleration conditions will change the final velocity after parameter adjustment, feedrate interpolation strategy was adjusted. For pure acceleration process and pure deceleration process with zero final velocity, a bidirectional interpolation strategy with backtracking correction was proposed to improve reliability and continuity of feedrate scheduling.

The rest of paper is organized as follows: Section 2 analyzes the S-shaped ACC/DEC algorithm. Section 3 presents the time-rounding scheme and jerk recalculation principle. Section 4 develops the bidirectional interpolation strategy with backtracking correction. The simulations are carried out and compared with previous research work in Section 5. Section 6 gives the conclusions.

Fig. 1
figure 1

The typical S-shaped ACC/DEC profile

Full size image

2 S-shaped ACC/DEC algorithm

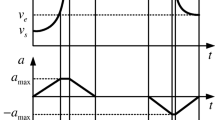
The S-shaped ACC/DEC control realizes the continuous change of acceleration during ACC/DEC, and effectively reduces the impact and oscillation in the motion process. As shown in Fig. 1, a typical S-shaped ACC/DEC profile contains seven stages, which are composed of three processes: acceleration (ACC), constant feedrate (CF) and deceleration (DEC). Analytical or numerical methods can obtain the section time \({[T_1,T_2,T_3,T_4,T_5,T_6,T_7]}\), start feedrate \({[v_1,v_2,v_3,v_4,v_5,v_6,v_7]}\) and the corresponding cumulative displacement \({[S_1,S_2,S_3,S_4,S_5,S_6,S_7]}\) according to the specified conditions, such as the maximum jerk \(J_{max}\), maximum acceleration \(a_{max}\), maximum velocity \(v_{max}\), displacement S, start velocity \(v_s\) and end velocity \(v_e\). However, the arbitrarily given conditions and numerical calculation methods prevent the exact discretization of the durations \(T_i\) (i = 1, 2, …, 7) in an integer multiple of the interpolation period \(T_s\).

Its displacement, feedrate and acceleration equations can be expressed as follows:

$$\begin{aligned} s(t)= {\left\{ \begin{array}{ll} v_{s} t+\frac{1}{6} J_{\max } t^{3} &{} 0 \le t \le t_{1} \\ s_{1}+v_{1} t+\frac{1}{2} a_{\max } t^{2} &{} t_{1}<\textrm{t} \le t_{2} \\ s_{2}+v_{2} t+\frac{1}{2} a_{\max } t^{2}-\frac{1}{6} J_{\max } t^{3} &{} t_{2}<\textrm{t} \le t_{3} \\ s_{3}+v_{3} t &{} t_{3}<\textrm{t} \le t_{4} \\ s_{4}+v_{4} t-\frac{1}{6} J_{\max } t^{3} &{} t_{4}<\textrm{t} \le t_{5} \\ s_{5}+v_{5} t-\frac{1}{2} a_{\max } t^{2} &{} t_{5}<\textrm{t} \le t_{6} \\ s_{6}+v_{6} t-\frac{1}{2} a_{\max } t^{2}+\frac{1}{6} J_{\max } t^{3} &{} t_{6}<\textrm{t} \le t_{7} \end{array}\right. } \end{aligned}$$
(1)
$$\begin{aligned} v(t)= {\left\{ \begin{array}{ll} v_{s}+\frac{1}{2} J_{\max } t^{2} &{} 0 \le t \le t_{1} \\ v_{1}+a_{\max } t &{} t_{1}<\textrm{t} \le t_{2} \\ v_{2}+a_{\max } t-\frac{1}{2} J_{\max } t^{2} &{} t_{2}<\textrm{t} \le t_{3} \\ v_{3} &{} t_{3}<\textrm{t} \le t_{4} \\ v_{4}-\frac{1}{2} J_{\max } t^{2} &{} t_{4}<\textrm{t} \le t_{5} \\ v_{5}-a_{\max } t &{} t_{5}<\textrm{t} \le t_{6} \\ v_{6}-a_{\max } t+\frac{1}{2} J_{\max } t^{2} &{} t_{6}<\textrm{t} \le t_{7} \end{array}\right. } \end{aligned}$$
(2)
$$\begin{aligned} a(t)= {\left\{ \begin{array}{ll} J_{\max } t &{} 0 \le t \le t_{1} \\ a_{\max } &{} t_{1}<\textrm{t} \le t_{2} \\ a_{\max }-J_{\max } t &{} t_{2}<\textrm{t} \le t_{3} \\ 0 &{} t_{3}<\textrm{t} \le t_{4} \\ -J_{\max } t &{} t_{4}<\textrm{t} \le t_{5} \\ -a_{\max } &{} t_{5}<\textrm{t} \le t_{6} \\ -a_{\max }+J_{\max } t &{} t_{6}<\textrm{t} \le t_{7} \end{array}\right. } \end{aligned}$$
(3)

The durations \(T_i\) (i = 1, 2, …, 7) of the seven phases are calculated by the start/end velocity \(v_s\)/\(v_e\) , the maximum velocity \(v_{max}\) , the tangential acceleration/jerk \(a_{max}/J_{max}\) , the cumulative displacement of ACC phase \(S_{acc}\) , the cumulative displacement of DEC phase \(S_{dec}\) and the desired arc length S, as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{T}_{1}}=\frac{{{a}_{\max }}}{{{J}_{\max }}} \\&{{T}_{2}}=\frac{{{v}_{\max }}-{{v}_{s}}}{{{a}_{\max }}}-\frac{{{a}_{\max }}}{{{J}_{\max }}} \\&{{T}_{3}}=\frac{{{a}_{\max }}}{{{J}_{\max }}}\\&{{T}_{4}}=\frac{S-{{S}_{acc}}-{{S}_{dec}}}{{{v}_{\max }}} \\&{{T}_{5}}=\frac{{{a}_{\max }}}{{{J}_{\max }}} \\&{{T}_{6}}=\frac{{{v}_{\max }}-{{v}_{e}}}{{{a}_{\max }}}-\frac{{{a}_{\max }}}{{{J}_{\max }}} \\&{{T}_{7}}=\frac{{{a}_{\max }}}{{{J}_{\max }}} \\ \end{aligned} \right. \end{aligned}$$
(4)

3 The time rounding scheme and jerk recalculation principle

This section introduces an optimal feedrate scheduling method based on S-shape ACC/DEC algorithm to eliminate rounding error and make the velocity and acceleration curves continuously smooth. The method includes time rounding schemes and details the corresponding jerk recalculations for various ACC/DEC situations.

3.1 Time rounding scheme

The motion parameters were given arbitrarily and involved numerical calculations based on standard S-shape ACC/DEC profile. This may cause the durations \(T_i \)(i = 1, 2,… 7) to be not an integer multiple of the interpolation period \(T_s\), resulting in rounding errors that affect the scheduled acceleration, feedrate and displacement profile and the smoothness of the motion. There are two schemes in the existing time rounding. One is to round the whole time period and distribute each sub-time period according to a certain proportion. The other is to round each sub-time period separately. Although the former scheme only needs one round calculation, it is too complicated to distribute each small period of time and the calculation is also cumbersome. The latter has a simpler calculation process, so this paper adopts this scheme for time rounding. Suppose \(T_1 = T_3\) and \(T_5 = T_7\), after the time rounding, the adjusted section time \(T_{i}^{\prime }\)(i = 1, 2,… 7) which can be expressed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{T_{1}^{\prime }={\text {ceil}}\left( \frac{T_{1}}{T_{s}}\right) T_{s} }\\&{T_{2}^{\prime }={\text {round}}\left( \frac{T_{2}}{T_{s}}\right) T_{s}} \\&{T_{4}^{\prime }={\text {round}}\left( \frac{T_{4}}{T_{s}}\right) T_{s} }\\&{T_{6}^{\prime }={\text {round}}\left( \frac{T_{6}}{T_{s}}\right) T_{s}} \\&{T_{7}^{\prime }={\text {ceil}}\left( \frac{T_{7}}{T_{s}}\right) T_{s}} \end{aligned} \right. \end{aligned}$$
(5)

where round rounds to the nearest integer, ceil rounds up to the next integer. Different rounding methods are used in different sub-time period to ensure that the actual velocity, acceleration and jerk are close to but do not exceed the system limitation.

3.2 Jerk recalculation principle

The traditional methods treat the feedrate scheduling and rounding error compensation as completely independent processes. It usually only considers the principle of constant total displacement, which leads to a non-smooth feedrate profile with discontinuities. Alternatively, it only considers the continuity of the velocity and ensures a smooth feedrate profile, but the rounding error still exists. This paper proposes a new calculation principle for feedrate scheduling that combines both principles: constant total displacement and continuity of velocity. The constant total displacement means that the sum of the displacements of each segment is equal to the total displacement. The principle of velocity continuity was used to calculate the maximum achievable velocity from the start point and the end point respectively. Then, the expression of jerk was deduced by using these two principles. Acceleration and feedrate are recalculated according the new jerk to ensure their continuity. Depending on different S-shaped ACC/DEC situations, three cases are distinguished. Recalculate the maximum jerk \(J_1\) during the ACC phase and the maximum jerk \(J_2\) during the DEC phase.

Fig. 2
figure 2

Bidirectional interpolation strategy

Full size image
  1. (1)

    The situation with CF phase

Taking the typical S-shaped e ACC/DEC profile as an example, it contains three phases: ACC phase, CF phase and DEC phase. The final velocity of the ACC phase \(v_3\) can be calculated from the start velocity \(v_s\) as follows:

$$\begin{aligned} {{v}_{3}}={{v}_{s}}+\frac{1}{2}{{J}_{\max }}T_{1}^{2}+{{a}_{\max }}{{T}_{2}}+{{a}_{\max }}{{T}_{3}}-\frac{1}{2}{{J}_{\max }}T_{3}^{2} \end{aligned}$$
(6)

Substituting \(T_{i}^{\prime }\)(i = 1, 2,… 7) into Eq. (6) can be expressed as follows:

$$\begin{aligned} {{v}_{3}}={{v}_{s}}+{{J}_{1}}{{{T}'}_{1}}{{{T}'}_{2}}+{{J}_{1}}{{T}'_{1}}^{2} \end{aligned}$$
(7)

Similarly, The initial velocity of the DEC phase \(v_4\) can be calculated from the end velocity \(v_e\) as follows:

$$\begin{aligned} {{v}_{4}}={{v}_{e}}+{{J}_{2}}{{{T}'}_{7}}{{{T}'}_{6}}+{{J}_{2}}{{T}'_{7}}^{2} \end{aligned}$$
(8)

According to the properties of the S-shaped ACC/DEC profile, the final velocity of ACC phase is equal to both the velocity of CF phase and the initial velocity of DEC phase,

$$\begin{aligned} {{v}_{3}}={{v}_{4}} \end{aligned}$$
(9)

The total displacement can be expressed as the sum of displacements in each phase,

$$\begin{aligned} {{S}_{acc}}+{{S}_{cf}}+{{S}_{dec}}=S \end{aligned}$$
(10)

where \(S_{acc}\) is the cumulative displacement in ACC phase, \(S_{cf}\) is the displacement in CF phase and \(S_{dec}\) is the cumulative displacement in DEC phase. Then, \(S_{acc}\) , \(S_{cf}\) and \(S_{dec}\) can be expressed as follows based on Eq. (2):

$$\begin{aligned} {\begin{matrix} {{S}_{acc}} &{}={{v}_{s}}(2{{T}_{1}}^{\prime }+{{{{T}'}}_{2}})+\frac{1}{2}{{J}_{1}}{{T}_{1}}{{^{\prime }}^{2}}\text {(}{{{{T}'}}_{1}}+{{{{T}'}}_{2}})+\frac{1}{2}{{J}_{1}}{{{{T}'}}_{1}}{{\text {(}{{{{T}'}}_{1}}+{{{{T}'}}_{2}})}^{2}} \\ {{S}_{cf}} &{}={{v}_{3}}{{T}_{4}}^{\prime } \\ {{S}_{dec}} &{}={{v}_{e}}(2{{T}_{7}}^{\prime }+{{{{T}'}}_{6}})+\frac{1}{2}{{J}_{2}}{{T}_{7}}{{^{\prime }}^{2}}\text {(}{{{{T}'}}_{7}}+{{{{T}'}}_{6}})+\frac{1}{2}{{J}_{2}}{{{{T}'}}_{7}}{{\text {(}{{{{T}'}}_{7}}+{{{{T}'}}_{6}})}^{2}} \\ \end{matrix}} \end{aligned}$$
(11)

Finally, \(J_1\) and \(J_2\) can be expressed as follows based on Eqs. (7)-(11):

$$\begin{aligned} {\begin{matrix} J_{1} &{}=\frac{2 S-v_{s}\left( 4 T_{1}^{\prime }+2 T_{2}^{\prime }+2 T_{4}^{\prime }+T_{6}^{\prime }+2 T_{7}^{\prime }\right) -v_{e}\left( T_{6}^{\prime }+2 T_{7}^{\prime }\right) }{\left( T_{1}^{\prime 2}+T_{1} T_{2}^{\prime }\right) \left( 2 T_{1}^{\prime }+T_{2}^{\prime }+2 T_{4}^{\prime }+T_{6}^{\prime }+T_{7}^{\prime }\right) } \\ J_{2} &{}=\frac{2 S-v_{s}\left( 2 T_{1}^{\prime }+2 T_{2}^{\prime }\right) -v_{e}\left( 2 T_{1}^{\prime }+T_{2}^{\prime }+2 T_{4}^{\prime }+2 T_{6}^{\prime }+4 T_{7}^{\prime }\right) }{T_{7}^{\prime 2}\left( 2 T_{1}^{\prime }+T_{2}^{\prime }+2 T_{4}^{\prime }+3 T_{6}^{\prime }+2 T_{7}^{\prime }\right) +T_{6}^{\prime } T_{7}^{\prime }\left( 2 T_{1}^{\prime }+T_{2}^{\prime }+2 T_{4}^{\prime }+T_{6}^{\prime }\right) } \end{matrix}} \end{aligned}$$
(12)
  1. (2)

    The situation only with ACC and DEC phases

Fig. 3
figure 3

Test curve and its curvature curve.a Butterfly-shaped curve.b Curvature curve

Full size image

This situation is computed analogously to its predecessor. According to the characteristics of the S-shaped ACC/DEC profile, the final velocity of ACC phase is equal to the initial velocity of DEC phase,

$$\begin{aligned} {{v}_{3}}={{v}_{4}} \end{aligned}$$
(13)

Furthermore, the total displacement can be expressed as the sum of displacements in each phase,

$$\begin{aligned} {{S}_{acc}}+{{S}_{dec}}=S \end{aligned}$$
(14)

Finally, \(J_1\) and \(J_2\) can be expressed as follows based on Eqs. (7), (8), (13) and (14):

$$\begin{aligned} {\begin{matrix} J_{1} &{}=\frac{2 S-v_{s}\left( 4 T_{1}^{\prime }+2 T_{2}^{\prime }+T_{6}^{\prime }+2 T_{7}^{\prime }\right) -v_{e}\left( T_{6}^{\prime }+2 T_{7}^{\prime }\right) }{\left( T_{1}^{\prime 2}+T_{1}^{\prime } T_{2}^{\prime }\right) \left( 2 T_{1}^{\prime }+T_{24}^{\prime }+T_{6}^{\prime }+T_{7}^{\prime }\right) } \\ J_{2} &{}=\frac{2 S-v_{s}\left( 2 T_{1}^{\prime }+2 T_{2}^{\prime }\right) -v_{e}\left( 2 T_{1}^{\prime }+T_{2}^{\prime }+2 T_{6}^{\prime }+4 T_{7}^{\prime }\right) }{T_{7}^{\prime 2}\left( 2 T_{1}^{\prime }+T_{2}^{\prime }+3 T_{6}^{\prime }+2 T_{7}^{\prime }\right) +T_{6}^{\prime } T_{7}^{\prime }\left( 2 T_{1}^{\prime }+T_{2}^{\prime }+T_{6}^{\prime }\right) } \end{matrix}} \end{aligned}$$
(15)
  1. (3)

    The situation only with ACC or DEC phase

According to the total displacement, the jerk was recalculated. This method ensured that the displacement remained unchanged,although it causes the end velocity to be lower than the look-ahead feedrate. Taking the pure acceleration process as an example, \(J_1\) can be calculated as follows:

$$\begin{aligned}&S=S_{a c c} \end{aligned}$$
(16)
$$\begin{aligned}&S=v_{s}\left( 2 T_{1}^{\prime }+T_{2}^{\prime }\right) +\frac{1}{2} J_{1}{T_{1}}^{2}\left( T_{1}^{\prime }+T_{2}^{\prime }\right) +\frac{1}{2} J_{1} T_{1}^{\prime }\left( T_{1}^{\prime }+T_{2}^{\prime }\right) ^{2} \end{aligned}$$
(17)
$$\begin{aligned}&J_{1}=\frac{2 S-2 v_{s}\left( 2 T_{1}^{\prime }+T_{2}^{\prime }\right) }{T_{1}^{\prime }\left( T_{1}^{\prime }+T_{2}^{\prime }\right) ^{2}+T_{1}^{\prime 2}\left( T_{1}^{\prime }+T_{2}^{\prime }\right) } \end{aligned}$$
(18)

The pure deceleration case was calculated similarly to the pure acceleration case. However, a special case occurred when the pure deceleration case with the end velocity being 0. Using this method would lead to a negative end velocity which was unacceptable. The next section explained how this situation was handled.

In summary, different S-shaped ACC/DEC situations has different feedrate scheduling processes. Finally, put \(J_1\), \(J_2\) and \(T_{i}^{\prime }\)(i = 1, 2,… 7) into Eqs. (1)-(3) to recalculate acceleration, velocity and displacement.

4 Bidirectional interpolation strategy with backtracking correction

To obtain the look-ahead feedrate, using the look-ahead scheme in [16]. Since the forward and reverse calculations of the look-ahead process are based on the typical S-shaped ACC/DEC algorithm, it cannot match the feedrate scheduling method given in this paper. This may cause problems for normal feedrate scheduling based on the look-ahead results, especially in pure acceleration and pure deceleration processes,and it may also affect interpolation stability. To solve this issue, this paper propose a bidirectional interpolation strategy with backtracking correction that matches our improved feedrate scheduling method. The strategy has two layers: firstly, when the final velocity of the pure acceleration or pure deceleration process is slightly lower than the look-ahead feedrate, the look-ahead feedrate is corrected; secondly, the pure deceleration process with the end velocity of 0 is transformed into a pure acceleration process with an start velocity of 0 by using the reverse interpolation method. This avoids negative velocities that can occur when time rounding is used. The specific strategies are as follows:

If the last curve segment of the trajectory curve is a pure deceleration process, as illustrated in Fig. 2 , its start point is used as a split point to divide the entire curve into two sections. Feedrate scheduling is performed from both ends of the trajectory curve and converges at the split point. Firstly, feedrate scheduling is performed from the end point of the trajectory curve. According to the proposed feedrate scheduling method, the velocity of the split point will be lower than the look-ahead feedrate, and the velocity is updated to the look-ahead feedrate of the split point. This ensures that the meeting velocity of the two directions on the split point is equal and has 0 acceleration, ensuring the smoothness of the movement. Then carry out feedrate scheduling from the start point of the trajectory curve. If the curve segment is a pure acceleration or a deceleration process, according to the proposed feedrate scheduling method, the velocity at the end of the curve segment will be less than the look-ahead feedrate. Update this velocity as the start velocity of the next curve segment to ensure the continuity of feedrate. Because the forward and reverse feedrate profile are equal in velocity at the split point and have 0 acceleration, the two feedrate profile are finally merged into a complete feedrate profile.The bidirectional interpolation strategy with backtracking correction is described in Algorithm 1:

Algorithm 1
figure a

 .

Full size image
Table 1 Interpolation parameters
Full size table
Fig. 4
figure 4

Simulation results by the method given in [16]. a Feedrate. b Acceleration. c Jerk

Full size image

where \(v_i(i=0,1,...,n)\) is look-ahead feedrate, \(s_i(i=1,2...n)\) is arc length of each segment of the NURBS curve, and \(v'_e\) is the velocity at the end of the curve segment after eedrate scheduling. When the curve segment is a pure acceleration or deceleration process, \(v'_e<v_e\).

If the last curve segment of the trajectory curve isn’t a pure deceleration process, only forward feedrate scheduling is required. If the curve segment is a pure acceleration or pure deceleration process, according to the proposed feedrate scheduling method, the velocity at the end of the curve segment will be less than the look-ahead feedrate. Update this velocity as the start velocity of the next curve segment to ensure the continuity of feedrate. Ultimately, this completes feedrate scheduling.

5 Simulation results and analysis

In this section, in order to verify the good performance of the method proposed in this paper, NURBS curve interpolation is performed for simulation comparison with the method given in [16].

5.1 Test cases and simulation environment

As shown in Fig. 3,the butterfly-shaped curve [14] is selected as the case study. The feedrate look-ahead method and the interpolation procedures given in [16] is applied to the simulations in this paper. The degrees, control points, knot vectors, and weight vectors of the test curves are given in [19].

The simulations are performed on a laptop equipped with Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz, 8.00GB SDRAM and Windows 10 operating system. And all the algorithms for simulations are developed and implemented on Matlab2018b. The interpolation parameters are listed in Table 1.

5.2 Analysis of the simulation results

The butterfly-shaped curve is divided into 26 segments by break points. The simulation results obtained by [16] methods are shown in Fig. 4 a-c.The acceleration profile exceeds the limits at some interpolation points and so does the jerk profile. This can lead to excessive machine vibration, which affects interpolation quality and efficiency. In rounding error compensation, only the continuity of velocity is considered and not the principle of constant total displacement, so the rounding error still exists. In Fig. 5 a-c, simulation results of the proposed method are presented. It can be seen that the feedrate profile is smooth, and the acceleration profile is continuous. At the same time, the actual feedrate at the end points of each segment never exceeds the feedrate look-ahead result during real-time interpolation. And the acceleration and jerk profile never go beyond the limits.

Fig. 5
figure 5

Simulation results by the proposed method. a Feedrate. b Acceleration. c Jerk

Full size image
Table 2 Comparisons of rounding error and maximum motion parameter
Full size table

The comparisons of rounding error and maximum motion parameter by two methods is shown in Table 2. The feedrate scheduling of the Method in [16] has a rounding errors of 1.42mm, and the maximum acceleration and the maximum jerk are all out of the limited range. The feedrate scheduling of the proposed method has no rounding errors, and none of the motion parameters exceeds the limit range. However, due to the rounding of each interpolation time, the actual maximum feedrate is slightly smaller than the commanded feedrate.

6 Conclusion

This paper proposes a S-shape feedrate scheduling method with rounding error elimination.The main conclusions are as follows:

A new time rounding scheme is designed in this study, which employs distinct time rounding methods for different time intervals to guarantee that the recalculated parameters remain within the prescribed limit. Then, according to the principles of constant displacement and continuity of feedrate, the jerk expression is derived, and an series of feedrate scheduling methods is are designed for different S-shaped ACC/DEC situations. Additionally, a bidirectional interpolation strategy with backtracking correction is designed to adapt to the proposed feedrate scheduling methods, ensuring the continuity of the velocity. Simulation results verify the feasibility and applicability of the proposed method, with rounding error of 0 and feedrate, acceleration, and jerk all within the limit range.