1 Introduction

In many industries, such as the aerospace industries, automobile, biomedical technologies, and electronics, plastic materials are irreplaceable materials due to their flexibility, corrosion resistance, and transparency. For example, plastic materials are used in different applications, such as automobile windows, medical components, and food industries. Most plastic end-products are manufactured using injection-molding processes. Three steps are involved in the injection-molding process: (1) filling phase, in which molten polymers are injected into the cavity; (2) phase of packing, during which high packing pressure is applied to ensure that the cavity is properly filled; and (3) cooling phase, during which polymers solidify and mold temperature drops. Injection molding produces an end-product whose quality is determined by several parameters, including the process, design, and materials used. Here, three common defects leading to a reduction in end-product quality are examined: (1) warpage, (2) short shot, and (3) shrinkage. An injection-molded warped component is considered a serious defect, especially the thin-walled components [1].

A part shrinks when it comes into contact with its cavity during injection molding. It is important to understand how shrinkage affects the final dimensions of molded plastic parts [2]. When a mold cavity is not filled, an incomplete part is called a short shot. When a mold is not injected with enough material, short shots result or when materials freeze before filling a cavity [3]. There are several reasons for this: incorrect selection of plastic materials, incorrect processing parameters, incorrect mold design, and incorrect design of parts.[4]. Moayyedian et al. [5] mentioned that the shape of the gate or runner at the filling stage contributes to short shots. Another investigation of the influence of gate design on injected parts was reported by Tsai [6]. An optical lens mold utilized a rectangular flow restrictor within a tertiary runner for having a uniform distribution of the melt temperature and residual thermal stress and warpage reduction. Using numerical analysis, Kim et al. [7] investigated different gate locations result in different polymer flow patterns, and found that incorrect positioning resulted in short shots when the gate was not positioned correctly.

Pandelidis and Kao [6] employed a fuzzy inference system (FIS) for the detection of defects in the injection molding process. Lee and Kim [7] introduced the modified complex method to minimize the numeric warpage value by considering six injection-molded part parameters, including injection time, cooling, packing pressure, packing time, melt temperature, and coolant temperature. Their proposed method achieved more than 70% reduction in the warpage of injection-molded parts. The minimization of the warpage defects is the goal of recent studies via different methods. He et al. [8] extracted the optimal process parameters of injection molding using an adaptive neuro-fuzzy inference system (ANFIS) in order to reduce the number of trials. The defects of the injection molding process are reduced using their proposed method based on the tested real case results. ANFIS is used in manufacturing fields for the prediction of optimal process parameters such as metal cutting [9]. Lotti et al. [10] proposed the first machine learning-based prediction model of the injection-molded plastic plaques shrinkage using mold temperature, meld temperature, flow rate, and holding pressure. They used the simple feedforward neural network as the suitable machine learning method for developing the prediction model because of the simplicity and cheap computational load. Mok and Kwong [11] determined the process parameters of injection molding based on MLP and FIS. The preliminary validation tests prove the efficiency of their proposed method. Later, Kurtaran and Erzurumlu [12] extract the dataset via the finite element method (FEM) of thin shell plastic parts injection molding. Then, they used analysis of variance (ANOVA) and response surface methodology (RSM) to develop a mathematical relation between the process condition parameters, including melt temperature, mold temperature, cooling time, packing pressure, and packing time toward the warpage of thin shell plastic parts. Also, they employed a genetic algorithm (GA) to extract the optimal parameters of the thin shell plastic parts using the extracted mathematical model via RSM. Gao et al. [13] employed the global optimization-based Kriging surrogate linked to the FEM environment to extract the optimal process and geometrical parameters of a box-shape part for various wall thicknesses. Hassan et al. [14] and Tang et al. [15] investigated the installation of the cooling system in designing the multi-cavity injection molds in points of location and size of the channel for the elimination of shrinkage via uniform solidification. Yin et al. [16] employed the feedforward neural network to estimate plastic parts’ warpage based on melt temperature, mold temperature, cooling time, packing time, and packing pressure. Tsai et al. [17] proposed the hybrid model using GA and to develop an injection molding algorithm for optical lens. The validation experiment proves the higher accuracy of the lens using their proposed method. Abbasalizadeh et al. [18] investigated the optimized amorphous thermoplastics and shrinkage behavior of semi-crystalline using experimental extracted datasets. They discovered that the most effective parameter on shrinkage behavior of polycarbonate using ANOVA. Khosravani et al. [19] reviewed the injection molding manufacturing process based on implementation of artificial intelligence methods. Abdul et al. [20] estimate the width and length shrinkages of the injection molded in high-density polyethylene parts using multilayer perceptron (MLP) under different processing parameters, including holding time, injection speed, and cooling time. They also developed the automatic machine lineaging-based tuning algorithm for mold machines to reduce the number of experiments compared to the error-and-trial method. Song et al. [21] predicted the warpage and shrinkage of injection-molded thin-walled parts using a hybrid machine learning method which is the combination of MLP, GA, and support vector regression (SVR) with higher accuracy compared to previous methods.

Researchers have proposed a hybrid cooling model utilizing fluted conformal cooling channels with inserts manufactured from Fast cool material to create different cooling models. Traditional or conformal standard cooling methods cannot adequately cool the industrial part because of its geometry and the mold’s ejection system requirements. With a Fast-cool insert, heat is optimally transferred to the slender core of the plastic part. Comparing the hybrid design to traditional cooling systems, a transient numerical analysis showed a 27.442% reduction in cycle time for the analyzed part [22]. There is also a proposal for conformal cooling channels with triple hook shapes for thick optical parts that have deep cores and high dimensional and optical requirements. Traditionally, conformal cooling channels are not suitable for these applications due to the small core dimensions and high requirements regarding warping and residual stresses [23]. Optical plastic collimators with conformal cooling channels are also proposed. This study presents conformal channels that outperform traditional and standard conformal channels in terms of thermal and dynamic performance, by implementing new sections of complex topology in order to meet both the geometric and functional requirements of an optical part, as well as the technological requirements of the additive manufacturing process for mold cavities [24].

In recent years, there has been a highly focused focus on optimizing the injection molding process parameters.

Gao et al. [25] used MLP and global optimization methods to design and develop the new machine learning-aided conformal cooling design injection molding to extract the optimal cooling process in order to minimize the injection molding process. Li et al. [26] proposed the Taguchi- and multiple linear regression-based prediction models in injection molding to predict the optimized molding parameters to reach the lowest dimensional deviation of the final product. Speranza et al. [27] predicted the variation of the fibrillar layer thickness in micro–injection molding using the mathematical model. Mahmoudian et al. [24] proposed that to improve the interaction of alumina nanoparticles and PMMA, in situ polymerization of methyl methacrylate was performed on alumina nanoparticles. The modified nanoparticles were dispersed appropriately in the polymer matrix to act as effective additives. To design experiments and optimize input parameters, the Taguchi method was used. Jung et al. [28] assessed the performance of different machine learning methods, including logistic regression, SVR, random forest, gradient boosting, XGBoost, CatBoost, LightGBM, and autoencoder, in the prediction of injection molding quality. Uğuroğlu [29] used machine learning methods, including logistic regression, k-nearest neighbor, random forest, and MLP, to propose a real-time application for plastic injection molding machines. Párizs et al. [30] investigated the performance of different machine learning methods, including a k-nearest neighbor, naïve Bayes, linear discriminant analysis, and decision tree (DT) in the prediction of multi-cavity injection molding’s quality. They discovered that the DT is the most accurate model among all the investigated methods, with more than 90% accuracy in the presence of little training data. Ke and Huang [31] proposed the optimized multilayer perceptron (MLP) using different types of stochastic gradient descent with momentum to predict the quality of injection-molded parts. They reached 95.8% accuracy during the testing process of the model using the Sigmoid activation function and learning rate = 0.1.

Based on the reviewed studies in this section, the prediction model of the injection-molding process quality, such as shrinkage, warpage, short shot, etc., using the process parameters can be categorized into two main groups, including mathematical-based neural network-based models. The neural network-based models are more accurate than the mathematical-based model. However, the neural network-based models cannot be easily defined without an advanced controller machine for molding machines. In addition, the lower config CPU controllers cannot handle the computational load of the neural network-based prediction model in real-time applications. Then, this research gap is filled in this study by developing the model, which combines these two groups, including mathematical and neural networks. Genetic programming (GP) is invented by Koza [32, 33], which is an extension of the GA. It is used to generate the mathematical relation of the injection-molding process as inspired by Darwin’s theory of natural selection. The mathematical model can calculate the injection-molding process, such as shrinkage or warpage, quickly without computing complicated computing. In the second step of the project, the mathematical optimization method using an interior point nonlinear programming solver is employed to extract optimal processing parameters faster than the meta-heuristic algorithm.

The injection-molding process for the thin-walled polypropylene part is explained in the next section. Also, the strategy for gathering the datasets is explained in this section. The methodology of this study is the combination of GP and interior point nonlinear programming solver is explained in Sect. 3. The proposed method is developed in MATLAB, and the results are generated and compared with previous methods in Sect. 4. The conclusions are remarked in Sect. 5.

2 Thin-walled polypropylene parts molded through injection molding

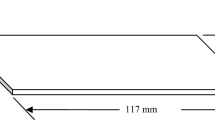
Regarding the literature survey, different defects have been considered in injection molding, and three different defects are selected, namely warpage, volume shrinkage, and short shot. Taguchi’s experimental design is applied to minimize the trial numbers and to determine the most significant parameters for the optimum design affecting the quality of the thin shell plastic part. The modeling of the selected part, including the sprue, runner, and gate, is conducted using SolidWorks, as shown in Fig. 1, and the simulation process is implemented using finite element analyses (FEA) and SolidWorks Plastic. The part selected is a plastic plate with a diameter of 100 mm and a thickness of 1 mm. The dimensional details of two different gates are shown in Fig. 2. The runner and gate length in total are 280 mm for two circular parts. The sprue is of 60 mm length and 1.5 draft angle. Based on the selected defects like warpage and short shot in this study, it is necessary to consider the most critical conditions. Running the simulation trails for a part with a thickness of 1 mm will cover the critical conditions. Hence, the optimum result will be applicable for any thicknesses of any plastic parts. Cool pipe model is selected in order to cool the plastic part and operates by drawing the cooling channels on the solid body representation of the mold. As the mold and cavity are heated, the transient thermal fields are calculated iteratively using the Cool solver. When the mold is heated for the first time, the ambient temperature is used. The solver uses the melting temperature of the uniform melt for the initial part temperature of the next cycle, but uses the mold temperature from the previous cycle to determine the initial part temperature of the next cycle.

Fig. 1
figure 1

The 3D modeling of thin-walled polypropylene part of the injection channels (sprue, runner, and gate)

Full size image
Fig. 2
figure 2

A Rectangular cross-section of an age gate; b elliptical cross-section of modified edge gate; c edge gate; d modified edge gate

Full size image

A key role played by FEM in the simulation will be to ensure the analysis results are accurate. Finite element analysis uses triangle meshes for surface meshes based on the geometry of samples, as shown in Fig. 3. For the injection part, a surface mesh size of 1 mm was chosen after evaluating different sizes. However, smaller sizes were considered for the injection system, which includes the sprue, runner, and gate, due to the sensitivity of the injection system that was a critical component of the simulation. For both elliptical and round cross-sectional shapes of runner in SolidWorks Plastic, surface mesh size of 0.3 mm is selected for sprues and runners, and 0.2 mm for gates. The direct solver option optimizes the Fill and Pack analyses. When hexahedral elements mesh with relatively thick parts, the Direct solver provides a more accurate prediction of inertial effects.

Fig. 3
figure 3

Finite element analysis of the designed part

Full size image

2.1 Injection molding machine and the selected material

Different processes and geometrical parameters are evaluated for this research. Based on the literature survey, 5 parameters have been selected: injection machine inputs and the gate design. The selected injection machine is the Poolad-Bch series, and the chosen material is PP (polypropylene).

2.2 Selection of parameter level and Taguchi orthogonal array

The selected parameters in different levels are gate type, filling time, cooling time, holding pressure time, and melt temperature in three levels (low, mid, and high), based on Taguchi’s experimental design, as shown in Table 1. The first and most significant reason for Taguchi’s application is to reduce the number of trials, which reduces time and cost. Level selection for the selected parameters is based on different simulations to determine the effective minimum and maximum levels (level 1 and level 3, respectively) of each parameter. Level 2 is the average of two other levels. The main reason for having three different levels is to evaluate the effect of each parameter on the selected plastic defects.

Table 1 The selected parameters are at different levels
Full size table

Table 2 shows the selected L18 orthogonal array of Taguchi according to the number and level of parameters. For any engineering application, the Taguchi method proposes three different quality evaluation concepts: smaller the better, nominal the best, and larger the better [34]. This paper aims to reduce the selected defects to their minimum level. Hence, smaller, better-quality characteristics are applied according to the Taguchi method and relevant tools such as Signal to noise ratio (S/N ratio). The simulation of each trial is conducted using SolidWorks Plastic to determine the value of individual defects.

Table 2 L18 orthogonal array of Taguchi
Full size table

For quality evaluation, three plastic defects are considered, namely warpage, volume shrinkage, and short shot, as illustrated in Fig. 4. The initial weight of each plastic defect is calculated via analytic hierarchy process (AHP), as illustrated in Table 3, with reference to their classification illustrated in Fig. 4. AHP can be applied in different engineering fields. For instance, in air gasification of plastic waste, studies showed that in conventional biomass gasification, hydrogen production decreased linearly with an increasing equivalence ratio, but in plastic waste gasification, an optimum equivalence ratio achieved the highest hydrogen output [35,36,37]. Based on Table 3, out of 100%, short shot has 50% contribution, volume shrinkage 20%, and warpage have 30% contribution.

Fig. 4
figure 4

The quality evaluation criteria

Full size image
Table 3 The calculation of initial weight
Full size table

The calculation of S/N ratio is conducted as shown in Table 4, based on Eq. (1) and Eq. (2) as follows, where \({\varvec{N}}\) is the number of experiments per trial and \({{\varvec{y}}}_{{\varvec{i}}}\) is the sum of the selected defects [38, 39].

Table 4 Signal to noise ratio calculation for 18 experiments
Full size table
$$\frac{S}{N}=-10\mathrm{log}\left(MSD\right)$$
(1)
$$MSD=\frac{1}{N}\left({\sum }_{i}^{n}{{y}_{i}}^{2}\right)$$
(2)

Concerning Table 4, the minimum and maximum defects value is related to trial 18 and trial 1, respectively. The simulation result for trials 1 and 18 is shown in Fig. 5a, b.

Fig. 5
figure 5

The short shot, shrinkage, and warpage for trial 1 (a): maximum; (b): minimum

Full size image

The next step is to determine the optimum level of the selected parameters based on the response table of Taguchi. Concerning Table 5, the highest value of individual parameters shows the optimum level of the selected parameters. Hence, gate design at level 2 (edge gate), filling time at level 3, cooling time at level 3, holding pressure time at level 3, and melt temperature at level 2 is the best combination. Also, the most important parameters affecting the selected defects are melt temperature and holding pressure time, followed by gate type, cooling time, and filling time, respectively, based on the difference value extracted from Table 5.

Table 5 The response table of Taguchi
Full size table

After finding the optimum level of individual parameters, the next step is to run the simulation to determine the value of the defect for the optimum design, as shown in Fig. 6. Regarding Table 6, the sum of the defects for the optimum design is 0.18, which is less than the minimum sum related to trial 18 in Table 6.

Fig. 6
figure 6

The short shot, shrinkage, and warpage analysis for the optimum design

Full size image
Table 6 The sum of defects for the optimum design using the Taguchi method
Full size table

3 Methodology

The neural network and meta-heuristic methods have been employed recently by many researchers to calculate the optimal processing parameters of the injection-mold machine to reach the highest quality in point of lowest shrinkage, warpage, and short shot. However, the high computational load of the neural network and meta-heuristic algorithms are the main disadvantages of these methods despite their accuracy. Figure 7 shows the graphical abstract of this paper, which is the whole proposed methodology in this research. It consists of 9 stages, from selecting experiment parameters to extracting optimal injection-molding process parameters. In the first stage, the different sets of injection-molding process parameters, including part cooling time, filling time, melt temperature, and holding pressure time, are established using the Taguchi method to reduce the number of experiments.

Fig. 7
figure 7

The graphical abstract of the proposed method

Full size image

The motivation is to reduce the total run time of the FEM to reach the highest accuracy. In the second stage, the SolidWork Plastics software, as the selected candidate for the FEM environment, calculates the shrinkage rate, warpage, and short shot. As explained in the previous section, the objective values combine these three down facts of the injection-molding process in the third stage of the work, which is calculated based on Eqs. (1–2).

In the fourth stage and after finishing the simulation stage, the datasets are gathered as.CSV files to be called and used in the next stages of the study. These four stages are straightforward, and they have been explained in detail in the previous sections. The datasets should be pre-processed before employing the machine learning method for training and developing the prediction model to reach the highest accuracy of the proposed method (stage 5). In this research, GP is employed to generate the mathematical formulation of the injection-molding process with acceptable accuracy. GP is a machine learning method, while the outcome is in the form of a mathematical or statistical model. This job has been done in the sixth stage of the proposed work in Fig. 7. The method has been analyzed and evaluated with previous methods such as DT, SVR, and MLP to prove the acceptable accuracy of the proposed method in stage 7 of the work. Stages 6 and 7 are related to the first contribution of the research. The second part of the contribution is accomplished in the eighth stage of Fig. 7. The interior-point nonlinear programming solver extracts the optimal process parameters of the injection-molding process in a fraction of the time. This section is composed of three subsections, including the description of data pre-processing (stage 5), GP (stage 6), and mathematical-based optimization (stage 8), respectively.

3.1 Data pre-processing

Three tasks should be implemented in the data before developing the model and applying the dataset. Initially, the data out of range should be removed to increase the robustness of the system. The second step is related to the normalization or standardization of the system to decrease the data complexity for a system before training. Both methods are employed to decrease the complexity of the network’s input data and increase the system’s accuracy. The following formula is used to calculate the data standardization:

$${\sigma }_{{x}_{i}}=\frac{{x}_{i}-\overline{x}}{{\sigma }_{x}}$$
(3)

where \({{\varvec{x}}}_{{\varvec{i}}}\), and \({{\varvec{\sigma}}}_{{{\varvec{x}}}_{{\varvec{i}}}}\) are respectively the ith raw and standardized input data. \({{\varvec{\sigma}}}_{{\varvec{x}}}\) and \(\overline{{\varvec{x}} }\) are also the functions for extracting the standard and average deviation of the data. The normalized data can also be obtained as:

$${n}_{{x}_{i}}=\frac{{x}_{i}-\underline{x}}{\overline{x}-\underline{x}}$$
(4)

where \({{\varvec{n}}}_{{{\varvec{x}}}_{{\varvec{i}}}}\) is the ith normalized input data. \(\underset{\_}{{\varvec{x}}}\) and \(\overline{{\varvec{x}}}\) are also the functions for extracting the minimum and maximum values of the data. During the final network pre-tuning process, the data is divided into 95% and 5% for the testing and training process of the network. The testing data is not shown to the system till the testing stage of the network in order to reach realistic results via the proposed models.

3.2 Genetic programming

Nowadays, due to the incompetency of classical optimization methods, applying nature-inspired optimization algorithms has found great popularity in various engineering fields. One of the most important sources of inspiration is the evolutionary behavior of chromosomes in living beings which leads to generations with fewer defects and more efficiency. Genetic algorithm, GA, is a sample of algorithms that imitate chromosomes’ behaviors in searching for the best solution to a given problem. GA aims to search the global optimum of a defined objective function in a limited search space by applying various operators on a population of number strings. One of the most applicable alternatives for GA that operates on the string of codes and functions, in addition to numbers, is GP. Firstly introduced by Koza in 1992 [32, 33], GP combines the principles of automatic programming and core precepts of evolutionary characteristics of chromosomes to approach a model-based optimization methodology. Applying various operators, chiefly crossover and mutation, on the strings of functions, numbers, and codes, GP, compared to GA, is more capable of solving more complicated problems. Introducing an accurate mathematical model based on input independent parameters and output measured values is another unique ability of the GP technique. In Fig. 8, samples of chromosomes in GP and operators to generate new offspring are illustrated.

Fig. 8
figure 8

Mathematical operations and members in GP

Full size image

In order to regenerate the mathematical model using GP, the below steps are as follows:

  • 1.The initial population is created via the random selection of the genome using different lengths.

  • 2.The fitness function is estimated for every genome.

  • 3.The initial population’s genomes are sorted using the fitness functions.

  • 4.The next generation’s genome is selected based on the minimum cost function value.

  • 5.The generation is calculated using the selected genomes and the GP’s probabilities.

  • 6.The termination criteria are checked. The unsatisfied termination criteria lead to step 2. The satisfied termination criteria lead to the evaluation of the next iterations.

The depth of the tree is defined using initial depth and operation depth. The operations of GP, including mutation, reproduction, and crossover, act in the tree’s different branches and components. There are two types of random mutation in GP, including replacement/termination of function with other function and swapping the sub-branches, as shown in Fig. 8.

GP is used to express the mathematical relation of the model known as the symbolic regression tool, which is the optimized version of the system based on the provided datasets. Based on the represented steps of GP, the initial version of the equation is generated via random combinations of mathematical functions, constant values, independent variables, and arithmetic operations. Based on Fig. 8, the terminal branches are the system’s variable or constant values.

In this paper, a genetic equation was extracted to the model of the cost function based on input molding parameters, including filling time (\({\varvec{B}}\)), part cooling time (\({\varvec{C}}\)), holding pressure time (\({\varvec{D}}\)), and melt temperature (\({\varvec{E}}\)) in injection-molding process of thin-walled polypropylene. To obtain the genetic equation, arithmetic functions are defined as follows:

$$T=\left\{+,-,\times,\div,1/x,x^2,x^3,\sqrt x,\sqrt[3]x\right\}$$
(5)

The number of chromosomes, mutation rate, and crossover rate were selected as 30, 0.1, and 0.044, respectively. The algorithm was terminated after 200,000 generations, and the best model was presented as the answer to the modeling process.

3.3 An interior point nonlinear programming solver

An interior-point method for solving the nonlinear programming problem is initially introduced by Fiacco and McCormick in the 1960s [40]. It is one of the powerful algorithms for solving large-scale nonlinear problems. The concept of the interior point is more complicated because of adding some new challenges, such as updating interior-point parameters, progress toward the solution, and nonconvexity treatment. The interest in the usage of interior-point solvers was raised in the 1980s after showing its power in solving the linear problem. It was used to solve the nonlinear problem by the late 1990s as there was a need to generate new methods and software. The interior-point proves its efficiency in handling large-scale nonlinear problems faster than other methods, such as the active set. The main motivation of the interior point method is to create the barrier function for keeping the constraints inside the objective function. This strategy leads the potential solutions inside the feasible area with higher efficiency compared with other nonlinear solvers in the point of computational time.

A perturbation factor (\({\varvec{\mu}}\)) is defined as the nonlinear solver program inside the feasible area via penalizing solutions close to the boundaries. The movement of the selected solutions toward the boundaries will increase the perturbation factor. Then, the feasible region center is selected if the perturbation factor is very large. On the other hand, the optimal solution is traced out of the central path with the small perturbation factors. Then, reducing the perturbation factor at every iteration leads to a smooth curve for the central path. This mentioned method is accurate and extremely intense in the point of computational load. Then, Newton’s method is employed to reduce the computational load of the solver in an approximation of the central path of the nonlinear programming. The logarithmic interior-point function is used as:

$$A\left(x,\mu \right)=f\left(x\right)-\mu \mathrm{log}\left(x\right)=f\left(x\right)-\mu \sum_{i=1}^{m}\mathrm{ln}\left({x}_{i}\right)$$
(6)

The interior-point is used mostly in the solution of the week-known optimal power flow problems. In optimal power flow problems, the goal is to extract the optimal solution of a power network using reliability and speed. In order to solve the nonlinear programming, the general form of the optimization can be defined as follows:

$$\mathrm{min}f\left(x\right)$$
(7)
$$\mathrm{s}.\mathrm{t}. h\left(x\right)=0$$
(8)
$$g\left(x\right)\le 0$$
(9)

The equations are modified using the slack variables convergence properties, Karush–Kuhn–Tucker conditions, and perturbation factor as:

$${\nabla }_{x}L\left(x,{\lambda }_{h},{\lambda }_{g}\right)=0h\left(x\right)=0$$
(10)
$$g\left(s\right)+s=0$$
(11)
$$\left[{\lambda }_{g}\right]s-\mu e=0$$
(12)
$$\left(s,{\lambda }_{g},\mu \right)\ge 0$$
(13)

The nonlinear equations are solved iteratively using Newton’s methods. Initially, \(\Delta {\varvec{x}}\) and \(\Delta {{\varvec{\lambda}}}_{{\varvec{h}}}\) are determined by reducing the linear equations. Then, slack variables \(\Delta {\varvec{s}}\) and corresponding multipliers \(\Delta {{\varvec{\lambda}}}_{{\varvec{g}}}\) are calculated using:

$$\Delta s=-g\left(s\right)-s-\nabla g\left(s\right)\Delta x$$
(14)
$$\Delta {\lambda }_{g}=-{\lambda }_{g}+\left[{s}^{-1}\right]\times \mu e-\left[{\lambda }_{g}\right]\Delta s$$
(15)

The perturbation factor μ can be extracted via the primal–dual distances as follows:

$$\mu =\sigma \times pdad=\sigma \times \frac{{\lambda }_{g}^{t}s}{niq}$$
(16)

where \({\varvec{\sigma}}\), \({\varvec{p}}{\varvec{d}}{\varvec{a}}{\varvec{d}},\) and \({\varvec{n}}{\varvec{i}}{\varvec{q}}\) are the optimal solution trajectory, the average distance of the primal–dual and inequality constraints. It should be noted that \({\varvec{\sigma}}\) varies from 0 to 1, while \({\varvec{\sigma}}=0\) refers to the affine-scaling direction, and \({\varvec{\sigma}}=1\) uses to centralization direction.

4 Results and discussions

The presented method in Sect. 3 consists of two main models, including GP and the interior point method. The GP model is designed and trained using the captured datasets via the GPLAB toolbox of MATLAB developed by S. Silva [41]. It is used to extract the mathematical model of the investigated system. Then, the interior point method is implemented using the fmincon of MATLAB software based on the extracted mathematical model using GP.

In order to evaluate the proposed methodology:

  • 1.The first contribution of the work related to the extraction of the mathematical models using GP has been compared with the common previous methods, including DT, SVR, Taguchi, and MLP, to show the efficiency of the proposed method in the point of accuracy and extraction of the full mathematical model.

  • 2.The second step extracts the optimal process parameters using the interior point method. It has been compared with GA as the most common phrase of the meta-heuristic method. The accuracy is in the acceptable range, while the computational load of the interior point method is extremely lower than the GA method.

A genetic equation was developed to determine the relationship between input molding parameters and output cost function in the injection-molding process of thin-walled polypropylene. The best genetically reached model considering mentioned arithmetic functions in Eqs. (1–2) using mathematical operation (+ , − , × and /), exponential, root, and trigonometric functions were presented as follows:

$${J}_{1}\left(B,C,D,E\right)=12.48\times {\mathrm{tan}}^{-1}\left(\left(\frac{\mathrm{coth}B}{\mathrm{cot}E}\right)-2.83\right)+\mathrm{sech}\left(\mathrm{csc}\left(B+4.15\right)\times {e}^{B}\right)-\mathrm{tanh}\left(\mathrm{sec}\left(\mathrm{csch}C\right)\right)+{\mathrm{tan}}^{-1}\left(\left({\mathrm{csc}}^{-1}\frac{{D}^{2}}{C}\right)\times \left(\mathrm{tan}\sqrt[3]{E}-0.0245\right)\right)+\mathrm{sin}\left(\left(-1.03D+19.18\right)+D-4.68-\mathrm{sech}B\right)+\mathrm{csch}\left(\mathrm{cot}\left({\mathrm{tanh}}^{-1}\left(\sqrt[3]{\mathrm{sech}\left(-0.15BE\times \mathrm{tan}C\right)}\right)\right)\right)$$
(17)

where \({\varvec{B}}\), \({\varvec{C}}\), \({\varvec{D}},\) and \({\varvec{E}}\) are filling time (s), part cooling time (s), holding pressure time (s), and melt temperature (○C), respectively. Equations (1–2) are the complicated version of the extracted GP-based prediction model of the cost function concerning the process parameter. This model is named GP1 in the rest of the paper.

In addition, the simpler mathematical model (named GP2) is extracted via the GP using mathematical operation (+ , − , × , and /), exponential, and root as follows:

$${J}_{2}\left(B,C,D,E\right)=-1.82\frac{D}{E}-2.02-\sqrt{6.8+B}+E+\frac{{B}^{4}C}{109.66-E}+4.39+\frac{\sqrt[3]{C}}{0.38B{E}^{3}}+\frac{{B}^{4}{C}^{2}+8.45E}{2.4B{E}^{4}}$$
(18)

Also, other methods, including DT, SVR, and MLP, are used to estimate the cost function value in Eqs. (1–2). The estimation of a cost function based on Eqs. (1–2) using FEM, DT, SVR, MLP, GP1, and GP2 are presented in Table 7. The best-estimated value for each trial in comparison with FEM is shown in the bold mod. Based on the represented results in Table 7, the prediction power of the MLP and GP1 during the training process is equal to 3-times best estimations of the cost function. However, the traditional methods, including DT and SVR methods, reach the weakest power of cost function estimation during the training process of the network. It should be mentioned that the highest accurate model should be selected based on the represented results during the testing process of the network, as the model should be used for all possible situations. Our proposed GP models (including GP1 and GP2) are the most accurate in predicting the cost function value during the testing process, with five times best value extraction out of 6 times trials.

Table 7 The obtained results using different sets of process parameters via FEM, DT, SVR, MLP, and GP
Full size table

In addition, the accuracy of obtained methods including DT, SVR, MLP, GP1, and GP2 using mean square error (MSE), root means square error (RMSE), normalized root means square error (NRMSE), and correlation coefficient (CC) are given in Table 8. Based on the represented result, the GP2 is the best accurate model among others, with the lowest MSE, RMSE, mean of error, variation of error, and higher CC.

Table 8 The obtained results using different sets of process parameters via FEM, DT, SVR, MLP, and GP
Full size table

Figure 9 shows the calculated objective function value based on Eqs. (1–2) using FEM, DT, SVR, MLP, GP1, and GP2. Based on the represented results in Fig. 9, CC between the actual value (using FEM) and predicted value via GP1 improved by 2.07%, 70.59%, and 20.19% compared to those of DT, SVR, and MLP, respectively. Then, GP1 can reach better results while representing the mathematical model used in a real-time application with a little computational load. In addition, the CC of GP2 is 0.78% higher than GP1.

Fig. 9
figure 9

The calculated objective function using FEM (Target), DT, SVR, MLP, GP1, and GP2

Full size image

In addition, Fig. 10 shows the error between the calculated objective function between the target (via FEM) and the predicted value (via DT, SVR, MLP, GP1, and GP2). Based on the represented results in Fig. 10, the RMSE of predicted objective value using GP is 16.30%, 71.29%, and 53.95% better than DT, SVR, and MLP models. In addition, GP2 is more accurate than GP1, with 25%, 8.14%, 26.89%, and 8.19% lower MSE, RMSE, mean error, and STD, respectively.

Fig. 10
figure 10

The error of the calculated objective function between the target (via FEM) and predicted value (via DT, SVR, MLP, GP1, and GP2)

Full size image

Figure 11a–d shows the regression of the investigated method in this study, including DT, SVR, MLP, GP1, and GP2, during the training and testing processing of the networks, respectively. It shows the acceptable accuracy of using GPs compared to other methods as the most accurate method in the point of higher regression. The GP models, including GP1 and GP2, are the most accurate models among the investigated models, including DT, SVR, and MLP. Among the previously studied models (including DT, SVR, and MLP), it should be noted that MLP is the most accurate model. However, the extracted MLP model has some short come. Firstly, the proposed model is Blackbox. The information inside the box is complicated. Secondly, based on the deepness of the MLP structure, the model gets computationally heavy. It is the biggest disadvantage of this model against its real-time applicability.

Fig. 11
figure 11

The regression between the actual objective function value via FEM and predicted value using (a): DT; (b): SVR; (c): MLP; (d): GP1; (e): GP2

Full size image

However, the main novelty of this study is the lower computational load of the system compared to the neural network-based models. The computational time for calculation of the cost function in the injection-molding process is evaluated using the tic/toc function of MATLAB, and the results show that the average computational time of 18 trials using DT, SVR, MLP, GP1, and GP2 is 0.0560, 0.0445, 0.4859, 0.0383, and 9.4710 × 10−4 (seconds), respectively. It proves the efficiency of the proposed GP-based prediction method in handling the real-time application computational complexity even in the presence of lower specification PCs. As it is obvious, the simplicity of the GP2 model in comparison with the GP1 model can decrease the computational time of the model from 0.0383 to 9.4710 × 10−4 (seconds). Also, MLP is the highest computationally expensive model, with 0.4859 (seconds) in each iteration. It should be noted that the code has been tested using a PC with Intel(R) Core(TM) i7-9007 CPU @ 3.60 GHz.

In the next step, the extracted mathematical model is solved using the interior point method, and the results are reported in Fig. 12a–d. Figure 12a, b shows the selected optimal solution and the convergence plot using the fmincon function of MATLAB, which is terminated after 20 iterations for the GP1-based prediction model, respectively. Also, Fig. 12c, d shows the selected optimal solution and the convergence plot using the fmincon function of MATLAB, which is terminated after 20 iterations for the GP2-based prediction model, respectively. Then, the selected optimal solution parameters using GP1 model are filling time = 0.9944 (seconds), part cooling time = 4.300 (seconds), holding pressure time = 9.9363 (seconds), and melt temperature = 256.0398 (○C). In addition, the selected optimal process parameters are filling time = 0.9944 (seconds), part cooling time = 4.300 (seconds), holding pressure time = 9.9363 (seconds), and melt temperature = 256.0398 (○C) using the GP2 model, which is extracted via fmincon function of MATLAB.

Fig. 12
figure 12

The results of fmincon for GP1 (a): selected optimal solution (b): convergence of the solution after 20 iterations. The results of fmincon for GP2 (c): selected optimal solution (d): convergence of the solution after 20 iterations

Full size image

This study’s contribution was to propose the appropriate model to predict the optimal molding process parameters without facing the higher computational load, which is common in neural networks and meta-heuristic methods. Also, the results prove the acceptable accuracy of the proposed model using GP and fmincon compared to previous models, including DT, SVR, and MLP.

5 Conclusion

In order to reduce the defects in the injection molding process, a quality evaluation model consisting of Taguchi, AHP, and SolidWorks plastics was applied to evaluate the optimum process and geometric parameters. According to the simulation results, the proposed quality evaluation model can establish injection molding process parameters that are efficient and geometrically accurate. Previously, DT, SVR, and MLP models are investigated in extracting optimal process parameters of the injection-molding process as traditional (DT and SVR) and neural network (MLP) models. However, the accuracy of the traditional model, including DT and SVR, is not appropriate. Also, the neural network-based models are computationally expensive regarding the deepness of the network. In addition, the extracted neural network-based model is like a Blackbox without any knowledge from inside of the function. In this study, the lower computational load is targeted to extract the optimal process parameters of the injection-molding process. Two GP-based models are trained and extracted with the definition of mathematical operation (+ , − , × , and /), exponential, root, and with/without trigonometric functions called GP1 and GP2, respectively. The GP-based mathematical model is extracted using the GPLAB toolbox of MATLAB. The proposed GP1 and GP2 prove the higher efficiency compared with the DT, SVR, and MLP models in point of accuracy with lower MSE, RMSE, and higher CC. Also, the lower computational time of the GP2-based prediction model is the most interesting discovery of this study. In the next step, the proposed mathematically based prediction models, including GP1 and GP2, are solved using the fmincon function of MATLAB software interior point method. The extracted solutions are tested in SolidWorks Plastics, and the results show the lower objective functions using the extracted optimal process parameters with higher efficiency. As a future study, the other highly advanced shape of machine learning methods as well as meta-huerestic optimization can be employed to increase the efficiency of the model [42,43,44,45,46,47].