A novel intelligent approach based on WOAGWO-VMD and MPA-LSSVM for diagnosis of bearing faults

Abstract

The bearing fault diagnosis plays an important role to reduce catastrophic failures and ensure the continuity of running machines to avoid heavy economic loss. The vibration signals of rolling bearings are often nonlinear and nonstationary; it is difficult to extract sensitive features and diagnose faults by traditional signal processing methods. To solve this problem, a novel intelligent fault-diagnosis approach based on whale optimization algorithm grey wolf optimization-variational mode decomposition (WOAGWO-VMD) algorithm and the marine predators algorithm optimization-least squares support vector machine (MPA-LSSVM) is proposed in this paper. Firstly, hybrid algorithm WOAGWO is used to optimize the parameters of VMD and obtain the optimal combination (K; α). Then, the optimized VMD algorithm is utilized to decompose the vibration signal of the rolling bearing into several intrinsic mode functions, and a new sensitive indicator is created to select the components containing the most information. For these components, the dispersion entropy feature, permutation entropy feature, and singular value feature are extracted to form the multi-feature vector. Finally, the feature vectors obtained are input to the MPA-LSSVM for diagnosis and identification. The validity and strength of the proposed method is verified by experimental data under different bearing conditions. The results have shown that the proposed method can extract the fault feature information of 16 bearing signals of different fault types effectively and identify them accurately.

1 Introduction

Rotating machines are one of the necessary equipment widely used in modern industry as they represent the mainstay of various vital industries such as nuclear power plants, petrochemical plants, and others, and due to their great importance, the continuity of the work of these machines is necessary, and despite their reliability, their work regularly under unstable conditions, such as variable rotational speed, overload, and unsteady thermal condition, makes it vulnerable to several failures. It can lead to massive financial and economic losses or even human life safety problems if left undetected [1, 2]. One of the main causes responsible for stopping rotating machines is bearings defects, because they are often exposed to rigorous environments during long-term operation. According to many studies, more than 45% of rotating machinery failures are due to bearing failures [3]. Therefore, it is crucial to identify the fault state, timely, necessarily and accurately to ensure the safe and continuous operation of machinery. The diagnosis of bearing faults has become the concern of many researchers from various fields, where, at the present time, it has formed a multi-disciplinary research structure. Its detection and diagnostic technologies mainly include vibration diagnostic technology, acoustic diagnostic technology, and temperature diagnostic technology [4]. The combination of these technologies can improve diagnosis accuracy. Currently, vibration signal analysis (vibration diagnosis) is one of the most widely used techniques. According to Mohd Ghazali and Rahiman [5], the vibrational diagnosis technique represents more than 82% of the overall other techniques used in fault diagnosis. Due to the complex working conditions that bearings are subjected to, the vibration signal will inevitably be nonlinear and non-stationary and contain noise, which considerably increases the difficulties in diagnosing bearing faults [6, 7]. In the field of rolling bearing fault vibration signal processing, there are some popular signal processing methods for example wavelet transform (WT) [8], Hilbert-Huang transform (HHT) [9], empirical mode decomposition (EMD) [10], ensemble empirical mode decomposition (EEMD) [11, 12], complete ensemble empirical mode decomposition adaptive noise (CEEMDAN) [13], and local mean decomposition (LMD) [14]. Although these methods gave some results, there are some problems, where WT needs to select the wavelet basis and decomposition level, which partially limits their application, while HHT’s limitation is energy leakage produced by the endpoint effect and unexpected negative frequency [15]. As for EMD, EEMD, and LMD methods, they have some adverse effects such as mode mixing and endpoint effect [16]. To solve the problems found in the aforementioned methods such as mode mixing and endpoint effect, Dragomiretskiy [17] proposed a non-iterative and adaptive signal processing method called variational mode decomposition (VMD) that has a solid mathematical basis, where it can adaptively decompose the vibration signal into several narrow-band signals of different frequencies. Marco Civera derived an effective comparison between the VMD, EMD, and CEEMDAN for the vibration-based structural health monitoring purposes and denoted the feasibility of VMD over the later methods [18]. Ye et al. [19] used VMD to decompose the original bearing vibration signal into several intrinsic mode functions (IMFs) and used the feature energy ratio to reconstruct the bearing vibration signal, then the multiscale permutation entropy is calculated to construct multidimensional feature vectors. And then the PSO-SVM model optimized is used in classification and identification of different faults of the rolling bearing. Fu et al. [20] proposed a new hybrid approach, coupling VMD algorithm, composite multiscale fine-sorted dispersion entropy (CMFSDE), and support vector machine (SVM) for fault diagnosis of rolling bearings. The original signal was decomposed into several IMFs by VMD, and then calculated the CMFSDE value of each IMF to form fault features. Finally, these features are used as input to SVM classifier optimized by MSCAHHO to identify the fault types. The previous studies have proved the effectiveness of the VMD algorithm in signal decomposition. However, the selection of the main two parameters, the decomposition level K and the penalty factor α, has always limited the improvement of the performance of VMD. Nowadays, with the development of smart algorithms, many researchers have proposed algorithms to solve this problem. Li et al. [21] utilized the genetic algorithm (GA) to optimize VMD parameters and used the sample entropy as the fitness function. Yao et al. [22] proposed a hybrid gearbox fault diagnosis method based on GWO‐VMD and DE‐KELM. Where they used the grey wolf optimizer (GWO) to optimize the parameters of the VMD in order to eliminate effectively the noise present in the vibration signals. Zhang et al. [23] proposed a method to select the optimal parameters [k, $\alpha$] in the VMD algorithm based on improved particle swarm optimization and the envelope entropy value as the fitness function. Feng et al. [24] applied the whale optimization algorithm (WOA) to optimize the parameters of VMD in order to reduce noise and obtain adaptive decomposition of vibration signals.

After decomposing the signal into several IMFs, the next procedure is to extract fault features from IMFs. With the evolution of artificial intelligence, bearing fault diagnosis is highly treated as a category of pattern recognition. Its feasibility and reliability largely related to the choice of feature vector [25]. Zhang et al. [26] decomposed the experiment gear fault data into several IMFs by the adaptive local iterative filtering, and calculated the permutation entropy of each IMF as the fault feature vector. Jin et al. [27] proposed a fault diagnosis method of train rolling bearing based on VMD to decompose the original signal into several intrinsic mode components (IMF) and calculated the distribution entropy of each component as the feature vector. Cheng et al. [28] proposed a bearing fault diagnosis method based on VMD and singular value feature (SVD) for feature extraction and G-G fuzzy clustering for fault identification. Therefore, we consider in this paper the multi-features based on dispersion entropy feature (DE), permutation entropy feature (PE), and SVD as the fault feature vector of rolling bearing vibration signal.

Obviously, the key step after feature extraction is to use an effective classifier for fault identification. Currently and with the continuous development of machine learning and deep learning, there are several classifiers that have been presented and used for fault diagnosis in rotating machines, such as artificial neural network (ANN) [29], extreme learning machines (ELMs) [30], SVM [31, 32], and deep learning [33]. In addition to these methods, we mention least-square support vector machines (LSSVM). The LSSVM can successfully process non-linear data. Hence, it was effectively investigated by many literatures in diagnosing and fault classification caused by bearings [34], and gears [35]. However, the accuracy of the LSSVM classification is highly sensitive to the selection of the penalty parameter C and kernel parameter g. To determine the values of the optimal parameters, a combination of intelligent optimization algorithms and LSSVM can be used. There are many smart optimization algorithms, including GA, particle swarm optimization (PSO), WOA, and GWO. Gao et al. [36] used the PSO to optimize LSSVM and applied it to fault classification of rolling bearings. Hanoi University of Industry et al. [37] proposed an automatic fault diagnosis approach for rolling bearing based on EEMD-LaS and Optimized Classifier BSO-LSSVM. Although the previously mentioned intelligent algorithms have been successful in improving the LSSVM classifier parameter, they still have some limitations, where it is not accurate at finding the global optimum parameter optimization, and this is confirmed by the theory of no free lunch [38]. To solve this defect, novel meta-heuristic optimization algorithm called MPA has been applied. In this paper an, intelligent model was developed for fault diagnosis of rolling bearing. This model was based firstly on hybrid algorithm WOAGWO to optimize the parameters of VMD. Then, the optimized VMD algorithm is used to decompose the vibration signal into several IMFs. Secondly, a new sensitive indicator (SI) is created to define the components containing the most information and calculate DE, PE, and SVD of each IMF to form the multi-feature vector. Finally, we used the marine predator algorithm MPA to optimize the parameters of classifier LSSVM; hence, the optimized model is used to classify and identify the different fault types of rolling bearing.

This paper is organized as follows. Section 2 presents the techniques used for fault feature extraction, including WOAGWO-VMD algorithm, and SI. Section 3 elaborates the fault feature classification using MPA-LSSVM. Section 4 describes the proposed intelligent diagnosis method based on WOAGWO-VMD and MPA-LSSVM. Section 5 presents the experimental analysis to check the validity of the proposed method for rolling bearing fault diagnosis; finally, the conclusion of this paper is given in Sect. 6.

2 Fault feature extraction

2.1 Variational mode decomposition

VMD is a novel signal processing method, which is adopted to decompose the original signal into several IMFs. In VMD algorithm, the vibration signal is adaptively decomposed into several IMFs in order to find the variational problem. The variational problem can be expressed as follows:

$$\left\{\begin{array}{l}\mathrm{min}\left\{\sum_{k}{\Vert {\partial }_{t}\left[(\delta \left(t\right)+\frac{j}{\pi t}*{u}_{k}(t)\right]{e}^{-j{\omega }_{k}t}\Vert }_{2}^{2}\right\}\\ s.t. \sum_{k}{u}_{k}\left(t\right)=f\left(t\right) \quad \quad k= 1, 2\dots ..K\end{array}\right.$$

(1)

where ${u}_{k}$ is the kth IMF and ${\omega }_{k}$ is the bandwidth center frequency. $K$ denotes the decomposition number. $f (t)$ is the original signal. ${\partial }_{t}$ is the partial derivative function and $\delta \left(t\right)$ is the Dirichlet function. In order to solve the variational problem, the parameters of penalty factor α and the Lagrange multiplication operator λ(t) are introduced to transform the constrained variational problem into an unconstrained problem as follows:

$$\begin{aligned}\mathrm{L}(\left\{{\mathrm{u}}_{\mathrm{k}}\right\},\left\{{\upomega }_{\mathrm{k}}\right\},\lambda )&=\alpha \sum_{k}{\Vert {\partial }_{t}\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*{u}_{k}(t)\right]{e}^{-j{\omega }_{k}t}\Vert }_{2}^{2}\\&+{\Vert f(t)\_\sum_{k}{u}_{k}(t)\Vert }_{2}^{2}+\langle \lambda \left(t\right),f(t)-\sum_{k}{u}_{k}(t)\rangle\end{aligned}$$

(2)

where α is the penalty parameter; λ is the Lagrange multiplier.

To find the optimal solution of Eq. (2), the alternating direction method of multipliers is utilized [16]. The implementation steps for the algorithm are as follows:

• Step 1. Perform an iterative loop n = n + 1;

• Step 2. Update $\left\{{\widehat{u}}_{k}(\omega )\right\}$ for all $\omega$ ≥ 0;

  $${\widehat{u}}_{k}^{n+1}\left(\omega \right)=\frac{\widehat{f}\left(\omega \right)-\sum_{i\ne K}{\widehat{u}}_{i}\left(\omega \right)+\frac{\widehat{\lambda }(\omega )}{2}}{1+2\alpha {(\omega -{\omega }_{k})}^{2}}$$

  (3)

• Step 3. Update the modal center frequency $\left\{{\widehat{\omega }}_{k}\right\}$

  $${{\widehat{\omega }}_{k}}^{n+1}=\frac{\underset{0}{\overset{\infty }{\int }}\omega {\left|{\widehat{u}}_{k}(\omega )\right|}^{2}d\omega }{{\int }_{0}^{\infty }{\left|{\widehat{u}}_{k}(\omega )\right|}^{2}d\omega }$$

  (4)

• Step 4. Update Lagrange multiplication operator $\widehat{\lambda }(\omega )$

  $${\widehat{\lambda }}^{n+1}\left(\omega \right)={\widehat{\lambda }}^{n}\left(\omega \right)+\tau \left((\widehat{f}\left(\omega \right)-\sum_{K}{\widehat{u}}_{K}^{n+1}\left(\omega \right)\right)$$

  (5)

• Step 5. Repeat steps 1–4 until the iteration stop condition is satisfied

  $$\sum_{K}\frac{{\Vert {\widehat{u}}_{k}^{n+1}-{\widehat{u}}_{k}^{n}\Vert }_{2}^{2}}{{\Vert {\widehat{u}}_{k}^{n}\Vert }_{2}^{2}}<\varepsilon$$

  (6)

• Step 6. End.

  where ε represents the tolerance of convergence criterion.

2.2 WOAGWO algorithm

2.2.1 Whale optimization algorithm

WOA is a new optimization algorithm introduced in metaheuristic algorithms by Mirjalili and Lewis. WOA simulates humpback whale hunting behavior [39]. These whales generally prefer to hunt small fish near the surface of the sea, where they use a special fishing technique called the bubble net feeding technique. WOA includes three types of mathematical behavioral simulations, which are as follows:

• (a) Encircling prey

In order to begin the hunt, humpback whales locate the prey and then surround it, and this behavior can be represented by the following formulas:

$$\overrightarrow{X}\left(\mathrm{t}+1\right)=\overrightarrow{{X}^{*}}\left(t\right)-\overrightarrow{A}\cdot \overrightarrow{D}$$

(7)

$$\overrightarrow{D}=\left|\overrightarrow{C}\cdot \overrightarrow{{X}^{*}}\left(\mathrm{t}\right)-\overrightarrow{X}(\mathrm{t})\right|$$

(8)

$$\overrightarrow{A}=2\cdot \overrightarrow{a}\cdot \overrightarrow{r}+ \overrightarrow{a}$$

(9)

$$\overrightarrow{C}=2 \cdot \overrightarrow{r}$$

(10)

where $\overrightarrow{{X}^{*}}\left(t\right)$ is the best position of search agent (whale) obtained so far, t is the current iteration, and $\overrightarrow{X}(t)$ is the present positon of search agent at iteration t. $\overrightarrow{A}$ and $\overrightarrow{C}$ are coefficient vectors. $\overrightarrow{r}$ is a random number in [0, 1]. $\overrightarrow{a}$ is linearly decreased from 2 to 0.

• (b) Bubble-net attacking

This hunting method includes the following two behaviors: reducing the ring and continuing to surround the prey. These two behaviors are represented by the following equation:

$$\overrightarrow{X}\left(\mathrm{t}+1\right)=\overrightarrow{{D}^{*}}\cdot {e}^{bl}\cdot \mathrm{cos}\left(2\pi l\right) +\overrightarrow{{X}^{*}}\left(t\right)$$

(11)

$$\overrightarrow{{D}^{*}}=\left|\overrightarrow{{X}^{*}} \left(\mathrm{t}\right)- \overrightarrow{X}(t)\right|$$

(12)

where $b$ is a constant value that identifies the logarithmic spiral shape, $l$ is a random number in the range [− 1, 1], and $\overrightarrow{{D}^{*}}$ represents the distance between the whale and prey. Humpback whales rotate around their prey during predation and shrink their range, so each behavior has a 50% chance. It is expressed mathematically as follows:

$$\overrightarrow{X}\left(\mathrm{t}+1\right)=\left\{\begin{array}{lc}\overrightarrow{{X}^{*}} - \overrightarrow{A\cdot}\overrightarrow{D} & if\;p<0.5\\ \overrightarrow{{D}^{*}} \cdot {e}^{bl} \cdot \mathrm{cos}\left(2\pi l\right) + \overrightarrow{{X}^{*}}\left(t\right) & if\;p \ge 0.5\end{array}\right.$$

(13)

where $p$ is an arbitrary number between [0 and 1].

• (iii) Search for prey

Exploration step: At this point, the humpback whales search each other’s positions at random. They are represented mathematically as follows:

$$\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{rand}-\overrightarrow{A}.\overrightarrow{D}$$

(14)

$$\overrightarrow{D}=\left|\overrightarrow{C}.{\overrightarrow{X}}_{rand}-\overrightarrow{X}\right|$$

(15)

${\overrightarrow{X}}_{rand}$ is the random whales in current iteration.

2.2.2 Grey wolf optimization

GWO was proposed by Mirjalili [40], an optimization algorithm that simulates the hunting of grey wolves in wildlife. This algorithm was inspired by the social hierarchy of grey wolves as these wolves are categorized into four classes: ($\alpha$) wolf leader, ($\beta$) helping the leader, ($\delta$) follows both previous wolves, and omega ($\omega$).

• (a) Social hierarchy

To emulate the social hierarchy of grey wolves, the fittest solution is regarded as $\alpha$ then $\beta$, and the third best solution is $\delta$, and the remaining candidate solutions are considered $\omega$.

• (b) Encircling prey

The grey wolves encircle the prey in order to hunt, according to the following equation:

$$\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{p}\left(t\right)-\overrightarrow{A}\cdot \overrightarrow{D}$$

(16)

$$\overrightarrow{D}= \left|\overrightarrow{C}\cdot {\overrightarrow{X}}_{p}\left(t\right)-\overrightarrow{X}(t)\right|$$

(17)

where $t$ is the current number of iterations, ${\overrightarrow{X}}_{p}\left(t\right)$ represents the position vector of the prey, and $\overrightarrow{X}(t)$ is the position vector of a grey wolf. $\overrightarrow{A}$ and $\overrightarrow{C}$ are coefficient vectors that are calculated from the following equations:

$$\overrightarrow{A}=2\overrightarrow{a}\cdot {\overrightarrow{r}}_{1}-\overrightarrow{a}$$

(18)

$$\overrightarrow{C} = {2\cdot \overrightarrow{r}}_{2}$$

(19)

where $\overrightarrow{a}$ decreases linearly from 2 to 0 over the course of iterations, and ${\overrightarrow{r}}_{1}$ and ${\overrightarrow{r}}_{2}$ are random vectors between [0, 1].

• (iii) Hunting

After the encircling process, a grey wolf begins to hunt for the best solution. Despite the reality that the best solution must be optimized, alpha wolf saves the best solution in each iteration and updates it if the solution is improved. Beta and delta can be used to identify the location of the prey. Thus, the best solutions are stored by each type of grey wolf and employed to update the position of grey wolves using the equations below.

$$\left\{\begin{array}{c}{\overrightarrow{D}}_{\alpha }=\left|{\overrightarrow{C}}_{1}\cdot {\overrightarrow{X}}_{\alpha }-\overrightarrow{X}\right|\\ {\overrightarrow{D}}_{\beta }=\left|{\overrightarrow{C}}_{2}\cdot {\overrightarrow{X}}_{\beta }-\overrightarrow{X}\right| \\ {\overrightarrow{D}}_{\delta }=\left|{\overrightarrow{C}}_{3}\cdot {\overrightarrow{X}}_{\delta }-\overrightarrow{X}\right|\end{array}\right.$$

(20)

$$\left\{\begin{array}{c}{\overrightarrow{X}}_{1}={\overrightarrow{X}}_{a}-{\overrightarrow{A}}_{1}\cdot {\overrightarrow{D}}_{\alpha }\\ {\overrightarrow{X}}_{2}={\overrightarrow{X}}_{\beta }-{\overrightarrow{A}}_{2}\cdot {\overrightarrow{D}}_{\beta }\\ {\overrightarrow{X}}_{3}={\overrightarrow{X}}_{\delta }-{\overrightarrow{A}}_{3}\cdot {\overrightarrow{D}}_{\delta }\end{array}\right.$$

(21)

$$\overrightarrow{X}\left(t+1\right)=\frac{{\overrightarrow{X}}_{1}+{\overrightarrow{X}}_{2}+{\overrightarrow{X}}_{3}}{3}$$

(22)

• (iv) Attacking prey (exploitation)

In this step, a grey wolf can perform hunting mechanism to try to stop the movement of the prey for attack them. This mechanism works by decreasing the value of $\overrightarrow{a}$, where the value of $\overrightarrow{A}$ is also decreased by the value $\overrightarrow{a}$, resulting in a value in the range [− 1, 1]. A grey wolf can be attacking the prey, if $\overrightarrow{A}$ is less than − 1 or greater than 1. However, the GWO is prone to stagnation in local solutions. Therefore, the researchers are attempting to discover various mechanisms for resolving this issue.

• (e) Search for prey (exploration)

The searching mechanism is influenced by alpha, beta, and delta. These three categories are distinct from one another. As a result, a mathematical equation is required for them to converge and attack the prey. Thus, the value of $\overrightarrow{A}$ must be between 1 and − 1; if its value is greater than 1 or less than − 1, this forces the search agents to diverge from the prey. Furthermore, if $\overrightarrow{A}$ is greater than 1, the search agent will try to find a better prey. $\overrightarrow{C}$ is another component factor that affects the exploration phase of GWO. Overall, the GWO algorithm generates a random population. The prey’s location is assumed by alpha, beta, and delta. The distance between candidate solutions is then updated. After that, a is reduced from 2 to 0 in order to achieve a balance between the two phases. After that, if $\overrightarrow{A}>1$, the search agents then move away from attacking the prey and if $\overrightarrow{A}<1$ they go forward the prey. Finally, the GWO reached a satisfactory result and was terminated.

2.2.3 WOAGWO

WOA is a recently implemented optimization algorithm to solve many optimization problems. Standard WOA may work well for the best solution. However, refining the optimal solution with each iteration is not enough. To solve this limitation, we introduce an algorithm called WOAGWO, proposed by Mohammed H [41]; this algorithm is a hybrid between the WOA and GWO algorithm in order to improve the performances of WOA and to obtain better solutions. The WOA algorithm is hybridized by adding two sections. Firstly, to improve the hunting mechanism, a condition has been added in the exploitation phase in WOA according to Eq. (22). The effects of A1, A2, and A3 on exploitation performance are greater. As a result, a new condition has been added to WOA’s standard exploitation phase to bypass local optima where each A is greater than − 1 or less than 1. Secondly, Eqs. (20), (21) and (22) have been adapted, and used within the conditions that have been added to the exploitation phase which contains A1, A2, and A3. Finally, to make the current solution progress toward the best solution and prevent the whale from changing to a position that is not better than the previous position as well, for these purposes, another new condition has been added to the exploration phase. The pseudocodes of WOAGWO are presented in Algorithm 2.

2.2.4 Hybrid WOA with GWO

Pseudocodes of WOAGWO algorithm:

2.3 Parameter adaptive optimization of VMD method based on WOAGWO

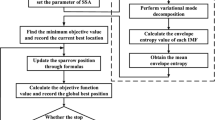
It is noteworthy that the parameter settings [k, α] of VMD need to be set in advance when decomposing signals due to their high impact on results [42], where alpha is directly proportional to bandwidth since smaller alpha gives a smaller bandwidth and vice versa; on the other hand, smaller K will give raise to mode aliasing and if K is too large it will lead to useless component generation [46]. In this paper, after tremendous trials, and investigating multiple manuscripts [21, 22, 42,43,44], we finally chose a reasonable range of α which is [200, 4000], and the selection range of K is [2, 12]. Therefore, in this section, we are introducing the hybrid algorithm WOAGWO to optimize the parameters of VMD. The WOAGWO-VMD algorithm needs to define the fitness function. According to reference [43], information entropy is an eminent indicator for judging signal sparseness, where the higher the entropy value, the higher the noise content of the signal, while the smaller indicates that the signal contains more fault information [44]. In this paper, we consider the average of the weighted permutation entropy of modes obtained by VMD as an objective function of the WOAGWO optimization algorithm, as shown in Fig. 1. The purpose of the parameter optimization process of VMD using WOAGWO is clearly interpreted as an efficient search for the minimum value of the objective function, as illustrated in Eq. (23):

Fig. 1

Objective function of WOAGWO algorithm

$$\left\{\begin{array}{l}fitness = min \left(\frac{1}{k}\sum\limits_{i=1}^{k}\mathrm{wpe}\left(i\right)\right)\\ s.t \;\;K=\left[\mathrm{2,12}\right], \alpha =\left[200, 4000\right]\end{array}\right.$$

(23)

where $\mathrm{wpe}(i)$ is the weighted permutation entropy of the ith IMF component. K and $\mathrm{\alpha }$ denote the mode number and the penalty factor respectively. The details of $wpe(i)$ is shown in [45], and its parameters used in this paper are embedding dimension m = 4 and time delay τ = 1, and the parameters of WOAGWO are population size = 20 and maximum iteration = 15, and its initial parameters are shown in Table 1. The flowchart of WOAGWO-VMD algorithm is shown in Fig. 2, and its steps are as follows:

• Step 1: Set the parameters of the WOAGWO algorithm, including the maximum number of iterations, the number of search agents, and the iteration range of K and α, and the parameters of the VMD algorithm also should be set.

• Step 2: Initialize the search agents.

• Step 3: Calculate the objective function of each search agent and choose the search agent with minimum objective function as the initial best search

• Step 4: To update the best search agent execute an iteration loop within the maximum number of iterations

• For each search agent update, the values of a, A, C, l, and p of WOA and A1, C1, A2, C2, A3, and C3 of GWO.

• Select the corresponding update formula to update the appropriate search agent to the different values of p and A.

• Calculate the updated objective function of each agent and select the best one to retain.

• Step 5: At the end of iterations, the best search agent is the best parameter combination (K, α).

Table 1 Parameter setting

Fig. 2

Flowchart of WOAGWO-VMD

2.4 Simulation signal analysis

In order to validate the effectiveness of the WOAGWO-VMD algorithm proposed in this paper, it is applied to decompose the simulation signal mentioned in the literature [43]. The simulation signal is shown as follows:

The time domain waveform of the simulated signal $y(t)$ and its four components ($y1(t)$, $y2(t)$, $y3(t)$, and $y4(t)$) are shown as follows:

$$\left\{\begin{array}{c}y1\left(t\right)=5\times sin\times (2\pi \times 50\times t)\\ y2\left(t\right)=4\times cos(2\pi \times 100\times t)\\ \genfrac{}{}{0pt}{}{y3\left(t\right)=\left\{\begin{array}{cc}3\times \mathrm{sin}\left(2\pi \times 300\times t\right) & t \in \left[\left[\mathrm{0,0.1}\right],\left[\mathrm{0.3,0.4}\right],\left[\mathrm{0.6,0.7}\right],\left[\mathrm{0.9,1}\right]\right]\\ 0 & t \in [\left[\mathrm{0.1,0.3}\right],\left[\mathrm{0.4,0.6}\right],\left[\mathrm{0.7,0.9}\right]]\end{array}\right.}{y\left(t\right)=y1(t) + y2(t) + y3(t) + y4(t)}\end{array}\right.$$

(24)

where $y1(t)$ is the sine signal with amplitude 5 and frequency 50; $y2(t)$ is the cosine signal with amplitude 4 and frequency 100; $y3(t)$ is high-frequency intermittent signal; $y4(t)$ is Gaussian white noise and $y(t)$ is the simulation signal. The time domain waveform of all these signals is shown in Fig. 3.

Fig. 3

The time domain waveform of each component signal and simulation signal

Firstly, WOAGWO is used to optimize the parameter combination [K, α] in the VMD algorithm. After that, the optimized VMD algorithm with the optimal combination [K, α] is used to decompose the simulation signal. The decomposition results of WOAGWO-VMD are shown in Fig. 4. Secondly, the EMD algorithm is used to decompose the same simulation signal. The decomposition results of EMD are shown in Fig. 5.

Fig. 4

WOAGWO-VMD decomposes the simulation signal

Fig. 5

EMD decomposes the simulation signal

According to Fig. 4, it can be seen that the proposed method WOAGWO-VMD decomposed the simulation signal into 3 IMF components with 50 Hz, 100 Hz, and 300 Hz successfully. Therefore, the effectiveness of WOAGWO-VMD algorithm can be obtained. As shown in Fig. 5, it can be seen that IMF1 and IMF3 extracted 300-Hz and 50-Hz signals successfully, but mode-mixing still occurs in IMF2 and IMF3. From the results obtained, it can be concluded that the proposed WOAGWO-VMD algorithm can decompose the frequency components in the simulation signal successfully, and overcome the mode mixing phenomenon in EMD algorithm.

2.5 Selection of sensitive components

The selection of components containing the most information is an important step in fault diagnosis, so for fault feature extraction a new method must be used to determine the sensitive components that have the largest contribution. Pearson correlation coefficient ($Pcc$) is an effective tool in the selection of IMF which contains the fault characteristics [47], where the bigger value of $Pcc$ denotes the greater impact features. The sparseness is a statistical index that effectively reflects the amplitude distribution of the vibration signal [42]. The largest value of sparseness denotes the stronger data sparsity. Given the superiority of both Pearson correlation coefficient and sparseness, a new index called sensitive indicator ($\mathrm{SI}$) was formulated based on the product of Pearson correlation coefficient and sparseness to select adaptively the sensitive components. The mathematical expression of $\mathrm{SI}$ is defined as:

$$S=\frac{\sqrt{\frac{1}{N}{\sum }_{n=1}^{N}{x(n)}^{2}}}{\frac{1}{N{\sum }_{n=1}^{N}\left|x(n)\right|}}$$

(25)

$$Pcc=\frac{E[\left(x-\overline{x }\right)\left(y-\overline{y }\right)]}{E\left[{\left(x-\overline{x }\right)}^{2}\right]E[{\left(y-\overline{y }\right)}^{2}]}$$

(26)

$$SI=Pcc\times S$$

(27)

where $S$ is the sparseness of the signal $x(n)$, and $N$ is the length of the signal $x(n)$; Pcc denotes the Pearson correlation coefficient between two signals ($x$ and $y$), and $E[.]$ represents the expectation operator.

2.6 Multi-features

To extract bearing fault feature vectors, we propose a multi-feature feature extraction method based on DE, PE, and SVD.

2.6.1 Dispersion entropy

Dispersion entropy results from the integration of symbolic dynamics with Shannon entropy for the development of an algorithm capable of characterizing the irregularity of time series with a low computation time [48]. The calculation steps of dispersion entropy for the time series $x=\left\{{x}_{i}, i=\mathrm{1,2},\dots ,N\right\}$ are as follows:

• 1. Use normal cumulative distribution function to map the time series x to $y=\left\{{y}_{1},{y}_{2},\dots ,{y}_{N}\right\}$ from 0 to 1

$${y}_{j}=\frac{1}{\sigma \sqrt{2\pi }}{\int }_{-\infty }^{xj}{e}^{\frac{{-(t-\mu )}^{2}}{2{\sigma }^{2}}}dt$$

(28)

where σ and $\mu$ represent mean and standard deviations of time series x respectively.

• 2. Employ the linear algorithm to map ${y}_{i}$ into integer from 1 to c and obtain a sequence ${z}_{j}^{c}$

$${Z}_{j}^{c}=\mathrm{round}\left(c.{y}_{j}+0.5\right)$$

(29)

where c represents the number of classes after mapping, ${Z}_{j}^{c}$ is the jth member of the classified time series, and round is the rounding function.

• 3. Calculate the embedding vector ${z}_{j}^{m,c}$ by exploiting the following formula:

$${Z}_{i}^{m,c}=\left\{{Z}_{i}^{c},{Z}_{i+d}^{c},\dots ,{Z}_{i+\left(m-1\right)d}^{c}\right\}, i=\mathrm{1,2},\dots ,N-\left(m-1\right)d$$

(30)

where $m$ and $d$ represent the embedded dimension and the delay time respectively.

• 4. Calculate the dispersion entropy patterns ${\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1,}}(v=\mathrm{1,2},\dots ,c)$ of each vector ${Z}_{i}^{m,c}$. ${Z}_{i}^{c}={v}_{0}, {Z}_{i+d}^{c}={v}_{1},\dots ,{Z}_{i+\left(m-1\right)d}^{c}={v}_{m-1}.$ ${c}^{m}$ is the number of possible patterns.

• 5. For each dispersion pattern, the relative frequency of potential dispersion patterns can be calculated as

$$p\left({\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1,}}\right)=\frac{\mathrm{number}({\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1,}})}{N-\left(m-1\right)d}$$

(31)

where number ${\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1}}$ represent the number of dispersion patterns. $p\left({\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1,}}\right)$ equal to the number of ${Z}_{i}^{m,c}$ mapped to ${\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1}}$ divided by the number of elements in ${Z}_{i}^{m,c}$.

• 6. The dispersion entropy is calculated as:

$$\mathrm{DE}\left(x,m,c,d\right)=-\sum_{\pi =1}^{{c}^{m}}P({\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1,}})\mathrm{ln}(P({\pi }_{{v}_{0,}{v}_{1,}\dots {v}_{m-1,}}))$$

(32)

2.6.2 Permutation entropy

Bandt and Pompe [49] proposed an approach called PE; this approach allows to analyze the complexity of the signal and detect dynamic changes in time series using the comparison of neighboring values. Its advantages are simplicity, robustness, and stability in addition to good noise resistance. The mathematical theory of PE is described briefly below. For a time series $x=\left\{{x}_{1},{x}_{2},\dots ,{x}_{N}\right\}$, the m-dimensional embedding vector is constructed as:

$${X}_{i}=\left\{x\left(i\right),x\left(i+\tau \right),\dots ,x(i+\left(m-1\right)\tau )\right\}, i=\mathrm{1,2},\dots ,N- \left(m-1\right)\tau$$

(33)

where $m$ represents the embedding dimension and $\tau$ is the time delay.

Each ${X}_{i}$ can be rearranged in an increasing order as

$$x(i+({j}_{1}-1)\tau \le x(i+({j}_{2}-1)\tau \le \dots \le x\left(i +\left({j}_{m}-1\right)\tau \right)$$

(34)

If there exist two elements in ${X}_{i}$ that have the same value, like:

$$x\left(i+\left({j}_{1}-1\right)\tau \right)=\tau \left(i+\left({j}_{2}-1\right)\tau \right)$$

(35)

Then their order can be denoted as:

$$x\left(i+ \left(j1- 1\right)\uptau \right)\le x\left(i+\left(j2- 1\right)\uptau \right)\;{j}_{1}<{j}_{2},$$

(36)

For any ${X}_{i}$, it can be mapped onto a group of symbols as

$$S\left(g\right)= \left({j}_{1}, {j}_{2}, \dots , {j}_{m}\right)$$

(37)

where $g=\mathrm{1,2},\dots , k\mathrm{ and }k \le m!$. $m!$ is the largest number of distinct symbols, and $S\left(g\right)$ is the one of $m!$ symbol sequence. The probability distribution of each symbol sequence is calculated as ${P}_{1}, {P}_{2}\dots , {P}_{k}$. The PE for the time series is defined as follows:

$${H}_{p}\left(m\right)=-\sum_{j=1}^{k}{P}_{j}Ln {P}_{j}$$

(38)

where $0 \le {H}_{p}\left(m\right)\le \mathrm{ln}(m!)$, ${H}_{p}(m)$ reaches the maximum ln(m!) when ${P}_{j}=\frac{1}{m!}$. ${H}_{p}(m)$ can be further normalized as:

$${H}_{p}=\frac{{H}_{p}\left(m\right)}{\mathrm{ln}\left(m!\right)}$$

(39)

2.6.3 Singular value decomposition

SVD is a very important matrix decomposition technique in linear algebra proposed by Beltrami in 1873. It has been regularly used in feature extraction and signal processing. SVD of an m × n matrix A is given by:

$$A=US{V}^{T}=\sum_{i=1}^{P}{A}_{i}=\sum_{i=1}^{P}{u}_{i}{\sigma }_{i}{v}_{i}^{T}$$

(40)

where $U=(m \times m)$ and $V = ( n \times n)$ are the orthogonal matrix, and $S = ( m \times n)$ being a matrix containing the singular values σi on the main diagonal and 0 elsewhere.

3 Fault feature classification using MPA-LSSVM

3.1 Marine predators algorithm

The MPA is a nature-inspired heuristic optimization algorithm proposed by A. Faramarzi [50]. The detailed steps of the algorithm are presented as follows:

3.1.1 Stage 1

This is the most important process in the initial iteration of improvement where exploration is important; at this point, when the movement of the predator is faster than the prey, the best strategy for the predator is to not move. So this stage is represented mathematically as follows:

while Iter < $\frac{1}{3}$ Max_Iter

$$\left\{\begin{array}{cr}{\overrightarrow{\mathrm{stepsize}}}_{i}={ \overrightarrow{R}}_{B}\otimes ({ \overrightarrow{\mathrm{Elite}}}_{i}-{ \overrightarrow{R}}_{B}\otimes { \overrightarrow{\mathrm{Prey}}}_{i} ) & i=1,\dots n\\ { \overrightarrow{\mathrm{Prey}}}_{i}={ \overrightarrow{\mathrm{Prey}}}_{i}+P.\overrightarrow{R}\otimes { \overrightarrow{\mathrm{stepsize}}}_{i}\end{array}\right.$$

(41)

where ${\overrightarrow{R}}_{B}$ represents a random vector indicating Brownian motion. ⊗ is the entry-wise multiplications, and Prey and Elite are the prey locations and best predator, respectively. Moreover $\overrightarrow{R}$ is a vector of uniform random numbers in [0,1]. And $P$ is a constant equal to 0.5. Max_iter is the maximum iteration and Iter represents the current iteration. This scenario is mainly encountered in the first third of iterations when step size or movement velocity is high.

3.1.2 Stage 2

At this stage, predator and prey movements are at the same pace. This simulates that they are both searching for the prey. This situation occurs mainly in the middle of the improvement process as exploration is gradually replaced by exploitation. Therefore, the population is divided into two parts. The first part was chosen for exploration while the second part was chosen for exploitation, in another way. The prey is responsible for the exploitation process, while the predatory animal is responsible for the exploration process.

$${While}\frac{1}{3}{{Max}}_{{Iter}}<{Iter}<\frac{2}{3}{Max}\_{iter}$$

For the first half of the population

$$\left\{\begin{array}{cr}{\overrightarrow{\mathrm{stepsize}}}_{i}={ \overrightarrow{R}}_{L}\otimes ({ \overrightarrow{\mathrm{Elite}}}_{i}-{ \overrightarrow{R}}_{L}\otimes { \overrightarrow{\mathrm{Prey}}}_{i} ) & i=1,\dots n/2\\ { \overrightarrow{\mathrm{Prey}}}_{i}=\overrightarrow{{\mathrm{ Prey}}_{i}}+P.\overrightarrow{R}\otimes { \overrightarrow{\mathrm{stepsize}}}_{i}\end{array}\right.$$

(42)

where ${\overrightarrow{R}}_{L}$ is a vector including random numbers based on Lévy distribution. The multiplication of ${\overrightarrow{R}}_{L}$ by Prey represents the simulation of the movement of prey in the manner of Luff. Since the step size of the Lev distribution is usually smaller, this will aid in exploration. The rule applied to the second half of the populations can be written as

$$\left\{\begin{array}{cr}{\overrightarrow{\mathrm{stepsize}}}_{i}={ \overrightarrow{R}}_{B}\otimes ({{ \overrightarrow{R}}_{B} \otimes \overrightarrow{\mathrm{Elite}}}_{i}-{\overrightarrow{\mathrm{ Prey}}}_{i} ) & i=n/2,\dots n\\ { \overrightarrow{\mathrm{Prey}}}_{i}={\overrightarrow{\mathrm{Elite}}}_{i}+P.CF\otimes { \overrightarrow{\mathrm{stepsize}}}_{i}\end{array}\right.$$

(43)

$$CF={(1-\frac{\mathrm{Iter}}{{\mathrm{Max}}_{\mathrm{Iter}}})}^{(2\frac{\mathrm{Iter}}{{\mathrm{Max}}_{\mathrm{Iter}}})}$$

where $\mathrm{CF}$ represents the adaptive parameter to control the step size for predator. The multiplication of ${\overrightarrow{R}}_{B}$ by the Elite represents the simulation movement of predator in Brownian, where the position of the prey is updated based on the movement of predator.

3.1.3 Stage 3

At this stage (low velocity ratio), the predator’s movement is faster than the prey. This phenomenon occurs in the last stage of the optimization process when the utilization capacity is high. Additionally, levy movement is the predator’s best strategy. The mathematical model of the last stage is represented as follows:

$$\mathrm{while\;Iter}> \frac{2}{3}{Max}\_{Iter}$$

$$\left\{\begin{array}{cr}{\overrightarrow{\mathrm{stepsize}}}_{i}={ \overrightarrow{R}}_{L}\otimes ({{ \overrightarrow{R}}_{L} \otimes \overrightarrow{\mathrm{Elite}}}_{i}-{ \overrightarrow{\mathrm{Prey}}}_{i} ) & i=1,\dots n\\ { \overrightarrow{\mathrm{Prey}}}_{i}={\overrightarrow{\mathrm{Elite}}}_{i}+P.CF\otimes { \overrightarrow{\mathrm{stepsize}}}_{i}\end{array}\right.$$

(44)

3.1.4 Stage 4

Eddy formation or fish aggregation devices (FADs) are an example of environmental issues affecting the behavior of marine predators as FADs represent local optima in the field of exploration. The mathematical model that describes the effects of FAD is formulated as follows:

$${\overrightarrow{\mathrm{Prey}}}_{i}=\left\{\begin{array}{l}{\overrightarrow{\mathrm{Prey}}}_{i}+CF\left[{\overrightarrow{X}}_{\mathrm{min}}+\overrightarrow{R}\otimes \left({\overrightarrow{X}}_{\mathrm{max}}-{\overrightarrow{X}}_{\mathrm{min}}\right)\right]\otimes \overrightarrow{U} \; if\; r<{\mathrm{FAD}}_{s}\\ {\overrightarrow{\mathrm{Prey}}}_{i}+\left[{\mathrm{FAD}}_{s}\left(1-r\right)+r\right]\left({\overrightarrow{\mathrm{Prey}}}_{r1}-{\overrightarrow{\mathrm{Prey}}}_{r2}\right) \; if\;r> {\mathrm{FAD}}_{s}\end{array}\right.$$

(45)

where FAD = 0.2, and $U$ is a binary solution with values 0 or 1; $r1$ and $r2$ are the indices of the prey, and ${X}_{\mathrm{max}}$ and ${X}_{\mathrm{min}}$ represent the upper and lower bounds, respectively.

3.1.5 Stage 5

Predators have a good and detailed memory of successful foraging sites. This ability is simulated using MPA, and the matrix fitness can be evaluated to refresh Elite after updating the Prey and the FADs. The fit value of each solution is compared with the previous value, so the optimum solution is saved in memory. Computational complexity of MPA algorithm is O(t(nd + cof × n)), where cof is the evaluation function, t is the iteration number, d is the optimization problem dimension, and n is the number of populations. The pseudo-codes of MPA is shown as follows:

3.2 LSSVM algorithm

SVM is a machine learning method that can be used for data classification or regression. It is based on statistical learning and the minimization of structural risks [34]. Its main role is to create an optimal hyperplane to maximize the separation margin between the two classes. The LSSVM is an improved algorithm based on SVM, where it converts the inequality constraints in SVM to equality and utilizes the least square linear formula as the loss function rather than the quadratic programming method used in SVM. The optimization objective function of LSSVM is defined as follows:

$$f\left(x\right)=sgn\left\{\omega .\mathrm{\varnothing }\left(x\right)+b\right\}$$

(46)

where $\omega$ is the weight vector, $\varnothing \left(x\right)$ represents nonlinear mapping function, and $b$ is deviation vector, the final optimization problem becomes

$$\left\{\begin{array}{c}\mathrm{min}J\left(\omega , \xi \right)= \frac{1}{2}{\Vert \omega \Vert }^{2}+\gamma \sum\limits_{i=1}^{N}{\xi }_{i}^{2}\\ s.t. {y}_{i}\left[{\omega }^{T}\phi \left({x}_{i}\right)+b\right]=1-{\xi }_{i}\\ i=\mathrm{1,2},\dots ,N.\end{array}\right.$$

(47)

J is the optimized objective function, ξ is the error variable, and γ represents the penalty factor. To solve the problem of optimization and obtain a better classification model, the Lagrange multiplier α_i was introduced and the Lagrange function was constructed as follows: (48).

$$L\left(\omega ,b,\xi ,{\alpha }_{i}\right)=J\left(\omega ,{\xi }_{i}\right)-\sum_{i=1}^{N}{\alpha }_{i}\left\{{y}_{i}\left[{\omega }^{T}\phi \left({x}_{i}\right)+b\right]-1+{\xi }_{i}\right\}$$

(48)

By using the constraints on the Karush–Kuhn–Tucker (KKT) condition, at the extreme points sought, the related parameters of the Lagrange function are independently subjected to a partial derivative operation, with the result being 0. The linear matrix expression that results is as follows:

$$\left[\genfrac{}{}{0pt}{}{O}{E}\quad \genfrac{}{}{0pt}{}{{E}^{T}}{\psi {\psi }^{T}+{E.\gamma }^{-1}}\right] \left[\frac{b}{\alpha }\right]=\left[\genfrac{}{}{0pt}{}{O}{y}\right]$$

(49)

where $E={[\mathrm{1,1}\dots .,1]}^{T}$, E, $y={[{y}_{1},{y}_{2},\dots ..{y}_{n}]}^{T}$, $\alpha ={[{\alpha }_{1},{\alpha }_{2},\dots \dots ,{\alpha }_{n}]}^{T}$, and $\psi ={[\phi \left({x}_{1}\right),\phi \left({x}_{2}\right),\dots \dots ..,\phi ({x}_{n})]}^{T}$. In the LSSVM algorithm, the decision function for classification is given as follows

$$f\left(x\right)=sgn\left[\sum_{i=1}^{n}{\alpha }_{i}K\left(x,{x}_{i}\right)+b\right]$$

(50)

where $k(x,{x}_{i})$ is the kernel function satisfying the mercer condition.

3.2.1 MPA-LSSVM

The LSSVM is an improved algorithm based on a SVM, which can be widely used in the mechanical fault diagnosis domain to solve classification and regression problems. However, the classification performance of LSSVM is mostly affected by the selection of parameters c and g [51]. To improve the classification feasibility of LSSVM, an algorithm should be used to optimize the parameters (c and g). MPA is a new optimization algorithm that was illustrated through benchmark functions and practical engineering problems. The results have demonstrated that MPA can obtain the optimal solution with a lower numerical cost compared to available optimization algorithms [50]. These comparison results encouraged us to use the MPA algorithm to optimize LSSVM parameters. The fitness function of MPA-LSSVM algorithm is shown in Eq. (51). In this study, the range of parameters c and g is [0, 1000] chosen according to Refs. [21] and [52]; the populations size = 20 and max iterations = 100 based in [55] and the initial parameter settings of MPA algorithm are shown in Table 1. The flowchart of the MPA-LSSVM proposed is shown in Fig. 6, and the specific steps of this proposed method are as follows:

• Step 1: Input the training set and test set normalized to the interval [0, 1].

• Step 2: Initialize the MPA and LSSVM parameters. Set the number of populations to 20, maximum number of iterations to 100. Then setting the range of (c, g), where the lower and upper bounds of c and g are 0 and 1000, respectively.

Fig. 6

Flowchart of MPA-LSSVM model

The position of each predator is defined as (c, g).

• Step 3: Use the following equation as fitness function of MPA-LSSVM.

$$\mathrm{fitness}=1-\frac{{N}_{t}}{{N}_{t}+{N}_{f}}$$

(51)

where ${N}_{t}$ and ${N}_{f}$ represent the number of true and false classification, respectively.

Evidently, a lower fitness value recorded a higher classification accuracy. The aim of the LSSVM parameter optimization problem is to minimize the fitness function.

• Step 4: Update the predators and preys position according to Eqs. (41)–(45) in Sect. 3.1.

• Step 5: Fitness evaluations:

• Updating the prey position.

The effect of updating the prey position on the fitness value can be evaluated using the FADs effects reported in stage 5 (Sect. 3.1). If the fitness value of the new prey position is lower compared to the previous position, then the new prey position replaces the previous one.

• Step 6: Export the optimal values of (c_best, g_best) once the maximum number of iterations is reached and trained LSSVM model.

• Step 7: The trained model is used to identify and classify the test dataset.

4 Fault diagnosis method based on WOAGWO-VMD and MPA-LSSVM

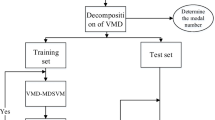
In order to improve the bearing fault identification accuracy, a novel intelligent fault diagnosis method is proposed in this paper. The structural framework of the proposed method is illustrated in Fig. 7. The specific steps of this method are summarized as follows:

• Step 1: The bearing vibration acceleration signals in various states (i.e., normal, ball fault, inner race fault and outer race fault) are collected using the acceleration sensors.

• Step 2: The hybrid algorithm (WOAGWO) is used to search the optimal parameters combination [K₀, α₀] of VMD.

• Step 3: Utilize VMD with optimal parameter combination [K₀, α₀] to decompose the vibration signal into several IMFs.

• Step 4: Analyze the correlation between each IMF component and the original signal by calculating the sensitive indicator (SI) of each IMF component and the original signal.

• Step 5: Select four IMF components with greater correlation with the original signal, and calculate DE, PE, and SVD of each IMFs, then construct the multiple features vector.

• Step 6: Normalize the sample feature value to [0, 1], using function mapminmax in matlab.

• Step 7: The obtained feature vectors normalized are randomly divided into two groups, a training sample set and a testing sample set.

• Step 8: The training samples is used as input to the MPA-LSSVM classifier, for obtaining the best LSSVM prediction model, while the testing samples is included in the prediction model to recognize and classifier different fault types.

Fig. 7

Fault diagnosis method based on WOAGWO-VMD and MPA-LSSVM

5 Experimental verification and result analysis

The experimental data of rolling bearings used in our paper is provided by Case Western Reserve University (CWRU) USA [53] in order to verify the validity of the suggested method in diagnosing rolling bearing faults. The test stand of the rolling bearing experiment is shown in Fig. 8. It consists mainly of a 2 HP motor (left), a torque sensor (middle), a dynamometer (right), and control electronics. The rolling bearing used in the experiment is a SKF6205 deep groove ball bearing. The vibration acceleration signal of the bearing is obtained from the driving end under the condition of a rotation speed of 1730 r/min, a load of 3HP, and a sampling frequency of 12 kHz. The bearing vibration signals are first classified into four categories, namely ordinary rolling bearings (normal) and rolling bearings with ball failure (B), outer ring failure (OR), and inner ring failure (IR). The faulty bearing is formed on the normal bearing by using electro-discharge machining (EDM). The diameter of the fault is 0.007, 0,014, 0.021, and 0.028 in. respectively. The damage points of the bearing outer ring are at 3 o’clock, 6 o’clock, and 12 o’clock respectively. The bearing vibration signal is classified into of 16 different types of failures. Each class has 50 samples with 4096 points for a total of 800 samples. Four hundred eighty groups are randomly selected for the training set and 320 groups are selected for the test sets. The time domain waveforms of vibration signal of rolling bearing are shown in Fig. 9. The detailed description of the class label is given in Table 2. This paper takes the ball fault signal with a fault severity of 0.028 in. as an example. The WOAGWO is utilized to optimize the parameters [K, α] of the VMD algorithm. The change curve of the minimum value of the average of the weighted permutation entropy with the number of iterations is shown in Fig. 10. It can be seen from Fig. 10 that the minimum value of the average of the weighted permutation entropy of 1.9280 appeared in the third iteration, which indicates that the optimization algorithm is quickly converging and has global optimization capabilities, and is appropriate for searching for the best parameter combination of VMD. The corresponding optimal parameter combination [K, α] is [6, 3835]. This obtained parameters are entered into the parameter settings of the VMD. Figure 11 shows the time domain diagram and spectrum diagram of 6 IMF components after the decomposition of the inner ring fault signal by VMD.

Fig. 8

The bearing test stand (a), and its Schematic diagram (b)

Fig. 9

Time domain waveform of the original bearing vibration

Table 2 Detailed description of the considered bearing working conditions

Fig. 10

Fitness value curve. Signal under different health conditions

Fig. 11

Waveform and spectrum of 6 IMF components. (a) Time domain, (b) FFT spectrum

For the vibration signals of 16 status, the best optimal combination [K₀, α₀] obtained by the hybrid optimization algorithm WOAGWO is shown in Table. 3

Table 3 Optimal parameter combination [K, α]

In order to demonstrate the superiority and efficacy of the multi-feature feature extraction method, the VMD method with the optimal parameter combination [K, α] obtained by WOAGWO-VMD algorithm is used to decompose different bearing vibration signals. Four IMF components with large correlation with the original signal are selected by the sensitive indicator (SI). For the IMF components selected, DE, PE, SVD, and multi-features are extracted from three perspectives of different fault types, different damage points, and different severity levels. Dimensionality reduction visualization t-SNE is used to visualize and compare the effects of the four feature extraction methods, such as shown in Fig. 12. Through t-SNE visual comparison in Fig. 12, it is shown that the multiple features have good intra-class aggregation and inter-class separation from three perspectives of different fault types, different damage points, and different severity levels, and exhibit the dispersion entropy feature, permutation entropy feature, and singular value feature results solely. Using the t-SNE dimensionality reduction method, we can see the distribution of multi-features extracted from 16 different bearing vibration signals previously analyzed by the WOAGWO-VMD algorithm, as shown in Fig. 13.

Fig. 12

Low-dimensional fault feature distribution. (a) Different fault types, (b) different severity, (c) different damage points

Fig. 13

Low-dimensional feature distribution of 16 kinds of bearing signals

It can be observed from Fig. 13 that the distinction of 16 types of data features is clear and the aggregation of data features is accurate. In summary, from Figs. 12 and 13, we conclude that multi-features can characterize the fault information of bearing signal accurately. To achieve the intelligent bearing fault diagnosis, the matrix of multi-features vector obtained were input to the MPA-LSSVM classifier for fault classification and recognition. The optimal LSSVM parameters (c_best, g_best) are obtained using MPA which are 67.12 and 72.64 respectively. To check the capacity of the proposed approach, it is compared with seven relevant methods. Fault diagnosis results of these methods are exhibited in Table 4. The recognition results and confusion matrix of the VMD-LSSVM method are illustrated in Fig. 14, while the recognition results and confusion matrix of the proposed method WOAGWO-VMD-MPA-LSSVM are illustrated in Fig. 15. We can notice from Figs. 14 and 15, and Table 4 that:

• 1. The diagnosis effect of using the optimized VMD is better than that of the unoptimized VMD method, which indicates the optimized VMD can more accurately extract the fault feature information of the rolling bearing.

• 2. The proposed method achieved a higher classification accuracy in the diagnosis of various types of faults than the other methods. The classification accuracy of the proposed method reached 99%. In addition, compared with other optimization algorithms, MPA-LSSVM achieves higher classification accuracy, which proves the good performance of MPA algorithm in parameter optimization. Therefore, the validity and superiority of the proposed approach in bearing fault diagnosis are confirmed.

Table 4 Comparison data of the comprehensive performance using different methods

Fig. 14

(a) Recognition results, and (b) confusion matrix (%) of the VMD-LSSVM method

Fig. 15

(a) Recognition results, and (b) confusion matrix (%) of the WOAGWO-VMD-MPA-LSSVM method

In order to further verify the effectiveness and superiority of the proposed method for diagnosis of bearing faults, we verify the superiority of our method used for feature extraction (WOAGWO-VMD decomposition and multi-features) as first approach by using the fault classifiers ELM, LSSVM, PSO-LSSVM, and PSO-SVM applied in the literature [54], [06], [21], and [25] respectively to diagnose and identify 16 bearing signals. The results are illustrated in Table 5. To ensure superiority of our fault classification method as well, it was compared with the classifiers also used in the previously mentioned literature as second approach. The results of the comparison are shown in Table 5. From the results table we can highlight the following:

• 1. When we use the same classifier mentioned in references [54], [6], [21], and [25], it turns out that our classification accuracy is always better than the classification accuracy of each reference. The present findings confirm the superiority of our feature extraction method.

• 2. When comparing the classifier we used MPA-LSSVM with other classifiers (RCFOA-ELM, MACGSA-LSSVM, VNWOA-LSSVM, ANN) employed in the same previous literature, it became clear that the classification accuracy of our classifier is better than the other classifiers. The result now provides evidence to effectiveness and superiority of the proposed fault classification method.

Table 5 Comparison of our proposed method with some related published literature for diagnosis of bearing faults

6 Conclusions

This paper presented a novel intelligent rolling bearing fault diagnosis method based on WOAGWO-VMD and MPA-LSSVM. In this method, the WOAGWO-VMD algorithm and multi-features were used for fault feature extraction, and the MPA-LSSVM algorithm for fault classification. In summary, this paper argued the following:

• 1. Through the simulated signal that was analyzed, the WOAGWO-VMD algorithm can extract the fault feature information of the signal more powerfully and significantly compared to EMD, which is critical for the diagnosis of rolling bearing faults.

• 2. In the WOAGWO-VMD algorithm, picking the minimum value of the average weighted permutation entropy as the fitness function helped to obtain the optimal parameter combination [k, α] of VMD quickly and efficiently.

• 3. Through the results obtained, the multi-features composed of dispersion entropy feature, permutation entropy feature, and singular value feature can more accurately characterize the fault information of the bearing signal based on t-SNE dimensionality reduction visualization.

• 4. The proposed MPA-LSSVM adaptively selects the optimal parameters [c, g] for fault recognition of rolling bearings and demonstrates superior classification accuracy compared with the GWO-LSSVM, PSO-LSSVM, GA-LSSVM, SVM, and ELM.

• 5. The effectiveness and feasibility of the proposed method in this paper is verified by using experimental data of rolling bearing fault vibration signal. It can be also applied to the fault diagnosis of other mechanical parts for upcoming works.