Introduction

Rotating machines is widely used in social production activities, and the rolling bearing is an important part of it. Due to the complex working environment and other reasons, rolling bearing is more likely to fail compared to other parts. Therefore, it is necessary to ensure the normal operation of rolling bearings [1,2,3]. A large number of experiments and cases show that monitoring and analyzing vibration signals is a reliable method to judge the running status of roller bearings [4,5,6,7,8]. With the change of rolling bearing state (i.e. the bearing has different faults), the relevant characteristics contained in its vibration signal will also change.

Empirical mode decomposition (EMD) has been pioneered by Huang et al. and it has been widely used as an effective method in fault diagnosis [9, 10]. However, there are some phenomena of mode mixing and terminal point effect in EMD. Based on EMD theory, a variety of signals processing methods had been proposed: ensemble empirical mode decomposition (EEMD) [11, 12], local mean decomposition (LMD) [13, 14] and complete ensemble empirical mode decomposition adaptive noise (CEEMDAN) [15, 16]. However, the essence of the above method is still based on the principle of recursive decomposition, which will lead to the accumulation of errors and cannot fundamentally overcome the phenomenon of mode mixing.

A new signal decomposition method based on adaptive Wiener filter which called variational mode decomposition (VMD) was first proposed [17]. This method can effectively decompose the test signal into a set of limited bandwidth with central frequency, and it has noise robustness than EMD [18]. Compares the decomposition performance using EMD and VMD, the results show that the latter has a better effect than the former in bearing defect feature extraction. However, in the above-mentioned literature, the selection of \(\alpha\) and K are all classical values when the author uses VMD to decompose the vibration signal. The Experiments show that the choice of parameters largely determines the decomposition efficiency of VMD [19, 20]. To weaken the influence of parameter selection on the decomposition effect, we can choose an optimization algorithm to adaptively select the appropriate combination of parameters. A novel bionic algorithm which is named sparrow search algorithm (SSA) is proposed [21]. The SSA has good performance in terms of convergence speed and robustness. So, this paper uses SSA to optimize the parameters of VMD. The minimum mean envelop entropy as the optimization objective. Based on the above explanation, this paper proposed a VMD parameter adaptation method based on SSA (SSA-VMD), which can obtain the relevant parameters of the VMD quickly and effectively.

The type of the classifier is an important factor that determines the accuracy of fault diagnosis. Researchers have made an in-depth study on the fault classification algorithm of rolling bearings, commonly used fault classification algorithms include: random forest (RF) [22, 23], deep belief network (DBN) [24, 25], support vector machines (SVM) [26,27,28]. Among them, SVM can better deal with the classification of small samples. As we all know, the parameter value of SVM affects the accuracy of classification [29]. Therefore, SSA is used to optimize SVM parameters. Through the above introduction, this paper proposed a method combined with SSA-VMD and SVM (SSA-VMD-SVM) for fault diagnosis of rolling bearing. To verify the effectiveness of the proposed method, two published data sets from different experimental platform are used.

The rest sections of this paper are arranged as follows. Section 2 introduces the principles and process of VMD parameter adaptive. including the theory of VMD, the principles of SSA and the specific steps of SSA-VMD. Section 3 describes the complete fault diagnosis process, including the introduce of FE, the theory of SVM and the process of SSA-VMD-SVM. Section 4 shows the effectiveness of the proposed method through the experimental results. Section 5 gives the conclusion of this study.

SSA-VMD Method

Variational Mode Decomposition

The VMD algorithm is different from EMD for IMF and it can be redefined as:

$$\begin{aligned} \left\{ \begin{array}{l} {u_k}(t) = {A_k}(t)\cos ({\phi _k}(t))\\ {\omega _k}(t) = \phi _k^{'}(t) = \frac{{d{\phi _k}}}{{dt}} \end{array} \right. \end{aligned}$$
(1)

where \({A_k}(t)\) and \({\omega _k}(t)\) are the instantaneous amplitude and instantaneous phase of \({u_k}(t)\), respectively. The original signal is decomposed into K mode functions, each of which has a center frequency. In this paper, the shorthand \({\omega _k}\) is used to represent center frequency. To achieve the purpose of decomposition, it is necessary to solve the constrained variational problem:

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{\left\{ {{u_k}} \right\} ,\left\{ {{\omega _k}} \right\} } \left\{ {\sum \limits _k {\left\| {{\partial _t}\left[ {(\delta (t) + \frac{j}{{\pi t}}) * {u_k}(t)} \right] {e^{ - j{\omega _k}t}}} \right\| _2^2} } \right\} \\ s.t.\sum \limits _k {{u_k}} = f \end{array} \end{aligned}$$
(2)

where t is the time scripts and \(\delta (t)\) is the Dirac distribution. \({u_k}\) and \({\omega _k}\) are abbreviation for the set of all modes and their corresponding center frequencies, respectively. By introducing Lagrangian multipliers \(\lambda\), the transformed expression is obtained as follows:

$$\begin{aligned} L(\left\{ {{u_k}} \right\} ,\left\{ {{\omega _k}} \right\} ,\lambda ) & = \alpha \sum \limits _k {\left\| {{\partial _t}\left[ {(\delta (t) + \frac{j}{{\pi t}}) * {u_k}(t)} \right] {e^{ - j{\omega _k}t}}} \right\| _2^2}n\nonumber \\& + \left\| {f(t) - \sum \limits _k {{u_k}(t)} } \right\| _2^2\mathrm{{ }} + \left\langle {\left. {\lambda (t),f(t) - \sum \limits _k {{u_k}(t)} } \right\rangle } \right. \end{aligned}$$
(3)

where \(\alpha\) is the secondary punitive factor, and its function is used to reducing the interference of Gaussian noise.

Sparrow Search Algorithm

A new optimization algorithm, which is called sparrow search algorithm, was proposed in 2020. In the SSA, sparrows are divided into two types: explorers and follower. Explorers lead followers to find food. The roles of followers and followers can be changed to each other, but the ratio of them in the population remains the same. This paper uses the following matrix to represent the position and fitness values of the sparrows:

$$\begin{aligned} X = \left[ \begin{array}{ccccc} x_{11}&{} x_{12} &{}\cdots &{}\cdots &{} x_{1d}\\ x_{21}&{} x_{22} &{}\cdots &{}\cdots &{} x_{2d}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ x_{n1}&{} x_{n2} &{}\cdots &{}\cdots &{}x_{nd} \end{array} \right] \end{aligned}$$
(4)

where n is the quantity of the sparrows in the population and d is the dimension of the issue to be optimized. Each sparrow has its own fitness, it can be showed as the following.

$$\begin{aligned} F_X = \left[ \begin{array}{ccccc} f(x_{11}&{} x_{12} &{}\cdots &{}\cdots &{} x_{1d})\\ f(x_{21}&{} x_{22} &{}\cdots &{}\cdots &{} x_{2d})\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ f(x_{n1}&{} x_{n2} &{}\cdots &{}\cdots &{}x_{nd}) \end{array} \right] \end{aligned}$$
(5)

In SSA, the position of explorers in each iteration is updated as follows:

$$\begin{aligned} X_{i,j}^{t + 1} = \left\{ \begin{array}{l} X_{i,j}^t \cdot exp{\left( {\frac{{ - i}}{{\alpha \cdot ite{r_{\max }}}}} \right) } \text {if} \,{R_2} < \text {ST}\mathrm{{ }}\\ X_{i,j}^t + Q \cdot L\mathrm{{ }} if {R_2} \ge \text {ST} \end{array} \right. \end{aligned}$$
(6)

where \(X_{i,j}^t\) represents the value of the j-th dimension of the i-th sparrow at the t iteration. t represents the current number of the iteration. \(ite{r_{\max }}\) is the maximum number of the iteration. \({R_2} \in \left( {0,1} \right]\) and \(\text {ST} \in \left( {0.5,1.0} \right]\) represent the warning value and the warning threshold respectively. L is a d-dimensional column vector whose every element is all 1. Q is a random number with normal distribution.

The followers need to update their location according the follow formula:

$$\begin{aligned} X_{i,j}^{t + 1} = \left\{ \begin{array}{l} Q \cdot exp\left( {\frac{{X_{\text {worst}}^t - X_{i,j}^t}}{{{i^2}}}} \right) {\text{ if }} \quad i > n/2\mathrm{{ }}\\ X_p^{t + 1} + \mid {X_{i,j}^t - X_p^{t + 1}} \mid \cdot {A^ + } \cdot L \text {otherwise} \end{array} \right. \end{aligned}$$
(7)

The position of these sparrows in the population is random. The following mathematical models can be established:

$$\begin{aligned} X_{i,j}^{t + 1} = \left\{ \begin{array}{l} X_{\text {best}}^t + \beta \cdot \mid {X_{i,j}^t - X_{\text {best}}^t} \mid \quad if {f_i} > {f_g}\mathrm{{ }}\\ X_{i,j}^t + B \cdot \left( {\frac{{\mid {X_{i,j}^t - X_{\text {worst}}^t} \mid }}{{\left( {{f_i} - {f_w}} \right) + \varepsilon }}} \right) if {f_i} = {f_g}\mathrm{{ }} \end{array} \right. \end{aligned}$$
(8)

where \(X_{\text {best}}^t\) is the current best location. \(\beta\) is a random number with a mean value of 1 and a variance of 0, and it obeys normal distribution. \(B(B \in [0,1])\) is a random number. \({f_i}\) represents the fitness of sparrow in the current situation, \({f_g}\) is the best fitness in the current global situation and \({f_w}\) is the worst one. \(\varepsilon\) is the smallest constant.

Improved VMD Based on SSA

The objective function selected by SSA-VMD is mean envelope entropy (MEE). The definition of envelope entropy is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {E_P} = - \sum \limits _{j = 1}^N {{p_j}\lg } ({p_j})\\ {p_j} = a(j)/\sum \limits _{j = 1}^N {a(j)} \end{array} \right. \end{aligned}$$
(9)

where \(j = 1,2, \ldots ,d\). The original signal x(t) undergoes the Hilbert transformation to get a(j). \({p_j}\) is the regularization result of a(j). The expression of the objective function MEE is as follows:

$$\begin{aligned} \text {MEE} = \text {mean} \left\{ {{E_{P1}}, \ldots ,{E_{Pk}}} \right\} = \frac{1}{K}\sum \limits _{i = 1}^K {{E_{Pi}}} \end{aligned}$$
(10)

where K represents the number of IMF component obtained by VMD. Obviously, when the value of MME is smaller, the complexity of IMFs is lower and the signal is more stable. Therefore, this paper chooses the minimum MME as the optimization objective function of SSA-VMD.

Fig. 1
figure 1

The flow chart of the SSA-VMD

Full size image

The structural block diagram for SSA-VMD is shown in Fig. 1 and the steps as follows.

  1. 1.

    Initialize the sparrows population and define the relevant parameters. The current position of the sparrow is taken as the parameter combination, i.e. \({X_i} =[x{}_{i,1},{x_{i,2}}] =[{x_k},{x_\alpha }]\)

  2. 2.

    Calculate the objective value of each sparrow, find the minimum objective value \(MEE^t\) and record the best position \(X_{\text {best}}^t\).

  3. 3.

    Update the position of the sparrows according to Eq. (6)–(8). If the fitness value of new position is better than the previous, sparrows move to the new location. Otherwise, the position of the sparrows remains the same.

  4. 4.

    Calculate the objective value \(MEE^{t+1}\) of the sparrow in the new position, and record the best position \(X_{\text {best}}^{t+1}\). If the objective value \(MEE^{t+1}\) is better than \(MEE^t\), the old best position \(X_{\text {best}}^t\) is replaced by \(X_{\text {best}}^{t+1}\).

  5. 5.

    Determine whether the stop condition is reached. If not, return to step 3 until the quantity of iterations reaches the set value, output the best parameter combination \([k,\alpha ]\).

The Proposed Fault Diagnosis

Fuzzy Entropy

FE is an efficient and complete method to judge the complexity of time series, and it is widely used in fault diagnosis [30]. It is necessary for FE to set corresponding calculation parameters: embedded dimension m and similar tolerance limit r. For a given N-dimensional time series \(\left[ {u(1),u(2), \ldots ,u(N)} \right]\). It is necessary for fuzzy entropy to set corresponding calculation parameters: embedded dimension m and Similar tolerance limit r. When the value of m is larger, the amount of information it contains will be more, but a larger m requires a larger data set \((N=10^m-30^m)\). Based on this reason, the embedded size m is set to 2. Generally, The larger the value of r, the more information will be ignored. When the value of r is small, it will increase the sensitivity of the result to noise [31]. So the values of r are usually 0.1 SD and 0.25 SD (SD is the standard deviation of the data set). In this paper, we set up \(r=0.2\) SD.

Support Vector Machine

Support vector machine (SVM) is an effective tool to solve the problem of small data classification. For a given set of samples \(\left\{ X={{x_1},{x_2},\ldots , {x_N}} \right\}\) to be classified, each vector in the sample has its own label. N is the quantity of the input samples. The vectors in sample space can be mapped to high-dimensional space, and a hyperplane in hyperspace can divide the space. Samples with the same labels are divided into the same area, and samples with different labels are divided, thus the sample sets can be classified. The hyperplane can be expressed as follows:

$$\begin{aligned} f(x) = \omega x + b \end{aligned}$$
(11)

where \(\omega\) represents the weight vector and b is the bias. In order to achieve a better result of classification. We need to select appropriate parameters to maximize the distance between various samples. The optimization problem of SVM is shown below:

$$\begin{aligned} \text {min}\mathrm{{ }}J(\omega ,C,\xi ) = \frac{1}{2}{\omega ^T}\omega + C\sum \limits _{i = 1}^N {{\xi _i}} \end{aligned}$$
(12)

where \({\xi _i}\) represents the slack variable of the given sample \({x_i}\), and the value of parameter C controls the generalization ability of SVM. Introduce the Lagrangian coefficient in Eq. (12) and get the expression is as follows

$$\begin{aligned} \begin{array}{l} \text {max} \,\mathrm{{ }}W(\alpha ) = \sum \limits _{i = 1}^N {{\alpha _i}} - \frac{1}{2}\sum \limits _{i = 1}^N \mathrm{{ }} \sum \limits _{j = 1}^N {{\alpha _i}} {\alpha _j}{y_i}{y_j}L({x_i},{y_i})\\ s.t.\mathrm{{ }}\sum \limits _{i = 1}^N {{\alpha _i}} {y_i} = 0,0 \le \alpha \le C \end{array} \end{aligned}$$
(13)

where \(L({x_i},{y_i})\) is the kernel, the advantage of kernel function is to make the value of samples in the original space equal to the value of samples in high-dimensional space. Radial basis kernel function (RBF) is a widely used kernel function. It can promote the generalization ability of SVM. The expression of RBF is as follows.

$$\begin{aligned} L({x_i},{y_i})= \text {exp}(-g \mid x_i-x_j\mid ^2) \end{aligned}$$
(14)

where g is the kernel parameter. The parameter of C and g are vital for the SVM. In [32], the author discussed the influence of the parameters on the results of SVM classification. Therefore, the SSA is used to optimize C and g to improve the performance of SVM in this paper.

SSA-VMD-SVM

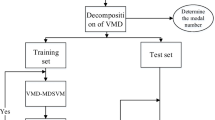
On the basis of the above theories, a fault diagnosis method of rolling bearings based on SSA-VMD and SVM is proposed in this paper, and the flow chart is shown in Fig. 2.

Fig. 2
figure 2

The flow chart of the SSA-VMD-SVM

Full size image

The specific steps are shown below.

  1. 1.

    The vibration signal is decomposed by SSA-VMD and Obtain the best parameters \(\left[ {K,\alpha } \right]\).

  2. 2.

    Use the parameter optimized VMD to decompose the signal and get the K different IMF components.

  3. 3.

    Fuzzy entropy of each IMF is calculated and the results is regarded as the feature vectors.

  4. 4.

    Input the feature vectors into SVM and get the classification results.

Experiment Verification

Experiment 1

The data sets used are derived from the Bearing Data Center of Case Western Reserve University (CWRU), and the structures of its equipment are shown in Fig. 3.

Fig. 3
figure 3

CWRU bearing platform

Full size image

The experimental platform is mainly composed of three parts. The left end is a two horsepower motor, the middle part is a torque sensor, and the right end is a power meter. The electrical discharge machining technology is used to punch out the fault point on the bearing, and the diameter of the fault range is 0.007 inches to 0.040 inches. Collect a data set containing the normal (NOR) conditions of the rolling bearing and the other three failure conditions [inner race (IR), outer race (OR) and ball (B)]. The bearing data parameters used in this paper: sampling frequency is 12kHz, bearing speed is 1797 rpm, load is 0HP. Select 1024 points in the data set as a sample, and the sampling duration is about 0.0853 second of each sample. The original signals in four different cases, such as inner ring fault and outer ring fault, are shown in Fig. 4.

Fig. 4
figure 4

Waveforms of vibration signal in four cases

Full size image

The Analysis of Experimental Results

This paper uses the parameters of SSA are shown in the Table 1. Where Num represents the population size, Iter is the maximum number of iterations. Ub and Lb represent the upper and lower boundaries of parameter values, respectively. Dim is the number of decision variables.

Table 1 Parameter setting of SSA
Full size table

The vibration signals are decomposed by SSA-VMD, the obtained optimal parameter combinations are \(\left[ {6, 4460} \right]\), \(\left[ {5, 5842} \right]\), \(\left[ {4, 5912} \right]\) and \(\left[ {3, 3346} \right]\). Fig. 5 shows the frequency spectrum of IMF after the signal is decomposed by VMD. From the decomposition results of the four cases, there are no mode mixing phenomenon in the decomposed signal, and each mode is successfully separated from the original signals.

Fig. 5
figure 5

Frequency spectrum of IMFs

Full size image

SSA-VMD not only has good decomposition performance for the original signal, but also has better decomposition speed than other intelligent algorithms. Figure 6 shows the time spend by SSA-VMD and the other three algorithms to find the best combination of parameters optimize: optimize VMD parameters by particle swarm optimization (PSO-VMD), optimize VMD parameters by whale optimization algorithm (WOA-VMD) and optimize VMD parameters by firefly algorithm (FA-VMD). The time value in the figure is obtained by calculating the average running time of the algorithm under four cases. The abscissa in Fig. 6 has two parameters, they are the basic parameters of the algorithm. Iter represents the number of iterations and Num represents the number of population. For example, [10, 30] represents that the four optimization algorithms search for the best parameter combination \([K,\alpha ]\) in the same population number (Num = 10) and iteration number (Iter = 30).

Fig. 6
figure 6

The time taken for the four methods to run under different iterations and populations

Full size image

When the number of iterations is fixed at 10, and the populations are respectively 30, 60, and 100, SSA-VMD spends the least time in finding the best parameters. SSA-VMD spends the least time compared with other methods. With the increase of the population, the speed advantage of the SSA-VMD is more obvious. When the number of populations is fixed at 30, and the iterations are respectively 10, 20, and 30, SSA also has certain advantages in terms of speed. In general, the optimization speed of SSA-VMD is faster than the other four optimization methods. With the increase of the number of iterations and populations, the speed advantage of SSA-VMD becomes more obvious.

Space of Feature Vectors

The dimension of feature vectors to affect the quality of the SVM classification results. From the optimization results of VMD parameters in four different situations, it can be seen that the optimized value of k under normal conditions (the value of k is 3) is smaller than the other three fault types. At the same time, the SVM model requires that dimensions of input feature vectors should be consistent. Therefore, the maximum dimension of the feature vectors is 3 in this paper. Figure 7a and b show the distribution of the feature vectors in space when their dimensions are 3 and 2, respectively. Compare these two pictures, the distribution of the features in Fig. 7a is more compact than the other one. So, the feature vector with dimension 3 is used in this part.

Fig. 7
figure 7

The space of sample feature

Full size image

Result Classification

The main function of training set is to train the model through a large amount of data, reduce the error of the experimental model and improve the generalization ability. The main role of the testing set is evaluating and verifying this model. Low dependence on training data is also an advantage of a model. Collect 100 samples under each working condition, a total of 400 groups. The first 20 samples are training sets, and the last 80 samples are test sets. The classification results are shown in Fig. 8.

Fig. 8
figure 8

The Diagnosis results of SSA-VMD-SVM model

Full size image

At the same time, this paper compares SSA-VMD-SVM with the other three methods in terms of classification, and the results are shown in Table 2. It can be seen that SSA-VMD-SVM has higher accuracy in the final decomposition result.

Table 2 Accuracy of various methods
Full size table

To verify the influence of SVM hyperparameters (i.e. C and g) on the classification results, we compared the classification accuracy between SSA-SVM and SVM with FE as the feature value. The specific results are shown in Table 3. It can be seen from the table that the classification accuracy of SVM in inner ring faults and rolling element faults is lower than SSA-SVM. These show that optimizing hyperparameters by SSA can improve the classification accuracy and efficiency of SVM.

Table 3 Classification results of SVM and SSA-SVM on CWRU data
Full size table

In [33], the authors divided the CWRU data into three categories: diagnosable (category Y), partially diagnosable (category P) and non-diagnosable (category N), and gave detailed annotations in the appendix. According to the classification of data, the IR and OR data used belong to category Y, and the B data belongs to category N in this paper. Meanwhile, this reference argued that new algorithms might be tested by P categories or N categories. Therefore, the data used in the paper accords with the relevant conclusions in this reference regarding the validation of the new algorithm on the CWRU data. To enhance the persuasiveness of the proposed method, this part increased a category P data, and the result as shown in Table 4.

Table 4 Performance of SSA-VMD-SVM on CWRU data
Full size table

Experiment 2

The data sets used are derived from the Center for Intelligent Maintenance Systems (IMS), University of Cincinnati. And the structures of its equipment are shown in Fig. 9.

Fig. 9
figure 9

IMS bearing platform

Full size image

The experimental platform consists of four ZA-2115 bearings, a motor with a speed of 2000rpm and several sensors. Two highly sensitive accelerometers are installed on each bearing, and the sampling frequency is 20kHz [34]. This platform mainly records the full cycle life of the bearing, and a total of three experimental tests have been carried out. In the first test, the inner ring (IR) of bearing 3 was damaged, and both the ball (B) elements and outer ring (OR) of bearing 4 have failed. The second and third test ended with outer ring failures of bearing 1 and bearing 3 respectively. In the first test, the bearing 3 and bearing 4 had been damaged by the 30th day [35]. Therefore, this paper regards the data of bearing 3 and bearing 4 on the 30th day of the first test as the early failure data. At the same time, the data of the first test of bearing 1 is taken as the data under normal (NOR). Select 2000 points in the data set as a sample, and the sampling duration is about 0.1 second of each sample. The original signals in three different cases, such as inner ring fault and outer ring fault are shown in Fig. 10.

Fig. 10
figure 10

Waveforms of vibration signal in three cases

Full size image

The Analysis of Experimental Results

The parameters of SSA used in this part are the same as those in experiment 1, the obtained optimal parameter combinations are \(\left[ {5, 5873} \right]\), \(\left[ {9, 4908} \right]\) and \(\left[ {3, 5350} \right]\). Fig. 11 shows the frequency spectrum of IMF after decomposition.

Fig. 11
figure 11

Frequency spectrum of IMFs

Full size image

Compared with the single fault in experiment 1, the compound fault types (i.e. mixed roller element and outer race faults) appeared in experiment 2. It can be seen from the decomposition of the frequency spectrum of IMFs that the method proposed in this paper can successfully decompose the various modes of the original signal for compound faults, and there are no phenomenon of modal mixing. In the same way as the experiment 1, this part also compares the decomposition speed of SSA-VMD and three other methods of the same type in IMS data set, and the specific results are shown in Fig. 12. The time value in the figure is the average running time of the decomposition algorithm under three different working conditions.

Fig. 12
figure 12

The time taken for the four methods to run under different iterations and populations

Full size image

Compared with experiment 1, the samples used in this part of the experiment contain more data points, and there are compound failures (i.e. mixed roller element and outer race faults). Therefore, in experiment 2, the average decomposition time of the method proposed in this paper under various working conditions is longer than that in experiment 1, compared with the other three methods, SSA-VMD still has the fastest decomposition speed. For example, when the number of iterations is 10 and the number of population is 30, SSA-VMD with the fastest decomposition speed is nearly half less than WOA-VMD with the slowest decomposition speed. With the increase of iteration number and population number, the method proposed in this paper has more and more advantages in decomposition speed. Moreover, compared with the other three methods, SSA-VMD has a smaller fluctuation of decomposition time when the population number and iteration times change.

Space of Feature Vectors

Based on the results of VMD optimization parameters in experiment 2 and the requirement of SVM input feature values, the dimension of the feature vector in this experiment is the same as experiment 1, that is, the dimension of the input feature vector is 3. Figure 13 shows the distribution of feature values in space, from the figure, we can see that using the method proposed in this paper to decompose and extract features, the distinction between different types of feature values is obvious, and single fault and mixed fault types can be well distinguished.

Fig. 13
figure 13

The space of sample feature

Full size image

Result Classification

Collect 100 samples under each working condition, a total of 400 groups. The 20 samples are training sets, and the last 80 samples are test sets. The classification results are shown in Fig. 14.

Fig. 14
figure 14

The diagnosis results of SSA-VMD-SVM model

Full size image

This part compared the classification accuracy of SSA-VMD-SVM with the other three methods under the IMS data set. The specific results are shown in Table 5. It can be seen from the table that the method proposed in this paper is higher in accuracy than the other three methods. At the same time, it also has a good classification effect for mixed fault types.

Table 5 Accuracy of various methods
Full size table

Meanwhile, experiment 2 also compared the classification results of SVM and SSA-SVM, and the specific results are shown in Table 6. It can be seen from the table that SSA-SVM is superior to SVM in classification accuracy. In particular, SSA-SVM is much more accurate than SVM in identifying mixed fault types (i.e. B + OR ). In experiment 2, the advantage of SSA-SVM over SVM is much greater than that of experiment 1.

Table 6 Classification results of SVM and SSA-SVM on IMS data
Full size table

In summary, two experimental results show that SSA-VMD-SVM can quickly extract effective information from vibration signals and accurately identify the failure of rolling bearings. It can also effectively distinguish between single fault type and mixed fault type. At the same time, compared with algorithms of the same type, the method proposed in this paper has certain advantages in terms of speed and accuracy.

Conclusion

To reduce the influence of VMD parameter value on signal decomposition results and improve the accuracy of fault diagnosis, this paper proposes a fault diagnosis method of rolling bearing, namely SSA-VMD-SVM. With MME as the objective function, SSA is used to find the best parameter combination. Then, the fuzzy entropy of each IMF is extracted as the feature value and input to the SVM to obtain the classification result. The parameters of SVM are optimized by SSA to improve accuracy. Two public data sets are used to verify the effectiveness of the proposed method. Experimental results show that SSA-VMD-SVM can extract fault features contained in vibration signals more quickly and distinguish various fault types more accurately than other methods of the same type. At the same time, the single fault type and the mixed fault type can also be distinguished well, which is accordant to the current trend of multiple fault diagnosis in the field of fault diagnosis.