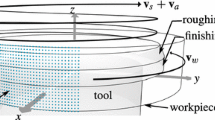
Abstract
The grinding process is one of the most important and widely used machining processes to achieve the desired surface quality and dimensional accuracy. Due to the stochastic nature of the grinding process and process conditions, the instantaneous micro-mechanisms between each grain and the workpiece are momentarily changing and are different from the other grains. Thus, the resultant normal and tangential grinding forces could be obtained by making the vector superposition of the instantaneous forces resulting from the contact of each grain and the workpiece. Previous studies in grinding forces have largely ignored the effects of micro-mechanisms of grain-workpiece in the grinding forces. On the other hand, most of these models are performed to predict grinding forces in the dry state that only can predict the maximal grinding forces based on the maximal value of undeformed chip thickness. In this research, a comprehensive model was used to analyze and predict the grinding forces both under dry conditions and in the presence of grinding fluid. In this research, the instantaneous undeformed chip thickness was calculated by a new method to determine the grinding forces at better accuracy. The proposed model can predict the components of normal and tangential grinding forces (including sliding, plowing, and cutting) based on the instantaneous undeformed chip thickness resulting from the kinematic analysis of abrasive grain trajectory and micro-mechanisms of cutting between abrasive grain and workpiece. By this method, the grinding forces were calculated more accurately than previous analytical models. In addition, a 2D slip line model was employed to separate dry and lubricated stages along with friction coefficient estimation for every single grain instantaneously. By this approach, the normal and tangential grinding forces could be predictable without the need for constant coefficients and additional experimental tests in both dry and lubricated stages. According to the proposed method, the effects of grinding parameters on each component of grinding forces were analyzed in both dry and lubricated grinding. The proposed model can also increase the accuracy of modeling in other grinding situations such as wheel loading issue, surface topography analysis, heat analysis, and specific grinding energy. In the end, experimental tests were performed to validate the theoretical model.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The grinding process is one of the most important machining processes and involves complex interactions between a large number of variables, such as machine tools, grinding wheel, workpieces, and other machining parameters. Grinding forces are a crucial factor influencing grinding performance, the durability of the grinding wheel, workpiece surface quality, and deformation of the processing system. Grinding forces are caused by elastic and plastic deformation, plowing, and chip formation, resulting from contact between the grinding wheel’s abrasives and the workpiece [1]. Modeling of the grinding process describes the relationship between the input and output values of the process to estimate the static and dynamic performance of the process. Modeling is an extensive concept; however, it can be divided into empirical, semi-analytical, and analytical models. In analytical models, the conformity of the model is determined from the physical laws using mathematical equations. Thus, analytical models depend on the physical understanding of the process and the earlier models to describe the mechanism. The accuracy of analytical modeling depends on the theories and how close they are to reality. Empirical models are determined from the information obtained from the grinding process. According to the requirement, the relationship between input and output parameters is specified in the selected model and validated in subsequent experimental tests.
Due to the random nature of the grinding wheel, including grain size, grain shape, and the random grain distribution on the grinding wheel, most studies on grinding forces are empirical. One of the first empirical models in the grinding forces is the Werner and Koenig model [2], which is based on the physical and kinetic theories. This model is a regression function between the grinding force and primary process variables such as depth of cut, wheel speed, feed rate, wheel diameter, and grain density where every parameter had a constant. Tönshoff et al. [3] reviewed the previous empirical models and obtained a basic form of the force model. Mishra and Salonitis [4] proposed a method to predict the factors for the basic form of force model by adding the two-way sensitivity analysis in the regression calculation. Fuh and Wang [5] used a backpropagation neural network (BPNN) to predict grinding forces. The results demonstrated the proper ability of the proposed model in self-learning based on the limited amount of data. Liu et al. [6] and Guo et al. [7] proposed new empirical models with multivariate regression analysis to accurately estimate the grinding forces. Malkin et al. [8] argued that grinding forces consist of two components: chip formation forces and sliding forces. Li et al. [9] assumed grinding forces as turning forces and improved Werner’s model by considering grinding forces as cutting and frictional forces. Younis et al. [10] proposed a new model for the grinding forces considering grinding forces in three stages: rubbing, plowing, and cutting forces. Younis’s model [10] was proved by Durgumahanti et al. [11]. They developed a similar model, which almost resolved the drawbacks of previous models. They modeled the rubbing, plowing, and cutting forces for all three components and ultimately combined them in a final model. In this model, they incorporated the effects of the variable coefficient of friction and plowing forces. Tang et al. [12] proposed a mathematical model with a focus on the chip formation forces. They classified the chip formation forces in two categories of static and dynamic forces according to the shear strain region and grinding zone temperature. The experiments validated the accuracy of the proposed model. Furthermore, Yao et al. [13] proposed a mathematical model to predict the grinding forces of the Aermet 100 steel. The least-square method was used to determine five constants in the model. The experimental results showed the reasonable accuracy of the model.
Most of the analytical models in the field of grinding forces are based on single-grain motion analysis. One of these models was an analytical one presented by Hecker et al. [14] in which a Rayleigh probability density distribution was presented for the equivalent undeformed chip thickness. They claimed that the resultant grinding forces could be obtained based on the undeformed chip thickness distribution, the wheel microstructure characteristics (i.e., grain density and geometry), and the workpiece material property. Besides, Cao et al. [15] tried to present a grinding force model by the geometrical analysis of the relative motions between the single grit and the workpiece. By calculating the undeformed chip cross-section area, chip length, and the number of active grains, grinding forces were obtained by aggregating the tangential and normal forces induced by each grain. A new model for grinding specific energy was presented by Azizi et al. [16]. Considering the influence of grinding wheel topography parameters (such as the number of active grits per unit area and their slope), they developed an analytical model to predict grinding forces. In this case, another similar model based on single-grain analysis was derived considering the random grain density [17]. Li et al. [18] developed an analytical model for dry grinding by modeling the actual wheel topography considering the variable stages of grain-workpiece micro-interactions for each grain. However, some constants like critical undeformed chip thickness for transition to plowing and cutting stages must be experimentally determined in this model. Ma et al. [19] focused on the time-varying dynamic phenomena induced by unstable factors in cylindrical grinding. They provided an analytical time-domain grinding force model by considering the effects of spindle run-out, vibrations, and machining parameters on grinding forces. Experimental results validated the proposed model. Another modeling was represented to estimate the micro-grinding forces [20]. In this case, a probabilistic modeling approach was employed to calculate chip thickness and specific forces by considering the effects of dressing parameters and tool deflection. Experiments showed that the proposed model could predict micro-grinding specific forces with acceptable accuracy. Zhang et al. [1] presented an improved force model by synthesizing every single grain grinding force that considered plastic-stacking and material removal mechanisms. Also, the effects of MQL and nanoparticles were investigated on the grinding forces and the performance of the grinding process [21,22,23,24]. Yang et al. [25, 26] developed the prediction models of minimum chip thickness and ductile–brittle transition chip thickness during single diamond grain grinding of zirconia ceramics under dry and different lubricating conditions; the size effect was also considered in the prediction model, and it showed that the predicted values were consistent with the experimental values. On the other hand, a model was proposed to predict the grinding specific force and energy [27]. In this study, the effects of undeformed chip thickness on the grinding specific force and energy were investigated by measuring and determining the topography of the grinding wheel. Besides, an analytical model was presented to predict the grinding forces by Jamshidi et al. [28], which was based on the micro-interactions between the grains and the workpiece. In this modeling, the grinding forces are divided into three categories: DMZ (dead metal zone) forces, plowing forces, and cutting forces. The proposed analytical model was in good agreement with the experimental results. However, the coefficient of friction is the only parameter in this model that must be experimentally determined. Also, the effects of abrasive wear behavior of white alumina (WA) and microcrystalline alumina (MA) wheels on the surface morphology of the ground workpiece were investigated [29]. In addition, the grinding forces, grain wear patterns, and ground surface integrity were studied in the grinding process by porous metal bonded aggregated CBN wheels [30]. Using CBN grinding wheel for grinding of Inconel 718 nickel-based superalloy with other alternatives like ultrasonic-vibration assisted grinding has demonstrated that it can reduce the grinding forces and improve the surface quality of the ground workpiece [31].
Furthermore, some researchers also considered the effects of undeformed chip thickness and abrasive grains on the grinding forces. A novel undeformed chip thickness model is proposed according to the grinding mechanisms, distribution of grains, kinematic theory, and mass conservation to describe the grinding conditions [32]. The theoretical results calculated by the suggested model are in good agreement with those of grinding [33, 34]. In addition, to investigate the fundamental mechanisms of grinding, a novel single grain approach is developed at a nanoscale depth of cut and 8.4 m/s scratching speed [35]. In the approach, the speeds used are three to six orders magnitude higher than those employed in nano scratching [36]. With the breakthrough of theories, novel diamond wheels and machining methods are developed to fabricate high-performance surfaces for use in semiconductor, microelectronics, and optoelectronics industries [37, 38]. These studies are a breakthrough to traditional grinding and manufacturing [39].
Although these models could predict grinding forces with reasonable accuracy, they still had some empirical constants that had to be determined by experiments. Moreover, these models are mostly provided to only predict normal and tangential grinding forces for dry grinding. On the other hand, since most of the previous models were based on the average undeformed chip thickness, they are only able to predict average values of process outputs such as grinding force and energy, Therefore, providing an analytical model capable of predicting grinding forces is essential. In this study, the normal and tangential grinding forces were calculated in both dry and lubricated states by momentarily determining the undeformed chip thickness based on the kinematic analysis of the grains and obtaining the instantaneous grain-workpiece micro-mechanisms (including sliding, plowing, and cutting).
2 Procedure of modeling grinding forces
2.1 Background and motivation
A grinding wheel cuts through the workpiece material as it passes underneath. A grain that cuts deeply into the workpiece carves out a chip. In contrast, a grain that rubs without penetration causes mild wear of the surface which may be hardly detectable. Also, there is a third situation where the grain penetrates and plows the surface, causing wedge formation without necessarily removing material called plowing [40]. In the plowing state, especially in dry grinding, the material piles up, and wedge formation in front of the abrasive is possible due to high adhesion [41]. This phenomenon occurs by adhering the piled-up material to the grain, which causes occasional material transfer. These cases can cause wheel loading and increase the grinding forces, damaging the workpiece and influencing its roughness [42]. Also, it can result in grinding wheel wear which has a direct relationship with wheel lifetime. On the other hand, the grinding force is directly related to grinding power \(\left\{P={F}_{\mathrm{t}}\left({V}_{\mathrm{s}}\pm {V}_{\mathrm{w}}\right)\right\}\) [43], where, \(P\) is the grinding power, \({F}_{\mathrm{t}}\) is the tangential grinding force, \({V}_{\mathrm{s}}\) shows the wheel speed, and \({V}_{\mathrm{w}}\) represents the feed speed. Furthermore, the sign “ + ” is used for down grinding, and the sign “_” is used for up grinding. Thus to determine the grinding power, it is necessary to specify the grinding forces [8]. Also, the dimensional accuracy in the grinding process has a connection with heat transferring or thermal deformation of the workpiece surface [44]. Moreover, the surface integrity of the workpiece is related to the grinding power and forces that mainly transfer to the workpiece by heat. Thus, investigating the components of grinding forces separately and presenting an analytical model that can enhance the understanding of the grinding forces in both dry and lubricated states sounds essential. During modeling, the following issues were considered:
-
In this model, it was assumed that the wear of the grinding wheel during the process is negligible.
-
The resultant normal and tangential forces are determined by making the vector superposition of the instantaneous forces of all the grains that are in contact with the workpiece at a particular moment.
-
In this model, Challen and Oxley’s theory [45] was used to determine the coefficients of friction for sliding, plowing, and cutting tangential forces. The friction coefficient is considered non-constant, which changes depending on the micro-mechanism type, the penetration depth of the abrasive, and the interfacial friction factor during the grinding process.
This study is novel due to proposing a new analytical model to determine the undeformed chip thickness for every single grain in the grinding process momentarily. In this study, by calculating the instantaneous undeformed chip thickness instead of the average amount of it and subsequently determining the forces for all three stages of cutting (including sliding, plowing, and cutting), the prediction of the forces led to more accurate values of grinding forces rather than previous analytical models. Also, setting boundary conditions reduced the calculation time and improved its speed by determining the forces for involved grains in the arc of cut area instead of all grains. Besides, this research is novel due to adding a 2D slip line model to the proposed model for separating the dry and wet grinding. Subsequently, the coefficient of friction for every single grain was determined instantaneously. This approach led to reasonable amounts of tangential grinding forces.
2.2 Flowchart
In this research, the algorithm shown by Fig. 1 was used to determine the grinding forces.
The mentioned algorithm includes:
-
1)
Calculation of instantaneous undeformed chip thickness for each grain at a specific moment, based on the kinematic analysis of grain cutting path and grain location resulting from random topography of wheel.
-
2)
Calculation of critical penetration depths or critical undeformed chip thicknesses based on the workpiece material properties and wheel geometry and parameters.
-
3)
Determination of instantaneous micro-mechanism for each grain
-
4)
Determination of normal and tangential grinding forces for each grain based on the instantaneous undeformed chip thickness and micro-mechanism, and finally, their superposition.
2.3 Modeling of grinding wheel topography
Since the actual topography of the grinding wheel is irregular, in this research, a model was presented for the grinding wheel topography with more conformity with the actual conditions. For this purpose, the shape and size of the grains and their position on the grinding wheel must be considered.
In the grinding process, the grinding wheel surface comprises randomly shaped grains held together by the grinding bond. Also, according to Ref. [46], choosing grain shape as spherical shaped has minor errors relative to experimental results. Thus, in this research, a spherical shape was considered for the grain shape.
In the first step to determine the initial location of the grains, a primary topography is considered a single layer of grains on the surface of a grinding wheel (Fig. 2a). Then, the surface of the grinding wheel was simulated by the grains with the size equal to the average grain diameter. The distribution of the grains is such that each adjacent grain is separated by a distance \({L}_{\mathrm{r}}\) [46]:
Modeling of the random grinding wheel topography [46]
In these equations, \({d}_{\mathrm{gmean}}\) is the average grain diameter, \(M\) shows the mesh number, \(N\) is the structure number, \({L}_{\mathrm{r}}\) is the distance between two adjacent grains, and \({V}_{\mathrm{g}}\) is the volume percentage of the grains in the wheel.
The number of the grains on the grinding wheel can be also obtained from the following equations:
where \({N}_{\mathrm{x}}\) is the number of the grains around the wheel circumference, \({N}_{\mathrm{y}}\) shows the number of the grains across the width of the grinding wheel, \(L\) is the wheel’s circumference, \(W\) represents the width of the wheel, and \(n\) is the total number of grains on the grinding wheel surface.
In the second step for abrasive grain size, Fig. 2b, due to the stochastic nature of the grain size, the simulation was carried out by considering of grain size between the minimum and the maximum grain diameter [18]:
\({d}_{\mathrm{gmin}}\) and \({d}_{\mathrm{gmax}}\) are the minimum and maximum diameter of the grain, respectively, which could be obtained according to Ref. [47]. Also, \(\xi\) is the random variable, and \(\delta\) is the is the range of grain size distribution.
In the third step, the final grain locations must be determined (Fig. 2c). For the final topography model, the grains must be randomly spaced, so the shaking process is established in a specific range to randomize the location of the abrasive grains on the XY plane [46, 48]:
where \(\left[\begin{array}{c}{x}_{n0}\\ {y}_{n0}\end{array}\right]\) and \(\left[\begin{array}{c}{x}_{nk}\\ {y}_{nk}\end{array}\right]\) are the initial and final location of the grains, respectively. n is the grain number, \({\lambda }_{\mathrm{x}}\) and \({\lambda }_{\mathrm{y}}\) are the random displacement between \(\left[-L_{\mathrm r}\;L_{\mathrm r}\right]\), and \(k\) denotes the shaking number taken as 1000 according to Ref. [46]. For preventing the overlapping of the grains, the following equation should be established between two neighboring abrasive grains [46, 48]:
where \(x\) and \(y\) are the grain coordinates in X and Y directions, and \(i\) is the grain’s number.
2.4 Determination of instantaneous undeformed chip thickness
During the modeling, the interaction between the single abrasive grain and the workpiece should be specified. For this purpose, a kinematic-geometric analysis of the abrasive grains was presented to determine the instantaneous undeformed chip thickness. Grain trajectory analysis for both X and Z directions according to Ref. [8] could be expressed as:
In these equations, “ + ” and “_” signs correspond to the down grinding and up grinding, respectively. Regarding the insignificant amount of \(\theta\) in the grinding process, and by combining Eq. (11) with Eq. (12), \({z}^{(i)}\) could be expressed as Eq. (13)
\({d}^{\left(i\right)}\) is the distance between the center of the grinding wheel and endpoint of the abrasive grain (Fig. 3), which could be obtained by
where \({{d}_{\mathrm{g}}}^{(i)}\) and \({d}_{\mathrm{s}}\) are the diameters of the grain and the grinding wheel, respectively. Finally, by combining the above equations, for single grain abrasive trajectory, we will have
A new coordinate is created to determine the trajectory of multiple abrasive grains. According to Fig. 3, the starting point is the contact point of the first grain with the workpiece. For this grain, it could be stated that.
Due to the small interval distance between the abrasives, the grain trajectory for the rest of the abrasive grains could be expressed as
\({s}^{\left(i\right)}\) is the interval distance between each grain and the first grain, which can be obtained from Eq. (18), and \(\Delta \mathrm{s}\) is the interval distance between two adjacent grains, which can be determined by Eq. (19):
As shown in Fig. 3, the undeformed chip thickness is considered as the difference between the momentary paths of two adjacent abrasive grains. For this purpose, the path of grain (i + 1) is calculated by subtracting the time interval with the grain (i):
In the above equation, \(\theta''^{\left(i+1\right)}\) is the instantaneous peripheral angle after removing the time interval with previous grain, and \(z_{t''}^{(i+1)}\) is the corresponding z coordinate. To solve the above equation, \(\theta''^{(i+1)}\) is considered as follows:
where \(\theta\) is the instantaneous peripheral angle for each grain, and \(\theta'\) is the peripheral angle resulting from the time interval between two neighboring abrasive grains, which could be expressed by
Also, \({\theta }^{(i)}\) could be expressed based on the time (\(t\)) as the following equation [49]:
Therefore, Eq. (21) could be rewritten as
Eventually, \({z}_{\mathrm{t}}^{(i)}\) and \(z_{\mathrm t''}^{(i+1)}\) could be represented as
The instantaneous undeformed chip thickness is calculated by implementing the boundary conditions and \({\theta }^{(i)}\le \frac{\pi }{2}, \mathrm{cos}{\theta }^{\left(i\right)}\le {d}^{\left(i\right)}\) \(\left(1-\frac{{a}_{\mathrm{p}}}{{d}^{\left(i\right)}}\right)\) as follows:
where \({a}_{\mathrm{p}}\) is the cutting depth, and \({h}_{\mathrm{t}}\) is the instantaneous undeformed chip thickness.
2.5 Determination of the contact micro-mechanism between grain and workpiece
The micro-mechanism that each grain is experiencing at any time depends on the undeformed chip thickness, material properties, and friction conditions. In this research, diagrams resulted from Challen and Oxley’s theory [45] were used for sliding-to-plowing and plowing-to-cutting transitions, and also for transitions within sliding mode in ductile materials. These stages could be defined as follows:
-
1)
Sliding: if \({h}_{\mathrm{t}}^{(i)}\le {h}_{\mathrm{plow}}^{(i)}\), the grain is in the sliding stage. \({h}_{\mathrm{plow}}^{(i)}\) is the critical penetration depth for the transition from sliding to the plowing stage. This stage is divided into three parts:
-
○ Elastic deformation: when \({h}_{\mathrm{t}}^{(i)}\le {h}_{\mathrm{elastio}-\mathrm{plastic}}^{(i)}\), the movement of the grain on the surface leads to elastic deformation. \({h}_{\mathrm{elastio}-\mathrm{plastic}}^{(i)}\) is the critical penetration depth for transition from elastic to elastoplastic deformation. At this stage, the penetration depth of the grain at a given moment is so small that it does not exceed the elastic limit of the workpiece. The elastoplastic phase begins when the pressure between the abrasive and workpiece material is lower than the yield point of the material [50]. This critical pressure is defined as \(P=0.39H\), where \(H\) is the workpiece hardness (MPa). For calculation of the deformation between grain and workpiece, by assuming a spherical and rigid grain, the deformation could be extracted based on the Hertz contact theory [51]:
In this equation, \(P\) is the pressure between grain and workpiece, and \({E}^{*}\) denotes the equivalent elastic modulus which can be obtained through Eq. (30):
where \({E}_{1}\),\({\upsilon }_{1}\) and \({E}_{2}\),\({\upsilon }_{2}\) are the elastic modulus and Poisson’s ratio for the workpiece and the grain, respectively.
Finally, the critical indentation depth for the transition from elastic into elastoplastic deformation could be expressed as
-
○ Elasto-plastic deformation: when \({h}_{\mathrm{elasto}-\mathrm{plastic}}^{(i)}\le {h}_{\mathrm{t}}^{(i)}\le {h}_{\mathrm{plastic}}^{(i)}\), the penetration depth of the grain exceeds the elastic limit, but it is less than the fully plastic limit. \({h}_{\mathrm{plastic}}^{(i)}\) is the critical penetration depth for transition from elastoplastic to plastic deformation. This stage is the beginning of plastic deformation. At this stage, the pressure between the grain and the workpiece exceeds the critical level of the previous stage. As mentioned, the lower critical limit of this deformation was calculated using Eq. (31). This deformation continues until the pressure between the spherical grain and the workpiece reaches the hardness of the workpiece [50]. The critical upper limit of deformation for this stage could be obtained by
$$h_{\mathrm{plastic}}^{(i)}=\left(\frac{3\pi}4\right)^2\left(\frac H{E^\ast}\right)^2\left(\frac{d_{\mathrm g}^{\left(i\right)}}2\right)\cdot$$(32)
-
○ Fully plastic deformation: when \({h}_{\mathrm{plastic}}^{(i)}\le {h}_{\mathrm{t}}^{(i)}\le {h}_{\mathrm{plow}}^{(i)}\), by increasing penetration depth, deformation exceeds the plastic limit, but it is less than the value for transition into the plowing state
-
2)
Plowing: If \({h}_{\mathrm{plow}}^{(i)}\le {h}_{\mathrm{t}}^{(i)}\le {h}_{\mathrm{cut}}^{(i)}\), the penetration depth of the grain is such that it can cause groove formation on the surface of the workpiece, but it is too low to lead to transition into the cutting mode. \({h}_{\mathrm{cut}}^{(i)}\) is the critical penetration depth for transition to cutting mode.
-
3)
Cutting: if \({h}_{\mathrm{t}}^{(i)}\ge {h}_{\mathrm{cut}}^{(i)}\), the penetration depth of the grain is large enough to perform chip formation and cutting operation.
In this research, a two-dimensional slip-line model proposed by Challen and Oxley [45] was used to separate the three stages, including sliding, plowing, and cutting. According to this model, the plowing stage is highly dependent on the process conditions. In this model, two variables (interfacial friction factor (\({f}_{\mathrm{hk}}\)) and attack angle (α)) were used to determine the status of the instantaneous micro-mechanism between each grain and the workpiece. The interfacial friction factor is defined as the ratio of the interfacial shear strength (\(\tau\)) to the bulk shear strength of the substrate (\(\kappa\)). According to Ref. [41], the transition from the sliding stage into the plowing stage is represented by Eq. (33), and also transition between the cutting stage with other modes can be described by Eq. (34) (as shown in Fig. 4).
In these equations, “\({f}_{\mathrm{hk}}\)” is a value between 0 and 1. As \({f}_{\mathrm{hk}}\) approaches 1, the condition tends towards dry grinding and higher wheel loading. As \({f}_{\mathrm{hk}}\) reduces, the lubrication condition improves. During dry grinding, the material is subjected to significant friction between the tool and the workpiece, resulting in high temperatures and wedge formation in front of the abrasive. Using lubricant decreases the friction between the grains and the workpiece and has a cooling influence during grinding [52]. However, it causes a higher plastic deformation and reduces wedge formation during grinding. The fluid type, its lubrication and cooling capability, its reaction with the workpiece surface, workpiece surface roughness, and process conditions affect \({f}_{\mathrm{hk}}\). According to Ref. [53], for dry grinding, this function is usually in the range of 0.7 to 0.9; for grinding with lubricant, the value of this function is in the range of 0.4 to 0.7. In this study, the interfacial friction factor corresponding to dry and lubricated grinding was considered as \({f}_{\mathrm{hk}}^{\mathrm{dry}}=0.8\) and \({f}_{\mathrm{hk}}^{\mathrm{dry}}=0.55\), respectively. Using the following equations, the critical attack angle can be obtained for the transition from sliding to plowing and plowing to cutting at both dry and lubricated conditions:
In the above equations, \({{\alpha }_{\mathrm{sl}-\mathrm{pl}}^{\mathrm{dry}}}^{(i)}\) and \({{\alpha }_{\mathrm{sl}-\mathrm{pl}}^{\mathrm{lub}}}^{(i)}\) are the critical attack angles for the transition from sliding to plowing in dry and lubricated conditions, respectively. Moreover, \({{\alpha }_{\mathrm{pl}-\mathrm{cut}}^{\mathrm{dry}}}^{(i)}\) and \({{\alpha }_{\mathrm{pl}-\mathrm{cut}}^{\mathrm{lub}}}^{(i)}\) are the critical attack angles for the transition from plowing to cutting in dry and lubricated conditions, respectively.
Based on the geometry of the grain movement in Fig. 5, the attack angle could be expressed as
By expanding the above equation, penetration depth could be determined based on the attack angle and grain diameter:
On the other hand, the slip line models do not cover all cutting mechanisms; thus, transition to plowing and cutting modes may occur at lower values of \({\alpha }^{(i)}\) [41]. Based on the experiments performed by Hokkirigawa [54] on carbon steel and stainless steel, the average attack angles required for the transition to plowing and cutting modes are 60 and 70% of the corresponding theoretical values. Thus, by solving Eq. (40) and establishing exact values of \({\alpha }^{(i)}\) in the equation, critical penetration depths for transition could be obtained as
In these equations, \({{h}_{\mathrm{sl}-\mathrm{pl}}^{\mathrm{lub}}}^{(i)}\) and \({{h}_{\mathrm{pl}-\mathrm{cut}}^{\mathrm{lub}}}^{(i)}\) are the critical penetration depths for the transition from sliding to plowing and plowing to cutting modes in the lubricated stage, respectively. Moreover, \({{h}_{\mathrm{sl}-\mathrm{pl}}^{\mathrm{dry}}}^{(i)}\) and \({{h}_{\mathrm{pl}-\mathrm{cut}}^{\mathrm{dry}}}^{(i)}\) are the critical penetration depths for the transition from sliding to plowing and plowing to cutting modes in the dry stage, respectively.
2.6 Calculation of normal grinding forces
2.6.1 Normal sliding forces
-
I.
Elastic deformation:
If the grain penetration depth is within the elastic range of the workpiece, based on Hertz theory, the sliding force can be expressed as [55]
$${F}_{\mathrm{ns}-\mathrm{e}}=\frac{4}{3}{E}^{*}.{\left(\frac{{d}_{\mathrm{g}}^{\left(i\right)}}{2}\right)}^\frac{1}{2}.{\left({h}_{\mathrm{t}}^{\left(i\right)}\right)}^\frac{3}{2}$$(45) -
II.
Elastoplastic deformation:
The normal force for elastoplastic deformation of the workpiece induced by a spherical grain could be calculated by the following equation [56]:
$${F}_{\mathrm{ns}-\mathrm{ep}}=\frac{\pi .H.{h}_{\mathrm{t}}^{\left(i\right)}{.d}_{\mathrm{g}}^{\left(i\right)}}{2}\left[1-0.6\frac{\mathrm{ln}{h}_{\mathrm{plastic}}^{\left(i\right)}-\mathrm{ln}{h}_{\mathrm{t}}^{\left(i\right)}}{\mathrm{ln}{h}_{\mathrm{plastic}}^{\left(i\right)}-\mathrm{ln}{h}_{\mathrm{elasto}-\mathrm{plastic}}^{\left(i\right)}}\right]$$$$\left[1-2{\left(\frac{{h}_{\mathrm{t}}^{\left(i\right)}-{h}_{\mathrm{elastio}-\mathrm{plastic}}^{\left(i\right)}}{{h}_{\mathrm{plastic}}^{\left(i\right)}-{h}_{\mathrm{elasto}-\mathrm{plastic}}^{\left(i\right)}}\right)}^{3}+3{\left(\frac{{h}_{\mathrm{t}}^{\left(i\right)}-{h}_{\mathrm{elasto}-\mathrm{plastic}}^{\left(i\right)}}{{h}_{\mathrm{plastic}}^{\left(i\right)}-{h}_{\mathrm{elasto}-\mathrm{plastic}}^{\left(i\right)}}\right)}^{2}\right]$$(46) -
III.
Fully plastic deformation:
For fully plastic deformation at the sliding stage, the normal force supported by a grain could be derived by the following equation [56]:
2.6.2 Normal plowing forces
The normal forces induced by an abrasive grain for plowing mode can be calculated by
where \(\Delta \gamma\) is the specific adhesion energy.
2.6.3 Normal cutting forces
The normal cutting forces of an abrasive during indentation in the cutting stage can be determined by [18]:
where \(HB\) is the Brinell hardness of the workpiece.
2.7 Calculation of tangential grinding forces
Since tangential forces are obtained by multiplying the normal forces by the friction coefficient, the calculation of this value is of great importance. Considering the various interactions of grains in the grinding process, it is now clear that the friction coefficient of grinding is not a constant value for each grain. In this research, to calculate the friction coefficient, according to the Challen and Oxley model [45], the friction coefficient will be obtained based on the attack angle and interfacial friction factor for each type of grain interaction (sliding, plowing, and cutting).
2.7.1 Tangential sliding forces:
According to the mentioned theory, the friction coefficient in the sliding stage could be obtained by
where \({A}_{\mathrm{t}}^{\left(i\right)}\) can be extracted as
Therefore, the tangential sliding forces will be
2.7.2 Tangential plowing forces
Furthermore, the tangential plowing force component can be calculated as
where \({\beta }_{\mathrm{t}}^{\left(i\right)}\) can be obtained by
So, the tangential plowing forces will be
2.7.3 Tangential cutting forces
The instantaneous friction coefficient in the cutting phase is also obtained according to the following equation:
Therefore, the tangential forces in this phase can be represented as
2.8 Superposition of grinding forces
The resultant grinding forces can be expressed as the sum of the sliding forces, plowing forces, and chip formation forces induced by all cutting grains in the contact zone [57]. Thus, by vector superposition of instantaneous forces resulting from the contact of each grain with the workpiece, the resultant grinding forces in X and Z directions could be calculated as [14]
3 Experimental setup and procedure
3.1 Procedure
The experiment setup is illustrated in Fig. 6. For experimental tests, each specimen is mounted and fixed on a special clamp located on the dynamometer. After fixing each specimen on the clamp and before starting the data acquisition, the specimen surface must be polished uniformly so that in each grinding pass, the contact of the grinding wheel with the entire surface of the workpiece is provided. Therefore, before each test, the specimen was ground in several passes to eradicate the effects of earlier scratches until the surface roughness of the workpiece reached to Ra = 0.5 µm. For maintaining the same conditions for all samples, the grinding wheel was dressed before each experiment using a single-point diamond dresser. The dressing depth was fixed at 100 μm, which was dressed in two cycles with a depth of 50 μm per cycle, 0.02 mm/s infeed rate, and 2500 rpm grinding wheel rotational speed. The applied grinding machine was a BLOHM Surface Grinder (model HFS204). The grinding process was conducted as a standard surface grinding operation in the up-grinding mode. Then, the tests were performed for the first 12 samples in dry condition, while 5% emulsions cutting fluid was employed for the subsequent 12 samples with 5.5 lit/min flow rate. The impact of the cutting depth, wheel speed, and workpiece speed on the grinding forces was also examined. The input grinding parameters for the experiment series are given in Table 1.
3.2 Force measurement
For measuring the grinding forces in this research, the KISTLER dynamometer (type 9255B) was used. This dynamometer has four sensors, which can measure grinding forces in three X, Y, and Z directions at a frequency of 10,000 data per second. In this experiment, the frequency was set to 2000 data per second. Due to the sensitivity of the signals sent from the dynamometer, a three-channel piezoelectric charge amplifier (type 5019B) was used to stabilize the signals. The generated voltage is amplified and converted into force signals, which are eventually displayed on the monitor screen.
3.3 Material and grinding tool
The AISI 1060 heat-treated steel was used in these tests whose chemical composition and mechanical properties are listed in Tables 2 and 3, respectively. Based on the workpiece material, aluminum oxide grinding wheel number 32A46 JVBE 268,445 was utilized for grinding the workpiece. The specification and mechanical properties of the grinding wheel and aluminum oxide grains are also presented in Table 4.
4 Result and discussion
4.1 Effects of grinding parameters on the force components at dry stage
The proposed model was implemented in MATLAB software, and the resulted were compared with the experimental findings.
The normal and tangential force changed based on the cutting depth as presented in Figs. 7 and 8 for the wheel speed of 22 m/s and the feed rate of 5 m/min. Based on the results, by increasing the cutting depth and arc of cut, more abrasives participated in the process; thus, all three force components, including sliding, plowing, and cutting, increase, causing an enhancement in total grinding forces. Additionally, due to the increase in cutting depth, the grinding abrasives are involved in higher penetration depths of the workpiece, leading to more cutting forces.
The average discrepancies in normal and tangential forces were 13.6% and 21.1%, respectively.
The effects of wheel speed on the normal and tangential forces are shown in Figs. 9 and 10 for the cutting depth of 15 µm and feed rate of 7 m/min. As seen, the model could predict the grinding forces at proper accuracy. The average discrepancies in normal and tangential forces were 12.2% and 12.4%, respectively. According to the figures, as the wheel speed increased, the grain trajectory and undeformed chip thickness instantly changed, and the cutting forces showed a slight enhancement. On the other hand, the sliding forces decreased; moreover, the plowing forces exhibited a drastic decrement, which eventually declined both normal and tangential forces at a low slope.
To examine the effects of workpiece feed rate on grinding forces, the cutting depth and wheel speed were fixed at 20 µm and 25 m/s, respectively. Figures 11 and 12 show the contribution of normal and tangential grinding force components with increasing the feed rate. As observed, by increasing the feed rate, the sliding forces increase at higher intensity, whereas the slope of the plowing forces enhancement was milder. The cutting forces, however, decreased with increasing feed rate. Finally, the sum of these changes incremented the grinding forces with a low slope. A comparison between analytical and experimental results (Figs. 11 and 12) shows good accuracy and low discrepancies of the proposed model. The average discrepancies in normal and tangential forces were 8.5% and 10.5%, respectively. On the other hand, by increasing the feed rate to 15 m/min, the engagement of the grinding wheel with the workpiece increased to such an extent that the grinding wheel self-sharpening occurred which reduced the experimental grinding forces.
4.2 Effects of grinding parameters on the force components at lubricated state
To further examine the validity of the model, the calculation was tested for the lubricated state in MATLAB software using different grinding parameters. The influence of input parameters was investigated on the grinding forces and the components. First, to investigate the effect of cutting depth on normal and tangential grinding forces in the lubricated state, wheel speed and workpiece feed rate were set at 22 m/s and 5 m/min, respectively. Figures 13 and 14 show the effect of cutting depth on the normal and tangential grinding forces, respectively. As the cutting depth and engagement increased, all three components of sliding, plowing, and cutting forces were enhanced. The increase in cutting forces is more noticeable than the other parts. Also, the figures show an agreement between the theoretical model and the experimental results. The average discrepancies in the normal and tangential forces were 20.1% and 17.9%, respectively.
For investigating the force changes based on the wheel speed, the depth of cut and the feed rate were respectively set at 15 µm and 7 m/min. Figures 15 and 16 depict the variations in normal and tangential grinding forces with increasing wheel speed. As seen, a rise in the wheel speed resulted in an increase in both normal and tangential forces. These changes are accompanied by a noticeable reduction in sliding forces, a slight reduction in plowing forces, and a subtle decline in cutting forces. Also, a comparison between normal and tangential grinding forces with wheel speed could be observed in the figures. The average discrepancies were 13.6% and 19.3% for normal and tangential directions, respectively.
The influences of workpiece feed rate on the normal and tangential forces are shown in Figs. 17 and 18 at the cutting depth of 20 µm and wheel speed of 25 m/s. By enhancing the feed rate, the grain trajectories and instantaneous undeformed chip thickness varied which altered the normal and tangential forces, as shown in Figs. 17 and 18. Increasing the feed rate enhanced the sliding and plowing components and caused slight changes in the cutting part, which led to an enhancement in both normal and tangential forces. The average discrepancies were 15.9% and 14.1% for normal and tangential directions, respectively. As it can be seen, except for the feed rate of 12 m/min where the forces were reduced, the results are ascending. The force reduction at this point could be due to the self-sharpening phenomena of the grinding wheel. The brittle behavior of the grinding wheel due to the cooling in lubricated grinding led to this phenomenon at lower feed rates compared to dry grinding.
4.3 Comparison between specific grinding forces with specific material removal rate
The comparison between the specific normal and tangential grinding forces with specific material removal rates was investigated to analyze the proposed model further. As shown in Figs. 19 and 20, the low deviation between the theoretical and experimental results demonstrates the reasonable accuracy of the proposed model in both dry and lubricated states. Also, it is clear that the theoretical grinding forces are smaller than the experimental results in most of the cases because of the wheel wear and wheel loading during the process. The grinding forces and material removal are two relevant variables so that with increasing the material removal rate, the normal and tangential grinding forces also increase. These changes in grinding forces increase significantly with increasing cutting depth rather than feed rate. As can be seen, the normal and tangential grinding forces decrease in the lubricated state for the equal material removal rates (Figs. 19 and 20).
Also, another point is the undeniable role of the cutting speed in grinding forces. According to the figures, the results of No. 2 and No. 14 tests for grinding forces in both dry and lubricated grinding show higher amounts rather than No. 9 and No. 21 tests despite having a lower value of the feed rate. According to these data, the undeniable role of cutting speed appears. In such a way, reducing the cutting speed by 3 m/s with equal cutting depth and lower feed rate increases the normal and tangential forces in dry grinding and grinding with coolant. Furthermore, tests No. 12 and 24 are the optimum points of the process because of the highest specific material removal rate and low value of grinding forces. These results show the feasibility of the proposed model and how this model can be employed in future studies to achieve optimal grinding parameters for different types of wheels and workpieces.
5 Conclusions
In this research, a new analytical model was developed for predicting the grinding forces of the ductile materials. The proposed model offered higher accuracy in the prediction of the grinding force components (sliding, plowing, and cutting) at both in the dry and lubricated conditions. Then, the accuracy of the proposed model was validated and confirmed with the experimental tests. The main differences between the proposed model and previous models can be summarized as:
-
1.
By modeling the random grinding wheel topography, this simulation tried to offer a model closer to the actual topography of the grinding wheel. Moreover, a new method was used to determine the instantaneous undeformed chip thickness. Using this variable, the grinding forces were determined based on the instant interaction types between the workpiece and the grains. In this study a 2D slip line model was added to the simulation. By this novel approach, the modeling extended to the lubricated state. Furthermore, the friction coefficient was calculated based on the micro-interaction type for every single grain. The coefficient of friction was considered as a variable function, which changed based on the type of kinematic micro-mechanisms, the penetration depth of the abrasive grain, and the interfacial friction factor during the grinding process. Based on this method, the grinding forces in both dry and lubricated states were determined.
-
2.
For validation of the proposed model, a series of experimental tests were performed. For this purpose, the effects of grinding parameters (including depth of cut, cutting speed, and workpiece feed rate) on grinding force components (sliding, plowing, and cutting) and the resultant normal and tangential forces were analyzed separately. In addition, the portion of sliding, plowing, and cutting stages from total normal and tangential grinding forces were obtained for all 24 tests. Besides, a comparison between specific normal and tangential forces with specific material removal rates in dry and wet grinding was essential to find the optimum points of the process. These results confirmed the feasibility and the accuracy of the proposed model in predicting the grinding forces.
-
3.
According to the results, the average contributions of normal sliding, plowing, and cutting forces in the dry state were about 18.1%, 41.8%, and 39.9%, respectively. As a comparison, the average contributions of normal sliding, plowing, and cutting forces in the lubricated mode were 29.8%, 29.2%, and 41%, respectively. Moreover, the average portions of tangential sliding, plowing, and cutting forces in the dry state were about 24.2%, 31.8%, and 14%, respectively, from the total forces. In the lubricated state, the average contributions of tangential sliding, plowing, and cutting forces were 35.8%, 33.4%, and 30.8% from the total tangential forces. By decreasing the portion of plowing forces in the lubricated stage, the formation of the wedges in front of the grains showed a decrement, giving rise to more proper grinding conditions compared to the dry mode.
-
4.
To determine the error of the analytical model with experimental results (i.e., the accuracy of the analytical model), the root mean square error (RMSE) function \(\left(RMSE=\pm \sqrt{\frac{1}{n}\sum_{i=1}^{n}{\left({F}_{m}^{(i)}-{F}_{a}^{(i)}\right)}^{2}}\right)\) was employed whose value was 17.36%.
-
5.
Also, adding a model for wheel wear behavior and wheel loading to this simulation can be beneficial to predict the grinding forces more accurately. Besides, this model is utilized for the common grinding conditions in which there is no workpiece burning and chatter. For special conditions or robot grinding that dynamic forces and regenerative chatter are involved in the operation, the effects of dynamic forces must be added to the proposed model.
References
Zhang Y, Li C, Ji H et al (2017) Analysis of grinding mechanics and improved predictive force model based on material-removal and plastic-stacking mechanisms. Int J Mach Tools Manuf 122:81–97. https://doi.org/10.1016/j.ijmachtools.2017.06.002
Werner G (1978) Influence of work material on grinding forces. Gen Assem CIRP, 28th. Manuf Technol 27:243–248
Tönshoff HK, Peters J, Inasaki I, Paul T (1992) Modelling and simulation of grinding processes. CIRP Ann - Manuf Technol 41:677–688. https://doi.org/10.1016/S0007-8506(07)63254-5
Mishra VK, Salonitis K (2013) Empirical estimation of grinding specific forces and energy based on a modified Werner grinding model. Procedia CIRP 8:287–292. https://doi.org/10.1016/j.procir.2013.06.104
Fuh KH, Bin WS (1997) Force modeling and forecasting in creep feed grinding using improved BP neural network. Int J Mach Tools Manuf 37:1167–1178. https://doi.org/10.1016/S0890-6955(96)00012-0
Liu Q, Chen X, Wang Y, Gindy N (2008) Empirical modelling of grinding force based on multivariate analysis. J Mater Process Technol 203:420–430. https://doi.org/10.1016/j.jmatprotec.2007.10.058
Guo M, Li B, Ding Z, Liang SY (2016) Empirical modeling of dynamic grinding force based on process analysis. Int J Adv Manuf Technol 86:3395–3405. https://doi.org/10.1007/s00170-016-8465-z
Malkin S, Guo C (2008) Grinding technology: theory and application of machining with abrasives. Industrial Press Inc.
Lichun L, Jizai F, Peklenik J (1980) A study of grinding force mathematical model. CIRP Ann - Manuf Technol 29:245–249. https://doi.org/10.1016/S0007-8506(07)61330-4
Younis M, Sadek MM, El-Wardani T (1987) A new approach to development of a grinding force model. J Manuf Sci Eng Trans ASME 109:306–313. https://doi.org/10.1115/1.3187133
Patnaik Durgumahanti US, Singh V, Venkateswara Rao P (2010) A new model for grinding force prediction and analysis. Int J Mach Tools Manuf 50:231–240. https://doi.org/10.1016/j.ijmachtools.2009.12.004
Tang J, Du J, Chen Y (2009) Modeling and experimental study of grinding forces in surface grinding. J Mater Process Technol 209:2847–2854. https://doi.org/10.1016/j.jmatprotec.2008.06.036
Yao C, Wang T, Xiao W et al (2014) Experimental study on grinding force and grinding temperature of Aermet 100 steel in surface grinding. J Mater Process Technol 214:2191–2199
Hecker RL, Ramoneda IM, Liang SY (2003) Analysis of wheel topography and grit force for grinding process modeling. Trans North Am Manuf Res Inst SME 31:281–288
Cao J, Wu Y, Li J, Zhang Q (2015) A grinding force model for ultrasonic assisted internal grinding (UAIG) of SiC ceramics. Int J Adv Manuf Technol 81:875–885. https://doi.org/10.1007/s00170-015-7282-0
Azizi A, Adibi H, Rezaei SM, Baseri H (2011) Modeling of specific grinding energy based on wheel topography. In: Advanced Materials Research. Trans Tech Publ, pp 72–78
Chang HC, Wang JJJ (2008) A stochastic grinding force model considering random grit distribution. Int J Mach Tools Manuf 48:1335–1344. https://doi.org/10.1016/j.ijmachtools.2008.05.012
Li HN, Yu TB, Wang ZX et al (2017) Detailed modeling of cutting forces in grinding process considering variable stages of grain-workpiece micro interactions. Int J Mech Sci 126:319–339. https://doi.org/10.1016/j.ijmecsci.2016.11.016
ma Y, yang J, li B, lu J, (2017) An analytical model of grinding force based on time-varying dynamic behavior. Int J Adv Manuf Technol 89:2883–2891. https://doi.org/10.1007/s00170-016-9751-5
Kadivar M, Azarhoushang B, Krajnik P (2021) Modeling of micro-grinding forces considering dressing parameters and tool deflection. Precis Eng 67:269–281. https://doi.org/10.1016/j.precisioneng.2020.10.004
Zhang Y, Li C, Jia D, et al (2016) Experimental study on the effect of nanoparticle concentration on the lubricating property of nanofluids for MQL grinding of Ni-based alloy. Elsevier B.V.
Guo S, Li C, Zhang Y et al (2017) Experimental evaluation of the lubrication performance of mixtures of castor oil with other vegetable oils in MQL grinding of nickel-based alloy. J Clean Prod 140:1060–1076. https://doi.org/10.1016/j.jclepro.2016.10.073
Li B, Li C, Zhang Y et al (2017) Heat transfer performance of MQL grinding with different nanofluids for Ni-based alloys using vegetable oil. J Clean Prod 154:1–11. https://doi.org/10.1016/j.jclepro.2017.03.213
Gao T, Li C, Yang M et al (2021) Mechanics analysis and predictive force models for the single-diamond grain grinding of carbon fiber reinforced polymers using CNT nano-lubricant. J Mater Process Technol 290:116976. https://doi.org/10.1016/j.jmatprotec.2020.116976
Yang M, Li C, Zhang Y et al (2019) Effect of friction coefficient on chip thickness models in ductile-regime grinding of zirconia ceramics. Int J Adv Manuf Technol 102:2617–2632. https://doi.org/10.1007/s00170-019-03367-0
Yang M, Li C, Zhang Y et al (2019) Predictive model for minimum chip thickness and size effect in single diamond grain grinding of zirconia ceramics under different lubricating conditions. Ceram Int 45:14908–14920. https://doi.org/10.1016/j.ceramint.2019.04.226
Dai C, Yin Z, Ding W, Zhu Y (2019) Grinding force and energy modeling of textured monolayer CBN wheels considering undeformed chip thickness nonuniformity. Int J Mech Sci 157–158:221–230. https://doi.org/10.1016/j.ijmecsci.2019.04.046
Jamshidi H, Budak E (2020) An analytical grinding force model based on individual grit interaction. J Mater Process Technol 283:116700. https://doi.org/10.1016/j.jmatprotec.2020.116700
Li M, Yin J, Che L et al (2021) Influence of alumina abrasive tool wear on ground surface characteristics and corrosion properties of K444 nickel-based superalloy. Chinese J Aeronaut. https://doi.org/10.1016/j.cja.2021.06.008
Zhao B, Ding W, Xiao G et al (2021) Effects of open pores on grinding performance of porous metal-bonded aggregated cBN wheels during grinding Ti–6Al–4V alloys. Ceram Int 47:31311–31318. https://doi.org/10.1016/j.ceramint.2021.08.004
Cao Y, Zhu Y, Ding W et al (2021) Vibration coupling effects and machining behavior of ultrasonic vibration plate device for creep-feed grinding of Inconel 718 nickel-based superalloy. Chinese J Aeronaut. https://doi.org/10.1016/j.cja.2020.12.039
Zhang Z, Huo Y, Guo D (2013) A model for nanogrinding based on direct evidence of ground chips of silicon wafers. Sci China Technol Sci 56:2099–2108. https://doi.org/10.1007/s11431-013-5286-2
Zhang Z, Song Y, Xu C, Guo D (2012) A novel model for undeformed nanometer chips of soft-brittle HgCdTe films induced by ultrafine diamond grits. Scr Mater 67:197–200. https://doi.org/10.1016/j.scriptamat.2012.04.017
Zhang Z, Huo F, Zhang X, Guo D (2012) Fabrication and size prediction of crystalline nanoparticles of silicon induced by nanogrinding with ultrafine diamond grits. Scr Mater 67:657–660. https://doi.org/10.1016/j.scriptamat.2012.07.016
Zhang Z, Wang B, Kang R et al (2015) Changes in surface layer of silicon wafers from diamond scratching. CIRP Ann - Manuf Technol 64:349–352. https://doi.org/10.1016/j.cirp.2015.04.005
Zhang Z, Guo D, Wang B et al (2015) A novel approach of high speed scratching on silicon wafers at nanoscale depths of cut. Sci Rep 5:1–9. https://doi.org/10.1038/srep16395
Zhang Z, Cui J, Wang B et al (2017) A novel approach of mechanical chemical grinding. J Alloys Compd 726:514–524. https://doi.org/10.1016/j.jallcom.2017.08.024
Zhang Z, Huang S, Wang S et al (2017) A novel approach of high-performance grinding using developed diamond wheels. Int J Adv Manuf Technol 91:3315–3326. https://doi.org/10.1007/s00170-017-0037-3
Wang B, Zhang Z, Chang K et al (2018) New deformation-induced nanostructure in silicon. Nano Lett 18:4611–4617. https://doi.org/10.1021/acs.nanolett.8b01910
Rowe WB (2013) Principles of modern grinding technology. William Andrew
van der Linde G (2011) Predicting galling behaviour in deep drawing processes
Adibi H, Rezaei SM, Sarhan AAD (2013) Analytical modeling of grinding wheel loading phenomena. Int J Adv Manuf Technol 68:473–485. https://doi.org/10.1007/s00170-013-4745-z
Wei J, Wang H, Lin B et al (2019) A force model in single grain grinding of long fiber reinforced woven composite. Int J Adv Manuf Technol 100:541–552. https://doi.org/10.1007/s00170-018-2719-x
Onishi T (2018) Grinding force and grinding heat: thermal deformation of a workpiece and compensation system. Toraibarojisuto/Journal Japanese Soc Tribol 63:145–152. https://doi.org/10.18914/tribologist.63.03_145
Challen JM, Oxley PLB (1979) An explanation of the different regimes of friction and wear using asperity deformation models. Wear 53:229–243. https://doi.org/10.1016/0043-1648(79)90080-2
Liu Y, Warkentin A, Bauer R, Gong Y (2013) Investigation of different grain shapes and dressing to predict surface roughness in grinding using kinematic simulations. Precis Eng 37:758–764. https://doi.org/10.1016/j.precisioneng.2013.02.009
Hou ZB, Komanduri R (2003) On the mechanics of the grinding process—Part I. Stochastic nature of the grinding process. Int J Mach Tools Manuf 43:1579–1593. https://doi.org/10.1016/S0890-6955(03)00186-X
M Kang L Zhang W Tang (2020) Study on three-dimensional topography modeling of the grinding wheel with image processing techniques. Int J Mech Sci 167 https://doi.org/10.1016/j.ijmecsci.2019.105241
Sun Y, Su ZP, Gong YD et al (2020) An experimental and numerical study of micro-grinding force and performance of sapphire using novel structured micro abrasive tool. Int J Mech Sci 181 https://doi.org/10.1016/j.ijmecsci.2020.105741
Bowden FP, Bowden FP, Tabor D (2001) The friction and lubrication of solids. Oxford University Press
Xie Y, Williams JA (1996) The prediction of friction and wear when a soft surface slides against a harder rough surface. Wear 196:21–34. https://doi.org/10.1016/0043-1648(95)06830-9
Winter M, Thiede S, Herrmann C (2015) Influence of the cutting fluid on process energy demand and surface roughness in grinding—a technological, environmental and economic examination. Int J Adv Manuf Technol 77:2005–2017. https://doi.org/10.1007/s00170-014-6557-1
van der Heide E, Schipper DJ (2003) Galling initiation due to frictional heating. Wear 254:1127–1133. https://doi.org/10.1016/S0043-1648(03)00324-7
Hokkirigawa K, Kato K (1988) An experimental and theoretical investigation of ploughing, cutting and wedge formation during abrasive wear. Tribol Int 21:51–57. https://doi.org/10.1016/0301-679X(88)90128-4
Johnson KL, Johnson KL (1987) Contact mechanics. Cambridge University Press
Jourani A (2015) Modelling of ploughing-cutting transition regime during abrasive manufacturing process. Int J Mechatronics Manuf Syst 8:19–32. https://doi.org/10.1504/IJMMS.2015.071664
Dai CW, Yu TY, Ding WF et al (2019) Single diamond grain cutting-edges morphology effect on grinding mechanism of Inconel 718. Precis Eng 55:119–126. https://doi.org/10.1016/j.precisioneng.2018.08.017
Author information
Authors and Affiliations
Contributions
HA conceived of the presented idea. FJ developed the theory and performed the computations. HA and AR verified the analytical methods. HA and AR encouraged FJ to investigate and supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Highlights
• A comprehensive analytical model is proposed to predict grinding forces for ductile materials.
• The model is established based on the superposition of grinding forces caused by abrasives in the contact zone with various micro-interaction types (sliding, plowing, and cutting).
• A novel method is used to calculate instantaneous undeformed chip thickness for every individual grain.
• The model can predict grinding forces in both dry and lubricated states with acceptable accuracy.
Rights and permissions
About this article
Cite this article
Adibi, H., Jamaati, F. & Rahimi, A. Analytical simulation of grinding forces based on the micro-mechanisms of cutting between grain-workpiece. Int J Adv Manuf Technol 119, 4781–4801 (2022). https://doi.org/10.1007/s00170-021-08280-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-08280-z