1 Introduction

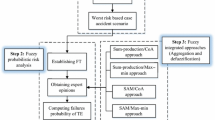
Fault tree analysis (FTA) is a useful tool for reliability analysis of industrial systems, such as nuclear reactor, aerospace, electric power, chemical, and mechanical. A fault tree (FT) is a logic diagram, or directed acyclic graph, that determines the relationship between the top event (i.e., system failure) and the basic events (i.e., component failures). It uses logic gates and events to model how component failures lead to system failures [1,2,3,4,5]. The traditional FTA procedure can be described as 8 steps in Fig. 1 [6].

Fig. 1
figure 1

Traditional FTA procedure

Full size image

One limitation of the conventional FTA is that the probability of failure of basic events must be known and considered as crisp values. However, in practice, the failure rates of the components are imprecise, deficient, or vague in the system modeling [7]. To overcome the limitation in FTA, the fuzzy set theory has been introduced into the FTA (aka. fuzzy fault tree analysis (FFTA)) to deal with ambiguous, qualitatively incomplete, ill-defined, and inaccurate information.

The fuzzy set theory was introduced in 1965 by Lotfizadeh [8] to deal with uncertainty due to imprecision and vagueness. More and more investigators successfully used the FFTA technique in various areas. Lin et al. [9] combined fuzzy set theories with expert elicitation to solve the safety problem of unexpected robot motion in an aircraft wing drilling system. Yazdi et al. [10] established a fuzzy fault tree (FFT) using expert opinion aggregated by fuzzy set theory and applied it to the risk assessment of the spherical storage hydrocarbon tank in case of fire and explosion. Abad et al. [11] introduced a framework which employed FFTA to identify the causes of a potential change and predict the probability of occurrence of the change in the construction industry.

However, there are still some problems that have not been fully considered:

  1. 1.

    The magnitude of failure and effect on the system has not been taken into account [5]. The state of the system is only identified in two conditions: either be 0 or 1 (i.e., normal or faulty). However, some failures do not occur randomly, which is dependent on the component degradation process. For this reason, the state of the system can be any real value from 0 to 1.

  2. 2.

    The logic gates are fixed and linguistic information such as the operators’ experiences and experts’ knowledge cannot be incorporated into the method [12, 13].

For these reasons, Song et al. [13] and Yao et al. [14] developed a novel FTA based on the Takagi and Sugeno (T-S) fuzzy model [15]. In their work, fuzzy possibilities are used to describe the events, and fuzzy variables are used to describe the magnitude of failure. The T-S fuzzy gates are constructed according to historical data and expert experience to represent the uncertainties in the relationships among events. The use of fuzzy variables and the T-S fuzzy gates reduces the need to collect a large number of failure data for computing the failure probabilities. The proposed T-S FFTA method has the advantages in handling imprecision in the probabilities of failure of components arising from inadequate failures data, uncertainties relationships among events, and considering the magnitude of failure. Tao et al. [16] introduced T-S gate rules for binary and polymorphic fault trees, extended component importance analysis to T-S FTA, and proposed the concept and calculation of T-S importance. In order to solve the disadvantages of calculation complexity and single inference of T-S FFTA, Chen et al. [17] combined the Bayesian network with T-S FTA, proposed a reliability analysis method for the multi-state hydraulic system. In addition to calculating the system reliability indices and importance by forward inference, the method can carry out fault diagnosis by backward inference. Bi et al. [18] verified the accuracy of the method combining T-S fuzzy gate fault tree and Bayesian network by comparing with the methods based on traditional Bayesian network and BP neural network. Yao et al. [19] presented an enhanced reliability optimization method based on the T-S fault tree and extended particle swarm optimization (PSO) algorithm that overcomes problems in constructing the reliability optimization model of multi-state systems, as well as early convergence problems in the PSO algorithm. Although the above studies can help solve the limitations of FFTA, they also created a new problem that when the historical data is insufficient, the construction of T-S fuzzy gates will inevitably rely too much on expert experience, resulting in inevitable subjective errors.

Therefore, an improved T-S FFTA method is proposed to reduce the subjective error caused by overdependence and require as little expert knowledge as possible. Firstly, the importance index of basic events of FFTA is obtained by MC simulation. Then, the improved T-S gate rules are constructed by the degree to which the basic events affect the top event in different states in a new way (i.e., importance index). Finally, the improved T-S FFTA method is constructed according to the above method, and the reliability analysis of the sealing subsystem, which is one of the most important and most faulty components of the numerical control (NC) turret, proves the correctness and provides data for fault diagnosis and preventive maintenance of the system.

The remainder of this paper is organized as follows: In Sect. 2, the T-S fuzzy fault tree model is briefly reviewed. In Sect. 3, an improved T-S FFTA method is proposed. In Sect. 4, the T-S probability importance algorithm is described. Then, in Sect. 5, a case study about the reliability analysis of the NC turret sealing subsystem is discussed and the effectiveness and superiority of the proposed approach are illustrated. Finally, in Sect. 6, the study is summarized.

2 T-S fuzzy fault tree

2.1 T-S fuzzy fault model

T-S fuzzy fault tree (FFT) is based on the T-S fuzzy theory. To put it simply, the logic gates such as AND or OR among events are generalized by the T-S fuzzy gates as shown in Fig. 2.

Fig. 2
figure 2

T-S FFT

Full size image

In Fig. 2, \({x}_{1},{x}_{2},...,{x}_{n}\) are basic events and y is a top event. Then, the fault degree of basic and top events are respectively represented by fuzzy numbers\(({x}_{1}^{1},{x}_{1}^{2},...,{{x}_{1}}^{{k}_{1}})\), …,\(({x}_{n}^{1}, {x}_{n}^{2} ,...,{x}_{n}^{{k}_{n}})\), and\(({y}^{1},{y}^{2},...,{y}^{n})\), where\(0\le {x}_{1}^{1}<{x}_{1}^{2}<...<{{x}_{1}}^{{k}_{1}}\le 1\), …,\(0\le {x}_{n}^{1}<{x}_{n}^{2}<...<{x}_{n}^{{k}_{n}}\le 1\), and\(0\le {y}^{1}<{y}^{2}<...<{y}^{n}\le 1\). Usually, the fault degree can be described by language information as small, medium, and large or no fault, degradation, and serious fault. Such language information corresponds to the fuzzy numbers in interval [0, 1].

2.2 T-S fuzzy gates

T-S fuzzy theory describes a universal approximation composed of if–then fuzzy rules, which can be represented as follows [13, 20]:

$$if x is A, then y=f(x)$$
(1)

where \(f(x)\) is a linear function of x=. The T-S fuzzy rules can be represented in Table 1:

Table 1 T-S fuzzy gates rules
Full size table

The fault status of the input basic event \({x}_{1}\) can be expressed as \({x}_{1}^{{a}_{1}}\),…, the fault status of the input basic event \({x}_{n}\) can be expressed as \({x}_{n}^{{a}_{n}}\). Then, the occurrence probability of the failure state of the output top event \({y}^{1}\) can be expressed as \({P}^{l}({y}^{1})\),…, the occurrence probability of the failure state \({y}^{{k}_{y}}\) can be expressed as \({P}^{l}({y}^{{k}_{y}})\), where \({a}_{1}=\mathrm{1,2},...,{k}_{1},\)…, \({a}_{n}=\mathrm{1,2},...,{k}_{n}\).

When the fuzzy possibility of component is known, suppose the fault state of the input basic event is \({x}_{i}^{{a}_{i}}(i=\mathrm{1,2},...,n)\) and the occurrence probability of this fault state is \({\text{P}}({x}_{\text{i}}={x}_{i}^{{a}_{i}})\); then, the execution probability of rule l is:

$${\mathrm{P}}_{0}^{1}=\prod_{i=1}^{n}P({x}_{i}={x}_{i}^{{a}_{i}})$$
(2)

The occurrence probability of the output top event y corresponding to the fault state is:

$$\left\{\begin{array}{l}{\text{p}}(y={y}^{1})=\sum_{l=1}^{r}{P}_{0}^{l}{P}^{l}(y={y}^{1})\\ {\text{p}}(y={y}^{2})=\sum_{l=1}^{r}{P}_{0}^{l}{P}^{l}(y={y}^{2})\\ \begin{array}{l}...\\ {\text{p}}(y={y}^{{k}_{y}})=\sum_{l=1}^{r}{P}_{0}^{l}{P}^{l}(y={y}^{{k}_{y}})\end{array}\end{array}\right\}$$
(3)

3 Improved T-S fuzzy fault tree

To solve the subjective error caused by overdependence [13,14,15,16,17,18,19], this paper constructs a new T-S fuzzy gates based on the importance index of basic events, which would require as little expert knowledge as possible. The importance index of basic events can be solved through Monte Carlo (MC) simulation.

MC simulation is a method that uses random sampling analysis to estimate the problem and to compute the variance of the estimate. By sampling the random variables in the model enough times and analyzing the statistical results of the sampling, one can estimate the problem and the variance of the estimated value. This is one of the most effective methods for reliability assessment due to its ability of good expression of statistical nature of the events [21,22,23]. The flowchart of the MC simulation algorithm of T-S FFTA model is shown in Fig. 3:

Fig. 3
figure 3

The flowchart of the MC simulation algorithm of the T-S FFTA model

Full size image

The construction process of the improved T-S fuzzy gates is as follows:

To simplify the calculation process of the T-S fuzzy gate rule algorithm, this paper considers the algorithms under three fault states of “0,” “0.5,” and “1” of the output event, i.e., \({y}^{1}=0\), \({y}^{2}=0.5\), and \({y}^{3}=1\).

The greater the importance is, the more easily the components will fail, which is a weak link of the system.

The relationship between the importance interval of the basic events and the influence of the output event in different states can be linearized.

First, we consider the influence of the importance of a single basic event xi on the overall output event y. When constructing a new T-S fuzzy gate rule, interval judgment is first made on the importance of the input events in the gates rules to obtain the influence value of the corresponding output events in different states, i.e., interval interpolation corresponding to the linear relationship. The results are shown in Table 2:

Table 2 Importance influence of a single basic event
Full size table

Therefore, we have the fuzzy possibility of the output event in the state of a given rule l in Eq. (4):

$$\left\{\begin{array}{c}{K}^{l}({y}^{l})=\frac{{W}_{N}\left({x}_{i}\right)-{a}_{i}}{\Delta {l}_{m}}\cdot \Delta O({y}^{i})+O({y}_{l}^{i}),({y}^{i}=0.5,\\ {y}^{i}=1)\\ {K}^{l}({y}^{i})=O({y}_{u}^{i})-\frac{{W}_{N}({x}_{i})-{a}_{i}}{\Delta {l}_{m}}\cdot \Delta O({y}^{i}),{y}^{i}=0\end{array}\right.$$
(4)

where \({K}^{l}({y}^{i})\) represents the fuzzy possibility under the output event \({y}^{i}\); \({a}_{l}\) represents the lower limit of the interval division of the importance; \({a}_{u}\) represents the upper limit of the interval division of the importance; \(\Delta {l}_{m}\) is the length of the interval division of the importance; \(O({y}^{i})\) represents the influence of the corresponding state of the output event; and \({W}_{N}({x}_{i})\) represents the importance of the basic event, obtained through MC simulation, whose calculation method is given in Fig. 2.

\({K}^{l}({y}^{1})\), \({K}^{l}({y}^{2})\),…, and \({K}^{l}({y}^{i})\) satisfy the following relation:

$$\begin{array}{c}\frac{{K}^{l}({y}^{1})}{{K}^{l}({y}^{1})+{K}^{l}({y}^{2})+...+{K}^{l}({y}^{i})}+...\\ +\frac{{K}^{l}({y}^{i})}{{K}^{l}({y}^{1})+{K}^{l}({y}^{2})+...+{K}^{l}({y}^{i})}=1\end{array}$$
(5)

Then, we consider the influence of correlation among components in a single gate rule:

When two or more components are in the fault state of \({y}^{i}\) at the same time, the calculation of the fuzzy possibility of the output events shall be judged by adding the importance values of all components in the fault state of \({y}^{i}\). The calculation process is the same as the case of a single component.

4 T-S probability importance analysis

Importance is an important part of FTA quantitative analysis. It describes the contribution of a component failure to the occurrence probability of top events, which is based upon time, component reliability parameters, and the system structure. Importance can not only be used for reliability analysis of the system, but also for optimization design of the system and guidance for maintenance and diagnosis of the system.

An algorithm for determining the probability importance of T-S FFTA is studied. When the fuzzy probability of basic event \({x}_{j}^{^{\prime}}s\) fault state \({x}_{j}^{{i}_{j}}\) is\(P({x}_{j}^{{i}_{j}} )({i}_{j}=\mathrm{1,2},...,{k}_{j})\), the T-S probability importance \({I}_{{T}_{q}}^{\mathrm{Pr}}({x}_{j}^{{i}_{j}})\) in fault state \({T}_{q}\) of fault tree top event T is:

$${I}_{{T}_{q}}^{\text{Pr}}({x}_{j}^{{i}_{j}})=P({T}_{q},P({x}_{j}^{{i}_{j}})=1)-P({T}_{q},P({x}_{j}^{{i}_{j}})=0)$$
(6)

where \(P({T}_{q},P({x}_{j}^{{i}_{j}})=1)\) represents the fuzzy possibility at the fault state \({T}_{q}\) of the top event T when the component \({x}_{j}\) fault state is \(P({x}_{j}^{{i}_{j}})=1\); \(P({T}_{q},P({x}_{j}^{{i}_{j}})=0)\) represents the fuzzy possibility of at the fault state \({T}_{q}\) of the top event T when the component \({x}_{j}\) fault state is \(P({x}_{j}^{{i}_{j}})=0\). It can be understood that the fuzzy possibility \({T}_{q}\) at the fault state is \({T}_{q}\) irrelevant with \({x}_{j}\). \({I}_{{T}_{q}}^{\text{Pr}}({x}_{j}^{{i}_{j}})\) can also be considered as the fuzzy possibility that component \({x}_{j}\) alone causes top event T with fault state \({x}_{j}^{{i}_{j}}\) when the fault state is \({T}_{q}\).

By calculating the T-S probability importance of the basic event \({x}_{j}\) in each fault state, the T-S probability importance \({I}_{{T}_{q}}^{\text{Pr}}({x}_{j})\) of the top event T is obtained as

$${I}_{{T}_{q}}^{\text{Pr}}({x}_{j})=\frac{\sum_{{i}_{j}=1}^{{k}_{j}^{^{\prime}}}{I}_{{T}_{q}}^{\text{Pr}}({x}_{j}^{{i}_{j}})}{{k}_{j}^{^{\prime}}}$$
(7)

where \({k}_{j}^{^{\prime}}\) is the number of fault states in which the jth event is not 0.

5 Case study

As a core functional component of the CNC lathe, the NC turret is one of the most prone to failure, whether they can operate safely affects the function and efficiency of the CNC lathe directly [24,25,26,27,28,29]. NC turret can be divided into five function modules according to its composition and working principle. The sealing system is the fault-prone component. Therefore, the reliability analysis of the NC turret sealing subsystem is discussed using the improved T-S FFTA method in this paper.

5.1 T-S FFTA model for NC turret sealing subsystem

The T-S fuzzy fault tree was constructed with the failure of the sealing subsystem as the top event, as shown in Fig. 4.

Fig. 4
figure 4

T-S FFT of NC turret sealing subsystem

Full size image

The reliability data for the components of the sealing subsystem are shown in Table 3 [29].

Table 3 Reliability data for the components of sealing subsystem
Full size table

5.2 MC reliability simulation of NC turret sealing subsystem

Through the trial algorithm, determining input parameters: NS = 100,000 times and the maximum working time Tmax = 150,000 h.

According to the MC simulation process in Fig. 3, the life distribution function of the 10 basic events of the NC turret sealing subsystem was randomly sampled and sorted, and the simulation curve of the importance of the basic events was shown in Fig. 5. The stable value of the importance of the basic events was shown in Table 4.

Fig. 5
figure 5

Importance distribution curve of basic events

Full size image
Table 4 Importance for the components of sealing subsystem
Full size table

The mean time between failures of the NC turret sealing subsystem obtained from MC simulation is \(MTB{F}_{MC}=11933h\). The theoretical value of the mean time between failures of the NC turret sealing subsystem is calculated as follows.

$$MTB{F}_{t}=\frac{1}{\sum_{i=1}^{n}{\lambda }_{i}}=\frac{1}{(389.8+...+13.22)\times {10}^{-7}}=11481h$$

The error between the simulation result and the theoretical calculation is

$${\Delta }_{MC}=\frac{11933-11481}{11481}=3.9\%<5\%$$

5.3 Reliability analysis of improved T-S FFTA for NC turret sealing subsystem

For the convenience of calculation, assume that the fuzzy numbers 0, 0.5, and 1 are used to indicate the three states of no fault, degradation, and serious fault of the NC turret sealing subsystem [13, 15, 29]. “0” failure state usually involves the following situations: no fault. The turret works normally but produces environmental noise and oil pollution or the turret works normally but the performance of some parts decreases, which has little influence on the machining accuracy of the workpiece. “0.5” failure state usually involves the following situations: The turret works normally, but the performance decreases seriously, which has a great influence on the machining accuracy of the workpiece. The turret does not work, it will not cause damage to other parts when the fault occurs, and the maintenance difficulty is low. “1” failure state usually involves the following situations: The turret does not work. When the fault occurs, it causes extensive damage to other parts, and the turret needs to be replaced.

According to the expert experience, the importance index of the basic events obtained in Table 4 is divided into intervals to obtain the degree of influence of the output event in different fault states. The criteria for dividing the importance interval can be shown in Table 5.

Table 5 Criteria for dividing the importance interval
Full size table

According to Eqs. (4) and (5), it can be calculated that when the fault states of basic events are \({x}_{1}\text{=}0.5,{x}_{2}\text{=}0\), the fuzzy possibility of the corresponding state \({y}^{1}=0\), \({y}^{2}=0.5\), and \({y}^{3}=1\) of the output event \({T}_{1}\) are \({K}_{{T}_{1}}^{l} ({y}^{1}=0\text{|}{x}_{1}\text{=}0.5,{x}_{2}\text{=}0)=0.25\), \({K}_{{T}_{1}}^{l}({y}^{1}=0.5)=0.40\), and \({K}_{{T}_{1}}^{l}({y}^{1}=1)=0.35\).

Similarly, when the fault states of basic events are \({x}_{1}\text{=}0,{x}_{2}\text{=}0.5\), the fuzzy possibility corresponding to the output event \({T}_{1}\) in different states are \({K}_{{T}_{1}}^{l}({y}^{1}=0\text{|}{x}_{1}\text{=}0,{x}_{2}\text{=}0.5)=0.57\), \({K}_{{T}_{1}}^{l}({y}^{1}=0.5)=0.24\), and \({K}_{{T}_{1}}^{l}({y}^{1}=1)=0.19\).

When the fault states of basic events are \({x}_{1}\text{=}0.5,{x}_{2}\text{=}0.5\), the sum of the importance of \({x}_{1}\) and \({x}_{2}\) is:

$$\sum {W}_{N}({\text{X}})={W}_{N}({x}_{1})+{W}_{N}({x}_{2})=0.5927$$

Then, the fuzzy possibility corresponding to the output event \({T}_{1}\) in different states is \({K}_{{T}_{1}}^{l}({y}^{1}=0\text{|}{x}_{1}\text{=}0.5,{x}_{2}\text{=}0.5)=0.15\), \({K}_{{T}_{1}}^{l}({y}^{1}=0.5)=0.46\), and \({K}_{{T}_{1}}^{l}({y}^{1}=1)=0.39\).

According to the above analysis, T-S fuzzy gate rules 1–4 before and after improvement can be shown in Tables 6, 7, 8, and 9.

Table 6 T-S gate rules 1 before and after improvement for NC turret sealing subsystem
Full size table
Table 7 T-S gate rules 2 before and after improvement for NC turret sealing subsystem
Full size table
Table 8 T-S gate rules 3 before and after improvement for NC turret sealing subsystem
Full size table
Table 9 T-S gate rules 4 before and after improvement for NC turret sealing subsystem
Full size table

According to Eq. (3), the fuzzy probability at different fault degrees of the top event before and after improvement can be calculated, as shown in Table 10.

Table 10 The fuzzy possibility at different failure degrees of the top events before and after improvement
Full size table

From the fuzzy failure probability of the top event T, the mean time between failures of the NC turret sealing subsystem before and after improvement can be solved as follows:

$$MTB{F}_{after}=\frac{1}{{P}_{after}(T=1)}=\frac{1}{89.7\times {10}^{-6}}=11148h$$
$$MTB{F}_{before}=\frac{1}{{P}_{before}(T=1)}=\frac{1}{98.3\times {10}^{-6}}=10172h$$

The error between the before and after improvement result and the theoretical calculation is

$${\Delta }_{after}=\frac{11481-11148}{11481}=2.9\%<5\%$$
$${\Delta }_{before}=\frac{11481-10172}{11481}=11.4\%>5\%$$

The relationship between the three errors of MC FFTA and T-S FFTA before improvement and improved T-S FFTA can be expressed as \({\Delta }_{after}<{\Delta }_{MC}<5\%<{\Delta }_{before}\).

It can be seen from the error analysis that the result of the proposed method in this paper and the result of the MC FFTA are within the error allowance, and the improved T-S FFTA has the smallest error, so the effectiveness of the method proposed in this paper is demonstrated. Moreover, the result of T-S FFTA before improvement has the largest error, which is caused by subjective errors from expert experience. Hence, the method proposed in this paper can rely as little as possible on expert experience in the case of insufficient data, thus reducing subjective errors.

Combined with Eqs. (6) and (7), the T-S probability importance of the NC turret sealing subsystem is calculated. The results are shown in Table 11:

Table 11 T-S probability importance of each component in different fault states
Full size table

As can be seen from Table 11, when the failure states of the NC turret sealing subsystem are 0.5 and 1 respectively, the order of probability importance of each component from large to small is as follows:

When failure status is 0.5, X1 > X2 > X4 > X10 > X3 > X9 > X5 > X7 > X8 > X6.

When failure status is 1, X1 > X2 > X10 > X4 > X3 > X9 > X5 > X7 > X8 > X6.

Statistical analysis was made on 152 post-sale data of SLT NC turret in a CNC machine tool factory, among which the fault frequency of NC turret sealing subsystem was the highest, accounting for 35% of the total fault data. The failure frequency distribution of its components is shown in Fig. 6 [30].

Fig. 6
figure 6

Failure frequency distribution of sealing subsystem components

Full size image

It can be found from the actual fault data that the failure frequency of the key components of the NC turret sealing subsystem is sorted as follows: X1 > X2 > X4 > X3 > X5.

The result is consistent with the ranking of the system in the “1” fault state obtained by the improved T-S FFTA method, which verifies the correctness of the method.

The greater the importance is, the more easily the components will fail, which is a weak link of the system. It can be seen that when the system is in the “0.5” fault state, the oil circuit sealing ring has the greatest impact on the system, followed by the pipe seal, water distributor sealing ring, and driveline bearing, so when the system runs to the set preventive maintenance time point, the system needs to be incompletely repaired, and the abovementioned parts should be repaired and replaced first to extend the service cycle of the system.

When the system is in the “1” fault state, the oil circuit sealing ring has the greatest impact on the system, followed by pipe seal, driveline bearing, and water distributor sealing ring; servo motor connecting screws have the least impact.

6 Conclusions

An improved T-S FFTA had been provided in this paper by introducing the importance index of basic events with T-S FFTA. The proposed method, in which fuzzy possibilities are used to describe the events, fuzzy variables are used to describe the magnitude of failure, and the T-S fuzzy gates are constructed to represent the uncertainties in the relationships among events, could not only solve the problem of imprecision in the probabilities of failure of components arising from inadequate failures data, uncertainties relationships among events and considering the magnitude of failure, making the result better than MC FFTA method, but also require as little expert knowledge as possible and reduce the subjective error caused by overdependence. The T-S probabilistic importance analysis of the basic events in different fault states indicates that oil circuit sealing ring, pipe seal, driveline bearing, and water distributor sealing ring play important role in affecting failure of the NC turret sealing subsystem.