1 Introduction

The performance of HMC is mainly reflected in whether the quality of the products meets the accuracy requirements of users [1]. Machining accuracy is the main parameter and final goal of evaluating the working performance of machine tool [2]. Affected by many factors, such as the axial elongation [3] or “hot rise” of the spindle caused by heat during the long-term use of the spindle of HMC, which will directly affect the accuracy of machine tool [4]. In addition, the installation and wear of the tool [5], the compression and deformation of the guide rail, the manufacturing error of the parts, and the complex human factors will reduce the machining accuracy of CNC machine tool. Among many factors, geometric error and thermal error account for about 50–70% of the total error, especially geometric error accounts for about 40% [6]. Machine tool geometric error has various types according to different forms, mainly including positioning error, straightness error, rolling error, Britain swing error, yaw error, and perpendicularity and parallelism error between motion axes. These errors interact with each other to influence the machine tool [7]. How to find and control effectively the key geometric errors which have great impact on machine tool is the main problem to improve machining accuracy.

To solve this problem, a novel global sensitivity analysis (GSA) is proposed. Sensitivity analysis (SA) can be used to study the influence of input uncertainty on system output [8], and also to identify the impact of system response by uncertainty changes from system parameters [9]. SA includes local sensitivity analysis (LSA) and GSA [10]. For CNC machine tools, LSA mainly analyzes the impact of a single error change on machining accuracy [11]. GSA considers the complex coupling effect of several geometric errors. Because the CNC machine tool is affected by many factors, the geometric errors have randomness, uncertainty, and mutual coupling and interaction [12]. Therefore, it is reasonable and effective to use GSA to identify critical geometric errors.

Many scholars have done a lot of research on GSA. Considering the randomness of geometric errors, Cheng et al. proposed the Sobol method to get the critical errors of a three-axis vertical machining center [13]. Xia used the improved Sobol method to identify globally the critical errors for a five-axis gear forming grinder [14]. Based on the Extended Fourier amplitude sensitivity test method, Guo et al. established the global sensitivity quantitative analysis method of geometric error for three-axis machining center [15]. Through the screw theory, Wu established the volume error model for three-axis machine tool, and studied the sensitivity of geometric error with this model [16]. However, in many sensitivity methods, it is neglected that the geometric error value changes with the displacement of motion axes. At different positions, the fluctuation of geometric errors should be considered. Therefore, a novel GSA method is proposed based on MBS and geometric error characteristics analysis.

Error modeling technology can clearly express the nonlinear mapping relationship between geometric error and machining accuracy. At present, modeling technology is becoming more and more mature, and MBS and screw theory are widely used [27]. Through the screw theory, Moon et al. carried out geometric error modeling and error compensation for CNC machine tools [17]. By the screw theory, Yang proposed a method to identify and correct position-independent geometric errors for multi-axis machine tools [18]. Based on MBS theory, Guo used homogeneous transformation matrix to establish geometric error model [19]. Similarly, Guo carried out geometric error modeling for five-axis machine tool with MBS theory and homogeneous transformation matrix [20]. With the development of MBS theory, it has become the mainstream choice of geometric error modeling [13, 14, 21].

Before studying the fluctuation of geometric errors with displacement, the fitting relationship between them must be established. At present, most polynomials with position coordinates as variables are chosen as fitting functions between single geometric error and displacement [16, 22, 23]. However, it is necessary to solve the order problem of the prediction model which has great influence on the fitting quality. Otherwise, the preset error will be introduced. Fu et al. [24] used automatic modeling technology to model single geometric error and selected the order of polynomials based on F-test. However, with the improvement of polynomial order, more measurement points were needed, and the fitting effect of polynomial form was not ideal compared with the actual error. Compared with polynomial function fitting, composite function fitting with trigonometric function is better. According to the integral relationship between straightness error and angle error, Ekinci et al. used the composite function composed of sine and cosine function as the fitting function, which has a good fitting effect [25]. Tang et al. used the composite function composed of sine cosine function and parabola function to fit the surface curve of the guide rail scanned by the electron microscope, and then, the geometric error is predicted, which also revealed the internal relationship between the geometric error and the trigonometric function [26].

In this paper, Fourier series including constant term and sine cosine function is used to fit the relationship between single geometric error and displacement in a certain stroke of moving axis of machine tool. In the machining stroke (i.e., the stroke of the moving parts of the machine tool), the geometric error parameters vary greatly at different displacement points. This paper defines it as the fluctuation of error. The rapid fluctuation of geometric errors will inevitably have a dynamic impact on the machining accuracy of machine tools. After obtaining the function formula with a high fitting degree, the derivative of function to displacement is used to analyze the fluctuation of error. The derivative function is defined as the fluctuation function of geometric error. After the coordinates of each position point are substituted into the derivative function, the variation trend of the error at that point is obtained. Finally, the overall fluctuation of geometric error in the stroke will be obtained by averaging.

The correlation of geometric errors is objective [27, 28]. Cheng et al. introduced the Pearson correlation coefficient to analyze the correlation between geometric errors, and classified them by SPSS [29]. Chen et al. introduced the spearman rank correlation to study the relation between single error parameter and tool attitude error in the whole sampling space, and calculated and selected ten key error parameters with large absolute correlation coefficient [30]. In this paper, an improved second-order partial correlation coefficient based on the Pearson product moment is introduced to analyze the correlation between geometric errors. Partial correlation coefficient has been successfully applied to systems biology [31], genomics [32], and acoustics [33].

The general structure of this paper. Section 2 introduces the framework of the novel global sensitivity analysis method. In Section 3, an overview of the sensitivity analysis method is introduced. In Section 4, a case study is carried out to elaborate the methods used. Section 5 is the conclusion.

2 The framework of analysis method

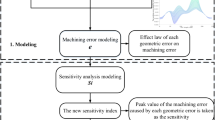
In this paper, the machine tool geometric error model is established based on MBS theory, and the partial derivative of each geometric error is obtained. At the same time, considering the fluctuation and correlation of errors in the motion stroke, the global sensitivity analysis model is constructed. The key geometric errors affecting the machining accuracy are identified by the sensitivity coefficient. The framework of the global sensitivity analysis method involved in this paper is shown in Fig. 1.

Fig. 1
figure 1

Framework of global sensitivity analysis

Full size image

3 Overview of sensitivity analysis method

3.1 Establishment of geometric error model

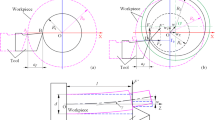
The machine tool structure is shown in Fig. 2. The mechanism of motion for the machine tool is analyzed, and the topological structure is established to represent the relative motion between moving axes. According to the motion transfer mode of the machine tool, the topological structure can be divided into two chains, as shown in Fig. 3. Set the fixed bed and column as inertia body with the mark of 0. X, Y, and Z guide rails are labeled 1, 2, and 4 respectively. The electric spindle and worktable are marked as 3 and 5 respectively. Table 1 shows the structural parameters of the machine tool.

Fig. 2
figure 2

Structure of machine tool

Full size image
Fig. 3
figure 3

Topological structure of machine tool

Full size image
Table 1 Structural parameters of the machine tool
Full size table

This paper only studies the fluctuation of the errors with the displacement in the stroke of the motion axis. Therefore, during the error measurement, keep the workbench fixed and motionless with the workpiece, that is, the B-axis is still and there is no error. Table 2 shows the symbols and meanings of geometric errors. Based on MBS theory, the motion characteristic matrix of the CNC machine tool is established by using homogeneous coordinate transformation, as shown in Table 3.

Table 2 Geometric error of HMC
Full size table
Table 3 The motion characteristic matrix of machine tool
Full size table

In the table:

The superscript p is static; The subscript s is motion;

T is the error characteristic matrix in an ideal state;

ΔT represents the error characteristic matrix in the actual state;

I4 × 4 denotes that when the error is relatively small, it can be ignored as the unit matrix;

Set the coordinates of the tool forming point in the tool coordinate system as:

$$ {P}_t={\left[{P}_{tx}{P}_{ty}{P}_{tz}1\right]}^T $$
(1)

Set the coordinates of the workpiece forming point in the workpiece coordinate system as:

$$ {P}_w={\left[{P}_{wx}{P}_{wy}{P}_{wz}1\right]}^T $$
(2)

When the machine tool works in the ideal state without error, the ideal coordinates of the workpiece forming point in the tool coordinate system can be written as:

$$ {P}_{\boldsymbol{tideal}}={\left[{T}_{01}^p{T}_{01}^s{T}_{12}^p{T}_{12}^s{T}_{23}^p{T}_{23}^s\right]}^{-1}{T}_{04}^{\mathrm{p}}{T}_{04}^{\mathrm{s}}{P}_w $$
(3)

In the case of actual machining, the actual coordinates of the workpiece forming point in the tool coordinate system are:

$$ {P}_{\mathrm{t}\boldsymbol{actual}}={\left[\Delta {T}_{03}\right]}^{-1}\Delta {T}_{04}{P}_w $$
(4)

Here, \( \Delta {T}_{03}={T}_{01}^p\Delta {T}_{01}^{\mathrm{p}}{T}_{01}^s\Delta {T}_{01}^{\mathrm{s}}{T}_{12}^p\Delta {T}_{12}^{\mathrm{p}}{T}_{12}^s\Delta {T}_{12}^{\mathrm{s}}{T}_{23}^p\Delta {T}_{23}^{\mathrm{p}}{T}_{23}^s\Delta {T}_{23}^{\mathrm{s}} \); \( \Delta {T}_{04}={T}_{04}^p\Delta {T}_{04}^p{T}_{04}^s\Delta {T}_{04}^s \).

The comprehensive error matrix can be written by symbol E(G) as follows:

$$ E(G)={P}_{\boldsymbol{tideal}}-{P}_{\mathrm{t}\boldsymbol{actual}}=\left[\begin{array}{c}{E}_x(G)\\ {}{E}_y(G)\\ {}{E}_y(G)\\ {}0\end{array}\right] $$
(5)

The machining process of this paper is to analyze the machining accuracy when simulating the machining of fixed size workpiece under the fixed workpiece and cutter installation position. Therefore, Pw and x, y, z in Table 3 are predetermined values. Ex(G), Ey(G), Ez(G) represent the machining accuracy function with geometric error as variable in three directions.

G = [g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15, g16, g17, g18] represents a vector composed of 18 errors, making δxx, δyx, δzx, εαx, εβx, εγx, δxy, δyy, δzy, εαy, εβy, εγy, δxz, δyz, δzz, εαz, εβz, εγz = g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15, g16, g17, g18.

3.2 Local influence analysis of geometric error

To analyze the local influence of single geometric error on machining accuracy of the machine tool, according to the formula (5), the partial derivative of the error is calculated by using the machining accuracy function according to formula (5). Taking the error δxx(=g1) as an example, after the partial derivative of g1 is calculated, the average value of the error measurement data is brought in, and the local influence on the machining accuracy in three directions when it changes slightly is analyzed. The matrix form represented by the symbol \( {f}_{g_1}^{(1)} \) is:

$$ {f}_{g_1}^{(1)}=\left[\begin{array}{ccc}\frac{\partial {E}_x}{\partial {g}_1}& 0& 0\\ {}0& \frac{\partial {E}_y}{\partial {g}_1}& 0\\ {}0& 0& \frac{\partial {E}_z}{\partial {g}_1}\end{array}\right] $$
(6)

Similarly, the local influence of the remaining 17 errors of \( {f}_{g_2}^{(1)},{f}_{g_3}^{(1)},\cdots {f}_{g_{18}}^{(1)} \) on machining accuracy in three directions can be obtained.

3.3 Fluctuation analysis of geometric error

In this paper, a fitting function based on the Fourier series is proposed to find the internal relationship between geometric error and motion displacement. The fitting function of error gi is represented by symbol \( {F}_{g_i}(u) \). u is the position of measurement point (i.e., movement axis displacement).

$$ {F}_{g_i}(u)={a}_0+{a}_1\mathit{\cos}(wu)+{b}_1\mathit{\sin}(wu)+{a}_2\mathit{\cos}\left(2 wu\right)+{b}_2\mathit{\sin}\left(2 wu\right)+{a}_3\mathit{\cos}\left(3 wu\right)+{b}_3\mathit{\sin}\left(3 wu\right)+\cdots +{a}_l\mathit{\cos}(lwu)+{b}_l\mathit{\sin}(lwu)\left(l=1,2,\cdots \right) $$
(7)

Where a0 is the constant term, a1, b1, a2, b2, ⋯al, bl; w are the coefficients of the fitting function, and l is the order of the Fourier series.

In addition, the sine series will be used for fitting. The form of the sine series represented by the symbol \( {S}_{g_i}(u) \) is

$$ {S}_{g_i}(u)={p}_1\mathit{\sin}\left({c}_1u+{d}_1\right)+{p}_2\mathit{\sin}\left({c}_2u+{d}_2\right)+\cdots +{p}_m\mathit{\sin}\left({c}_mu+{d}_m\right)\left(m=1,2,\cdots \right) $$
(8)

Where p1, c1, d1⋯pm, cm, dm are coefficients of the fitting function and m is the order of the sine function.

According to the fitting functions above, this paper uses the fitting function to derive the u. Taking g1 as an example, formula 9 can be written as follows:

$$ {f}_{g_1}^{(2)}=\frac{1}{n}\left[\sum \limits_{t=1}^n{\left.\frac{dF_{g_1}(u)}{d(u)}\right|}_{u={u}_t}\right] $$
(9)

Where n(=11) is the number of measurement points, ut(=50, 130, ⋯850) is the position of measurement points, and \( \frac{dF_{g_1}(u)}{d(u)} \) is the fluctuation function of geometric error. The position of the measurement point is brought into the function in turn and then the mean value is calculated. The overall fluctuation of geometric error in the machining stroke can be obtained. Taking the same steps, we can get the fluctuation of the remaining 17 geometric errors, such as \( {f}_{g_2}^{(2)},{f}_{g_3}^{(2)},\cdots, {f}_{g_{18}}^{(2)} \).

3.4 Partial correlation analysis of geometric errors

Pearson product moment correlation is usually used to study the correlation between continuous random variables. In this paper, an improved second-order partial correlation coefficient based on the Pearson product moment is introduced to analyze the correlation between geometric errors. The calculation of the correlation coefficient is shown in Eq. 10–12.

$$ {\displaystyle \begin{array}{c}{R}_{g_i,{g}_j}^0=\mathrm{corrcoef}\left({\mathrm{g}}_i,{\mathrm{g}}_j\right)\\ {}\left(i,j=1,2,\cdots 18\right)\end{array}} $$
(10)
$$ {\displaystyle \begin{array}{c}{R}_{g_i-{g}_j,{g}_k}^1=\frac{R_{g_i,{g}_j}^0-{R}_{g_i,{g}_k}^0\times {R}_{g_j,{g}_k}^0}{\sqrt{\left[1-{\left({R}_{g_i,{g}_k}^0\right)}^2\right]\left[1-{\left({R}_{g_j,{g}_k}^0\right)}^2\right]}}\\ {}\left(i,j,k=1,2,\cdots 18\right)\end{array}} $$
(11)
$$ {\displaystyle \begin{array}{c}{R}_{g_i-{g}_j,{g}_k-{g}_h}^2=\frac{R_{g_i-{g}_j,{g}_k}^1-{R}_{g_i-{g}_k,{g}_h}^1\times {R}_{g_j-{g}_k,{g}_h}^1}{\sqrt{\left[1-{\left({R}_{g_i-{\mathrm{g}}_k,{g}_h}^1\right)}^2\right]\left[1-{\left({R}_{g_j-{\mathrm{g}}_k,{g}_h}^1\right)}^2\right]}}\\ {}\left(i,j,k,h=1,2,\cdots 18\right)\end{array}} $$
(12)

\( {R}_{g_i,{g}_j}^0 \), \( {R}_{g_i-{g}_j,{g}_k}^1 \), and \( {R}_{g_i-{g}_j,{g}_k-{g}_h}^2 \) denote zero-, first-, and second-order partial correlation coefficients, respectively. The result of \( {R}_{g_1,{g}_2}^0 \) is the same as that of \( {R}_{g_2,{g}_1}^0 \), i.e., the result of zero-order correlation can be written as a symmetric matrix with the main diagonal of one. However, in the calculation of the first- and second-order partial correlation, when the errors are the same, the result will be infinite. To ensure that the calculated results can still be written as a matrix form of 18 × 18, so as to clearly show the correlation between the errors, the following provisions are made.

  1. 1)

    When two errors are the same (i.e., i = k), the calculation result of the first- or second-order partial correlation coefficient is infinite. In this case, refer to the 0-order partial correlation results, and set them to 1. In each case, there are two times of infinity, so it does not affect the calculation results.

  2. 2)

    After calculating the first-order partial correlation, 2448 sets of data will be obtained. In order to simplify the calculation, the matrix form of 18 × 18 is still written according to the 0-order calculation results after the average value is calculated for each case. Then, according to the first-order partial correlation formula, the second-order partial correlation coefficient is calculated.

After the second-order partial correlation coefficients of geometric errors in each case are obtained, the mean value is calculated for each case, and the result was still written as the matrix form of 18 × 18. The mean value of each line is calculated again, and the result is taken as the overall correlation between the geometric error and the rest errors. Second-order partial correlation coefficient of single error expressed by \( {R}_{g_i}^2 \).

3.5 Establishment of global sensitivity analysis model

Through the above analysis, the global sensitivity model of geometric error is established in the form of sequential multiplication. The symbols fX(gi), fY(gi), fZ(gi) respectively represent the global sensitivity coefficients of errors to the three machining directions of X, Y, and Z. Equation 13 shows the global sensitivity of the i-th error.

$$ {\displaystyle \begin{array}{c}f\left({\mathrm{g}}_i\right)={R}_{{\mathrm{g}}_i}^2\cdotp {f}_{{\mathrm{g}}_i}^{(1)}\cdotp {f}_{{\mathrm{g}}_i}^{(2)}=\left[\begin{array}{ccc}{f}_X\left({\mathrm{g}}_i\right)& 0& 0\\ {}0& {f}_Y\left({\mathrm{g}}_i\right)& 0\\ {}0& 0& {f}_Z\left({\mathrm{g}}_i\right)\end{array}\right]\\ {}{R}_{{\mathrm{g}}_i}^2=\left[\begin{array}{ccc}\frac{\partial {E}_x}{\partial {\mathrm{g}}_i}& 0& 0\\ {}0& \frac{\partial {E}_y}{\partial {\mathrm{g}}_i}& 0\\ {}0& 0& \frac{\partial {E}_z}{\partial {\mathrm{g}}_i}\end{array}\right]\frac{1}{n}\left[\sum \limits_{t=1}^n{\left.\frac{dF_{g_1}(u)}{d(u)}\right|}_{u={u}_t}\right]\end{array}} $$
(13)

The global sensitivity coefficient of any error gi to the whole machining space is expressed as fGlobal(gi):

$$ {f}_{\boldsymbol{Global}}\left({g}_i\right)=\sqrt{{\left[{f}_X\left({g}_i\right)\right]}^2+{\left[{f}_Y\left({g}_i\right)\right]}^2+{\left[{f}_Z\left({g}_i\right)\right]}^2} $$
(14)

4 Case study

4.1 Geometric error measurement and digital characteristics

Under the condition that the testing instrument and the moving axis of the machine tool do not interfere, the same 800 mm stroke is selected on each axis. Take 50 mm as the starting point and set a measuring point at an interval of 80 mm. The moving axis runs twice in both positive and negative directions respectively. Using 6D laser interferometer, each point is measured four times, and the geometric error data at different positions are recorded, as shown in Fig. 4. Statistics and calculation of measured data are shown in Table 4, 5, 6, 7.

Fig. 4
figure 4

Error data collection site

Full size image
Table 4 Geometric error data of X-axis (mm)
Full size table
Table 5 Geometric error data of Y-axis (mm)
Full size table
Table 6 Geometric error data of Z-axis (mm)
Full size table
Table 7 Orientation errors data (mm)
Full size table

4.2 Global sensitivity calculation of geometric errors

According to Section 3.3, some fitting results are shown in Table 8. Figure 5, 6, 7 shows the fitting function of some geometric errors and displacements. All fitting functions of position dependent geometric errors and displacements are shown in Appendix 1 Table 12. Appendix 2 is the second-order partial correlation coefficient of all geometric errors. The direct interaction and potential correlation between errors can be obtained by calculation and analysis.

Table 8 Fitting functions of partial geometric errors and displacement
Full size table
Fig. 5
figure 5

δxx − u fitting curve and residual error

Full size image
Fig. 6
figure 6

δyx − u fitting curve and residual error

Full size image
Fig. 7
figure 7

εβx − u fitting curve and residual error

Full size image

Among them, R-square represents the quality of a fitting effect. The normal value range is [0,1], the closer it is to 1, it indicates that the variables of the equation have a stronger ability to interpret the function. This model also fits the data well. It can be seen from Appendix 1 Table 12 that most of the R-squares are above 0.98, some are very close to 1. Compared with the low-order Fourier series fitting error-displacement curve based on the least square method of the same guideway in literature [34], the fitting degree of this paper is higher than its 1.7%–8.2%, which can show the relationship between geometric error and displacement more clearly. Table 9 shows the fitting comparison results. High fitting degree is helpful to analyze the fluctuation of geometric error.

Table 9 Comparison results of R-square
Full size table

After all the data are brought into the model, Table 10 lists the calculation results of the global sensitivity coefficients of errors. For visual display, the results are shown in histogram 8–9 (Figs. 8 and 9).

Table 10 The results of global sensitivity coefficients
Full size table
Fig. 8
figure 8

Global sensitivity coefficients of geometric errors in X, Y, and Z machining directions

Full size image
Fig. 9
figure 9

Global sensitivity of geometric errors in the whole machining space

Full size image

From the above figures, the following conclusions can be drawn:

  1. (1)

    For the X direction, the global sensitivity coefficients of εγx, δxx, εβx are larger. For the Y direction, the global sensitivity coefficients of δyy, εαy, δzz are larger. For the Z direction, the global sensitivity coefficients of εβx, εβz, εαy are larger. The analysis results show that when the moving parts move along each axis, these three geometric errors and other errors have a great influence on the machining accuracy of each axis through the interaction between them.

  2. (2)

    For the whole machining space of machine tools, the global sensitivity coefficients of εγx, εβx, δyy, δxx, εβz, εαy are relatively large, accounting for 74.6% of the total.

4.3 Application and improvement

From the overall analysis results, the geometric error of X-axis has the greatest impact on the machining accuracy. Therefore, this paper proposes to replace the X-axis with two more accurate guide rails, as shown in Fig. 10. After the improvement, the error is remeasured, and the measurement data is counted and brought into the machine space geometric error model in formula 5. Table 11 shows the accuracy of the machine tool before and after improvement.

Fig. 10
figure 10

Replacing high precision guide rail

Full size image
Table 11 Accuracy of machine tool before and after improvement
Full size table

The experimental results show that this method can effectively identify the geometric errors which have a great influence on the machining accuracy of HMC. The manufacturing and assembly of machine tools should be strictly controlled to fundamentally improve the processing quality of products. At the same time, the validity of the proposed method is proved.

5 Conclusion

The method proposed in this paper has the following features:

  1. (1)

    This paper analyzes the overall effect of geometric error on machining accuracy in a certain stroke. By introducing different displacement points into the fluctuation function, the fluctuation of geometric error at this point can be obtained, and then, the global sensitivity coefficient at this point can be calculated. This method reveals the influence of geometric error on the machining accuracy of machine tool due to the change of movement position. At the same time, it shows that the sensitivity coefficient changes with the change of displacement.

  2. (2)

    In this paper, the Fourier series is used to fit a single geometric error. The results show that the fitting degree is high and the residual error is small. In fact, if the trigonometric function terms in the Fourier series and sine series expand according to Taylor series and ignore the higher-order terms, they are polynomial functions. Therefore, trigonometric functions are more fitting accurate than polynomials. In addition, the dynamic effects of the fluctuation and correlation of geometric errors on machining accuracy are considered in the global sensitivity analysis model proposed in this paper. The analysis results are closer to the actual production process.

  3. (3)

    In this paper, only the geometric errors related to the moving axis are studied, but the errors related to the rotating axis (B-axis) have not found good fitting functions. And the research is carried out under the quasi-static condition of machine tool. The dynamic fluctuation of error and thermal error caused by different axial acceleration and dynamic load of machine tool should be further considered.