A stability prediction method research for milling processes based on implicit multistep schemes

Abstract

Chatter suppression during milling operations is of great significant for tool life, surface quality, and cutting efficiency. Based on the Hamming and Simpson methods, a Hamming–Simpson–based method is presented in this paper for accurately and efficiently determining the milling stability. The milling dynamic model with consideration of the regeneration effect is expressed by delay differential equations (DDEs) with time-periodic coefficients. After separating the tooth-passing period into two different phases, the two linear multistep methods are simultaneously adopted to estimate the state term by discretizing the forced vibration phase into time intervals of equal length. Subsequently, the state transition matrix can be determined over one period and the chatter-free borderline can be searched according to the Floquet theory. On this basis, the precision and efficiency of the Hamming–Simpson–based method are analyzed in detail through comparing with the three benchmark methods. Analysis results indicate that the Hamming method is required to convert variables which may affect the prediction accuracy. To overcome this shortcoming and promote the computational accuracy, a three-step implicit multistep exponential fitting method is applied to predict chatter stability; meanwhile, the Simpson method is responsible for the correction of the prediction. The effectiveness of the proposed method has been comparatively analyzed through two benchmark examples. Numerical simulations illustrate that the proposed method exhibits better prediction accuracy and computational efficiency.

1 Introduction

Chatter is already recognized as a typical undesired phenomenon in machining operations, which always seriously affects the production efficiency and machining quality, even accelerated tool wear and reduce machine tool’s life [1]. Therefore, chatter stability prediction is an effective and significant way for assisting the machinist to select optimal cutting parameters to improve the production efficiency and avoid chatter [2,3,4]. Theoretically speaking, chatter vibration caused by the frictional, mode-coupling, thermo-mechanical, and regenerative mechanisms. During the milling processes, regenerative chatter [5, 6] is regarded as a typical and undesirable self-excited vibration because of its deteriorative effects on the surface quality and machining productivity. The corresponding model of milling dynamics can be formulated as delay differential equations (DDEs) [7, 8], and numerous researches have been conducted by solving the DDEs for predicting the stability lobe diagram (SLD). To achieve stable machining and good surface finish, the chatter-free cutting parameters can be obtained according to the obtained SLD.

It is well known that different methods for prediction of regenerative chatter stability have been developed. When taking the mean component of Fourier series into account, Altintas and Budak [9, 10] firstly proposed a wide and classical analytical method for predicting the SLD using the zero-order approximation (ZOA), which is of low computational cost. However, it may not give better prediction accuracy for low radial immersion conditions. To overcome this shortcoming and expand the scope of applications, Merdol and Altintas [11] brought the higher order harmonics of the directional factors into the milling dynamic system and reported a multifrequency solution for determining the stable boundary. In the abovementioned researches [9,10,11], the nonlinear factors of the milling system are not considered; thus, the differential equation of the milling system is linear. When the nonlinear dynamics is taken into consideration, Balachandran et al. [12,13,14] found the nonlinear dynamical models have a certain impact on the accurate and efficient prediction of chatter stability, which explored the nature of chatter. The linear dynamics models can achieve quite good accuracy for milling stability prediction without consideration of the post-instability motions, and they are used for determining suitable machining parameters. Bayly and his co-authors [15] put forward a temporal finite element analysis to simultaneously calculate the SLD and surface location error. Butcher and his co-authors [16] utilized a Chebyshev collocation method (CCM) to deal with stability prediction. With the aid of shifted Chebyshev polynomials, a stability prediction method was proposed by Yan et al. [17] for thin-walled workpiece milling. By discretizing the delayed term with piecewise constant functions, two different order semi-discretization methods (0th and 1st SDMs) were firstly introduced by Insperger and Stepan [18, 19] for chatter stability prediction, and the convergence rates and stability lobes of the two SDMs were carefully studied in [20]. Furthermore, the two SDMs can be utilized for milling process stability analysis with various situations. By using improved precise time-integration algorithm, Jiang et al. [21] interpolated the terms of DDEs using the Newton interpolation and developed the second-order SDM (2nd SDM) to predict the SLD, which is of high computational efficiency in low- and high-speed milling processes. Nevertheless, the SDMs have relatively low computational efficiency.

To enhance the computational efficiency without any loss of prediction accuracy, Ding et al. [22] discretized the state and time-delay terms of DDEs and presented the so-called full-discretization method (1st FDM), which can be widely used for predicting the stability lobes. By using direct integration scheme (DIS), different prediction methods for higher approximation accuracy were developed. Ding et al. [23] expanded the 1st FDM and explored the second-order FDM (2nd FDM) for predicting the stability lobes based on the second-order Lagrange polynomial. Quo et al. [24] subsequently presented the third-order FDM (3rd FDM) to derive the milling stability. Ozoegwu et al. [25] further developed the fourth- and fifth-order FDMs for determining the stability lobes based on least squares approximation. Liu et al. [26] reported a third-order Hermite approximation method (3rd HAM) to calculate the SLD. Ji et al. [27] further developed a third-order Hermite–Newton approximation method (3rd H-NAM) to predict chatter stability; simulation results illustrate that the 3rd H-NAM has faster convergence rate and higher computational accuracy in most complex situations. However, the calculation speed can be reduced due to more complex structures.

With the aim of reducing the computational time, the second-order updated FDM (2nd UFDM) was proposed by Tang et al. [28] for predicting the SLD, which employs linear interpolation techniques directly to establish the transition matrix. Yan et al. [29] subsequently extended the 2nd UFDM to the third-order UFDM (3rd UFDM). The UFDMs have been verified to be accurate and efficient methods. The UFDMs achieve a better performance, but all elements of dynamical equations do not discretize completely. On the other hand, Li et al. [30] employed the Euler’s method to discretize the differential term and reported the complete discretization scheme (CDS) for determining the stability lobes. Under the same framework of complete discretization scheme, Xie [31] utilized the linear interpolation to approximate the period coefficient matrices and further developed an improved CDS (ICDS) for chatter stability prediction. Li et al. [32] utilized the dichotomy search to determine the stability boundaries and reported the Runge–Kutta CDM (RKCDM) for determining the stability lobes. Besides, two Runge–Kutta methods (CRKM and GRKM) were investigated by Niu et al. [33]. The GRKM exhibits higher computational accuracy and efficiency; however, its complex structure leads to the large calculation of the exponential matrix. Subsequently, based on the precise integration method (PIM), Dai et al. [34] proposed an explicit PIM to predict the chatter stability. By using the golden search to substitute the sequential search, Dai et al. [35] developed the improved FDM (IFDM) to calculate the SLD. Later, Li et al. [36] expanded the PIM method and developed an improved PIM (IPIM) for milling process stability analysis by using the second-order Taylor formula. Additionally, Ding et al. [37] investigated on SLD using the numerical integration schemes and reported the numerical integration method (NIM) to search stability limits under three different conditions. With the help of differential quadrature method, a semi-analytical method was subsequently suggested by Ding and his co-authors [38] to calculate the SLD. By using the Simpson method to approximate the state term over a discrete interval, a new approach was presented by Zhang et al. [39] for predicting the stability lobes. With the aid of the numerical extrapolation and the finite difference methods, Zhang and co-workers [40] suggested the numerical differentiation method (NDM) for high-speed milling.

In recent years, by using the Adams-Moulton-method (AMM) to approximate the state term, Qin et al. [41] presented an AMM for more efficiently and accurately prediction of chatter stability. Tao et al. [42] extended the AMM to obtain the stability lobes with multiple delays. Qin et al. [43] improved the AMM and reported the Adams–Simpson–based method (ASM) to predict the SLD. The comparative results showed that the ASM converges much faster than the AMM by using the predictor–corrector technique. To further improve the convergence rate and prediction accuracy, a Hamming–Simpson–based method (HSM) is proposed for predicting the SLD. Nevertheless, the Hamming method is required to convert variables which may affect the prediction accuracy of the SLD. To develop the HSM with higher prediction accuracy and computational efficiency based on the predictor–corrector technique; the authors combine the third-order implicit multistep exponential fitting method [44, 45] and the Simpson method to predict chatter stability, known as the implicit multistep exponential fitting–Simpson–based method (ISM). The simulations reveal that the ISM exhibits much higher accuracy and efficiency.

The rest of this paper is organized as follows. In Sect. 2, mathematical models of milling processes are constructed. In Sect. 3, a Hamming–Simpson–based method (HSM) is proposed to calculate the SLD. In Sect. 4, the accuracy of the single-DOF SLD is discussed in detail. In Sect. 5, a three-step implicit multistep exponential fitting–Simpson–based method (ISM) is presented to predict milling stability. In Sect. 6, the convergence rate and SLD with the ISM are investigated through making comparison with the three benchmark methods. In Sect. 7, it draws several conclusions.

2 Mathematical model of milling processes

On the basis of stability analysis, single- and two-DOF dynamic models with regenerative effect are described, respectively.

2.1 The single-DOF milling model

According to regenerative chatter theory, the single-DOF milling model from [18, 19] is formulated as the following dynamic equation:

$$ {m}_t\overset{\cdot \cdot }{x}(t)+2{m}_t{\zeta \omega}_n\overset{\cdot }{x}(t)+{m}_t{\omega}_n^2x(t)={a}_ph(t)\left[x\left(t-T\right)-x(t)\right] $$

(1)

where

$$ h(t)=\sum \limits_{j=1}^{N_f}g\left({\phi}_j(t)\right)\left[{K}_n{s}^2+{K}_t sc\right]\kern0.5em $$

(2)

where x(t) stands for the displacement vector in x direction with the modal parameters of system represented bym_t, ζ, and ω_n. a_p refers to the axial cutting depth. T stands for the regenerative delay or tooth passing period, which is decided by the tool number N_fand the spindle speed Ω, namelyT  = 60/(N_fΩ). In Eq. (2), given the normal and tangential cutting force coefficientK_n and K_t, the angular position of jth toothϕ_j(t) = (2πΩ/60)t + 2π(j − 1)/N_f. Besides, s  = sin(ϕ_j(t)), c = cos(ϕ_j(t)).

The window function g(ϕ_j(t)) is defined as

$$ g\left({\phi}_j(t)\right)=\left\{\begin{array}{c}1\kern4em {\phi}_{st}<{\phi}_j(t)<{\phi}_{ex}\\ {}0\kern7.5em \mathrm{otherwise}\end{array}\right. $$

(3)

where ϕ_st and ϕ_ex denote the start and exit angles of tooth, respectively. It is defined as

$$ \left\{\begin{array}{c}{\phi}_{st}=0,{\phi}_{ex}=\operatorname{arccos}\left(1-\frac{2a}{D}\right)\kern10em \mathrm{up}\hbox{-} \mathrm{milling}\\ {}{\phi}_{st}=\operatorname{arccos}\left(\frac{2a}{D}-1\right),{\phi}_{ex}=\pi \kern7.5em \mathrm{down}\hbox{-} \mathrm{milling}\kern1.5em \end{array}\right. $$

(4)

where a/D signifies the radial immersion ratio.

Through using state-space transformation, chatter stability analysis is carried out. Therefore, Eq. (1) is rewritten in the first-order milling model:

$$ \overset{\cdot }{U}(t)= AU(t)+B(t)\left[U\left(t-T\right)-U(t)\right] $$

(5)

where

$$ A=\left[\begin{array}{cc}-{\zeta \omega}_n& 1/{m}_t\\ {}{m}_t\left({\zeta}^2{\omega}_n^2-{\omega}_n^2\right)& -{\zeta \omega}_n\end{array}\right],B(t)=\left[\begin{array}{cc}0& 0\\ {}{a}_ph(t)& 0\end{array}\right] $$

(6)

2.2 The two-DOF milling model

According to regenerative chatter theory, the two-DOF milling model from [18, 19] is formulated as the following dynamic equation:

$$ {\displaystyle \begin{array}{c}\left[\begin{array}{cc}{m}_t& 0\\ {}0& {m}_t\end{array}\right]\left[\begin{array}{c}\overset{\cdot \cdot }{x}(t)\\ {}\overset{\cdot \cdot }{y}(t)\end{array}\right]+\left[\begin{array}{cc}2\zeta {\omega}_n{m}_t& 0\\ {}0& 2\zeta {\omega}_n{m}_t\end{array}\right]\left[\begin{array}{c}\overset{\cdot }{x}(t)\\ {}\overset{\cdot }{y}(t)\end{array}\right]+\left[\begin{array}{cc}{\omega}_n^2{m}_t& 0\\ {}0& {\omega}_n^2{m}_t\end{array}\right]\left[\begin{array}{c}x(t)\\ {}y(t)\end{array}\right]\\ {}\kern4.29em =\left[\begin{array}{cc}{a}_p{h}_{xx}(t)& {a}_p{h}_{xy}(t)\\ {}{a}_p{h}_{yx}(t)& {a}_p{h}_{yy}(t)\end{array}\right]\left[\begin{array}{c}x\left(t-T\right)-x(t)\\ {}y\left(t-T\right)-y(t)\end{array}\right]\end{array}} $$

(7)

where h_xx(t) = h(t) is defined by Eq. (2). Besides, the other three cutting force coefficients read

$$ {h}_{xy}(t)=\sum \limits_{j=1}^{N_f}g\left({\phi}_j(t)\right)\left[{K}_n sc+{K}_t{c}^2\right]\kern0.5em $$

(8)

$$ {h}_{yx}(t)=\sum \limits_{j=1}^{N_f}g\left({\phi}_j(t)\right)\left[{K}_n sc-{K}_t{s}^2\right]\kern0.5em $$

(9)

$$ {h}_{yy}(t)=\sum \limits_{j=1}^{N_f}g\left({\phi}_j(t)\right)\left[{K}_n{c}^2-{K}_t sc\right]\kern0.5em $$

(10)

Similarly, Eq. (7) is rewritten in the first-order milling model:

$$ \overset{\cdot }{U}(t)= AU(t)+B(t)\left[U\left(t-T\right)-U(t)\right] $$

(11)

where

$$ A=\left[\begin{array}{cccc}-{\zeta \omega}_n& 0& 1/{m}_t& 0\\ {}0& -{\zeta \omega}_n& 0& 1/{m}_t\\ {}{m}_t{\omega}_n^2\left({\zeta}^2-1\right)& 0& -{\zeta \omega}_n& 0\\ {}0& {m}_t{\omega}_n^2\left({\zeta}^2-1\right)& 0& -{\zeta \omega}_n\end{array}\right] $$

$$ B(t)=\left[\begin{array}{cccc}0& 0& 0& 0\\ {}0& 0& 0& 0\\ {}{a}_p{h}_{xx}(t)& {a}_p{h}_{xy}(t)& 0& 0\\ {}{a}_p{h}_{yx}(t)& {a}_p{h}_{yy}(t)& 0& 0\end{array}\right]\kern0.24em U(t)=\left[\begin{array}{c}x(t)\\ {}y(t)\\ {}{m}_t\left(\overset{\cdot }{x}(t)+{\zeta \omega}_nx(t)\right)\\ {}{m}_t\left(\overset{\cdot }{y}(t)+{\zeta \omega}_ny(t)\right)\end{array}\right] $$

(12)

According to state-space theory, the dynamical Eq. (5) and Eq. (11) of the milling system based on the DIS can be deduced as

$$ U(t)={e}^{A\left(t-{t}_0\right)}U\left({t}_0\right)+{\int}_{t_0}^t{e}^{A\left(t-\xi \right)}B\left(\xi \right)\left[U\left(\xi -T\right)-U\left(\xi \right)\right] d\xi $$

(13)

where t₀ denotes the initial time instant.

According to whether the tool is not cutting the part, the tooth-passing period can be precisely separated into two different stages: the free and forced vibration phases [37]. In the free vibration process, the term B(ξ) equals to zero matrix. Therefore, Eq. (13) is simplified as

$$ U(t)={e}^{A\left(t-{t}_0\right)}U\left({t}_0\right) $$

(14)

Subsequently, dividing the forced vibration phase [t₀ + t_f, t₀ + T] into m small subintervals, h stands for the discrete step, that is h = (T − t_f)/m. Obviously, the time for each sampling point t_n(n = 1, 2, ⋯, m + 1) is given by the following:

$$ {t}_n={t}_0+{t}_f+\left(n-1\right)h $$

(15)

At the start of the forced vibration duration, ${U}_1={e}^{At_f}{U}_{m+1-T}$ is the state term at the start time point. In addition, at arbitrary time point t_n, Eq. (13) is further equivalently re-expressed to become

$$ U(t)={e}^{A\left(t-{t}_n\right)}U\left({t}_n\right)+{\int}_{t_n}^t{e}^{A\left(t-\xi \right)}B\left(\xi \right)\left[U\left(\xi -T\right)-U\left(\xi \right)\right] d\xi $$

(16)

3 Hamming–Simpson–based method

As is well known, quite a few problems in the milling process can be eventually presented in the form of DDEs, while many traditional numerical integration methods to analyze and compute the DDEs have some advantages and shortcomings. Therefore, as a kind of convenient and simple numerical methods, the various linear multistep methods are employed to establish the state transition matrix. Therefore, the authors combine the Hamming and Simpson methods to predict the SLD, in which this method can not only ensure the computational efficiency but also improve the prediction accuracy. For being easy to describe, U(t_n), U(t_{n − T}), and B(t_n) are abbreviated as U_n, U_{n − T}, and B_n, respectively. Hence, the state term U_{n + 1} can be obtained by the Hamming method, resulting in

$$ {\displaystyle \begin{array}{l}{U}_{n+1}=\frac{1}{8}\left(9{e}^{Ah}{U}_n-{e}^{3 Ah}{U}_{n-2}\right)+\\ {}\kern3.5em \frac{3h}{8}\left\{-{e}^{2 Ah}{B}_{n-1}\left[{U}_{n-1-T}-{U}_{n-1}\right]+2{e}^{Ah}{B}_n\left[{U}_{n-T}-{U}_n\right]+{B}_{n+1}\left[{U}_{n+1-T}-{U}_{n+1}\right]\right\}\end{array}} $$

(17)

Then, Eq. (17) can be rewritten as

$$ {G}_{n-1}{U}_{n-1}+{G}_n{U}_n+{G}_{n+1}{U}_{n+1}+\frac{1}{8}{e}^{3 Ah}{U}_{n-2}={H}_{n-1}{U}_{n-1-T}+{H}_n{U}_{n-T}+{H}_{n+1}{U}_{n+1-T} $$

(18)

where

$$ \left\{\begin{array}{c}{G}_{n-1}=-\frac{3h}{8}{e}^{2 Ah}{B}_{n-1},{G}_n=-\frac{9}{8}{e}^{Ah}+\frac{3h}{4}{e}^{Ah}{B}_n,{G}_{n+1}=I+\frac{3h}{8}{B}_{n+1}\\ {}{H}_{n-1}=-\frac{3h}{8}{e}^{2 Ah}{B}_{n-1},{H}_n=\frac{3h}{4}{e}^{Ah}{B}_n,{H}_{n+1}=\frac{3h}{8}{B}_{n+1}\kern8em \end{array}\right. $$

(19)

If the variable U_{n − 2} in two adjacent time periods are out of the required range, it needs to be converted into the required range with corresponding substitutions. In Eq. (18), when n = 2, the left variable U_{n − 2} is equal to U₀. With the substitution U₀ = U_{n − n} = U_{n − T}, Eq. (18) can be rewritten as

$$ {G}_{n-1}{U}_{n-1}+{G}_n{U}_n+{G}_{n+1}{U}_{n+1}={H}_{n-1}{U}_{n-1-T}+{H}_n{U}_{n-T}+{H}_{n+1}{U}_{n+1-T}-\frac{1}{8}{e}^{3 Ah}{U}_{n-T} $$

(20)

Meanwhile, according to the Simpson method [39], the state term U_{n + 1} can be expressed as

$$ {U}_{n+1}={e}^{2 Ah}{U}_{n-1}+\frac{h}{3}\left\{{e}^{2 Ah}{B}_{n-1}\left[{U}_{n-1-T}-{U}_{n-1}\right]+4{e}^{Ah}{B}_n\left[{U}_{n-T}-{U}_n\right]+{B}_{n+1}\left[{U}_{n+1-T}-{U}_{n+1}\right]\right\} $$

(21)

Then, Eq. (21) can be rewritten as follows:

$$ {R}_{n-1}{U}_{n-1}+{R}_n{U}_n+{R}_{n+1}{U}_{n+1}={S}_{n-1}{U}_{n-1-T}+{S}_n{U}_{n-T}+{S}_{n+1}{U}_{n+1-T} $$

(22)

where

$$ \left\{\begin{array}{l}{R}_{n-1}=-{e}^{2 Ah}+\frac{h}{3}{e}^{2 Ah}{B}_{n-1},{R}_n=\frac{4h}{3}{e}^{Ah}{B}_n,{R}_{n+1}=I+\frac{h}{3}{B}_{n+1}\\ {}{S}_{n-1}=\frac{h}{3}{e}^{2 Ah}{B}_{n-1},{S}_n=\frac{4h}{3}{e}^{Ah}{B}_n,{S}_{n+1}=\frac{h}{3}{B}_{n+1}\kern8em \end{array}\right. $$

(23)

Combining Eqs. (18), (20), and (22), the discrete map is defined as

$$ {E}_1\left[\begin{array}{c}{U}_1\\ {}{U}_2\\ {}\vdots \\ {}{U}_{m+1}\end{array}\right]=\left({F}_1+{C}_1\right)\left[\begin{array}{c}{U}_{1-T}\\ {}{U}_{2-T}\\ {}\vdots \\ {}{U}_{m+1-T}\end{array}\right] $$

(24)

where

$$ {E}_1=\left[\begin{array}{ccccccc}I& & & & & & \\ {}{G}_1& {G}_2& {G}_3& & & & \\ {}{R}_1& {R}_2& {R}_3& & & & \\ {}& \frac{1}{8}{e}^{3 Ah}& {G}_3& {G}_4& {G}_5& & \\ {}& & {R}_3& {R}_4& {R}_5& & \\ {}& & \ddots & \ddots & \ddots & \ddots & \\ {}& & & \frac{1}{8}{e}^{3 Ah}& {G}_{m-1}& {G}_m& {G}_{m+1}\\ {}& & & & {R}_{m-1}& {R}_m& {R}_{m+1}\end{array}\right] $$

(25)

and

$$ {F}_1=\left[\begin{array}{ccccccc}& & & & & & {e}^{A{t}_f}\\ {}{H}_1& {H}_2& {H}_3& & & & \\ {}{S}_1& {S}_2& {S}_3& & & & \\ {}& & {H}_3& {H}_4& {H}_5& & \\ {}& & {S}_3& {S}_4& {S}_5& & \\ {}& & & \ddots & \ddots & \ddots & \\ {}& & & & {H}_{m-1}& {H}_m& {H}_{m+1}\\ {}& & & & {S}_{m-1}& {S}_m& {S}_{m+1}\end{array}\right]\kern0.24em {C}_1=\left[\begin{array}{cccc}0& \cdots & 0& 0\\ {}0& \cdots & -\frac{1}{8}{e}^{3 Ah}& 0\\ {}\vdots & \ddots & \vdots & \vdots \\ {}0& \cdots & 0& 0\end{array}\right] $$

(26)

The state transition matrix Ψ₁ with the HSM is constructed in Eq. (27):

$$ {\Psi}_1={\left({E}_1\right)}^{-1}\left({F}_1+{C}_1\right) $$

(27)

Finally, the eigenvalues of Ψ₁ can be used to extract the crucial stability contour curve based on Floquet theory [22]. The milling system is unstable when the maximal magnitude of all eigenvalues surpasses one. Otherwise, it is stable. Hence, the stability criterion can be obtained to judge whether system is unstable or not.

4 Result comparison and discussion

In this section, three benchmark methods are employed to dissect the effectiveness of the HSM, and the SLD can be obtained under two different radial immersion conditions.

4.1 Analysis of convergence rate

In general, the local discretization error can be generally considered as the most difficult issue of numerical approximation, which can be utilized to analyze the stability and prediction accuracy over a discrete time interval. The system parameters in this paper are from [18, 22], which are displayed in Table 1. Besides, the programs of each method are implemented using Matlab R2014a, and executed on the same computation platform with a central processing unit 2.8 GHZ (Intel Core(TM) i5-8400, 8 GB), to compare the computational accuracy and efficiency equally.

Table 1 Milling parameters

With the aim of comparing the prediction accuracy of different numerical methods, the absolute value of two different solutions is utilized to study the convergence rate. As is known to all, for the 1st SDM in literature [19], the local discretization error can be proven as O(h³) [20]. In addition, the local discretization error of the NIM was calculated and given as O(h³) [37]. As for the two-step Adams–Moulton method [41], the local approximation order is O(h⁴) [43]. In terms of the Hamming and Simpson methods, the local approximation orders are both O(h⁵). The Hamming and Simpson methods together constitute the predictor–corrector scheme to predict milling stability. Consequently, for the HSM in this brief paper, the theoretical local discretization error can be determined as O(h⁶). For the purpose of studying the convergence rate of the HSM, the approximate critical eigenvalues of state transition matrix are marked as |μ|, which are calculated by using different methods with respect to various computational parameters m. The exact critical eigenvalue is marked as μ₀, which is calculated by the HSM with m = 1000. For the purpose of demonstrating the accuracy of the HSM, the four machining parameter combinations (a/D  =  1, Ω  =  5000 rpm_,a_p = 0.1, 0.5, 0.7, and 1.0 mm) are selective for convergence comparison.

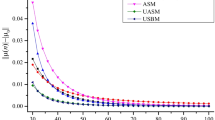
Figure 1 reveals the convergence rates with four different cutting parameters for four different methods. As shown in Fig. 1, the HSM converges much faster compared with the other three benchmark methods, which means that the HSM has a better numerical stability. For example, the HSM can achieve numerical stability with m = 48; nevertheless, the computational parameter m of other three benchmark methods significantly surpasses 48, respectively. It means that the HSM achieves much faster converse rate than the three benchmark methods. Hence, the HSM can obviously improve the prediction accuracy.

Fig. 1

Convergence rates of the HSM, ASM, NIM, and 1st SDM with a/D = 1

4.2 Stability lobe prediction

Based on the regeneration theory, theoretical analysis is used to investigate the milling stability for developing and perfecting the theory in this realm. To further compare the computational precision of the HSM, the stability lobes that are calculated by using the four different methods with the time interval m  =  40 and 50 are shown in Fig. 2. To begin with, the authors set a/D  =  1 for full immersion milling. The cutting parameters with Ω ∈ [5 × 10³,  25 × 10³] rpm and a_p ∈ [0,  5 × 10⁻³] mm are utilized in construction of the SLDs over a 200 × 100-sized grid. In the diagrams, the SLDs are determined by the HSM withm = 500, which serves as the exact reference stability boundaries in red curves. As the computation times are unstable, every program runs five times and the average time consumption can be conducted.

Fig. 2

Comparison of SLDs using the 1st SDM, NIM, ASM, and HSM with a/D = 1

Figure 2 shows the HSM achieves better prediction accuracy than the other three methods, which means that the SLDs obtained by the HSM have very good agreement with the reference stability boundaries. Hence, from the accuracy aspect, it signifies the HSM is applicable and reliable for chatter stability prediction and could ascertain the stability lobes more accurate for full immersion milling with the small time intervals. For example, the HSM can generate accurate stability lobes with m = 50; nevertheless, the time interval m of other three benchmark methods is greater than 50, respectively. Hence, the HSM takes less time compared with the other three benchmark methods to calculate the SLD with small time intervals. Meanwhile, Fig. 4 illustrates the average computational time of the four different methods under different radial immersion ratio a/D and time interval m. According to Fig. 4a, it is obvious that the HSM is more efficient than the classic 1st SDM, which can be dropped about 88% computational time. Nevertheless, compared with the NIM and ASM methods, the HSM has higher prediction accuracy with only a slight increase in computational cost. This is because the calculation of matrix exponentials with the HSM can be increased, which leads to more costs in computational time. In addition, the NIM and the ASM have been verified as an efficient method to obtain the SLD. For example, the computational time of 1st SDM, NIM, and ASM with a/D = 1 and m = 50 costs 811.8, 84.5, and 96.3 s, respectively. Nevertheless, for the HSM, its corresponding computational time consumes 103.5 s. In summary, the HSM has better prediction accuracy and numerical stability than the other three benchmark methods.

To better verify the performance of the HSM, the stability lobes that are calculated by using the four different methods with time interval m  =  10 and 20 are shown in Fig. 3. Subsequently, the authors set a/D  =  0.5 for half immersion milling. Similarly, in the stability charts, the exact stability boundaries computed by the HSM with m = 500. The cutting parameters with Ω ∈ [5 × 10³,  25 × 10³] rpm and a_p ∈ [0,  3.5 × 10⁻³] mm are utilized in construction of the SLDs over a 200 × 100-sized grid. Figure 3 shows the HSM achieves better prediction accuracy than the classic 1st SDM under the same time intervals, which means that the SLDs obtained by the HSM have very good agreement with the reference stability boundaries. Consequently, from the accuracy aspect, it signifies the HSM is feasible and reliable for chatter stability prediction and could ascertain the stability lobes more accurate for half immersion milling with the same time intervals. For example, the HSM can generate accurate stability lobes with m = 20; nevertheless, the time interval m of other three benchmark methods surpasses 20, respectively. Hence, the HSM consumes less time compared with the other three benchmark methods to calculate the SLD with small time intervals. In addition, according to Fig. 4b, it is clear that the HSM is more efficient than the classic 1st SDM, which can be dropped almost 88% computational time. Therefore, it is concluded that the HSM achieves satisfactory computational efficiency and prediction accuracy. For example, the computational time of 1st SDM, NIM, and ASM with a/D = 0.5 and m = 20 costs 86.4, 18.6, and 24.4 s, respectively. Nevertheless, for the HSM, its corresponding computational time is 25.4 s. Due to the out of the required range variable U_{n − 2}, values of the HSM need to convert into the required range, which may affect the prediction accuracy of SLD. Additionally, the state transition matrix of the HSM has an asymmetric structure. To solve the problem and enhance the performance of the HSM, the authors develop the three-step implicit multistep exponential fitting method to predict the milling stability.

Fig. 3

Comparison of SLDs using the 1st SDM, NIM, ASM, and HSM with a/D = 0.5

Fig. 4

Comparison of computational time using the 1st SDM, NIM, ASM, and HSM with a, ba/D = 1 and 0.5

5 Implicit multistep exponential fitting–Simpson–based method

Combined with traditional numerical integration techniques, several numerical algorithms with high accuracy and efficiency for the analytical solution of delay differential equations (DDEs) have been constructed. A novel method that combines the three-step implicit multistep exponential fitting method with the Simpson method (ISM) is proposed to predict milling stability [44, 45]. The proposed method can not only ensure the computational efficiency but also improve the computational accuracy. Similarly, Based on the implicit multistep exponential fitting–Simpson–based method, the state term U_{n + 1} can be obtained as follows:

$$ {\displaystyle \begin{array}{l}{U}_{n+1}={e}^{Ah}{U}_n+{hN}_2{B}_{n-1}\left[{U}_{n-1-T}-{U}_{n-1}\right]-h\left({N}_1+2{N}_2\right){B}_n\left[{U}_{n-T}-{U}_n\right]\\ {}\kern3.5em +h\left({N}_0+{N}_1+{N}_2\right){B}_{n+1}\left[{U}_{n+1-T}-{U}_{n+1}\right]\end{array}} $$

(28)

The coefficients N₀, N₁, N₂ can be derived by Eq. (28).

$$ N={e}^{Ah} $$

(29)

$$ {N}_0=-\frac{A^{-1}}{h}\left(I-N\right) $$

(30)

$$ {N}_1=-{\left(\frac{A^{-1}}{h}\right)}^2\left(I-N\right)-\frac{A^{-1}}{h}N $$

(31)

$$ {N}_2=-{\left(\frac{A^{-1}}{h}\right)}^3\left(I-N\right)-{\left(\frac{A^{-1}}{h}\right)}^2\left(\frac{1}{2}I+\frac{1}{2}N\right) $$

(32)

Then, Eq. (28) can be rewritten as follows:

$$ {K}_{n-1}{U}_{n-1}+{K}_n{U}_n+{K}_{n+1}{U}_{n+1}={L}_{n-1}{U}_{n-1-T}+{L}_n{U}_{n-T}+{L}_{n+1}{U}_{n+1-T} $$

(33)

where

$$ \left\{\begin{array}{c}{K}_{n-1}=h{N}_2{B}_{n-1},{L}_{n-1}=h{N}_2{B}_{n-1}\kern13.86em \\ {}{K}_n=-{e}^{Ah}-h\left({N}_1+2{N}_2\right){B}_n,{L}_n=-h\left({N}_1+2{N}_2\right){B}_n\kern4.62em \\ {}{K}_{n+1}=I+h\left({N}_0+{N}_1+{N}_2\right){B}_{n+1},{L}_{n+1}=h\left({N}_0+{N}_1+{N}_2\right){B}_{n+1}\kern0.99em \end{array}\right. $$

(34)

Combining Eqs. (22) and (33), the discrete map is defined as

$$ {E}_2\left[\begin{array}{c}{U}_1\\ {}{U}_2\\ {}\vdots \\ {}{U}_{m+1}\end{array}\right]={F}_2\left[\begin{array}{c}{U}_{1-T}\\ {}{U}_{2-T}\\ {}\vdots \\ {}{U}_{m+1-T}\end{array}\right] $$

(35)

where

$$ {E}_2=\left[\begin{array}{ccccccc}I& & & & & & \\ {}{K}_1& {K}_2& {K}_3& & & & \\ {}{R}_1& {R}_2& {R}_3& & & & \\ {}& & {K}_3& {K}_4& {K}_5& & \\ {}& & {R}_3& {R}_4& {R}_5& & \\ {}& & & \ddots & \ddots & \ddots & \\ {}& & & & {K}_{m-1}& {K}_m& {K}_{m+1}\\ {}& & & & {R}_{m-1}& {R}_m& {R}_{m+1}\end{array}\right] $$

(36)

and

$$ {F}_2=\left[\begin{array}{ccccccc}& & & & & & {e}^{At_f}\\ {}{L}_1& {L}_2& {L}_3& & & & \\ {}{S}_1& {S}_2& {S}_3& & & & \\ {}& & {L}_3& {L}_4& {L}_5& & \\ {}& & {S}_3& {S}_4& {S}_5& & \\ {}& & & \ddots & \ddots & \ddots & \\ {}& & & & {L}_{m-1}& {L}_m& {L}_{m+1}\\ {}& & & & {S}_{m-1}& {S}_m& {S}_{m+1}\end{array}\right] $$

(37)

The state transition matrix Ψ₂ with the ISM is constructed in Eq. (38):

$$ {\Psi}_2={\left({E}_2\right)}^{-1}{F}_2 $$

(38)

Then, the chatter stability can be determined in the same way as in Sect. 3.

6 Numerical result analysis and discussion

This section focuses on the introduction of implicit multistep exponential fitting–Simpson–based method (ISM) to predict milling stability, and three benchmark examples are employed to verify the ISM for milling processes. The parameters of this milling model are the same as those used in Sect. 4; only the analytical method is different.

6.1 Comparison of convergence rate

To verify the computational precision of the ISM, the convergence rate of the ISM is analyzed by comparing with the other three benchmark methods. Following the same way used in [20], for the ISM in this brief paper, the local discretization error can be determined as O(h⁶). Meanwhile, the four machining parameter combinations (a/D  =  1, Ω  =  5000 rpm, a_p = 0.1, 0.5, 0.7, and 1.0 mm) are selective for convergence comparison. Similarly, the exact critical eigenvalue μ₀ is also computed by the ISM with m = 1000 in this section. Figure 5 reveals the convergence rates with four different cutting parameters for the three benchmark methods and the ISM. As shown in Fig. 5, the ISM converges much faster compared with the other three benchmark methods, which means that the ISM achieves high numerical stability and precision. For example, the ISM can achieve convergence withm = 35, but the value of discretization parameter m of the other three benchmark methods clearly surpasses 35, respectively. It means that the ISM obtains much faster converse rate than the three benchmark methods. Hence, the ISM can significantly enhance the prediction accuracy of stability lobes.

Fig. 5

Convergence rates of the ISM, ASM, NIM, and 1st SDM with a/D = 1

For the purpose of further illustrating the calculate accuracy of the ISM, the four machining parameter combinations (a/D  =  0.05,Ω  =  5000 rpm,a_p = 0.5, 1.0, 1.5 and 2.0 mm) are selective for convergence comparison. In the same way, the system parameters of previous cases are still used in this section. The exact reference critical eigenvalueμ₀is also determined by the ISM with m = 1000. As shown in Fig. 6, the ISM converges much faster than the other three benchmark methods under the same time intervals, which means that the ISM achieves excellent numerical stability. Hence, it is concluded from the convergence analysis results that the ISM is more suitable for stability prediction under two different radial immersion conditions.

Fig. 6

Convergence rates of the ISM, ASM, NIM, and 1st SDM with a/D = 0.05

6.2 Stability lobe prediction

For the purpose of providing comparison for the prediction accuracy and computational time, we will make comparisons with the three benchmark methods and the ISM, in which the same dynamic model parameters are adopted.

6.2.1 Single-DOF milling system

Without loss of generality, to evaluate the validity and effectiveness of the ISM, the stability lobes are calculated by using the three benchmark methods and the ISM with the time interval m  =  10 and 20are shown in Fig. 7. To begin with, the authors set a/D  =  0.6 for medium immersion milling. The cutting parameters with Ω ∈ [5 × 10³,  25 × 10³] rpm and a_p ∈ [0,  5 × 10⁻³] mm are utilized in construction of the SLDs over a 200 × 100-sized grid. In the diagrams, the SLDs are determined by the ISM withm = 500, which serves as the exact reference stability boundaries in red curves. Figure 7 shows the ISM achieves better prediction accuracy than those of the other three methods under the same conditions, which means that the SLDs obtained by the ISM have very good agreement with the reference stability boundary curves. Consequently, from the accuracy aspect, it signifies the ISM is reliable and feasible for chatter stability prediction and could ascertain the stability lobes more accurate for medium immersion milling with the same time intervals. For example, the HSM can generate accurate stability lobes with m = 20; nevertheless, the time interval m of other three benchmark methods is greater than 20, respectively. Hence, the ISM takes less time compared with the other three benchmark methods to calculate the SLD with small time intervals. Meanwhile, Fig. 9 illustrates the average computational time of the three benchmark methods and the ISM under different radial immersion ratios a/D and time interval m. According to Fig. 9a, it is clear that the ISM is more efficient than the classic 1st SDM, which can be dropped almost 89% computational time. Nevertheless, compared with the NIM, the ISM has higher prediction accuracy with only a slight increase in computational cost. This is because that the number of exponential matrix calculations with the NIM can be reduced. The ISM and the ASM take about the same amount of computational time to predict the stability lobes. For example, the computational time of 1st SDM, NIM, and ASM with a/D =  0.6 and m = 20 costs 86.1, 20.5, and 25.3 s, respectively. Nevertheless, for the ISM, its corresponding computational time costs 26.8 s. Hence, the conclusions indicate that the ISM is much higher than the NIM and ASM in terms of computational accuracy within the same computational efficiency.

Fig. 7

Comparison of SLDs using the 1st SDM, NIM, ASM, and ISM with a/D = 0.6

For the purpose of investigating calculation accuracy and efficiency of the ISM, the stability lobes are calculated by using the three benchmark methods and the ISM with time interval m  =  4 and 10 are shown in Fig. 8. Meanwhile, the authors set a/D  =  0.06 for low immersion milling. Similarly, in the stability charts, the exact stability boundaries computed by the ISM withm = 500. The cutting parameters with Ω ∈ [5 × 10³,  25 × 10³] rpm and a_p ∈ [0,  10 × 10⁻³] mm are utilized in construction of the SLDs over a 200 × 100-sized grid. Figure 8 shows the ISM achieves better precision compared with the classic 1st SDM under the same time intervals, which means that the SLDs obtained by the HSM have very good agreement with the reference stability boundaries. Hence, from the accuracy aspect, it signifies the HSM is feasible and reliable for chatter stability prediction and could ascertain the stability lobes more accurate for low immersion milling with the same time intervals. For example, the ISM can generate accurate stability lobes withm = 10; nevertheless, the time interval m of other three benchmark methods suppresses 10, respectively. Consequently, the ISM spends less time compared with the other three benchmark methods to calculate the SLD with small time intervals. Additionally, according to Fig. 9b, it is clear that the ISM is more efficient than the classic 1st SDM, which can be dropped about 88% computational time. Compared with the NIM and the ASM, the ISM has higher prediction accuracy with only marginally increase in time loss. For example, the computational time of 1st SDM, NIM, and ASM with a/D =  0.06 and m = 10 costs 44.2, 3.6, and 4.7 s, respectively. Nevertheless, for the ISM, its corresponding computational time is 4.8 s. As a consequence, the ISM achieves higher prediction accuracy without loss of any computational efficiency under both low and medium immersion conditions.

Fig. 8

Comparison of SLDs using the 1st SDM, NIM, ASM, and ISM with a/D = 0.06

Fig. 9

Comparison of computational time using the 1st SDM, NIM, ASM, and ISM with a, b a/D = 0.6 and 0.06

6.2.2 Two-DOF milling system

Through the above research, the characteristics of single-DOF milling process are understood. The parameters of two-DOF milling dynamic system are similar to those of single-DOF milling system, and the model parameters in the two directions correspondingly are further assumed equal. Furthermore, to compare the effectiveness of the ISM, the stability lobes are calculated by using the three benchmark methods and the ISM with the time interval m  =  4 and 10 are shown in Fig. 10. To begin with, the authors set a/D  =  0.06 for low immersion milling. The cutting parameters with Ω ∈ [5 × 10³,  25 × 10³] rpm and a_p ∈ [0,  10 × 10⁻³] mm are utilized in construction of the SLDs over a 200 × 100-sized grid. In the diagrams, the SLDs are determined by the ISM with m = 500, which serves as the exact reference stability boundaries in red curves.

Fig. 10

Comparison of SLDs using the 1st SDM, NIM, ASM, and ISM with a/D = 0.06

It is clear from Fig. 10 that the prediction accuracy of the ISM is superior to that of the other three methods, which means that the SLDs obtained by the ISM have very good agreement with the reference stability boundaries curves. Consequently, from the accuracy aspect, it signifies the ISM is applicable and reliable for chatter stability prediction and could ascertain the stability lobes more accurate for low immersion milling with the same time intervals. For example, the ISM can generate accurate stability lobes with m = 10; nevertheless, the time interval m of other three benchmark methods is greater than 10, respectively. Hence, the ISM takes less time compared with the other three benchmark methods to calculate the SLD with small time intervals. Meanwhile, Fig. 11 illustrates the average computational time of the three benchmark methods and the ISM under different radial immersion ratios a/D and time intervals m. According to Fig. 11, it is obvious that the 1st SDM consumes the most computational time and the INM takes the least amount of computational time among the four methods. For example, the computational time of 1st SDM, NIM, and ASM with a/D =  0.06 and m = 10 costs 49.5, 13.2, and 15.3 s, respectively. Nevertheless, for the ISM, its corresponding computational time consumes 16.0 s. Hence, it is clear that the ISM is more efficient than the 1st classic SDM, which can be dropped almost 85% computational time. Nevertheless, when compared with the NIM and ASM methods, the computational time of the ISM is increased by about 19% and 3% is very small. Obviously, the abovementioned research consequence shows the ISM has higher computational efficiency and accuracy to predict the milling stability.

Fig. 11

Comparison of computational time using the 1st SDM, NIM, ASM, and ISM with a/D = 0.06

7 Conclusions

In this paper, two highly accurate and efficient methods are proposed for determining the milling stability. The state transition matrix is directly constructed by using a predictor–corrector scheme. Some conclusions are summarized from this research work.

• (1) The milling dynamic model with consideration of the regeneration effect can be expressed as DDEs, and the linear multistep methods are simultaneously utilized to approximate the state term.

• (2) Based on the predictor–corrector technique, a Hamming–Simpson–based method (HSM) is presented to calculate the stability lobe diagram. The convergence rate of the HSM is analyzed in detail by comparisons with the three benchmark methods. Numerical results illustrate that the HSM converges faster to the exact critical eigenvalue than those of the other three methods, which means that the HSM can obviously enhance the prediction accuracy of the SLD.

• (3) The calculation accuracy and efficiency of the HSM are investigated by using half immersion and full immersion, which proves that the HSM not only has higher computational efficiency but also better prediction accuracy when compared with the classical 1st SDM. Nevertheless, when compared with the NIM and ASM methods, the HSM has higher prediction accuracy with only a slight increase in computational cost. Consequently, it is concluded that the HSM achieves satisfactory computational efficiency and accuracy. Due to the variable, U_{n − 2} of the Hamming method located out of the required range into the required range, which will lead to the computational accuracy of the HSM, can be reduced. Hence, the performance of the HSM in terms of accuracy and efficiency needs to be improved.

• (4) For the purpose of improving the performance of the HSM, we use a three-step implicit multistep exponential fitting method to predict milling stability and then use the Simpson method to correct this prediction. Three benchmark methods are adopted to demonstrate the effectiveness of the three-step implicit multistep exponential fitting–Simpson–based method (ISM). Simulation results indicate that the ISM simultaneously exhibits better computational efficiency and accuracy under the same time intervals.