Linear stability analysis of surface waves of liquid jet injected in transverse gas flow with different angles

Abstract

A theoretical and experimental study was conducted to investigate the effect of injection angle on surface waves. Linear stability theory was utilized to obtain the analytical relation. In the experimental study, high-speed photography and shadowgraph techniques were used. Image processing codes were developed to extract information from photos. The results obtained from the theoretical relation were validated with the experimental results at different injection angles. In addition, at the injection angle of 90${^\circ }$, the theoretical results were evaluated with the experimental results of other researchers. This evaluation showed that the theory results were in good agreement with the experimental data. The proper orthogonal decomposition (POD) and the power spectra density (PSD) analysis were also used to investigate the effect of the injection angle on the flow structures. The results obtained from the linear stability were used to determine the maximum waves’ growth rate, and a relation was presented for the breakup length of the liquid jet at different injection angles. The breakup length results were compared with theory and published experimental data. The presented relation is more consistent with experimental data than other theories due to considering the nature of waves. The results showed that the instability of the liquid jet is influenced by three forces: inertial, surface tension, and aerodynamic. Therefore, Rayleigh–Taylor, Kelvin–Helmholtz, Rayleigh–Plateau, and azimuthal instabilities occur in the process. Decreasing the injection angle changes the nature of waves and shifts from Rayleigh–Taylor to Kelvin–Helmholtz. That reduces the wavelength and increases the growth rate of the waves. Axial waves have a significant impact on the physics of the waves and influence parameters. If axial waves are not formed, the growth rate of the waves is independent of the injection angle. An increase in the gas Weber number causes a change in the type of dominant waves and a greater instability of the liquid jet. In contrast, an increase in the liquid Weber number causes an enhancement in the resistance of the liquid jet against the transverse flow without changing the type of the dominant waves. Decreasing the density ratio reduces the effect of Rayleigh–Taylor waves and strengthens the Kelvin–Helmholtz waves. It causes two trends to be observed for the growth rate of waves at low spray angles, while one trend occurs at high spray angles.

Graphical abstract

1 Introduction

By injecting a liquid jet into the transverse airflow, the momentum exchange between the flows increases. This makes it possible to utilize liquid jet injection in cross flow (LJIC) in engineering applications. Combustion systems of gas turbines and jet engine augmenters are among the most important parts in which this phenomenon occurs [1]. In addition to aerospace applications, it has many usages in various other industries, such as agriculture, painting, petrochemical, etc. Also, one of the most critical issues now is reducing the toxic air pollutants released by burning fossil fuels [2]. That adds to the importance of studies and a more accurate understanding of liquid jet injection in the transverse stream.

The process of breakup, its mechanisms, and its types have been investigated by researchers in detail [1,2,3,4,5]. At the interface surface of the two flows, waves begin to appear. Two types of waves can be distinguished: column and surface waves. Surface waves occur near the orifice and lead to the surface breakup, while column waves can be detected at distances away from the orifice and eventually cause column breakup. These two types of waves are also different in terms of wavelength. Column waves have a larger wavelength than surface waves. However, increasing the gas Weber number decreases the wavelength in both [6]. Generally, two types of disturbances occur at the interface: axial disturbances that make column waves and column breakup and azimuthal disturbances that lead to surface breakup. The three Kelvin–Helmholtz, Rayleigh–Taylor, and Rayleigh–Plateau (capillary) instabilities play a key role in creating these disturbances [7]. The difference in velocity and non-discontinuous properties of the two fluids at the interface causes waves due to Kelvin–Helmholtz instability on the front face. In addition, on the liquid jet’s upstream side, near the upstream stagnation point, crossflow accelerates the gas in the transverse direction toward the liquid jet and creates Rayleigh–Taylor waves [8]. The wavelength of both types of waves is reduced by increasing the gas Weber number, but this decrease is more severe for Kelvin–Helmholtz waves [9, 10].

Most researchers have experimentally studied the breakup process and its effective parameters by flow visualization [11,12,13,14,15,16,17,18,19,20,21,22,23]. In addition, numerous numerical studies have been conducted to understand better flow physics and effective parameters [8,9,10, 24, 25]. Various theory studies have been performed based on the stability analysis [26, 27]. Investigation of the linear instability of a liquid jet into quiescent air was adopted by Sterling and Sleicher [28], Lin and Lian [29], Funada and Joseph [30], Liu and Liu [31], Yang et al. [32], Boronin et al. [33], and Pillai et al. [34]. Although using linear stability analysis in jet spray in transverse flow is found in several studies, most of them have perused single-phase flow [35,36,37,38,39]. Several studies also utilized it in two-phase transverse flow [40,41,42,43,44,45,46,47]. Wang [43] studied the Rayleigh–Taylor waves and showed the growth rate of waves with small wave numbers is more influenced by aerodynamic forces and transverse air velocity, while jet velocity plays a major role in the growth rate of waves with large wave numbers. Behzad et al. [44] utilized stability analysis to identify azimuthal shear instability as the primary mechanism in the surface breakup. Amini [26] modeled the injection of liquid jets in weak crossflow with the help of stability theory and addressed the role of axial disturbances in liquid jets’ breakup.

Fig. 1

Influence of the injection angle on the surface waves at ${\textrm{We}}_{l}=65,{\textrm{We}}_{g}=6.5$, a 90${^\circ }$, b 60${^\circ }$, (c) 30${^\circ }$

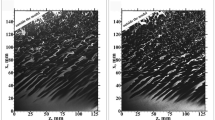
One of the topics that has received less attention from researchers but is of great importance is the effect of injection angle on the breakup mechanism of the liquid jet. Broumand et al. [48] presented a theoretical relation for the path of the injected liquid jet at an arbitrary angle. Kasmaiee and Tadjfar [49, 50] investigated the effect of injection angle on flow parameters. In our previous articles [49, 50], we discussed the influence of the angle in the flow regimes, trajectory, breakup point, drop size and its distribution, distribution of drop orientation and its aspect ratio, as well as the wavelength of column wave (not the surface wave) experimentally and presented semi-empirical (semi-theoretical) correlations. One of the parameters that play an important role in the progress of the breakup process is surface waves, which were not discussed in our previous articles. Also, using linear stability theory, we presented a completely theoretical (not semi-empirical) relation for its wavelength. In addition, the use of the proper orthogonal decomposition (POD) analysis for a better description of flow structures was also investigated in this article. Although there are several studies on these issues, none of them have perused the injection angle impacts on the surface wave growth rate and POD analysis. Surface waves are affected by the injection angle. By reducing the injection angle, the wavelength decreases. In addition, the amplitude of fluctuations also decreases. Figure 1 shows an example of surface waves at different spray angles. In this study, surface waves are investigated theoretically and experimentally. Though experimental studies provide helpful and valuable information, they are of rare use on the breakup mechanisms and the waves formed at the interface due to the difficulty of visualization. Numerical methods also face severe problems in implementing the effect of operating conditions on the details of physics. In addition, it is complicated and challenging to capture the sharp moving and deforming interface due to complex, multiscale, and multiphase physical structures [26]. These issues justify the development of a simple and low-cost theoretical model. In this study, the theory of linear stability was utilized to study the role of injection angle in wave growth rate and breakup length. The influence of other effective parameters, such as gas and liquid Weber numbers and density ratio, was surveyed at different injection angles. The influence of flow structures and injection angle on them was investigated using POD analysis.

2 Experimental method

The experimental method can be divided into two parts: (1) laboratory setup and experimental equipment. (2) Extracting data and image processing. The first part is mostly the hardware aspect, while the second part is based on the software aspect. The laboratory setup consists of three separate components. Figure 2 schematically represents these parts. A view of the used support base and the utilized injector is provided in Fig. 3. More details about the experimental setup and the injector are in Kasmaiee and Tadjfar [49, 50]. In this research, two cameras were employed. The first was a high-speed camera recording flow dynamics in POD analysis. Details of this camera are in our previous papers [49, 50]. The second was applied to visualize surface waves. The Canon EOS 700D digital camera and Godox TT600 light pulse with a pulse length of 50 microseconds were used for better and clearer detection of surface waves.

Fig. 2

The schematic of the laboratory setup

Fig. 3

The view of the support base and the injector, a front view, b view A-A

Image processing algorithms were utilized to extract and determine the liquid jet characteristics. We developed in-house codes for extracting different flow parameters such as trajectory [49], break length [49] and size, orientation, and aspect ratio of drops [50]. In this study, the aim is to detect surface waves and determine their wavelength by in-house code. The general algorithm is shown in Fig. 4. The Sobel edge detection algorithm was used to identify the waves better. The Sobel filter is a spatial filter based on the first derivative, which uses two masks Further details of this algorithm are provided in Vincent and Folorunso’s research [52]. Finally, the windward side of the liquid jet was identified as a wave. In the next step, it is necessary to determine the direction of wave movement. According to previous research [49], the path of the liquid jet can be considered a power function. Based on that, the best power function that fits the data was determined. The obtained function was utilized to transfer the coordinates from the Cartesian x–z reference to the local tangential-vertical S–N coordinate. At last, by identifying the peaks in the resulting diagram and determining the distance between two consecutive peaks, the wavelength of surface waves is obtained by averaging them over all photos.

One of the challenges is to determine the distance from the nozzle exit to identify the surface waves. In other researchers’ papers, no criterion for this distance was determined. By considering five times the nozzle diameter as the maximum distance of formation of surface waves and the linearity of the changes, the experimental results for the wavelength of surface waves were extracted. In order to ensure the appropriateness of the considered distance, the obtained experimental results were compared with other researcher’ experimental data and their correlations [4, 5]. The result of this comparison is presented in Fig. 4b. As can be seen, there is a good agreement between the extracted experimental data and the experimental results of other researchers, which indicates the appropriateness of the considered distance.

Fig. 4

a The general algorithm for wave detection, b comparison of the obtained experimental data of surface wavelength with the experimental results of other researchers

3 Theoretical framework and linear stability analysis

Consider a 3D liquid jet injected into the gas at an angle $\psi _{0}$ with respect to the direction of transverse flow from a circular nozzle with radius R. The liquid jet with $\rho _{l}$ density and $\sigma$ surface tension exits the nozzle at $v_{l}$ velocity in the direction of spraying. The transverse flow is a gas with $\rho _{g}$ density flowing at $v_{g}$ velocity. Both Newtonian fluids were assumed to be incompressible and inviscid, and this assumption has been justified by the research of Wang et al. [43], Vadivukkarasan and Panchagnula [53, 54], and Liu et al. [46]. The effect of Gravity force was ignored. A cylindrical coordinate system was used to analyze the problem. The problem’s configuration, its related parameters, and the coordinate system axes are shown in Fig. 5.

Fig. 5

Schematic model of a liquid jet injected with the desired angle in transverse flow

The mass and momentum conservation equations for an incompressible Newtonian fluid are written in a tensor form as follows:

$$\begin{aligned} {\partial _{j}V}_{j}= & {} 0 \end{aligned}$$

(1)

$$\begin{aligned} {\partial _{t}V}_{i}+V_{j}{\partial _{j}V}_{i}= & {} -\frac{1}{\rho }\partial _{i}P+\upsilon {\partial _{jj}V}_{i}+f_{i} \end{aligned}$$

(2)

where i and j are the tensor indices, and t index is time. The $\partial _{j}$ symbol represents $\frac{\partial }{\partial x_{j}}$. Removing the expression viscosity by considering non-viscosity flow, also ignoring external forces, and assuming irrotational flow, the equation governing the flow is as follows:

$$\begin{aligned} \partial _{jj}\varphi =0 \end{aligned}$$

(3)

In this relation, $\varphi$ is the velocity potential function obtained from $\varphi =\partial _{j}V_{j}$. The $\partial _{jj}$ symbol indicates $\frac{\partial ^{2}}{\partial x_{j}^{2}}$. The deviation of the liquid jet at the initial cross section, which is actually the nozzle outlet, is neglected. Karagozian [55] and Sedarsky et al. [56] showed that the perturbations are displaced by the liquid jet so that the surface wavelength does not alter significantly in a moment. In fact, aerodynamic forces take time to deform and overcome surface tension. Amini [26] demonstrated that the assumption of transverse flow passing through a cylinder to model the problem is sufficiently accurate. Therefore, according to the coordinate axis directions, the velocity vectors of the liquid jet and gas flow in the nozzle outlet are as follows:

$$\begin{aligned} V_{l}= & {} v_{l}{\hat{e}}_{k} \end{aligned}$$

(4)

$$\begin{aligned} V_{g}= & {} v_{g}\sin \psi _{0}\left( 1-\frac{R^{2}}{r^{2}} \right) \cos \beta {\hat{e}}_{r}-v_{g}\sin \psi _{0}\left( 1+\frac{R^{2}}{r^{2}} \right) \sin \beta {\hat{e}}_{\theta }+v_{g}\cos \psi _{0}{\hat{e}}_{k} \end{aligned}$$

(5)

The ${\hat{e}}_{r}, {\hat{e}}_{\theta }, {\hat{e}}_{k}$ are unit vectors of the reference coordinate. The l and g subtitles determine the type of fluid. The circumferential angle was shown with $\beta$. The velocity potential function can be rewritten in terms of the base conditions and perturbation quantities as follows:

$$\begin{aligned} \varphi _{g}= & {} v_{g}\sin \psi _{0}\left( r+\frac{R^{2}}{r} \right) \cos \beta +v_{g}\cos \psi _{0}Z+\varphi _{g}^{\prime } \end{aligned}$$

(6)

$$\begin{aligned} \varphi _{l}= & {} v_{l}Z+\varphi _{l}^{\prime } \end{aligned}$$

(7)

where $v_{j}^{\prime }=\partial _{j}\varphi ^{\prime }$. By replacing the velocity potential functions in Eq. 3:

$$\begin{aligned} \partial _{jj}\varphi _{l}^{\prime }= & {} 0 \end{aligned}$$

(8)

$$\begin{aligned} \partial _{jj}\varphi _{g}^{\prime }= & {} 0 \end{aligned}$$

(9)

According to the classical normal mode analysis, the perturbation potential functions can be rewritten as extensions of the Fourier modes as follows:

$$\begin{aligned} \varphi _{l}^{\prime }= & {} \sum \limits _{m=-\infty }^{+\infty } {F_{m}\left( r \right) e^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(10)

$$\begin{aligned} \varphi _{g}^{\prime }= & {} \sum \limits _{m=-\infty }^{+\infty } {G_{m}\left( r \right) e^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(11)

By definition,

$$\begin{aligned} F_{m}\left( r \right)= & {} \frac{e^{-(kzi+\omega t)}}{2\pi }\int _0^{2\pi } {\varphi _{l}^{\prime }e}^{-im\theta } \textrm{d}\theta \end{aligned}$$

(12)

$$\begin{aligned} G_{m}\left( r \right)= & {} \frac{e^{-(kzi+\omega t)}}{2\pi }\int _0^{2\pi } {\varphi _{g}^{\prime }e}^{-im\theta } \textrm{d}\theta \end{aligned}$$

(13)

where k is the wavenumber of the perturbation in the axial direction and m is the azimuthal wavenumber which shows the perturbation wavenumber in $\uptheta$ direction. $\omega$ is the complex frequency whose real and imaginary parts show growth rate and disturbance wave frequency, respectively. The interface displacement of the liquid jet and transverse flow can be written as follows:

$$\begin{aligned} \eta =\sum \limits _{m=-\infty }^{+\infty } {\eta _{0}e^{i\left( kz+m\theta \right) +\omega t}=r-R} \end{aligned}$$

(14)

$F_{m}\left( r\right)$ and $G_{m}\left( r\right)$ must satisfy $F_{m}\left( r = 0\right) =0$ and $G_{m}\left( r\rightarrow \infty \right) =0$. Therefore, the general solution of Eqs. 10 and 11 can be written as below:

$$\begin{aligned} \varphi _{l}^{\prime }= & {} \sum \limits _{m=-\infty }^{+\infty } {{c_{m_{1}}I}_{m}(kr)e^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(15)

$$\begin{aligned} \varphi _{g}^{\prime }= & {} \sum \limits _{m=-\infty }^{+\infty } {c_{m_{2}}K_{m}(kr)e^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(16)

where $c_{m_{1}}$ and $c_{m_{2}}$ are constants. $I_{m}(kr)$ and $K_{m}(kr)$ are the mth-order of the first- and second-kind modified Bessel function, respectively, which are obtained from the following relations:

$$\begin{aligned} I_{m}(x)= & {} \sum \limits _{n=0}^\infty {\frac{1}{n{!\Gamma }\left( {n+m+1} \right) }\left( \frac{x}{2} \right) ^{2n+m}} \end{aligned}$$

(17)

$$\begin{aligned} K_{m}(x)= & {} \frac{-\pi }{2}\left( \frac{I_{m}\left( x \right) -I_{-m}(x)}{{\sin }(m\pi )} \right) \end{aligned}$$

(18)

where ${\Gamma }\left( x \right)$ is the gamma function and calculated from the following relation:

$$\begin{aligned} {\Gamma }\left( x \right) =\int _0^\infty t^{x-1} e^{-t}\textrm{d}t=(x-1)! \end{aligned}$$

(19)

Assuming Re$(x)\ge 0$, the following equations can be used to calculate the modified Bessel functions:

$$\begin{aligned} I_{m}\left( x \right)= & {} \frac{1}{\pi }\int _0^\pi {e^{x\textrm{cos}t}\cos \left( mt \right) \textrm{d}t} -\frac{\sin \left( m\pi \right) }{\pi }\int _0^\infty {e^{-\left( x\textrm{cos}ht+mt \right) }\textrm{d}t} \end{aligned}$$

(20)

$$\begin{aligned} K_{m}(x)= & {} \int _0^\infty {e^{-x\textrm{cos}ht}{\cosh }(mt)\textrm{d}t} \end{aligned}$$

(21)

The absence of a net mass flux across the surface of the liquid column, which is equivalent to the absence of an across velocity at the interface, is considered the kinematic boundary condition. So at $r=R$:

$$\begin{aligned} {{v_{r}^{\prime }}_{l}}= & {} \partial _{r}\varphi _{l}^{\prime }=\partial _{t}\eta +v_{l}\partial _{z}\eta \end{aligned}$$

(22)

$$\begin{aligned} {{v_{r}^{\prime }}_{g}}= & {} \partial _{r}\varphi _{g}^{\prime }=\partial _{t}\eta -\frac{{2v}_{g}}{R}\sin \psi _{0} \sin \beta \partial _{\theta }\eta +v_{g}\cos \psi _{0}\partial _{z}\eta \end{aligned}$$

(23)

By placing $\eta , \varphi _{l}^{\prime }$ and $\varphi _{g}^{\prime }$ from 14, 15 and 16 relationships:

$$\begin{aligned}{} & {} \sum \limits _{m=-\infty }^{+\infty } {{c_{m_{1}}k\partial _{r}I}_{m}(kR)e^{i\left( kz+m\theta \right) +\omega t}} =\sum \limits _{m=-\infty }^{+\infty } {\eta _{0}\omega e^{i\left( kz+m\theta \right) +\omega t}} +v_{l}\sum \limits _{m=-\infty }^{+\infty } {\eta _{0}kie^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \sum \limits _{m=-\infty }^{+\infty } {c_{m_{2}}k{\partial _{r}K}_{m}(kR)e^{i\left( kz+m\theta \right) +\omega t}} =\sum \limits _{m=-\infty }^{+\infty } {\eta _{0}\omega e^{i\left( kz+m\theta \right) +\omega t}}\nonumber \\{} & {} \quad -\frac{{2v}_{g}}{R}\sin \psi _{0}\sin \beta \sum \limits _{m=-\infty }^{+\infty } {\eta _{0}mie^{i\left( kz+m\theta \right) +\omega t}} +v_{g}\cos \psi _{0}\sum \limits _{m=-\infty }^{+\infty } {\eta _{0}kie^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(25)

By arranging the above equations, $c_{m_{1}}$and $c_{m_{2}}$ are obtained as follows:

$$\begin{aligned} c_{m_{1}}= & {} \eta _{0}\left( \frac{\left( \omega +v_{l}(ik) \right) }{kI_{m}^{\prime }(kR)} \right) \end{aligned}$$

(26)

$$\begin{aligned} c_{m_{2}}= & {} \eta _{0}\frac{\left( \omega -\frac{2v_{g}\sin \psi _{0}}{R}\sin \beta (im)+v_{g}\cos \psi _{0}(ik) \right) }{{kK}_{m}^{\prime }(kR)} \end{aligned}$$

(27)

where $I_{m}^{\prime }\left( kR \right) =\partial _{r}I_{m}\left( kR \right)$, $K_{m}^{\prime }\left( kR \right) =\partial _{r}K_{m}\left( kR \right)$. Assuming that the flow is non-rotational and the gas is non-viscous, according to the Bernoulli relation:

$$\begin{aligned} \frac{p_{g}}{\rho _{g}}+\frac{V_{g}^{2}}{2}=\frac{p_{g_{\infty }}}{\rho _{g}}+\frac{V_{g_{\infty }}^{2}}{2} \end{aligned}$$

(28)

The $\infty$ sign indicates the conditions where the gas is away from the liquid jet and has no disturbance. According to the assumption of the cylinder model, the gas pressure on the interface can be determined as follows:

$$\begin{aligned} p_{g}-p_{g_{\infty }}=\frac{1}{2}{\rho _{g}v}_{g}^{2}(1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0}) \end{aligned}$$

(29)

The phrase on the right actually indicates the effect of aerodynamic forces on the liquid column. This expression can be considered equivalent to the aerodynamic acceleration that affects the liquid jet. Liquid jet instabilities are a local phenomenon and their dimensions are much smaller than those of liquid jets [4, 43]. The following relationship can be obtained by defining the effective thickness:

$$\begin{aligned} \frac{1}{2}{\rho _{g}v}_{g}^{2}\left( 1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0} \right) =\rho _{l}a\left( \beta ,\psi _{0} \right) \xi \end{aligned}$$

(30)

$a\left( \beta ,\psi _{0} \right)$ is the aerodynamic acceleration induced by aerodynamic forces on the liquid jet. It is a function of the spray angle and the circumferential angle $\xi$ indicates the amount of liquid thickness that aerodynamic forces affect. For example, consider the wind blowing and passing through an outdoor swimming pool. These winds cause acceleration and surface waves. All pool water does not affect these accelerations and waves, but a certain depth of water plays a role in forming of them. Similarly, when a helicopter is flying over an ocean, the aerodynamic forces influence a certain water thickness. If the propeller-induced aerodynamic force acts at full depth, there are almost no acceleration and surface waves which is not real. Wang et al. [43] suggested a value of R/8 for the effective thickness. Accordingly, in this study, $\xi =R/8$ was considered. The condition of the continuity of the stress tensor across the interface is known as the dynamic boundary condition. So at $r=R$:

$$\begin{aligned} \left( p_{l}^{\prime }-p_{g}^{\prime } \right) -\Delta p^{\prime }=-\rho _{l}a\left( \beta ,\psi _{0} \right) \eta =-\frac{1}{2}{\rho _{g}v}_{g}^{2}(1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0})\frac{\eta }{\xi } \end{aligned}$$

(31)

where $\Delta p$ is the pressure jump because of the liquid surface tension and $\Delta p^{\prime }$ is instantaneous surface tension created by disturbance. The following relation was suggested for $\Delta p^{\prime }$ on the interface [32, 43]:

$$\begin{aligned} \Delta p^{\prime }=-\sigma \left\{ \frac{1}{R^{2}}\left[ 1-m^{2}-{(kR)}^{2} \right] \eta \right\} \end{aligned}$$

(32)

By writing the unsteady Bernoulli relation for a point before and after perturbations and linearizing the relation, the following equation for perturbation pressure is obtained:

$$\begin{aligned} p^{\prime }=-\rho \left( \partial _{t}\varphi ^{\prime }+V_{j}V_{j}^{\prime } \right) \end{aligned}$$

(33)

By using Eqs. 15 and 16, the following expressions are obtained for gas and liquid pressures at $r=R$:

$$\begin{aligned} p_{l}^{\prime }= & {} -\rho _{l}\sum \limits _{m=-\infty }^{+\infty } {{c_{m_{1}}I}_{m}\left( kR \right) \left[ \omega +v_{l}(ik) \right] e^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(34)

$$\begin{aligned} p_{g}^{\prime }= & {} -\rho _{g}\sum \limits _{m=-\infty }^{+\infty } {c_{m_{2}}K_{m}\left( kR \right) \left[ \omega -\frac{2v_{g}}{R}{\sin \psi }_{0}\sin \beta (im)+v_{g}\cos \psi _{0}(ik) \right] e^{i\left( kz+m\theta \right) +\omega t}} \end{aligned}$$

(35)

By replacing relations 32, 34 and 35 in relation 31 and using relations 26 and 27, the following relation is obtained:

$$\begin{aligned}{} & {} -\rho _{l}\frac{I_{m}\left( kR \right) }{I_{m}^{\prime }\left( kR \right) }\left[ \omega +v_{l}\left( ik \right) \right] ^{2}+\rho _{g}\frac{K_{m}\left( kR \right) }{K_{m}^{\prime }\left( kR \right) }\left[ \omega -\frac{{2v}_{g}}{R}{\sin \psi }_{0}\sin \beta (im)+v_{g}\cos \psi _{0}(ik) \right] ^{2}\nonumber \\{} & {} \quad +\frac{\sigma k}{R^{2}}\left[ 1-m^{2}-\left( kR \right) ^{2} \right] =-\frac{k}{2\xi }{\rho _{g}v}_{g}^{2}(1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0}) \end{aligned}$$

(36)

By defining ${\Upsilon }_{m}=\frac{I_{m}\left( kR \right) }{I_{m}^{\prime }\left( kR \right) }$ and ${\Lambda }_{m}=\frac{K_{m}\left( kR \right) }{K_{m}^{\prime }\left( kR \right) }$, simplifying and sorting the above relation:

$$\begin{aligned}{} & {} \left( \rho _{l}{\Upsilon }_{m}-\rho _{g}{\Lambda }_{m} \right) \omega ^{2}+2i\left[ \rho _{l}v_{l}k{\Upsilon }_{m}+\rho _{g}v_{g}{\Lambda }_{m}\left( \frac{2m}{R}{\sin \psi }_{0}\sin \beta -k \cos \psi _{0} \right) \right] \omega \nonumber \\{} & {} \quad -\left[ \rho _{l}\left( v_{l}k \right) ^{2}{\Upsilon }_{m}-\rho _{g}v_{g}^{2}{\Lambda }_{m}\left( k \cos \psi _{0}-\frac{2m}{R}{\sin \beta \sin \psi }_{0} \right) ^{2} \right] -\frac{k}{2\xi }{\rho _{g}v}_{g}^{2}\left( 1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0} \right) \nonumber \\{} & {} \quad -\frac{\sigma k}{R^{2}}\left[ 1-m^{2}-\left( kR \right) ^{2} \right] =0 \end{aligned}$$

(37)

4 Result and discussion

Equation 37 is a quadratic equation with two roots according to the basic theorem of algebra. The equation can be rewritten in the following relation:

$$\begin{aligned} a\omega ^{2}+bi\omega +c=0 \end{aligned}$$

(38)

where a, b and c are defined as follows:

$$\begin{aligned} a= & {} \rho _{l}{\Upsilon }_{m}-\rho _{g}{\Lambda }_{m} \end{aligned}$$

(39)

$$\begin{aligned} b= & {} 2\left[ \rho _{l}v_{l}k{\Upsilon }_{m}+\rho _{g}v_{g}{\Lambda }_{m}\left( \frac{2m}{R}{\sin \psi }_{0}\sin \beta -k \cos \psi _{0} \right) \right] \end{aligned}$$

(40)

$$\begin{aligned} c= & {} -\frac{k}{2\xi }{\rho _{g}v}_{g}^{2}\left( 1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0} \right) -\frac{\sigma k}{R^{2}}\left[ 1-m^{2}-\left( kR \right) ^{2} \right] \nonumber \\{} & {} \quad -\left[ \rho _{l}\left( v_{l}k \right) ^{2}{\Upsilon }_{m}-\rho _{g}v_{g}^{2}{\Lambda }_{m}\left( k \cos \psi _{0}-\frac{2m}{R}{\sin \beta \sin \psi }_{0} \right) ^{2} \right] \end{aligned}$$

(41)

The complex frequency can be obtained from the following relation:

$$\begin{aligned} \omega= & {} \frac{-bi\pm \sqrt{-b^{2}-4ac} }{2a} \end{aligned}$$

(42)

For the equation to have a real part (growth rate), it is necessary to satisfy the two conditions of $a.c<0$ and $\left| a.c \right| >b^{2}/4$. Otherwise, the equation will not have a real part, and in fact, we will face waves whose temporal growth rate is zero. The real and imaginary parts of the frequency can be obtained as follows:

$$\begin{aligned} \omega _{R}= & {} Re\left( \omega \right) =\frac{\pm \sqrt{-b^{2}-4ac} }{2a}=\pm \sqrt{\frac{-b^{2}}{4a^{2}}-\frac{c}{a}} \end{aligned}$$

(43)

$$\begin{aligned} \omega _{I}= & {} Im\left( \omega \right) =\frac{-b}{2a} \end{aligned}$$

(44)

By squaring and replacing the a, b and c parameters we have:

$$\begin{aligned} \omega _{R}^{2}= & {} -\frac{\left[ \rho _{l}v_{l}k{\Upsilon }_{m}+\rho _{g}v_{g}{\Lambda }_{m}\left( \frac{2m}{R}{\sin \psi }_{0}\sin \beta -k \cos \psi _{0} \right) \right] ^{2}}{\left[ \rho _{l}{\Upsilon }_{m}-\rho _{g}{\Lambda }_{m} \right] ^{2}}\nonumber \\{} & {} +\frac{\left[ \rho _{l}\left( v_{l}k \right) ^{2}{\Upsilon }_{m}-\rho _{g}v_{g}^{2}{\Lambda }_{m}\left( k \cos \psi _{0}-\frac{2m}{R}{\sin \beta \sin \psi }_{0} \right) ^{2} \right] }{\left[ \rho _{l}{\Upsilon }_{m}-\rho _{g}{\Lambda }_{m} \right] }\nonumber \\{} & {} \quad +\frac{\frac{\sigma k}{R^{2}}\left[ 1-m^{2}-\left( kR \right) ^{2} \right] }{\left[ \rho _{l}{\Upsilon }_{m}-\rho _{g}{\Lambda }_{m} \right] }+\frac{\frac{k}{2\xi }{\rho _{g}v}_{g}^{2}\left( 1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0} \right) }{\left[ \rho _{l}{\Upsilon }_{m}-\rho _{g}{\Lambda }_{m} \right] } \end{aligned}$$

(45)

$$\begin{aligned} \omega _{I}^{2}= & {} \frac{\left[ \rho _{l}v_{l}k{\Upsilon }_{m}+\rho _{g}v_{g}{\Lambda }_{m}\left( \frac{2m}{R}{\sin \psi }_{0}\sin \beta -k \cos \psi _{0} \right) \right] ^{2}}{\left[ \rho _{l}{\Upsilon }_{m}-\rho _{g}{\Lambda }_{m} \right] ^{2}} \end{aligned}$$

(46)

In Eq. 45, the first two terms can be attributed to inertial forces related to liquid and gas velocities. The third term of Eq. 45 is due to the capillary force created by the liquid surface tension. The fourth expression shows the role of aerodynamic acceleration in the wave frequency growth rate. The first two terms greatly contribute to the growth rate of Kelvin–Helmholtz waves. The third statement plays an important role in Rayleigh–Plateau instability. The aerodynamic acceleration and effective thickness expressed in the fourth term have a significant role in the Rayleigh–Taylor wave growth rate. Equation 46 shows that the disturbance wave frequency is induced by inertial forces. These inertial forces are formed by the velocities of the transverse flow and the liquid jet The dimensionless numbers associated with this problem are (1) the gas Weber number, (2) the liquid Weber number, (3) the density ratios between two fluids, and (4) the ratio of velocities between two fluids. Mathematically, these dimensionless numbers can be expressed as follows:

$$\begin{aligned} {\textrm{We}}_{l}=\frac{\rho _{l}v_{l}^{2}R}{\sigma }, {\textrm{We}}_{g}=\frac{\rho _{g}v_{g}^{2}R}{\sigma }, \rho ^{*}=\frac{\rho _{g}}{\rho _{l}}, v^{*}=\frac{v_{g}}{v_{l}} \end{aligned}$$

(47)

The other stability parameters can also be presented dimensionless as follows:

$$\begin{aligned} \omega ^{*}=\frac{\omega R}{v_{l}}, k^{*}=kR, R^{*}=\frac{R}{2\xi } \end{aligned}$$

(48)

Circumferential wavenumber (m) is dimensionless. Based on the dimensionless parameters defined, Eqs. 45 and 46 can be rewritten as follows:

$$\begin{aligned} {{\omega _{R}^*}}^{2}= & {} \frac{\omega _{R}^{2}R^{2}}{v_{l}^{2}}=-\frac{\left[ k^{*}{\Upsilon }_{m}+\rho ^{*}v^{*}{\Lambda }_{m}\left( 2m{\sin \psi }_{0}\sin \beta -k^{*} \cos \psi _{0} \right) \right] ^{2}}{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] ^{2}}\nonumber \\{} & {} \quad +\frac{\left[ {{k^{*}}^{2}} {\Upsilon }_{m}-\rho ^{*} {{v^{*}}^{2}}{\Lambda }_{m}\left( k^{*}\cos \psi _{0}-2m{\sin \beta \sin \psi }_{0} \right) ^{2} \right] }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] }\nonumber \\{} & {} \quad +\frac{\frac{k^{*}}{{\textrm{We}}_{l}}\left[ 1-m^{2}-{{k^{*}}^{2}} \right] }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] }+\frac{R^{*}k^{*}\frac{{\textrm{We}}_{g}}{{\textrm{We}}_{l}}\left( 1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0} \right) }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] } \end{aligned}$$

(49)

$$\begin{aligned} {\omega _{I}^{*}}^{2}= & {} \frac{\omega _{I}^{2}R^{2}}{v_{l}^{2}}= \frac{\left[ k^{*}{\Upsilon }_{m}+\rho ^{*}v^{*}{\Lambda }_{m}\left( 2m{\sin \psi }_{0}\sin \beta -k^{*}\cos \psi _{0} \right) \right] ^{2}}{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] ^{2}} \end{aligned}$$

(50)

The dominant grow rate frequency and the unstable axial and circumferential wavenumbers can be determined by specifying the flow conditions. According to the three-dimensional nature of the problem, four different modes of instability can be defined [53, 54]. These modes are Taylor$\left( k^{*}>0, m=0 \right)$, sinuous $\left( k^{*}=0, m=1 \right)$, flute $\left( k^{*}=0, m>1 \right)$, and helical $\left( k^{*}>0, m>0 \right)$. These four different modes of instability are presented in Fig. 6. Equations 49 and 50 take into account all the instabilities (Rayleigh–Taylor, Kelvin–Helmholtz, Rayleigh–Plateau, and azimuthal) that affect the liquid jet injection with an arbitrary angle in transverse air. The main source of the Rayleigh–Taylor instabilities formation is the density difference between the two fluids, so it is sufficient to consider the dimensionless number of the density ratio equal to 1 ($\rho ^{*}=1)$. In other words, assuming the density of the two fluids is the same, the resulting instabilities on the interface will be of the Kelvin–Helmholtz type. Accordingly, Eq. 49 can be rewritten as follows:

$$\begin{aligned} {\omega _{R}^{*}}^{2}= & {} -\frac{\left[ k^{*}{\Upsilon }_{m}+v^{*}{\Lambda }_{m}\left( 2m{\sin \psi }_{0}\sin \beta -k^{*}\cos \psi _{0} \right) \right] ^{2}}{\left[ {\Upsilon }_{m}-{\Lambda }_{m} \right] ^{2}}\nonumber \\{} & {} \quad +\frac{\left[ {{k^{*}}^{2}} {\Upsilon }_{m}-{{v^{*}}^{2}}{\Lambda }_{m}\left( k^{*}\cos \psi _{0}-2m{\sin \beta \sin \psi }_{0} \right) ^{2} \right] }{\left[ {\Upsilon }_{m}-{\Lambda }_{m} \right] }\nonumber \\{} & {} \quad +\frac{\frac{k^{*}}{{\textrm{We}}_{l}}\left[ 1-m^{2}-{{k^{*}}^{2}} \right] }{\left[ {\Upsilon }_{m}-{\Lambda }_{m} \right] }+\frac{R^{*} k^{*} {{v^{*}}^{2}}\left( 1-4{\sin }^{2}\beta {\sin }^{2}\psi _{0} \right) }{\left[ {\Upsilon }_{m}-{\Lambda }_{m} \right] } \end{aligned}$$

(51)

In non-viscous two-phase flow, the Kelvin–Helmholtz instability is caused by the velocity difference between the two fluids at the interface. Therefore, to eliminate the effect of Kelvin–Helmholtz instability, it is sufficient to consider the velocity of both fluids as equal at the interface. In other words, the velocity ratio at the interface must be equal to 1 ($v^{*}\cos \psi _{0}=1)$. So, Eq. 49 can be rewritten as follows:

$$\begin{aligned} {\omega _{R}^{*}}^{2}= & {} \quad -\frac{\left[ k^{*}{\Upsilon }_{m}+\rho ^{*}{\Lambda }_{m}\left( 2m{\tan \psi }_{0}\sin \beta -k^{*} \right) \right] ^{2}}{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] ^{2}}\nonumber \\{} & {} \quad +\frac{\left[ {{k^{*}}^{2}}{\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m}\left( k^{*}-2m{\sin \beta \tan \psi }_{0} \right) ^{2} \right] }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] }\nonumber \\{} & {} \quad +\frac{\frac{k^{*}}{{\textrm{We}}_{l}}\left[ 1-m^{2}-{{k^{*}}^{2}} \right] }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] }+\frac{R^{*}k^{*}\rho ^{*}\left( 1/{\cos }^{2}\psi _{0}-4{\sin }^{2}\beta {\tan }^{2}\psi _{0} \right) }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] } \end{aligned}$$

(52)

Different parameters affect the dimensionless wave growth rate and dimensionless disturbance wave frequency. In the following, the effect of these parameters will be examined in detail.

Fig. 6

Different modes of instability [53]. a the Taylor mode, b the sinuous mode, c the flute mode, d the helical mode

4.1 Validation

In order to investigate the accuracy and confirm the validity, the final relation for the growth rate of waves was compared with other relations resulting from classical linear instability. For an injection angle of 90${^\circ }$, by placing $\psi _{0} = \frac{\pi }{2}$ in Eq. 49, Wang et al.’s [43] equation is obtained. The result of this simplification is shown in Eq. 53, which is the same as Wang et al.’s relation 24. In addition to the spray angle of 90${^\circ }$ if the gas Weber number is considered zero, Eq. 49 reduces to Yang’s [40] equation. Excluding the liquid jet viscosity terms in Sterling and Sleicher’s [28] dispersion equation, a relation is obtained a special case of Eq. 37 without the effective thickness term and $m = 0, \psi _{0} = \frac{\pi }{2}$. By omitting the viscosity terms in Amini’s [26] dispersion relation, the reduced relation 37 will be obtained for the 90${^\circ }$ injection angle. Regardless of the mass and heat transfer effects in Liu et al.’s [46] dispersion relation, an equation is obtained that can also be acquired by omitting the effective thickness term and writing Eq. 37 for vertical spraying. If no transverse gaseous flow exists, the equation of 37 becomes the same as Rayleigh’s [57] relation.

$$\begin{aligned} {\omega _{R}^{*}}^{2}= & {} \frac{\omega _{R}^{2}R^{2}}{v_{l}^{2}}=-\frac{\left[ k^{*}{\Upsilon }_{m}+{2m\textrm{sin}\beta \rho }^{*}v^{*}{\Lambda }_{m} \right] ^{2}}{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] ^{2}}+\frac{\left[ {{k^{*}}^{2}}{\Upsilon }_{m}-\rho ^{*} {{v^{*}}^{2}}{\Lambda }_{m}\left( 2m\textrm{sin}\beta \right) ^{2} \right] }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] }\nonumber \\{} & {} \quad +\frac{\frac{k^{*}}{{\textrm{We}}_{l}}\left[ 1-m^{2}-{{k^{*}}^{2}} \right] }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] } +\frac{R^{*}{k^{*}}\frac{{\textrm{We}}_{g}}{{\textrm{We}}_{l}}\left( 1-4{\sin }^{2}\beta \right) }{\left[ {\Upsilon }_{m}-\rho ^{*}{\Lambda }_{m} \right] } \end{aligned}$$

(53)

The maximum growth rate and the corresponding wave number determine the waves with the fastest growth at the liquid jet surface. These waves eventually lead to the breakup of the liquid jet column. In addition, the size of the isolated ligaments is proportional to their wavelength. In order to validate the relation obtained from the linear stability theory in this study, the wavelengths related to the axial waves with the maximum growth rate in different gas Weber numbers were compared with the results of Mazallon et al. [4], Sallam et al. [5] and Wang et al. [43]. This comparison is shown in Fig. 7. In this figure, the data are related to the upstream axial surface waves, in other words, $m=0$ and $\beta =0$ are assumed Since the studies of other researchers were limited to the injection angle of 90${^\circ }$, $\psi _{0}$was considered to be 90${^\circ }$. It can be seen that our relationship is in good agreement with the relations of other researchers. The general trend is that the wavelength decreases with increasing gas Weber number. In addition to the fact that both Rayleigh–Taylor and Kelvin–Helmholtz waves show a decrease in wavelength by increasing the gas Weber number, the transition from Rayleigh–Taylor to Kelvin–Helmholtz and the dominance of shear forces at high gas Weber numbers occurs. That causes a more severe wavelength reduction. In order to evaluate the accuracy of the theory developed for the effect of injection angle, the results of the theory were compared with our experimental results. This comparison is shown in Fig. 8. For comparison, no data were found from other researchers who studied the spray angle impacts at a wavelength. As can be seen, there is a good agreement between theory results and the experimental data at different angles. The differences between theory and experimental results are in the range of error bars. This difference in results can be attributed to theoretical assumptions, such as effective thickness or non-viscous flow. Of course, it should be noted that these waves are difficult to detect experimentally, and in the study of other researchers for a 90${^\circ }$ angle, there are similar differences between the theoretical and experimental results

Fig. 7

Comparison of the upstream axial surface waves for $\psi _{0}=90{^\circ }$

Fig. 8

Comparison of the upstream axial surface waves between theory and experimental data for injection angle of a $90{^\circ }$, b $60{^\circ }$, c $30{^\circ }$

4.2 The effect of injection angle

To evaluate the injection angle effects, velocity ratio, liquid to gas density ratio, and gas and liquid Weber numbers were considered 9, 810, 13 and 130, respectively. Figure 9 shows the impact of spray angle on the wave growth rate for different azimuthal modes. As can be seen, with decreasing injection angle in all azimuthal modes, the growth rate and the corresponding wave number increase. In other words, decreasing the injection angle in different azimuthal modes, the wavelength of surface waves reduces, but their growth rate will be enhanced As the injection angle decreases, the liquid jet velocity component increases in the airflow direction. That causes the tangential velocity difference at the common boundary to increase, making the jet more unstable and the wave growth rate more intense, reducing the wavelength due to a change in mechanism from Rayleigh–Taylor to Kelvin–Helmholtz. When the azimuthal mode is zero, it represents axial symmetric waves, while when the azimuthal wave number is non-zero, non-axial waves are generated. Axial waves play an important role in column breakup, while non-axial waves affect surface breakup. Therefore, the maximum growth rate of axial and non-axial waves is effective in column and surface breakup. Ng et al. [6] and Amini [26] have also mentioned this issue for 90${^\circ }$ injection angles in their studies. Figure 10 shows the wave growth rate in terms of the circumferential wave number. As can be seen, with increasing ${ k}^{*}$, the effect of the angle on the growth rate becomes more pronounced. So when ${ k}^{*}$is zero, the growth rate diagrams in terms of the circumferential wave number at different spray angles overlap completely and are independent of the injection angle. In contrast, when ${ k}^{*}=6$, the impact of the spray angle is clearly visible. When a liquid jet is injected with a desired angle in the transverse flow, in addition to the liquid jet momentum difference with air on the interface direction leads to axial Kelvin–Helmholtz waves, the pressure difference upstream and downstream of the liquid column causes axial Rayleigh–Taylor waves. Therefore, the axial waves are the primary stimulus for making the effect of the spray angle on the liquid column. When these waves are ignored, the injection angle effect will disappear. That is why at $k^{*}=0,$ the growth rate diagrams are the same for different injection angles. In all $k^{*}>0$, as the spray angle increases, the wave growth rate increases in all circumferential wave numbers. This gain can be attributed to the enlargement in peripheral perturbations caused by the tangential velocity at the joint surface. Generally, the maximum peripheral wavelength reduces with increasing injection angle in samples whose ${ k}^{*}$ has not reached the maximum ${ k}^{*}$(cases of b, c). In larger ${ k}^{*}(case d)$, the maximum growth rate occurs initially and the spray angle has no effect on its wavelength. Also, reducing the injection angle expands the stability zone for both longitudinal and azimuthal wavenumbers

Fig. 9

Effect of the injection angle on growth rate at different azimuthal modes, a $m=0$, b $m=1,$ c $m=2,$ d $m=3$

Fig. 10

Effect of the injection angle on growth rate at different wave numbers, a ${ k}^{*}=0$, b ${ k}^{*}=2,$ c ${ k}^{*}=4,$ d ${ k}^{*}=6$

4.3 The effect of gas and liquid Weber numbers

Figure 11 shows how increasing the gas Weber number affects surface waves at different injection angles For this purpose, the density ratio and liquid Weber number were considered constant and the same as the values of the previous section. When a liquid jet is issued into the transverse airflow, different regimes can be defined by the interaction of different forces, including aerodynamic drag, surface tension, and momentum. In different regimes, the effect of these forces on the liquid jet varies. Changing these regimes is a function of the gas Weber number. In this study, the gas Weber number has increased from 5 to 100. The range of the gas Weber number is such that it includes different regimes of liquid jet injected in the transverse stream. When the gas Weber number is 5, the flow regime is the arc regime. In addition, the cross section of the liquid jet at distances away from the orifice, due to the reduction of lateral pressures relative to the upstream stagnation pressure, goes out of the circle and toward the ellipse, increasing the effective drag surface and bending more. The predominant instability in this regime is Rayleigh–Taylor instability. By increasing the gas Weber number to 10, structures are created in the flow called bags. In fact, nodes appear in the liquid jet trajectory, which swells due to the aerodynamic forces of these nodes and form bag structures. Eventually, the bags remain stable until the surface tension of their membranes resists drag, after which they break. Rayleigh–Taylor instability is dominant in this regime as well. Further increasing the gas Weber number, the shear forces are strengthened, which causes a surface breakup. This mode occurs in gas Weber numbers (based on radius) of 50 and above. In this regime, Kelvin–Helmholtz instability is important. Intermediate Weber numbers, such as the 20, are called multimode regimes. In this regime, bags appear, also shear forces are effective, and none of the Kelvin- Helmholtz and Rayleigh–Taylor instabilities can be ignored. With increasing gas Weber number due to increasing aerodynamic forces, the growth rate of waves and perturbations of the jet surface increases, and the liquid jet experiences a faster breakup. Since the wavelength of both Rayleigh–Taylor and Kelvin–Helmholtz waves decreases with increasing the gas Weber number [8, 9], this decrease is also visible at the wave with maximum growth rate. By increasing the spray angle, the effect of the gas Weber number changes on the growth rate is significant, so that in the 90 $^\circ$ injection angle, by raising it from 5 to 100, the dimensionless growth rate reaches from 0.48 to 4.78. In contrast, it gains from 0.67 to 32.4 for the injection angle 0$^\circ$. It also should be noted that as the injection angle increases, the relative velocity between the jet and the air increases, and consequently the aerodynamic drag force on the liquid jet increases [49]. In addition, the maximum growth rate of the waves diminishes, and the wavelength of the structures rises because of the reduction of the velocity difference in the interface. Figure 12 presents the impact of increasing the liquid Weber number on the growth rate of waves at different spray angles. The value of other dimensionless parameters is fixed and the same as in the previous section and only the liquid Weber number changes between 13 and 130. As can be seen, for the 90${^\circ }$ injection angle, a perfectly regular trend is formed and the growth rate is increased by decreasing the liquid Weber number. By reducing the liquid Weber number in the fixed gas Weber number, the resistance of the liquid jet to transverse air decreases. In addition to intensifying instabilities and increasing the waves’ growth rate, this decline will cause the liquid jet column to break up sooner. Since neither the gas Weber number nor the type of the wave (in this case, Rayleigh–Taylor instability is predominant) has changed, the wavelength of the maximum growth rate has not changed. As the angle decreases, in addition to intensifying the instabilities and increasing the growth rate, the effect of changes in the liquid Weber number on the jet column becomes more apparent. The Kelvin–Helmholtz waves become more visible due to the tangential velocity difference at the common surface as the angle reduces. So, the wavelength of the highest growth and the corresponding wavenumber change at different liquid Weber numbers. In fact, although at an injection angle of 90${^\circ }$, the wavelength with the maximum growth rate can be considered independent of the liquid Weber number, this assumption will not be true by changing the angle.

Fig. 11

Effect of the gas Weber number on growth rate of the upstream axial surface waves at injection angle of a ${90}{^{\circ }}$, b ${60}{^{\circ }},$ c ${30}{^{\circ }}$ d $0{^{\circ }}$

Fig. 12

Effect of the liquid Weber number on growth rate of the upstream axial surface waves at injection angle of a ${90}{^{\circ }}$, b ${60}{^{\circ }},$ c ${30}{^{\circ }}$ d $0{^{\circ }}$

4.4 The effect of densities ratio

The effect of the density ratio on the growth rate of axial waves is shown in Fig. 13. This figure is related to the conditions in which the gas and liquid Weber numbers are considered 13 and 130, respectively. At a spray angle of 90$^\circ$, it is observed that by decreasing the ratio of liquid to gas ($1/\rho ^{*})$, the wavelength with the maximum growth rate diminishes. This reduction can be attributed to the change of Rayleigh–Taylor instability to Kelvin–Helmholtz. Kelvin–Helmholtz waves are generally shorter wavelengths. As the gas to liquid density ratio ($\rho ^{*})$ increases, the Atwood number ($At=\frac{\rho _{l}-\rho _{g}}{\rho _{l}+\rho _{g}})$ decreases, and the effect of Rayleigh–Taylor waves on the instabilities reduces. This decline provides the basis for strengthening the Kelvin–Helmholtz instability. In addition, it can be seen that increasing the liquid to gas density ratio ($1/\rho ^{*})$ from a threshold does not affect the growth rate and the associated wavelength. That means that Rayleigh–Taylor waves for fluids with very high-density ratios are independent of the Atwood number. By decreasing the injection angle, as the effect of Kelvin–Helmholtz waves on the instabilities increases, two trends are observed by changing the density ratio. In the high ratio of liquid to gaseous densities, the opposite trend can be seen with the spray angle of 90${^\circ }$, while in the low ratio, a similar trend occurs for the 90$^\circ$ angle. At high-density ratios, on the one hand, the effect of Kelvin–Helmholtz waves is amplified by decreasing the spray angle, and on the other hand, the Rayleigh–Taylor instability is strengthened by raising the density gradient, which causes the trend to be opposite to the 90 $^\circ$ injection angle. By reducing the density ratio, the predominant instability is Kelvin–Helmholtz, which has higher growth rates and shorter wavelengths. So, the trend for low-density ratio conditions is similar to the injection angle of 90 $^\circ$.

Fig. 13

Effect of the density ratio on growth rate of the upstream axial surface waves at injection angle of a ${ }{90}{^{\circ }}$, b ${60}{^{\circ }},$ c ${30}{^{\circ }}$ d $0{^{\circ }}$

4.5 Prediction of the breakup length

The breakup length is one of the basic parameters measured in the liquid jet injection process. This length determines the distance required to form the ligaments and droplets from the nozzle exit. For estimation of the breakup length, it can be assumed that the amplitude of the dominant wave is equal to the radius of the exit liquid jet [26, 43]. Therefore, the following equation can be used to determine the breakup length:

$$\begin{aligned} L=\frac{v_{l}}{{\omega _{{R}_{\textrm{opt}}}}} Ln\left( \frac{\eta _{b}}{\eta _{0}} \right) \end{aligned}$$

(54)

We used linear theory to determine the breakup point, similar to other researchers [28, 43, 58, 59, 67], assuming that the waves grow linearly to the breakup point, the nonlinear part occurs quickly, and its effects can be ignored. In this equation, it is assumed that when the surface wave reaches a critical amplitude, the ligaments are separated from the jet column and cause the jet column to break. Although the maximum growth rate can be determined by linear stability theory, this theory is not able to estimate critical wave amplitude for the breakup [59]. In fact, although the assumption of linearity is used to estimate the growth rate, the Ln$\left( \frac{\eta _{b}}{\eta _{0}} \right)$ is extracted from experimental data [28, 43, 58, 59, 67]. Thus, the maximum growth rate significantly affects the breakup process. For a more detailed study, the impact of the gas Weber number on the optimal growth rate at different injection angles is shown in Fig. 14. In this figure, the liquid Weber number is ${{\textrm{We}}}_{{l}}=65$. As can be seen in all spraying angles with increasing gas Weber number, the optimal growth rate has risen, and this increase follows the power form. In low gas Weber numbers, the growth rate is independent of the angle, but the higher gas Weber number, the more pronounced the injection angle effect becomes. This figure shows well that reducing the angle enhances the instability due to the difference in tangential velocity at the joint surface. The changing of the optimal longitudinal and peripheral wave numbers at different injection angles is shown in Fig. 15. As can be seen, with reducing spray angle, the axial wave has a more important role in the maximum growth rate than the peripheral wave. These effects are exacerbated by increasing the gas Weber number. Because the liquid jet velocity component is amplified in the direction of the transverse flow with decreasing the angle, the possibility of the axial waves’ formation increases.

Fig. 14

Effect of gas Weber number on the maximum wave growth rate at ${\textrm{We}}_{l}=65$

Fig. 15

Effect of gas Weber number at ${\textrm{We}}_{l}=65$ on the optimum, a axial wavenumber b circumferential wavenumber

The effect of the liquid Weber number on the maximum growth rate at ${\textrm{We}}_{g}=6.5$ is presented in Fig. 16. In all injection angles, a decreasing trend is observed with increasing liquid Weber number. In fact, as the liquid Weber number reduces, the resistance of the liquid jet to disturbance decreases, and the maximum growth rate increases. These changes follow the form of power function at all injection angles. Although the spray angle is one of the effective parameters in low liquid Weber numbers, in high liquid Weber numbers, the maximum growth rate is independent of the injection angle, which can be attributed to the significant increase in liquid jet resistance to disturbance. The variations of the optimum axial and circumferential wave numbers in terms of the liquid Weber number are shown in Fig. 17. As the spray angle increases, the peripheral wave number rises, while the axial wave number reduces. Raising the angle increases the difference between the transverse flow direction and the liquid exit direction from the nozzle, and the non-axial instability factors are found to be more important.

Fig. 16

Effect of liquid Weber number on the maximum wave growth rate at ${\textrm{We}}_{g}=6.5$

Fig. 17

Effect of liquid Weber number at ${\textrm{We}}_{g}=6.5$ on the optimum, a axial wavenumber b circumferential wavenumber

The only unknown expression to determine the breakup length is $\textrm{Ln}\left( \frac{\eta _{b}}{\eta _{0}} \right)$. This term is obtained from experimental results. Researchers have stated that this parameter is subject to operating conditions [58, 59, 67]. Therefore, it can be estimated as follows:

$$\begin{aligned} \textrm{Ln}\left( \frac{\eta _{b}}{\eta _{0}} \right) =c_{1}{\textrm{We}}_{l}^{c_{2}}{\textrm{We}}_{g}^{c_{3}} \end{aligned}$$

(55)

In this relation, the coefficients are a function of the injection angle. The changes of these coefficients relative to the injection angle were assumed to be linear. The variations of these coefficients in terms of spray angle are shown in Fig. 18. The angle of 90${^\circ }$ is considered the reference angle so $\psi _{\textrm{ref}}=\frac{\pi }{2}$. With the distance from the exit nozzle, both the wavelength and the amplitude of the disturbances increase. Hence, the ratio of the perturbation amplitude at the breaking point to the starting point is always greater than one. Although the amount of disturbance amplitude decreases with the injection angle along the entire wave path, this reduction is more severe at the beginning of the nozzle exit. In such a way, the ratio of disturbances at the breakup point to the initial disturbances increases with reducing injection angle. Hence, the change in coefficient $c_{1}$relative to the spray angle is a downward trend. As the liquid Weber number increases, the jet momentum to counteract distortion rises, reducing the amount of distortion at the breaking point. That is why $c_{2}$ is negative. While the gas Weber number is enhanced the amplitude of fluctuations reduces, and the coefficient $c_{3}$ is positive. By increasing the spray angle, the effect of gas and liquid Weber numbers on the amplitude ratio of distortions decreases, which is the cause of the observed trends for $c_{3 }$in the figure.

Fig. 18

The variations of coefficients with respect to injection angle

Figure 19 presents the breakup length estimated with instability theory. In order to evaluate the theory’s accuracy, the results of this theory were compared with the experimental data and the results of the theory developed by the authors based on the jet trajectory and Wu’s assumptions. As can be seen, although the difference between the two theories at high injection angles is small and both are consistent with the experimental data, as the angle decreases, the present theory is more consistent with the experimental results. Kasmaiee and Tadjfar [49] attributed the reason for this discrepancy with the experimental results to the assumptions of Wu’s theory and stated that Wu’s theory is more accurate for flows with the shear breakup mechanism. However, the present theory has accurate predictions for all flows with different breakup mechanisms, which can be attributed to the determination of breakup length based on wavelength, its growth rate and the nature of the waves. So, it is also accurate when the mechanism changes This semi-theoretical relation (semi-empirical correlation) is very useful and practical, especially for design applications, and it helps the physical understanding of the problem. Because of its theoretical-empirical base, it can be used by researchers to model the role of injection angle. The results obtained were compared with the results of Ragucci et al. [12] to ensure the performance of these models in similar problems. This comparison is presented in Fig. 19f and shows that the present model is consistent with the experimental correlation of the other researchers for the 90${^\circ }$ injection angle

Fig. 19

Breakup length at ${\textrm{We}}_{l}=65$ for a $\psi _{0}=90,$ b $\psi _{0}=75,$ c $\psi _{0}=60,$ d $\psi _{0}=45,$ e $\psi _{0}=30,$ f Comparison with the results of Ragucci et al. [12] for $\psi _{0}=90$

4.6 Proper orthogonal decomposition (POD) analysis

Proper orthogonal decomposition (POD) is used to study flow physics in more detail. This tool allows the detection of dominant modes and structures. POD is a statistical method to reduce the dimensions of the problem. This dimension reduction makes it easier to identify and understand the main features [60]. The POD method provides useful results for analysis by separating coherent structures from fluctuations. The POD utilizes a linear single value decomposition process to reduce dimensions. Although its first applications in fluid mechanics were related to the analysis of vector fields in turbulent flows [61, 62], it was also utilized to analyze scalar fields [63]. In POD, the two main parameters, the orthonormal basis functions ${\Gamma }_{j}$ and time dependent orthonormal amplitude coefficients (temporal coefficients)${ a}_{j,i}$, must be specified. These parameters are determined by minimizing the squares truncation error. The detail of this algorithm was explained by Arienti and Soteriou [63]. Since the modes are arranged according to energy, the primary modes have the highest energy; this makes it possible to separate the characteristics of large structures from small ones [63, 64]. Different researchers applied it to analyze two-phase transverse flow physics deeply and detect its structures better in their studies [8, 15, 18, 65, 66].

By changing the injection angle, the breakup point and the penetration of the liquid jet in the transverse flow, as well as the flow structures and dynamics, are changed. In this study, to investigate the effect of the angle on the flow structures, POD analysis was performed for the different injection angles under flow conditions where the gas and liquid Weber numbers are 6.5 and 65, respectively. Since the flow structures are dynamic phenomena, this work provided the opportunity to analyze the dominant structures of the flow and the influence of the angle on them. In order to utilize POD analysis, 3600 photos with a frequency of 1200 were provided for each case. The number of images and the frequency are appropriate and sufficient for POD analysis [15]. Different modes of POD analysis for spray angles from 30${^\circ }$ to 90${^\circ }$ are shown in Fig. 20. Higher modes are less dominant and have much higher dominant frequencies and can be ignored without affecting the interpretation of dominant phenomena. The first mode is the mean flow, which shows the average behavior of the jet, and as the mode increases, the occurrence of phenomena decreases. In the second mode, it can be seen that the structures are more elongated by reducing the angle, and 30 and 90${^\circ }$ angles, respectively, have the longest and shortest structures. These structures are related to a whiplash action before the break of the liquid jet [18]. In other words, with the reduction of the spray angle, because the impact of the gas Weber number is declined on the liquid jet, the jet experiences less twisting and entanglement and remains more continuous. The third mode is completely different. At the spray angle of 90${^\circ }$, the beginning of oscillations can be seen, which relates to after the breakup. In comparison, at the angle of 30${^\circ }$, the continuous jet is observed, and oscillations are not seen. In the third mode of other angles, it is also observed that the oscillating structures are being formed. Strictly, it is a state between an oscillatory state and a continuous jet. In fact, the act of whiplash is in progress and is separating the continuous jet. This mode shows well that the jet will break faster with increasing the angle. In the third mode of the 30${^\circ }$, the continuous jet has waves that can be attributed to Kelvin–Helmholtz instabilities. By reducing the spraying angle and strengthening the tangential velocity difference at the interface, these waves become more visible. Oscillating structures can be seen from mode four to mode six in different injection angles. As the injection angle decreases, these structures appear at farther distances from the nozzle. So, these disturbances can be seen downstream of the flow and at distances far from the nozzle for the angle of 30${^\circ }$, while these structures emerge nearer distances for the angle of 90${^\circ }$. For other angles, structures are created in the distance between these two states. The distance between two oscillating structures of the same color is attributed to the wavelength of column waves [15]. Their wavelength decreases as the angle reduces. Accordingly, the wavelength of these structures will be lower for the angle of 30${^\circ }$ compared to 90${^\circ }$.

Fig. 20

POD analysis for different injection angles at ${\textrm{We}}_{l}=65, {\textrm{We}}_{g}=6.5$, a 30${^\circ }$, b 45${^\circ }$, c 60${^\circ }$, d 75${^\circ }$, e 90${^\circ }$

For further investigation, the energy content of the modes is presented in Table 1 and Fig. 21. Figure 21 shows well that the energy content rises with increasing angle in all modes. This causes the liquid jet column to break faster and the atomization process to improve with increasing angle. Moreover, as the mode increases, its energy content decreases at all angles, indicating that the lower modes contain the more dominant flow structures. The first mode at all angles is the average behavior of the flow and, therefore, has the highest energy content. As discussed in the description of Fig. 20, the second mode is related to the flow structures before the breakup, while the fourth to sixth modes are related to the structures after the breakup of the liquid jet column. The third mode is also an intermediate mode. The energy content of structures reduces with advancing mode number. In Table 1, the relative energy content of the modes in each angle is presented to the total energy for that angle. This table clearly shows that these six modes allocate more than 85% of the energy in each angle, and therefore, they are sufficient for reconstructing images and examining the dominant structures. Arienti and Soteriou [63], who used POD to reconstruct two-phase flow images in transverse air, stated that the first four modes provide 82% of the total content, and therefore, the first four modes are sufficient to reconstruct their investigated flow and structures.

Fig. 21

Energy content of POD modes for different injection angles at ${\textrm{We}}_{l}=65, {\textrm{We}}_{g}=6.5$

Table 1 Relative energy content of POD modes for different injection angles

Fig. 22

PSD results at ${\textrm{We}}_{l}=65, {\textrm{We}}_{g}=6.5$ for injection angle of a 30${^\circ }$ b 45${^\circ }$, c 60${^\circ }$, d 75${^\circ }$, e 90${^\circ }$

In addition, by carrying out a fast Fourier transform (FFT), the power spectra density (PSD) extracted from modes 2, 3, and 4 for different injection angles has been compared. The result of this comparison is shown in Fig. 22. The PSD graphs of the first mode are very similar at different angles. Modes 5 and 6 are also related to non-dominant structures after the breakup process and are less important. Modes 2 and 4, which respectively represent the dominant structures before and after the liquid jet column breakup, can help us understand the physics of the problem and the effect of injection angle on dominant structures. Mode 3 is also an intermediate mode. Therefore, investigating the PSD of these three modes is enough to extract information. It should be noted that since the photography frequency is 1200 Hz, according to the Nyquist sampling theorem, the phenomena can be detected with a maximum frequency of 600 Hz. As can be seen, the dominant frequencies have moved to the right with the mode increment at different injection angles. In other words, with the increment of the mode, they have larger frequencies because the structures have less dominance and energy. Mode 3 is the middle mode in which the liquid jet column collapses and breaks. So, their PSD diagrams are completely different at different angles, and a regular trend cannot be found in them. In this mode, the breakup has not occurred at some angles, and in some cases, the process is developing, and in others, the breakup has occurred. In the second mode, with the angle increase, the dominant frequencies have moved to the right. The second mode shows the structure before the breakup. Since these structures become more elongated as the angle decreases, their wavelength is longer, and their frequency is lower. In the fourth mode, contrary to the second mode, the dominant frequencies have moved to the left by increasing the angle. The wavelength of the oscillating structures after the break is equivalent to the wavelength of the column waves, and as the angle decreases, the wavelength reduces, and their frequency increases

5 Conclusion

This study used a theoretical and experimental investigation of surface waves and the effect of the injection angle on their growth rate and wavelength. Linear stability analysis was utilized to obtain the theoretical relation for the growth rate of surface waves. These waves occur near the nozzle exit of the liquid jet. Thus, the cross section of the exit jet can be considered constant and its changes can be ignored in theoretical analysis The shadowgraphy technique was applied to visualize the flow in the experimental study. The flow visualization was recorded by high-speed photography. Relevant results were extracted by implementing in-house image processing codes. An image processing code was developed to determine the wavelength at different injection angles. Sobel algorithm was used to detect edges and liquid jet surface waves. The trajectory of the liquid jet was estimated as a power function, and the wavelength was determined by transferring the wave to the local tangential-vertical coordinate. In the theory study, aerodynamics, inertial and surface tension forces were considered as effective forces. Fluid viscosity against aerodynamic forces was neglected. The theoretical results were in good agreement with the experimental data at different injection angles. In order to validate the theory, the results obtained from the theory were compared with the theoretical and experimental data of other researchers for the wavelength at the injection angle of 90${^\circ }$. This evaluation showed that the theory is consistent with the other researchers’ results.

The theoretical relation showed that gas and liquid Weber numbers, density ratio, velocity ratio, axial and peripheral wave numbers, effective thickness, and injection angle are impressive in the growth rate of waves. Surface waves are caused by Rayleigh–Taylor, Kelvin–Helmholtz, Rayleigh–Plateau, and azimuthal instabilities. As the injection angle decreases due to the enhancement of the tangential velocity component of the jet, the wave growth rate increases, although it is associated with a reduction in wavelength due to the change of the instability mechanism from Rayleigh–Taylor to Kelvin–Helmholtz. While the injection angle significantly affects the formation of azimuthal waves, its main effect is on axial waves. So, if the axial waves are ignored, the growth rate of azimuthal waves will be independent of the angle. With the increase in gas Weber number, the liquid jet is facing changes in the breakup wave types, and more instability. The increment of the gas Weber number enhances the shear forces and the resulting surface breakup, which is a factor for strengthening the Kelvin–Helmholtz instability. However, the decrease in liquid Weber number causes a decrease in the resistance of the jet and, as a result, an increase in the growth rate waves. However, it does not change the type of waves. The reason for the formation of Rayleigh–Taylor waves is the density difference between two fluids. Therefore, with the gain of the density ratio, the Rayleigh–Taylor waves are strengthened. In other words, reducing the density ratio provides an opportunity for the flow to reinforce the Kelvin–Helmholtz waves. The impact of the injection angle in these changes is such that a uniform trend is observed at high angles for waves’ growth rate, while at low angles, two different trends are observed and a change of trend occurs. This difference is caused by the influence of the injection angle on the growth of waves. At low spray angles, the growth of Kelvin–Helmholtz waves is intensified due to the increase in the tangential velocity difference of the two fluids at the interface.

One of the important parameters in the process of liquid jet atomization in transverse flow is the breakup length. The maximum growth rate of waves was obtained from linear stability analysis and the breakup length of the liquid jet was determined at different injection angles based on it. The growth rate of the waves occurs in conditions where both the axial wave number and the peripheral wave number are nonzero and greater than one, so the instability mode is the helical mode. The effect of gas and liquid Weber numbers on the maximum growth rate and axial and peripheral wave numbers at different injection angles was investigated. The results of this theory for breakup length were compared with the theory and experimental data of other researchers. In the present theory, the nature of the waves and the effect of the injection angle on their growth rate were considered for specifying the breakup length. Therefore, the present theory is in better agreement with the experimental results. In order to investigate the effect of spray angle on flow structures, proper orthogonal decomposition (POD) analysis was used to reveal the dominant structure. The structures before and after the liquid jet breakup were analyzed in different modes. In order to investigate more precisely, the power spectra density (PSD) was obtained by applying the fast Fourier transform (FFT) for several modes. The results showed that decreasing the injection angle reduces the frequency of the structures before the breakup, while the frequency of the oscillating structures rises after the break.