1 Introduction

Municipal and industrial thermal wastewater is often discharged into water bodies such as seas, lakes, estuaries and rivers. Presence of thermal effluent on a body of water and any perturbation in ambient temperature leads to modifying the physical, biological and chemical properties of water, which can have severe adverse effects on the aquatic environment [1, 2]. For example, cold-blooded animals such as fish are particularly sensitive to changes in the thermal environment because they are unable to adjust their body temperature and vulnerable by a decrease or increase in their metabolic rate. Therefore, the proper understanding of the dispersion, transport and mixing processes of the thermal effluent discharged into water bodies is essential to water quality control, environmental impact and risk assessment.

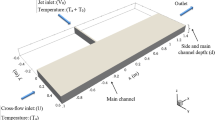
The wastewater dispose of in water bodies takes place from the outfalls of waste-carrying pipes, ditches, swales and other structures [3]. Surface discharges by lateral channels are traditional means and a very cost-effective method to discharge large volumes of effluent into the water body [4]. The buoyant lateral surface discharge usually forms turbulent surface jets and turbulent surface plumes in the receiving water body [5]. The surface jet spread is generally affected by the discharge rate \(({Q}_{0})\), cross-flow velocity \(({U}_{\mathrm{a}})\), water free surface, solid walls and bed. The spread rate of the surface plumes is further influenced by a stable stratification. Moreover, the surface jets and surface plumes exhibit a different flow structure and mixing pattern depending on the depth of the lateral channel relative to the cross-flow. Abdelwahed [6] reported two regimes for the surface discharge in the deep cross-flow and three regimes for the full-depth discharge in the cross-flow. The flow force (\({M}_{0}= {V}_{{0}} {Q}_{0}+0.5\mathrm{g}^{\prime }{d}_{{0}} {A}_{0})\), buoyancy flux (\({F}_{0}={g}^{\prime }{Q}_{0})\) and cross-flow velocity are important dependent variables for the surface discharge in the deep cross-flow. In more detailed investigations, Abdelwahed [6] divided the surface plumes discharge in deep cross-flow into two different types using the cross-flow parameter (\(\lambda )\), where the ratio of two timescales (\({t}_{\mathrm{B}} = {M}_{{0}}\)/\({F}_{{0}}\), \({t}_{\mathrm{U}} =\) (\({M}_{{0}}\)/\({U}^{4})^{0.5})\) is defined as the cross-flow parameter (\(\lambda = {t}_{{\mathrm{U}}}\)/\({t}_{\mathrm{B}})\). The different regions of these two types are affected by the variables illustrated in Fig. 1.

Fig. 1
figure 1

The flow regimes of the surface plume in deep cross-flow

Full size image

Despite the wide application of lateral jets and plumes discharge, their behavior is still quite complicated. Over the past decades, considerable experimental [7,8,9,10] and field [11, 12] efforts have been carried out to predict the behavior of discharged wastewater, and a lot of primary findings have been reported. However, performing laboratory and field studies not only are time-consuming and costly, but also cannot elucidate the evolution of vortex structures and produce detailed flow information. In recent decades, the use of computational fluid dynamics to predict the behavior of jets and plumes has attracted attention due to the growth of computing systems, [13,14,15].

McGuirk and Rodi [16] carried out the first two-dimensional numerical simulation of pollutant discharge from a lateral channel in a cross-flow. McGuirk and Rodi [17] developed a steady three-dimensional mathematical model to study the discharge of heated surface jets in a stagnant water body. Wang and Cheng [18] performed a three-dimensional numerical simulation of lateral discharge in a cross-flow channel with the RNG k–\(\varepsilon \) turbulence model defined in the commercial code FLUENT 4.4. They compared their results with laboratory data and those obtained from the standard k–\(\varepsilon \) turbulence model focusing on the effects of bed roughness and jet width ratio on the flow structure of the recirculation zone. Yu and Righetto [19] developed a depth-averaged turbulence model and carried out a two-dimensional steady-state simulation of thermal pollutant discharge from the lateral channel into a rectangular cross-flow channel. Kalita et al. [13] modeled a two-dimensional steady-state turbulent plane jets discharge in a moderate and weak and cross-flow. Kim and Cho [20] studied the hot water flow field discharged from a lateral surface channel based on the renormalization group (RNG) k–\(\varepsilon \) turbulence model and compared the results with a submerged side channel. Tang et al. [21] numerically simulated the discharge mixing of heat pollutants in the near region of a real-life configuration. The domain decomposition method with multilevel embedded overset grids is used because of the complexity of the geometry. Peng et al. [22] solved the two-dimensional shallow water equations using the lattice Boltzmann equation to steady simulate the discharge of thermal contaminants from the side channel. Tay et al. [23] examined the main circulation patterns and effects of temperature and salinity on the southern basin of Tauranga harbor using the ELCOM model. Khosravi and Javan [24] studied three-dimensional flow structures and mixing patterns in the near and far-field of the discharged full-depth thermal buoyant flow from the lateral channel in the cross-flow using the OpenFOAM model. They have extracted and studied three-dimensional and two-dimensional flow structures using the lambda-2 (\(\lambda _{2} )\) and LIC methods. They also performed parametric studies and statistical analyses to investigate the mixing properties of the flow for different values of R and \(\hbox {Fr}_{{0}}\). Khosravi and Javan [25] used a new data mining technique called multi-objective evolutionary polynomial regression (EPR-MOGA) to study the side thermal plume discharge in the full-depth cross-flow and compared the results with the OpenFOAM numerical model and the laboratory data. They proposed three mathematical relations to calculate the temperature distribution, temperature half-thickness and spread of thermal contamination at the free surface.

The numerical simulation of the lateral plume discharge in the deep cross-flow requires a high-resolution grid in the computational domain. Computational costs increase with an increase in the number of cells. Adaptive mesh refinement (AMR) is a technique dynamically adapting the mesh in specific regions of the simulation during the time solution. AMR allows an accurate solution with low computational costs compared to a refined uniform mesh. The AMR method has been employed successfully in a wide variety of application from single-phase flows [26,27,28] to multiphase flows [29,30,31]. Berger and Oliger [32] carried out the first studies on the dynamic mesh refinement for structured grids and developed an algorithm for the dynamic gridding. Theodorakakos and Bergeles [33] evaluated the capability of the AMR approach with the volume of fluid method (VOF) on the convection of bubbles under specified flow velocities and droplet impact. They concluded that AMR has been able to reduce the computational cost for simulations, while obtain excellent accuracy of the interfacial area. Cooke et al. [34] investigated the VOF method along with local AMR to study the isothermal, non-reacting, gravity-driven flow. The findings revealed that AMR led to the results with a much better agreement to experimental data. Schillaci et al. [35] adopted a finite-volume numerical model with an adaptive mesh refinement strategy to optimize the computational resources to perform the DNS of different three-dimensional liquid injection phenomena. Lucchini et al. [36] simulated the evaporating of high-pressure diesel sprays using the Eulerian–Lagrangian approach included dynamically refine the grid.

Previous studies on the lateral thermal plume discharge in the deep cross-flow have mainly focused on the steady-state flow behavior, while formations and developments of unsteady coherent structures have been less investigated. However, understanding evaluating coherent structures and the mixing process is essential to controlling and designing a lateral surface waste-disposal system. In this paper, the lateral plume discharge in the deep cross-flow is simulated with a developed OpenFOAM heat transfer solver with the emphasis on the development and the spread of the thermal plume along with the related transport and mixing processes. The unsteady Reynolds-averaged Navier–Stokes equations (URANS), equations closed with the realizable k–\(\varepsilon \) turbulence model, have been applied to evaluate three-dimensional features and the mixing characteristics. The adaptive mesh refinement (ARM) method has been used in simulations to save computing time. The \(\hbox {Fr}_{0\, }\) effect on the buoyant plume has been studied in detail. Instantaneous snapshots of flow and scalar fields have been applied to identify three-dimensional coherent structures, flow patterns and instability mechanisms. Three-dimensional streamlines based on the instantaneous velocity vectors along with two statistical analysis temporal mixing deficiency (TMD) and spatial mixing deficiency (SMD) are presented for further exploration about the mixing process.

2 Computational model and numerical framework

2.1 Geometry and flow conditions

The experiment of the lateral plume discharge in the deep cross-flow by Abdelwahed [6] is reproduced here. Figure 2 depicts the computational domain with some details. Abdelwahed [6] conducted lots of experiments on discharging heat pollutant from a side-channel into a wide-open channel influenced by a cross-flow and measured a wide variety of laboratory data under different temperatures and geometries conditions. The side channel has a square cross section with a size of 0.0254 m. The lateral channel exit is located at a distance 1 m downstream of the main channel inlet and is perpendicular to the cross-flow. The length, width and height of the cross-flow channel are 3.00, 0.61 and 0.1354 m, respectively. The origin of the coordinate system is located at the junction of the cross-flow and lateral channel at the bottom of the cross-flow channel. The lateral channel length is set at 0.6 m to develop the flow parameters.

Fig. 2
figure 2

The computational domain of a lateral plume discharged in the deep cross-flow

Full size image

The flow conditions, included the uniform velocity at the cross-flow channel entrance \(({U}_{\mathrm{a}})\), uniform velocity at the lateral channel inlet \(({U}_{\mathrm{jet}})\), velocity ratio (\(R= {U}_{{\mathrm{jet}}}\)/\({U}_{\mathrm{a}})\), temperature in the cross-flow entrance \(({T}_{\mathrm{a}})\), temperature difference between the lateral and cross-flow channel \(({T}_{0})\), and buoyancy flux (\({F}_{0} ={g}\left( {{\Delta \rho } / \rho } \right) {Q}_{0} )\), are presented in Table 1.

The value of the Reynolds number (Re\(={\rho UD} / \mu )\) for each test at the jet exit \((\hbox {Re}_{\mathrm{Jet}})\) and cross-flow entrance \((\hbox {Re}_{\mathrm{CrossFlow}})\) is given in Table 1. D is the hydraulic diameter. The molecular viscosity (\(\nu _{0_\mathrm{{CrossFlow}} } )\) is equal to 9.34E−07 kg/m s. The density value in the computational domain is calculated by the state equation, which is explained in the next section. Presented in Table 1 the values of expansion coefficient (\(\beta )\) are required to calculate the density.

Table 1 The parameters of experiments conducted by Abdelwahed (1981)
Full size table

2.2 Governing equations

The unsteady Reynolds-averaged Navier–Stokes (URANS) equations and temperature equation for incompressible flows in conjunction with the Boussinesq approximation for buoyancy effects are as follows [37]:

$$\begin{aligned}&\displaystyle \frac{\partial \bar{{u}}_{j} }{\partial x_{j} }=0\end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle \frac{\partial \bar{{u}}_{i} }{\partial t}+\frac{\partial }{\partial x_{j} }\left( {\bar{{u}}_{j} \bar{{u}}_{i} } \right) -\frac{\partial }{\partial x_{j} }\left\{ {\left( {\nu _{0} +\nu _{t} } \right) \left( {\frac{\partial \bar{{u}}_{i} }{\partial x_{j} }+\frac{\partial \bar{{u}}_{j} }{\partial x_{i} }} \right) -\frac{2}{3}\left( {\frac{\partial \bar{{u}}_{k} }{\partial x_{k} }} \right) \delta _{ij} } \right\} =-\frac{\partial {\widetilde{p}}}{\partial x_{i} }+\frac{\rho -\rho _{0} }{\rho _{0} }g_{i}\end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle \frac{\partial \bar{{T}}}{\partial t}+\frac{\partial }{\partial x_{j} }\left( {\bar{{T}}\bar{{u}}_{j} } \right) -\frac{\partial }{\partial x_{k} }\left( {\left( {\frac{\nu _{t} }{\Pr _{t} }+\frac{\nu _{0} }{\Pr }} \right) \frac{\partial \bar{{T}}}{\partial x_{k} }} \right) =0 \end{aligned}$$
(3)

where \({x}_{\mathrm{i}}\), \({x}_{\mathrm{j}}\), \({x}_{\mathrm{k}}\) are the spatial coordinates, \({g}_{\mathrm{i}}\) is the acceleration due to gravity, t is the evolution time, \({u}_{\mathrm{i}}\), \({u}_{\mathrm{j}}\), \({u}_{\mathrm{k}}\) are the velocity components, \(\delta _{ij} \) is the Kronecker delta, \({\widetilde{p}}=\left( {{\bar{{p}}} / {\rho _{0} }} \right) +\left( {2 / 3k} \right) \) is the corrected pressure, \(\rho _{0} \) is the ambient fluid density, \(\nu _{t} \) is the eddy viscosity closed by using the realizable k–\(\upvarepsilon \) model turbulence model in the present study, and k is the turbulent kinetic energy. The fluid density ( \(\rho \) ) is calculated as follows:

$$\begin{aligned} \rho =\rho _{0} \times \left( {1-\beta \left( {\bar{{T}}-T_{k} } \right) } \right) \end{aligned}$$
(4)

where \(\bar{{T}}\) and \(T_{{k}} \) are the temperature and a reference temperature. The turbulent Prandtl number \((\hbox {Pr}_{\mathrm{t}})\) and Prandtl number (Pr) are set to 0.85 and 7, respectively.

In this study, the realizable k–\(\varepsilon \) turbulent model is hired to compute \(\nu _{\mathrm{t}} \). The realizable k–\(\varepsilon \) turbulence model can provide a good prediction of mixing layers, separate flow and vortex shading that have a considerable effect on the mixing pattern [24]. Moreover, this model has been widely used to study jet and plume discharge in the cross-flow [38,39,40]. The detailed information of the realizable k–\(\varepsilon \) turbulent model can be found in Shih et al. [41]. The transport equations for k and \(\varepsilon \) (dissipation rate equation) are expressed as,

$$\begin{aligned}&\displaystyle \frac{\partial k}{\partial t}+\frac{\partial }{\partial x_{j} }\left( {\bar{{u}}_{j} k} \right) =\frac{\partial }{\partial x_{j} }\left[ {\left( {\nu _{0} +\nu _{t} } \right) \frac{\partial k}{\partial x_{j} }} \right] +G_{k} -\varepsilon \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle \frac{\partial \varepsilon }{\partial t}+\frac{\partial }{\partial x_{j} }\left( {\bar{{u}}_{j} \varepsilon } \right) =\frac{\partial }{\partial x_{j} }\left[ {\left( {\nu _{0} +\frac{\nu _{t} }{1.2}} \right) \frac{\partial \varepsilon }{\partial x_{j} }} \right] +C_{1} \sqrt{2S_{ij} S_{ji} } \varepsilon -\frac{1.9\varepsilon ^{2}}{k+\sqrt{\nu \varepsilon } } \end{aligned}$$
(6)

in which \({S}_{{ij}} =0.5\times \left( {{\partial \bar{{{u}}}_{{j}} } / {\partial {x}_{{i}} }+{\partial \bar{{u}}_{{i}} } / {\partial {x}_{{j}} }} \right) \) is the mean strain rate. The turbulent viscosity is calculated by:

$$\begin{aligned} \nu _{t} =\left( {\frac{1}{4.0+A_{s} U^{*}\frac{k}{\varepsilon }}} \right) \frac{k^{2}}{\varepsilon } \end{aligned}$$
(7)

Shih et al. [41] presented relationships to calculate \({C}_{{1}}\), \({U}^{*}\) and \({A}_{\mathrm{s}}\).

2.3 Numerical methods and boundary conditions

The governing equations are numerically solved by a finite volume method based on the OpenFOAM (open-source field operation and manipulation) platform. In this study, the basic buoyantBoussinesqPimpleFoam solver equipped with an AMR method has been used for simulations [42]. This solver is a transient solver for the turbulent and buoyant flow of incompressible fluids.

The pressure implicit with splitting of operators (PISO) algorithm was applied in the velocity and pressure coupling [43]. The time terms are discretized by the implicit second-order accurate backward method. The cell limited by the Gauss linear method is adopted for the gradient interpolation. The Gauss limited linear schemes have been used to discretize the space for all the convective terms except the ones in momentum, which is used a combined scheme called filteredLinear2V. The Laplacian terms are discretized using limited Gauss linear schemes. The generalized geometric-algebraic multi-grid (GAMG) method with Gauss-Seidel smoother is applied to solve the pressure field with a tolerance of 10e−6 at each time step. The preconditioned bi-conjugate gradient (Pre-BiCG) solver with the diagonal incomplete LU (DILU) preconditioner is applied for the velocity field. The stabilized preconditioned (bi-) conjugate gradient (Pre-BiCG-STAB) method, for both symmetric and asymmetric matrices, with the DILU preconditioner is used for \(\bar{{T}}\), k, and \(\varepsilon \). More details on solvers, discretization techniques and solving methods can be found in Greenshields [42]. Convergence criterion for velocity components, temperature, k and \(\varepsilon \) transport equations are set to achieve absolute tolerance up to 10e−8 at each time step. All simulations are done in the Intel Corei7-4710HQ, 2.50 GHz, 12 GB RAM.

The symmetry boundary condition is employed for the upper side of the main and cross-flow channel. All walls are set adiabatic (zero gradients) and non-slip. The static pressure condition is set at the outlet of the cross-flow channel. A uniform velocity and constant temperature are imposed at the inlet of the jet and cross-flow. The standard wall function provided by OpenFOAM was used for k, epsilon in walls. A zero gradient boundary condition was applied for other boundaries. The effects of air in all simulations are neglected.

2.4 Mesh generation: adaptive mesh refinement

The easiest way to accomplish precise numerical simulations is to apply high-resolution grids in the computational domain, although the problem is that computational costs increase with increasing the number of cells. The adaptive mesh refinement (AMR) was proposed to solve this dilemma. AMR is a technique which dynamically refines the mesh in the regions of interest to capture essential flow characteristics such as the formation of coherent structures and small-scale mixing of scalar fields.

There are three categories of mesh adaptation [44]:

  • h-refinement The mesh resolution is refined by adding computational nodes and reducing the size of the cell. Conversely, the mesh is coarsened by deleting nodes. In this method, the grid connectivity is altered.

  • r-refinement The number of grid points is kept constant inside the computational domain, but their location is changed by moved or stretched.

  • p-refinement The increase in mesh resolution is obtained by decreasing or increasing the order of accuracy of the discretization schemes. In this approach, the mesh connection remains unchanged.

The most common approach is h-refinement, which is also known as AMR. The general methodology of the mesh refinement and coarsening process in h-refinement approach can be described as follows:

  1. 1.

    A scalar field and a range of it, along with the maximum number of allowed cells in the domain, are determined as the refinement criterion.

  2. 2.

    The cells whose values belong to the user-specified refinement range are refined via cell splitting.

  3. 3.

    The cells that have values outside the range in step 1 are coarsened.

  4. 4.

    The computed flow-field is mapped from the old mesh to the new mesh, and the fluxes are corrected in the solver using the new values of the velocity.

  5. 5.

    The governing equations are solved on the new mesh.

  6. 6.

    The time step is advanced, and all the steps are repeated until the end of the simulation.

Figure 3 shows the refinement and coarsening algorithm that is used by the AMR procedure.

Fig. 3
figure 3

Flow chart for the adaptive mesh refinement (AMR) algorithm

Full size image

2.5 The grid and time-step independence analysis

This section studies the mesh independence to determine an adequate limit on the number of cell divisions. This investigation hired two different approaches to meshing procedure. Firstly, simulations were run using the buoyantBoussinesqPimpleFoam solver on a structured uniform hexahedral static mesh, using four different conditions on the refinement and accordingly time step. Then, a simulation was run using the solver equipped with AMR.

The mean excess temperature (T) field is used as a criterion to identify the regions that need to be refined or coarsened. Abdelwahed [6] recorded 25 times of the temperature at each node per second. He reported the mean excess temperature for 55 seconds as:

$$\begin{aligned} T=\frac{1}{n}\sum \limits _{i=1}^n {T_{i} } \end{aligned}$$
(8)

where \(n (=1375)\) is the number of excess temperature \(({T}_{{i}})\) recorded at each node. The excess temperature parameter is defined as the subtraction of the instantaneous temperature (\(\bar{{T}})\) from the temperature of the cross-flow entrance \(({T}_{\mathrm{a}})\). After the jet stream reaches the outlet of the cross-flow channel, the results are recorded for 55 s.

The sensitivity analysis of numerical simulation results is carried out for 1T test by different static square cube meshes. Simulations were run initially with a mesh of approximately 400,000 cells and time step 0.08 s (coarse case). The refined meshes (moderate, fine and very fine cases) are obtained from the coarse mesh by reducing the size of the grids in each direction by a factor of 0.8, respectively. The number of cells are 0.00391, 0.00312, 0.0025 and 0.002 m for the coarse, medium, fine and very fine grid, respectively. The numbers of grids is 2624952, 4273230 and 7979480 in the medium, fine and vary fine grid, respectively. The time step (\(\Delta \,t\)) is also simultaneously reduced by a coefficient of 0.8 in the medium and fine grids to evaluate the independence of the results to the time step. It is set 0.06 s, 0.05 s and 0.04 s in the medium, fine and very fine grid, respectively.

The number of cells increased in subsequent calculations until a minimal difference was observed in the solution. Figure 4 illustrates a closer plane view of the static mesh for the very fine case. Here, it can be seen that the static mesh is highly refined throughout the whole domain, even in regions where it is not required. Therefore, by using a static mesh, the entire mesh has to be refined, causing an increase in the CPU time dramatically.

Fig. 4
figure 4

Closer plane view of the static mesh

Full size image

For AMR analysis, an initial mesh was selected with approximately 250,000 structured uniform hexahedral cells with a cell size of 0.00635 m, and the mesh refinement process will continue automatically until the very fine grid size case similar to static mesh is reached (Fig. 5).

The mesh refining procedure is conducted in case the temperature value in the computational domain is more than 0.15 of the temperature at the cross-flow entrance. In all analyses, the refining operation was performed on two levels and one buffer layer was used to transfer from the large mesh to the smaller mesh. The number of cell layers between two refinement levels is referred to as buffer layers. It is critical to ensure a smooth transition between refinement levels in meshes by taking the buffer layers in order to reduce discretization errors caused by mesh skewness at refinement transitions. Figure 5b shows a close-up view of refined meshes using one buffer layers.

The AMR mesh is much more highly refined at the buoyant area, where the high grid density is required for the accurate resolution. In other parts of the domain, the mesh is coarser, which helps to maintain reasonable simulation run times. Therefore, AMR meshing will be a better option to do the refinement with a much-reduced CPU time.

Fig. 5
figure 5

Closer a plane and b cross-section view of the AMR mesh

Full size image

Figure 6 depicts the mean excess temperature profile for the 1T test at a distance of \(x=0.2\) m near the free surface for different meshes. The coefficient of correlation (r), relative error (RE) and mean absolute error (MAE) indices are used to assess the accuracy of the numerical simulation results as follows:

$$\begin{aligned} r= & {} \frac{\sum \nolimits _{i=1}^n {\left( {\mathrm{{Fr}}_{\mathrm{observed}_{{i} }} -{\sum \limits _{i=1}^n {\mathrm{{Fr}}_{\mathrm{observed}_{{i} } } }} \Bigg / n} \right) \left( {\mathrm{{Fr}}{_{\mathrm{{predicted}}_{i}} } -{\sum \limits _{i=1}^n {\mathrm{{Fr}}_{\mathrm{\mathrm {predicted}}_{i} } } } \Bigg / n} \right) } }{\sqrt{\sum \nolimits _{i=1}^n {\left( {\mathrm{{Fr}}_{\mathrm{observed}_{{i} }} -{\sum \limits _{i=1}^n {\mathrm{{Fr}}_{\mathrm{observed}_{{i} } } }} \Bigg / n} \right) ^{2}} } \sqrt{\sum \nolimits _{i=1}^n {\left( {\mathrm{{Fr}}_{\mathrm{{predicted}}_{i} } -{\sum \limits _{i=1}^n {\mathrm{{Fr}}_{\mathrm{{predicted}}_{i} } } } \Bigg / n} \right) ^{2}} } } \end{aligned}$$
(9)
$$\begin{aligned} \mathrm{{RE}}= & {} \frac{1}{n}\sum \limits _{i=1}^n {\frac{\left| {\mathrm{{Fr}}_{\mathrm{observed}_{{i} }} -\mathrm{{Fr}}_{\mathrm{{predicted}}_{i} } } \right| }{\mathrm{{Fr}}_{\mathrm{observed}_{{i} }} }} \end{aligned}$$
(10)
$$\begin{aligned} \mathrm{{MAE}}= & {} \frac{1}{n}\sum \limits _{i=1}^n {\left| {\mathrm{{Fr}}_{\mathrm{observed}_{{i} }} -\mathrm{{Fr}}_{\mathrm{{predicted}}_{i} } } \right| } \end{aligned}$$
(11)

where \(\mathrm{{Fr}}_{\mathrm{observed}_{{i} }} \) and \(\mathrm{{Fr}}_{\mathrm{{predicted}}_{i} } \) are the experimental and simulation results, respectively.

r values are 60.56%, 93.61%, 95.57, 97.92 for the coarse, moderate, fine and very fine meshes, respectively, and 97.50% for AMR. The coarse mesh is insufficient since the numerical results are inaccurate compared to the numerical results of the moderate, fine and very fine meshes. There was very little difference in the numerical results with approximately 4 (fine) and 8 (very fine) million cells. A cell count of roughly 8 million cells allowed mesh dependency errors to be minimized, while keeping run times to a reasonable level. The buoyantBoussinesqPimpleFoam results on the very fine mesh show almost identical results with those equipped with AMR in terms of temperature where the difference between the curves is negligible (Fig. 6).

Fig. 6
figure 6

The grid and time independence analysis for temperature profiles at the free surface along the horizontal line \(x = 0.20\) m at the time, \(t =\) 55 s for test 1T

Full size image

To further validate the grid and time-step independence analysis, Fig. 7 exhibits MAE values in different static and AMR meshing. As can be seen, the values of the MAE are reduced with the mesh and time step reduction, and eventually we arrive at a convergence in the results. The MAE value for the AMR model is approximately equal to that of the “very fine” model.

Fig. 7
figure 7

The grid and time-step independence analysis with and without AMR

Full size image

Based on the results provided by the mesh independence study, we could discern the resolution needed to obtain grid-independent results. A fine uniform three-dimensional hexahedral static mesh having the same dimensions throughout the domain would have required ~8 million cells, while it finally requires approximately ~1.5–2.0 million cells to AMR simulate. Using the adaptive mesh strategy, each simulation reported in the present study took a total of approximately 45–55 h of the active CPU time, while with the static mesh, this time is about one week. As a result, two solvers give similar results with a big difference in the CPU time. In the following, all analyses are performed with AMR simulate.

3 Model validation

In the current study, the laboratory findings from the buoyant surface plume from a side channel in deep cross-flow performed by Abdelwahed [6] are selected to verify the numerical model. The experimental conditions of the chosen experiments are summarized in Table 1.

The thermal pollutants spread on the main channel after discharging into the cross-flow and create a plum surface due to the buoyancy. The temperature half-thickness profile, where the temperature is equal to half of the temperature at the water free surface, is used to introduce the thermal cross section. Figure 8 shows the cross section of the plume flow at \(x = 5\) and 10 cm of the 2T test and at \(x = 28\) and 56 cm of the 4T test. The numerical model well simulates the separation of the plume flow. The length of the spreading plume is simulated with excellent precision at \(x=5\) and 10 cm at the free surface of the 2T test and \(x = 28\) cm at the free surface of the 4T. However, at \(x = 56\) cm of the 4T test the length of the spreading plume flow at free surface is predicted less than the experimental result.

Fig. 8
figure 8

Temperature half-thickness of the depth cross-flow in the a 2T test and b 4T test; experimental results (dashed line), numerical results (solid line)

Full size image

Figure 9 presents the simulated and measured results of T for the 1T test in different depths (\(z=\) 12.85, 8.35, 5.85 cm) of cross sections located at \(x=10\) and 40 cm. The experimental and numerical results of T have a good agreement.

Fig. 9
figure 9

Numerical (solid line) and experimental results (\(\circ \)) of the mean excess temperature for the 1T test: a \(x=10\) cm and b \(x=40\) cm

Full size image

Abdelwahed [6] reported the location of the maximum mean excess temperature \(({T}_{\mathrm{m}})\) at different cross sections to describe the jet trajectory \(({y}_{\mathrm{m}})\) at the free surface. He defined the length (\(l_\mathrm{s} =\left( {{M_{0}^{2} } / {UF_{0} }} \right) ^{1/3})\), time (\(t_{s} ={M_{0} } / {F_{0} })\) and temperature (\(T_\mathrm{s} ={\Gamma _{0} } / {Ul_\mathrm{s}^{2} })\) scales to establish a correlation among the measured data, where \(M_{0} =V_{0}^{2} A_{0} +0.5\times g_{0}^{'} d_{0} A_{0} \) is the flow force, \(F_{0} =g_{0}^{'} V_{0} A_{0} \) is the buoyancy flux, and \(\Gamma _{0} =T_{0} Q_{0} \) is the heat flux of the discharged jet. \({A}_{{0}}\) and \(g_{0}^{'} =g\left( {\Delta \rho } \right) /\rho \) are cross-section area in the side channel inlet and reduced gravity, respectively.

The simulated results of \({T}_{\mathrm{m}}\) and \({y}_{\mathrm{m}}\) are compared with the experimental results of the 1–4T tests in Fig. 10. RE values of the results presented in Fig. 10a, b are 14.24% and 12.15, respectively. r values are 98.95% and 98.58% for these results. MAE values of the \({T}_{\mathrm{m}}\) and \({y}_{\mathrm{m}}\) are 0.66 K and 1.93 cm, respectively. A good agreement can be seen between the experimental and numerical results. In general, the numerical model well simulates the flow characteristics of the hot water discharged from the side channel in the cross-flow.

Fig. 10
figure 10

a The maximum mean excess temperature and b the transverse location of the maximum mean excess temperature at different locations along the cross-flow of the 1–4T tests

Full size image

In this paper, the \(\lambda _{2}\) vortex criterion is applied to visualize three-dimensional coherent structures. The \(\lambda _{2}\)-criterion is defined as the negative values of the second eigenvalue of the symmetry square of the velocity gradient tensor [45]. Figure 11 shows a comparison of the vortical structures in the static and AMR grid simulations. The snapshots were selected from the 1T test with \(R = 3.96\) at the time, \(t = 55\) s. The \(\lambda _{2}\) isosurfaces are colored with the mean excess temperature. On the right, it can be seen that the AMR mesh captures large-scale turbulence and reduces the resolution of fine-scale structures, which is better captured on the static mesh (on the left). However, these fine-scale structures are weak and do not play an important role in the mixing process. As shown in the previous section, the most important feature of the flow is captured in both static and AMR grid simulations. Other details of the flow pattern, including mean excess temperature distribution, large vortex structure and jet trajectory in both simulations, are similar.

Fig. 11
figure 11

Instantaneous coherent structures in the main channel colored by the mean excess temperature: a AMR grid and b static grid (color figure online)

Full size image

4 Results and discussion

Figure 12 shows the bottom view of the instantaneous vortical structures in terms of \(\lambda _{2}\) for the 1T and 3T tests. The focus value is \(\lambda _{2}=0.5\), and isosurfaces are colored with the mean excess temperature. The vorticity is shown from the bottom view to highlight the coherent structures that were concealed under the surface. Close to the lateral channel exit, shear layer roll-up appears around the jet core, demonstrating the shear layer in the initial jet region arises from the Kelvin–Helmholtz instability. As the jet enters the cross-flow, the shear layer roll-up becomes unstable and gradually fades away. These structures are then advected downstream and further enhanced by the entraining cross-flow and rolls-up into small vortices. From temperature contours, it is visible that the cross-flow deflection in the initial jet zone increases its temperature and induces a mixing region.

Fig. 12
figure 12

The isosurface of the \(\lambda _{2}\) criterion for tests 1T (left) and 3T (right), colored by the mean excess temperature (color figure online)

Full size image

The cross-flow view of the instantaneous coherent structures colored by the mean excess temperature for four of the densimetric Froude number \((\hbox {Fr}_{0})\) is visualized in Fig. 13. Many studies have shown that \(\hbox {Fr}_{0}\) is an important dimensionless parameter [39]. The value of \(\hbox {Fr}_{{0}}\) gives an indication of the magnitude of plume inertia over plume buoyancy. Besides, \(\hbox {Fr}_{0}\) allows to compare and scale different model results. The \(\hbox {Fr}_{{0}}\) is given by the following equation

$$\begin{aligned} \mathrm{Fr}_{0} =\frac{{U}_{\mathrm{jet}} }{\sqrt{{{g}}'_{0} \sqrt{{A}_{0} } } } \end{aligned}$$
(12)

where \(\hbox {A}_{{0}}\) is the cross-section area of the lateral channel and \(g_{0}^{'} =g\left( {\Delta \rho } \right) /\rho \) is reduced gravity. The change in vortex dynamics with \(\hbox {Fr}_{{0}}\) is clearly observed. Shear layer roll-up vortices are also evident in the shear layer close to the lateral channel exit for all tests except for the 4T test, which is difficult to detect because of the vortex weakness. At \(\hbox {Fr}_{0}= 10.30\), large-scale vortices are seen in the free surface, inner wall and channel floor, with large streamwise structures and less fine-scale turbulence. As the \(\hbox {Fr}_{{0}}\) decreases, the coherent structures become increasingly weak, with the faster breakdown of the shear layer roll-up, and disappearance of vortices in the inner wall and bottom.

Fig. 13
figure 13

The isosurface of the \(\lambda _{2}\) (= 0.5) criterion for tests a 1T with \(\hbox {Fr}_{0} = 10.30\), b 2T with \(\hbox {Fr}_{0} = 6.10\), c 3T with \(\hbox {Fr}_{0} = 4.08\) and d 4T with \(\hbox {Fr}_{0} = 2.24\), colored with the mean excess temperature (color figure online)

Full size image

To perform a complete environmental assessment of lateral thermal plume discharge in the deep cross-flow, the spreading, mixing and transporting processes need to be understood. Thermal buoyant discharges should be carried out in such a way guaranteeing that ambient water temperatures do not exceed a specified temperature rise outside an established mixing region. The environmental constraints given by the World Bank define the mixing region as a zone where initial dilution of discharge occurs and where exceedance of the water quality standards is allowed [46]. There is no standard to specify the mixing region for a particular project, and the maximum temperature increase is determined through an environmental assessment process. Figure 14 shows the three-dimensional volume of a thermal plume discharge with a threshold of \(\Delta T = 0.5\, ^\circ \mathrm{C}\) and cross sections along the cross-flow for different \(\hbox {Fr}_{{0}}\) colored with y coordinate component. The y contour profiles can provide important insight into the distribution of the temperature plume along with the channel depth. Every point within this plume has a temperature difference larger than 0.5 \(^\circ \mathrm{C}\) than cross-flow. The mixing zone pattern is strongly influenced by the initial \(\hbox {Fr}_{{0}}\). With increasing the \(\hbox {Fr}_{{0}}\), the buoyant plume penetrates more in the deep and fewer spread in the free surface. For plume with \(\hbox {Fr}_{0} =\)10.30, which has the largest amount of \(\hbox {Fr}_{{0}}\), the maximum emission depth is significantly lower. The plume with \(\hbox {Fr}_{{0}} =2.24\) has the least amount of \(\hbox {Fr}_{{0}}\) and the smallest amount of thermal discharge volumes which is located near the free surface. As a consequence, the spreading of the temperature over the water column is dominated by varying \(\hbox {Fr}_{{0}}\).

Fig. 14
figure 14

Three-dimensional threshold (\(\Delta \,T= 0.5\) \(^\circ \mathrm{C}\)) of a lateral thermal plume discharge for a \(\hbox {Fr}_{{0}} = 10.30\), b \(\hbox {Fr}_{0} = 6.10\), c \(\hbox {Fr}_{{0}} = 4.08\) and d \(\hbox {Fr}_{0} = 2.24\), colored with y coordinate component (color figure online)

Full size image

Figures 15 and 16 depict three-dimensional streamlines based on the instantaneous velocity vectors derived from the lateral channel, colored by the mean excess temperature for four of the \(\hbox {Fr}_{{0}}\). The discharged plume acts as an obstacle in the cross-flow near the discharge location which makes the stream to divert to the under of the discharged plume, and forms a swirl flow at the edge of the jet boundary and cross-flow. The swirl flow pattern formed continues to downstream the main channel. Increasing the \(\hbox {Fr}_{{0}}\) results in weakening the swirl flow around the discharged jet core.

Fig. 15
figure 15

Three-dimensional streamlines based on the instantaneous velocity vectors and colored by the mean excess temperature: (test: 1T) \(\hbox {Fr}_{0} = 10.30\), (test: 2T) \(\hbox {Fr}_{0} = 6.10\) (color figure online)

Full size image
Fig. 16
figure 16

Three-dimensional streamlines based on the instantaneous velocity vectors and colored by the mean excess temperature: (test: 3T) \(\hbox {Fr}_{0} = 4.08\) and (test: 4T) \(\hbox {Fr}_{0} = 2.24\) (color figure online)

Full size image

Figure 17 illustrates the temporal evolution of the temperature contour in plane views located at \(z=12.00\) cm for the 1–4T test. The counterclockwise-rotating vortices called backward-rolling vortices are observed at the confluence of the discharged plume and cross-flow because of the Kelvin–Helmholtz instability. Zhang and Yang [15] and Khosravi and Javan [24] reported vortices similar to these for the jet flow from the channel bottom with a circular cross section and side thermal discharge in the cross-flow, respectively. The gaps formed at the shear layer mix the lateral discharged fluid with the cross-flow. The scale of the backward-rolling vortices becomes larger toward the main channel downstream, and they disappear approximately at \(x =\) 0.5–0.6 m. In other words, they slightly move downstream and then shed in the cross-flow channel (vortex shedding). As shown in the figures, the increase in \(\hbox {Fr}_{{0}}\) has led to more spread of the plume in the main channel.

Fig. 17
figure 17

The temporal evolution of the temperature contours near the free surface for a \(\hbox {Fr}_{0}\) = 10.30, b \(\hbox {Fr}_{{0}}\) = 6.10, c \(\hbox {Fr}_{0}\) = 4.08 and d \(\hbox {Fr}_{{0}}\) = 2.24

Full size image

The mixing indices, TMD (temporal mixing deficiency), which is a spatial heterogeneity measure of the time-averaged quantity and SMD (spatial mixing deficiency), which is a temporal heterogeneity of the spatial average at various points over a plane, are evaluated based on the instantaneous temperature over the cross sections at several locations (\(0.05< x< 0.55, 0.1345< z< 0.005, 0.00< y< 0.61\)). SMD and TMD at point i over n snapshots are calculated as [15]:

$$\begin{aligned} \mathrm{{SMD}}= & {} \frac{\mathrm{{RMS}}_\mathrm{{plane}} \left( {\left\langle {T_{i} } \right\rangle } \right) }{\mathrm{{Avg}}_\mathrm{{plane}} \left( {\left\langle T \right\rangle } \right) } \end{aligned}$$
(13)
$$\begin{aligned} \mathrm{{TMD}}= & {} \mathrm{{Avg}}_\mathrm{{plane}} \left( {\frac{\mathrm{{RMS}}_{i} }{\left\langle {T_{i} } \right\rangle }} \right) \end{aligned}$$
(14)

where

$$\begin{aligned} \left\langle {T_{i} } \right\rangle&=\frac{1}{n}\sum \limits _{k=1}^n {T_{i,k} } \end{aligned}$$
(15)
$$\begin{aligned} \mathrm{{RMS}}_{i}&=\sqrt{\frac{1}{n-1}\sum \limits _{k=1}^n {\left( {\left\langle {T_{i} } \right\rangle -T_{i,k} } \right) ^{2}} } \end{aligned}$$
(16)
$$\begin{aligned} \mathrm{{Avg}}_{\mathrm{{plane}}} \left( {\left\langle T \right\rangle } \right)&=\frac{1}{m}\sum \limits _{i=1}^m {\left\langle {T_{i} } \right\rangle } \end{aligned}$$
(17)
$$\begin{aligned} \mathrm{{RMS}}_{\mathrm{{plane}}} \left( {\left\langle {T_{i} } \right\rangle } \right)&=\sqrt{\frac{1}{m-1}\sum \limits _{i=1}^m {\left( {\left\langle {T_{i} } \right\rangle -\mathrm{{Avg}}_{\mathrm{{plane}}} \left( {\left\langle {T_{i} } \right\rangle } \right) } \right) ^{2}} } \end{aligned}$$
(18)

Figure 18 shows the results of the TMD and SMD for tests 1–4T. Temperature data are recorded every 0.04 s during a period of 55 s. Both TMD and SMD indices are the most in the 1T test due to the most homogeneous of the mixing field. Conversely, both mixing indices are less in 4T test, which is denoting the most inhomogeneity of the mixing field. According to Table 1, increasing the reduced gravity (\(g_{0}^{'} )\) has a large contribution to the overall increase of the TMD and SMD profiles along the main channel. The TMD and SMD increase by increasing reduced gravity. TMD and SMD gradient profiles are approximately equal for distances greater than \(x>\) 30 cm. The difference in TMD is substantial for distances smaller than \(x<\) 15 cm. Generally, TMD and SMD gradually decrease for 1–4T tests by getting away from the lateral channel denoting the homogeneity mixing field in the far fields. Zhang and Yang [15] and Khosravi and Javan [24] reported a similar trend of SMD and TMD for the transverse jet with a circular cross section discharged in the cross-flow and side thermal discharge in the cross-flow, respectively.

Fig. 18
figure 18

TMD and SMD spatial evolution of mixing indices for tests 1–4T

Full size image

5 Conclusions

In this paper, the detailed three-dimensional structure and mixing characteristics of the lateral thermal plume discharge in the deep cross-flow are investigated using the OpenFOAM model. The realizable k-\(\upvarepsilon \) turbulence model is applied to close the URANS equations. The emphasis is on the development and the spreading of the buoyant plume along with the related transport and mixing processes. The standard heat transfer OpenFOAM solver equipped with an adaptive mesh refinement (AMR) method has been applied to reduce the computational cost. The numerical simulation results are in good agreement with the experimental data of Abdelwahed [6] in terms of the maximum mean excess temperature, temperature half- thickness and jet trajectory at different cross sections of the main channel.

The coherent structures, contours and streamlines are examined for the different \(\hbox {Fr}_{{0}}\) to evaluate the link between the scaler mixing and flow dynamics. The vortex structures are visualized by the Lambda-2 technique. The large-scale structures are the most dominant transport process for this unsteady situation. Shear layer roll-up vortices occur near the discharge location and at the confluence of the surface jet and cross-flow. \(\hbox {Fr}_{{0}}\) plays an essential role in the flow pattern and temperature distribution. High \(\hbox {Fr}_{{0}}\) induces larger turbulent shear layer roll-up vortices. As the \(\hbox {Fr}_{{0}}\) decreases, the coherent structures become increasingly weak, with the faster breakdown of the shear layer roll-up, and disappearance of vortices in the inner wall and bottom area. Consequently, the spreading of the temperature over the water column is dominated by varying \(\hbox {Fr}_{{0}}\). The increase in \(\hbox {Fr}_{0}\) has led to more spread of the plume in the main channel and fewer spread in the free surface. The instantaneous temperature contours near the free surface exhibit a vortex shedding phenomenon and gaps between the cross-flow and discharged plume at the shear layer. The three-dimensional streamlines show a swirl flow at the edge of the jet boundary and cross-flow. The swirl flow pattern formed continues to downstream the main channel. Increasing the \(\hbox {Fr}_{{0}}\) results in weakening the swirl flow around the discharged jet core. Mixing efficiency is quantified using the temporal mixing deficiency (TMD) and spatial mixing deficiency (SMD). The TMD and SMD show the direct relationship between the mixing efficiency and reduced gravity (\(g_{0}^{'} )\).