1 Introduction

The study of elastic fields resulting from the presence of rigid line inhomogeneities continues to attract increasing attention in the literature. These rigid line inhomogeneities are especially useful in the modeling of composites; for example, they can be used to represent thin hard fibers as part of a reinforcing phase in composite materials. Accordingly, researchers have considered material microsystems incorporating rigid line inhomogeneities in various different scenarios ranging from those involving the influence of rigid inhomogeneities placed near material interfaces [1,2,3,4], the interaction of dislocations with rigid line inhomogeneities [5] and the singular stress fields induced near the tips of rigid line inhomogeneities [6,7,8,9]. In all of the aforementioned studies, the rigid line inhomogeneity is either embedded in a homogeneous material [3, 5,6,7,8,9] or lies at the interface of a bimaterial [1,2,3,4]. In the design of fibrous composites, a coating layer is usually inserted between the internal inhomogeneity (representing the fiber) and the surrounding matrix with the objective of improving the bonding between the inhomogeneity and the matrix and also to reduce the material mismatch induced stress concentration at the interface [10]. It is of interest to examine the influence of a rigid line inhomogeneity when it is entirely embedded inside such an intermediate coating layer especially with respect to its interaction with an edge dislocation located nearby inside the matrix region. We know, for example, that dislocations are always present in a composite and the embedded rigid line inhomogeneity will tend to repel the dislocation so that an analysis of the interaction between the two becomes crucial in the design of the corresponding composite. We mention in closing this paragraph that a rigid line inhomogeneity is often referred to as an ‘anticrack’ [2, 7] originating from the point of view put forward by Dundurs and Markenscoff in [7] that a rigid line inhomogeneity can be considered as the ‘opposite’ of a crack [7]:

“The opposite of a crack, in a certain sense, is a cut in the material that is filled with a rigid lamella: A crack is a cut that transmits no tractions, but allows a displacement discontinuity. The rigid lamella transmits tractions, but prevents a displacement discontinuity. There is no uniform terminology for the latter, and we shall call them anticracks for brevity.”

In this paper, we present an analytical study of the interaction of an edge dislocation located inside the matrix region and a finite anticrack entirely embedded in a confocal elliptical coating. The confocal geometry permits an analytical treatment of the interaction problem. The coating and the matrix have identical shear moduli but distinct Poisson’s ratios. Using conformal mapping, analytic continuation and an application of the generalized Liouville’s theorem, we construct a closed-form representation of an auxiliary function defined in the entire image plane. This auxiliary function is then used to derive the two pairs of complex potentials (whose expressions contain convergent series) in the image plane which characterize the corresponding stress and displacement distributions everywhere in the composite. By satisfying moment balance on a circular disk with sufficiently large radius, the rigid-body rotation of the anticrack can be uniquely determined and expressed in closed-form. We also obtain the stress intensity factors at the two anticrack tips induced by the edge dislocation. Our solution is verified by careful comparison with its classical counterpart in Dundurs and Markenscoff [7].

2 Complex variable formulation

We first establish a Cartesian coordinate system \(\left\{ {x_{i} } \right\} \,(i=1,2,3)\). For plane deformations of an isotropic elastic material, the three in-plane stresses \((\sigma _{11} ,\,\sigma _{22} ,\,\sigma _{12} )\), two in-plane displacements \((u_{1} ,\,u_{2} )\) and two stress functions \((\phi _{1} ,\,\phi _{2} )\) are given in terms of two analytic functions \(\varphi (z)\) and \(\psi (z)\) of the complex variable \(z=x_{1} +\text{ i }x_{2} \) as [11]

$$\begin{aligned}&\sigma _{11} +\sigma _{22} =2\left[ {{\varphi }'(z)+\overline{{\varphi }'(z)} } \right] , \nonumber \\&\sigma _{22} -\sigma _{11} +2\text{ i }\sigma _{12} =2\left[ {\bar{{z}}{\varphi }''(z)+{\psi }'(z)} \right] , \end{aligned}$$
(1)
$$\begin{aligned}&2\mu (u_{1} +\text{ i }u_{2} )=\kappa \varphi (z)-z\overline{{\varphi }'(z)} -\overline{\psi (z)} , \nonumber \\&\phi _{1} +\text{ i }\phi _{2} =\text{ i }\left[ {\varphi (z)+z\overline{{\varphi }'(z)} +\overline{\psi (z)} } \right] , \end{aligned}$$
(2)

where \(\kappa =3-4\nu \) for plane strain and \(\kappa ={(3-\nu )} / {(1+\nu )}\) for plane stress, \(\mu \) and \(\nu \, (0\leqslant \nu \leqslant 1 / 2)\) are the shear modulus and Poisson’s ratio, respectively. In addition, the stresses are related to the stress functions through [3]

$$\begin{aligned} \sigma _{11}= & {} -\phi _{1,2} ,\quad \sigma _{12} =\phi _{1,1} , \nonumber \\ \sigma _{21}= & {} -\phi _{2,2} ,\quad \sigma _{22} =\phi _{2,1} . \end{aligned}$$
(3)

3 Analytic solution

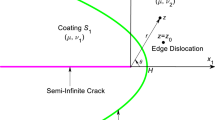
As shown in Fig. 1, we consider an edge dislocation interacting with a confocally coated finite anticrack. The two sides of the anticrack of half-length a lying on the interval \(-a<x_{1} <a,\, x_{2} =0^{\pm }\) remain perfectly bonded to a confocal elliptical coating, which is in turn surrounded by an unbounded matrix. Let \(S_{1} \) and \(S_{2} \) denote the coating and the matrix, respectively, which are perfectly bonded through the elliptical interface L whose two foci are located at \(z=\pm a\). The edge dislocation with Burgers vector \((b_{1} ,\,b_{2} )\) is located at \(z=z_{0} \) in the matrix. In what follows, the subscripts 1 and 2 are appended to quantities formerly free of subscripts to identify the respective quantities in \(S_{1} \) and \(S_{2} \) (for example, \(\varphi _{\mathrm {1}}\), \(\psi _{\mathrm {1}}\), \(\kappa _{\mathrm {1}}\) will denote the values of \(\varphi \), \(\psi \), \(\kappa \) in the region \(S_{1} \), etc—this notation should not be confused with the use of existing subscripts corresponding to the complex variable \(z=x_{1} +\text{ i }x_{2} )\). In order to arrive at an analytical solution, we further assume that the coating and the matrix have equal shear moduli but distinct Poisson’s ratios.

As shown in Fig. 2, by introducing the following conformal mapping function

$$\begin{aligned} z=\omega (\xi )=\frac{a}{2}\left( {\xi +\frac{1}{\xi }} \right) ,\quad \left| \xi \right| \geqslant 1, \end{aligned}$$
(4)

the two sides of the anticrack are mapped onto the unit circle \(\left| \xi \right| =1\); the elliptical interface L is mapped onto the outer concentric circle \(\left| \xi \right| =R>1\); the location of the edge dislocation at \(z=z_{0} \) is mapped onto \(\xi =\xi _{0} \,(\left| {\xi _{0} } \right| >R)\). Evidently, the semi-major and semi-minor axes of the ellipse L are given, respectively, by \(\frac{a}{2}(R+R^{-1})\) and \(\frac{a}{2}(R-R^{-1})\). For convenience, we write \(\varphi _{i} (\xi )=\varphi _{i} (\omega (\xi )),\,\psi _{i} (\xi )=\psi _{i} (\omega (\xi ))\, (i=1,\,2)\).

Fig. 1
figure 1

An edge dislocation interacting with a confocally coated finite anticrack

Full size image
Fig. 2
figure 2

The image \(\xi \)-plane

Full size image

As noted above, the two sides of the anticrack remain perfectly bonded to the coating. We disregard any rigid body translation of the anticrack and assume that the anticrack undergoes only an unknown rigid-body rotation. Using Eq. (2)\(_{\mathrm {1}}\), we thus impose the condition of rigid-body displacements on the two sides of the anticrack, i.e., that \(u_{1} +\text{ i }u_{2} =\text{ i }\varepsilon z\), where \(\varepsilon \) is the unknown rigid-body rotation of the anticrack (to be determined), leading to the introduction of the following analytic continuation

$$\begin{aligned} \psi _{1} (\xi )=\kappa _{1} \bar{{\varphi }}_{1} \left( {\frac{1}{\xi }} \right) -\frac{\xi (\xi ^{2}+1)}{\xi ^{2}-1}{\varphi }'_{1} (\xi )+\text{ i }a\mu \varepsilon \left( {\xi +\frac{1}{\xi }} \right) . \end{aligned}$$
(5)

Equation (5) implies that \(\varphi _{1} (\xi )\) has been extended to the annulus \(1 / R\leqslant \left| \xi \right| \leqslant 1\).

Using Eq. (5), the continuity of tractions and displacements across the perfectly bonded elliptical coating-matrix interface L can be written as

$$\begin{aligned} \varphi _{1} (\xi )=\frac{\kappa _{2} +1}{\kappa _{1} +1}\varphi _{2} (\xi ),\quad \frac{1}{R}\leqslant \left| \xi \right| <+\infty ; \end{aligned}$$
(6)

and

$$\begin{aligned}&\bar{{\psi }}_{2} \left( {\frac{R^{2}}{\xi }} \right) -\frac{R^{4}(\kappa _{1} -\kappa _{2} )(\xi ^{2}+1)+R^{2}(\kappa _{2} +1)(\xi ^{2}+R^{4})}{\xi (\xi ^{2}-R^{4})(\kappa _{1} +1)}{\bar{{\varphi }}}'_{2} \left( {\frac{R^{2}}{\xi }} \right) +\frac{\text{ i }a\mu \varepsilon }{R^{2}}\xi \nonumber \\&\quad =\frac{\kappa _{2} -\kappa _{1} }{\kappa _{1} +1}\varphi _{2} (\xi )+\frac{\kappa _{1} (\kappa _{2} +1)}{\kappa _{1} +1}\varphi _{2} \left( {\frac{\xi }{R^{2}}} \right) -\frac{\text{ i }a\mu \varepsilon R^{2}}{\xi },\quad \left| \xi \right| =R. \end{aligned}$$
(7)

A detailed derivation of Eqs. (6) and (7) can be found in Appendix A. Equation (6) is an analytic continuation of the two analytic functions \(\varphi _{1} (\xi )\) and \(\varphi _{2} (\xi )\) in view of the fact that \(\varphi _{1} (\xi )\) is now extended to \(R\leqslant \left| \xi \right| <+\infty \) while \(\varphi _{2} (\xi )\) is extended to \(\frac{1}{R}\leqslant \left| \xi \right| \leqslant R\) by using Eq. (6). In view of Eq. (7), an auxiliary function \(H(\xi )\) can be constructed as follows

$$\begin{aligned} H(\xi )=\left\{ {{\begin{array}{*{20}l} {\bar{{\psi }}_{2} \left( {\frac{R^{2}}{\xi }} \right) -\frac{R^{4}(\kappa _{1} -\kappa _{2} )(\xi ^{2}+1)+R^{2}(\kappa _{2} +1)(\xi ^{2}+R^{4})}{\xi (\xi ^{2}-R^{4})(\kappa _{1} +1)}{\bar{{\varphi }}}'_{2} \left( {\frac{R^{2}}{\xi }} \right) +\frac{\text{ i }a\mu \varepsilon }{R^{2}}\xi ,\quad \left| \xi \right| \leqslant R;} \\ {\frac{\kappa _{2} -\kappa _{1} }{\kappa _{1} +1}\varphi _{2} (\xi )+\frac{\kappa _{1} (\kappa _{2} +1)}{\kappa _{1} +1}\varphi _{2} \left( {\frac{\xi }{R^{2}}} \right) -\frac{\text{ i }a\mu \varepsilon R^{2}}{\xi },\quad \left| \xi \right| \geqslant R.} \\ \end{array} }} \right. \end{aligned}$$
(8)

We can see from Eqs. (7) and (8) that \(H(\xi )\) is continuous across the circle \(\left| \xi \right| =R\) and is then analytic in the whole \(\xi \)-plane except at the four points \(\xi =0,\,\xi _{0} ,\,R^{2}\xi _{0} ,\,{R^{2}} / {\bar{{\xi }}_{0} }\). By applying the generalized Liouville’s theorem, a closed-form expression for the auxiliary function \(H(\xi )\) can be obtained as follows

$$\begin{aligned} H(\xi )= & {} \frac{\text{ i }\mu (\kappa _{1} -\kappa _{2} )(b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{1} +1)(\kappa _{2} +1)}\ln (\xi -\xi _{0} )-\frac{\text{ i }\mu \kappa _{1} (\kappa _{2} +1)(b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{1} +1)(\kappa _{2} +1)}\ln (\xi -R^{2}\xi _{0} ) \nonumber \\&-\, \frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\ln \left( {\frac{R^{2}}{\xi }-\bar{{\xi }}_{0} } \right) \nonumber \\&-\, \frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )\left[ {\xi _{0} (\kappa _{1} -\kappa _{2} )(R^{2}-1)(R^{2}-\bar{{\xi }}_{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(1-\left| {\xi _{0} } \right| ^{2})} \right] }{\pi (\kappa _{1} +1)(\kappa _{2} +1)\left| {\xi _{0} } \right| ^{2}(\bar{{\xi }}_{0}^{2} -1)}\frac{1}{\xi -R^{2}\bar{{\xi }}_{0}^{-1} }.\nonumber \\ \end{aligned}$$
(9)

Remark

The auxiliary function \(H(\xi )\) defined in Eq. (8) is quite different from that for a crack in a confocal elliptical inhomogeneity in Wu and Chen [12]. In deriving Eq. (9), we have utilized the fact that the singular parts of \(\varphi _{2} (\xi )\) and \(\psi _{2} (\xi )\) at \(\xi =\xi _{0} \), denoted, respectively, by \(\varphi _{s} (\xi )\) and \(\psi _{s} (\xi )\), are given by \(\varphi _{s} (\xi )=-\frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\ln (\xi -\xi _{0} ),\,\psi _{s} (\xi )=\frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\ln (\xi -\xi _{0} )+\frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\frac{\xi _{0}^{2} (\bar{{\xi }}_{0}^{2} +1)}{\bar{{\xi }}_{0} (\xi _{0}^{2} -1)}\frac{1}{\xi -\xi _{0} }\)(see Suo [13] for more details).

Consequently, the pair of analytic functions \(\varphi _{2} (\xi )\) and \(\psi _{2} (\xi )\) can be derived from Eqs. (8) and (9) as follows

$$\begin{aligned} \varphi _{2} (\xi )= & {} -\frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\ln (\xi -\xi _{0} )+\frac{\text{ i }a\mu \varepsilon R^{2}(\kappa _{1} +1)}{\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)}\frac{1}{\xi }\nonumber \\&-\, \frac{\text{ i }\mu (\kappa _{1} +1)(b_{1} +\text{ i }b_{2} )}{\pi \kappa _{1} (\kappa _{2} +1)^{2}}\sum \limits _{n=0}^{+\infty } {M^{n}\ln \left( {\frac{1}{R^{2n}\xi }-\bar{{\xi }}_{0} } \right) } \nonumber \\&-\, \frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )\left[ {\xi _{0} (\kappa _{1} -\kappa _{2} )(R^{2}-1)(R^{2}-\bar{{\xi }}_{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(1-\left| {\xi _{0} } \right| ^{2})} \right] }{\pi \kappa _{1} (\kappa _{2} +1)^{2}R^{2}\left| {\xi _{0} } \right| ^{2}(\bar{{\xi }}_{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\xi -\bar{{\xi }}_{0}^{-1} }} , \nonumber \\ \end{aligned}$$
(10)
$$\begin{aligned} \psi _{2} (\xi )= & {} \frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\ln (\xi -\xi _{0} )+\frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\frac{\xi _{0}^{2} (\bar{{\xi }}_{0}^{2} +1)}{\bar{{\xi }}_{0} (\xi _{0}^{2} -1)}\frac{1}{\xi -\xi _{0} } \nonumber \\&+\, \frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )\left( {\begin{array}{l} (\kappa _{1} -\kappa _{2} )\left[ {\xi ^{2}(\xi _{0}^{2} -1)-\xi \xi _{0} (R^{4}+1)-(\xi _{0}^{2} +R^{4})} \right] \\ +R^{2}(\kappa _{2} +1)\left[ {\xi ^{2}(\xi _{0}^{2} -1)-2\xi _{0} \xi -(\xi _{0}^{2} +1)} \right] \\ \end{array}} \right) }{\pi R^{2}(\kappa _{1} +1)(\kappa _{2} +1)(\xi _{0}^{2} -1)(\xi ^{2}-1)} \nonumber \\&+\, \frac{\text{ i }a\mu \varepsilon \left\{ {(\kappa _{1} -\kappa _{2} )(R^{4}+1)+R^{2}(\kappa _{2} +1)\left[ {\xi ^{2}(\kappa _{1} +1)+\kappa _{1} -1} \right] } \right\} }{\xi (\xi ^{2}-1)\left[ {\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)} \right] } \nonumber \\&+\, \frac{\text{ i }\mu (\kappa _{2} -\kappa _{1} )(b_{1} -\text{ i }b_{2} )}{\pi (\kappa _{1} +1)(\kappa _{2} +1)}\ln (R^{2}\xi ^{-1}-\bar{{\xi }}_{0} )+\frac{\text{ i }\mu \kappa _{1} (\kappa _{2} +1)(b_{1} -\text{ i }b_{2} )}{\pi (\kappa _{1} +1)(\kappa _{2} +1)}\ln (\xi ^{-1}-\bar{{\xi }}_{0} ) \nonumber \\&+\, \frac{\xi (\kappa _{2} -\kappa _{1} )(\xi ^{2}+R^{4})-\xi R^{2}(\kappa _{2} +1)(\xi ^{2}+1)}{R^{2}(\xi ^{2}-1)(\kappa _{1} +1)} \nonumber \\&\times \, \left\{ {\begin{array}{l} -\frac{\text{ i }\mu (\kappa _{1} +1)(b_{1} +\text{ i }b_{2} )}{\pi \kappa _{1} (\kappa _{2} +1)^{2}}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{\xi (R^{2n}\bar{{\xi }}_{0} \xi -1)}} \\ +\frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )\left[ {\xi _{0} (\kappa _{1} -\kappa _{2} )(R^{2}-1)(R^{2}-\bar{{\xi }}_{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(1-\left| {\xi _{0} } \right| ^{2})} \right] }{\pi \kappa _{1} (\kappa _{2} +1)^{2}R^{2}\left| {\xi _{0} } \right| ^{2}(\bar{{\xi }}_{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}\xi -\bar{{\xi }}_{0}^{-1} )^{2}}} \\ \end{array}} \right\} , \end{aligned}$$
(11)

where

$$\begin{aligned} M=\frac{\kappa _{1} -\kappa _{2} }{\kappa _{1} (\kappa _{2} +1)},\quad \left| M \right| <1. \end{aligned}$$
(12)

The appearance of the series in Eqs. (10) and (11) is due to the fact that the singularities in \(H(\xi )\) can be located at points other than \(\xi =0,\,\infty \). By using D’Alembert’s ratio test, the series appearing in Eqs. (10) and (11) are found to be always convergent. By satisfying moment balance on the circular disk: \(\left| z \right| =\rho ,\,\rho \rightarrow +\infty \), the rigid-body rotation of the anticrack can be uniquely determined as

$$\begin{aligned} \varepsilon= & {} \frac{\kappa _{1} (R^{2}-M)}{\pi a(\kappa _{1} +1)(\kappa _{2} +1)}\left[ {\frac{(R^{2}-1)^{2}(\kappa _{1} -\kappa _{2} )}{R^{4}(\kappa _{1} +1)}-\frac{(\xi _{0} -\bar{{\xi }}_{0} )^{2}}{R^{2}\left| {\xi _{0} } \right| ^{2}}} \right] \text{ Re }\left\{ {\frac{\xi _{0} (b_{1} +\text{ i }b_{2} )}{\xi _{0}^{2} -1}} \right\} \nonumber \\&+\, \frac{\kappa _{1} (R^{2}-M)\left[ {\kappa _{1} (\kappa _{2} +1)+R^{2}(\kappa _{2} -\kappa _{1} )} \right] }{\pi aR^{2}(\kappa _{1} +1)^{2}(\kappa _{2} +1)} \text{ Re }\left\{ {\xi _{0}^{-1} (b_{1} +\text{ i }b_{2} )} \right\} \nonumber \\&-\frac{\kappa _{1} -\kappa _{2} +R^{2}(\kappa _{2} +1)}{\pi aR^{2}(\kappa _{1} +1)(\kappa _{2} +1)^{2}}\text{ Re }\left\{ {\bar{{\xi }}_{0}^{-1} (b_{1} +\text{ i }b_{2} )} \right\} \nonumber \\&+\, \frac{\kappa _{1} -\kappa _{2} +R^{2}(\kappa _{2} +1)}{\pi aR^{4}\left| {\xi _{0} } \right| ^{2}(\kappa _{1} +1)^{2}(\kappa _{2} +1)^{2}}\nonumber \\&\times \mathrm{Re} \left\{ {\frac{(b_{1} +\text{ i }b_{2} )\left[ {\bar{{\xi }}_{0} (\kappa _{1} -\kappa _{2} )(R^{2}-1)(R^{2}-\xi _{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(\left| {\xi _{0} } \right| ^{2}-1)} \right] }{\xi _{0}^{2} -1}} \right\} . \end{aligned}$$
(13)

Although both \(\varphi _{2} (\xi )\) and \(\psi _{2} (\xi )\) contain series, the rigid-body rotation of the anticrack in Eq. (13) is in closed-form. When the edge dislocation is located on the\(x_{1} \)-axis with \(\xi _{0} =\bar{{\xi }}_{0} \), the rigid-body rotation in Eq. (13) becomes

$$\begin{aligned} \varepsilon =\frac{(\kappa _{1} -\kappa _{2} )(R^{2}-1)^{2}}{\pi aR^{2}(\kappa _{1} +1)(\kappa _{2} +1)}\frac{b_{1} }{\xi _{0} (\xi _{0}^{2} -1)}+\frac{\kappa _{2} -1}{\pi a(\kappa _{2} +1)}\frac{b_{1} }{\xi _{0} }. \end{aligned}$$
(14)

It is deduced from Eq. (14) that \(\varepsilon =0\) when the edge dislocation is located at

$$\begin{aligned} \xi _{0} =\pm \sqrt{1+\frac{(\kappa _{2} -\kappa _{1} )(R-R^{-1})^{2}}{(\kappa _{1} +1)(\kappa _{2} -1)}} ,\quad \kappa _{2} >\kappa _{1} \geqslant 1. \end{aligned}$$
(15)

When \(\kappa _{1} =\kappa _{2} =\kappa \), Eq. (13) becomes

$$\begin{aligned} \varepsilon =\frac{1}{a\pi }\text{ Re }\left\{ {\left[ {\frac{2\bar{{\xi }}_{0} -\xi _{0} (\xi _{0}^{2} +\bar{{\xi }}_{0}^{2} )}{(\kappa +1)\left| {\xi _{0} } \right| ^{2}(\xi _{0}^{2} -1)}+\frac{1}{\xi _{0} }} \right] (b_{1} +\text{ i }b_{2} )} \right\} . \end{aligned}$$
(16)

Furthermore, when the edge dislocation is located on the \(x_{1}\)-axis, Eq. (16) reduces to

$$\begin{aligned} \varepsilon =\frac{b_{1} (\kappa -1)}{\pi a\xi _{0} (\kappa +1)}, \end{aligned}$$
(17)

which is simply the classical result by Dundurs and Markenscoff [7].

Using the relationships in Eqs. (5) and (6), the pair of analytic functions \(\varphi _{1} (\xi )\) and \(\psi _{1} (\xi )\) can be further developed to the form

$$\begin{aligned} \varphi _{1} (\xi )= & {} -\frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{1} +1)}\ln (\xi -\xi _{0} )+\frac{\text{ i }a\mu \varepsilon R^{2}(\kappa _{2} +1)}{\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)}\frac{1}{\xi }-\frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi \kappa _{1} (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {M^{n}\ln \left( {\frac{1}{R^{2n}\xi }-\bar{{\xi }}_{0} } \right) } \nonumber \\&-\, \frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )\left[ {\xi _{0} (\kappa _{1} -\kappa _{2} )(R^{2}-1)(R^{2}-\bar{{\xi }}_{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(1-\left| {\xi _{0} } \right| ^{2})} \right] }{\pi \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\left| {\xi _{0} } \right| ^{2}(\bar{{\xi }}_{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\xi -\bar{{\xi }}_{0}^{-1} }} , \nonumber \\\end{aligned}$$
(18)
$$\begin{aligned} \psi _{1} (\xi )= & {} \frac{\text{ i }\kappa _{1} \mu (b_{1} -\text{ i }b_{2} )}{\pi (\kappa _{1} +1)}\ln (\xi ^{-1}-\bar{{\xi }}_{0} )+\frac{\text{ i }a\mu \varepsilon (\kappa _{2} -\kappa _{1} )\xi }{\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)}+\frac{\text{ i }a\mu \varepsilon }{\xi }+\frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )}{\pi (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {M^{n}\ln (\xi -R^{2n}\xi _{0} )} \nonumber \\&+\, \frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )\left[ {\bar{{\xi }}_{0} (\kappa _{1} -\kappa _{2} )(R^{2}-1)(R^{2}-\xi _{0}^{2} )+R^{2}(\kappa _{1} +1)(\bar{{\xi }}_{0} -\xi _{0} )(1-\left| {\xi _{0} } \right| ^{2})} \right] }{\pi (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\left| {\xi _{0} } \right| ^{2}(\xi _{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\xi ^{-1}-\xi _{0}^{-1} }} \nonumber \\&+\, \frac{\xi (\xi ^{2}+1)}{\xi ^{2}-1}\left\{ {\begin{array}{l} \frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi (\kappa _{1} +1)}\frac{1}{\xi -\xi _{0} }+\frac{\text{ i }a\mu \varepsilon R^{2}(\kappa _{2} +1)}{\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)}\frac{1}{\xi ^{2}}+\frac{\text{ i }\mu (b_{1} +\text{ i }b_{2} )}{\pi \kappa _{1} (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{\xi (R^{2n}\bar{{\xi }}_{0} \xi -1)}} \\ +\frac{\text{ i }\mu (b_{1} -\text{ i }b_{2} )\left[ {\xi _{0} (\kappa _{2} -\kappa _{1} )(R^{2}-1)(R^{2}-\bar{{\xi }}_{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(\left| {\xi _{0} } \right| ^{2}-1)} \right] }{\pi \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\left| {\xi _{0} } \right| ^{2}(\bar{{\xi }}_{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}\xi -\bar{{\xi }}_{0}^{-1} )^{2}}} \\ \end{array}} \right\} .\nonumber \\ \end{aligned}$$
(19)

The singular stress field near the right tip of the anticrack can be extracted from the full-field solution derived in Eqs. (18) and (19) as follows

$$\begin{aligned} \sigma _{11}= & {} \frac{S_{\mathrm{I}} }{\sqrt{2\pi r} (1-\kappa _{1} )}\left[ {(3+\kappa _{1} )\cos \frac{\theta }{2}-\sin \theta \sin \frac{3\theta }{2}} \right] \nonumber \\&-\, \frac{S_{\mathrm{II}} }{\sqrt{2\pi r} (1-\kappa _{1} )}\left[ {(3-\kappa _{1} )\sin \frac{\theta }{2}+\sin \theta \cos \frac{3\theta }{2}} \right] , \nonumber \\ \sigma _{22}= & {} \frac{S_{\mathrm{I}} }{\sqrt{2\pi r} (1-\kappa _{1} )}\left[ {(1-\kappa _{1} )\cos \frac{\theta }{2}+\sin \theta \sin \frac{3\theta }{2}} \right] \nonumber \\&+\, \frac{S_{\mathrm{II}} }{\sqrt{2\pi r} (1-\kappa _{1} )}\left[ {-(1+\kappa _{1} )\sin \frac{\theta }{2}+\sin \theta \cos \frac{3\theta }{2}} \right] , \nonumber \\ \sigma _{12}= & {} \frac{S_{\mathrm{I}} }{\sqrt{2\pi r} (1-\kappa _{1} )}\left[ {(1+\kappa _{1} )\sin \frac{\theta }{2}+\sin \theta \cos \frac{3\theta }{2}} \right] \nonumber \\&+\frac{S_{\mathrm{II}} }{\sqrt{2\pi r} (1-\kappa _{1} )}\left[ {(1-\kappa _{1} )\cos \frac{\theta }{2}-\sin \theta \sin \frac{3\theta }{2}} \right] , \end{aligned}$$
(20)

where \(z-a=r\text{ e}^{\text{ i }\theta }\) with r and \(\theta \) being the usual local polar coordinates, and \(S_{\mathrm{I}} \) and \(S_{\mathrm{II}} \) are, respectively, the mode I and mode II stress intensity factors determined explicitly as

$$\begin{aligned}&S_{\mathrm{I}} -\text{ i }S_{\mathrm{II}} =(1-\kappa _{1} )\sqrt{\frac{\pi }{a}} {\varphi }'_{1} (1) \nonumber \\&\quad =\frac{\text{ i }\mu (\kappa _{1} -1)(b_{1} +\text{ i }b_{2} )}{\sqrt{\pi a} (\kappa _{1} +1)}\frac{1}{1-\xi _{0} }+\frac{\text{ i }\sqrt{\pi a} \mu \varepsilon R^{2}(\kappa _{1} -1)(\kappa _{2} +1)}{\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)}+\frac{\text{ i }\mu (\kappa _{1} -1)(b_{1} +\text{ i }b_{2} )}{\sqrt{\pi a} \kappa _{1} (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\bar{{\xi }}_{0} -1}} \nonumber \\&\qquad +\, \frac{\text{ i }\mu (\kappa _{1} -1)(b_{1} -\text{ i }b_{2} )\left[ {\xi _{0} (\kappa _{2} -\kappa _{1} )(R^{2}-1)(R^{2}-\bar{{\xi }}_{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(\left| {\xi _{0} } \right| ^{2}-1)} \right] }{\sqrt{\pi a} \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\left| {\xi _{0} } \right| ^{2}(\bar{{\xi }}_{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}-\bar{{\xi }}_{0}^{-1} )^{2}}} .\nonumber \\ \end{aligned}$$
(21)

The derivation of Eqs. (20) and (21) can be found in Appendix B. When the edge dislocation lies on the \(x_{1} \)-axis with \(\xi _{0} =\bar{{\xi }}_{0} \), we have from Eq. (22) that

$$\begin{aligned} S_{\mathrm{I}}= & {} \frac{b_{2} \mu (\kappa _{1} -1)}{\sqrt{\pi a} (\kappa _{1} +1)}\frac{1}{\xi _{0} -1}-\frac{b_{2} \mu (\kappa _{1} -1)}{\sqrt{\pi a} \kappa _{1} (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\xi _{0} -1}} \nonumber \\&+\, \frac{b_{2} \mu (\kappa _{1} -1)(\kappa _{2} -\kappa _{1} )(R^{2}-1)(R^{2}-\xi _{0}^{2} )}{\sqrt{\pi a} \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\xi _{0} (\xi _{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}-\xi _{0}^{-1} )^{2}}} , \nonumber \\ S_{\mathrm{II}}= & {} \frac{b_{1} \mu (\kappa _{1} -1)}{\sqrt{\pi a} (\kappa _{1} +1)}\frac{1}{\xi _{0} -1}-\frac{b_{1} \mu (\kappa _{1} -1)}{\sqrt{\pi a} \left[ {\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)} \right] \xi _{0} }\left[ {\frac{(\kappa _{1} -\kappa _{2} )(R^{2}-1)^{2}}{(\kappa _{1} +1)(\xi _{0}^{2} -1)}+R^{2}(\kappa _{2} -1)} \right] \nonumber \\&-\, \frac{b_{1} \mu (\kappa _{1} -1)}{\sqrt{\pi a} \kappa _{1} (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\xi _{0} -1}} -\frac{b_{1} \mu (\kappa _{1} -1)(\kappa _{2} -\kappa _{1} )(R^{2}-1)(R^{2}-\xi _{0}^{2} )}{\sqrt{\pi a} \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\xi _{0} (\xi _{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}-\xi _{0}^{-1} )^{2}}} .\nonumber \\ \end{aligned}$$
(22)

Furthermore, when \(\kappa _{1} =\kappa _{2} =\kappa \), Eq. (22) reduces to

$$\begin{aligned} S_{\mathrm{I}} =\frac{b_{2} \mu (\kappa -1)^{2}}{\sqrt{\pi a} \kappa (\kappa +1)}\frac{1}{\xi _{0} -1},\quad S_{\mathrm{II}} =\frac{b_{1} \mu (\kappa -1)^{2}}{\sqrt{\pi a} \kappa (\kappa +1)}\frac{1}{\xi _{0} (\xi _{0} -1)}. \end{aligned}$$
(23)

In a similar manner, the mode I and mode II stress intensity factors at the left anticrack tip can be determined as

$$\begin{aligned} S_{\mathrm{I}} -\text{ i }S_{\mathrm{II}}= & {} (1-\kappa _{1} )\sqrt{\frac{\pi }{a}} {\varphi }'_{1} (-1) \nonumber \\= & {} -\frac{\text{ i }\mu (\kappa _{1} -1)(b_{1} +\text{ i }b_{2} )}{\sqrt{\pi a} (\kappa _{1} +1)}\frac{1}{\xi _{0} +1}+\frac{\text{ i }\sqrt{\pi a} \mu \varepsilon R^{2}(\kappa _{1} -1)(\kappa _{2} +1)}{\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)}+\frac{\text{ i }\mu (\kappa _{1} -1)(b_{1} +\text{ i }b_{2} )}{\sqrt{\pi a} \kappa _{1} (\kappa _{2} +1)}\nonumber \\&\times \sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\bar{{\xi }}_{0} +1}} \nonumber \\&+\, \frac{\text{ i }\mu (\kappa _{1} -1)(b_{1} -\text{ i }b_{2} )\left[ {\xi _{0} (\kappa _{2} -\kappa _{1} )(R^{2}-1)(R^{2}-\bar{{\xi }}_{0}^{2} )+R^{2}(\kappa _{1} +1)(\xi _{0} -\bar{{\xi }}_{0} )(\left| {\xi _{0} } \right| ^{2}-1)} \right] }{\sqrt{\pi a} \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\left| {\xi _{0} } \right| ^{2}(\bar{{\xi }}_{0}^{2} -1)}\nonumber \\&\times \sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}+\bar{{\xi }}_{0}^{-1} )^{2}}} . \end{aligned}$$
(24)

When the edge dislocation lies on the \(x_{1} \)-axis, Eq. (24) becomes

$$\begin{aligned} S_{\mathrm{I}}= & {} \frac{b_{2} \mu (\kappa _{1} -1)}{\sqrt{\pi a} (\kappa _{1} +1)}\frac{1}{\xi _{0} +1}-\frac{b_{2} \mu (\kappa _{1} -1)}{\sqrt{\pi a} \kappa _{1} (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\xi _{0} +1}} \nonumber \\&+\, \frac{b_{2} \mu (\kappa _{1} -1)(\kappa _{2} -\kappa _{1} )(R^{2}-1)(R^{2}-\xi _{0}^{2} )}{\sqrt{\pi a} \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\xi _{0} (\xi _{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}+\xi _{0}^{-1} )^{2}}} , \nonumber \\ S_{\mathrm{II}}= & {} \frac{b_{1} \mu (\kappa _{1} -1)}{\sqrt{\pi a} (\kappa _{1} +1)}\frac{1}{\xi _{0} +1}-\frac{b_{1} \mu (\kappa _{1} -1)}{\sqrt{\pi a} \left[ {\kappa _{2} -\kappa _{1} +R^{2}\kappa _{1} (\kappa _{2} +1)} \right] \xi _{0} }\left[ {\frac{(\kappa _{1} -\kappa _{2} )(R^{2}-1)^{2}}{(\kappa _{1} +1)(\xi _{0}^{2} -1)}+R^{2}(\kappa _{2} -1)} \right] \nonumber \\&-\, \frac{b_{1} \mu (\kappa _{1} -1)}{\sqrt{\pi a} \kappa _{1} (\kappa _{2} +1)}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{R^{2n}\xi _{0} +1}} -\frac{b_{1} \mu (\kappa _{1} -1)(\kappa _{2} -\kappa _{1} )(R^{2}-1)(R^{2}-\xi _{0}^{2} )}{\sqrt{\pi a} \kappa _{1} (\kappa _{1} +1)(\kappa _{2} +1)R^{2}\xi _{0} (\xi _{0}^{2} -1)}\sum \limits _{n=0}^{+\infty } {\frac{R^{2n}M^{n}}{(R^{2n}+\xi _{0}^{-1} )^{2}}} .\nonumber \\ \end{aligned}$$
(25)

Furthermore, when \(\kappa _{1} =\kappa _{2} =\kappa \), Eq. (25) reduces to

$$\begin{aligned} S_{\mathrm{I}} =\frac{b_{2} \mu (\kappa -1)^{2}}{\sqrt{\pi a} \kappa (\kappa +1)}\frac{1}{\xi _{0} +1},\quad S_{\mathrm{II}} =-\frac{b_{1} \mu (\kappa -1)^{2}}{\sqrt{\pi a} \kappa (\kappa +1)}\frac{1}{\xi _{0} (\xi _{0} +1)}. \end{aligned}$$
(26)

It is verified that Eqs. (23) and (26) can also be extracted from the full-field expression of the stresses along the entire \(x_{1} \)-axis given in Dundurs and Markenscoff [7].

We see from the asymptotic singular stress field in Eq. (20) that the definition of \(S_{\mathrm{I}} \) is in complete agreement with that introduced by Wang et al. [9] for a rigid line inhomogeneity as opposed to the definition of \(S_{\mathrm{II}} \) which is quite different. In the discussion by Wang et al. [9], mode I and mode II deformations are in fact identical after excluding the pre-factors. The present mode II deformation has not been identified by Wang et al. [9] mainly because they considered only uniform stresses at infinity, and, as a result, the actual mode II deformation observed here is not excited by the uniform remote loading.

The driving force on either the right or the left anticrack tip, denoted by J, can be determined as [4]

$$\begin{aligned} J=-\frac{\kappa _{1} (1+\kappa _{1} )}{2\mu (1-\kappa _{1} )^{2}}(S_{\mathrm{I}}^{2} +S_{\mathrm{II}}^{2} ). \end{aligned}$$
(27)

As a result of the geometry, the right anticrack tip tends to contract toward the left while the left anticrack tip tends to contract toward the right. Using the Peach–Koehler formula [14] or evaluating of the J integrals around the center of the edge dislocation [15], the image force acting on the edge dislocation can also be obtained (we omit its rather lengthy expression). Here, we point out that the image force gives a quantitative description of changes in the interaction energy [14, 16].

It follows from Eqs. (23), (26) and (27) that when \(\kappa _{1} =\kappa _{2} =\kappa \) and the dislocation lies on the \(x_{1} \)-axis, the \(x_{1} \) component of the image force acting on the edge dislocation, denoted as \(F_{1} \), which is equal to the driving force on the left anticrack tip minus that on the right anticrack tip, is given by

$$\begin{aligned} F_{1} =\frac{2\mu (\kappa -1)^{2}(b_{1}^{2} +\xi _{0}^{2} b_{2}^{2} )}{\pi a\kappa (\kappa +1)\xi _{0} (\xi _{0}^{2} -1)^{2}}, \end{aligned}$$
(28)

which is found to be consistent with the result in Dundurs and Markenscoff [7].

4 Conclusions

We have presented an analytical solution of the interaction problem associated with an edge dislocation in the vicinity of a confocally coated anticrack. An auxiliary function defined in the whole image plane is constructed in Eq. (8) with its closed-form representation given by Eq. (9) following an application of the generalized Liouville’s theorem. Subsequently, the two pairs of analytic functions \(\varphi _{i} (\xi ),\,\psi _{i} (\xi )\,\, (i=1,2)\) are given by Eqs. (10), (11), (18) and (19). A closed-form expression of the rigid-body rotation of the anticrack is given by Eq. (13). The singular stress field near the two anticrack tips is completely governed by two stress intensity factors \(S_{\mathrm{I}} \) and \(S_{\mathrm{II}} \) which are explicitly determined by Eq. (21) at the right tip and Eq. (24) at the left tip. The rationales for the introduced stress intensity factors and the driving force on the two anticrack tips are demonstrated through the indirect determination of the image force on the edge dislocation in Eq. (28).

When the coating and matrix have distinct shear moduli, the two pairs of complex potentials \(\varphi _{i} (\xi ),\,\psi _{i} (\xi ) \,\, (i=1,\,2)\) must be expanded in standard Laurent series. The coefficients in the Laurent series together with the rigid-body rotation of the anticrack would then be determined through the solution of a coupled set of an infinite number of linear algebraic equations.