1 Introduction

The interaction of dislocations with elastic inhomogeneities has attracted the attention of theoreticians and practitioners alike (see, for example, [3–7, 12, 19, 23–25]). The inhomogeneity–matrix interface remains a critical focus point in the analysis of the dislocation–inhomogeneity interaction problem. In an effort to allow tractability of the ensuing mathematical models, early studies assumed an idealized model of the interface, for example, perfectly bonded [5, 6] or sliding [4]. In an effort to more accurately model the influence of the interface, in particular to account for interface damage (for example, debonding, sliding and/or micro-cracking across the interface), the linear spring model has been introduced into the dislocation–inhomogeneity interaction problem [7, 19, 23]. This more comprehensive interface model is based on the assumption that tractions are continuous, but displacements are discontinuous across the interface. More precisely, jumps in the displacement components are proportional to their respective interface traction components in terms of ‘spring-factor-type’ interface parameters [16]. The linear spring interface model is also referred to as a ‘soft interface’ since it is particularly appropriate when modeling a soft and thin interphase layer lying between two elastic media [1]. It is well known that when composite assemblies involving elastic inhomogeneities are analyzed at much smaller length scales (for example, at the nanoscale), the increasing surface area-to-bulk volume ratio means that the effects of surface mechanics (on all surfaces involved in the assembly) play a significant role in the overall deformation of the composite [17]. One of the most commonly adopted ‘surface models’ is the continuum-based surface/interface model of Gurtin and Murdoch [9–11]. In the absence of residual surface tension, the Gurtin–Murdoch model is strictly equivalent to the membrane-type stiff interface referred to in [1, 2]. The Gurtin–Murdoch model has recently been incorporated into the study of the dislocation–inhomogeneity interaction problem [8, 13, 20]. Most recently, the current authors [21, 22] have proposed the so-called mixed-type imperfect interface model to account for the most accurate representation of possible interface damage in nanosized inhomogeneities. In this interface model, both the inhomogeneity and the matrix are endowed with separate and distinct surface elasticities and bonded through a spring-type imperfect interface. This allows for a comprehensive account of the contribution of each of the surfaces involved in the mechanical analysis.

In this paper, the mixed-type imperfect interface is incorporated into the interaction problem of an edge dislocation near a circular elastic inhomogeneity. A simple and effective method based on analytic continuation is proposed to solve the interaction problem with highly unusual and nonstandard boundary/interface conditions. The image force acting on the edge dislocation is also derived using the analytic solution obtained and the Peach–Koehler formula [3]. The size dependency of the induced stress field and the normalized image force is clearly demonstrated. The correctness of the obtained solution is carefully verified by comparison with the classical solutions of Dundurs [3] for a perfectly bonded interface and Dundurs and Gangadharan [4] for a sliding interface.

The paper is structured as follows: In Sect. 2, the bulk elasticity, the surface elasticity and the spring-type imperfect interface models are reviewed briefly for completeness. In Sect. 3, an analytic solution to the dislocation–inhomogeneity interaction problem is subsequently derived. Explicit expressions for the image force in the case of gliding and climbing dislocations are presented in Sect. 4 as well as analytic results for the long-range interaction results when the dislocation is located remotely with respect to the inhomogeneity.

2 Formulation

2.1 The bulk elasticity

In what follows, unless otherwise stated, Latin indices i, j, k take the values 1,2,3 and we sum over repeated indices. In a Cartesian coordinate system \(\left\{ {x_i } \right\} \), the equilibrium equations and the constitutive relations describing the deformation of a linearly elastic, homogeneous and isotropic bulk solid are given by

$$\begin{aligned} \sigma _{ij,j} =0,\sigma _{ij} =2\mu \varepsilon _{ij} +\lambda \varepsilon _{kk} \delta _{ij} ,\varepsilon _{ij} =\frac{1}{2}(u_{i,j} +u_{j,i} ), \end{aligned}$$
(1)

where \(\lambda \) and \(\mu \) are Lamé constants, \(\sigma _{ij} \) and \(\varepsilon _{ij} \) are, respectively, the Cartesian components of the stress and strain tensors in the bulk material, \(u_i \) is the ith component of the displacement vector, and \(\delta _{ij} \) is the Kronecker delta.

For plane strain problems, the stresses, displacements and associated stress functions \(\phi _1 ,\phi _2 \) can be expressed in terms of two analytic functions \(\varphi \)(z) and \(\psi (z)\) of the complex variable \(z=x_1 +\hbox {i}x_2 \) as [14, 18]

$$\begin{aligned} \sigma _{11} +\sigma _{22}= & {} 2\left[ {{\varphi }'(z)+\overline{{\varphi }'(z)} } \right] , \nonumber \\ \sigma _{22} -\sigma _{11} +2\hbox {i}\sigma _{12}= & {} 2\left[ {\bar{{z}}{\varphi }''(z)+{\psi }'(z)} \right] , \nonumber \\ 2\mu (u_1 +\hbox {i}u_2 )= & {} \kappa \varphi (z)-z\overline{{\varphi }'(z)} -\overline{\psi (z)} , \nonumber \\ \phi _1 +\hbox {i}\phi _2= & {} \hbox {i}\left[ {\varphi (z)+z\overline{{\varphi }'(z)} +\overline{\psi (z)} } \right] , \end{aligned}$$
(2)

where \(\kappa =3-4\nu \) in which \(\nu (0\le \nu \le 1/2)\) is Poisson’s ratio. In addition, the stresses are related to the stress functions through [18]

$$\begin{aligned} \sigma _{11}= & {} -\phi _{1,2} ,\;\sigma _{12} =\phi _{1,1} , \nonumber \\ \sigma _{21}= & {} -\phi _{2,2} ,\;\sigma _{22} =\phi _{2,1} . \end{aligned}$$
(3)

Let \(t_1 \) and \(t_2 \) be traction components along the \(x_{1}\)- and \(x_{2}\)-directions, respectively, on a boundary L. If s is the arc length measured along L such that, when facing the direction of increasing s, the material remains on the left-hand side, and it can be shown that [18]

$$\begin{aligned} t_1 +\hbox {i}t_2 =-\frac{\mathrm{d}(\phi _1 +\hbox {i}\phi _2 )}{\mathrm{d}s}. \end{aligned}$$
(4)

2.2 The Gurtin–Murdoch surface elasticity

The equilibrium conditions on a surface incorporating interface/surface elasticity according to the Gurtin–Murdoch theory can be expressed as [9–11, 15]:

$$\begin{aligned}&{[}\sigma _{\alpha j} n_j \underline{e}_\alpha ]+\sigma _{\alpha \beta ,\beta }^\mathrm{s} \underline{e}_\alpha =0,\;(\hbox {tangential direction}) \nonumber \\&{[}\sigma _{ij} n_{i} n_{j} ]=\sigma _{\alpha \beta }^{s} \kappa _{\alpha \beta } ,\quad (\hbox {normal direction}) \end{aligned}$$
(5)

where \(n_{i}\) is the ith component of the outward unit normal vector to the surface, \([{*}]\) denotes the jump across the surface, and \(\sigma _{\alpha \beta }^\mathrm{s} \) and \(\kappa _{\alpha \beta } \) are the components of the surface stress tensor and the surface curvature tensor, respectively. In addition, the constitutive equations on the isotropic surface are given by

$$\begin{aligned} \sigma _{\alpha \beta }^\mathrm{s} =\sigma _0 \delta _{\alpha \beta } +2(\mu _s -\sigma _0 )\varepsilon _{\alpha \beta }^\mathrm{s} +(\lambda _s +\sigma _0 )\varepsilon _{\gamma \gamma }^\mathrm{s} \delta _{\alpha \beta } , \end{aligned}$$
(6)

where \(\varepsilon _{\alpha \beta }^\mathrm{s} \) are the components of the surface strain tensor, \(\sigma _0 \) is the surface tension, and \(\lambda _s \) and \(\mu _s \) are the two surface Lamé constants.

We mention that in Eqs. (5) and (6), the Greek indices \(\alpha \), \(\beta \) and \(\gamma \) take on values of the surface components. For example, in the case of circular cylindrical fibers, \(\alpha \), \(\beta \), \(\gamma \) each takes on the values \(\theta \), z.

2.3 The spring-type imperfect interface

Denote by \(u_r \) and \(u_\theta \) the respective components of the displacement vector, normal and tangential to the inhomogeneity–matrix interface L and \(\sigma _{rr} \),\(\sigma _{r\theta } \) the normal and shear components, respectively, of the traction along the interface L. The interface conditions on the spring-type imperfect interface are [1].

$$\begin{aligned}{}[\sigma _{rr} +\hbox {i}\sigma _{r\theta } ]=0,\sigma _{rr} =k_r [u_r ],\hbox { }\sigma _{r\theta } =k_\theta [u_\theta ], \quad \hbox { on }\quad L, \end{aligned}$$
(7)

where \(k_r \) and \(k_\theta \) are two nonnegative interface parameters and \([{*}]=[{*}]_M -[{*}]_I \) denotes the jump across L (with subscripts ‘M’ and ‘I’ denoting the matrix and inhomogeneity, respectively).

3 An edge dislocation near a circular inhomogeneity with a mixed-type imperfect interface

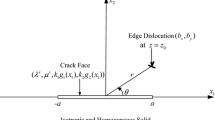
Consider a domain in \(\mathfrak {R}^{2}\), infinite in extent, containing a single circular elastic inhomogeneity with elastic properties different from those of the surrounding matrix, as shown in Fig. 1. The inhomogeneity, with its center at the origin of the coordinate system and radius R, occupies a region denoted by \(S_1 \). The matrix occupies the region \(S_2\), and the inhomogeneity–matrix interface is represented by the curve L. In what follows, the subscripts 1 and 2 [or the superscripts (1) and (2)] are used to identify the respective quantities in \(S_1 \) and \(S_2 \). Separate surface elasticities are simultaneously incorporated into the surface of the inhomogeneity and into that of the matrix. In addition, the two phases are bonded through a spring-type imperfect interface as described above. An edge dislocation with Burgers vector \((b_1 ,b_2 )\) is located at \((\xi ,0)\) on the \(x_1 \)-axis in the matrix. The composite remains free from any other external loading.

Fig. 1
figure 1

An edge dislocation near a circular inhomogeneity with a mixed-type imperfect interface

Full size image

If we assume that the interface L is coherent (i.e., \(\varepsilon _{\alpha \beta }^\mathrm{s} =\varepsilon _{\alpha \beta } )\) with respect to either the inhomogeneity or the matrix, it follows from Eqs. (5) and (6) that the boundary conditions on the surfaces of the circular inhomogeneity and the surrounding matrix can be written in the form

$$\begin{aligned} (\sigma _{rr}^{(1)} +\hbox {i}\sigma _{r\theta }^{(1)} )-(\sigma _{rr}^- +\hbox {i}\sigma _{r\theta }^- )=-\frac{\sigma _0^{(1)} }{R}+\frac{J_0^{(1)} }{R^{2}}\left[ {\hbox {i}\frac{\partial ^\mathrm{2}u_\theta ^{(1)} }{\partial \theta ^{2}}+\hbox {i}\frac{\partial \hbox {(}u_r^{(1)} +\hbox {i}u_\theta ^{(1)} )}{\partial \theta }-u_r^{(1)} } \right] ,\nonumber \\ \hbox {on the surface of the inhomogeneity}, \end{aligned}$$
(8)
$$\begin{aligned} (\sigma _{rr}^+ +\hbox {i}\sigma _{r\theta }^+ )-(\sigma _{rr}^{(2)} +\hbox {i}\sigma _{r\theta }^{(2)} )=-\frac{\sigma _0^{(2)} }{R}+\frac{J_0^{(2)} }{R^{2}}\left[ {\hbox {i}\frac{\partial ^\mathrm{2}u_\theta ^{(2)} }{\partial \theta ^{2}}+\hbox {i}\frac{\partial \hbox {(}u_r^{(2)} +\hbox {i}u_\theta ^{(2)} )}{\partial \theta }-u_r^{(2)} } \right] ,\nonumber \\ \hbox {on the surface of the matrix,} \end{aligned}$$
(9)

where \(J_0^{(j)} =2\mu _s^{(j)} +\lambda _s^{(j)} -\sigma _0^{(j)} \ge 0,j=1,2\), and

$$\begin{aligned} \sigma _{rr}^- +\hbox {i}\sigma _{r\theta }^-= & {} \sigma _{rr}^+ +\hbox {i}\sigma _{r\theta }^+ =\frac{k_r +k_\theta }{2}\left[ {\hbox {(}u_r^{(2)} +\hbox {i}u_\theta ^{(2)} )-\hbox {(}u_r^{(1)} +\hbox {i}u_\theta ^{(1)} )} \right] \nonumber \\&+\frac{k_r -k_\theta }{2}\left[ {\hbox {(}u_r^{(2)} -\hbox {i}u_\theta ^{(2)} )-\hbox {(}u_r^{(1)} -\hbox {i}u_\theta ^{(1)} )} \right] , \end{aligned}$$
(10)

According to Eq. (7), Eqs. (8)–(10) describe a mixed-type imperfect interface under inplane deformations. The imperfect interface model in Eqs. (8)–(10) contains six nonnegative imperfect interface parameters \(J_0^{(1)} ,\hbox { }J_0^{(2)} ,\hbox { }\sigma _0^{(1)} ,\hbox { }\sigma _0^{(2)} ,\hbox { }k_r ,\hbox { }k_\theta \). In order to solve the boundary value problem, we introduce the following analytical continuations:

$$\begin{aligned} \varphi _1 (z)=-z{\bar{{\varphi }}}'_1 ({R^{2}}/z)-\bar{{\psi }}_1 ({R^{2}}/z),\quad \left| z \right| >R,\nonumber \\ \varphi _2 (z)=-z{\bar{{\varphi }}}'_2 ({R^{2}}/z)-\bar{{\psi }}_2 ({R^{2}}/z),\quad \left| z \right| <R. \end{aligned}$$
(11)

Consequently, the boundary conditions in Eqs. (8)–(10) can be concisely expressed in terms of \(\varphi _1 (z),\hbox { }\varphi _2 (z)\) and their analytic continuations are as follows

$$\begin{aligned}&\begin{array}{l} {\varphi '}_{1}^{+} (z)-{\varphi '}_{1}^{-} (z)-\frac{k_r +k_\theta }{4}\left[ {\frac{R}{\mu _2 }\left( {\kappa _2 z^{-1}\varphi _2^- (z)+z^{-1}\varphi _2^+ (z)} \right) -\frac{R}{\mu _1 }\left( {\kappa _1 z^{-1}\varphi _1^+ (z)+z^{-1}\varphi _1^- (z)} \right) } \right] \\ -\frac{k_r -k_\theta }{4}\left[ {\frac{R^{-1}}{\mu _2 }\left( {\kappa _2 z\bar{{\varphi }}_2^+ ({R^{2}}/z)+z\bar{{\varphi }}_2^- ({R^{2}}/z)} \right) -\frac{R^{-1}}{\mu _1 }\left( {\kappa _1 z\bar{{\varphi }}_1^- ({R^{2}}/z)+z\bar{{\varphi }}_1^+ ({R^{2}}/z)} \right) } \right] \\ = -\,\frac{\sigma _0^{(1)} }{R} +\frac{J_0^{(1)} }{2R\mu _1 } \left( {\begin{array}{l} -\hbox {i}\hbox {Im}\left\{ {\kappa _{1} z^{-1}\varphi _{1}^{+} (z)-\kappa _1 {\varphi '}_{1}^{+} (z)+\kappa _{1} z{\varphi ''}_{1}^{+} (z)+{z^{-1}}{\varphi _{1}^{-}} (z)-{{\varphi }_{1}^{'-}} (z)+z{\varphi ''}_{1}^{-} (z)} \right\} \\ +\kappa _{1} z^{-1}\varphi _{1}^{+} (z)-\kappa _1 {{\varphi }_{1}^{'+}} (z)+z^{-1}\varphi _{1}^{-} (z)-{\varphi }_{1}^{'-} (z)-\hbox {Re}\left\{ {\kappa _1 z^{-1}\varphi _1^+ (z)+z^{-1}\varphi _{1}^{-} (z)} \right\} \\ \end{array}} \right) , \\ \end{array} \quad \left| z \right| =R, \end{aligned}$$
(12)
$$\begin{aligned}&\begin{array}{l} {\varphi }_{2}^{'+} (z)-{\varphi }_{2}^{'-} (z)+\frac{k_r +k_\theta }{4}\left[ {\frac{R}{\mu _2 }\left( {\kappa _2 z^{-1}\varphi _2^- (z)+z^{-1}\varphi _2^+ (z)} \right) -\frac{R}{\mu _1 }\left( {\kappa _1 z^{-1}\varphi _1^+ (z)+z^{-1}\varphi _1^- (z)} \right) } \right] \\ +\frac{k_r -k_\theta }{4}\left[ {\frac{R^{-1}}{\mu _2 }\left( {\kappa _2 z\bar{{\varphi }}_2^+ ({R^{2}}/z)+z\bar{{\varphi }}_2^- ({R^{2}}/z)} \right) -\frac{R^{-1}}{\mu _1 }\left( {\kappa _1 z\bar{{\varphi }}_1^- ({R^{2}}/z)+z\bar{{\varphi }}_1^+ ({R^{2}}/z)} \right) } \right] \\ = -\,\frac{\sigma _0^{(2)} }{R}+\frac{J_0^{(2)} }{2R\mu _2 }\left( {\begin{array}{l} -\hbox {i}\hbox {Im}\left\{ {\kappa _2 z^{-1}\varphi _2^- (z)-\kappa _2 {\varphi }_{2}^{'-} (z)+\kappa _2 z{\varphi }_2^{''-} (z)+z^{-1}\varphi _2^+ (z)-{\varphi }_{2}^{'+} (z)+z{\varphi }_2^{''+} (z)} \right\} \\ +\kappa _2 z^{-1}\varphi _2^- (z)-\kappa _2 {{\varphi }_{2}^{'-}} (z)+z^{-1}\varphi _2^+ (z)-{\varphi }_{2}^{'+} (z)-\mathrm{Re}\left\{ {\kappa _2 z^{-1}\varphi _2^- (z)+z^{-1}\varphi _2^+ (z)} \right\} \\ \end{array}} \right) , \\ \end{array} \quad \left| z \right| =R,\nonumber \\ \end{aligned}$$
(13)

where the superscripts ‘+’ and ‘−’ denote limiting values as we approach the interface L from either the inside or outside, respectively.

The two analytic functions \(\varphi _1 (z),\hbox { }\varphi _2 (z)\) and their analytic continuations can be written in terms of the following convergent series:

$$\begin{aligned} \begin{array}{l} \varphi _1 (z)=\left\{ {{\begin{array}{l} {\sum _{n=0}^{+\infty } {X_n R^{-n}z^{n}},\quad \hbox { }\left| z \right|<R,} \\ {-\bar{{X}}_1 R^{-1}z+\sum _{n=0}^{+\infty } {Y_n R^{n}z^{-n}} ,\quad \left| z \right|>R,} \\ \end{array} }} \right. \\ \varphi _2 (z)=\left\{ {{\begin{array}{l} {-A\ln \frac{z-{R^{2}}/\xi }{z}+\frac{R^{2}(R^{2}-\xi ^{2})}{\xi ^{3}}\frac{\bar{{A}}}{z-{R^{2}}/\xi }+\sum _{n=0}^{+\infty } {B_n R^{-n}z^{n}} ,\quad \left| z \right| <R,} \\ {A\ln (z-\xi )+\sum _{n=0}^{+\infty } {A_n R^{n}z^{-n}} ,\quad \left| z \right| >R,} \\ \end{array} }} \right. \\ \end{array} \end{aligned}$$
(14)

where \(X_n ,Y_n ,A_n ,B_n ,n=0,1,2,\ldots ,+\infty \) are unknown complex coefficients to be determined and

$$\begin{aligned} A=\frac{\mu _2 (b_2 -\hbox {i}b_1 )}{\pi (\kappa _2 +1)}. \end{aligned}$$
(15)

Substituting Eq. (14) into the boundary conditions in Eqs. (12) and (13), and equating coefficients of like-powers of \(z=R\hbox {e}^{\hbox {i}\theta }\), we finally arrive at the following sets of linear algebraic equations

$$\begin{aligned}&\left[ {2+\rho (\kappa _1 -1)+\chi (\kappa _1 +1)+\gamma _1 (\kappa _1 -1)} \right] X_1 +\left[ {2+\rho (\kappa _1 -1)-\chi (1+\kappa _1 )+\gamma _1 (\kappa _1 -1)} \right] \bar{{X}}_1 \nonumber \\&\qquad -\Gamma (\rho +\chi )B_1 -\Gamma (\rho -\chi )\bar{{B}}_1 =-4R\delta _1 \mu _1 +\Gamma \kappa _2 (\rho +\chi )E_1 +\Gamma \kappa _2 (\rho -\chi )\bar{{E}}_1 , \nonumber \\&\left[ {\rho (1-\kappa _1 )-\chi (1+\kappa _1 )} \right] X_1 +\left[ {\rho (1-\kappa _1 )+\chi (1+\kappa _1 )} \right] \bar{{X}}_1 \nonumber \\&\qquad +\left[ {2+\Gamma (\rho +\chi )+\gamma _2 } \right] B_1 +\left[ {\Gamma (\rho -\chi )+\gamma _2 } \right] \bar{{B}}_1 \nonumber \\&\quad =-4R\delta _2 \mu _2 +\left[ {2-\Gamma \kappa _2 (\rho +\chi )-\gamma _2 \kappa _2 } \right] E_1 -\left[ {\Gamma \kappa _2 (\rho -\chi )+\gamma _2 \kappa _2 } \right] \bar{{E}}_1 , \end{aligned}$$
(16)
$$\begin{aligned}&(1+\kappa _1 \gamma _1 )X_2 +\frac{\rho \chi }{\rho -\chi }\left[ {\Gamma (\kappa _2 \bar{{A}}_0 +\kappa _2 \bar{{E}}_0 +\bar{{B}}_0 )-(\kappa _1 \bar{{X}}_0 +\bar{{Y}}_0 )} \right] =0, \nonumber \\&(1+\gamma _2 )B_2 -\frac{\rho \chi }{\rho -\chi }\left[ {\Gamma (\kappa _2 \bar{{A}}_0 +\kappa _2 \bar{{E}}_0 +\bar{{B}}_0 )-(\kappa _1 \bar{{X}}_0 +\bar{{Y}}_0 )} \right] =(1-\kappa _2 \gamma _2 )E_2 ,\nonumber \\&\Gamma (\kappa _2 E_2 +B_2 )-\kappa _1 X_2 =-\frac{\rho +\chi }{\rho -\chi }\left[ {\Gamma (\kappa _2 \bar{{A}}_0 +\kappa _2 \bar{{E}}_0 +\bar{{B}}_0 )-(\kappa _1 \bar{{X}}_0 +\bar{{Y}}_0 )} \right] , \end{aligned}$$
(17)
$$\begin{aligned}&\left[ {2n+\kappa _1 (\rho +\chi )+n^{2}\kappa _1 \gamma _1 } \right] X_n +\left[ {\rho -\chi -n(n-2)\gamma _1 } \right] \bar{{Y}}_{n-2} -\Gamma (\rho +\chi )B_n -\kappa _2 \Gamma (\rho -\chi )\bar{{A}}_{n-2} \nonumber \\&\quad =\Gamma \kappa _2 (\rho +\chi )E_n +\Gamma (\rho -\chi )\bar{{F}}_{n-2} , \nonumber \\&\kappa _1 \left[ {\rho -\chi -\gamma _1 n(n-2)} \right] X_n +\left[ {2(n-2)+\rho +\chi +\gamma _1 (n-2)^{2}} \right] \bar{{Y}}_{n-2} -\Gamma (\rho -\chi )B_n -\Gamma \kappa _2 (\rho +\chi )\bar{{A}}_{n-2} \nonumber \\&\quad =\Gamma \kappa _2 (\rho -\chi )E_n +\Gamma (\rho +\chi )\bar{{F}}_{n-2} , \nonumber \\&\qquad -\kappa _1 (\rho +\chi )X_n -(\rho -\chi )\bar{{Y}}_{n-2} +\left[ {2n+\Gamma (\rho +\chi )+\gamma _2 n^{2}} \right] B_n +\kappa _2 \left[ {\Gamma (\rho -\chi )-\gamma _2 n(n-2)} \right] \bar{{A}}_{n-2} \nonumber \\&\quad =\left[ {2n-\kappa _2 \Gamma (\rho +\chi )-n^{2}\kappa _2 \gamma _2 } \right] E_n +\left[ {\gamma _2 n(n-2)-\Gamma (\rho -\chi )} \right] \bar{{F}}_{n-2} , \nonumber \\&\qquad -\kappa _1 (\rho -\chi )X_n -(\rho +\chi )\bar{{Y}}_{n-2} +\left[ {\Gamma (\rho -\chi )-n(n-2)\gamma _2 } \right] B_n \nonumber \\&\qquad +\left[ {2(n-2)+\kappa _2 \Gamma (\rho +\chi )+\kappa _2 \gamma _2 (n-2)^{2}} \right] \bar{{A}}_{n-2} \nonumber \\&\quad =\kappa _2 \left[ {\gamma _2 n(n-2)-\Gamma (\rho -\chi )} \right] E_n +\left[ {2(n-2)-\Gamma (\rho +\chi )-\gamma _2 (n-2)^{2}} \right] \bar{{F}}_{n-2} ,\nonumber \\&\qquad n=3,4,\ldots ,+\infty , \end{aligned}$$
(18)

where the dimensionless parameters \(\rho ,\chi ,\gamma _1 ,\gamma _2 ,\delta _1 ,\delta _2 \) and \(\Gamma \) are defined by

$$\begin{aligned} \rho =\frac{Rk_r }{2\mu _1 },\chi =\frac{Rk_\theta }{2\mu _1 },\gamma _1 =\frac{J_0^{(1)} }{2R\mu _1 },\gamma _2 =\frac{J_0^{(2)} }{2R\mu _2 },\delta _1 =\frac{\sigma _0^{(1)} }{2R\mu _1 },\delta _2 =\frac{\sigma _0^{(2)} }{2R\mu _2 },\Gamma =\frac{\mu _1 }{\mu _2 }, \end{aligned}$$
(19)

and the loading parameters \(E_0 ,E_n ,F_n ,n=1,2,\ldots ,+\infty \) by

$$\begin{aligned} E_0 =A\ln (-\xi ),E_n =-\frac{A}{n}\left( {\frac{R}{\xi }} \right) ^{n},F_n =\left( {\frac{A}{n}-\bar{{A}}} \right) \left( {\frac{R}{\xi }} \right) ^{n}+\bar{{A}}\left( {\frac{R}{\xi }} \right) ^{n+2},\quad n=1,2,\ldots ,+\infty . \end{aligned}$$
(20)

It is clear from the definitions in Eq. (19) that the four size-dependent parameters \(\gamma _1 ,\gamma _2 ,\delta _1 \) and \(\delta _2 \) arise from surface elasticities and that the two size-dependent parameters \(\rho \) and \(\chi \) arise from the spring-type imperfect interface. The two coefficients \(X_1 \) and \(B_1 \) can then be uniquely determined by solving Eq. (16), leading to

$$\begin{aligned} X_1= & {} \frac{\Gamma \rho {E}'_1 (\kappa _2 +1)-2R\delta _1 \mu _1 (1+\Gamma \rho +\gamma _2 )-2R\rho \delta _2 \mu _2 \Gamma }{(1+\Gamma \rho +\gamma _2 )\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] -\rho ^{2}\Gamma (\kappa _1 -1)}+\hbox {i}\frac{\Gamma (\kappa _2 +1)}{\kappa _1 +1}{E}''_1 ,\nonumber \\ B_1= & {} \frac{\rho (\kappa _1 -1)(\rho \Gamma \kappa _2 {E}'_1 -2R\delta _1 \mu _1 )+\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] \left[ {(1-\gamma _2 \kappa _2 -\rho \Gamma \kappa _2 ){E}'_1 -2R\delta _2 \mu _2 } \right] }{(1+\Gamma \rho +\gamma _2 )\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] -\rho ^{2}\Gamma (\kappa _1 -1)}+\hbox {i}{E}''_1 ,\nonumber \\ \end{aligned}$$
(21)

where \({E}'_1 \) and \({E}''_1 \) are, respectively, the real and imaginary parts of \(E_1 \). Interestingly, the imaginary parts of \(X_1 \) and \(B_1 \) are independent of \(b_2 \) and the existence of the mixed-type interface. In addition, the imaginary part of \(X_1 \) is also independent of the elastic properties of the matrix, while that of \(B_1 \) is independent of the elastic properties of the inhomogeneity.

The three coefficients \(X_2 ,B_2 \) and \(\kappa _1 X_0 +Y_0 -\Gamma (\kappa _2 A_0 +B_0 )\) can be uniquely determined as follows by solving Eq. (17)

$$\begin{aligned} X_2= & {} \frac{E_2 \rho \chi \Gamma (\kappa _2 +1)}{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1+\gamma _2 )+\rho \chi \left[ {\Gamma +\kappa _1 (1+\Gamma \gamma _1 +\gamma _2 )} \right] },\nonumber \\ B_2= & {} \frac{E_2 \left\{ {(\rho +\chi )(1+\kappa _1 \gamma _1 )(1-\kappa _2 \gamma _2 )+\rho \chi \left[ {\kappa _1 -\kappa _2 \Gamma -\kappa _1 \kappa _2 (\Gamma \gamma _1 +\gamma _2 )} \right] } \right\} }{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1+\gamma _2 )+\rho \chi \left[ {\Gamma +\kappa _1 (1+\Gamma \gamma _1 +\gamma _2 )} \right] },\nonumber \\ \kappa _1 X_0 +Y_0 -\Gamma (\kappa _2 A_0 +B_0 )= & {} \frac{\bar{{E}}_2 \Gamma (\rho -\chi )(\kappa _2 +1)(1+\kappa _1 \gamma _1 )}{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1+\gamma _2 )+\rho \chi \left[ {\Gamma +\kappa _1 (1+\Gamma \gamma _1 +\gamma _2 )} \right] }+\Gamma \kappa _2 E_0 .\nonumber \\ \end{aligned}$$
(22)

The four coefficients \(X_0 ,Y_0 ,A_0 \) and \(B_0 \) are constrained by Eq. (22)\(_{3}\). Setting \(X_0 =B_0 =0\) and \(A_0 =-\kappa _2 E_0 \), the left coefficient \(Y_0 \) can be uniquely determined from Eq. (22)\(_{3}\) as

$$\begin{aligned} Y_0 =\frac{\bar{{E}}_2 \Gamma (\rho -\chi )(\kappa _2 +1)(1+\kappa _1 \gamma _1 )}{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1+\gamma _2 )+\rho \chi \left[ {\Gamma +\kappa _1 (1+\Gamma \gamma _1 +\gamma _2 )} \right] }. \end{aligned}$$
(23)

The coefficients \(X_n ,Y_{n-2} ,B_n ,A_{n-2} ,n=3,4,\ldots ,+\infty \) are then uniquely determined by solving Eq. (18):

$$\begin{aligned} \left[ {{\begin{array}{c} {\kappa _1 X_n } \\ {\bar{{Y}}_{n-2} } \\ {\Gamma B_n } \\ {\Gamma \kappa _2 \bar{{A}}_{n-2} } \\ \end{array} }} \right] =-\Gamma \left[ {{\begin{array}{c} 0 \\ 0 \\ {\kappa _2 E_n } \\ {\bar{{F}}_{n-2} } \\ \end{array} }} \right] +\frac{2(\kappa _2 +1)}{\kappa _2 }\mathbf{Q}_n^{-1} \left[ {{\begin{array}{c} 0 \\ 0 \\ {n\kappa _2 E_n } \\ {(n-2)\bar{{F}}_{n-2} } \\ \end{array} }} \right] ,\quad n=3,4,\ldots ,+\infty , \end{aligned}$$
(24)

where

$$\begin{aligned} \begin{array}{l} \mathbf{Q}_n =\left[ {{\begin{array}{cccc} {\rho +\chi }&{} {\rho -\chi }&{} {-(\rho +\chi )}&{} {\chi -\rho } \\ {\rho -\chi }&{} {\rho +\chi }&{} {\chi -\rho } &{}{-(\rho +\chi )} \\ {-(\rho +\chi )} &{}{\chi -\rho } &{}{\rho +\chi }&{} {\rho -\chi } \\ {\chi -\rho } &{}{-(\rho +\chi )} &{}{\rho -\chi } &{}{\rho +\chi } \\ \end{array} }} \right] \\ \qquad \qquad +\left[ {{\begin{array}{cccc} {\frac{2n}{\kappa _1 }+\gamma _1 n^{2}}&{}{-\gamma _1 n(n-2)}&{} 0&{} 0 \\ {-\gamma _1 n(n-2)}&{} {2(n-2)+\gamma _1 (n-2)^{2}} &{}0&{} 0 \\ 0&{} 0&{}{\frac{2n+\gamma _2 n^{2}}{\Gamma }}&{} {-\frac{\gamma _2 n(n-2)}{\Gamma }} \\ 0 &{}0&{} {-\frac{\gamma _2 n(n-2)}{\Gamma }} &{} {\frac{2(n-2)}{\Gamma \kappa _2 }+\frac{\gamma _2 (n-2)^{2}}{\Gamma }} \\ \end{array} }} \right] . \\ \end{array} \end{aligned}$$
(25)

It can be shown in a relatively straightforward manner that \(\mathbf{Q}_n \) is a positive definite real symmetric matrix. From Eq. (24), we can see that to determine the unknown coefficients it is sufficient to find the inverse of the 4\(\times \)4 matrices \(\mathbf{Q}_n ,n=3,4,\ldots ,+\infty \).

All of the coefficients in the expressions for \(\varphi _1 (z),\varphi _2 (z)\) and their analytic continuations have now been completely determined. The two original analytic functions \(\psi _1 (z)\) defined in the inhomogeneity and \(\psi _2 (z)\) defined in the matrix can also be conveniently obtained from Eqs. (11) and (14) as

$$\begin{aligned} \psi _1 (z)= & {} -\sum _{n=0}^{+\infty } {\left[ {\bar{{Y}}_n +(n+2)X_{n+2} } \right] R^{-n}z^{n}} ,\left| z \right| <R; \nonumber \\ \psi _2 (z)= & {} \bar{{A}}\ln (z-\xi )-\frac{\xi A}{z-\xi }-\left[ {\bar{{A}}\ln (-\xi )+\frac{A(\xi ^{2}-R^{2})}{\xi ^{2}}+\bar{{B}}_0 } \right] \nonumber \\&\quad +\left( {\frac{R}{\xi }A-\bar{{B}}_1 } \right) Rz^{-1}+\sum _{n=2}^{+\infty } {\left[ {(n-2)A_{n-2} -\bar{{B}}_n } \right] R^{n}z^{-n}} , \quad \left| z \right| >R. \end{aligned}$$
(26)

By substituting the analytic functions obtained into Eq. (2), we arrive at the stress field in the composite. It is clear from the above analysis that the induced stress field in the composite depends on the six size-dependent parameters \(\rho ,\chi ,\gamma _1 ,\gamma _2 ,\delta _1 \) and \(\delta _2 \).

In particular, the average mean stress within the inhomogeneity and the rigid body rotation at the center of the circular inhomogeneity can be given quite simply by

$$\begin{aligned} <\sigma _{11} +\sigma _{22} >= & {} -\frac{4\mu _1 \left[ {\frac{\rho b_2 }{\pi \xi }+2\delta _1 (1+\Gamma \rho +\gamma _2 )+2\rho \delta _2 } \right] }{(1+\Gamma \rho +\gamma _2 )\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] -\rho ^{2}\Gamma (\kappa _1 -1)}, \end{aligned}$$
(27)
$$\begin{aligned} \varpi _{21}= & {} \frac{1}{2}(u_{2,1} -u_{1,2} )=\frac{b_1 }{2\pi \xi }, \quad \mathrm{at} \,z=0, \end{aligned}$$
(28)

where <*> denotes the average. From Eq. (27), we can see that the sign of the average mean stress is simply opposite to that of the sum of the three terms in the square brackets in the numerator. Interestingly, the rigid body rotation at the center of the inhomogeneity in Eq. (28) is independent of the elastic properties of the composite, the imperfection of the interface and the component \(b_2 \) of the Burgers vector.

4 Image force on the edge dislocation

Using the Peach–Koehler formula [3], we can derive the image force acting on the edge dislocation. We will discuss two cases in detail: (1) The Burgers vector is normal to the interface with \(b_1 \ne 0\) and \(b_2 =0\); (2) the Burgers vector is directed tangentially to the interface with \(b_2 \ne 0\) and \(b_1 =0\).

4.1 The case \(b_1 \ne 0,b_2 =0\)

The image force acting on the gliding dislocation can be given explicitly by

$$\begin{aligned} \begin{array}{l} \displaystyle F^{{*}}=\frac{\pi R(\kappa _2 +1)}{\mu _2 b_1^2 }F_1 =-\frac{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1-\kappa _2 \gamma _2 )+\rho \chi \left[ {\kappa _1 -\kappa _2 \Gamma -\kappa _1 \kappa _2 (\Gamma \gamma _1 +\gamma _2 )} \right] }{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1+\gamma _2 )+\rho \chi \left[ {\Gamma +\kappa _1 (1+\Gamma \gamma _1 +\gamma _2 )} \right] }\eta ^{5} \\ \qquad \quad \, \displaystyle +\sum _{n=3}^{+\infty } {\eta ^{2n-3}\left\{ {\kappa _2^{-1} (n-1)^{2}(1-2\eta ^{2})+\eta ^{4}\left[ {\kappa _2 +\kappa _2^{-1} n(n-2)} \right] } \right\} } \\ \qquad \quad \, \displaystyle +\,\frac{2(\kappa _2 +1)}{\Gamma \kappa _2 }\sum _{n=3}^{+\infty } {\eta ^{2n-3}\left[ {{\begin{array}{l} {0,}\; {0,}\; {-n\eta ^{2},}\; {\kappa _2^{-1} (n-2)(n\eta ^{2}-n+1)} \\ \end{array} }} \right] \mathbf{Q}_n^{-1} \left[ {{\begin{array}{l} \qquad 0 \\ \qquad 0 \\ \qquad {\kappa _{2} \eta ^{2}} \\ {n-1-(n-2)\eta ^{2}} \\ \end{array} }} \right] } , \\ F_2 =0, \\ \end{array} \end{aligned}$$
(29)

where \(F_1 \) and \(F_2 \) are, respectively, the image force components along the \(x_1 \)- and \(x_2 \)-directions and \(\eta =R/\xi ,-1<\eta <1\). It is seen from the above expression that the normalized image force \(F^{{*}}\) depends on the four size-dependent parameters \(\gamma _1 ,\gamma _2 ,\rho \) and \(\chi \). In other words, the normalized image force is also size dependent. It is also clear from the above expression that \(F^{{*}}\) is an odd function of \(\eta \). It has been verified numerically (using MATLAB) that: (1) when choosing \(\gamma _1 =\gamma _2 =0\) and \(\rho ,\chi \rightarrow \infty \), Eq. (29) recovers Eq. (7.8) in [3] in the case of a perfect interface; (2) when choosing \(\gamma _1 =\gamma _2 =\chi =0\) and \(\rho \rightarrow \infty \), Eq. (29) recovers Eq. (15) in [4] for a sliding interface. These results verify numerically, to a certain extent, the correctness of the solution obtained. We illustrate in Fig. 2 the normalized image force for different values of the parameters \(\gamma _1 ,\gamma _2 ,\rho \) and \(\chi \) with \(\Gamma =5,\kappa _1 =\kappa _2 =2\). The set of parameters \(\gamma _1 =\gamma _2 =0,\rho =\chi =\infty \) corresponds to a perfect interface [3], while the set \(\gamma _1 =\gamma _2 =0,\rho =\infty ,\chi =0\) describes the sliding interface [4]. From Fig. 2, we can see that the gliding dislocation is repelled from the inhomogeneity when the interface is assumed to be perfect or sliding; there exist inner stable and outer unstable equilibrium positions for the gliding dislocation (recall that \(\eta =R/\xi )\) when \(\gamma _1 =1,\gamma _2 =3,\rho =30,\chi =0\). This fact implies that the mixed-type imperfect interface will exert a significant influence on the stability of the dislocation.

Fig. 2
figure 2

Normalized image force \(F^{{*}}\) on a gliding dislocation for different values of the parameters \(\gamma _1 ,\gamma _2 ,\rho \) and \(\chi \) with \(\Gamma =5,\kappa _1 =\kappa _2 =2\)

Full size image

When the dislocation is located far from the inhomogeneity, the asymptotic expression for the image force can be obtained from Eq. (29) as

$$\begin{aligned} F^{{*}}= & {} \frac{4\eta ^{3}}{\kappa _2 }\left[ {1-\frac{(\kappa _2 +1)\left( {\begin{array}{l} 3(2+3\gamma _2 )\left[ {2+\gamma _1 (3\kappa _1 +1)} \right] \\ +\rho \left[ {6+2\kappa _1 +2\Gamma +\gamma _1 (\Gamma +16\kappa _1 +3\Gamma \kappa _1 )+3\gamma _2 (3+\kappa _1 )+24\kappa _1 \gamma _1 \gamma _2 } \right] \\ +\chi \left[ {6+2\kappa _1 +2\Gamma +\gamma _1 (\Gamma +4\kappa _1 +3\Gamma \kappa _1 )+3\gamma _2 (3+\kappa _1 )+6\kappa _1 \gamma _1 \gamma _2 } \right] \\ +2\rho \chi \left[ {2(\Gamma +\kappa _1 )+3\kappa _1 (\Gamma \gamma _1 +\gamma _2 )} \right] \\ \end{array}} \right) }{\left( {\begin{array}{l} 3\left[ {2+\gamma _1 (3\kappa _1 +1)} \right] \left[ {2+\gamma _2 (\kappa _2 +3)} \right] \\ +\rho \left[ {\begin{array}{l} \gamma _1 \left[ {\Gamma +(16+3\Gamma )\kappa _1 +3\Gamma \kappa _2 +9\Gamma \kappa _1 \kappa _2 } \right] +\gamma _2 \left[ {9+3\kappa _1 +(3+16\Gamma )\kappa _2 +\kappa _1 \kappa _2 } \right] \\ +8\gamma _1 \gamma _2 \left[ {3\kappa _1 +\Gamma \kappa _2 +(1+3\Gamma )\kappa _1 \kappa _2 } \right] +2(3+\Gamma +\kappa _1 +3\Gamma \kappa _2 ) \\ \end{array}} \right] \\ +\chi \left[ {\begin{array}{l} \gamma _1 \left[ {\Gamma +(4+3\Gamma )\kappa _1 +3\Gamma \kappa _2 +9\Gamma \kappa _1 \kappa _2 } \right] +\gamma _2 \left[ {9+3\kappa _1 +(3+4\Gamma )\kappa _2 +\kappa _1 \kappa _2 } \right] \\ +2\gamma _1 \gamma _2 \left[ {3\kappa _1 +\Gamma \kappa _2 +(1+3\Gamma )\kappa _1 \kappa _2 } \right] +2(3+\Gamma +\kappa _1 +3\Gamma \kappa _2 ) \\ \end{array}} \right] \\ +2\rho \chi \left[ {2(\Gamma +\kappa _1 )(\Gamma \kappa _2 +1)+(\Gamma \gamma _1 +\gamma _2 )\left[ {3\kappa _1 (\Gamma \kappa _2 +1)+\kappa _2 (\Gamma +\kappa _1 )} \right] } \right] \\ \end{array}} \right) }} \right] \nonumber \\&+O(\eta ^{5}), \eta \rightarrow 0. \end{aligned}$$
(30)

Below, we present several typical examples to illustrate the solution and simultaneously verify its correctness.

  • \(\rho ,\chi \rightarrow \infty \)

In this case, Eq. (30) reduces to

$$\begin{aligned} F^{{*}}=\frac{4\eta ^{3}\left[ {2(\Gamma +\kappa _1 )(\Gamma -1)+(\Gamma \gamma _1 +\gamma _2 )(3\kappa _1 \Gamma +\Gamma -2\kappa _1 )} \right] }{2(\Gamma +\kappa _1 )(\Gamma \kappa _2 +1)+(\Gamma \gamma _1 +\gamma _2 )\left[ {3\kappa _1 (\Gamma \kappa _2 +1)+\kappa _2 (\Gamma +\kappa _1 )} \right] }, \end{aligned}$$
(31)

which indicates that \(\Gamma \gamma _1 +\gamma _2 ={(J_0^{(1)} +J_0^{(2)} )}/{(2R\mu _2 )}\) can now be taken whole. If we further assume that \(\gamma _1 =\gamma _2 =0\), Eq. (31) becomes

$$\begin{aligned} F^{{*}}=\frac{4\eta ^{3}(\Gamma -1)}{\Gamma \kappa _2 +1}, \end{aligned}$$
(32)

which is just Eq. (7.13) in [3] for a perfect interface.

  • \(\gamma _1 =\gamma _2 =0\)

In this case, the surface elasticities are absent. Consequently, Eq. (30) reduces to

$$\begin{aligned} F^{{*}}=\frac{4\eta ^{3}\left[ {-6+(\rho +\chi )(2\Gamma -3-\kappa _1 )+2\rho \chi (\Gamma -1)(\Gamma +\kappa _1 )} \right] }{6+(\rho +\chi )(3+\Gamma +\kappa _1 +3\Gamma \kappa _2 )+2\rho \chi (\Gamma +\kappa _1 )(\Gamma \kappa _2 +1)}. \end{aligned}$$
(33)

If we further assume that \(\chi =0\) and \(\rho \rightarrow \infty \), Eq. (33) becomes

$$\begin{aligned} F^{{*}}=\frac{4\eta ^{3}(2\Gamma -3-\kappa _1 )}{3+\Gamma +\kappa _1 +3\Gamma \kappa _2 }, \end{aligned}$$
(34)

which is just Eq. (19) in [4] for a sliding interface.

  • \(\rho =\chi =0\)

In this case, Eq. (30) becomes

$$\begin{aligned} F^{{*}}=\frac{8\eta ^{3}(\gamma _2 -\kappa _2 )}{\kappa _2 \left[ {2+\gamma _2 (\kappa _2 +3)} \right] }, \end{aligned}$$
(35)

which is independent of the elastic properties of the inhomogeneity. If we further assume that \(\gamma _2 =0\), Eq. (35) becomes

$$\begin{aligned} F^{{*}}=-4\eta ^{3}, \end{aligned}$$
(36)

which is just the result of a gliding dislocation located far from a traction-free hole. Equation (36) can also be obtained by setting \(\Gamma =0\) in Eqs. (32) or (34).

4.2 \(b_2 \ne 0,b_1 =0\)

The image force acting on the climbing dislocation can be given explicitly by

$$\begin{aligned} F_{*}= & {} \frac{\pi R(\kappa _2 +1)}{\mu _2 b_2^2 }F_1 =-\frac{2\pi R(\kappa _2 +1)}{b_2 }\frac{\rho (\kappa _1 -1)\delta _1 \Gamma +\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] \delta _2 }{(1+\Gamma \rho +\gamma _2 )\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] -\rho ^{2}\Gamma (\kappa _1 -1)}\eta ^{2}\nonumber \\&-\frac{\rho ^{2}\Gamma (\kappa _1 -1)(\kappa _2 -1)+\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] \left[ {2+(1-\kappa _2 )(\Gamma \rho +\gamma _2 )} \right] }{(1+\Gamma \rho +\gamma _2 )\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] -\rho ^{2}\Gamma (\kappa _1 -1)}\eta ^{3} \nonumber \\&-\frac{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1-\kappa _2 \gamma _2 )+\rho \chi \left[ {\kappa _1 -\kappa _2 \Gamma -\kappa _1 \kappa _2 (\Gamma \gamma _1 +\gamma _2 )} \right] }{(\rho +\chi )(1+\kappa _1 \gamma _1 )(1+\gamma _2 )+\rho \chi \left[ {\Gamma +\kappa _1 (1+\Gamma \gamma _1 +\gamma _2 )} \right] }\eta ^{5} \\&+\sum _{n=3}^{+\infty } {\eta ^{2n-3}\left\{ {\kappa _2^{-1} (n-3)^{2}-2\eta ^{2}\kappa _2^{-1} (n-1)(n-3)+\eta ^{4}\left[ {\kappa _2 +\kappa _2^{-1} n(n-2)} \right] } \right\} }\nonumber \\&+\frac{2(\kappa _2 +1)}{\Gamma \kappa _2 }\sum _{n=3}^{+\infty } {\eta ^{2n-3}\left[ {{\begin{array}{l} {0,}\; {0,}\; {n\eta ^{2},}\; {\kappa _2^{-1} (n-2)(n-3-n\eta ^{2})} \nonumber \\ \end{array} }} \right] } \mathbf{Q}_n^{-1} \left[ {{\begin{array}{l} \qquad 0 \\ \qquad 0 \\ \qquad {-\kappa _2 \eta ^{2}} \\ {(n-2)\eta ^{2}-n+3} \\ \end{array} }} \right] . \nonumber \end{aligned}$$
(37)

It is clear from the above expression that the normalized image force \(F_{*} \) depends on all six size-dependent parameters \(\gamma _1 ,\gamma _2 ,\delta _1 ,\delta _2 \hbox {, }\rho \) and \(\chi \). The existence of residual surface tensions means that \(F_{*} \) in Eq. (37) is no longer an odd function of \(\eta \). It has been verified numerically (using MATLAB) that: (1) when choosing \(\gamma _1 =\gamma _2 =\delta _1 =\delta _2 =0\) and \(\rho ,\chi \rightarrow \infty \), Eq. (37) recovers Eq. (7.9) in [3] for a perfect interface; (2) when choosing \(\gamma _1 =\gamma _2 =\delta _1 =\delta _2 =\chi =0\) and \(\rho \rightarrow \infty \), Eq. (37) recovers Eq. (16) in [4] for a sliding interface. Thus, the correctness of the solution has also been verified numerically. Figure 3 shows the normalized image force on a climbing dislocation for different values of the parameters \(\gamma _1 ,\gamma _2 ,\rho \) and \(\chi \) with \(\Gamma =3,\kappa _1 =\kappa _2 =2\) and \(\delta _1 =\delta _2 =0\). It is observed from Fig. 3 that the climbing dislocation is repelled from the inhomogeneity when the interface is perfect with \(\gamma _1 =\gamma _2 =0,\rho =\chi =\infty \); there is an unstable equilibrium position for the climbing dislocation when the interface is sliding freely with \(\gamma _1 =\gamma _2 =0,\rho =\infty ,\chi =0\); and there exist an inner stable equilibrium position and an outer unstable equilibrium position for the climbing dislocation when \(\gamma _1 =\gamma _2 =0.1,\rho =30,\chi =0\). The results in Figs. 2 and 3 indicate that it is possible to find multiple equilibrium positions for an edge dislocation interacting with a circular inhomogeneity with a mixed-type imperfect interface.

Fig. 3
figure 3

Normalized image force \(F_{*} \) on a climbing dislocation for different values of the parameters \(\gamma _1 ,\gamma _2 ,\rho \) and \(\chi \) with \(\Gamma =3,\kappa _1 =\kappa _2 =2\) and \(\delta _1 =\delta _2 =0\)

Full size image

When the dislocation is located far from the inhomogeneity, the asymptotic expression for the image force can be extracted from Eq. (37) as

$$\begin{aligned} F_1= & {} -\frac{2\mu _2 b_2 \left\{ {\rho (\kappa _1 -1)\delta _1 \Gamma +\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] \delta _2 } \right\} }{(1+\Gamma \rho +\gamma _2 )\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] -\rho ^{2}\Gamma (\kappa _1 -1)}\eta ^{2} \nonumber \\&\quad -\frac{\mu _2 b_2^2 }{\pi R(\kappa _2 +1)}\frac{\rho ^{2}\Gamma (\kappa _1 -1)(\kappa _2 -1)+\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] \left[ {2+(1-\kappa _2 )(\Gamma \rho +\gamma _2 )} \right] }{(1+\Gamma \rho +\gamma _2 )\left[ {2+(\rho +\gamma _1 )(\kappa _1 -1)} \right] -\rho ^{2}\Gamma (\kappa _1 -1)}\eta ^{3}+O(\eta ^{5}),\nonumber \\&\qquad \eta \rightarrow 0, \end{aligned}$$
(38)

which is independent of \(\chi \). The existence of residual surface tensions means that the magnitude of the image force on a climbing dislocation decays slower than that on a gliding dislocation as the dislocation moves away from the inhomogeneity. It is seen from Eq. (38) that the sign of \(F_1 \) is simply opposite to that of \(b_2 \) when the climbing dislocation is very far from the inhomogeneity. Below, several examples are presented to illustrate the solution serving also to verify the correctness of the solution.

  • \(\rho \rightarrow \infty \)

In this case, Eq. (38) reduces to

$$\begin{aligned} F_1= & {} -\frac{2\mu _2 b_2 (\kappa _1 -1)(\delta _1 \Gamma +\delta _2 )}{2\Gamma +(\kappa _1 -1)(\Gamma \gamma _1 +\gamma _2 +1)}\eta ^{2}\nonumber \\&-\frac{\mu _2 b_2^2 }{\pi R(\kappa _2 +1)}\frac{2(\kappa _1 -1)-2\Gamma (\kappa _2 -1)-(\Gamma \gamma _1 +\gamma _2 )(\kappa _1 -1)(\kappa _2 -1)}{2\Gamma +(\kappa _1 -1)(\Gamma \gamma _1 +\gamma _2 +1)}\eta ^{3}, \end{aligned}$$
(39)

which also indicates that both \(\Gamma \gamma _1 +\gamma _2 ={(J_0^{(1)} +J_0^{(2)} )}/{(2R\mu _2 )}\) and \(\Gamma \delta _1 +\delta _2 ={(\sigma _0^{(1)} +\sigma _0^{(2)} )}/{(2R\mu _2 )}\) are now taken as whole. If we further assume that \(\gamma _1 =\gamma _2 =\delta _1 =\delta _2 =0\), Eq. (39) becomes

$$\begin{aligned} F_{*} =\frac{2\eta ^{3}\left[ {\Gamma (\kappa _2 -1)-(\kappa _1 -1)} \right] }{2\Gamma +\kappa _1 -1}, \end{aligned}$$
(40)

which is just Eq. (7.14) in [3] for a perfect interface and Eq. (20) in [4] for a sliding interface. Clearly, Eq. (40) is valid for any value of \(\chi \).

  • \(\gamma _1 =\gamma _2 =\delta _1 =\delta _2 =0\)

Now the surface elasticities are absent. In this case, Eq. (38) reduces to

$$\begin{aligned} F_{*} =-\frac{4+2\rho \left[ {\kappa _1 -1-\Gamma (\kappa _2 -1)} \right] }{2+\rho (2\Gamma +\kappa _1 -1)}\eta ^{3}. \end{aligned}$$
(41)

  • \(\rho =0\)

In this case, Eq. (38) reduces to

$$\begin{aligned} F_1 =-\frac{2\mu _2 b_2 \delta _2 }{1+\gamma _2 }\eta ^{2}-\frac{\mu _2 b_2^2 }{\pi R(\kappa _2 +1)}\frac{2+\gamma _2 (1-\kappa _2 )}{1+\gamma _2 }\eta ^{3}, \end{aligned}$$
(42)

which is independent of the elastic properties of the inhomogeneity. If we further assume that \(\gamma _2 =\delta _2 =0\), Eq. (42) becomes

$$\begin{aligned} F_{*} =-2\eta ^{3}, \end{aligned}$$
(43)

which is just the result of a climbing dislocation located far from a traction-free hole. Equation (43) can also be obtained by setting \(\Gamma =0\) in Eqs. (40) or (41).

5 Conclusions

In this work, we have derived a rigorous solution to the problem of an edge dislocation interacting with a circular elastic inhomogeneity with a mixed-type imperfect interface. The mixed-type imperfect interface is introduced to reflect the complicated and more realistic scenario in which a soft interface represented by the spring model is bounded by two stiff interfaces arising from Gurtin–Murdoch surface elasticities. The boundary conditions on the mixed-type interface are concisely expressed in terms of \(\varphi _1 (z),\varphi _2 (z)\) and their analytic continuations. All of the complex coefficients appearing in each of these four analytic functions are obtained in a quasi-decoupled manner: \(X_1 \) and \(B_1 \) are determined by solving the two coupled linear algebraic equations in Eq. (16); \(X_2 ,B_2 \) and \(\kappa _1 X_0 +Y_0 -\Gamma (\kappa _2 A_0 +B_0 )\) are determined by solving the three coupled linear algebraic equations in Eq. (17); and \(X_n ,Y_{n-2} ,B_n \) and \(A_{n-2} \) for a certain value of \(n(\ge 3)\) can be determined by solving the four coupled linear algebraic equations in Eq. (18). The stress field and the image force acting on the edge dislocation can then be conveniently derived from the obtained analytic functions. Analytic expressions for the image force on gliding and climbing dislocations are presented. It is observed that in general the normalized image force depends on six size-dependent parameters \(\gamma _1 ,\gamma _2 ,\delta _1 ,\delta _2 \hbox {, }\rho \) and \(\chi \), the first four of which result from surface elasticities and the latter two from the linear spring model. The solution to the problem of an edge dislocation inside a circular inhomogeneity with a mixed-type imperfect interface can be derived quite similarly.