Determination of metamaterial parameters by means of a homogenization approach based on asymptotic analysis

Abstract

By using modern additive manufacturing techniques, a structure at the millimeter length scale (macroscale) can be produced showing a lattice substructure of micrometer dimensions (microscale). Such a system is called a metamaterial at the macroscale, because its mechanical characteristics deviate from the characteristics at the microscale. Consequently, a metamaterial is modeled by using additional parameters. These we intend to determine. A homogenization approach based on asymptotic analysis establishes a connection between these different characteristics at micro- and macroscales. A linear elastic first-order theory at the microscale is related to a linear elastic second-order theory at the macroscale. Small strains (and, correspondingly, small gradients) are assumed at both scales. A relation for the parameters at the macroscale is derived by using the equivalence of energy at macro- and microscales within a so-called representative volume element (RVE). The determination of the parameters becomes possible by solving a boundary value problem within the framework of the finite element method. The proposed approach guarantees that the additional parameters vanish if the material is purely homogeneous; in other words, it is fully compatible with conventional homogenization schemes based on spatial averaging techniques. Moreover, the proposed approach is reliable, because it ensures that the obtained additional parameters are insensitive to choices of the RVE consisting of a repetition of smaller RVEs depending upon the intrinsic size of the structure.

1 Introduction

Periodic lattice-type structures involving large number of repetitive substructures continue to attract the interest of many researchers because of their fascinating properties, such as relatively low manufacturing costs and high specific stiffness [19, 46,47,48, 64, 67]. The mechanical response of such a structure depends not only on the material, but also on the morphology of its substructure [62, 63]. Hence, an appropriate “metamaterial description” must be used for mimicking the dependence on its substructure.

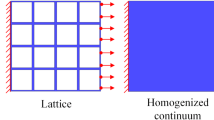
In order to design and fabricate metamaterials for engineering applications, an accurate and efficient prediction of their mechanical performances is important [28, 32, 51, 94, 98]. Indeed, standard numerical techniques, such as the finite element method (FEM), can be used for modeling a structure including every detail of its subunits [100, 101]. However, this requires the mesh size to be at least one order smaller than the geometric size of the substructure leading to very high computational costs. Hence, homogenization techniques are developed to upscale the mechanical response at the microscale—the presence of the substructure leads to a composite material, which can be seen as a heterogeneous material—to the macroscale by defining an appropriate constitutive equation. Particularly in composite materials, with fibers embedded in a matrix building a periodic substructure, micro- and macroscale behaviors are modeled by the same linear elastic model, also a.k.a. Cauchy continuum. The homogenization of such periodic structures toward an equivalent Cauchy continuum has been investigated thoroughly [20, 45, 57, 68, 72, 102].

Many approaches in the literature assume that there exists a representative volume element (RVE) with periodic boundary conditions that precisely captures the deformation behavior of the whole geometry. Such an approach utilizes the energy equivalence of the RVE at both macroscale and microscale, and it was also used in [52]. The effective properties of such homogenized continua are in good agreement with experiments [93] under the condition that $L\gg l$, where L represents the macroscopic length scale, i.e., (mean value of) the geometric dimensions of the whole structure, and l represents the length scale of the microscale namely, the geometric dimensions of the substructure. The quantity l will be used as the “length scale” of a basic cell of the structure, as indicated in Fig. 1. Note that the concept of a basic cell is different from that of an RVE. It is evident that a basic cell can be regarded as an RVE, and stacking or gathering several basic cells can construct an RVE as well. Classical homogenization encounters limitations [10, 60] when L is of a comparable order with respect to l.

Size effects fail to be captured by a standard homogenization having the same-order theory at both scales. A feasible approach is to use a first-order theory at the microscale and a second-order one at the macroscale. This leads to additional parameters at the macroscale, which need to be determined. We refer to various formulations of a second-order theory in [1,2,3, 6,7,8, 33, 37, 66, 70, 80, 81, 83, 84, 86, 87, 91, 95]. Higher-order approaches are also referred to as generalized continuum theories and homogenization within that framework is a challenging task pursued by many scientists, among others by [17, 31, 40, 49, 56, 76, 85]. In most cases, it is agreed that homogenization of an RVE by involving so-called higher gradient terms of the macroscopic field is a natural way to include a size effect [14, 41,42,43,44, 60]. By using gamma convergence, homogenization results have been obtained in [4, 5, 75]. A remarkable class of structures described at the macroscale by using a second gradient elasticity theory are pantographic objects [18, 89, 92]. They have received a notable follow-up in the literature [30, 34, 69, 82, 97, 99], also from a mathematically rigorous standpoint regarding fundamental issues, such as well-posedness [36].

A possibly promising homogenization technique is asymptotic analysis, which has been used to obtain homogenized material parameters in [90]. This method decomposes the variables into their global variations and into local fluctuations. Such a decomposition was used to generate closed-form equations to determine constitutive parameters in one-dimensional problems, for example in the analysis of composites [16, 22], while 2D problems [13, 15, 23, 29, 78] have been investigated numerically. FEM was applied in [73] demonstrating that higher-order terms start dominating when the difference between the parameters of the composite materials increases. A second-order asymptotic and computational homogenization technique is proposed by [13]. Here, the boundary value problems generated by the asymptotic homogenization were solved with a quadratic ansatz. However, there are still two main issues that are not well addressed when trying to homogenize structures in the framework of generalized mechanics [96]:

• The first one concerns compatibility, in the sense that parameters of the strain gradient stiffness tensor should vanish when the structure is purely homogeneous.

• The second one concerns reliability, such that the strain gradient stiffness tensor has to be insensitive to a repetition of the basic cell.

A successful attempt is made in [59, 60] establishing a connection between microscale parameters and macroscale parameters (by using the strain gradient theory). A “correction” term was proposed, such that the strain gradient stiffness tensor satisfied compatibility and reliability requirements. Different numerical solution methods are used for this approach: Fast Fourier technique (FFT) is employed in [61] and FEM was used in [15]. We follow their methodology and propose an alternative derivation for this “correction” term in Sect. 3 in a somewhat pedagogical manner. Furthermore, we apply and validate the method for simple yet general 2D metamaterials in Sects. 4 and 5 by using FEM. In order to demonstrate its versatility, computations of the square lattice are performed in Sect. 6. The computations are performed with the aid of open-source codes developed by the FEniCS project [2]. The proposed method delivers all metamaterial parameters in 2D by using a linear elastic material model at the microscale after a computational procedure as investigated in what follows.

2 A preliminary remark on objective strain energy densities

The following analysis at the macroscale and at the microscale is heavily based on expressions for the strain energy densities. In fact, in the end these will be formulated in terms of derivatives of the displacement, which puts the objectivity of these expressions at stake and makes us wonder what the limits of application of the proposed approach are. Let it be said here and now: The proposed approach holds for small deformations on the microscale as well as on the macroscale. However, the aforementioned pantographic structures can undergo large reversible deformations. It was also for this reason that the authors of [33], who are protagonists of this class of metamaterials, decided to formulate the strain energy density such that it is ready for a mathematical treatment of isotropic second-order gradient elastic materials at large deformations. We will use their results and specialize them to our case of interest, which are expressions for the strain energy density of a Cauchy material on the microscale and of a second-order material on the macroscale subjected to small deformations. In this context, the interested reader is also referred to Chapter 3 of [21], where the case of third-order elastic continua for large deformations is examined.

In [33], the strain energy density is first expressed in terms of the deformation gradient and its gradient, $F_{\alpha i}$ and $F_{\alpha i,j}$, respectively. Following [33], we use small Latin indices to indicate Cartesian coordinates of the reference placement, $\varvec{X}$. Later on, we will depart from this nomenclature and also use a similar symbol for centers of mass. If required, Greek indices are used to characterize the current configuration. The principles of rational mechanics are now applied to arrive at the following (objective) form for the strain energy density:

$$\begin{aligned} w=\tfrac{1}{2}\left( E_{ij}C_{ijkl}E_{kl}+2E_{ij}H_{ijklm}E_{kl,m}+E_{ij,k}D_{ijklmn}E_{lm,n}\right) . \end{aligned}$$

(1)

The (constant) stiffness tensors $\varvec{C}$, $\varvec{H}$, $\varvec{D}$ are of fourth, fifth, and sixth rank, respectively. They observe certain symmetry properties, which follow from the semi-positiveness of the strain energy density and from the symmetries of the Green–Lagrange tensor $\varvec{E}=\frac{1}{2}\left( \varvec{F}^\top \cdot \varvec{F}-\varvec{\mathrm {I}}\right)$ and its derivative w.r.t. to the reference placement:

$$\begin{aligned} \begin{aligned}&C_{ijkl}=C_{jikl}=C_{ijlk}=C_{klij}\;,\;\;H_{ijklm}=H_{jiklm}=H_{ijkml}=H_{lmijk}\\&D_{ijklmn}=D_{jiklmn}=D_{ijkmln}=D_{lmnijk}. \end{aligned} \end{aligned}$$

(2)

If the material is centrosymmetric, then $\varvec{H}$ vanishes and $\varvec{C}$ and $\varvec{D}$ can be expressed by sums of products of two and three unit tensors of second rank, respectively. This way $\varvec{C}$ is reduced to two stiffness parameters (the two Lamé coefficients) and $\varvec{D}$ to five:

$$\begin{aligned} \begin{aligned} C_{ijkl}&=\lambda \delta _{ij}\delta _{kl}+\mu \left( \delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}\right) \;,\;\;H_{ijklp}=0\;,\;\;\\ D_{ijklpq}&= c_1\left( \delta _{ij}\delta _{kl}\delta _{pq}+ \delta _{ij}\delta _{kp}\delta _{lq}+ \delta _{ik}\delta _{jq}\delta _{lp}+ \delta _{iq}\delta _{jk}\delta _{lp}\right) \\&\quad +c_2\delta _{ij}\delta _{kq}\delta _{lp}+c_3\left( \delta _{ij}\delta _{jl}\delta _{pq}+ \delta _{ik}\delta _{jp}\delta _{lq} \right. \\&\quad +\left. \delta _{ik}\delta _{jq}\delta _{lp}+ \delta _{il}\delta _{jk}\delta _{lp}+ \delta _{ip}\delta _{jk}\delta _{lq}\right) \\&\quad +c_{4}\left( \delta _{il}\delta _{jp}\delta _{kq}+ \delta _{ip}\delta _{jl}\delta _{kq}\right) \\&\quad +c_{5}\left( \delta _{il}\delta _{jq}\delta _{kp}+ \delta _{ip}\delta _{jq}\delta _{kl}+ \delta _{iq}\delta _{jl}\delta _{kp}+ \delta _{iq}\delta _{jp}\delta _{kl}\right) . \end{aligned} \end{aligned}$$

(3)

It should be noted that in this form Eqs. (1) and (3) are the extension to what is known as the St. Venant–Kirchhoff generalization of Hooke’s law for small strain linear elasticity to large strains, where the gradient of the Green–Lagrange tensor is not present ([53], p. 250).

Recall that the Green–Lagrange tensor can be written in terms of displacement derivatives as follows:

$$\begin{aligned} E_{ij}=\tfrac{1}{2}\left( u_{i,j}+u_{j,i}+u_{k,i}u_{k,j}\right) . \end{aligned}$$

(4)

Consequently its derivative reads:

$$\begin{aligned} E_{ij,k}=\tfrac{1}{2}\left( u_{i,jk}+u_{j,ik}+u_{l,ik}u_{l,j}+u_{l,i}u_{l,jk}\right) . \end{aligned}$$

(5)

We define small strain second gradient theory such that we neglect all products of displacement derivatives and if no distinction needs to be made between current and reference placement. Then, for an centrosymmetric material we arrive at:

$$\begin{aligned} w=\tfrac{1}{2}\left( C_{ijkl}u_{i,j}u_{k,l}+D_{ijklmn}u_{i,jk}u_{l,mn}\right) . \end{aligned}$$

(6)

By right, following [33], all indices should be in Greek letters, since it is the current configuration which is meant in the linear theory, but for convenience we refrain from doing so. Of course, if the classical Cauchy continuum of linear elasticity with small strains is concerned, the second part in Eq. (6) must be omitted. It should also be mentioned that this result is in agreement with Eq. (16) of [65], if third-order gradients in displacement are neglected, and Eq. (19) of [58], where it is attempted to determine the seven stiffness coefficients experimentally. It should be pointed out that these authors do not address the issue of objectiveness of the strain energy and the small strain approximation, most likely because they were educated in the spirit of classical Hookean elasticity.

In order to formulate boundary value problems for the displacement and their gradients, equations of motions are required. They follow from the balance of momentum which will be reduced to the static case. Hence, we need an expression for the stress tensor in terms of displacement gradients. The general theory for stresses and the equations of motion of higher-order gradient continua undergoing large deformations are outlined in [21], Chapters 1 and 2. We do not need such generality in the sequel. Hence, we follow the way indicated in [65] and calculate hyperstresses of second and third rank, where according to Castigliano’s principle, the strain energy density (6) can be used as their potential:

$$\begin{aligned} \overset{\scriptscriptstyle {(2)}}{\sigma }_{ij}=\frac{\partial w}{\partial u_{i,j}}\;,\;\;\overset{\scriptscriptstyle {(3)}}{\sigma }_{ijk}=\frac{\partial w}{\partial {u_{ij,k}}}. \end{aligned}$$

(7)

Note that in the case of the traditional Cauchy continuum, the hyperstress of second rank, $\overset{\scriptscriptstyle {(2)}}{\varvec{\sigma }}$, becomes the ordinary Cauchy stress and the hyperstress of third rank, $\overset{\scriptscriptstyle {(3)}}{\varvec{\sigma }}$, vanishes. The corresponding balance of momentum reads in the static case:

$$\begin{aligned} \overset{\scriptscriptstyle {(2)}}{\sigma }_{ij,j}-\overset{\scriptscriptstyle {(3)}}{\sigma }_{ijk,jk}+f_i=0, \end{aligned}$$

(8)

where $f_i$ indicate the body forces.

3 Connection of micro- and macroscale parameters

Consider a continuum body occupying a domain $\Omega$ in two-dimensional space, $\Omega \in \mathbb R^2$. The metamaterial is embodied in an RVE, $\Omega ^P$, where periodically aligned RVEs constitute metamaterial domains,

$$\begin{aligned} \cup \Omega ^P = \Omega \ , \ \ \Omega ^P \cap \Omega ^Q = \emptyset \ , \ \ \qquad P,Q = 1,2,3,\ldots M, P \ne Q. \end{aligned}$$

(9)

The RVE at the microscale represents the detailed substructure, such as the fibers and the matrix in a composite material. The same RVE at the macroscale is modeled as a homogeneous metamaterial. We assume that the corresponding stored energies are equal although the definitions at both scales differ. We use a first-order theory for defining the volumetric energy (volume) density of an RVE at the microscale “m,” and a second-order theory at the macroscale, “M,” for the energy density, i.e., $w^\text {m}$, and $w^\text {M}$, respectively:

$$\begin{aligned} \int _{\Omega ^P} { w^\text {m}} \, \mathrm d V= & {} \int _{\Omega ^P} { w^\text {M}} \, \mathrm d V,\nonumber \\ \int _{\Omega ^P} \frac{1}{2} C^\text {m}_{ijkl} u^\text {m}_{i,j} u^\text {m}_{k,l} \, \mathrm d V= & {} \int _{\Omega ^P} \frac{1}{2} \big ( C^\text {M}_{ijkl} u^\text {M}_{i,j} u_{k,l}^\text {M} + D_{ijklmn}^\text {M} u_{i,jk}^\text {M} u_{l,mn}^\text {M} \big ) \, \mathrm d V. \end{aligned}$$

(10)

Note that all fields are expressed in Cartesian coordinates. The microscale stiffness tensor, $C^\text {m}_{ijkl}$, is a function in space. Consider a lattice substructure. Even if the trusses are made of a homogeneous material, the voids between the trusses generate a heterogeneous substructure at the microscale, such that the microscale stiffness tensor depends on space coordinates and possesses either the value of the truss material or is equal to zero due to the voids. In contrast to that, the macroscale material tensors, $C^\text {M}_{ijkl}$ and $D^\text {M}_{ijklmn}$, are constant in space, because they are generated by the homogenization procedure to be explained in the following. The continuum body at the reference frame has particles at coordinates $X_i$, where they move to $x_i$ under a mechanical loading. The displacement is the deviation from the reference frame, and we emphasize that the microscale displacement, $u^\text {m}_i$, is different than the macroscale displacement, $u^\text {M}_i$,

$$\begin{aligned} {u^\text {m}_i}= & {} { x_i^\text {m}} - X_i , \nonumber \\ {u^\text {M}_i}= & {} { x_i^\text {M}} - X_i , \end{aligned}$$

(11)

because the current positions of particles differ. This difference between ${x_i^\text {m}}$ and ${ x_i^\text {M}}$ is illustrated in Fig. 1. For demonstrating the microscale deformation, the substructure is visualized as well. For simplicity, a well-known example is used, namely composite materials with the red inclusion (fibers) embedded in the blue material (matrix). For the homogenized case, the same particle moves to $x_i^\text {M}$ expressed at the macroscale without the substructure. We emphasize that micro- and macroscales are both expressed in the same coordinate system. Two different cases are examined, a heterogeneous one on the microscale with known material properties versus a homogeneous one on the macroscale with sought parameters. In order to identify the material parameters, strain energy expressions for macro- and microscales are derived in what follows.

Fig. 1

Left: Continuum body in the reference frame. Right top: Deformation at the microscale. Right bottom: Corresponding deformation at the macroscale

3.1 The macroscale energy for an RVE

Consider the macroscale case for an RVE, $\Omega ^P$. As customary in spatial averaging, we define the geometric center $\overset{\text {c}}{{\varvec{X}}}$ of the RVE:

$$\begin{aligned} \overset{\text {c}}{{\varvec{X}}} = \frac{1}{V} \int _{\Omega } {\varvec{X}} \, \mathrm d V, \end{aligned}$$

(12)

approximate the macroscale displacement by a Taylor expansion around the value at the geometric center by truncating after quadratic terms (in order to account for the strain gradient effect), and calculate displacement gradients of this approximation

$$\begin{aligned} {u^\text {M} _i}({\varvec{X}})&= {u^\text {M} _i}\Big |_{\overset{\text {c}}{{\varvec{X}}}} + u^\text {M}_{i,j} \Big |_{\overset{\text {c}}{{\varvec{X}}}} (X_j-\overset{\text {c}}{X}_j) + \frac{1}{2} u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{{\varvec{X}}}} (X_j-\overset{\text {c}}{X}_j) (X_k-\overset{\text {c}}{X}_k), \nonumber \\ u^\text {M}_{i,l}({\varvec{X}})&= u^\text {M}_{i,j} \Big |_{\overset{\text {c}}{{\varvec{X}}}} \delta _{jl} + \frac{1}{2} u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{{\varvec{X}}}} ( \delta _{jl} (X_k-\overset{\text {c}}{X}_k) + (X_j-\overset{\text {c}}{X}_j) \delta _{kl} ), \nonumber \\&= u^\text {M}_{i,l} \Big |_{\overset{\text {c}}{{\varvec{X}}}} + u^\text {M}_{i,lk} \Big |_{\overset{\text {c}}{{\varvec{X}}}} (X_k-\overset{\text {c}}{X}_k), \nonumber \\ u^\text {M}_{i,lm}({\varvec{X}})&= u^\text {M}_{i,lk} \Big |_{\overset{\text {c}}{{\varvec{X}}}} \delta _{km} = u^\text {M}_{i,lm} \Big |_{\overset{\text {c}}{{\varvec{X}}}}. \end{aligned}$$

(13)

According to Eq. (13), spatial averaging the gradient terms of the displacement field leads to

$$\begin{aligned} \begin{aligned} \langle {u}_{i,j}^\text {M} \rangle&=\frac{1}{V}\int _{\Omega ^P} u^\text {M} _{i,j} \, \mathrm d V= u^\text {M}_{i,j}\Big |_{\overset{\text {c}}{{\varvec{X}}}} + u^\text {M}_{i,jk}\Big |_{\overset{\text {c}}{{\varvec{X}}}} \bar{I}_k \ , \ \ \bar{I}_k = \frac{1}{V} \int _{\Omega ^P} (X_k-\overset{\text {c}}{X}_k) \, \mathrm d V, \\ \langle {u}_{i,jk}^\text {M} \rangle&=\frac{1}{V}\int _{\Omega ^P} u^\text {M} _{i,jk}\, \mathrm d V= u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{{\varvec{X}}}}. \end{aligned} \end{aligned}$$

(14)

Since we require $\bar{I}_k = 0$ from Eq. (12),

$$\begin{aligned} \langle {u}_{i,j}^\text {M} \rangle = u^\text {M}_{i,j}\Big |_{\overset{\text {c}}{{\varvec{X}}}} \ , \ \ \langle {u}_{i,jk}^\text {M} \rangle = u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{{\varvec{X}}}}. \end{aligned}$$

(15)

After inserting Eq. (15) into Eq. (13), we obtain

$$\begin{aligned} \begin{aligned}&u_i^\text {M}({\varvec{X}}) = u^\text {M} _i\Big |_{\overset{\text {c}}{{\varvec{X}}}} + \langle {u}_{i,j}^\text {M} \rangle (X_j-\overset{\text {c}}{X}_j) + \frac{1}{2} \langle {u}_{i,jk}^\text {M} \rangle (X_j-\overset{\text {c}}{X}_j) (X_k-\overset{\text {c}}{X}_k), \\&u^\text {M} _{i,j}({\varvec{X}}) = \langle {u}_{i,j}^\text {M} \rangle + \langle {u}_{i,jk}^\text {M}\rangle (X_k-\overset{\text {c}}{X}_k), \\&u^\text {M}_{i,jk}({\varvec{X}}) = \langle {u}_{i,jk}^\text {M} \rangle . \end{aligned} \end{aligned}$$

(16)

Now, by using the last relation in Eq. (16) on the right-hand side of Eq. (10), the macroscale energy of an RVE reads as follows, because the macroscale stiffness tensors are constant in space:

$$\begin{aligned}&\int _{\Omega ^P} \frac{1}{2} \big ( C^\text {M}_{ijlm} u^\text {M}_{i,j} u^\text {M}_{l,m} + D^\text {M}_{ijklmn} u^\text {M}_{i,jk} u^\text {M}_{l,mn} \big ) \, \mathrm d V = \frac{1}{2} C^\text {M}_{ijlm} \int _{\Omega ^P} u^\text {M}_{i,j} u^\text {M}_{l,m} \, \mathrm d V \nonumber \\&\qquad +\frac{1}{2} D^\text {M}_{ijklmn} \int _{\Omega ^P} u^\text {M}_{i,jk} u^\text {M}_{l,mn} \, \mathrm d V = \frac{1}{2} C^\text {M}_{ijlm} \int _{\Omega ^P} \Big ( \langle {u}_{i,j}^\text {M} \rangle +\langle {u}_{i,jk}^\text {M} \rangle (X_k-\overset{\text {c}}{X}_k) \Big )\nonumber \\&\qquad \times \Big (\langle {u}_{l,m}^\text {M} \rangle + \langle {u}_{l,mn}^\text {M}\rangle (X_n-\overset{\text {c}}{X}_n) \Big ) \, \mathrm d V + \frac{1}{2} D^\text {M}_{ijklmn} \int _{\Omega ^P} \langle {u}_{i,jk}^\text {M}\rangle \langle {u}_{l,mn}^\text {M}\rangle \, \mathrm d V \nonumber \\&\quad = \frac{1}{2}V \Big ( C^\text {M}_{ijlm} \langle {u}_{i,j}^\text {M}\rangle \langle {u}_{l,m}^\text {M}\rangle + ( C^\text {M}_{ijlm} \bar{I}_{kn} + D^\text {M}_{ijklmn} ) \langle {u}_{i,jk}^\text {M}\rangle \langle {u}_{l,mn}^\text {M}\rangle \Big ), \end{aligned}$$

(17)

where

$$\begin{aligned} \bar{I}_{kn} = \frac{1}{V} \int _{\Omega ^P} \left( X_k-\overset{\text {c}}{X}_k\right) \left( X_n-\overset{\text {c}}{X}_n\right) \, \mathrm d V. \end{aligned}$$

(18)

Consequently, the macroscale energy of an RVE is expressed in terms of the gradient of macroscopic deformation. In what follows, it will be shown, by making use of asymptotic homogenization analysis, that the microscale energy can be formulated in terms of the gradient of macroscopic deformation as well leading to connections between the parameters.

3.2 The microscale energy for an RVE

Following the asymptotic homogenization method in [77], we reformulate the left-hand side of Eq. (10). The asymptotic homogenization method separates length scales by using global coordinates, ${\varvec{X}}$, for describing the global variation of the displacement, and by using local coordinates, $\varvec{y}$, for describing the local fluctuation of the displacement. We refer to [74] and [35, Appendix B] for a more detailed investigation of the multiscale asymptotic analysis applied in this work. We introduce the local coordinates:

$$\begin{aligned} y_j= \frac{1}{\epsilon }\left( X_j - \overset{\text {c}}{X}_j \right) , \end{aligned}$$

(19)

where $\epsilon$ is a homothetic ratio scaling global and local coordinates. We stress that the dimensions of an RVE in local coordinates can be arbitrarily chosen by varying $\epsilon$. For example, as depicted in Fig. 2, the size of an RVE is given by l in global coordinates, whereas it is denoted by w in local coordinates. If we choose $l=0.001$ mm, as measured in global coordinates, ${\varvec{X}}$, then it can be homothetically scaled to any dimension, such as $w=0.001$ mm or $w=1000$ mm in local coordinates, $\varvec{y}$, by setting the homothetic ratio to $\epsilon = 1.0$ or $\epsilon = 10^{-6}$, in such a way that the size of the RVE is kept constant in the global coordinates. We remark that the homothetic ratio is used to describe the relationship for the sizes of an RVE between global and local coordinates; however, the ratio between macroscale and microscale remains the same, $L/l=\text {const}$. We assume that the displacement field is a smooth function on the macroscopic level and $\varvec{y}$-periodic in local coordinates resulting in vanishing mean local fluctuations within each RVE. Hence, the decomposition of the microscale displacement is additively decomposed into a macroscale displacement and into local fluctuations defined on different scales—they are independent.

Fig. 2

Illustration of the approximation of the asymptotic expansion

Following [61], the displacement field of an RVE, $\Omega ^P$, at global coordinates ${\varvec{X}}$, is expanded by using an asymptotic series with homothetic ratio $\epsilon$, where, in general, the corresponding coefficients depend on global coordinates, ${\varvec{X}}$, as well as on local coordinates, $\varvec{y}$, which are related by Eq. (19):

$$\begin{aligned} \varvec{u ^\text {m}}({\varvec{X}}) = \overset{0}{\varvec{u}}( {\varvec{X}}, \varvec{y}) + \epsilon \overset{1}{\varvec{u}}({\varvec{X}},\varvec{y}) + \epsilon ^2 \overset{2}{\varvec{u}}({\varvec{X}}, \varvec{y}) + \cdots , \end{aligned}$$

(20)

where $\overset{n}{\varvec{u}}( {\varvec{X}}, \varvec{y})$ (n = 0, 1, 2, ...) are assumed to be $\varvec{y}$-periodic. We shall see later that the first term $\overset{0}{\varvec{u}}( {\varvec{X}}, \varvec{y})$ is independent of $\varvec{y}$. We apply now the elasticity problem in statics [by using Eq. (8) for a Cauchy continuum] as it needs to be fulfilled within the RVE:

$$\begin{aligned} \big ( C_{ijkl}^\text {m} u^\text {m}_{k,l} \big )_{,j} + f_{i} = 0 \qquad \forall {\varvec{X}} \in \Omega ^P, \end{aligned}$$

(21)

where the body force, $\varvec{f}$, is a given function. By inserting Eq. (20) as well as using the chain rule with the aid of the relation in Eq. (19), we obtain

$$\begin{aligned} u^\text {m}_{i,j}= & {} \Big ( \overset{0}{u}_i( {\varvec{X}}, \varvec{y}) + \epsilon \overset{1}{u}_i ({\varvec{X}},\varvec{y}) + \epsilon ^2 \overset{2}{u}_i({\varvec{X}}, \varvec{y}) + \cdots \Big )_{,j} \nonumber \\= & {} \overset{0}{u}_{i,j} + \frac{\partial \overset{0}{u}_i}{\partial y_k} \frac{\delta _{kj}}{\epsilon } + \epsilon \overset{1}{u}_{i,j} + \epsilon \frac{\partial \overset{1}{u}_i}{\partial y_k} \frac{\delta _{kj}}{\epsilon } + \epsilon ^2 \overset{2}{u}_{i,j} + \epsilon ^2 \frac{\partial \overset{2}{u}_i}{\partial y_k} \frac{\delta _{kj}}{\epsilon } + \cdots \end{aligned}$$

(22)

Using the latter in Eq. (21),

$$\begin{aligned}&\bigg ( C_{ijkl}^\text {m} \Big ( \overset{0}{u}_{k,l} + {\frac{1}{\epsilon }} \frac{\partial \overset{0}{u}_k}{\partial y_l} + \epsilon \overset{1}{u}_{k,l} + \frac{\partial \overset{1}{u}_k}{\partial y_l} + \epsilon ^2 \overset{2}{u}_{k,l} + \epsilon \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big ) \bigg )_{,j} \nonumber \\&\quad + \frac{\partial }{\partial y_j}\bigg ( C_{ijkl}^\text {m} \Big ( {\frac{1}{\epsilon }} \overset{0}{u}_{k,l} + {\frac{1}{\epsilon ^2}} \frac{\partial \overset{0}{u}_k}{\partial y_l} + \overset{1}{u}_{k,l} + {\frac{1}{\epsilon }} \frac{\partial \overset{1}{u}_k}{\partial y_l} + \epsilon \overset{2}{u}_{k,l} + \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big ) \bigg ) + f_{i} = 0, \end{aligned}$$

(23)

and then, gathering terms having the same order in $\epsilon$ leads to the following terms:

• of the order $\epsilon ^{-2}$,

  $$\begin{aligned} \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{0}{u}_k}{\partial y_l} \Big ) = 0, \end{aligned}$$

  (24)

• of the order $\epsilon ^{-1}$,

  $$\begin{aligned} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{0}{u}_k}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m} \overset{0}{u}_{k,l} \big ) + \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{1}{u}_k}{\partial y_l} \Big ) = 0, \end{aligned}$$

  (25)

• and of the order $\epsilon ^{0}$,

  $$\begin{aligned} \big ( C_{ijkl}^\text {m} \overset{0}{u}_{k,l} \big )_{,j} + \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{1}{u}_k}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m} \overset{1}{u}_{k,l} \big ) + \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big ) + f_i = 0. \end{aligned}$$

  (26)

By solving these partial differential equations, Eq. (20) can be rewritten as:

$$\begin{aligned} u^\text {m}_i({\varvec{X}},\varvec{y}) = \overset{0}{u}_i({\varvec{X}}) + \epsilon \varphi _{abi}(\varvec{y}) \overset{0}{u}_{a,b}({\varvec{X}}) + \epsilon ^2 \psi _{abci}(\varvec{y}) \overset{0}{u}_{a,bc}({\varvec{X}}) + \cdots , \end{aligned}$$

(27)

where $\varphi _{abi}(\varvec{y})$ and $\psi _{abci}(\varvec{y})$ are both $\varvec{y}$-periodic, and they are the solutions of the following two partial differential equations:

$$\begin{aligned}&\frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \Big ( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ak} \delta _{bl} \Big ) \bigg ) = 0, \end{aligned}$$

(28)

$$\begin{aligned}&\frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \Big ( \frac{\partial \psi _{abck}}{\partial y_l} + \varphi _{abk} \delta _{lc} \Big ) \bigg ) + C_{ickl}^\text {m} \Big ( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ka} \delta _{lb} \Big ) - {C}_{icab}^\text {M} = 0. \end{aligned}$$

(29)

It should be noted that the choice of the indices of the third-order tensor $\varvec{\varphi }$ and fourth-order tensor $\varvec{\psi }$ differs from those in [15, 61]. Since $\varvec{\varphi }$ and $\varvec{\psi }$ are expressed in the Cartesian coordinates, we choose to use lower indices like $\varphi _{abk}$ and $\psi _{abck}$ here. They are mathematically and physically exactly identical to those in [15, 61]. We refer to the appendix for a derivation of Eqs. (27), (28), and (29). Since the first term $\overset{0}{u}_i({\varvec{X}})$ depends only on the macroscopic coordinates, ${\varvec{X}}$, it is assumed to be the known macroscopic displacement $\overset{0}{u}_i({\varvec{X}}) =u^\text {M}_i({\varvec{X}})$ such that Eq. (20) provides

$$\begin{aligned} u^\text {m}_i({\varvec{X}},\varvec{y}) = {u}_i({\varvec{X}})^\text {M} + \epsilon \varphi _{abi}(\varvec{y}) {u}_{a,b}^\text {M}({\varvec{X}}) + \epsilon ^2 \psi _{abci}(\varvec{y}) {u}_{a,bc}^\text {M}({\varvec{X}}) + \cdots . \end{aligned}$$

(30)

We wish to express the energy on the microscale; thus, we need the gradient of the microscale displacement:

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j}&= \Big ( u_i^\text {M} + \epsilon \varphi _{abi} u_{a,b}^\text {M} + \epsilon ^2 \psi _{abci} u_{a,bc}^\text {M} + \cdots \Big )_{,j} \\&= u_{i,j}^\text {M} + \frac{\partial \varphi _{abi}}{\partial y_j} u^\text {M}_{a,b} + \epsilon \varphi _{abi} u_{a,bj}^\text {M} + \epsilon \frac{\partial \psi _{abci}}{\partial y_j} u^\text {M}_{a,bc} + \epsilon ^2 \psi _{abci} u^\text {M}_{a,jbc} + \cdots , \end{aligned} \end{aligned}$$

(31)

with the same accuracy, i.e., after neglecting higher than second gradients and inserting Eq. (16) with the aid of Eq. (19), we write

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j}&= \Big (\delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \Big ) u^\text {M}_{a,b} + \epsilon u^\text {M}_{a,bc} \Big ( \varphi _{abi} \delta _{jc} + \frac{\partial \psi _{abci} }{\partial y_j} \Big ) + \cdots \\&= \Big (\delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \Big ) \Big ( \langle {u}_{a,b}^\text {M} \rangle + \epsilon y_c \langle u_{a,bc}^\text {M} \rangle \Big ) + \epsilon \langle u_{a,bc}^\text {M} \rangle \Big ( \varphi _{abi} \delta _{jc} + \frac{\partial \psi _{abci} }{\partial y_j} \Big ) + \cdots \\&= L_{abij}\langle {u}_{a,b}^\text {M} \rangle + \epsilon M_{abcij} \langle {u}_{a,bc}^\text {M} \rangle + \cdots , \end{aligned} \end{aligned}$$

(32)

where

$$\begin{aligned} \begin{aligned} L_{abij}&= \delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j}, \\ M_{abcij}&= y_{c} \Big ( \delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \Big ) + \Big ( \varphi _{abi} \delta _{jc} + \frac{\partial \psi _{abci} }{\partial y_j} \Big ). \end{aligned} \end{aligned}$$

(33)

By using the latter on the left-hand side of Eq. (10), the microscale energy becomes

$$\begin{aligned} \int _{\Omega ^P} \frac{1}{2} C^\text {m}_{ijkl} u^\text {m}_{i,j} u^\text {m}_{k,l} \, \mathrm d V= & {} \frac{1}{2} \int _{\Omega ^P} \Big ( C_{ijkl}^\text {m} L_{abij} L_{cdkl} \langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,d}^\text {M} \rangle \nonumber \\&+\, \epsilon ^2 C_{ijkl}^\text {m} M_{abcij} M_{defkl} \langle {u}_{a,bc}^\text {M}\rangle \langle {u}_{d,ef}^\text {M}\rangle +2 \epsilon C_{ijkl}^\text {m} L_{abij} M_{cdekl} \langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,de}^\text {M}\rangle \Big ) \, \mathrm d V \nonumber \\= & {} \frac{V}{2}\Big ( \bar{C}_{abcd} \langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,d}^\text {M}\rangle + \bar{D}_{abcdef}\langle {u}_{a,bc}^\text {M}\rangle \langle {u}_{d,ef}^\text {M}\rangle + \bar{G}_{abcde}\langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,de}^\text {M}\rangle \Big ) \ \end{aligned}$$

(34)

where

$$\begin{aligned} \bar{C}_{abcd}= & {} \frac{1}{V} \int _{\Omega ^P} C_{ijkl}^\text {m} L_{abij} L_{cdkl} \, \mathrm d V, \nonumber \\ \bar{D}_{abcdef}= & {} \frac{\epsilon ^2}{V} \int _{\Omega ^P} C_{ijkl}^\text {m} M_{abcij} M_{defkl} \, \mathrm d V, \nonumber \\ \bar{G}_{abcde}= & {} \frac{2\epsilon }{V} \int _{\Omega ^P} C_{ijkl}^\text {m} L_{abij} M_{cdekl} \, \mathrm d V. \end{aligned}$$

(35)

Because we have assumed centrosymmetric materials, the rank 5 tensor vanishes, $\bar{\varvec{G}}=0$. We realize immediately by comparison with Eq. (17) that

$$\begin{aligned} C^\text {M}_{ijlm}= & {} \bar{C}_{ijlm}, \nonumber \\ C^\text {M}_{ijlm} \bar{I}_{kn} + D^\text {M}_{ijklmn}= & {} \bar{D}_{ijklmn}, \end{aligned}$$

(36)

where

$$\begin{aligned} \bar{I}_{kn} = \int _{\Omega ^P} (X_k-\overset{\text {c}}{X}_k)(X_n-\overset{\text {c}}{X}_n) \, \mathrm d V =\epsilon ^2 \int _{\Omega ^P}y_k y_n \, \mathrm d V. \end{aligned}$$

(37)

Therefore, we have generated an algorithm delivering effective parameters:

$$\begin{aligned} C^\text {M}_{abcd}= & {} \frac{1}{V} \int _{\Omega ^P} C_{ijkl}^\text {m} L_{abij} L_{cdkl} \, \mathrm d V, \nonumber \\ D^\text {M}_{abcdef}= & {} \epsilon ^2 \Bigg ( \frac{1}{V} \int _{\Omega ^P} C_{ijkl}^\text {m} M_{abcij} M_{defkl} \, \mathrm d V - C^\text {M}_{abef} \int _{\Omega ^P}y_c y_d \, \mathrm d V \Bigg )\ , \end{aligned}$$

(38)

after computing $\varvec{\varphi }$ and $\varvec{\psi }$ in an RVE.

4 Numerical solution of strain gradient homogenization problems

The final goal is to obtain the coefficients in the classical stiffness tensor $C^\text {M}_{ijlm}$ and for the strain gradient stiffness tensor $D^\text {M}_{ijklmn}$. For their determination, we need to solve Eqs. (28), (29). For the sake of simplicity, we restrict the analysis to a 2D case, such that all indices are from $\{1,2\}$. Within the RVE, which is the computational domain, $\Omega$, Eqs. (28), (29) are solved by using the Galerkin procedure in the FEM with continuous shape functions. All boundary conditions are assumed to be periodic; in other words, the values of $\phi _{abi}$, $\psi _{abci}$ are given by Dirichlet boundary conditions.

Indeed, the solutions of Eqs. (28), (29) are determined for specific a, b indices (classical coefficients) as well as a, b, c indices (strain gradient coefficients). Consider the case where $a=1$ and $b=1$ leading to the weak form of Eq. (28) after multiplying by an arbitrary test function vanishing on Dirichlet boundaries and integrating by parts:

$$\begin{aligned} \int _\Omega \bigg ( C_{ijkl}^\text {m} \Big (\frac{\partial \varphi _{11k}}{\partial y_l} + \delta _{1k} \delta _{1l} \Big ) \bigg ) \frac{\partial \updelta \varphi _{11i}}{\partial y_j} \, \mathrm d V = 0, \end{aligned}$$

(39)

from which we determine $\varphi _{abi}$ after solving for $ab={11,12,21,22}$. By knowing $\varvec{\varphi }$, for example in the case of $a=1$, $b=1$, and $c=2$, we then solve

$$\begin{aligned}&\int _\Omega \Bigg ( \bigg ( C_{ijkl}^\text {m} \Big ( \frac{\partial \psi _{112k}}{\partial y_l} + \varphi _{11k} \delta _{l2} \Big ) \bigg ) \frac{\partial \updelta \psi _{112i}}{\partial y_j} \nonumber \\&\quad - C_{i2kl}^\text {m} \Big ( \frac{\partial \varphi _{11k}}{\partial y_l} + \delta _{k1} \delta _{l1} \Big ) \updelta \psi _{112i} + {C}_{i211}^\text {M} \updelta \psi _{112i} \Bigg ) \, \mathrm d V= 0. \end{aligned}$$

(40)

The result for $\varvec{\psi }$ follows after solving for $abc=\{111, 112, 121, 122, 211, 212, 221, 222\}$. By inserting $\varvec{\varphi }$ and $\varvec{\psi }$ in Eq. (33) and then applying Eq. (38), we determine $\varvec{C}^\text {M}$ and $\varvec{D}^\text {M}$.

We have used the open-source software FEniCS for our computations. The CAD models of the RVE have been created on the open-source platform SALOME 7.6, and FEM discretizations of the CAD models were realized by the mesh generator NetGen built in SALOME 7.6. Application of the periodic conditions and creating the matrices was done via Python. We emphasize that the generated mesh has to possess perfectly matching vertices on opposite (periodic) boundaries for consistency. Via NetGen, this has been automatically fulfilled by mapping the meshes between periodic surfaces. The mesh is then transferred to FEniCS, and the numerical solution of weak forms has been obtained by using the iterative solver gmres with the preconditioner jacobi with relative tolerance $10^{-5}$ and absolute tolerance $10^{-10}$ to ensure the accuracy of the calculations.

5 Identification of the classical and strain gradient stiffness tensors

In order to demonstrate the approach, the classical and strain gradient stiffness tensors are identified for specific cases. First, consistency is examined by computing $\varvec{C}^\text {M}$ and $\varvec{D}^\text {M}$ for the case of a homogeneous material. As expected, the approach delivers zero for $\varvec{D}^\text {M}$ (within the numerical tolerance). Concretely, the implementation leads to $\varvec{D}^\text {M}$ components $10^{-6}$ N or smaller for a material with a Young’s modulus, E, of 100 MPa and a Poisson’s ratio, $\nu$, of 0.3. This is consistent with the interpretation that for a homogeneous material, all corresponding strain gradient material parameters must vanish.

Fig. 3

Geometry of square lattice structures and different selections of RVE

Then a simple geometry, the so-called square lattice structure in 2D, is investigated. The square lattice structure has been widely used in engineering practice [9], as shown in Fig. 3, where gray lines build up a truss- like structure. This inner structure is expected to deliver a $D_4$ invariant material symmetry group [11, 12, 79].

For the microscale material parameters of the lattice structure, isotropic material properties are used:

$$\begin{aligned} C_{ijkl}^\text {m}= & {} \lambda \delta _{ij} \delta _{kl} + \mu \delta _{ik} \delta _{jl} + \mu \delta _{il} \delta _{jk}, \nonumber \\ \lambda= & {} \frac{E \nu }{(1+\nu ) (1-2\nu )}, \ \mu = \frac{E}{2(1+\nu )}. \end{aligned}$$

(41)

Voigt notation is used for representing the tensors; for convenience, we refer to Tables 1 and 2 for the chosen convention based on the work by [12].

Table 1 Voigt notation used for 2D strain tensors

Table 2 Voigt notation used for 2D strain gradient tensors

5.1 Parameter determination for the square lattice structure

In the case of the square lattice structure, we assume that the material parameters of the inclusion are much smaller than those of the matrix. Simply stated, we consider an additively manufactured truss-like structure with rods made out of a polymer and voids being the inclusions. By choosing material properties as compiled in Table 3 and the volume fraction of the inclusion to be $81\%$, we select different RVEs and determine the parameters. The RVEs are generated by repeating the corresponding basic cell, while the size of the basic cell is kept constant. Specifically, the RVEs constitute of one cell, four cells, and nine cells, as depicted in Fig. 3. The results for

$$\begin{aligned} \varvec{C}^\text {M}= & {} \begin{pmatrix} C_{1111} &{} C_{1122} &{} 0 \\ &{} C_{1111} &{} 0 \\ \text {sym.} &{} &{} C_{1212} \\ \end{pmatrix}\ , \nonumber \\ \varvec{D}^\text {M}= & {} \begin{pmatrix} D_{111111}&{} D_{111221} &{} D_{111122} &{}0 &{} 0 &{} 0 \\ &{} D_{221221} &{} D_{221122} &{} 0 &{} 0 &{} 0 \\ &{} &{} D_{122122} &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} D_{111111} &{} D_{111221} &{} D_{111122} \\ &{}\text {sym.} &{} &{} &{} D_{221221} &{} D_{221122} \\ &{} &{} &{} &{} &{} D_{122122} \\ \end{pmatrix} \ . \end{aligned}$$

(42)

are compiled in Table 4.

Table 3 Material properties used in lattice structures

Table 4 Parameters determined for the square lattice

Fig. 4

Different sizes of basic cell with the same volume ratio

Table 5 Identified nonzero strain gradient stiffness parameters for the square lattice structure in units of N

In order to investigate how the size of the basic cell affects classical and strain gradient stiffness tensors, different sizes of basic cells ($0.2\times 0.2$, $0.5\times 0.5$) are selected and the corresponding results are compared with those obtained with the basic cells size $1\times 1$, see Fig. 4 for the basic cells. Due to the fact that these three structures have the same topology, the same material properties, and the same inclusion volume fraction, the corresponding classical stiffness tensors are identical. However, this is not so in the case of the strain gradient stiffness tensors, as compiled in Table 5. All nonvanishing parameters approach zero as the size of basic cells is decreasing. We remark that this fact is intuitively correct. Indeed, when the size of basic cells vanishes, the material becomes homogeneous resulting in a vanishing $\varvec{D}^\text {M}$. This computation also illustrates the role of the homothetic ratio $\epsilon$. To this end, let us consider the parameter $D_{221221}$ as shown in Table 5. In the case of a basic cell 1$\times$1, this parameter is four times larger than that computed for the case of a basic cell 0.5$\times$0.5, and it is 25 times larger than that computed for the case of a basic cell 0.2$\times$0.2. The magnification factors (4 or 25) are equal to the square of homothetic ratios of these three basic cells as directly given in Eq. (35).

6 Computational validation of determined parameters

In order to verify and to validate the numerical values of the determined parameters, we perform three different computations: a computation on the microscale by incorporating the inner structure, a computation only with the determined classical stiffness tensor on the macroscale by using the homogenized structure, and another computation with both the determined classical stiffness tensor and the strain gradient tensor on the macroscale by using the homogenized structure.

As suggested in [39, 71, 88], the problem of strain gradient elasticity is solved by using a weak form that, in the linear setting, leads to an $H^2$ norm about the trial solutions as well as test functions. Hence, the corresponding finite-dimensional approximations are guaranteed to lie in a function space that is at least of $C^1$ continuity. In order to obtain this property, isogeometric FEM is employed with non-uniform rational Bezier splines (NURBS)-based shape functions. The isogeometric FEM is able to ensure $C^n$ continuity in one single patch, which is appropriate for 2D simple geometries as in the present case. A detailed discussion of the NURBS basis and isogeometric FEM as well as the weak formulation of strain gradient elasticity can be found in [24,25,26,27, 38, 50, 54, 55]. The deformation energy that quantitatively describes the overall deformation behavior of the structures is used to compare the results.

Fig. 5

Boundary conditions for computations

The boundary conditions for the simulations are shown in Fig. 5. The left side of the structure is clamped, and on the right side of the structure, a rotation is prescribed along the center of the right edge. Two different types of computations are performed in the following subsections. In Sect. 6.1, the computations are done for the lattice structures with different macrosizes but the same sizes of basic cell, and in Sect. 6.2, we conduct computations for lattice structures with the same macrosizes but with different sizes of internal basic cells. The total volume remains the same in this case due to the fact that the ratio of the cell wall length to thickness of the basic cell is held constant with a ratio 1 to 10.

6.1 Computations for square lattices with the same basic cell sizes and varied macrosizes

In this section, computations for the square lattice with the same sizes of the basic cell but with different macrosizes as shown in Fig. 6 are performed. The size of the basic cell is 1 mm $\times$ 1 mm, and the selected lattices are of the macrosizes:

• 2 mm $\times$ 2 mm,

• 4 mm $\times$ 4 mm,

• 6 mm $\times$ 6 mm,

• 10 mm $\times$ 10 mm.

Fig. 6

Selected simulations for square lattice with the same size microstructure

The results of the simulations are shown in Fig. 7, where the vertical axis stands for the strain energy of the structures (in mJ) and the horizontal axis stands for the prescribed rotation (in rad). The black solid lines in Fig. 7 represent the results on the microscale. We consider this solution to be the correct one. The blue dashed line with square markers represents the computations of the homogenized structure by using the classical stiffness tensor. The yellow dashed line with circle markers represents the simulations for the homogenized structure when taking the strain gradient effect into account.

The blue lines show a smaller strain energy with regard to the microscale due to the absence of the higher-order strain gradient energy. We remark that while keeping the sizes of the basic cells unchanged, with increasing macrosizes of the structures, namely L / l becoming larger and larger, the computational results of the classical elasticity theory approach that on the microscale. We may say that in a large macroscale $L/l>10$, classical elasticity is adequate to guarantee the accuracy of the computation. However, when the macroscopic length scale is of the same order of its sizes of the internal substructures, the strain gradient effect becomes significant. This phenomenon is also known as size effect.

Fig. 7

Comparison of strain energies for square lattice structures with different macroscale sizes

6.2 Computations for square lattices with varied basic cell sizes and the same macrosizes

In order to verify the identified parameters for square lattices with different basic cell sizes but the same macrosizes even further, computations are conducted in this section. Three square lattices are selected as shown in Fig. 8. These three lattices possess the same macrosizes 4 mm $\times$ 4 mm. Their basic cell sizes are 1 mm $\times$ 1 mm, 0.5 mm $\times$ 0.5 mm, and 0.2 mm $\times$ 0.2 mm for the left, the middle, and the right lattice as shown in Fig. 8, respectively, which divides the macro-domain into 16, 64, and 400 basic cells. The computations are shown in Figs. 9 and 10. Figure 9 indicates that with increasing basic cell sizes, the strain energy at the rotation of 0.2 radian shows an increasing trend at the microscale. As it was mentioned above, this scale-dependent (depends on L / l) phenomenon is also known as size effect.

Fig. 8

Selected simulations for square lattices with basic cells of varied sizes

Fig. 9

Comparative computations between microscale and macroscale of elasticity

Fig. 10

Comparisons between computations in microscale, macroscale of elasticity, and macroscale of strain gradient for square lattice structures with different number of cells

The computations on the macroscale of elasticity are identical for these three cases due to the fact that the ratio of the cell wall length to the thickness of the basic cell is fixed with a ratio 1 to 10. The computation on the macroscale of elasticity is independent of the scale ratio, and they show a significant error compared with the microscale where the scale ratio (L / l) is getting smaller, and the size effect could not be ignored. When the scale ratio (L / l) is getting larger, which means the basic cell sizes is decreasing, the computations on the macroscale of elasticity are gradually approaching those of the microscale. In such a case, for example $L/l>20$, the size effect can be ignored. It can be also observed from Fig. 10a–c that the computations with strain gradient show a good quantitative match with the microscale, which means that by taking the strain gradient stiffness tensor into account, the size effect of the lattice structure is fully resolved.

7 Conclusions

A homogenization approach based on the asymptotic analysis has been exploited for developing a methodology in order to determine stiffness parameters of a metamaterial. Specifically, the strain gradient theory was used on the macroscale. The expressions of classical stiffness tensor and strain gradient stiffness tensor have been derived, and the FEM has been successfully used to solve the partial differential equations generated from the homogenization procedure. The so-called square lattice structure has been investigated, and their material parameters are explicitly computed. The proposed approach guarantees that the parameters of strain gradient stiffness tensors vanish as the material becomes homogeneous. Moreover, it ensures that strain gradient-related parameters are independent on the repetition of RVE, but dependent on the intrinsic size of the material. In order to validate the parameters determined by this methodology, additional numerical computations of the square lattice with different sizes have been performed. The numerical results show that the size effect of the lattice can be accurately captured by using the strain gradient theory with the parameters determined by the methodology applied herein. We emphasize that this methodology can be applied to any metamaterial made of a substructure with an RVE.

Appendix: Asymptotic solution for the displacement field

The asymptotic solution for an RVE is derived. Specifically, the solutions of Eqs. (24), (25), and (26) are shown.

We start with Eq. (24). Because $C_{ijkl}^\text {m}$ is a function of $\varvec{y}$, the only possible general solution of Eq. (24) is to restrict $\overset{0}{u}_i({\varvec{X}})$, since it is $\varvec{y}$-periodic and has a bounded gradient. The solution in the order of $\epsilon ^{-2}$ can be given as:

$$\begin{aligned} \overset{0}{u}_i = \overset{0}{u}_i({\varvec{X}}). \end{aligned}$$

(43)

Note that $\overset{0}{u}_i({\varvec{X}})$ depends only on the macroscopic coordinates. It is assumed to be the known macroscopic displacement $\overset{0}{u}_i({\varvec{X}}) =u^\text {M}_i({\varvec{X}})$. By substituting Eq. (43) into Eq. (25), by introducing $\varphi _{abc}=\varphi _{abc}(\varvec{y})$, for the inverse operation, we obtain

$$\begin{aligned}&\frac{\partial C_{ijab}^\text {m}}{\partial y_j} \frac{\partial \overset{0}{u}_a}{\partial X_b} = - \frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \frac{\partial \overset{1}{u}_k}{\partial y_l} \bigg ), \nonumber \\&\frac{\partial C_{ijab}^\text {m} }{\partial y_j} = - \frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \frac{\partial \varphi _{abk} }{\partial y_l} \bigg ), \nonumber \\&\frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \Big ( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ak} \delta _{bl} \Big ) \bigg ) = 0. \end{aligned}$$

(44)

Then, the general solution of Eq. (25) can be given as:

$$\begin{aligned} \overset{1}{u}_i = \varphi _{abi} \overset{0}{u}_{a,b} + \overset{1}{\bar{u}}_i({\varvec{X}}), \end{aligned}$$

(45)

where $\overset{1}{\bar{u}}_i =\overset{1}{\bar{u}}_i({\varvec{X}})$ are integration constants in $\varvec{y}$.

Substitution of Eqs. (43) and (45) (with $\overset{1}{\bar{u}}_i({\varvec{X}}) = 0$) into Eq. (26) leads to

$$\begin{aligned} C_{ijkl}^\text {m} \overset{0}{u}_{k,lj} + C_{ijkl}^\text {m} \frac{\partial \varphi _{abk}}{\partial y_l} \overset{0}{u}_{a,bj} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m} \varphi _{abk} \big ) \overset{0}{u}_{a,bl} + \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big ) + f_i = 0. \end{aligned}$$

(46)

Please note that the body force $\varvec{f}$ keeps unchanged on the micro- and macroscales. We recall the governing equation in the macroscale which reads [3]:

$$\begin{aligned}&\Bigg (\frac{\partial w^\text {M}}{\partial u_{i,j}^\text {M}} - \Big (\frac{\partial w^\text {M}}{\partial u_{i,jk}^\text {M}}\Big )_{,k} \Bigg )_{,j} + f_i= 0, \nonumber \\&C^\text {M}_{ijkl} u^\text {M}_{k,lj} - D_{ijklmn}^\text {M} u_{l,mnkj}^\text {M} + f_i= 0. \end{aligned}$$

(47)

By neglecting the fourth-order term in Eq. (47) and by using $\overset{0}{u}_i({\varvec{X}}) =u^\text {M}_i({\varvec{X}})$, we obtain

$$\begin{aligned} f_i = -C^\text {M}_{ijkl} u^\text {M}_{k,lj} = -C^\text {M}_{ijkl} \overset{0}{u}_{k,lj}. \end{aligned}$$

(48)

Substituting Eq. (48) into Eq. (46) leads to

$$\begin{aligned} \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big ) = -\Big ( C_{icab}^\text {m} + C_{ijkl}^\text {m} \frac{\partial \varphi _{abk}}{\partial y_l} \delta _{jc} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m} \varphi _{abk} \big ) \delta _{lc} - C^\text {M}_{icab} \Big ) \overset{0}{u}_{a,bc}. \end{aligned}$$

(49)

Because $\overset{0}{u}_{a,bc}$ is constant in $\varvec{y}$, we can introduce $\psi _{abci}$ depending on $\varvec{y}$ and decompose as follows:

$$\begin{aligned} \overset{2}{u}_i = \psi _{abci} \overset{0}{u}_{a,bc} + \overset{2}{\bar{u}}_i({\varvec{X}}), \end{aligned}$$

(50)

where $\psi _{abcd}=\psi _{abcd}(\varvec{y})$ and $\overset{2}{\bar{u}}_i({\varvec{X}})$ are integration constants in $\varvec{y}$. By substituting Eq. (50) (with $\overset{2}{\bar{u}}_i({\varvec{X}}) = 0$) into Eq. (49), it is found that the tensor $\psi _{abcd}$ must fulfill the following equation:

$$\begin{aligned} \frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \Big ( \frac{\partial \psi _{abck}}{\partial y_l} + \varphi _{abk} \delta _{lc} \big ) \bigg ) + C_{ickl}^\text {m} \Big ( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ka} \delta _{lb} \Big ) - {{C}}_{icab}^\text {M} = 0, \end{aligned}$$

(51)

such that Eq. (20) provides

$$\begin{aligned} u^\text {m}_i({\varvec{X}},\varvec{y}) = \overset{0}{u}_i({\varvec{X}}) + \epsilon \varphi _{abi}(\varvec{y}) \overset{0}{u}_{a,b}({\varvec{X}}) + \epsilon ^2 \psi _{abci}(\varvec{y}) \overset{0}{u}_{a,bc}({\varvec{X}}) + \cdots . \end{aligned}$$

(52)