Keywords

1 Introduction

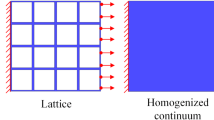
In continuum mechanics, conventional theory of elasticity fails to model structures, where the inner substructure starts affecting the material response. An intuitive explanation for this phenomenon relies on the length scale of the geometry, macroscale, ratio with respect to the inner substructure, microscale. As this ratio approaches one and the length scales are in the same order, then the effects of the substructure shall be incorporated and we call this structure related material system metamaterial. This inner substructure might be simply the molecular structure. For example, in the case of crystalline materials with a lattice type substructure, the grain orientation leads to material anisotropy or change in parameters like the yield stress, these phenomena have been studied among others also in Reuss (1929); Hashin and Shtrikman (1962); Sharo and Kachanov (2000); Lebensohn et al. (2004). Such an inner substructure can be generated by adhering different materials, which is the case in composite materials and “effective” parameters read as a result of a homogenization procedure, see for example Levin (1976); Willis (1977); Kushnevsky et al. (1998); Sburlati et al. (2018). A system with inclusions like a porous material can be seen as a metamaterial, where the voids affect the material properties at the macroscale, we refer to Eshelby (1957); Mori and Tanaka (1973); Kanaun and Kudryavtseva (1986); Hashin (1991); Nazarenko (1996); Dormieux et al. (2006). Additive manufacturing—as in the case of 3D printing—is another prominent example to build up a metamaterial as applied in Kochmann and Venturini (2013); Placidi et al. (2016); Turco et al. (2017); Solyaev et al. (2018); Ganzosch et al. (2018); Yang et al. (2018). Often it is assumed that the substructure is periodic in a sense that the same cell is repeated for generating the structure at the macroscale. This so-called representative volume element is useful for an analysis of effective parameters. All these approaches are based on the assumption that the material response is modeled with the same phenomenological models at both scales.

By using the homogenization approach as in Pideri and Seppecher (1997); Bigoni and Drugan (2007); Seppecher et al. (2011); Abdoul-Anziz and Seppecher (2018); Mandadapu et al. (2018), we understand that the assumption of having the same material model can lead to inaccurate results such that a higher order theory needs to be incorporated at the macroscale as developed by Eringen and Suhubi (1964); Mindlin (1964); Eringen (1968); Steinmann (1994); Eremeyev et al. (2012); Polizzotto (2013a; 2013b); Ivanova and Vilchevskaya (2016); Abali (2018). Various times it has been observed that a generalized mechanics description is necessary for modeling mechanical response accurately as the thinner or smaller structure starts deviating from classical results as detected in Namazu et al. (2000); Lam et al. (2003); McFarland and Colton (2005); Gruber et al. (2008); Chen et al. (2010); dell’Isola et al. (2019). For a simple beam bending problem, conventional theory of elasticity fails to estimate the experimental results, as a remedy, for example the strain gradient theory in Abali and Müller (2016) is capable of capturing this effect, as applied by Abali et al. (2015), Abali et al. (2017); however, we need to know the additional parameters introduced for incorporating higher order effects.

As the inner substructure and its material response is set, a detailed model of the microscale can be used to determine the additional parameters at the macroscale. Thus, the parameter determination in generalized mechanics is not a new approach, see for example Forest et al. (1999); Pietraszkiewicz and Eremeyev (2009); Giorgio (2016) or also by using the asymptotic analysis in Bensoussan et al. (1978); Hollister and Kikuchi (1992); Chung et al. (2001); Temizer (2012) with an application in Forest et al. (2001); Li (2011); Eremeyev (2016) Barboura and Li (2018); Ganghoffer et al. (2018); Turco (2019). Often a representative volume element has been used, we remark that it is difficult to justify that the higher order theory has to inherit one, see the discussion in Rahali et al. (2015). Thus, we search for a method without implementing a representative volume element at all. In this work we briefly show the second order theory and the additional parameters occurring in this theory. Then we apply the general algorithm proposed by Abali et al. (2019) and define the parameters for a specific geometry.

2 Computational Approach

We strictly follow Abali et al. (2019) and use the equivalence of the stored energy at the microscale,

$$\begin{aligned} \ \! ^{\text {m}}\!w = \frac{1}{2} \ \! ^{\text {m}}\!\varepsilon _{ij} \ \! ^{\text {m}}\!C_{ijkl} \ \! ^{\text {m}}\!\varepsilon _{kl}, \end{aligned}$$
(1)

to the stored energy at the macroscale,

$$\begin{aligned} \ \! ^{\text {M}}\!w = \frac{1}{2} \ \! ^{\text {M}}\!\varepsilon _{ij} \ \! ^{\text {M}}\!C_{ijkl} \ \! ^{\text {M}}\!\varepsilon _{kl} + \ \! ^{\text {M}}\!\varepsilon _{ij} G_{ijklm} \ \! ^{\text {M}}\!\varepsilon _{kl,m} + \frac{1}{2} \ \! ^{\text {M}}\!\varepsilon _{ij,k} D_{ijklmn} \ \! ^{\text {M}}\!\varepsilon _{lm,n}, \end{aligned}$$
(2)

such that we have

$$\begin{aligned} \begin{aligned} \int _{\mathcal {B}}\ \! ^{\text {m}}\!w \, \mathrm {d} \mathrm {v}=&\int _{\mathcal {B}}\ \! ^{\text {M}}\!w \, \mathrm {d} \mathrm {v}, \\ \int _{\mathcal {B}}\ \! ^{\text {m}}\!\varepsilon _{ij} \ \! ^{\text {m}}\!C_{ijkl} \ \! ^{\text {m}}\!\varepsilon _{kl} \, \mathrm {d} \mathrm {v}=&\ \! ^{\text {M}}\!C_{ijkl} \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij} \ \! ^{\text {M}}\!\varepsilon _{kl} \, \mathrm {d} \mathrm {v}+ 2 G_{ijklm} \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij} \ \! ^{\text {M}}\!\varepsilon _{kl,m} \, \mathrm {d} \mathrm {v}\\&+ D_{ijklmn} \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij,k} \ \! ^{\text {M}}\!\varepsilon _{lm,n} \, \mathrm {d} \mathrm {v}. \end{aligned} \end{aligned}$$
(3)

Consider that we assume that the macroscale material properties are appropriate for an isotropic and centrosymmetric material

$$\begin{aligned} \begin{aligned} \ \! ^{\text {M}}\!C_{ijkl} =&\, c_1 \delta _{i j} \delta _{k l} + c_2 (\delta _{i k} \delta _{j l} + \delta _{i l} \delta _{j k}), \\ D_{ijklmn} =&\, c_3 (\delta _{i j} \delta _{k l} \delta _{m n} + \delta _{i n} \delta _{j k} \delta _{l m} + \delta _{i j} \delta _{k m} \delta _{l n} + \delta _{i k} \delta _{j n} \delta _{l m} ) + c_4 \delta _{i j} \delta _{k n} \delta _{m l}\\&+ c_5 (\delta _{i k} \delta _{j l} \delta _{m n} + \delta _{i m} \delta _{j k} \delta _{l n} + \delta _{i k} \delta _{j m} \delta _{l n} + \delta _{i l} \delta _{j k} \delta _{m n})\\&+ c_6 (\delta _{i l} \delta _{j m} \delta _{k n} + \delta _{i m} \delta _{j l} \delta _{k n} )\\&+ c_7 (\delta _{i l} \delta _{j n} \delta _{m k} + \delta _{i m} \delta _{j n} \delta _{l k} + \delta _{i n} \delta _{j l} \delta _{k m} + \delta _{i n} \delta _{j m} \delta _{k l}),\\ G_{ijklm} =&\, 0 \ , \end{aligned} \end{aligned}$$
(4)

with the unknown material parameters, \(\varvec{c} = \{c_1, c_2, c_3, c_4, c_5, c_6, c_7\}\), which we obviously intend to determine. By simply inserting the latter into the energy equivalence and writing in a linear algebra fashion, as an example for one case denoted by the index 1 as follows:

$$\begin{aligned} \sum _{\alpha =1}^7 A_{1\alpha } c_\alpha = R_1, \end{aligned}$$
(5)

we observe that the coefficient matrix, \(\varvec{A}\), as well as the right hand side, R, can be computed

$$\begin{aligned} \begin{aligned} A_{11} =&\delta _{i j} \delta _{k l} \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij} \ \! ^{\text {M}}\!\varepsilon _{kl} \, \mathrm {d} \mathrm {v}\\ A_{12} =&(\delta _{i k} \delta _{j l} + \delta _{i l} \delta _{j k}) \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij} \ \! ^{\text {M}}\!\varepsilon _{kl} \, \mathrm {d} \mathrm {v}\\ A_{13} =&(\delta _{i j} \delta _{k l} \delta _{m n} + \delta _{i n} \delta _{j k} \delta _{l m} + \delta _{i j} \delta _{k m} \delta _{l n} + \delta _{i k} \delta _{j n} \delta _{l m} ) \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij,k} \ \! ^{\text {M}}\!\varepsilon _{lm,n} \, \mathrm {d} \mathrm {v}\\ A_{14} =&\delta _{i j} \delta _{k n} \delta _{m l} \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij,k} \ \! ^{\text {M}}\!\varepsilon _{lm,n} \, \mathrm {d} \mathrm {v}\\ A_{15} =&(\delta _{i k} \delta _{j l} \delta _{m n} + \delta _{i m} \delta _{j k} \delta _{l n} + \delta _{i k} \delta _{j m} \delta _{l n} + \delta _{i l} \delta _{j k} \delta _{m n}) \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij,k} \ \! ^{\text {M}}\!\varepsilon _{lm,n} \, \mathrm {d} \mathrm {v}\\ A_{16} =&(\delta _{i l} \delta _{j m} \delta _{k n} + \delta _{i m} \delta _{j l} \delta _{k n} ) \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij,k} \ \! ^{\text {M}}\!\varepsilon _{lm,n} \, \mathrm {d} \mathrm {v}\\ A_{17} =&(\delta _{i l} \delta _{j n} \delta _{m k} + \delta _{i m} \delta _{j n} \delta _{l k} + \delta _{i n} \delta _{j l} \delta _{k m} + \delta _{i n} \delta _{j m} \delta _{k l}) \int _{\mathcal {B}}\ \! ^{\text {M}}\!\varepsilon _{ij,k} \ \! ^{\text {M}}\!\varepsilon _{lm,n} \, \mathrm {d} \mathrm {v}\\ R_1 =&\int _{\mathcal {B}}\ \! ^{\text {m}}\!\varepsilon _{ij} \ \! ^{\text {m}}\!C_{ijkl} \ \! ^{\text {m}}\!\varepsilon _{kl} \, \mathrm {d} \mathrm {v}, \end{aligned} \end{aligned}$$
(6)

for a problem with given, \(\ \! ^{\text {M}}\!\varvec{\varepsilon }\), and computed, \(\ \! ^{\text {m}}\!\varvec{\varepsilon }\). By defining 7 distinct cases, the system, \(\varvec{A} \varvec{c} = \varvec{R}\), with \(\varvec{A}\) of rank 7 provides a unique determination of unknowns by \(\varvec{c} = \varvec{A}^{-1} \varvec{R}\).

These seven cases are the one of the key choices in the approach and we use the following seven cases:

$$\begin{aligned} \begin{array}{c} \text {case} 1: \ \! ^{\text {M}}\!\varvec{u} = \Big ( \frac{y}{2} , \frac{x}{2} , 0 \Big ) \quad \text {case} 2: \ \! ^{\text {M}}\!\varvec{u} = \Big ( x , 0 , 0 \Big ) \quad \text {case} 3: \ \! ^{\text {M}}\!\varvec{u} = \Big ( -x z , 0, x y \Big ) \\ \text {case} 4: \ \! ^{\text {M}}\!\varvec{u} = \Big ( x z , 0, -\frac{x^2}{2} \Big ) \quad \text {case} 5: \ \! ^{\text {M}}\!\varvec{u} = \Big ( -y z , 0, x y \Big ) \\ \text {case} 6: \ \! ^{\text {M}}\!\varvec{u} = \Big ( 0 , -y , \frac{y^2}{2} \Big ) \quad \text {case} 7: \ \! ^{\text {M}}\!\varvec{u} = \Big ( 0 , \frac{y^2}{2} , 0 \Big ), \end{array}\end{aligned}$$
(7)

where the only necessary condition seems to be such a choice generating a rank 7 coefficient matrix. It is challenging (if even possible) to suggest experimental designs for constructing this given homogenized displacement on the structure. If we use a linear strain measure,

$$\begin{aligned} \ \! ^{\text {M}}\!\varepsilon _{ij} = \frac{1}{2} \Big ( \frac{\partial \ \! ^{\text {M}}\!u_i}{\partial X_j} + \frac{\partial \ \! ^{\text {M}}\!u_j}{\partial X_i} \Big ) = \ \! ^{\text {M}}\!u_{(i,j)} , \end{aligned}$$
(8)

we can easily calculate the coefficient matrix for one of the aforementioned cases. For the right hand side, we compute \(\ \! ^{\text {m}}\!\varvec{u}\) for the detailed microscale of the continuum body, \({\mathcal {B}}\), by applying the boundary conditions acquired from the given \(\ \! ^{\text {M}}\!\varvec{u}\) evaluated on boundaries. Solving \(\ \! ^{\text {m}}\!\varvec{u}\) at the microscale is established by satisfying the weak form:

$$\begin{aligned} \text {Form} = \int _{\mathcal {B}}\ \! ^{\text {m}}\!C_{ijkl} \ \! ^{\text {m}}\!u_{(k,l)} \updelta u_{i,j} \, \mathrm {d} V , \end{aligned}$$
(9)

with the corresponding test functions, \(\updelta \varvec{u}\), from the same Hilbertian Sobolev space as the unknown, \(\ \! ^{\text {m}}\!\varvec{u}\), known as the Galerkin method,

$$\begin{aligned} \hat{{\mathcal {V}}} = \big \{ \ \! ^{\text {m}}\!\varvec{u} , \updelta \varvec{u} \in [{\mathcal {H}}^n(\varOmega )]^3 : \ \! ^{\text {m}}\!\varvec{u} , \updelta \varvec{u} = \text {given} \ \forall \varvec{x} \in \partial {\mathcal {B}}\big \}. \end{aligned}$$
(10)

The construction is automatized by using open-source programs like Salome, NetGen, and FEniCS (Alnaes et al. 2009; Logg et al. 2012), by using a Python code, we refer to Abali (2017) for a standard introduction of this weak form as well as the whole implementation.

3 Application

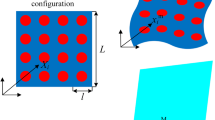
A pantographic structure has been studied for several systems, see for example Misra et al. (2018); Turco et al. (2019); dell’Isola et al. (2018); Solyaev et al. (2018); Harrison et al. (2018); Spagnuolo and Andreaus (2019); Greco et al. (2019). We aim at determining effective parameters in a strain gradient theory by applying the procedure from the last section for the pantographic structure as shown in Fig. 1. We emphasize that no representative volume element is used, instead, we simulate only a part of the whole structure as the macroscale displacement is provided as a function applied on this part.

Fig. 1.
figure 1

Pantographic structure CAD model designed in Salome open-source platform. Left: the whole structure. Right: part of the structure used for the computation with the shown mesh generated by Netgen.

Full size image

For a 3D printed pantographic structure out of ABS or PP, we may approximate a linear elastic response with Young’s modulus of \(E=400\times 10^6\) Pa and Poisson’s ratio of \(\nu =0.3\) leading to the following Lame parameters:

$$\begin{aligned} \lambda = \frac{E \nu }{(1+\nu )(1-2\nu )} \, , \ \mu = \frac{E}{2(1+\nu )}. \end{aligned}$$
(11)

They are used in the microscale material response

$$\begin{aligned} \ \! ^{\text {m}}\!C_{ijkl} = \lambda \delta _{i j} \delta _{k l} + \mu \delta _{i k} \delta _{i l} + \mu \delta _{i l} \delta _{j k}, \end{aligned}$$
(12)

which is simply the Hooke’s phenomenological model in isotropic linear elasticity. We emphasize that we use this assumption for clarity and fail to know if the material response of an additively manufactured polymer material is accurately captured by this model. Especially in semi-crystalline materials like PP, fused deposition modeling 3D printers may introduce extrusion orientation dependent anisotropic response. Moreover, the polymer material may behave hyperelastic. Another model is possible for obtaining the right hand side in Eq. (6) in order to increase the accuracy. Herein we use linear elastic model for demonstrating the methodology.

After solving 7 cases subsequently, computing the coefficient matrix, we have determined the 7 material and structure related parameters as follows:

$$\begin{aligned} \begin{aligned} c_{1}=\,&231\times 10^6\,\text {Pa} \\ c_{2}=\,&154\times 10^6\,\text {Pa} \\ c_{3}=\,&287\times 10^{-6}\,\text {N} \\ c_{4}=\,&58\times 10^{-6}\,\text {N} \\ c_{5}=\,&-264\times 10^{-6}\,\text {N} \\ c_{6}=\,&-32\times 10^{-6}\,\text {N} \\ c_{7}=\,&-32\times 10^{-6}\,\text {N} \end{aligned} \end{aligned}$$
(13)

4 Discussion and Conclusion

A simple yet elegant computational approach has been applied for obtaining the effective parameters as a result of a homogenization procedure in space in order to reduce the complexity of the structure modeling greatly. As an expense of additional parameters, we aim at incorporating the inner substructure effects by using higher gradients in the displacement. These additional parameters have been obtained by a purely computational methodology under the following assumptions:

  • At the microscale, the material model is linear elastic and isotropic.

  • At the macroscale, the material model is linear strain gradient elastic and isotropic as well as centrosymmetric.

Both assumptions are difficult to verify or falsify. We use these assumptions in the modeling for simplicity, more sophisticated approaches can be implemented as well, the general methodology remains still valid. The only possible validation for a concrete structure relies on an experimental study, which is left to further research endeavors.