Automating adjoint sensitivity analysis for multidisciplinary models involving partial differential equations

Abstract

We present a general framework for incorporating partial differential equation (PDE)-based models into gradient-based optimization of multidisciplinary systems by integrating FEniCSx with the recently developed Computational System Design Language (CSDL). CSDL is a domain-specific language designed to facilitate adjoint sensitivity analysis multidisciplinary design optimization (MDO). We use CSDL’s abstractions to link together sub-models representing different disciplines, not all of which are necessarily modeled by PDEs. For the subsystems which are modeled by PDEs, we use FEniCSx to compute partial derivatives of problem residuals, which CSDL can combine with derivatives from other disciplines using the chain rule and the adjoint method. The development of this framework is motivated by the problem of optimizing designs of electric vertical takeoff and landing (eVTOL) aircraft where, due to the relative novelty of this class of vehicle, there is currently a large, unexplored design space. Predicting the performance of eVTOL aircraft requires PDE-based modeling of various sub-problems, including electric motors, composite shell structures, and thermoelasticity and electrochemistry of battery packs. For system-level analysis and optimization, these must be coupled to non-PDE components, such as low-fidelity aerodynamic models, geometric design tools, and lumped-parameter battery and circuit models. In this work, we demonstrate the modeling flexibility and efficiency of this framework through classic optimal control and topology optimization problems with known solutions, and also challenging eVTOL-related applications including shape optimization of an electric motor, and aeroelastic coupling for gust response of an eVTOL wing. Given the generality of this framework, we expect it to facilitate research on a wide range of PDE-constrained MDO problems beyond eVTOL applications.

1 Introduction

The design and optimization of electrical vertical takeoff and landing (eVTOL) aircraft poses significant challenges due to the complexity in modeling and analyzing multiphysics systems. This includes predicting the stability and performance of eVTOL aircraft under different flight conditions, which requires evaluating a system-level model that integrates sub-models from various disciplines, such as weights, battery design, flight dynamics, and aeroelasticity. In order to achieve a reasonable turnaround time while maintaining sufficient accuracy for global evaluation, the system-level model may contain both high-fidelity PDE-based sub-models and low-fidelity non-PDE sub-models, highlighting the need for a multifidelity computational tool.

Multidisciplinary design optimization (MDO) is a widely used approach in this kind of problems, as it can incorporate all of the disciplines simultaneously, in conjunction with the numerical optimization algorithms (de Weck et al. 2007; Martins and Lambe 2013). MDO stands as a promising modeling technique used to solve complex engineering challenges such as coupled subsystems involving multiple disciplines, especially in the early stage of the design process. Its applications span a broad spectrum, including aircraft wing design (Benaouali and Kachel 2019), wind turbines (Ashuri et al. 2014), and spacecraft design (Taylor 2000; Jilla and Miller 2002). In the context of eVTOL aircraft design, gradient-based MDO is preferable over gradient-free methods, as evaluating high-fidelity sub-models can be extremely expensive in terms of computational cost.

To numerically solve the PDE components in gradient-based MDO problems, we can utilize the finite element method (FEM) to approximate the desired PDE solution in a finite-dimensional function space over a discretized domain. While the finite element method is widely used in structural analysis, it is also applicable to problems in any discipline that can be described by PDEs, such as heat transfer simulations of battery packs (Nelson et al. 2011), fluid–structure interaction of blood vessels (Kamensky 2021), or even weather predictions (Cotter and Shipton 2012).

However, existing tools for finite element analysis and MDO are not naturally compatible with each other and do not fulfill all the requirements mentioned above. Commercial finite element tools, such as Nastran, may come with fully integrated optimization modules, like Nastran SOL200 (Siemens 2014). However, it is challenging to export essential gradient information from a closed-source commercial solver for coupling with other sub-models, such as a low-fidelity particle-based aerodynamic solver built on purely algebraic equations.

Open-source finite element tools are easier to extract derivative information from, but not general enough to suit all disciplines involving PDE models. For example, while TACS (Kennedy and Martins 2014) specializes in structural optimization with beams and shells, it is challenging to be extended to multidisciplinary problems like aeroelasticity, as it can only provide finite element solutions for existing disciplines implemented in its C++ library, which currently supports structures and heat transfer.

FEniCS (Logg et al. 2011) is an open-source tool for solving PDEs that automates the efficient implementation of the finite element method through its abstraction of mathematical modeling and its automatic code generation capability. It uses the Python interface of the Unified Form Language, UFL (Alnæs et al. 2014a) to provide a user-friendly front end, where users only need to provide the mathematical model as a variational form of the PDE residual, and FEniCS will call the FEniCS Form Compiler, FFC (Ølgaard and Wells 2010) to generate finite element code in C++ and solve the problem in the backend of DOLFIN (Logg and Wells 2010).

The library dolfin-adjoint (Mitusch et al. 2019) is an adjoint-based optimization extension of FEniCS that minimizes the effort required to build an adjoint model based on a forward solver. However, due to its dependency on FEniCS, it requires that all sub-models be implemented in the Python interface of FEniCS or Firedrake (Rathgeber et al. 2016), limiting the use of non-PDE components like models represented by algebraic equations for preprocessing and postprocessing steps.

CSDL (Gandarillas et al. 2024) is a recently developed algebraic modeling language that automates the exact derivative computation for its native operations including array operations such as reshaping, reordering, and matrix–vector products, and fundamental operations such as logarithmic, exponential, and trigonometric functions. CSDL is designed to be compatible with external solvers using customized operations, requiring users to define the operations and the associated partial derivatives in the format that CSDL specifies. This allows CSDL to connect the external solvers with the rest of the model automatically and compute the total derivatives needed for the optimization using the chain rule and the adjoint method.

The aforementioned FEniCS is a prototypical external solver that would extend the capability of CSDL for PDE-based high-fidelity modeling. In this paper, we use FEniCSx (Scroggs et al. 2022; Baratta et al. 2023), the new version of the FEniCS library with significant improvements, including support for a broader range of element types and complex number computation, among others. We will refer to them as FEniCSx and the legacy FEniCS, respectively, in the remainder of this paper. In this work, we present a general framework that integrates FEniCSx with CSDL for efficient modeling, simulation and optimization of multidisciplinary and multifidelity systems involving some, but not exclusively, PDE-based subsystems.

We present FEMO,¹ a generalized tool that enables PDE solutions for multiphysics problems and provides automated derivative computation for optimization process. FEMO offers the following key features that enhance research in PDE-constrained MDO:

• (1) Highly modularized design that can be extended to interface external solvers, meeting the needs of large-scale multidisciplinary modeling and optimization

• (2) User-friendly API that minimizes the barrier of FEniCSx programming for optimization users, allowing them to focus on the modeling itself

• (3) Demonstrations of eVTOL-related applications, showcasing efficient modeling for coupling aerodynamic and structural solvers of different levels of fidelity, as well as innovative approach to incorporate shape parametrization into PDE solutions in the motor design application

The remainder of this paper is organized as follows. Section 2 introduces a model problem—namely, the optimal control of a nonlinear elliptic PDE—to illustrate the proposed methodology. It is followed with the implementation of FEMO in Sect. 3. In Sect. 4, we demonstrate the capabilities of this approach through a wide range of applications relevant to eVTOL subsystems, including topology optimization of a cantilever beam, shape optimization of an electric motor, and gust response simulation of an eVTOL wing and the associated sensitivity analysis. Section 5 draws conclusions and discusses possible future extensions of this work and anticipated challenges of applying it to system-level eVTOL aircraft design and optimization.

2 Methodology

We start with the definition of a PDE-constrained MDO problem in Sect. 2.1, and introduce a specific model problem—the optimal control of a nonlinear elliptic PDE. This model problem is used to illustrate the workflow of solving this optimization problem, which includes formulating the finite element equation with Nitsche’s method, and obtaining derivatives for gradient-based optimization through the automatic code generation capabilities in FEniCSx.

2.1 A glimpse at a PDE-constrained MDO problem

The diagram in Fig. 1 illustrates a representative PDE-constrained MDO process, which involves one or two high-fidelity PDE sub-models, and multiple mid- to low-fidelity algebraic sub-models. The sub-model that computes objective function could be a weighted combination of several sub-functions such as efficiency, cost, weight, or maximum loads.

In this process, coupling can occur in various ways among the sub-models, including one-way coupling and two-way coupling between disciplines. For instance, the two-way coupling between Discipline 1 and Discipline 2 could be used for load and displacement updates between an aerodynamic solver and a structural solver in aeroelastic analysis; the one-way coupling between Discipline n and Discipline $n-1$ could represent postprocessing for electric power losses based on solutions of the Maxwell’s equations in electromagnetic modeling.

Fig. 1

A representative MDO process that encapsulates the most challenging aspects typically encountered in such problems: (a) coupling multiple high-fidelity PDE sub-models; (b) combining sub-models for disciplines with and without PDEs. The orange boxes represent the high-fidelity PDE sub-models, while the green boxes represent the mid- to low-fidelity non-PDE sub-models. The pink box represents the sub-model that computes the objective function. (Color figure online)

2.2 A model problem: optimal control of a nonlinear elliptic PDE

The methodology for solving a PDE-constrained MDO problem is presented as a generalized approach. To illustrate the workflow, we walk through the modeling process using the optimal control of a nonlinear elliptic PDE as the model problem (Pörner and Wachsmuth 2017). This problem is commonly referred to as an inverse problem in the mathematical community, as the goal involves determining the source term given the analytical solution of the PDE. The mathematical model of this problem is formulated as

$$\begin{aligned} \text {minimize}&~~~ J(u,f) = \frac{1}{2}||u-g||_{L^2}^2 + \frac{\alpha }{2}||f||_{L^2}^2 \nonumber \\ \text {with respect to}&~~~ f \end{aligned}$$

(1a)

$$\begin{aligned} \text {such that}&~~~ -\varDelta u + u^3 = f ~~~ \text { in } \varOmega \nonumber \\&\quad \quad u = g ~~~ \text { on } \varGamma , \end{aligned}$$

(1b)

where $\varOmega$ is the domain of interest, $\varGamma$ is the outer boundary of $\varOmega$. The state variable $u:\varOmega \rightarrow \mathbb {R}$ and the control variable (or design variable) $f:\varOmega \rightarrow \mathbb {R}$ are constrained by a boundary value problem (BVP) represented by (1b). The BVP consists of a nonlinear elliptic equation, specifically a nonlinear Helmholtz equation in this case, and subject to a Dirichlet boundary condition. The objective function, defined in (1a), is formulated as the sum of the $L^2$ norm of the difference between the state variable u and the analytical solution g, and an $L^2$ regularization term that depends on the control variable f.

The goal of this optimal control problem is to determine the optimal values of f that lead to a state variable u with the desired profile matching the analytical solution g, while satisfying the nonlinear elliptic PDE associated with f. This model problem is relatively simple and easily abstracted in the optimization problem setting, but due to the nonlinearity in the PDE it still presents a challenge.

2.3 Finite element solution of the model problem

Recall the strong form of the nonlinear Helmholtz equation in (1b). Find u, such that

$$\begin{aligned} \begin{aligned} -\varDelta u + u^3&= f ~~~ \text { in } \varOmega { ,}\\ u&= g ~~~ \text { on } \varGamma { .} \end{aligned} \end{aligned}$$

The weak form is formulated as below. Find $u\in \mathcal {V}_\textrm{g}$, such that $\forall \,v\in \mathcal {V}_0$,

$$\begin{aligned} \int _{\varOmega } \nabla u \cdot \nabla v \,\textrm{d}\varOmega + \int _{\varOmega } u^3 v \,\textrm{d}\varOmega = \int _{\varOmega } f v \,\textrm{d}\varOmega \text {,} \end{aligned}$$

(2)

where $\mathcal {V}_\textrm{g}$ and $\mathcal {V}_0$ are the trial and the test spaces defined as

$$\begin{aligned} \begin{aligned} \mathcal {V}_\textrm{g}&:= \left\{ u \in H^1(\varOmega ): u|_{\partial \varOmega } = g \right\} { ,}\\ \mathcal {V}_0&:= \left\{ v \in H^1(\varOmega ): v|_{\partial \varOmega } = 0 \right\} { .} \end{aligned} \end{aligned}$$

(3)

Let $u_h$, $v_h$ be the Galerkin approximation of u, v. The discrete problem then becomes find $u_h\!\in \!\mathcal {V}_h$, such that $\forall \,v_h\!\in \!\mathcal {V}_h$,

$$\begin{aligned} \int _{\varOmega } \nabla u_h \cdot \nabla v_h \,\textrm{d}\varOmega + \ \int _{\varOmega } {u_h}^3 v_h \,\textrm{d}\varOmega = \int _{\varOmega } f v_h \,\textrm{d}\varOmega \text {,} \end{aligned}$$

(4)

where $\mathcal {V}_h$ is a finite-dimensional subspace of $H^1(\varOmega )$.

In order to handle the Dirichlet boundary condition in a more systematic manner throughout the optimization process, Nitsche’s method (1971) is employed for weak enforcement. This approach involves introducing additional boundary terms to both sides of (4). By doing so, the boundary condition is automatically incorporated into the weak form and its associated partial derivatives with respect to the state variable u. With the boundary terms added to (4), we have

$$\begin{aligned} \begin{aligned}&\int _{\varOmega } \nabla u_h \cdot \nabla v_h \,\textrm{d}\varOmega + \int _{\varOmega } {u_h}^3 v_h \,\textrm{d}\varOmega \ - \int _{\varGamma } (\nabla u_h \cdot \varvec{n}) v_h \,\textrm{d}\varGamma \\&\qquad \mp \int _{\varGamma } (\nabla v_h \cdot \varvec{n}) u_h \,\textrm{d}\varGamma \ + \int _{\varGamma } \frac{C_\text {pen}}{h} u_h v_h \,\textrm{d}\varGamma \\&\quad = \int _{\varOmega } f v_h \,\textrm{d}\varOmega \mp \int _{\varGamma } (\nabla v_h \cdot \varvec{n}) g \,\textrm{d}\varGamma \ + \int _{\varGamma } \frac{C_\text {pen}}{h} g v_h \,\textrm{d}\varGamma { ,} \end{aligned} \end{aligned}$$

(5)

where $\varvec{n}$ is the unit normal vector pointing outwards of the outer boundary $\varGamma$, h is a parameter indicating the refinement of the mesh (i.e., the cell diameter of the discretized domain), and $C_\text {pen}$ is a positive constant independent of the mesh refinement. Rearranging terms we obtain the residual form of the nonlinear Helmholtz equation:

$$\begin{aligned} \begin{aligned} R(u_h,f) =&\int _{\varOmega } \nabla u_h \cdot \nabla v_h \,\textrm{d}\varOmega + \int _{\varOmega } {u_h}^3 v_h \,\textrm{d}\varOmega \ \\&\quad - \int _{\varOmega } f v_h \,\textrm{d}\varOmega - \int _{\varGamma } ( \nabla u_h \cdot \varvec{n}) v_h \,\textrm{d}\varGamma \\&\quad \mp \int _{\varGamma } ( \nabla v_h \cdot \varvec{n}) (u_h - g) \,\textrm{d}\varGamma \\&\quad + \int _{\varGamma } \frac{C_\text {pen}}{h} (u_h - g) v_h \,\textrm{d}\varGamma { .} \end{aligned} \end{aligned}$$

(6)

The $\mp$ sign in (6) corresponds to the symmetric (−) and nonsymmetric ($+$) variants of Nitsche’s method. In this paper’s applications, the symmetric variant is utilized. It is widely accepted by the finite element community and offers optimal accuracy in both $L^{2}$ and $H^{1}$ norms (Annavarapu et al. 2012; Jiang et al. 2015). The nonsymmetric Nitsche’s method has also gained increasing attention for its independence of the choice of penalty parameter $C_\text {pen}$ (Schillinger et al. 2016). However, we do not delve into the detailed comparison of these two variants as it is beyond the scope of this paper.

2.4 Automated derivative computation for gradient-based optimization

Gradient-based optimization is a preferred approach in MDO problems that involves evaluating high-fidelity sub-models, such as finite element solvers. It uses derivative information from the model to determine the direction of design variable updates, offering efficiency and accuracy. However, a major challenge in gradient-based optimization is ensuring that each component of the model has the required partial derivatives of its outputs with respect to its inputs. These derivatives are essential for computing the total derivative of the objective function with respect to the design variables.

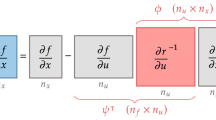
To address this challenge, FEMO automates derivative computation as much as possible. It leverages the automatic differentiation capabilities of FEniCSx to compute partial derivatives of PDE residuals with respect to function inputs (i.e., $\partial R/\partial u$ and $\partial R/\partial f$), and utilizes CSDL for partial derivatives of algebraic operations, such as matrix–vector multiplications, occupying in preprocessing and postprocessing code.

For the model problem in (1b), the total derivative of the objective function J with respect to the inputs f can be computed using the chain rule

$$\begin{aligned} \begin{aligned} \frac{\textrm{d} J}{\textrm{d} f} = \frac{\partial J}{\partial f} + \ \frac{\partial J}{\partial u}\frac{\textrm{d} u}{\textrm{d} f} { .} \end{aligned} \end{aligned}$$

(7)

With $\partial R/\partial u$ and $\partial R/\partial f$ provided by FEniCSx, we can obtain $\textrm{d}u/\textrm{d}f$ by solving the linear system in (8), and insert it to (7) to compute the total derivative $\textrm{d}J/\textrm{d}f$.

$$\begin{aligned} \begin{aligned} R(u,f) = 0 \Rightarrow \ \frac{\textrm{d} R}{\textrm{d} f} = 0 \Rightarrow \ \frac{\partial R}{\partial u}\frac{\textrm{d} u}{\textrm{d} f} = - \frac{\partial R}{\partial f} { .} \end{aligned} \end{aligned}$$

(8)

The assembly of partial derivatives to obtain total derivatives is handled automatically by CSDL, where it employs the direct or adjoint method based on the computational cost.

3 Implementation

In this section, we present a detailed explanation of how FEMO is used to solve PDE-constrained MDO problems. We begin with examples of FEniCSx and CSDL implementation, and then walk through the steps involved in solving the model problem using FEMO.

In Sect. 3.1, we introduce the native operations in CSDL such as matrix–vector products, and the $\texttt {CustomOperation}$ class object, which serves as a wrapper for FEniCSx related operations. In Sect. 3.2, we provide a detailed explanation of FEniCSx programming workflow, accompanied by code examples for essential functionalities, such as computing partial derivatives and solving linear or nonlinear systems. In Sect. 3.3, we demonstrate how all the components are assembled together using the Python API of FEMO.

3.1 System-level modeling construction using CSDL

CSDL is a domain-specific language for constructing computational models in MDO. It provides access to a diverse set of operations such as summation, averaging, trigonometric functions, and array operations. Listing 1 demonstrates a simple model that utilizes built-in CSDL operations. In CSDL, the computation of partial derivative associated with built-in operations is automated. The execution of CSDL models is performed by the $\texttt {Simulator}$ object in the Python backend of CSDL, which is implemented using Numpy.

In addition to the built-in operations, CSDL also supports user-defined custom operations, including implicit and explicit custom operations. Implicit custom operations typically involve solving a linear or nonlinear system to compute the output, making them suitable for wrapping PDE solvers. We will demonstrate how we utilize custom operations as wrappers for FEniCSx operations in Sect. 3.3. A CSDL model can contain multiple sub-models, where each of them has its own operation defined, whether built-in or custom. The total derivatives of models with coupled sub-models are computed using either direct or adjoint methods, depending on the number of design variables and the number of objectives. If there are more design variables than objectives, the adjoint method is executed, which is often the case for MDO problems.

3.2 Automated finite element solutions and derivatives with FEniCSx

FEniCSx is a collection of scientific libraries (UFL, DOLFINx, FFCx, Basix) written in Python and C++, where each library has a specific functionality in solving finite element problems. Figure 2 illustrates the workflow between these libraries and their respective functionalities.

In the workflow for writing a FEniCSx program in Python, the user begins by importing the mesh using the XDMF file reader in DOLFINx. Next, they specify the variational form of the PDE residual using the Uniform Form Language, UFL (Alnæs et al. 2014b), which is a domain-specific language for variational expressions. DOLFINx then automatically interfaces with FFCx to generate high-performance finite element code in C++ on the backend.

Fig. 2

FEniCSx workflow

For example, when solving the model problem, we first create a unit square mesh with triangular elements as the analysis domain. We then define a Lagrange finite element space for the solution u of the nonlinear elliptic PDE of $C^1$ continuity, as shown in Listing 2.

Next, we express the interior terms and the boundary terms with symmetric Nitsche’s method of the PDE residual using UFL operations. The code snippet in Listing 3 corresponds to the mathematical formulation described in (6).

The UFL also provides analytical computation of partial derivatives, such as $\partial R/\partial u$ and $\partial R/\partial f$ for the PDE residual R defined in Listing 3, i.e.,

Fig. 3

FEMO framework

The analytical derivatives computed by UFL can be assembled into discrete form using DOLFINx, resulting in PETSc arrays. These arrays can be further converted to Numpy or Scipy arrays to interface with CSDL. This process is generalized by FEMO as described in Sect. 3.3.

FEniCSx offers convenient build-in linear and nonlinear solvers for users and allows for the flexibility of custom solvers tailored to specific problem requirements. In FEMO, we utilize customized nonlinear solvers such as $\texttt {NewtonSolver}$ and $\texttt {SNESSolver}$ with $\texttt {MUMPS}$ as the linear solver from PETSc. The code in FEMO is designed to be case-independent, enabling the solution of PDE problems in any discipline. The implementation details of the solvers, as well as other modularized components such as derivative form assembly and function value extraction, will be discussed in Sect. 3.3.

3.3 Coupling of FEniCSx and CSDL through FEMO

Integrating FEniCSx and CSDL for PDE-constrained MDO can be challenging due to their different domain-specific languages and data storage methods. FEniCSx uses UFL to express variational terms, such as integration and differentiation and stores data as PETSc sparse arrays. On the other hand, CSDL utilizes Numpy arrays for algebraic operations. Translating between these two software can be a tedious task, but it can be streamlined through the use of generic class objects. FEMO addresses this challenge by providing a generalized modeling framework for FEA-related computations and automating the data communication between the two libraries, as illustrated in Fig. 3.

The code example below showcases two convenient utility functions provided by FEMO: assembleMatrix converts analytical expression to discrete form, and solveNonlinear solves the finite element problem. These functions can be easily utilized within the CSDL modeling environment.

By integrating all the utility functions within FEMO’s FEA class object, we can provide essential functionalities required by CSDL’s CustomOperation. This integration enables the construction of a generic StateModel for computing PDE solutions, and an OutputModel for assembling variational forms. Listing 4 is a code snippet illustrating the implementation of the generic StateModel in FEMO’s source code. It takes a user-defined FEA object, along with input and output names, as parameters.

For the model problem, we utilize these generic models to create problem-specific CSDL custom operation models. These models can take FEniCSx Function or Form objects (i.e., u is a Function object defined in Listing 2) as the inputs and use generalized FEniCSx operations in FEMO to compute the outputs, as shown in Listing 5. The type="scalar" argument specifies that this model returns a scalar output, i.e., an integral over a certain domain. There is also a "field" type output, which computes distributed field outputs on the finite element mesh, i.e., element-wise and point-wise properties. The FEAModel class is employed to group finite element-related operations together. It provides the flexibility to connect multiple PDE systems by including multiple FEA objects in its list argument, i.e., FEAModel(fea=[fea1,fea2]). This is used in the motor example in Sect. 4.3.

The coupling of sub-models in FEMO is automatically handled based on the names of the variables. Each input or output variable in the sub-models has a unique name associated with the object that stores its values. These names are automatically propagated throughout the system by CSDL and are used to connect to sub-models of other disciplines. Therefore, it is crucial to maintain consistency in variable names throughout the modeling process.

Finally, we utilize the SNOPT library—a powerful software for solving nonlinear optimization problems (Gill et al. 2005)—as the optimizer for our numerical tests. We leverage the Python binding of SNOPT in modOpt,² which can interface with CSDL by creating a CSDLProblem object with the simulator, as demonstrated in Listing 6.

4 Numerical examples

In this section, we demonstrate the versatility and effectiveness of FEMO through four numerical examples that span various disciplines and complexity levels in modeling. The problem set includes three well-posed optimization problems and one sensitivity analysis example. In Sect. 4.1, we continue using the model problem discussed in previous sections as an example of a pure PDE-constrained problem, as there is no other algebraic sub-models coupled with it. In Sect. 4.2, we solve a classic density-based topology optimization problem for a 2D cantilever beam. This example demonstrates the coupling of a PDE with non-PDE components, specifically the use of a density filter as a preprocessor. We compare its runscript with pure FEniCS implementation in “Appendix A” to show the differences between them. In Sect. 4.3, we tackle a more complex real-world problem for shape optimization of an electric motor. This problem involves solving two coupled PDEs: one for mesh deformation and the other for Maxwell’s equations. Additionally, the PDE components are coupled with external preprocessors implemented in CSDL for shape parametrization. In Sect. 4.4, we construct a multifidelity aeroelastic solver that combines the Vortex Lattice Method, VLM (Anderson 2010) implemented in CSDL with the Reissner–Mindlin shell solver implemented in FEniCSx. We utilize this aeroelastic solver in a dynamic test case simulating the gust response of an eVTOL wing. We also showcase the automatic computation of derivatives for this coupled system in a static test case.

Fig. 4

The MDO process for the optimal control of a nonlinear Helmholtz equation. The orange box represents the finite element solver, and corresponds to the StateModel in FEMO; the pink box represents the objective function written as a variational form, corresponding to the OutputModel in FEMO. (Color figure online)

Fig. 5

Snapshots of the optimization process for the model problem with a $128\times 128$ mesh. The control variable f has a uniform value of 0.1 across the entire domain at the first optimization iteration ($N=1$) and the optimization converges at $N=570$

All three optimization examples utilize the Python binding of SNOPT, accessible through modOpt, as the optimizer. We tune the optimizer using two settings: the (major) optimization tolerance, closely linked to the objective gradient, and the (major) feasibility tolerance, determining the tightness of the constraint enforcement. The values of these two tolerances along with the number of iterations are discussed in the numerical results of each example.

4.1 Optimal control of a nonlinear elliptic PDE

4.1.1 Mathematical formulation

The MDO process for the model problem described in (1b) is illustrated in Fig. 4. The optimal solution of the problem is denoted as $f^*$, and the associated state variable is represented by $u^*$. The objective function value at the end of the optimization iterations is denoted as $J^*$, i.e., $J^* = J(u^*, f^*)$.

4.1.2 Numerical results

For numerical analysis, we consider a unit square domain $\varOmega =[0,1]\times [0,1]$ and choose $g(\varvec{x})= \sin (2\pi x_1)\cos (\pi x_2)$ as the analytical solution of u on $\varOmega$. We use symmetric Nitsche’s method to weakly enforce the Dirichlet boundary condition $u=g$ on $\varGamma$. $\alpha$ is a dimensionless constant used in the regularization term of the objective function in (1a). For our specific case, we have selected $\alpha =6\times 10^{-7}$. With the known analytical solution g, the optimal solution of f can be calculated analytically using the strong form of the nonlinear Helmholtz equation in (1b). Specifically, we have $f_\textrm{d} = -\varDelta g + g^3$, which can be easily implemented using UFL as

where g is a UFL form object defined beforehand.

The optimization is terminated when the optimality drops below a predefined tolerance. At the end of the optimization, we expect that the results for u and f will closely approximate their respective analytical solutions, i.e., $u^* \rightarrow g$ and $f^* \rightarrow f_\textrm{d}$. To evaluate the success of the optimization problem, we calculate the $L_2$ norms for both pairs. Figure 5 illustrates the evolution of the control variable f and the state variable u during the optimization test with a $128\times 128$ mesh. The initial guess for all degrees of freedom in f is set to 0.1. This optimization run requires 570 iterations to converge to a tolerance of $10^{-11}$. In this problem, the control variable f is represented as a discontinuous Lagrange function of degree 0. Initially, the distribution of f exhibits a scattering profile for $N=200$. As the optimization progresses, it gradually becomes smoother. This smoothing effect can be attributed to the presence of f in the regularization term of the objective function J.

We perform a convergence study on mesh sensitivity by running optimization tests with different meshes. The results are summarized in Table 1. As observed, all the values in the last three columns decrease as the mesh becomes finer. Specifically, the error of the control variable $f^*$ exhibits the expected first-order convergence, as reported in Arada et al. (2002). Another observation is that as the mesh size decreases, tightening the optimality tolerance becomes necessary, along with an increased number of SNOPT optimization iterations, to ensure this first-order convergence of the error in control. We showcase the convergence history for the test case with a $16\times 16$ mesh in Fig. 6 by plotting the objective function J and optimality over the optimization iterations. This plot demonstrates a monotonic convergence for the objective function, which serves as verification for both accuracy and efficiency of the adjoint computation.

Table 1 A mesh sensitivity study for the optimal control of the nonlinear Helmholtz problem

4.2 Topology optimization of a cantilever plate

We demonstrate the versatility of this software by applying it to a classical 2D cantilever beam topology optimization problem using a density-based approach. This problem is a well-known benchmark in the field of topology optimization, and has been extensively studied using various optimization approaches. Notably, Chung et al. (2019) implemented the problem using OpenMDAO (Gray et al. 2019), a NASA developed MDO framework, while Yan et al. (2022) automated gradient-based topology optimization by coupling the legacy FEniCS and OpenMDAO in their previous work.

4.2.1 Mathematical formulation

We aim to optimize the density distribution of the material, denoted as $\rho$, subjected to a constant volume constraint. The structural behavior of the beam is governed by the PDE of linear elasticity. The objective of this optimization problem is to minimize the compliance of the beam, which is defined as the inverse of the stiffness, as indicated in the first equation of (9).

$$\begin{aligned} \begin{aligned} \text {minimize}&~~~ J(\varvec{u}) = \int _\varGamma {\varvec{u}} \cdot \varvec{f}\,\textrm{d}\varGamma \\ \text {with respect to}&~~~ \rho \\ \text {such that}&~~~ \tilde{\rho } = \tilde{\rho }(\rho ) \\&~~\int _\varOmega \tilde{\rho }\,\textrm{d}\varOmega = \text {constant} \\&~~~ -\nabla \cdot \sigma (\varvec{u},\tilde{\rho }) = \varvec{f} \\&~~~~ \rho _{\min } < \rho \le 1. \end{aligned} \end{aligned}$$

(9)

Fig. 6

Convergence history for the model problem with a $16\!\times \!16$ mesh. The optimization converges after 93 iterations with a total runtime of 28 s

To smooth the density distribution and prevent checkerboard patterns, which can cause instability, a distance-based method is employed to map the original density $\rho$ to the filtered density $\tilde{\rho }$. For each element i, its filtered density is computed by summing the weighted contributions of nearby elements, given by the equation:

$$\begin{aligned} \tilde{\rho }_i=\sum _j w_{ij} \rho _j\text {,} \end{aligned}$$

(10)

where $\tilde{\rho }_i$ is the filtered density of element i, $\rho _j$ is the unfiltered density of a nearby element j, and $w_{ij}$ is the weight function that connects element i and j, which satisfies $\sum _j w_{ij} = 1$. In this example, we use a simple conic weight function to compute $w_{ij}$ based on the distance between element i and j, whose formula can be found in Svanberg and Svärd (2013).

The solid isotropic material with penalization (SIMP) method is employed to incorporate the density distribution into the PDE constraint, which was initially developed by Bendsøe and Kikuchi (1988). In this specific application, the local material property is proportional to the power product of the local density, i.e., $E_i(\tilde{\rho }_i)=\tilde{\rho }_i^3E_0$. Additionally, a minimum value of density, denoted as $\rho _{\min }$, is imposed to avoid material singularity and maintain numerical stability during the finite element analysis. Figure 7 shows the MDO process of this problem. The distance-based density filter sub-model is implemented with CSDL linear algebra operations, and marked in green as it is considered as an external component, while the finite element sub-models are marked in pink (OutputModel) and orange (StateModel).

Fig. 7

The MDO process for topology optimization of a cantilever beam

4.2.2 Numerical results

The physical setting of the boundary value problem is shown in Fig. 8a. The compliance of a cantilever beam is minimized with a volume fraction constraint of 0.4. The beam has a clamped boundary condition on the left edge, and a downward traction force applied in the middle of the right edge. The beam has a length of 160 and a height of 80. It is discretized into a structured quadrilateral mesh, with user-defined number of elements on each side. Linear elasticity is assumed in this example, but it can be extended to nonlinear cases as discussed in Yan et al. (2022). The Young’s modulus is set to 1.0 and the Poisson’s ratio is set to 0.3. The traction force, denoted as F, has a magnitude of 0.25 and is directed downwards. $\rho _{\min }$ is set to $10^{-4}$ as the lower bound of the design variable. Note that all of the parameters are dimensionless.

Fig. 8

Topology optimization of a cantilever beam under linear elasticity with a $80\times 40$ mesh. a The problem setting, b the optimized density distribution $\tilde{\rho }$, and c convergence history of the objective function and the optimality

We showcase the optimization results and convergence history for the test case with a $80\times 40$ mesh in Fig. 8b and c, which demonstrates a generally monotonic convergence for the compliance. The optimization terminates within 338 major iterations with a total runtime of 177 s. The optimality tolerance is set to be $10^{-8}$ and the feasibility tolerance for enforcing the volume constraint is set to be $10^{-6}$ in SNOPT. Given that the feasibility is always zero for most of the iterations (indicating that the linear constraints are always satisfied), the focus of Fig. 8c is on the convergence history of the objective function and the optimality. The optimized solution in Fig. 8b for the penalized density $\tilde{\rho }$ exhibits a tapered shape as anticipated in prior studies (Chung et al. 2019; Yan et al. 2022). Furthermore, due to the symmetric boundary condition and load, the density distribution displays a symmetric profile with linear elastic material model.

4.3 Electric motor design

In this section, we tackle a practical problem including the shape optimization of an electric motor. This problem is an essential part for the system-level modeling and optimization of eVTOL aircraft. Using the presented tool, we are able to build a high-fidelity model that can accurately capture the precise mesh movement near the motor components and their impact on the electromagnetic performance of the motor. This is achieved by formulating the relevant processes as coupled PDEs and connecting them with an external solver for shape parametrization. Specifically, we focus on studying a permanent magnet synchronous motor (PMSM), and analyze the behavior of a single static phase within its periodic operation.

4.3.1 Optimization problem definition

The optimization problem is formulated shown in (11), where $\varvec{x}$ represents a vector of design variables that define the shape of the motor. $\varOmega _\textrm{bc}$ is a vector of boundary movements on the finite element mesh. $\varOmega$ denotes the original mesh and $\tilde{\varOmega }$ represents the moved mesh. The objective function $J(\cdot )$ depends on the deformed mesh $\tilde{\varOmega }$ and the solution of Maxwell’s equations $A_z$—the z-component of magnetic potential vector A.

(11)

The problem is governed by two nonlinear PDEs: one for mesh movement (hyperelasticity) and another for electromagnetic modeling (Maxwell’s equations). These PDEs are coupled in a way that the solution of the former—the nodal deformation—is incorporated in the PDE residual of the latter. Hence the nodal deformation can have an impact on the final solution of the magnetic flux density. The corresponding MDO process is abstracted in Fig. 9.

Fig. 9

The MDO process for shape optimization of an electric motor

4.3.2 Shape parametrization with free-form deformation

We start with an initial configuration of the motor geometry as shown in Fig. 10a. We use the vector of design variables $\varvec{x}$ to describe the changes in the geometric parameters of the motor, such as the inner radius of the rotor and the positions of the magnets.

To incorporate these changes into the physical domain, we employ free-form deformation (FFD), which is a technique commonly used for modeling the deformation of rigid objects and is analogous to parametrization with B-splines (Kenway et al. 2010; Sederberg and Parry 1986). FFD allows us to map the geometric changes $\varvec{x}$ to the movements of a specific group of boundary-defining points in the physical domain. These points are denoted as $\varOmega _\textrm{bc}$.

It is important to note that this problem involves numerous modeling specifications and steps in the preprocessing and postprocessing stages. A comprehensive discussion on the FFD method can be found in Scotzniovsky et al. (2024), which uses FEMO for geometric design of electric motor. However, for the purpose of this paper, these details are omitted, and the focus is primarily on the PDE-related aspects of the formulation.

Fig. 10

a The baseline geometry of the permanent magnet synchronous motor model. The red box highlights 1 of the 12 magnets. b The zoomed view of the red-boxed region with the undeformed mesh. The magnet is highlighted in fuchsia color. c The zoomed view of the red-boxed region with the deformed mesh. The magnet highlighted in fuchsia has been moved inwards along the radial direction

4.3.3 Automated mesh movement

For the sake of notation convenience, we introduce $\varvec{u_\textrm{bc}}$ to represent the boundary movement $\varOmega _\textrm{bc}$ on the finite element domain. Additionally, we denote $\varvec{u}$ as the displacements for all the mesh vertices in the entire domain:

$$\begin{aligned} \varvec{u(X)}=\phi (\varvec{X})-\varvec{X} \text {,} \end{aligned}$$

(12)

where $\phi {:} ~\varvec{X}\rightarrow \varvec{\tilde{X}}$ represents the mapping from the original domain $\varOmega$ to the deformed domain $\tilde{\varOmega }$. This approach for updating mesh based on the mesh movement is analogous to the approach used in fluid–structure interaction applications (Neighbor et al. 2023).

To simulate the mesh movement, we formulate a BVP where the displacements of the boundary vertices $\varvec{u_\textrm{bc}}$ are imposed as Dirichlet boundary conditions. The BVP is governed by a hyperelastic equation. By solving this BVP, we obtain the smooth movements $\varvec{u}$ throughout the entire domain, including both the on-boundary and off-boundary vertices. The strong form of the hyperelasticity problem is as follows

$$\begin{aligned} \begin{aligned} - \nabla \cdot \varvec{P(u)}&= \varvec{f} ~~~ \text { in } \varOmega \text {,} \\ \varvec{u}&= \varvec{u_\textrm{bc}} ~ \text { on } \varGamma _\textrm{bc} \text {,} \end{aligned} \end{aligned}$$

(13)

where $\varvec{f}$ represents the body force, which is assumed to be zero in our case. The first Piola–Kirchhoff stress $\varvec{P}$ is given by

$$\begin{aligned} \varvec{P} := J\sigma \varvec{F}^{-\textrm{T}}, \end{aligned}$$

(14)

where $\sigma$ represents the Cauchy stress, $\varvec{F}$ is the deformation gradient, and J is its determinant. $\varvec{F}$ can be computed by

$$\begin{aligned} \varvec{F} = \frac{\partial \phi }{\partial \varvec{X}} = \ \nabla \varvec{u} + \varvec{I} , \end{aligned}$$

(15)

which can be conveniently implemented in UFL as follows:

For the material model, we adopt the modified St. Venant–Kirchhoff constitutive model, where the second Piola–Kirchhoff stress is defined as

$$\begin{aligned} \varvec{S}(\varvec{F}) = 2\mu \left[ \varvec{E}-\frac{\textrm{tr}(\varvec{E})}{3}\varvec{I} \right] + K \text {tr}(\varvec{E}) \varvec{I} \text {.} \end{aligned}$$

(16)

Here, $\varvec{E}=\frac{1}{2}(\varvec{F}^\textrm{T}\varvec{F}-I)$ is the Green–Lagrange strain. $\mu$ and K are the material parameters that can be chosen based on the deformation to introduce artificial stiffness in regions of the mesh that experience crushing. In our numerical tests, we set $\mu = K = J^{-p}$, where p is a positive integer (set to 3).

Then the first Piola–Kirchhoff stress can be computed by

$$\begin{aligned} \varvec{P}(\varvec{F}) = \varvec{F}\cdot \varvec{S}(\varvec{F}) \text {.} \end{aligned}$$

(17)

In the finite element formulation, the boundary condition is weakly enforced to the weak form of (13) using the symmetric Nitsche’s method applied on the subdomains. To specify the relevant facets for the boundary condition, we define an integral operator using UFL, such as

Here, ds represents the integral operator on facets in the finite element domain that are not on the outer boundary, and dss is a user-specified integral operator on the selected facets based on the provided boundary data, which contains the indices of the desired facet entities. The group of those facets corresponds to $\varGamma _\textrm{bc}$ in (13), which is a subset of the total boundary $\varGamma$.

Figure 10 illustrates how the mesh deforms when moving a magnet inwards along the radial direction. Figure 10b represents the undeformed mesh. Nonzero displacements are assigned to the vertices located on the outer edges of the magnet, while the vertices on the unmoved boundaries, such as the air gap (the finely discretized area above the magnet), are restrained to remain unmoved. Figure 10c shows the deformed mesh obtained by warping the domain using the solution of the hyperelastic problem. The deformed mesh captures the movements of the vertices both inside and surrounding the magnet, resulting in a smooth mesh of the new configuration.

We note that the mesh is not actually moved during the optimization process. Instead, the mesh movement is incorporated into Maxwell’s equations, allowing us to compute the electromagnetic solution as if it were on the deformed mesh. This coupling method will be further explained in the next subsection.

An important advantage of this approach is that the number of vertices and their connectivity relationship remain constant throughout the optimization process. By computing the displacements of the vertices and incorporating them into the subsequent steps, we eliminate the need to regenerate or move the mesh, resulting in reduced computational cost.

To enhance the robustness of this algorithm for handling large deformation during the optimization process, we employ a customized nonlinear solver with load-stepping to incrementally apply the subdomain movements. The number of steps is dynamically determined based on the mesh size and the maximum expected deformation. This adaptive approach helps prevent inverted elements, which can cause the subsequent electromagnetic solver to fail.

4.3.4 Magnetostatic problem on the deformed mesh

Maxwell’s equations are

$$\begin{aligned} \begin{aligned} \nabla \times \varvec{H}&= \varvec{J}_\textrm{w}+\varvec{J}_\textrm{m},\\ \nabla \cdot \varvec{B}&= 0\text {,} \end{aligned} \end{aligned}$$

(18)

where $\varvec{J}_\textrm{w}$ and $\varvec{J}_\textrm{m}$ are source terms representing the effective current densities within the stator windings and the magnets, respectively. $\varvec{B}$ represents the magnetic flux density, and $\varvec{H}$ represents the magnetizing field.

The relationships between $\varvec{B}$, $\varvec{H}$, and $\varvec{A}$ (the magnetic vector potential) are given by

$$\begin{aligned} \begin{aligned} \varvec{B}&=\mu \varvec{H} \text {,}\\ \varvec{B}&=\nabla \times \varvec{A}\text {,} \end{aligned} \end{aligned}$$

(19)

where $\mu$ is the magnetic permeability, which is a nonlinear function of B and depends on the local material properties.

Rewriting Maxwell’s equations in (18) by using $\varvec{A}$ as the solution gives us

$$\begin{aligned} \nabla \times (\mu ^{-1} \nabla \times \varvec{A}) = \varvec{J}_\textrm{w}+\varvec{J}_\textrm{m}\text {.} \end{aligned}$$

(20)

This can be reduced by considering only the z-component of $\varvec{A}$ as the other two components are both zero

$$\begin{aligned} \begin{aligned} - \nabla \cdot ({\mu }^{-1} \nabla A_z)&= \varvec{J}_z ~~\text {in} ~~\varOmega \text {,}\\ A_z&= g ~~~~\text {on} ~~\varGamma \text {.} \end{aligned} \end{aligned}$$

(21)

We choose $g=0$ for a homogeneous boundary condition of $A_z$. Then, $\varvec{B}$ can be obtained from $A_z$ in the postprocessing steps by

$$\begin{aligned} \varvec{B}(x, y) = \left( \frac{\partial A_z}{\partial y}, -\frac{\partial A_z}{\partial x}\right) \text {.} \end{aligned}$$

(22)

The weak form of (21) can be formulated as

$$\begin{aligned} \int _{\varOmega } \mu ^{-1} \nabla A_z \cdot \nabla v\,\textrm{d}\varOmega = \int _{\varOmega } J_z v\,\textrm{d}\varOmega \text {,} \end{aligned}$$

(23)

where v is a test function of $A_z$. By moving the right-hand side term to the left and applying the Dirichlet boundary condition with Nitsche’s method, we obtain the PDE residual in variational form on the undeformed mesh:

$$\begin{aligned} R(A_z, \varOmega ) & = \int _{\varOmega } \mu ^{-1} \nabla A_z \cdot \nabla v\,\textrm{d}\varOmega \ - \int _{\varOmega } J_z v\,\textrm{d}\varOmega \nonumber \\ & \quad - \int _{\varGamma } \mu ^{-1} (\nabla A_z \cdot \varvec{n} \cdot v \ \mp \nabla v \cdot \varvec{n} \cdot (A_z-g))\,\textrm{d}\varGamma \nonumber \\ & \quad + \int _{\varGamma }\frac{C_\textrm{pen}}{h}\mu ^{-1}v (A_z-g)\,\textrm{d}\varGamma \text {.} \end{aligned}$$

(24)

To obtain the variational form on the deformed mesh, we adopt a seamless coupling method for hyperelasticity and electromagnetism by incorporating $\varvec{u}$ into the weak form in (24). This is inspired by the body-fitted method for Fluid–Structure Interaction (FSI) problems (Bazilevs et al. 2008), where the integral and differential operators are modified by Nanson’s formula into the weak forms. For example,

$$\begin{aligned} \begin{aligned} \textrm{d}\varOmega&\rightarrow J \textrm{d}\varOmega , \\ \varvec{n}\textrm{d}\varGamma&\rightarrow J\varvec{F}^{-\textrm{T}} \varvec{n} \textrm{d}\varGamma , \\ \textrm{d}\varGamma&\rightarrow |J\varvec{F}^{-\textrm{T}} \varvec{n}| \textrm{d}\varGamma , \\ \nabla v&\rightarrow \nabla v \cdot \varvec{F^{-1}} \\&\ldots \end{aligned} \end{aligned}$$

(25)

Here, J represents the determinant of $\varvec{F}$, which is computed by $J = \textrm{det}(\varvec{F})$. These modifications can be easily handled by UFL, i.e., $\nabla v \cdot \varvec{F^{-1}}$ can be conveniently implemented as

where F(u) is the predefined function as described in Sect. 4.3.3.

4.3.5 Numerical results

For the numerical tests, we set up a simplified optimization problem with a single design variable—the change of magnet position in the radial direction. The objective is to minimize the natural core losses due to the magnets during no-load operation. In the simplified setting, the total core loss $P_\textrm{L}$ is given by the sum of the eddy current loss $P_\textrm{ec}$ and the hysteresis loss $P_\textrm{h}$, i.e., $P_\textrm{L} = P_\textrm{ec} + P_\textrm{h}$. The losses are computed by

$$\begin{aligned} P_\textrm{ec}= & 2\pi ^2 f^2 l K_\textrm{ec} \int _{\varOmega _\textrm{ec}}|\varvec{B}|^{2} \textrm{d}\varOmega \quad \text { and } \quad \nonumber \\ P_{h}= & 2\pi f l K_\textrm{h} \int _{\varOmega _\textrm{h}}|\varvec{B}|^{\beta } \textrm{d}\varOmega \text {,} \end{aligned}$$

(26)

where f is the frequency of the input signal in Hertz, l is the motor length, and they are both set to unit values. $K_\textrm{ec}$ is the eddy current coefficient, and $K_\textrm{h}$ is the Steinmetz hysteresis coefficient. $\varOmega _\textrm{ec}$ and $\varOmega _\textrm{h}$ represent the subdomains where the power loss effects are observed (typically the rotor and the stator). $\beta$ is the Steinmetz exponent that depends on material, ranging from 1.5 to 2.5. $\beta$ is set to 1.76835 for the chosen Hiperco 50 the alloy material, which is the material used for the rotor and the stator. Again, we need to convert the integral operators in (26) to the deformed mesh using the substitutions given in (25).

As shown in Fig. 11, this single-variable single-objective optimization converges successfully. The optimality drops below $10^{-8}$ within 9 iterations. The problem is always feasible throughout the optimization process as the linear constraints, i.e., the bounds on the design variable, are always satisfied. The total runtime for this problem is 571 s, involving the evaluation of the coupled PDE system on a mesh with 28,410 elements as well as the adjoint computation.

Fig. 11

Convergence history for the shape optimization of the electric motor

The magnitude of the magnetic flux density $\varvec{B}$ is plotted on both sides of the motor in Fig. 12. The left side represents the magnetic flux solution field on the undeformed mesh, while the right half shows the results obtained on the deformed mesh. Although it is not obvious to notice the difference of the two sides as they use the same color scale, it is worth mentioning that the maximum magnitude of $\varvec{B}$ on the right is 2.1, which is $8.7\%$ smaller than the maximum value of 2.3 on the left as in the color legend. Also, in the optimized configuration, a lighter color of $\varvec{B}$ magnitude can be observed in the stator area between the stator teeth. This indicates a reduction in the power loss in this region, leading to improved performance. The decrease in peak magnetic flux density can be explained by the enlarged area of the rotor between the magnets and the air gap. The movement of the magnets increases the area for flux to permeate through this tight zone, which decreases the effective flux density. The movement of the magnets also decreases the flux that permeates from the rotor to the stator, reducing the flux density magnitudes in the stator teeth.

Fig. 12

The magnetic flux density on the initial configuration (pink) and the optimized configuration (orange). (Color figure online)

4.4 Aeroelastic analysis on an eVTOL wing

This application employs aeroelastic coupling of a high-fidelity structural solver based on Reissner–Mindlin shell theory and a low-fidelity aerodynamics solver: the vortex lattice method (VLM). A solver-independent method (Van Schie et al. 2023) is used for coupling these two solvers. Numerical tests include a static aeroelastic analysis with analytical derivative computation and a dynamic case for gust response on an eVTOL wing. We use the Uber eCRM-001 model in the following test cases, which is an electric common reference model (eCRM) for electric air taxi.

4.4.1 Aerodynamic solver with vortex lattice method

VLM is a widely used approach for analyzing aerodynamic performance, such as force or pressure distribution on lifting surfaces (Anderson 2010). VLM makes a potential flow assumption, which means the flow can be characterized by an irrotational velocity field given by

$$\begin{aligned} \nabla ^2 \varPhi = 0 \text {,} \end{aligned}$$

(27)

where $\varPhi$ is the fluid potential.

Other assumptions of VLM include that (1) the fluid is incompressible; and (2) the lifting surfaces are thin and have a small angle of attack and sideslip.

Fig. 13

VLM workflow for aerodynamic analysis

The VLM model is built in CSDL to enable automated derivative computation. It is implemented in an inertial frame with a constant freestream velocity and assumes steady-state conditions during each mission segment. Figure 13 demonstrates the inputs, model, and outputs of the VLM model. The inputs of the VLM model are the meshes and the states of the lifting surfaces. Then, the model creates structured quadrilateral panels and uses vortex rings located at the quarter-chord of each panel for computation. The system of equations to be solved in (28) corresponds to the flow-tangency condition meaning zero normal velocity on the lifting surface panels.

$$\begin{aligned} \varvec{A}\varvec{\varGamma _\text {b}} + \varvec{B}\varvec{\varGamma _\text {w}} + \varvec{v} \cdot \varvec{n}=0 \text {,} \end{aligned}$$

(28)

where $\varvec{v}$ is the freestream velocity, and $\varvec{n}$ is the normal vector of the lifting surface panels. $\varvec{\varGamma _\text {b}}$ and $\varvec{\varGamma _\text {w}}$ represent the bound and the wake vortex circulation strengths, respectively. $\varvec{A}$ and $\varvec{B}$ are the aerodynamic influence coefficient matrices.

The outputs of the VLM model are the traction forces on each panel given by the panel forces divided by the areas. The panel forces are calculated using the Kutta–Joukowski theorem (Katz and Plotkin 2001) as below

$$\begin{aligned} \varvec{F}=\rho \varvec{\varGamma _\text {b}} \varvec{v_\text {ind} } \times \varvec{s} \text {,} \end{aligned}$$

(29)

where $\rho$ is the density of air, $\varvec{v_\text {ind}}$ is the induced velocity evaluated at the bound vortex collocation points, and $\varvec{s}$ represents the bound vector.

4.4.2 Thin-shell structural solver with Reissner–Mindlin plate theory

We implement the Reissner–Mindlin shell formulation in FEniCSx,³ based on the geometrically linear, quadrilateral-element variant of the fully nonlinear unconventional shell formulation developed by Campello et al. (2003). This formulation considers six-parameter solution fields (three for displacements and three for rotations).

There are other openly available implementations of this shell formulation in the FEniCS community, such as the pedagogical example by Bleyer (2018), with slight difference in the formulation of the drilling stabilization term. Moreover, the existing implementation is implemented in legacy FEniCS with limited support for quadrilateral elements, while our shell solver is implemented in FEniCSx, which provides robust support for quadrilateral elements.

While our shell solver can deal with both triangular and quadrilateral elements, it currently cannot handle meshes containing multiple types of elements, i.e., meshes containing both triangular and quadrilateral elements, due to a limitation in the FEniCSx mesh importing module.

4.4.3 Work-conservative aeroelastic coupling

The VLM aerodynamic solver is loosely coupled with the FEniCSx structural solver by linearly mapping the aerodynamic loads and structural displacements between both solvers. We use the approach presented in Van Schie et al. (2023) to construct these linear load and displacement maps. In this approach, we start by expressing the aeroelastic work with each solver. This is achieved by defining a matrix M for each solver, such that the aeroelastic work can be computed as the product $\varvec{u}^\textrm{T} M \varvec{F}$. Here, $\varvec{u}$ and $\varvec{F}$ are the vectors containing the degrees of freedom of the displacements and the loads, respectively. The product $\varvec{u}^\textrm{T} M \varvec{F}$ encodes all solver-specific information used in computing aeroelastic work.

Next, we define a linear map to transfer the displacements from the structural solver to the VLM solver. Then, we construct the linear map that transfers aerodynamic loads from the VLM solver to the structural solver following the expressions of aeroelastic work and the displacement map. The resulting load map ensures that the load-displacement mapping pair conserves aeroelastic work and can also be designed to conserve the total aerodynamic load in each principal direction. In this application, both the displacement map and the load map are linear, which allows them to be used in gradient-based optimization algorithms.

4.4.4 Static aeroelastic simulation with constant wind velocity

We start with a simple static case of aeroelasticity, where a constant wind velocity $V_{\infty }=50 \,\textrm{m}/\textrm{s}$ is applied. We consider an angle of attack $\textrm{AoA}=6^\circ$, and the air density is set to the International Standard Atmosphere air density at sea level, $\rho = 1.225$ kg/m$^{3}$. The aerodynamic solver initiates with an original VLM mesh and outputs the aerodynamic loads, which are then projected onto the structural domain. The structural solver computes the displacements, which in turn lead to updates in the VLM mesh. This iterative process continues until the updates in the VLM mesh coordinates between the previous and the current iterations fall below $10^{-6}$. We use an embedded nonlinear block CG solver for this iterative coupling relationship. The results of the von Mises stress and the aerodynamic load are shown in Fig. 14.

Fig. 14

Static aeroelastic analysis of the eCRM-001 wing model with constant wind velocity and clamped boundary condition at the wing root. The deformation of the wing structure is scaled by a factor of 40 for visualization

4.4.5 Dynamic aeroelastic simulation of wind gust response

For the dynamic scenario, we study the response of the eVTOL wing subjected to gust excitation. The eVTOL aircraft is initially cruising at a constant speed of $v_0=50$ m/s under steady wind in the x direction, $V_{\infty }=50$ m/s. Then, we apply a gust wind in the z-direction with a sinusoidal profile given by $V_\textrm{gust}=v_0\times (1-\cos (2\pi (t-T_0)/T_1))$, where $T_0$ is the time when the gust is activated and $T_1$ is the duration of the gust application.

We simulate the aeroelastic response of the wing under this gust excitation, considering three phases: the steady state, the gust application period, and the oscillation after gust removal. We choose the implicit midpoint rule in FEniCSx as the time integration method for the dynamic structural solver, and the steady VLM solver. In Fig. 15, the gust velocity and the tip displacement of the eVTOL wing are shown over time. The peak tip displacement occurs slightly after the maximum gust velocity. This aligns with our expectation since the velocity of wing tip is not zero yet at the maximum gust velocity, leading to a continued upward movement of the wing until the velocity of the wing itself decreases to zero. The amplitude of the tip displacement is constant during the oscillation phase because there is no damping in the elastic model. In the plot of tip displacements, a convergence study of time step size is performed and the solution converges when $\varDelta t=0.001$ (Nsteps=50).

Fig. 15

Numerical results for wind gust response of the eCRM-001 wing model under a sinusoidal gust excitement. The plot on top shows the velocity of the gust over time. The plot on the bottom shows the corresponding aeroelastic response of the wing measured by the tip displacement with different time step sizes

Fig. 16

The MDO process for thickness sensitivity analysis of the eCRM-001 wing structure under aerodynamic loads

4.4.6 Sensitivity analysis and validation of compliance with respect to thickness

As the aeroelastic solver is fully integrated with FEMO, it allows us to compute the total derivatives of any specified outputs with respect to design variables automatically. The MDO process is shown in Fig. 16. These automated derivatives are the key to solve any optimization problems involving aeroelasticity efficiently. In Fig. 17, we demonstrate the capability of automatic adjoint computation for aeroelasticity by performing sensitivity analysis of structural compliance with respect to thickness distribution in a static scenario. We represent the thickness $\varvec{t}$ using a first-order continuous polynomial function, which is equivalent to nodal thickness. A constant thickness of 0.03 m is assigned as the initial value. The compliance C in this problem is defined as the dot product of the force vector $\varvec{f}$ and the displacement vector $\varvec{u}$ (Christensen and Klarbring 2008),

$$\begin{aligned} {C = \varvec{f}^\textrm{T} \varvec{u} \text {,}} \end{aligned}$$

(30)

which estimates the inverse of the stiffness in the structure model. The runscript for sensitivity analysis is shown in Listing 7, “Appendix B,” where we also provide a comprehensive comparison of estimated implementation efforts involved in utilizing FEMO versus employing Nastran. It is worth mentioning that while compliance and thickness are structural parameters, the aerodynamic solver is also involved in this derivative computation. This is because the aerodynamic mesh will be affected by structural deformation, leading to changes in the aerodynamic loads, which in turn impact the compliance, computed from the displacements.

Fig. 17

The gradients of compliance with respect to the thickness distribution are represented as a first-order continuous function in the top contour plot. The locations of the nodes used for adjoint validation are shown in the bottom plot

Table 2 Adjoint validation at selected nodes by comparing the gradients computed, respectively, by FEMO and finite difference method for the two-way coupled aeroelastic model

We validate the gradients computed through FEMO’s automatic adjoint method by comparing them with finite difference results at selected nodes. Specifically, we use the first-order forward difference approximation for validation. Thirteen nodes along the span-wise direction of the wing skin are chosen for this comparison, with their locations shown in Fig. 17. Given the gradients’ varying magnitudes ranging from $10^{-4}$ to $10^{-1}$, the choice of perturbation step size h can significantly affect the finite difference results. After conducting several numerical experiments with different step sizes, we opt for a step size of $10^{-4}$ to achieve a good balance of accuracy and stability. Detailed results are provided in Fig. 18, “Appendix C.” The gradients at the selected nodes are summarized in Table 2, demonstrating good agreement between the two approaches, with a maximum relative error of $1.31\%$.

5 Conclusion

In this work, we have presented a generalized approach for modeling PDE-constrained MDO problems, and developed the computational tool FEMO, with the goal to minimize the time, effort, and expertise required for development. FEMO leverages the powerful finite element solver FEniCSx to effectively and accurately solve PDEs, and integrates with CSDL, a domain-specific language for MDO modeling, to enable coupling with non-PDE components and automatic adjoint sensitivity analysis.

The effectiveness of this approach has been demonstrated through verification using benchmark problems, including the optimal control of a nonlinear elliptic PDE and topology optimization of a cantilever beam, both of which have known analytical solutions. Additionally, its capability to tackle real-world problems, such as the design and optimization of electric vertical takeoff and landing (eVTOL) aircraft, which motivated this research, has been established.

The shape optimization of an electric motor has converged successfully, which couples two nonlinear PDEs—the hyperelastic equation and Maxwell’s equations—to simulate the magnetic flux density field under geometry deformation, and then coupled with non-PDE postprocessing model to compute the power loss as the objective function.

We applied this method to large-scale aeroelastic analysis of an eVTOL wing, where there are thousands of design variables corresponding to node-wise structural thickness. Here, the FEniCSx-based structural solver is loosely coupled with the CSDL-based VLM solver through FEMO, and both static and dynamic cases have been discussed. For the static case, we also performed sensitivity analysis for structural compliance of the wing with respect to thickness distribution, which provided qualitatively reasonable results for the gradients. In the dynamic case, the structural response of the wing under gust excitation was studied, and the wing tip displacement profile achieved convergence through the reduction of the time step size.

While the presented methodology and implementation have shown promising results, there are still some challenges to overcome. Expertise is required for applying case-dependent Dirichlet boundary conditions weakly with Nitsche’s method, including formulation, tuning, and testing. Additionally, the efficiency needs to be improved for large-scale problems with a large number of design variables. Potential solutions could be reduced-order modeling, parallel computing, or tuning for nonlinear/linear solvers. For future work, we plan to address the above-mentioned challenges, and extend FEMO to include additional features and applications, such as sensitivity analysis for dynamic aeroelastic models. Another goal could be to incorporate other finite element modules based on the legacy FEniCS to fulfill specific analysis requirements, such as using PENGoLINS for isogeometric analysis with non-matching shells (Zhao et al. 2022).

Appendices

Appendix A: Code comparison of FEMO and FEniCS for topology optimization problem

We utilize the topology optimization problem described in Sect. 4.2 to compare FEMO code⁴ with pure FEniCS code.⁵ To elucidate the structures of the two platforms, we have streamlined both scripts by removing secondary lines, including import statements, unnecessary comments, and postprocessing. In addition, the GeneralFilterModel class in FEMO code is also omitted, as it primarily consists of simple CSDL-based algebraic operations. Even in this simple example, several benefits of using FEMO become apparent:

• (1) FEMO naturally separates the finite element analysis and optimization code through a modular design, facilitating easy debugging and modification. For instance, in this case, only Lines 115–117 in the FEMO code need to be changed if a different density filter is desired.

• (2) The FEMO code incorporates fewer FEniCS implementations (Lines 12–50) compared to pure FEniCS (throughout the entire script). This is attributed to the automation of FEniCS utility functions, such as variable updates in the backend of FEMO.

• (3) The remaining sections of the FEMO code are straightforward to implement, mainly involving filling in the blank spaces of parameters in the dictionary object, such as in fea.add_input(), fea.add_state() and fea.add_output() (Lines 81–93).

Appendix B: Implementation effort comparison of FEMO and Nastran for aeroelasticity

We compare the implementation efforts involved in using FEMO and Nastran for aeroelasticity analysis. We present the full FEMO runscript in Listing 7 for sensitivity analysis of an eVTOL wing under static aeroelastic coupling. The FEniCS-based dolfin-adjoint library is excluded from our comparison due to its inability to interface with other non-FEniCS-based solvers, such as low-/mid-fidelity aerodynamic solvers.

Given that Nastran primarily serves as a finite element analysis solver for structural and thermal analysis, while FEMO offers a generic PDE solver platform coupled with an optimization environment, our comparison focuses on two main aspects: the shell solver integrated with FEMO versus Nastran, and the respective workflows of using them in aeroelasticity. It is worth noting that most source code using Nastran for high-fidelity aeroelastic coupling are either inaccessible to public or challenging to reproduce because of the lack of maintenance or license constraints (Kenway and Martins 2014; Benaouali and Kachel 2019). For this reason, discussions of implementation efforts are estimated based the authors’ experience with these software tools and the literature.

The breakdown of implementation efforts is as follows:

• Learning curve we use the time required to master the shell solver as the learning curve estimation. Nastran, being a widely accepted finite element solver in aerospace and other engineering fields, typically has a lower learning curve for its pre-compiled commercial software products. In contrast, FEMO’s FEA capability relies on FEniCSx, necessitating the users to possess basic knowledge of FEniCSx and Python programming. Consequently, the learning curve for the FEMO shell solver is slightly steeper

• Coupling we specifically consider the integration of forward simulation for this aspect, as the coupling of derivatives is addressed separately in the next item. In contrast to FEMO’s automated coupling capability as easy as model.add(submodel), as shown in Lines 302–309 in Listing 7, Nastran demands significant effort as well as expertise in compiling multi-language code, given that the original solver is written in Fortran.⁶ While tools like pyNastran⁷ exist, they are primarily utilized for pre/postprocessing of Nastran.

• Derivatives similar to coupling, derivative computation for the coupled system is significantly easier in FEMO. While Nastran does provide derivatives for the structure solver, computing derivatives for the coupled system requires manual derivation and implementation, whereas FEMO utilizes automatic adjoint methods for derivative computation.

• Lines of code since FEMO automates coupling and derivative computation, it can save hundreds to thousands of lines of code for those processes.

• Code maintenance code maintenance is considerably easier in FEMO. It is fully open-source and can be easily extended to other application scenarios by simply changing the sub-model to be added to the full model. Additionally, thanks to its utilization of dictionaries, FEMO code is much easier to read.

Appendix C: Numerical experiments on finite difference step size in the aeroelastic example

For adjoint validation of the aeroelastic model, we use the finite difference method to compare the gradients of compliance with respect to thickness ($\textrm{d}C/\textrm{d}t$) at selected nodes. Figure 18 shows the relative errors in $\textrm{d}C/\textrm{d}t$ for various finite difference step sizes h. The results show that smaller h generally reduces errors, but increases errors significantly for some nodes. Specifically, $h = 10^{-5}$ and $h = 10^{-6}$ have smaller errors for the first ten nodes but increase for node 11–13 due to round-off error from lower magnitudes of the gradients at these nodes. Therefore, $h = 10^{-4}$ is optimal, balancing low errors and stability. The accuracy of the adjoint method in FEMO has been verified as the relative errors for the first ten nodes (whose gradients’ magnitude exceeds 0.1) remain reasonable across different step sizes.

Fig. 18

Relative errors for the gradients of compliance with respect to thickness ($\textrm{d}C/\textrm{d}t$) using different finite difference step sizes h