Yet another parameter-free shape optimization method

Abstract

The use of node coordinates as design variables in shape optimization offers a larger design space than computer-aided design (CAD)-based shape parameterizations. It also allows for the optimization of legacy designs, i.e., a finite element mesh from an existing design can be readily optimized to meet new performance requirements without involving a CAD model. However, it is well known that the node coordinate parameterization method is fraught with numerical difficulties, which makes it impractical to use. This has led to several of “parameter-free” shape optimization methods that seek the advantages and avoid the pitfalls of the naïve node coordinate parameterization method. These methods come in two main varieties: sensitivity filtering (or gradient smoothing) and consistent filtering. The latter is analogous to the density filter method used in topology optimization (TO). Herein, we use the PDE filter from TO and energy-based filters to implement consistent shape optimization filtering schemes easily and efficiently. Numerical experiments demonstrate that consistent methods are more robust than sensitivity filtering methods.

1 Introduction

Shape optimization morphs material boundaries to achieve optimal design performance. When compared to topology optimization, shape optimization exhibits less design freedom; however, it provides an explicit boundary/interface description. Thus, when simulations involve boundary or interface-dominant physics, e.g., stress computations for optimization metrics or solid–fluid interaction, shape optimization is often advantageous. Further, shape optimization results are easily communicated to manufacturing processes due to the explicit boundary and interface representations.

Shape optimization poses two key challenges. First, a parameterization must be defined that allows design flexibility while maintaining adequate design control. Unfortunately, these two desires are often contradictory. Second, a conforming mesh of each iterate design must be generated for use in the finite element simulation. The difficulty of mesh generation depends on the complexity of the parameterization. To ease this process, we combine the parameterization with the finite element mesh. Namely, we use the mesh nodal coordinates as the optimization variables. Users only generate a mesh via their favorite preprocessor for the initial design. Thereafter, the optimizer controls the mesh updates. This “parameter-free” approach reduces design limitations imposed by restrictive parameterizations.

To motivate our work, we optimize the shape of a hole in a biaxially loaded plate to minimize the compliance subject to a maximum volume constraint Fig. 1.¹ In our so-called parameterized optimization, we require the hole to be an ellipse and optimize the lengths of the axes, Fig. 2. The compliance of the optimized design is 79% of the initial design’s compliance. The analytical solution, assuming the plate is infinite, is an ellipse with 2:1 axes ratio, so our design with 1.81 axes ratio is nearly optimal. Nonetheless, to improve the design, we no longer restrict it to the 2 parameter elliptical hole optimization. Rather, an “independent node” optimization is performed in which all of the finite element node coordinates (except those that would affect the plate’s outer boundary) serve as design parameters. However, as seen in Fig. 2, after 3 iterations, the mesh gets tangled so the optimization is terminated. This is expected since the compliance and volume are insensitive to internal node movements and hence the optimizer only moves the boundary nodes. To resolve this mesh tangling deficiency, various “parameter-free” shape optimization methods have been proposed; we propose yet another.

We aim to develop a parameter-free shape optimization method that uses readily available nonlinear programming (NLP) solvers, e.g., IPOPT (Wächter and Biegler 2006) and fmincon (Matlab 2017). In this way, we can readily accommodate an arbitrary number of constraints, verify the Karush-Kuhn-Tucker (KKT) optimality conditions, and avoid writing-specialized NLP solvers. We seek a robust method that does not require extensive parameter tuning when solving a range of optimization problems. Finally, we aim to develop an efficient method that converges rapidly and utilizes high-performance computing (HPC).

Fig. 1

Plate with hole (left), symmetry domain with biaxial loading boundary conditions (center) and design boundary conditions (right)

Fig. 2

Finite element meshes for optimized plate with hole

To achieve our parameter-free shape optimization goals, we mimic the implicit PDE density filter developed by Lazarov and Sigmund (2011) from topology optimization. The use of a consistent sensitivity analysis, i.e., we filter nodal coordinates and their sensitivities, provides robust convergence during the design optimization.

We aim to optimize the shape of three-dimensional continuum structures using the finite element method, and hence, we do not review literature that concerns optimization of plate and shell structures and isogeometric analysis.² Notwithstanding this omission, the shape optimization literature is vast, please refer to Samareh (2001); Martinelli and Jameson (2012); Upadhyay et al. (2021) for thorough reviews of the subject. Our discussion focuses on parameter-free methods. The use of node coordinates as design variables in shape optimization has the advantage of offering a large design space and eliminating the reliance on computer-aided design (CAD)-based shape parameterizations (Braibant and Fleury 1984; Chen and Tortorelli 1997) that are troublesome for industrially relevant optimization problems. This is because industrially relevant CAD models are created using numerous boolean, blending, rounding, and trimming operations. In the optimization, finite element meshes must be created from the CAD models and derivatives of the node coordinates with respect to the optimization parameters, e.g., select dimensions must be computed. While this task is easily accomplished for the simple optimization problem illustrated in Figs. 1 and 2, it is often extremely challenging for industrially relevant problems. CAD models associated with legacy designs may also be unavailable. However, if finite element models for such designs are available, they can be shape optimized via the parameter-free method to meet new design specifications. That said, the node coordinate parameterizations may lead to an ill-posed optimization problems (Chenais 1975; Bängtsson et al. 2003; Mohammadi and Pironneau 2004; Harbrecht 2008; Mohammadi and Pironneau 2008), but most definitely, it is well known that naively using the node coordinates as design variables produces designs with tangled meshes which are artifacts of the finite element discretization (Braibant and Fleury 1984; Le et al. 2011), cf. the simple example above.

We compute the derivatives of the optimization cost and constraint functions using the adjoint method. The derivatives can be expressed as a combination of volumetric and surface integrals in the so-called domain method or solely with surface integrals in the so-called boundary method. Sensitivities computed via the “domain” method agree, within machine precision, to those computed via finite difference approximations (Choi and Seong 1986; Yang and Botkin 1987) because the differentiate-then-discretize and discretize-then-differentiate operations commute (Yang and Botkin 1987; Berggren 2010). However, sensitivities computed via the boundary method are error prone due to a lack of continuity in the gradient computations across the inter element boundaries (Berggren 2010). Fortunately, these errors diminish with mesh refinement and may also be reduced by using nonconventional $C^1$ interpolation.

Gradient smoothing is analogous to sensitivity filtering in topology optimization (Sigmund 1997) where it is well known that the filtered sensitivities are inconsistent with the NLP solver and hence the NLP convergence suffers (Matsumori et al. 2017). Two types of shape optimization gradient smoothing methods exist, explicit and implicit. The explicit approach uses a convolution filter, much like how Sigmund (1997) computes a “smooth” gradient from the “raw” gradient, e.g. (Stück and Rung 2011; Gerzen et al. 2012). In the implicit approach, a careful distinction is made between the derivative and the gradient, e.g., Pironneau (1984). We generally compute the derivative via adjoint methods as described below. But, the gradient, not the derivative, is often required by popular NLP algorithms, e.g., the method of steepest descent. The gradient belongs to an inner product space, and hence, it depends on the definition of the inner product. This is the impetus of the $H^1$ smoothing methods (Pironneau 1984; Jameson 2004; Gournay 2006; Nonogawa et al. 2020; Azegami 2021; Allaire et al. 2021) which roughly project the derivative onto the chosen inner product space. The projected gradient requires the solution of a PDE and hence the “implicit” filter terminology.

The traction method presented by Shimoda et al. (1997) can be viewed as a gradient smoothing method in which the $H^1$ inner product is replaced with the energy inner product from linear isotropic elasticity. The method applies the shape derivative as a traction to compute the smoothed gradient and hence its name. In another variant, Azegami and Takeuchi (2006) treat the shape derivative as an “ambient” displacement in a Robin-like boundary condition to obtain additional smoothness of the gradient. This latter approach is more closely related to the $H^1$ smoothing methods. Riehl and Steinmann (2014) extend the traction method by incorporating an adaptive mesh refinement step to ensure suitable meshes and accurate simulations.

As noted by Schwedes et al. (2017), the inconsistency introduced by only filtering the sensitivity in the implicit methods can be resolved by incorporating the chosen inner product into the NLP solver. Unfortunately, this is seldom the case as most NLP libraries work in ${\mathbb {R}}^n$ rather than the underlying function space in which the optimization problem is naturally formulated, e.g., $H^1$. Perhaps this is why most of the shape optimization methods cited above do not use popular NLP libraries; rather, they rely on augmented Lagrangian methods that incorporate a single constraint combined with inefficient steepest descent methods (Gournay 2006; Nonogawa et al. 2020; Ertl et al. 2019). Nonetheless, gradient smoothing algorithms prove effective as seen below and demonstrated by Ertl et al. (2019).

Riehl et al. (2014) and Bletzinger (2014) provide efforts to maintain consistency in the optimization formulation. Therein explicit filters are used to compute the gradient from the derivative and its transpose is used to smooth the design update. This is akin to the density filter (Bruns and Tortorelli 2001) from topology optimization where the element volume fraction vector $\varvec{\nu }$ is optimized, but the filtered element volume fraction vector $\widetilde{\varvec{\nu }} = {\varvec{F}} \, \varvec{\nu }$ obtained from the filter matrix ${\varvec{F}}$ is used to define the design over which the response is computed. Sensitivities ${\partial \theta }/{\partial \widetilde{\varvec{\nu }}}$ of the cost and constraint functions ${\widetilde{\theta }}(\widetilde{\varvec{\nu }})$ are computed via adjoint methods and the chain-rule is used to evaluate the sensitivities that are input to the NLP algorithm ${\partial \theta }/{\partial { \varvec{\nu }}} = {\varvec{F}}^T \, {\partial {\widetilde{\theta }}}/{\partial \widetilde{\varvec{\nu }}}$. Here, the smoothed and unsmoothed element volume fraction vectors $\widetilde{\varvec{\nu }}$ and $\varvec{\nu }$ are replaced by the smoothed and unsmoothed nodal coordinate vectors $\widetilde{\varvec{X}}$ and $\varvec{X}$; however, an inconsistency arises that does not appear in topology optimization. Namely, in the work by Riehl et al. (2014) and Bletzinger (2014), the mesh over which ${\varvec{F}}$ is computed is defined by the smoothed node coordinate vector $\widetilde{\varvec{X}}$, which continues to evolve during the optimization and consequently ${\varvec{F}}$ changes during the optimization. This observation has led to the development of adaptive filter schemes, Antonau et al. (2022).³

In the end, it is difficult to know precisely what optimization problem is solved. Notably, the filter is recomputed at each optimization iteration using the configuration corresponding to the previous design iterate and hence the optimized design depends on the “trajectory” of the NLP algorithm. One cannot obtain KKT conditions to a predefined optimization problem, without taking this “trajectory” into account.

In the natural design variable method, Belegundu and Rajan (1988) apply “design loads” $\varvec{P}_d$ to the initial design and use separate “shape morphing” analyses to deform the initial design configuration $\Omega _0$ into the optimized configuration $\Omega$. The load $\varvec{P}_d$ serves as the design variable vector in the optimization, Weeber et al. (1992); Tortorelli (1993). The initial design with node coordinate vector $\varvec{X}_0$ is morphed into the optimized structure with node coordinate vector ${\varvec{X}} = \varvec{X}_0 + \varvec{D}$. Here, $\varvec{D}$ is the solution to the discretized shape morphing elasticity equation ${\varvec{K}}_d \, \varvec{D} = \varvec{P}_d$. Mimicking the sensitivity filtering discussion above, we have $\varvec{D} = {\varvec{K}}_d^{-1} \, \varvec{P}_d$ and ${\partial \theta }/{\partial \varvec{P}} = {\varvec{K}}_d^{-T} \, {\partial {\widetilde{\theta }}}/{\partial {\varvec{X}}}$, i.e., $\varvec{K}_d^{-1}$ plays the role of the filter matrix $\varvec{F}$. This consistent method has a well-defined optimization problem that quickly converges.

The “fictitious energy method” is similar the natural design variable method; however, Scherer et al. (2010) use prescribed displacements rather than loads to morph the initial design into the optimized design. Mesh quality is ensured by using a “special” nonlinear, isotropic, hyperelastic material that is unaffected by rigid motions and dilations/contractions in the morphing analysis. In this way, rigid motions and dilations/contractions of elements are allowed whereas shear and unequal triaxial extensions/compressions of the elements are minimized. To further limit mesh distortion, an additional constraint on the total strain energy of the morphing deformation is imposed.

The explicit consistent filtering approach to shape optimization (Le et al. 2011) can be viewed as the shape optimization equivalent of the popular density-based topology optimization method (Bruns and Tortorelli 2001). The latter uses a consistent filter to formulate as well-posed optimization problem and hasten convergence of the NLP algorithm. Herein, we build upon the work of Le et al. (2011) by replacing the explicit filter with various implicit filters, another idea borrowed from topology optimization (Lazarov and Sigmund 2011) and used by Matsumori et al. (2017) in their shape optimization study. These implicit filters are more suitable to HPC and, in our opinion, easier to implement, although they require the solutions of additional PDEs. Indeed, the solvers are implemented using efficient numerical techniques leveraging scalable parallel computer architectures. On the other hand, the explicit filters require interprocessor communication to evaluate the filter convolution integrals and HPC libraries that support such computations are not generally available. A comparison of consistent explicit and implicit filters is presented by Najian and Bletzinger (2023).

Our approach is very similar to the $H^1$ filter approach described by Matsumori et al. (2017); however, we do not constrain a mesh quality energy or limit the extent of the filter to the boundary region. Similarities also exist between our approach and that presented by Liatsikouras et al. (2022).

Therein the coordinates of duplicate “handle nodes” on the boundary serve as the design parameters. The initial mesh is morphed into the optimized design by minimizing the morphing strain energy subject to the constraint that the “follower” surface nodes are close to the handle nodes. Because the constraint is enforced via the penalty method, the design smoothness can be controlled by varying the penalty value. To a lesser extent, our approach is similar to the fictitious energy approach (Scherer et al. 2010); however, we replace their morphing displacement boundary conditions with Robin boundary conditions so we are able to filter all of the node coordinate updates, i.e., both in the domain’s interior and on its boundary and we do not constrain the fictitious energy. Tikhonov regularization is used by Bängtsson et al. (2003) to obtain a smooth boundary; the idea is motivated by Gunzburger et al. (2000). Their approach requires the solution of an ODE (for their two-dimensional study) to map the optimization’s jagged boundary to a smooth boundary over which the optimization cost and constraint functions are computed. Interior nodes are relocated by solving an elasticity problem as done in the fictitious energy approach (Scherer et al. 2010); however, their problem is linear so the mesh motion is more limited. Gradients of the cost and constraint functions are computed in a consistent manner using a combination of direct and adjoint methods. Their thorough study compares many different problem formulations.

We experiment with different filters based on the vector Helmholtz PDE used by Matsumori et al. (2017), a nonlinear filter based on the fictitious energy approach of Scherer et al. (2010), and a linearized version of this nonlinear filter. To solve the optimization problems, we use popular NLP libraries IPOPT (Wächter and Biegler 2006) and fmincon (Matlab 2017) to leverage their efficient algorithms and their abilities to incorporate numerous constraints and compute KKT optimality conditions. Some of our computations utilize the MFEM library (Anderson et al. 2021), and hence, we can readily invoke parallelism and employ a wide variety of discretizations, e.g., high-order polynomials. Derivatives for the algorithms are computed consistently via adjoint methods and accurately using domain, rather than boundary, sensitivity integrations. Summarizing the salient features in our work, we highlight

• 1. Domain shape derivative computations,

• 2. Consistency with the NLP algorithm,

• 3. PDE and energy-based filters,

• 4. Multiple filter functions,

• 5. Use of popular NLP libraries.

We compare our consistent approaches to the fictitious energy approach of Scherer et al. (2010) and the gradient smoothing approaches of Allaire et al. (2021) and Azegami (2021). These three methods are also integrated with the popular NLP libraries and utilize the accurate domain shape derivative computations.

2 Independent node coordinate formulation

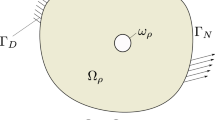
In the independent node coordinate formulation, the node coordinates contained in $\varvec{X}$ that define the physical domain $\Omega$ serve as the design variable. A linear elastic finite element analysis is performed over $\Omega$ to compute the physical displacement field $\varvec{u}$. The cost and constraint functions $\theta _i, i = 0, 1, 2, \cdots$ and their shape sensitivities ${D \theta _i}/{D \varvec{X}}$ are then evaluated. The values of the coordinates $\varvec{X}$, cost and constraint functions $\theta _i$ , and sensitivities ${D \theta _i}/{D \varvec{X}}$ are input to the NLP algorithm to update the coordinates $\varvec{X} \leftarrow \varvec{X} + \Delta \varvec{X}$. Iterations continue until convergence, or more likely until the appearance of a tangled mesh which causes the algorithm to crash.

In the finite element analysis, we find the physical displacement ${\varvec{u}} \in {{\mathcal {H}}}(\varvec{u}^p)$ that satisfies the linear elastic residual equation

$$\begin{aligned} \begin{aligned} 0&= \; r(\varvec{u}, \varvec{w}) \\&= \int _{\Omega } \nabla {\varvec{w}} \cdot {\mathbb {C}}[ \nabla {\varvec{u}}] \, dv - \int _\Omega {\varvec{w}} \cdot \varvec{b} \, dv \\&- \int _{A^t} {\varvec{w}} \cdot \varvec{t}^n \, da - \int _{A^p} {\varvec{w}} \cdot p \, \varvec{n} \, da \\&= a(\varvec{u}, \varvec{w}) - \ell (\varvec{w}) \end{aligned} \end{aligned}$$

(1)

for all ${\varvec{w}} \in {{\mathcal {H}}}(\varvec{0})$. In the above ${\mathbb {C}}$ is the elasticity tensor which exhibits the usual symmetries, $\varvec{b}$ is the prescribed body force per unit volume. $\partial \Omega$ is the boundary of $\Omega$ with outward unit normal vector $\varvec{n}$; it is divided into three complementary regions $A^u$, $A^t$ , and $A^p$ over which the displacement $\varvec{u}^p$, traction $\varvec{t}^p$ , and normal pressure p are prescribed. Finally, a is the bilinear form, $\ell$ is the load linear form, and the space of admissible functions is

$$\begin{aligned} {{\mathcal {H}}}(\varvec{u}^p) = \{ \varvec{u} \in H^1 \,: \, \varvec{u} = \varvec{u}^p \ \forall \ \varvec{x} \in A^u\}. \end{aligned}$$

(2)

Without loss of generality, we assume $\varvec{u}^p = \varvec{0}$ henceforth.

Upon evaluating the displacement field, we compute the optimization cost and constraint functions $\theta _i$

$$\begin{aligned} \begin{aligned} \theta _i(\varvec{x})&= \int _\Omega \Lambda (\nabla \varvec{u}, \varvec{u}, \varvec{x}) \, dv + \int _{A^t} \tau (\varvec{u}, \varvec{x}) \, da \\ {}&+ \int _{A^p} \varvec{\tau }(\varvec{u}, \varvec{x}) \cdot \varvec{n} \, da \end{aligned} \end{aligned}$$

(3)

where $\varvec{x}$ denotes the location of material particles in $\Omega$ and $\Lambda$, $\tau$ , and $\varvec{\tau }$ are generic functions that can be used to compute, e.g., the volume of $\Omega$ by equating $\Lambda = 1$, $\tau = 0$ , and $\varvec{\tau } = \varvec{0}$ or compliance by equating $\Lambda = \nabla \varvec{u} \cdot {\mathbb {C}}[\nabla \varvec{u}]$, $\tau = 0$ , and $\varvec{\tau } = \varvec{0}$. The shape sensitivity of the above is evaluated using the adjoint method (Haug and Choi 1986). Details of the sensitivity analysis and finite element discretization are provided in Appendix.

In practice, many of the node coordinates are not moved during the optimization. To illustrate this, we optimize the shape of a hole in the center of a homogeneous isotropic $2 \times 2$ square plate that is subjected to biaxial traction, Fig. 1. To facilitate the plane stress analysis, we utilize domain symmetry whence the optimized hole geometry is necessarily symmetric with respect to reflections about the $\varvec{e}_1$ and $\varvec{e}_2$ axes. Since we are only optimizing the hole shape, the node coordinates are constrained such that the nodes on the vertical edges cannot move in the $\varvec{e}_1$ direction and the nodes on the horizontal edges cannot move in the $\varvec{e}_2$ direction.

One iteration for the independent node coordinate optimization algorithm is partially summarized in Algorithm 1. For each iteration of the optimization, we have a design $\Omega$ defined by the node coordinates $\varvec{X}$ over which we compute the $\theta _i$ and their derivatives ${D \theta _i}/{D \varvec{X}}$. The optimizer updates the design, i.e., $\varvec{X} \leftarrow \varvec{X} + \Delta \varvec{X}$, whereafter another iteration commences if the convergence criterion has not been satisfied. Unfortunately, this independent node coordinate formulation invariably produces tangled meshes which cause the optimization to prematurely crash, Fig. 2.

Independent node coordinate iteration, Appendix 1 for the discretization

2.1 Gradient smoothing algorithm

The gradient smoothing formulation is similar to the independent node coordinate formulation as we are given a body with material points identified by their positions $\varvec{x}$ in the initial design configuration $\Omega _0$ and $\varvec{x} \leftarrow \varvec{x} + \delta \varvec{x}$ in the optimized design configuration $\Omega$. The mesh tangling incurred by the independent node coordinate formulation is resolved using numerous variants of explicit (Stück and Rung 2011) or implicit (Pironneau 1984; Jameson 2004; Gournay 2006; Scherer et al. 2010; Allaire et al. 2021; Müller et al. 2021; Welker 2021) gradient smoothing algorithms. Mimicking the sensitivity filter in topology optimization (Sigmund 1997), the explicit method computes a smooth shape sensitivity by filtering the raw gradient, i.e., shape sensitivity. Implicit smoothing uses the Riesz representation theorem to relate the derivative $\delta \theta$ to the gradient $\text {grad} \theta$. In ${\mathbb {R}}^n$, under the standard Euclidean inner product, there is no difference in the representation of the derivative and the gradient. Thus, when the design, i.e., the node coordinate vector $\varvec{X}$, is viewed as an element of ${\mathbb {R}}^n$, the design derivative and gradient are (numerically) interchangeable. However, this is no longer the case when one views the design as an element of a function space $\mathcal{H}$, which is the case if we use a perturbation $\Delta \varvec{x}\in {{\mathcal {H}}}$ to deform the current design into the next design iterate, i.e., points originally located at $\varvec{x}$ in the current design are displaced to locations $\varvec{x} = \varvec{x} + \Delta \varvec{x}$ in the next design iterate. Assuming the inner product on $\mathcal{H}$ is not the Euclidean inner product, the shape derivative is no longer (numerically) interchangeable with the gradient. Instead, assuming it exists, the derivative at $\Omega$, $\delta \theta (\varvec{x}; \cdot ) \in \text {Lin}( {{\mathcal {H}}} \rightarrow {\mathbb {R}})$, is a linear operator from ${{\mathcal {H}}}$ into ${\mathbb {R}}$ and hence by the Riesz representation theorem there exists a unique $\text {grad} \theta (\varvec{x}) \in {{\mathcal {H}}}$ such that $\delta \theta (\varvec{x}, \delta \varvec{x}) = a(\text {grad} \theta (\varvec{x}), \delta \varvec{x})$ for all $\delta \varvec{x}\in {{\mathcal {H}}}$. In this equality $a(\cdot , \cdot )$ is the inner product for ${{\mathcal {H}}}$ and this is where things get murky as there are multiple choices for the space ${{\mathcal {H}}}$ and inner product $a(\cdot , \cdot )$. For example if we choose ${{\mathcal {H}}} = L^2$ and the standard inner product

$$\begin{aligned} a (\varvec{u}, \varvec{w}) = \int _\Omega \varvec{u} \cdot \varvec{w} \, dv \end{aligned}$$

(4)

we obtain the “rough” gradient $\text {grad} \theta (\varvec{x})$ via

$$\begin{aligned} a(\text {grad} \theta (\varvec{x}), \delta \varvec{x}) = \int _\Omega \text {grad} \theta (\varvec{x}) \cdot \delta \varvec{x} \, dv = \delta \theta (\varvec{x}; \delta \varvec{x} ) \end{aligned}$$

(5)

⁴ However, if we choose ${{\mathcal {H}}} = H^1$ and the nonstandard inner product

$$\begin{aligned} {\widetilde{a}}(\varvec{u}, \varvec{w}) = \int _\Omega (\nabla \varvec{u} \cdot \gamma \, \nabla \varvec{w} + \varvec{u} \cdot \varvec{w}) \, dv \end{aligned}$$

(6)

with $\gamma >0$ , we obtain the “smooth” gradient $\widetilde{\text {grad} \theta }(\varvec{x})$ via

$$\begin{aligned} \begin{aligned} {\widetilde{a}}( \widetilde{\text {grad} \theta }(\varvec{x}), \delta \varvec{x})&= \int _\Omega \left( \nabla \widetilde{\text {grad}\theta }(\varvec{x}) \cdot \gamma \, \nabla \delta \varvec{x} + \right. \\ {}&\hspace{.3in} \left. \widetilde{\text {grad} \theta }(\varvec{x}) \cdot \delta \varvec{x} \right) \, dv \\ {}&= \delta \theta (\varvec{x}; \delta \varvec{x} ) \end{aligned} \end{aligned}$$

(7)

In the above, we emphasize that $\widetilde{\text {grad} \theta }(\varvec{x})$ is a vector field in $H^1$ and $\nabla \widetilde{\text {grad} \theta }(\varvec{x})$ is the spatial derivative of this field.

To see why we refer to $\text {grad} \theta (\varvec{x})$ and $\widetilde{\text {grad} \theta }(\varvec{x})$ as the rough and smooth gradients, consider the following minimization problem

$$\begin{aligned} \begin{aligned}&\mathop {\min }_{\widetilde{\text {grad} \theta } \in H^1 }{} & {} \int _{\Omega } |\widetilde{\text {grad} \theta } - \text {grad} \theta |^2 \, dv \\&\text {such that }{} & {} \int _{\Omega _0} |\nabla \widetilde{\text {grad} \theta } |^2 \, dv = 0 \end{aligned} \end{aligned}$$

(8)

where $\text {grad} \theta \in L^2$ is the known rough gradient and we have dropped the arguments for conciseness. Solving the above via the penalty method results in the unconstrained problem

$$\begin{aligned} \begin{aligned}&\mathop {\min }_{\widetilde{\text {grad} \theta }(\varvec{x}) \in H^1 }&\int _{\Omega } |\widetilde{\text {grad} \theta } (\varvec{x}) - \text {grad} \theta (\varvec{x}) |^2 \, dv + \\{} & {} \gamma \, \int _{\Omega _0} |\nabla \widetilde{\text {grad} \theta }(\varvec{x}) |^2 \, dv \end{aligned} \end{aligned}$$

(9)

where $\gamma >0$ is the penalty parameter. The stationary condition of (9) requires $\widetilde{\text {grad} \theta } (\varvec{x}) \in H^1$ to satisfy

$$\begin{aligned} \begin{aligned} {\widetilde{a}}( \widetilde{\text {grad} \theta }(\varvec{x}), \varvec{w}) = a(\text {grad} \theta (\varvec{x}), \varvec{w}) = \delta \theta (\varvec{x}; \varvec{w}) \end{aligned} \end{aligned}$$

(10)

for all $\varvec{w} \in H^1$. Larger values of $\gamma$ increase the enforcement of the $\int _{\Omega _0} |\nabla \widetilde{\text {grad} \theta }(\varvec{x}) |^2 \, dv = 0$ constraint, i.e., lessen the spatial variations in $\widetilde{\text {grad} \theta }(\varvec{x})$. An excellent tutorial on the need for using $\widetilde{\text {grad} \theta }(\varvec{x})$ rather than ${\text {grad} \theta }(\varvec{x})$ appears in Jameson (2004).

The $H^1$ smoothing algorithm uses the smooth gradient $\widetilde{\text {grad} \theta }(\varvec{x})$ to compute the design updates $\delta \varvec{x}$. Smoother gradients result in smoother updates and hence less mesh tangling. Setting $\gamma = 1$ we see that ${\widetilde{a}}$ reduces to the standard inner product for $H^1$ and hence the $H^1$ terminology.

We finish the derivation with the imposition of the “boundary conditions.” To fix the location of portions of the boundary $\partial \Omega$ during the shape optimization, we replace $H^1$ in (10) with

$$\begin{aligned} H^1_0 = \{ \varvec{u} \in H^1 |\, \varvec{u} \cdot \varvec{e} = 0 \ \textrm{on} \ A^{f} \} \end{aligned}$$

(11)

in which $A^{f} \subset \partial \Omega _0$ are the surface regions which are fixed in the $\varvec{e}$ direction during the optimization. E.g. in the Fig. 1 example $\varvec{u} \cdot \varvec{e}_2 = 0$ on the horizontal edges and $\varvec{u} \cdot \varvec{e}_1 = 0$ on the vertical edges. Telling the nonlinear programming algorithm that $\widetilde{\text {grad} \theta }(\varvec{x}) \cdot \varvec{e} = 0$ on $A^f$ ensures that these surfaces remain unchanged in these directions during the optimization.

The $H^1$ smoothing algorithm is analogous to the PDE filter in topology optimization (Lazarov and Sigmund 2011). However, it is not performed in a consistent manner, and hence, it is also analogous to the sensitivity filtering approach in topology optimization (Sigmund 1997).⁵ As such, the optimization algorithm may converge slowly or not at all.

We note that the traction method (Shimoda et al. 1997) is a variant of the $H^1$ smoothing algorithm in which the elasticity bilinear form a of (1) replaces ${\widetilde{a}}$ of (6), i.e., we use the energy inner product. As such, “infinitesimal rigid motions” characterized by skew $\nabla \widetilde{\text {grad} \theta }(\varvec{x})$ are not penalized, as these do not adversely affect mesh quality. Multiple variants of the traction method are described by Azegami (2021).

The $H^1$ smoothing algorithm is only a slight modification to the independent node coordinate formulation. For each iteration of the optimization, we are given the node coordinates $\varvec{X}$ whereupon we complete Algorithm 2 to compute the $\Theta _i$ and their $H^1$ smoothed gradients $\widetilde{\text {Grad}} {\Theta _i}$. The optimizer processes these quantities and either updates the design, i.e., $\varvec{X}\leftarrow \varvec{X} + \Delta \varvec{X}$ or declares convergence.

H¹ smoothing algorithm iteration, Appendix 2 for the discretization

2.2 Fictitious energy formulation

In the fictitious energy formulation of Scherer et al. (2010), an initial design $\Omega _0$ is deformed into the optimized design $\Omega$ such that points located at $\varvec{x}_0$ in the initial design $\Omega _0$ are displaced to the locations $\varvec{x} = \varvec{x}_0+ \varvec{d}$ in the optimized design. As such, the design displacement field $\varvec{d}$ serves as the control in the optimization. To be clear, $\varvec{d}$ is only optimized on the boundary $\partial \Omega _0 {\setminus } A^f$ where $A^f$ is defined in the discussion surrounding (11). For the Fig. 1 example, $d^p = \varvec{d}\cdot \varvec{e}_1$ and $d^p = \varvec{d}\cdot \varvec{e}_2$ are optimized over the circular arc, $d^p = \varvec{d}\cdot \varvec{e}_1$ is optimized over the horizontal edges and $d^p = \varvec{d}\cdot \varvec{e}_2$ is optimized over the vertical edges. Over the remainder of the boundary $A^f$, $\varvec{d}\cdot \varvec{e} = 0$. To obtain the displacement $\varvec{d}$ on the interior ${\overline{\Omega }}_0$ , a “fictitious” nonlinear elasticity analysis is performed. The analysis assumes an isotropic hyperelastic material that is unaffected by rigid deformations and dilations/contractions.

The morphing analysis finds the $\varvec{d}$ that solves the minimization problem

$$\begin{aligned} \mathop {\min }_{\varvec{d} \in {{\mathcal {H}}}_f( d^p)} \int _{\Omega _0} {\Psi _f}(\varvec{F}_d) \, dv \end{aligned}$$

(12)

where $\Psi _f$ is the fictitious energy density defined in Appendix 3, $\varvec{F}_d = \varvec{I} + \nabla \varvec{d}$ is the fictitious deformation gradient,

$$\begin{aligned} \begin{aligned} {{\mathcal {H}}}_f (d^p)= \{&\varvec{d} \in H^1 |\, \varvec{d} \cdot \varvec{e} = 0 \ \textrm{on} \ A^{f} \ \text {and}\\ {}&\varvec{d}\cdot \varvec{e} = d^p \ \text {on} \ \partial \Omega _0 \setminus A^{f} \} \end{aligned} \end{aligned}$$

(13)

is the space of admissible fictitious displacements, and $d^p$ is the prescribed displacement that is optimized. Stationarity of (12) requires $\varvec{d}\in {{\mathcal {H}}}_f( d^p)$ to satisfy the residual equation

$$\begin{aligned} r_f(\varvec{d}, \varvec{w}) = \int _{\Omega _0} \nabla \varvec{w} \cdot \varvec{P}_f \, dv = 0 \end{aligned}$$

(14)

for all $\varvec{w} \in {{\mathcal {H}}}_f( 0)$ where $\varvec{P}_f= {\partial \Psi _f}/{\partial \varvec{F}_d}$ is the fictitious First Piola-Kirchhoff stress. In the finite element method, we express $\varvec{d}= \varvec{d}^0 + \varvec{d}^p$ where $\varvec{d}^0 \in {{\mathcal {H}}}_f(0)$ and $\varvec{d}^p \in {{\mathcal {H}}}_f(d^p)$ is a known extension function that satisfies the prescribed displacement boundary condition. In this way, we solve (12) by finding the $\varvec{d}^0\in {{\mathcal {H}}}_f( 0)$ that satisfies

$$\begin{aligned} r_f(\varvec{d}^0, \varvec{w}, \varvec{d}^p) = \int _{\Omega _0} \nabla \varvec{w} \cdot \frac{\partial \Psi _f}{\partial \varvec{F}_d} \, dv = 0 \end{aligned}$$

(15)

for all $\varvec{w} \in {{\mathcal {H}}}_f( 0)$. We then trivially compute $\varvec{d}= \varvec{d}^0 + \varvec{d}^p$. The solution of the above residual equation for $\varvec{d}^0$ is obtained via Newton’s method, Appendix 3 for details.

As an added measure to prevent severe mesh distortion during the shape optimization, the fictitious energy approach places a constraint on the total fictitious energy, i.e.,

$$\begin{aligned} \theta _f(d^p) = \int _{\Omega _0} \Psi _f(\varvec{F}_d) \, dv - {\overline{\Psi }}_f \le 0 \end{aligned}$$

(16)

where ${\overline{\Psi }}_f$ is the maximum permissible total fictitious energy. The above is enforced in addition to the $\theta _i(d^p) \le 0$ and $i = 1, 2, \cdots$ constraints.

The fictitious energy approach is a consistent approach; thereby, it exhibits faster convergence verses the $H^1$ smoothing formulation. However, the consistency comes with a price with regard to the sensitivity analysis as two adjoint analyses are now required to evaluate the sensitivity of each cost and constraint function with respect the boundary displacement $d^p$, Appendix 3 for details.

In each iteration of the fictitious energy formulation, we are given the initial node coordinates $\varvec{X}_0$ and the node design displacement vector $\varvec{D}^p$ whereupon we complete Algorithm 3 to compute the $\Theta _i$ and their derivatives ${D \Theta _i}/{D \varvec{D}^p} , \, i=f, 0, 1, 2, \cdots$. The optimizer subsequently uses these quantities to either update the design, i.e., $\varvec{D}^p \leftarrow \varvec{D}^p + \Delta \varvec{D}^p$ or declare the convergence.

Fictitious energy formulation, Appendix 3 for the discretization

2.3 Consistent filtering formulation

The consistent filtering formulation is similar to the fictitious energy formulations as we again deform an initial design $\Omega _0$ into the optimized design $\Omega$ and the design displacement field $\varvec{d}$ controls the design. Here, however, points at locations $\varvec{x}_0$ in the initial design $\Omega _0$ are displaced to locations $\varvec{x} = \varvec{x}_0 + \widetilde{\varvec{d}}$ in the optimized design $\Omega$, where $\widetilde{\varvec{d}}$ is the filtered version of $\varvec{d}$. The method is analogous to PDE sensitivity filtering in topology optimization (Lazarov and Sigmund 2011). As such, it eliminates the inconsistency of the $H^1$ smoothing formulation and filters the boundary updates which the fictitious energy formulation does not.

To obtain the filtered design in our “PDE filter” variant, we find $\widetilde{\varvec{d}} \in {{\mathcal {H}}}_c$ such that

$$\begin{aligned} \begin{aligned} 0&= r_c(\widetilde{\varvec{d}}, \varvec{w}, \varvec{d}) \\&=\int _{\Omega _0} \left( \nabla \varvec{w} \cdot \gamma \, \nabla \widetilde{\varvec{d}} + \varvec{w} \cdot \widetilde{\varvec{d}} \right) \, dv \\&\hspace{1em}- \int _{\Omega _0} \varvec{w} \cdot \varvec{d}\, dv \\&=a_c( \widetilde{\varvec{d}}, \varvec{w} ) - \ell _c(\varvec{w}, \varvec{d}) \end{aligned} \end{aligned}$$

(17)

for all $\varvec{w} \in {{\mathcal {H}}}_c$ where

$$\begin{aligned} {{\mathcal {H}}}_c = \{\widetilde{\varvec{d}} \in H^1 |\, \widetilde{\varvec{d}} \cdot \varvec{e} = \varvec{0} \;\; \text {on} \;\; A^{f} \} \end{aligned}$$

(18)

(11).

Similar to the $H^1$ smoothing discussion, to obtain physical insight into the filter, we consider the minimization problem

$$\begin{aligned} \begin{aligned} \mathop {\min }_{\widetilde{\varvec{d}} \in {{\mathcal {H}}}_c}&\int _{\Omega _0} |\widetilde{\varvec{d}} - \varvec{d} |^2 \, dv \\ \text {such that }&\int _{\Omega _0} |\nabla \widetilde{\varvec{d}} |^2 \, dv = 0 \end{aligned} \end{aligned}$$

(19)

and solve it via the penalty method, i.e., we solve

$$\begin{aligned} \begin{aligned} \mathop {\min }_{\widetilde{\varvec{d}} \in {{\mathcal {H}}}_c}&\int _{\Omega _0} |\widetilde{\varvec{d}} - \varvec{d} |^2 \, dv \\&+ \gamma \, \int _{\Omega _0} |\nabla \widetilde{\varvec{d}} |^2 \, dv \end{aligned} \end{aligned}$$

(20)

. The stationarity condition of (20) requires $\widetilde{\varvec{d}} \in {{\mathcal {H}}}_c$ to satisfy (17) for all $\varvec{w} \in {{\mathcal {H}}}_c$. In this way, $\widetilde{\varvec{d}}$ is “close” to $\varvec{d}$, but $|\nabla \widetilde{\varvec{d}}|$ will be “small,” i.e., $\widetilde{\varvec{d}}$ is the smoothed version of $\varvec{d}$. The smoothness of $\widetilde{\varvec{d}}$ increases with increasing $\gamma$ because the enforcement of the $\int _{\Omega _0} |\nabla {\widetilde{\varvec{d}}} |^2 \, dv = 0$ constraint increases with increasing $\gamma$. Our filter is very similar to that used by Matsumori et al. (2017); however, they only integrate $|{\widetilde{\varvec{d}}} - \varvec{d} |^2$ over regions that are close to the boundary $\partial \Omega _0$ so the interior nodes are less constrained, which is most likely fine.

A comparison of the filtering approaches is worthy of discussion. The fictitious energy residual Eq. (15) for $\varvec{d}^0$ and consistent filter residual Eq. (17) for ${\widetilde{\varvec{d}}}$ are solved over the initial design configuration $\Omega _0$ whereas the $H^1$ smoothing Eq. (10) for $\widetilde{\text {grad} \theta _i}$ is solved over the current design configuration $\Omega$. One difference between the fictitious energy and consistent approaches lies in the definitions of the spaces of the admissible displacements ${{\mathcal {H}}}_f$ and ${{\mathcal {H}}}_c$, (13) and (18). In the fictitious energy method, $\varvec{d}= d^p \, \varvec{e}$ is prescribed by the optimizer over $\partial \Omega _0 \backslash A^f$ whereas in the consistent approach, $\widetilde{\varvec{d}}$ is not prescribed over this surface. Because of this, no smoothing is performed on this boundary in the fictitious energy method. Another difference between these methods is that the fictitious energy method requires the solution of a nonlinear PDE; albeit in the second variant of our consistent approach described next, we must also solve a nonlinear PDE.

The $\nabla \varvec{w} \cdot \gamma \, \nabla \widetilde{\varvec{d}}$ term in (17) penalizes $|\nabla \widetilde{\varvec{d}} |$. As such, rigid transformations or dilations/contractions are penalized even though they do not adversely affect mesh quality. Motivated by this observation and by Scherer et al. (2010), in our second variant “energy filter” approach, we solve a nonlinear PDE by replacing $\int _{\Omega _0} \nabla \varvec{w} \cdot \gamma \, \nabla \widetilde{\varvec{d}} \, dv$ with $\int _{\Omega _0} \nabla \varvec{w} \cdot \gamma \, {\partial \Psi _f(\widetilde{\varvec{F}}_d )}/{\partial \widetilde{\varvec{F}}_d} \, dv$ where $\widetilde{\varvec{F}}_d = \varvec{I} + \nabla \widetilde{\varvec{d}}$. This has the effect of weakly enforcing the constraint $\int _{\Omega _0} {\Psi _f(\widetilde{\varvec{F}}_d )} \, dv = 0$ rather than $\int _{\Omega _0} |\nabla \widetilde{\varvec{d}} |^2 \, dv = 0$. And in our third variant, the “linearized energy filter,” we alternatively penalize the linearized energy by replacing $\int _{\Omega _0} |\nabla \widetilde{\varvec{d}} |^2 \, dv$ with $1/2 \, \int _{\Omega _0} \nabla \widetilde{\varvec{d}} \cdot {\mathbb {A}}_f[ \nabla \widetilde{\varvec{d}} ]\, dv = 0$ where ${\mathbb {A}}_f = \partial ^2 \Psi _f(\varvec{I})/\partial \widetilde{\varvec{F}}_d^2$ provides the linearized energy, Appendix 3 for details.

In these consistent approaches, we maintain a clear distinction between the filtered field $\widetilde{\varvec{d}}$ that is used to define $\Omega$ and the design displacement field $\varvec{d}$ that we optimize. So like the fictitious energy approach, this has ramification in the sensitivity analysis, namely we again have to solve two adjoint problems, Appendix 4 for details.

In each iteration of the consistent PDE filtering formulation, we are given the initial node coordinates $\varvec{X}_0$ and the design displacement $\varvec{D}$ whereupon we complete Algorithm 4 to compute the $\Theta _i$ and their derivatives ${D \Theta _i}/{D \varvec{D}} .$ The optimizer subsequently uses these quantities to either update the design, i.e., $\varvec{D}\leftarrow \varvec{D} + \Delta \varvec{D}$ or declare the convergence.

Consistent filtering formulation, Appendix 4 for the discretization

As expected, filtering $\varvec{d}$ reduces numerical anomalies due to the discretization and hastens convergence of the optimization problem by reducing the effective design space. Indeed, the many design parameters in $\varvec{d}$ are “mollified” into a fewer number of influential parameters. To see this, we use the spectral decomposition theorem to express⁶$\varvec{\Phi }^T \,(\varvec{K}_c + \varvec{M}_c) \, \varvec{\Phi } = \text {diag} \left( \lambda _1, \lambda _2, \cdots \right)$ where $(\lambda _i, \varvec{\Phi }_i)$ are the eigenpairs of $\varvec{K}_c + \varvec{M}_c$ that are arranged such that $\lambda _i \le \lambda _{i+1}$, and the eigenvectors are mass normalized such that $\varvec{\Phi }_i^T \, \varvec{M}_c \, \varvec{\Phi }_j = \delta _{ij}$ and $\varvec{\Phi } = \begin{bmatrix} \varvec{\Phi }_1&\varvec{\Phi }_2&\cdots \end{bmatrix}$. In this way, with $\widetilde{ \varvec{D}} = \varvec{\Phi } \, \widetilde{\varvec{D}}^*$ and $\varvec{D} = \varvec{\Phi } \, \varvec{D}^*$ , we have

$$\begin{aligned} \widetilde{\varvec{D}}^* = \begin{Bmatrix} \frac{1}{\lambda _1} \, D^*_{1} \\ \frac{1}{\lambda _2} \, D^{*}_{2} \\ \vdots \end{Bmatrix} \end{aligned}$$

(21)

We see that the “modes” associated with the smaller eigenvalues contribute more to $\widetilde{\varvec{D}}$ than those associated with the larger eigenvalues. And the mode shapes associated with smaller eigenvalues are smoother than those associated with larger eigenvalues. Hence, $\widetilde{\varvec{D}}$ is smoother than $\varvec{D}$, i.e., by replacing $\varvec{D}$ with $\widetilde{\varvec{D}}$ , we have mollified the space of possible design configurations $\Omega$.

3 Filter comparison

To illustrate the parameter-free methods described in Sect. 2, we return to the problem discussed in Sect. 1 and optimize the shape of a hole in a plane stress plate, initially a circle with radius $r =1/(2 \, \sqrt{ \pi })$, to minimize the compliance (or maximum stress) subject to a constraint that the area be less than ${\overline{A}} = 0.75 \, V$ where A is the area of the plate without the hole, Fig. 1. The $2\times 2$ plate is comprised of an isotropic linear elastic material with Young’s modulus $E = 10.0$ and Poisson ratio $\nu = 0.3$ and subjected to a biaxial tensile load with prescribed traction $\varvec{t}^p = 2 \, \varvec{e}_1$ and $\varvec{t}^p = \varvec{e}_2$ over the vertical and horizontal boundaries. Quarter symmetry is utilized to reduce the computational burden. For the $H^1$ and traction methods with $\Delta \varvec{x} = \varvec{d}$, and consistent method, we solve

$$\begin{aligned}&\mathop {\min }_{\varvec{d}\in {{\mathcal {H}}}_H}{} {} \theta _0\\&\text {such that }{} \theta _1 = \int _{\Omega } \, da - {\overline{A}} = 0 \\{} &{} {}{\underline{d}} \le \varvec{d}\cdot \varvec{e}_i \le {\overline{d}} \;\;\text {for} \;\;i = 1, 2 \end{aligned}$$

(22)

. And for the fictitious energy method, we solve

$$\begin{aligned}&\mathop {\min }_{d^p }{} {} \theta _0 \\&\text {such that }{} \theta _1 = \int _{\Omega } \, da - {\overline{A}} = 0 \\{}&\theta _f = \int _{\Omega _0} \Psi _f(\varvec{F}_f) \, da - {\overline{\Psi }}_f \le 0 \\{} &{} {\underline{d}} \le d^p \le {\overline{d}} \end{aligned}$$

(23)

In our reduced space optimization, we use the adjoint sensitivity analyses to account for the implicit dependence of the response, e.g., $\varvec{u}$ with respect to the design. For the $H^1$, traction, and fictitious energy approaches, it is easy to place box constraints on the design because $\varvec{d}$ and $d^p$ directly affect the shape as $\varvec{x} = \varvec{x}_0 + \varvec{d}$; for all of these cases ${\underline{d}}, {\overline{d}} = \mp 0.25$. On the other hand, in the consistent approaches, $\varvec{x} = \varvec{x}_0 + \widetilde{\varvec{d}}$ where $\widetilde{\varvec{d}}$ is implicitly defined by the design $\varvec{d}$. So while we do provide box constraints on $\varvec{d}$, their range is large in comparison with those in the other approaches. As a guide, we choose ${\underline{d}},{\overline{d}} \approx \mp \lambda _i \, \underline{{\widetilde{d}}}$ where $\underline{{\widetilde{d}}}$ is the bound we desire on ${\widetilde{d}}$ and $\lambda _i$ is the $i-th$ smallest eigenvalue of $\varvec{K}_c + \varvec{M}_c$ where $i \approx 4, 5, 6$. For all of these cases, $\underline{ {d}}, \overline{ {d}} = \mp 20 \approx \mp 0.25 \cdot \lambda _4 = 18.25$. In all cases, these box constraints are necessary to obtain well-posed problems. Indeed, removing them could result in designs with fine scale shape oscillations in the continuum setting and tangled finite element meshes in the discrete setting. All of the above functions $\theta _i$ are scaled so that the sensitivities of each function has a unit norm for the initial design, e.g., $|{D \theta _i}/{D \varvec{D}} |= 1$ for $\varvec{D}= \varvec{0}$. An exception for this is the maximum energy constraint in the fictitious energy approach which is normalized for $d^p = 0.02$ as ${D \theta _f}/{D d^p} = 0$ for $d^p = 0$. To keep things relatively equal, the $H^1$ smoothing and consistent PDE filter use $\gamma = 10$, the traction uses $E=10$ and $\nu = 0.3$ ,and the fictitious energy and consistent approaches with the linearized energy function use $\gamma = 5$. On the other hand, the fictitious energy and consistent approaches with the nonlinear energy function use $\gamma = 1$. We conjecture that the lower $\gamma$ value is needed due to the stiffening effect of the nonlinear energy function $\Psi _f$, i.e., a higher nonlinear energy is required to achieve the same level of mesh morphing as compared to the linearized energy. Loosely based on the ${\overline{\Psi }}_f =.006 \, {\overline{A}} = 0.0045$ suggested by Scherer et al. (2010) (which does not include the $\gamma$ factor), we assign ${\overline{\Psi }}_f = \gamma \, 0.030 \, {\overline{A}}= 0.1125$ for the maximum energy for the fictitious energy method with the linearized energy. We decreased the maximum to ${\overline{\Psi }}_f = 4 \, \gamma \, \Psi _f(0.02) = 0.0285$, i.e., $4 \, \gamma$ times the “normalization” energy for the nonlinear energy case. The selection of these maximum energy bounds definitely requires some “experimentation.”

The optimization cost function $\theta _0$ is either the compliance

$$\begin{aligned} \Theta = \int _\Omega \nabla \varvec{u} \cdot {\mathbb {C}}[\nabla \varvec{u}] \, da \end{aligned}$$

(24)

or the p-norm aggregation of the von Mises stress $\sigma _{VM}$

$$\begin{aligned} \Upsilon = \left( \int _\Omega \sigma _{VM}^p \, da \right) ^{\frac{1}{p}} \end{aligned}$$

(25)

in which $p=6$ throughout Sect. 3. We use $\Theta$ and $\Upsilon$ to denote compliance and p-norm aggregation of the von Mises stress, respectively, throughout, and the superscript $^0$ to denote the metric value of the initial design; e.g., $\Theta ^0$ refers to the compliance of the initial design.

The interior-point method of Matlab’s fmincon with a limit of 100 function evaluations is used for the optimizations. The accuracies of the user supplied derivatives are verified for the fictitious energy and consistent approaches. None of the methods produce the expected elliptical hole with 2:1 axis ratio due to the finite domain size; however, they all tend in that direction.

3.1 Compliance minimization

We first minimize the compliance $\theta _0=\Theta$ of (24). This is an easy problem so all of the methods should and do perform admirably. Results from the various algorithms are presented in Table 1.

Table 1 Compliance minimization results

The fictitious energy values for the optimized designs obtained via the linear and nonlinear energy functions are 0.117 and 0.0271; hence, the maximum energy constraints are, respectively, violated and relatively active. The nonlinear energies for the fictitious energy and consistent approaches required some special care in that the Newton solver did not always converge. To resolve this, the load was incrementally applied over numerous load steps as needed; as such, the morphing analysis dominated the computational expense. Figure 3 illustrates the designs and their strain energy distributions. The contour plots qualitatively compare the methods with a consistent coloring scheme whereas the tables provide a quantitative comparison. The designs exhibit subtle differences which are seen through their energy distributions. The consistent methods with linearized energy filter $1/2 \, \gamma \, \nabla \varvec{d}\cdot {\mathbb {A}}_f[\nabla \varvec{d}]$ and nonlinear energy filter $\gamma \, \Psi _f$ produce the best designs, although all of the designs are reasonable. The consistent method with nonlinear energy filter $\gamma \, \Psi _f$ produces the best mesh based on the “eyeball” norm. The inconsistent $H^1$ and traction methods converge in the fewest number of iterations because the change in the design between iterations is too small, presumably because the optimizer gets “confused” by the inconsistent sensitivity analysis, as evidenced by greater compliance values.

Fig. 3

Strain energy distributions of compliance optimized designs

3.2 Stress minimization

We next minimize the p-norm of the von Mises stress, i.e., in the optimization, we replace (24) with (25) so that $\theta _0 = \Upsilon$. This is a more difficult problem as we replace the compliance which is a global quantity with an approximation of the maximum stress which is a local quantity. All of the other parameters are the same as those described above. Results from the various algorithms are denoted in Table 2 and Fig. 4. Descriptions of the table and figures are the same as those for the compliance minimization. The fictitious energy values for the optimized designs obtained via the linear and nonlinear energy functions are 0.115 and 0.0246; hence, the maximum energy constraints are again, respectively, violated and relatively active. The design obtained by the fictitious energy method with nonlinear energy is quite good; however, its nonlinear morphing analysis dominates the computational cost. All of the designs obtained by the consistent methods appear to be reasonable. And again the consistent method with nonlinear energy filter $\gamma \, \Psi _f$ produces the best mesh based on the “eyeball” norm. Anomalies exist in the designs obtained with the remaining methods. Parameter tuning could be used to improve these designs, but the point of this exercise is to find methods that are amenable to common nonlinear programming algorithms that do not require excessive parameter tuning.

Fig. 4

Von Mises stress distributions of stress optimized designs

Table 2 Stress minimization results

4 Test problems

The advantages of consistent filtering methods were demonstrated in Sect. 3. Here, we further showcase the three consistent filtering approaches when used to design both 2D and 3D structures. Specifically, tradeoffs between ease of implementation, computational burden, and mesh quality are explored. A summary of relevant parameters used throughout this section is presented in Table 3. All results in this section used the MFEM library (Anderson et al. 2021) to solve the PDEs and the IPOPT library (Wächter and Biegler 2006) to solve the optimization problems. The Livermore Design Optimization (LiDO) code was utilized to compute the required sensitivities, and the Targeted Matrix Optimization Paradigm (TMOP) (Knupp 2012; Dobrev et al. 2019; Barrera et al. 2022) is used to implement the consistent nonlinear energy filter.⁷

Table 3 Parameters used throughout Sect. 4

4.1 2D plate design

To compare the filtering methods, we revisit the design of the plane stress plate, but under biaxial or shear loading and with an initially square $1\times 1$ hole rather than a circular hole, Fig. 5. Morphing the square into the optimal circle (biaxial loading) or diamond (shear loading) is challenging since it requires a right angle to be morphed into an arc or straight line, respectively. All optimizations presented in this section solve the stress minimization problem of Equations (22) and (25). We chose to minimize the maximum stress since it is generally more challenging than compliance, which could hide deficiencies in the methods.

Fig. 5

2D plate test problem, design/analysis symmetry cell outlined by dashed line

4.1.1 Consistent method with the PDE filter

We first consider the consistent PDE filter, which has one parameter $\gamma$ that controls the tradeoff between how “smooth” the mesh is and how closely $\widetilde{\varvec{d}}$ matches $\varvec{d}$, as well as a set of parameter bounds ${\underline{d}}, {\overline{d}}$. A smaller $\gamma$ requires smaller, i.e., more restrictive, parameter bounds to avoid mesh entanglement, while a larger $\gamma$ permits more liberal parameter bounds.

Figure 6 illustrates how $\gamma$, ${\underline{d}}$, and ${\overline{d}}$ affect the optimized design. The two optimal designs boast similar performance with $\Upsilon / \Upsilon ^0$ values of 0.38 and 0.39. The first takeaway is that we can use values of $\gamma$ that are two orders of magnitude apart and obtain satisfactory results by tuning the ${\underline{d}}$ and ${\overline{d}}$ bounds. However, both of our optimized designs tend to “smash” elements along the symmetry planes, and further, this effect worsens for the larger value of $\gamma$. The advantage of this approach is the smooth boundary, which comes at the expense of element quality. In Fig. 7, we present the optimal design for shear loading, using the same $\gamma = 10^{-1}$ value that produced the higher quality mesh under biaxial loading. We again see a smooth boundary but notice many highly distorted elements near the symmetry planes. The stress contour plots, which use consistent color schemes for each load case, are provided to qualitatively compare designs, whereas Tables 4 and 5 quantitatively compare them.

Fig. 6

Design of 2D plate under biaxial loading with the PDE filter

Table 4 Summary of 2D plate under biaxial loading optimization results

Table 5 Summary of 2D plate under shear loading optimization results

To summarize, this PDE filter is simple to implement, especially for those familiar with the PDE filter from topology optimization. Indeed, repeated use of a scalar-valued PDE filter could be used to compute each component of $\widetilde{\varvec{d}}$, although a vector-valued implementation was used here. This method is computationally inexpensive since it only requires linear PDE solves. Optimizations using this filter generally produce smooth boundaries at the expense of poor element quality and consequently reduced simulation accuracy.

4.1.2 Consistent method with the linearized energy filter

The linearized energy filter promotes higher element quality than the PDE filter as seen in the designs for biaxial and shear loading illustrated in Fig. 8. Specifically, the elements are nearly squareshaped throughout the domain. Notably, the high mesh quality near the symmetry planes is in stark contrast to the results in Sect. 4.1.1; however, the tradeoff is that the optimizer struggles to remove the “corner” in the initial design’s square hole. Thus, the maximum von Mises ratios in Fig. 8 are slightly higher than their counterparts in Sect. 4.1.1, i.e., 0.40 and 0.36 for the designs in this section, compared with 0.38 and 0.34 for the designs in Sect. 4.1.1.

Fig. 7

Design of 2D plate under shear loading with the PDE filter

When compared to the PDE filter, we see that the linearized energy filter ensures higher mesh quality at the expense of design freedom. It is also simple to implement, especially since a linear elasticity solver can be re-purposed for this filter with proper selection of the Lamé parameters, i.e., $\lambda = -\frac{1}{3}$ and $\mu = \frac{1}{2}$ (see Appendix 3 for details), and the computational expense is therefore equivalent to a single linear elasticity PDE solve.

4.1.3 Consistent method with the nonlinear energy filter

Finally, we consider the nonlinear energy filter (with quality metric $\mu _2$ from Dobrev et al. (2019) which is the same as the $\Psi _f$ function of (40)). Although this filter is more computationally expensive, it proves to be more capable than the linear filters presented in Sects. 4.1.1 and 4.1.2. The robustness of the formulation is demonstrated by the mesh refinement study for the biaxial loaded design illustrated in Fig. 9. Indeed, the same parameters, $\gamma = 10^{-1}, {\underline{d}}, {\overline{d}} \mp 0.1$, were used to obtain each result, despite their differing element size. Additionally, we see very similar optimized designs, demonstrating the mesh independence of this technique. Similar observations hold for the mesh refinement study performed on the shear loaded designs, Fig. 10. Notably, the same values of $\gamma$, ${\underline{d}}$, and ${\overline{d}}$ were used for both loadings, and again, we see consistent designs for the different mesh resolutions. When compared to the consistent PDE filter in Sect. 4.1.1, we notice higher element quality throughout Figs. 9 and 10, and when compared to the linearized energy filter in Sect. 4.1.2, we notice a smoother boundary. The nonlinear energy filter produces the lowest maximum stress in the optimal design when comparing equivalent meshes across the three consistent filters, as listed in Tables 4 and  5. Thus, the nonlinear filter exhibits the advantages of both linear filters, i.e., high mesh quality and smooth boundaries, at the cost of additional computational burden.

Fig. 8

Optimal 2D plate designs obtained via the linearized energy filter

Fig. 9

Effect of h-refinement on the design of 2D plate under biaxial loading with the nonlinear energy filter. Left column is initial (init) designs, and right column is optimized (opt) designs

Fig. 10

Effect of h-refinement on the design of 2D plate under shear loading with the nonlinear energy filter. Left column is initial (init) designs, and right column is optimized (opt) designs

As an alternative to increasing the number of elements, i.e., h-refinement, simulation accuracy can also be improved by increasing the polynomial order of the mesh, i.e., p-refinement. Figures 11 and 12 present optimal designs corresponding to linear, quadratic, and cubic elements. The p-refinement study used the same values of $\gamma$, ${\underline{d}}$ , and ${\overline{d}}$ as the h-refinement study. The sharp corner is much improved when using quadratic elements, and nearly entirely removed when using cubic elements. Further, the element quality is high throughout the domain. The designs obtained using the cubic meshes and the nonlinear energy filter appear to be the best when considering mesh quality, design performance, and number of degrees-of-freedom.

Fig. 11

Effect of p-refinement on the design of 2D plate under biaxial loading with the nonlinear energy filter. Left column is initial (init) designs, and right column is optimized (opt) designs. p denotes the order of the solution basis functions

Fig. 12

Effect of p-refinement on the design of 2D plate under shear loading with the nonlinear energy filter. Left column is initial (init) designs, and right column is optimized (opt) designs. p denotes the order of the solution basis functions

The consistent nonlinear energy filter can be summarized as an extremely effective, but computationally expensive alternative to the consistent linear filters. Indeed morphing computations may dominate the physics computations, especially if the latter are linear. Additionally, the implementation of a nonlinear filter is more difficult than the linear filters. However, the improved optimization performance may warrant the added effort. Further, the combination of a smooth boundary representation and high element quality throughout the domain, especially when using meshes with higher-order elements, is unmatched by the other techniques. As design problems require more complex physics, the improved element quality obtained via the nonlinear energy filter may become even more important for accurate response predictions. Moreover, the computational cost will be less significant when compared to the cost of the complex nonlinear physics simulations.

4.2 3D dam design

We use the design of a 3D dam subject to a design-dependent hydrostatic pressure load to further challenge the optimization scheme. Indeed, the direction of the applied load changes as the mesh morphs. The problem is summarized in Fig. 13 by overlaying the pressure load and mechanical displacement boundary conditions on the mesh of the initial design. As pictured, we enforce homogeneous essential boundary conditions, i.e., $\varvec{u} \cdot \varvec{n} = 0$, on the surfaces with normals $\varvec{n} = - \varvec{e}_2$ and $\varvec{n} = \pm \varvec{e}_3$. We also enforce design constraints by fixing the normal displacement $\varvec{d} \cdot \varvec{n} = 0$ over the surfaces with normals $\varvec{n} = \pm \varvec{e}_2$ and $\varvec{n} = \pm \varvec{e}_3$. The initial design has dimensions [200, 700, 1200] in the $\varvec{e}_1$, $\varvec{e}_2$, and $\varvec{e}_3$ directions, respectively. We consider both compliance and maximum stress minimization.

Fig. 13

Dam design problem loads and boundary conditions applied to the initial design

4.2.1 Consistent method with the PDE filter

The PDE filter achieves satisfactory results for the 3D dam design problem. The minimum compliance design pictured in Fig. 14 has 50% of the initial design’s compliance. Element quality is difficult to qualitatively compare for 3D structures, but we note that there are highly distorted elements near the bottom corners of the design.

Fig. 14

Compliance min. with the PDE filter

A minimization of the maximum von Mises stress produces a design that resembles the compliance minimization design. The initial and optimized von Mises stress distributions are presented in Figs. 15 and  16, respectively. The optimal design reduces the peak von Mises stress by nearly half; however, this filter provides the worst performance of the three consistent filters, Table 7. Generally, the PDE filter is not able to displace the initial mesh as far as the energy-based filters before mesh entanglement occurs. Since this filter simply “smooths” the node coordinates without regard for element quality, the elements become distorted quite easily and therefore the optimal performance is limited by how far the mesh is able to distort before it tangles.

Fig. 15

Initial von Mises stress distribution

Fig. 16

Maximum von Mises stress minimization with the PDE filter

4.2.2 Consistent method with linearized energy

The linearized energy filter was effective in the dam optimization. An h-refinement study of the compliance minimization problem was performed to investigate the mesh independence of the shape optimization framework, Fig. 17. Two important behaviors were observed: the same filter and bound parameters were effective for all three meshes, and the same performance, i.e., $\Theta /\Theta ^0_0 = 0.42$ was obtained for all three designs. The final mesh contained 1,904,163 design variables, demonstrating the scalability of the method to large design problems. The robustness provided by mesh-independent filter parameters allows designers to tune optimization parameters on coarser meshes before using them on refined meshes.

Fig. 17

Effect of h-refinement on compliance minimization with the linearized energy filter

The linearized energy filter produced a design with less compliance than the PDE filter, Table 6. This trend was consistent with the minimum von Mises stress designs. Inspection of Fig. 18 reveals a superior design to that in Fig. 16; the linearized energy filter allows the mesh to morph further while keeping elements from tangling and therefore allows the final design to mitigate stress more effectively.

The astute civil engineer might notice, however, that our optimal dams are to this point concave with respect to the hydrostatic pressure load, whereas real-world dams are often convex with respect to the water they are retaining. The main driver of this inconsistency is the von Mises stress metric, which assumes materials are equally strong in tension and compression. Thus, a better stress metric to design for is the Drucker-Prager criterion (Drucker and Prager 1952) since most dams are made of concrete, which is strong in compression and weak in tension. If we assume that our constituent material is 10 times stronger in compression than in tension and use the Drucker-Prager stress criterion, we obtain the initial stress field pictured in Fig. 19. Designing for the Drucker-Prager criterion has a fascinating effect on the optimal geometry; the top surface of the dam switches from concave to convex with respect to the hydrostatic pressure load, which is a trait of arch dams, and two reinforcement columns appear on the front face, which is a trait of buttress dams, Fig. 20. In summary, when we account for the type of materials typically used to build dams, the optimized design resembles dams seen in the real world.

Fig. 18

Maximum von Mises stress minimization with the linearized energy filter

Fig. 19

Initial Drucker-Prager stress distribution

Fig. 20

Maximum Drucker-Prager stress minimization with the linearized energy filter

4.2.3 Consistent method with nonlinear energy

We attempted to use the nonlinear energy filter (with quality metric $\mu _{303}$ from Dobrev et al. (2019) which equals $\Psi _f$ from (40)) in the same manner as in Sect. 4.1. A value was selected for $\gamma$ and then the parameter bounds ${\underline{d}}, {\overline{d}}$ were tuned accordingly. Through trial and error, it was determined that this technique was not effective when using the nonlinear energy filter for the 3D dam optimization problem. Specifically, the optimal dam design required a much larger mesh distortion than the optimal plate design, which caused convergence issues during the filtering operation. Thus, a slightly different technique was developed for this problem. Rather than selecting a large bound range $[{\underline{d}}, {\overline{d}}]$, we follow Scherer et al. (2010) and solve a series of optimizations with smaller ranges, wherein the initial design for each subsequent optimization was the optimized design from the previous optimization. In this way, the design was allowed to distort incrementally through many, more constrained, design problems. The key difference between solving the design problem in a single pass versus breaking it into numerous steps, as outlined here, is that the reference element is incrementally updated in the latter technique which introduces inconsistencies with respect to the initial design optimization problem.

Figure 21 depicts the optimized design for compliance minimization using the nonlinear energy filter. The final design is superior to those obtained with the linear filters, Table 6. Similarly, the best designs with respect to von Mises and Drucker-Prager metrics were obtained using the nonlinear energy filter with the incremental design process, Tables 7 and 8. The final designs are displayed in Figs. 22 and 23, for von Mises and Drucker-Prager metrics, respectively. The design stress field histories for the Drucker-Prager minimization are presented in Fig. 24 to demonstrate the sequential optimization process described above. We emphasize that although 14 optimizations were required to obtain optimal designs, each of the optimizations converged quickly due to the smaller range $[{\underline{d}}, {\overline{d}}]$. In fact, the total number of design iterations for all of the design steps combined was similar to that required for the single-pass optimizations in Sect. 4.2.2. That said, the overall computational cost remains higher for the nonlinear filter since each design iteration requires the solution of the nonlinear filter PDE.

Again, we emphasize the tradeoff between computational cost and optimization performance must be considered. For example, the design problems using the highly refined meshes in Figs. 17e and 17f would have an increased execution time, perhaps an order of magnitude more, if using the nonlinear energy filter compared to the linearized energy filter to obtain only marginal compliance improvement, i.e., $\Theta / \Theta ^0$ of 0.42 vs. 0.39. However, the design for Drucker-Prager stress using the nonlinear energy filter was significantly more effective than that obtained using the linear filter, i.e., $\Theta / \Theta ^0$ of 0.33 vs. 0.19, possibly justifying the increased computational cost.

Table 6 Summary of 3D dam compliance minimization results

Table 7 Summary of 3D dam von Mises stress optimization results

Table 8 Summary of 3D dam Drucker-Prager stress optimization results

Fig. 21

Compliance minimization with nonlinear energy filter

Fig. 22

Maximum von Mises stress minimization with nonlinear energy filter

Fig. 23

Maximum Drucker-Prager stress minimization with nonlinear energy filter

Fig. 24

History of Drucker-Prager stress minimization designs with ${\underline{d}}, {\overline{d}} \mp 50$

5 Conclusions

Shape optimization provides an attractive option over topology optimization, especially when the boundary phenomena dominate the design, e.g., in stress-based design. Shape optimizations typically use CAD-based parameterizations which move the positions of the finite elements through globally supported basis functions. This type of design description can be difficult to implement for industry applications and limits the design to these predefined parameterizations.

Independent node parameterization has been extensively used, but numerical difficulties, e.g., mesh entanglement, still pose a challenge. Significant progress has been made to alleviate this challenge and here we add to this body of work. Specifically, we demonstrate that consistent filtering, i.e., filtering both updated nodal positions and their sensitivities, is advantageous over filtering only sensitivities. We unify a technique for parameterizing locally supported finite element quantities, i.e., element “densities” in topology optimization and nodal coordinates in shape optimization, to minimize human intervention in the design process.

We demonstrate consistent filtering by designing a 2D plate under biaxial and shear loading and a 3D dam subject to a hydrostatic pressure load. We show that the consistent PDE, linearized energy, and nonlinear energy filters all produce satisfactory designs, although each has pros and cons relative to the others. In summary, the PDE filter maintains design regularity, is computationally inexpensive and simple to implement, but suffers from poor element quality. The linearized energy filter is computationally inexpensive and simple to implement and produces higher element quality at the expensive of less design freedom. Finally, the nonlinear energy filter exhibits superior performance by simultaneously ensuring design freedom and high element quality, but incurs a steep computational cost. The choice of an appropriate filter is therefore problem dependent; the tradeoff between design freedom, ease of implementation, and computational cost must be analyzed on a case-by-case basis.

Appendices

Appendix 1: Independent node coordinate derivations

The variation of $\theta$ at $\varvec{x}$ with respect to the shape perturbation $\delta \varvec{x}$ is expressed as the sum of an explicit variation $\delta \theta ^E$ and implicit variation $\delta \theta ^I$, i.e., $\delta \theta = \delta \theta ^E + \delta \theta ^I$. The former is expressed

$$\begin{aligned} \begin{aligned} \delta&\theta ^E(\varvec{x}; \delta \varvec{x}) \\&= \int _\Omega \left( (-\nabla ^T \varvec{u} \,\frac{\partial \Lambda }{\partial \nabla \varvec{u}} + \Lambda \, \varvec{I}) \cdot \nabla \delta \varvec{x}+\frac{\partial \Lambda }{\partial \varvec{x}} \cdot \delta \varvec{x} \right) dv \\&+ \int _{A^t} \left( \frac{\partial \tau }{\partial \varvec{x}} \cdot \delta \varvec{x} +\tau \, (\varvec{I} - \varvec{n} \otimes \varvec{n}) \cdot \nabla \delta \varvec{x} \right) \, da \\&+ \int _{A^p} \left( \left( \frac{\partial \varvec{\tau }}{\partial \varvec{x}} \right) ^T \varvec{n} \cdot \delta \varvec{x} \right. \\&\left. + ((\varvec{\tau } \cdot \varvec{n}) \, \varvec{I} -(\varvec{n} \otimes \varvec{\tau }) )\cdot \nabla \delta \varvec{x} \right) \, da \end{aligned} \end{aligned}$$

(26)

and the latter as

$$\begin{aligned} \begin{aligned} \delta \theta ^I(\varvec{x}; {\mathop {\varvec{u}}\limits ^{\star }} )&= \int _\Omega \left( \frac{\partial \Lambda }{\partial \nabla \varvec{u}} \cdot \nabla {\mathop {\varvec{u}}\limits ^{\star }} + \frac{\partial \Lambda }{\partial \varvec{u}} \cdot {\mathop {\varvec{u}}\limits ^{\star }} \right) \, dv \\&+ \int _{A^t} {\mathop {\varvec{u}}\limits ^{\star }} \cdot \frac{\partial \tau }{\partial \varvec{u}} da + \int _{A^p} {\mathop {\varvec{u}}\limits ^{\star }} \cdot \left( \frac{\partial \varvec{\tau }}{\partial \varvec{u}}\right) ^T \varvec{n} \, da \end{aligned} \end{aligned}$$

(27)

To obtain the above, we define the material derivative with respect the design velocity $\delta \varvec{x}$ as ${\mathop {\varvec{u}}\limits ^{\star }} \! \! \!(\varvec{x}) = \delta \varvec{u}(\varvec{x}; \delta \varvec{x}) + \nabla \varvec{u}(\varvec{x}) \, \delta \varvec{x}$; it is implicitly defined by (1).⁸ We also use the commuter identity ${\mathop {\overline{\nabla \varvec{u}}}\limits ^{\star }} = -\nabla {\varvec{u}} \nabla \delta {\varvec{x}} + \nabla {\mathop {\varvec{u}}\limits ^{\star }}$.

In the adjoint sensitivity method, we annihilate the implicit variation $\delta \theta ^I$. To do this, we take the variation of the residual Eq. (1) and, as above, express it as the sum of an explicit variation $\delta r^E$ and implicit variation $\delta r^I$, i.e., $\delta r = \delta r^E + \delta r^I$. The explicit and implicit variations are

$$\begin{aligned} \begin{aligned}&\delta r^E (\varvec{u}, \varvec{w}, \varvec{x}; \delta \varvec{x}) = \\&\int _\Omega \left( \left( -\nabla ^T \varvec{w} \, {\mathbb {C}}[\nabla \varvec{u}] - \nabla ^T \varvec{u} \,{\mathbb {C}} [ \nabla \varvec{w}] \right. \right. \\&\left. \left. + (\nabla \varvec{w} \cdot {\mathbb {C}}[\nabla \varvec{u}] - \varvec{w} \cdot \varvec{b})\, \varvec{I}\right) \cdot \nabla \delta \varvec{x} \right. \\&\left. + \left( \left( \frac{\partial {\mathbb {C}}[\nabla \varvec{u}]}{\partial \varvec{x}}\right) ^T [\nabla \varvec{w}] - \left( \frac{\partial \varvec{b}}{\partial \varvec{x}} \right) ^T \varvec{w} \right) \cdot \delta \varvec{x} \right) \, dv \\&- \int _{A^t} \left( \left( \frac{\partial \varvec{t}^p}{\partial \varvec{x}}\right) ^T \varvec{w} \cdot \delta \varvec{x} \right. \\&\left. + (\varvec{w} \cdot \varvec{t}^p) \, (\varvec{I} - \varvec{n} \otimes \varvec{n}) \cdot \nabla \delta \varvec{x} \, \right) \, da \\&- \int _{A^p} \left( \left( \frac{\partial p}{\partial \varvec{x}} \otimes \varvec{w} \right) \, \varvec{n} \cdot \delta \varvec{x} + p\, \left( ( \varvec{w} \cdot \varvec{n} ) \varvec{I} \right. \right. \\&\left. \left. - (\varvec{n} \otimes \varvec{w} ) \right) \cdot \nabla \delta \varvec{x} \right) \, da \end{aligned} \end{aligned}$$

(28)

and

$$\begin{aligned} \begin{aligned} \delta r^I(\varvec{u}, \varvec{w}, \varvec{u}; {\mathop {\varvec{u}}\limits ^{\star }} )&= \int _{\Omega } \nabla {\varvec{w}} \cdot {\mathbb {C}}[ \nabla {\mathop {\varvec{u}}\limits ^{\star }} ] \, dv \\&= a( {\mathop {\varvec{u}}\limits ^{\star }} , \varvec{w}) \end{aligned} \end{aligned}$$

(29)

Now we subtract the zero $\delta r = \delta r^E + \delta r^I= 0$ from $\delta \theta = \delta \theta ^E + \delta \theta ^I$ and rearrange to obtain

$$\begin{aligned} \begin{aligned} \delta _i \theta (\varvec{x}, \delta \varvec{x})&= \delta \theta ^E(\varvec{x}, \delta \varvec{x}) \\ {}&- \delta r^E(\varvec{u}, \varvec{w}, \varvec{x}; \delta \varvec{x}) \\&+\left( \delta \theta ^I(\varvec{x}, {\mathop {\varvec{u}}\limits ^{\star }} ) - \delta r^I(\varvec{u}, \varvec{w}, \varvec{u}; {\mathop {\varvec{u}}\limits ^{\star }} ) \right) \end{aligned} \end{aligned}$$

(30)

To eliminate the implicit variations $\delta \theta ^I(\varvec{x}, {\mathop {\varvec{u}}\limits ^{\star }} ) - \delta r^I(\varvec{u}, \varvec{w}, \varvec{u}; {\mathop {\varvec{u}}\limits ^{\star }} )$, we solve the following adjoint equation for the heretofore arbitrary $\varvec{w} \in {{\mathcal {H}}}(\varvec{0})$

$$\begin{aligned} \begin{aligned} 0&= a( {\mathop {\varvec{u}}\limits ^{\star }} , \varvec{w}) \\&- \int _\Omega \left( \nabla {\mathop {\varvec{u}}\limits ^{\star }} \cdot \frac{\partial \Lambda }{\partial \nabla \varvec{u}} + {\mathop {\varvec{u}}\limits ^{\star }} \cdot \frac{\partial \Lambda }{\partial \varvec{u}} \right) dv \\&- \int _{A^t} {\mathop {\varvec{u}}\limits ^{\star }} \cdot \frac{\partial \tau }{\partial \varvec{u}} \, da \\&-\int _{A^p} {\mathop {\varvec{u}}\limits ^{\star }} \cdot \left( \frac{\partial \varvec{\tau }}{\partial \varvec{u}}\right) ^T \varvec{n} \, da \end{aligned} \end{aligned}$$

(31)

for all ${\mathop {\varvec{u}}\limits ^{\star }} \in {{\mathcal {H}}}(\varvec{0})$. As such, the sensitivity reduces to

$$\begin{aligned} \begin{aligned} \delta \theta (\varvec{x}; \delta \varvec{x})&= \delta \theta ^E(\varvec{x}; \delta \varvec{x}) \\&- \delta r^E(\varvec{u}, \varvec{w}, \varvec{x}; \delta \varvec{x}). \end{aligned} \end{aligned}$$

(32)

Note that $\delta \theta$ can be expressed as a boundary integral by applying the divergence method, Haug and Choi (1986), but it is well known that this introduces error in the finite element computations as mentioned in Sect. 1. Consequently, we use the “domain” expression (32) in all of our computations.⁹

We now discuss the finite element discretization. The Equilibrium Equation (1) becomes

$$\begin{aligned} {\varvec{W}}^T (\varvec{K} \, {\varvec{U}} - \varvec{P} ) = 0 \end{aligned}$$

(33)

where $\varvec{U}$ and ${\varvec{W}}$ are the degrees-of-freedom vectors corresponding to $\varvec{u}$ and ${\varvec{w}}$, $\varvec{K}$ is the symmetric stiffness matrix defined such that ${\varvec{W}}^T \varvec{K} \, {\varvec{U}} = a(\varvec{u}, \varvec{w}) = \int _{\Omega } \nabla {\varvec{w}} \cdot {\mathbb {C}}[ \nabla {\varvec{u}} ] \, dv$ and $\varvec{P}$ is the load vector defined such that ${\varvec{W}}^T \varvec{P} = \ell (\varvec{w}) = \int _\Omega {\varvec{w}} \cdot \varvec{b} \, dv + \int _{A^t} {\varvec{w}} \cdot \varvec{t}^n \, da + \int _{A^p} {\varvec{w}} \cdot p \, \varvec{n} \, da$. The arbitrariness of $\varvec{W}$ yields the linear equation $\varvec{K} \, \varvec{U} = \varvec{P}$ that we solve for $\varvec{U}$.

After evaluating $\varvec{U}$ , we can interpolate $\varvec{u}$ and $\nabla \varvec{u}$ within the elements as $\varvec{u}(\varvec{x}) = \varvec{N}(\varvec{x}) \, \varvec{U}$ and $\nabla \varvec{u}(\varvec{x}) = \varvec{B}(\varvec{x}) \, \varvec{U}$ where $\varvec{N}$ contains the element shape functions, $\varvec{B} = {\partial \varvec{N} }/{\partial \varvec{x}}$ and the gradient $\nabla \varvec{u}$ is expressed in the usual vector representation formed by stacking its columns. These interpolations allow us to evaluate the cost and constraint functions $\theta$ of (3) by summing over the elements $\Omega _e$ and performing the usual quadratures. The same interpolation is used to express $\varvec{x} = \varvec{N}(\varvec{x}) \, \varvec{X}$, $\delta \varvec{x} = \varvec{N}(\varvec{x}) \, \delta \varvec{X}$ , and $\nabla \delta \varvec{x} = \varvec{B}(\varvec{x}) \, \delta \varvec{X}$. In this way, $\delta \theta ^E(\varvec{x}; \delta \varvec{x}) = \delta \varvec{X}^T \, {\partial \Theta }/{\partial \varvec{X}}$ where

$$\begin{aligned} \begin{aligned}&\frac{\partial \Theta }{\partial \varvec{X}} = \mathbb {A}_{e=1}^{n_{\text {elem}}} \left[ \right. \\&\left. \int _{\Omega _e} \left( \varvec{B}^T \, \left( - \nabla ^T \varvec{u} \,\frac{\partial \Lambda }{\partial \nabla \varvec{u}} + \Lambda \, \varvec{I} \right) ^T + \varvec{N}^T \frac{\partial \Lambda }{\partial \varvec{x}} \right) \, dv \right. \\&\left. + \int _{A^t_e} \left( \varvec{N}^T \, \frac{\partial \tau }{\partial \varvec{x}} +\varvec{B}^T \, \tau \, (\varvec{I} - \varvec{n} \otimes \varvec{n}) \right) \, da \right. \\&\left. + \int _{A^p_e} \left( \varvec{N}^T \left( \frac{\partial \varvec{\tau }}{\partial \varvec{x}} \right) ^T \varvec{N} \right. \right. \\&\left. \left. + \varvec{B}^T ((\varvec{\tau } \cdot \varvec{n}) \, \varvec{I} - (\varvec{n} \otimes \varvec{\tau }) ) \right) \, da \right] \end{aligned} \end{aligned}$$

(34)

in which $\mathbb {A}$ is the usual finite element assembly operator and all tensors, e.g., $- \nabla ^T \varvec{u} \,\frac{\partial \Lambda }{\partial \nabla \varvec{u}} + \Lambda \, \varvec{I}$ are expressed in their vector representations. We similarly have $\delta \theta ^I(\varvec{x}; {\mathop {\varvec{u}}\limits ^{\star }} ) = {\mathop {\varvec{U}}\limits ^{\star }} ^T \! \! {\partial \Theta }/{\partial \varvec{U}}$ where

$$\begin{aligned} \begin{aligned} \frac{\partial \Theta }{\partial \varvec{U}}&= \mathbb {A}_{e=1}^{n_{\text {elem}}} \left[ \int _{\Omega _e} \left( \varvec{B}^T \, \frac{\partial \Lambda }{\partial \nabla \varvec{u}} +\varvec{N}^T \, \frac{\partial \Lambda }{\partial \varvec{u}} \right) \, dv \right. \\&\left. + \int _{A^t_e} \varvec{N}^T \, \frac{\partial \tau }{\partial \varvec{u}} \, da +\int _{A^p_e} \varvec{N}^T \, \left( \frac{\partial \varvec{\tau }}{\partial \varvec{u}}\right) ^T \varvec{N} \, da \right] \end{aligned} \end{aligned}$$

(35)

Further, $\delta r^E(\varvec{u}, \varvec{w}, \varvec{x}; \delta \varvec{x}) = \delta \varvec{X}^T \, {\partial R}/{\partial \varvec{X}}$ where

$$\begin{aligned} \begin{aligned}&\frac{\partial R}{\partial \varvec{X}} = \mathbb {A}_{e=1}^{n_{\text {elem}}} \left[ \int _{\Omega _e} \left( \varvec{B}^T \, \left( -\nabla ^T \varvec{w} \, {\mathbb {C}}[\nabla \varvec{u}] \right. \right. \right. \\&\left. \left. \left. - \nabla ^T \varvec{u} \,{\mathbb {C}} [ \nabla \varvec{w}] + (\nabla \varvec{w} \cdot {\mathbb {C}}[\nabla \varvec{u}] - \varvec{w} \cdot \varvec{b})\, \varvec{I} \right) \right. \right. \\&+\left. \left. \varvec{N}^T \left( \left( \frac{\partial {\mathbb {C}}[\nabla \varvec{u}]}{\partial \varvec{x}}\right) ^T [\nabla \varvec{w}] - \left( \frac{\partial \varvec{b}}{\partial \varvec{x}} \right) ^T \varvec{w} \right) \right) \, dv \right. \\&\left. -\int _{A^t_e} \left( \varvec{N}^T \, \left( \frac{\partial \varvec{t}^p}{\partial \varvec{x}}\right) ^T \varvec{w} \right. \right. \\&\left. \left. + \varvec{B}^T \, (\varvec{w} \cdot \varvec{t}^p) \, (\varvec{I} - \varvec{n} \otimes \varvec{n}) \right) \, da \right. \\&\left. -\int _{A^p_e} \left( \varvec{N}^T \, \left( \frac{\partial p}{\partial \varvec{x}} \otimes \varvec{w} \right) \, \varvec{n} \right. \right. \\&\left. \left. +\varvec{B}^T \, p\, \left( ( \varvec{w} \cdot \varvec{n} ) \varvec{I} - (\varvec{n} \otimes \varvec{w} ) \right) \right) \, da \right] \end{aligned} \end{aligned}$$

(36)

in which $\varvec{w}$ and $\nabla \varvec{w}$ are interpolated similarly to $\varvec{u}$ and $\nabla \varvec{u}$. Finally

$$\begin{aligned} \delta r^I(\varvec{u}, \varvec{w}, \varvec{x}; {\mathop {\varvec{u}}\limits ^{\star }} ) = a(\varvec{w}, {\mathop {\varvec{u}}\limits ^{\star }} ) = \, {\mathop { \varvec{U}}\limits ^{\star }} ^T \! \! \varvec{K} \, \varvec{W} \end{aligned}$$

(37)

so that

$$\begin{aligned} \begin{aligned} \delta \theta ^I(\varvec{x}, {\mathop {\varvec{u}}\limits ^{\star }} )&- \delta r^I(\varvec{u}, \varvec{w}, \varvec{x}; {\mathop {\varvec{u}}\limits ^{\star }} ) \\&= \, {\mathop {\varvec{U}}\limits ^{\star }} ^T \! \! \left( ({\partial \Theta }/{\partial \varvec{U}})^T - \varvec{K} \, \varvec{W} \right) . \end{aligned} \end{aligned}$$

(38)

To annihilate this implicit term, we equate ${\mathop {\varvec{U}}\limits ^{\star }} ^T \! \! \left( ({\partial \Theta }/{\partial \varvec{U}})^T - \varvec{K} \, \varvec{W} \right) = 0$ and use the arbitrariness of ${\mathop {\varvec{U}}\limits ^{\star }}$ to define the adjoint problem $\varvec{K}~\varvec{W}~=~({\partial \Theta }/{\partial \varvec{U}})^T$ that we solve for $\varvec{W}$. Finally, we evaluate the sensitivity ${D \Theta }/{D \varvec{X}} = {\partial \Theta }/{\partial \varvec{X}} - {\partial R}/{\partial \varvec{X}}$.

Appendix 2: Gradient smoothing derivations

The finite element implementation of (10) gives the sensitivity filter equation

$$\begin{aligned} {\varvec{W}}^T \left( (\widetilde{\varvec{K}} + \widetilde{\varvec{M}}) \, {\widetilde{\text {Grad} \Theta }} - \left( \frac{D \Theta }{D \varvec{X}} \right) ^T \right) = 0 \end{aligned}$$

(39)

where we define $\widetilde{\text {Grad} \Theta }$ as the degrees-of-freedom vector corresponding to $\widetilde{\text {grad} \theta }$, $\widetilde{\varvec{K}}$ as the symmetric smoothing stiffness matrix that satisfies ${\varvec{W}}^T \widetilde{\varvec{K}} \, {\varvec{U}} = \int _{\Omega } \nabla {\varvec{w}} \cdot \gamma \, \nabla {\varvec{u}} \, dv$ and $\widetilde{\varvec{M}}$ as the symmetric smoothing mass matrix that satisfies ${\varvec{W}}^T \widetilde{\varvec{M}} \, {\varvec{U}} = \int _{\Omega } {\varvec{w}} \cdot {\varvec{u}} \, dv$. The arbitrariness of $\varvec{W}$ gives the linear equation $(\widetilde{\varvec{K}} + \widetilde{\varvec{M}}) \, \widetilde{\text {Grad} \Theta } = ({D \theta }/{D \varvec{X}} )^T$ that we solve for $\widetilde{\text {Grad} \Theta }$.

Appendix 3: Fictitious energy derivations

1.1 Fictitious energy function

We desire a fictitious energy density functional $\Psi _f$ that is unaffected by rigid motions and dilations/contractions as we do not want to penalize an element that is subjected to such a shape preserving transformation. To these ends, we use pose the fictitious energy function

$$\begin{aligned} \begin{aligned} \Psi _f(\varvec{F}_d)&= \frac{\textrm{tr} \varvec{C}_d}{(\det \varvec{C}_d)^{\frac{1}{n}}} - n \\ \end{aligned} \end{aligned}$$

(40)

where $\varvec{C}_d = \varvec{F}_d^T \, \varvec{F}_d$ is the fictitious symmetric right-Cauchy-Green strain and $n=2(3)$ for two(three)-dimensional domains. It is readily verified that for $\varvec{F}_d = \alpha \, \varvec{R}_d$, i.e., a combined rotation $\varvec{R}_d$ and dilation/contraction $\alpha \, \varvec{I}$ that $\Psi _f(\varvec{F}_d) = 0$.

To obtain the Eq. (40) energy density functional $\Psi _f$ , we note that

$$\begin{aligned} \varvec{F}_d = \varvec{R}_d \, \varvec{U}_d= \varvec{R}_d \, (\det \varvec{F}_d)^{1/n} \, \overline{\varvec{U}}_d \end{aligned}$$

(41)

where $\varvec{R}_d$ is a rotation and $\varvec{U}_d$ is symmetric positive definite. The first equality is a result of the polar decomposition theorem and the second uses the definition $\overline{\varvec{U}}_d = (\det \varvec{F}_d)^{-1/n} \, \varvec{U}_d$ so that $\det \overline{\varvec{U}}_d = 1$. As seen above, the fictitious deformation gradient consists of an isochoric distortion/contraction $\overline{\varvec{U}}_d$, followed by a dilation $(\det \varvec{F}_d)^{1/n} \, \varvec{I}$ followed by a rotation $\varvec{R}_d$. Based on this decomposition, we pose the Neo-Hookean like fictitious energy function that does not depend on the dilation/contraction $\det \varvec{F}_d \, \varvec{I}$ nor the rotation $\varvec{R}_d$

$$\begin{aligned} \begin{aligned} \Psi _f(\varvec{F}_d)&= \textrm{tr} \overline{\varvec{U}}_d^2 - n \\ \end{aligned} \end{aligned}$$

(42)

which is equivalent to (40). Using the spectral decomposition theorem, we can express the above for two dimensions as

$$\begin{aligned} \Psi _f(\varvec{F}_d) = \lambda ^2 + \frac{1}{\lambda ^2} - 2 \end{aligned}$$

(43)

where $\lambda$ and $1/\lambda$ are the positive eigenvalues of $\overline{\varvec{U}}_d$ and for three dimensions as

$$\begin{aligned} \Psi _f(\varvec{F}_d) = \lambda _1^2 + \lambda _2^2 + \frac{1}{\lambda _1^2 \, \lambda _2^2} - 3 \end{aligned}$$

(44)

where $\lambda _1, \, \lambda _2$ and $1/(\lambda _1\, \lambda _2)$ are the positive eigenvalues of $\overline{\varvec{U}}_d$. A simple derivation subsequently indicates that the minimum energy is obtained for $\lambda = 1$ in two dimensions and for $\lambda _1=\lambda _2 = 1$ in three dimensions which implies $\overline{\varvec{U}}_d = \varvec{I}$, i.e., there is no distortion. This further confirms that $\varvec{F}_d = \alpha \, \varvec{R}_d$ is an energy minimizer for which $\Psi _f(\alpha \, \varvec{R}_d) = 0$.

1.2 Newton’s method

To solve the residual Eq. (15), we use Newton’s method and iterate by finding the $\Delta \varvec{d}\in \mathcal{H}_f( 0)$ such that

$$\begin{aligned} \begin{aligned} \delta _{d^0} r_f(\varvec{d}^0, \varvec{w}, \varvec{d}^p; \Delta \varvec{d}^0)&= \int _{\Omega _0} \nabla \varvec{w} \cdot \frac{\partial ^{2} \Psi _f}{\partial \varvec{F}_d^{2} } [\nabla \Delta \varvec{d}^0] \, dv \\ {}&= -r_f(\varvec{d}, \varvec{w}, \varvec{d}^p) \end{aligned} \end{aligned}$$

(45)

for all $\varvec{w} \in {{\mathcal {H}}}_f( 0)$. Upon evaluating $\Delta \varvec{d}^0$ we update $\varvec{d}^0\leftarrow \varvec{d}^0+ \Delta \varvec{d}^0$ and continue iterating until $r(\varvec{d}, \varvec{w}, \varvec{d}^p) \le \epsilon$ for some suitable convergence tolerance $\epsilon$. Note that the fictitious energy residual Eq. (14) for $\varvec{d}^0$ is solved over the initial configuration $\Omega _0$ whereas the $H^1$ smoothing Eq. (10) for $\widetilde{\text {grad} \theta }$ is solved over the current design configuration $\Omega$.

To evaluate the residual and tangent, we need

$$\begin{aligned} \begin{aligned} \frac{\partial \Psi _f}{\partial \varvec{F}_d}&= 2 \, \varvec{F}_d\, \frac{\partial \Psi _f}{\partial \varvec{C}_d} \\ \frac{\partial ^{2} \Psi _f}{\partial \varvec{F}_d^{2} }&= 2 \, \varvec{I} \boxtimes \frac{\partial \Psi _f}{\partial \varvec{C}_d} \\&+4 (\varvec{F} \boxtimes \varvec{I}) \, \frac{\partial ^{2} \Psi _f}{\partial \varvec{C}_d^{2} } \, (\varvec{F} \boxtimes \varvec{I})^T \end{aligned} \end{aligned}$$

(46)

where, for any 2-tensors $\varvec{A}$ and $\varvec{B}$, the conjugate product $\varvec{A} \boxtimes \varvec{B}$ is the 4-tensor that satisfies $(\varvec{A}~\boxtimes ~\varvec{B})[\varvec{C}]~=~\varvec{A}~\varvec{C}~\varvec{B}^T$ for any 2-tensor $\varvec{C}$. For the energy function of (40), we have

$$\begin{aligned} \begin{aligned} \frac{\partial \Psi _f}{\partial \varvec{C}_d}&= (\det \varvec{C}_d)^{-\frac{1}{n}} \, \left( \varvec{I} - \frac{1}{n} \, \textrm{tr} \varvec{C}_d \, \varvec{C}_d^{-1} \right) \\ \frac{\partial ^{2} \Psi _f}{\partial \varvec{C}_d^{2} }&= \frac{1}{n} (\det \varvec{C}_d)^{-\frac{1}{n}} \, \left( -\varvec{I} \otimes \varvec{C}_d^{-1} - \varvec{C}_d^{-1} \otimes \varvec{I} \right. \\&\left. +\frac{1}{n} \textrm{tr} \varvec{C}_d \, \varvec{C}_d^{-1} \otimes \varvec{C}_d^{-1} + \textrm{tr} \varvec{C}_d \, \varvec{C}_d^{-1} \boxtimes \varvec{C}_d^{-1}\right) \end{aligned} \end{aligned}$$

(47)

where the dyadic product $\varvec{A} \otimes \varvec{B}$ is the 4-tensor that satisfies $(\varvec{A}~\otimes ~\varvec{B})[\varvec{C}]~=~(\varvec{B}\cdot \varvec{C})~\varvec{A}$ for any 2-tensor $\varvec{C}$.

A linearization about $\varvec{F}_d = \varvec{I}$, which is accurate when $\nabla \varvec{d}$ is “small,” provides

$$\begin{aligned} \begin{aligned} \Psi _f&= \frac{1}{2} \, \nabla \varvec{d}\cdot {\mathbb {A}}_f[\nabla \varvec{d}] \\ \frac{\partial \Psi _f}{\partial \varvec{F}_d}&= {\mathbb {A}}_f[\nabla \varvec{d}] \\ \frac{\partial ^{2} \Psi _f}{\partial \varvec{F}_d^{2} }&= {\mathbb {A}}_f \end{aligned} \end{aligned}$$

(48)

where

$$\begin{aligned} {\mathbb {A}}_f = \frac{\partial ^{2} \Psi _f}{\partial \varvec{F}_d^{2} } \bigg |_{\varvec{F}_d = \varvec{I}} = 4 \left( {\mathbb {I}}_{\text {sym}} - \frac{1}{n} \varvec{I} \otimes \varvec{I} \right) \end{aligned}$$

(49)

wherein the symmetrizer ${\mathbb {I}}_{\text {sym}}$ is the 4-tensor that satisfies ${\mathbb {I}}_{\text {sym}} [\varvec{C}] = \frac{1}{2}( \varvec{C} + \varvec{C}^T)$ for any 2-tensor $\varvec{C}$. Note that ${\mathbb {A}}_f [\varvec{C}] = 4\, ({\mathbb {I}}_{\text {sym}}[\varvec{C}] - \textrm{tr} C \, \varvec{I})$ is deviatoric and symmetric and hence as expected ${\mathbb {A}}_f[\nabla \varvec{d}] = \varvec{0}$ for $\nabla \varvec{d}= \alpha \, \varvec{I}$ an infinitesimal dilation/contraction, for $\nabla \varvec{d}= \varvec{W}$ where $\varvec{W}$ is skew, i.e., an infinitesimal rotation and for their combination $\nabla \varvec{d}= \alpha \, \varvec{W}$. The stiffness tensor ${\mathbb {C}}$ for a linear elastic isotropic material can be expressed as ${\mathbb {C}} = 2 \, \mu \, {\mathbb {I}}_{\text {sym-dev}} + 3 \, \kappa \, {\mathbb {I}}_{\text {sph}}$ where ${\mathbb {I}}_{\text {sym-dev}} = {\mathbb {I}}_{\text {sym}} - \frac{1}{n} \varvec{I} \otimes \varvec{I}$ and ${\mathbb {I}}_{\text {sph}} = \frac{1}{n} \varvec{I} \otimes \varvec{I}$ are the projections onto the spaces of symmetric deviatoric tensors and spherical tensors, respectively. And hence, the “fictitious” material can be thought of as an elastic material with shear stiffness $\mu = 1/2$ and bulk modulus $\kappa = 0$ which also implies it has first Lamé parameter $\lambda = -1/3$, Poisson ratio $\nu = -1$, and Young’s modulus $E = 0$.¹⁰¹¹

1.3 Sensitivity analysis

Noting that $\delta \varvec{x} = \delta \varvec{d}$ allows us to write

$$\begin{aligned} \begin{aligned} \delta \theta ( \varvec{d}; \delta \varvec{d})&= \delta \theta ^E(\varvec{x}; \delta \varvec{x}) \\ {}&- \delta r^E(\varvec{u}, \varvec{w}, \varvec{x}; \delta \varvec{x}) \end{aligned} \end{aligned}$$

(50)

from (32). The problem arises because $\varvec{d}$ is an implicit function of $d^p$ as seen through (15), i.e., we have $\varvec{d}= \varvec{d}^0(d^p) + \varvec{d}^p(d^p)$ and hence, with a slight abuse of notation, we have

$$\begin{aligned} \theta = \theta (d^p) = \theta ( \varvec{d}(d^p) ) = \theta ( \varvec{d}^0(d^p), \varvec{d}^p(d^p) ). \end{aligned}$$

(51)

We annihilate the implicit variation $\delta \varvec{d}^0(d^p; \delta d^p)$ in (50) by again applying the adjoint method. To do this, the total variation of (15) with respect to $d^p$ in the direction $\delta d^p$, which equals zero, is subtracted from (50) to give

$$\begin{aligned} \begin{aligned}&\delta \theta ( d^p; \delta d^p) = \delta _{d^0} \theta ( \varvec{d}^0(d^p),\varvec{d}^p(d^p); \delta \varvec{d}^0(d^p; \delta d^p )) \\&+\delta _{d^p} \theta ( \varvec{d}^0(d^p), \varvec{d}^p(d^p); \delta \varvec{d}^p(d^p;\delta d^p) \\&- \left\{ \delta _{{d^0}} r_f(\varvec{d}^0(d^p), \varvec{w}, \varvec{d}^p(d^p); \delta \varvec{d}^0(d^p; \delta d^p )) \right. \\ {}&\left. + \delta _{d^p} r_f(\varvec{d}^0(d^p), \varvec{w}, \varvec{d}^p(d^p); \delta \varvec{d}^p(d^p;\delta d^p) )\right\} \end{aligned} \end{aligned}$$

(52)

where $\delta _{d^0} r_f$ is the tangent operator of (45) and the term in braces equals zero. Upon requiring the heretofore arbitrary $\varvec{w} \in {{\mathcal {H}}}_f(0)$ to satisfy

$$\begin{aligned} \begin{aligned} \delta _{{d^0}} r_f(\varvec{d}^0(d^p), \varvec{w},&\varvec{d}^p(d^p); \delta \varvec{d}^0(d^p; \delta d^p )) \\&= \delta \theta ( \varvec{d}(d^p); \delta \varvec{d}^0(d^p; \delta d^p )) \end{aligned} \end{aligned}$$

(53)

for all $\delta \varvec{d}^0 \in {{\mathcal {H}}}_f(0)$, (62) reduces to

$$\begin{aligned} \begin{aligned} \delta \theta ( d^p; \delta d^p)&= \delta _{d^p} \theta ( \varvec{d}^0(d^p), \varvec{d}^p(d^p); \delta \varvec{d}^p(d^p;\delta d^p)) \\&-\delta _{d^p} r_f(\varvec{d}^0(d^p), \varvec{w}, \varvec{d}^p(d^p); \delta \varvec{d}^p(d^p;\delta d^p) ) \end{aligned} \end{aligned}$$

(54)

which is the desired explicit sensitivity expression. The fact that $r_f$ and $\theta$ are defined over different domains $\Omega _0$ and $\Omega$ is not a concern as the change-of-variable theorem can always be used to express $\theta$ over $\Omega _0$. Indeed, the change-of-variable theorem is often used to obtain the shape sensitivity expressions $\delta \theta ^E_i$ and $\delta r^E$ of (26) and (28).

A simplification arises for the sensitivity analysis of the Equation (16) constraint on the total fictitious energy. Indeed, using the adjoint sensitivity analysis, one can show that

$$\begin{aligned} \begin{aligned} \delta \theta _f( d^p; \delta d^p)&= \int _{\Omega _0} \frac{\partial \Psi _f(\varvec{F}_d)}{\partial \varvec{F}_d} \cdot \nabla \delta \varvec{d}_p(d^p; \delta d^p ) \, dv \\&\hspace{1em} -\delta _{d^p} r_f(\varvec{d}^0(d^p), \varvec{w}, \varvec{d}^p(d^p); \delta \varvec{d}^p(d^p;\delta d^p) ) \\&= r_f(\varvec{d}^0(d^p), \delta \varvec{d}^p(d^p; \delta d^p), \varvec{d}^p(d^p) ) \end{aligned} \end{aligned}$$

(55)

where we use (15) with $\varvec{w} = \delta \varvec{d}^p(d^p; \delta d^p )$¹² and the fact that the adjoint response $\varvec{w}=\varvec{0}$. The latter claim is true since, for all $\delta \varvec{d}^0 \in \mathcal{H}_f(0)$, $\varvec{w} \in {{\mathcal {H}}}_f(0)$ must satisfy

$$\begin{aligned} \begin{aligned}&\delta _{d^0} r_f(\varvec{d}^0(d^p), \varvec{w}, \varvec{d}^p(d^p);\delta \varvec{d}^0(d^p; \delta d^p) ) \\&=\int _{\Omega _0} \frac{\partial \Psi _f(\varvec{F}_d)}{\partial \varvec{F}_d} \cdot \nabla \delta \varvec{d}^0(d^p; \delta d^p ) \, dv \\&= r_f(\varvec{d}^0(d^p), \delta \varvec{d}^0(d^p; \delta d^p ), \varvec{d}^p(d^p)) \end{aligned} \end{aligned}$$

(56)

where we used (15) with $\varvec{w} = \delta \varvec{d}^0(d^p; \delta d^p )\in {{\mathcal {H}}}_f(0)$ to obtain the last equality. We trivially obtain $\varvec{w}=\varvec{0}$ since the load linear term on right-hand side equals zero.

1.4 Discretization

In the finite element discretization, we partition $\varvec{D}$ the degrees-of-freedom vector corresponding to $\varvec{d}= \varvec{d}^0 + \varvec{d}^p$, into the degrees-of-freedom vectors $\varvec{D}^0$ and $\varvec{D}^p$ that correspond to $\varvec{d}^0$ and $\varvec{d}^p$; the discretization and partition of $\varvec{w}$ are similarly performed. The residual Equation (15) is then expressed as

$$\begin{aligned} {\varvec{W}}^{0^T} \, \varvec{R}_f^0 (\varvec{D}^0, \varvec{D}^p) = 0 \end{aligned}$$

(57)

where $\varvec{R}_f$ is the residual vector defined such that $\varvec{W}^T \varvec{R}_{f} = \int _{\Omega _0} \nabla \varvec{w} \cdot \frac{\partial \Psi _f}{\partial \varvec{F}_d} \, dv$ and $\varvec{R}_f^{0}$ is the partition of $\varvec{R}_f$ that corresponds to $\varvec{W}^0$. Notably, we only solve the residual equation $r_f=0$ for the degrees-of-freedom that corresponds to the unknown $\varvec{D}^0$. The discretization of the Newton update equation (45) yields

$$\begin{aligned} \varvec{W}^{0^T} \left( \varvec{K}^{00}_f \, \Delta \varvec{D}^0 + \varvec{R}_f^0 \right) = 0 \end{aligned}$$

(58)

where $\varvec{K}_f$ is the symmetric tangent stiffness matrix defined such that $\varvec{W}^T \varvec{K}_f \, \Delta \varvec{D}= \int _{\Omega _0} \nabla \varvec{w}\cdot {\partial ^{2} \Psi _f}/{\partial \varvec{F}_d^{2} } [\nabla \Delta \varvec{d}] \, dv$ and $\varvec{K}^{00}_f$ is the partition of $\varvec{K}_f$ that corresponds to $\varvec{W}^0$ and $\Delta \varvec{D}^0$. The arbitrariness of $\varvec{W}^{0}$ renders the linear update equation $\varvec{K}^{00}_f \, \Delta \varvec{D}^0 = - \varvec{R}_f^0$ that we solve for $\Delta \varvec{D}^0$. Updates $\varvec{D}^0 \leftarrow \varvec{D}^0 + \Delta \varvec{D}^0$ continue until $|\varvec{R}_f^0|\le \epsilon$ for suitably small tolerance $\epsilon$.

The adjoint Eq. (53) is discretized as

$$\begin{aligned} \delta \varvec{D}^{0^T} \left( \varvec{K}^{00}_f \, \varvec{W}^0 - \left( \frac{D \theta }{D \varvec{X}^0} \right) ^T \right) = 0 \end{aligned}$$

(59)

where ${D \theta }/{D \varvec{X}^0}$ is the partition of ${D \theta }/{D \varvec{X}}$ that is associated with the $\varvec{D}^0$ degrees-of-freedom. The arbitrariness of $\delta \varvec{D}^{0}$ renders the linear adjoint equation $\varvec{K}^{00}_f \, \varvec{W}^0 = \left( {D \theta }/{D \varvec{X}^0} \right) ^T$ that we solve for $\varvec{W}^0$. Finally, the sensitivity Eq. (54) is discretized such that

$$\begin{aligned} \frac{D \theta }{D \varvec{D}^p} = \frac{D \theta }{D \varvec{X}^p} - \varvec{W}^{0^T} \, \varvec{K}^{0p}_f \end{aligned}$$

(60)

where ${D \theta }/{D \varvec{X}^p}$ is the partition of ${D \theta }/{D \varvec{X}}$ that is associated with $\varvec{D}^p$ and $\varvec{K}^{0p}_f$ is the partition of $\varvec{K}_f$ that is associated with $\varvec{W}^0$ and $\Delta \varvec{D}^p$. The sensitivity of the energy constraint (16) is obtained directly by evaluating ${D \Theta _f}/{D \varvec{D}^p} = {\partial \Theta _f}/{\partial \varvec{D}^p}$. The computation of ${\partial \Theta _f}/{\partial \varvec{D}^p} = \varvec{R}^p_f$ follows from (15) and (55) where $\varvec{R}_f^{p}$ is the partition of $\varvec{R}_f$ that corresponds to the $\varvec{D}^p$ degrees-of-freedom.

Appendix 4: Consistent filtering derivations

Noting that $\delta \varvec{x} = \delta \widetilde{\varvec{d}}$ allows us to trivially obtain

$$\begin{aligned} \begin{aligned} \delta \theta (\widetilde{\varvec{d}}; \delta \widetilde{\varvec{d}})&= \delta \theta ^E(\varvec{x}; \delta \varvec{x})\\&- \delta r^E(\varvec{u}, \varvec{w}, \varvec{x}; \delta \varvec{x}) \end{aligned} \end{aligned}$$

(61)

from (32). The problem arises because $\widetilde{\varvec{d}}$ is an implicit function of $\varvec{d}$ as seen through (17), i.e., we have $\widetilde{\varvec{d}}= \widetilde{ \varvec{d}}(\varvec{d})$ and hence, using our abusive notation, we have $\theta = \theta (\varvec{d}) = \theta (\widetilde{\varvec{d}}(\varvec{d}))$. We annihilate the implicit variation $\delta \widetilde{\varvec{d}}(\varvec{d}; \delta \varvec{d})$ in (61) by again applying the adjoint method. The variation of (17) with respect to $\varvec{d}$ in the direction $\delta \varvec{d}$, which equals zero, is subtracted from (61) to give¹³

$$\begin{aligned} \begin{aligned} \delta \theta ( \varvec{d}; \delta \varvec{d})&= \delta \theta (\widetilde{\varvec{d}}; \delta \widetilde{\varvec{d}}) \\&\overbrace{- a_c ( \delta \widetilde{\varvec{d}}, \varvec{w} ) + \ell _c(\varvec{w}, \delta \varvec{d})}^{=0} \end{aligned} \end{aligned}$$

(62)

Upon requiring the heretofore arbitrary $\varvec{w} \in {{\mathcal {H}}}_c$ to satisfy

$$\begin{aligned} a_c ( \delta \widetilde{\varvec{d}}, \varvec{w} ) =\delta \theta (\widetilde{\varvec{d}}; \delta \widetilde{\varvec{d}}) \end{aligned}$$

(63)

for all $\delta \widetilde{\varvec{d}} \in {{\mathcal {H}}}_c$, (62) reduces to the desired explicit sensitivity expression

$$\begin{aligned} \delta \theta ( \varvec{d}; \delta \varvec{d}) = \ell _c(\varvec{w}, \delta \varvec{d}) \end{aligned}$$

(64)

As discussed above, the fact that $a_c$, $\ell _c$ and $\delta \theta$ are defined over different domains in (62) - (64) is not a concern.

The finite element discretization of (17) yields the equation

$$\begin{aligned} \varvec{W} ^T ((\varvec{K}_c + \varvec{M}_c) \, \widetilde{\varvec{D}} - \varvec{M}_c \, \varvec{D}) = 0 \end{aligned}$$

(65)

where $\varvec{D}$, $\widetilde{\varvec{D}}$ , and $\varvec{W}$ are the degrees-of-freedom vectors corresponding to $\varvec{d}$, $\widetilde{\varvec{d}}$ , and $\varvec{w}$, $\varvec{K}_c$ is the symmetric filter stiffness matrix defined such that¹⁴$\varvec{W} ^T \varvec{K}_c \, \widetilde{\varvec{D}} = \int _{\Omega _0} \nabla \varvec{w} \cdot \gamma \, \nabla \widetilde{\varvec{d}} \, dv$ and $\varvec{M}_c$ is the symmetric filter mass matrix defined such that $\varvec{W} ^T \varvec{M}_c \, {\varvec{D}} = \int _{\Omega _0} \varvec{w} \cdot {\varvec{d}} \, dv$. Using the symmetries of $\varvec{K}_c$ and $\varvec{M}_c$, the adjoint problem (63) is discretized as

$$\begin{aligned} \delta \widetilde{\varvec{D}}^T (\varvec{K}_c + \varvec{M}_c) \, \varvec{W} = \delta \widetilde{\varvec{D}}^T \left( \frac{D \theta }{D \varvec{X}} \right) ^T \end{aligned}$$

(66)

. The arbitrariness of $\delta \widetilde{\varvec{D}}$ renders the linear adjoint equation $(\varvec{K}_c + \varvec{M}_c) \, \varvec{W} = ({D \Theta }/{D \varvec{X}} )^T$ that we solve for $\varvec{W}$. Finally, the derivative of (64) is computed from ${D \Theta }/{D \varvec{D}} = \varvec{M}_c \, \varvec{W}$.