1 Introduction

An understanding of the wheel–rail relationship on railways is becoming increasingly important with the continuous development of the railway industry. The irregularity of the wheel–rail contact geometry causes uneven distribution of the contact stress on the wheel–rail surface and structural fatigue of the vehicle, which in turn causes rail damage and becomes a major factor affecting the stability of train operation and rail maintenance costs. Target profile design is an effective means of ensuring good wheel–rail matching characteristics and is gradually being used in various types of railway systems, such as high-speed, metro, and heavy-haul systems (Jahed et al. 2008; Choi et al. 2013a; Wang et al. 2016).

Profile design is a scientific problem with a long history, and numerous ideas for it have been proposed. The earliest wheel–rail profile was designed by the trial-and-error method (Heumann 1934; Heller and Harry Law 1979), but it is difficult to obtain ideal results because of the many variables involved and methodological shortcomings.

With continuous advancements in numerical methods, there has been a gradual increase in the use of single-objective optimization methods to address this complex design problem. One class of methods involves a single-objective solution based on the minimization of certain requirements, including the dynamic response of the vehicle body, contact stress, wear, profile conformability, etc. Zhai et al. (2014) analyzed the problem of rail wear in a curved section of a heavy-haul railway with a small radius and proposed a rail profile optimization method based on the dynamic contact between the wheel and rail profile. It was demonstrated that the wheel–rail dynamic interaction of the optimized profile was significantly improved. Based on the variation in contact stress between the wheel and rail, Smallwood et al. (1991) proposed a method aimed at reducing contact stress to optimize the rail. The results showed that the maximum contact stress between the wheel and rail was reduced by approximately 50% by optimizing the outer rail profile. Zong and Dhanasekar (2013a, 2013b) proposed minimizing the contact stress as the objective based on the finite element method and genetic algorithm to obtain the optimal profile. The results showed that the optimized rail profile effectively reduced the stress concentration on the working side of the rail head. Choi et al. (2013a) proposed an asymmetric rail profile optimization design method with the rail wear index as the objective function and the wheel–rail dynamic performance as the constraint and solved the wear problem for curved sections in urban rail transport. A rail profile design method based on a genetic algorithm was proposed by Wang et al. (2017), with the rail wear rate as the objective function, the vertical coordinate of the rail profile as the design variable, and the geometric characteristics and grinding depth as the constraint conditions. Spangenberg et al. (2019) analyzed the impact of the conformal profile on wear and rolling contact fatigue and then optimized the wheel–rail profile according to this idea. The wheel designed according to this conformal idea had a more stable equivalent conicity.

The other class of methods involves single-objective design based on the inverse solution of contact characteristics. By setting the contact relationship of the target in advance, the profile is obtained with an optimization algorithm. The key is to study the internal relationship between the contact relationship and actual requirements. Markine et al. (2007) and Shevtsov et al. (2008) proposed a design method based on the inverse of the rolling circle radius difference function for the wheel profile, considering the maximum equivalent conicity and the profile geometry as constraints, and a method based on response surface fitting was used to achieve the target profile design. The obtained wheel profile had good dynamic performance and obvious wear reduction, achieving a balance between stability, curve passing performance, wear and fatigue relief in the Netherlands. Mao and Shen (2017, 2018) obtained the analytical formula of the wheel–rail relationship with a theoretical derivation and took the wheel-diameter difference curve as the design parameter and the expected wheel–rail contact distribution as the design boundary condition to obtain the rail grinding profile using an inverse solution method. With the goal of improving the wheel–rail contact state, Jun et al. (2014) proposed an inverse method based on the contact angle curve and used the bilateral wheel–rail contact angle difference curve to evaluate and obtain the optimal profile by continuous correction. Among such methods, the design of rolling circle radius differences is favored by researchers and designers because it is more effective.

Wheel–rail profile matching affects vehicle-rail dynamics, wheel–rail contact fatigue and wear at the same time, and single-objective optimization is not sufficient for all application scenarios. Gradually, multi-objective optimization has been applied to profile design issues. Magel and Kalousek (2002) evaluated the optimized rail profile by comprehensively considering the development of wear, fatigue, wavy wear, optimal stability, and noise reduction, effectively extending the service life of the rail. Persson and Iwnicki (2004), Persson et al. (2010) took the weighted sum of penalty factors related to dynamics such as the maximum contact stress, wheel–rail lateral force, derailment coefficient, wear number, and so on as the objective function and used a genetic algorithm to solve for the optimal wheel and rail profile. They achieved good results in rolling contact fatigue, wear, noise, and other issues, and the matching performance was also improved to a certain extent by the Stockholm Metro. Choi et al. (2013b) presented a numerical method for multi-objective optimization of wheel profiles based on the energy transfer model. They designed an optimized profile that simultaneously reduced wheel flange wear and profile fatigue. Tang et al. (2020) designed a multi-objective optimization method for rail profiles based on a genetic algorithm and hierarchical analysis, in which the multi-objective parameters are safety indicators, wheel–rail wear and wheel–rail contact stress, and the weight coefficient is allocated for optimization. However, research on the interactions between sub-objectives in existing multi-objective methods is lacking, making it difficult to ensure that the design results are globally optimal, and many details need to be further investigated.

In recent years, numerous new optimization methods and strategies have emerged. To improve train punctuality, Wang et al. (2020) developed a train trajectory optimization method based on fuzzy rules and genetic algorithms. This method effectively optimizes the train’s travel trajectory and addresses the impacts of parameter uncertainties on train operations. Zhu et al. (2021) compared the advantages and limitations of six hybrid heuristic models, including genetic algorithm, particle swarm optimization, and ant colony optimization algorithms. They provided model recommendations for different problem requirements, offering guidance for the design and optimization of load-bearing hierarchical hardening shells. Li et al. (2023) proposed a hierarchical linking strategy based on multiple sets, combining the ideas of multiple sets and hierarchical linking. This method comprehensively considers various uncertainties and correlations, providing more accurate reliability evaluation results. Kolahchi et al. (2022) proposed an optimization method called AK-GWO, which combines the adaptive Kriging model with the gray wolf optimization algorithm to achieve more precise optimization in the design of layered hardening shells. Regarding approximate optimizations, Zhang et al. (2022) proposed a method that combines a gradient-assisted metamodel with a trust region optimization framework for wing fixture shape optimization. The gradient-assisted metamodel reduces the computational cost of the real model by establishing a surrogate model, while the trust region optimization framework provides an effective optimization strategy.

In summary, the optimization design of wheels and rails has gradually evolved from using a trial method to a single-objective optimization method with various kinetic indicators or contact relations. In addition, multi-objective optimization is also a trend in profile design development. In recent years, optimization methods that can be implemented to structural design have become increasingly rich and complex, and optimization strategies have become more efficient. In the research process, we often want to obtain an excellent rail profile in all directions, but it is difficult to obtain a unified answer due to various factors in the actual operation, and most multi-objective optimization methods are relatively complex and inefficient, which are not practical for the rapid design and solution of actual lines with multiple sections. The single-objective optimization method with the contact relationship as the objective can quickly obtain results, but the choice of the objective function is crucial and needs to include as much wheel–rail information as possible. The rolling radius difference (RRD) is an objective function that meets this requirement but also has its own shortcomings. Therefore, in this paper, an inverse design method that performs rail profile optimization is proposed based on the distribution of contact points. The distribution of the contact points contains much information regarding the direct wheel–rail contact. All static wheel–rail relationships, including the rolling radius difference, contact angle difference, and equivalent conicity, are calculated based on the calculated contact points. Additionally, the distribution of the contact points encompasses many implicit relationships. The denser the adjacent contact points are, the more concentrated the stress distribution at the contact points and the greater the potential for wear. Conversely, more dispersed adjacent points may affect the dynamic operation performance of the vehicle body. Thus, it can satisfy most requirements through the intuitive control of contact points for engineering practice.

2 Objective curve of inverse design

In the inverse design method, the design goal should include as many design requirements as possible, and RRD is one of the functions satisfying this property. The RRD is one of the main parameters of wheel–rail contact geometry, which is closely related to vehicle dynamics performance, and the wheel–rail contact relationship can be obviously improved by optimizing the RRD curve. The author has also created a rail profile design program based on RRD as the objective function, which has been widely used in practice (Shi et al. 2021). The design process with RRD as the objective function has produced some inevitable contradictions in practical applications.

Figure 1 shows a case of rail profile design based on RRD that was encountered, in which yw is the lateral displacement of the wheelset. The rail profile satisfying the target RRD curve was obtained by the program. The RRD curve meets the design requirements formulated in advance. However, it can be seen that the contact point distribution is discontinuous at lateral displacements of 2–3 mm. The transverse gap between two adjacent rail contact points with 0.5 mm lateral displacement reaches 6.4 mm. The vehicle dynamic performance will be affected when the wheelset moves in this part. On the other hand, this discontinuity has the potential to cause the occurrence of two or even more contact points on the rail or wheel, which will further degrade the dynamic performance.

Fig. 1
figure 1

Profile optimization case based on RRD target curve: a RRD curve b wheel–rail contact relationship

Full size image

In addition, a common problem is the same contact point for multiple consecutive lateral displacements. The rail contact point is still in the same position, although the position of the wheelset has changed, which causes greater stress concentration and has a major impact on wear. Works departments pay special attention to rail wear in small radius curves and heavy-load sections to reduce maintenance costs.

The reason for these problems is that RRD is an indirect objective function in the wheel–rail contact relationship, which is defined by the left and right contact positions of the wheel. It responds directly to changes in contact point position on the wheel tread but fails to do so for points on the rail. In other words, a continuous and homogeneous distribution of wheel contact points is basically ensured through the design of the RRD curve. However, it may be subject to several conditions on the rail:

  1. (1)

    The contact points of the rails are deviated far from each other under adjacent lateral displacement, resulting in the jumping phenomenon. This easily gives rise to multipoint contact, which is detrimental to the passage of trains.

  2. (2)

    Under adjacent lateral displacement, the contact points of the rail are close to each other, even in the same position. This will cause stress concentration, which is not conducive to the long-term use of the rail.

  3. (3)

    The rail contact points are continuous and evenly distributed. The stress is kept low, which facilitates stable train operation and prolongs the life of the rail.

In general, the ideal rail design profile satisfies the third criterion, but it is not always perfectly achieved in the target RRD design. The wheel tread design process can basically satisfy all the requirements. However, in the optimization design of the rail, the position of the rail contact point is the key design requirement. For these reasons, the idea of taking the distribution of rail contact points as the objective function was applied to the optimization design of the profile. Two objective functions, contact position on the left (CPL) and contact position on the right (CPR), are proposed to be freely selected in the optimization design of rail profiles. A single-objective function can be used in the design of a one-sided rail and symmetrical rails on both sides, and two can also be used together in the asymmetrical design.

Such an optimization objective directly affects the contact distribution in the rail and indirectly reflects the contact stress distribution. The principle of the optimized target curve is to satisfy the third condition above as much as possible. All these concepts will be discussed in detail in the following sections.

3 Design method

3.1 Rail profile optimization method

Based on the above idea, an inverse design method of rail profiles with the objective of contact point location distribution is developed.

Most optimization problems can be expressed in the following form:

$$ {\text{Minimize}} \; F_{0} (X) \to \min ,X \in R^{N} $$
(1)
$$ {\text{subject to}} \; \begin{array}{*{20}l} {F_{i} \left( X \right) \le 1\left( {i = 1, \cdots ,N_{0} } \right)} \hfill \\ \end{array} $$
(2)
$$ {\text{and}} \; A_{j} \le x_{j} \le B_{j} \left( {j = 1, \cdots ,N_{{\text{mov }}} } \right) $$
(3)

where \(F_{0}\) is the objective function;

\(\begin{array}{*{20}l} {F_{i} (i = 1, \cdots ,N_{{0}} )} \hfill \\ \end{array}\) are the constraint functions;

\(X = \left[ {x_{1} ,x_{2} \cdots ,x_{{N_{{\text{mov }}} }} } \right]\) is the vector of design variables;

N0 is the number of constraints;

Nmov is the number of optimization points;

\(A_{j}\) and \(B_{j}\) are the side limits, which define the lower and upper bounds of the j-th design variable, respectively.

3.1.1 Design variables

To transform the rail profile optimization problem into a general optimization problem, it is necessary to design some variables to control the rail profile.

The first step is to determine the optimization region according to the design requirements. In general, the range of wheelset lateral movement will not be significantly different before and after profile optimization. To find the appropriate range of rail profile adjustment, a reasonable approach is to conduct vehicle–track dynamics analysis for the optimized line section. The scope of wheelset lateral displacement can be obtained by substituting the actual parameters of the vehicle, line, and wheel–rail profile. Then, the region to be optimized can be obtained by appropriate expansion.

The next step is to select several points in the optimization region as the design points and set the variable vertical coordinates as the design variables. The optimization region and design points are shown in Fig. 2. Points A and B are the fixed points, and \(\left[ {\left( {y_{1} ,z_{1} } \right) \cdot \cdot \cdot \left( {y_{i} ,z_{i} } \right) \cdot \cdot \cdot \left( {y_{Nl} ,z_{Nl} } \right)} \right]\) are the coordinates of the design points in the left rail. \(X = \left[ {z_{1} ,z_{2} , \ldots ,z_{{N_{mov} }} } \right]\) are the design variables in the whole rail profile design. Inside, the design points are not necessarily uniformly distributed in the optimization region, and the key areas can be targeted according to the design requirements.

Fig. 2
figure 2

Optimize areas and control points: a Left rail b Right rail

Full size image

The selection of the left- and right-side rail profiles does not necessarily need to be symmetrical due to the different design requirements. In symmetrical grinding design, only one side of the rail needs to be selected for design variables, such as in the pre-grinding design of a new rail profile. Once the rail profile is determined on one side, the other side only needs to be symmetrical. In some asymmetric grinding designs, such as curve designs, the left and right rails must be selected separately.

3.1.2 Constraint functions

  1. (1)

    Rail convex function restriction

    The inherent convex curvature of the rail profile entails a monotonically decreasing slope between two adjacent points from left to right of the rail data. Therefore, the constraint equation function can be automatically established after the fixed points and design points are determined. Then, the constraint relation of rail profile design is

    $$ k_{i} > k_{i + 1} (i = A,1,2,...Nl), $$
    (4)

    where \(k_{i}\) is the slope of the connection between the i-th data point and the i + 1st data point, and \(k_{i + 1}\) is the connection between i + 1st and the i + 2nd. i includes fixed points and all design points, and the left and right rail profiles are considered separately. The constraint equation of the left design point is as follows:

    $$ K_{L} \cdot Z_{L} < b_{L}, $$
    (5)

    where

    $$ \begin{gathered} K_{L} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {} & {} & {} & {} & {} \\ {a_{21} } & {a_{22} } & {a_{23} } & {} & {} & {} & {} \\ {} & {...} & {...} & {...} & {} & {} & {} \\ {} & {} & {a_{i(i - 1)} } & {a_{ii} } & {a_{i(i + 1)} } & {} & {} \\ {} & {} & {} & {...} & {...} & {...} & {} \\ {} & {} & {} & {} & {a_{(n - 1)(n - 2)} } & {a_{(n - 1)(n - 1)} } & {a_{(n - 1)n} } \\ {} & {} & {} & {} & {} & {a_{n(n - 1)} } & {a_{nn} } \\ \end{array} } \right] \hfill \\ b_{L} = \left[ {\begin{array}{*{20}c} { - a_{1A} z_{A} } \\ 0 \\ {...} \\ 0 \\ {...} \\ 0 \\ { - a_{nB} z_{B} } \\ \end{array} } \right]\quad a_{ij} = \left\{ {\begin{array}{*{20}c} {y_{i + 2} - y_{i + 1} } & {{\text{j}} = {\text{i}} - 1} \\ {y_{i} - y_{i + 2} } & {{\text{j}} = {\text{i}}} \\ {y_{i + 1} - y_{i} } & {{\text{j}} = {\text{i}} + 1} \\ \end{array} } \right. \hfill \\ \end{gathered} $$
    (6)

    where \(y_{i}\) and \(z_{i}\) are the lateral and vertical coordinates of each design point of the left rail, respectively; \(z_{A}\) and \(z_{B}\) are the vertical coordinates of the two fixed points of the left rail.

    In the multipoint approximation method, the constraint equations are formulated algebraically as

    $$ F_{i} (X) = K_{L} \cdot Z_{L} - b_{L} + 1 < 1 $$
    (7)
  2. (2)

    Continuous boundary slope.

    This condition is realized in the rail profile connection, which is smoothed using nonuniform rational B-splines (NURBS) to ensure slope continuity.

  3. (3)

    Grinding restriction.

    In practical applications, this is not necessarily a new rail profile design constraint. Sometimes it is necessary to fulfill grinding restrictions in the actual profile, which is reflected in the constraint boundary conditions.

    $$ A_{j} = X_{0} - D_{g} = \left[ {z_{10} - d_{g1} ,z_{20} - d_{g2} , \ldots ,z_{{N_{{{\text{mov}}}} 0}} - d_{{gN_{{{\text{mov}}}} }} } \right] $$
    (8)
    $$ B_{j} = X_{0} = \left[ {z_{10} ,z_{20} , \ldots ,z_{{N_{{{\text{mov}}}} 0}} } \right] $$
    (9)

    where \(D_{g} = \left[ {d_{g1} ,d_{g2} , \ldots ,d_{{gN_{{{\text{mov}}}} }} } \right]\) is the grinding limit vector and \(d_{gi}\) is the maximum grinding depth of each point.

3.1.3 Objective function

It is clear from the previous analysis that the distribution of rail contact points directly expresses the wheel–rail contact relationship. A proper distribution can improve the stability and comfort of train operation and reduce contact stress and rail wear. The objective function proposed is therefore based on the contact point distribution curve, and the rail profile with a predetermined wheel–rail matching relationship is solved in reverse according to a given objective. The target distribution curve designed should ensure that the wheel–rail contact point distribution is continuous and able to provide sufficient curve passing capacity, while the practicalities of matching the wear wheel profile can be taken into account.

The objective function is to minimize the difference between the target rail contact point location distribution curve and the calculated curve in the optimization process. The formula is as follows:

$$ \begin{gathered} \min \, F_{o} \left( Z \right) = a_{1} \frac{{\sum\nolimits_{i = 1}^{N} {\left( {\Delta CPL_{t} \left( {y_{wi} } \right) - \Delta CPL_{c} \left( {Z,y_{wi} } \right)} \right)^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {\Delta CPL_{t} \left( {y_{wi} } \right)} \right)^{2} } }} \hfill \\ \, + a_{2} \frac{{\sum\nolimits_{i = 1}^{N} {\left( {\Delta CPR_{t} \left( {y_{wi} } \right) - \Delta CPR_{c} \left( {Z,y_{wi} } \right)} \right)^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {\Delta CPR_{t} \left( {y_{wi} } \right)} \right)^{2} } }} \hfill \\ \end{gathered} $$
(10)

where \(\Delta CPL_{t}\) and \(\Delta CPR_{t}\) are the distribution curves of the contact points of the target rails on the left and right sides, respectively;

\(\Delta CPL_{c}\) and \(\Delta CPR_{c}\) are calculated curves according to the optimized profile;

\(Z\) is the design variable;

\(y_{w}\) is the lateral displacement of the wheelset;

\(N\) is the number of traverse calculation points;

\(a_{1}\) and \(a_{2}\) are the weight coefficients.

The weight coefficients of the left and right contact points are set here, and different weight ratios can also be set according to the importance of different lateral displacements to meet the needs of an actual operation.

3.1.4 Optimization method

After completing the above steps, a general optimization problem in the form of formula (1) can be formed according to the objective function, constraint equation, and boundary conditions. With the purpose of solving this optimization problem, the multipoint approximate optimization method is used (Markine et al. 2007; Yan et al. 2014). The essence of this method is to continuously replace the original optimization problem with an approximation function, forming one simple optimization problem after another. During the k-th iteration, the above optimization problem can be transformed into

$$ {\text{Minimize}} \; \tilde{F}_{0}^{k} (X) \to \min ,X \in R^{N} $$
(11)
$$ {\text{subject to}} \; \tilde{F}_{i}^{k} (X) \le 1\quad \left( {i = 1, \cdots ,N_{0} } \right) $$
(12)
$$ {\text{and}} \; A_{j}^{k} \le X_{j}^{k} \le B_{j}^{k} \left( {j = 1, \cdots ,N_{mov} } \right) \, \begin{array}{*{20}l} {A_{j} \le A_{j}^{k} ,B_{j} \le B_{j}^{k} } \hfill \\ \end{array} $$
(13)

where the superscript k is the number of iteration steps, \(\tilde{F}_{i}^{k}\) is the approximation of the original function \(\begin{array}{*{20}l} {F_{i} } \hfill \\ \end{array}\), and \(A_{j}^{k}\) and \(B_{j}^{k}\) are move limits defining the approximation applicability range.

In this case, the approximation function is replaced by a linear equation such that each optimization step solves a linear optimization problem, and the calculation speed is further improved.

$$ \tilde{F}(Z) = a_{0} + \sum\limits_{j = 1}^{{N_{{\text{mov }}} }} {a_{j} x_{j} } \left( {j = 1, \cdots ,N_{{\text{mov }}} } \right) $$
(14)

where \(a_{j}\) is a tuning parameter.

Depending on the optimal solution at each iteration step in the optimization process, the size and position of the search subregion must be continuously adjusted to ensure the validity of the approximation equation. Each search subregion is determined using the following:

$$ h_{j}^{k} = \left( {B_{j}^{k} - A_{j}^{k} } \right)H_{m} {\text{sgn}} \left( {X_{{*_{j} }}^{k} - X_{{*_{j} }}^{k - 1} } \right)\left( {j = 1, \cdots ,N_{{\text{mov }}} } \right) $$
(15)
$$ \left\{ {\begin{array}{*{20}c} {A_{j}^{k + 1} = X_{{*_{j} }}^{k} - \lambda \left| {h_{j}^{k} } \right|} \\ {B_{j}^{k + 1} = X_{{*_{j} }}^{k} + \mu \left| {h_{j}^{k} } \right|} \\ \end{array} } \right. $$
(16)

where \(A_{j}^{k + 1}\) and \(B_{j}^{k + 1}\) are the constraint boundaries for the next step; \(X_{*}^{k}\) is the most recent optimal solution; \(X_{*}^{k - 1}\) is the previous optimal solution; \(\left( {X_{*}^{k} - X_{*}^{k - 1} } \right)\) determines the direction of search subregion change; and \(h_{j}^{k}\) is the moving step size of the design variable, which can be determined according to the two adjacent optimal solutions and the relative moving step size. If \(h_{j}^{k} < 0\),\(\lambda { = }1.6\) and \(\mu = 0.5\); if \(h_{j}^{k} > 0\), \(\lambda { = }0.5\) and \(\mu = 1.6\) in formula (16).

The termination condition is

$$ e^{k} = \sum\limits_{i = 1}^{K} {\left( {\Delta CP_{t} \left( {y_{{{\text{w}}i}} } \right) - \Delta CP_{c} \left( {X,y_{{{\text{w}}i}} } \right)} \right)^{2} } = 0,{\text{ or }}X_{*}^{k - 4} = \cdots = X_{*}^{k} $$
(17)

where \(\Delta CP_{c}\) and \(\Delta CP_{t}\) are the current calculated and target values of the objective function CPL/CPR.

3.1.5 Design procedure

Figure 3 shows the complete flowchart of the rail profile design procedure implemented using MATLAB software. The optimized procedure includes the following steps.

Fig. 3
figure 3

Flowchart of rail profile design procedure

Full size image

First, the measured profile is processed to obtain the determined wheelset profile and the original rail profile to be optimized. Then, the original wheel–rail contact relationship is determined based on the track line method (Wang 1984). The area of the rail to be optimized is obtained by analyzing the dynamic response of the corresponding line based on the established three-dimensional vehicle–track mode.

Next, the CPL or CPR curve is designed in the optimization region, and the objective function is generated from it. The design variables and constraints are obtained by selecting appropriate design points in the region.

The optimized rail profile is calculated according to the designed objective function by applying the multipoint approximate optimization method. If the termination conditions are not satisfied, the search subregion is varied, and the optimization process is repeated so that it forms a closed-loop process until an optimized pair of rail profiles is obtained. Next, it is necessary to determine whether the error in the target curve is satisfied, and if not, return to modify the initial CPL or CPR curve until the error is respected. In this process, a variety of design schemes can also be provided for comparison in combination with different target CPL/CPR curves and design points.

Finally, the optimized rail profile is imported into the three-dimensional vehicle–track model and simulated by applying an actual line to evaluate the wheel–rail contact relationship before and after optimization to determine whether it is acceptable as the final result.

3.2 Evaluation indicators

The evaluation criteria are mainly divided into static evaluation and dynamic evaluation criteria. Among them, the contact stress is closely related to rail wear, which is our key indicator. The calculation of wheel–rail contact stress often involves a laborious process. This study presents a method for evaluating static contact stress based on the average undeformed gap between the wheel and rail. As shown in Fig. 4, once the location of the wheel–rail contact point is determined, the area around the contact point is selected to calculate the average distance:

$$ p_{s} (y_{w} ) = \frac{{\sum\nolimits_{j = 1}^{m} {\left| {z_{w}^{(j)} \left( {y_{w} } \right) - z_{r}^{(j)} \left( {y_{w} } \right)} \right|} }}{m}, $$
(18)

where m is the number of profile description points within the scope of 10 mm from the lateral coordinates of the contact points. \(z_{w}^{(j)}\)、\(z_{r}^{(j)}\) are the spatial positions of the wheelset and rail at the j-th point within this range, respectively. Notably, the static contact stress here refers to the average distance between the wheel and rail, so the unit is millimeters (mm) rather than pascals (Pa).

Fig. 4
figure 4

Static contact stress based on contact clearance

Full size image

The dynamic contact stress refers to the force per unit area on the contact surface, which is based on complex wheel–rail contact theories. It is adopted from Kalker’s non-Hertzian contact theory based on virtual interpenetration (Piotrowski and Kik 2008). The normal compression is extracted throughout the vehicle–track coupling simulation to determine the virtual interpenetration area of the surface. The contact patch shape is then corrected according to the KP method to obtain the corrected virtual penetration area, which leads to the calculation of the normal contact pressure at the contact origin.

In the dynamic response, some conventional indicators, such as wheelset lateral displacement, vehicle acceleration, and wheel–rail force, are also included to evaluate the wheel–rail optimization performance.

4 Numerical examples

4.1 Pre-grinding design for new profile

Two design examples are given here to illustrate the feasibility of this rail optimization method. The first case is the pre-grinding design for a new rail profile. A combination of LM and CN60 (gauge: 1435 mm, rail cant: 1/40) is selected here. The original wheel–rail contact relationship is shown in Fig. 5.

Fig. 5
figure 5

Wheel–rail contact relationship of original profile: a Left rail b Right rail

Full size image

As stated in the previous rail contact position distribution curve (CPL and CPR) discussion, a suitable target curve is conducive to finding the optimal contact state between the rigid wheelset and rail. The setting principles of the contact point curve primarily include the following:

  1. (1)

    The rail contact positions are distributed as evenly as possible under the calculated lateral displacement to maintain great operational stability;

  2. (2)

    In consideration of the wear demand, the rail contact position should have as wide a distribution range as possible to minimize the wear;

  3. (3)

    The lateral spacing of the contact points should be adjusted appropriately in response to changes in the grinding angle.

The design of the new rail requires consideration of universality under various conditions. The new rail needs to meet not only the stability of the straight runs but also the smooth transitions on curves; thus, the following design principles are proposed for the pre-sanding design of the new rails to ensure efficient operation on straight and curve:

  1. (1)

    Rail contact in areas with small lateral displacement should be evenly distributed in a small range to maintain stability on a straight track.

  2. (2)

    Rail contact in areas with medium lateral displacement should be evenly distributed and connected as smoothly as possible to reduce the impact of the train on the track during the transition from straight to curve.

  3. (3)

    Rail contact in areas with large lateral displacement should be as close to the gauge angle as possible so that the wheels have a large rolling circle to pass through the curve.

To improve the train passing performance and reduce rail wear, the original CPR function needs to be modified. Several control points on the curve are chosen here to achieve this objective by linear fitting, as shown in Fig. 6. The rail profile is designed using the proposed rail optimization method, and the corresponding optimized rail profile is shown in Fig. 7.

Fig. 6
figure 6

Contact position distribution curve

Full size image
Fig. 7
figure 7

Comparison between original and optimized profile

Full size image

Figures 8 and 9 show the validation results of the CPR function and the new contact distribution of the design profile. The overall difference between the target CPR and the calculated CPR is small. Compared to the original contact relationship, the uneven contact distribution has been eliminated, and the rail contact points are more evenly distributed over the entire contact range, in line with the design principles presented above.

Fig. 8
figure 8

Contact position distribution curve of optimized profile

Full size image
Fig. 9
figure 9

Wheel–rail contact relationship of optimized profile: a Left rail b Right rail

Full size image

Figures 10 and 11 show the comparison of the rolling circle radius difference and the right wheel contact point clearance before and after the design, respectively. It can be seen that the target design of the contact point distribution has improved the RRD performance even though there is no direct control of the wheelset operating capability. The optimized RRD is straighter in the straight line, and the steps in the curve have been eliminated, resulting in a smoother RRD curve.

Fig. 10
figure 10

Rolling circle radius differences comparison

Full size image
Fig. 11
figure 11

Static contact stress comparison

Full size image

The static contact stress is expressed by the wheel–rail contact point clearance. In terms of wear, the optimized profile shows a reduction in contact point clearance over most of the moving range. This increases the commonality between the wheelset and the rail to better control the local stress concentration and improve the service life of the rail. Moreover, the distribution on the wheelset is also more uniform, which also helps to reduce wheelset wear.

4.2 Asymmetric design in curve

4.2.1 General information

The previous case illustrates that this design method greatly improves the symmetrical profile design. However, in practice, asymmetrical rail profile design problems arise frequently. It is necessary to optimize the design of the rails according to actual lines, vehicle parameters, wheelset profiles, etc., to improve the train dynamic performance and reduce rail wear.

This case provides an example encountered in actual operation. In the subway of a city, a rail was severely deformed after long periods of wear and tear, and a targeted rail profile design was carried out. To this end, the profiles of the whole line were collected and designed by applying the method in this paper. Here, the design of only one curve is demonstrated. The working condition in this case is a curve (radius of 700 m, length of 300 m, transition curve of 60 m, superelevation of 120 mm, and operating speed of 80 km/h) where there is widening of the gauge.

The profile was measured by the MiniProf instrument. According to the lathing records, the wheel profile of the train in different seasons was measured. At 0 to 3 months, 4 to 6 months, and 7 to 9 months after wheel turning, 2–3 trains for each period were selected for a total of 7 wagons with 24 wheelsets each, and the left and right profiles were measured. There are 11 measurement points for the rail, including 4 points on transition curves at both ends and 7 points on circular curves. The profile measurement contains the rail inclination information. The collected rail and wheel profiles are determined by the averaging method. The field diagram of information collection is shown in Fig. 12.

Fig. 12
figure 12

Information collection: a Wheel information b Rail information

Full size image

4.2.2 Optimization region

In this paper, a three-dimensional vehicle–track dynamics model is established, as shown in Fig. 13. A metro vehicle is chosen, the vehicle model is considered a multi-rigid body system, and the body, bogie, and wheelset structures are simplified to rigid bodies. The vehicle structures are connected by primary and secondary suspensions simplified as springs and damping elements. The rail is simplified as a continuous Euler beam on the basis of discrete elastic point support, considering its lateral, vertical, and torsional vibrations. Hertz linear contact theory is used to solve for the wheel–rail normal force, and the tangential creep force is solved using Shen-Hedrick-Elkins theory. A two-step numerical integration method was used to solve the vehicle–track dynamic equations (Gao et al. 2019), and model validation was completed by comparison with the results of SIMPACK (Shi et al. 2021).

Fig. 13
figure 13

Vehicle–track dynamics model

Full size image

Applying the established vehicle–track dynamics model, the actual line information and the measured urban rail irregularity with a sampling interval of 0.25 m are substituted, which is superimposed on the shortwave component. Figure 14 shows the lateral displacement of the four wheelsets obtained from the simulation. It can be seen from the figure that in the curved section, the lateral displacement of the first and third wheelsets is between 8 and 14 mm, and the second and fourth wheelsets move between 2 and 8 mm. Therefore, the rail profile is optimized with a focus on 2 to 14 mm, and the scope is expanded to − 10 to 20 mm in the optimization process.

Fig. 14
figure 14

Lateral displacement of original profile

Full size image

4.2.3 Optimized design and process

The static original profile of wheel–rail contact relationship is obtained in the optimization area of the previous section, as shown in Fig. 15. The red line segment between the wheel and rail is the primary contact point, and the green and blue line segments are the second and third points of contact, respectively.

Fig. 15
figure 15

Wheel–rail contact relationship of original profile: a Left rail b Right rail

Full size image

The left rail has severe vertical wear in the central zone, and the wheel–rail contact relationship is divided into two contact areas near the 0 lateral displacement due to long-term wear, and multipoint contact occurs during the intermediate jump. Although the effective contact range calculated above is 2–14 mm, it should be noted that the dynamic simulation is only one possible scenario for mimicry. In actual operation, it may be easy to run to the contact area where the lateral displacement is less than 0 due to the influence of other external environments, such as excessive irregularities and track slab offset, which have a significant effect on the running performance. In addition, because the contact relationship with 2–20 mm is too concentrated on the nonworking side, it is true that running only on this part does not have an obvious impact on performance but is not conducive to rail wear and maintenance, which is why the rail top gradually wears, so that the contact position is divided into two areas.

The right rail wear is not very obvious just after the rail change. However, the contact relationship of the working side is relatively discrete, and there is a locally uneven distribution. In particular, there are multiple points of contact within the range of 2 ~ 8 mm of lateral displacement, and there are three contact points at 7 mm, which will cause a very negative impact on traffic.

To this end, the optimized objective function is developed for the rail profile in this curved section. The principle of determining the objective function satisfies the previously mentioned requirements. A larger range of uniform distribution is used for the positions 5–15 mm in the curve section, and a smaller range of uniform distribution is used for the other positions. The left contact position keeps the contact region generally at the gauge angle position, so there is a large gap in the CPL of the original left rail. The CPR is adjusted to use a relatively small contact interval of 60 degrees, where the influence of the grinding angle is taken into account.

The contact point distribution curves before and after optimization are shown in Fig. 16. The overall difference between the calculated curve and the target curve is small, meeting the optimization goal set before design. Figure 17 shows the profile comparison before and after optimization.

Fig. 16
figure 16

Contact position distribution curve: a CPL curve b CPR curve

Full size image
Fig. 17
figure 17

Comparison between original and optimized profile: a Left rail b Right rail

Full size image

4.2.4 Static comparison

First, the wheel–rail contact performance before and after optimization is analyzed from the static point of view.

Figure 18 shows the contact distribution of the optimized new profile. Compared with the original profile, the contact points are more evenly distributed throughout the contact region, and the uneven contact distribution has been eliminated. The main contact positions are located near the working edge and the gauge angle, and the large radius of curvature of this part of the profile effectively reduces the contact pressure. The original issues of jumping and multipoint contact have been eliminated, effectively reducing the likelihood of vehicle shaking. At the same time, with the homogeneity of the rail contact points, the wheelset contact points are also more evenly distributed along the contact region, which reduces wheel wear.

Fig. 18
figure 18

Wheel–rail contact relationship of optimized profile: a Left rail b Right rail

Full size image

Figures 19 and 20 show the difference in the rolling circle radius and static contact stress before and after optimization, where only the first point of contact is calculated for multipoint contacts. In the asymmetric optimized design of the curve, the optimized RRD curve is smoother, and steps are eliminated in the contact range. As shown in Fig. 20, the contact clearance of the optimized profile is reduced in most of the lateral displacement range, which increases the commonality between the wheelset and rail, thus playing a better control role in local stress concentration and improving rail life. A good correspondence is noticed in Fig. 16, where the contact stresses are higher in the parts with a smaller distribution of contact points. It is worth noting that the static contact stress in the right-hand rail at 13–15 mm is larger than in the original, which is due to the smaller region of adjusted contact points and the manifest jump in the original contact points.

Fig. 19
figure 19

Rolling circle radius differences comparison

Full size image
Fig. 20
figure 20

Static contact stress comparison: a Left rail b Right rail

Full size image

4.2.5 Dynamic performance comparison

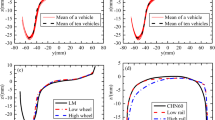
The optimized profile is substituted into the dynamic model to obtain the new response. The performance of the kinetic index is shown in Figs. 21, 22, 23, and the peak response is listed in Table 1.

Fig. 21
figure 21

Comparison of lateral displacement between original and optimized profile

Full size image
Fig. 22
figure 22

Comparison of lateral force of axle between original and optimized profile

Full size image
Fig. 23
figure 23

Mean value of dynamic contact stress comparison: a Left rail b Right rail

Full size image
Table 1 Peak dynamic response comparison
Full size table

Figure 21 shows a comparison of the lateral displacement for the front bogie before and after optimization. There is no significant difference in the position of the lateral displacement within the original key design contact range (5 ~ 15 mm). However, under constant irregularity, the range of the wheelset running on the rail is relatively reduced, indicating that the stability of the wheelset has been improved. The results for the rear bogie are similar to those for the front bogie and will not be further discussed here.

There is a significant reduction in the dynamic response from Table 1. In particular, the optimized profile performs better in terms of lateral forces on the axle (Fig. 22). This is related to the reduction in the range of the lateral displacement and the uniform distribution of the contact area, which reduces the motion impact of the wheelset in the lateral direction and increases the lateral stability.

Figure 23 shows the comparison of the dynamic contact stresses, from which it can be seen that there are obvious differences in the wheel–rail contact stresses between the original and optimized profiles. When the optimized profile is adopted, the wheel–rail contact stresses are significantly reduced, with a 22.33% reduction in the right-hand wheel of the second wheelset. Overall, the optimized profile effectively increases the contact area and reduces the contact stress by increasing the conformality of the wheel–rail profile, which reduces wear and contact fatigue damage and increases the service life of the wheel and rail.

4.2.6 Wear prediction

Applying Kalker’s non-Hertz contact theory based on virtual interpenetration (Piotrowski and Kik 2008), the local contact properties of a wheel–rail system can be obtained, including the contact range and contact force in all directions. Archard’s wear model (Li et al. 2011) is used in calculating the wear of a rail:

$$ V_{w} = K\frac{NS}{H}, $$
(19)

where Vw is the wear of the contact unit, H is the hardness of the worn material, K is the wear coefficient, N is the normal pressure, and S is the sliding distance of the element.

For rail profiles with wear, it is specified that the rail profile needs to be updated when the maximum wear depth reaches 0.1 mm. The rail profile is smoothed using the NURBS spline function for the calculated section.

Figure 24 shows the wear distribution of the original profile and the optimized profile after three updates. As seen from the figure, the wear of the rail along the circular curve is significantly greater than at the other positions. The calculated rail light band is basically flat and parallel to the longitudinal direction of the rail, but the wear depth is unevenly distributed along the longitudinal direction of the rail. The contact range of the original profile at the contact position of the left rail is small, the light band is narrow, and there is large local wear, while the light band of the optimized profile is wide, indicating that the wear is relatively scattered and evenly distributed. Although the original profile has a wide distribution along the right rail contact region, there is also obvious local wear caused by stress concentration, which is not conducive to the long-term development of wear, while the scope of the optimized profile wear area is slightly increased, which greatly reduces the development of wear depth.

Fig. 24
figure 24

Wear prediction results after 3rd iteration: a left rail of original profile b right rail of original profile c left rail of optimized profile d right rail of optimized profile

Full size image

The cumulative number of passing vehicles with different update times is shown in Fig. 25. The cumulative number of vehicles passing the optimized rail profile is significantly greater than that of the original rail profile at all renewal stages. After the 1st iteration and the 10th iteration, the cumulative number of vehicles passing through increased by 41% and 27%, respectively, compared with the original profile. This shows that the optimized rail profile effectively reduces the rail wear rate in the curved section.

Fig. 25
figure 25

Number of vehicles with different update times

Full size image

5 Conclusions

To address the issues of adjacent contact point jumping and local contact point stress concentration in existing rail profile optimization with rolling radius difference (RRD) as the objective, an inverse design method targeting the distribution of contact points (CPL/CPR) is proposed. The design procedure adopts a multipoint approximate optimization method, and complete code is implemented in MATLAB.

  1. (1)

    The ideal rail profile is obtained by setting the CPL/CPR curve in advance. This method optimizes the contact distribution of the rails, eliminates the multipoint contact of the original profile, optimizes the dynamic performance of the vehicle in real operating scenarios, and reduces the wear of the rails and wheels. The effectiveness and efficiency of this design procedure have been demonstrated through the application of two design examples.

  2. (2)

    The profile optimization method proposed features a more comprehensive objective function compared to other single-objective solving methods. It exhibits superior computational efficiency compared to multi-objective optimization methods with more complex requirements. Additionally, the adoption of a multipoint approximation optimization method, which aligns with the profile design progress of multiple control points, further enhances its calculation efficiency and accuracy.

  3. (3)

    Although there is no direct control over the running performance of the wheelset and the wheel–rail wear, the RRD curve and stress reduction are still improved by the design of the CPL/CPR curve. The RRD of the optimized profile is smoother, and steps are eliminated. This achieves the goal of reducing wear and is more convenient and efficient compared to multi-objective optimization methods that include wear optimization.

The grinding work discussed in Sect. 4.2 has already been started on the whole line. We look forward to the subsequent analysis of the results as a means of verifying the feasibility of the proposed design approach.