1 Introduction

The curve radius of a typical metro line is small, and it is very common for metro vehicles to accelerate and brake frequently during operation (Arizon et al. 2007). Consequently, the wheel and rail profile shapes are affected by wheel–rail wear, which can greatly influence the geometrical characteristics of the contacts between wheels and rails. Several important factors, such as the dynamic behavior of vehicle-track systems as well as their safety and ride comfort (Jin and Ahmadian 2012), are affected by the geometrical shapes of the wheel and rail profiles and their contact region characteristics.

The LM wheel profile and profile of Chinese 60 kg/m rail (LM&CHN60) used in Chinese metro systems work well together when they are new. However, both the wheels and rails wear over time; hollow wear and flange wear are the main wear types for wheels (Huang et al. 2013), whereas side wear of the rails on curves is a normal phenomenon in metro systems. The worn profiles may result in worse wheel–rail interaction, which can lead to abnormal vehicle vibrations and have a significant influence on the development of wheel–rail wear. Compatible wheel and rail profiles can ensure appropriate creep forces for negotiating a curve (Li et al. 2011; Jahed et al. 2008). To determine the optimal combinations of wheel and rail profiles, various approaches have been developed to design profiles that achieve satisfactory matching between wheels and rails. Heller and Harry (1979) presented a procedure for designing wheel profiles by analyzing the vehicle performance for the initial profile and systematically adjusting the profile until certain dynamic performance and wear tendency objectives are met or a satisfactory compromise is reached. Leary et al. (1991) proposed an approach based on the average worn wheel or expansions of rail shapes that ensure single-point contact for designing custom wheel profiles to optimize their performance characteristics. Choromański and Zboiński (1992) presented a method based on a window function defined on the basis of the Chebyshev series for optimizing wheel profiles. This method accounts for the nonlinear theory of wheel–rail contact, including two-point contact, and considers the dynamic properties of railway vehicles and wheel–rail life. Magel and Kalousek (2002) developed a pummeling model for optimizing rail profiles by quantifying the contact performance with a large number of measured new and worn wheels. Shen et al. (2003) developed a unique method for designing railway wheel profiles to be compatible with a typical rail profile by employing the contact angles as the optimization target. Persson and Iwnicki (2004) presented a method for the design of wheel profiles for railway vehicles using a genetic algorithm, in which a penalty index was calculated to evaluate the offspring profiles. Shevtsov et al. (2005, 2008) and Markine et al. (2007) presented an inverse shape design method for adjusting the shape of a wheel profile based on a given rolling radius difference (RRD) function and a given rail profile to improve the dynamic performance of a metro system suffering from severe wheel–rail wear. Cui et al. (2009) proposed an optimization method for the design of a rail profile based on the normal gap between the wheel and rail. The optimized rail profile, which achieves good conformal contact with the LM wheel profile, significantly reduces the wheel–rail contact stress without sacrificing dynamic performance. Polach (2011) proposed a method for profile design with a given target conicity that is suitable for vehicles running on straight tracks. Mao and Shen (2018) presented an inverse design method for designing rail grinding profiles with a target RRD and contact distribution.

The aforementioned studies have shown the development of profile optimization methods from field experience to attractive approaches applied in computer-based development environments. Benefiting from the development of optimization methods, the limitations on the profile forms are eliminated. However, previous research has typically focused on wheel profile optimization and related vehicle dynamic behavior on tangent tracks. Only a few studies have considered the influence of the worn wheel (rail) profile on rail (wheel) profile optimization and verified the optimized profile wear. Therefore, the optimization design target combined with dynamic behavior and wear prediction on a specific line cannot be directly reflected.

In fact, poor matching between wheel and rail profiles caused by wear often occurs on curves of a metro line, and wheel–rail contact regions on the low and high rails on a curve are typically different. Meanwhile, wheel–rail surface wear is a function of sliding and contact stresses on the contact patch (Piotrowski and Chollet 2005) and is influenced by the curve parameters and type of track. In view of this, this study establishes a comprehensive optimization system that includes a coupled vehicle-track model with different types of curved tracks, an inverse shape design method, and a wear model. Based on the comprehensive optimization system, the profile design procedure is developed to optimize the rail profiles to match the worn wheel profiles. Moreover, low and high rail profiles are optimized simultaneously with different optimized regions. Through the evaluation of dynamic performance and the verification of wear on a specific curve, the optimum rail profiles for given worn wheel profiles are determined to ensure the optimization effect in practical application.

To obtain an optimum pair of rail profiles for the given worn wheel profiles on a specific curve, the vehicle-track dynamic behavior and wheel–rail contact geometry characteristics of worn wheel and rail profiles (WW&WR) and LM&CHN60 are evaluated by a three-dimensional vehicle-track coupled model. The coupled model is established considering the structural characteristics of metro. Then, an inverse design method is developed for rail profile optimization with an asymmetrical design of low and high rails to improve the wheel–rail contact properties. Several pairs of optimized rail profiles are obtained in terms of the optimization method under different design schemes. Finally, the material loss due to wear is calculated to evaluate the optimized rail profiles to choose the optimum rail profiles with two types of track, namely, a steel spring floating slab track and a nonballasted track on a solid bed, for a specific curve. A comparison of the dynamic behaviors of worn and optimum rail profiles is discussed to further demonstrate the effects.

2 Analysis of LM&CHN60 and WW&WR

2.1 General information

The given worn wheel profiles are taken as the mean of the measured profiles from 10 operating vehicles, as shown in Fig. 1a, b. Comparisons between the LM&CHN60 profiles and the WW&WR profiles are shown in Fig. 1c, d. The worn rail profiles were measured on a curve of a Beijing metro, as shown in Fig. 2, while the CHN60 profile has a cant of 1/40. Hollow wear was observed on the wheel treads and flanges, while severe side wear had occurred on the high rail. The worn wheel tread with increased curvature is obviously inappropriate for the worn rail. To obtain more compatible rail profiles for the worn wheel profiles, a three-dimensional coupled vehicle-track model is established in view of the structural characteristics of metro to analyze the dynamic properties of the vehicle-track system with LM&CHN60 and WW&WR, respectively.

Fig. 1
figure 1

Worn and unworn wheel and rail profiles: a mean of the low wheel profiles, b mean of the high wheel profiles, c wheel profiles, and d rail profiles

Full size image
Fig. 2
figure 2

Images of rail profile measurements on a curve: a low rail and b high rail

Full size image

2.2 Three-dimensional coupled vehicle-track model of metro

2.2.1 Vehicle model

A vehicle passing over a curved track is illustrated in Fig. 3. The vehicle is modeled as a rigid multibody system with 35 degrees of freedom (Zhang et al. 2008). Each component of the vehicle has five degrees of freedom, namely, lateral displacement, vertical displacement, roll angle, pitch angle, and yaw angle. The structural elastic deformation of the vehicle components is neglected. The vehicle model considered here consists of a pair of two-axle bogies with double suspension systems.

Fig. 3
figure 3

The coupled vehicle-track model: a the vehicle passing over a curved track, b elevation of the vehicle model, and c side elevation of the vehicle model

Full size image

The car body and the bogies are connected by the secondary suspension, while the bogie is supported on the wheelsets through the primary suspension. Relative to the running direction, the front and rear bogies are numbered 1 and 2, respectively. Similarly, the front and rear wheelsets of the front bogie are numbered 1 and 2, respectively, while the front and rear wheelsets of the rear bogie are numbered 3 and 4, respectively. The equations of motion for the vehicle are expressed as follows:

$$ {\displaystyle \begin{array}{c}\left[\begin{array}{ccc}{\mathbf{M}}^{\mathrm{c}\mathrm{c}}& & \\ {}& {\mathbf{M}}^{\mathrm{t}\mathrm{t}}& \\ {}& & {\mathbf{M}}^{\mathrm{w}\mathrm{w}}\end{array}\right]\left(\begin{array}{c}{\ddot{\mathbf{u}}}^{\mathrm{c}}\\ {}{\ddot{\mathbf{u}}}^{\mathrm{t}}\\ {}{\ddot{\mathbf{u}}}^{\mathrm{w}}\end{array}\right)+\left[\begin{array}{ccc}{\mathbf{C}}^{\mathrm{c}\mathrm{c}}& {\mathbf{C}}^{\mathrm{c}\mathrm{t}}& \\ {}{\mathbf{C}}^{\mathrm{t}\mathrm{c}}& {\mathbf{C}}^{\mathrm{t}\mathrm{t}}& {\mathbf{C}}^{\mathrm{t}\mathrm{w}}\\ {}& {\mathbf{C}}^{\mathrm{w}\mathrm{t}}& {\mathbf{C}}^{\mathrm{w}\mathrm{w}}\end{array}\right]\left(\begin{array}{c}{\dot{\mathbf{u}}}^{\mathrm{c}}\\ {}{\dot{\mathbf{u}}}^{\mathrm{t}}\\ {}{\dot{\mathbf{u}}}^{\mathrm{w}}\end{array}\right)\\ {}+\left[\begin{array}{ccc}{\mathbf{K}}^{\mathrm{c}\mathrm{c}}& {\mathbf{K}}^{\mathrm{c}\mathrm{t}}& \\ {}{\mathbf{K}}^{\mathrm{t}\mathrm{c}}& {\mathbf{K}}^{\mathrm{t}\mathrm{t}}& {\mathbf{K}}^{\mathrm{t}\mathrm{w}}\\ {}& {\mathbf{K}}^{\mathrm{w}\mathrm{t}}& {\mathbf{K}}^{\mathrm{w}\mathrm{w}}\end{array}\right]\left(\begin{array}{c}{\mathbf{u}}^{\mathrm{c}}\\ {}{\mathbf{u}}^{\mathrm{t}}\\ {}{\mathbf{u}}^{\mathrm{w}}\end{array}\right)={\mathbf{F}}_{\mathrm{g}}+{\mathbf{F}}_{\mathrm{c}}+{\mathbf{F}}_{\mathrm{d}}+{\mathbf{F}}_{\mathrm{q}}\end{array}} $$
(1)

where M, C, and K denote the mass, damping, and stiffness sub-matrices, respectively, \( \ddot{u} \), \( \dot{u} \) and u denote the acceleration, velocity and displacement sub-vectors, respectively; Fg denotes the gravity component vector; Fq denotes the wheel–rail contact force vector; and the superscripts “c,” “t,” and “w” denote car body, bogie and wheelset, respectively. Fc = (Fcc Fct1 Fct2 Fcw1 Fcw2 Fcw3 Fcw4) is the additional force caused by the centrifugal effect when the vehicle passes the curve. \( {F}_d=\left({F}_{dc}\kern0.5em {F}_{dt1}\kern0.5em {F}_{dt2}\kern0.5em {F}_{dw1}\kern0.5em {F}_{dw2}\kern0.5em {F}_{dw3}\kern0.5em {F}_{dw4}\right) \) is the additional force generated by the geometric eccentricity of the component on the curve.

2.2.2 Track model

The three-dimensional slab track submodels, as illustrated in Fig. 4, represent two most commonly used slab track structures in metro systems, namely, a steel spring floating slab track (Fig. 4b) and a nonballasted track on a solid bed (Fig. 4c), consisting of rails, fasteners, track slabs, and the subground. Additionally, a shear spring and a bending spring are installed at the ends of two adjacent slabs as dowel joints to reduce the slab discontinuity, as shown in Fig. 4a.

Fig. 4
figure 4

The three-dimensional slab track model: a model of a slab track, b model of a steel spring floating slab track, and c model of a nonballasted track on a solid bed

Full size image

Both the low and high rails are modeled as continuous Bernoulli–Euler beams that are discretely supported on the track slabs by springs and dampers, representing the elasticity and damping of the fasteners (Zhai et al. 2009). The considered vibrations of each rail are vertical, lateral and torsional. The equations of motion for each rail (on the low side and high side) can be written in the form of fourth-order partial differential equations, as shown below.

For the vertical direction:

$$ {\displaystyle \begin{array}{l}{EI}_y\frac{\partial^4{Z}_{\mathrm{r}}\left(x,t\right)}{\partial {x}^4}+{m}_{\mathrm{r}}\frac{\partial^2{Z}_{\mathrm{r}}\left(x,t\right)}{\partial {t}^2}=\\ {}-\sum \limits_{i=1}^{N_{\mathrm{V}}}{F}_{\mathrm{V}i}(t)\delta \left(x-{x}_i\right)+\sum \limits_{j=1}^4{P}_j(t)\delta \left(x-{x}_{\mathrm{w}i}\right)\end{array}} $$
(2)

For the lateral direction:

$$ {\displaystyle \begin{array}{l}{EI}_z\frac{\partial^4{Y}_{\mathrm{r}}\left(x,t\right)}{\partial {x}^4}+{m}_{\mathrm{r}}\frac{\partial^2{Y}_{\mathrm{r}}\left(x,t\right)}{\partial {t}^2}=\\ {}-\sum \limits_{i=1}^{N_{\mathrm{L}}}{F}_{\mathrm{L}i}(t)\delta \left(x-{x}_i\right)+\sum \limits_{j=1}^4{Q}_j(t)\delta \left(x-{x}_{\mathrm{w}i}\right)\end{array}} $$
(3)

For the torsional direction:

$$ {\displaystyle \begin{array}{l}\mathrm{GK}\frac{\partial^2{\phi}_{\mathrm{r}}\left(x,t\right)}{\partial {x}^2}+{\rho}_{\mathrm{r}}{I}_0\frac{\partial^2{\phi}_{\mathrm{r}}\left(x,t\right)}{\partial {t}^2}=\\ {}-\sum \limits_{i=1}^{N_{\mathrm{T}}}{M}_{\mathrm{s}i}(t)\delta \left(x-{x}_i\right)+\sum \limits_{j=1}^4{M}_{\mathrm{w}j}(t)\delta \left(x-{x}_{\mathrm{w}i}\right)\end{array}} $$
(4)

Here, E is the Young’s modulus of the rail material; Iy and Iz are the second moments of the area of the rail cross-section about the lateral and vertical axes, respectively; mr is the mass per unit longitudinal length; ρr is the rail density; I0 is the torsional inertia of the rail; GK is the torsional stiffness of the rail; Zr(x, t), Yr(x, t), and ϕr(x, t) are the vertical, lateral, and torsional displacements of the rail, respectively; FVi and FLi are the vertical and lateral supporting forces in the ith mode at position xsi on the rail, respectively; Pj and Qj are the jth vertical and lateral wheel–rail forces, respectively, at position xwj on the rail; Msi and Mwj are the moments acting on the rail; δ(x − xi) is the Dirac delta function; and NV, NL, and NT are the total numbers of rail mode functions calculated in the vertical, lateral, and torsional directions, respectively.

The track slabs are described as elastic rectangular plates supported on viscoelastic foundations (Zhai et al. 2009), which are also simplified as springs and dampers. The slab track model permits the adjustment of various track parameters, such as the support spacing, stiffness and damping, for different types of tracks.

A series of two-dimensional beam mode functions is used to approximate the vertical displacement of a slab. Each track slab is modeled as an elastic rectangular plate with four free edges, with asymmetric boundary conditions on the diagonal. The equations of motion for each track slab in the vertical direction can be written as follows:

$$ {\displaystyle \begin{array}{c}\frac{\partial^4w\left(x,y,t\right)}{\partial {x}^4}+2\frac{\partial^4w\left(x,y,t\right)}{\partial {x}^2\partial {y}^2}+\frac{\partial^4w\left(x,y,t\right)}{\partial {y}^4}+\frac{C_{\mathrm{s}}}{D_{\mathrm{s}}}\frac{\partial w\left(x,y,t\right)}{\partial t}+\frac{\rho_{\mathrm{s}}{h}_{\mathrm{s}}}{D_{\mathrm{s}}}\frac{\partial^2w\left(x,y,t\right)}{\partial {t}^4}\\ {}=\frac{1}{D_{\mathrm{s}}}\left[\begin{array}{c}\sum \limits_{i=1}^{2{N}_{\mathrm{V}}}{F}_{\mathrm{V}i}(t)\delta \left(x-{x}_{\mathrm{p}i}\right)\delta \left(y-{y}_{\mathrm{p}i}\right)-\sum \limits_{j=1}^{N_{\mathrm{b}}}{F}_{\mathrm{s}\mathrm{ubV}j}(t)\delta \left(x-{x}_{\mathrm{b}j}\right)\delta \left(y-{y}_{\mathrm{b}j}\right)\\ {}-\sum \limits_{j=1}^{N_{\mathrm{s}}}{F}_{\mathrm{s}j}(t)\delta \left(x-{x}_{\mathrm{s}j}\right)\delta \left(y-{y}_{\mathrm{s}j}\right)\end{array}\right]\end{array}} $$
(5)

Here, Es is the elastic (Young’s) modulus of the track slab; Cs is the damping of the slab; xpi and ypi are the longitudinal and lateral positions of the ith fastener node on the track plate, respectively; Fsjis the jth shear hinge force of the shear springs and bending springs at the longitudinal and lateral positions of xsj and ysj on the track slab; and FsubVj is the jth vertical supporting force of the subground acting through the steel springs or solid bed at the longitudinal and lateral positions of xbj and ybj under the track slab.

Since the thickness of a track slab is much less than its length, its lateral bending stiffness is very large. Therefore, it is sufficient to consider only the rigid modes of the slab vibrations in the lateral and rotational directions. The lateral and rotational motions can be regarded as rigid-body motions. The equation of motion in the lateral direction is expressed as follows:

$$ {\rho}_{\mathrm{s}}{L}_{\mathrm{s}}{W}_{\mathrm{s}}{h}_{\mathrm{s}}{\ddot{y}}_{\mathrm{s}}=\sum \limits_{i=1}^{N_{\mathrm{V}}}{F}_{\mathrm{L}i}-2\sum \limits_{j=1}^{N_{\mathrm{b}}}{F}_{\mathrm{s}\mathrm{ubL}j} $$
(6)

The equation of motion in the rotational direction is expressed as follows:

$$ {J}_{\mathrm{s}\mathrm{z}}{\ddot{\phi}}_{\mathrm{s}}=\sum \limits_{i=1}^{N_{\mathrm{V}}}{F}_{\mathrm{L}i}{d}_{\mathrm{f}i}-2\sum \limits_{j=1}^{N_{\mathrm{b}}}{F}_{\mathrm{s}\mathrm{ubL}j}{d}_{\mathrm{b}j} $$
(7)

Here, Ls, Ws, and hs are the length, width, and thickness, respectively, of the slab; ρs is the density of the slab; FsubL is the lateral supporting force of the subground acting through the steel springs or solid bed; Jszis the moment of inertia about the vertical axis; dfiis the longitudinal distance from the ith fastener support point to the center of the slab; and dbj is the longitudinal distance from the jth subground support point to the center of the slab.

According to the Rayleigh–Ritz method, (2)–(5) can be simplified to second-order ordinary equations to be solved (Jin et al. 2006; Zhai et al. 2009).

2.2.3 Coupled wheel–rail model

The coupled wheel–rail model is crucial to the geometrical characteristics of the wheel–rail contact. The rails are assumed to be fixed without any movement, while lateral (yw), roll (ϕw), and yaw (ψw) motions are considered for the wheelset. The contact line (Wang 1984; Tang and Lu 2011), which consists of the possible positions of wheel–rail contact points, can be calculated as follows:

$$ x=\cos \left({\psi}_{\mathrm{w}}\right)\sin \left({L}_{\mathrm{w}}\right){W}_z-\sin \left({\phi}_{\mathrm{w}}\right){W}_y $$
(8a)
$$ {\displaystyle \begin{array}{c}y=\cos \left({\phi}_{\mathrm{w}}\right)\sin \left({\psi}_{\mathrm{w}}\right)\sin \left({L}_{\mathrm{w}}\right){W}_z\\ {}+\cos \left({\phi}_{\mathrm{w}}\right)\cos \left({\psi}_{\mathrm{w}}\right){W}_y-\sin \left({\phi}_{\mathrm{w}}\right)\cos \left({L}_{\mathrm{w}}\right){W}_z+{y}_{\mathrm{w}}\end{array}} $$
(8b)
$$ {\displaystyle \begin{array}{l}z=\sin \left({\phi}_{\mathrm{w}}\right)\sin \left({\psi}_{\mathrm{w}}\right)\sin \left({L}_{\mathrm{w}}\right){W}_z\\ {}+\sin \left({\phi}_{\mathrm{w}}\right)\cos \left({\psi}_{\mathrm{w}}\right){W}_y+\cos \left({\phi}_{\mathrm{w}}\right)\cos \left({L}_{\mathrm{w}}\right){W}_z\end{array}} $$
(8c)

where x, y, and z are the coordinates of the possible wheel–rail contact points; Wy and Wz are the coordinates of the wheel profile; and Lw is an advanced or lagged roller angle.

Until the minimum vertical wheel–rail distances are equal between the low and high sides, the positions of the wheel–rail contact points pL and pR are determined by adjusting ϕw and Lw, as shown in Fig. 5.

Fig. 5
figure 5

The coupled wheel–rail model

Full size image

The coupled wheel–rail contact model consists of a normal contact model and a tangential contact model. The normal wheel–rail force is described by a Hertzian linear contact spring (Nguyen et al. 2009). The tangential creep forces at the wheel–rail contact point are first calculated using Kalker’s linear creep theory and then modified by means of the Shen–Hedrick–Elkins nonlinear model (Shen et al. 1983).

2.2.4 Numerical integration method

A two-step composite time integration scheme (Gao et al. 2019) is applied to solve the coupled vehicle-track dynamic model. In the two-step integration scheme, under the assumption that the response at the nth time step is known, all unknown variables at the (n + 1/2)th time step are calculated based on the assumptions of the trapezoidal rule. Then, in accordance with the known responses at the nth and (n + 1/2)th time steps, the response at the (n + 1)th time step can be solved by using the 3-point backward Euler method. More information about the integration scheme can be found in the paper of Gao et al. (2019). However, the track length on a curve may be very long, which can significantly increase the size of the matrix that is formed via the mode-superposition method. To solve this problem, the sliding window method is used to divide the track into constant-length segments for iterative calculations (Song et al. 2018). The combination of the two-step integration method and the sliding window method can increase the computational efficiency while significantly ensuring the accuracy of the solutions.

2.3 Model cross-verification

The model was verified by comparing the dynamic responses of a vehicle model implemented in Simpack (Simpack 9.10.1 2016) with the results of the proposed three-dimensional coupled vehicle-track model using the steel spring floating slab track submodel. The main parameters of the metro vehicle and the track used in the simulations are listed in Table 1. The track is arranged on a curve with a radius of 650 m and a superelevation of 120 mm. The lengths of the curve and transition curve sections are 482 m and 85 m, respectively. The fastener spacing of the track is 0.6 m, and the support spacing of the steel springs is twice that of the fastener spacing. The running speed of the vehicle is 100 km/h, and the integration time step is 10−4 s.

Table 1 Main parameters of the vehicle-track model
Full size table

Figures 6 and 7 show the dynamic responses obtained with the LM&CHN60 profiles from the Simpack model and the proposed three-dimensional coupled vehicle-track model, respectively. It should be noted that the track in the Simpack model is rigid and without deformation. Since the wheelsets of the front bogie and rear bogie exhibit the same behavior, only the wheelsets of the front bogie are discussed. As seen from Figs. 6 and 7, the trends of lateral displacement, yaw angle, derailment coefficients, and rates of wheel load reduction for both the 1st and 2nd wheelsets in the three-dimensional coupled vehicle-track model are in excellent agreement with those in the Simpack model, except that the derailment coefficients and rates of wheel load reduction of the three-dimensional coupled vehicle-track model are much smoother. In other words, the track elasticity in the three-dimensional coupled vehicle-track model has an obvious influence on the wheel–rail dynamic responses. Due to the consideration of the track elasticity, the dynamic responses of the three-dimensional coupled vehicle-track model show obvious periodic vibrations, with the period of the vibration being equal to the track slab length, as shown in Figs. 6 and 7. In contrast, because the track in the Simpack model is rigid, the vehicle is obviously impacted when entering and leaving the transition curve sections.

Fig. 6
figure 6

Dynamic responses of the wheelsets: a lateral displacements of the wheelsets and b yaw angles of the wheelsets

Full size image
Fig. 7
figure 7

Dynamic vehicle-rail interaction responses: a derailment coefficients of the 1st wheelset, b derailment coefficients of the 2nd wheelset, c rates of wheel load reduction for the 1st wheelset, and d rates of wheel load reduction for the 2nd wheelset

Full size image

2.4 Performances of LM&CHN60 and WW&WR

Comparisons between the dynamic responses of the proposed three-dimensional coupled vehicle-track model using the steel spring floating slab track submodel with LM&CHN60 and WW&WR are shown in Figs. 8, 9, and 10. The curve parameters used are the same as in Section 2.3. The difference between the wheel and rail shapes results in different dynamic behaviors of the vehicle-track system. Figure 8 gives the lateral accelerations of the wheelset. It can be clearly seen that the lateral accelerations of both the 1st wheelset and 2nd wheelset with LM&CHN60 are much smaller than those of the WW&WR. The wheelset with the worn profiles is more likely to generate large abnormal oscillations, especially on the transition section. By comparing Fig. 7 with Fig. 9, it can be found that the derailment coefficients and rates of wheel load reduction of both the 1st and 2nd wheelsets with WW&WR are larger than those of the LM&CHN60. Obviously, wheel–rail wear can affect the stability of the vehicle on a curve.

Fig. 8
figure 8

Lateral acceleration of the wheelset: a 1st wheelset and b 2nd wheelset

Full size image
Fig. 9
figure 9

Dynamic vehicle-rail interaction responses with WW&WR: a derailment coefficients and b rates of wheel load reduction

Full size image
Fig. 10
figure 10

Lateral displacement of the wheelset with WW&WR

Full size image

The lateral displacement of the wheelset with WW&WR is approximately 8 mm on the tangent section of the line, which is equal to the lateral displacement of the 1st wheelset with LM&CHN60 to negotiate the curve, as shown in Fig. 10. Since the lateral displacement of the 1st wheelset is larger than that of the 2nd wheelset, the motion of the 1st wheelset under different curve radius is analyzed to research the wheel–rail contact characteristics. Most of the metro lines are composed of curves with a radius greater than 300 m. The lateral displacements of the 1st wheelset to negotiate curves with LM&CHN60 and WW&WR with a radius in the range of 300–900 m are simulated in Fig. 11. The lateral displacements of the 1st wheelset with LM&CHN60 and WW&WR can both increase as the radius decreases. The lateral displacements of the 1st wheelset with WW&WR do not exceed 15 mm when operated on a curve with a radius greater than 300 m, which are much larger than those of the LM&CHN60.

Fig. 11
figure 11

Lateral displacement of the 1st wheelset with the LM&CHN60 and WW&WR under curves with different radii

Full size image

In view of this, the rolling radius difference (RRD) and the wheel–rail contact points for the LM&CHN60 and WW&WR with 0–20-mm lateral displacements of a wheelset, as calculated using the contact line method in Section 2.2.3, are shown in Figs. 12, 13, and 14. The RRD is considered to be an indirect index of the geometrical characteristics of the contacts between wheels and rails. The RRD of LM&CHN60 can be classified into three regions, as shown in Figs. 12 and 13. The first region corresponds to the tread contact within the 3-mm lateral displacement of a wheelset, which is responsible for motion on a tangent track. The second region is related to a 3–9-mm lateral displacement of a wheelset, which is designed to negotiate curves with a large radius. The third region corresponds to the negotiation on a sharp curve with the flange contact beyond 9-mm lateral displacement of a wheelset. It can be seen that the RRD of LM&CHN60 is much larger than that of WW&WR within 15-mm lateral displacement of a wheelset. When the lateral displacement of the wheelset is beyond 15 mm, the flange contact of WW&WR occurs, and the flange contact region is the same as the third region of LM&CHN60, as shown in Figs. 13 and 14. From the above dynamic analysis, the deficiency of the RRD of WW&WR within the 15-mm lateral displacement of the wheelset can generate severe oscillations of a vehicle. Meanwhile, there is a discontinuity in the contact region of WW&WR for the 10–15-mm lateral displacements of a wheelset, which could be seen as the “stairs” of the RRD. When a vehicle passes a curve, such discontinuity in the contact region can further deteriorate the operational stability.

Fig. 12
figure 12

Comparison between LM&CHN60 and WW&WR RRDs

Full size image
Fig. 13
figure 13

Positions of contact points of LM&CHN60 depending on the lateral displacement of a wheelset: a low rail and b high rail

Full size image
Fig. 14
figure 14

Positions of contact points of WW&WR depending on the lateral displacement of a wheelset: a low rail and b high rail

Full size image

3 Rail profile design

3.1 Design variables

To describe the shape of a rail profile, a number of points on the rail are chosen. The points on the surface of the rail profile are expressed as the coordinates (y, z), and the region of y < 0 is the inner side of the rail. Through dynamic analysis and wheel–rail contact properties of worn and unworn profiles, the ends of the optimized region points A and B with the coordinates of (yA, zA) and (yB, zB) are determined, as shown in Fig. 14. To ensure the size of the rail profile, the points that are not in the optimized region remain fixed. Meanwhile, the number of control points Nmov selected in the optimized region can significantly influence the shape of the rail profile during the optimization process. The control points should be evenly distributed in the optimized region, while the number of them can be considered as an adjustable parameter to obtain more rail shapes. The formula can be expressed as follows:

$$ \frac{y_j-{y}_{\mathrm{A}}}{y_{\mathrm{A}}-{y}_{\mathrm{B}}}<1,\kern0.5em j=1,2,\cdots, {N}_{\mathrm{mov}} $$
(9)

Once the position of the control points is determined, the vertical coordinates \( Z=\left[{z}_1,\cdots, {z}_{N_{\mathrm{mov}}}\right] \) of the adjustable control points are chosen as the design variables, and their lateral positions are fixed. Based on the selected points, a connected profile is generated using the uniform rational B-spline interpolation algorithm. Then, a complete rail profile can be created and expressed by Z.

Considering the different contact regions of the low and high rails on the curve, a design that is asymmetric between the low and high rails is adopted. The design variables of the low and high rail should be determined separately.

3.2 Objective function

Based on the above research and dynamic analysis of the vehicle-track system, the main objective is to create compatible rail profiles to the worn wheel profiles so as to improve the stability of vehicle operation and wheel–rail wear. Since RRD defines, to a large extent, the behavior of a wheelset on a track, the optimization approach presented is based on the RRD function. The RRD function contains a priori defined wheel–rail contact characteristics, which can be established by mathematical expressions. When the optimum RRD function is defined as the target RRD, one can try to solve an inverse problem to find the rail profiles that satisfy such an RRD. Based on the above analysis of worn and unworn profiles before optimization, the actual and ideal matchings between wheels and rails are known. To achieve the purpose of optimization, the target RRD is designed to ensure the continuous distribution of wheel–rail contact points and provide sufficient curve passing capacity, which should not be much different from the actual wheel–rail contact properties.

The objective function is formulated to minimize the discrepancy between the target RRD and the calculated RRD of the designed rail profile (Shevtsov et al. 2008). To obtain a smoother RRD during the optimization process without “stairs,” the rate of change of the curvature of the calculated RRD is also considered in this paper to prevent discontinuity of the wheel–rail contact points. The objective function can be written as follows:

$$ {F}_{\mathrm{o}}(Z)=\frac{\sum_{i=1}^N{\left(\Delta {r}_{\mathrm{t}}\left({y}_{\mathrm{w}i}\right)-\Delta {r}_c\left(Z,{y}_{\mathrm{w}i}\right)\right)}^2}{\sum_{i=1}^N{\left(\Delta {r}_t\left({y}_{\mathrm{w}i}\right)\right)}^2}+\frac{\sum_{i=1}^N\left|\Delta {r_{\mathrm{c}}}^{\hbox{'}\hbox{'}}\left(Z,{y}_{\mathrm{w}i}\right)\right|{\sum}_{i=1}^K{\left(\Delta {r}_t\left({y}_{\mathrm{w}i}\right)\right)}^2}{\sum_{i=1}^N{\left(\Delta {r}_{\mathrm{t}}\left({y}_{\mathrm{w}i}\right)-\Delta {r}_{\mathrm{c}}\left(Z,{y}_{\mathrm{w}i}\right)\right)}^2}\to \min $$
(10)

where Δrt is the target RRD, Δrc is the calculated RRD of the designed profile, X is the position of a control point, yw is the lateral displacement of the wheelset, and N is the number of points at which the lateral displacement is calculated.

3.3 Constraint function

The design variables must meet the requirement of the monotonicity of the rail profile curve. Considering the convex property of the curved rail profile, as shown in Fig. 15, the position of each control point should be limited to ensure that an effective profile is obtained during the optimization process, which also makes this process computationally less time-consuming. The constraint function is expressed as follows:

$$ \left(\frac{z_j-{z}_{j-1}}{y_j-{y}_{j-1}}\right)/\left(\frac{z_{j+1}-{z}_j}{y_{j+1}-{y}_j}\right)\le 1\left(j=2,2,\cdots, {N}_{\mathrm{mov}}-1\right) $$
(11)
Fig. 15
figure 15

Illustration of the rail profile

Full size image

To ensure continuous curvature of the rail profile, some boundary conditions are set as follows:

$$ \left\{\begin{array}{c}\left({z}_1-{z}_{\mathrm{A}}\right)/\left({y}_1-{y}_{\mathrm{A}}\right)\ge {S}_{\mathrm{A}}\kern0.5em \\ {}\left({z}_{\mathrm{B}}-{z}_{N_{\mathrm{mov}}}\right)/\left({y}_{\mathrm{B}}-{y}_{N_{\mathrm{mov}}}\right)\le {S}_{\mathrm{B}}\end{array}\right. $$
(12)

where SA and SB are the slopes of start point A and end point B, respectively.

3.4 Optimization method

The optimization problem mentioned above can be stated in a general form as follows:

Minimize

$$ {F}_{\mathrm{o}}(Z),Z\in {R}^N $$
(13a)

subject to

$$ {F}_i(Z)\le 1\kern1em \left(i=1,\dots, {N}_0\right) $$
(13b)

and

$$ {D}_j\le {z}_j\le {U}_j\left(j=1,\dots, {N}_{\mathrm{mov}}\right) $$
(13c)

where \( Z=\left[{z}_1,\cdots, {z}_{N_{\mathrm{mov}}}\right] \) denotes the design variables; Dj and Uj are the lower and upper bounds on the design variable, which define a search region of the jth design variable; Fo is the objective function; Fi is the ith constraint function, and N0 is the number of the optimization sample.

To solve the optimization problem formulated as (13), the multipoint approximation optimization method based on response surface fitting (Markine et al. 2007; Yan et al. 2013) is used. The essence of this method is to replace the initial function with the approximation function iteratively, which is effective in a subregion.

In every mth step of this iterative procedure, the problem of (13) is formulated and solved as:

Minimize

$$ {\tilde{F}}_{\mathrm{o}}^m(Z),Z\in {R}^N $$
(14a)

Subject to

$$ {\tilde{F}}_{\mathrm{o}}^m(Z)\le \kern1em \left(i=1,\cdots, {N}_0\right) $$
(14b)

and

$$ {D}_j^m\le {Z}_j^m\le {U}_j^m\left(j=1,\cdots, {N}_{\mathrm{mov}}\right) $$
(14c)

where \( \tilde{F}(Z) \) is the approximation function of the initial function F(Z).

To obtain the analytical expressions that reflect the optimization problems considered to be a function of its parameters, the methods of regression analysis are implemented (Toropov 1989). Based on a set of numerical results of the initial function, the approximate function can be formed as follows:

$$ \tilde{F}(Z)={a}_{\mathrm{o}}+\sum \limits_{j=1}^{N_{\mathrm{mov}}}{z}_j{a}_j\left(j=1,\cdots, {N}_{\mathrm{mov}}\right) $$
(15)

where a is a tuning parameter.

Hence, the extremum problem of (14) can be solved simply by the form of (15). It should be noted that the solution of the optimization problem in (14) is found in the search subregion, which is determined by the moving side limits Dm andUm. The size and location of the search subregion can also be changed according to the solution. The solution Zm obtained in the mth step is chosen as the starting point for the (m + 1)th step (Yan et al. 2013); the side limits of the design variables in each iteration step can be expressed as follows:

$$ {h}_j^m=\left({B}_j^m-{A}_j^m\right){H}^m\operatorname{sgn}\left({Z}_{\ast_j}^m-{Z}_{\ast_j}^{m-1}\right)\left(j=1,\cdots, {N}_{\mathrm{mov}}\right) $$
(16a)
$$ {\displaystyle \begin{array}{l}{D}_j^{m+1}={Z}_{\ast_j}^m-\lambda \left|{h}_j^m\right|\\ {}{U}_j^{m+1}={Z}_{\ast_j}^m+\mu \left|{h}_j^m\right|\end{array}} $$
(16b)

If \( {h}_j^m<0 \), λ = 1.6, and μ = 0.5; if \( {h}_j^m>0 \), λ = 0.5, and μ = 1.6 (Markine 1999). \( {Z}_{\ast}^m \) and \( {Z}_{\ast}^{m-1} \) are the last and previous approximations, respectively, of the optimal solution that has been found. The direction of change of the side limits is determined by the adjacent optimal solutions\( \left({Z}_{\ast}^m-{Z}_{\ast}^{m-1}\right) \). Hm is a constant. Adjusting the side limits D and U of the design variables in each iteration step to control the shape of the rail profile ensures that the optimization result remains close to the target.

The termination conditions of iteration can be determined as follows:

$$ \left\{\begin{array}{l}{e}^m={\sum}_{i=1}^K{\left(\Delta {r}_t\left({y}_{\mathrm{w}i}\right)-\Delta {r}_c\left(Z,{y}_{\mathrm{w}i}\right)\right)}^2=0, or\\ {}{Z}_{\ast}^{m-4}=\cdots ={Z}_{\ast}^m\end{array}\right. $$
(17)

The optimized rail profiles are obtained until the convergence criteria have been satisfied.

4 Optimum rail profile design procedure

The flowchart of the optimum rail profile design procedure is shown in Fig. 16 and the procedure has been implemented using MATLAB software. The optimum rail profile design procedure consists of the following steps.

  • Step 1: Definition of the rail optimized region and target RRD.

Fig. 16
figure 16

Flowchart of the optimum rail profile design procedure

Full size image

The first step of the procedure is to determine the rail optimized regions yA and yB and the target RRD function. For this purpose, wheel and rail profile measurements are used to collect data on worn and unworn profiles. Based on the three-dimensional vehicle-track model proposed in Section 2, the lateral displacement of a wheelset with different curve radius is analyzed on worn and unworn profiles. Through the comparative analysis of the wheel–rail contact characteristics between the worn and unworn profiles within the required lateral displacement of a wheelset, the optimized regions of low and high rails and the target RRD are obtained.

  • Step 2: Rail profile optimization based on the inverse design method.

The second step is to set the number of control points Nmov in the optimized region. Then, N0 groups of Z are produced in random according to (11) and (12) and N0 pairs of rail profiles are fitted by connecting each set of Z using the uniform rational B-spline interpolation algorithm. The optimization problem can be formulated and solved with the worn wheel profiles according to (10) and (15) to generate rail profiles. If the optimized results do not meet (17), the side limits Dm + 1 and Um + 1 of Z will be adjusted according to (16), and other N0 pairs of rail profiles will be generated. The whole shape optimization progress based on the inverse method proposed in Section 3 is in a close-loop until a pair of optimized rail profiles is obtained. A variety of design schemes are provided by combining different target RRD and control points, and multiple pairs of optimized rail profiles are obtained.

  • Step 3: Selection of optimum rail profiles based on dynamic properties.

The dynamic properties of a vehicle-track system are not directly controlled during the shape optimization process, which reduces the computational cost of the optimization, and does not reflect the influence of the curved track. When the optimized profile has been obtained, the wear of the obtained rail profile should be evaluated. Import the optimized rail profiles into the three-dimensional vehicle-track model considering two types of tracks and perform the simulation on a specific curve. Then, the wear of the rail passing over the specified curved track is analyzed to compare and select the optimum rail profiles for the given worn wheel profiles among the optimized rail profiles.

In step 3, Archard’s wear model (Li et al. 2011) for sliding contact is used in calculating the wear of a rail. According to the related theory, the wear depth in one element of the contact patch is defined as follows:

$$ {V}_{\mathrm{d}J}=K\frac{p_J{S}_J}{H} $$
(18)

where H is the hardness of the worn material, K is the wear coefficient, pJ is the normal pressure on element J as shown in Fig. 17, and SJ is the sliding distance of element J, which can be expressed as follows:

$$ {S}_J=\left|{v}_{\mathrm{slip}J}\right|\frac{\Delta x}{v} $$
(19)
$$ {v}_{\mathrm{slip}J}=v\left[\left(\begin{array}{c}{\zeta}_1-{y}_J{\zeta}_3\\ {}{\zeta}_2-{x}_J{\zeta}_3\end{array}\right)-\frac{\partial {u}_J}{\partial x}\right] $$
(20)
Fig. 17
figure 17

Wheel–rail contact patch

Full size image

Here, v is the running speed of the vehicle; Δx is the length of the element in the rolling direction (note that the area of an element is 0.1 × 0.1 mm2); vslipJ is the slip velocity of element J; ζ1, ζ2, and ζ3 are the longitudinal, lateral and torsional creepages, respectively; uJ is the elastic displacement; and xJ and yJ are the coordinates of the contact ellipse.

Kalker’s non-Hertzian contact theory based on virtual interpenetration (Piotrowski and Kik 2008) is used to solve the pressure distribution on wheel–rail contact patch. It is assumed that the wheel is a revolute body of radius R and that the rolling surface of the rail is cylindrical. By introducing a virtual penetrationδ0, the virtual interpenetration region at the wheel–rail interface in the x- and y-coordinates can be defined as follows:

$$ g(y)=\left\{\begin{array}{l}{\delta}_0-f(y)\\ {}0\end{array}\right.{\displaystyle \begin{array}{c}\kern0.5em f(y)\le {\delta}_0\\ {}\begin{array}{cc}& f(y)>{\delta}_0\end{array}\end{array}} $$
(21)
$$ {x}_{\mathrm{l}}(y)=-{x}_{\mathrm{t}}(y)\approx \sqrt{2 Rg(y)} $$
(22)

where g(y) is the interpenetration function, f(y) is the interpenetration of the wheel–rail interface at position y, and xl(y) and xt(y) are the front and rear edges, respectively, of the interpenetration region in the x-coordinate.

According to the properties of Hertzian contact, the pressure distribution p(x, y) in the contact area and the normal force N can be given as follows:

$$ p\left(x,y\right)=\frac{p_0}{x_{\mathrm{l}}(0)}\sqrt{x_{\mathrm{l}}^2(y)-{x}^2} $$
(23)
$$ N=\frac{p_0}{x_{\mathrm{l}}(0)}{\int}_{y_{\mathrm{r}}}^{y_{\mathrm{l}}}{\int}_{-{x}_{\mathrm{l}}}^{x_{\mathrm{l}}}\sqrt{x_{\mathrm{l}}^2(y)-{x}^2} dxdy $$
(24)

where p0 is the maximum pressure.

Assuming that the normal pressure p(x, y) is known, to satisfy the contact conditions at the point (0, 0) by using Boussinesq’s influence function, (23) and (24) can be transformed into the following:

$$ N=\frac{\pi E\delta}{2\left(1-{\sigma}^2\right)}{\left({\int}_{y_{\mathrm{r}}}^{y_{\mathrm{l}}}{\int}_{-{x}_{\mathrm{l}}}^{x_{\mathrm{l}}}\frac{\sqrt{x_{\mathrm{l}}^2(y)-{x}^2}}{\sqrt{x^2+{y}^2}} dxdy\right)}^{-1}{\int}_{y_{\mathrm{r}}}^{y_{\mathrm{l}}}{\int}_{-{x}_{\mathrm{l}}}^{x_{\mathrm{l}}}\sqrt{x_{\mathrm{l}}^2(y)-{x}^2} dxdy $$
(25)
$$ {p}_0=N\sqrt{2R{\delta}_0}{\left({\int}_{y_{\mathrm{r}}}^{y_{\mathrm{l}}}{\int}_{-{x}_{\mathrm{l}}}^{x_{\mathrm{l}}}\sqrt{x_{\mathrm{l}}^2(y)-{x}^2} dxdy\right)}^{-1} $$
(26)

The virtual penetration δ0 is found to be δ0 = 0.55δ. Thus, the wheel–rail normal contact problem is solved.

The wear coefficient K can be obtained through laboratory tests or by performing extensive field measurements (Jendel 2002) and is determined by the contact pressure and slip velocity of each individual element, as shown in Fig. 18.

Fig. 18
figure 18

The wear coefficient

Full size image

The wear distribution on a wheel–rail contact patch forms through the accumulation of the wear depth at each time step along the travel distance within the width of the contact patch, as shown in Fig. 19. Finally, once the maximum wear depth for all elements in the rolling direction on the same strip has been determined, the wear depth distribution of the contact patch on the rail cross-section is obtained.

Fig. 19
figure 19

Wear depth of a contact patch

Full size image

5 Results

In this section, the application of the optimization design procedure is shown, and the optimum rail profiles for the given worn wheel profiles of a specific curve are obtained by considering two types of track, that is, the steel spring floating slab track and the nonballasted track on a solid bed. Additionally, the dynamic behavior of the metro vehicle and the two types of track with the optimum rail profiles are verified by comparison with the worn rail profiles. The proposed three-dimensional coupled vehicle-track model is considered and subjected to measured track irregularities superimposed with short vertical wavelength irregularities, as shown in Fig. 20. The parameters of the metro vehicle and the two kinds of tracks used in the simulation are listed in Table 1. The running speed of the vehicle is 93 km/h, and the integration time step is 10−4 s. The curve with the parameters is the same as that used in Section 2.3.

Fig. 20
figure 20

Samples of the measured track irregularities: a lateral irregularity of the high rail, b lateral irregularity of the low rail, c vertical irregularity of the high rail, and d vertical irregularity of the low rail

Full size image

5.1 Rail profile design

On the basis of eliminating the large changes in the wheel–rail contact point and increasing RRD within a 15-mm lateral displacement of a wheelset, two kinds of target RRDs, labeled “Target RRD_1” and “Target RRD_2,” are considered by referring to the performances of WW&WR and LM&CHN60 in Section 2.4, as shown in Fig. 21. Considering the distribution of wheel–rail contact points of WW&WR, two sets of design variables, labeled “Control points_1” and “Control points_2,” are shown in Fig. 22. In accordance with the different design schemes defined in Table 2, four pairs of optimized rail profiles are obtained in terms of the inverse design method, labeled “Opt_1,” “Opt_2,” “Opt_3,” and “Opt_4,” as shown in Fig. 23. By comparing the target and optimized RRDs, as shown in Figs. 24a, b, the inverse shape design method presented can be used to obtain an optimized result without “stairs” that is close to the target. It can also be seen that different numbers of control points can cause different rail shape changes, resulting in obvious differences in the optimized profile even with the same target RRD.

Fig. 21
figure 21

The RRD as a function of the lateral displacement of the wheelset

Full size image
Fig. 22
figure 22

The control points on the rails: a control points on the low rail and b control points on the high rail

Full size image
Table 2 Optimization design schemes
Full size table
Fig. 23
figure 23

Optimized rail profiles: a low rail and b high rail

Full size image
Fig. 24
figure 24

Comparisons between the target and optimized RRDs: a Target RRD_1 and b Target RRD_2

Full size image

5.2 Analysis of wear for choosing the optimum rail profiles

The wear of the worn and optimized rail profiles for the steel spring floating slab track and the nonballasted track on a solid bed are compared here. For each wheel–rail contact, 10 sections were calculated in the middle of the curve at intervals of 0.2 m; thus, a total of 40 cross-sections were calculated for the contact of all four wheels with the rails on each side.

Figures 25 and 26 illustrate the wear depths of the 40 cross-sections calculated for each pair of rail profiles for the steel spring floating slab track and the nonballasted track on a solid bed, respectively. A comparison of Figs. 25 and 26 reveals that the wear depths of the worn rails on both sides are much greater for the nonballasted track on a solid bed than they are for the steel spring floating slab track. By comparing Figs. 25a and 26a with Figs. 25b and 26b, respectively, it can be seen that the wear depth of the low rail is greater than that of the high rail. The wear depths of both the low and high rails of the two types of curved track with Opt_1, Opt_2, Opt_3 and Opt_4 are significantly decreased in comparison with the worn rails. However, the wear depths of the optimized profiles obtained by different optimization schemes are quite different. Additionally, the wear of the low rail is distributed near the center of the rail with both Opt_1 and Opt_4.

Fig. 25
figure 25

Wear depths of the steel spring floating slab track: a the low rail and b the high rail

Full size image
Fig. 26
figure 26

Wear depths of the nonballasted track on a solid bed: a the low rail and b the high rail

Full size image

Figure 27 shows the maximum wear depth for the cross-sections calculated for each pair of rail profiles for both types of curved tracks. It can be seen that the maximum wear depths of Opt_4 on both low and high rails are minimum among the optimized rail profiles and much lower than those of the worn rail profiles. With Opt_4, the maximum wear depths are 1.08% of the maximum wear depth of the worn rail for the low rail of the steel spring floating slab track and 0.62% of the maximum wear depth of the worn rail for the low rail of the nonballasted track on a solid bed, whereas the corresponding percentages for the high rail are 9.61% for the steel spring floating slab track and 11.19% for the nonballasted track on a solid bed. From the above comparison, it can be seen that the Opt_4 profiles show a better effect than the other optimized rail profiles.

Fig. 27
figure 27

Maximum wear depth on the rails: a the low rail and b the high rail

Full size image

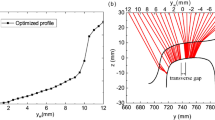
Furthermore, Fig. 28 shows the distributions of the contact points for Opt_4 with 0–20-mm lateral displacements of a wheelset. It can be seen that Opt_4 effectively eliminates the discontinuity in the contact point due to the hollow wear of the wheel treads. Therefore, considering the vehicle stability requirements and the development of rail wear, Opt_4 is the most compatible pair of rail profiles for the given worn wheel profiles of the specific curve.

Fig. 28
figure 28

Positions of the contact points between the worn wheels and Opt_4 depending on the lateral displacement of the wheelset: a low rail and b high rail

Full size image

5.3 Comparison of the dynamic responses between worn and optimum rail profiles

A dynamic analysis of the interaction of the worn and Opt_4 rail profiles with the worn wheel profiles is presented as follows. The lateral displacements of the wheelsets of the front bogie with the worn and Opt_4 rail profiles are shown in Fig. 29. It can be seen by comparing Fig. 29a and b or Fig. 29c and d that the two different types of curved tracks have no obvious effect on the lateral displacements of the wheelsets. From a comparison of the lateral displacements of the wheelsets between the worn and optimum rail profiles, it is evident that the optimum rail profiles can effectively reduce the maximum lateral displacement of the 1st wheelset on the curve from 15 to 14 mm and that of the 2nd wheelset from 11 to 6 mm. At the same time, Opt_4 can ensure that the lateral displacements of the wheelsets oscillate near 0 on a straight track (as shown in Fig. 29 at distances of 700–800 m). This means that the optimum rail profiles can appropriately match the given wheel profiles with hollow wear. Since the results for the wheelsets of the rear bogie are similar to those for the front bogie, no further discussion will be presented here.

Fig. 29
figure 29

Lateral displacements of the wheelsets on the curved tracks: a the 1st wheelset on the steel spring floating slab track, b the 1st wheelset on the nonballasted track on a solid bed, c the 2nd wheelset on the steel spring floating slab track, and d the 2nd wheelset on the nonballasted track on a solid bed

Full size image

Figures 30 and 31 show the lateral accelerations of the rails and the centers of the track slabs on the curve for both types of curved tracks with the worn and Opt_4 rail profiles. The lateral accelerations of low and high rails and the track slabs are significantly reduced for the track with the floating slab structure compared with the nonballasted track on a solid bed. When Opt_4 is applied, the lateral vibrations of both rails and track slabs are obviously improved. Meanwhile, the optimum profiles effectively solve the problem of large differences in lateral acceleration amplitudes between the low and high rails.

Fig. 30
figure 30

Lateral acceleration of the rails on the curved tracks: a low rail of the steel spring floating slab track, b high rail of the steel spring floating slab track, c low rail of the nonballasted track on a solid bed, and d high rail of the nonballasted track on a solid bed

Full size image
Fig. 31
figure 31

Lateral acceleration of the centers of the track slabs on the curved tracks: a the steel spring floating slab track and b the nonballasted track on a solid bed

Full size image

Figures 32 and 33 present the derailment coefficients and rates of wheel load reduction, respectively, for the 1st wheelset for the two types of curved tracks with the worn and Opt_4 rail profiles. By comparing Fig. 32a, b with Fig. 32c, d, respectively, and comparing Fig. 33a, b with Fig. 33c, d, respectively, it can be seen that for the rails on both sides, the derailment coefficients and rates of wheel load reduction for the 1st wheelset are higher with the nonballasted track on a solid bed than they are with the steel spring floating slab track. It can also be seen that Opt_4 effectively reduces the derailment coefficients and rates of wheel load reduction for the 1st wheelset for the rails on both sides for both types of curved tracks. Thus, the optimum rail profiles have significant improvements in the dynamic properties of the vehicle-track system.

Fig. 32
figure 32

Derailment coefficients for the 1st wheelset: a low rail of the steel spring floating slab track, b high rail of the steel spring floating slab track, c low rail of the nonballasted track on a solid bed, and d high rail of the nonballasted track on a solid bed

Full size image
Fig. 33
figure 33

Rates of wheel load reduction for the 1st wheelset: a low rail of the steel spring floating slab track, b high rail of the steel spring floating slab track, c low rail of the nonballasted track on a solid bed, and d high rail of the nonballasted track on a solid bed

Full size image

6 Conclusions

In this paper, a comparative analysis of the performances of the LM&CHN60 and WW&WR is used as the basis to define wheel–rail contact characteristics. Then, according to the predefined wheel–rail contact characteristics, an inverse shape design method is presented to optimize rail profiles for the given wheel profiles. Through the analysis of the wear depth of the worn and optimized rail profiles with two types of specified curved track, the optimum rail profiles can be selected among the optimized rail profiles. The dynamic properties of the vehicle-track system with the optimum rail profiles are discussed. The total procedure can be completed by the MATLAB program. The following conclusions can be drawn:

  1. (1)

    With wear, the distribution of the wheel–rail contact points can become discontinuous due to the incompatibility of the worn wheel and rail profiles. The RRDs of the worn wheels and rails decrease, resulting in much larger lateral displacements of the wheelset, derailment coefficients, and rates of wheel load reduction of the wheels when passing through a curve. Consequently, the stability of the running vehicle on the curve degrades.

  2. (2)

    With the proposed optimization design method for metro rail profiles, one can easily obtain an optimization result that is close to the target design. Multiple optimized rail profiles can be designed by adjusting the number of control points considered in the optimization calculations and the target RRD, and these optimized profiles can then be compared with the wear model to select the optimum profiles with the best performance of a specific curve.

  3. (3)

    With the optimum profiles, the wear depths of the rails with both the steel spring floating slab track and the nonballasted track on a solid bed, especially the low rail, on the curved track are significantly reduced. The optimum rail profiles are more compatible with the worn wheels, ensuring continuity of the contact point positions with 0–20-mm lateral displacements of a wheelset. Moreover, the optimum rail profiles effectively improve the dynamic responses of the metro vehicle-track system when negotiating the curve.

  4. (4)

    The results of the field testing of the optimized rail profile on a curve with a radius of 650 m in a Beijing metro have shown that due to the application of the optimum rail profile, the growth rate of rail wear has been slowed down. The maintenance intervals for rail reprofiling have been doubled.