Structural reliability analysis based on analytical maximum entropy method using polynomial chaos expansion

Abstract

The maximum entropy (ME) method is a promising tool for structural reliability analysis by estimating the unknown probability density function (PDF) of given model response from its moment constraints. However, the classic ME algorithm has to resort to an iterative procedure due to non-linear constraints, and the required high order moment estimations may have large statistical error. In this paper, we (i) propose an analytical ME method based on integration by parts algorithm to transform the non-linear constraints to a system of linear equations and (ii) derive the polynomial chaos expansion (PCE) multiplication for improving higher order moment calculation required in the previous step efficiently. Thus, an analytical formula of response PDF is obtained directly without intensively iterative procedure and associated convergence error, and it is followed by probability failure estimation using numerical integration computation. Two structural engineering cases are implemented to illustrate the accuracy and efficiency of the proposed method.

1 Introduction

Structure reliability analysis is one of the most important issues in engineering practice because of uncertainties in geometry parameters, operating conditions, material properties, applied loadings, etc. It is usually concerned with the probability of a limit state violation of a structural component. For simplicity, the failure probability is the integration of joint probability density function (PDF) of the input variables over failure domain.

Generally speaking, except for some very simple cases, it is an intractable problem to solve the failure probability. Such difficulty arises due to implicit limit state function as well as associated failure domain. In this way, the numerical simulation methodology, such as the Monte Carlo simulation (MCS) and versions including various importance sampling strategies, is widely employed for failure probability or reliability calculation (Zio 2013). Although these numerical methods are straightforward, it could lead to huge computation burden when structures or systems in consideration are large and complex, e.g., the finite element model. Therefore, researchers have developed the semi-analytical methodology, e.g., the first order reliability method (FORM) and the second order reliability method (SORM) (Zhao and Ono 1999), to mitigate this problem. These methods find an approximate analytical solution of procedure instead of many samplings. However, the gradients required in these methods are often calculated by the finite difference algorithm, and it is also time-consuming for complicated structures.

In addition, the response surface methodology is proposed to deal with the issue of implicit limit state function. The basic idea is to fit the true limit state function by approximate technologies, which makes function evaluation much easier for further computation (Shi et al. 2014). And such approximation is known as the response surface. Typically, it is chosen to be first or second order polynomials, high-dimensional model representation (HDMR) or dimensional reduction method (DRM) (Rabitz 1999), Kriging model (Kaymaz 2005), radial basis function (Jamshidi and Kirby 2010), etc. Then, the numerical simulation methodology and the approximate methodology could execute using the response surface instead of the original one. However, all these methods are computationally efficient but at the expense of accuracy (Chakraborty and Chowdhury 2015). Besides, Bucher and Most also concluded that relative accuracy of various response surface approaches might depend on the specific problem under consideration (Bucher and Most 2008).

Another distinguished idea is the statistical response characterization methodology (Shi et al. 2014). Unlike those discussed above whose foundation is input joint PDF integration over failure domain, this methodology represents PDF of limit state function response explicitly and obtains the probability of failure by employing numerical integration of this PDF directly. Researchers have extended the spectral stochastic finite element method (SSFEM) for PDF estimation of any response quantity by combining FORM sensitivity analysis (Sudret and Der Kiureghian 2002), and taken MCS for assumed PDF fitting (Huang et al. 2014). However, the former one may become a weakness when it comes to small failure probabilities, while the latter one might not be able to capture the response characterization when the assumed PDF form is far from the truth, and it is also short of computational efficiency.

An alternative way to obtain the PDF of response is the maximum entropy (ME) method, which is proposed by Jaynes as a rational approach to estimate unknown PDF (Jaynes 1957). The ME principle states that the PDF of response is the one having the maximum entropy under given moment constraints. Thus, a typical three-step method is widely adopted (Li and Zhang 2011; Shi et al. 2014; Chakraborty and Chowdhury 2015; Lasota et al. 2015). In the first step, several moments of response are obtained. In the second step, the explicit response PDF is derived from ME principle with moment constraints, where the Newton algorithms are employed in computation process since the constraints are non-linear in most cases. Finally, failure probability or some other results could come out. In the last few decades, a number of ME algorithms have been developed and applied in various fields, like structural reliability analysis (Zhang and Pandey 2013; Dai et al. 2016; Fan et al. 2018), structural damage assessment (Meruane and Ortiz-Bernardin 2015), extreme significant wave heights prediction (Petrov et al. 2013), and rotor-shaft dynamic responses modeling (Lasota et al. 2015).

However, there are practical difficulties suffered by ME method. First of all, Newton algorithms are iterative, which causes additional computation and convergence issue. And there might be unbalanced non-linearities and ill-conditioned Jacobian matrices in Newton algorithms (Abramov 2007). Besides, the moment estimations may have large statistical errors by traditional sampling approach, especially for high order moment. In order to overcome these shortcomings, researchers have conducted many studies. For one thing, Bandyopadhyay proposed an improved scaling iterative approach without matrix inversion (Bandyopadhyay et al. 2005). Some researchers use Chebyshev polynomials (Gotovac and Gotovac 2009), Fup basis functions (Gotovac and Gotovac 2009), or other orthogonal polynomials in fitting response PDF (Abramov 2007). Although these approaches make the ME method more stable and suitable when high order moments are given, the iterative procedure remains and the algorithm convergence is a potential problem. Zhang introduced the fractional moment concept to avoid high order moment (Zhang and Pandey 2013), but this approach introduces additional constraints and associated iterative resolution process for fractional values. It would increase algorithm complexity, while fractional moment might not apply in the case where the moment value is negative. For another, Shi made an attempt to get response PDF by classic ME fitting method and FORM was combined to compute failure probability, while K-S tests are used to check goodness of both moment estimations and PDF fitting (Shi et al. 2014). Chakraborty (Chakraborty and Chowdhury 2015) and Lasota (Lasota et al. 2015) use polynomial chaos expansion (PCE), which is a typical surrogate response under HDMR, to obtain low order moment instead of sampling accurately, because PCE converges in the L₂ sense for any arbitrary stochastic process with finite second moment, and the accuracy of PCE could be improved by increasing PCE degree (Xiu and Em Karniadakis 2002; Sudret 2008). But higher order moment calculation is obtained by PCE sampling, which may introduce additional sampling error and computational costs. Moreover, the univariate dimension reduction method (UDR) is also proposed to compute high order moments efficiently (Rahman and Xu 2004), but previous research indicated that the lack of accuracy of UDR is inherent to its mathematical formulation and may not be reduced (Gherlone et al. 2013). As a whole, these works also do not change the existing framework of iterative algorithm, and the moment estimations are mostly based on consuming sampling principle.

In this paper, we explore an analytical method to improve the existing ME method, which could mitigate problems discussed above. Since the formula of response PDF is an exponential form according to ME principle, the key idea is to separate parameters in PDF using integration by parts. So, the constraints could be converted into a system of linear equations. Thus, the PDF would be obtained without convergence error. However, it may lead to a higher moment estimation requirement in solving procedure than classic ME method. To deal with this challenge, we make an attempt to use PCE and multiplication algorithm to obtain high order moments within limited statistical error.

The presentation of this work is structured as follows. Section 2 presents the proposed analytical maximum entropy method. In Section 3, the polynomial chaos expansion for high order statistical moment calculation is introduced. The procedure of proposed method is presented in Section 4. The proposed method for structural reliability analyses is illustrated by two examples in Section 5. Conclusions are summarized in the last section as well as Appendix 1, 2, 3, and 4.

2 Maximum entropy method for reliability analysis

2.1 Maximum entropy principle and classic algorithm

The maximum entropy principle is of particular use in characterizing the specific PDF of a random variable (Jaynes 1957; Bandyopadhyay et al. 2005; Petrov et al. 2013). According to information theory, the entropy of a continuous random variable y∈Ω_y with PDF f(y) is defined as

$$ S\left(f(y)\right)=-{\int}_{y\in {\Omega}_y}\ln \left(f(y)\right)f(x) dx $$

(1)

The ME principle states that the PDF which best represents the current information or constraints is the one with the largest entropy. Thus, if these constraints are known as statistical moments of arbitrary basis functions (h_i(y); i = 0, ..., m), the ME method can be defined as the following optimization problem:

$$ {\displaystyle \begin{array}{l}\max \kern0.4em \mathrm{S}\left(f(y)\right)\\ {}\mathrm{subject}\kern0.4em \mathrm{to}\\ {}{\int}_{y\in {\Omega}_y}{h}_i(y)f(y) dy={\mu}_i;\kern0.5em i=0,\cdots, m\end{array}} $$

(2)

where μ_i is the moment of the ith basis function.

The above optimization problem could be solved by introducing Lagrangian function L with the corresponding multiplier λ_i, written as

$$ L\left(f(y),\lambda \right)=S\left(f(y)\right)-\sum \limits_{i=0}^m{\lambda}_i\left({\int}_{y\in {\Omega}_y}{h}_i(y)f(y) dy-{\mu}_i\right) $$

(3)

Thus, this optimization problem is reduced to find the maximum value of (3):

$$ \frac{\partial L\left(f(y),\lambda \right)}{\partial f(y)}={\int}_{y\in {\Omega}_y}\left(-1-\ln \left(f(y)\right)-\sum \limits_{j=0}^m{\lambda}_j{h}_j(y)\right) dy=0 $$

(4)

Therefore, the generic form of the PDF f(y) is

$$ f(y)=\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{h}_j(y)\right) $$

(5)

where λ_i becomes undetermined parameter which makes PDF satisfy constraints in (2). Furthermore, if basis function h_i(y) is taken as monomial yⁱ, the zeroth normalized condition is given as ${\int}_{y\in {\Omega}_y}f(y) dy=1$.

Since (2) and (5) are non-linear, a number of optimization techniques, such as Newton method or its improved versions (Kelley 1999) and the BFGS procedure (Abramov 2009), could be utilized to solve this problem. We would not go into detail on these algorithms here. However, the common feature of them is that all of these methods suffer the iterative procedure which is confronted with the challenge of convergence, especially when it comes to high order moment. However, high order moment information may be necessary for more accurate estimation of PDF in general. So, it might pose a dilemma for ME method. Although some researchers propose to mitigate this problem by introducing orthogonal polynomials like Chebyshev or Lagrange polynomials for PDF fitting, many numerical difficulties still remain. In addition, the high order moment evaluations are also a problem in practice.

2.2 Proposed analytical maximum entropy method

To overcome the problems discussed above, we first attempt to solve the optimization problem analytically. And then, we employ PCE algorithm to deal with high order moment calculation. The later one will be discussed in Section 3. The original idea behind the proposed method is to avoid iterative procedure by using the exponential form of response PDF f(y). In other words, the undetermined parameters λ_i could be separated from exponential function using integration by parts for each moment constraint in (2), while the form of exponent remains and it could be converted to several different order moment constraints. Note the fact that the moment constraint itself could be treated as a whole and replaced by a known moment value, λ_i could become independent from original non-linear PDF f(y) after separation. In this way, with the known moment information, the optimization problem could be transformed into a system of linear equations, and λ_i could be solved analytically.

However, there is a potential problem with this idea, that is, higher order moments required in our method may be computationally instable. This phenomenon would lead to unbalanced non-linearities and ill-conditioned matrix for linear equations mentioned above. To deal with this problem, we introduce the well-known Chebyshev polynomials to improve the quality of matrix. The detail is given as follows.

Consider the limit state function y = g(x) where x = (x₁,…,x_n) ∈Ωⁿ is an n-dimensional random input. We assume that the form of response PDF is given as

$$ f(y)=\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) $$

(6)

where T_j(y) is the jth Chebyshev polynomial (see Appendix 1 (Mason and Handscomb 2002)). Without loss of generality, we would solve this problem and associated unknown λ_i in the interval [− 1, 1]. Other cases could be discussed at the end of this section. Thus, (6) is subject to the following constraints:

$$ {\int}_{-1}^1{T}_i(y)f(y) dy={M}_i;\kern0.5em i=0,\cdots, m $$

(7)

where M_i is the moment associated with ith Chebyshev polynomial T_i(y). To avoid confusion with the classic monomial moment, e.g., E(y), E(y²), etc., we call M_i as Chebyshev moment here.

According to the recurrence relation of Chebyshev polynomials in Appendix 1, a linear transformation is available as (8) or (9)

$$ {\displaystyle \begin{array}{l}\frac{1}{4}{M}_1-\frac{1}{4}{M}_3\\ {}={\int}_{-1}^1\frac{1}{4}{T}_1(y)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy-{\int}_{-1}^1\frac{1}{4}{T}_3(y)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\\ {}={\int}_{-1}^1\frac{1}{4}\left({T}_1(y)-{T}_3(y)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right)\\ {}={\int}_{-1}^1\left({T}_1(y)-\frac{1}{4}\left({T}_1(y)+{T}_3(y)\right)-\frac{1}{2}{T}_1(y)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\\ {}={\int}_{-1}^1\left({T}_1(y)-\frac{1}{2}{xT}_2(y)-\frac{1}{2}{xT}_0(y)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\\ {}={\int}_{-1}^1\left({T}_1(y)-{x}^2{T}_1(y)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\end{array}} $$

(8)

and for i ≥ 2

$$ {\displaystyle \begin{array}{l}\frac{1}{2}{M}_i-\frac{1}{4}{M}_{i+2}-\frac{1}{4}{M}_{i-2}\\ {}={\int}_{-1}^1\left(\frac{1}{2}{T}_i(y)-\frac{1}{4}{T}_{i+2}(y)-\frac{1}{4}{T}_{i-2}(y)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\\ {}={\int}_{-1}^1\left({T}_i(y)-\frac{1}{2}\left(\frac{T_{i+2}(y)+{T}_i(y)}{2}\right)-\frac{1}{2}\left(\frac{T_i(y)+{T}_{i-2}(y)}{2}\right)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\\ {}={\int}_{-1}^1\left({T}_i(y)-\frac{1}{2}{xT}_{i+1}(y)-\frac{1}{2}{xT}_{i-1}(y)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\\ {}={\int}_{-1}^1\left({T}_i(y)-{x}^2{T}_i(y)\right)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\end{array}} $$

(9)

In this way, the key step of the proposed method is to separate unknown λ_i in (5) with integration by parts. The reason why we take (1 − y²)T_i(y) instead of T_i(y) as basis function is to avoid definite integral term after parameter separation. For all i > 0, we have

$$ {\displaystyle \begin{array}{l}{\int}_{-1}^1\left(1-{y}^2\right){T}_i(y)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}={\int}_{-1}^1\left(1-{y}^2\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\frac{1}{2\left(i+1\right)}{dT}_{i+1}(y)\\ {}\kern0.8000001em -{\int}_{-1}^1\left(1-{y}^2\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\frac{1}{2\left(i-1\right)}{dT}_{i-1}(y)\end{array}} $$

(10)

By implementing the relations among Chebyshev polynomials, (10) is derived as (11)-(12) if all Chebyshev moment information is given

$$ \frac{1}{16}\left(2{M}_2-{M}_4-{M}_0\right){\lambda}_1+\frac{1}{8}\left({M}_3-{M}_5\right){\lambda}_2+\frac{1}{16}\sum \limits_{j=3}^mj\left({M}_{j+1}-{M}_{j+3}+{M}_{j-3}-{M}_{j-1}\right){\lambda}_j=\frac{1}{4}\left({M}_1-{M}_3\right) $$

(11)

and for i ≥ 2

$$ {\displaystyle \begin{array}{l}\frac{1}{8\left(i+1\right)}\sum \limits_{j=1}^ij\left({M}_{i+j}-{M}_{i+j+2}-{M}_{i-j}+{M}_{i-j+2}\right){\lambda}_j+\frac{1}{8}\left({M}_{2i+1}-{M}_{2i+3}\right){\lambda}_{i+1}\kern0.1em \\ {}+\frac{1}{8\left(i+1\right)}\sum \limits_{j=i+2}^mj\left({M}_{i+j}-{M}_{i+j+2}+{M}_{j-i-2}-{M}_{j-i}\right){\lambda}_j\\ {}-\frac{1}{8\left(i-1\right)}\sum \limits_{j=1}^{i-2}j\left({M}_{i+j-2}-{M}_{i+j}-{M}_{i-j-2}+{M}_{i-j}\right){\lambda}_j-\frac{1}{8}\left({M}_{2i-3}-{M}_{2i-1}\right){\lambda}_{i+1}\kern0.1em \\ {}-\frac{1}{8\left(i-1\right)}\sum \limits_{j=i+2}^mj\left({M}_{i+j-2}-{M}_{i+j}+{M}_{j-i}-{M}_{j-i+2}\right){\lambda}_j\\ {}=\left(\frac{1}{2}-\frac{1}{2\left(i+1\right)}+\frac{1}{2\left(i-1\right)}\right){M}_i-\left(\frac{1}{4}+\frac{1}{2\left(i+1\right)}\right){M}_{i+2}-\left(\frac{1}{4}-\frac{1}{2\left(i-1\right)}\right){M}_{i-2}\end{array}} $$

(12)

Appendix 2 provides the details of solving procedure. The (11)-(12) is a system of linear equations, and it could be rewritten as the following matrix form:

$$ \left[\begin{array}{cccc}{A}_{11}& {A}_{12}& \cdots & {A}_{1m}\\ {}{A}_{21}& {A}_{22}& \cdots & {A}_{2m}\\ {}\vdots & \vdots & \ddots & \vdots \\ {}{A}_{m1}& {A}_{m2}& \cdots & {A}_{mm}\end{array}\right]\left[\begin{array}{c}{\lambda}_1\\ {}{\lambda}_2\\ {}\vdots \\ {}{\lambda}_m\end{array}\right]=\left[\begin{array}{c}{B}_1\\ {}{B}_2\\ {}\vdots \\ {}{B}_m\end{array}\right] $$

(13)

where ${A}_{11}=\frac{1}{16}\left(2{M}_2-{M}_4-{M}_0\right)$

$$ {A}_{12}=\frac{1}{8}\left({M}_3-{M}_5\right) $$

$$ {A}_{1m}=\frac{m}{16}\left({M}_{m+1}-{M}_{m+3}+{M}_{m-3}-{M}_{m-1}\right) $$

$$ {A}_{21}=\frac{1}{24}\left(2{M}_3-{M}_5-{M}_1\right) $$

$$ {A}_{22}=\frac{1}{12}\left({M}_4-{M}_6-{M}_0+{M}_2\right) $$

$$ {A}_{2m}=\frac{m}{24}\left({M}_{m+2}-{M}_{m+4}+{M}_{m-4}-{M}_{m-2}\right)-\frac{m}{8}\left({M}_{m-2}-{M}_{m+2}\right) $$

$$ {A}_{m1}=\frac{1}{8\left(m+1\right)}\left(2{M}_{m+1}-{M}_{m+3}-{M}_{m-1}\right)-\frac{1}{8\left(m-1\right)}\left(2{M}_{m-1}-{M}_{m+1}-{M}_{m-3}+{M}_{m-1}\right) $$

$$ {A}_{m2}=\frac{1}{4\left(m+1\right)}\left({M}_{m+2}-{M}_{m+4}-{M}_{m-2}+{M}_m\right)-\frac{1}{4\left(m-1\right)}\left({M}_m-{M}_{m+2}-{M}_{m-4}+{M}_{m-2}\right) $$

$$ {A}_{mm}=\frac{m}{8\left(m+1\right)}\left({M}_{2m}-{M}_{2m+2}-{M}_0+{M}_2\right)-\frac{m}{8\left(m-1\right)}\left({M}_{2m-2}-{M}_{2m}+{M}_0-{M}_2\right) $$

$$ {B}_1=\frac{1}{4}\left({M}_1-{M}_3\right) $$

$$ {B}_2=\frac{3}{4}{M}_2-\frac{1}{2}{M}_3+\frac{1}{4}{M}_0 $$

$$ {B}_m=\left(\frac{1}{2}-\frac{1}{2\left(m+1\right)}+\frac{1}{2\left(m-1\right)}\right){M}_m-\left(\frac{1}{4}+\frac{1}{2\left(m+1\right)}\right){M}_{m+2}-\left(\frac{1}{4}-\frac{1}{2\left(m-1\right)}\right){M}_{m-2} $$

The equations could be used to solve λ_i analytically. The result is an exact solution without convergence error.

Moreover, if i = 0, we have the following equation:

$$ {M}_0={\int}_{-1}^1{T}_0(y)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy={\int}_{-1}^1\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy=\exp \left(-1-{\lambda}_0\right){\int}_{-1}^1\exp \left(-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy $$

(14)

That is, λ₀ is derived as

$$ {\lambda}_0=-1-\ln \left({\int}_{-1}^1\exp \left(-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy\right) $$

(15)

Therefore, the failure probability of given model could be computed by integration as follows:

$$ {P}_f={\int}_{-1}^0f(y) dy={\int}_{-1}^0\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy $$

(16)

In addition, since T_i(y) itself is a polynomial form based on monomial y lower than ith order, the Chebyshev moment M_i corresponding to T_i(y) could be calculated by the linear combination of traditional monomial moments, e.g., M₄ = 8E(y⁴) − 8E(y²) + 1. It is shown that each Chebyshev moment includes both high order and low order classical monomial moment information. This property could avoid unbalanced non-linearities. It is because the value of response domain is within the interval [− 1, 1], and there would not be divergence of monomial moments as well as Chebyshev moments. In addition, even if the moment value is close to zero as the order of monomial moment increase, the low order monomial moment in Chebyshev moment could compensate for this and the high order Chebyshev moment would not be zero, which makes the matrix of (13) non-singular.

It should be noted that the analytical method mentioned above requires that the response of given model should belong to the interval [− 1, 1], which may be violated in many cases. Thus, the arc-tangent transformation is taken as (17) where the value domain of response is [− 1, 1].

$$ y=\frac{2}{\pi}\mathrm{arc}\tan \left(g\left(\boldsymbol{x}\right)/k\right) $$

(17)

The reasons of this transformation are (1) the magnitude of high order moment is under control without divergence; (2) The interval [− 1, 1] is in accord with Chebyshev polynomials, and the fitting accuracy is assured; (3) it could avoid truncated error of integral interval during calculation procedure if the interval of response is unknown and an assumed interval is taken.

In general, the existing methods are developed based on classic ME algorithm framework, which obtains results by iterative procedure using low order moments, and the accuracy of these methods depends on iteration times. Compared with these ME methods, the efficiency of our analytical method could be significantly improved, because it could avoid iterative procedure based on high order moment.

2.3 Example

The efficiency of our method is inherently better than classic methods, and we test two examples to illustrate the accuracy of proposed method. The first one is a complicated bi-model, which is used to test failure PDF fitting in structural reliability analysis, and the second one is a difficult step function, which is used to test the stability of our algorithm. Without loss of generality, the initial values of unknowns in classic ME are all zeros. In addition, the evaluation criteria of PDF fitting is the root mean square error (RMSE), which is defined as

$$ MSE=\sqrt{\frac{1}{n}\sum \limits_{i=1}^n{\left(f\left({x}_i\right)-{f}_{ME}\left({x}_i\right)\right)}^2} $$

(18)

where f(x) is the original PDF and f_ME(x) is the ME PDF obtained by our method or classic ME method. n is the number of discrete points within the interval [− 1, 1], and x_i is the sequential discrete point. In our cases, n is chosen to be 10,000.

The bi-modal PDF is a sum of two Gaussian PDFs. Its total area is normalized to [− 1, 1]. The results presented in Fig. 1 and Table 1 indicate that the accuracy and efficiency of our method are both better than the classic method. When m is 8, RMSE of our method is 4.3026 × 10⁻², and RMSE of the classic method is 4.8732 × 10⁻² with 30 iteration. What’s more, if the accuracy is not acceptable when m is 8, our method could improve the accuracy using larger moments, e.g., when m = 16, the PDF fitting is close to the exact one, whose RMSE is about 0.00125. While, the classic method may not be able to execute due to unbalanced non-linearities and ill-conditioned Jacobian matrices.

Fig. 1

The approximation of bi-modal PDF. a The results obtained by proposed method. b The results obtained by classic method

Table 1 The comparison between proposed method and classic method for bi-modal PDF fitting

Then, we would compare the results of step PDF fitting with our method and the classic method in Fig. 2 and Table 2. Since the step PDF is a difficult function, both methods may not be able to describe it precisely. The accuracy of our method is less than that of the classic method; however, our method could improve its performance by increasing the moment constraints. When m is 16, RMSE of step PDF fitting using our method is 6.3264. While, the classic method may not execute due to unbalanced non-linearities and ill-conditioned Jacobian matrices. Besides, there is no iterative procedure using our method, which is more efficient than the classic method. With equivalent calculation cost, our method is more accurate than the classic method. For example, when m is 2, the RMSE of our method is 13.8951 × 10⁻², and that of the classic method is 19.3571 × 10⁻² with 1 iteration.

Fig. 2

The approximation of step PDF. a The results obtained by proposed method. b The results obtained by classic method

Table 2 The comparison between proposed method and classic method for step PDF fitting

Thus, the proposed method may be an efficient algorithm for PDF fitting in reliability analysis compared with the classic method at similar accuracy.

When it comes to engineering applications, it may not be able to obtain moment information directly. The traditional MCS approach is time-consuming and unstable for high order moment calculation. Thus, we propose to take PCE algorithm to provide such information as in Ref. (Chakraborty and Chowdhury 2015; Lasota et al. 2015). However, it may not be convenient for PCE to offer high order moments except for the first two moments. Therefore, the key point of proposed method then becomes high order computation based on PCE.

3 PCE for high order moment calculation

In this section, the classic PCE would be extended for high order moment calculation, which then would be used as inputs for ME method above. We would first introduce the classic PCE and its global statistical properties for the first two order moments. Then, the classic PCE would be developed for high order moments by PCE multiplication, while the accuracy of these results would be proved.

3.1 The PCE algorithm

PCE, which was originally introduced by Wiener, employs the Hermite polynomials in the random space to approximate the Gaussian stochastic processes. In Xiu and Em Karniadakis (2002), Xiu and Karniadakis developed the PCE under Wiener-Askey scheme that could be applied for non-Gaussian scenarios. It could uniformly approximate any random process with finite second order moments.

Consider the model y = g(x) in Section 2.1 again. Then, let ${\left\{{\xi}_i\right\}}_{i=0}^n$ be independent standardized orthogonal random variables associated with ${\left\{{x}_i\right\}}_{i=1}^n$. For example, if x_i~N(2, 0.5), then we have x_i = 0.5ξ_i + 2 where ξ_i is subject to the standardized normal distribution N(0, 1).

Then, the PCE of the limit state function is (Sudret 2008)

$$ {\displaystyle \begin{array}{l}y={g}_{\mathrm{PCE}}\left(\boldsymbol{\xi} \right)={c}_0{\psi}_0+\sum \limits_{i_1=1}^n{c}_{i_1}{\psi}_1\left({\xi}_{i_1}\right)+\sum \limits_{i_1=1}^n\sum \limits_{i_2=1}^{i_1}{c}_{i_1{i}_2}{\psi}_2\left({\xi}_{i_1},{\xi}_{i_2}\right)\\ {}\kern5.699997em +\sum \limits_{i_1=1}^n\sum \limits_{i_2=1}^{i_1}\sum \limits_{i_3=1}^{i_2}{c}_{i_1{i}_2{i}_3}{\psi}_3\left({\xi}_{i_1},{\xi}_{i_2},{\xi}_{i_3}\right)+\cdots \end{array}} $$

(19)

where ${\left\{{c}_j\right\}}_{j=0}^{\infty }$ are the coefficients, and ${\psi}_s\left({\xi}_{i_1},\cdots, {\xi}_{i_s}\right)$ denotes the polynomial chaos basis of sth degree in terms of multi-dimensional standardized random variables ξ = (ξ₁, ⋯, ξ_n)^T. In addition, the expansion bases ${\left\{{\psi}_s\right\}}_{s=0}^{\infty }$ are multi-dimensional hyper-geometric polynomials, which are defined as tensor products of the corresponding one-dimensional orthogonal polynomial ${\left\{{\phi}_k\right\}}_{k=0}^{\infty }$, that is,

$$ {\psi}_s\left({\xi}_1,{\xi}_2,\cdots, {\xi}_s\right)=\prod \limits_{k=1}^s{\phi}_{\alpha_k}\left({\xi}_k\right)\kern0.1em $$

(20)

where ϕ_i is a one-dimensional orthogonal basis with orthogonality relation

$$ \left\langle {\phi}_i,{\phi}_j\right\rangle =\left\langle {\phi}_i^2\right\rangle {\delta}_{ij} $$

(21)

where δ_ij is the Kronecker delta, <•,•> denotes the ensemble average which is the inner product in Hilbert space. And αk is the vector of index, which is subjected to non-negative integer.

The type of orthogonal polynomials depends on the distributed type of input variables, e.g., the orthogonal polynomials corresponding to normal distribution are Hermite polynomials, while the orthogonal polynomials corresponding to uniform distribution are Legendre polynomials. If the distribution types of input variables are not the same, Isukapalli provided several distribution transformation relationships that map different distributions as functions of normal random variables (Isukapalli 1999). With the pre-processing, the problem of inconsistent distribution could be overcome.

In engineering practice, the PCE is truncated to finite terms. So, considering an n-dimensional orthogonal polynomial with the degree not exceeding p, (19) can be rewritten as another form with limited terms, that is,

$$ {\displaystyle \begin{array}{l}y\approx {y}_p={g}_{PCE}\left(\boldsymbol{\xi} \right)={c}_0+\sum \limits_{i=1}^n\sum \limits_{\boldsymbol{\alpha} \in {\varphi}_i}{c}_{\boldsymbol{\alpha}}{\psi}_{\boldsymbol{\alpha}}\left({\xi}_i\right)+\sum \limits_{1\le {i}_1<{i}_2\le n}\sum \limits_{\boldsymbol{\alpha} \in {\varphi}_{i_1{i}_2}}{c}_{\boldsymbol{\alpha}}{\psi}_{\boldsymbol{\alpha}}\left({\xi}_{i_1},{\xi}_{i_2}\right)+\cdots +\\ {}\sum \limits_{1\le {i}_1<\cdots <{i}_s\le n}\sum \limits_{\boldsymbol{\alpha} \in {\varphi}_{i_1\cdots {i}_s}}{c}_{\boldsymbol{\alpha}}{\psi}_{\boldsymbol{\alpha}}\left({\xi}_{i_1},\cdots, {\xi}_{i_s}\right)+\cdots +\sum \limits_{\boldsymbol{\alpha} \in {\varphi}_{1, 2,\cdots, n}}{c}_{\boldsymbol{\alpha}}{\psi}_{\boldsymbol{\alpha}}\left({\xi}_1,\cdots, {\xi}_n\right)\end{array}} $$

(22)

where the subscript α is a tuple defined as α = (α₁,…, α_n), and ${\varphi}_{i_1,\cdots, {i}_s}$ is defined as a realization of α = tuple so that only the indices {i₁,…,i_s} are non-zeros:

$$ {\varphi}_{i_1,\cdots, {i}_s}=\left\{\boldsymbol{\alpha} :\kern0.4em \begin{array}{c}{\alpha}_k>0\kern0.9000001em \forall k=1,2,\cdots, n.\kern0.5em k\in \left({i}_1,\cdots, {i}_s\right)\\ {}{\alpha}_k=0\kern0.9000001em \forall k=1,2,\cdots, n.\kern0.5em k\notin \left({i}_1,\cdots, {i}_s\right)\end{array}\right\} $$

(23)

Correspondingly, the expansion bases ${\psi}_{\boldsymbol{\alpha}}\left(\boldsymbol{\xi} \right)=\prod \limits_{k=1}^n{\phi}_{\alpha_k}\left({\xi}_k\right)$, where $\sum \limits_{k=1}^j{\alpha}_k\le p$. Denote N as the total number of polynomials, and then we have

$$ N=\left(\begin{array}{c}n+p\\ {}p\end{array}\right)=\frac{\left(n+p\right)!}{n!p!} $$

(24)

Generally, (22) can be further simplified as

$$ {y}_p=\sum \limits_{j=0}^{N-1}{c}_j{\psi}_j\left(\boldsymbol{\xi} \right),\kern0.8000001em for\kern0.7em \boldsymbol{\xi} =\left({\xi}_1,\cdots, {\xi}_n\right) $$

(25)

where coefficient c_j and expansion base ψ_j(ξ) are corresponding to (22) sequentially.

Let ${\left\{{\xi}^i\right\}}_{i=1}^M$ denote a set of the random variable samples, and it could be determined by probabilistic collocation method (PCM). Again Let ${\left\{g\left({\boldsymbol{\xi}}^i\right)\right\}}_{i=1}^M$ denote the corresponding set of model output or response, where M is the number of samples. Denoting c = (c₀,…,c_N − 1)^T, an approximation $\hat{\boldsymbol{c}}$ could be given by least squares algorithm:

$$ \hat{c}=\arg \underset{\boldsymbol{c}}{\min}\sum \limits_{i=1}^M{\left(g\left({\boldsymbol{\xi}}^i\right)-\sum \limits_{j=0}^N{c}_j{\psi}_j\left({\boldsymbol{\xi}}^i\right)\right)}^2 $$

(26)

where M is suggested to be selected as M = 2(N + 1) (Isukapalli 1999).

Due to the orthogonality of the basis, the mean value and the variance of y in (25) can be calculated as (Sudret 2008)

$$ {\displaystyle \begin{array}{l}E\left({y}_p\right)={c}_0\\ {}V\left({y}_p\right)=\sum \limits_{j=1}^{N-1}{c}_j^2E\left({\psi}_j^2\left(\boldsymbol{\xi} \right)\right)\end{array}} $$

(27)

3.2 PCE for high order moment calculation

As could be seen above, the PCE could provide the first two order moments accurately. However, there are some difficulties for high order moment calculation. Consider the fact that PCE consists of orthonormal bases, and the product of two PCEs in (25) can be expanded as a linear combination of Hermite polynomials, we could make multiplication of orthogonal polynomials to obtain high order moments by (27). In Luo (2006), the generalization form of PCE multiplication based on (19) is presented. In this paper, we would apply this theory to the truncated PCE, and prove that the multiplication form could provide an accurate high order moment estimation under appropriate PCE degree.

Suppose u and v have PCE formula with the same n-dimensional standardized random variables ξ = (ξ₁, ⋯, ξ_n)^T but different degree p_α and p_β respectively. That is, $u=\sum \limits_{\left|\boldsymbol{\alpha} \right|\le {p}_{\alpha }}{u}_{\boldsymbol{\alpha}}{\psi}_{\boldsymbol{\alpha}}\left(\boldsymbol{\xi} \right)$, $v=\sum \limits_{\left|\boldsymbol{\beta} \right|\le {p}_{\beta }}{v}_{\boldsymbol{\beta}}{\psi}_{\boldsymbol{\beta}}\left(\boldsymbol{\xi} \right)$. If E(|uv|²) < ∞, then the product of u and v has the PCE formula

$$ uv=\sum \limits_{\left|\boldsymbol{\theta} \right|\le {p}_{\alpha }+{p}_{\beta }}\sum \limits_{0\le \boldsymbol{\beta} \le \boldsymbol{\theta}}\sum \limits_{\begin{array}{l}\left|\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\right|\le {p}_{\alpha },\\ {}\left|\boldsymbol{\beta} +\boldsymbol{r}\right|\le {p}_{\beta}\end{array}}C\left(\boldsymbol{\theta}, \boldsymbol{\beta}, \boldsymbol{r}\right){u}_{\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}}{v}_{\boldsymbol{\beta} +\boldsymbol{r}}{\psi}_{\boldsymbol{\theta}}\left(\boldsymbol{\xi} \right) $$

(28)

and

$$ C\left(\boldsymbol{\theta}, \boldsymbol{\beta}, \boldsymbol{r}\right)={\left[\left(\begin{array}{c}\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\boldsymbol{\beta} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\boldsymbol{\theta} \\ {}\boldsymbol{\theta} -\boldsymbol{\beta} \end{array}\right)\right]}^{\frac{1}{2}} $$

(29)

where the subscripts α, β, r, and θ are tuples associated with PCE terms, e.g., α = (α₁, α₂, …, α_n). We say β ≤ θ if β_i ≤ θ_i for all i = 1,2,…,n. The operation of these subscripts, such as + or −, is also defined as component-wise. Especially, the factorial of tuples is defined like α! = ∏_i α_i!. The proof is provided in Appendix 3.

Specifically, the mean of uv is

$$ E(uv)=\sum \limits_{\left|\boldsymbol{r}\right|\le \min \left({p}_{\alpha },{p}_{\beta}\right)}C\left(\boldsymbol{\theta} =\boldsymbol{0},\boldsymbol{\beta} =\boldsymbol{0},\boldsymbol{r}\right){u}_{\boldsymbol{r}}{v}_{\boldsymbol{r}}=\sum \limits_{\left|\boldsymbol{r}\right|\le \min \left({p}_{\alpha },{p}_{\beta}\right)}{u}_{\boldsymbol{r}}{v}_{\boldsymbol{r}} $$

(30)

Based upon the preparation above, we could calculate the high order moments of PCE by replacing u and v with two PCEs respectively. That is, u and v in (28) could be replaced by y_p, ${y}_p^2$, ${y}_p^3$, …, respectively as (31). Thus, the high order moments could be computed analytically.

$$ {\displaystyle \begin{array}{l}E\left({y}^2\left(\boldsymbol{\xi} \right)\right)\approx E\left({y}_p^2\left(\boldsymbol{\xi} \right)\right)=E\left({y}_p\left(\boldsymbol{\xi} \right)\cdot {y}_p\left(\boldsymbol{\xi} \right)\right)\\ {}E\left({y}^3\left(\boldsymbol{\xi} \right)\right)\approx E\left({y}_p^3\left(\boldsymbol{\xi} \right)\right)=E\left({y}_p^2\left(\boldsymbol{\xi} \right)\cdot {y}_p\left(\boldsymbol{\xi} \right)\right)\\ {}\kern5.199997em \vdots \\ {}E\left({y}^k\left(\boldsymbol{\xi} \right)\right)\approx E\left({y}_p^k\left(\boldsymbol{\xi} \right)\right)=E\left({y}_p^{\left\lfloor \frac{k}{2}\right\rfloor}\left(\boldsymbol{\xi} \right)\cdot {y}_p^{\left\lceil \frac{k}{2}\right\rceil}\left(\boldsymbol{\xi} \right)\right)\end{array}} $$

(31)

where ⌊•⌋ is rounded down and ⌈•⌉ is rounded up.

In addition, if E(y^k(ξ)) is required, it is not necessary to calculate the coefficients of y^k(ξ) when k is a positive even number. Instead, it could be obtained by an alternative approach as

$$ E\left({y}^k\left(\boldsymbol{\xi} \right)\right)=E{\left({y}^{\frac{k}{2}}\left(\boldsymbol{\xi} \right)\right)}^2+V\left({y}^{\frac{k}{2}}\left(\boldsymbol{\xi} \right)\right)\approx E{\left({y}_p^{\frac{k}{2}}\left(\boldsymbol{\xi} \right)\right)}^2+V\left({y}_p^{\frac{k}{2}}\left(\boldsymbol{\xi} \right)\right) $$

(32)

Since the PCE is L₂ convergence in the corresponding Hilbert functional space, that is

$$ \underset{p\to \infty }{\lim }E{\left({y}_p-y\right)}^2=0 $$

(33)

We could prove that moment evaluations by (32) are also accurate with L₂ convergence as

$$ \underset{p\to \infty }{\lim }E{\left({y}_p^k-{y}^k\right)}^2=0,\kern0.6em k=1,2,\dots $$

(34)

The detail is presented in Appendix 4. Specifically, for a given function or model, the main source of error for high order moment estimation comes from PCE approximation procedure itself, and there is no additional source of error in following PCE multiplication for high order moment estimation. In addition, the error of PCE decreases as the increasing of PCE degree, which in turn leads to error reduction of high order moment estimation. In this way, we could obtain the moment information precisely and efficiently using PCE multiplication above. And we also employ an example to show the accuracy of this method for high order moment estimation. Consider a function

$$ g=1.5-0.25{x}_1-0.05{x}_2^2{x}_3-0.05{x}_3^2\sin \left(\pi {x}_1\right) $$

(35)

where x₁~N(2, 0.2), x₂~N(3, 0.5), and x₃~N(1, 0.3). PCE of increasing degrees (p = 3, 5, 7) are used to estimate high order moments. The results are presented in Table 3 and Fig. 3. It is shown that the relative error of PCE for higher order moment estimation becomes larger as the order of moment increases. However, the relative error of moment estimations decreases with the increasing degree of PCE. This means that the error of proposed method could be controlled.

Table 3 The high order moment estimations and associated relative error with different PCE degrees

Fig. 3

The relative error of high order moment estimations with different PCE degrees

In real engineering application, it may introduce much computational burden if PCE degree is taken too large. A practical way is to calculate PCEs with small p and p + 1 degree respectively, which is followed by comparing the difference. If the difference is less than a pre-defined threshold, the PCE with p + 1 degree are adopted. Otherwise, PCE with p + 2 degree is used to repeat this procedure. Thus, the accuracy and efficiency are balanced for engineering practice.

4 Summary of proposed method

With the preparation of moment calculation algorithm and response PDF solving algorithm based on ME, this section presents a summary for structural reliability analysis using proposed analytical ME method. The difference between classic ME method and the proposed method is illustrated in Fig. 4. The general procedure of our method is shown as follows:

• (i) Compute the high order moment estimations by PCE and associated multiplication algorithm.

• Provide distribution type and distribution parameters of the input random variables, and then map these distributions into the same standard normal distribution.

• Compute PCE for limit state function using (26) where the response is converted to the interval [− 1, 1] by arc-tangent function as (17).

• Determine the number of moment constraints, which is marked as m. During this procedure, make multiplication of PCE and derive the moment order as (32), which is followed by computing associated Chebyshev moments according to the form of Chebyshev polynomials.

• (ii) Compute (13) and (15) analytically, which leads to explicit ME PDF. First, a pre-defined threshold value is taken. And then execute the proposed method with m constraints and m + 2 constraints respectively. If the difference of failure probabilities of two computations is less than a threshold value, we terminate the solving process and take the latter failure probability as the final result. Otherwise, another two higher moment constraints are used. The entire procedure is repeated until the convergence condition or threshold value is reached.

• (iii) Compute the failure probability by integration in interval [− 1, 0] as (16).

Fig. 4

The difference between classic ME method and proposed method

5 Application

In this section, two examples are taken to illustrate the performance of proposed method. The first example is a composite beam, and the second one is about a truss bridge structure. Both examples are conducted by MCS, FORM, SORM, the classic methods as well as the proposed method for comparison in accuracy and efficiency. Besides, the classic methods are implemented by two different moment calculation algorithms, that is, the sampling algorithm and the PCE algorithm.

5.1 A composite beam example

This example is taken from Ref. (Chakraborty and Chowdhury 2015). It is about a composite beam with an enhancement layer fastened to its bottom face as shown in Fig. 5. There are 20 independent random variables including cross-section geometric parameters of beam A and B with associated Young’s modulus E_w, cross-section geometric parameters of enhancement layer C and D with associated Young’s modulus E_a. Besides, six external forces P₁, P₂, P₃, P₄, P₅, and P₆ and their location are at a distance of L₁, L₂, L₃, L₄, L₅, and L₆ from the left end. Finally, the allowable stress is S. The details of these variables are presented in Table 4. And the limit state function is given as

$$ g\left(\boldsymbol{x}\right)=S-\frac{\left[\frac{\sum \limits_{i=1}^6{P}_i\left(L-{L}_i\right)}{L}{L}_3-{P}_1\left({L}_3-{L}_1\right)-{P}_2\left({L}_3-{L}_2\right)\right]K}{\frac{1}{12}{AB}^3+ AB{\left(K-0.5B\right)}^2+\frac{1}{12}\frac{E_a}{E_w}{CD}^3+\frac{E_a}{E_w} CD{\left(B+0.5D-K\right)}^2} $$

(36)

where

$$ K=\left[\frac{0.5{AB}^2+\frac{E_a}{E_w} CD\left(B+0.5D\right)}{AB+\frac{E_a}{E_w} CD}\right] $$

(37)

Fig. 5

The composite beam considered in Section 5.1

Table 4 The distribution parameters of input variable considered in Section 5.1

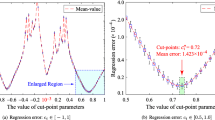
The results obtained from various methods are listed in Table 5. It is shown that proposed method could obtain an accurate result compared with other methods. Compared with the classic ME method, our method takes significantly fewer function evaluations. And compared to the classic ME method whose moment information is provided by PCE (Chakraborty and Chowdhury 2015), our method could generate a more accurate result without any iterative procedure even when the times of function evaluations are the same. Also, compared with the FORM or SORM when number of function evaluation is similar to our method, the accuracy of FORM and SORM is close to that of our method. Besides, the error of FORM or SORM is inherent to its mathematical formulation, and it may not be able to mitigate within its calculation process. When it comes to the proposed method, the error could be reduced by increasing the PCE degree, which is marked as p, and moment constraints, which is marked as m. For further demonstrating the performance, the convergent tendency of proposed method is presented in Table 6 where m = 2, 4, 6, and 8 are implemented successively. Besides, the relative error of power moments is also presented in Fig. 6 which takes m = 8 as example. It should be noted that the original response is transformed to interval [− 1, 1] by 2/π *atan(y/10), so the moments are less than 1. It is shown that the proposed method is convergent and both moment calculation and response PDF unknown solving are precise.

Table 5 Failure probability using various methods

Table 6 The failure probability obtained by different m when p = 4

Fig. 6

The error curve of example 1 by proposed method

5.2 A truss bridge example

In this example, a truss bridge is considered. The problem consists of steel bars and concrete deck subjected to gravity load and external force as shown in Figs. 7 and 8. For simplicity, all steel bars are the same I-steel. The length of each bar is 12 m, while width and thickness of the I-steel are 400 and 16 mm respectively. The thickness of concrete deck is 30 mm. The external force considered in this example is 10 kN. Six input variables, including the size of steel bar, Young’s modulus, and the external force, are all normally distributed, and their distribution parameters can be seen in Table 7. Besides, the limit state function is assumed to be g = 0.0085 − Δy, where Δy is the maximum displacement of the truss bridge.

Fig. 7

The front view of truss bridge considered in Section 5.2

Fig. 8

The finite element model considered in Section 5.2

Table 7 The distribution parameters of input variable considered in Section 5.2

The MCS, FORM, SORM, two classic ME methods with different moment calculation algorithms, and the proposed method are employed to calculate the failure probability, and the results are presented in Table 8.

Table 8 Failure probability using various methods

It could be seen that the proposed method with p = 5 and m = 6 obtains the best approximate result compared to the benchmark solution obtained using MCS. And the number of function evaluations of the proposed method is significantly less than MCS and the classic ME methods with traditional moment calculation algorithm. Thus, the performance of our method is better than classic ME method. On the other hand, if the efficiency is preferred, the proposed method could reduce the computational burden by decreasing PCE degree and moment constraints. Although the number of function evaluation of proposed method is slightly less than FORM or SORM when p = 3 and m = 2, the accuracies of these methods are also close. Therefore, the proposed method may be an alternative method for structural reliability analysis.

6 Conclusion

The paper presents a generic method for calculating structural reliability analytically. It is based on the maximum entropy principle in which Chebyshev polynomials are employed and unknown parameters in response probability density function are solved by an analytical approach. In addition, the polynomial chaos expansion and associated multiplication are introduced for accurate high order moment calculation, and the results are presented as inputs for analytical ME method above. The proposed method mainly has two advantages:

First of all, in contrast to popular ME algorithm, this method could exhibit excellent efficiency and convergence because the parameters in ME PDF is obtained analytically without iterative procedure. And the Chebyshev polynomials adopted in ME PDF mitigate the ill-conditional matrix during calculation procedure above.

Second, the PCE-based multiplication algorithm decreases the number of original limit state function evaluations to about 2(n + p)!/n!/p!, where p is the PCE order and n is the dimension of input. It could make high order moment evaluations efficient and accurate with a mean square convergent.

Third, compared with well-known FORM and SORM, the accuracy of proposed method is similar to that of FORM or SORM when the number of function evaluation is close. Moreover, the proposed method could improve the accuracy by increasing the PCE degree and moment constraints.

Several examples are presented to illustrate the numerical accuracy and efficiency of proposed method. It is shown that this method provides an alternate and efficient approach to analyze structural reliability problems.

Appendices

Appendix 1

1.1 Chebyshev polynomials

The definition of Chebyshev polynomials is

$$ {\displaystyle \begin{array}{l}{T}_0(x)=1,\\ {}{T}_n(x)=\frac{n}{2}\sum \limits_{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor }{\left(-1\right)}^k\frac{\left(n-k-1\right)!}{k!\left(n-2k\right)!}{(2x)}^{n-2k},\kern0.6em n\ge 1\end{array}} $$

(38)

and the most well-known form of Chebyshev polynomials is given by the recurrence relation

$$ {\displaystyle \begin{array}{l}{T}_0(x)=1,\\ {}{T}_1(x)=x,\\ {}{T}_{n+1}(x)=2{xT}_n(x)-{T}_{n-1}(x),\kern0.8000001em n\ge 2\end{array}} $$

(39)

where x∈[− 1, 1]. This definition is also referred as Chebyshev polynomials of the first kind, and there is another definition of Chebyshev polynomials of the second kind:

$$ {\displaystyle \begin{array}{l}{U}_0(x)=1,\\ {}{U}_1(x)=2x,\\ {}{U}_{n+1}(x)=2{xU}_n(x)-{U}_{n-1}(x),\kern0.8000001em n\ge 2\end{array}} $$

(40)

The relationship between these two kinds of Chebyshev polynomials are given as (41)-(44):

$$ \frac{dT_n(x)}{dx}={nU}_{n-1}(x) $$

(41)

$$ {T}_j(x){U}_k(x)=\left\{\begin{array}{cc}\frac{1}{2}\left({U}_{j+k}(x)+{U}_{k-j}(x)\right),& k\ge j-1,\\ {}\frac{1}{2}\left({U}_{j+k}(x)-{U}_{j-k-2}(x)\right),& k\le j-2.\end{array}\right. $$

(42)

with the convention U₋₁ ≡ 0.

$$ {T}_n(x)=\frac{1}{2\left(n+1\right)}\frac{dT_{n+1}(x)}{dx}-\frac{1}{2\left(n-1\right)}\frac{dT_{n-1}(x)}{dx},\kern0.9000001em \forall i\ge 1. $$

(43)

$$ \left(1-{x}^2\right){U}_{n-1}(x)={xT}_n(x)-{T}_{n+1}(x)=\frac{T_{n-1}(x)-{T}_{n+1}(x)}{2} $$

(44)

1.2 Hermite polynomials

The Hermite polynomials {H_n(x)}_n ≥ 0 are defined as

$$ {H}_n(x)={\left(-1\right)}^n{e}^{\frac{x^2}{2}}\frac{d^n}{dx^n}\left({e}^{-\frac{x^2}{2}}\right) $$

(45)

and the well-known recursive relation of the Hermite polynomials is

$$ \left\{\begin{array}{l}{H}_0(x)\equiv 1,\\ {}{H}_1(x)=2x,\\ {}{H}_{n+1}(x)=2{xH}_n(x)-2{nH}_{n-1}(x)\kern0.2em \end{array}\right. $$

(46)

Appendix 2

In this section, the derivation details of (12) is provided.

Consider (10), and take ${F}_1^{(i)}(y)={\int}_{-1}^1\left(1-{y}^2\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\frac{1}{2\left(i+1\right)}{dT}_{i+1}(y)$ and ${F}_2^{(i)}(y)={\int}_{-1}^1\left(1-{y}^2\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\frac{1}{2\left(i-1\right)}{dT}_{i-1}(y)$ for simplicity. Then, we would solve the two parts separately.

First of all, F₁⁽ⁱ⁾(x) could be transformed as

$$ {\displaystyle \begin{array}{l}{F}_1^{(i)}(y)={\left[\frac{1}{2\left(i+1\right)}\left(1-{y}^2\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\right]}_{-1}^1\\ {}\kern3.099999em -{\int}_{-1}^1\frac{1}{2\left(i+1\right)}{T}_{i+1}(y)\left[-2x+\left(1-{y}^2\right)\frac{d}{dy}\left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\right]\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}\kern2.4em =\frac{1}{i+1}{\int}_{-1}^1{yT}_{i+1}(y)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}\kern3.099999em +\frac{1}{2\left(i+1\right)}{\int}_{-1}^1{T}_{i+1}(y)\left(1-{y}^2\right)\frac{d}{dy}\left(\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\end{array}} $$

(47)

Take (39) into consideration, the first integral term above is derived as

$$ {\displaystyle \begin{array}{l}\frac{1}{i+1}{\int}_{-1}^1{yT}_{i+1}(y)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}=\frac{1}{i+1}{\int}_{-1}^1\frac{T_{i+1}(y)+{T}_i(y)}{2}\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}=\frac{1}{2\left(i+1\right)}\left({M}_{i+2}+{M}_i\right)\end{array}} $$

(48)

Then, take (41) and (42) into consideration, the second integral term in (47) is derived as

$$ {\displaystyle \begin{array}{l}\frac{1}{2\left(i+1\right)}{\int}_{-1}^1{T}_{i+1}(y)\left(1-{y}^2\right)\frac{d}{dy}\left(\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}=\frac{1}{2\left(i+1\right)}{\int}_{-1}^1{T}_{i+1}(y)\left(1-{y}^2\right)\left(\sum \limits_{j=1}^mj{\lambda}_j{U}_{j-1}(y)\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(x)\right) dy\\ {}=\frac{1}{2\left(i+1\right)}{\int}_{-1}^1\left(1-{y}^2\right)\left(\sum \limits_{j=1}^mj{\lambda}_j{T}_{i+1}(y){U}_{j-1}(y)\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}=\frac{1}{2\left(i+1\right)}{\int}_{-1}^1\left(1-{y}^2\right)\left[\begin{array}{l}\left(\sum \limits_{j=1}^ij{\lambda}_j\frac{U_{i+j}(y)-{U}_{i-j}(y)}{2}\right)+\left(i+1\right){\lambda}_{i+1}\frac{U_{2i+1}}{2}\\ {}+\left(\sum \limits_{j=i+2}^mj{\lambda}_j\frac{U_{i+j}(y)+{U}_{j-i-2}(y)}{2}\right)\end{array}\right]\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\end{array}} $$

(49)

where the Chebyshev polynomials of the second kind come as intermediate polynomials.

By using (44), the polynomial multiplication of Chebyshev polynomials in (49) is given as the following:

$$ {\displaystyle \begin{array}{l}\left(1-{y}^2\right)\frac{U_{i+j}(y)-{U}_{i-j}(y)}{2}=\frac{T_{i+j}(y)-{T}_{i+j+2}(y)}{2}-\frac{T_{i-j}(y)-{T}_{i-j+2}(y)}{2}\\ {}\left(1-{y}^2\right)\frac{U_{2i+1}}{2}=\frac{T_{2i+1}(y)-{T}_{2i+3}(y)}{2}\\ {}\left(1-{y}^2\right)\frac{U_{i+j}(y)+{U}_{j-i-2}(y)}{2}=\frac{T_{i+j}(y)-{T}_{i+j+2}(y)}{2}+\frac{T_{j-i-2}(y)-{T}_{j-i}(y)}{2}\end{array}} $$

(50)

Substitute (50) into (49), the second integral term in (47) is derived as follows:

$$ {\displaystyle \begin{array}{l}\frac{1}{2\left(i+1\right)}{\int}_{-1}^1{T}_{i+1}(y)\left(1-{y}^2\right)\frac{d}{dy}\left(\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}=\frac{1}{2\left(i+1\right)}{\int}_{-1}^1\left[\sum \limits_{j=1}^i\frac{j}{2}{\lambda}_j\left(\frac{T_{i+j}(y)-{T}_{i+j+2}(y)}{2}-\frac{T_{i-j}(y)-{T}_{i-j+2}(y)}{2}\right)\right]\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}\kern0.7em +\frac{1}{2\left(i+1\right)}{\int}_{-1}^1\frac{i+1}{2}{\lambda}_{i+1}\frac{T_{2i+1}(y)-{T}_{2i+3}(y)}{2}\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}\kern0.7em +\frac{1}{2\left(i+1\right)}{\int}_{-1}^1\sum \limits_{j=i+2}^m\frac{j}{2}{\lambda}_j\left(\frac{T_{i+j}(y)-{T}_{i+j+2}(y)}{2}+\frac{T_{j-i-2}(y)-{T}_{j-i}(y)}{2}\right)\exp \left(-1-\sum \limits_{j=0}^m{\lambda}_j{T}_j(y)\right) dy\\ {}=\frac{1}{8\left(i+1\right)}\sum \limits_{j=1}^ij\left({M}_{i+j}-{M}_{i+j+2}-{M}_{i-j}+{M}_{i-j+2}\right){\lambda}_j+\frac{1}{8}\left({M}_{2i+1}-{M}_{2i+3}\right){\lambda}_{i+1}\\ {}\kern0.9000001em +\frac{1}{8\left(i+1\right)}\sum \limits_{j=i+2}^mj\left({M}_{i+j}-{M}_{i+j+2}+{M}_{j-i-2}-{M}_{j-i}\right){\lambda}_j\end{array}} $$

(51)

By Combining (48) and (51), we have the following relationship:

$$ {\displaystyle \begin{array}{l}{F}_1^{(i)}(y)=\frac{1}{2\left(i+1\right)}\left({M}_{i+2}+{M}_i\right)+\frac{1}{8\left(i+1\right)}\sum \limits_{j=1}^ij\left({M}_{i+j}-{M}_{i+j+2}-{M}_{i-j}+{M}_{i-j+2}\right){\lambda}_j\\ {}\kern3.099999em +\frac{1}{8}\left({M}_{2i+1}-{M}_{2i+3}\right){\lambda}_{i+1}+\frac{1}{8\left(i+1\right)}\sum \limits_{j=i+2}^mj\left({M}_{i+j}-{M}_{i+j+2}+{M}_{j-i-2}-{M}_{j-i}\right){\lambda}_j\end{array}} $$

(52)

Secondly, when it comes to F₂⁽ⁱ⁾(x), it is a little more complicated. When i = 1, since T₀(x) is a constant according to the definition of Chebyshev polynomials. Otherwise, when i ≥ 2, we could derive F₂⁽ⁱ⁾(x) with a similar procedure as (47)-(51) with the following result:

$$ {\displaystyle \begin{array}{l}{F}_2^{(i)}(y)=\frac{1}{2\left(i-1\right)}\left({M}_i+{M}_{i-2}\right)+\frac{1}{8\left(i-1\right)}\sum \limits_{j=1}^{i-2}j\left({M}_{i+j-2}-{M}_{i+j}-{M}_{i-j-2}+{M}_{i-j}\right){\lambda}_j\\ {}\kern3.099999em +\frac{1}{8}\left({M}_{2i-3}-{M}_{2i-1}\right){\lambda}_{i+1}+\frac{1}{8\left(i-1\right)}\sum \limits_{j=i+2}^mj\left({M}_{i+j-2}-{M}_{i+j}+{M}_{j-i}-{M}_{j-i+2}\right){\lambda}_j\end{array}} $$

(53)

What is more, consider (8) and (9), we would establish the following equations. When i = 1, we have

$$ {\displaystyle \begin{array}{l}{\int}_{-1}^1\left(1-{y}^2\right){T}_1(y)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy={F}_1^{(1)}(y)\\ {}{\int}_{-1}^1\left(1-{y}^2\right){T}_i(y)\exp \left(-1-\sum \limits_{j=1}^m{\lambda}_j{T}_j(y)\right) dy={F}_1^{(i)}(y)-{F}_2^{(i)}(y)\end{array}} $$

(54)

and it could be rewritten as

$$ \frac{1}{16}\left(2{M}_2-{M}_4-{M}_0\right){\lambda}_1+\frac{1}{8}\left({M}_3-{M}_5\right){\lambda}_2+\frac{1}{16}\sum \limits_{j=3}^mj\left({M}_{j+1}-{M}_{j+3}+{M}_{j-3}-{M}_{j-1}\right){\lambda}_j=\frac{1}{4}\left({M}_1-{M}_3\right) $$

(55)

and for i ≥ 2

$$ {\displaystyle \begin{array}{l}\frac{1}{8\left(i+1\right)}\sum \limits_{j=1}^ij\left({M}_{i+j}-{M}_{i+j+2}-{M}_{i-j}+{M}_{i-j+2}\right){\lambda}_j+\frac{1}{8}\left({M}_{2i+1}-{M}_{2i+3}\right){\lambda}_{i+1}\kern0.1em \\ {}+\frac{1}{8\left(i+1\right)}\sum \limits_{j=i+2}^mj\left({M}_{i+j}-{M}_{i+j+2}+{M}_{j-i-2}-{M}_{j-i}\right){\lambda}_j-\frac{1}{8\left(i-1\right)}\sum \limits_{j=1}^{i-2}j\left({M}_{i+j-2}-{M}_{i+j}-{M}_{i-j-2}+{M}_{i-j}\right){\lambda}_j\\ {}-\frac{1}{8}\left({M}_{2i-3}-{M}_{2i-1}\right){\lambda}_{i+1}-\frac{1}{8\left(i-1\right)}\sum \limits_{j=i+2}^mj\left({M}_{i+j-2}-{M}_{i+j}+{M}_{j-i}-{M}_{j-i+2}\right){\lambda}_j\\ {}=\left(\frac{1}{2}-\frac{1}{2\left(i+1\right)}+\frac{1}{2\left(i-1\right)}\right){M}_i-\left(\frac{1}{4}+\frac{1}{2\left(i+1\right)}\right){M}_{i+2}-\left(\frac{1}{4}-\frac{1}{2\left(i-1\right)}\right){M}_{i-2}\end{array}} $$

(56)

Appendix 3

In this section, we would prove the formula of two PCEs multiplication.

First of all, for any non-negative integer α and β, the product of two Hermite polynomials can be expressed as (Savin and Faverjon 2017)

$$ {H}_{\alpha }(x){H}_{\beta }(x)=\sum \limits_{r\le \min \left(\alpha, \beta \right)}{\left[\left(\begin{array}{l}\alpha \\ {}r\end{array}\right)\left(\begin{array}{l}\beta \\ {}r\end{array}\right)\left(\begin{array}{c}\alpha +\beta -2r\\ {}\alpha -r\end{array}\right)\right]}^{\frac{1}{2}}{H}_{\alpha +\beta -2r}(x) $$

(57)

Then, this formula could be generalized to multi-dimensional form as (58).

$$ {\psi}_{\boldsymbol{\alpha}}\left(\boldsymbol{\xi} \right){\psi}_{\boldsymbol{\beta}}\left(\boldsymbol{\xi} \right)=\sum \limits_{r\le \min \left(\boldsymbol{\alpha}, \boldsymbol{\beta} \right)}B\left(\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{r}\right){\psi}_{\boldsymbol{\alpha} +\boldsymbol{\beta} -2\boldsymbol{r}}\left(\boldsymbol{\xi} \right) $$

(58)

where $B\left(\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{r}\right)={\left[\left(\begin{array}{l}\boldsymbol{\alpha} \\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{l}\boldsymbol{\beta} \\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\boldsymbol{\alpha} +\boldsymbol{\beta} -2\boldsymbol{r}\\ {}\boldsymbol{\alpha} -\boldsymbol{r}\end{array}\right)\right]}^{\frac{1}{2}}$, and the meaning of the notations above is shown in Section 3.2.

With the preparation, we could derive the multiplication of two PCEs as follows.

Suppose u and v have PCE formula with the same n-dimensional standardized random variables ξ = (ξ₁, ⋯, ξ_n)^T but different order p_α and p_β respectively. Namely, we have $u=\sum \limits_{\left|\boldsymbol{\alpha} \right|\le {p}_{\alpha }}{u}_{\boldsymbol{\alpha}}{\psi}_{\boldsymbol{\alpha}}\left(\boldsymbol{\xi} \right)$, $v=\sum \limits_{\left|\boldsymbol{\beta} \right|\le {p}_{\beta }}{v}_{\boldsymbol{\beta}}{\psi}_{\boldsymbol{\beta}}\left(\boldsymbol{\xi} \right)$. So the multiplication of u and v is

$$ {\displaystyle \begin{array}{l} uv=\sum \limits_{\left|\boldsymbol{\alpha} \right|\le {p}_{\alpha }}\sum \limits_{\left|\boldsymbol{\beta} \right|\le {p}_{\beta }}{u}_{\boldsymbol{\alpha}}{v}_{\boldsymbol{\beta}}{\psi}_{\boldsymbol{\alpha}}\left(\boldsymbol{\xi} \right){\psi}_{\boldsymbol{\beta}}\left(\boldsymbol{\xi} \right)\\ {}=\sum \limits_{\left|\boldsymbol{\alpha} \right|\le {p}_{\alpha }}\sum \limits_{\left|\boldsymbol{\beta} \right|\le {p}_{\beta }}{u}_{\boldsymbol{\alpha}}{v}_{\boldsymbol{\beta}}\sum \limits_{r\le \min \left(\boldsymbol{\alpha}, \boldsymbol{\beta} \right)}B\left(\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{r}\right){\psi}_{\boldsymbol{\alpha} +\boldsymbol{\beta} -2\boldsymbol{r}}\left(\boldsymbol{\xi} \right)\\ {}=\sum \limits_{\left|\boldsymbol{\alpha} \right|\le {p}_{\alpha }}\sum \limits_{\left|\boldsymbol{\beta} \right|\le {p}_{\beta }}{u}_{\boldsymbol{\alpha}}{v}_{\boldsymbol{\beta}}\sum \limits_{\boldsymbol{r}\le \min \left(\boldsymbol{\alpha}, \boldsymbol{\beta} \right)}\left(\begin{array}{c}\boldsymbol{\alpha} \\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\boldsymbol{\beta} \\ {}\boldsymbol{r}\end{array}\right)r!\frac{\sqrt{\left(\boldsymbol{\alpha} +\boldsymbol{\beta} -2\boldsymbol{r}\right)!}}{\sqrt{\boldsymbol{\alpha} !\boldsymbol{\beta} !}}{\psi}_{\boldsymbol{\alpha} +\boldsymbol{\beta} -2\boldsymbol{r}}\left(\boldsymbol{\xi} \right)\end{array}} $$

(59)

Let $\tilde{\boldsymbol{\alpha}}=\boldsymbol{\alpha} -\boldsymbol{r}$, $\tilde{\boldsymbol{\beta}}=\boldsymbol{\beta} -\boldsymbol{r}$, then r = min(α, β) is equivalent to $\tilde{\boldsymbol{\alpha}},\tilde{\boldsymbol{\beta}}\ge 0$. Alternatively, $\boldsymbol{\alpha} =\tilde{\boldsymbol{\alpha}}+\boldsymbol{r}$, $\boldsymbol{\beta} =\tilde{\boldsymbol{\beta}}+\boldsymbol{r}$ and the above summation can be rewritten as

$$ uv=\sum \limits_{\left|\tilde{\boldsymbol{\alpha}}\right|\le {p}_{\alpha }}\sum \limits_{\left|\tilde{\boldsymbol{\beta}}\right|\le {p}_{\beta }}\sum \limits_{\begin{array}{l}\left|\boldsymbol{r}+\tilde{\boldsymbol{\alpha}}\right|\le {p}_{\alpha },\\ {}\left|\boldsymbol{r}+\tilde{\boldsymbol{\beta}}\right|\le {p}_{\beta}\end{array}}{u}_{\tilde{\boldsymbol{\alpha}}+\boldsymbol{r}}{v}_{\tilde{\boldsymbol{\beta}}+\boldsymbol{r}}\left(\begin{array}{c}\tilde{\boldsymbol{\alpha}}+\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\tilde{\boldsymbol{\beta}}+\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)r!\frac{\sqrt{\left(\tilde{\boldsymbol{\alpha}}+\tilde{\boldsymbol{\beta}}\right)!}}{\sqrt{\left(\tilde{\boldsymbol{\alpha}}+\boldsymbol{r}\right)!\left(\tilde{\boldsymbol{\beta}}+\boldsymbol{r}\right)!}}{\psi}_{\tilde{\boldsymbol{\alpha}}+\tilde{\boldsymbol{\beta}}}\left(\boldsymbol{\xi} \right) $$

(60)

For simplicity, we still denote $\boldsymbol{\alpha} =\tilde{\boldsymbol{\alpha}}$ and $\boldsymbol{\beta} =\tilde{\boldsymbol{\beta}}$. Then, let θ = α + β, thus α = θ − β ≥ 0 and 0 ≤ β ≤ θ. The above summation is equivalent to

$$ {\displaystyle \begin{array}{l} uv=\sum \limits_{\left|\boldsymbol{\theta} \right|\le {p}_{\alpha }+{p}_{\beta }}\sum \limits_{\boldsymbol{\alpha} +\boldsymbol{\beta} =\boldsymbol{\theta}}\sum \limits_{\begin{array}{l}\left|\boldsymbol{\alpha} +\boldsymbol{r}\right|\le {p}_{\alpha },\\ {}\left|\boldsymbol{\beta} +\boldsymbol{r}\right|\le {p}_{\beta}\end{array}}{u}_{\boldsymbol{\alpha} +\boldsymbol{r}}{v}_{\boldsymbol{\beta} +\boldsymbol{r}}\left(\begin{array}{c}\boldsymbol{\alpha} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\boldsymbol{\beta} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)r!\frac{\sqrt{\boldsymbol{\theta} !}}{\sqrt{\left(\boldsymbol{\alpha} +\boldsymbol{r}\right)!\left(\boldsymbol{\beta} +\boldsymbol{r}\right)!}}{\psi}_{\boldsymbol{\theta}}\left(\boldsymbol{\xi} \right)\\ {}=\sum \limits_{\left|\boldsymbol{\theta} \right|\le {p}_{\alpha }+{p}_{\beta }}\sum \limits_{0\le \boldsymbol{\beta} \le \boldsymbol{\theta}}\sum \limits_{\begin{array}{l}\left|\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\right|\le {p}_{\alpha },\\ {}\left|\boldsymbol{\beta} +\boldsymbol{r}\right|\le {p}_{\beta}\end{array}}{u}_{\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}}{v}_{\boldsymbol{\beta} +\boldsymbol{r}}\left(\begin{array}{c}\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\boldsymbol{\beta} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)r!\frac{\sqrt{\boldsymbol{\theta} !}}{\sqrt{\left(\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\right)!\left(\boldsymbol{\beta} +\boldsymbol{r}\right)!}}{\psi}_{\boldsymbol{\theta}}\left(\boldsymbol{\xi} \right)\end{array}} $$

(61)

For simplicity, denote

$$ C\left(\boldsymbol{\theta}, \boldsymbol{\beta}, \boldsymbol{r}\right)=\left(\begin{array}{c}\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)\left(\begin{array}{c}\boldsymbol{\beta} +\boldsymbol{r}\\ {}\boldsymbol{r}\end{array}\right)r!\frac{\sqrt{\boldsymbol{\theta} !}}{\sqrt{\left(\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\right)!\left(\boldsymbol{\beta} +\boldsymbol{r}\right)!}} $$

(62)

Thus, we have

$$ uv=\sum \limits_{\left|\boldsymbol{\theta} \right|\le {p}_{\alpha }+{p}_{\beta }}\sum \limits_{0\le \boldsymbol{\beta} \le \boldsymbol{\theta}}\sum \limits_{\begin{array}{l}\left|\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}\right|\le {p}_{\alpha },\\ {}\left|\boldsymbol{\beta} +\boldsymbol{r}\right|\le {p}_{\beta}\end{array}}C\left(\boldsymbol{\theta}, \boldsymbol{\beta}, \boldsymbol{r}\right){u}_{\boldsymbol{\theta} -\boldsymbol{\beta} +\boldsymbol{r}}{v}_{\boldsymbol{\beta} +\boldsymbol{r}}{\psi}_{\boldsymbol{\theta}}\left(\boldsymbol{\xi} \right) $$

(63)

which completes the proof.

Appendix 4

In this section, we would prove the statement in Section 3.2 that the multiplication of two PCEs converges in the L₂ sense. Let us consider a system as y = g(x) with independent distribution input x. And assume that the PCE approximation of this system is expressed as y_p = g_PCE(ξ), where p is the order of PCE, and ξ is the standard normal variable associated with input x. Then, since PCE is L₂ convergence, we have

$$ \underset{p\to \infty }{\lim }E{\left({y}_p-y\right)}^2=\underset{p\to \infty }{\lim }{\int}_{\Omega}{\left({y}_p-y\right)}^2f\left(\boldsymbol{x}\right)d\boldsymbol{x}=0 $$

(64)

where Ω is the domain of input x, and f(x) is the joint PDF that subjects to ∫_Ωf(x)dx = 1.

Therefore, ∀ 0 < ε < 1, ∃ n > N where N is a positive integer,

$$ \left|{\int}_{\Omega}{\left({y}_p-y\right)}^2f\left(\boldsymbol{x}\right)d\boldsymbol{x}\right|<\varepsilon <1 $$

(65)

Now considering the fact that (y_p − y)² ≥ 0, if (y_p − y)² ≥ 1, we would derive that

$$ \left|{\int}_{\Omega}{\left({y}_p-y\right)}^2f\left(\boldsymbol{x}\right)d\boldsymbol{x}\right|\ge \left|{\int}_{\Omega}f\left(\boldsymbol{x}\right)d\boldsymbol{x}\right|=1 $$

(66)

which is in contradiction with (65). So, we would have 0 ≤ (y_p − y)² < 1. This means that |y_p − y| is bounded.

Noting that the absolute value of response of given system is less than 1 in our proposed method, namely, |y| ≤ 1. So, we could obtain that

$$ \left|{y}_p\right|\le 2 $$

(67)

Now, we would prove the convergence of PCE multiplication. First of all, we would prove a basis inequality as

$$ {\displaystyle \begin{array}{l}{\left({y}_p^k-{y}^k\right)}^2={\left({y}_p-y\right)}^2{\left({y}_p^{k-1}+{y}_p^{k-2}y+\cdots {y}_p{y}^{k-2}+{y}^{k-1}\right)}^2\\ {}\kern4.599998em \le {\left({y}_p-y\right)}^2{\left(\left|{y}_p^{k-1}\right|+\left|{y}_p^{k-2}\right|\left|y\right|+\cdots \left|{y}_p\right|\left|{y}^{k-2}\right|+\left|{y}^{k-1}\right|\right)}^2\\ {}\kern4.499998em \le {\left({y}_p-y\right)}^2{\left({2}^{k-1}+{2}^{k-2}+\cdots 2+1\right)}^2\\ {}\kern4.499998em ={\left({y}_p-y\right)}^2{\left({2}^k-1\right)}^2\end{array}} $$

(68)

where k means the order of required moment.

Then, with this preparation, we could derive that for a limited number k,

$$ {\displaystyle \begin{array}{l}\underset{p\to \infty }{\lim }E{\left({y}_p^k-{y}^k\right)}^2=\underset{p\to \infty }{\lim }{\int}_{\Omega}{\left({y}_p^k-{y}^k\right)}^2f\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}\le \underset{p\to \infty }{\lim }{\int}_{\Omega}{\left({y}_p-y\right)}^2f\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}\le {\left({2}^k-1\right)}^2\underset{p\to \infty }{\lim }{\int}_{\Omega}{\left({y}_p-y\right)}^2f\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}=0\end{array}} $$

(69)

This means that if y_p is L₂ convergence with given system, the k-power of y_p also converges to y^k in L₂ sense. Thus, the approach of PCE multiplication could provide an accurate estimation of high order moment information. So, the proof completes.