Topology optimization of compliant mechanisms and structures subjected to design-dependent pressure loadings

Abstract

This article presents an extended algorithm for topology optimization of compliant mechanisms and structures with design-dependent pressure loadings using the moving iso-surface threshold (MIST) method. In this algorithm, the fluid-structure interface is modeled using the finite element method via considering equivalent virtual strain energy and work and is tracked by an element-based searching scheme. Design-dependent pressure loads are directly applied on interface boundary and are calculated as virtual work equivalent nodal forces in the interface elements based on the finite element formulation. Several numerical examples are presented for topology optimization of mean compliance and compliant mechanisms. The present algorithm is validated through benchmarking with the results in literature and/or full finite element analysis (FEA) results of the optimum compliant mechanism and structure designs.

1 Introduction

Compliant mechanism has promising applications in small-scaled morphing wing structures, due to its smooth shape movements and cost-effective manufacturing and maintenance, compared to rigid body mechanism (Sofla et al. 2010; Vasista et al. 2012; Weisshaar 2013). Inspired by cellular fluidic systems in natural plants, adaptive fluid pressurized actuators have exhibited large actuation, and their control can be implemented by regulating fluid pressures (Vos and Barrett 2011; Gramüller et al. 2015; Lv et al. 2016). Thus, by using compliant mechanism or structure with pneumatic or hydraulic pressure actuation, the generated structural configurational changes are expected to be smoother and more compatible compared to those actuated via concentrated or point load(s). For example, this is particularly important for achieving smooth morphing wing structures in aerospace applications and for achieving compatible shape changes in matching with surrounding structures in soft robots or wearable devices in biomedical applications.

Topology optimization of compliant mechanism has attracted a great research interest. Vast existing works focus on compliant mechanism actuated by fixed input load, such as single-input-single-output (SISO) (Sigmund 1997) and multi-input-multi-output (MIMO) (Saxena 2005) problems. Only very few works (Panganiban et al. 2010; Vasista and Tong 2012) have studied topology optimization of pressure-actuated compliant mechanism. In this type of problems, the loads involve design-dependent surface loadings, where the locations and directions of pressure can change with designs due to evolutions of interface boundary (Hammer and Olhoff 2000; Chen and Kikuchi 2001). Thus, major challenges are tracking and modeling of the fluid-structure interface.

To identify the fluid-structure interface boundary, a number of methods have been developed. For example, fictitious thermal or electrical field (Chen and Kikuchi 2001; Zheng et al. 2009) or iso-line (Hammer and Olhoff 2000; Du and Olhoff 2004; Lee and Martins 2012) have been adopted in solid isotropic material with penalization (SIMP) method. In the level set method (LSM), techniques were developed to track loaded boundaries from zero level set and topology boundary (Wang et al. 2015; Xia et al. 2015; Emmendoerfer et al. 2018). Moreover, element-based algorithm searching schemes using a criterion such as element density (Zhang et al. 2008) or element types (Chen and Kikuchi 2001; Picelli et al. 2019) to systematically identify interface elements in the fixed-grid mesh were also developed. In terms of modeling fluid-structure interface, methods such as equivalent nodal forces (Lee and Martins 2012; Wang et al. 2015; Emmendoerfer et al. 2018; Picelli et al. 2019) and enrichment via extended finite element method (XFEM) (Jenkins and Maute 2016) have been studied.

An alternative method is using hydrostatic incompressible fluid to transfer pressure loads to structure, in which determining and tracking the pressurized boundary is unnecessary (Sigmund and Clausen 2007). Based on this method, mixed displacement-pressure (u/P) coupling formulation (Sigmund and Clausen 2007; Bruggi and Cinquini 2009; Vasista and Tong 2012, 2013) and displacement-based nonconforming element (Jang and Kim 2009; Panganiban et al. 2010) have been developed to deal with the incompressibility.

Most research on topology optimization with design-dependent pressure loadings focuses on minimum compliance problems. In terms of topology optimization of pressure-actuated compliant mechanism problems, Panganiban et al. (2010) applied displacement-based nonconforming element and method of moving asymptotes (MMA) and Vasista and Tong (2012) employed mixed u/P formulation associated with the SIMP or MIST method, in which fluid-structure interface was not identified. In solving such a problem, the calculation of the sensitivity of the design-dependent force vector with respect to design variables and the searching of interface boundaries can be difficult (Hammer and Olhoff 2000; Chen and Kikuchi 2001; Du and Olhoff 2004; Sigmund and Clausen 2007). In MIST (Tong and Lin 2011), a physical response function and its threshold level are used in each iteration to define and update topology with a clear boundary without involving direct sensitivity analysis. These two features render MIST a potential candidate for solving the design-dependent topology optimization problem.

In this work, we develop an extended MIST-based algorithm to study topology optimization with design-dependent fluidic pressure loadings. For the sake of simplicity, fluid-structure interaction is handled by considering the structure subjected to fluidic pressure load without modeling of fluid field. Fluidic pressure is directly applied on interface boundary to simulate the real scenario of a pneumatic or hydraulic actuator and applied to interface elements as work equivalent nodal forces. A new general formulation of pressurized fluid-structure interface element based on the finite element method and equivalent virtual strain energy and work is also developed. Although equivalent nodal forces using Gaussian quadrature (Lee and Martins 2012; Wang et al. 2015; Picelli et al. 2019) have been studied, we derive and evaluate equivalent loads analytically via exact integration for iso-parametric bilinear rectangular elements and compared with Gaussian quadrature. Interface boundary is identified and tracked via an element-based algorithm searching scheme—fluid flooding method (Chen and Kikuchi 2001; Picelli et al. 2019). Numerical examples, including benchmark problems and typical compliant mechanism design cases, are presented to validate the present extended MIST algorithm and compare different methods of load calculations.

2 Problem formulation and discretization

2.1 Problem formulation

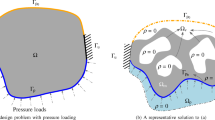
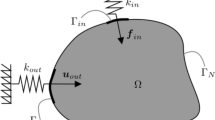
Considering a linear elastic body Ω subjected to general loading, including design-dependent load such as pressure, as shown in Fig. 1, the elastic body that produces a movement u_out at selected output port under a given loading forms a compliant mechanism. For such compliant mechanism, by using the concept from Frecker et al. (1997), the optimization problem can be defined as finding the optimum topology of the elastic body that maximizes the output displacement subject to satisfying the equilibrium equation and a given material volume constraint, and it can be mathematically formulated as follows:

$$ \max :{u}_{\mathrm{out}} $$

(1a)

$$ s.t.:\left\{\begin{array}{l}{\int}_{\Omega}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ \boldsymbol{\upsigma} d\Omega ={\int}_{\Omega}\ \updelta {\boldsymbol{u}}^{\mathrm{T}}\ {\mathbf{f}}_{\mathrm{b}}d\Omega +{\int}_{\Gamma}\ \updelta {\boldsymbol{u}}^{\mathrm{T}}\ {\mathbf{f}}_{\mathrm{p}}d\Gamma +\sum_{i=1}^{{\mathrm{N}}_{\mathrm{F}}}\updelta {{\mathbf{u}}_i}^{\mathrm{T}}{\mathbf{F}}_i\\ {}{\int}_{\Omega}d\Omega \le {V}_fV\end{array}\right. $$

(1b,c)

where u_out denotes the displacement at the output port; σ, f_b, f_p, and F_i (i = 1,2,…, N_F) represent the vectors of stress, body force, surface traction, and point loads, respectively; δε and δu are the vectors of virtual strain and displacement with T being transpose; Ω is the domain of the elastic body; Γ is the boundary of Ω on which a surface traction, whether design-dependent or independent, is known; and V_f and V denote the prescribed volume fraction and the total volume of Ω. In this study, we focus on design-dependent surface traction loading, such as pressure, by assuming f_b = 0 and F_i = 0. In addition to the compliant mechanism problem as defined in (1), we also consider the minimum mean compliance problem.

Fig. 1

An elastic body subjected to general loading, including design-dependent pressure load

The finite element method (FEM) has been used to solve the equilibrium equation in (1b) and to describe the topology of domain Ω through its discretization with a finite number of elements, each of which may contain one or more materials.

In order to describe the topology and conduct finite element (FE) analysis, we discretize the design domain Ω with a finite number of elements, $\Omega ={\bigcup}_{e=1}^{N_e}{\Omega}_{\mathrm{e}}$ (where e represents the eth element; N_e denotes the total number of elements, and Ω_e represents the domain of the eth element). In this case, assuming f_b = 0 and F_i = 0 and considering pressure loading only (Panganiban et al. 2010; Vasista and Tong 2012), the topology optimization problem in (1) can be rewritten as follows:

$$ \max :{u}_{\mathrm{out}} $$

(2a)

$$ s.t.:\left\{\begin{array}{l}\sum_{e=1}^{N_e}{\int}_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ \boldsymbol{\upsigma} d{\Omega}_{\mathrm{e}}=\sum_{e=1}^{N_e}{\int}_{\Gamma_{\mathrm{e}}}\ \updelta {\boldsymbol{u}}^{\mathrm{T}}\ {\mathbf{f}}_{\mathrm{p}}d{\Gamma}_{\mathrm{e}}\\ {}\sum_{e=1}^{N_e}{\int}_{\Omega_{\mathrm{e}}}d{\Omega}_{\mathrm{e}}\le {V}_fV\end{array}\right. $$

(2b,c)

In this study, the design-dependent surface traction f_p is assumed to be applied via quasi-static fluidic pressure loading, such as hydrostatic or air pressure. Hence, there are three types of fluid-structure interface elements with and without fluidic pressure as illustrated in Fig. 2. For a solid element with a pressure acting on one or more sides, the relevant equivalent load vector can be determined routinely. For a void element with internal pressure (or an internally pressurized void element), there is no need to consider an equivalent load vector because the internal fluid pressure acting on the element’s four sides can be balanced by neighboring adjacent elements. For an interface element with a solid and a pressurized void sub-element, because the void sub-element behaves similar to the void element, we only need to determine the equivalent nodal force vector of the pressure acting on the solid-void interface Γ_e in element Ω_e as shown in Fig. 3a, b or in an illustrative structure in Fig. 3c, d.

Fig. 2

Three types of elements with and without pressure

Fig. 3

Illustrative examples for a an interface element with two materials and a pressure; b the interface element homogenized based on equivalent strain energy and work; c fluid-structure interface, and d equivalent FE model homogenized based on equivalent strain energy and work

Without losing generality, let us consider an element Ω_e with two subdomains, Ω_ei (i = 1,2), of two different materials with or without design-dependent pressure acting on the interface Γ_e from materiel 2 to 1, as illustrated in Fig. 3a. This creates a requirement to evaluate the virtual strain energy and the associated virtual work done by such pressure for all elements. Our aim is to transform the element in Fig. 3a to a homogenized one with equivalent virtual strain energy and equivalent virtual work, such as the element shown in Fig. 3b with one material in Ω_e and equivalent nodal forces.

2.2 Equivalent strain energy

The virtual strain energy for an element with two subdomains in the equilibrium equation in (2b) can be evaluated as:

$$ {\displaystyle \begin{array}{c}{\int}_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ \boldsymbol{\upsigma} d{\Omega}_{\mathrm{e}}={\int}_{\Omega_{\mathrm{e}1}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_1d{\Omega}_{\mathrm{e}}+{\int}_{\Omega_{\mathrm{e}2}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_2d{\Omega}_{\mathrm{e}}\\ {}\kern4em ={f}_1\left({\Omega}_{\mathrm{e}1},\boldsymbol{\upvarepsilon}, {\boldsymbol{\upsigma}}_1\right){\int}_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_1d{\Omega}_{\mathrm{e}}+{f}_2\left({\Omega}_{\mathrm{e}2},\boldsymbol{\upvarepsilon}, {\boldsymbol{\upsigma}}_2\right){\int}_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_2d{\Omega}_{\mathrm{e}}\ \end{array}} $$

(3a)

where

$$ {\displaystyle \begin{array}{c}{f}_1\left({\Omega}_{\mathrm{e}1},\boldsymbol{\upvarepsilon}, {\boldsymbol{\upsigma}}_1\right)=\frac{\int_{\Omega_{\mathrm{e}1}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_1d{\Omega}_{\mathrm{e}}}{\int_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_1d{\Omega}_{\mathrm{e}}}\\ {}{f}_2\left({\Omega}_{\mathrm{e}2},\boldsymbol{\upvarepsilon}, {\boldsymbol{\upsigma}}_2\right)=\frac{\int_{\Omega_{\mathrm{e}2}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_2d{\Omega}_{\mathrm{e}}}{\int_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_2d{\Omega}_{\mathrm{e}}}\end{array}} $$

(3b)

where σ_i = D_iε (i = 1,2) represents the stress vectors in subdomain Ω_ei (i = 1,2).

To evaluate (3b), since stress and virtual strain vectors are continuous functions of global coordinates x and y (where (x, y) ∈ Ω_e or Ω_ei (i = 1, 2), the virtual strain energy densities δε^T σ_i (i = 1,2) are also continuous functions of x and y in Ω_ei (i = 1,2) and Ω_e. Thus, by using the first mean value theorem for definite integral, (3b) can be written as:

$$ {\displaystyle \begin{array}{c}{f}_i\left({\Omega}_{\mathrm{e}\mathrm{i}},\boldsymbol{\upvarepsilon}, {\boldsymbol{\upsigma}}_{\mathrm{i}}\right)=\frac{\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\left({\mathrm{x}}_{\mathrm{i}}^{\ast },{\mathrm{y}}_{\mathrm{i}}^{*}\right)\ {\boldsymbol{\upsigma}}_{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{i}}^{\ast },{\mathrm{y}}_{\mathrm{i}}^{*}\right)}{\updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right)\ {\boldsymbol{\upsigma}}_{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right)}\ \frac{\int_{\Omega_{\mathrm{e}\mathrm{i}}}d{\Omega}_{\mathrm{e}}}{\int_{\Omega_{\mathrm{e}}}d{\Omega}_{\mathrm{e}}\ }\ \end{array}} $$

(4)

where $\updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\left({\mathrm{x}}_{\mathrm{i}}^{\ast },{\mathrm{y}}_{\mathrm{i}}^{*}\right)\ {\boldsymbol{\upsigma}}_{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{i}}^{\ast },{\mathrm{y}}_{\mathrm{i}}^{*}\right)$ denotes the mean values of δε^T σ_i at $\left({\mathrm{x}}_{\mathrm{i}}^{\ast },{\mathrm{y}}_{\mathrm{i}}^{*}\right)\in {\Omega}_{\mathrm{ei}}$ (i = 1,2); δε^T(x_i, y_i) σ_i(x_i, y_i) represents the mean values of δε^T σ_i at (x_i, y_i) ∈ Ω_e (i = 1,2).

It is evident that the second ratio on the right-hand side of (4) represents the area ratio of material 1 or 2. For material 1, the area ratio can be expressed as:

$$ {\displaystyle \begin{array}{c}{x}_e=\frac{\ {\int}_{\Omega_{\mathrm{e}1}}d{\Omega}_{\mathrm{e}}}{\int_{\Omega_{\mathrm{e}}}\ d{\Omega}_{\mathrm{e}}}\ \end{array}} $$

(5)

The area ratio for material 2 can be defined as 1 − x_e. However, the virtual strain energy density ratio on the right-hand side of (4) depends on the real and virtual nodal displacements of the element and material properties. This makes it impossible to evaluate this ratio prior to solving the equilibrium equation in (2b). Therefore, as an approximation, one can assume that this energy density ratio is a function of the area ratio x_e. Thus, (3a) can be simplified approximately via (4)–(5) as follows:

$$ {\int}_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ \boldsymbol{\upsigma} d{\Omega}_{\mathrm{e}}=f\left({x}_e\right){\int}_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_1d{\Omega}_{\mathrm{e}}+g\left({x}_e\right){\int}_{\Omega_{\mathrm{e}}}\ \updelta {\boldsymbol{\upvarepsilon}}^{\mathrm{T}}\ {\boldsymbol{\upsigma}}_2d{\Omega}_{\mathrm{e}} $$

(6)

where f(x_e) is a user-defined function of the area ratio x_e and f(x_e) + g(x_e) = 1.

For the linear case, σ₁ = D₁ε and σ₂ = D₂ε, (6) can used in the displacement-based FE formulation to define the element stiffness matrix as:

$$ {\displaystyle \begin{array}{c}{\int}_{\Omega_{\mathrm{e}}}\ {\mathbf{B}}^{\mathbf{T}}{\mathbf{D}}_{\mathrm{e}}\mathbf{B}d{\Omega}_{\mathrm{e}}=f\left({x}_e\right){\int}_{\varOmega_e}{\mathbf{B}}^{\mathbf{T}}{\mathbf{D}}_1\mathbf{B}d{\varOmega}_e+g\left({x}_e\right){\int}_{\Omega_{\mathrm{e}}}{\mathbf{B}}^{\mathbf{T}}{\mathbf{D}}_2\mathbf{B}d{\Omega}_{\mathrm{e}}\ \end{array}} $$

(7)

or the material matrix for the homogenized element in Fig. 3b:

$$ {\displaystyle \begin{array}{c}{\mathbf{D}}_{\mathrm{e}}\left({x}_e\right)=f\left({x}_e\right){\mathbf{D}}_1+g\left({x}_e\right){\mathbf{D}}_2\ \end{array}} $$

(8)

where D_e, D₁, and D₂ represent the constitutive matrix of the element, material 1 and material 2, respectively and B denotes the strain-displacement matrix. Equation (8) can be viewed as a material interpolation or homogenization based on equivalent strain energy with function f(x_e). A number forms of such function have been proposed in the literature with material density or area ratio as a variable (e.g., power function in solid isotropic material with the penalization (SIMP) model (Bendsoe and Sigmund 2003) and the rational function in a rational approximation of material properties (RAMP) model (Stolpe and Svanberg 2001)). Among various proposed functions, the power function is probably the most common and classical choice, such as the following two-phase material interpolation (Bendsøe and Sigmund 1999; Emmendoerfer et al. 2018):

$$ {\displaystyle \begin{array}{c}{\mathbf{D}}_{\mathrm{e}}\left({x}_e\right)={x}_e^p{\mathbf{D}}_1+\left(1-{x}_e^p\right){\mathbf{D}}_2\ \end{array}} $$

(9)

The equivalent strain energy formulation in (7) together with (8) or (9) has been used in various topology optimization methods with x_e being either material density or area ratio, for example, in the SIMP method (Bendsoe and Sigmund 2003) or in the ersatz material model used in LSM (Emmendoerfer et al. 2018; Picelli et al. 2019) and MIST (Vasista and Tong 2012).

2.3 Equivalent nodal forces

The virtual work done by the pressure in the equilibrium (2b) needs to be discretized using the displacement-based FE formulation in order to determine the work equivalent nodal force vector. Consider a distributed pressure acting on the interface of an element in the direction pointing towards material 1 (from materials 2 to 1): f_p = P(ζ ) n, where P(ζ ) and n indicate its magnitude and direction vector as illustrated in Fig. 4. Linearly distributed pressure P(ζ ) = P₀ + P₁ζ is considered in this work, where ζ is a local parametric coordinate along Γ_e ranging between − 1 and 1 as shown in Fig. 4, and P₀ and P₁ are constants (for example, as shown in Fig. 4, P₀ = (P₅ + P₆)/2 and P₁ =  − (P₅ − P₆)/2, where P₅ and P₆ denote the pressure at nodes 5 and 6 with ζ =  − 1 and ζ = 1, respectively). From (2b), the work equivalent nodal force vector can be determined by:

$$ {\displaystyle \begin{array}{c}{\mathbf{F}}_{\mathrm{e}}={\int}_{\Gamma_{\mathrm{e}}}\ {\mathbf{N}}^{\mathbf{T}}\ {\mathbf{f}}_{\mathrm{p}}d{\Gamma}_{\mathrm{e}}=\left({\mathrm{P}}_0{\int}_{\Gamma_{\mathrm{e}}}\ {\mathbf{N}}^{\mathbf{T}}d{\Gamma}_{\mathrm{e}}+{\mathrm{P}}_1{\int}_{\Gamma_{\mathrm{e}}}\ {\mathbf{N}}^{\mathbf{T}}\upzeta d{\Gamma}_{\mathrm{e}}\right)\mathbf{n}=\left({\mathrm{P}}_0\ {\mathbf{N}}_{0\Gamma}+{\mathrm{P}}_1{\mathbf{N}}_{1\Gamma}\right)\ \mathbf{n}\ \end{array}} $$

(10)

where F_e is the equivalent load vector of element e; N represents the matrix of shape functions of an element, and

$$ {\displaystyle \begin{array}{c}{\mathbf{N}}_{0\Gamma}={\int}_{\Gamma_{\mathrm{e}}}\ {\mathbf{N}}^{\mathrm{T}}d{\Gamma}_{\mathrm{e}}={\int}_0^{{\mathrm{L}}_{\mathrm{c}}}\mathbf{N}{\left(\mathrm{S}\right)}^{\mathrm{T}}\ \mathrm{dS};\kern2em {\mathbf{N}}_{1\Gamma}={\int}_{\Gamma_{\mathrm{e}}}\ {\mathbf{N}}^{\mathrm{T}}\upzeta d{\Gamma}_{\mathrm{e}}={\int}_0^{{\mathrm{L}}_{\mathrm{c}}}\mathbf{N}{\left(\mathrm{S}\right)}^{\mathrm{T}}\ \upzeta \mathrm{dS}\end{array}} $$

(11)

where L_c denotes the length of the interface Γ_e and S represents the curvilinear coordinate along Γ_e, which is the interface boundary between materials 1 and 2 in element e. As an illustrative example, for the 4-node rectangular element with pressure applied on Γ_e as illustrated in Fig. 4, (10) and (11) define the equivalent nodal forces at the four nodes of the element. Hence, it is important to determine the integral in (11).

Fig. 4

Work equivalent nodal forces calculation and coordinate systems

Consider 4-node iso-parametric quadrilateral element with the following shape function matrix being used for displacements and global coordinates (x, y):

$$ {\displaystyle \begin{array}{c}\mathbf{N}=\left[\begin{array}{cccccccc}{N}_1& 0&{N}_2& 0&{N}_3& 0&{N}_4& 0\\ {}0&{N}_1& 0&{N}_2& 0&{N}_3& 0&{N}_4\end{array}\right]\ \end{array}} $$

(12a)

where

$$ {N}_i\left(\upxi, \upeta \right)=\frac{1}{4}\left(1+{\upxi}_{\mathrm{i}}\upxi\ \right)\left(1+{\upeta}_{\mathrm{i}}\upeta \right)\kern0.75em \left(i=1,2,3,4\right) $$

(12b)

and ξ and η are the usual parametric coordinates. We assume that the interface Γ_e is straight in the (ξ, η) space with (ξ_g, η_g) being the midpoint along its length. Thus, the straight line Γ_e can be defined in a parametric form as:

$$ {\displaystyle \begin{array}{c}\upxi \left(\upzeta \right)={\upxi}_g+{\upxi}_d\upzeta; \kern3em \upeta \left(\upzeta \right)={\upeta}_g+{\upeta}_d\upzeta \kern1em \end{array}} $$

(13)

where ζ is a local parametric coordinate along Γ_e similar to (ξ,η) and ranges between − 1 and 1. Substituting (13) into (12), we can define the integrand N(S)^T in (11) in terms of the local coordinate ζ as N(ξ(ζ), η(ζ))^T by using the iso-parametric definition of global coordinates (x, y), i.e., $x=\sum_{i=1}^4{N}_i\left(\upxi, \upeta \right){x}_i$ and $y=\sum_{i=1}^4{N}_i\left(\upxi, \upeta \right){y}_i$. Furthermore, we can also derive dS in (11) as:

$$ {\displaystyle \begin{array}{c}\mathrm{dS}=\sqrt{dx^2+{dy}^2}={S}_e\left(\upzeta \right)d\upzeta\ \end{array}} $$

(14a)

where

$$ {\displaystyle \begin{array}{c}{S}_e\left(\upzeta \right)={\left({\boldsymbol{d}}_{\upzeta}^T{\boldsymbol{J}}^T\left(\upzeta \right)\boldsymbol{J}\left(\upzeta \right){\boldsymbol{d}}_{\upzeta}\right)}^{\frac{1}{2}}\end{array}} $$

(14b)

and

$$ {\displaystyle \begin{array}{c}\boldsymbol{J}\left(\upzeta \right)=\left[\begin{array}{cc}{x}_{,\upxi}\left(\upzeta \right)&{x}_{,\upeta}\left(\upzeta \right)\\ {}{y}_{,\upxi}\left(\upzeta \right)&{y}_{,\upeta}\left(\upzeta \right)\end{array}\right];\kern3em {\boldsymbol{d}}_{\upzeta}={\left\{\begin{array}{cc}{\upxi}_d&{\upeta}_d\end{array}\right\}}^T\end{array}} $$

(14c)

where J(ζ) is the Jacobian matrix and d_ζ is the directional coefficient vector according to (13). Thus, (11) can be rewritten as follows:

$$ {\displaystyle \begin{array}{c}{\mathbf{N}}_{0\Gamma}={\int}_{-1}^1\mathbf{N}{\left(\upxi \left(\upzeta \right),\upeta \left(\upzeta \right)\right)}^{\mathrm{T}}{S}_e\left(\upzeta \right)\mathrm{d}\upzeta; \kern2.25em {\mathbf{N}}_{1\Gamma}={\int}_{-1}^1\mathbf{N}{\left(\upxi \left(\upzeta \right),\upeta \left(\upzeta \right)\right)}^{\mathrm{T}}{S}_e\left(\upzeta \right)\upzeta \mathrm{d}\upzeta \end{array}} $$

(15a)

Due to the presence of the term S_e(ζ), the matrices N_0Γ and N_1Γ in (15a) can be only evaluated via numerical integration methods. By using Gaussian quadrature, we have

$$ {\displaystyle \begin{array}{c}{\mathbf{N}}_{0\Gamma}=\sum_{\boldsymbol{i}=\mathbf{1}}^{N_g}\mathbf{N}{\left(\upxi \left({\upzeta}_i\right),\upeta \left({\upzeta}_i\right)\right)}^{\mathrm{T}}\ {S}_e\left({\upzeta}_i\right){w}_i;\kern1em {\mathbf{N}}_{1\Gamma}=\sum_{\boldsymbol{i}=\mathbf{1}}^{N_g}\mathbf{N}{\left(\upxi \left({\upzeta}_i\right),\upeta \left({\upzeta}_i\right)\right)}^{\mathrm{T}}\ {S}_e\left({\upzeta}_i\right){\upzeta}_i{w}_i\end{array}} $$

(15b)

where ζ_i and w_i are the coordinate and weight of the ith Gaussian point and N_g is the total number of Gaussian points. For the case of one or two Gaussian points, we have:

$$ {\displaystyle \begin{array}{c}{\mathbf{N}}_{0\Gamma}=2\mathbf{N}{\left(\upxi (0),\upeta (0)\right)}^{\mathrm{T}}\ {S}_e(0);\kern1.75em {\mathbf{N}}_{1\Gamma}=0\kern0.5em \end{array}} $$

(16)

or

$$ {\displaystyle \begin{array}{c}{\mathbf{N}}_{0\Gamma}=\mathbf{N}{\left(\upxi \left(-\frac{1}{\sqrt{3}}\right),\upeta \left(-\frac{1}{\sqrt{3}}\right)\right)}^{\mathrm{T}}\ {S}_e\left(-\frac{1}{\sqrt{3}}\right)+\mathbf{N}{\left(\upxi \left(\frac{1}{\sqrt{3}}\right),\upeta \left(\frac{1}{\sqrt{3}}\right)\right)}^{\mathrm{T}}\ {S}_e\left(\frac{1}{\sqrt{3}}\right)\ \end{array}} $$

(17a)

$$ {\displaystyle \begin{array}{c}{\mathbf{N}}_{1\Gamma}=-\frac{1}{\sqrt{3}}\mathbf{N}{\left(\upxi \left(-\frac{1}{\sqrt{3}}\right),\upeta \left(-\frac{1}{\sqrt{3}}\right)\right)}^{\mathrm{T}}\ {S}_e\left(-\frac{1}{\sqrt{3}}\right)+\frac{1}{\sqrt{3}}\mathbf{N}{\left(\upxi \left(\frac{1}{\sqrt{3}}\right),\upeta \left(\frac{1}{\sqrt{3}}\right)\right)}^{\mathrm{T}}\ {S}_e\left(\frac{1}{\sqrt{3}}\right)\ \end{array}} $$

(17b)

As in structural topology optimization, rectangular elements are often used. Thus, let us consider the 4-node rectangular element with side length 2a and 2b and pressure applied on Γ_e as illustrated in Fig. 4. Let (x_c, y_c) and (x_g, y_g) denote the global coordinates of the center of the element and the midpoint of the interface Γ_e respectively, one has x = x_c + a ξ and y = y_c + bη, and thus,

$$ {\displaystyle \begin{array}{c}{\xi}_g=\frac{x_{\mathrm{g}}-{x}_{\mathrm{c}}}{\mathrm{a}}=\upxi (0);\kern4.50em {\upeta}_g=\frac{y_{\mathrm{g}}-{y}_{\mathrm{c}}}{\mathrm{b}}=\upeta (0)\end{array}} $$

(18a)

$$ {\displaystyle \begin{array}{c}{\xi}_d=\frac{x_{\mathrm{d}}}{\mathrm{a}}=\frac{x_6-{x}_5}{2\mathrm{a}};\kern4.50em {\upeta}_d=\frac{y_{\mathrm{d}}}{\mathrm{b}}=\frac{y_6-{y}_5}{2\mathrm{b}}\end{array}} $$

(18b)

$$ {\displaystyle \begin{array}{c}{S}_e\left(\upzeta \right)=\sqrt{x_d^2+{y}_d^2}=\frac{L_{\mathrm{c}}}{2}\end{array}} $$

(18c)

and L_c is the length of the interface Γ_e. Thus, for the 4-node rectangular element, we can obtain the explicit expressions for (16) and (17); in addition, we can also work out the explicit exact analytical expression for (15a). These formulations are listed below for three cases:

• 1) Gaussian quadrature with one Gauss point

Equation (16) can be rewritten as follows:

$$ {\displaystyle \begin{array}{c}{\mathbf{N}}_{0\Gamma}={\mathrm{L}}_{\mathrm{c}}\mathbf{N}{\left(x\left(\upzeta =0\right),\mathrm{y}\left(\upzeta =0\right)\right)}^{\mathrm{T}}={\mathrm{L}}_{\mathrm{c}}\mathbf{N}{\left(x={x}_g,y={y}_g\right)}^{\mathrm{T}}\\ {}={\mathrm{L}}_{\mathrm{c}}\mathbf{N}{\left(\upxi =\frac{{\mathrm{x}}_{\mathrm{g}}-{\mathrm{x}}_{\mathrm{c}}}{a},\upeta =\frac{{\mathrm{y}}_{\mathrm{g}}-{\mathrm{y}}_{\mathrm{c}}}{b}\right)}^{\mathrm{T}}\\ {}{\mathbf{N}}_{1\Gamma}=\mathbf{0}\ \end{array}} $$

(19)

which is the same as (Picelli et al. 2019) for uniform pressure.

• 2) Gaussian quadrature with two Gauss points

Equation (17) now becomes:

$$ {\displaystyle \begin{array}{c}\begin{array}{c}{\mathbf{N}}_{0\Gamma}=\frac{L_c}{2}\left[\mathbf{N}{\left(x\left(\upzeta =-\sqrt{1/3}\right),\mathrm{y}\left(\upzeta =-\sqrt{1/3}\right)\right)}^{\mathrm{T}}+\mathbf{N}{\left(x\left(\upzeta =\sqrt{1/3}\right),\mathrm{y}\left(\upzeta =\sqrt{1/3}\right)\right)}^{\mathrm{T}}\right]\\ {}=\frac{L_c}{2}\left[\mathbf{N}{\left(x={x}_g-\sqrt{\frac{1}{3}}{x}_d,y={y}_g-\sqrt{\frac{1}{3}}{y}_d\right)}^{\mathrm{T}}+\mathbf{N}{\left(x={x}_g+\sqrt{\frac{1}{3}}{x}_d,y={y}_g+\sqrt{\frac{1}{3}}{y}_d\right)}^{\mathrm{T}}\right]\end{array}\\ {}{\mathbf{N}}_{1\Gamma}=\frac{L_c}{2\sqrt{3}}\left[-\mathbf{N}{\left(\upxi \left(-\frac{1}{\sqrt{3}}\right),\upeta \left(-\frac{1}{\sqrt{3}}\right)\right)}^{\mathrm{T}}+\mathbf{N}{\left(\upxi \left(\frac{1}{\sqrt{3}}\right),\upeta \left(\frac{1}{\sqrt{3}}\right)\right)}^{\mathrm{T}}\right]\\ {}=\frac{L_c}{2\sqrt{3}}\left[-\mathbf{N}{\left(x={x}_g-\sqrt{\frac{1}{3}}{x}_d,y={y}_g-\sqrt{\frac{1}{3}}{y}_d\right)}^{\mathrm{T}}+\mathbf{N}{\left(x={x}_g+\sqrt{\frac{1}{3}}{x}_d,y={y}_g+\sqrt{\frac{1}{3}}{y}_d\right)}^{\mathrm{T}}\right]\end{array}} $$

(20)

• 3) Exact integration

To derive an exact formula for the equivalent nodal force vector F_e in (10), one needs to work out the analytical expressions for N_0Γ and N_1Γ in (11) or (15a) for the rectangular element. The exact formula for each term in N_0Γ and N_1Γ corresponding to the relevant shape function N_i(ξ, η) (i = 1, 2, 3, 4) in (15a) can be derived using (13) and (18) as follows:

$$ {\displaystyle \begin{array}{c}\begin{array}{c}{\mathrm{N}}_{0{\Gamma}_{\mathrm{i}}}=\frac{L_c}{2}{\int}_{-1}^1{N}_i\left(\mathrm{x}\left(\upzeta \right),\mathrm{y}\left(\upzeta \right)\right)d\upzeta \\ {}\begin{array}{c}=\frac{L_c}{2}{\int}_{-1}^1\frac{1}{4}\left[\frac{x_i-{x}_c}{a^2}{x}_d\upzeta +\frac{\left({x}_g-{x}_c\right)\left({x}_i-{x}_c\right)}{a^2}+1\right]\left[\frac{y_i-{y}_c}{b^2}{y}_d\upzeta +\frac{\left({y}_g-{y}_c\right)\left({y}_i-{y}_c\right)}{b^2}+1\right]d\upzeta \\ {}=\frac{L_c}{8}\left\{\frac{2}{3}\frac{\left({x}_i-{x}_c\right)\left({y}_i-{y}_c\right)}{a^2{b}^2}{x}_d{y}_d+2\left[\frac{\left({x}_g-{x}_c\right)\left({x}_i-{x}_c\right)}{a^2}+1\right]\left[\frac{\left({y}_g-{y}_c\right)\left({y}_i-{y}_c\right)}{b^2}+1\right]\right\}\end{array}\\ {}{\mathrm{N}}_{1{\Gamma}_{\mathrm{i}}}=\frac{L_c}{2}{\int}_{-1}^1{N}_i\left(\mathrm{x}\left(\upzeta \right),\mathrm{y}\left(\upzeta \right)\right)\upzeta d\upzeta \end{array}\\ {}=\frac{L_c}{12}\left\{\frac{x_i-{x}_c}{a^2}{x}_d\left(\frac{\left({y}_g-{y}_c\right)\left({y}_i-{y}_c\right)}{b^2}+1\right)+\frac{y_i-{y}_c}{b^2}{y}_d\left(\frac{\left({x}_g-{x}_c\right)\left({x}_i-{x}_c\right)}{a^2}+1\right)\right\}\\ {}\left(i=1,2,3,4\right)\end{array}} $$

(21)

where (x_i − x_c)/a and (y_i − y_c)/b are equal to ±1 depending on i value. Substituting (21) into (10) and noting (15a) yields the exact formula.

By using (19), (20), or (21), the equivalent nodal force vector for the 4-node rectangular element as shown in Fig. 4 can be calculated via (10). This equivalent force vector of the interface pressure load can be employed in topology optimization methods that involve clear topology boundary, such as LSM or MIST.

It is worth noting that the present formulation for the equivalent nodal force vector of a non-uniformly distributed pressure can be used to capture variation in both pressure magnitude and direction once the fluidic pressure field is determined by using a method, such as FEM (Picelli et al. 2019).

3 Algorithm and implementation

The compliant mechanism problem of maximizing u_out is equivalent to that of maximizing the mutual potential energy or mutual energy expressed in terms of the symmetric global stiffness matrix and nodal displacement vectors due to the applied loads and the dummy load (Frecker et al. 1997). In FEM, this mutual energy can also be equivalent to the total mutual strain energy as in (22a). Thus, the problem of maximizing the total mutual strain energy can be formulated using FEM discretization in (2b) together with (7) and (10) as finding a topology such that

$$ {\displaystyle \begin{array}{c}\max :\kern0.5em J={u}_{\mathrm{out}}^{(1)}={\int}_{\Omega}{\boldsymbol{\upsigma}}^{(2)^{\mathrm{T}}}{\boldsymbol{\upvarepsilon}}^{(1)}\ d\Omega\ \end{array}} $$

(22a)

$$ s.t.:\left\{\begin{array}{l}\left(\sum_{e=1}^{N_e}{\int}_{\Omega_{\mathrm{e}}}\ {\mathbf{B}}^{\mathrm{T}}{\mathbf{D}}_e\left({x}_e\right)\mathbf{B}d{\Omega}_{\mathrm{e}}\right){\mathbf{u}}^{(1)}=\sum_{e=1}^{N_e}{\int}_{\Gamma_{\mathrm{e}}}\ {\mathbf{N}}^{\mathrm{T}}{\mathbf{f}}_{\mathrm{p}}d{\Gamma}_{\mathrm{e}}\\ {}\left(\sum_{e=1}^{N_e}{\int}_{\Omega_{\mathrm{e}}}\ {\mathbf{B}}^{\mathrm{T}}{\mathbf{D}}_e\left({x}_e\right)\mathbf{B}d{\Omega}_{\mathrm{e}}\right){\boldsymbol{u}}^{(2)}={\mathbf{F}}_{\mathrm{out}}\\ {}\sum_{e=1}^{N_e}{\int}_{\Omega_{\mathrm{e}}}d{\Omega}_{\mathrm{e}}\le {V}_fV\\ {}0\le {x}_e\le 1\end{array}\right. $$

(22b,c,d,e)

where J denotes the objective function defined using mutual strain energy, the displacement u, and strain ε and stress σ with superscripts (1) and (2) refer, respectively, to those obtained under the real load f_p and the virtual load F_out. As there is only one non-zero unit dummy load acting in the direction of ${u}_{\mathrm{out}}^{(1)}$ at the output port, (22a) can also be obtained according to the unit load method as: ${\mathbf{F}}_{\mathrm{out}}^T{\mathbf{u}}^{(1)}=1\times {u}_{\mathrm{out}}^{(1)}={\int}_{\Omega}{\boldsymbol{\upsigma}}^{(2)^{\mathrm{T}}}{\boldsymbol{\upvarepsilon}}^{(1)}\ d\Omega$. Equation (22b, c) is the equilibrium equations for the real and virtual load cases respectively, and (22d) is the material volume constraint. x_e is an element-based variable calculated and updated iteratively to facilitate the transformation of a topology to a finite element model for structural analysis as shown in Fig. 3.

It is worth noting that, for both real and virtual load cases, an artificial spring of stiffness k_out is attached to the output port only, because it is difficult to attach artificial springs to input ports on evolving and moving pressurized surfaces. A relatively large k_out is employed and added in the present study in solving (22b, c).

3.1 Objective function

In using the MIST (Tong and Lin 2011), the objective function in (22a) at the kth iteration can be expressed using a response function Φ in terms of both mutual strain energy density and strain energy density in domain Ω as follows:

$$ {\displaystyle \begin{array}{c}{J}^k={J}^k\left({\Phi}^k,{t}^k\right)={\int}_{\Omega}{\Phi}^kH\left({\Phi}^k-{t}^k\right)d\Omega \kern2em \left(k=1,2,\dots \right)\end{array}} $$

(23)

in which the response function is given by

$$ {\displaystyle \begin{array}{c}{\Phi}^k={\overline{\Phi}}^k\left({\boldsymbol{x}}_e^{k-1}\right)\kern2em \left(k=1\right)\\ {}{\Phi}^k=\left(1-{k}_{\varPhi}\right){\Phi}^{k-1}+{k}_{\varPhi }\ {\overline{\Phi}}^k\left({\boldsymbol{x}}_e^{k-1}\right)\kern2em \left(k\ge 2\right)\end{array}} $$

(24a)

where

$$ {\overline{\Phi}}^k\left({\boldsymbol{x}}_e^{k-1}\right)=\left(1-\alpha \right){E}_{med}^k\left({\boldsymbol{x}}_e^{k-1}\right)+\alpha {E}_{sed}^k\left({\boldsymbol{x}}_e^{k-1}\right)\kern0.5em \left(k=1,2,\dots \right) $$

(24b)

and

$$ {\displaystyle \begin{array}{c}{E}_{med}^k\left({\boldsymbol{x}}_e^{k-1}\right)=\frac{1}{2}{\boldsymbol{\sigma}}_{(2)}^T\left({\boldsymbol{x}}_e^{k-1}\right){\boldsymbol{\varepsilon}}_{(1)}\left({\boldsymbol{x}}_e^{k-1}\right)\kern4.25em \left(k=1,2,\dots \right)\\ {}{E}_{sed}^k\left({\boldsymbol{x}}_e^{k-1}\right)=\frac{1}{2}{\boldsymbol{\sigma}}_{(1)}^T\left({\boldsymbol{x}}_e^{k-1}\right){\boldsymbol{\varepsilon}}_{(1)}\left({\boldsymbol{x}}_e^{k-1}\right)\kern4.5em \left(k=1,2,\dots \right)\end{array}} $$

(24c)

where J^k, Φ^k and t^k (k = 1, 2, …) denote the objective function, response function, and the iso-surface threshold level at the kth iteration, respectively; H is the Heaviside function; ${\boldsymbol{\sigma}}_{(1)}\left({\boldsymbol{x}}_e^{k-1}\right)$, ${\boldsymbol{\varepsilon}}_{(1)}\left({\boldsymbol{x}}_e^{k-1}\right)$, ${\boldsymbol{\sigma}}_{(2)}\left({\boldsymbol{x}}_e^{k-1}\right)$, ${E}_{\mathrm{med}}^k\left({\boldsymbol{x}}_e^{k-1}\right)$, and ${E}_{\mathrm{sed}}^k\left({\boldsymbol{x}}_e^{k-1}\right)$ (k = 1, 2, …) denote the real stress, real strain, virtual stress, mutual strain energy density, and the strain energy density calculated at the kth iteration using the topology, or, area ratio vector, ${\boldsymbol{x}}_e^{k-1}$, of the previous (k-1)th iteration; for each element, ${\boldsymbol{\sigma}}_{(1)}\left({\boldsymbol{x}}_e^{k-1}\right)={\mathbf{D}}_{\mathrm{e}}\left({\boldsymbol{x}}_e^{k-1}\right){\boldsymbol{\varepsilon}}_{(1)}\left({\boldsymbol{x}}_e^{k-1}\right)$, ${\boldsymbol{\sigma}}_{(2)}\left({\boldsymbol{x}}_e^{k-1}\right)={\mathbf{D}}_{\mathrm{e}}\left({\boldsymbol{x}}_e^{k-1}\right){\boldsymbol{\varepsilon}}_{(2)}\left({\boldsymbol{x}}_e^{k-1}\right)$; and α and k_Φ are user-chosen coefficients (0 ≤ α ≤ 1; 0 < k_Φ ≤ 1). In this study, D_e is interpolated using a modified SIMP scheme as ${\mathbf{D}}_{\mathrm{e}}\left({x}_e^{k-1}\right)=\left({\left(1-{x}_{\mathrm{min}}\right)\left({x}_e^{k-1}\right)}^p+{x}_{\mathrm{min}}\right){\mathbf{D}}_{\mathrm{solid}}$ (i.e., (9) with D₁ = D_solid and D₂ = x_min D_solid). This interpolation is selected for the purpose of comparing the present results with those available in the literature (Emmendoerfer et al. 2018; Picelli et al. 2019).

Since the objective function in (22a) is the total mutual strain energy in the domain, thus, the mutual strain energy density should be chosen as the response function. However, to circumvent potential discontinuity on pressurized surfaces (interface boundaries), the response function should be revised as a combination of both mutual strain energy density and strain energy density as in (24b) with a coefficient α. Here α represents the weight of strain energy density and mutual strain energy density in the response function. When α = 1, the objective becomes minimizing the overall compliance; when α = 0, the objective is to maximize u_out. However, topological discontinuity may occur on the pressurized boundary when α = 0. Therefore, to maximize u_out, α should be chosen as small as possible but also sufficiently large to avoid topological discontinuity (in this study α = 0.2 is chosen).

In addition, the response function is also re-constructed by the combined energy in the current ${\overline{\Phi}}^k$ and previous Φ^k − 1 iterations as in (24a) to reduce possible fluctuations due to moving and evolving pressured interfaces via introducing a new coefficient k_Φ, which denotes the weight distribution between the previous and current iterations. In present computations, k_Φ = 0.5 is chosen for maximizing u_out. For the minimum compliance problem, α = 1, the response function is stable during optimization and thus there is no need to include the previous iteration, i.e., k_Φ = 1.

3.2 Implementation

The basic algorithm and implementation of MIST are presented in details in (Tong and Lin 2011; Vasista and Tong 2014). The basic MIST includes initialization, structural model and analysis, calculation of the response function and threshold level, and update of the topology and structural model. The present extension to the original MIST consists of the following new elements: (a) modified update scheme for physical response function; (b) equivalent design-dependent load vector formula and update scheme; and (c) design-dependent pressure-loaded interface tracking scheme.

The element-based fluid flooding method for interface tracking (Picelli et al. 2019) is adopted in this work, and the element type (i.e., fluid, interface, or solid) can be determined by checking the area ratio of each element using the present material model. Thus, the solution procedure for the extended algorithm can be given as follows:

• Step 1: Initialization (k = 0)

• Create fixed-grid finite element mesh and model, including initial equivalent nodal force $\sum_{e=1}^{N_e}{\mathbf{F}}_e^0$ using (10) and ${\mathbf{f}}_p^0$;

• Assign initial ${x}_e^0\ \left(e=1,2,\dots {N}_e\right)$ in Ω⁰;

• Select parameters: α, k_Φ, k_mv, x_min, and p.

• Step 2: FE analysis with iteration index k = 1, 2, 3, …

• Assign material properties using ${\mathbf{D}}_{\mathrm{e}}\left({x}_e^{k-1}\right)=\left({\left(1-{x}_{\mathrm{min}}\right)\left({x}_e^{k-1}\right)}^p+{x}_{\mathrm{min}}\right){\mathbf{D}}_{\mathrm{solid}}$, e = 1, 2, …N_e);

• Conduct FEA in (22b, c) for virtual and real load cases using ${\mathbf{D}}_{\mathrm{e}}\left({x}_e^{k-1}\right)$;

• Output nodal stresses, strains and displacements.

• Step 3: Constructing Φ^k, determining t^k, and creating ${\overline{\Omega}}_t^k$

• Calculate initial nodal Φ^k by using (24) and nodal stresses and strains from step 2;

• Construct Φ^k function after filtering and normalizing initial nodal Φ^k (e.g., with a filter radius being 2.5 times of element edge length L_x; normalized between − 1 and 1);

• Determine t^k for the prescribed volume constraint via the bisection method;

• Generate the kth topology ${\overline{\Omega}}_t^k$ and the associated area ratio ${\overline{x}}_e^k$, including solid, void, and interface elements with interface boundaries ${\overline{\Gamma}}_e^k$, by the intersection of Φ^k and t^k;

• Calculate J^k using (23) and ΔJ^k = J^k − J^k − 1 for k ≥ 2;

• Step 4: Interface tracking and update of equivalent loads

• Track pressurized element interfaces in the kth topology ${\overline{\Omega}}_t^k$ via ${\overline{x}}_e^k$ using the element-based fluid flooding method (Chen and Kikuchi 2001; Picelli et al. 2019), with criteria ${\overline{x}}_e^k\le {x}_{\mathrm{min}}$,${x}_{\mathrm{min}}<{\overline{x}}_e^k<1$, and ${\overline{x}}_e^k=1$ for fluid, interface, and solid element respectively;

• Calculate equivalent nodal forces ${\overline{\mathbf{F}}}_e^k$ for each pressurized element interface ${\overline{\Gamma}}_e^k$ via (10);

• Update equivalent nodal forces to $\sum_{e=1}^{N_e}{\overline{\mathbf{F}}}_e^k$ in the FE model;

• Step 5: Updating ${x}_e^k$ and material properties

• Update ${x}_e^k$ using:

$$ {\displaystyle \begin{array}{c}{x}_e^k={x}_e^{k-1}+{k}_{\mathrm{mv}}\left({\overline{x}}_e^k-{x}_e^{k-1}\right)\end{array}} $$

(25)

where k_mv is a dynamic move limit;

• Modify material properties using (9), ${x}_e^k$ and penalty p;

• Step 6: Convergence check

• Calculate the change in response function:

$$ {\displaystyle \begin{array}{c}\varDelta {\varPhi}^k=\frac{1}{N_n}\left(\sum_{n=1}^{N_n}\left|{\varPhi}^k\left({r}_n\right)-{\varPhi}^{k-1}\left({r}_n\right)\right|\right)\kern2.75em \left(k\ge 2\right)\end{array}} $$

(26)

where r_n and N_n are node number and the total number of nodes;

• If ΔΦ^k > ε or k < designated iteration number, update k as k+1 and go to step 2 and repeat steps 2–5; otherwise terminate iteration.

It is worth noting that, although the above algorithm is presented for the linear compliant mechanism and structure problems, it can be extended to take into account the geometrical nonlinearity by modifying the relevant structural analyses and using the response function determined from nonlinear solutions (Luo and Tong 2016).

4 Numerical examples

In this section, an example of equivalent nodal forces at the element level is first presented to illustrate the present equivalent nodal force calculation method. Then, four examples are presented to validate the present extended MIST algorithm.

In all the present computations, ${\boldsymbol{x}}_e^0$ (e = 1, 2, …N_e) are initialized as the material being evenly distributed, and pressure loads ${\mathbf{f}}_p^0$ are initialized as being applied to external boundaries of the design domain as defined in each example. In the minimum compliance examples 4.2 and 4.3, material properties are E = 1, υ = 0.3 and polyurethane with E = 100 MPa and υ = 0.3 is chosen for the compliant mechanism examples 4.4 and 4.5. Material penalization factor is set as p = 3 for the minimum compliance problems, whereas it is initially chosen as 1 and gradually increased to 3 with an increment of 0.05 per iteration for the compliant mechanism problems in order to reduce the effect of low-density elements at the beginning of optimization. The filter radius is 2.5 times of element size L_x, and x_min = 10⁻³. In addition, k_Φ = 0.5, α = 0.2, and k_Φ = 1, α = 1 are chosen for the maximum u_out compliant mechanism and the minimum compliance problems, respectively. In the dynamic move limit, k_mv is initialized as 0.5 and then reduced by half if an oscillation in the objective function occurs (i.e., ΔJ^k > 0, ΔJ^k − 1 < 0, and ΔJ^k − 2 > 0 or ΔJ^k < 0, ΔJ^k − 1 > 0, and ΔJ^k − 2 < 0 (k ≥ 4)) and k_mv ≥ k_{mv, min} (where ${k}_{\mathrm{mv},\min }=\frac{0.5}{2^4}$ is the minimum value of the move limit).

Although equivalent nodal force vectors are derived for linearly distributed pressure P(ζ ) = P₀ + P₁ζ in 2.3, uniform pressure loadings (P(ζ ) = P, i.e., P₀ = P and P₁ = 0) are applied to be consistent with the literature. In examples 4.3 and 4.4, non-uniform hydrostatic fluidic pressures that vary linearly with depth h are considered.

4.1 A comparison of equivalent nodal forces at the element level

In this example, the virtual work-based equivalent nodal forces are calculated by (10) with (19), (20), or (21), respectively, for a varying geometry of a pressurized interface element. As shown in Fig. 5, the pressurized boundary of the rectangular interface element of size 1 × 1 is pivoted on the midpoint of the right edge, and the other end of the pressurized boundary can move along the top edge for S₁ = 0 to 1. The uniform pressure load applied is P = 1. In addition, the relative error between the equivalent nodal forces predicted using the exact integration and the 1-point or 2-point Gaussian quadrature are defined as usual. For example, $\left|{F}_{1x}^{1 pt}/{F}_{1x}^{ex}-1\right|\%$ denotes the relative error between the results predicted by using the 1-point Gaussian quadrature and the exact integration for the force at node 1 in the x-direction.

Fig. 5

An interface element with node 5 pivoted and node 6 moving along S₁

The largest error between the 2-point Gaussian quadrature and the exact integration are in the order of 10⁻¹³%, which indicates the errors of the 2-point Gaussian quadrature are negligible. Therefore, only the results of the exact integration and the 1-point Gaussian quadrature are presented. The nodal forces in x- and y-directions at nodes 1 to 4 are shown in Fig. 6 a to d, respectively. The variations and trends of the nodal forces along S₁ for both methods are very much similar. However, the magnitudes of the nodal forces in the x-direction at nodes 2 and 3, F_2x and F_3x, decrease with S₁, whereas those of all the remaining nodal forces increase with S₁. This is due to the variation in the pressure direction and the increase in the length of the 5–6 interface as S₁ varies from 0 to 1. The relative errors for nodes 1 to 4 are calculated and plotted in Fig. 6e. For nodes 3 and 4, the 1-point Gaussian quadrature gives reasonable predictions with a maximum relative error about 10%. However, for nodes 1 and 2, the relative errors between the exact integration and the 1-point Gaussian quadrature methods are relatively large and close to 50%.

Fig. 6

Equivalent nodal forces using the 1-point Gaussian quadrature and exact integration for varying S₁ of a node 1; b node 2; c node 3 and d node 4; and e relative error between the 1-point Gaussian quadrature and the exact integration versus S₁

In the following four topology optimization examples, the 1-point Gaussian quadrature and exact integrations methods are used to illustrate the influences of these two equivalent nodal force formulations. The 1-point Gaussian quadrature results are presented for the purpose of comparison as they are available in the literature.

4.2 Piston

Figure 7 depicts the design domain, supported and loading conditions for the piston design example that has been studied by using other topology optimization methods (Sigmund and Clausen 2007; Lee and Martins 2012; Xia et al. 2015; Emmendoerfer et al. 2018; Picelli et al. 2019). The cylindrical piston is pressurized from the top with a uniform pressure of P = 1, and the center of the bottom edge is fixed. Both the left and right edges are constrained in the horizontal direction as the cylinder walls. A 150 × 50 mesh is used to minimize the mean compliance for the design domain with a volume fraction of 30%.

Fig. 7

The design domain and support and loading conditions for the piston problem

The present extended MIST algorithm for the compliant mechanism problem can be easily adapted to solve the minimum compliance problem by letting α = 1. The response function in (24b) becomes the strain energy density and the objective function in (22a) becomes:

$$ {\displaystyle \begin{array}{c}\min :J={\int}_{\Omega}\frac{1}{2}{\upsigma}^{(1)^{\mathrm{T}}}{\upvarepsilon}^{(1)}\ d\Omega \end{array}} $$

(27)

To prevent the structure from collapsing, as pointed out in (Lee and Martins 2012), fixed-point loads are applied to the top-left and top-right corner. The magnitude of the fixed loads is 0.0005, which is 2.5% of P × L_x; therefore, the fixed loads can be considered as negligible compared with the applied pressure load.

The optimized topologies and compliances using both equivalent nodal force methods are shown in Fig. 8. The optimized topology with the exact integration (Fig. 8a) is very similar to Fig. 15 in (Xia et al. 2015), except for a small hole near the upper center part. The minimum compliance (C = 27.90) is comparable to and slightly lower than the values in literature by using LSM (Emmendoerfer et al. 2018) (C = 30.22) and (Xia et al. 2015) (C = 29.88), which also involve clear topology boundaries. The optimal topology using 1-point Gaussian quadrature (Fig. 8b) is comparable to Fig. 16 in (Bruggi and Cinquini 2009) and Fig. 7e in (Sigmund and Clausen 2007).

Fig. 8

Optimal topologies and compliances of the piston subjected to equivalent loads using a exact integration (C = 27.90) and b 1-point Gaussian quadrature (C = 33.43)

The curves of the compliance versus iteration are shown in Fig. 9a. As is shown in Fig. 9a for the exact integration case, the topology and objective function almost converge at around iteration 50. However, there is an abrupt change in the local topology of the upper boundaries of the two center cavities (see the second topology in Fig. 9a at iteration 57), and this change of interface boundary generates an oscillation in the objective function. Thereafter, as these local upper boundaries evolve back to those prior to iteration 57, the oscillation disappears and the convergence is achieved. The magnitude and iteration ranges of the oscillation appear smaller than those observed for the 1-point Gaussian quadrature case. Compared with the load calculation via 1-point Gaussian quadrature (C = 33.43), the use of exact integration provides less oscillations and lower optimal compliance.

Fig. 9

a Compliance versus iteration of the piston design case and the topologies at iteration 50, 57 (oscillating iteration), and 70 using exact integration; b the normalized Φ surface and the corresponding threshold level of the optimized topology using the exact integration (Fig. 8a); and c schematic of deformation (scaled to 0.005 times) and the von Mises stress distribution of the optimized topology in Fig. 8a (where the wireframe indicates the un-deformed structure and the contour denotes the deformation)

The 3D surface of the normalized Φ ranging between − 1 and + 1 and the corresponding threshold level t for the optimized topology in Fig. 8a are shown in Fig. 9b. Since the single-point constraining boundary condition is applied to the center of the bottom edge in this example, the strain energy level at the fixed point is extremely high compared to the rest of the design domain. Thus, only the Φ surface plot excluding the steep peak around the fixed point is presented. Additionally, a full FEA is conducted for the optimized topology using the exact integration, which gives compliance: C = 31.54. The deformation (shown in 0.005× scale) and von Mises stress distribution are shown in Fig. 9c.

4.3 Externally pressurized lid

As illustrated in Fig. 10, the minimum compliance design of an underwater structure subjected to external hydrostatic pressure load is studied. This is another classical problem for topology optimization under pressure load (Sigmund and Clausen 2007; Picelli et al. 2014; Emmendoerfer et al. 2018) with a series of different material properties and constrained regions used in literature. The imposed uniform pressure is P = 1, and a regular 80 × 40 mesh is used. In the present computation, the design domain is fixed at the bottom-left and bottom-right corner, and the volume fraction is set as 20%.

Fig. 10

The design domain of an externally pressure-loaded structure

As expected, the optimal topologies using both methods are arch-like structures to support the external pressures as shown in Fig. 11a and b. The heights of optimized arch-like topologies via the two methods are almost identical and agree well with those reported in literature (Sigmund and Clausen 2007; Picelli et al. 2014; Emmendoerfer et al. 2018). The uptake of the exact integration method provides a lightly lower objective function value (C = 11.30). The histories of the objective function for both methods are shown in Fig. 11d. The full FEA of the optimized topology using the exact integration shows C = 17.42, where the deformation (shown in 0.004× scale) and the von Mises stress distribution are shown in Fig. 11e.

Fig. 11

Optimal topologies and compliances of the externally pressurized lid subjected to uniform pressures using a exact integration (C = 11.30) and b 1-point Gaussian quadrature (C = 12.17); c non-uniform hydrostatic pressures with P_s = 1 and P_h = 1 (C = 20.32); d the compliance versus iteration of a and b; and e schematic of deformation (scaled to 0.004 times) and von Mises stress distribution of the optimized topology using the exact integration, where the wireframes indicate the un-deformed structure and the contours denote the deformation

For this underwater structure, a non-uniform hydrostatic pressure loading is also studied. For this case, the pressure can be considered as linear to depth h. Thus, for each element as shown in Fig. 4 P(ζ ) = P₀ + P₁ζ, where P₀ = (P₅ + P₆)/2, P₁ =  − (P₅ − P₆)/2, and the hydrostatic pressures P₅ = P_s + P_hh₅ and P₆ = P_s + P_hh₆. In this example, as shown in Fig. 10, P_s = P = 1 and P_h = 1. By using the exact integration, one can obtain the topology as shown in Fig. 11c. The thickness at the root and midpoint of the arch are 29% and 7% larger than these for uniform pressure case (Fig. 11a) respectively.

4.4 Compliant gripper

In this example, half of a compliant gripper is studied using the present extended MIST algorithm. As illustrated in Fig. 12, half of the gripper is constrained around the top-right corner and pressurized from the top side. The dimension of the design domain is 80 mm × 40 mm, and the non-design domains include two solid and one void regions. The objective is to maximize the gripping displacement at the output port. The mesh used is 80 × 40 and the prescribed volume fraction is 25%, with an imposed uniform pressure load P = 0.5 MPa.

Fig. 12

The design domain of the compliant gripper case

If α = 0 (the response function is a mutual strain energy density only) is used, material separation can occur on the thin hinge connected to the inclined bar-like member in the top-right (see Figs. 13 and 14). Therefore, α = 0.2 is applied to stabilize the interface boundary. An artificial spring is attached to the output port only, and thus, relatively high stiffness is used in the present computation: k_out = 10N/mm. Because the ${u}_{\mathrm{out}}^{(1)}$ value calculated from solving (22b) is dependent on the choice of k_out, the exact ${u}_{\mathrm{out}}^{(1)}$ of the final optimal topology must be calculated via FEA without the artificial spring included. The FEA is conducted via ANSYS, with final optimal topologies converted and imported as CAD models.

Fig. 13

Optimal topologies and output displacements of the compliant gripper subjected to uniform pressures using a exact integration (${u}_{\mathrm{out}}^{(1)}$= –21.19 mm) and b 1-point Gaussian quadrature (${u}_{\mathrm{out}}^{(1)}$= –16.85 mm); non-uniform hydrostatic pressures with P_s = 0.5 MPa and c P_h = 1/160 MPa/mm (${u}_{\mathrm{out}}^{(1)}$= –22.12 mm) and d P_h = 1/80 MPa/mm (${u}_{\mathrm{out}}^{(1)}$= –26.84 mm)

Fig. 14

Output displacements versus iteration of the gripper design case and the topologies at iteration 10, 25, 50, and 100 using exact integration

The optimal topologies and displacements by using both methods are shown in Fig. 13a and b, and the histories of the output displacements as well as the topologies of iterations 10, 25, 50, and 100 using the exact integration are presented in Fig. 14. Similar to the previous examples, the optimized output displacement is larger with less oscillation when using the exact integration method. As shown in Fig. 14, the interface surface evolves quickly in the first 15 iterations and then moves downwards iteratively to reduce the thickness of the pressure-carrying part of the structure and improve the flexibility of the gripper. A thin hinge is observed on the bar-like pressure-loaded member from iteration 25, but it is eliminated gradually during iterations. The optimal topologies for both cases are imported to ANSYS and are used to conduct FEA with the polyurethane material (E = 100 MPa, υ = 0.3), and the deformation of optimal topologies with the von Mises stress are presented in true scale as Fig. 15, which shows that the desired deformation of the gripper is achieved. With a pressure load of 25 kPa applied to the gripper, the optimal topology obtained using the exact integration shows much larger deformation.

Fig. 15

Schematic of deformation and the von Mises stress distribution under 25 kPa pressure for the gripper design using a the exact integration (${u}_{\mathrm{out}}^{(1)}$= –8.32 mm) and b the 1-point Gaussian quadrature (${u}_{\mathrm{out}}^{(1)}$= –3.60 mm) (where the wireframes indicate the un-deformed structures and the contours denote the true scale deformations)

Non-uniform hydrostatic pressure, similar to example 4.3, is also considered using the exact integration with P_s = P = 0.5 MPa and P_h = 1/160 or 1/80 MPa/mm, and the optimized topologies and output displacements are shown in Fig. 13c and d. The locations of the thin hinge in both cases are lower than that for the uniform pressure case (Fig. 13a) and notable differences can be observed in the internal structural topological members. The optimal output displacements are larger than that in Fig. 13a as expected as the pressure loads are higher.

4.5 Inverter

Force inverter is another type of classical compliant mechanism problem, which generates displacement output in the reverse direction of the input force. In this case, the input force is replaced by a design-dependent uniform pressure load. Half of the inverter is demonstrated in Fig. 16. It is pressurized from the bottom edge and constrained at the bottom-right corner, and the downward displacement at the output port is maximized. The dimension of design domain, material properties, uniform pressure imposed, spring stiffness, and finite element mesh are the same as in example 4.4.

Fig. 16

The design domain of the inverter case

The optimal topologies using both methods are similar, except for the interface boundaries, as shown in Fig. 17. The surface area of the pressure-loaded boundary using exact integration is larger, which offers a larger input load and thus larger output displacement. Figure 18 presents the histories of the output displacements and the topologies of iterations 15, 50, 100, and 150 with the exact integration. Oscillations occur around the 15th iteration and end about the 100th iteration, due to the iterative changes of interface boundary, while the oscillation is eliminated after the interface boundary converges after 100 iterations. Although the changes of interface boundary are slight in these iterations, the oscillation in objective function can be large, as can be seen from Fig. 18. It should be noted that a relatively large dynamic move limit is used in the present computations for achieving faster convergence, and the oscillation can be reduced by using a small k_mv.

Fig. 17

Optimal topologies and output displacements of the inverter subjected to equivalent loads using a exact integration (${u}_{\mathrm{out}}^{(1)}$= –13.83 mm) and b 1-point Gaussian quadrature (${u}_{\mathrm{out}}^{(1)}$= –11.90 mm)

Fig. 18

Output displacements versus iteration of the inverter design case and topologies at iteration 15, 50, 100, and 150 using exact integration

As illustrated in Fig. 19, a pressure of 15 kPa is applied to the optimized topologies of the inverter with the same polyurethane material properties as in example 4.4, where the deformations are shown in true scale. This FEA validation shows that the desired deformations are achieved for both methods, and the output displacement predicted using the exact integration is larger.

Fig. 19

Schematic of the deformation and von Mises stress distributions under a 15 kPa pressure for the inverter design using a the exact integration (${u}_{\mathrm{out}}^{(1)}$= (${u}_{\mathrm{out}}^{(1)}$–6.50 mm) and b the 1-point Gaussian quadrature (${u}_{\mathrm{out}}^{(1)}$= -3.93mm) (where the wireframes indicate the un-deformed structures and the contours denote the true scale deformations

The final optimized topologies, near the output port, of the present gripper and inverter look similar to these of the conventional compliant mechanism structures under design independent load settings (e.g., (Tong and Lin 2011) with single-input-single-output (SISO). However, the topological configurations near the input port(s) are substantially different.

5 Conclusion

This work presents an extended MIST algorithm for structural topology optimization with design-dependent loads. This algorithm has the following features: a a general formulation of element stiffness matrix and material interpolation derived based on equivalent virtual strain energy; b a general formulation for equivalent nodal forces for pressure acting on interface boundary of an iso-parametric rectangular element derived based on equivalent virtual work using exact integration or Gaussian quadrature; c a novel physical response function defined via a linear combination of strain energy and mutual strain energy densities re-constructed from previous and current iterations for compliant mechanism problems; and d element type can be determined using the present material model directly from element area ratio, with which an element-based interface searching scheme can be easily implemented. The present algorithm is benchmarked by two well-studied examples, and the optimized topologies and compliances with the exact integration agree well with those obtained in the literature using LSM. Two typical compliant mechanism design cases are studied and validated by full FEA solutions. It is noted that the exact integration method is more appropriate in calculating equivalent load, compared with 1-point Gaussian quadrature, as it provides better convergence and better-optimized objectives with lower compliances or larger displacements in the compliance or compliant mechanism problems.