Topological-derivative-based design of stiff fiber-reinforced structures with optimally oriented continuous fibers

Abstract

We use topological derivatives to obtain fiber-reinforced structural designs with non-periodic continuous fibers optimally arranged in specific patterns. The distribution of anisotropic fiber material within isotropic matrix material is determined for given volume fractions of void and material as well as fiber and matrix simultaneously, for maximum stiffness. In this three-phase material distribution approach, we generate a Pareto surface of stiffness and two volume fractions by adjusting the level-set plane in the topological sensitivity field. For this, we utilize topological derivatives for interchanging (i) isotropic material and void; (ii) fiber material and void; and (iii) isotropic and fiber materials, during iterative optimization. While the isotropic topological derivative is well known, the latter two required modification of the anisotropic topological derivative. Furthermore, we used the polar form of the topological derivative to determine the optimal orientation of the fiber at every point. Thus, in the discretized finite element model, we get element-wise optimal fiber orientation in the portions where fiber is present. Using these discrete sets of orientations, we extract continuous fibers as streamlines of the vector field. We show that continuous fibers are aligned with the principal stress directions as first reported by Pedersen. Three categories of examples are presented: (i) embedding fiber everywhere in the isotropic matrix without voids; (ii) selectively embedding fiber for a given volume fraction of the fiber without voids; and (iii) including voids for given volume fractions of fiber and matrix materials. We also present an example with multiple load cases. Additionally, in view of practical implementation of laying up or 3D-printing of fibers within the matrix material, we simplify the dense arrangement of fibers by evenly spacing them while retaining their specific patterns.

1 Introduction

Topology optimization, with its beginning in homogenization-based parameterization (Bendsoe and Kikuchi 1988), is a well-established method for designing structures made of a single isotropic material using power-law material interpolation techniques (e.g., Bendsoe and Sigmund 2003; Stolpe and Svanberg 2001). Optimality criteria method (Bendsoe and Sigmund 2003), method of moving asymptotes (Svanberg 1987), level-set method (Wang et al. 2003), phase-field technique (Wang and Zhou 2004), etc., are some of the widely used methods for topology optimization today. Extension of these methods to the design of stiff structures (Wang and Wang 2004; Zou and Saitou 2017) and compliant mechanisms (Yin and Ananthasuresh 2001) with multiple isotropic materials is also reported. As explained next, topology optimization with anisotropic materials (fiber-reinforced structures, in particular) has also been extensively investigated. These techniques use a two-phase material (void and anisotropic material) approach. In the present study, we describe a three-phase approach to topology optimization of composite structures comprising optimally oriented continuous fibers patterned in an isotropic material. That is, the optimized structure consists of voids, only isotropic material, and isotropic material embedded with optimally oriented fibers. We first review analytical and computational approaches used to obtain optimal fiber orientations.

1.1 Analytically derived fiber orientation

In a pioneering study, Pedersen (1989, 1990, 1991) analytically derived conditions for optimal orientation of orthotropic materials. He gave closed-form expressions where the orientation depends on a non-dimensional parameter and the ratio of principal strains. His work also stated that principal stress and principal strain directions coincide for optimal designs. Thus, one can define orientations along the maximum principal strain direction for materials with low shear stiffness to achieve the global extremum. In another work (Bendsoe et al. 1994), properties of general material were optimized analytically to obtain orthotropic material following principal strain directions. The analytical investigation of parameters for optimal laminate design subjected to single and multiple loads was reported in Hammer et al. (1997). The stress- and strain-based approaches were compared in Cheng et al. (1994) and Gea and Luo (2004) for obtaining optimal orientation of orthotropic material. As an alternative to energy-based formulations, analytical sensitivity with respect to orientation variables was derived in Majak and Hannus (2003) subjected to Hill and Tsai-Wu failure criteria to study material failure.

1.2 Numerically computed fiber orientations

In later years, gradient-based optimization emerged as the primary approach for determining orientation of fibers in composites. Level-set modeling was used to optimize evenly spaced continuous fiber paths in (Brampton et al. 2015) where slope of the level-set function decides material orientation for every element in the finite element discretization. Similarly, a level-set model-based topology optimization of thermally active composites was presented in Maute et al. (2015). In this work, the spatial arrangement of shape memory polymers within a matrix was obtained for a target deformed shape of the composite, which could be printed directly without any post-processing of the obtained design. Alternatively, optimal orientation of fibers is determined from a limited set of discrete fiber angles (Kiyono et al. 2017). In this, a normal distribution function was proposed to assign one variable at a point to select an optimized angle among several discrete candidate angles. In another example, both orientation and size of the fibers were optimized for the stiffest orthotropic membrane structures (Klarbring et al. 2019). Laminated composites were designed for optimal orientations wherein each layer had a different objective (Petrovic et al. 2018). Furthermore, material orientations of large-scale composite shell structures were studied in Muramatsu and Shimoda (2019) where sensitivity with respect to the orientation variables was applied as a virtual heat source while the structural compliance was minimized. In Shen and Branscomb (2020), orientation of anisotropic materials was optimized using gradient-based mathematical programming.

1.3 Topology optimization using anisotropic materials with optimal orientations

Gradient-based numerical techniques were adopted for optimizing the topology and fiber orientations concurrently (Bruyneel and Fleury 2002; Setoodeh et al. 2005). Fictitious material density (as is common in topology optimization), fiber density, and fiber orientation were considered as design variables (Thomsen 1992). It is reported that conventional continuous fiber angle optimization (CFAO), where the solution is highly dependent on initial fiber configuration, falls in the local minimum (Stegmann and Lund 2005). As an alternative, Discrete Material Optimization (DMO) was proposed in Stegmann and Lund (2005), where the material model was formulated by combining multiple elasticity tensors incorporating different orientation variables, which are further penalized to force the solution to arrive at a single angle for each element. A composite model subjected to multiple load cases was optimized in Zhou and Li (2006) to enable the material orientation to follow principal stress directions. The optimization approach proposed in Nomura et al. (2014) offers continuous design with orientation pertaining to both continuous and discrete sets of angles. It improves local minimum issue inherent to CFAO because the evolving design is independent of previous iterative design. It was shown in Zhou et al. (2018) that fiber orientation aligns with the direction of a segment in multi-component topology optimization.

In view of additive manufacturing of composite structures, the effect of build direction on the resulting material anisotropy was examined in Chiu et al. (2018) using a parametric study. Build direction, topology, and fiber orientation were simultaneously considered in Chandrasekhar et al. (2019). Toward developing practically useful designs, Safonov A.A. (2019) and Nomura et al. (2018) presented 3D topologies with optimally oriented fibers. In particular, tensor field variables were used to optimize fiber orientations. Additionally, simultaneous optimization of the topology and material microstructure was done in Yan et al. (2019).

All the aforementioned works are concerned with topology optimization of only anisotropic material with either optimally oriented fiber or microstructure. In contrast to these two-phase approaches (i.e., void and anisotropic material), a three-phase approach was proposed in Lee et al. (2018), wherein fiber fraction was considered along with material fraction in a given design space. Such a composite structure could be characterized as functionally graded because fiber is present in a fraction of the structure with voids and that too with variable fiber density. The approach taken in Lee et al. (2018) was sequential in the sense that three steps were followed, beginning with the design of isotropic-material matrix with voids, and then inserting fiber selectively, followed by optimally orienting the fiber. Our work utilizes topological derivative and combines all three steps into one by simultaneously interchanging three phases, namely, isotropic matrix material, fiber-reinforced orthotropic material, and voids, as illustrated in Fig. 1. The next part of this section briefly introduces topological derivative and its applicability in topology optimization.

Fig. 1

Graphical illustration of topological-derivative-based design algorithm for extracting fiber-reinforced structural design: a Initial isotropic matrix with specified boundary conditions. The desired fiber fraction and void fraction are given by FF^∗ and V F^∗ respectively. b Design algorithm to replace isotropic matrix with optimally oriented fiber inclusions for desired FF^∗ while void fraction V F is held constant. It utilizes topological derivatives for interchanging matrix (isotropic) and fiber material, i.e., TD_I→F and TD_F→I. c Design algorithm to create voids in the material for desired V F^∗ while fiber fraction FF is held constant. It utilizes topological derivatives for interchanging matrix material and void, i.e., TD_I→V and TD_{V →I} as well as fiber material and void TD_F→V and TD_{V →F}. d Pareto design surface which compares mean compliance of the structure with void and fiber fractions as displayed in the projected Pareto curves. e Three-phase material distribution and fiber orientation for specified V F^∗ and FF^∗. f Fiber-reinforced structure with evenly spaced continuous fiber trajectories

1.4 Topological derivative

Topological derivative is the closed form analytical expression that quantifies the sensitivity of a given performance functional with respect to an infinitesimal domain perturbation (Novotny and Sokolowski 2013). Consider an unperturbed (reference) domain Ω that is perturbed by introducing a finite size circular inclusion B_ε, centered at x̂ with radius ε. The topological derivative is mathematically computed as:

$$ TD(\hat{\mathbf{x}}) = \lim_{\varepsilon\to 0}\frac{\psi_{\varepsilon}({\Omega}) - \psi({\Omega})}{f(\varepsilon)} $$

(1)

In the above equation, TD(x̂) is the first-order topological derivative, ψ_ε(Ω) and ψ(Ω) are the performance measures of the perturbed and unperturbed domains, respectively, and f(ε) is the positive first-order correction factor such that when ε → 0,f(ε) vanishes.

The topological derivative has been successfully applied in determining optimal topology of structures. The analytical derivative is computed for the homogenous isotropic and anisotropic domains, where voids are created in order to obtain the optimal topology for a given volume fraction (Bonnet and Delgado 2013; Giusti et al. 2016). One can also insert anisotropic inclusions into the already existing isotropic domain while achieving the specified objective. This method is not only computationally efficient but also offers Pareto front of the optimal design for the performance functional and volume of the material used (Suresh 2010; Mirzendehdel and Suresh 2015). The optimal solution for multimaterial isotropic model wherein level-set-based topological derivative representation is generalized for multiple isotropic materials is reported in Gangl (2020) and Onco and Giusti (2020).

1.5 Scope of the work

In the present study, we use topological derivatives to obtain optimal material distribution and orientation of fibers within the matrix and voids, simultaneously. We modify anisotropic topological derivative to replace isotropic matrix with fiber inclusions and then determine Pareto-optimal three-phase material distribution using topological-derivative-based design algorithm. The optimal fiber orientation is achieved by computing anisotropic topological derivative in the polar coordinate system. This comprehensive multi-phase study offers Pareto surface which encapsulates stiff fiber-reinforced designs at various void and fiber fractions. Additionally, the resulting orientation vector field is further processed to achieve evenly spaced continuous fiber trajectories along which the long fiber strands can be laid.

The procedure of obtaining fiber-reinforced structural design is illustrated in Fig. 1. As shown in the figure, we consider a structure with homogeneous isotropic material (Fig. 1a) to begin with. For the purpose of illustration, the structure is fixed at one edge and a point load is applied at the center of the opposite edge. We analyze the discretized finite element model of the structure and generate the topological sensitivity field for incorporating fiber inclusions at optimal locations in the matrix. This requires two topological derivatives TD_I→F and TD_F→I to interchange isotropic matrix with fiber material as shown in (Fig. 1b). The void fraction, V F, is held constant during this procedure of material replacement and reorientation using transformed topological derivative. Once we reach the desired fiber fraction incrementally toward FF^∗, the resulting material distribution is called by the second loop where voids are created while fiber fraction FF is held constant, as shown in (Fig. 1c). In this void-creation step, we use four topological derivatives to create voids in the matrix material TD_I→V, voids in the fiber material TD_F→V, adding matrix material to voids TD_{V →I} and adding anisotropic fiber material back to voids TD_{V →F}. This procedure is incrementally repeated to cover the desired range of void and fiber fractions resulting in the development of Pareto surface in (Fig. 1d) where we compare mean compliance with respective volume fraction of voids and fiber. The optimal material distribution and fiber orientation is presented in (Fig. 1e). The material and orientation information is further processed in data visualization software to create uniformly spaced fiber paths as illustrated in (Fig. 1f).

The paper is organized as follows: The problem statement is defined in Section 2 where the sets of governing equation and boundary conditions for reference and perturbed domains, respectively, are explained. In Section 3, the analytical derivatives required to compute topological sensitivity are encapsulated. Section 4 is devoted to the implementation of topological derivatives to obtain optimal topologies in fiber-reinforced composites. The Pareto optimality conditions are presented and element-wise optimal fiber orientations are obtained using the polar form of the topological derivative. Several numerical examples with different loading and boundary conditions are demonstrated in Section 5. The last section offers an approach of generating continuous fiber paths. It provides an insight into the manufacturability of the resulting topology, which in turn leads to non-periodic fiber arrangement following specific patterns.

2 Problem statement

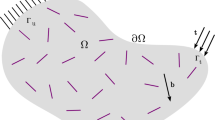
In this section, we present the mathematical statement of the elasticity problem. The initial unperturbed domain is fully isotropic as shown in Fig. 2a. The displacement field u for the unperturbed domain solves the following variational problem:

$$ \boldsymbol{u}\in\mathcal{U}({\Omega}):\quad {\int}_{\Omega} \boldsymbol{\sigma}(\boldsymbol{u})\cdot\boldsymbol{\epsilon}(\boldsymbol{\eta}) = {\int}_{{\Gamma}_{N}} \bar{\boldsymbol{q}}\cdot\boldsymbol{\eta}, \quad\forall \boldsymbol{\eta}\in\mathcal{U}({\Omega}) $$

(2)

where, q̄ is the traction applied at Γ_N, u is the displacement, and η is perturbation in the displacement. The term 𝜖(η) represents the engineering strain expressed in Voigt notation, i.e.:

$$ \boldsymbol{\epsilon}(\boldsymbol{\eta}) = \left[ {\begin{array}{c} \epsilon_{xx} \\ \epsilon_{yy} \\ \gamma_{xy} \end{array} } \right] = \left[ {\begin{array}{c} \partial \eta_{x}/\partial x \\ \partial \eta_{y}/\partial y \\ \partial \eta_{x}/\partial y + \partial \eta_{y}/\partial x \end{array} } \right] $$

(3)

with η_x and η_y being the components of perturbed displacement η. The stress vector σ(u) in (2) is related to 𝜖(u) by:

$$ \boldsymbol{\sigma}(\boldsymbol{u}) = \boldsymbol{C}\boldsymbol{\epsilon}(\boldsymbol{u}) $$

(4)

Here, C is the constitutive relation for isotropic material expressed in matrix (Voigt notation). The space (Ω) is defined as $\mathcal {U}({\Omega }):= \big \{\boldsymbol {\phi }\in H^{1}({\Omega }:\mathbb {R}^{2}):\boldsymbol {\phi }|_{{\Gamma }_{D}} = \boldsymbol {0}\big \}$, with Γ_D is the part of the boundary ∂Ω, where displacement is prescribed. The performance functional ψ(Ω), which is the strain energy associated to the system, is given by:

$$ \psi({\Omega}) = \frac{1}{2}{\int}_{\Omega}\boldsymbol{\sigma}(\boldsymbol{u})\cdot\boldsymbol{\epsilon}(\boldsymbol{u}) $$

(5)

Fig. 2

Domain representation for topological derivative

Next, the domain in Fig. 2a is perturbed by introducing a circular inclusion of finite size with a different constitutive matrix C^∗ shown in Fig. 2b, such that the displacement of the perturbed domain is obtained by solving the following variational form:

$$ \boldsymbol{u}_{\varepsilon}\in\mathcal{U}({\Omega}): {\int}_{\Omega} \boldsymbol{\sigma}_{\varepsilon}(\boldsymbol{u}_{\varepsilon})\cdot\boldsymbol{\epsilon}(\boldsymbol{\eta}_{\varepsilon}) = {\int}_{{\Gamma}_{N}} \bar{\boldsymbol{q}}\cdot\boldsymbol{\eta}_{\varepsilon}, \quad\forall \boldsymbol{\eta}_{\varepsilon}\in\mathcal{U}({\Omega}) $$

(6)

with Ω := (Ω∖B_ε¯) ∪ B_ε. The stress vector is given by σ_ε(u_ε) = C_ε(x)𝜖(u_ε) with C_ε(x) defined as:

$$ \boldsymbol{C}_{\varepsilon}(\boldsymbol{x}) = \begin{cases} \boldsymbol{C} & \text { if } \boldsymbol{x}\in {\Omega}\backslash \overline{B_{\varepsilon}}\\ \boldsymbol{C}^{*} & \text{ if } \boldsymbol{x}\in B_{\varepsilon} \end{cases} $$

(7)

where C^∗ is the constitutive matrix of inclusion. If the inclusion is void, then C^∗ = γC, γ denotes the contrast parameter that mimics void. For the anisotropic fiber inclusions, we need to replace C^∗ with the constitutive matrix pertaining to the anisotropy that represents the fiber material. The performance functional for the perturbed domain is given by:

$$ \psi_{\varepsilon}({\Omega}) = \frac{1}{2}{\int}_{\Omega}\boldsymbol{\sigma}_{\varepsilon}(\boldsymbol{u}_{\varepsilon})\cdot\boldsymbol{\epsilon}(\boldsymbol{u}_{\varepsilon}) $$

(8)

By using (1), (5), and (8), one can obtain the topological derivative for the elastic system; see for instance, Novotny and Sokolowski (2013). In the next section, we have encapsulated all the topological derivatives required to obtain the topology of the fiber-reinforced composite.

3 Topological derivative evaluation

In this section, we present the topological derivatives for exchanging: (i) isotropic matrix material to voids (I → V); (ii) voids to isotropic matrix material (V → I); (iii) fiber material to voids (F → V); (iv) voids to fiber material (V → F); (v) matrix to fiber material (I → F); and (vi) fiber to matrix material (F → I).

3.1 Topological derivative for isotropic ⇌ void phase

According to Novotny and Sokolowski (2013), the analytical expressions of topological derivatives for interchanging isotropic matrix material and void are given by:

$$ \begin{array}{@{}rcl@{}} TD_{I\rightarrow V}(\hat{\boldsymbol{x}}) &=& \frac{2}{1+\nu}\boldsymbol{\sigma}(\hat{\boldsymbol{x}})\cdot\boldsymbol{\epsilon}(\hat{\boldsymbol{x}}) - \frac{1-3\nu}{2(1-\nu^{2})}\\ &&\times(\sigma_{xx}(\hat{\boldsymbol{x}})+\sigma_{yy}(\hat{\boldsymbol{x}}))(\epsilon_{xx}(\hat{\boldsymbol{x}})+\epsilon_{yy}(\hat{\boldsymbol{x}})) \end{array} $$

(9a)

$$ \begin{array}{@{}rcl@{}} TD_{V\rightarrow I}(\hat{\boldsymbol{x}}) &=& -\frac{2}{3-\nu}\boldsymbol{\sigma}(\hat{\boldsymbol{x}})\cdot\boldsymbol{\epsilon}(\hat{\boldsymbol{x}}) - \frac{1-3\nu}{2(1+\nu)(3-\nu)}\\ &&\times(\sigma_{xx}(\hat{\boldsymbol{x}})+\sigma_{yy}(\hat{\boldsymbol{x}}))(\epsilon_{xx}(\hat{\boldsymbol{x}})+\epsilon_{yy}(\hat{\boldsymbol{x}})) \end{array} $$

(9b)

Here, we denote σ(u(x̂)) and 𝜖(u(x̂)) by σ(x̂) and 𝜖(x̂), respectively, for the sake of convenience.

3.2 Topological derivative for fiber ⇌ void phase

The topological derivative in anisotropic elasticity derived in Bonnet and Delgado (2013) and Giusti et al. (2016) uses the polarization tensor for anisotropic inclusions. We utilize this fourth order polarization tensor in second order using standard subscript notations to evaluate topological derivative for interchanging fiber material and voids, which is given by

$$ TD_{F\rightleftharpoons V}(\hat{\boldsymbol{x}}) = \frac{1-\gamma}{2\gamma}\Big(\gamma \boldsymbol{I} + \boldsymbol{T}_{\gamma}\Big)\boldsymbol{\sigma}(\hat{\boldsymbol{x}})\cdot\boldsymbol{\epsilon}(\hat{\boldsymbol{x}}) $$

(10)

Here, I is the identity matrix of order 3 while T_γ in the matrix notation, determines the stress-state inside the inclusion B_ε, see for instance, Giusti et al. (2016). We substitute γ → 0 and γ →∞ in (10) to obtain TD_F→V and TD_{V →F}, respectively.

3.3 Topological derivative for isotropic ⇌ fiber phase

In order to determine topological derivatives for inserting anisotropic fiber inclusions in the isotropic matrix, the polarization tensors in anisotropic elasticity requires a modification. We express the fourth order anisotropic polarization tensor (Giusti et al. 2016) in second order matrix notation as follows:

$$ \boldsymbol{P} = \frac{1}{2}{\Delta} \boldsymbol{C}(\hat{\boldsymbol{x}})\big(\boldsymbol{C}^{-1}(\hat{\boldsymbol{x}}) + \boldsymbol{C}^{*^{-1}}(\hat{\boldsymbol{x}})\boldsymbol{T}(\hat{\boldsymbol{x}})\big) $$

(11)

Here, ΔC = C −C^∗ and the matrix T is computed as

$$ \boldsymbol{T} = -\boldsymbol{A}\boldsymbol{S}, \quad \boldsymbol{S} = \boldsymbol{I} - \boldsymbol{C}^{*}\boldsymbol{C}^{-1} $$

(12)

where A is the matrix of order 3 × 3, obtained by using complex variable method for anisotropic elasticity. In this, the stress and displacement fields inside the inclusion are expressed in terms of complex potentials and a system of equations is obtained to solve A by incorporating prescribed boundary conditions, as explained in Giusti et al. (2016). The constitutive matrix C is denoted as C_I for the isotropic phase, and C^∗ as C_F for the anisotropic fiber phase. Thus, the topological derivatives for interchanging isotropic matrix and fiber inclusions are given by:

$$ \begin{array}{@{}rcl@{}} TD_{I\rightarrow F}(\hat{\boldsymbol{x}}) &=& \boldsymbol{P}_{IF}\boldsymbol{\sigma}(\hat{\boldsymbol{x}})\cdot\boldsymbol{\epsilon}(\hat{\boldsymbol{x}}), \quad \text{with}\\ \boldsymbol{P}_{IF} &=& \frac{1}{2}\big(\boldsymbol{C}_{I} - \boldsymbol{C}_{F}\big)\big(\boldsymbol{C}_{I}^{-1} + \boldsymbol{C}_{F}^{-1}\boldsymbol{T}_{IF}\big) \end{array} $$

(13a)

$$ \begin{array}{@{}rcl@{}} TD_{F\rightarrow I}(\hat{\boldsymbol{x}}) &=& \boldsymbol{P}_{FI}\boldsymbol{\sigma}(\hat{\boldsymbol{x}})\cdot\boldsymbol{\epsilon}(\hat{\boldsymbol{x}}), \quad \text{with}\\ \boldsymbol{P}_{FI} &=& \frac{1}{2}\big(\boldsymbol{C}_{F} - \boldsymbol{C}_{I}\big)\big(\boldsymbol{C}_{F}^{-1} + \boldsymbol{C}_{I}^{-1}\boldsymbol{T}_{FI}\big) \end{array} $$

(13b)

In the preceding equations, T_IF and T_FI are different as they are dependent on C_I and C_F.

Polar form of anisotropic topological derivative

In order to determine optimal fiber angle for each element in the discretized finite element model, we compute anisotropic topological derivative in polar coordinates. This is done by transforming the stiffness matrix of anisotropic material using the following relation:

$$ \bar{\boldsymbol{C}} = \boldsymbol{\mathcal{T}}_{1}^{-1}\boldsymbol{C}\boldsymbol{\mathcal{T}}_{2} $$

(14)

where the transformation matrices ₁ and ₂ are given by:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\mathcal{T}}_{1} &=& \left[ {\begin{array}{ccc} m^{2} & n^{2} & 2mn \\ n^{2} & m^{2} & -2mn \\ -mn & mn & m^{2}-n^{2} \end{array} } \right] \quad\text{and}\\ \boldsymbol{\mathcal{T}}_{2} &=& \left[ {\begin{array}{ccc} m^{2} & n^{2} & mn \\ n^{2} & m^{2} & -mn \\ -2mn & 2mn & m^{2}-n^{2} \end{array} } \right] \end{array} $$

(15)

with m = cos𝜃 and n = sin𝜃 where 𝜃 is the orientation of the fiber with respect to the reference coordinate system. Once the stiffness matrix is obtained as a function of 𝜃, the polarization tensors P_IF and P_FI in (13a) and (13b), respectively, are expressed in terms of the orientation variable leading to the evaluation of minimum transformed topological derivative:

$$ \min_{\theta} TD(\theta) = \boldsymbol{P}^{*}(\theta)\boldsymbol{\sigma}(\hat{\boldsymbol{x}})\cdot\boldsymbol{\epsilon}(\hat{\boldsymbol{x}}) $$

(16)

Here, P^∗ is either P_IF or P_FI for interchanging fiber and matrix material. Similarly, topological derivative in (10) for interchanging fiber material and void can be written in polar form using (16). The transformed topological derivative in (16) is computed for different values of 𝜃. And then material orientation for which the topological derivative is the lowest is chosen as the optimal orientation for the particular element.

4 Solution method

In this section, we explain the algorithm that guides us to the optimal topology of fiber-reinforced composite structures. The topological derivatives mentioned in Section 3 are utilized to obtain the optimal structural design and the fiber angle is determined for each element by computing the anisotropic topological derivative in polar form. The continuous fibers are generated in the form of streamlines by visualizing the obtained data of element-wise fiber angles in the form of a vector field. The method of determining Pareto-optimal isotropic designs as explained in Suresh (2010) is exploited in our work, where the set of all the evolving topologies satisfy validity and Pareto-optimality conditions. In this section, we will explain two algorithms where algorithm 1 offers optimal replacement of partial/full volume of isotropic matrix with anisotropic inclusions thereby maximizing the stiffness of the structure. The second algorithm provides optimal fiber-reinforced topology which constitutes only isotropic matrix, optimally oriented fibers within the matrix and voids. In both the algorithms, we compute fiber angles pertaining to elements with anisotropic material property. Such element-wise fiber angles help us generate continuous fibers.

4.1 Algorithm 1

This algorithm is the extension of the design methodology adopted in Suresh (2010) where the optimal distribution of isotropic material and void is determined. Here, we address the solution method for optimal replacement of isotropic matrix material with anisotropic fiber inclusions. The algorithm to extract fiber-reinforced structural design without voids is shown in Fig. 3 and the details of the steps are as follows:

• 0. We initialize our design by setting matrix volume Ω^m equal to the design space D which means that the fiber fraction (FF) in the matrix is 0. The initial design is fully isotropic with angle set to 0 and the fraction of matrix material to be replaced with fiber inclusions is set to ΔFF = 0.05.

• 1. Finite element analysis is carried over the matrix volume Ω^m and the polar topological sensitivity field is computed using (16). We use Gaussian filter to smoothen the sensitivity field and also store mean compliance J in this step.

• 2. We check whether the desired volume fraction of fiber inclusions in the matrix FF^∗ has attained or not.

• 3. If the condition in Step 2 is not satisfied, then we move to the next material replacement step by modifying FF.

• 4. Next, we compute the level-set value τ by adjusting the level-set plane in the topological sensitivity field. In this step, bisection method is adopted to obtain level-set value between the maximum and minimum values of field and a fixed point iteration scheme is used to arrive at a design such that the fiber volume Ω^f is equal to FF. The area of isotropic matrix below the level-set plane is replaced by fiber inclusions, as illustrated in Fig. 4a.

• 5. We follow step 1 to perform finite element analysis and obtain filtered topological sensitivity field for the composite volume Ω^τ = Ω^m ∪Ω^f.

• 6. The Pareto optimality condition for interchanging matrix and fiber material is given by:

  $$ min(TD_{I\rightarrow F}) + min(TD_{F\rightarrow I}) \geq 0 $$

  (17)

  If the condition follows, we move to step 2. If not, then we move to step 4 and search for the Pareto optimal design at the same fiber fraction.

• 7. If the condition in step 2 is satisfied, then we extract the topology in the form of iso-surface and optimal orientations as illustrated in Fig. 4b.

• 8. This material distribution with optimal orientation of fiber material requires further processing to determine continuous fiber trajectories.

Algorithm 1 determines optimal distribution of fiber and matrix materials which can be visualized while designing composite structures, e.g., the design of fan blades in aircraft engines, where fiber-reinforced composite materials are predominantly used. The critical parameters like weight, efficiency, and clearances are optimized by varying the orientation of fibers in the composite structure. During the manufacturing phase, these optimal orientations of the fibers in the matrix are realized through the state-of-the-art additive manufacturing techniques.

Fig. 3

Algorithm 1: To determine Pareto-optimal fiber-reinforced structural design without voids

Fig. 4

Topological-derivative-based level-set visualization for two-phase material distribution

4.2 Algorithm 2

We use an approach for obtaining three-phase material distribution of only matrix, fibers embedded within the matrix, and voids in the design space, as illustrated in Fig. 5. As shown in the figure, we optimally add fiber inclusions in the matrix for desired value of fiber fraction (FF^∗) while void fraction (V F) is held constant. Once we arrive at FF^∗, voids are created at constant fiber fraction (FF). Since the voids may add or remove some material from the fibers, thereby changing the fiber fraction in the matrix, we again distribute them in the resulting topology to retain FF^∗ while simultaneously maintaining V F^∗. Alternatively, one can also interchange between FF^∗ and V F^∗ to first create voids in the matrix material followed by insertion of fibers. In this paper, we intend to create voids in the composite structure for which the algorithm is designed to obtain optimal distribution of material and void as well as fiber or no fiber where there is material. It consists of two loops where the first loop maintains the fiber fraction in the material while void fraction is held constant and the second loop creates optimal locations of voids with fiber fraction held constant. The steps in the algorithm, as illustrated in Fig. 6, are as follows:

• 0. We start with an initial isotropic domain Ω^m which is equal to the design space D. The void fraction V F, fiber fraction FF, and orientation set to 0. The fraction of isotropic matrix to be replaced by fiber material is set as ΔFF = 0.05 and the volume fraction of voids to be created in the material domain is given by ΔV F = 0.05.

• 1. We carry finite element analysis over Ω^m and filtered topological sensitivity field is evaluated using (16) to interchange between matrix and fibers.

• 2. We check whether we have attained the desired fiber fraction FF^∗.

• 3. If not, then we move to next material replacement step by modifying fiber fraction FF.

• 4. Now, we compute the level-set value τ₁ in the sensitivity field by adjusting the level-set plane, as explained in algorithm 1. The motive is to arrive at fiber volume Ω^f equal to FF. The area below the level-set plane is replaced by fiber material, as shown in Fig. 7a.

• 5. We perform finite element analysis on ${\Omega }^{\tau _{1}} = {\Omega }^{m} \cup {\Omega }^{f}$ and evaluate the corresponding topological sensitivity field as we did in Step 1.

• 6. The Pareto optimality condition for replacing isotropic matrix by fiber inclusions is given by:

  $$ min(TD_{I\rightarrow F}) + min(TD_{F\rightarrow I}) \geq 0 $$

  (18)

  If the condition in step 6 follows, then we move to step 2; otherwise, we go to step 4.

• 7. If the condition in step 2 follows, then we check for the void fraction in the design space to attain desired value V F^∗.

• 8. If not, then we move to next void creation step by modifying V F.

• 9. We compute level-set value τ₂ by bisection method and adjust the level-set plane such that the volume occupied by voids Ω^v is equal to V F. The area below the level-set plane is the region with optimal void locations, as illustrated in Fig. 7b.

• 10. We perform finite element analysis over ${\Omega }^{\tau _{2}} = {\Omega }^{m} \cup {\Omega }^{f}\cup {\Omega }^{v}$ and compute composite topological derivatives using (9a) and (16) for interchanging matrix and voids as well as fiber and voids, respectively.

• 11. We check the Pareto optimality condition for creation of voids which is given by:

  $$ min(TD_{M\rightarrow V}) + min(TD_{V\rightarrow M}) \geq 0 $$

  (19)

  Here, M represents matrix material or fiber. If the condition does not follows, we move to step 9. If yes, then we go to step 2 for redistributing fibers in the design such that we arrive at FF^∗ while maintaining V F.

• 12. We need to check whether steps 2 and 7 follow simultaneously. If yes, then we extract the resulting iso-surface and the optimized orientations.

• 13. This three-phase material distribution with optimally oriented fibers requires further processing to determine continuous fiber trajectories (explained in Section 6).

In this three-phase topology optimization procedure, we develop a Pareto surface for designs for different void and fiber fractions.

Fig. 5

An approach to arrive at three-phase material distribution and orientation

Fig. 6

Algorithm 2: To determine Pareto optimal fiber-reinforced structural design with voids

Fig. 7

Topological-derivative-based level-set visualization for three-phase material distribution

5 Numerical examples

In this section, we present various fiber-reinforced structures designed for maximum stiffness. In the first part of this section, we utilize algorithm 1 to obtain Pareto optimal homogeneous distribution of matrix material (isotropic) and fiber material (orthotropic) for desired volume fraction of fiber and matrix. In this process, we also present optimal orientation of fiber in each orthotropic element of the finite element mesh. We discuss three examples of cantilever with different loading conditions and their respective Pareto curves. The second part of this section will present optimal fiber orientations for multiple load cases. In the third part of this section, we will utilize algorithm 2 to present three-phase structural topology for a given void fraction in the material and fiber fraction in matrix.

In all the examples, we have considered the following material properties:

• 1. For isotropic matrix, we have E = 1.0 GPa (Young’s modulus) and ν = 0.3 (Poisson’s ratio).

• 2. For fiber inclusions, we consider orthotropic constitutive properties with E_x = 4.0 GPa (Young’s modulus in longitudinal direction), E_y = 2.0 GPa (Young’s modulus in transverse direction), ν_xy = 0.3, (Poisson’s ratio), and G = 0.7 GPa (shear modulus).

• 3. The contrast parameter to mimic void is taken as γ = 1.0 × 10^− 4. In addition, we consider plane stress assumption for all the loading conditions and the domain is discretized into 60 × 30 bilinear quad elements.

5.1 Fiber-reinforced structural designs without voids

The first example is that of a cantilever with load case-1 shown in Fig. 8a. We use algorithm 1 to determine Pareto optimal distribution of fiber and matrix materials at different fiber fractions (FF) and demonstrate the same through a Pareto curve shown in Fig. 8b. The black and gray colors represent fiber and matrix materials, respectively. We consider the fiber elements in the finite element model and compute topological derivative in polar coordinates for different values of 𝜃, using (16) where fiber angle corresponding to minimum topological derivative value offers optimal orientation for the particular element. The orientation field for a given fiber fraction, say FF^∗ = 0.6, is illustrated in Fig. 9a. Note that there will be a slight deviation in the Pareto curves for oriented and non-oriented topological derivatives as shown in Fig. 9b.

Fig. 8

Pareto optimal material distribution for load case-1

Fig. 9

Optimal orientation at given fiber fraction and deviation in the Pareto curves for load case 1

One can generate element-wise fiber orientations at any fiber fraction by following a similar procedure. Furthermore, we obtained principal stress direction for the mentioned load case using COMSOL Multiphysics and we observe that the resulting orientation field for completely orthotropic structure is in agreement with principal stress directions, as illustrated in Fig. 10. The red and blue arrows represent tensile and compressive nature of stresses respectively in Fig. 10b.

Fig. 10

Optimal fiber orientations in agreement with principal stress directions for load case 1

The second loading case of cantilever is shown in Fig. 11a for which the Pareto optimal material distribution is shown in Fig. 11b. The vector field of orientations at FF^∗ = 0.6 for this specific load case is shown in Fig. 12a and the deviation in the value of mean compliance for the polar topological derivative is identified in the Pareto curve as shown in Fig. 12b. Next, we perform a regular check of resulting orientations with principal stress directions, which is presented in Fig. 13

Fig. 11

Pareto optimal material distribution for load case 2

Fig. 12

Optimal orientation at given fiber fraction and deviation in the Pareto curves for load case 2

Fig. 13

Optimal fiber orientations in agreement with principal stress directions for load case 2

The third loading case of the cantilever is shown in Fig. 14a where we are applying uniformly distributed load.

Fig. 14

Benchmark result on orientation of orthotropic fibers reported by Pedersen (1991) for distributed load case

In this case, we compute optimal orientations for fully orthotropic material in the domain, i.e., with FF^∗ = 1 and compare these with the one reported by Pedersen (1991) in Fig. 14b. In the work, the author states that the orientations for orthotropic material should follow principal stress directions (Pedersen 1989). Thus, we observe in our case that the orientation field agrees with the direction of principal stresses, as illustrated in Fig. 15.

Fig. 15

Comparison with the results by Pedersen for load case 3

5.2 Fiber-reinforced structure for multiple load case

We investigate the optimal fiber orientations in the cantilever subjected to multiple loads. The point loads are as shown in Fig. 16a. In this case, we individually compute topological derivative field corresponding to two loads using (16) and generate a sensitivity field with the minimum value of the topological derivative. This idea of taking the minimum value of derivative provides stiffest composite structure and the resulting vector field of optimal fiber angles is then obtained as shown in Fig. 16b. Here, we have depicted the element-wise fiber angles corresponding to both the loads. If the optimal fiber angles pertaining to both the loads are equal, they are represented by a single red line, whereas intersecting red and blue lines depict that the angles are unequal corresponding to both the loads.

Fig. 16

Orientation field in multiple load case

5.3 Fiber-reinforced structural design with voids (a three-phase topology)

In this three-phase design approach, we use algorithm 2 to arrive at Pareto optimal material distribution to incorporate matrix, fiber, and voids. We first take an initial matrix which constitutes isotropic material for the cantilever with load case 1. The topological sensitivity field for this initial design is computed using (16) to optimally place fiber material while void fraction is held constant. Once, we reach the desired value of fiber fraction FF^∗, we intend to create voids by keeping fiber fraction constant. The material sensitivity field is generated by evaluating topological derivatives in (9a) and (16) to create void locations. This iterative process of simultaneously distributing matrix, fiber, and voids in the design space eventually offers three-phase optimized topology for various fiber and void fractions.

We check for the three-phase design to satisfy Pareto optimality conditions in (17) and (18). Once, this Pareto optimal material distribution is determined, we also plot the orientation field for the resulting topology. The three-phase material distribution is illustrated in Fig. 17a and the resulting orientation field is shown in Fig. 17b. The material distribution and orientation for load case 2 (end load) are presented in Fig. 17c and d respectively.

Fig. 17

Optimal material distribution and orientations of fiber-reinforced structure for two load cases

The fiber-reinforced structural design with optimal orientation of fibers can be obtained for the range of fiber and void fractions thereby providing a Pareto surface of stiffness and volume fraction of void and material as well as fiber and matrix as shown in Fig. 18. In the next section, we present the fiber trajectories for all the designs that we have obtained, along which the continuous fiber strands can be laid.

Fig. 18

Pareto surface of stiffness and two volume fractions for center load on the right edge

6 Continuous fiber trajectories

The two- and three-phase optimal material distributions are achieved for several loading conditions, using topological-derivative-based design algorithm. The polar form of anisotropic topological derivative provided us the optimal fiber orientation of all the elements in the finite element model. In view of embedding fibers within the matrix, element-wise fiber orientation is not amenable for manufacturing or 3D printing. This points to a need to develop continuous fiber tracks such that the long fibers can be laid along them. In this section, we explain the procedure for obtaining long and evenly spaced continuous fibers.

Long fibers are generated with the help of stream2 function in MATLAB. This function requires the vector field of the domain and the starting points of the streamlines (or fibers) as inputs and returns the data points of the fibers paths as output. The optimal element-wise orientations are visualized in the form of vector field and the starting points are obtained from the center of the elements. Therefore, the number of starting points (and hence the number of fibers) will be same as the number of elements. While it generates long fibers as per the obtained orientations, such density of fibers can impose heavy manufacturing constraints since it is difficult to lay large number of fibers in a small volume of the domain. Hence, there is a need to space the fibers uniformly such that they lie within the print tolerance of the machine. The following steps are followed to achieve the evenly spaced long fibers:

• 1. The domain is divided into smaller domains. The size of the smaller domains can be varied depending on the allowable range of spacing between the fibers.

• 2. The set of smaller domains through which each fiber passes is identified; to ensure appropriate spacing between the fibers, a constraint of allowing only one fiber to pass through the smaller domain is enforced.

• 3. Among the entire density of fibers, each fiber is prioritized based on a metric which is calculated using the following expression:

  $$ {\Sigma}_{i=1}^{n} \alpha_{i} \sigma_{i} $$

  (20)

  where α_i is the arc length of fiber inside the smaller domain i, σ_i is the largest absolute value of the principal stress in i, and n is the number of smaller domains through which the fiber passes. This metric tries to capture the contribution of a fiber for improving the stiffness by giving priority to those domains which have higher principal stress values. Therefore, the fiber which has the highest value of this metric is plotted first and hence dominates the smaller domain after the constraint mentioned in step 2 is enforced.

• 4. Once the priority of laying fibers is set, the redundant fibers must be removed. This is achieved by eliminating the starting points of the fibers which lie within the print tolerance (or spacing between the fibers). Hence, the fibers are plotted sequentially so that they terminate either at the boundary or an element where there is fiber already present, as presented in Fig. 19.

  Fig. 19

  

  Uniformly spaced continuous fibers for two load cases

This procedure of obtaining long fibers does not necessarily provide fiber continuity as there are uneven breaks in the fiber paths which may not comply with the print tolerance associated with the minimum length for laying fibers. This drawback is overcome using data visualization software, ParaView, for obtaining continuous fiber trajectories. The element-wise fiber orientation for all the loading cases can be visualized in the form of a vector field. The evenly spaced fibers are obtained using “Evenly Spaced Streamlines 2D” filter in ParaView, as illustrated in Fig. 20. Long fiber paths in multiple load cases are obtained using Tecplot, as depicted in Fig. 20d. The simplified fiber arrangement is achieved while retaining non-periodic and specific pattern of the fiber.

Fig. 20

Evenly spaced continuous fibers for all the load cases

7 Closure

In this paper, we present stiffest composite designs with and without voids by using topological derivatives. The Pareto optimal distribution of matrix material (isotropic), fiber material (orthotropic), and voids is achieved for a given void fraction in material and fiber fraction in matrix. The intent of this study is to obtain fiber-reinforced structures with evenly spaced continuous fibers. We also developed a Pareto surface of structural stiffness with two volume fractions, namely void and fiber fractions.

Simultaneously varying void and fiber fractions using six topological derivatives in a level-set methodology is a key feature of the technique presented in this paper. Using the polar form of the topological derivative enabled choosing the optimum fiber angle effortlessly. Unlike some previous works, here optimal fiber angle can assume any value rather than from the predetermined discrete set. The optimal orientations for uniformly distributed load are in agreement with the results from the literature. We also observed that the optimal orientations agree with the principal stress directions in all the design examples.

We implemented an algorithm to incorporate only matrix material, fibers embedded within matrix material, and voids in a given design space for two loading conditions. The fiber fraction and void fraction are controlled simultaneously which lead to optimal distribution of the three phases. The orientations are determined for the resulting multimaterial distribution by representing topological derivative in polar coordinates. These set of orientations provide continuous fiber paths along which the long fiber strands can be laid. We evenly space the continuous fibers such that the manufacturability constraints are satisfied while retaining their non-periodic and specific pattern. The simplification of the dense fiber arrangement led to a question on how much we have lost or gained in terms of structural stiffness. The evaluation of mean compliance is non-trivial as elements in the finite element grid possess anisotropic fibers embedded within the isotropic matrix, which requires a different constitutive model to address the issue. The proposed methodology in this paper is applicable to the work in Amstutz and Novotny (2010) and Sales et al. (2015), to obtain fiber orientations and trajectories of Kirchhoff and Reissner/Mindlin plates.