Abstract
This study presents a novel computational framework for designing optimal dissipative (damping) metamaterials under time-dependent loading conditions at finite deformations. In this framework, finite strain computational homogenization is integrated with a density-based multimaterial topology optimization. In addition, a thermodynamically consistent finite strain viscoelasticity model is incorporated together with an analytical path-dependent sensitivity analysis. Optimization formulations with and without stiffness and mass constraints are considered, and various new damping metamaterial designs are obtained that combine soft viscoelastic and stiff hyperelastic material phases. Multiscale stability analysis using the Bloch wave analysis and rank-1 convexity checks is also carried out to investigate stability of the optimized designs. Stability analyses demonstrate that the inclusion of voids or soft material phases can make a metamaterial more prone to lose micro and macro-stability. Furthermore, the concept of tunable metamaterials is explored wherein metamaterial’s response is steered towards a stable deformation path by tailoring the design with a preselected micro buckling mode.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mechanical metamaterials with tailored functionalities have received considerable attention in recent years due to the unprecedented progress in additive manufacturing technologies (Gibson et al. 2014; Gao et al. 2015). In essence, these metamaterials are obtained by carefully designing the underlying material microstructure, and the exotic properties of these metamaterials are dependent on the tailored material microstructures rather than on the material’s chemical constitution. While many metamaterials have been obtained by experimental design and trial-and-error methods (Surjadi et al. 2019), advanced computational methods based on multiscale mechanics and mathematical optimization can provide a rigorous framework for designing such metamaterials (Sigmund 1994). This study is concerned with the design of optimized metamaterials with desirable damping and stiffness properties under finite strains using nonlinear homogenization and topology optimization methods.
Homogenization theories, starting with the pioneering work of Hill (1972) and Mandel (1972), provide a rigorous mathematical framework for predicting the effective properties of composites based on analysis of the underlying metamaterial microstructure. For comprehensive reviews of homogenization theories and various computational aspects, the readers are referred to Saeb et al. (2016) and Blanco et al. (2016). While homogenization analysis under small deformations is straightforward, the consideration of stability under finite strain homogenization is nontrivial (Geymonat et al. 1993). As shown in previous studies (Geymonat et al. 1993; Triantafyllidis et al. 2005), both microscale stability (leading to short wavelength bifurcations) and macroscale stability (i.e., loss of macroscopic rank-1 convexity associated with long wavelength bifurcations) can be lost under finite deformations. Topology optimization, first proposed by Bendsøe and Kikuchi (1988), on the other hand, seeks optimum material layout to minimize/maximize predefined objectives, and these methods have undergone significant progress and are now routinely used in engineering designs (Sigmund and Maute 2013; Deaton and Grandhi 2014). Combining with asymptotic homogenization theory, Sigmund (1994) first used topology optimization in material design and optimization. Following Sigmund’s work, a large amount of research has been devoted to the discovery of novel metamaterials with a wide range of properties, such as extreme thermal expansion (Sigmund and Torquato 1997), extreme bulk and shear modulus (Gibiansky and Sigmund 2000; Huang et al. 2011), desirable band-gaps (Sigmund and Jensen 2003), negative Poisson’s ratio (Sigmund 1994) and optimal plastic energy dissipation (Alberdi and Khandelwal 2019b) and damping characteristics (Andreassen and Jensen 2014; Asadpoure et al. 2017; Yun and Youn 2018), among others. Though promising, the metamaterial design by inverse homogenization based topology optimization is mostly restricted to small deformation regime. Design via inverse homogenization under finite deformation is challenging due to a number of issues, including the difficulties in the nonlinear finite element analysis (FEA), where the mesh distortion can occur in low/intermediate density elements that would prevent the convergence in FEA (Buhl et al. 2000). The other challenge is related to the validity of nonlinear homogenization due to the presence of potential multiscale, i.e., micro and macro scale, instabilities (Geymonat et al. 1993; Triantafyllidis et al. 2005), as mentioned above. Recently, some efforts have been made in designing metamaterials at finite strains (Nakshatrala et al. 2013; Kato et al. 2018; Zhang and Khandelwal 2019a).
Metamaterials with optimal damping and stiffness properties are needed in many applications for energy dissipation and vibration control in aerospace, automotive, mechanical, and civil engineering (Hagood and von Flotow 1991; Rao 2003; Nakra 1998). Energy dissipation in these metamaterials is due to the viscoelastic behavior of the underlying material. Most of the previous studies on viscoelastic metamaterial design have been confined to the small strain regime wherein frequency domain analyses under steady-state conditions are considered (Andreassen and Jensen 2014; Yi et al. 2000; Chen and Liu 2016; Huang et al. 2015). This is a rather restrictive design framework, since arbitrary time-dependent loadings, such as pulse, irregular cyclic loadings, etc., cannot be considered. Extension to time domain is not trivial, however, due to the path-/time-dependent design sensitivity analysis (Michaleris et al. 1994), and only in the recent studies efforts have been made to incorporate consistent and accurate path-/time-dependent sensitivities in design optimization (Alberdi et al. 2018b; Zhang et al. 2017; Li et al. 2018; Ivarsson et al. 2018; Bogomolny and Amir 2012; Li et al. 2017; Nakshatrala and Tortorelli 2015; Nakshatrala and Tortorelli 2016; Alberdi and Khandelwal 2017; Alberdi and Khandelwal 2019a). Another important restriction is due to the small strain assumption that has been considered in the previous studies on design of viscoelastic metamaterials. As has been demonstrated in previous studies with hyperelastic materials (Buhl et al. 2000; Jung and Gea 2004; Zhang et al. 2018; Wallin et al. 2018), nonlinear designs under finite strains can be significantly different from linear designs. This is critical since damping metamaterials such as viscoelastic metamaterials can undergo large deformations during a loading process. As a result, designs based on small strain assumptions can lead to suboptimal or even misleading designs. Moreover, nonlinear metamaterial designs should also account for macro and micro instabilities (Zhang and Khandelwal 2019a; Triantafyllidis and Schraad 1998), which is a non-issue in the design of viscoelastic metamaterials under small strains.
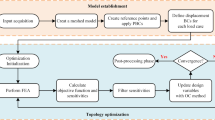
To address the aforementioned challenges, a computational design framework is proposed in this study for the design of optimal damping metamaterials at finite strains based on nonlinear homogenization and density-based multimaterial topology optimization. This work is inspired by the previous studies (Zhang et al. 2015; Zhang and Khandelwal 2019b), where it has been demonstrated that combining softer viscoelastic material with stiffer elastic material can vastly improve the damping performance of a structure or material. The main contributions of this work are as follows: (a) An effective design framework is achieved by combining a series of methods, models, and techniques including finite strain homogenization analysis that enables a clear transition from the microstructural behavior to the macroscale properties, a thermodynamically consistent finite strain viscoelasticity model with analytical path-dependent sensitivities, multimaterial optimization formulations, and an adaptive linear energy interpolation scheme for mitigating mesh distortion issues; (b) parametric studies are conducted for providing important insights on the damping metamaterial design; (c) multiscale stability investigations on the optimized designs based on Bloch wave analysis and rank-1 convexity checks are carried out, and the use of short-wavelength buckling mode for obtaining a tunable design performance is numerically demonstrated. Stability investigations are only carried out as post-design checks and stability constraints are not directly included in the optimization process. The rest of the paper is organized as follows: in Section 2, finite deformation homogenization method is reviewed. In Section 3, finite strain viscoelastic model is presented. Sections 4 and 5 give the density-based multimaterial topology optimization formulations and path-dependent sensitivity analysis, respectively. Section 6 shows illustrative numerical examples, which is followed by multiscale stability investigations in Section 7. Final remarks and conclusions are given in Section 8.
2 Finite deformation homogenization
Finite deformation homogenization theory is used for describing the overall macroscale response of metamaterials with periodic microstructures. To this end, a representative unit cell (RUC) is considered that characterizes the underlying periodic microstructure of a metamaterial. Based on homogenization theory, this RUC can be used to describe the overall macroscale metamaterial behavior (Saeb et al. 2016). For example, Fig. 1 shows the deformation of a bulk of metamaterial with microstructure characterized by the periodic arrangement of a unit cell that can be taken as RUC. To fulfill the scale separation assumptions, the characteristic length of RUC should be much smaller than the dimensions of the macroscale continuum body (Saeb et al. 2016). Note that an overbar is used for denoting variables at macroscale, e.g., \(\boldsymbol {\overline {X}}\) and \(\overline {\boldsymbol {x}}\) are the position vectors of a material point in the initial and current configurations, respectively, at macroscale, while X and x are position vectors of a material point in the initial and current configurations, respectively, at microscale.
At macroscale, the initial configuration Ω0 is mapped to the current configuration Ωt by a nonlinear deformation \(\overline {\boldsymbol {\varphi }}\), i.e., \(\overline {\boldsymbol {x}}(t) = \overline {\boldsymbol {\varphi }}(\overline {\boldsymbol {X}},t)\) at \(\overline {\boldsymbol {X}}\in {\Omega }_{0}\), \(t\in \mathbb {R}^{+}\). The resulted deformation gradient field at macroscale is \(\overline {\boldsymbol {F}}(\overline {\boldsymbol {X}},t)=\boldsymbol {I}+{\boldsymbol {\nabla }}\overline {\boldsymbol {u}}\), where \(\overline {\boldsymbol {u}}\) is the macroscopic displacement field satisfying \(\overline {\boldsymbol {x}}(t)=\overline {\boldsymbol {X}}+\overline {\boldsymbol {u}}(t)\) and ∇ represents the gradient operator w.r.t. the macroscale coordinates \(\overline {\boldsymbol {X}}\). At microscale, the initial configuration of RUC is denoted by \({\Omega }_{0}^{\mu }\) that consists of solid part \({\mathcal{B}}_{0}\) and void part \({\mathcal{H}}_{0}\), i.e., \({\Omega }_{0}^{\mu }={\mathcal{B}}_{0}\cup {\mathcal{H}}_{0}\), which is mapped to the current configuration \({\Omega }_{t}^{\mu }(={\mathcal{B}}_{t}\cup {\mathcal{H}}_{t})\) by a nonlinear deformation φ. In the deformation-driven homogenization framework, deformation of the microstructure is driven by a local deformation \(\overline {\boldsymbol {F}}(\overline {\boldsymbol {X}},t)\) of the macro-continuum associated with the point \(\overline {\boldsymbol {X}}\) at macroscale. That is, with the macroscopic deformation gradient \(\overline {\boldsymbol {F}}\) as the input, the microscale problem is solved for the homogenized/macroscopic stress and tangent moduli. In FE2 formulation (Saeb et al. 2016), the micro-problem is defined and solved at each integration point in the macro-problem and the two problems are solved in a nested way. In the current study, the macroscopic deformation \(\overline {\boldsymbol {F}}(\overline {\boldsymbol {X}},t)\) with \(t\in \mathbb {R}^{+}\) is prescribed at certain fixed \(\overline {\boldsymbol {X}}\in {\Omega }_{0}\), without referring to any specific macro-problem. The macroscopic material properties are then evaluated under this deformation mode. Thus, the explicit dependence on \(\overline {\boldsymbol {X}}\) is omitted in further discussions.
The microscopic displacement field u(X, t) over the RUC domain \({\Omega }_{0}^{\mu }\) is assumed to be driven by a prescribed macroscopic deformation \(\overline {\boldsymbol {F}}(t)\), i.e.,
where \(\tilde {\boldsymbol {u}}(\boldsymbol {X},t)\) is defined as the displacement fluctuation field. The microscopic deformation gradient can be expressed as
where ∇X denotes the gradient operator w.r.t. the microscale coordinates X. Following Hill (1972), the macro deformation gradient \(\overline {\boldsymbol {F}}\) is assumed to be fully described by the kinematics on the boundary of RUC
which, combined with a rigid-body translation removal constraint, i.e., \({\int \limits }_{{\mathcal{B}}_{0}}\boldsymbol {u}(\boldsymbol {X},t)dV=\boldsymbol {0}\), constitutes the kinematical admissibility constraints for the microscale displacement field of the micro-problem (de Souza Neto et al. 2015). Here, V is the volume of the domain \({\Omega }_{0}^{\mu }\) and N the unit normal vector on the boundary \(\partial {\Omega }_{0}^{\mu }\). Note that \(\partial {\mathcal{B}}_{0}=\partial {\Omega }_{0}^{\mu }\cup \partial {\mathcal{H}}_{0}\) where \(\partial (\blacksquare )\) denotes the boundary of \(\blacksquare \). As a result, the kinematically admissible displacement fluctuation field \(\tilde {\boldsymbol {u}}(\boldsymbol {X},t)\) is defined in a functional space \(\mathcal {V}_{\min \limits }\)
where the constraint \({\int \limits }_{{\mathcal{B}}_{0}}\tilde {\boldsymbol {u}}(\boldsymbol {X},t)dV=\boldsymbol {0}\) is for removing rigid-body translation and the constraint \({\int \limits }_{\partial {\Omega }_{0}^{\mu }}\tilde {\boldsymbol {u}}(\boldsymbol {X},t)\otimes \boldsymbol {N}(\boldsymbol {X})dS=\boldsymbol {0}\) is obtained by substituting (1) into (3), which implicitly suppresses the rigid-body rotations. The functional space \(H^{1}({\mathcal{B}}_{0})=\{\boldsymbol {v}|v_{i}\in L^{2}({\mathcal{B}}_{0}),\partial v_{i}/\partial X_{j}\in L^{2}({\mathcal{B}}_{0}),i,j=1,2,...,d\}\) and \(L^{2}({\mathcal{B}}_{0})\) represents the space of square integrable functions defined on \({\mathcal{B}}_{0}\) and d is the number of space dimensions. The subscript \(\min \limits \) means that this set of constraints is the minimal set required for kinematical admissibility. It has been shown in de Souza Neto et al. (2015) that this set of constraints corresponds to the constant traction boundary conditions. Additional constraints can be introduced in a consistent way that may lead to periodic boundary conditions or linear displacement boundary conditions (de Souza Neto et al. 2015).
The micro-to-macro transition is governed by the principle of multiscale virtual power (de Souza Neto et al. 2015), which is expressed as, \(\forall t\in \mathbb {R}^{+}\)
where \(\overline {\boldsymbol {P}}\) and P are the macro and micro 1st Piola-Kirchhoff (PK) stress tensors, respectively, and the space of virtual kinematically admissible fluctuation field \(\delta \tilde {\boldsymbol {u}}\) is identical to that of the kinematically admissible fluctuation field \(\tilde {\boldsymbol {u}}\), \(\mathcal {V}\), which is a subspace of \(\mathcal {V}_{\min \limits }\). Equation (5) can be seen as the variational form of the Hill-Mandel condition (Hill 1972; Mandel 1972) that states the incremental internal energy equivalence between the macroscale and microscale. In (5), inertia and body forces have been assumed zero and the interested readers are referred to Ref. (de Souza Neto et al. 2015) for further extensions to dynamic cases.
The stress homogenization relation
and the microscale equilibrium equation
can be obtained from (5) by choosing \(\delta \tilde {\boldsymbol {u}}=\boldsymbol {0}\) and \(\delta \boldsymbol {\overline {F}}=\boldsymbol {0}\), respectively. Note that the second equality in (6) can be proved using divergence theorem and the fact that ∇X.P = 0 (Saeb et al. 2016), while the third equality is due to the traction-free void boundaries, i.e., t0 = 0 on \(\partial {\mathcal{H}}_{0}\). For dissipative constituent materials, the homogenized/macroscopic mechanical dissipation rate per unit reference volume is assumed to be defined by the volume average
where Dint(X, t) represents the energy dissipation rate per unit reference volume at microscale.
2.1 Periodic boundary condition
As the underlying metamaterial microstructure is assumed to be periodic with repeating unit cells (Fig. 1), periodic boundary conditions are used to evaluate the homogenized response. In this study, 2D plane strain problems are considered in the numerical implementations where no microscale fluctuations are on the out-of-plane surface. However, all the presented methods can be canonically extended to 3D cases. For a 2D RUC, the boundary can be decomposed into a pair of negative and positive sides, denoting as \(\partial {\Omega }_{0}^{\mu -}\) and \(\partial {\Omega }_{0}^{\mu +}\), respectively (see Fig. 2), where points on the positive side can be reached by translating the corresponding points on the negative side using a periodic lattice vector a1 or a2 or ± (a1 ±a2). For periodic boundary conditions, the displacement fluctuations on the negative side is equal to the corresponding ones on the positive side, i.e.,
which can be proved to automatically satisfy the constraint in (3). Hence, the kinematically admissible displacement fluctuation field considering periodic boundary condition is defined in a functional space \(\mathcal {V}\)
and the micro-problem is completely defined by (5).
For a given discretized RUC (Fig. 2), the constraints in (9) are given by
where m pairs of nodes lying on the negative and positive boundary sides are identified. The rigid-body translation constraint can be equivalently replaced by fixing one arbitrary point, e.g., \(\tilde {\boldsymbol {u}}_{o}=\boldsymbol {0}\) in \({\mathcal{B}}_{0}\). Thus, the discretized functional space \(\mathcal {V}^{h}\) is defined by
2.2 Principle of multiscale virtual power with Lagrange multiplier: discrete form
Given a discretized microstructure, the principle of multiscale virtual power together with the periodic boundary conditions can be formulated in a variational form with constraint-free variational spaces using the Lagrange multiplier method. To this end, the constrained variational form in (5) is considered where the Lagrange multipliers are introduced to enforced the boundary conditions [(12)] as follows:
where λ and μ = [μ1,..., μm]T are the Lagrange multipliers, and the constraints are restated in terms of the displacement field u(X, t) instead of fluctuation field \(\tilde {\boldsymbol {u}}(\boldsymbol {X},t)\). Note that uo(t) = 0 is equivalent to \(\tilde {\boldsymbol {u}}_{o}(t)=\boldsymbol {0}\) in the sense of removing rigid-body translation. The vector Lq in (13) represents the translation vector that satisfies \(\boldsymbol {X}_{q}^{+}=\boldsymbol {X}_{q}^{-}+\boldsymbol {L}_{q}\) where \(\boldsymbol {X}_{q}^{+}\) and \(\boldsymbol {X}_{q}^{-}\) are the coordinates of the nodes on a pair of positive and negative sides (see Fig. 2).
2.2.1 Interpretation of Lagrange multipliers
The Lagrange multipliers λ and μ can be interpreted as discrete nodal forces on the boundary. For instance, assuming \(\delta \overline {\boldsymbol {F}}=\boldsymbol {0}\), δλ = 0, δμ = 0, and δu = c0 (with c0 being constant in \({\mathcal{B}}_{0}\)) in (13) gives \(\lambda ^{T}\boldsymbol {c}_{0}=0\). Therefore,
has to be satisfied, which means that for a self-equilibrated system, fixing one arbitrary point for removing rigid-body translation does not create any reaction forces. Next, taking \(\delta \overline {\boldsymbol {F}}=\boldsymbol {0}\), δλ = 0, and δμ = 0 with δu(X) = A0.X in \({\mathcal{B}}_{0}\) where A0 ∈Lin (a constant 2nd-order tensor) in (13), it can be shown that
where μq and Lq (q = 1,..., m) are both vectors (or 1st-order tensors) while P and A0 are 2nd-order tensors. Since A0 can be chosen arbitrarily, it follows from (6) and (15) that
which when combined with (6)3 shows that μq represents the traction force at node q. Therefore, it can be seen that the homogenized stress can be computed from the Lagrange multipliers μ.
2.3 Finite element formulation
The rigid-body translation and periodic boundary constraints can be expressed in matrix-vector forms as
with matrices M1 and M2, and vector h constructed such that
where u is the global nodal displacement vector, \(\boldsymbol {u}^{+}=\left [\boldsymbol {u}_{1}^{+},...,\boldsymbol {u}_{m}^{+}\right ]^{T}\), and \(\boldsymbol {u}^{-}=\left [\boldsymbol {u}_{1}^{-},...,\boldsymbol {u}_{m}^{-}\right ]^{T}\) includes m nodal displacements defined on the positive and negative boundary sides, respectively. \(\boldsymbol {L}_{q}=\left [\tilde {X}_{q},\tilde {Y}_{q}\right ]^{T}\) is the translational vector from the q th node on the negative side to the q th node on the positive side. The expression of h vector is written for 2D case in (18).
Considering the unknown variables to be solved as u, λ, and μ, the resulting set of nonlinear constrained equilibrium equations, from (13), can be written as
where Fint represents the global internal force vector defined by
where B is the shape function derivative matrix, Ωe represents the e th element integration domain satisfying \({\mathcal{B}}_{0}=\bigcup \limits _{e=1}^{n_{ele}}{\Omega }^{e}\) and nele are the total number of elements in the RUC. In the topology optimization, with the design domain defined as the RUC, a fictitious domain approach is adopted in which void area \({\mathcal{H}}_{0}\) is also included in FEA and is assigned vanishing material properties, i.e., \({\Omega }_{0}^{\mu }=\bigcup \limits _{e=1}^{n_{ele}}{\Omega }^{e}\).
The nonlinear system in (19) is solved using the Newton-Raphson (NR) method and the Jacobian matrix, which is needed for NR solver, can be calculated as
where the term KT = ∂Fint/∂u is the tangent structural stiffness matrix calculated by
in which the element tangent stiffness matrix \(\boldsymbol {k}_{T}^{e}\) is obtained by the F-bar formulation given in Section 4.5 and is not symmetric.
2.4 Homogenized stress and tangent moduli
Using (16)2 and the definition of matrix \(\left [\boldsymbol {L}_{M}\right ]\) given in (18), the homogenized stress \(\overline {\boldsymbol {P}}\) is computed as
where the bracket outside \(\boldsymbol {\overline {P}}\) means that it is arranged in a 4 × 1 vector form, similarly as \([\boldsymbol {\overline {F}}]\) used in (18).
The 4th-order tensor homogenized tangent moduli \(\overline {\mathbb {A}}\) is defined by
and can be rephrased in a matrix form as \(\left [\overline {\mathbb {A}}\right ]=\partial \left [\overline {\boldsymbol {P}}\right ]/\partial \left [\overline {\boldsymbol {F}}\right ]\), which is of size 4 ×4 for 2D case. From (23), it is clear that \(\left [\overline {\mathbb {A}}\right ]\) is determined by the derivative of Lagrange multiplier μ with respect to \(\overline {\boldsymbol {F}}\). To this end, the set of global equilibrium equation (19) is perturbed at the equilibrium state by a perturbation \({\Delta }\overline {\boldsymbol {F}}\), i.e.,
which results in
Combining (24) with (23) and (26), it can be shown that
where the matrix \(\left [\hat {\boldsymbol {L}}_{M}\right ]\) is of size (N + 2 + 2m) × 4 and is defined by
where N is the number of total DOFs in the displacement field, i.e., the size of u vector.
3 Finite strain viscoelastic model
The finite strain viscoelastic model proposed by Reese and Govindjee (1998) is adopted in this study. This model is based on a thermodynamically consistent framework, and therefore, the energy dissipation through viscous effects is clearly defined in the model. As compared to other finite strain viscoelastic formulations, e.g., Holzapfel (1996) and Holzapfel and Simo (1996), where inequilibrium perturbations are assumed to be infinitesimal, this model can accommodate large perturbations away from the equilibrium states. Moreover, due to thermodynamic consistency, this model is free from dynamic instabilities, as shown by Govindjee et al. (2014). The model is briefly reviewed below and the implementation details can be found in Appendix A.
3.1 Free energy
The finite strain viscoelastic model assumes multiplicative split of the deformation gradient
where Fe represents the elastic deformation gradient and Fv denotes the inelastic deformation gradient resulting from the viscous motion. The free energy is considered to be additively decomposed into stored equilibrium state (ψeq) and non-equilibrium state (ψneq) energies, i.e.,
where C = FT.F is the right Cauchy-Green strain tensor. For isotropic materials, the free energy can be equivalently expressed in terms of b = F.FT and \(\boldsymbol {b}^{e}\triangleq \boldsymbol {F}^{e}.{\boldsymbol {F}^{e}}^{T}\) as
where be represents the Finger tensor corresponding to the elastic deformation Fe.
3.2 Thermodynamics and flow rules
The energy dissipation rate per unit reference volume (Dint) is non-negative during any deformation process and is expressed in the form of Clausius-Planck inequality as
where \(\boldsymbol {d}\triangleq \text {sym}(\boldsymbol {l})\) with \(\boldsymbol {l}\triangleq \dot {\boldsymbol {F}}.\boldsymbol {F}^{-1}\). Equation (32) leads to the following relationships
where the Kirchhoff stress tensor τ is symmetric and τeq (or τneq) is coaxial with b (or be).
Considering the arbitrariness of rates d and \({\mathcal{L}}_{v}\left [\boldsymbol {b}^{e}\right ]\), this gives
To fulfill (34), a quadratic form is often used, i.e.,
where \(\mathbb {D}\) is a fourth-order positive definite isotropic tensor defined by
where \(\mathbb {P}_{dev}^{s}\triangleq \mathbb {I}_{4}^{s}-\frac {1}{3}\boldsymbol {I}\otimes \boldsymbol {I}\) is the fourth-order symmetric deviatoric projection tensors (see the context following (B.30) for the definition of \(\mathbb {I}_{4}^{s}\)). In (36), only the energy dissipation due to isochoric deformations is considered since many viscoelastic materials such as polymers are nearly incompressible and the energy dissipation due to volumetric deformations is limited. The extension to include volumetric viscosity is straightforward and can be found in Reese and Govindjee (1998). The relaxation time (τ) near thermodynamic equilibrium state is given by τ = ηd/μ, where μ is the initial shear modulus of the non-equilibrium part of the viscoelastic response.
3.3 Viscoelastic energy dissipation
Using (34) and (35), the energy dissipation rate per unit reference volume can be calculated as
With Dint considered as energy dissipation at microscale, the homogenized/macroscopic energy dissipation rate per unit reference volume (8) can be calculated as
which leads to a total energy dissipation per unit macroscopic reference volume under a loading process during time t ∈ [0, T]
4 Density-based multimaterial topology optimization
Topology optimization seeks the optimal material layout within a given design domain. In the density-based framework, the domain is discretized by a finite element (FE) mesh where each element is assigned with single/multiple density variable(s) representing the presence or absence of the material candidate(s). For example, with three phases (material-0, material-1, and material-2), each element is assigned with two density variables ρ1 and ρ2, where ρ1 indicates if material-0 is present (ρ1 = 0) or absent (ρ1 = 1) and ρ2 denotes the proportion of material-1 as compared to material-2 within ρ1 percentage of solid, i.e., ρ2 = 1 means full of material-1 while ρ2 = 0 means full of material-2. For design involving void and two solid phases, for instance, material-0 can be taken as the void phase. Moreover, in order to use gradient-based optimization algorithms, the discrete density variables are relaxed to continuous values, i.e., ρ1, ρ2 ∈ [0,1].
4.1 Topology optimization formulation
With the aim of designing metamaterials with optimal damping properties, the objective is to maximize the homogenized total dissipated energy density \(\overline {W}_{d}\) (39). Three optimization formulations are considered in this study to design such metamaterials.
- Optimization formulation-1 (OF-1): :
-
$$ \begin{array}{@{}rcl@{}} \min && f_{0}(\boldsymbol{x}_{1},\boldsymbol{x}_{2})=-\overline{W}_{d} \\ \mathrm{s.t.}&& f_{1}(\boldsymbol{x}_{1})=V_{f}(\boldsymbol{x}_{1})/V_{T}-1\leq 0 \\ && 0\leq {x_{1}^{e}}\leq 1,\quad 0\leq {x_{2}^{e}}\leq 1, \quad \!e = 1,2,...,n_{ele} \end{array} $$(40)
- Optimization formulation-2 (OF-2): :
-
$$ \begin{array}{@{}rcl@{}} \min && f_{0}(\boldsymbol{x}_{1},\boldsymbol{x}_{2})=-\overline{W}_{d} \\ \mathrm{s.t.}&& f_{1}(\boldsymbol{x}_{1},\boldsymbol{x}_{2})=1-\left[\overline{\mathbb{A}}_{0}\right]_{11}/\overline{k}\leq 0 \\ && f_{2}(\boldsymbol{x}_{1},\boldsymbol{x}_{2})=1-\left[\overline{\mathbb{A}}_{0}\right]_{44}/\overline{k}\leq 0 \\ && 0\leq {x_{1}^{e}}\leq 1,\quad 0\leq {x_{2}^{e}}\leq 1, \quad \!e = 1,2,...,n_{ele} \end{array} $$(41)
- Optimization formulation-3 (OF-3): :
-
$$ \begin{array}{@{}rcl@{}} \min && f_{0}(\boldsymbol{x}_{1},\boldsymbol{x}_{2})=-\overline{W}_{d} \\ \mathrm{s.t.}&& f_{1}(\boldsymbol{x}_{1},\boldsymbol{x}_{2})=M_{f}(\boldsymbol{x}_{1},\boldsymbol{x}_{2})-1\leq 0 \\ && 0\leq {x_{1}^{e}}\leq 1,\quad 0\leq {x_{2}^{e}}\leq 1, \quad \!e = 1,2,...,n_{ele} \end{array} $$(42)
In the above formulations, x1 and x2 denote the design variables that are mapped to the density variables ρ1 and ρ2, respectively, through the density and projection filters; nele is the total number of elements in the design domain; \(\left [\overline {\mathbb {A}}_{0}\right ]_{ij}\) represents the ij component of the matrix \(\left [\overline {\mathbb {A}}\right ]\) defined in (27) evaluated at the initial undeformed state whereas \(\overline {k}\) stands for the predefined macroscopic required initial stiffness value. Vf(x1) and Mf(x1, x2) represent the total volume fractions and the total mass fractions of material-1 and material-2, respectively, calculated as
where ve denotes the volume of e th element, ω0, ω1, and ω2 are the physical densities of the three phases and M∗ is the allowable upper limit on the total mass. VT in (40) denotes the upper bound of Vf(x1) set in the constraint.
Remarks 1
For nonlinear metamaterials, the stiffness varies along the loading process due to the nonlinear nature of the system. To achieve a better control over a designed metamaterial stiffness, the stiffness constraints can include the homogenized tangent moduli at all loading steps. This can be achieved by constraining the components in the homogenized tangent moduli \(\overline {\mathbb {A}}\) given by (27) at each step; however, this will also result in increased computational cost. For simplification, in (41), only the initial metamaterial stiffness \(\overline {\mathbb {A}}_{0}\) is considered in the stiffness constraint. This initial stiffness represents the metamaterial’s stiffness in the undeformed state where the contributions to stiffness by the viscous mechanisms are not present.
It can be seen that there is no volume or mass constraint in OF-2 and also in OF-1 when it is used for two phase, i.e., hyperelastic and viscoelastic, metamaterial design. This is in contrast with the traditional stiffness design, where volume or mass constraint has to be included for generating discrete topologies. There are two underlying reasons for this behavior. First, unlike the traditional stiffness design where fully solid phase leads to the highest stiffness and including void phase decreases the stiffness, in the energy dissipation designs considered in this study, fully viscoelastic phase may not lead to the best design and incorporating non-dissipative stiffer hyperelastic phase can yield better designs. Second, the penalizations used in the material interpolation schemes (i.e., the penalization power p in (51) and (52) is greater than 1) also make the mixture of the two phases inefficient in both stiffness as compared to hyperelastic phase and in energy dissipation as compared to viscoelastic phase.
4.2 Density and projection filters
Density filter – periodic formulation
Density filter (Bourdin 2001; Bruns and Tortorelli 2001), which is adopted to address the mesh dependency and checkerboarding issues, can be expressed in a matrix form as
where \(\tilde {\boldsymbol {\rho }}_{1}\) and \(\tilde {\boldsymbol {\rho }}_{2}\) are the vectors containing the filtered design variables; W is the filtering matrix that can be expressed in component form as
where \(r_{\min \limits }\) is the filter radius and Xi denotes the coordinates of the centroid of i th element. The distance between points Xi and Xj should take the spatial periodicity of the RUC into account, i.e.,
where \(\mathbb {Z}\) stands for the set of integers.
Heaviside projection filter
Due to the averaging effect brought by the density filter, the boundaries of optimized design tend to be blurry. To achieve discrete designs, Heaviside projection filter (Wang et al. 2011) is used, where the filtered design fields are projected by the following filter operations
where \(\hat {\beta }\) controls the slope of the Heaviside function while η determines the cutoff location.
4.3 Multimaterial interpolation scheme
As intermediate densities are allowed, i.e., ρ1, ρ2 ∈ [0,1], appropriate material interpolation scheme has to be constructed for the representation of material properties of mixtures, i.e., ρ1 ∈ [0,1] and/or ρ2 ∈ [0,1]. The properties of the three considered materials are listed in Table 1. As shown, all material candidates, except for void phase, are nearly incompressible. Depending on the choice of candidates for material-0, two different material interpolation schemes are used.
4.3.1 Material-0: void phase
When void phase (ρ1 = 0) is included, the mixture with ρ1 < 1 (∀ρ2) will lead to a compressible composite. An appropriate material interpolation dealing with incompressibility for this case has been proposed in Zhang and Khandelwal (2019b) and is adopted in this study. For completeness, this scheme is presented in this section. The material interpolation is carried out on the free energy of the material phases
where ψ0, ψ1, and ψ2 denote the interpolated free energy of the material-0 (void phase), material-1 (hyperelastic phase), and material-2 (viscoelastic phase), respectively. Free energy of the material-0 (compressible void phase) is interpolated as
where \(\hat {\psi }_{0}\) and \(\tilde {\psi }_{0}\) are the volumetric and isochoric contributions, respectively. Free energy of the material-1 (hyperelastic phase) is interpolated as
where the volumetric (\(\hat {\psi }_{1}\)) and isochoric contributions (\(\tilde {\psi }_{1}\)) are separately interpolated. Next, the free energy of the material-2 (viscoelastic phase) is interpolated as
where the volumetric (\(\hat {\psi }_{2}^{eq}\), \(\hat {\psi }_{2}^{neq}\)) and isochoric contributions (\(\tilde {\psi }_{2}^{eq}\), \(\tilde {\psi }_{2}^{neq}\)) are separately interpolated for both the equilibrium and non-equilibrium contributions. The penalization parameters pe > 1 and p > 1 are used for penalizing the intermediate densities and mixtures. A quadratic form is used for the volumetric energies (\(\hat {\psi }_{0}\), \(\hat {\psi }_{1}\), \(\hat {\psi }_{2}^{eq}\), and \(\hat {\psi }_{2}^{neq}\)) and the Ogden model is used to formulate isochoric components (\(\tilde {\psi }_{0}\), \(\tilde {\psi }_{1}\), \(\tilde {\psi }_{2}^{eq}\), and \(\tilde {\psi }_{2}^{neq}\)), i.e.,
with \(J=\sqrt {\det (\boldsymbol {b})}\) and \(\hat {\lambda }_{a}=J^{-1/3}\lambda _{a}\) where λa (a = 1,2,3) are the principal stretches (i.e., the eigenvalues of \(\sqrt {\boldsymbol {b}}\)). For non-equilibrium strain energies \(\hat {\psi }_{2}^{neq}\) and \(\tilde {\psi }_{2}^{neq}\), the input variable b is replaced with be and accordingly J is replaced with Je and \(\hat {\lambda }_{a}\) are replaced with \(\hat {\lambda }_{a}^{e}={J^{e}}^{-1/3}{\lambda _{a}^{e}}\) (a = 1,2,3), the elastic principal stretches. The initial shear modulus which is defined by \(\mu \triangleq \frac {1}{2} {\sum }_{q=1}^{N}\mu _{q}\alpha _{q}\) can be used together with the initial bulk modulus κ to determine initial Poisson’s ratio. In material interpolation, from (49) to (52), the interpolation can be seen as conducted on material parameters κ and μq (q = 1,…, N). In this way, for the non-equilibrium strain energy, the viscosity ηd = τμ is also interpolated, where the relaxation time τ is assumed as a fixed constant. It is noted that even though the material interpolation on the non-equilibrium strain energy in (52)3 can be put outside the strain energy, the calculation of be is based on a set of coupled nonlinear constitutive equations with interpolated parameters (see Appendix A).
The interpolation functions ζκ(ρ1) and ζμ(ρ1) in (51) and (52) are evaluated using material parameters according to the phase to which it is attached and are defined based on the E-ν interpolation rule proposed in Zhang et al. (2018) wherein the functions ζκ(ρ1) and ζμ(ρ1) are determined by
where the bulk modulus κ(ρ1) and shear modulus μ(ρ1) are related to Young’s modulus E(ρ1) and Poisson’s ratio ν(ρ1) by κ(ρ1) = E(ρ1)/[3(1 − 2ν(ρ1))] and μ(ρ1) = E(ρ1)/[2(1 + ν(ρ1))]. Here, κ0 and μ0 are the initial bulk and shear modulus of the solid material phase, respectively. Young’s modulus E(ρ1) and Poisson’s ratio ν(ρ1) are interpolated using the E-ν interpolation scheme as
where E0 and ν0 are initial Young’s modulus and Poisson’s ratio, respectively, of the solid phase; 𝜖ν is the lower bound parameter for Poisson’s ratio and is chosen as 𝜖ν = 0.4 and pν is the penalization power. In addition, a non-zero lower bound parameter 𝜖 = 10− 3 is included in the non-equilibrium energy to avoid singularities in the interpolated viscous moduli \(\mathbb {D}\) where term 1/ηd is present.
4.3.2 Material-0: soft incompressible hyperelastic phase
When material-0 is chosen to be incompressible hyperelastic phase (2nd candidate of material-0 in Table 1), the mixture with ρ1 < 1 (∀ρ2) still remains nearly incompressible. As a result, the incompressibility is not relaxed for the intermediate densities, and a three-phase material interpolation scheme similar to the one proposed by Sigmund and Torquato (1997) is used. In this case, the material interpolation in (50) is replaced by
for penalization on material-0, and (54) is replaced by
Equation (55) is not needed in this case.
4.4 FE mesh distortion
The convergence of NR solver is affected by FE mesh distortions, and mesh distortions are exacerbated in topology optimization under finite deformation when void regions are considered within a fictitious domain approach (Buhl et al. 2000; Wang et al. 2014). This is due to the fact that void regions are modeled with elements of vanishing stiffness. However, these low stiffness elements can undergo severe distortions, preventing FEA from converging. This convergence issue can be mitigated by the linear energy interpolation scheme proposed in Wang et al. (2014), which was later extended to an adaptive scheme in Zhang et al. (2018). The main idea of this scheme is to interpolate between the linear and nonlinear kinematics based on the solid/void density field. For instance, with ρ1 = 0 representing void phase, the deformation gradient F is interpolated using the solid/void density variable ρ1 as
where c and β are interpolation parameters. Following Zhang et al. (2018), the element internal force is modified to
where BL denotes the derivative of the shape functions of a regular 4-node element, \(\boldsymbol {\varepsilon }=\boldsymbol {\nabla }_{\boldsymbol {X}}^{s}\boldsymbol {u}\) represents the small strain measure, and \(\mathbb {C}\) is the linear isotropic elastic moduli determined by interpolated Young’s modulus \(E(\rho _{1})=\left [\epsilon _{E}+(1-\epsilon _{E})\rho _{1}^{p_{L}}\right ]E_{0}\) and constant Poisson’s ratio ν = 0.2, where \(\epsilon _{E}={10}^{-8}\) and E0 = 2μ0(1 + ν) with μ0 to be chosen identical to that of the initial shear modulus of hyperelastic material, and pL is the penalization power. The remaining parameters are β = 120 and c = 0.08, where c is adaptively updated (if needed) using the scheme proposed in Zhang et al. (2018). It should be noted that for fully solid designs, e.g., two solid-phase designs and three solid-phase designs, the stiffness of each material phase is high enough for avoiding excessive mesh distortions, and this strategy is not incorporated in these cases.
4.5 F-bar element formulation
For FEA, F-bar element formulation (de Souza Neto et al. 1996) is adopted to avoid volumetric locking, where the deformation gradient F is modified to
where F0 is the deformation gradient evaluated at the centroid of the element, and the in-plane part is obtained by removing all terms related to the out-of-plane quantities such as Fi3 and F3i where i = 1,2,3. As a result, the 1st PK stress tensor is modified to
where the pair (Fb, Pb) serves as the input-output of the material subroutine. Note that both F and F0 in (60) are evaluated based on the interpolated displacement field when the linear energy interpolation scheme (see (58) in Section 4.4) is included. Further details on the implementation and performance of F-bar elements can be found in de Souza Neto et al. (1996). It should be mentioned that the resulted structural tangent stiffness matrix KT is not symmetric with the F-bar element formulation.
5 Path-dependent sensitivity analysis
The path-dependence of the viscoelastic material behavior leads to a path-dependent sensitivity calculation. Adjoint method is used for sensitivity analysis, since the number of design variables far exceeds the number of objective and constraint functions. The calculations follow the adjoint sensitivity analysis framework proposed in Michaleris et al. (1994), which was adopted and expanded in many recent studies on topology optimization with inelastic materials (Alberdi et al. 2018b; Bogomolny and Amir 2012; Kato et al. 2015; Nakshatrala and Tortorelli 2015; Wallin et al. 2016; Ivarsson et al. 2018).
5.1 Adjoint formulation
The adjoint function is constructed as
where F represents the objective (or constraint) function, \(\hat {\boldsymbol {u}}^{k}\) and vk are the solution and auxiliary variables at step k and are determined by the corresponding global equilibrium (Rk = 0) and local constitutive equations (Hk = 0), γk and ηk are the corresponding adjoint variables, and the density variables ρ1 and ρ2 are functions of the design variables x1 and x2 through mappings by the density and projection filters. The goal of sensitivity analysis is to calculate the derivatives dF/dx1 and dF/dx2. In the following, the computation of the derivatives dF/dρ1 and dF/dρ2 are elaborated and the simple chain rules by dρ1/dx1 and dρ2/dx2 due to density and projection filters are omitted.
Since equilibrium and constitutive equations are always satisfied irrespective of the density variables ρ1 and ρ2, it is obvious that \(d\hat {F}/d\boldsymbol {\rho }_{1}\equiv dF/d\boldsymbol {\rho }_{1}\) and \(d\hat {F}/d\boldsymbol {\rho }_{2}\equiv dF/d\boldsymbol {\rho }_{2}\). Taking derivatives of \(\hat {F}\) with respect to ρ1 (or ρ2) and eliminating all the terms that contain the implicit derivative \(d\hat {\boldsymbol {u}}^{k}/d\boldsymbol {\rho }_{1}\) and \(d\boldsymbol {v}^{k}/d\boldsymbol {\rho }_{1}\) (k = 1,..., n) yields
where the adjoint variables γk and ηk are calculated in a backward order from the following system of equations:
Finally, all the explicit derivatives needed to complete the adjoint sensitivity calculation using (63) are
For the purpose of sensitivity analysis, the solution variables (\(\hat {\boldsymbol {u}}\)) are chosen as the displacement field and Lagrange multipliers, i.e., \(\hat {\boldsymbol {u}}{\equiv }\left [\boldsymbol {u} \boldsymbol {\lambda } \boldsymbol {\mu })\right ]^{T}\), while the auxiliary variables (v) are chosen to include elastic Finger tensor be. Corresponding constraints are the global equilibrium equations for \(\hat {\boldsymbol {u}}\) and local constitutive equations for be, which are formulated as
where \(\boldsymbol {B}_{e_{s}}\) and \(\boldsymbol {B}_{L,e_{s}}\) are the shape function derivative matrices for finite and small strains, respectively. The subscript e means the e th element and the subscript s means the s th quadrature point, and \(w_{e_{s}}\) is the weight of the s th quadrature point in the e th element. There are nipt (= 4) quadrature points in each element. The local constitutive equation \(\boldsymbol {H}_{e_{s}}^{k}\) (67)3) defined at s th quadrature point in e th element at step k is obtained by using the backward exponential map-based integrator of the rate (35) (see Appendix A). In (67)3, \({\boldsymbol {b}^{e}}^{tr}\triangleq {\boldsymbol {F}^{e}}^{tr}.{{\boldsymbol {F}^{e}}^{tr}}^{T}\) with \({\boldsymbol {F}^{e}}^{tr}=\boldsymbol {F}_{\delta }.\boldsymbol {F}_{k-1}^{e}\) and \(\boldsymbol {F}_{\delta }\triangleq \boldsymbol {F}.\boldsymbol {F}_{k-1}^{-1}\), and \(\boldsymbol {A}\triangleq \mathbb {D}:\boldsymbol {\tau }^{neq}\) where the current step notation k and quadrature index s are omitted. It is noted that due to the symmetry of be tensor, only the symmetric part of be is included in \(\boldsymbol {H}_{e_{s}}^{k}\). The calculation of the derivatives in (65) is given in Appendix B. A verification of the sensitivity analysis is provided in Appendix C.
Remarks 2
As mentioned in Section 4.4, for no-void designs, e.g., two solid-phase and three solid-phase designs, the linear energy interpolation is excluded. In these cases, γ ≡ 1 in (66).
It is possible that a small perturbation on the design might lead to a design that needs a different number of time steps in the FEA due to the adaptivity of the NR solver. As there is always a solution to the underlying mechanics problem at any time under the specified loading and boundary conditions, there is no theoretical differentiability issue. The only issue is that due to the nonlinearity of the problem solutions cannot be obtained via large or fixed time steps in the NR solver, and the time-step size might need to be adaptively changed in order to find the solution. However, this does not lead to non-differentiability of the cost and/or constraints functions. Thus, when computing the sensitivities of the cost or constraints with respect to the design variables, the potential change of the time-step size in an analysis is not crucial.
6 Numerical examples
In the following examples, the material candidates considered in the multimaterial topology optimization are given in Table 1. When considering finite deformations, continuation is usually needed to avoid analysis failure during early optimization iterations when the design is evolving from the initial intermediate density design. The employed continuation scheme incrementally updates pe and p from 1 to 3, pL from 4 to 6, and pν from 3 to 1, with an increment/decrement of 0.1 every 20 iterations. This increased penalization of pL compared to pe is done so that the optimizer does not use low-density values to exploit small deformation kinematics. The optimization runs up to 450 iterations after which a Heaviside projection, i.e., (48), is initiated with η = 0.5, and \(\hat {\beta }\) is increased from 1 to 10 with an increment of 1 every 20 iterations. The optimization is terminated at 670 iterations in total. Note that the projection is used only to resolve the boundaries of the design, after a clear topology has already emerged after 450 iterations.
In nonlinear FEA, the NR scheme with an adaptive step-size strategy is used and convergence is assumed when the energy residual drops below 10− 12 (Crisfield 1991). The Method of Moving Asymptotes (MMA) (Svanberg 1987) is used as an optimizer with default parameter settings. All the design domains—with square, parallelogram, and hexagonal unit cells—are discretized by a 80 × 80 FE mesh with density filter radius \(r_{\min \limits } = 0.0375\) for all problems (spanning over 3 elements for square domain). These different unit cell shapes all have a side length of 1, which results in different areas, e.g., Area (square) = 1, Area (45∘ parallelogram) = 0.707, Area (60∘ parallelogram) = 0.866, and Area (hexagon) = 2.598. All the numerical computations are carried out in a Matlab-based in-house finite element library CPSSL-FEA developed at the University of Notre Dame.
Numerical examples presented in the following sections can be divided into three categories: The first category (Sections 6.2 – 6.7) considers two solid-phase designs with material-1 (hyperelastic phase) and material-2 (viscoelastic phase) using optimization formulation OF-1 (Sections 6.2 – 6.6) or OF-2 (Section 6.7), and ρ1 ≡ 1 is not updated during optimization and the total material volume constraint is not activated. The initial design for the first category is chosen as shown in Fig. 3a, unless otherwise stated. The second category (Section 6.8) considers three phase designs with void chosen for material-0 (see Section 4.3.1) and uses optimization formulation OF-1. The initial design for this case is shown in Fig. 3b. The third category (Section 6.9) considers three solid-phase designs with a soft hyperelastic material chosen for material-0 and uses optimization formulation OF-3 with the initial design shown in Fig. 3c.
6.1 Macroscopic deformation gradient loading \(\overline {\mathbf {\mathit {F}}}(t)\)
The proposed framework can account for different types of time-dependent loading such as harmonic loading, pulse-like loading, or other waveforms. For illustration purposes, harmonic loading is considered in the following numerical examples. The macroscopic deformation gradient \(\overline {\boldsymbol {F}}(t)\) is prescribed in the deformation-driven framework. Without loss of generality, the macroscopic rigid-body rotation is ignored \((\overline {\boldsymbol {R}}=\boldsymbol {I})\) and the principal macro stretch ratios \(\overline {\lambda }_{a}(t)\) are at a fixed angle 𝜃 with respect to the standard Euclidean bases {ea}, i.e.,
where \(\overline {\boldsymbol {F}}^{Q}(t)=\text {diag}\left (\overline {\lambda }_{1}(t),\overline {\lambda }_{2}(t)\right )\) and Q the bases transformation matrix expressed as
Since all solid phases are considered to be nearly incompressible, without void, the composite material should still exhibit incompressibility. Thus, it is assumed that \(\overline {\lambda }_{1}(t)=\overline {\lambda }(t)\) and \(\overline {\lambda }_{2}(t)=1/\overline {\lambda }(t)\), which result in an isochoric deformation mode. Moreover, cyclic loading is considered with the logarithm of the principal stretch following a sinusoidal function, i.e.,
where \(\overline {\Lambda }\) represents the magnitude of the principal stretch. The loading frequency f = 0.009s− 1 with time duration t ∈ [0,1/f], i.e., one cycle, is used, unless stated otherwise. The frequency f is chosen such that the energy dissipation achieves the maximum value with the chosen material parameters for the viscoelastic phase (material-2 in Table 1).
6.2 Dependence on the loading magnitude
The first example investigates the effect of loading magnitude on the optimized metamaterial topologies. The loading parameters are 𝜃 = 45∘ with various magnitudes \(\overline {\Lambda }\in \{1.2, 1,4, 1.8, 2.0\}\). The design optimization considers two phases, material-1 (hyperelastic) and material-2 (viscoelastic), with ρ1 ≡ 1. The optimized metamaterial designs are provided in Table 2. Since material-1 represents a hyperelastic material (red color) that is much stiffer than the material-2, which is viscoelastic (blue color), the inclusion of material-1 helps to localize deformation in dissipative material-2 region, which finally increases the energy dissipation capacity (Zhang and Khandelwal 2019b). This can be seen from the deformed shapes and energy dissipation distributions in Table 2, and as a result the proportion of material-1 increases as the loading magnitude decreases. Moreover, the geometric nonlinear effects, which can be observed in the hysteresis response, increases as the loading magnitude increases. The optimization histories demonstrate that smooth convergence can be obtained within the proposed framework.
6.3 Initial design influence
As compared to structural design optimization, where an initial design can be taken as one with homogeneous density distribution, the metamaterial design has to start from non-homogeneous design. If homogeneous density distribution is used, the design sensitivities would be equal to each other, as the homogenized properties are optimized under periodic boundary conditions. This example is used to demonstrate the dependence of the optimized topology on the initial design in the optimization. With the loading condition given in (70) with \(\overline {\Lambda }=1.4\) and 𝜃 = 0∘ (again ρ1 ≡ 1), the results shown in Table 3 demonstrate that starting from different initial designs leads to different optimized designs, as expected. This result shows that multiple local minima exist due to the non-convexity of the optimization problem. Also, by comparing these results, it can be seen that the initial design-3 is a better choice for this case in terms of the energy dissipation capacity. Thus, in practice, different initial designs can be considered for designing such metamaterials.
6.4 Different unit cell geometries
For periodic metamaterial designs, the basic unit cell shape is first chosen, which specifies the periodicities of the designed metamaterial. For 2D case, for example, the most general unit cell shape is parallelogram with two sides as the two periodic lattice vectors (Podestá et al. 2019). Square and hexagon can be seen as special cases of a parallelogram unit cell. Depending on the angle of parallelogram, different unit cell shapes can be adopted. The proposed framework can be used with different unit cell geometries. To illustrate this, a square, two parallelograms (45∘ and 60∘), and a hexagon unit cells are used in design optimization. For loading, the macroscopic deformation gradient with \(\overline {\Lambda }=1.4\) and 𝜃 = 0∘ is used. The optimized designs for different unit cells are shown in Table 4. From this result, it can be seen that the square unit cell leads to a design with the least energy dissipation (\(\overline {W}_{d}\)) as compared to other unit cells. This result suggests that different unit cells can be examined in practice in order to achieve desirable optimized designs.
6.5 Designs under different loadings
This example shows the metamaterial designs for different macroscopic deformations. Again, ρ1 ≡ 1 and the macroscopic deformations \(\overline {\boldsymbol {F}}(t)\) with magnitude \(\overline {\Lambda }=1.4\) and different orientations (𝜃) (68) – (70) are considered. The results are presented in Table 5, where the third column corresponds to the maximization of the energy dissipation under two orientations, one with 𝜃 = 0∘ and the other one with 45∘, i.e., \(\overline {W}_{d}\equiv \overline {W}_{d}\left (\overline {\boldsymbol {F}}(\theta =0^{\circ })\right )+\overline {W}_{d}\left (\overline {\boldsymbol {F}}(\theta ={45}^{\circ })\right )\). This means that two FEAs and sensitivity analyses are required for one optimization step in this case. As expected, different types of macro deformations correspond to different optimized designs. Moreover, as the results show, the energy dissipation is \(\overline {W}_{d}=0.2472\) for \(\overline {\boldsymbol {F}}(\theta =0^{\circ })\) design under the \(\overline {\boldsymbol {F}}(\theta ={45}^{\circ })\) loading, while \(\overline {W}_{d}=0.3097\) for 𝜃 = 45∘ design under the \(\overline {\boldsymbol {F}}(\theta =0^{\circ })\) loading. Thus, the optimality of a design under multiple loading scenarios can be balanced, as demonstrated in the last column in Table 5.
6.6 Dependence on the loading frequency
This example examines whether the optimality of the design changes towards the loads of the same type but with different frequencies. To begin with, a uniaxial test of one element filled with material-2 (viscoelastic phase) is carried out (see Fig. 4). The uniaxial load considers three cycles with different frequencies, e.g., 0.001 s− 1 (f1), 0.009 s− 1 (f2), and 0.05 s− 1 (f3). The corresponding hysteretic results are shown in Fig. 5, where it can be seen that as frequency increases it takes more time for the response to settle into steady state. Besides, the material stiffness increases with the increase of frequency due to the viscous effect. The unit cell optimization results for \(\overline {\Lambda }=1.4\) and 𝜃 = 0∘ are given in Table 6, where again ρ1 ≡ 1. As can be seen, different optimized topologies are obtained for different loading frequencies. Moreover, as these designs are only local optima, although good local optima as continuation strategies are used, the global optimality of the designs cannot be ensured for a given frequency. Thus, the results shown in Table 6 cannot conclusively affirm the dependency of the optimized designs on the loading frequency. For instance, the design optimized for frequency f1 outperforms other designs for frequency f1 and also frequency f2, but not for frequency f3. However, the results still suggest dependency of optimized designs on the loading frequency. Furthermore, as for high loading frequencies, more time is needed for the response to settle into steady state, Table 7 examines the optimized topologies with three cycles. As demonstrated in Table 7, in this test case, no obvious difference can be observed as compared to the results with one loading cycle.
6.7 Initial stiffness constraint
Depending on the application at hand, damping metamaterials with adequate stiffness may be needed for other functionalities. Hence, it is important for a design framework to be able to incorporate stiffness constraints. Compared to a linear system, where stiffness remains constant during loading process, the stiffness of nonlinear systems changes, due to both material and geometric nonlinearities. In this study, the initial elastic moduli of a homogenized metamaterial is used for applying stiffness constraints. The initial stiffness represents the stiffness that a metamaterial exhibits at the start of loading when no deformation has occurred. The optimization formulation OF-2 (41) is adopted with ρ1 ≡ 1 and various \(\overline {k}\) values to explore how the stiffness constraints affect the optimized metamaterial topologies. The loading condition is prescribed with \(\overline {\Lambda }=1.4\) and 𝜃 = 0∘. Figure 6 shows the optimization histories with various stiffness constraints, i.e., none, \(\overline {k}=30\), 40 and 50. As can be seen, due to the increase in the stiffness constraint, the objective function value gets deteriorated. The resulted optimized topologies are given in Table 8, where the proportion of the soft viscoelastic phase (material-2) decreases as the stiffness requirement increases, as expected. Figure 7 shows how the stiffness indicators \([\overline {\mathbb {A}}]_{11}\) and \([\overline {\mathbb {A}}]_{44}\) changes during loading process, where note that \([\overline {\mathbb {A}}]_{11}\equiv \overline {\mathbb {A}}_{1111}\) and \([\overline {\mathbb {A}}]_{44}\equiv \overline {\mathbb {A}}_{2222}\). The clear discontinuity in the curve slope at the first loading step is due to the fact that the initial stiffness does not include the stiffness from the non-equilibrium energy that accounts for viscous effect.
6.8 Designs with void phase
While bi-material designs that combine softer viscoelastic phase with stiffer hyperelastic phase help in improving energy dissipation, the metamaterial is fully dense. Including void phase in a design can help achieving metamaterials with overall lower material usage. In this example, to consider this case, voids are introduced as a third phase, i.e., material-0 in (49). Using optimization formulation OF-1, which constrains the overall material volume fraction, with both ρ1 and ρ2 vectors as design variables, optimized metamaterials with voids are obtained. The loading condition again considers (70) with \(\overline {\Lambda }=1.4\) and 𝜃 = 0∘. Moreover, in this case, the symmetries of the design along the horizontal and vertical as well as two diagonal lines are enforced, which results in a design domain occupying only one-eighth of the original unit cell domain (see Fig. 8). The optimization results with different total material volume fractions, VT = 0.5, 0.55, 0.7, and 0.8, are shown in Table 9. The deformed shapes of each design at two loading peaks of one cycle are plotted together with the hysteresis loops. As mentioned in Section 4.4, it is important to note that including void phase can lead to mesh distortion issues, which needs changes as shown in (58) and (59). Figure 9 shows the updates of the cutoff parameter c in (58) for optimization with VT = 0.5. Besides the fact that smaller step size in the adaptive NR solver has to be used due to mesh distortions, an extra number of FEAs are also needed in order to achieve convergence due to c parameter updates (Fig. 9). Furthermore, stability issues are not considered during the optimization process, and both the micro and macro-stability can be lost during the loading process. Such stability issues will be discussed in Section 7.3.2.
6.9 Lightweight design with light-soft fillers
As mentioned in the last example and shown in Section 7, a metamaterial may lose stability when voids are introduced in the design. To improve the design stability, this section investigates replacing voids with a light and soft incompressible hyperelastic phase. Thus, the overall purpose is to achieve lightweight designs with improved metamaterial stability. Using the optimization formulation OF-3 with the 2nd candidate chosen as material-0 in Table 1 and material physical densities ω0 = 30, ω1 = 200, and ω2 = 100, the optimization results under the same loading condition, i.e., \(\overline {\Lambda }=1.4\) and 𝜃 = 0∘, are given in Table 10 for various weight constraints wherein material-0 is shown in yellow. This result shows that when the weight constraint is relaxed, more softer hyperelastic phase is replaced with the viscoelastic phase. The volume of the stiffer hyperelastic phase increases little due to its high physical density. As will be shown in Section 7.3.3, only the design with M∗ = 70 loses stability during the loading process.
7 Multiscale stabilities
For periodic metamaterial designs based on nonlinear homogenization, an important assumption is that a single unit cell can serve as a representative unit cell during the entire loading process. For finitely strained periodic metamaterials, this assumption, however, does not always hold (Geymonat et al. 1993). Upon loading, buckling can happen with wavelengths possibly across arbitrary scales, which can lead to a change of the periodicity of the underlying microstructure or even macroscopic localization, i.e., loss of rank-1 convexity of the homogenized material. For rate-independent materials, the multiscale stability has been investigated in the past (Geymonat et al. 1993; Triantafyllidis et al. 2005; Triantafyllidis and Schraad 1998; Triantafyllidis and Maker 1985). As shown in (Triantafyllidis et al. 2005), the micro-stability can be studied by the Bloch analysis in which only one unit cell is analyzed by the Bloch wave representation of a buckling mode, while the macro-stability can be examined by a rank-1 convexity check on the homogenized tangent moduli. The multiscale stability under rate-dependent material behavior, however, is not well established, although the more general Lyapunov method can be used for stability investigation in dynamic cases (Govindjee et al. 2014). In this study, the viscous effects, which account for rate dependency, is neglected in the stability examinations and the multiscale stability checks are carried out based on the methods proposed in (Triantafyllidis et al. 2005).
7.1 Microscale stability
For rate-independent solids, the stability is governed by the Hill’s stability criterion (Hill 1958), which states that the principal solution branch ceases to be stable if the functional β(λ) defined by
loses positive definiteness. In (71), v is taken from the kinematically admissible displacement variation space \({H_{0}^{1}}({\Omega }_{0})\) for the corresponding macroscale boundary value problem. For periodic solids of infinite extent (\({\Omega }_{0}\rightarrow \mathbb {R}^{d}\)), v is taken from locally integrable, bounded functions that ensures the finiteness of the ratio Q (Triantafyllidis et al. 2005). The symbol ∗ denotes the complex conjugate and λ stands for the load parameter, which in this study can be taken as identical to the macroscopic stretch ratio \(\overline {\lambda }\) (Section 6.1). The tensor \(\mathbb {A}\) represents the tangent moduli under the loading parameter λ with the same periodicity as one unit cell. It was shown in (Geymonat et al. 1993) that this infimum β(λ) can be computed through Bloch wave analysis, where the calculation is carried out within one unit cell \({\Omega }_{0}^{\mu }\) and is expressed as
where vB is the Bloch wave function representing the eigenmode and u is periodic functions with the same periodicity as the unit cell, while the wavevector k is chosen in the 1st Brillouin zone (BZ) in the reciprocal space spanned by the reciprocal bases bi (i = 1,..., d) defined by ai.bj = 2πδij (Kittel and McEuen 1996). For a square unit cell, for example, the 1st BZ can be simply chosen as ki ∈ [0,1), i = 1,..., d with \(\boldsymbol {k}={\sum }_{i}{k_{i}\boldsymbol {b}_{i}}\).
7.2 Macroscale stability
As a measure of the macroscopic stability, the strict rank-1 convexity of the homogenized tangent moduli ensures the absence of discontinuities in the deformation gradient field on the macroscale. It is assessed by examining the positive definiteness of the ellipticity indicator B(λ) defined by
where \(\overline {\boldsymbol {m}}\) and \(\overline {\boldsymbol {M}}\) span over all possible directions with \(\left \Vert \overline {\boldsymbol {m}}\right \Vert =\left \Vert \overline {\boldsymbol {M}}\right \Vert =1\). When there is a discontinuous deformation corresponds to the loss of strict rank-1 convexity, i.e., B(λ) = 0, the corresponding minimizing vector \(\overline {\boldsymbol {M}}\) represents the normal to the curves across which the jump discontinuities appear and \(\overline {\boldsymbol {m}}\) determines the nature of the discontinuous mode, i.e., simple shear if \(\overline {\boldsymbol {m}}\) is orthogonal to \(\overline {\boldsymbol {M}}\) or pure splitting if \(\overline {\boldsymbol {m}}\) is parallel to \(\overline {\boldsymbol {M}}\) or mixture otherwise (Ortiz et al. 1987). Also, as shown in Geymonat et al. (1993), the loss of strict rank-one convexity corresponds to a long wavelength microscale buckling, i.e.,
Remark 1
It is worth noting that two physically different types of buckling modes exist in the neighborhood of k = 0, i.e., the long wavelength mode with \(\boldsymbol {k}\rightarrow \boldsymbol {0}\) that leads to the loss of rank-1 convexity of the homogenized tangent moduli at the macroscale, and the highly localized buckling mode with k = 0 which has the same periodicity as one unit cell. The following relationship was also established in Geymonat et al. (1993)
which states that the short wavelength instabilities always precede the long wavelength instabilities which in turn precede the highly localized ones. Interested readers are referred to Refs. (Geymonat et al. 1993; Triantafyllidis et al. 2005; Alberdi et al. 2018a) for further theoretical details and numerical implementations.
7.3 Examples: Stability investigation of the optimized topologies
All the examples presented in Sections 6.2, 6.3, 6.8, and 6.9 are examined for their multiscale stabilities during the loading process. For two solid-phase (bi-material) and three solid-phase designs, all the optimized topologies except one, i.e., the first design in Table 10, are stable on both macro and micro scales, while for three phase designs with voids, all topologies lose both macro and micro stabilities during the loading. To illustrate these stability issues, three designs are discussed in details. To this end, the multiscale stability analysis is carried out as follows: (a) discrete designs of the optimized unit cells are obtained by applying a discrete Heaviside projection filter with cutoff located at ρ1 = ρ2 = 0.5, followed by which the void elements are removed from the FE mesh; (b) the macroscale stability is examined via rank-1 convexity check by slowly increasing the loading factor λ (\(\equiv \overline {\lambda }\)) with load step size \({\Delta }\overline {\lambda }=0.01\) up to the target magnitude until B(λ) ≤ 0 at every π/720 radian increment in both \(\boldsymbol {\overline {m}}\) and \(\boldsymbol {\overline {M}}\) space; and (c) the microscopic stability is investigated using the Bloch wave analysis which seeks k ∈ 1st BZ for which β(λ) < 0, where the 1st BZ, i.e., k = (k1, k2) ∈ [0,1) × [0,1), is discretized with a 100 × 100 uniform mesh together with 100 × 100 uniform meshes in three refined zones (0,0.001) × (0.001,1], (0.001,1] × (0,0.001), and (0,0.001) × (0,0.001).
7.3.1 Two solid-phase designs
The optimized topologies in Sections 6.2 and 6.3 are examined for their multiscale stabilities during the applied loading. These results indicate that both micro and macro stabilities are preserved during the loading process. For example, the rank-1 convexity curves of the third design in Table 3 are shown in Fig. 10, which demonstrates the macroscale stability, where \(B_{\alpha }\triangleq \underset {\overline {\boldsymbol {m}}}{\min \limits }(\overline {\boldsymbol {m}}\otimes \overline {\boldsymbol {M}}):\overline {\mathbb {A}}:(\overline {\boldsymbol {m}}\otimes \overline {\boldsymbol {M}})\) with \(\overline {\boldsymbol {M}}=\left [\cos \limits \alpha \sin \limits \alpha \right ]^{T}\) and α ∈ [0, π).
Macroscale stability of the third design in Table 3
7.3.2 Three phase with void designs
With void phase in the design, all the optimized topologies in Section 6.8 lose both micro and macro stabilities during the applied loading. As an illustration, Fig. 11 shows the microscale stability surface obtained through Bloch analysis and the macroscale stability curve by rank-1 convexity analysis of the second design in Table 9 at macro loading \(\overline {\lambda }=1.07\). In this case, \({\upbeta }_{\boldsymbol {k}}\triangleq \underset {\boldsymbol {u}}{\inf } Q(\boldsymbol {v}_{B}(\boldsymbol {k},\boldsymbol {u}); {\Omega }_{0}^{\mu })\) computed at each discretized point k in the 1st BZ serves as the micro-stability indicator. To detect the critical points, stability checks are carried out with a fixed loading step size of \({\Delta }\overline {\lambda }=0.01\). This study does not intend to find the numerically exact 1st critical point, but serves to demonstrate the potential instabilities that exist due to the geometric nonlinearities. Table 11 reports the detected 1st critical loads for all designs in Table 9.
Loss of both micro and macro stabilities at \(\overline {\lambda }=1.07\) of second design in Table 9
7.3.3 Three solid-phase designs
With void replaced by soft hyperelastic material phase, the multiscale stability is seen to be significantly improved. As shown in the results in Table 12, only the first design in Table 10 loses stability at \(\overline {\lambda }=1.37\) which is close to the target loading magnitude 1.4, while all the other designs are stable during the loading process. Figure 12 shows the microscale stability surface and macroscale rank-1 convexity curve at the critical step \(\overline {\lambda }=1.37\).
Loss of both micro and macro stabilities at \(\overline {\lambda }=1.37\) of first design in Table 10
7.4 Tailored stable metamaterials
Instead of considering instabilities as a potential drawback, they can also be utilized to tailor metamaterial designs. Indeed, in recent years, pattern transformations due to microscale instabilities have been used for achieving desired mechanical properties (Kochmann and Bertoldi 2017). Though promising, it is not yet clear how the stability response can be explicitly controlled during the optimization process. As demonstrated in Section 7.3, without incorporating multiscale stability constraints in the design phase, both macro and micro stabilities can be lost. This poses additional challenges on the homogenization, as the wavelength of the buckling mode, and therefore, the fundamental unit cell is not a priori known. However, if a metamaterial design can be appropriately tailored to harness multiscale instabilities, then rich mechanical behavior can be obtained.
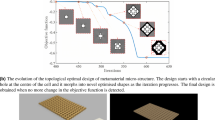
In this section, an illustrative example is presented to show the use of microscale instabilities for tailoring a metamaterial design. The basic idea is to create a design for which the first microscale bifurcation mode is separated from the other higher modes, and the first microscale bifurcation mode is then use to tailor the metamaterial design. To illustrate this idea, a metamaterial with unit cell design (Design-A) shown in Fig. 13a is considered, where the red and blue phases represent hyperelastic phase (with κ = 518.02 MPa, μp = 10.43 MPa, αp = 2, N = 1) and viscoelastic phase (material-2 in Table 1), respectively. This design is subjected to uniaxial loading during which the macroscopic deformation \(\overline {\boldsymbol {F}}=\text {diag}(\overline {\lambda }_{1},\overline {\lambda }_{2} )\) is applied such that the principal stretch \(\overline {\lambda }_{2}\) along vertical axis is prescribed and the other principal stretch \(\overline {\lambda }_{1}\) along the horizontal axis is determined by the condition \(\overline {P}_{11}=0\). The results of the multiscale stability analysis for this design are shown in Fig. 13b. In this case, the 1st bifurcation occurs at microscale, i.e., short wavelength buckling, with buckling mode periodic in terms of 2 × 2 unit cells, as shown in Fig. 13c.
This 2 × 2 buckling mode is used to tailor the metamaterial design by applying a perturbation in this mode on the Design-A in Fig. 13a. The resulted metamaterial design (Design-B) still remains periodic but with an enlarged unit cell, as shown in Fig. 14a. The response of this new metamaterial Design-B (Fig. 14b) shows no bifurcation during the loading process, as compared to the response of Design-A. The deformed shape of Design-B in Fig. 14c shows that the deformation of this design follows the added buckling mode. Moreover, the homogenized energy dissipation per cycle per unit volume of Design-B is 6.627 × 10− 3, which is even higher than the energy dissipation of the Design-A following principal branch, i.e., 4.087 × 10− 3. This example demonstrates that a metamaterial design can be tailored to have a stable response by carefully designing the microstructure. However, a direct consideration of multiscale stability in the design optimization process needs further investigations.
8 Conclusions
In this study, a computational framework is presented for designing damping metamaterials at finite deformations based on the nonlinear deformation-driven homogenization and density-based multimaterial topology optimization. The main idea is to combine a soft viscoelastic material phase with a stiffer hyperelastic phase to achieve a metamaterial with improved damping performance. The inclusion of void or lighter hyperelastic phase is also investigated for a lightweight damping metamaterial design. In the proposed framework, a thermodynamically consistent finite strain viscoelastic model is incorporated together with F-bar formulation for addressing volumetric locking. An analytical path-dependent sensitivity analysis is considered within a nonlinear homogenization framework. Numerical issues related to mesh distortions is addressed using an adaptive linear energy interpolation scheme. Based on the numerical studies carried out in this work, a number of observations can be made: (a) To achieve desired optimal designs, various unit cell shapes (periodicities) and different initial designs should be explored since they both influence optimized designs; (b) both loading frequency and magnitude may influence an optimized metamaterial design; (c) multiple loading scenarios can be incorporated in the optimization process to a design metamaterial for more than one deformation mode; (d) stiffness constraints based on the initial homogenized tangent moduli can be used for an effective stiffness control; (e) multiscale stability analysis reveals that the inclusion of void or soft material phases can make a metamaterial more prone to lose micro and macro stability.
The concept of tuning metamaterial’s performance using a desired buckling mode is also explored, wherein a buckling mode is incorporated into metamaterial’s design, which in turn steers the response towards the preferred stable deformation path. The resulting damping performance is improved compared to the one following the unstable principal branch. However, it should be noted that this design is not optimized for energy dissipation, since it is not obtained through optimization. Future work should investigate direct consideration of rate-dependent multiscale stability in the design of nonlinear metamaterials.
References
Alberdi R, Khandelwal K (2017) Topology optimization of pressure dependent elastoplastic energy absorbing structures with material damage constraints. Finite Elem Anal Des 133:42–61. https://doi.org/10.1016/j.finel.2017.05.004
Alberdi R, Khandelwal K (2019a) Bi-material topology optimization for energy dissipation with inertia and material rate effects under finite deformations. Finite Elem Anal Des 164:18–41. https://doi.org/10.1016/j.finel.2019.06.003
Alberdi R, Khandelwal K (2019b) Design of periodic elastoplastic energy dissipating microstructures. Struct Multidiscip Optim 59(2):461–483. https://doi.org/10.1007/s00158-018-2076-2
Alberdi R, Zhang G, Khandelwal K (2018a) A framework for implementation of rve-based multiscale models in computational homogenization using isogeometric analysis. Int J Numer Methods Eng 114(9):1018–1051. https://doi.org/10.1002/nme.5775
Alberdi R, Zhang G, Li L, Khandelwal K (2018b) A unified framework for nonlinear path-dependent sensitivity analysis in topology optimization. Int J Numer Methods Eng 115(1):1–56. https://doi.org/10.1002/nme.5794
Andreassen E, Jensen JS (2014) Topology optimization of periodic microstructures for enhanced dynamic properties of viscoelastic composite materials. Struct Multidiscip Optim 49(5):695–705. https://doi.org/10.1007/s00158-013-1018-2
Asadpoure A, Tootkaboni M, Valdevit L (2017) Topology optimization of multiphase architected materials for energy dissipation. Comput Methods Appl Mech Eng 325:314–329. https://doi.org/10.1016/j.cma.2017.07.007
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224. https://doi.org/10.1016/0045-7825(88)90086-2
Blanco PJ, Sánchez PJ, de Souza Neto EA, Feijóo RA (2016) Variational foundations and generalized unified theory of rve-based multiscale models. Arch Comput Methods Eng 23 (2):191–253. https://doi.org/10.1007/s11831-014-9137-5
Bogomolny M, Amir O (2012) Conceptual design of reinforced concrete structures using topology optimization with elastoplastic material modeling. Int J Numer Methods Eng 90(13):1578–1597. https://doi.org/10.1002/nme.4253
Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50 (9):2143–2158. https://doi.org/10.1002/nme.116
Bruns TE, Tortorelli DA (2001) Topology optimization of non-linear elastic structures and compliant mechanisms. Comput Methods Appl Mech Eng 190(26):3443–3459. https://doi.org/10.1016/S0045-7825(00)00278-4
Buhl T, Pedersen CB, Sigmund O (2000) Stiffness design of geometrically nonlinear structures using topology optimization. Struct Multidiscip Optim 19(2):93–104. https://doi.org/10.1007/s001580050089
Chen W, Liu S (2016) Microstructural topology optimization of viscoelastic materials for maximum modal loss factor of macrostructures. Struct Multidiscip Optim 53(1):1–14. https://doi.org/10.1007/s00158-015-1305-1
Crisfield MA (1991) Non-linear finite element analysis of solids and structures, vol 1. Wiley, New York
Deaton JD, Grandhi RV (2014) A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct Multidiscip Optim 49(1):1–38. https://doi.org/10.1007/s00158-013-0956-z
Gao W, Zhang Y, Ramanujan D, Ramani K, Chen Y, Williams CB, Wang CC, Shin YC, Zhang S, Zavattieri PD (2015) The status, challenges, and future of additive manufacturing in engineering. Comput Aided Des 69:65–89. https://doi.org/10.1016/j.cad.2015.04.001
Geymonat G, Müller S, Triantafyllidis N (1993) Homogenization of nonlinearly elastic materials, microscopic bifurcation and macroscopic loss of rank-one convexity. Arch Ration Mech Anal 122(3):231–290. https://doi.org/10.1007/BF00380256
Gibiansky LV, Sigmund O (2000) Multiphase composites with extremal bulk modulus. J Mech Phys Solids 48(3):461–498. https://doi.org/10.1016/S0022-5096(99)00043-5
Gibson I, Rosen DW, Stucker B, et al. (2014) Additive manufacturing technologies, vol 17. Springer, Boston
Govindjee S, Potter T, Wilkening J (2014) Dynamic stability of spinning viscoelastic cylinders at finite deformation. Int J Solids Struct 51(21):3589–3603. https://doi.org/10.1016/j.ijsolstr.2014.06.022
Hagood N, von Flotow A (1991) Damping of structural vibrations with piezoelectric materials and passive electrical networks. J Sound Vib 146(2):243–268. https://doi.org/10.1016/0022-460X(91)90762-9
Hill R (1958) A general theory of uniqueness and stability in elastic-plastic solids. J Mech Phys Solids 6 (3):236–249. https://doi.org/10.1016/0022-5096(58)90029-2
Hill R (1972) On constitutive macro-variables for heterogeneous solids at finite strain. Proceedings of the Royal Society of London A Mathematical and Physical Sciences 326(1565):131–147. https://doi.org/10.1098/rspa.1972.0001
Holzapfel GA (1996) On large strain viscoelasticity: continuum formulation and finite element applications to elastomeric structures. Int J Num Methods Eng 39(22):3903–3926. https://doi.org/10.1002/(SICI)1097-0207(19961130)39:22<3903::AID-NME34>3.0.CO;2-C
Holzapfel GA, Simo JC (1996) A new viscoelastic constitutive model for continuous media at finite thermomechanical changes. Int J Solids Struct 33(20):3019–3034. https://doi.org/10.1016/0020-7683(95)00263-4
Huang X, Radman A, Xie Y (2011) Topological design of microstructures of cellular materials for maximum bulk or shear modulus. Comput Mater Sci 50(6):1861–1870. https://doi.org/10.1016/j.commatsci.2011.01.030
Huang X, Zhou S, Sun G, Li G, Xie YM (2015) Topology optimization for microstructures of viscoelastic composite materials. Comput Methods Appl Mech Eng 283:503–516. https://doi.org/10.1016/j.cma.2014.10.007
Ivarsson N, Wallin M, Tortorelli D (2018) Topology optimization of finite strain viscoplastic systems under transient loads. Int J Numer Methods Eng 114(13):1351–1367. https://doi.org/10.1002/nme.5789
Jung D, Gea HC (2004) Topology optimization of nonlinear structures. Finite Elem Anal Des 40 (11):1417–1427. https://doi.org/10.1016/j.finel.2003.08.011
Kato J, Hoshiba H, Takase S, Terada K, Kyoya T (2015) Analytical sensitivity in topology optimization for elastoplastic composites. Struct Multidiscip Optim 52(3):507–526. https://doi.org/10.1007/s00158-015-1246-8
Kato J, Yachi D, Kyoya T, Terada K (2018) Micro-macro concurrent topology optimization for nonlinear solids with a decoupling multiscale analysis. Int J Numer Methods Eng 113(8):1189–1213. https://doi.org/10.1002/nme.5571
Kittel C, McEuen P (1996) Introduction to solid state physics, vol 8. Wiley, New York
Kochmann DM, Bertoldi K (2017) Exploiting microstructural instabilities in solids and structures: from metamaterials to structural transitions. Applied Mechanics Reviews 69(5):050801. https://doi.org/10.1115/1.4037966
Li L, Zhang G, Khandelwal K (2017) Design of energy dissipating elastoplastic structures under cyclic loads using topology optimization. Struct Multidiscip Optim 56(2):391–412. https://doi.org/10.1007/s00158-017-1671-y
Li L, Zhang G, Khandelwal K (2018) Failure resistant topology optimization of structures using nonlocal elastoplastic-damage model. Struct Multidiscip Optim 58(4):1589–1618. https://doi.org/10.1007/s00158-018-1984-5
Mandel J (1972) Plasticité classique et viscoplasticité Volume 97 of CISM Lecture Notes. Springer, Wien
Michaleris P, Tortorelli DA, Vidal CA (1994) Tangent operators and design sensitivity formulations for transient non-linear coupled problems with applications to elastoplasticity. Int J Numer Methods Eng 37 (14):2471–2499. https://doi.org/10.1002/nme.1620371408
Nakra B (1998) Vibration control in machines and structures using viscoelastic damping. J Sound Vib 211 (3):449–466. https://doi.org/10.1006/jsvi.1997.1317
Nakshatrala P, Tortorelli D (2015) Topology optimization for effective energy propagation in rate-independent elastoplastic material systems. Comput Methods Appl Mech Eng 295:305–326. https://doi.org/10.1016/j.cma.2015.05.004
Nakshatrala P, Tortorelli D (2016) Nonlinear structural design using multiscale topology optimization. part ii: Transient formulation. Comput Methods Appl Mech Eng 304:605–618. https://doi.org/10.1016/j.cma.2016.01.003
Nakshatrala P, Tortorelli D, Nakshatrala K (2013) Nonlinear structural design using multiscale topology optimization. part i: Static formulation. Comput Methods Appl Mech Eng 261-262:167–176. https://doi.org/10.1016/j.cma.2012.12.018
Ortiz M, Leroy Y, Needleman A (1987) A finite element method for localized failure analysis. Comput Methods Appl Mech Eng 61(2):189–214. https://doi.org/10.1016/0045-7825(87)90004-1
Podestá J, Méndez C, Toro S, Huespe A (2019) Symmetry considerations for topology design in the elastic inverse homogenization problem. J Mech Phys Solids 128:54–78. https://doi.org/10.1016/j.jmps.2019.03.018
Rao MD (2003) Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. J Sound Vib 262(3):457–474. https://doi.org/10.1016/S0022-460X(03)00106-8, 2001 India-USA Symposium on Emerging Trends in Vibration and Noise Engineering
Reese S, Govindjee S (1998) A theory of finite viscoelasticity and numerical aspects. Int J Solids Struct 35 (26):3455–3482. https://doi.org/10.1016/S0020-7683(97)00217-5
Saeb S, Steinmann P, Javili A (2016) Aspects of computational homogenization at finite deformations: a unifying review from Reuss’ to Voigt’s bound. Appl Mech Rev 68(5):050801. https://doi.org/10.1115/1.4034024
Sigmund O (1994) Materials with prescribed constitutive parameters: an inverse homogenization problem. Int J Solids Struct 31(17):2313–2329. https://doi.org/10.1016/0020-7683(94)90154-6
Sigmund O, Maute K (2013) Topology optimization approaches. Struct Multidiscip Optim 48(6):1031–1055. https://doi.org/10.1007/s00158-013-0978-6
Sigmund O, Jensen SJ (2003) Systematic design of phononic band - gap materials and structures by topology optimization. Philosophical Transactions of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences 361(1806):1001–1019. https://doi.org/10.1098/rsta.2003.1177
Sigmund O, Torquato S (1997) Design of materials with extreme thermal expansion using a three-phase topology optimization method. J Mech Phys Solids 45(6):1037–1067. https://doi.org/10.1016/S0022-5096(96)00114-7
de Souza Neto E, Perić D, Dutko M, Owen D (1996) Design of simple low order finite elements for large strain analysis of nearly incompressible solids. Int J Solids Struct 33(20):3277–3296. https://doi.org/10.1016/0020-7683(95)00259-6
de Souza Neto E, Blanco P, Sánchez P, Feijóo R (2015) An rve-based multiscale theory of solids with micro-scale inertia and body force effects. Mech Mater 80:136–144. https://doi.org/10.1016/j.mechmat.2014.10.007
de Souza Neto EA, Peric D, Owen DR (2011) Computational methods for plasticity: theory and applications. John Wiley & Sons, West Sussex. https://doi.org/10.1002/9780470694626
Surjadi JU, Gao L, Du H, Li X, Xiong X, Fang NX, Lu Y (2019) Mechanical metamaterials and their engineering applications. Adv Eng Mater 21(3):1800864. https://doi.org/10.1002/adem.201800864
Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373. https://doi.org/10.1002/nme.1620240207
Triantafyllidis N, Maker BN (1985) On the comparison between microscopic and macroscopic instability mechanisms in a class of Fiber-Reinforced composites. J Appl Mech 52(4):794–800. https://doi.org/10.1115/1.3169148
Triantafyllidis N, Schraad M (1998) Onset of failure in aluminum honeycombs under general in-plane loading. J Mech Phys Solids 46(6):1089–1124. https://doi.org/10.1016/S0022-5096(97)00060-4
Triantafyllidis N, Nestorović MD, Schraad MW (2005) Failure surfaces for finitely strained two-phase periodic solids under general in-plane loading. J Appl Mech 73(3):505–515. https://doi.org/10.1115/1.2126695
Wallin M, Jönsson V, Wingren E (2016) Topology optimization based on finite strain plasticity. Struct Multidiscip Optim 54(4):783–793. https://doi.org/10.1007/s00158-016-1435-0
Wallin M, Ivarsson N, Tortorelli D (2018) Stiffness optimization of non-linear elastic structures. Comput Methods Appl Mech Eng 330:292–307. https://doi.org/10.1016/j.cma.2017.11.004
Wang F, Lazarov BS, Sigmund O (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidiscip Optim 43(6):767–784. https://doi.org/10.1007/s00158-010-0602-y
Wang F, Lazarov BS, Sigmund O, Jensen JS (2014) Interpolation scheme for fictitious domain techniques and topology optimization of finite strain elastic problems. Comput Methods Appl Mech Eng 276:453–472. https://doi.org/10.1016/j.cma.2014.03.021
Weber G, Anand L (1990) Finite deformation constitutive equations and a time integration procedure for isotropic, hyperelastic-viscoplastic solids. Comput Methods Appl Mech Eng 79(2):173–202. https://doi.org/10.1016/0045-7825(90)90131-5
Yi YM, Park SH, Youn SK (2000) Design of microstructures of viscoelastic composites for optimal damping characteristics. Int J Solids Struct 37(35):4791–4810. https://doi.org/10.1016/S0020-7683(99)00181-X
Yun KS, Youn SK (2018) Microstructural topology optimization of viscoelastic materials of damped structures subjected to dynamic loads. Int J Solids Struct 147:67–79. https://doi.org/10.1016/j.ijsolstr.2018.04.022
Zhang G, Khandelwal K (2019a) Computational design of finite strain auxetic metamaterials via topology optimization and nonlinear homogenization. Comput Methods Appl Mech Eng 356:490–527. https://doi.org/10.1016/j.cma.2019.07.027
Zhang G, Khandelwal K (2019b) Design of dissipative multimaterial viscoelastic-hyperelastic systems at finite strains via topology optimization. Int J Numer Methods Eng 119(11):1037–1068. https://doi.org/10.1002/nme.6083
Zhang G, Li L, Khandelwal K (2017) Topology optimization of structures with anisotropic plastic materials using enhanced assumed strain elements. Struct Multidiscip Optim 55(6):1965–1988. https://doi.org/10.1007/s00158-016-1612-1
Zhang G, Alberdi R, Khandelwal K (2018) Topology optimization with incompressible materials under small and finite deformations using mixed u/p elements. Int J Numer Methods Eng 115(8):1015–1052. https://doi.org/10.1002/nme.5834
Zhang P, Heyne MA, To AC (2015) Biomimetic staggered composites with highly enhanced energy dissipation: modeling, 3d printing, and testing. J Mech Phys Solids 83:285–300. https://doi.org/10.1016/j.jmps.2015.06.015
Funding
The presented work is supported in part by the US National Science Foundation through Grant CMMI-1762277. Any opinions, findings, conclusions, and recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the sponsors.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflict of interest.
Additional information
Responsible Editor: Julián Andrés Norato
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Replication of results
Appendices A, B and C provide the supplementary information that is needed to replicate the results presented in this study.
Appendices
Appendix A:: Finite strain viscoelasticity model implementation
In this appendix, numerical implementation of the finite strain viscoelastic model is presented. In the context of strain-driven finite element analysis, given data at an integration point: Fk and \(\boldsymbol {b}_{k}^{e}\) at previous step k, and F at current step k + 1, the goal is to find the unknown variables: P, be and the consistent tangent moduli at the current step k + 1. Note that the subscript k + 1 for the current step, the element number, and integration point number are removed for clarity. In addition to standard tensor notations, the following nonstandard tensor notations are used:
where A and B are any 2nd-order tensors and \(\boldsymbol {\mathcal {A}}\) and \(\mathbb {A}\) are any 3rd- and 4th-order tensors, respectively.
The viscoelastic model consists of equilibrium and non-equilibrium parts. The equilibrium part is handled in the same way as the hyperelastic model. For the non-equilibrium part, the material interpolation cannot be applied outside the material subroutine since the internal variable be is not known and has to be solved from a set of nonlinear constitutive equations where interpolated material parameters are used. In the following derivations, the material parameters κ, μq, and ηd are interpolated based on the material interpolation given in Section 4.3.
1.1 A.1 Integration of rate equations
The internal variable given in (35) is integrated using the exponential map integrator (Weber and Anand 1990). With \({\mathcal{L}}_{v}[\boldsymbol {b}^{e}]=\boldsymbol {F}.\dot {\overline {{\boldsymbol {C}^{v}}^{-1}}}.\boldsymbol {F}^{T}\) where Cv = FvT.Fv, (35) can be written as
Using the backward exponential integrator, (A.2) is integrated as
where the subscript k denotes the term evaluated at the last time step tk, with the time interval Δt = tk+ 1 − tk. Noticing that \(\exp [\boldsymbol {Y}^{-1}.\boldsymbol {Z}.\boldsymbol {Y}]=\boldsymbol {Y}^{-1}.\exp [\boldsymbol {Z}].\boldsymbol {Y}\) for any 2nd-order tensor Y and Z (Y is invertible) and the relation \(\boldsymbol {b}^{e}=\boldsymbol {F}.{\boldsymbol {C}^{v}}^{-1}.\boldsymbol {F}^{T}\), (A.3) can be simplified to
with \({\boldsymbol {b}^{e}}^{tr}={\boldsymbol {F}^{e}}^{tr}.{\boldsymbol {F}^{e}}^{{tr}^{T}}\) where \({\boldsymbol {F}^{e}}^{tr}\triangleq \boldsymbol {F}_{\delta }.\boldsymbol {F}_{k}^{e}\) and \(\boldsymbol {F}_{\delta }=\boldsymbol {F}.\boldsymbol {F}_{k}^{-1}\). Due to the isotropy, the non-equilibrium stress τneq and the tensor be are coaxial, which results in the coaxiality of tensor betr with τneq and be. As a result, it is possible to express the evolution rule in the principal space. Denote the elastic principal stretch at the current step as \({\lambda _{a}^{e}}\), while \({{\lambda _{a}^{e}}}^{tr}\) (a = 1, 2, 3) for the trial step, which are the square-root of the eigenvalues of tensors be and betr, respectively. The non-equilibrium principal stresses are denoted by \(\tau _{a}^{neq}\), which are the eigenvalues of the tensor τneq. Employing logarithmic strain, where \({\varepsilon _{a}^{e}}{\triangleq \ln \lambda _{a}^{e}}\) and \({{\varepsilon _{a}^{e}}}^{tr}\triangleq {{\ln \lambda _{a}^{e}}}^{tr}\), (A.4) can be expressed in the principal space as
where \(p^{neq}=(\tau _{1}^{neq}+\tau _{2}^{neq}+\tau _{3}^{neq})/3\) represents the pressure which equals \(\frac {1}{3}\text {tr}\left (\tau ^{neq}\right )\).
1.2 A.2 Stress tensor and consistent tangent moduli
For the non-equilibrium part, since the elastic Finger tensor be is not known, the non-equilibrium Kirchhoff stress τneq and be have to be calculated by using Eq. (33)3 and (A.5). This set of nonlinear equations are solved using Newton-Raphson (NR) method. Due to the coaxiality of be and τneq, (33)3 can be expressed in the principal space as
with the principal space spanned by \(\boldsymbol {G}_{a}^{e}\) which are the same as \({\boldsymbol {G}_{a}^{e}}^{tr}\) that span the principal space of betr (see (A.4)). Combining (A.5) and (A.6), the unknown variables \(\tau _{a}^{neq}\) and \({\varepsilon _{a}^{e}}\) are solved using the Newton-Raphson method. Taking \(\tau _{a}^{neq}\) as implicit functions of \({\varepsilon _{a}^{e}}\) determined by (A.6), the unknown variables are reduced to \({\varepsilon _{a}^{e}}\) and the set of nonlinear equations to be solved becomes
with the Jacobian matrix calculated, by employing (A.6), as
where κ, μq, and αq (q = 1,..., N) are parameters related to the non-equilibrium strain energy. Tangent modulus for the non-equilibrium part is obtained as
where the derivative ∂τneq/∂betr is computed using chain rule
in which \({\boldsymbol {\varepsilon }^{e}}^{tr}={\sum }_{a=1}^{3} {{\varepsilon _{a}^{e}}}^{tr}\boldsymbol {G}_{a}^{e}\) and the term ∂τneq/∂εetr can be derived from the (A.6) and (A.7) following the procedure given in de Souza Neto et al. (2011). The term ∂εetr/∂betr is computed in the same way, since εetr and betr are coaxial.
Appendix B:: Explicit derivatives required for the adjoint sensitivity analysis
For the objective and constraint functions, beside the energy dissipation (\(f_{0}=-\overline {W}_{d}\)) which depends on the solution and auxiliary variables, all the other constraints, e.g., material volume constraint and initial stiffness constraint, are only functions of the density field and their sensitivities are not path-dependent, and thus easy to compute. This appendix gives the derivatives that are used in the path-dependent sensitivity calculation of f0. For illustration purposes, the material interpolation scheme assuming void phase for Material-0 (Section 4.3.1) is considered in the sensitivity derivation in this appendix. In the following derivations, the tensor form and matrix-vector form are both utilized for notational simplicity and the appropriate form should be clear from the context. Moreover, to simplify the derivation process, the following functions are defined
where the functions ζκ(ρ1) and ζμ(ρ1) are evaluated using the associated material parameters, e.g., g2(ρ1, ρ2) and g3(ρ1, ρ2) are evaluated using Material-1 parameters, g4(ρ1, ρ2) and g5(ρ1, ρ2) are using equilibrium part of the viscoelastic material (Material-2), while g6(ρ1, ρ2) and g7(ρ1, ρ2) are based on non-equilibrium part of the viscoelastic material.
1.1 B.1 Derivatives of f0
After time and spatial domains discretization, the homogenized energy dissipation defined in (39) can be approximated by
where \(\mathbb {D}\) depends on the density variables \({\rho _{1}^{e}}\) and \({\rho _{2}^{e}}\); \(\boldsymbol {\tau }_{e_{s}}^{neq}\) is the Kirchhoff stress of the non-equilibrium viscoelastic phase at s th integration point in e th element; and Δtk = tk − tk− 1 is the time interval between step (k − 1) and step k. This leads to
The derivatives ∂f0/∂ρ1 and ∂f0/∂ρ2 are arranged as
with their components computed based on chain rule as
where \(\mu _{0}^{neq}\) is the initial shear modulus of the non-equilibrium viscoelastic solid phase, ηd is the interpolated value, and \(\hat {\psi }^{neq}\) and \(\tilde {\psi }^{neq}\) are the volumetric and isochoric non-equilibrium viscoelastic strain energy of solid phase.
The derivative \(\partial f_{0}/\partial \boldsymbol {v}^{k}\) is arranged as
where element number and integration point indices on elastic Finger tensor be are avoided with the understanding that the derivative \(\partial \boldsymbol {\tau }_{e_{s}}^{neq}/\partial \boldsymbol {b}^{e}\) is evaluated at the s th integration point inside e th element.
1.2 B.2 Derivatives of Rk
Due to the linear energy interpolation (Section 4.4) and F-bar formulation (Section 4.5), the 1st PK stress P is computed as
where r = r(ρ1, u) is a function of ρ1 and u, and \(\boldsymbol {P}_{0}^{b}\), \(\boldsymbol {P}_{1}^{b}\), \(\boldsymbol {P}_{2}^{b,eq}\), and \(\boldsymbol {P}_{2}^{b,neq}\) are 1st PK stresses contributed from different material phases, where the superscript “b” is used to denote that they are evaluated based on Fb. Based on this, it is straightforward that
where \(\boldsymbol {\nabla }_{\boldsymbol {X}}^{0}\) denotes the gradient operator evaluated at the centroid of the element. Also,
where B and B0 are the shape functions derivative matrices evaluated at the integration point and the centroid, respectively. Besides, due to the dependence of Fb on ρ1 and u, the following derivatives are obtained
1.2.1 B.2.1 Derivatives of \(\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{1}\) and \(\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{2}\)
The explicit dependence of Rk on ρ1 comes from the linear energy interpolation parameter γ(ρ1) as well as the interpolated constitutive model parameters. Thus, the derivative \(\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{1}\) is computed as
in which \(\mathbb {A}_{0}^{b}\), \(\mathbb {A}_{1}^{b}\), and \(\mathbb {A}_{2}^{b,eq}\) are the tangent moduli evaluated from each constitutive model with material interpolation, i.e., \(\mathbb {A}_{0}^{b}\triangleq \partial \boldsymbol {P}_{0}^{b}/\partial \boldsymbol {F}^{b}\), \(\mathbb {A}_{1}^{b}\triangleq \partial \boldsymbol {P}_{1}^{b}/\partial \boldsymbol {F}^{b}\) and \(\mathbb {A}_{2}^{b,eq}\triangleq \partial \boldsymbol {P}_{2}^{b,eq}/\partial \boldsymbol {F}^{b}\); \(\frac {\partial \boldsymbol {P}^{b}}{\partial \rho _{1}}\big |_{\boldsymbol {F}^{b} \text {fixed}}\) is computed by
where
where “s” in the subscript denotes that the term is evaluated with the non-interpolated solid material parameters. Again, the upper hat denotes the volumetric part while upper tilde denotes the isochoric part, e.g., \(\hat {\boldsymbol {P}}_{2,s}^{b,eq}=\partial \hat {\psi }_{2}^{eq}/\partial \boldsymbol {F}^{b}\), where \(\hat {\psi }_{2}^{eq}\) is evaluated with solid phase parameters. It should be noted that in sensitivity analysis the calculation of \(\hat {\boldsymbol {P}}_{2,s}^{b,neq}\) and \(\tilde {\boldsymbol {P}}_{2,s}^{b,neq}\) are based on \(\hat {\psi }_{2}^{neq}(\boldsymbol {b}^{e})\) and \(\tilde {\psi }_{2}^{neq}(\boldsymbol {b}^{e})\) where solid material phase parameters are used, however, the computation of be is based on the interpolated material parameters. Since be is chosen as independent variable, its dependence on ρ1 and ρ2 fields is not explicitly accounted. On the other hand, the dependence of Rk on ρ2 comes from the constitutive model parameters. As a result, the derivative \(\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{2}\) is computed as
1.2.2 B.2.2 Derivatives of \(\partial \boldsymbol {R}^{k}/\partial \hat {\boldsymbol {u}}^{k}\) and \(\partial \boldsymbol {R}^{k}/\partial \hat {\boldsymbol {u}}^{k-1}\)
The derivative \(\partial \boldsymbol {R}^{k}/\partial \hat {\boldsymbol {u}}^{k}\) is derived as
where the term ∂Pb/∂Fb is calculated in (B.15). Also, Rk does not depend on \(\hat {\boldsymbol {u}}^{k-1}\) explicitly and
1.2.3 B.2.3 Derivatives of ∂Rk/∂vk and ∂Rk/∂vk− 1
Since in the free energy only \(\psi _{2}^{neq}(\boldsymbol {b}^{e})\) depends on the auxiliary variable (v ≡be), the derivative ∂Rk/∂vk can be derived as
Without dependence of Rk on vk− 1
1.3 B.3 Derivatives of Hk
1.3.1 B.3.1 Derivatives of \(\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{1}\) and \(\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{2}\)
The derivatives \(\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{1}\) and \(\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{2}\) are obtained as
where
and
in which \(\tilde {\tau }_{a}^{neq}=\tau _{a}^{neq}-p^{neq}\) is the isochoric part of the principal non-equilibrium Kirchhoff stress and the relationship \({\boldsymbol {b}^{e}}^{tr}=\boldsymbol {F}_{\delta }^{b}.\boldsymbol {b}_{k-1}^{e}.\boldsymbol {F}_{\delta }^{b^{T}}\) with \(\boldsymbol {F}_{\delta }^{b}\triangleq \boldsymbol {F}^{b}.\boldsymbol {F}_{k-1}^{b^{-1}}\) is used in the derivation (where Fb is at step k), and the derivative \(\partial \tilde {\tau }_{a}^{neq}/{\partial \rho _{A}^{e}}\) is calculated by
where the subscript “s” in \(\tilde {\tau }_{a,s}^{neq}\) means that it is computed from the solid phase.
1.3.2 B.3.2 Derivatives of \(\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k}\) and \(\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k-1}\)
The derivative \(\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k}\) is obtained as
Similarly, the derivative \(\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k-1}\) is obtained in the same way but with
1.3.3 B.3.3 Derivatives of ∂Hk/∂vk and ∂Hk/∂vk− 1
The derivative ∂Hk/∂vk is obtained as
where \(\mathbb {I}_{4}^{s}\) is the symmetric identity 4th-order tensor, i.e., \(\mathbb {I}_{4}^{s}\triangleq \frac {1}{2}(\boldsymbol {I}\boxtimes \boldsymbol {I}+\boldsymbol {I}\boxdot \boldsymbol {I})\), \(\boldsymbol {I}\rightarrow \) second-order identity tensor and the derivatives \(\partial (\exp [-2 {\Delta } t_{k}\boldsymbol {A}])/\partial \boldsymbol {\tau }^{neq}\) and ∂τneq/∂be are computed in the principal space. Finally, the derivative ∂Hk/∂vk− 1 is formulated in the same way as ∂Hk/∂vk, but with
Appendix C: Verifications of the path-dependent sensitivity analysis
In this appendix, the path-dependent sensitivity calculation given in Section 5 and Appendix B is verified for two types of material interpolations as given in Section 4.3 for different candidates chosen for material-0. The first verification, referred to as verification-1, considers the material interpolation given in Section 4.3.1 with void phase chosen as material-0. The second verification, referred to as verification-2, considers the material interpolation in Section 4.3.2 with a soft hyperelastic phase chosen as material-0.
1.1 C.1 Sensitivity verification-1: Void for material-0
For verification-1, a parallelogram-shaped RUC with a random design shown in Fig. 15a is used. The density vectors ρ1 and ρ2 are plotted in Fig. 15c. The macroscopic deformation loading considers (68) to (70) with 𝜃 = 0∘, Λ = 1.4, f = 0.009s− 1, and t ∈ [0, 1/f]. The sensitivity comparison between the proposed adjoint method and the central difference method (with perturbation \({\Delta }\rho _{1}={\Delta }\rho _{2}={10}^{-6}\)) is shown in Fig. 16 where good matches can be observed with relative error around 10− 6 to 10− 8. Here, the relative error is computed as the absolute value of the ratio of the difference between the central difference results and the adjoint results to the central difference results.
1.2 C.2 Sensitivity verification-2: Soft hyperelastic phase for material-0
For verification-2, a hexagon-shaped RUC with prescribed design shown in Fig. 15b is used. The design is with the same density vectors ρ1 and ρ2 shown in Fig. 15c. The macroscopic deformation loading considers (68) to (70) with 𝜃 = 45∘, Λ = 1.4, f = 0.009s− 1 and t ∈ [0, 1/f]. The sensitivity comparison between the proposed adjoint method and the central difference method (with perturbation \({\Delta }\rho _{1}={\Delta }\rho _{2}={10}^{-6}\)) is shown in Fig. 17 where again good matches can be observed with relative error around 10− 6 to 10− 8.
Rights and permissions
About this article
Cite this article
Zhang, G., Khandelwal, K. Topology optimization of dissipative metamaterials at finite strains based on nonlinear homogenization. Struct Multidisc Optim 62, 1419–1455 (2020). https://doi.org/10.1007/s00158-020-02566-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-020-02566-8