Failure resistant topology optimization of structures using nonlocal elastoplastic-damage model

Abstract

For energy absorbing structures made up of ductile materials, the plastic strain accumulation often leads to early material damage and failure, which can deteriorate the overall structural performance. The goal of this work is to limit this damage in elastoplastic designs using the density-based topology optimization framework such that the optimized structures can absorb energy in a more controllable manner. To this end, an implicit nonlocal coupled elastoplastic damage model is considered for simulating the material damage and softening behavior. The nonlocal effect from the void elements is removed by introducing a scaling scheme for the nonlocal parameters. Path-dependent sensitivity is derived analytically using an adjoint method whose accuracy is further verified by the central difference method. The effectiveness of the proposed method is demonstrated through several numerical examples. It is shown that the load-carrying capacity, ductility, as well as ultimate plastic work dissipation capacity of the optimized design, can be considerably improved by the proposed method.

1 Introduction

Topology optimization is an advanced design method that has been applied to numerous applications (Bendsøe and Sigmund 2003). Past studies have also investigated the utilization of topology optimization method to design elastoplastic energy absorbing structures (Maute et al. 1998; Schwarz et al. 2001; Nakshatrala and Tortorelli 2015; Kato et al. 2015; Wallin et al. 2016; Li and Khandelwal 2017; Li et al. 2017a, 2017b; Alberdi and Khandelwal 2017; Zhang et al. 2017). In ductile materials, the elastoplastic behavior is usually accompanied by material damage that leads to the deterioration of material properties, which is further reflected as the gradual loss of the load-carrying capacity. For instance, the damage in structural steels is due to the nucleation, growth and coalescence of microvoids that finally results in material fracture and failure (Kiran and Khandelwal 2013, 2014a, 2014b, 2015). This multiscale fracture process is controlled by the plastic strains and applied loading conditions. Thus, when enhancing plastic work dissipation capacity in topology optimization, it is also important to control the damage evolution such that optimized topologies can have large ductility and can dissipate sufficient plastic work before failure.

To date, the majority of damage-resistant topology optimization work has focused on limiting the local yield stresses in the optimized structures. The basic idea of the so-called stress-based topology optimization is to keep the structure within the linear elastic regime so that the potential damage due to inelastic behavior can be excluded (Duysinx and Bendsøe 1998). Despite the developments in addressing the inherent difficulties, i.e. stress singularity issues (Bruggi 2008; Cheng and Guo 1997), numerous local constraints (Duysinx and Bendsøe 1998; Yang and Chen 1996; Le et al. 2010; París et al. 2009) and highly nonlinear stress constraints (Duysinx and Bendsøe 1998; Svanberg and Werme 2007), stress-based topology optimization cannot be applied to energy absorbing structural designs, since it lacks the description of plastic energy dissipation. Another category is the damage-based topology optimization, in which the damage mechanics is explicitly considered in the topology optimization formulation. The early work in this category can be traced back to Bendsøe and Diaz (1998), in which the optimized layout was obtained by constraining the damage from an approximate elastic damage model. A level-set based topology optimization method for brittle elastic fracture resistant designs was proposed by Challis et al. (2008), wherein the energy release rate of crack propagation was used as the fracture measure. Amir and Sigmund (2013) and Amir (2013) used elastic damage model to simulate the behavior of concrete structures, and the optimal placement of reinforcement bars and shape of concrete structures were sought using the topology optimization. James and Waisman (2014) proposed a damage mitigation topology optimization method by constraining the aggregated maximum elastic-damage. Jansen et al. (2014) incorporated a simplified local failure model into topology optimization formulation to achieve the more robust design. Recently, Noël et al. (2017) combined nonlocal elastic-damage model with level-set based topology optimization method, and the stiffest structure is sought by accounting for the material stiffness loss introduced by the damage model. All of the aforementioned damage-based topology optimization studies were focused on the elastic damage models, which can only represent the damage in brittle materials. To account for the plastic energy dissipation in the design of energy absorbing ductile structures, the physics of elastoplastic dissipation should be further considered.

In recent studies, the authors have proposed two strategies to address the issue of damage in elastoplastic topology optimization. In the first strategy, the uncoupled fracture models – which describe the critical conditions for fracture initiation in terms of stress-states and accumulated plastic strain – were used (Alberdi and Khandelwal 2017; Li and Khandelwal 2017). In particular, additional material pointwise fracture constraints were incorporated in the optimization process using the p-norm constraint aggregation method. While this strategy is able to yield optimal topologies with robust performance, the actual material failure is only approximately considered using the uncoupled fracture models. In the second strategy, a coupled elastoplastic damage model was directly employed in topology optimization to describe the physics of underlying material damage (Li et al. 2017b), and the damage constraints were enforced on the internal damage variable. An important issue when considering coupled elastoplastic damage models in topology optimization is that the numerical solution obtained from the finite element analysis employing local damage models, where a local description of damage is used for modeling material softening, reveals pathological dependence on the size and orientation of the underlying finite element (FE) mesh (De Borst et al. 1993; Lasry and Belytschko 1988; Bažant et al. 1984). Accordingly, upon FE mesh refinement no convergence to a physically meaningful solution exists. This mesh-dependence is the direct consequence of the ill-posedness of the underlying mathematical formulation, i.e. the boundary value problem loses ellipticity for the quasi-static case. This change allows discontinuities in the strain distribution to appear, and deformation tends to localize into a zone of zero width, which in turn influence the energy dissipation capacity. In the past, many enhanced physical and phenomenological models have been proposed to overcome this deficiency, and an overview of these methods can be found in Refs (Belytschko et al. 2013; de Borst et al. 2012). Thus, in order to more accurately consider the damage and failure in elastoplastic topology optimization it is important to include these enhanced physical models in topology optimization. Although the nonlocal formulations of material damage/softening models have already been considered in various papers on topology or shape optimizations (Amir 2013, Amir and Sigmund 2013, James and Waisman 2014, Kato et al. 2008, Kato and Ramm 2010), all of them have focused on the elastic-brittle damage. Topology optimization of failure resistant structures accounting for the nonlocal elastoplastic-damage has not yet been explored in the literature to the authors’ best knowledge.

In this study, a density-based topology optimization method to design damage-resistant energy absorbing structures is proposed. In order to capture the softening behavior caused by material damage, a second-order implicit coupled elastoplastic damage model is considered. This model is capable of simulating the transition from hardening to softening behavior due to the initiation and evolution of ductile damage while simultaneously addressing the underlying FE mesh dependent issues by introducing a nonlocal plastic strain field. A novel SIMP-like material interpolation scheme is introduced to represent the mechanical behavior of intermediate density elements in a physically consistent manner, while a scaling scheme for nonlocal model parameters is used to eliminate the nonlocal effects from the void elements. As a result, accurate physics of nonlocal damage can be captured in both the finite element analyses and the topology optimization process. The goal of the optimizations is to design minimum volume topologies that can dissipate the prescribed amount of energy via plastic work while simultaneously constraining the material damage within acceptable limits. Numerically accurate and consistent path-dependent design sensitivities are derived analytically using the adjoint method, which is verified by the central difference method before being utilized in topology optimization. Various numerical studies are presented to demonstrate the effectiveness of the proposed methods. Note that the problems formulated in this study are restricted to quasi-static conditions, where strain rate and inertial effects are ignored. The corresponding applications can be found in earthquake engineering, such as metallic yielding dampers, shear links, etc. (Soong and Spencer 2002), in which the components dissipate energy via inelastic deformations.

The remainder of this paper is organized as follows: Section 2 describes the implicit nonlocal coupled elastoplastic damage model and its finite element formulation is given in Section 3. Section 4 discusses the design parametrization scheme as well as the problem formulation of the proposed topology optimization method. The detailed derivation of the path-dependent sensitivity analysis via the adjoint method for the coupled nonlocal damage model is presented in Section 5. Section 6 reports the sensitivity verification results and investigates three numerical examples with different configurations using the proposed method. Finally, concluding remarks are provided in Section 7.

2 Nonlocal damage model for ductile materials

Among the various methods proposed to handle the FE mesh dependency issues, the nonlocal integral-based and gradient enhanced damage models are effective from both the physical and computational points of view (Peerlings et al. 2001). An important feature of these models is the incorporation of an intrinsic length-scale, which can be related to the material microstructure and associated failure mechanisms. The nonlocal integral-based theories consider a nonlocal variable, which is calculated as the weighted average value of the corresponding local variable. The state of the stress then depends on this nonlocal variable so that the model can represent the spread of the strain softening effect from one material point to its neighboring material points. The nonlocal gradient models, on the other hand, consider higher-order gradient terms of the desired local variable in the constitutive model (Engelen et al. 2003). Essentially, a gradient model can be seen as the approximation of nonlocal integral-based model upon Taylor expansion (Engelen 2005). Two types of gradient approximations – explicit and implicit gradient approximations — have been proposed. Studies have shown that the implicit gradient approximation is superior to the explicit approximation, as it is able to model the complete failure while the explicit approximation cannot (Engelen et al. 2003). Besides, implicit approximation gives a closer approximation to a nonlocal integral-based formulation as compared to explicit model when the same order of gradient terms are considered (Askes et al. 2000). Accordingly, an implicit coupled elastoplastic damage model is considered in this work for simulation of damage and softening behavior in ductile materials. Specifically, the implicit nonlocal damage model for ductile materials developed by Engelen et al. (2003) is utilized. In this section, the brief description of the strong form governing equations and constitutive relations of the damage model are presented. The detailed description of the model can be found elsewhere (Engelen et al. 2003; Engelen 2005).

2.1 Governing equations

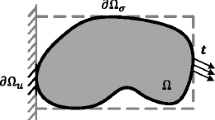
Consider a solid body occupying a bounded domain $\phantom {\dot {i}\!}{\Omega }$ as shown in Fig. 1. Its boundary $\phantom {\dot {i}\!}\partial {\Omega }$ is partitioned into two segments: $\phantom {\dot {i}\!} \partial {\Omega }=\partial {\Omega }_{u}\cup \partial {\Omega }_{\sigma }$ and $\phantom {\dot {i}\!}\partial {\Omega }_{u}\cap \partial {\Omega }_{\sigma } = \emptyset$. The body $\phantom {\dot {i}\!}{\Omega }$ is subjected to body forces $\phantom {\dot {i}\!}\boldsymbol {b}$, surface tractions $\phantom {\dot {i}\!}\overline {\boldsymbol {t}}$ are imposed on $\phantom {\dot {i}\!}\partial {\Omega }_{\sigma }$ while the prescribed displacement $\phantom {\dot {i}\!}\overline {\boldsymbol {u}}$ are applied on $\phantom {\dot {i}\!}\partial {\Omega }_{u}$. Restricting attention to quasi-static problems and small deformation case, the strong form of the governing equations is expressed as

$$ \left\{\begin{array}{l} {\boldsymbol{\nabla}}.\boldsymbol{\sigma}+\boldsymbol{b}=\boldsymbol{0}\\ {\overline{\alpha}}-\ell^{2}{\nabla}^{2}{\overline{\alpha}}=\alpha\\ \end{array}\right. \text{in}\quad{\Omega} $$

(1)

with boundary conditions

$$ \begin{array}{lll} {\boldsymbol{u}}=\overline{\boldsymbol{u}}\quad&\text{on}\quad&\partial{\Omega}_{u}\\ \boldsymbol{\sigma}.\overline{\boldsymbol{n}}=\overline{\boldsymbol{t}}\quad&\text{on}\quad&\partial{\Omega}_{\sigma}\\ \boldsymbol{\nabla}\overline{\alpha}.\overline{\boldsymbol{n}}= 0\quad&\text{on}\quad&\partial{\Omega}\\ \end{array} $$

(2)

where $\phantom {\dot {i}\!}\boldsymbol {\nabla }$ is the divergence operator and $\phantom {\dot {i}\!}\boldsymbol {\sigma }$ denotes the Cauchy stress tensor; $\phantom {\dot {i}\!}\alpha$ and $\phantom {\dot {i}\!}\overline {\alpha }$ are the local and nonlocal equivalent plastic strains, respectively, and $\phantom {\dot {i}\!}\ell$ denotes the length-scale parameter. For the boundary conditions, $\phantom {\dot {i}\!}\overline {\boldsymbol {u}}$ and $\phantom {\dot {i}\!}\overline {\boldsymbol {t}}$ are the prescribed displacements and tractions on $\phantom {\dot {i}\!}\partial {\Omega }_{u}$ and $\phantom {\dot {i}\!}\partial {\Omega }_{\sigma }$, respectively, where $\phantom {\dot {i}\!}\overline {\boldsymbol {n}}$ is the unit outward normal vector field on $\phantom {\dot {i}\!}\partial {\Omega }$. Only the Neumann boundary conditions, i.e. $\phantom {\dot {i}\!}\boldsymbol {\nabla }\overline {\alpha }.\overline {\boldsymbol {n}}= 0$ on $\phantom {\dot {i}\!}\partial {\Omega }$, is considred for the nonlocal field $\phantom {\dot {i}\!}\overline {\alpha }$ (Engelen 2005). It is noted that the parameter $\phantom {\dot {i}\!}\ell$ determines the length-scale of the zone in which the damage is approximately smeared out and can be related to the microstructure of the considered material.

Fig. 1

Schematic illustration of a solid body Ω and its boundary ∂Ω

2.2 Constitutive relations

The constitutive relations determine the coupling between both PDEs in (1). In the context of small deformation assumption, the strain field is calculated by $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }=\boldsymbol {\nabla }^{s}\boldsymbol {u}$, where $\phantom {\dot {i}\!}\boldsymbol {\nabla }^{s}\boldsymbol {u}$ denotes the symmetric gradient operator. The total strain is additively decomposed into an elastic strain $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }^{e}$ and a plastic strain $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }^{p}$ as

$$ \boldsymbol{\varepsilon} = \boldsymbol{\varepsilon}^{e} + \boldsymbol{\varepsilon}^{p}\ $$

(3)

Assuming the isotropic elasticity, the Cauchy stress tensor $\phantom {\dot {i}\!}\boldsymbol {\sigma }$ is computed by

$$ \boldsymbol{\sigma} = \mathbb{C}^{e} : \boldsymbol{\varepsilon}^{e}\\ $$

(4)

where $\phantom {\dot {i}\!}\mathbb {C}^{e}\;{\triangleq }\;3{{\kappa }}{\mathbb {P}_{vol}}+ 2{\mu }{\mathbb {P}_{dev}^{s}}$ is the isotropic elasticity tensor, and $\phantom {\dot {i}\!}{\kappa }$ and $\phantom {\dot {i}\!}\mu$ are the bulk and shear moduli, respectively. The fourth order volumetric $\phantom {\dot {i}\!}{\mathbb {P}_{vol}}$ and symmetric deviatoric $\phantom {\dot {i}\!}{\mathbb {P}_{dev}^{s}}$ projectors are given by $\phantom {\dot {i}\!}{\mathbb {P}_{vol}\:{\triangleq }\:\frac {1}{3}\boldsymbol {I}\otimes \boldsymbol {I}}$ and $\phantom {\dot {i}\!}{\mathbb {P}_{dev}^{s}\:{\triangleq }\:\mathbb {I}_{4}^{s}-\mathbb {P}_{vol}}$ where $\phantom {\dot {i}\!}{[\mathbb {I}_{4}^{s}]_{ijkl}\:{\triangleq }\:\frac {1}{2}(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})}$ and $\phantom {\dot {i}\!}{\boldsymbol {I}}$ is the second order identity tensor. To model the progression of damage, the von Mises yield criterion is coupled with a nonlocal damage function, $\phantom {\dot {i}\!}d({\kappa })$, as follows

$$ \begin{array}{l} \displaystyle\phi(\boldsymbol{\sigma},\alpha,{\kappa}) = \|\boldsymbol{s}\|-\sqrt{\frac{2}{3}}(1-d({\kappa}))\left(\sigma_{y}+\zeta(\alpha)\right)\\ \text{with}\\ \zeta(\alpha)=K^{h}\alpha\\ {\kappa}(t)=\max \{\overline{\alpha}(\tau)\;\;|\;\;0\leq\tau\leq t\} \end{array} $$

(5)

where $\phantom {\dot {i}\!}\boldsymbol {s}$ denotes the deviatoric part of the stress tensor $\phantom {\dot {i}\!}\boldsymbol {\sigma }$, $\phantom {\dot {i}\!}\sigma _{y}$ is the initial yield stress and $\phantom {\dot {i}\!}\zeta (\alpha )$ is the linear isotropic hardening function defined in terms of the local equivalent plastic strain $\phantom {\dot {i}\!}\alpha$ and hardening modulus $\phantom {\dot {i}\!}K^{h}$. In (5), $\phantom {\dot {i}\!}d({\kappa })$ serves as the ductile damage variable that is defined in terms of the maximum nonlocal strain measure $\phantom {\dot {i}\!}{\kappa }$ and $\phantom {\dot {i}\!}\tau$ is the time-like loading parameter. It is noted that the softening and degradation of the material are described by the damage variable d in this model. In (5), the term $\phantom {\dot {i}\!}(1-d({\kappa }))$ reduces the yield strength at a material point, and depends on the ductile damage variable $\phantom {\dot {i}\!}d\in [0,1]$, where $\phantom {\dot {i}\!}d = 1$ represents complete loss of material strength. An exponential function is employed to describe the dependence of d on the nonlocal strain measure $\phantom {\dot {i}\!}{\kappa }$ as follows

$$ d({\kappa})=\left(1-e^{-\beta({\kappa}-{\kappa}_{th})}\right){\Gamma}({\kappa})\\ $$

(6)

where $\phantom {\dot {i}\!}\beta$ is a material parameter that controls the speed of damage evolution, $\phantom {\dot {i}\!}{\kappa }_{th}$ is the threshold parameter that triggers the damage initiation and $\phantom {\dot {i}\!}{\Gamma }({\kappa })$ is a smooth threshold function. The threshold function $\phantom {\dot {i}\!}{\Gamma }({\kappa })$ is introduced to enable smooth transition from undamaged material state to damaged material state (Li et al. 2017b) which is given by

$$ {\Gamma}({\kappa})\,=\, \left\{\begin{array}{lll} 0 && {\kappa}\leq{\kappa}_{th}\\ \displaystyle\left(\frac{{\kappa}\,-\,{\kappa}_{th}}{{\Delta}{\kappa}}\right)^{2}\left(3\,-\,2\frac{{\kappa}\,-\,{\kappa}_{th}}{{\Delta}{\kappa}}\right)&& {\kappa}_{th}\!<\!{\kappa}\!<\!{\kappa}_{th}+{\Delta}{\kappa}\\ 1&& {\kappa}\geq{\kappa}_{th}\,+\,{\Delta}{\kappa}\\ \end{array}\right. $$

(7)

where $\phantom {\dot {i}\!}{\Delta }{\kappa }$ denotes the bandwidth for the threshold function to reach unity. By using this damage evolution, the damage is initiated only when $\phantom {\dot {i}\!}{\kappa }>{\kappa }_{th}$, and $\phantom {\dot {i}\!}{\kappa }_{th}$ can be considered as the effective plastic strain at damage initiation. The relationship between d and $\phantom {\dot {i}\!}{\kappa }$ in (6) and (7) is illustrated in Fig. 2 with different model parameters. It can be seen that a smooth and monotonically increasing relationship between d and $\phantom {\dot {i}\!}{\kappa }$ is obtained, which is differentiable for sensitivity analysis in optimization process. Moreover, while $\phantom {\dot {i}\!}{\kappa }_{th}$ determines when the damage starts to initiate, $\phantom {\dot {i}\!}\beta$ defines how fast the damage develops and $\phantom {\dot {i}\!}{\Delta }{\kappa }$ controls the bandwidth of the threshold function (Fig. 2).

Fig. 2

The smooth and monotonic increasing threshold functions for damage evolution, with different damage parameters

The flow rules for the evolution of plastic strain and internal variables are given by

$$ \dot{\boldsymbol{\varepsilon}}^{p}=\gamma\frac{\partial\phi}{\partial\boldsymbol{\sigma}}=\gamma\frac{\boldsymbol{s}}{\|\boldsymbol{s}\|}=\gamma\boldsymbol{n} $$

(8)

$$ \dot{\alpha}=\sqrt{\frac{2}{3}}{\|\boldsymbol{\dot{\varepsilon}}^{p}\|}=\sqrt{\frac{2}{3}}\gamma $$

(9)

$$ {\kappa}(t)=\max \{\overline{\alpha}(\tau)\;\;|\;\;0\leq\tau\leq t\} $$

(10)

where $\phantom {\dot {i}\!}\gamma$ is the plastic multiplier that represents the amount of plastic flow, and n is a unit vector defines the normal to the yield surface. To complete the constitutive model, the Karush-Kuhn-Tucker and consistency conditions are introduced to describe the plastic loading and unloading processes as follows

$$ \begin{array}{lll} \gamma\geq0,\;\phi\leq0,\;\gamma\phi= 0&&(\mathrm{KKT\;conditions})\\ \gamma\dot{\phi}= 0&&(\mathrm{Consistency\ condition})\ \end{array} $$

(11)

The nonlocal damage model mentioned above is implemented in the strain-driven finite element framework, and the implicit backward Euler scheme is adopted to discretize the evolution equations. The standard elastic predictor/return-mapping algorithm is employed to solve the local nonlinear problem (de Souza Neto et al. 2011). The elastic predictor/return-mapping algorithm and the associated consistent algorithmic tangent moduli are provided in Appendix AA.

3 Finite element implementation

This section presents the finite element implementation of the nonlocal damage model discussed in Section 2. It lays down the foundation for the optimization problem formulation presented in Section 4 and adjoint sensitivity analysis shown in Section 5.

3.1 Weak form

For the purpose of finite element implementation, the weak form of the problem is obtained from the strong form following the principle of virtual work: find $\phantom {\dot {i}\!}\boldsymbol {u}\in \mathscr {U}=\{\boldsymbol {u}:{\Omega }\to \mathbb {R}^{3}\;|\;\boldsymbol {u}=\overline {\boldsymbol {u}}\;\;\text {on}\;\; \partial {{\Omega }_{u}}\}$ and $\phantom {\dot {i}\!}\overline {\alpha }\in \mathscr {V}=\{\overline {\alpha }:{\Omega }\to \mathbb {R}\}$ such that

$$ \begin{array}{l} \displaystyle{\int}_{\Omega}\boldsymbol{\nabla}^{s}\delta\boldsymbol{u}:\boldsymbol{\sigma}dv\,=\,{\int}_{\Omega}\delta\boldsymbol{u}.\boldsymbol{b}dv+{\int}_{\partial{\Omega}_{\sigma}}\delta\boldsymbol{u}.\overline{\boldsymbol{t}}ds,\quad\forall\delta\boldsymbol{u}\in\hat{\mathscr{U}}\\ \displaystyle{\int}_{\Omega}\delta\overline{\alpha}\cdot\overline{\alpha}dv\,+\,{\int}_{\Omega}\ell^{2}\boldsymbol{\nabla}\delta\overline{\alpha}.\boldsymbol{\nabla}\overline{\alpha}dv\,=\,{\int}_{\Omega}\delta\overline{\alpha}\cdot\alpha dv,\;\;\:\forall\delta\overline{\alpha}\in\mathscr{V}\\ \end{array} $$

(12)

where $\phantom {\dot {i}\!}\delta \boldsymbol {u}\in \hat {\mathscr {U}}=\{\boldsymbol {u}:{\Omega }\to \mathbb {R}^{3}\;|\;\boldsymbol {u}=\boldsymbol {0}\;\;\text {on}\;\;\partial {{\Omega }_{u}}\}$ and $\phantom {\dot {i}\!}\delta \overline {\alpha }\in \mathscr {V}$ represent the virtual displacement and virtual nonlocal strain fields, respectively.

3.2 Finite element discretization

The presented implicit gradient-enhanced formulation for elastoplasticity based on ductile damage permits a straightforward $\phantom {\dot {i}\!}C^{0}$-continuous discretization within a finite element framework. In this study, plane strain condition is assumed and an 8-node quadrilateral (Q8) element with reduced integration (4 integration points) is utilized to interpolate the displacement field $\phantom {\dot {i}\!}\boldsymbol {u}$, while a 4-node quadrilateral (Q4) element is used to interpolate the nonlocal plastic strain field $\phantom {\dot {i}\!}\overline {\alpha }$, as shown in Fig. 3. This element is referred to as Q8/4 element.

Fig. 3

Nodes and integration points within a Q8/4 element

Substituting the displacement and nonlocal strain approximations and ignoring the body forces, the finite element discretized form can be derived as

$$ \boldsymbol{R}=\overset{n_{ele}}{\underset{e = 1}{\mathscr{A}}}\boldsymbol{R}^{e}=\boldsymbol{0}\\ \text{with}\\ \boldsymbol{R}^{e}=\left[\begin{array}{c} \boldsymbol{F}_{int,u}^{e}-\boldsymbol{F}_{ext,u}^{e}\\ \boldsymbol{F}_{int,\overline{\alpha}}^{e}\\ \end{array}\right] $$

(13)

where $\phantom {\dot {i}\!}\mathscr {A}$ is the standard finite element assembly operator, $\phantom {\dot {i}\!}n_{ele}$ is the total number of elements in the design domain. The corresponding element internal forces, $\phantom {\dot {i}\!}\boldsymbol {F}_{int,u}^{e}$ and $\phantom {\dot {i}\!}\boldsymbol {F}_{int,\overline {\alpha }}^{e}$, and the external force, $\phantom {\dot {i}\!}\boldsymbol {F}_{ext,u}^{e}$, read

$$ \begin{array}{l} \displaystyle\boldsymbol{F}_{int,u}^{e}={\int}_{{\Omega}^{e}}\boldsymbol{B}_{u}^{T}\boldsymbol{\sigma}dv\\ \displaystyle\boldsymbol{F}_{int,\overline{\alpha}}^{e}={\int}_{{\Omega}^{e}}\left(\boldsymbol{N}_{\overline{\alpha}}^{T}\boldsymbol{N}_{\overline{\alpha}}\overline{\boldsymbol{\alpha}}_{e}+\ell^{2}\boldsymbol{B}_{\overline{\alpha}}^{T}\boldsymbol{B}_{\overline{\alpha}}\overline{\boldsymbol{\alpha}}_{e}-\boldsymbol{N}_{\overline{\alpha}}^{T}\alpha\right)dv\\ \displaystyle\boldsymbol{F}_{ext,u}^{e}={\int}_{\partial{\Omega}_{\sigma}^{e}}\boldsymbol{N}_{u}^{T}\overline{\boldsymbol{t}}ds \end{array} $$

(14)

where $\phantom {\dot {i}\!}\boldsymbol {N}_{u}$ and $\phantom {\dot {i}\!}\boldsymbol {B}_{u}$ are the shape function and shape function derivative matrices for Q8 element, respectively; $\phantom {\dot {i}\!}\boldsymbol {N}_{\overline {\alpha }}$ and $\phantom {\dot {i}\!}\boldsymbol {B}_{\overline {\alpha }}$ are the shape function and shape function derivative matrices for Q4 element, respectively; $\phantom {\dot {i}\!}\overline {\boldsymbol {\alpha }}^{e}$ is the element nodal vector of the nonlocal quantities, while $\phantom {\dot {i}\!}\alpha$ is the local field defined at each integration point.

In this study, the discrete nonlinear global system in (12) is solved in an incremental manner based on the displacement control strategy. For each incremental step k, Newton-Raphson (NR) method is employed to seek the equilibrium state $\phantom {\dot {i}\!}\boldsymbol {U}^{k}=\left [\boldsymbol {u}^{k};\overline {\boldsymbol {\alpha }}^{k}\right ]$. Specifically, given the solution field predictor $\phantom {\dot {i}\!}\boldsymbol {U}_{0}^{k}$ at step k, the displacement at step k is iteratively (r = 1,2,3,...) updated through

$$ \begin{array}{l} {\Delta}\boldsymbol{U}_{r}^{k}=-\boldsymbol{K}_{T}^{-1}\boldsymbol{R}(\boldsymbol{U}_{r-1}^{k})\\ \boldsymbol{U}_{r}^{k}=\boldsymbol{U}_{r-1}^{k}+{\Delta}\boldsymbol{U}_{r}^{k} \end{array} $$

(15)

in which $\phantom {\dot {i}\!}\boldsymbol {K}_{T}{\triangleq }\frac {\partial \boldsymbol {R}}{\partial \boldsymbol {U}}|_{\boldsymbol {U}=\boldsymbol {U}_{r-1}^{k}}$ is the tangent stiffness matrix obtained as

$$ \boldsymbol{K}_{T}=\overset{n_{ele}}{\underset{e = 1}{\mathscr{A}}}\boldsymbol{K}_{T}^{e}\ $$

(16)

with

$$ \boldsymbol{K}_{T}^{e}\,=\,{\int}_{{\Omega}^{e}}\left[\begin{array}{llc} \!\displaystyle\boldsymbol{B}_{u}^{T}\left[\frac{\partial\boldsymbol{\sigma}}{\partial\boldsymbol{\varepsilon}}\right]\boldsymbol{B}_{u} && \boldsymbol{B}_{u}^{T}\left[\frac{\partial\boldsymbol{\sigma}}{\partial\overline{\alpha}}\right]\boldsymbol{N}_{\overline{\alpha}}\\ \!-\boldsymbol{N}_{\overline{\alpha}}^{T}\left[\frac{\partial\alpha}{\partial\boldsymbol{\varepsilon}}\right]\boldsymbol{B}_{u} && \boldsymbol{N}_{\overline{\alpha}}^{T}\boldsymbol{N}_{\overline{\alpha}}+\ell^{2}\boldsymbol{B}_{\overline{\alpha}}^{T}\boldsymbol{B}_{\overline{\alpha}}\,-\,\boldsymbol{N}_{\overline{\alpha}}^{T}\frac{\partial\alpha}{\partial\overline{\alpha}}\boldsymbol{N}_{\overline{\alpha}} \end{array}\right]dv $$

(17)

where the terms $\phantom {\dot {i}\!}\frac {\partial \boldsymbol {\sigma }}{\partial \boldsymbol {\varepsilon }}$, $\phantom {\dot {i}\!}\frac {\partial \boldsymbol {\sigma }}{\partial \overline {\alpha }}$, $\phantom {\dot {i}\!}\frac {\partial \alpha }{\partial \boldsymbol {\varepsilon }}$ and $\phantom {\dot {i}\!}\frac {\partial \alpha }{\partial \overline {\alpha }}$ are given in the calculation of $\phantom {\dot {i}\!}\boldsymbol {C}_{T}$ which is the algorithmic consistent tangent modulus provided in Appendix A. The symbol [■] denotes an appropriate matrix-vector form of the tensor ■. The NR iteration is terminated once the global energy residual $\phantom {\dot {i}\!}\text {abs}(\boldsymbol {R}(\boldsymbol {U}_{r}^{k})^{T}$ $\phantom {\dot {i}\!}{\Delta }\boldsymbol {U}_{r}^{k})$ $\phantom {\dot {i}\!}\leq 10^{-12}$ is reached. This tolerance is quadratically achieved using the consistent tangent operator used in this study. Typically, 3 to 6 NR iterations are needed for finding the solution at each displacement step.

Fig. 4

Portal frame configuration and finite element discretization (unit: mm)

3.3 Mesh convergence study

A two-dimensional portal frame with unit thickness as shown in Fig. 4a is considered for mesh convergence study to illustrate the mesh-independent behavior. The frame has a sharp corner where a damage zone can develop. A displacement of $\phantom {\dot {i}\!}u = 1$ mm is prescribed over 5 mm at the center of the top surface. The material model has a Young’s modulus $\phantom {\dot {i}\!}E = 20$ GPa, Poisson’s ratio $\phantom {\dot {i}\!}\nu = 0.3$, initial yield stress $\phantom {\dot {i}\!}\sigma _{y} = 20$ MPa, hardening modulus $\phantom {\dot {i}\!}K^{h} = 2$ GPa, damage parameters $\phantom {\dot {i}\!}\beta = 75$, $\phantom {\dot {i}\!}{\kappa }_{th}$= 0, $\phantom {\dot {i}\!}{\Delta }{\kappa } = 0$ and length scale parameter $\phantom {\dot {i}\!}\ell = 1.5$ mm. Note that a relatively large $\phantom {\dot {i}\!}\beta$ value has been used in order to show the material softening behavior even with a small applied displacement (u = 1 mm). More realistic damage parameter values have to be calibrated to fit the actual material behavior, which is out of the scope of this study. Due to the irregular geometry of the model, the domain is discretized into $\phantom {\dot {i}\!}nely\times nelx$ mesh with non-uniformly sized elements as illustrated in Fig. 4b. Mesh convergence studies are performed using different meshes $\phantom {\dot {i}\!} 24\times 48$, $\phantom {\dot {i}\!}48\times 96$ and $\phantom {\dot {i}\!}96\times 192$.

The load-displacement curves from different meshes are plotted in Fig. 5, in which typical elastoplastic hardening and softening phenomena can be observed. Figure 5 also shows satisfactory convergence is achieved with the mesh $\phantom {\dot {i}\!}96\times 192$. All the meshes exhibit very similar responses, implying the mesh independency achieved by the nonlocal damage formulation. This nonlocal effect can be also observed in Fig. 6, where the contours of local equivalent plastic strain $\phantom {\dot {i}\!}\alpha$ and nonlocal damage d in $\phantom {\dot {i}\!}48\times 96$ and $\phantom {\dot {i}\!}96\times 192$ meshes are plotted. A strong mesh dependency of local equivalent plastic strain $\phantom {\dot {i}\!}\alpha$ can be observed in the left column of Fig. 6. The maximum value and distribution of $\phantom {\dot {i}\!}\alpha$ are both changing with the mesh refinement. On the contrary, the contours and peak values of nonlocal damage d are almost identical in these two meshes, as shown in the right column of Fig. 6. This mesh independent property eventually results in similar force-displacement curves for different meshes as shown in Fig. 5.

Fig. 5

Mesh convergence study for the portal frame using Q8/4 elements with reduced integration

Fig. 6

Contours of local equivalent plastic strain α (left column) and nonlocal damage d (right column) in 48 × 96 and 96 × 192 FE mesh

4 Damage constrained topology optimization

This section presents the damage constrained topology optimization formulation with elastoplasticity and material nonlocal damage behaviors. In particular, density-based method (Bendsøe 1989) is used in this study as it provides an efficient and accurate connection between nonlinear FEA and optimization process via explicit design parametrization.

4.1 Material interpolation

In density-based topology optimization method, the design domain $\phantom {\dot {i}\!}{\Omega }$ is discretized by means of $\phantom {\dot {i}\!}n_{ele}$ finite elements and the structure is parametrized by assigning a density variable $\phantom {\dot {i}\!}\rho _{e}$ to each element (Bendsøe and Sigmund 2003). Here, $\phantom {\dot {i}\!}\rho _{e}= 0$ means void element and $\phantom {\dot {i}\!}\rho _{e}= 1$ indicates solid element. The goal is to find the optimal solution for $\phantom {\dot {i}\!}\rho _{e}$ that amplifies desired structural performance while satisfying certain constraints. However, seeking the discrete values of $\phantom {\dot {i}\!}\rho _{e}\in \{0,1\}$ leads to an integer programming problem which is challenging to solve. Thus, the density variable is usually allowed to vary continuously between void and solid, i.e., $\phantom {\dot {i}\!}0\leq \rho _{e}\leq 1$, which enables the update by efficient gradient-based algorithms (Christensen and Klarbring 2008). In this problem setting with relaxed design space, the intermediate density elements (0 < ρ_e < 1) usually lack physical interpretation and should be avoided in the final designs. In the well-known SIMP method for elastic materials (Bendsøe 1989; Zhou and Rozvany 1991), this is achieved by assigning an inferior mechanical property to the intermediate density elements using a penalized material interpolation scheme. In this way, the intermediate density elements become inefficient so that they can be successively removed during the optimization process.

Unlike the elastic material in which only one material parameter, i.e. Young’s modulus E, is interpolated, the nonlocal coupled elastoplastic damage model considered in this study involves five material parameters, namely, Young’s modulus E, initial yield stress $\phantom {\dot {i}\!}\sigma _{y}$, hardening modulus $\phantom {\dot {i}\!}K^{h}$, damage initiation threshold $\phantom {\dot {i}\!}{\kappa }_{th}$ and damage parameter $\phantom {\dot {i}\!}\beta$, that need to be appropriately interpolated. Each material parameter characterizes specific material behavior as illustrated in the stress-strain relation (black line) in Fig. 7. It can be seen that increase of the values of E, $\phantom {\dot {i}\!}\sigma _{y}$, $\phantom {\dot {i}\!}K^{h}$ and $\phantom {\dot {i}\!}{\kappa }_{th}$ has positive effect in increasing the plastic work dissipation (approximately the area enveloped by the stress-strain curve), while increase of $\phantom {\dot {i}\!}\beta$ value has a negative effect in increasing the plastic work dissipation. Therefore, to properly mimic the behavior of element with various densities, a SIMP-like material interpolation scheme is utilized to interpolate the four material parameters $\phantom {\dot {i}\!}E_{e}$, $\phantom {\dot {i}\!}\sigma _{y_{e}}$, $\phantom {\dot {i}\!}{K_{e}^{h}}$ and $\phantom {\dot {i}\!}{\kappa }_{{th}_{e}}$ for an element e with density $\phantom {\dot {i}\!}\rho _{e}$ as follows

$$ E_{e}=E_{min}+(E-E_{min}){\rho_{e}^{p_{1}}} $$

(18)

$$ {\sigma_{y}}_{e}={\sigma_{y}}_{min}+({\sigma_{y}}-{\sigma_{y}}_{min}){\rho_{e}^{p_{2}}} $$

(19)

$$ {K^{h}_{e}}=K^{h}_{min}+\left(K^{h}-K^{h}_{min}\right){\rho_{e}^{p_{3}}} $$

(20)

$$ {\kappa}_{{th}_{e}}={\kappa}_{{th}_{min}}+\left({\kappa}_{{th}}-{\kappa}_{{th}_{min}}\right){\rho_{e}^{p_{4}}} $$

(21)

where E, $\phantom {\dot {i}\!}\sigma _{y}$, $\phantom {\dot {i}\!}K^{h}$ and $\phantom {\dot {i}\!}{\kappa }_{th}$ are material parameters for solid elements while $\phantom {\dot {i}\!}E_{min}$, $\phantom {\dot {i}\!}\sigma _{y_{min}}$, $\phantom {\dot {i}\!}K_{min}^{h}$ and $\phantom {\dot {i}\!}{\kappa }_{{th}_{min}}$ are the ones for void elements; $\phantom {\dot {i}\!}p_{1}$ to $\phantom {\dot {i}\!}p_{4}$ are the penalization coefficients for each material parameters. Similar interpolations for these material parameters were also used in the studies by Maute et al. (1998), Bogomolny and Amir (2012) and Kato et al. (2015). Similar to the power-law interpolation for softening parameters used in (Kato et al. 2008), the damage parameter $\phantom {\dot {i}\!}\beta _{e}$ for element e is interpolated in an opposite way as follows

$$ \beta_{e}=\beta_{v}-(\beta_{v}-\beta){\rho_{e}^{p_{5}}} $$

(22)

in which $\phantom {\dot {i}\!}\beta$ and $\phantom {\dot {i}\!}\beta _{v}$ are the damage parameters for solid element and void element, respectively and $\phantom {\dot {i}\!}p_{5}$ is the corresponding penalization parameter. By adopting the above-mentioned material interpolation scheme, the stress-strain relation for an intermediate density element (i.e. $\phantom {\dot {i}\!}\rho _{e}<1$) is illustrated in blue line in Fig. 7. Using this scheme, it can be observed that the intermediate density element is inefficient in dissipating plastic work and easier to be damaged than the solid element (ρ_e = 1), which is physically plausible.

Fig. 7

Stress-strain relations of nonlocal damage model for solid element (in black) and intermediate density element (in blue)

Special attention should be drawn to the fact that even if the proposed material interpolation scheme is able to scale down the plastic work dissipated by the intermediate density elements in a physically consistent manner, the equivalent plastic strain $\phantom {\dot {i}\!}\alpha$ is not necessarily low in these elements since their yield stress is also scaled down by the densities. The high value of $\phantom {\dot {i}\!}\alpha$ may cause convergence difficulties for NR method in the nonlinear FEA, which eventually interrupts the optimization process. In many previous studies (Maute et al. 1998; Wallin et al. 2016; Amir 2017), this issue was addressed by setting a smaller $\phantom {\dot {i}\!}p_{2}$ and $\phantom {\dot {i}\!}p_{3}$ values than $\phantom {\dot {i}\!}p_{1}$ value, which postpones the intermediate density elements from reaching their yield limits. In our previous studies (Li et al. 2017b; Li and Khandelwal 2017), the same $\phantom {\dot {i}\!}p_{1}$, $\phantom {\dot {i}\!}p_{2}$ and $\phantom {\dot {i}\!}p_{3}$ values were utilized without encountering any problem by using an adaptive step size strategy in the global NR solver (de Borst et al. 2012). However, as the nonlocal damage is influenced by local $\phantom {\dot {i}\!}\alpha$, and $\phantom {\dot {i}\!}\beta$ and $\phantom {\dot {i}\!}{\kappa }_{th}$ values, in this study, the penalization parameter setting of $\phantom {\dot {i}\!}p_{1}= 3$, $\phantom {\dot {i}\!}p_{2}=p_{3}= 2.5$ and $\phantom {\dot {i}\!}p_{4}=p_{5}= 2$ is employed. The smaller $\phantom {\dot {i}\!}p_{4}$ and $\phantom {\dot {i}\!}p_{5}$ values are considered to stabilize the NR process when large intermediate densities exist. Meanwhile, the material parameters for void elements are set as $\phantom {\dot {i}\!}E_{min}= 10^{-8}E$, $\phantom {\dot {i}\!}\sigma _{y_{min}}= 10^{-4}\sigma _{y}$ and $\phantom {\dot {i}\!}K_{min}^{h}= 10^{-4}K^{h}$ to increase the yield stress and stiffness for void elements. The value for $\phantom {\dot {i}\!}{\kappa }_{{th}_{min}}= 0.001$ and $\phantom {\dot {i}\!}\beta _{v}= 50$ are used in the topology optimization studies.

A simple example is considered to show the stress-strain behavior based on the aforementioned material interpolation scheme. To this end, a uniaxial tensile test is carried out on a Q8/4 element with the boundary conditions illustrated in Fig. 8a. The reference material has Young’s modulus $\phantom {\dot {i}\!}E = 20$ GPa, Poisson’s ratio $\phantom {\dot {i}\!}\nu = 0.3$, initial yield stress $\phantom {\dot {i}\!}\sigma _{y} = 20$ MPa, hardening modulus $\phantom {\dot {i}\!}K^{h} = 2$ GPa, damage parameters $\phantom {\dot {i}\!}\beta = 15$, $\phantom {\dot {i}\!}{\kappa }_{th} = 0.01$ and $\phantom {\dot {i}\!}{\Delta }{\kappa } = 0.002$, which are the same as the ones used in Section 6. Figure 8b reports the stress-strain (σ₁₁ vs. ε₁₁) curves for various element densities up to the applied displacement $\phantom {\dot {i}\!}u = 0.12$ mm. It can be observed that the plastic work dissipation capacity decreases with the decrease in density, i.e. intermediate densities are less effective. Furthermore, at very small densities stress-strain behavior is linear as a higher lower bound for yield stress ($\phantom {\dot {i}\!}\sigma _{y_{min}}= 10^{-4}\sigma _{y}$) is used. This helps to avoid excessive plastic deformation in low-density elements, and thus stabilizes the NR solution process.

Fig. 8

Uniaxial test of a single Q8/4 element with various densities: a problem configuration; and b strain-stress curves

4.2 Scaling of nonlocal parameters

In the density-based material interpolation scheme, the void or low-density elements are considered in both the FEA analyses and optimization process. However, as discussed above, these elements are modeled with very low stiffness and strength so that they have insignificant effect on FEA response. This approach is also termed as fictitious domain approach. As the finite element mesh is fixed throughout the topology optimization process, this approach saves significant computational effort as the remeshing is avoided. It is worth pointing out that although the adopted material interpolation scheme is able to characterize the mechanical behavior for single element, the nonlocal PDE in (1)₂ still accounts for the plastic strains contributed by the void/low-density elements. However, these “artificial” elements are padded with weak material and are excluded in the final designs. Therefore, these low-density elements should not affect the nonlocal plastic-strain and damage distribution in the solid elements. To this end, for an accurate implementation based on the fictitious domain approach while getting accurate structural softening response, the nonlocal effect of the void/low-density elements is suppressed by scaling the length scale parameter $\phantom {\dot {i}\!}\ell _{e}$ of element e as

$$ \ell_{e}={\rho_{e}^{p_{6}}}\ell $$

(23)

where $\phantom {\dot {i}\!}\ell$ is the length scale parameter for solid element, $\phantom {\dot {i}\!}\rho _{e}$ is the element density and $\phantom {\dot {i}\!}p_{6}$ is the scaling exponent. Through (23), nonlocal plastic strains in the void/low-density elements will not be influenced by the neighboring solid elements. This idea was also used in our previous study (Li et al. 2017c) in which the length scale parameter for gradient elastic material was scaled in a similar way. In addition, the local equivalent plastic strain $\phantom {\dot {i}\!}\alpha$ of the void/low-density elements in the nonlocal equation is also suppressed and (1)₂ is modified as

$$ \overline{\alpha}-{\ell_{e}^{2}}\nabla^{2}\overline{\alpha}=p_{e}^{p_{7}}\alpha $$

(24)

where $\phantom {\dot {i}\!}p_{7}$ is the corresponding scaling exponent. By scaling $\phantom {\dot {i}\!}\alpha$ on the right hand side of (24), the nonlocal equivalent plastic strain $\phantom {\dot {i}\!}\overline {\alpha }$ as well as the nonlocal damage in solid element will not account for the artificial $\phantom {\dot {i}\!}\alpha$ in the surrounding void/low-density elements. For all the considered examples, the exponent values of $\phantom {\dot {i}\!}p_{6}=p_{7}= 3$ are used.

To show the necessity of scaling the nonlocal parameters, a C-shaped cantilever is investigated as illustrated in Fig. 9a. The cantilever has a hollow region Ω_low in the middle and is fixed at the left edge. An upward displacement of $\phantom {\dot {i}\!}u = 5$ mm is applied over 5 mm at the right bottom as shown. The material parameters considered here are $\phantom {\dot {i}\!}E = 20$ GPa, $\phantom {\dot {i}\!}\nu = 0.3$, $\phantom {\dot {i}\!}K^{h} = 2$ GPa, $\phantom {\dot {i}\!}\beta = 75$, $\phantom {\dot {i}\!}\beta _{v} = 100$, $\phantom {\dot {i}\!}{\kappa }_{th} = 0.005$, $\phantom {\dot {i}\!}{\Delta }{\kappa } = 0.002$ and $\phantom {\dot {i}\!}\ell = 7.5$ mm. The simulations are performed using a conforming mesh with 3750 square elements, wherein the $\phantom {\dot {i}\!}{\Omega }_{\text {low}}$ is excluded from the analyses and only the solid region is meshed, as well as using a density-based fictitious domain approach using a fixed $\phantom {\dot {i}\!}100\times 50$ mesh with 5000 elements. For the latter case, a small density $\phantom {\dot {i}\!}\rho _{e}= 10^{-6}$ is prescribed to the elements in the region of $\phantom {\dot {i}\!}{\Omega }_{\text {low}}$, while the solid elements have density $\phantom {\dot {i}\!}\rho _{e} = 1$. The damage map in the C-shaped cantilever with conforming mesh is shown in Fig. 9b. It is observed that the damage is located across the left side of horizontal arm and the maximum damage is $\phantom {\dot {i}\!}d_{max} = 0.672$. When fictitious domain approach is used without scaling the nonlocal parameters, the damage contours shown in Fig. 9c are significantly different from the true one in Fig. 9b. This is primarily due to the fact that the fictitious elements in $\phantom {\dot {i}\!}{\Omega }_{\text {low}}$ help to nonlocalize the damage from their neighboring solid elements. As a result, the damage inside the solid elements is decreased, i.e. $\phantom {\dot {i}\!}d_{max}= 0.663$, while the damage inside the void element increases, as shown in Fig. 9c. Using the proposed scaling scheme given in (23) and (24), the damage contours shown in Fig. 9d can accurately capture the damage occurrence locations as well as the peak damage value with $\phantom {\dot {i}\!}d_{max}= 0.672$.

Fig. 9

C-shaped cantilever with low density elements inside: a design domain (unit: mm); b damage contour with conforming mesh; c damage contour without the nonlocal parameters scaling; and d damage contour with the nonlocal parameters scaling

The load-displacement curve for the C-shaped cantilever using conforming mesh, fictitious domain approach with and without the proposed scaling scheme are also plotted in Fig. 10. One can see that although the curves are nearly identical in the elastic and early plastic hardening stages, fictitious domain approach without using the scaling scheme (blue-dot line) deviates from the correct response (red line) once the softening starts at about 2.6 mm. This discrepancy gradually grows and eventually leads to a significant difference at the design displacement of 5 mm. With the proposed scaling scheme, the FEA is capable of generating the result (black-hollow line) that is close to the one from conforming mesh, and the discrepancy is negligible as shown in Fig. 10.

Fig. 10

Load-displacement relations of the C-shaped cantilever using different schemes

4.3 Density filter

Density filter (Bruns and Tortorelli 2001; Bourdin 2001) is further utilized in this work to avoid the checkerboard issue and to ensure the mesh independency for the optimized design. It can be expressed in a matrix form as

$$ \boldsymbol{\rho}=\boldsymbol{Wx} $$

(25)

where $\phantom {\dot {i}\!}\boldsymbol {\rho }$ and $\phantom {\dot {i}\!}\boldsymbol {x}$ are the vectors collecting all the density and design variables, respectively; $\phantom {\dot {i}\!}\boldsymbol {W}$ is the filtering matrix with the following components

$$ W_{ej}=\frac{w_{ej}V_{j}}{{\sum}_{j = 1}^{n_{ele}}w_{ej}V_{j}} $$

(26)

where $\phantom {\dot {i}\!}V_{j}$ is the volume of element j and $\phantom {\dot {i}\!}w_{ej}$ is the distance weighting coefficient defined as

$$ w_{ej}=\max \left\{r_{min}-\|\boldsymbol{X}_{e}-\boldsymbol{X}_{j}\|_{2},0\right\} $$

(27)

in which $\phantom {\dot {i}\!}\boldsymbol {X}_{e}$ denotes the centroid coordinate of element e and $\phantom {\dot {i}\!}r_{min}$ is the prescribed density filter radius. The matrix $\phantom {\dot {i}\!}\boldsymbol {W}$ only needs to be calculated once prior to the optimization process, and the stored information can be reused within each optimization iteration.

4.4 Problem formulation

The objective of topology optimization is to minimize the material volume fraction while satisfying the constraints of target minimum plastic work dissipation together with material damage constraints. The aim is to find the design with high plastic work dissipation capacity per unit material volume while limiting amount of the damage to achieve robust designs. To this end, the optimization problem is formulated as

$$ \begin{array}{rl} \underset{\boldsymbol{0}\leq\boldsymbol{x}\leq\boldsymbol{1}}{\min }&\quad \displaystyle f_{0}(\boldsymbol{x})=\frac{1}{V_{0}}\left({\sum}_{e = 1}^{n_{ele}}V_{e}\rho_{e}(\boldsymbol{x})\right)\\ \mathrm{s.t.}&\quad \displaystyle f_{1}(\boldsymbol{x})= 1-\frac{W^{p}(\boldsymbol{x})}{\overline{W}^{p}}\leq0\\ &\quad f_{2}(\boldsymbol{x})=D_{max}(\boldsymbol{x})-\overline{D}\leq0\\ \text{with}&\quad \boldsymbol{R}^{k}(\boldsymbol{U}^{k},\boldsymbol{U}^{k-1},\boldsymbol{v}^{k},\boldsymbol{v}^{k-1},\boldsymbol{\rho}(\boldsymbol{x}))=\boldsymbol{0}\\ &\quad \boldsymbol{H}^{k}(\boldsymbol{U}^{k},\boldsymbol{U}^{k-1},\boldsymbol{v}^{k},\boldsymbol{v}^{k-1},\boldsymbol{\rho}(\boldsymbol{x}))=\boldsymbol{0}\\ &\quad k = 1,2,...,n \end{array} $$

(28)

In (28), $\phantom {\dot {i}\!}\boldsymbol {x}\in \mathbb {R}^{n_{ele}}$ is the vector of design variables that is updated by the optimizer. The volume fraction objective function $\phantom {\dot {i}\!}f_{0}(\boldsymbol {x})$ is the summation of multiplication of element volume $\phantom {\dot {i}\!}V_{e}$ and density $\phantom {\dot {i}\!}\rho _{e}$ over $\phantom {\dot {i}\!}n_{ele}$ elements, divided by the total volume of the design domain $\phantom {\dot {i}\!}V_{0}$. $\phantom {\dot {i}\!}f_{1}(\boldsymbol {x})$ is the plastic work constraint, requiring that the plastic work $\phantom {\dot {i}\!}W^{p}(\boldsymbol {x})$ should be larger than a prescribed value $\phantom {\dot {i}\!}\overline {W}^{p}$. The plastic work, $\phantom {\dot {i}\!}W^{p}$, is expressed in discrete form using trapezoidal rule as

$$ W^{p}(\boldsymbol{x})\,=\,\sum\limits_{k = 1}^{n}\left(\sum\limits_{e = 1}^{n_{ele}}\left(\sum\limits_{r = 1}^{n_{ipt}}\frac{1}{2}(\boldsymbol{\sigma}_{e_{r}}^{k}\,+\,\boldsymbol{\sigma}_{e_{r}}^{k-1}):(\boldsymbol{\varepsilon}_{e_{r}}^{p^{k}}\,-\,\boldsymbol{\varepsilon}_{e_{r}}^{p^{k-1}})w_{r}\right)\right) $$

(29)

where $\phantom {\dot {i}\!}n_{ipt}= 4$ is the number of integration point within one finite element.

The damage constraint is enforced using the constraint function $\phantom {\dot {i}\!}f_{2} (\boldsymbol {x})$. According to the material interpolation scheme shown in Section 4.1, the damage values in low-density elements can be high, which would keep the topology from a clear 0/1 design. To allow the optimizer to freely remove material from low-density regions while still being able to satisfy the damage constraints, a relaxed measure of damage is introduced as follows

$$ D_{e_{r}}={\rho_{e}^{q}}d_{e_{r}}^{n} $$

(30)

where $\phantom {\dot {i}\!}d_{e_{r}}^{n}$ is the final step (k = n) nonlocal damage at the $\phantom {\dot {i}\!}r^{th}$ integration point in element e, $\phantom {\dot {i}\!}\rho _{e}$ is the element density, and q is the relaxation parameter. A value of $\phantom {\dot {i}\!}q = 3$ is used in this study and a similar relaxation scheme has also been considered in James and Waisman (2014). By using the relaxed nonlocal damage $\phantom {\dot {i}\!}D_{e_{r}}$ at each integration point, the global maximum damage measure $\phantom {\dot {i}\!}D_{max}$ is constructed using p-norm function to approximate the actual maximum damage $\phantom {\dot {i}\!}d_{max}$ as follows

$$ D_{max}=\left(\sum\limits_{e = 1}^{n_{ele}}\left[\sum\limits_{r = 1}^{n_{ipt}}(D_{e_{r}})^{p_{a}}\right]\right)^{\frac{1}{p_{a}}}\approx\max \{D_{e_{r}}\}=d_{max} $$

(31)

where $\phantom {\dot {i}\!}p_{a}$ is the aggregation parameter. It is worth noting that the p-norm function shown in (31) approaches the true maximum value $\phantom {\dot {i}\!}d_{max}$ from above as $\phantom {\dot {i}\!}p_{a}$ increases. This means that the true maximum damage inside the design domain (d_max) is always lower than the aggregated value (D_max), and therefore, by constraining $\phantom {\dot {i}\!}D_{max}$ under a prescribed limit $\phantom {\dot {i}\!}\overline {D}$ ((28)₃) always leads to a conservative design. To better control the local damage, a regional aggregation method can be used (París et al. 2009; Le et al. 2010; Holmberg et al. 2013). However, in this study a high value of $\phantom {\dot {i}\!}p_{a}$ is used to provide a good approximation of the maximum damage. On the other hand, a very large value of $\phantom {\dot {i}\!}p_{a}$ makes the global constraint function highly non-convex. To have a balance between these two contradictory features, $\phantom {\dot {i}\!}p_{a} = 20$ is used throughout this study.

Finally, $\phantom {\dot {i}\!}\boldsymbol {R}^{k}=\boldsymbol {0}$ is the global equilibrium equation that should be satisfied at each load step k, while $\phantom {\dot {i}\!}\boldsymbol {H}^{k}=\boldsymbol {0}$ represents the extra constraints from constitutive equations at step k. Also, n is the total number of analyses steps used in the FEA, $\phantom {\dot {i}\!}\boldsymbol {U}^{k}$ is the global solution vector at step k while $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ are the auxiliary variables used to describe the constraints $\phantom {\dot {i}\!}\boldsymbol {H}^{k}$ at step k. The definitions of $\phantom {\dot {i}\!}\boldsymbol {H}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ will be further elaborated in Section 5. Using the nested solution approach (Christensen and Klarbring 2008), only the plastic work constraint $\phantom {\dot {i}\!}f_{1}(\boldsymbol {x})\leq 0$, damage constraint $\phantom {\dot {i}\!}f_{2}(\boldsymbol {x})\leq 0$ and the box constraints $\phantom {\dot {i}\!}\boldsymbol {0}\leq \boldsymbol {x}\leq \boldsymbol {1}$ are enforced by the gradient-based optimizer, while the constraints $\phantom {\dot {i}\!}\boldsymbol {R}^{k}=\boldsymbol {0}$ and $\phantom {\dot {i}\!}\boldsymbol {H}^{k}=\boldsymbol {0}$ are directly enforced during the finite element solution process. It is also noted that a purely plastic topology optimization formulation can be conveniently recovered from (28) by using a large damage initiation threshold $\phantom {\dot {i}\!}{\kappa }_{th}$, zero penalty factor for the damage threshold $\phantom {\dot {i}\!}p_{4}$, and by ignoring the information of constraint $\phantom {\dot {i}\!}f_{2}$ in the optimization process. To recover the purely plastic design, $\phantom {\dot {i}\!}{\kappa }_{th}= 1000$ and $\phantom {\dot {i}\!}p_{4}= 0$ are used in this study. The topology designs from this purely plastic topology optimization formulation are used as reference designs for comparison purposes in Section 6.

5 Path-dependent sensitivity analysis

Since the nonlocal coupled elastoplastic damage model is path-dependent, the design sensitivities for updating the optimization problem (28) should account for the history information of each converged incremental step. The adjoint method is preferred than the direct differentiation method for sensitivity analysis (Strang 2007) in topology optimization problems, as the number of design variables far exceeds the number of objective and constraint functions. In this section, the detailed derivation of path-dependent sensitivities is provided, which is based on the adjoint method framework for transient nonlinear coupled systems (Michaleris et al. 1994).

Consider a generalized target function F in terms of solution variable $\phantom {\dot {i}\!}\boldsymbol {U}^{k}$, auxiliary variables $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ and density variable $\phantom {\dot {i}\!}\boldsymbol {\rho }$. An augmented function $\phantom {\dot {i}\!}\widehat {F}$ is first constructed as

$$ \begin{array}{ll} \widehat{F}=&F(\boldsymbol{U}^{n},...,\boldsymbol{U}^{1},\boldsymbol{v}^{n},...,\boldsymbol{v}^{1},\boldsymbol{\rho})\\ &\displaystyle+{\sum}_{k = 1}^{n}\boldsymbol{\lambda}^{k^{T}}\boldsymbol{R}^{k}(\boldsymbol{U}^{k},\boldsymbol{U}^{k-1},\boldsymbol{v}^{k},\boldsymbol{v}^{k-1},\boldsymbol{\rho})\\ &\displaystyle+{\sum}_{k = 1}^{n}\boldsymbol{\mu}^{k^{T}}\boldsymbol{H}^{k}(\boldsymbol{U}^{k},\boldsymbol{U}^{k-1},\boldsymbol{v}^{k},\boldsymbol{v}^{k-1},\boldsymbol{\rho}) \end{array} $$

(32)

where $\phantom {\dot {i}\!}\boldsymbol {\lambda }^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {\mu }^{k}$ are the adjoint variables associated with the residual constraints $\phantom {\dot {i}\!}\boldsymbol {R}^{k}=\boldsymbol {0}$ and $\phantom {\dot {i}\!}\boldsymbol {H}^{k}=\boldsymbol {0}$, respectively. Since $\phantom {\dot {i}\!}\boldsymbol {R}^{k}=\boldsymbol {0}$ and $\phantom {\dot {i}\!}\boldsymbol {H}^{k}=\boldsymbol {0}$ are satisfied for each step k, $\phantom {\dot {i}\!}F=\widehat {F}$ and $\phantom {\dot {i}\!}dF/d\boldsymbol {\rho }=d\widehat {F}/d\boldsymbol {\rho }$. Taking derivative of $\phantom {\dot {i}\!}\widehat {F}$ with respect to $\phantom {\dot {i}\!}\boldsymbol {\rho }$ and eliminating all the coefficients that contain the implicit derivative terms $\phantom {\dot {i}\!}d\boldsymbol {U}^{k}/d{\boldsymbol {\rho }}$ and $\phantom {\dot {i}\!}d\boldsymbol {v}^{k}/d\boldsymbol {\rho }$ yield

$$ \frac{dF}{d\boldsymbol{\rho}}=\frac{d\widehat{F}}{d\boldsymbol{\rho}}=\frac{\partial{F}}{\partial\boldsymbol{\rho}}+{\sum}_{k = 1}^{n}\left(\boldsymbol{\lambda}^{k^{T}}\frac{\partial{\boldsymbol{R}^{k}}}{\partial{\boldsymbol{\rho}}}+\boldsymbol{\mu}^{k^{T}}\frac{\partial{\boldsymbol{H}^{k}}}{\partial{\boldsymbol{\rho}}}\right)\ $$

(33)

where the adjoint variables $\phantom {\dot {i}\!}\boldsymbol {\lambda }^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {\mu }^{k}$ are calculated in a backward manner from the last step $\phantom {\dot {i}\!}k=n$ to the first step $\phantom {\dot {i}\!}k = 1$ using the following adjoint systems

$$ \begin{array}{l} \text{step}\;n:\left\{\begin{array}{l} \frac{\partial{F}}{\partial{\boldsymbol{U}}^{n}}+{\boldsymbol{\lambda}^{n^{T}}}\frac{\partial{\boldsymbol{R}}^{n}}{\partial{\boldsymbol{U}}^{n}}+\boldsymbol{\mu}^{n^{T}}\frac{\partial{\boldsymbol{H}^{n}}}{\partial{\boldsymbol{U}}^{n}}=\boldsymbol{0} \\ \frac{\partial{F}}{\partial{\boldsymbol{v}}^{n}}+{\boldsymbol{\lambda}^{n^{T}}}\frac{\partial{\boldsymbol{R}}^{n}}{\partial{\boldsymbol{v}}^{n}}+\boldsymbol{\mu}^{n^{T}}\frac{\partial{\boldsymbol{H}^{n}}}{\partial{\boldsymbol{v}}^{n}}=\boldsymbol{0}\end{array}\right. \\ \text{step}\;k:\left\{\begin{array}{r} \frac{\partial{F}}{\partial{\boldsymbol{U}}^{k}}+{\boldsymbol{\lambda}^{{k + 1}^{T}}}\frac{\partial{\boldsymbol{R}}^{k + 1}}{\partial{\boldsymbol{U}}^{k}}+\boldsymbol{\mu}^{{k + 1}^{T}}\frac{\partial{\boldsymbol{H}^{k + 1}}}{\partial{\boldsymbol{U}}^{k}}\\ {\qquad\qquad}+{\boldsymbol{\lambda}^{{k}^{T}}}\frac{\partial{\boldsymbol{R}}^{k}}{\partial{\boldsymbol{U}}^{k}}+\boldsymbol{\mu}^{{k}^{T}}\frac{\partial{\boldsymbol{H}^{k}}}{\partial{\boldsymbol{U}}^{k}}=\boldsymbol{0} \\ \frac{\partial{F}}{\partial{\boldsymbol{v}}^{k}}+{\boldsymbol{\lambda}^{{k + 1}^{T}}}\frac{\partial{\boldsymbol{R}}^{k + 1}}{\partial{\boldsymbol{v}}^{k}}+\boldsymbol{\mu}^{{k + 1}^{T}}\frac{\partial{\boldsymbol{H}^{k + 1}}}{\partial{\boldsymbol{v}}^{k}}\\ {\qquad\qquad}+{\boldsymbol{\lambda}^{{k}^{T}}}\frac{\partial{\boldsymbol{R}}^{k}}{\partial{\boldsymbol{v}}^{k}}+\boldsymbol{\mu}^{{k}^{T}}\frac{\partial{\boldsymbol{H}^{k}}}{\partial{\boldsymbol{v}}^{k}}=\boldsymbol{0}\end{array}\right.\\ k = n-1,...,2,1 \end{array} $$

(34)

Considering the additional density filter $\phantom {\dot {i}\!}\boldsymbol {\rho }=\boldsymbol {Wx}$ given in (25), the design sensitivities is calculated using the chain rule as

$$ \frac{dF}{d\boldsymbol{x}}=\frac{d{F}}{d\boldsymbol{\rho}}\frac{d\boldsymbol{\rho}}{d\boldsymbol{x}}=\frac{dF}{d\boldsymbol{\rho}}\boldsymbol{W} $$

(35)

Note that F can be any function of interest such as the functions $\phantom {\dot {i}\!}f_{0}$, $\phantom {\dot {i}\!}f_{1}$ and $\phantom {\dot {i}\!}f_{2}$ in (28). By inspecting (32) to (34), the following explicit derivatives are needed to complete the adjoint sensitivity analysis

$$ \begin{array}{l} \text{For}\; F: \frac{\partial{F}}{\partial{\boldsymbol{\rho}}}, \frac{\partial{F}}{\partial{\boldsymbol{U}}^{k}}, \frac{\partial{F}}{\partial{\boldsymbol{v}}^{k}}\\ \text{For}\; \boldsymbol{R}^{k}: \frac{\partial\boldsymbol{R}^{k}}{\partial{\boldsymbol{\rho}}}, \frac{\partial\boldsymbol{R}^{k}}{\partial{\boldsymbol{U}}^{k}},\frac{\partial\boldsymbol{R}^{k}}{\partial{\boldsymbol{U}}^{k-1}}, \frac{\partial\boldsymbol{R}^{k}}{\partial{\boldsymbol{v}}^{k}},\frac{\partial\boldsymbol{R}^{k}}{\partial{\boldsymbol{v}}^{k-1}}\\ \text{For}\; \boldsymbol{H}^{k}: \frac{\partial\boldsymbol{H}^{k}}{\partial{\boldsymbol{\rho}}}, \frac{\partial\boldsymbol{H}^{k}}{\partial{\boldsymbol{U}}^{k}},\frac{\partial\boldsymbol{H}^{k}}{\partial{\boldsymbol{U}}^{k-1}}, \frac{\partial\boldsymbol{H}^{k}}{\partial{\boldsymbol{v}}^{k}},\frac{\partial\boldsymbol{H}^{k}}{\partial{\boldsymbol{v}}^{k-1}}\ \end{array} $$

(36)

The definitions of F, $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {U}^{k}$ are usually fixed by the optimization problem formulation and underlying nonlinear system. Therefore, the definitions of $\phantom {\dot {i}\!}\boldsymbol {H}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ will determine the final expressions for the required explicit derivatives listed above. As discussed in Section 3.2, the global solution variable $\phantom {\dot {i}\!}\boldsymbol {U}^{k}$ at current step k includes both displacement field $\phantom {\dot {i}\!}\boldsymbol {u}^{k}$ and the nonlocal equivalent plastic strain field $\phantom {\dot {i}\!}\overline {\boldsymbol {\alpha }}^{k}$, which is arranged as

$$ \boldsymbol{U}^{k}=\left[\begin{array}{l} \boldsymbol{u}^{k}\\ \overline{\boldsymbol{\alpha}}^{k}\\ \end{array}\right] $$

(37)

Since displacement control strategy is used ($\overline {\boldsymbol {t}}=\boldsymbol {0}$) and body forces are ignored (b = 0), with the scaling scheme for nonlocal parameters in (23) and (24), the global residual $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$ can be reformulated as

$$ \begin{array}{l} \boldsymbol{R}^{k}\,=\,\overset{n_{ele}}{\underset{e = 1}{\mathscr{A}}}\boldsymbol{R}^{e^{k}}=\boldsymbol{0}\quad\text{with}\\ \boldsymbol{R}^{e^{k}}\,=\,\left[\begin{array}{c} \boldsymbol{R}_{u}^{e^{k}}\\ \boldsymbol{R}_{\overline{\alpha}}^{e^{k}}\\ \end{array}\right]=\\ \left[\begin{array}{c} \sum\limits_{r = 1}^{n_{ipt}}\boldsymbol{B}_{u_{r}}^{T}\boldsymbol{\sigma}_{e_{r}}^{k}w_{r}\\ \sum\limits_{r = 1}^{n_{ipt}}\!\left(\boldsymbol{N}_{\overline{\alpha}_{r}}^{T}\boldsymbol{N}_{\overline{\alpha}_{r}}\overline{\boldsymbol{\alpha}}_{e}^{k}\,+\,(\rho_{e}^{p_{6}}\ell)^{2}\boldsymbol{B}_{\overline{\alpha}_{r}}^{T}\boldsymbol{B}_{\overline{\alpha}_{r}}\overline{\boldsymbol{\alpha}}_{e}^{k}\,-\,\rho_{e}^{p_{7}}\boldsymbol{N}_{\overline{\alpha}_{r}}^{T}{\alpha}_{e}^{k}\right)w_{r}\\ \end{array}\right] \end{array} $$

(38)

Unlike $\phantom {\dot {i}\!}\boldsymbol {U}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$, local residual $\phantom {\dot {i}\!}\boldsymbol {H}^{k}$ and auxiliary variables $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ are defined at each integration point. The auxiliary variable $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ is defined as a collection of Cauchy stress $\phantom {\dot {i}\!}\boldsymbol {\sigma }^{k}$, plastic strain $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }^{p^{k}}$, equivalent plastic strain $\phantom {\dot {i}\!}\alpha ^{k}$, plastic multiplier increment $\phantom {\dot {i}\!}{\Delta }\gamma ^{k}$ and nonlocal damage measure $\phantom {\dot {i}\!}{\kappa }^{k}$, which are arranged in a vector form as

$$ \boldsymbol{v}^{k}\,=\,\left[\begin{array}{c} \boldsymbol{v}_{1}^{k}\\ \vdots\\ \boldsymbol{v}_{n_{ele}}^{k} \end{array}\right] \;\;\text{with}\;\;\; \boldsymbol{v}_{e}^{k}\,=\,\left[\begin{array}{c} \boldsymbol{v}_{e_{1}}^{k}\\ \boldsymbol{v}_{e_{2}}^{k}\\ \boldsymbol{v}_{e_{3}}^{k}\\ \boldsymbol{v}_{e_{4}}^{k} \end{array}\right] \;\;\text{and}\;\;\; \boldsymbol{v}_{e_{r}}^{k}\,=\,\left[\begin{array}{c} \boldsymbol{\sigma}_{e_{r}}^{k}\\ \boldsymbol{\varepsilon}_{e_{r}}^{p^{k}}\\ \alpha_{e_{r}}^{k}\\ {\Delta}{\gamma}_{e_{r}}^{k}\\ {\kappa}_{e_{r}}^{k} \end{array}\right] $$

(39)

The local residual $\phantom {\dot {i}\!}\boldsymbol {H}^{k}=\boldsymbol {0}$ is defined as

$$ \boldsymbol{H}^{k}=\left[\begin{array}{c} \boldsymbol{H}_{1}^{k}\\ \vdots\\ \boldsymbol{H}_{n_{ele}}^{k} \end{array}\right] \text{with}\; \boldsymbol{H}_{e}^{k}=\left[\begin{array}{c} \boldsymbol{H}_{e_{1}}^{k}\\ \boldsymbol{H}_{e_{2}}^{k}\\ \boldsymbol{H}_{e_{3}}^{k}\\ \boldsymbol{H}_{e_{4}}^{k} \end{array}\right] \text{and}\; \boldsymbol{H}_{e_{r}}^{k}=\left[\begin{array}{c} \boldsymbol{h}_{e_{r1}}^{k}\\ \boldsymbol{h}_{e_{r2}}^{k}\\ {h}_{e_{r3}}^{k}\\ {h}_{e_{r4}}^{k}\\ {h}_{e_{r5}}^{k} \end{array}\right] $$

(40)

where $\phantom {\dot {i}\!}\boldsymbol {H}_{e_{r}}^{k}$ is different from elastic step to plastic step. For elastic step, it is

$$ \boldsymbol{H}_{e_{r}}^{k} = \left\{\begin{array}{l} \boldsymbol{h}_{e_{r1}}^{k}={\boldsymbol{\sigma}^{k}_{e_{r}}}-\mathbb{C}^{e}:\left({\boldsymbol{\varepsilon}^{k}_{e_{r}}}-{\boldsymbol{\varepsilon}_{e_{r}}^{p^{k}}}\right)=\boldsymbol{0}\\ \boldsymbol{h}_{e_{r2}}^{k}={\boldsymbol{\varepsilon}_{e_{r}}^{p^{k}}}-{\boldsymbol{\varepsilon}_{e_{r}}^{p^{k-1}}}=\boldsymbol{0}\\ {h}_{e_{r3}}^{k}=\alpha_{e_{r}}^{k}-\alpha_{e_{r}}^{k-1}= 0\\ {h}_{e_{r4}}^{k}={\Delta}{\gamma_{e_{r}}^{k}}= 0\\ {h}_{e_{r5}}^{k}={\kappa}_{e_{r}}^{k}-\max \{{\kappa}_{e_{r}}^{k-1},\;\boldsymbol{N}_{\overline{\alpha}_{r}}\overline{\boldsymbol{\alpha}}^{e}\}= 0 \end{array}\right. $$

(41)

while for plastic step, it is

$$ \boldsymbol{H}_{e_{r}}^{k} \,=\, \left\{\begin{array}{l} \boldsymbol{h}_{e_{r1}}^{k}\,=\,{\boldsymbol{\sigma}^{k}_{e_{r}}}-\mathbb{C}^{e}:\left({\boldsymbol{\varepsilon}^{k}_{e_{r}}}-{\boldsymbol{\varepsilon}_{e_{r}}^{p^{k}}}\right)=\boldsymbol{0}\\ \boldsymbol{h}_{e_{r2}}^{k}\,=\,{\boldsymbol{\varepsilon}_{e_{r}}^{p^{k}}}-{\boldsymbol\varepsilon_{e_{r}}^{p^{k-1}}}-{\Delta}{\gamma}_{e_{r}}^{k}\boldsymbol{n}_{e_{r}}^{k}=\boldsymbol{0}\\ {h}_{e_{r3}}^{k}\,=\,\alpha_{e_{r}}^{k}-\alpha_{e_{r}}^{k-1}-\sqrt{\frac{2}{3}}{\Delta}\gamma_{e_{r}}^{k}= 0\\ {h}_{e_{r4}}^{k}\,=\,\|\boldsymbol{s}_{e_{r}}^{k}\|\,-\,\sqrt{\frac{2}{3}}(1\,-\,d({\kappa}_{e_{r}}^{k}))\left(\sigma_{y_{e_{r}}}\,+\,\zeta(\alpha_{e_{r}}^{k})\right)= 0\\ {h}_{e_{r5}}^{k}\,=\,{\kappa}_{e_{r}}^{k}-\max \{{\kappa}_{e_{r}}^{k-1},\;\boldsymbol{N}_{\overline{\alpha}_{r}}\overline{\boldsymbol{\alpha}}^{e}\}= 0 \end{array}\right. $$

(42)

It can be seen that $\phantom {\dot {i}\!}\boldsymbol {H}_{e_{r}}^{k}$ is constructed by the discrete constitutive relations at an integration point. Specifically, $\phantom {\dot {i}\!}\boldsymbol {h}_{e_{r1}}^{k}$ denotes the stress-strain relation; $\phantom {\dot {i}\!}\boldsymbol {h}_{e_{r2}}^{k}$ and $\phantom {\dot {i}\!}{h}_{e_{r3}}^{k}$ are the updates for plastic strain and equivalent plastic strain, respectively; $\phantom {\dot {i}\!}{h}_{e_{r4}}^{k}$ represents the yield criterion and $\phantom {\dot {i}\!}{h}_{e_{r5}}^{k}$ indicates the update of nonlocal damage measure. The detailed expressions for the explicit derivatives in (36) are given in Appendix B.

6 Numerical examples

Numerical examples are presented in this section to investigate the effectiveness of the proposed elastoplastic nonlocal-damage constrained topology optimization method on different problem configurations. In all the examples, plane strain condition with unit thickness is assumed, and the design domains are discretized by Q8/4 elements with 4 point reduced integration, as discussed in Section 3.2. The reference elastoplastic material for solid elements has Young’s modulus $\phantom {\dot {i}\!}E = 20$ GPa, Poisson’s ratio $\phantom {\dot {i}\!}\nu = 0.3$, initial yield stress $\phantom {\dot {i}\!}\sigma _{y} = 20$ MPa and hardening modulus $\phantom {\dot {i}\!}K^{h} = 2$ GPa. The damage parameters for the candidate material are set as $\phantom {\dot {i}\!}\beta = 15$, $\phantom {\dot {i}\!}{\kappa }_{th} = 0.01$ and $\phantom {\dot {i}\!}{\Delta }{\kappa } = 0.002$ with the nonlocal length scale parameter $\phantom {\dot {i}\!}\ell = 2$ mm, unless otherwise stated. Note that $\phantom {\dot {i}\!}\ell$ is a material property and can be calibrated to experimental results. The selected $\phantom {\dot {i}\!}\ell$ value is used to demonstrate the idea of the proposed method. For further details about the nonlocal parameter calibration, readers are referred to the study by Le Bellégo et al. (2003).

In the nonlinear FEA, an adaptive step size strategy is employed to ensure the convergence of NR method within each incremental step (de Borst et al. 2012). In general, 25 to 30 number of increments are needed to finish the FEA. The optimization problems are updated using the method of moving asymptotes (MMA) (Svanberg 1987; Li and Khandelwal 2014) with default parameter settings. All the optimizations are initiated with homogenous solid designs (i.e. $\phantom {\dot {i}\!}x_{e}= 1$), and terminated after 400 iterations unless otherwise stated. The FEA, adjoint sensitivity analyses and optimizations are performed on a 64-bit dual Intel^® quadcore machine with 3.06 GHz processors and 24GB RAM, utilizing Matlab^® based in-house finite element library CPSSL-FEA developed at the University of Notre Dame.

6.1 Sensitivity verification

A preliminary study is performed to assess the accuracy of the adjoint sensitivity analysis derived in Section 5. For this purpose, left half of the portal frame shown in Fig. 4a is utilized as the verification model, whose boundary conditions are depicted in Fig. 11a. The design domain is discretized by 576 (nelx × nely = 24 × 24) elements. A downward displacement of $\phantom {\dot {i}\!}u = 3$ mm is applied over 3 nodes on the right top surface. For an element-wise sensitivity comparison, the finite elements are numbered in the order from the left to the right, and from the bottom to the top. The first 1 to 48 uniformly sized square elements are numbered within the left rectangular region, while the rest 49 to 576 non-uniformly sized elements are numbered within the right wedge region, as indicated in Fig. 11a. To verify the sensitivity under a more realistic optimization condition, the non-homogeneous density distribution shown in Fig. 11b is checked. The corresponding damage distribution with above problem settings is given in Fig. 11c. It can be seen that the damage has initiated at the locations where the displacement is applied, where the portal frame is supported as well as the reentrant corner. The maximum damage $\phantom {\dot {i}\!}d_{max}= 0.157$ indicates the sensitivities to be verified next has already accounted for the plasticity and damage initiations.

Fig. 11

Half portal frame model for sensitivity verification: a design domain and element numbering; b non-homogenous density distribution; and c damage distribution

According to (28), the sensitivities of plastic work (W^p) and relaxed aggregated maximum damage (D_max) with respect to density variable (ρ_e) are of particular interest to verify. To this end, sensitivities computed from adjoint method are compared with the ones obtained from central difference method. A perturbation value of $\phantom {\dot {i}\!}10^{-6}$ is used in the central difference method. It took 62.5 sec for the adjoint method to obtain all the sensitivities while the time is 34892.2 sec for the central difference method. Obviously, the adjoint sensitivity analyses are indispensable in this case. The element-wise comparisons of $\phantom {\dot {i}\!}d{W}^{p}/d{\rho }_{e}$ and $\phantom {\dot {i}\!}d{D}_{max}/d{\rho }_{e}$ between these two methods are plotted in Fig. 12a and c, respectively. It can be observed that the sensitivity curves of both quantities are practical identical and overlap with each other. The relative errors between the sensitivity values from the two methods are plotted in Fig. 12b and d, respectively. The plots show that the maximum relative errors for $\phantom {\dot {i}\!}d{W}^{p}/d{\rho }_{e}$ and $\phantom {\dot {i}\!}d{D}_{max}/d{\rho }_{e}$ are $\phantom {\dot {i}\!}6.83\times 10^{-4}$ and $\phantom {\dot {i}\!}2.05\times 10^{-6}$, respectively. Thus, the adjoint sensitivity results match the central difference results with high accuracy. Based on this verification study, it can be concluded that the adjoint sensitivity analysis is correctly implemented and can be safely used in the proposed topology optimization method.

Fig. 12

Sensitivity comparison between adjoint method and central difference method: a$d{W}^{p}/d{\rho }_{e}$; b relative error of $d{W}^{p}/d{\rho }_{e}$; cdD_max/dρ_e; and d relative error of dD_max/dρ_e

It is important to note that the existence of sensitivities is not guaranteed at the transitions from elastic behavior to plastic behavior, as well as due to the use of other non-differentiable operators. Thus, the design sensitivity can be theoretically discontinuous. However, such discontinuities have negligible impact on the numerical accuracy of overall design sensitivities, as these discontinuities are encountered locally at integration points and a limited number of such discontinuities does not cause a huge loss of accuracy. Moreover, in numerical simulations, it is rare to exactly hit the discontinuous point due to the finite numerical precision. As has been shown in previous studies (Li and Khandelwal 2017; Li et al. 2017a, 2017b; Zhang et al. 2017; Zhang and Der Kiureghian 1993; Michaleris et al. 1994) as well as the sensitivity verification results presented above, high accuracy is preserved during the adjoint sensitivity analysis.

6.2 Example 1: cantilever beam

As the first topology optimization example, the proposed method is applied to design a cantilever beam as illustrated in Fig. 13. The rectangular design domain is discretized into $\phantom {\dot {i}\!}144\times 72$ equally sized square Q8/4 elements. A downward design displacement of $\phantom {\dot {i}\!}u = 5$ mm is applied over 13 nodes on the right bottom surface. The minimum plastic work to be dissipated is specified as $\phantom {\dot {i}\!}\overline {W}^{p}= 750$ J and the density filter radius is set to $\phantom {\dot {i}\!}r_{min} = 2$ mm.

Fig. 13

Design domain of the cantilever beam (unit: mm)

For the sake of comparison, the von Mises plastic result without considering the coupled damage is first generated. Figure 14a presents the optimized plastic design and the corresponding damage distribution reanalyzed using the nonlocal damage model under the design displacement $\phantom {\dot {i}\!}u = 5$ mm. Note that only the elements with $\phantom {\dot {i}\!}\rho _{e}\geq 0.5$ are presented in the damage distributions throughout the paper. It is observed that the damage in plastic design is located at the regions where the cantilever is supported and the displacement is applied, with the maximum damage value $\phantom {\dot {i}\!}d_{max}= 0.368$.

Another linear elastic reference design is also generated for this cantilever example. Since linear elastic model does not have the plastic energy measure, the minimum compliance formulation with volume fraction constraint the same as the optimized one from plastic design (i.e., $\phantom {\dot {i}\!}V_{f}= 0.4302$), is used to generate the linear design for comparison. As shown in Fig. 14b, a different design is achieved in the linear case, but with higher maximum damage value (d_max = 0.451) compared to the plastic design.

Fig. 14

Optimized cantilever beams and corresponding damage distributions with different damage constraints: a plastic design; b linear design; c$\overline {D} = 0.2$ design; d$\overline {D} = 0.1$ design; and e$\overline {D} = 0.0.075$ design. (Note that scales of damage plots are varying)

In order to mitigate the damage, the designs from damage constrained formulation enforcing three constraint thresholds $\phantom {\dot {i}\!}\overline {D}= 0.2, 0.1$ and 0.075 are generated and depicted in Fig. 14c to e, respectively, together with their damage contour plots. Different material layouts are obtained as compared to the plastic and linear designs in order to satisfy the additional damage constraint. For example, thicker horizontal members are present at the supports in order to reduce the damage, and the thickness increases from approximately 6.3 mm to 10.2 mm, as measured in Fig. 14. Meanwhile, the right cantilever tip member becomes more vertical to mitigate the damage at the load application region, and the vertical angle changes from $\phantom {\dot {i}\!}32.4^{\circ }$ to $\phantom {\dot {i}\!}15.5^{\circ }$. This vertical member also offers a better force transition path through the entire structure to the supports. These features become more prominent with more restricted damage constraint thresholds, say $\phantom {\dot {i}\!}\overline {D} = 0.075$ as shown Fig. 14e.

It is worth pointing out that although the damage constrained designs are all feasible in terms of the aggregated damage constraints $\phantom {\dot {i}\!}D_{max}$, as confirmed by the fifth column in Table 1, the actual maximum damage $\phantom {\dot {i}\!}d_{max}$ in the design is smaller than the prescribed damage thresholds. This is due to the fact that the p-norm approximation overestimates the actual maximum damage, as discussed in Section 4.4.

Figure 15 presents the objective and constraint functions convergence histories of the damage constrained design with $\phantom {\dot {i}\!}\overline {D}= 0.075$ in Fig. 14e together with several intermediate results. Only first 200 iterations of the constraint function histories are plotted for the sake of clarity as the major convergence of the constraint functions occurs within the first 50 iterations. It can be seen in Fig. 15b that damage constraint is infeasible in the initial homogenous design while the plastic work constraint is inactive. With the reduction of material volume fraction and material redistribution, the damage constraint feasibility is gradually fulfilled and the plastic work dissipation decreases to the prescribed value ($\overline {W}^{p}$). Convergence oscillations take place mostly during the first 20 iterations, indicating the layout adjustment in the intermediate designs. Smooth convergences are obtained after 50 iterations and all the constraints are feasible and active in the final design.

Fig. 15

Convergence histories for the optimized cantilever beam in the case of Fig. 14(e): a objective function and intermediate designs; and b constraint functions

To investigate the ultimate performance of the optimized cantilever designs, the finite element analysis on each optimized design up to the failure point, i.e., $\phantom {\dot {i}\!}d_{max} = 1$, is carried out. Figure 16 shows the load-displacement curves for each design wherein the typical elastoplastic hardening and softening behavior is captured in the structural responses. It can be observed that although the performance in terms of load-displacement behavior of each design is similar up to the design displacement $\phantom {\dot {i}\!}u = 5$ mm, the damage distributions are significantly different (see Table 1) which in turn lead to significant differences in ultimate load carrying capacities. In general, by limiting the damage development at the design displacement, the optimized design has higher load-carrying capacity, better ductility together with postponed failure point compared with the plastic and linear designs. Figure 17 exhibits the damage distributions for cantilever beam designs at their failure points. One can see that the ultimate failure location switches from design to design due to the different optimized material layout. Moreover, the designs with more restricted damage constraints of $\phantom {\dot {i}\!}\overline {D}= 0.1$ and 0.075 have a much widely spread out damage at the failure points (Fig. 17d and e) compared to other three designs, indicating a better material utilization.

Fig. 16

Load-displacement curves of the optimized cantilever beams up to the failure points

Fig. 17

Damage distributions of the optimized cantilever beams at the failure points

Table 1 summarizes the optimized material volume fraction and ultimate performance of each cantilever beam shown in Fig. 14. One can see that the purely plastic design requires the least amount of material with volume fraction of 0.4302 to dissipate the prescribed amount of plastic work. If the maximum damage is constrained to be smaller than 0.2, more material (V_f = 0.4351) is needed to satisfy the damage constraint. However, with only 1.14% more material, the damage constrained design is able to achieve 23.97% increase in maximum load capacity and 65.40% increase ductility. Here, ductility is defined as the displacement at the maximum load point. More importantly, 3646.5 J plastic work can be dissipated before the complete failure, which is 99.32% more than the plastic design (1829.5 J). This trade-off is more prominent if more restricted damage constraint is considered, as indicated by the fourth and fifth row in Table 1. It can be observed that the minimum compliance design performs worst in terms of all indexes. This is expected since it is designed for minimum compliance instead of energy dissipation and damage mitigation.

Table 1 Performance comparison of the optimized cantilever beam designs

6.3 Example 2: L-shaped bracket

The second example has L-shaped design domain as shown in Fig. 18. The design domain is discretized by 9216 (120 × 48 + 72 × 48) uniform square Q8/4 elements and a downward displacement $\phantom {\dot {i}\!}u = 10$ mm is applied over 13 nodes on the right top tip to relax the stress concentration at the loading points. The minimum plastic work to be dissipated is specified as $\phantom {\dot {i}\!}\overline {W}^{p}= 1000$ J while the density filter radius is set to $\phantom {\dot {i}\!}r_{min}= 2$ mm.

Fig. 18

Design domain of the L-shaped bracket (unit: mm)

Fig. 19

Optimized L-shaped brackets and corresponding damage distributions with different damage constraints: a plastic design; b$\overline {D}= 0.2$ design; and c$\overline {D}= 0.075$ design (Note that scales of damage plots are different)

Table 2 Performance comparison of the optimized L-shaped bracket designs

Solving the purely plastic formulation with no damage constraint yields the optimized design shown in Fig. 19a. The corresponding damage distribution in this plastic design, obtained by reanalyzing this design with elastoplastic damage model, exhibits a damage at the location where the displacements are applied, and the maximum damage value reaches $\phantom {\dot {i}\!}d_{max} = 0.713$. Next, by constraining the maximum damage below $\phantom {\dot {i}\!}\overline {D} = 0.2$ in the damage constrained formulation, the optimized design and damage map are reported in Fig. 19b. This design features a vertical supporting member under the location where displacement is applied to provide a better load transition path. As a result, the damage concentration is significantly relieved, together with a more uniformly distributed damage. The maximum damage inside the domain is successfully constrained to $\phantom {\dot {i}\!}d_{max} = 0.173$, which is below $\phantom {\dot {i}\!}\overline {D} = 0.2$. Additional damage constrained design with a more restricted damage threshold $\phantom {\dot {i}\!}\overline {D} = 0.075$ is shown in Fig. 19c. Besides the vertical supporting member, topology with an additional inclined branching member and thicker inner vertical member is obtained to constrain the maximum damage to $\phantom {\dot {i}\!}d_{max} = 0.063$. It is also observed that the damage is much more uniformly distributed in the design domain.

The iteration histories of objective and constraint functions of the damage constrained design with $\phantom {\dot {i}\!}\overline {D} = 0.075$ in Fig. 19c are plotted in Fig. 20, together with selected intermediate results. Additional 300 iterations are executed on this case, as there were some gray area after 400 iterations. Again, the constraint functions convergence histories are plotted for 200 iterations, as no obvious oscillation occurs after 50 iterations. It is found that the objective function value decreases steadily and smoothly after 50 iterations, and the constraints are feasible and active when optimization is finished.

Fig. 20

Convergence histories for the optimized L-shaped bracket in the case of Fig. 19c: a objective function and intermediate designs; and b constraint functions

The load-displacement curves of the optimized L-shaped brackets are plotted in Fig. 23a until final failure to show the ultimate behavior. Representative response curves with softening behavior are again obtained for each case. One can see that the response diverges after the elastic phase in order to satisfy the damage constraints under the design displacement. The damage in plastic design evolves quickly, and this design reaches limit load and failure point right after the design displacement of $\phantom {\dot {i}\!}u = 10$ mm due to the high concentrated damage. On the contrary, the damage-constrained designs have a much more postponed softening behaviors and final failure points. The reason for this behavior can be deduced from the damage maps of the designs at their failure points as presented in left column of Fig. 24. The damage distribution and failure inside plastic design shown in left column of Fig. 24a is localized and the material is not fully utilized. Meanwhile, the failure locations are changing in other two damaged constrained designs with more evenly distributed damage and better material utilization (left column of Fig. 24b and c). This finally results in a better performance in both the overall load-carrying capacity and ductility, as shown in Fig. 23a.

Although the damage concentration in the vicinity of the applied displacements can be alleviated by distributing the displacements over multiple element nodes, it can be seen from Fig. 19a that the damage is still mostly accumulated around this region. The damage-constrained formulation tried to reconfigure this region into a vertical member to decrease the damage, as can be seen in Fig. 19b and c; however, the damage concentration is still present at the location where displacements are prescribed. To alleviate local strain concentrations, an additional exercise is carried out in which a selected group of elements are considered to be elastic and are excluded from the optimization process (Fig. 21). Similar element exclusion strategy has been used by Holmberg et al. (2013) in stress constrained topology optimization. In this study, an “8 × 4” block of elements at the upper right corner are excluded, as shown in Fig. 21.

Fig. 21

Elements in black are linear elastic and are excluded from optimization

The optimized L-shaped brackets with the element exclusion strategy are shown in Fig. 22. It can be seen from Fig. 22a that the damage in the plastic design is no longer concentrated at the displacement-applied location and the maximum damage under the design displacement is significantly decreased to $\phantom {\dot {i}\!}d_{max}= 0.248$. This indicates a better load transferring path achieved by the element exclusion strategy. Moreover, much less material is needed (V_f = 0.3149 in Table 2) in this case as the damage is more evenly distributed. Different topologies are also obtained for the cases of $\phantom {\dot {i}\!}\overline {D}= 0.2$ and 0.075 with less material consumption (Table 2) as reported in Fig. 22b and c, compared with the ones without the element exclusion strategy in Fig. 19b and c. To show the ultimate behavior, the load-displacement curves of the optimized L-shaped brackets with the element exclusion strategy until the failure points is plotted in Fig. 23b. It can be again concluded that the damage constrained designs have better performance over the plastic design in terms of the overall load-carrying capacity and ductility. The right column of Fig. 24 shows the damage distributions at the failure points for this case.

Fig. 22

Optimized L-shaped brackets with element exclusion strategy, and corresponding damage distributions with different damage constraints: a plastic design; b$\overline {D}= 0.2$ design; and c$\overline {D}= 0.075$ design (Note that scales of damage plots are different)

Fig. 23

Load-displacement curves of the optimized L-shaped brackets up to the failure points (ℓ = 2 mm): a without element exclusion strategy; and b with element exclusion strategy

Fig. 24

Damage distributions of the optimized L-shaped brackets at the failure points: (left column) without element exclusion strategy; and (right column) with element exclusion strategy

The first 3 rows in Table 2 shows the performance comparison of the optimized L-shaped brackets without element exclusion strategy. As expected, the enforcement of the damage constraint comes at the cost of increased amount of material being used, as indicated by the third column of Table 2. Compared to the material volume fraction of 0.3424 needed for plastic design, 4.56% and 14.34% more material is required by the damaged constrained designs with $\phantom {\dot {i}\!}\overline {D}= 0.2$ and $\phantom {\dot {i}\!}\overline {D}= 0.075$, respectively. However, this slight increase in material usage results in much more mechanical benefits, i.e. 34.40% and 52.85% higher load carrying capacities, 81.96% and 138.32% better ductilities, 98.65% and 176.59% more ultimate plastic work $\phantom {\dot {i}\!}W_{ult}^{p}$, are gained as the trade-offs, as shown in first 3 rows in Table 2. When using the element exclusion strategy, the performance comparison of the optimized L-shaped brackets is summarized in last 3 rows in Table 2. Similar trend can be seen in this case. For example, compared to the material volume fraction of 0.3149 needed for plastic design, 0.83% and 8.57% more material is required by the damaged constrained designs with $\phantom {\dot {i}\!}\overline {D}= 0.2$ and $\phantom {\dot {i}\!}\overline {D}= 0.075$, respectively. However, this slight increase in material usage results in much more mechanical benefits, i.e. 12.12% and 18.97% higher load carrying capacities, 31.58% and 41.29% better ductilities, 23.19% and 45.01% more ultimate plastic work $\phantom {\dot {i}\!}W_{ult}^{p}$, are gained as the trade-offs.

An additional study is carried out to investigate the influence of the length scale parameter l on the optimized designs. To this end, three different parameter values, i.e. ℓ = 1,0.5 and 0.2 mm are tested on the L-shaped bracket problem with damage constraint $\phantom {\dot {i}\!}\overline {D} = 0.2$ and without element exclusion strategy, while other parameters are kept unchanged. When $\phantom {\dot {i}\!}\ell$ decreases, the nonlocal effect becomes weaker such that the peak damage in the design domain increases. The increased damage might cause convergence issues in the NR method, especially during the early optimization iterations. To avoid this numerical issue, a continuation scheme on $\phantom {\dot {i}\!}\ell$ is used in this additional study, i.e. the optimization starts with $\phantom {\dot {i}\!}\ell = 2$ mm which gradually decreases by 0.1 every 10 iterations, and 200 more iterations are executed once the target $\phantom {\dot {i}\!}\ell$ value is reached. Figure 25 reports the optimized designs and the corresponding damage contours for each case. In comparison to the design in Fig. 19b, the designs with smaller $\phantom {\dot {i}\!}\ell$ have more concentrated damage at the reentrant corner, along with higher damage values due to the weaker nonlocal effect. This eventually leads to more material volume cost and reconfiguration of the design in order to suppress the increased damage. The contour plots of the designs in Fig. 25a and c are shown in Fig. 26, in which a clearer comparison can be observed for the design with different $\phantom {\dot {i}\!}\ell$.

Fig. 25

Optimized L-shaped brackets and corresponding damage distributions with different length scale parameters ($\overline {D}= 0.2$): aℓ = 1 mm; bℓ = 0.5 mm; and cℓ = 0.2 mm

Fig. 26

Contour comparison of L-shaped bracket designs with ℓ = 1 mm and ℓ = 0.2 mm ($\overline {D} = 0.2$)

6.4 Example 3: portal frame

The last example concerns the design of a portal frame as shown in Fig. 4. The design domain is discretized by a mesh with 18432 (nelx × nely = 192 × 96) non-uniformly sized Q8/4 elements. The design displacement $\phantom {\dot {i}\!}u = 3$ mm is applied over 17 nodes at the center of top surface. The topology optimization is solved with a minimum plastic work dissipation target $\phantom {\dot {i}\!}\overline {W}^{p}= 600$ J with the density filter radius $\phantom {\dot {i}\!}r_{min}= 1.5$ mm.

Figure 27a reports the purely plastic design using von Mises model along with the damage map obtained by reanalyzing this design using the elastoplastic nonlocal-damage model. It can be seen that under the design displacement, the plastic design has a maximum damage $\phantom {\dot {i}\!}d_{max}= 0.221$ concentrated at the corner and support locations. Figure 27b to d present the optimized designs and the relevant damage fields from the damage constrained formulation with $\phantom {\dot {i}\!}\overline {D}= 0.2, 0.1$ and 0.075, respectively. It can be observed that if the damage constraints are enforced, the designs are reconfigured and equipped with more members to limit the damage within the design domain, especially at the entrant corner and frame support locations. All of the maximum damages $\phantom {\dot {i}\!}d_{max}$ are successfully limited within the allowable thresholds. The converge history of the volume fraction and selected intermediate designs in the case of $\phantom {\dot {i}\!}\overline {D}= 0.075$ (Fig. 27d) are plotted in Fig. 28 together with the first 200 iteration convergence histories of the constraints. Smooth convergence is obtained after 50 iterations in Fig. 28a and feasible solution is achieved as indicated in Fig. 28b. It is worth noting that the topologies shown in Fig. 27b–d still preserve corners, which may induce the plastic strain concentrations. However, the influence of such concentrations on the final damage is not significant in the optimized topologies. The damage is alleviated by increasing the material volume fraction, and reconfiguring and resizing members instead of rounding out the corner location. Therefore, the suggested topologies in Fig. 27b–d are safe when considering the nonlocal elastoplastic-coupled damage model.

Fig. 27

Optimized portal frames and corresponding damage distributions with different damage constraints: a plastic design; b$\overline {D}= 0.2$ design; c$\overline {D}= 0.1$ design; and d$\overline {D}= 0.075$ design

Fig. 28

Convergence histories for the optimized portal frame in the case of Fig. 27d: a objective function and intermediate designs; and b constraint functions

The load-displacement curves for the optimized portal frame designs up to the failure points are plotted in Fig. 29. Similar performance improvement, as observed in previous two examples, is obtained in this case by constraining the damage. The failure points are postponed with higher maximum load carrying capacities and better ductilities. Figure 30 shows the damage contour of each design at its failure point, indicated by the cross in Fig. 29. One can see from Fig. 30a that the plastic design fails due to the damage localization at the support locations. The rest material is not fully utilized, as the damage is small in these regions. The damage constrained design with $\phantom {\dot {i}\!}\overline {D}= 0.2$ fails at the reentrant corner with a better material utilization, as shown in Fig. 30b. As presented in Fig. 30c and d, the failure locations for the damage constrained cases with $\phantom {\dot {i}\!}\overline {D} = 0.1$ and 0.075 are in the lower chord and leg of the frame with much better distributions of damage and material utilizations.

Fig. 29

Load-displacement curves of the optimized portal frames up to the failure points

Fig. 30

Damage distributions of the optimized portal frames at the failure points

The detailed performance comparison of the four optimized portal frames is summarized in Table 3. Once again, more material is needed in order to satisfy the more restricted damage constraint while dissipating the prescribed amount of plastic work, as indicated by the third column of Table 3. However, comparing the plastic design with the damaged constrained design with $\phantom {\dot {i}\!}\overline {D} = 0.075$, a 4.31% increase in material volume fraction leads to 18.03% increase in maximum load-bearing capacity, 48.38% better ductility and 47.74% more ultimate plastic work dissipation. The ultimate performance of the optimized design with less restricted damage constraint $\phantom {\dot {i}\!}\overline {D} = 0.2$ and 0.1 can be compared from the second and third rows of Table 3, respectively. The in-between tradeoffs are obtained in these two cases as expected. As previously discussed, these tradeoffs are worthwhile for the sake of structural performance and safety.

Table 3 Performance comparison of the optimized portal frame designs

7 Conclusions

This work proposes a topology optimization method to design energy absorbing structures that are subject to maximum damage constraint. An implicit nonlocal coupled elastoplastic model was incorporated with density-based topology optimization for the mesh independent description of the elastoplastic-damage softening behavior. The SIMP method was extended to interpolate five main material parameters introduced by the considered nonlocal damage model. Moreover, a special scaling scheme for nonlocal parameters was proposed that can capture the accurate structural response based on the fictitious domain approach. The path-dependent sensitivities were calculated analytically using the adjoint method for nonlinear coupled transient systems, whose accuracy was further verified numerically via the central difference method on a portal frame example.

The topology optimization problem was formulated to minimize the material volume fraction subject to the minimum plastic work constraint and the constraint on maximum damage. The damage relaxation was considered to relax the damage in low-density elements, and maximum damage was approximated by the p-norm function. Three numerical examples were used to demonstrate that the proposed method is capable of finding satisfactory and feasible solutions under the design displacement with smooth convergences. More importantly, the proposed method is able to generate optimized designs with higher load-carrying capacities, enhanced ductilities and much larger ultimate plastic work dissipation capacity with superior material utilization before complete failure. The trade-off is only a small increase in material volume. This trade-off becomes more worthwhile if more restricted damage constraints are enforced. Finally, to capture the full nature of energy absorbing process, this work can be extended to include finite strain plasticity, rate dependence and inertia effects. These important issues will be investigated in our future works.

Appendices

Appendix A: Return-mapping algorithm and consistent tangent modulus

In this appendix, numerical implementation of the nonlocal damage elastoplasticity model given in Section 2 is presented. In the context of the strain-driven finite element formulation, given data at an integration point: $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }_{m}^{p}$, $\phantom {\dot {i}\!}\alpha _{m}$ and $\phantom {\dot {i}\!}{\kappa }_{m}$ at previous step m, and $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }$ and $\phantom {\dot {i}\!}\overline {\alpha }$ at current step $\phantom {\dot {i}\!}m + 1$, the goal is to find the unknown variables: $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }_{m + 1}^{p}$, $\phantom {\dot {i}\!}\alpha _{m + 1}$ and the consistent tangent moduli at the current step. Note that the subscript $\phantom {\dot {i}\!}m + 1$ of the variables at current step is omitted for the sake of clarity, also the step index is put at subscript instead of superscript, and the element number, integration point number are removed for clarity. An elastic predictor/return-mapping algorithm is used to solve the constitutive model as follows.

1.1 Step 1: Elastic trial step

$$ \begin{array}{l} \text{Given}:\quad\quad{\boldsymbol{\varepsilon}^{p^{tr}}}=\boldsymbol{\varepsilon}_{m}^{p},\quad\alpha^{tr}=\alpha_{m}\\ \text{Evaluate}:\\ \quad\quad\boldsymbol{\sigma}^{tr}=\mathbb{C}^{e}:(\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}^{p^{tr}}),\quad\boldsymbol{s}^{tr}=\mathbb{P}_{dev}^{s}:\boldsymbol{\sigma}^{tr}\\ \quad\quad{\kappa}=\max \{{\kappa}_{m},\overline{\alpha}\},\quad \zeta^{tr}=K^{h}\alpha^{tr}\\ \quad\quad\phi^{tr}(\boldsymbol{\sigma}^{tr},\alpha^{tr},{\kappa})=\|\boldsymbol{s}^{tr}\|-\sqrt{\frac{2}{3}}(1-d({\kappa}))(\sigma_{y}+\zeta^{tr})\ \end{array} $$

(43)

where $\phantom {\dot {i}\!}\mathbb {C}^{e}$ is the fourth-order elasticity tensor and $\phantom {\dot {i}\!}\mathbb {P}_{dev}^{s}$ denotes the fourth-order deviatoric projection tensor; $\phantom {\dot {i}\!}\overline {\alpha }$ is the nonlocal equivalent plastic strain at the integration point.

If $\phantom {\dot {i}\!}\phi ^{tr}\leq 0$, then the current step is an elastic step and the following elastic updates are made

$$ \boldsymbol{\varepsilon}^{p}=\boldsymbol{\varepsilon}^{p^{tr}},\quad\alpha=\alpha^{tr}\quad\text{and}\quad\boldsymbol{\sigma}=\boldsymbol{\sigma}^{tr} $$

(44)

and the consistent algorithmic tangent modulus $\phantom {\dot {i}\!}\boldsymbol {C}_{T}$ is given by

$$ \frac{\partial{\boldsymbol{\sigma}}}{\partial{\boldsymbol{\varepsilon}}}=\mathbb{C}^{e},\quad\frac{\partial{\boldsymbol{\sigma}}}{\partial{\overline{\alpha}}}=\boldsymbol{0},\quad\frac{\partial{\alpha}}{\partial{\boldsymbol{\varepsilon}}}=\boldsymbol{0},\quad\frac{\partial{\alpha}}{\partial{\overline{\alpha}}}= 0 $$

(45)

$$ \boldsymbol{C}_{T}=\large\left[\begin{array}{cc} \frac{\partial{\boldsymbol{\sigma}}}{\partial{\boldsymbol{\varepsilon}}}& \frac{\partial{\boldsymbol{\sigma}}}{\partial{\overline{\alpha}}}\\ \frac{\partial{\alpha}}{\partial{\boldsymbol{\varepsilon}}}& \frac{\partial{\alpha}}{\partial{\overline{\alpha}}} \end{array}\right]=\normalsize\left[\begin{array}{cc} \mathbb{C}^{e}\;&\boldsymbol{0}\\ \boldsymbol{0}\;&0\\ \end{array}\right] $$

(46)

Else if $\phantom {\dot {i}\!}\phi ^{tr}>0$, then there is a plastic flow in this step and the algorithm proceeds to Step 2.

1.2 Step 2: Plastic return mapping

In this step, the plastic flow is nonzero (i.e., $\phantom {\dot {i}\!}\gamma >0$). Using backward Euler method, the flow rules in (8) and (9) are discretized as

$$ \boldsymbol{\varepsilon}^{p}=\boldsymbol{\varepsilon}_{m}^{p}+{\Delta}\gamma\boldsymbol{n}\quad\quad \alpha=\alpha_{m}+\sqrt{\frac{2}{3}}{\Delta}\gamma $$

(47)

$$ \boldsymbol{\sigma}=\boldsymbol{\sigma}^{tr}-2\mu{\Delta}\gamma\boldsymbol{n}\quad\text{and}\quad\boldsymbol{s}=\boldsymbol{s}^{tr}-2\mu{\Delta}\gamma\boldsymbol{n} $$

(48)

in which (48)₂ further leads to

$$ \|\boldsymbol{s}\|=\|\boldsymbol{s}^{tr}\|-2\mu{\Delta}\gamma\quad\text{and}\quad\boldsymbol{n}=\boldsymbol{n}^{tr}=\frac{\boldsymbol{s}^{tr}}{\|\boldsymbol{s}^{tr}\|}\ $$

(49)

The yield function can be then expressed as

$$ \phi=\|\boldsymbol{s}^{tr}\|-2\mu{\Delta}\gamma-\sqrt{\frac{2}{3}}(1-d({\kappa}))\left(\sigma_{y}+\zeta(\alpha)\right) $$

(50)

The NR method can then be used for solving (50) for $\phantom {\dot {i}\!}{\Delta }\gamma$ where the Jacobian is given by

$$ \frac{\partial\phi}{\partial{\Delta}\gamma}=-2\mu-\frac{2}{3}(1-d({\kappa}))\frac{\partial{\zeta}}{\partial{\alpha}} $$

(51)

After obtaining $\phantom {\dot {i}\!}{\Delta }\gamma$, the internal state variables $\phantom {\dot {i}\!}\boldsymbol {\varepsilon }^{p}$ and $\phantom {\dot {i}\!}\alpha$ can be calculated through (47) while the stress tensor $\phantom {\dot {i}\!}\boldsymbol {\sigma }$ can be obtained through (48)₁. Next, to calculate the tangent moduli $\phantom {\dot {i}\!}\partial \boldsymbol {\sigma }/\partial \boldsymbol {\varepsilon }$, $\phantom {\dot {i}\!}\partial \boldsymbol {\sigma }/\partial \overline {\alpha }$, $\phantom {\dot {i}\!}\partial {\alpha }/\partial \boldsymbol {\boldsymbol {\varepsilon }}$ and $\phantom {\dot {i}\!}\partial {\alpha }/\partial \overline {\alpha }$, some results due to tensor algebra have to be derived, which are

$$ \begin{array}{l} \displaystyle\frac{\partial{\|\boldsymbol{s}^{tr}\|}}{\partial\boldsymbol{\varepsilon}}= 2\mu\boldsymbol{n}^{tr}\\ \displaystyle\mathbb{B}=\frac{\partial\boldsymbol{n}}{\partial\boldsymbol{\varepsilon}}=\frac{2\mu}{\|\boldsymbol{s}^{tr}\|}(\mathbb{P}_{dev}^{s}-\boldsymbol{n}^{tr}\otimes\boldsymbol{n}^{tr})\\ \displaystyle\frac{\partial{d}}{\partial{\boldsymbol{\varepsilon}}}= 0,\quad\frac{\partial{\|\boldsymbol{s}^{tr}\|}}{\partial{\overline{\alpha}}}= 0 \end{array} $$

(52)

As a result of consistency condition, the total differential of the yield equation gives

$$ d\phi=\frac{\partial\phi}{\partial{\boldsymbol{\varepsilon}}}:d\boldsymbol{\varepsilon}+\frac{\partial\phi}{\partial{\overline{\alpha}}}d\overline{\alpha}= 0 $$

(53)

with

$$ \frac{\partial\phi}{\partial\boldsymbol{\varepsilon}}=\frac{\partial\|\boldsymbol{s}^{tr}\|}{\partial\boldsymbol{\varepsilon}}-2\mu\frac{\partial({\Delta}\gamma)}{\partial\boldsymbol{\varepsilon}}-\frac{2}{3}(1-d)K^{h}\frac{\partial({\Delta}\gamma)}{\partial\boldsymbol{\varepsilon}} $$

(54)

$$\begin{array}{@{}rcl@{}} \frac{\partial\phi}{\partial\overline{\alpha}}&=&\frac{\partial\|\boldsymbol{s}^{tr}\|}{\partial\overline{\alpha}}-2\mu\frac{\partial({\Delta}\gamma)}{\partial\overline{\alpha}}+\sqrt{\frac{2}{3}}\frac{\partial{d}}{\partial{\kappa}}\frac{\partial{\kappa}}{\partial\overline{\alpha}}(\sigma_{y}+\zeta({\Delta}\gamma))\\ &&-\frac{2}{3}(1-d)K^{h}\frac{\partial({\Delta}\gamma)}{\partial\overline{\alpha}} \end{array} $$

(55)

Due to the independency of $\phantom {\dot {i}\!}d\boldsymbol {\varepsilon }$ and $\phantom {\dot {i}\!}d\overline {\alpha }$, we further have $\phantom {\dot {i}\!}\partial \phi /\partial \boldsymbol {\varepsilon }= 0$ and $\phantom {\dot {i}\!}\partial \phi /\partial \overline {\alpha }= 0$, which lead to

$$ \frac{\partial({\Delta}\gamma)}{\partial\boldsymbol{\varepsilon}}=c_{1}\boldsymbol{n}^{tr}\quad\text{with}\quad{c_{1}}=\frac{2\mu}{2\mu+\frac{2}{3}(1-d)K^{h}} $$

(56)

$$ \frac{\partial({\Delta}\gamma)}{\partial\overline{\alpha}}= \left\{\begin{array}{lll} \frac{\sqrt{\frac{2}{3}}(\sigma_{y}+\zeta({\Delta}\gamma))}{2\mu+\frac{2}{3}(1-d)K^{h}}\frac{\partial{d}}{\partial{\kappa}}\quad&&\text{if}\;{\kappa}=\overline{\alpha}\\ 0\quad&&\text{otherwise}\\ \end{array}\right. $$

(57)

With the derivations in (52), (56) and (57), the consistent algorithmic tangent modulus $\phantom {\dot {i}\!}\boldsymbol {C}_{T}$ can be calculated as

$$ \begin{array}{lll} \displaystyle\frac{\partial\boldsymbol{\sigma}}{\partial\boldsymbol{\varepsilon}}=\mathbb{C}^{e}-2\mu{\Delta}\gamma\mathbb{B}-2\mu{c_{1}}\boldsymbol{n}^{tr}\otimes\boldsymbol{n}^{tr}\\ \displaystyle\frac{\partial\boldsymbol{\sigma}}{\partial\overline{\alpha}}=-2\mu\frac{\partial({\Delta}\gamma)}{\partial\overline{\alpha}}\boldsymbol{n}^{tr}\\ \displaystyle\frac{\partial{\alpha}}{\partial\boldsymbol{\varepsilon}}=\sqrt{\frac{2}{3}}c_{1}\boldsymbol{n}^{tr},\quad\frac{\partial\alpha}{\partial\overline{\alpha}}=\sqrt{\frac{2}{3}}\frac{\partial{\Delta}\gamma}{\partial\overline{\alpha}}\\ \end{array} $$

(58)

$$ \begin{array}{ll} \boldsymbol{C}_{T}&=\large\left[\begin{array}{ll} \frac{\partial\boldsymbol{\sigma}}{\partial\boldsymbol{\varepsilon}}&\frac{\partial\boldsymbol{\sigma}}{\partial\overline{\alpha}}\\ \frac{\partial\alpha}{\partial\boldsymbol{\varepsilon}}&\frac{\partial\alpha}{\partial\overline{\alpha}} \end{array}\right]\\ &=\normalsize\left[\begin{array}{cc} \mathbb{C}^{e}-2\mu{\Delta}\gamma\mathbb{B}-2\mu{c_{1}}\boldsymbol{n}^{tr}\otimes\boldsymbol{n}^{tr}\;&-2\mu\frac{\partial({\Delta}\gamma)}{\partial\overline{\alpha}}\boldsymbol{n}^{tr}\\ \sqrt{\frac{2}{3}}c_{1}\boldsymbol{n}^{tr}\;&\sqrt{\frac{2}{3}}\frac{\partial{\Delta}\gamma}{\partial\overline{\alpha}}\\ \end{array}\right] \end{array} $$

(59)

The above consistent evaluation of the tangent operator $\phantom {\dot {i}\!}\boldsymbol {C}_{T}$ ensures the quadratic convergence of the global NR solver.

Appendix B: Explicit derivatives for the adjoint sensitivity analysis

This Appendix presents the complete derivations of the explicit derivatives of F, $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {H}^{k}$ needed in (36).

2.1 Derivatives of objective and constraint functions

According to (28), three target functions (f₀, $\phantom {\dot {i}\!}f_{1}$ and $\phantom {\dot {i}\!}f_{2}$) need sensitivity calculation. The sensitivity of the volume fraction objective function $\phantom {\dot {i}\!}f_{0}$ is straightforward to calculate and is given as

$$ \frac{df_{0}}{d\boldsymbol{\rho}}=\frac{1}{V_{0}}\boldsymbol{V} $$

(60)

where $\phantom {\dot {i}\!}\boldsymbol {V}$ is the element volume vector that collects all the element volume $\phantom {\dot {i}\!}V_{e}$.

For the plastic work constraint $\phantom {\dot {i}\!}F=f_{1}$ defined in (28)₂, since $\phantom {\dot {i}\!}W^{p}$ only depends on $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {v}^{k-1}$ as indicated by (29), it implies

$$ \frac{\partial{f_{1}}}{\partial\boldsymbol{\rho}}=\boldsymbol{0},\quad\frac{\partial{f_{1}}}{\partial\boldsymbol{U}^{k}}=\boldsymbol{0} $$

(61)

The only non-zero derivatives $\phantom {\dot {i}\!}\partial {f_{1}}/\partial {\boldsymbol {v}}^{k}$ are arranged as

$$ \begin{array}{l} \frac{\partial{f_{1}}}{\partial\boldsymbol{v}^{k}}=\left[\begin{array}{l} \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{1}^{k}}\quad \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{2}^{k}}\quad\dots\quad \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{n_{ele}}^{k}} \end{array}\right]\quad\text{with}\\ \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{e}^{k}}=\left[\begin{array}{l} \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{e_{1}}^{k}}\quad \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{e_{2}}^{k}}\quad \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{e_{3}}^{k}}\quad \frac{\partial{f_{1}}}{\partial\boldsymbol{v}_{e_{4}}^{k}} \end{array}\right] \end{array} $$

(62)

while the expression of term $\phantom {\dot {i}\!}\partial {f_{1}}/\partial \boldsymbol {v}_{e_{r}}^{k}$ is distinguished from $\phantom {\dot {i}\!}k=n$ and $\phantom {\dot {i}\!}k\neq n$, which reads

$$ \begin{array}{l} \frac{\partial{f_{1}}}{\partial{\boldsymbol{v}_{e_{r}}^{n}}}=-\frac{1}{\overline{W}^{p}}\left[\begin{array}{lllllllll} \frac{1}{2}\left(\boldsymbol{\varepsilon}_{e_{r}}^{p^{n}}-\boldsymbol{\varepsilon}_{e_{r}}^{p^{n-1}}\right)w_{r}&&\frac{1}{2}\left(\boldsymbol{\sigma}_{e_{r}}^{n}+\boldsymbol{\sigma}_{e_{r}}^{{n-1}}\right)w_{r}&&0&&0&&0 \end{array}\right]\\ \frac{\partial{f_{1}}}{\partial{\boldsymbol{v}_{e_{r}}^{k}}}=-\frac{1}{\overline{W}^{p}}\left[\begin{array}{lllllllll} \frac{1}{2}\left(\boldsymbol{\varepsilon}_{e_{r}}^{p^{k + 1}}-\boldsymbol{\varepsilon}_{e_{r}}^{p^{k-1}}\right)w_{r}&&\frac{1}{2}\left(\boldsymbol{\sigma}_{e_{r}}^{k-1}-\boldsymbol{\sigma}_{e_{r}}^{{k + 1}}\right)w_{r}&&0&&0&&0 \end{array}\right] \end{array} $$

(63)

For the damage constraint $\phantom {\dot {i}\!}F=f_{2}$ defined in (28)₃, since $\phantom {\dot {i}\!}D_{max}(\boldsymbol {x})$ only depends on $\phantom {\dot {i}\!}\boldsymbol {\rho }$ and $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ as indicated by (30) and (31), implies $\phantom {\dot {i}\!}\partial {f_{2}}/\partial \boldsymbol {U}^{k}=\boldsymbol {0}$. The non-zero derivative $\phantom {\dot {i}\!}\partial {f_{2}}/\partial \boldsymbol {\rho }$ is arranged as

$$ \begin{array}{ll} \frac{\partial{f_{2}}}{\partial\boldsymbol{\rho}}=&\left[ \frac{\partial{f_{2}}}{\partial\rho_{1}}\quad \frac{\partial{f_{2}}}{\partial\rho_{2}}\quad\dots\quad \frac{\partial{f_{2}}}{\partial\rho_{n_{ele}}} \right]\quad\text{with}\\ \frac{\partial{f_{2}}}{\partial\rho_{e}}=&\displaystyle\left({\sum}_{e = 1}^{n_{ele}}\left({\sum}_{r = 1}^{n_{ipt}}\left({\rho_{e}^{q}}{d_{e_{r}}^{n}}\right)^{p_{a}}\right)\right)^{\frac{1}{p_{a}}-1}\times\\ &\displaystyle{\sum}_{r = 1}^{n_{ipt}}\left(({\rho_{e}^{q}}d_{e_{r}}^{n})^{p_{a}-1}\left(q\rho_{e}^{q-1}d_{e_{r}}^{n}+{\rho_{e}^{q}}\frac{\partial{d_{e_{r}}^{n}}}{\partial\rho_{e}}\right)\right) \end{array} $$

(64)

where $\phantom {\dot {i}\!}\partial {d}_{e_{r}}^{n}/\partial \rho _{e}$ can be derived based on (6) using chain rule, which reads

$$ \frac{\partial{d}_{e_{r}}^{n}}{\partial\rho_{e}}=\frac{\partial{d}_{e_{r}}^{n}}{\partial{\kappa}_{th_{e}}}\frac{\partial{\kappa}_{th_{e}}}{\partial\rho_{e}}+\frac{\partial{d}_{e_{r}}^{n}}{\partial{\Gamma}}\frac{\partial{\Gamma}}{\partial{\kappa}_{th_{e}}}\frac{\partial{\kappa}_{th_{e}}}{\partial\rho_{e}}+\frac{\partial{d}_{e_{r}}^{n}}{\partial\beta_{e}}\frac{\partial\beta_{e}}{\partial\rho_{e}} $$

(65)

in which the derivatives $\phantom {\dot {i}\!}\partial {d}_{e_{r}}^{n}/\partial {\kappa }_{th_{e}}$, $\phantom {\dot {i}\!}{\partial {d}_{e_{r}}^{n}}/{\partial {\Gamma }}$, $\phantom {\dot {i}\!}{\partial {\Gamma }}/{\partial {\kappa }_{th_{e}}}$ and $\phantom {\dot {i}\!}{\partial {d}_{e_{r}}^{n}}/{\partial \beta _{e}}$ can be straightforwardly obtained from (6) and (7), and are omitted here. The derivatives of damage parameters $\phantom {\dot {i}\!}{\partial {\kappa }_{th_{e}}}/{\partial \rho _{e}}$ and $\phantom {\dot {i}\!}{\partial \beta _{e}}/{\partial \rho _{e}}$ can be calculated by the material interpolation shown in (21) and (22) as

$$ \begin{array}{l} \frac{\partial{\kappa}_{th_{e}}}{\partial\rho_{e}}=p_{4}({\kappa}_{th}-{\kappa}_{th_{min}})\rho_{e}^{(p_{4}-1)}\\ \frac{\partial\beta_{e}}{\partial\rho_{e}}=-p_{5}(\beta_{v}-\beta)\rho_{e}^{(p_{5}-1)}\\ \end{array} $$

(66)

The other non-zero derivative $\phantom {\dot {i}\!}\partial {f_{2}}/\partial \boldsymbol {v}^{k}$ is given by

$$ \begin{array}{l} \frac{\partial{f_{2}}}{\partial\boldsymbol{v}^{k}}=\left[ \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{1}^{k}}\quad \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{2}^{k}}\quad\dots\quad \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{n_{ele}}^{k}} \right]\quad\text{with}\\ \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{e}^{k}}=\left[ \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{e_{1}}^{k}}\quad \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{e_{2}}^{k}}\quad \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{e_{3}}^{k}}\quad \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{e_{4}}^{k}} \right] \end{array} $$

(67)

where the term $\phantom {\dot {i}\!}{\partial {f_{2}}}/{\partial \boldsymbol {v}_{e_{r}}^{k}}$ is distinguished from $\phantom {\dot {i}\!}k=n$ and $\phantom {\dot {i}\!}k\neq n$, which is expressed as

$$ \begin{array}{ll} \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{e_{r}}^{k}}&=\displaystyle\rho_{e}^{qp_{a}}\left(d_{e_{r}}^{k}\right)^{p_{a}-1}\left({\sum}_{e = 1}^{n_{ele}}\left({\sum}_{r = 1}^{n_{ipt}}\left({\rho_{e}^{q}}{d_{e_{r}}^{k}}\right)^{p_{a}}\right)\right)^{\frac{1}{p_{a}}-1}\times\\ &\quad \left[\boldsymbol{0} \quad \boldsymbol{0} \quad 0 \quad 0 \quad \frac{\partial{d}_{e_{r}}^{k}}{\partial{\kappa}_{e_{r}}^{k}}\right]\quad(k=n)\\ \frac{\partial{f_{2}}}{\partial\boldsymbol{v}_{e_{r}}^{k}}&=\boldsymbol{0}\quad(k\neq n)\\ \end{array} $$

(68)

Based on (6), the following derivative is obtained

$$ \frac{\partial{d}_{e_{r}}^{k}}{\partial{\kappa}_{e_{r}}^{k}}\,=\,\beta_{e}{e}^{-\beta_{e}\left({\kappa}_{e_{r}}^{k}-{\kappa}_{th_{e}}\right)}{\Gamma}\left({\kappa}_{e_{r}}^{k}\right)+\left(1\,-\,e^{-\beta_{e}({\kappa}_{e_{r}}^{k}-{\kappa}_{th_{e}})}\right)\frac{\partial{\Gamma}}{\partial{\kappa}}|_{{\kappa}={\kappa}_{e_{r}}^{k}} $$

(69)

where $\phantom {\dot {i}\!}{\partial {\Gamma }}/{\partial {\kappa }}$ can be obtained from (7).

2.2 Derivatives of $\boldsymbol {R}^{\text {\textit {k}}}$

According to (38), the derivative of $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$ with respect to the solution variable $\phantom {\dot {i}\!}\boldsymbol {U}^{k}$ reads

$$ \frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{U}^{k}}=\overset{n_{ele}}{\underset{e = 1}{\mathscr{A}}}\left(\frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{U}_{e}^{k}}\right) $$

(70)

with

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} \frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{U}_{e}^{k}}&=\left[\begin{array}{ll} \frac{\partial\boldsymbol{R}_{u}^{e^{k}}}{\partial\boldsymbol{u}_{e}^{k}}&\frac{\partial\boldsymbol{R}_{u}^{e^{k}}}{\partial\overline{\boldsymbol{\alpha}}_{e}^{k}}\\ \frac{\partial\boldsymbol{R}_{\overline{\alpha}}^{e^{k}}}{\partial\boldsymbol{u}_{e}^{k}}&\frac{\partial\boldsymbol{R}_{\overline{\alpha}}^{e^{k}}}{\partial\overline{\boldsymbol{\alpha}}_{e}^{k}} \end{array}\right]\\ &=\left[\begin{array}{lc} \boldsymbol{0}&\boldsymbol{0}\\\boldsymbol{0}&\sum\limits_{r = 1}^{n_{ipt}}\left(\boldsymbol{N}_{\overline{\alpha}_{r}}^{T}\boldsymbol{N}_{\overline{\alpha}_{r}}+(\rho_{e}^{p_{6}}\ell)^{2}\boldsymbol{B}_{\overline{\alpha}_{r}}^{T}\boldsymbol{B}_{\overline{\alpha}_{r}}\right)w_{r} \end{array}\right] \end{array} \end{array} $$

(71)

while the derivative $\phantom {\dot {i}\!}\partial \boldsymbol {R}^{k}/\partial \boldsymbol {U}^{k-1}=\boldsymbol {0}$. The derivative of $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$ with respect to the auxiliary variable $\phantom {\dot {i}\!}\boldsymbol {v}^{k}$ is calculated as

$$ \begin{array}{l} \frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{v}^{k}}= \overset{n_{ele}}{\underset{e = 1}{\mathscr{A}}}\left(\frac{\partial\boldsymbol{R}_{e}^{k}}{\partial\boldsymbol{v}^{k}}\right)\quad\text{with}\\ \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}^{k}}=\left[ \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{1}^{k}}\quad\dots\quad\frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{n_{ele}}^{k}}\right] \end{array} $$

(72)

where the derivatives $\phantom {\dot {i}\!}\partial \boldsymbol {R}^{e^{k}}/\partial \boldsymbol {v}_{j}^{k}=\boldsymbol {0}$ for $\phantom {\dot {i}\!}j\neq e$. The only non-zero derivative $\phantom {\dot {i}\!}\partial \boldsymbol {R}^{e^{k}}/\partial \boldsymbol {v}_{e}^{k}$ is calculated as

$$ \begin{array}{ll} \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{e}^{k}}&=\left[ \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{e_{1}}^{k}}\,\, \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{e_{2}}^{k}}\,\, \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{e_{3}}^{k}}\,\, \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{e_{4}}^{k}}\right]\quad\text{with}\\ \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{v}_{e_{r}}^{k}}&=\left[ \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{\sigma}_{e_{r}}^{k}}\,\, \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\boldsymbol{\varepsilon}_{e_{r}}^{p^{k}}}\,\, \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\alpha_{e_{r}}^{k}}\,\, \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial{\Delta}\gamma_{e_{r}}^{k}}\,\, \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial{\kappa}_{e_{r}}^{k}}\right]\\ &=\left[\begin{array}{ccccc} w_{r}\boldsymbol{B}_{u_{r}}^{T} &\quad \boldsymbol{0} &\quad \boldsymbol{0} &\quad \boldsymbol{0} &\quad \boldsymbol{0}\\ \boldsymbol{0} &\quad \boldsymbol{0} &\quad -w_{r}\rho_{e}^{p_{7}}\boldsymbol{N}_{\overline{\alpha}_{r}}^{T} &\quad \boldsymbol{0} &\quad \boldsymbol{0} \end{array}\right] \end{array} $$

(73)

while the derivative of $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$ with respect to $\phantom {\dot {i}\!}\boldsymbol {v}^{k-1}$ is zero, i.e., $\phantom {\dot {i}\!}\partial \boldsymbol {R}^{k}/\partial \boldsymbol {v}^{k-1}=\boldsymbol {0}$. Finally, the derivative of $\phantom {\dot {i}\!}\boldsymbol {R}^{k}$ with respect to $\phantom {\dot {i}\!}\boldsymbol {\rho }$ is arranged as

$$ \begin{array}{l} \frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{\rho}}\,=\, \overset{n_{ele}}{\underset{e = 1}{\mathscr{A}}}\left(\frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\rho_{e}}\right)\quad\text{with}\\ \frac{\partial\boldsymbol{R}^{e^{k}}}{\partial\rho_{e}}\,=\,\left[\begin{array}{c} \boldsymbol{0}\\ 2p_{6}\ell^{2}\rho_{e}^{2p_{6}-1}\sum\limits_{r = 1}^{n_{ipt}}w_{r}\boldsymbol{B}_{\overline{\alpha}_{r}}^{T}\boldsymbol{B}_{\overline{\alpha}_{r}}\overline{\boldsymbol{\alpha}}_{e}^{k}-p_{7}\rho_{e}^{p_{7}-1}\sum\limits_{r = 1}^{n_{ipt}}w_{r}\boldsymbol{N}_{\overline{\alpha}_{r}}^{T}\alpha_{e_{r}}^{k} \end{array}\right] \end{array} $$

(74)

2.3 Derivatives of $\boldsymbol {H}^{\text {\textit {k}}}$

As indicated by (41) and (42), $\phantom {\dot {i}\!}\boldsymbol {H}^{k}$ only depends on the solution field $\phantom {\dot {i}\!}\boldsymbol {U}^{k}$ at current step. Thus, $\phantom {\dot {i}\!}\partial \boldsymbol {H}^{k}/\partial \boldsymbol {U}^{k-1}=\boldsymbol {0}$ and the expressions for non-zero derivatives $\phantom {\dot {i}\!}\partial \boldsymbol {H}^{k}/\partial \boldsymbol {U}^{k}$ are the same for elastic and plastic steps, which can be written as

$$ \frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{U}^{k}}=\left[\begin{array}{c} \frac{\partial\boldsymbol{H}_{1}^{k}}{\partial\boldsymbol{U}^{k}}\\ \vdots\\ \frac{\partial\boldsymbol{H}_{n_{ele}}^{k}}{\partial\boldsymbol{U}^{k}}\\ \end{array}\right]\quad \text{with}\quad \frac{\partial\boldsymbol{H}_{j}^{k}}{\partial\boldsymbol{U}^{k}}=\overset{n_{ele}}{\underset{e = 1}{\mathscr{A}}}\left(\frac{\partial\boldsymbol{H}_{j}^{k}}{\partial\boldsymbol{U}_{e}^{k}}\right)\\ $$

(75)

It can be seen that $\phantom {\dot {i}\!}\partial \boldsymbol {H}_{j}^{k}/\partial \boldsymbol {U}_{e}^{k}=\boldsymbol {0}$ for $\phantom {\dot {i}\!}j\neq e$, so the non-zero term $\phantom {\dot {i}\!}\partial \boldsymbol {H}_{e}^{k}/\partial \boldsymbol {U}_{e}^{k}$ is calculated as

$$ \begin{array}{l} \frac{\partial\boldsymbol{H}_{e}^{k}}{\partial\boldsymbol{U}_{e}^{k}}=\left[\begin{array}{c} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\boldsymbol{U}_{e}^{k}}\\ \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\boldsymbol{U}_{e}^{k}}\\ \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\boldsymbol{U}_{e}^{k}}\\ \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\boldsymbol{U}_{e}^{k}}\\ \end{array}\right]=\left[\begin{array}{cc} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\boldsymbol{u}_{e}^{k}}&\frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\overline{\boldsymbol{\alpha}}_{e}^{k}}\\ \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\boldsymbol{u}_{e}^{k}}&\frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\overline{\boldsymbol{\alpha}}_{e}^{k}}\\ \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\boldsymbol{u}_{e}^{k}}&\frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\overline{\boldsymbol{\alpha}}_{e}^{k}}\\ \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\boldsymbol{u}_{e}^{k}}&\frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\overline{\boldsymbol{\alpha}}_{e}^{k}}\\ \end{array}\right]\quad \text{with}\\ \frac{\partial\boldsymbol{H}_{e_{r}}^{k}}{\partial\boldsymbol{u}_{e}^{k}}=\left[\begin{array}{c} -\mathbb{C}^{e}:\frac{\partial\boldsymbol{\varepsilon}_{e_{r}}^{k}}{\partial\boldsymbol{u}_{e}^{k}}\\ \boldsymbol{0}\\\boldsymbol{0}\\\boldsymbol{0}\\\boldsymbol{0}\\ \end{array}\right]\quad\text{and}\quad\frac{\partial\boldsymbol{H}_{e_{r}}^{k}}{\partial\overline{\boldsymbol{\alpha}}_{e}^{k}}=\left[\begin{array}{c} \boldsymbol{0}\\\boldsymbol{0}\\\boldsymbol{0}\\\boldsymbol{0}\\\boldsymbol{z}_{1} \end{array}\right]\\ \text{where}\quad\boldsymbol{z}_{1}=\left\{\begin{array}{ll} \boldsymbol{0},& \,\,\text{if}{\;\;}{\kappa}_{e_{r}}^{k-1}>\boldsymbol{N}_{\overline{\alpha}_{r}}\overline{\boldsymbol{\alpha}}^{e}\\ -\boldsymbol{N}_{\overline{\alpha}_{r}},&\,\,\text{otherwise} \end{array}\right. \end{array} $$

(76)

For the derivatives $\phantom {\dot {i}\!}\partial \boldsymbol {H}^{k}/\partial \boldsymbol {v}^{k}$ and $\phantom {\dot {i}\!}\partial \boldsymbol {H}^{k}/\partial \boldsymbol {v}^{k-1}$, the structures of the derivative matrices are

$$ \begin{array}{l} \frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{v}^{k}}=\left[\begin{array}{cccc} \frac{\partial\boldsymbol{H}_{1}^{k}}{\partial\boldsymbol{v}_{1}^{k}} & \boldsymbol{0} & {\dots} & \boldsymbol{0}\\ \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{2}^{k}}{\partial\boldsymbol{v}_{2}^{k}} & {\dots} & \boldsymbol{0}\\ {\vdots} & {\vdots} & {\ddots} & \vdots\\ \boldsymbol{0} & \boldsymbol{0} & {\dots} & \frac{\partial\boldsymbol{H}_{n_{ele}}^{k}}{\partial\boldsymbol{v}_{n_{ele}}^{k}}\\ \end{array}\right]\\ \frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{v}^{k-1}}=\left[\begin{array}{cccc} \frac{\partial\boldsymbol{H}_{1}^{k}}{\partial\boldsymbol{v}_{1}^{k-1}} & \boldsymbol{0} & {\dots} & \boldsymbol{0}\\ \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{2}^{k}}{\partial\boldsymbol{v}_{2}^{k-1}} & {\dots} & \boldsymbol{0}\\ {\vdots} & {\vdots} & {\ddots} & \vdots\\ \boldsymbol{0} & \boldsymbol{0} & {\dots} & \frac{\partial\boldsymbol{H}_{n_{ele}}^{k}}{\partial\boldsymbol{v}_{n_{ele}}^{k-1}}\\ \end{array}\right]\\ \end{array} $$

(77)

This is because $\phantom {\dot {i}\!}\boldsymbol {v}_{i}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {v}_{j}^{k}$ are independent and $\phantom {\dot {i}\!}\boldsymbol {H}_{i}^{k}$ and $\phantom {\dot {i}\!}\boldsymbol {H}_{j}^{k}$ are uncoupled given $\phantom {\dot {i}\!}i\neq j$. As a result, only submatrices lying on the diagonal are non-zeros. Moreover, the non-zero submatrices share the same structure as

$$ \begin{array}{l} \frac{\partial\boldsymbol{H}_{e}^{k}}{\partial\boldsymbol{v}_{e}^{k}}=\left[\begin{array}{cccc} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\boldsymbol{v}_{e_{1}}^{k}} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0}\\ \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\boldsymbol{v}_{e_{2}}^{k}} & \boldsymbol{0} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\boldsymbol{v}_{e_{3}}^{k}} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\boldsymbol{v}_{e_{4}}^{k}}\\ \end{array}\right]\\ \frac{\partial\boldsymbol{H}_{e}^{k}}{\partial\boldsymbol{v}_{e}^{k-1}}=\left[\begin{array}{cccc} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\boldsymbol{v}_{e_{1}}^{k-1}} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0}\\ \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\boldsymbol{v}_{e_{2}}^{k-1}} & \boldsymbol{0} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\boldsymbol{v}_{e_{3}}^{k-1}} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\boldsymbol{v}_{e_{4}}^{k-1}}\\ \end{array}\right] \end{array} $$

(78)

For $\phantom {\dot {i}\!}\partial \boldsymbol {H}_{e}^{k}/\partial \boldsymbol {v}_{e}^{k-1}$, both elastic step and plastic step give

$$ \begin{array}{l} \frac{\partial\boldsymbol{H}_{e_{r}}^{k}}{\partial\boldsymbol{v}_{e_{r}}^{k-1}}=\left[\begin{array}{ccccc} \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0}\\ \boldsymbol{0} & -\mathbb{I}_{4}^{s} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & -1 & 0 & 0\\ \boldsymbol{0} & \boldsymbol{0} & 0 & 0 & 0\\ \boldsymbol{0} & \boldsymbol{0} & 0 & 0 & z_{2}\\ \end{array}\right]\quad \text{with}\\ z_{2}=\left\{\begin{array}{ll} -1,\quad&\qquad\text{if}\;\;{\kappa}_{e_{r}}^{k-1}>\boldsymbol{N}_{\overline{\alpha}_{r}}\overline{\boldsymbol{\alpha}}^{e}\\ 0,\quad&\qquad\text{otherwise} \end{array}\right. \end{array} $$

(79)

while for $\phantom {\dot {i}\!}\partial \boldsymbol {H}_{e}^{k}/\partial \boldsymbol {v}_{e}^{k}$, elastic step and plastic step have to be distinguished. For elastic step, it is

$$ \frac{\partial\boldsymbol{H}_{e_{r}}^{k}}{\partial\boldsymbol{v}_{e_{r}}^{k}}=\left[\begin{array}{ccccc} \mathbb{I}_{4}^{s} &\quad \mathbb{C}^{e} &\quad \boldsymbol{0} &\quad \boldsymbol{0} &\quad {\boldsymbol{0}}\\ \boldsymbol{0} &\quad \mathbb{I}_{4}^{s} &\quad \boldsymbol{0} &\quad \boldsymbol{0} &\quad \boldsymbol{0}\\ \boldsymbol{0} &\quad \boldsymbol{0} &\quad 1 &\quad 0 &\quad 0\\ \boldsymbol{0} &\quad \boldsymbol{0} &\quad 0 &\quad 1 &\quad 0\\ \boldsymbol{0} &\quad \boldsymbol{0} &\quad 0 &\quad 0 &\quad 0\\ \end{array}\right] $$

(80)

while for plastic step it is

$$ \frac{\partial\boldsymbol{H}_{e_{r}}^{k}}{\partial\boldsymbol{v}_{e_{r}}^{k}}\,=\,\left[\begin{array}{ccccc} \mathbb{I}_{4}^{s} & \mathbb{C}^{e} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0}\\ \!-{\Delta}\gamma_{e_{r}}^{k}\mathbb{A} & \mathbb{I}_{4}^{s} & \boldsymbol{0} & -\boldsymbol{n}_{e_{r}}^{k} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & 1 & -\sqrt{\frac{2}{3}} & 0\\ \boldsymbol{n}_{e_{r}}^{k} & \boldsymbol{0} & \!-\sqrt{\frac{2}{3}}(1\!-d_{e_{r}}^{k}){K_{e}^{h}} & 0 & \sqrt{\frac{2}{3}}(\sigma_{y_{e}}\,+\,\zeta_{e_{r}}^{k})\frac{\partial{d}_{e_{r}}^{k}}{\partial{\kappa}_{e_{r}}^{k}}\\ \boldsymbol{0} & \boldsymbol{0} & 0 & 0 & 1\\ \end{array}\right] $$

(81)

where $\phantom {\dot {i}\!}{\partial {d}_{e_{r}}^{k}}/{\partial {\kappa }_{e_{r}}^{k}}$ can be calculated using (69) and

$$ \mathbb{A}=\frac{\partial\boldsymbol{n}_{e_{r}}^{k}}{\partial\boldsymbol{\sigma}_{e_{r}}^{k}}=\frac{1}{\|\boldsymbol{s}_{e_{r}}^{k}\|}(\mathbb{P}_{dev}^{s}-\boldsymbol{n}_{e_{r}}^{k}\otimes\boldsymbol{n}_{e_{r}}^{k}) $$

(82)

Finally, since $\phantom {\dot {i}\!}\boldsymbol {H}_{e}^{k}$ only depends on $\phantom {\dot {i}\!}{\rho }_{e}$, the derivative $\phantom {\dot {i}\!}\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }$ is calculated as

$$ \frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{\rho}}\,=\,\left[\begin{array}{cccc} \frac{\partial\boldsymbol{H}_{1}^{k}}{\partial\rho_{1}} & \boldsymbol{0} & {\dots} & \boldsymbol{0}\\ \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{2}^{k}}{\partial\rho_{2}} & {\dots} & \boldsymbol{0}\\ {\vdots} & {\vdots} & {\ddots} & \vdots\\ \boldsymbol{0} & \boldsymbol{0} & {\dots} & \frac{\partial\boldsymbol{H}_{n_{ele}}^{k}}{\partial\rho_{n_{ele}}}\\ \end{array}\right] \mathrm{\!with} \frac{\partial\boldsymbol{H}_{e}^{k}}{\partial\rho_{e}}\,=\,\left[\begin{array}{c} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\rho_{e}}\\ \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\rho_{e}}\\ \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\rho_{e}}\\ \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\rho_{e}}\\ \end{array}\right] $$

(83)

where the calculation of the term $\phantom {\dot {i}\!}\partial \boldsymbol {H}_{e_{r}}^{k}/\partial {\rho }_{e}$ is different for elastic and plastic steps. For elastic step, it is

$$ \frac{\partial\boldsymbol{H}_{e_{r}}^{k}}{\partial\rho_{e}}=\left[\begin{array}{c} -\frac{\partial\mathbb{C}^{e}}{\partial\rho_{e}}:\boldsymbol{\varepsilon}_{e_{r}}^{e^{k}}\\ \boldsymbol{0}\\ 0\\ 0\\ 0\\ \end{array}\right] $$

(84)

while for plastic step, it is

$$ \frac{\partial\boldsymbol{H}_{e_{r}}^{k}}{\partial\rho_{e}}\,=\,\small\left[\begin{array}{c} -\frac{\partial\mathbb{C}^{e}}{\partial\rho_{e}}:\boldsymbol{\varepsilon}_{e_{r}}^{e^{k}}\\ \boldsymbol{0}\\ 0\\ \!\!-\sqrt{\frac{2}{3}}(1\,-\,d_{e_{r}}^{k})\left(\frac{\partial\sigma_{y_{e}}}{\partial\rho_{e}}\,+\,\frac{\partial\zeta_{e_{r}}^{k}}{\partial\rho_{e}}\right)\,+\,\sqrt{\frac{2}{3}}\frac{\partial d_{e_{r}}^{k}}{\partial\rho_{e}}(\sigma_{y_{e}}\,+\,\zeta_{e_{r}}^{k})\\ 0\\ \end{array}\right] $$

(85)

Here $\phantom {\dot {i}\!}\partial d_{e_{r}}^{k}/\partial \rho _{e}$ can be again calculated by (69). With the material parameters interpolation presented in Section 4.1, following derivatives complete the calculations shown in (85)

$$ \begin{array}{l} \frac{\partial\mathbb{C}^{e}}{\partial\rho_{e}}=p_{1}(E-E_{min})\rho_{e}^{(p_{1}-1)}\mathbb{C}_{0}\\ \frac{\partial\sigma_{y_{e}}}{\partial\rho_{e}}=p_{2}(\sigma_{y}-\sigma_{y_{min}})\rho_{e}^{(p_{2}-1)}\\ \frac{\partial\zeta_{e_{r}}^{k}}{\partial\rho_{e}}=\alpha_{e_{r}}^{k}{p_{3}}(K^{h}-K_{min}^{h})\rho_{e}^{(p_{3}-1)} \end{array} $$

(86)

where $\phantom {\dot {i}\!}\mathbb {C}_{0}$ is the isotropic elasticity tensor evaluated with $\phantom {\dot {i}\!}E = 1$.