1 Introduction

Incorporating the structural optimization method to improve structural fundamental frequencies is a classic technique used to avoid structural resonance, and this approach has attracted a great deal of attention. Typically, there are two fundamental issues regarding the geometric levels of the design variables that must be addressed to allow for realization of this concept. One issue involves the structural parameters, such as the topologies, the boundary curves, and the sizes of structural components, used as design variables (Olhoff 1989; Seyranian et al. 1994; Du and Olhoff 2007). In contrast, the other involves the microstructural parameters of periodic materials, such as the microstructural topologies of the unit cell, used as design variables (Niu et al. 2009; Du and Yang 2015; Du and Sun 2017). Both of these problems have been actively studied, and the classic monograph by Bendsøe and Sigmund (2003) provides information regarding the earlier developments on this topic.

In regard to microstructural design problems, the actual heterogeneous material containing periodic microstructures is typically replaced by a given homogeneous continuum that possesses effective properties, and the structural responses are then calculated using those effective properties. The homogenization of heterogeneous material therefore plays a key role in this topic. The homogenization method, which is based on the perturbation technique, is generally the most commonly used method. In this method, the microstructure is assumed to be infinitely small, and the effective constitutive constants are derived using the perturbation expansion technique (Hassani and Hinton 1999). By using this classic homogenization method, researchers have reported numerous microstructural design studies over the past two decades since Sigmund (1994b) proposed the inverse homogenization strategy of material design. The objective functions in the previous studies are not only confined to the structural frequencies but also include a range of physical properties, such as elastic stiffness (Neves et al. 2000; Chen et al. 2018; Gao et al. 2018), buckling strength (Thomsen et al. 2018), Poisson’s ratio (Sigmund 1994a), thermal expansion coefficient, and conductivity. Previously published reviews provide additional information regarding related studies (Cadman et al. 2013; Osanov and Guest 2016).

The basic assumption that the material microstructural size is infinitely small, however, is sometimes inadequate, as a structure may possess certain local dimensions that are comparable to those of the microstructural sizes. Based on this fact, in these local regions, the effective continuum properties of the actual heterogeneous material cannot be determined by the homogenization method. Prior studies have indicated that the structural responses computed using the effective properties are quite different from the results tested by experiments or computed using the full discretization of the real structures (Onck et al. 2001; Dai and Zhang 2008; Tekoglu and Onck 2008; Liu and Su 2009; Su and Liu 2014). Additionally, it was previously demonstrated that the structural response in regard to effective properties tends to mirror the real response as the material microstructural size becomes smaller. This procedure indicated that the effective properties of heterogeneous material are dependent upon the dimensions of the specimen and upon the size of the material microstructural scale. This phenomenon is typically termed the “size effect” (Onck et al. 2001; Tekoglu and Onck 2008).

It is expected that the optimal results for the microstructural optimization problems are size-dependent, as the effective continuum properties depend upon the size of actual heterogeneous material microstructures. Few studies, however, have focused on the size dependence of the optimal results for microstructural design problems (Zhang and Sun 2006; Huang and Xie 2008). These few studies did report that the optimal topologies of microstructures exhibit size dependence in regard to the maximization of global stiffness for structures composed of periodic cellular solids. In these studies, it was observed that the microstructures of the materials are fully discretized, and expensive computations are therefore required.

Owing to the expensive computations, an alternative means to provide economic computation is necessary. It is well-known that some high-order continuum theories, for example, the couple-stress continuum theory (Mindlin 1963), contain more information regarding the microstructures. This may, therefore, provide a reasonable approach to homogenize the actual heterogeneous material as an effective couple-stress continuum to reveal size dependence in the material design. The couple-stress theory incorporates a local rotation of points in addition to the translation that is assumed in classical elasticity and a couple-stress (a torque per unit area) and the force stress (force per unit area) (Anderson and Lakes 1994). This theory simulates the higher order deformations that occur on the microstructures of a given material, and it has been used successfully for size effects analyses. Additionally, it should be noted that there are other theories, such as the Cosserat theory, that incorporate couple-stress. For details regarding the differences among these theories, the reader is referred to the classic monograph (Eringen 1999).

Although these higher order theories have been widely applied to the size effect analysis of structures, little work has been performed regarding the size dependence of the optimal results for the structural optimization problems. Previous studies have indicated that the optimal results, including structural topologies and the objective functions for the topology design of higher order continuum, depend upon the structural dimensions (Rovati and Veber 2007; Liu and Su 2010; Bruggi and Taliercio 2012; Veber and Taliercio 2012; Su and Liu 2016). In one of our earlier related studies (Su and Liu 2010), we examined the microstructural design problems in regard to the minimization of the structural mean compliance based on the couple-stress continuum model, and we found that the optimal microstructural topologies exhibit remarkable size dependence.

The purpose of this study was to describe and examine the size dependence in regard to the microstructural topology design of periodic cellular solids to achieve the maximal fundamental frequencies of free vibration. We constructed our topology optimization model based upon the couple-stress continuum theory rather than upon the classic continuum theory. In this model, a modified bound formulation of objective and constraint functions was used to avoid the non-differentiability of the repeated frequencies. The numerical examples revealed that the present couple-stress-based optimization model details the size dependence of the optimal results in the microstructural design of periodic cellular solids and improves the weakness of the classic optimization models in regard to the description of the size effects.

2 Couple-stress theory

As mentioned earlier, the couple-stress theory introduces the rotation of points along with translation. This assumption implies that the dimension of a “point” within couple-stress continuum is finite rather than infinitely small. If this assertion were not the case, then the definition of rotation would be meaningless. Hence, a point in couple-stress continuum must have a property to resist its change of rotation motion, as the point has finite dimension. The measure of this resistance is named as the micro-rotation inertia and symbolized by Θ. Micro-rotation inertia plays an important role in the dynamic behavior of couple-stress continuum or Cosserat continuum (de Borst and Sluys 1991). This parameter does not exist in classic continuum, as a point in class continuum is infinitely small. In addition, an element of the couple-stress continuum must incorporate a curvature to represent its curve deformation. Note that this curvature is not included in the classic continuum, as an element of the classic continuum is infinitely small. Similarly, the stress on an element within the couple-stress continuum may vary along the sides due to the finite dimension of the element. The varying stress on the couple-stress continuum element is then approximately replaced by the mean stress and by a torque per unit area that is named as the couple-stress (see Fig. 1).

Fig. 1
figure 1

Effective couple-stress continuum model and classic continuum model for the approximation of the actual varying stress. a actual varying stress. b couples-stress continuum. d classic continuum

Full size image

The homogenization of actual heterogeneous material based on the couple-stress theory is necessarily more accurate than the classic theory. As presented in Fig. 1, the mean stress alone does not represent the varying stress on real microstructures if the stress possesses a significant gradient; however, the effective couple-stress continuum model improves the accuracy by allowing for the incorporation of the couple-stress.

We confined our study to the scope of 2D orthotropic problems in this paper, and we provide an example using the following planar problem. The degrees of freedom (DOF) of a particle is expressed as

$$ \boldsymbol{u}={\left(u,v,\varphi \right)}^T $$
(1)

where u, v, and φ denote the planar translations and the rotation, respectively. The stress and couple-stress components are provided in Fig. 2.

Fig. 2
figure 2

Components of stress and couple-stress in a planar problem

Full size image

It is determined that the cross-shearing stresses are not necessarily equal from the condition of the moment equilibrium of the element. Mindlin (1963) suggested decomposing the asymmetric shearing stresses into a symmetric part τS and an antisymmetric part τA.

$$ {\tau}_S=\left({\tau}_{xy}+{\tau}_{yx}\right)/2,\kern0.66em {\tau}_A=\left({\tau}_{xy}-{\tau}_{yx}\right)/2 $$
(2)

Hence, the constitutive relations of the planar orthotropic couple-stress continuum are expressed as

$$ \left\{\begin{array}{l}{\sigma}_x\\ {}{\sigma}_y\\ {}{\tau}_S\end{array}\right\}=\left[\begin{array}{ccc}{C}_{11}& {C}_{12}& 0\\ {}{C}_{21}& {C}_{22}& 0\\ {}0& 0& {C}_{66}\end{array}\right]\left\{\begin{array}{l}{\varepsilon}_x\\ {}{\varepsilon}_y\\ {}{\gamma}_{xy}\end{array}\right\},\left\{\begin{array}{l}{m}_{xz}\\ {}{m}_{yz}\end{array}\right\}=\left[\begin{array}{cc}{D}_{11}& 0\\ {}0& {D}_{22}\end{array}\right]\left\{\begin{array}{l}{\kappa}_{xz}\\ {}{\kappa}_{yz}\end{array}\right\} $$
(3)

or in a compact form:

$$ \boldsymbol{\sigma} =\boldsymbol{C}\boldsymbol{\varepsilon }, \kern0.66em \boldsymbol{m}=\boldsymbol{D}\boldsymbol{\kappa } $$
(4)

where the classic component C and the couple-stress component D are uncoupling for the orthotropic couple-stress continuum. The strain components εx, εx, and γxy and the curvature components κxz and κyz are defined as follows:

$$ {\displaystyle \begin{array}{l}{\varepsilon}_x=\partial u/\partial x,\kern1em {\varepsilon}_y=\partial v/\partial y,\kern1em {\gamma}_{xy}=\partial u/\partial y+\partial v/\partial x\\ {}{\kappa}_{xz}=\partial \varphi /\partial x,\kern1em {\kappa}_{yz}=\partial \varphi /\partial y\end{array}} $$
(5)

It has been well-documented that the nonzero components of matrix D are dependent on microstructural size while the components of matrix C are size-independent. Mindlin (1963) defined a characteristic length parameter l to denote the size dependence of the couple-stress constitutive constants. The nonzero components of D are thereby expressed as D11 = 4Gl2 and D22 = 4Gl2 for isotropic couple-stress continuum, where G denotes the shearing modulus. The characteristic length l depends on the microstructure of couple-stress continuum. For example, the characteristic length of couple-stress continuum deduced from a periodic heterogeneous material that has square unit cell and dilute circular inclusions is proportional to the length of the cell size (Bigoni and Drugan 2007). The definitions of characteristic lengths for orthotropic couple-stress continuum are more complicated. For a detailed discussion regarding the definitions, the related references should be consulted (Bouyge et al. 2002; Liu and Su 2009).

In addition to D11 and D22, another size-dependent parameter in couple-stress elasticity is the micro- rotational inertia Θ. In contrast, the effective density ρ is size-independent.

The finite element method (FEM) is typically required for the vibration analysis of general structures composed of a couple-stress continuum. The discrete FEM equation was derived from the principle of virtual work of couple-stress continuum.

$$ \boldsymbol{KX}=\boldsymbol{\lambda} \boldsymbol{MX} $$
(6)

where K denotes the structural global stiffness matrix and M is the global mass matrix, X denotes the vibrating mode corresponding to the eigenvalue λ that relates the natural frequency f by λ = (2πf) 2. K and M are assembled by the element stiffness matrix and the element mass matrix, respectively.

Note that the rotation depends upon the translations within the couple-stress elasticity, which is expressed as Eq. (7).

$$ \varphi =\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) $$
(7)

Hence, the C1 continuity is required for the interpolations of displacements of couple-stress elasticity.

3 Optimization formulation

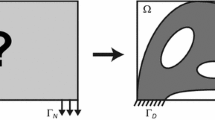
The purpose of this study was to study size dependence in regard to the microstructural design of periodic cellular solids to achieve the maximal structural fundamental frequencies (see Fig. 3). Topology optimization methods that have been widely recognized were used at the cell level. This approach was based upon the inverse homogenization problems defined by Sigmund (1994b). In this model, the topology of the base cell was identified for a given amount of admissible material in a manner that allowed the structural fundamental frequencies to be maximized. The geometry domain of the base cell was regarded as the design domain. A homogenization method was performed to calculate the effective couples-stress continuum constitutive constants that included the components of constitutive matrix C and D, the micro-rotation inertia Θ, and the effective density ρ. Then, the structural fundamental frequencies were computed using the FEM in combination with these effective constitutive constants. It should be noted that some higher order eigenmodes may be missed due to homogenization of the cellular solids to continuum. However, this limitation has little influence on this study, as our objective is to maximize the fundamental frequencies.

Fig. 3
figure 3

Sketch of the microstructural design of periodic cellular solids used for maximization of the structural fundamental frequencies

Full size image

In the procedure, the solid isotropic material with penalization (SIMP) interpolation scheme (Bendsøe 1989; Rozvany et al. 1992) was adopted at the cell level. In this scheme, the geometry domain of a base cell was discretized into small quadrilateral elements, and the artificial density ρi of element i was used as a design variable to describe the topology of that location. Based on the SIMP scheme, the element i has Young’s modulus Esi penalized by the artificial density as

$$ {E}_{si}={\rho}_i^p{E}_0 $$
(8)

where p = 3 is the penalty number and E0 is the Young’s modulus of base material of the real cellular solids. The physical density at element i, ρsi, which should be required in the vibration analysis of structures, was expressed as

$$ {\rho}_{si}={\rho}_i{\rho}_0 $$
(9)

where ρ0 is the physical density of the base material of the real cellular solids (see Fig. 4). Note that in the topology optimization problems regarding macrostructures for the maximization of fundamental frequencies, the interpolation as Eq.(8) and Eq.(9), occasionally results in local vibration modes; however, these local vibration modes did not appear in the present study, as we did not compute the vibration at the cell level.

Fig. 4
figure 4

SIMP scheme at the cell level

Full size image

Next, the effective continuum properties were determined from the analysis of the base cell. As mentioned earlier, to determine the size dependence of the optimal design of unit cells, the couple-stress continuum model was used in this procedure. The homogenization of the classic heterogeneous continuum into a homogeneous couple-stress continuum exhibiting effective properties has attracted a great deal of attention. Here, we used the technique proposed in our previous work (Liu and Su 2009; Su and Liu 2014) that is based on the equivalent strain energy methods. Six loading cases were performed to calculate the nonzero components in constitutive matrices C and D, and one loading case was used to calculate the effective micro-inertia Θ. To ensure that this study was self-contained, a brief introduction of the computation procedure is provided in the Appendix.

The frequencies of the structure composed of the effective couple-stress continuum were computed by the FEM. As mentioned earlier, the C1 continuity is required for the displacement interpolation scheme in the FEM of couple-stress continuum. It is typically difficult to directly develop an appropriate C1 continuous element for a couple-stress continuum. In this study, a penalty constraint was introduced to approximately implement the C1 continuity.

The objective of the optimization formulation was to maximize the fundamental frequencies of structures. The main issue with this type of optimization problem is the non-smoothness or non-differentiability of eigenvalues in common sense when the magnitudes of several eigenvalues coalesce (Seyranian et al. 1994; Bendsøe and Sigmund 2003). The phenomenon of repeated eigenvalues is more prominent in the design of symmetry structures possessing symmetry boundary conditions. This non-differentiability in common sense creates difficulties in finding sensitivities of repeated eigenvalues with respect to design changes and derivation of necessary optimal conditions for the optimization problems. Some special formulations or algorithms have been constructed to handle this non-differentiability problem (Clarke 1990; Seyranian et al. 1994; Rodrigues et al. 1995; Bendsøe and Sigmund 2003). A procedure that combined the bound formulation and the artificial frequency constraints (Bendsøe and Sigmund 2003) to prevent these repeating frequencies was adopted in this study.

The optimization formulation was stated as:

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.33em {\rho}_1,{\rho}_2,...,{\rho}_n,\beta \\ {}\max :\kern0.33em \beta \\ {}\mathrm{s}.\mathrm{t}.:\kern0.33em \boldsymbol{K}{\boldsymbol{X}}_{\boldsymbol{i}}={\boldsymbol{\lambda}}_{\boldsymbol{i}}\boldsymbol{M}{\boldsymbol{X}}_{\boldsymbol{i}},\kern0.33em i=1,2,...,N\\ {}\kern1.98em {\alpha}^i{\lambda}_i\ge \beta, \kern0.33em i=1,2,...,N\\ {}\kern1.98em \sum \limits_{e=1}^n{\rho}_e{v}_e\le {V}^{\ast}\\ {}\kern1.98em 0<{\rho}_{\mathrm{min}}\le {\rho}_e\le 1,\kern0.33em e=1,2,...,n\end{array}} $$
(10)

where ρi denoted the artificial density variables on the cell level while β was a bound variable. ve denoted the volume of element e, and V* denoted the permitted solid material amount. n denoted the number of the density variables. N was an integer number that was larger than the possible repeating number of fundamental frequencies of the designing structures, and N was set 3 in this study. The eigenvectors were M-orthonormalized as

$$ {\boldsymbol{X}}_{\boldsymbol{i}}^{\boldsymbol{T}}\boldsymbol{M}{\boldsymbol{X}}_{\boldsymbol{j}}={\delta}_{ij},\kern0.99em i,j=1,2,...,N $$
(11)

where δij denoted the Kronecker’s delta.

The purpose of the introduction of the artificial constraints αiλi ≥ β, i = 1,…, N, where each frequency was multiplied with α at the power i was to slightly separate the adjacent eigenvalues to prevent the repeated eigenvalues. The parameter α was a number that was less than and close to 1. Hence, these constraints required that the frequency be progressively larger from mode one to mode N (Bendsøe and Sigmund 2003). Although it is impossible to prove the validity of this formulation rigorously, it does work well for most cases in practice, according to Bendsøe and Sigmund (2003) and other experience (Tsai and Cheng 2013; Su and Liu 2016). The exact value of the parameter α in the modified bound constraint was heuristic. We chose α as 0.95 in this study.

The optimization problem was solved by the method of moving asymptotes (MMA) (Svanberg 1987), where the gradients of the objective function and the constraint functions with respect to changes in the design variables were required. This procedure of computing the gradients of objective or constraint functions with respect to design variables is usually termed “sensitivity analysis.” The focus of the sensitivity analysis in the present optimization formulation was to allow for the computations of the gradients of the eigenvalues to the density design variables. This procedure was implemented straightforward according to the method presented in Eq. (12), as the repeated frequencies were already prevented.

$$ \frac{\partial {\lambda}_i}{\partial {\rho}_e}={\boldsymbol{X}}_i^T\left(\frac{\partial \boldsymbol{K}}{\partial {\rho}_e}-{\lambda}_i\frac{\partial \boldsymbol{M}}{\partial {\rho}_e}\right){\boldsymbol{X}}_i,\kern0.99em i=1,2,...,N,\kern0.33em e=1,2,...,n $$
(12)

According to the global stiffness matrix and the mass matrix assembling procedure of the standard FEM, the key step in Eq. (12) was the computations of ∂ke/∂ρe and ∂me/∂ρe, where ke denoted the element stiffness matrix and me was the element mass matrix. Additionally, according to the definitions of element stiffness matrix and mass matrix, only the gradients of the effective constitutive constants with respect to the design variables required computation, and these values were ∂C/∂ρe, ∂D/∂ρe, ∂ρ/∂ρe, and ∂Θ/∂ρe. Among these terms, ∂C/∂ρe and ∂D/∂ρe were reported in our previous work (Su and Liu 2010). Hence, this study provided only the expressions of ∂ρ/∂ρe and ∂Θ/∂ρe.

From the definition of the effective density ρ

$$ \frac{\partial \rho }{\partial {\rho}_e}=\frac{\rho_0{v}_e}{\sum \limits_{i=1}^n{v}_i},\kern0.66em e=1,...,n $$
(13)

Similarly, from the definition of the effective micro-rotational inertia Θ

$$ \frac{\partial \varTheta }{\partial {\rho}_e}=\frac{1}{\sum \limits_{i=1}^n{v}_i}\left({\rho}_0{I}_{pe}-{I}_p\frac{\partial \rho }{\partial {\rho}_e}\right),\kern1.32em e=1,...,n $$
(14)

where Ipe denoted the polar moment of inertia of element e in the unit cell with respect to its centroid and Ip denoted the polar moment of inertia of the whole unit cell with respect to its centroid.

In addition, density filter (Bruns and Tortorelli 2001) was applied to prevent the checkerboard pattern and mesh dependency of the optimal topology.

4 Numerical examples

It is important to reiterate that the aim of this study was to explore the size dependence of the optimal results for the microstructural topology design of a periodic cellular solid for maximizing the structural fundamental frequencies. As this size dependence is difficult to determine using the homogenization method based on the classic continuum theory, we constructed our topology optimization formulation based on the couple-stress continuum theory.

In this section, two typical numerical examples were presented to verify the present topological optimization formulation. In each example, the structure was composed of periodic cellular solids and possessed fixed shape and size. The optimal microstructures of the unit cells possessing different sizes for the maximization of the structural fundamental frequencies were designed to investigate the size dependence of the optimal results. The unit cell was assumed to be centrosymmetric in each case for simplicity, as the effective couple-stress continuum of this material is orthotropic, and the constitutive matrices C and D are uncoupling. This symmetric assumption may slightly affect the optimal results, as it introduces an additional constraint. However, this constraint is valuable, as the symmetric cells are usually manufactured more easily. The base material used for each cellular solid was aluminum, as this material exhibits a Young’s modulus E0 = 69GPa, a Poisson’s ratio ν0 = 0.3, and a density ρ0 = 2.7 × 103 kg/m3 without a loss of generality.

4.1 Exampe 1

A simply supported beam-like structure shown in Fig. 5 was considered for this example. The structure possesses a fixed length L = 20 mm, a height H = 10 mm, and unit thickness. It was composed of periodic cellular solids with microstructure of unit cell that was designed to achieve maximal fundamental frequencies for the structures. The amount of the permitted material was 0.4. It was assumed that the unit cells of the cellular solids possessed square domains. Each square cell possessed a side length h that varied for different cases. To assess the size dependence of the results, a scale factor n = H/h was defined. The topology optimization problems with n = 2~5 were solved. In each case, 1/4 base cell was studied due to the symmetry.

Fig. 5
figure 5

Beam-like structure composed of periodic cellular materials

Full size image

Using the method described above, the topologies of the unit cells at different scale factor n were obtained. Taken together, the optimal microstructural topologies varied as the scale factor n or the microstructural size changed, and this is illustrated in Table 1. For the convenience of observation, the topologies of 1/4 cell, one cell, and 3 × 2 cells for each case were all listed in this table.

Table 1 Optimal microstructural topologies at different cell sizes for cellular solids described in Example 1
Full size table

The microstructural topologies based on the classic continuum theory were also listed in this table for comparison. These results demonstrated that the classic continuum model cannot reflect the size dependence of the optimal microstructural topologies.

Additionally, the optimal fundamental frequencies at different cell sizes obtained by the present method were reported in Fig. 6. Again, the corresponding results obtained by the classic continuum model were shown for comparison. In general, the fundamental frequencies based on the couple-stress continuum model exhibited size dependence, while the results based on the classic model possessed size-independence. The fundamental frequency of the couple-stress model was over 17% larger than that of the classic model for n = 2. Additionally, this value dropped rapidly as n increased and was nearly equal to the classic value for n = 5. Hence, the present couple-stress optimization model described the size dependence successfully.

Fig 6
figure 6

Maximal fundamental frequencies of the structures versus cell sizes for Example 1

Full size image

The size dependence of the structural fundamental frequencies could be due to the size dependence of the constitutive constants of the effective couple-stress continuum. As illustrated in Fig. 7, the effective bending constants D11 and D22 and the micro-rotational inertia Θ all possessed high values at n = 2 and decreased rapidly to almost zero as n increased from 2 to 5. These trends were similar to those of the fundamental frequencies (see Fig. 6); however, it should be noted that the influences of these two types of constants on the fundamental frequencies are totally opposite. In general, the decreasing of D11 and D22 decreases of the fundamental frequencies of a structure composed of a couple-stress continuum while the decreasing of Θ increases the frequencies. Hence, the above results indicated that the influence of the bending constants D11 and D22 on the size dependence of the maximal fundamental frequencies may be a primary factor, while the micro-rotational inertia may be a secondary factor. This observation was in good agreement with our previous conclusions (Su and Liu 2014, 2016).

Fig. 7
figure 7

Effective constitutive constants of the optimal cellular solids versus cell sizes in Example 1: (a) D11 and D22, (2) Θ

Full size image

Additionally, other effective constitutive constants also exhibited size dependence. The effective constants at different cell sizes were summarized in Table 2. Unlike the bending constants and the micro-rotational inertia, these rest constants did not exhibit evident trends. In fact, these classic constants were incapable of describing size dependence. Hence, these slight size-dependent differences may be caused by the size dependence of the higher order constants (e.g., D11 and D22).

Table 2 The constitutive constants of the optimal cellular solids versus cell size
Full size table

The aim of this study was to investigate the size dependence of microstructural design of periodic cellular solids to possess maximal fundamental natural frequencies. To avoid expensive computation, this study considered the cellular solids as couple-stress continuum. Hence, the comparison of the present method and the fully discrete method is interesting. We tried to compare these two methods in this example for the case n = 2 and 3, as they contained only small number cells; even then, the computation was still expensive. Hence, only coarser meshes were adopted in the discrete models. The results showed that the two methods obtained similar structural topologies and same size-dependent trends (see Table 3). Additionally, the optimal fundamental frequencies of discrete models were lower than those of the couple-stress models. This difference may be caused by the coarser meshes of discrete models, and better frequencies are expected for finer meshes. However, more efficient and stable computational technique is required, and this extends the scope of the present study.

Table 3 Comparison of couple-stress model and fully discrete model: topologies and fundamental frequencies
Full size table

4.2 Exampe 2

A rectangular structure possessing a small rectangular void was considered for this example. The structure was clamped at each of its four corners as shown in Fig. 8. The structure contained unit thickness and possessed the sizes L1 = 40 mm, L2 = 20 mm, H1 = 30 mm, and H2 = 10 mm. The scale factor n was defined as n = (H1-H2)/2h in this example, as it was expected that the bending deformation of a given portion was the dominant mode in the free vibration. Without a loss of generality, the amount of permitted solid material in the base cell of the solid material was still 0.4. Again, 1/4 cell was studied due to symmetry, and the topologies were obtained for n = 2~5.

Fig. 8
figure 8

Rectangular structure possessing a rectangular void composed of periodic cellular material

Full size image

In contrast to the previous example, repeated frequencies exhibiting different mode shapes were observed for this example. The iteration history of n = 2 was given in Fig. 9. As detailed in this figure, f1 and f2 were very close during the iteration process, and the relative error of these two frequencies in the optimal results was as small as 2.06%. The stable convergence indicated that the bound formulation used in the present study was effective. Additionally, the repeated frequencies were also found in other cases of n, and the iteration histories were summarized in Table 4. In each case, the repeated frequencies were separated numerically to ensure that the sensitivity analysis was performed correctly.

Fig. 9
figure 9

Iteration histories of the first three frequencies of the structure for n = 2

Full size image
Table 4 Optimal first two frequencies of the structure for n = 2~5
Full size table

Again, the topologies of the unit cells at n = 2~5 were identified to examine the size dependence of the optimal results in this example. All results from these analyses were listed in Table 5, and the optimal topologies from the classic continuum model were also included. Similar to example 1, it was evident from the results that the couple-stress-based results were size-dependent, while the classic theory-based results exhibited no size dependence.

Table 5 Optimal microstructural topologies at different cell sizes for cellular solids in Example 2
Full size table

The fundamental frequencies of the structure contained within the optimal unit cells also displayed remarkable size effects (Fig. 10). The fundamental frequency of the couple-stress model was higher by as much as 16.9% compared to that of the classic model for n = 2. As n increased, the fundamental frequencies dropped rapidly, and this value was 5.7% larger than that of the classic method for n = 5. It should be noted that this size dependence cannot be revealed by the classic continuum models.

Fig. 10
figure 10

Maximal fundamental frequencies of the structures versus cell sizes for Example 2

Full size image

As stated earlier, there was a strong possibility that the size dependence of the structural fundamental frequencies was the result of the size dependence of the constitutive constants of the studied effective continuum. Figure 11 indicated that the effective bending constants D11 and D22, as well as the effective micro-rotational inertia Θ, were strongly dependent upon cell size. The values of these constants were large at n = 2 and dropped rapidly toward zeros as n increased. Additionally, the slope of this drop gradually decreased as n increased. Note that D11 and D22 nearly coincided in this example; however, this was likely just a coincidence.

Fig. 11
figure 11

Effective constitutive constants of the optimal cellular solids versus cell sizes in Example 2: (a) D11 and D22, (2) Θ

Full size image

In addition to the above three constants, other constants, with the exception of the effective densities, exhibited size dependence. For convenience, all the effective constants versus the scale factor n were summarized in Table 6. Again we found that the size dependence of nonzero components of the sub-matrix C of constitutive was irregular, and this finding was different from those of D11, D22, and Θ.

Table 6 The constitutive constants of optimal cellular solids versus cell size
Full size table

5 Discussion

Prior studies (Sigmund 1994a; Sigmund 1994b; Neves et al. 2000; Niu et al. 2009; Cadman et al. 2013; Osanov and Guest 2016; Chen et al. 2018) have documented the feasibility of the design of microstructures in improving structural global properties such as the global stiffness, the bulk modulus, and the shearing modulus. Most of these studies, however, are based on the effective classic continuum model and have used the homogenization method to represent the effective properties of actual heterogeneous solids. Those formulations have ignored the influence of the cell size on the structural properties due to the assumption of infinitely small cell scale.

In this study, we developed a microstructural topology optimization model based on the effective couple-stress continuum model to maximize the fundamental frequencies of structures composed of periodic cellular solids. The numerical examples demonstrated that our optimization model recognized the size-dependent features of the optimal results. We found that the size effects of the optimal results influenced both the optimal fundamental frequencies and the corresponding microstructural topologies.

The size effects were described quantitatively along with the optimal fundamental frequencies in the present optimization model. When the cell sizes of the researched cellular solids were close to the key dimensions of structures (n = 2, for example), the structural fundamental frequencies based on the present couple-stress model could be more than 15% larger than those of the classic model. As the cell sizes decreased gradually, the couple-stress model-based fundamental frequencies tended to mirror the classic theory-based results. The relative error between these two models was often less than 5% for n = 5.

The size effects were also directly indicated by the optimal microstructural topologies in this model. When the cell sizes of the cellular solids were close to the key dimensions of the structures, the optimal topologies typically possessed a common layout, where the most material lay on the boundary regions of the cell domains. The optimal topologies tended to exist as a “truss-like” layout, however, as the cell sizes decreased gradually. It should be noted that the truss-like microstructures are typically the optimal layouts of the classic continuum for the maximal global stiffness.

These two different layouts of material influenced the constitutive constants and the optimal results in different ways. The material existing at the boundary regions of cell domains almost always produces larger bending constants D11 and D22 and micro-rotational inertia Θ (Bigoni and Drugan 2007; Liu and Su 2009; Su and Liu 2014). In contrast, the truss-like layout of material constructing the stretching-governed structures always produces structures that exhibit excellent stiffness per unit mass (Deshpande et al. 2001). This high specific stiffness of these structures often results in high fundamental frequencies of natural vibration.

Given this, it is highly probable that the size dependence is caused by the transition of these two mechanisms for the improvement of the structural fundamental frequencies. When the cell sizes are large, n = 2, D11 and D22 are also large. As these bending constants dominantly influence the natural vibration behavior, improvement of these two constants provides an economical means to maximize the structural fundamental frequencies. Therefore, finite amounts of solid materials tend to exist at the boundary regions of the cells, ultimately allowing for larger bending constants and larger fundamental frequencies. When the cell sizes are small, however, the bending constants become small, and they influence the structural fundamental frequencies slightly. Hence, an effective approach to enhance the structural fundamental frequencies is to improve the specific stiffness of the effective continuum, for a method that is used for the classic continuum. This size effect deduced by the transition of two mechanisms that allows for the improvement of structural global properties is also confirmed in our previous work, where we attempted minimization of the structural compliance (Su and Liu 2010).

Additionally, it should be noted that the maximal fundamental frequencies decrease as the cell sizes become small. As discussed earlier, the bending constants D11 and D22 approach zero as the cell sizes decrease. Hence, the global stiffness of structures declines, and the optimal fundamental frequencies drop accordingly. Similar trends have been reported in cell design studies examining the maximization of structural global stiffness (Zhang and Sun 2006; Huang and Xie 2008; Su and Liu 2010).

Interestingly, we observed that both the bending constants and the micro-rotational inertia show the same size-dependent trends; however, they influence the structural fundamental frequencies in completely opposite ways. In our previous work (Su and Liu 2014, 2016), we documented that the D11 and D22 are the dominant factors in regard to the free vibration of couple-stress continuum structures.

The present method is suitable for the design of structures possessing some local dimensions comparable to those of the microstructural sizes of the composed materials, as the effective couple-stress continuum model does not require that the microstructural size of a material is infinitely small. For example, the topology design of structures composed of geometry gradient materials, which can be manufactured by the additive manufacturing process, can be finished by this method. Note that constraints due to manufacturability must also be considered prior to the initiation of final engineering applications. These considerations, however, are beyond the scope of this study.

The present formulation is not recommended to design beam-like structures with only one cell in height, as local deformations on the cell level may sometimes be remarkable. The fully discrete method is suggested in such extreme case.

6 Conclusions

In this study, a topology optimization formulation to allow for the design of the microstructures of periodic cellular solids to maximize the structural fundamental frequencies was proposed. The cellular solids were homogenized as a couple-stress continuum rather than as a classic continuum in an attempt to interpret the influence of cell size on the optimal results.

Based on our results, we have formulated the following conclusions:

The present formulation based on the couples-tress continuum model confirms both the size dependence of the maximal structural fundamental frequencies and that of the corresponding optimal microstructures. Hence, it improves on the limitations of the classic continuum models that are unable to describe the size dependence of the optimal results.

The maximal structural fundamental frequencies based on the present couple-stress continuum optimization model are larger than those derived from the classic continuum optimization model, as the latter model ignores the influences of the microstructural scale on the global structural responses. Additionally, the optimal frequencies derived from the couples-tress model tend to mirror those of the classic model as the microstructural sizes decrease. Similar trends are also observed in regard to the microstructural topologies.

This couple-stress continuum-based optimization model is useful for the microstructural design of structures possessing local dimensions that are comparable to the microstructural size.