Optimization of elastic spring supports for cantilever beams

Abstract

In this study,a new approach of optimization algorithm is developed. The optimum distribution of elastic springs on which a cantilever Timoshenko beam is seated and minimization of the shear force on the support of the beam is investigated.The Fourier transform is applied to the beam vibration equation in the time domain and transfer function, independent from the external influence, is used to define the structural response. For all translational modes of the beam, the optimum locations and amounts of the springs are investigated so that the transfer function amplitude of the support shear force is minimized. The stiffness coefficients of the springs placed on the nodes of the beam divided into finite elements are considered as design variables. There is an active constraint on the sum of the spring coefficients taken as design variables and passive constraints on each of them as the upper and lower bounds. Optimality criteria are derived using the Lagrange Multipliers method. The gradient information required for solving the optimization problem is analytically derived. Verification of the new approach optimization algorithm was carried out by comparing the results presented in this paper with those ones from analysis of the model of the beam without springs, with springs with uniform stiffness and with optimal distribution of springs which support a cantilever beam to minimize the tip deflection of the beam found in the literature. The numerical results show that the presented method is effective in finding the optimum spring stiffness coefficients and location of springs for all translational modes.The proposed method can give designers an idea of how to support the cantilever beams under different harmonic vibrations.

1 Introduction

Beams are widely used in constructions, particularly in bridges, buildings, frame structures, beam-floors, supporting structures. Design of support for structures is an important element of engineering practise. In addition to the basic function of maintaining the structure in stability, proper support influences the optimal work of the structure. Beams are used as structural elements in many engineering problems and there are a large number of studies in the literature about transverse vibration of uniform isotropic beams (Gorman 1975). For many years, researchers have been interested in issues related to the optimization of structural support in order to improve the properties of elements such as reducing the maximum deflections, bending moments (Imam and Al-Shihri 1996), increasing natural frequency and buckling coefficient (Won and Park 1998; Liu et al. 1996), reducing stress and strain (Marcelin 2001). Prager and Rozvany (Prager and Rozvany 1975) presented the optimal locations of supports and steps in yield moment. Wang (Wang 1993; Wang 2003; Wang 2004; Wang 2006)and Wang et al. (Wang and Chen 1996; Wang et al. 2004; Wang et al. 2006; Wang et al. 2010) presented detailed analysis of the location of supports and parameters of supports for different cases. In the paper (Wang and Chen 1996), the formulas for computing eigenvalue sensitivity with respect to location of in-span occurrence with application of normal mode method are presented.The eigenvalue sensitivity depends on the slope of Eigen function as well as a force term which depends on the specific occurrence. The quantitative data can be used to find locations of in-span occurrences to maximize the fundamental eigenvalue of a structure member. Wang and Chen (Wang and Chen 1996) propose the genetic algorithms for the optimization problem of beam with rigid and elastic supports. Using genetic algorithms, the gradient information is not needed. The optimum location and the minimum stiffness of internal support for beams with different end conditions are presented in the work of Wang (Wang 2003). In another study, Wang (Wang et al. 2004) investigated the design sensitivity analysis for the deflection of a beam or plate structure with respect to the position of a simple support using the discrete method. Also a heuristic optimization algorithm, called the evolutionary shift method, is presented for support position optimization with the objective of minimizing the maximum deflections. The minimum stiffness of a simple support that increases a natural frequency of a beam to its upper limit is developed by Wang et al. (Wang et al. 2006) for various boundary conditions. The sensitivity analysis of the bending moment is investigated with regard to the movement of a simple support position by using the adjoint variable method. In this procedure, both elastic and rigid supports are taken into account, and a closed-form expression for the moment derivative is generated. On the basis of the design sensitivity, a heuristic optimization algorithm is applied to minimize the maximal bending moment under multiple load cases. In order to improve the structural performance, an optimization scheme of minimization of maximal absolute bending moment in a planar frame was presented by Wang (Wang 2006) to find optimal design of the support position. The structural deflection is substantially reduced without additional material. The Rayleigh–Ritz method is employed to determine the minimum stiffness location of the elastic point support for raising the fundamental natural frequency of a rectangular plate to the second frequency of the unsupported plate in thepaper of Wang et al. (Wang et al. 2010). Courant and Hilbert (Courant and Hilbert 1953) stated that the optimum locations, if the supports are rigid,should be at the nodal points of a higher vibration mode, and the fundamental frequency is correspondingly raised. Akesson and Olhoff (Akesson and Olhof 1988) studied the influence on Eigen frequencies of varying locations and stiffnesses of one or two additional lateral supports for a cantilever Euler-Bernoulli beam as well as sensitivities and cost optima are discussed. The application of Courant’s maximum-minimum principle to the problem of maximum increase of the lowest undamped Eigen frequency in flexural vibration of beams is reviewed.

Analysis of support stiffness is also important in buckling problems (Timoshenko and Gere 1961). In many cases, the choice of proper support stiffness or in the extreme case, the resignation from it in a specific location does not worsen the working conditions of the element. Maurizi and Rossit (Maurizi and Rossit 1987) analysed case of the effect of finite rigidity of the intermediate supports. They focused on characteristic equation of transverse vibrations of clamped beams with an intermediate translational constraint. Rao (Rao 1989) presented the explicit and exact frequency and mode-shape expressions for the clamped-clamped uniform beams with intermediate elastic support.Kukla (Kukla 1991) dealt with the problem of free vibration of a combined system consisting of a Timoshenko beam and multi-mass oscillators. The formulation and solution of the problem comprises the systems of the beam with many oscillators, which are attached to it at arbitrary points. The solution is found by applying the Green function method. The effect of an oscillator on the frequencies of the combined system is investigated. The author presents the influence of the location of two and three-degree-of-freedom oscillators attached to a cantilever beam on a few first frequencies of the vibration systems. Won and Park (Won and Park 1998) proposed a procedure to find the location of optimal support positions of a structure while varying its support stiffness in which the fundamental eigenvalue of the structure is maximized. The optimal design for beam structures including position and stiffness of supports are also discussed in other papers (Mroz and Rozvany 1975; Rozvany 1975; Szelag and Mroz 1978; Mroz and Lekszycki 1982; Garstecki and Mroz 1987; Dems and Turant 1997; Bojczuk and Mroz 1998; Mroz and Haftka 1994). Bojczuk and Mroz (Bojczuk and Mroz 1998b) had presented a method for trusses. Ching and Gene (Ching and Gene 1992) developed various sensitivity equations for eigenvalue sensitivity analysis of planar frames with variable joint and support locations. Liu et al. (Liu et al. 1996) presented a method to derive the equations of eigenvalue rate with respect to the support location using the generalized variational principles of the Rayleigh quotient. Son and Kwak (Son and Kwak 1993) developed a sensitivity formula of eigenvalues with respect to the change of boundary conditions by using material derivative concept based on variational formulation. A theoretical formulation was presented by Sinha and Friswell (Sinha and Frishwell 2001) for estimating support location. Buhl (Buhl 2001) demonstrated a method for support distribution using a continuum type topology optimization. Olhoff and Taylor (Olhoff and Taylor 1998) studied optimal design of non-uniform, elastic, continuous columns with unspecified number of available interior supports.Olhoff and Akesson (Olhoff and Akesson 1991) studied support optimization of a column to maximize the buckling load. Jihang and Weighong (Jihang and Weighong 2006) studied to maximize the natural frequency of structures and presented the support layout design that corresponds to optimization of boundary conditions. Albaracinet al. (Albaracin et al. 2004) investigated the problem of a uniform beam with intermediate constraints and theends areelastically restrained against rotation and translation. Friswell and Wang (Friswell and Wang 2007) developed a procedure to calculate the minimum stiffness and the optimal position of one or two elastic supports lying along the free edge opposite to the restrained boundary edge of the plate. Kong (Kong 2009) analysed the vibration of plates with various boundary and internal support conditions and proposed a computational technique to determine the optimal location and stiffness of discrete elastic supports in maximizing the fundamental frequency of both isotropic plates and composite plates. The magnitude of mass and stiffness of a linear spring that supports a beam element are well known key parameters affecting the free vibration characteristics of a beam in the existing literature. In addition to this, the offset of each linear spring, which supports a beam, is also the predominant parameter (Lin 2010). Zhu and Zhang (Zhu and Zhang 2010) proposed an integrated layout optimization method to deal with the simultaneous design of structure and support layout. Fayyah and Razak (Fayyah and Razak 2012) studied the effect of deterioration in the elastic bearing support stiffness on the dynamic properties of structural elements, in order to determine the sensitivity of dynamic properties as a tool for monitoring the condition of supports. Aydin (Aydin 2014) investigated the optimal spring distribution including both optimal value of the stiffness coefficients and optimal locations of springs at thefirst-three modes. The study of Aydin (Aydin 2014) includedthe minimizationofboth the tip displacement and the tip absolute acceleration of a cantilever beam.

In the vibration of cantilever beams constructed on elastic foundations, the position and the rigidity of these supports are a matter of concern. The design and distribution of elastic supports supporting these beams will vary in different vibrations of the beam. Commonly displacement-based methods and research can be demonstrated, as well as force-based methods. Sometimes internal forces can exceed the yield limits, which is important for damage.Furthermore, the effect of the springs above these internal forces in case of the different vibration modes should be examined and the sensitivity of the behaviour parameters according to these design variables must be revealed.In this study, the optimization of locations and amounts of the springs are investigated to minimize the support shear force corresponding to all translational modes of a cantilever beam supported by elastic springs. A new method has been shown for the analysis and design of the support conditions of the beams based on the elastic foundation, in order to find optimal values of the stiffness of the springs using transfer functions of support shear force for different modes of vibration. The equation of motion, the transfer function of the support shear force, and the equations for their amplitudes are derived. For the optimization problem defined on the basis of the Lagrange multipliers method, the optimality criteria and the analytical formulation of sensitivities are derived. An algorithm is proposed to find the optimal spring coefficient and the location of the springs. The proposed method is tested on a numerical example with both optimization-related analyses and frequency and time-domain calculations.

In many studies available in the literature, displacements and in some studies, the acceleration is minimized and they are displacement-based methods. Many studies are focused on maximizing the fundamental frequencies. In this study, a force based method is aimed. Reduction of displacements is important and the minimizing of the specified forces is also another important aspect of engineering. The main advantage of this study is that it is an alternative to displacement based methods. From the engineering point of view, the yield of internal forces is undesirable. In this way, it is important to minimize the forces. Furthermore, the sensitivity equations given in this study are analytically derived and are defined depending on the transfer functions. In the literature, there is a gap on optimal support design using different modes. This study proposes to find optimal springs whichare based oncantilever beams by using different vibration modes. Using the equations derived for the proposed method, it assists in selecting the most suitable support positions through the different spring-supported beams provided.

2 Theoretical background of the analysed problem

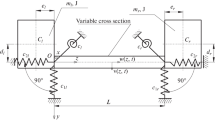
The problem is focused on a cantilever Timoshenko beam supported by elastic springs. For the proposed method, the structural system can be different as beams, frames and truss systems, while the general equations andthe method given here do not change. In the case where the cantilever beam subjected to supporting springs and its nodal displacements and rotations are shown in Fig. 1(a),let us consider cantilever Timoshenko beam of length L, solid square cross section A, bending stiffness EI and elastic springs supporting the beam. The beam is subjected to vertical support acceleration. There is a lumped mass at tip of the beam. In order to model the cantilever beam and the supporting springs, the beam is divided into n finite elements. Translational and a rotational component of the beam motion are defined at each node. The potential locations of the springs are defined at each node. The initial node is defined from the left except for the fixed end. The spring supports act only in the vertical direction. In the specified locations of the beam, stiffness coefficients k = {k₁,k₂,…,k_n} of supporting springs indicate the design variables; and n presents the number of design variables. Let u_i and θ_i be assigned as the dynamic transverse displacement and the angle of rotation at the i^th node of the beam. As shown in Fig. 1(a), while the dynamic displacement vector can be presented as u = {u₁,θ₁,…,u_n,θ_n}^T,M and K denotes the mass and stiffness matrices of beam model and C denotes the structural damping matrix that are determined as either mass proportional damping or stiffness proportional damping. The element stiffness matrix k for Timoshenko beams is given as (Przemieniecki 1968):

$$ k=\frac{\mathrm{EI}}{{\mathrm{L}}^3\left(1+\phi \right)}\left[\begin{array}{cccccc}& 12& & & & \mathrm{Sym}\\ {}6\mathrm{L}& & {\mathrm{L}}^2\left(4+\phi \right)& & & \\ {}-12& & \kern2em -6\mathrm{L}& & 12& \\ {}6\mathrm{L}& & \kern1em {\mathrm{L}}^2\left(2-\phi \right)& & -6\mathrm{L}& {\mathrm{L}}^2\left(4+\phi \right)\end{array}\right] $$

(1)

Fig.1

(a) Cantilever beam based on elastic springs and its nodal displacements and rotations (b) The amplitude of the transfer function of the support shear force for uncontrolled and controlled cases

whereI present the second moment of area and $\upphi =\frac{12\mathrm{EI}}{\mathrm{G}\upkappa \mathrm{A}{\mathrm{L}}^2}$, the element mass matrix m is written as follows

$$ m=\frac{\uprho \mathrm{AL}}{{\left(1+\phi \right)}^2}\left[\begin{array}{ccc}{\mathrm{m}}_1\kern0.5em & & \mathrm{Sym}\\ {}{\mathrm{m}}_2\kern0.5em {\mathrm{m}}_5& & \\ {}\begin{array}{cc}\begin{array}{c}{\mathrm{m}}_3\\ {}{\mathrm{m}}_4\end{array}& \begin{array}{c}-{\mathrm{m}}_4\\ {}\kern0.75em {\mathrm{m}}_6\end{array}\end{array}& \begin{array}{c}\kern0.75em {\mathrm{m}}_1\\ {}-{\mathrm{m}}_2\end{array}& \begin{array}{c}\\ {}{\mathrm{m}}_5\end{array}\end{array}\right]+\frac{\uprho \mathrm{AL}}{{\left(1+\phi \right)}^2}{\left(\frac{\mathrm{r}}{\mathrm{L}}\right)}^2\left[\begin{array}{ccc}\begin{array}{cc}{\mathrm{m}}_7& \end{array}& & \mathrm{Sym}\\ {}\begin{array}{cc}{\mathrm{m}}_8& {\mathrm{m}}_9\end{array}& & \\ {}\begin{array}{cc}\begin{array}{c}-{\mathrm{m}}_7\\ {}\kern0.75em {\mathrm{m}}_8\end{array}& \begin{array}{c}-{\mathrm{m}}_8\\ {}\kern0.5em {\mathrm{m}}_{10}\end{array}\end{array}& \begin{array}{c}\kern0.5em {\mathrm{m}}_7\\ {}-{\mathrm{m}}_8\end{array}& \begin{array}{c}\\ {}{\mathrm{m}}_9\end{array}\end{array}\right] $$

(2)

Let $r=\sqrt{\frac{I}{A}}$ denote the radius of gyration of cross-section and the elements of element mass matrix be given as

$$ {m}_1=\frac{13}{35}+\frac{7\phi }{10}+\frac{\phi^2}{3}{m}_2=\left(\frac{11}{210}+\frac{11\phi }{120}+\frac{\phi^2}{24}\right)L{m}_3=\frac{9}{70}+\frac{3\phi }{10}+\frac{\phi^2}{6}{m}_4=-\left(\frac{13}{420}+\frac{3\phi }{40}+\frac{\phi^2}{24}\right)L{m}_5=\left(\frac{1}{105}+\frac{\phi }{60}+\frac{\phi^2}{120}\right){L}^2\ {m}_6=-\left(\frac{1}{140}+\frac{\phi }{60}+\frac{\phi^2}{120}\right){L}^2{m}_7=\frac{6}{5}{m}_8=\left(\frac{1}{10}-\frac{\phi }{2}\right)L{m}_9=\left(\frac{2}{15}+\frac{\phi }{6}+\frac{\phi^2}{3}\right){L}^2{m}_{10}=\left(-\frac{1}{30}-\frac{\phi }{6}+\frac{\phi^2}{6}\right){L}^2 $$

(3)

When the system does not have any spring, the equation of motion can be written as follows:

$$ \boldsymbol{M}\ddot{\boldsymbol{u}}(t)+\boldsymbol{C}\dot{\boldsymbol{u}}(t)+\boldsymbol{Ku}(t)=-\boldsymbol{Mr}{\ddot{u}}_g(t) $$

(4)

where$\ddot{\boldsymbol{u}}(t),\kern0.5em \dot{\boldsymbol{u}}(t)$ andu(t) are acceleration, velocity and displacement vectors, respectively. The r denotestheinfluence vector asr={1,0,…,1,0}. ${\ddot{u}}_g(t)$is defined as vertical support acceleration. If Fourier Transformation is applied on Eq. (4), U(ω)and${\ddot{U}}_g\left(\omega \right)$are the Fourier Transformation of u(t)and${\ddot{\ u}}_g(t)$. In this case, the Eq. (4) is rewritten as

$$ \left(\boldsymbol{K}+ i\omega \boldsymbol{C}-{\omega}^2\boldsymbol{M}\right)\boldsymbol{U}\left(\omega \right)=-\boldsymbol{Mr}{\ddot{U}}_g\left(\omega \right) $$

(5)

whereω denotes the circular frequency of the excitation, and i denotes $\sqrt{-1}$. As shown in Fig. 1(a), if the beam is supported by elastic springs, Eq. (5) is modified into

$$ \left(\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right)+ i\omega \boldsymbol{C}-{\omega}^2\boldsymbol{M}\right){\boldsymbol{U}}_{\boldsymbol{s}}\left(\omega \right)=-\boldsymbol{Mr}{\ddot{U}}_g\left(\omega \right) $$

(6)

Here K_s denotes the stiffness matrix of the supporting springs. U_s(ω)is the Fourier Transform of the displacements after the springs are included. A transfer function is defined as follows

$$ \overset{\sim }{\boldsymbol{U}}\left(\omega \right)=\frac{{\boldsymbol{U}}_{\boldsymbol{s}}\left(\omega \right)}{{\ddot{U}}_g\left(\omega \right)} $$

(7)

If ω=ω_nis selected here, the ground motion will be defined as a harmonic motion with natural circular frequency ω_n. Using Eq. (7), Eq. (6) can be rewritten as

$$ \boldsymbol{A}\overset{\sim }{\boldsymbol{U}}\left({\omega}_n\right)=-\boldsymbol{Mr} $$

(8)

Making$\overset{\sim }{\boldsymbol{U}}\left({\omega}_n\right)$ here presents the transfer function of the displacements calculated at the n^thnatural circular frequency. The matrix A, which includes the design variables as {k₁,k₂,…,k_n}. A is given as

$$ \boldsymbol{A}=\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right)+i{\omega}_n\boldsymbol{C}-{\omega}_n^2\boldsymbol{M} $$

(9)

Here K, M and C are certain. The K_scovering the design variables will be found. If Eq. (8) is arranged as follows

$$ \overset{\sim }{\boldsymbol{U}}\left({\omega}_n\right)=-{\boldsymbol{A}}^{-1}\boldsymbol{Mr} $$

(10)

The transfer function of displacement vector is found in Eq. (10) (Takewaki 1998).The transfer function of elastic force in the nodes is obtained by multiplying the displacement vector with the total stiffness matrix and the transfer function vector of the elastic forces (Aydin and Boduroglu 2008) as follows

$$ \boldsymbol{F}\left({\omega}_n\right)=-\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right){\boldsymbol{A}}^{-1}\boldsymbol{Mr} $$

(11)

3 Optimization problem

In the literature, some optimization problems have been developed in order to find the optimum values of the spring locating points or spring constants:reducing the maximum deflections and bending moments (Imam and Al-Shihri 1996), increasing natural frequencyand buckling coefficient (Won and Park 1998; Liu et al. 1996), reducing the stress and strain (Marcelin 2001), minimizing the stiffness of internal support for beams (Wang 2003), minimizing tip deflection (Friswell and Wang 2007) and tip absolute acceleration (Aydin 2014).

In Fig. 1, the shear force response on the support of a cantilever beam implies the internal force behaviour of the beam. The yield of support shear force may cause shear damage in the beam. It is important to design the location and rigidity of the elastic supports that the cantilever beams often encounter in practical engineering applications to prevent shear damage. These vibrating beams can be exposed to different excitation frequencies. Thus, it is also important to use different modes in the design of the elastic supports of the beams under different harmonic excitations.

In this study, the optimization problem is defined as to find the stiffness coefficients of spring k_i which minimize the transfer function amplitude of the support shear force of cantilever beam evaluated at the n^th natural circular frequency ω_n of the model beam as shown in Fig. 1(a). The transfer function amplitude of support shear force is decreased to attain the minimum value in any modes as shown in Fig. 1(b). It should be noted that the springs attached to the cantilever beam increases the natural frequency of the beam as it causes an increase in rigidity as shown in Fig. 1(b).

The proposed optimization problem to find the optimal spring coefficients and the locations of the springs is expressed as

$$ Design\ variables\ \boldsymbol{k}=\left\{{k}_1,{k}_2,\dots, {k}_n\right\} $$

(12)

$$ MinimizeV\left(\boldsymbol{k}\right)={\sum}_{s=1}^n\mathit{\operatorname{sign}}\left({\varnothing}_{is}\right)\left|{F}_s\left(\boldsymbol{k}\right)\right| $$

(13)

$$ Subject\ to0\le {k}_j\le {k}_{up}\ \left(j=1,2,\dots, n\right) $$

(14)

$$ {\sum}_{i=1}^n{k}_j=\overline{K} $$

(15)

where|F_s(k)| and V(k) are transfer function amplitudes of shear force in nodes correspondingtothe vertical degrees of freedom and the transfer function amplitude of the support shear force, respectively. The mode number considered is noted as i and sign(∅_is) presenting the sign of the s^th elements of the i^thnormalizedmode vector.The transfer function amplitudes of the support shear force mentioned here can be calculated for any vibration mode as will be mentioned later. In Eq. (15), the parameter $\overline{K}$ denotes the total stiffness coefficient of the springs. Another important issue is the total amount of the coefficients of the springs on which the beam is based. If this amount passes a certain value, it will increase the support force. This will be checked in the algorithm that is intended to prevent thissituation. An active constraint on the sum of the stiffness coefficient of the springs in Eq. (15) and passive constraints on the upper k_upand lower bound of stiffness coefficient of each spring have been given in Eq. (14).

The sign (− or +) placed at the beginning of the amplitude of the transfer function of any elastic force |F_i| in Eq. (13) indicates the sign of i^th element (corresponds to translational degree) in the mode vector of consideration. The amplitudes of the transfer functions, which are used, do not indicate real displacement or forces. However, they are functions that express the dynamic behaviour of the system independent of the external force. Here, the displacement amplitude and internal forces amplitudes found by transfer functions are examined. Because the values of the transfer functions defined in the frequency domain are complex numbers. Therefore, since the absolute values are studied here, this sign is taken as a sign of the elements (in the translational degree) of the normalized mode vector to take into account the directional effects in modal behaviour. If the signs are taken into account in the problem, the value and the direction of support force changes. Otherwise, the transfer functions amplitude are always positive and in the same direction. We know that the sign of the behaviour values corresponding to the freedom of some modes are sometimes negativeorpositive. Therefore, the sign of the support shear force is sometimes positive and sometimes negative, and this results in the optimization of being the problem of maximization or minimization.For a better understanding of the proposed method, an Appendix section has been created, showing some basic calculations of a cantilever beam with two finite elements and four degrees of freedom.

The transfer function amplitude of support shear force is calculated by eq. (13) taking into account the absolute values of complex terms corresponding to the shear forces in the nodes. The method includes the transfer function amplitude ofF(ω) and taking into account the sign of the forces in modal behaviour. In order to better explain the relationship between |F_s(k)|and V(k), the following figure is given in detail for the first six modes Fig 2.

Fig. 2

The relationship betweenthe amplitudes of shear forces (|F_s(k)|) in nodes and the support shear force (V(k))

In thestudy of Aydin (Aydin 2014), the objective functions are the transfer function amplitude of the tip displacement and tip absolute acceleration. Minimizing displacements with optimum placement of springs is important to reduce deformations and is a common practice in engineering applications. This has led to the emergence of displacement-based methods. In addition to reducing displacements, it is also important to minimize the displacement of the structural elements and to support them with optimum springs for this purpose. In this study, a force-based optimum spring design method, which is expressed by transfer functions defined according to different discrete modes, is shown that different optimum spring designs can occur according to displacement based method. An increase in forces can cause stresses in the material to exceed the yield limit. In this respect, in addition to minimizing displacement or accelerations, minimizing forces can be important.

3.1 Optimality criteria for support shear force

The generalized Lagrangian L for the problem of optimal spring placement in terms ofthe support shear force can be written in terms of Lagrange Multipliers λ, {μ_j} and {ν_j}, objective function and the mentioned constraints as follows:

$$ L\left({k}_j,\lambda, {\mu}_j,{\upsilon}_j\right)=V\left(\boldsymbol{k}\right)+\lambda \left({\sum}_{j=1}^n\left({k}_j-\overline{K}\right)\right)+{\sum}_{j=1}^n{\mu}_j\left(0-{k}_j\right)+{\sum}_{j=1}^n{\upsilon}_i\left({k}_j-{k}_{up}\right) $$

(16)

The optimality criteria without upper and lower bound constraints on stiffness coefficients can be derived from stationary conditions of Lagrangian L (μ = 0, ν = 0) with respect to λ and k_j,

$$ \frac{\partial V}{\partial {k}_j}+\lambda =0\kern0.5em \left(j=1,2,\dots, n\right)\kern3em 0<{k}_j<{k}_{up} $$

(17)

$$ {\sum}_{j=1}^n{k}_j-\overline{K}=0 $$

(18)

Here the partial derivative of objective function according to design variable k_j is expressed as$\frac{\partial V}{\kern0.75em \partial {k}_j}$. Eq. (17) for lower and upper constraints is changed as follows:

$$ \frac{\partial V}{\partial {k}_j}+\lambda \ge 0\kern3.5em {k}_j=0 $$

(19)

$$ \frac{\partial V}{\partial {k}_j}+\lambda \le 0\kern3.5em {k}_j={k}_{up} $$

(20)

A new algorithm in case of support shear force as an objective function is proposed due to modified classical steepest direction search algorithm.For the solution of the problem, the method shown by Aydin (Aydin 2014) was used to minimize the tip deflection. In (Aydin 2014) for the optimization of the springs, the author adapted the SDSA method given by Takewaki (Takewaki 1998).

3.2 Sensitivity analyses

To determine the optimal position of spring supports, both the sensitivity of objective functions and the natural frequency corresponding to the position of the support areinvestigated. The sensitivity information allows both the search direction and the optimal position of the spring support. It will act according to the intended algebraic sensitivity information. Eq. (10) is differentiated with respect to k_j as given below

$$ \frac{\partial \boldsymbol{A}}{\partial {k}_j}\overset{\sim }{\boldsymbol{U}}+\boldsymbol{A}\frac{\partial \overset{\sim }{\boldsymbol{U}}}{\partial {k}_j}=0\ \left(\mathrm{j}=1,\dots, \mathrm{n}\right) $$

(21)

$$ \frac{\partial \overset{\sim }{\boldsymbol{U}}}{\partial {k}_j}=-{\boldsymbol{A}}^{-\mathbf{1}}\frac{\partial \boldsymbol{A}}{\partial {k}_j}\overset{\sim }{\boldsymbol{U}} $$

(22)

If Eq. (11) is differentiated with respect to k_j, the order derivatives of F is written as

$$ \frac{\partial \boldsymbol{F}}{\partial {k}_j}=\left(\frac{\partial {\boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}-\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right){\boldsymbol{A}}^{-\mathbf{1}}\frac{\partial \boldsymbol{A}}{\partial {k}_j}\right)\overset{\sim }{\boldsymbol{U}} $$

(23)

where$\overset{\sim }{\ \boldsymbol{U}}$ has been derived in Eq. (10). The calculation of $\frac{\partial {\boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}$ is easy since the components of the K_s are linear function of k_j. The quantity of F_iin Eq. (11) in a complex form can be written as

$$ {F}_i=\mathit{\operatorname{Re}}\left[{F}_i\right]+\mathit{\operatorname{Im}}\left[{F}_i\right] $$

(24)

whereF_iis the transfer function values of the i^th node displacement in complex form. The first order sensitivity of the quantityF_i in Eq. (23) can be expressed as

$$ \frac{\partial {F}_i}{\partial {k}_j}=\mathit{\operatorname{Re}}\left[\frac{\partial {F}_i}{\partial {k}_j}\right]+\mathit{\operatorname{Im}}\left[\frac{\partial {F}_i}{\partial {k}_j}\right] $$

(25)

The absolute values of F_ican be written as

$$ \left|{F}_i\right|=\sqrt{{\left(\mathit{\operatorname{Re}}\left[{F}_i\right]\right)}^2+{\left(\mathit{\operatorname{Im}}\left[{F}_i\right]\right)}^2} $$

(26)

If |F_i|is differentiated with respect to the j^th stiffness coefficient k_j, the first order sensitivities of the absolute values of transfer function amplitude of the i^th node forceis found to be

$$ \frac{\partial \left|{F}_i\right|}{\partial {k}_j}=\frac{1}{\left|{F}_i\right|}\left\{\mathit{\operatorname{Re}}\left[{F}_i\right]\left(\mathit{\operatorname{Re}}\left[\frac{\partial {F}_i}{\partial {k}_j}\right]\right)+\mathit{\operatorname{Im}}\left[{F}_i\right]\left(\mathit{\operatorname{Im}}\left[\frac{\partial {F}_i}{\partial {k}_j}\right]\right)\right\} $$

(27)

The first order sensitivity of the transfer function amplitude of the support shear force is expressed as the sum of the sensitivities of the transfer function of support shear forces

$$ \frac{\partial V}{\partial {k}_j}={\sum}_{s=1}^n\mathit{\operatorname{sign}}\left({\varnothing}_{is}\right)\frac{\partial \left|{F}_s\right|}{\partial {k}_j} $$

(28)

wherei is defined as the mode number considered and sign(∅_is) presents the sign according to the s^thelements of the i^th mode vector∅_i. The elementsof i^th mode vectorcorrespond to the translational components of motion, not rotational parts. The moments in the nodes do not have an effect on the calculation of the shear force of support.The parameter $\frac{\partial V}{\partial {k}_j}$represents the first order partial differentiation of transfer function amplitude of the support shear force with respect to design variable k_j.The components of matrix A consist of K, K_s, M, C and ω = ω_i. The added spring matrix K_s, the damping matrix C and the i^th natural circular frequency of the beam ω_i are functions of design variables. In order to derive the first order sensitivity of matrix A, the partial derivative with respect to design variables k_j should be obtained.

For a cantilever beam model, both eigenvector and eigenvalues are found from the following equation

$$ \left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right){\boldsymbol{\varPhi}}_i={\varOmega}_i\boldsymbol{M}{\boldsymbol{\varPhi}}_{\boldsymbol{i}} $$

(29)

whereΦ_i and Ω_iare the i^th eigenvector and the i^th eigenvalue of the beam structure, respectively. If both sides of Eq. (29) are multiplied by${\boldsymbol{\varPhi}}_{\boldsymbol{i}}^{\boldsymbol{T}}$, Eq. (29) can be rearranged as follows

$$ {\boldsymbol{\varPhi}}_{\boldsymbol{i}}^{\boldsymbol{T}}\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right){\boldsymbol{\varPhi}}_i={\varOmega}_i{\boldsymbol{\varPhi}}_{\boldsymbol{i}}^{\boldsymbol{T}}\boldsymbol{M}{\boldsymbol{\varPhi}}_{\boldsymbol{i}} $$

(30)

Let ${\overline{m}}_i={\boldsymbol{\varPhi}}_{\boldsymbol{i}}^{\boldsymbol{T}}\boldsymbol{M}{\boldsymbol{\varPhi}}_{\boldsymbol{i}}$ and ${\overline{k}}_i={\boldsymbol{\varPhi}}_{\boldsymbol{i}}^{\boldsymbol{T}}\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right){\boldsymbol{\varPhi}}_{\boldsymbol{i}}$ denote modal mass and modal stiffness evaluated at the i^th mode of the beam. Eq. (30) can be rewritten in the following form:

$$ {\varOmega}_i=\frac{{\overline{k}}_i}{{\overline{m}}_i} $$

(31)

The first order sensitivity of the eigenvalue Ω_i with respect to design variable k_j is given as

$$ \frac{\partial {\varOmega}_i}{\partial {k}_j}=\frac{1}{{\overline{m}}_i}\frac{\partial {\overline{k}}_i}{\partial {k}_j} $$

(32)

where sensitivity of the modal stiffness with respect to design parameter k_j can be given as

$$ \frac{\partial {\overline{k}}_i}{\partial {k}_j}={\boldsymbol{\varPhi}}_{\boldsymbol{i}}^{\boldsymbol{T}}\frac{\partial \left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right)}{\partial {k}_j}{\boldsymbol{\varPhi}}_{\boldsymbol{i}} $$

(33)

When Ω_i=ω_i²is substituted in Eq. (32), the first order sensitivity of the i^th natural circular frequency of the cantilever beam can be obtained in the following form

$$ \frac{\partial {\omega}_i}{\partial {k}_j}=\frac{1}{2{\overline{m}}_i{\omega}_i}\frac{\partial {\overline{k}}_i}{\partial {k}_j} $$

(34)

To derive the first order sensitivity of the matrix A, in addition to the sensitivity of the eigenvalue and the natural circular frequency, the sensitivity of the damping matrix C should be determined. Structural damping can be taken as either mass proportional or stiffness proportional damping. For both of the cases, structural damping matrix can be written as

$$ \boldsymbol{C}=2{\zeta}_i{\omega}_i\boldsymbol{M} $$

(35)

$$ \boldsymbol{C}=\frac{2{\zeta}_i}{\omega_i}\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right) $$

(36)

whereζ_i denotes the damping ratio in the i^th mode. The partial derivatives of Eqs. (35)–(36) with respect to design variable k_j can be obtained as follows:

$$ \frac{\partial \boldsymbol{C}}{\partial {k}_j}=2{\zeta}_i\frac{\partial {\omega}_i}{\partial {k}_j}\boldsymbol{M} $$

(37)

$$ \frac{\partial \boldsymbol{C}}{\partial {k}_j}=\frac{2{\zeta}_i}{\omega_i}\frac{{\partial \boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}-\frac{2{\zeta}_i}{{\left({\omega}_i\right)}^2}\frac{\partial {\omega}_i}{\partial {k}_j}\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right) $$

(38)

where the elements of matrix K_s are linear functions of design parameters k_j and the partial derivative of each term of K_s matrix with respect to both k₁ and k_j can be obtained for the cantilever beam as

$$ \frac{{\partial \boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_1}={\left[\begin{array}{cccccccc}1& 0& \dots & 0& 0& \dots & 0& 0\\ {}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}0& 0& \dots & 0& 0& \dots & 0& 0\end{array}\right]}_{2 nx2n}\frac{{\partial \boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}={\left[\begin{array}{cccccccc}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}0& 0& \dots & 1& 0& \dots & 0& 0\\ {}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}0& 0& \dots & 0& 0& \dots & 0& 0\\ {}0& 0& \dots & 0& 0& \dots & 0& 0\end{array}\right]}_{2 nx2n} $$

(39)

The first order sensitivity of the matrix A can be obtained by using the sensitivity formulations $\frac{{\partial \boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}$, $\frac{\partial \boldsymbol{C}}{\partial {k}_j}$, $\frac{\partial {\omega}_i}{\partial {k}_j}$ and $\frac{\partial {\varOmega}_i}{\partial {k}_j}$ as follows

$$ \frac{\partial \boldsymbol{A}}{\partial {k}_j}=\frac{{\partial \boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}\kern0.5em +i\frac{\partial {\omega}_i}{\partial {k}_j}\boldsymbol{C}+i{\omega}_i\frac{\partial \boldsymbol{C}}{\partial {k}_j}-\frac{\partial {\varOmega}_i}{\partial {k}_j}\boldsymbol{M} $$

(40)

In case of mass proportional structural damping, Eq. (40) can be written as

$$ \frac{\partial \mathbf{A}}{\partial {\mathrm{k}}_{\mathrm{j}}}=\frac{{\partial \mathbf{K}}_{\mathbf{s}}}{\partial {\mathrm{k}}_{\mathrm{j}}}\kern0.5em +\mathrm{i}\frac{1}{2{\overline{\mathrm{m}}}_{\mathrm{i}}{\upomega}_{\mathrm{i}}}\frac{\partial {\overline{\mathrm{k}}}_{\mathrm{i}}}{\partial {\mathrm{k}}_{\mathrm{j}}}2{\upzeta}_{\mathrm{i}}{\upomega}_{\mathrm{i}}\mathbf{M}+\mathrm{i}{\upomega}_{\mathrm{i}}2{\upzeta}_{\mathrm{i}}\frac{\partial {\upomega}_{\mathrm{i}}}{\partial {\mathrm{k}}_{\mathrm{j}}}\mathbf{M}-\frac{1}{{\overline{\mathrm{m}}}_{\mathrm{i}}}\frac{\partial {\overline{\mathrm{k}}}_{\mathrm{i}}}{\partial {\mathrm{k}}_{\mathrm{j}}}\mathbf{M} $$

(41)

If the structural damping is chosen to be proportional to stiffness, Eq. (40) is as follows

$$ \frac{\partial \boldsymbol{A}}{\partial {k}_j}=\frac{{\partial \boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}\kern0.5em +i\frac{1}{2{\overline{m}}_i{\omega}_i}\frac{\partial {\overline{k}}_i}{\partial {k}_j}\frac{2{\zeta}_i}{\omega_i}\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right)+i{\omega}_i\Big(\frac{2{\zeta}_i}{\omega_i}\frac{{\partial \boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_j}-\frac{2{\zeta}_i}{{\left({\omega}_i\right)}^2}\frac{\partial {\omega}_i}{\partial {k}_j}\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right)-\frac{1}{{\overline{m}}_i}\frac{\partial {\overline{k}}_i}{\partial {k}_j}\boldsymbol{M} $$

(42)

Proposed Algorithm based on first order approximation for support shear force is given as

• Step 1. Assume the stiffness coefficients of all springs to be k_j = 0 where j = 1,...,n.

• Step 2. Select vibration mode number of beam.

• Step 3. Find the Eigenvalue and Eigenvectors.

• Step 4. Assume the increment of the stiffnessas $\Delta K=\frac{\overline{K}}{d}$ where d is selected as the design step number.

• Step 5. Computethe transfer function amplitude (V) using Eq. (13) and the first order sensitivities$\frac{\partial V}{\partial {k}_j}$for all design variables (k_j) using Eq. (28).

• Step 6. Find an index z satisfying$\mathit{\operatorname{Max}}\left(\frac{\partial V}{\partial {k}_j}\right)-\frac{\partial V}{\partial {k}_z}=0$ if the sign of objective function is the negative. If the sign of objective function is the positive, find an index z satisfying$\mathit{\operatorname{Min}}\left(\frac{\partial V}{\partial {k}_j}\right)-\frac{\partial V}{\partial {k}_z}=0$

• Step 7. Update V by $V\pm \frac{\partial V}{\partial {k}_z}\Delta {k}_z$where ∆k_z = ∆K and the sign between the parameters should be negative in case of minimization. It should be negative in case of maximization.

• Step 8. If the new value of V is less than the previous value of V and the constraint ${\sum}_{i=1}^n{k}_i=\overline{K}$ is not provided, continue the process and return to step 3 by adding new stiffness coefficients.

• Step 9. The new value of V is higher than the previous value of V,stop the algorithm and calculate the sum of the stiffness coefficients ${\sum}_{i=1}^n{k}_i={\overline{K}}_{new}$that it is added up to that time.

A simplified feasible direction search algorithm isproposed to calculate the optimal placement of springs using only the first order approximation. The classical Steepest Direction Search Algorithm is invalid because of the more complex sensitivity calculations, when it is applied to the optimal spring distribution problem based on the support shear force for all modes control. This algorithm does not use the second order sensitivity.Therefore, the increment of the stiffness coefficient added in each step is fixed by increment of added stiffness coefficient (∆K) in any step. In this method, the eigenvalues and eigenvectors of the beam are renewed by the stiffness added to the springs in each step. At each step, it is checked whether the objective function falls or not. The objective function is reduced and updated according to direction obtained until the constraint ${\sum}_{i=1}^n{k}_i=\overline{K}$ is satisfied. If the new value of V is less than the previous value of V and the constraint ${\sum}_{i=1}^n{k}_i=\overline{K}$ is not provided, the process continues. When the new value of V is higher than the previous value of V, the algorithm should be stopped even if the equality constraint ${\sum}_{i=1}^n{k}_i=\overline{K}$ is not provided. If the increase in K exceeds a certain value, the value of the objective function will start to increase, which is undesirable. Then the algorithm should be stopped.If it is not stopped, the transfer function amplitude of the support shear force will begin to increase and will begin to move away from convergence in the first order derivatives.When the new value of V is higher than the previous value of V, the algorithm should be stopped and calculated as ${\sum}_{i=1}^n{k}_i={\overline{K}}_{new}$that you have added up to that time. Accordingly, the minimum supporting shear force response of the beam depends on the total stiffness capacity. First-order partial derivatives are also examined in this algorithm. The first order partial derivatives determine the direction of optimization and focus on the sensitive design parameter.

In this study, a gradient based method is proposed. There are many optimization methods to solve engineering problems. The gradient based methods need sensitivity information. Sensitivities give us sensitive design parameters and sensitive locations above the structural response. They may be discontinuous for various objective functions and constraints. The sensitivities in this paper are continuous for the proposed objective function and constraints. If the opposite situation appears, this difficulty can be overcome by using direct search approaches for optimization because direct search algorithms do not have many mathematical requirements (no derivatives needed, etc.) for the optimization problems. Also, direct search techniques explore the design space by generating a number of successive solutions to guide the algorithm to an optimal design. The main characteristic of these algorithms is the imitation of biological and physical events by evolving a near-optimal solution over a number of successive iterations (Saka et al. 2015; Sonmez 2010). One of direct search algorithms, which is called Grey Wolf Optimizer (GWO) method (Mirjalili et al. 2014), is used in this study to compare the results of the gradient-based method proposed to the results obtained from GWO.Because Sonmez (Sonmez 2018) found that GWO was computationally more effective than the Genetic algorithm, Harmony search and Ant colony optimization algorithm. Similar to other meta-heuristic algorithms, GWO has a stochastic nature when working with a set of potential solutions. The reader may find more specific information regarding GWO in (Mirjalili et al. 2014; Sonmez 2018).

This study also investigates the optimal spring distribution for each of them by considering discrete modes. Examining the problem under the influence of narrow and / or wide frequency band will give more realistic results as it will cover a wider frequency range, considering the unpredictable nature of random external effects. By using random vibration theory, the mean-square of support shear force can be defined and a power spectral density (PSD) function of the input support acceleration is taken as a constant value or a critical excitation. The proposed study focuses on how to optimally support the springs if the beam vibrates in each discrete mode. The beams examined here vibrate in certain specific resonance situations. It can be principally important to understand the optimal spring design that corresponds to each discrete mode response.

4 Numerical example

The 6 m long cantilever beam shown in Fig. 3 is modelled as a Timoshenko beam by dividing it into 1 m finite elements and assuming a vertical displacement and a rotation at each node.A vertical and anrotational displacement at each node are considered and a total of 12 degrees of freedom are defined in the system. The shear modulus is G = 7,94 10¹⁰ N/m², the correction factor κ = 5/6, the cross-sectional area A=0,05 m², the moment of inertia I = 2,08 10⁻⁴ m⁴, density of material ρ = 7,8 10³ kg/m³, the modulus of elasticity E = 2,06 10¹¹ N/m². A mass of 100 kg was also added to the end of the beam. Structural damping matrix is selected as mass proportionaland damping ratio is given as 0,02. Placements ofnodes of springs are defined at the nodal points. The design variables$\boldsymbol{k}=\left\{{k}_1\kern0.5em {k}_2\kern0.5em \begin{array}{ccc}{k}_3& {k}_4& \begin{array}{cc}{k}_5& {k}_6\end{array}\end{array}\right\}$ denote as spring stiffness coefficients. The first six modes of the cantilever beam, which correspond to the translational displacements, were considered to find the optimal spring design. Initially, the total amount of spring constant is estimated by the designer. By using the proposed algorithm, optimum values of spring coefficients are found. This is repeated for the first six modes. While the algorithm is running, if the objective function is increased, it is stopped, otherwise the objective function is continued and the convergence is observed in the first derivative. The local optimum problem encountered in gradient-based methods is also valid here. However, in the problem proposed here, the stiffness coefficients must be positive. If the optimization problem starts with a different initial value, it may not be possible to investigate or reach the global as the amount of stiffness to be added at each step will never be negative. Therefore, all design variables are initially set to zero and optimization is started.

Fig. 3

Model cantilever beam with supported springs

Verification of the method was carried out by comparing the results presented in this paper with those ones from analysis of the model of the beam without springs, with springs with uniform stiffness and with optimal distribution of springs which support a cantilever beam to minimize the tip deflection of the beam (Aydin 2014).The same problem is also solved using the GWO method and the gradient-based method in the paper is largely confirmed by a metaheuristic method. During the optimization, considering the first six translational modes, the variations of objective functions are shown in Fig. 4 for each step. Support shear force varies considerably with respect to the springs to which they are attached. The insertion of the springs can increase the elasticforcesin nodesand as a result the support shear force can be increased. Therefore, the objective function in the algorithm is controlled and decreased at every step. If there is an increase, the optimization is stopped.

Fig. 4

Variation of objective function for different mode control according to design step number

On the basis of the results presented in Fig. 4, for the first mode control, the application of optimal spring stiffness reduces the transfer function amplitude of the shear force compared to the case with no springs by 26.499%, for the fourth mode by 26.509% compared to the model presented in (Aydin 2014).Although it is seen that the value of the objective function is positive, it is seen that it is minimized in the positive region. On Fig. 4 (a) itis clearly visible that the proposed method reduces the transfer function amplitude of the support shear force in the best way comparing to other gradient basedmethod (Aydin 2014) and uniform design.The final values of the target transfer function of the method aimed at minimizing tip displacement and the result of the proposed method are very close to each other.When the variation of the objective functions for spring designs obtained according to the first mode are investigated, it is clear that the uniform design increases the objective function in the positive region. For the second, third, fifth and sixth modes, the variation of objective functionpresent the same trend, for both the proposed method and the method presented in (Aydin 2014).When the control of the fourth mode is examined, the minimum value of objective function is attained by the end of design steps in the proposed designand the result of (Aydin 2014) is also close to it.The sign of the objective function is negative and is considered to be a maximization problem.In the case of the control of the first, third and fifth modes, it can be seen that the sign of the objective function amplitude is positive, while in the case of the control of the second, fourth and sixth modes, the sign is negative. As mentioned above, this situation provides the problem to be a minimization or maximization problem, which is related to the direction of the shear force in the support.In different mode behaviour, the direction or sign of the shear forces in the nodes changes, and consequently the sign of the force in the support may change.

The minimization of transfer function amplitude of tip deflection is not the goal of the analysis in this paper. In order to make a comparison, the transfer function amplitude of the tip displacement is examined for different spring designs and different mode control cases.Fig. 5 shows the variation of transfer function amplitude of the tip displacement for different designs in case of first sixth mode control. For the second, third, fifth and sixth modes, the value of the transfer function are the same in the proposed model and arepresented in (Aydin 2014).In the case of control of the first modes, it is seen that the last transfer function value of all spring designsare attainat near point.When the control of the 2nd, 3rd, 4th, 5th and 6th modes is examined in terms of uniform design, the worst performance shows uniform design. In the first mode, the uniform design is similar inperformance withthe other designs.The control of the fourth mode showed the best displacement performance according to the displacement optimization design.

Fig. 5

Variation of transfer function for different mode control according to design step number

Fig.6(a) shows the optimal distributions of springs at the nodes. In the optimal design according to the first mode, the large part of the total amount of the spring is added to the fourth node (64%) and fifth node (36%). In the design according to the tip displacement, the springs are placed at the fourth node (52%), fifth node(41%) and sixth node (7%) so that the purpose of the design is to minimize the tip displacement.The large part of total springs focus close to the 4th and 5th nodes for both minimization of the support shear force and minimization of tip displacement.The example problem is also optimized by the GWO method, since it is the gradient-based method employed here and is on a similar basis with the other displacement minimization method compared.The results of GWO can also be observed in both Table 1 and Fig 6.When the results of GWO are considered for the first mode, it is seen that the total stiffness amount is distributed to all nodes, but mainly to the 4th (38%) and 5th (58%) nodes.According to the results of GWO, the nodes where the stiffness is predominantly distributed are the same as the nodes on which the proposed method is focused. Although the optimal spring locations are close to each other, the GWO performs better in the first mode in terms of transfer function values.

Fig. 6

Optimal spring distributions for thefirst six modes

Table 1 Optimal spring distributions for different mode controland different models.

The optimal designs for control of 2nd, 3rd, 5th and 6th modes give the sameor very approximatevalues and distributions as shown in Fig.6(b,c,e, f) in case of all optimal designs. In the second mode, the total amount is placed in the sixth node (Fig. 6(b)). When examining the optimum spring distribution for third mode controlin Fig. 6(c), it can be seen that a total spring coefficient at the 4th node is addedin the proposed method and the displacement minimization.In the GWO design, the total stiffness is largely added to node 4, with very small amounts distributed to other nodes. For the control of the fourth mode as shown in Fig.6(d), the total amount of springs is distributed in the 6th(70%),3rd(28%) and5^th(2%) node for proposed methodwhile it is added only to the 3rd node for displacement based design.In the control of the fourth mode, if the distribution of the GWO is examined, it can be seen that the springs are mainly distributed in the 3rd (69%)and 6th (30) nodes.In thefourth optimal control, although the optimum stiffness amounts of the springs differ with the proposed method and GWO method, the dominant locations are the same.As can also be seen from Table 1, the results of the proposed method are also best in terms of transfer functions.Both Fig. 6(e) and Table 1, it is necessary to add the total spring amount to node 5 according to all optimum designs to control the fifth mode. As a result of the control of sixth mode the total spring is focused in the second nodein case of all optimal designs (Fig. 6(f)). The springs with large values found in the analyses can also refer to a simple support. The value of the support force changes with the added springs. The addition of springs can increase or decrease this magnitude. The aim here is to reduce the force of support when adding the springs. The support force of a cantilever beam will also change with the vibrating of different modes. For beam model, the values of the optimum spring coefficients for the different modes are given in Table 1.

Figure 7 shows the variation of the frequency for each mode duringoptimization. In particular, if the control of the first mode is examined,at the end of the displacement optimization, it is seen that the frequency value reached is maximum.Since the aim of this study is to minimize the shear force on the support, the increase in frequency during design is clearly visible in Fig.7, although it does not maximize the frequency.In the case of the control of other modes, it appears that the two optimal designs follow the same or similar trend in terms of the frequency variations.

Fig. 7

The variation of the corresponding frequency for the first-six mode control

The springs added also change the natural circular frequencies and mode shapes of the model, as expected. Table 2 shows the variations in natural circular frequencies for different mode controls. In the first mode control, the first natural frequency varies from 178,55 rad/s (proposed) to 198,78 rad/s (uniform), while the change in the other frequencies is also remarkable. In the control of the second mode, the second natural circular frequency varies from 254,37 rad/s (proposed) to 210,54 rad/s (uniform). In the control of the third mode, the third natural circular frequency varies from 587,20 rad/s (proposed) to 567,24 rad/s (uniform). These changes can be seen in more detail in Fig.8. It is observed that the optimum spring designs have caused serious changes especially in the natural circular frequencies of the first-three modes.When the variations of all frequencies according to different designs are examined, the largest values are generally found in the case of uniform designs under the control of the 6^thmode.

Table 2 The variation of natural circular frequencies of first-six mode for different mode control and different models

Fig. 8

Changes of natural circular frequencies for different mode control

The convergance for the derivatives of both objective functions, as well as for first order derivative of transfer function amplitude with respect to design variables according to design step number in case of different mode control is achieved as shown in Fig.9 and Fig. 10.The negative region of the signs of the derivative points to a minimization problem, while being in the positive region is an indicator of a maximization problem. This situation should be considered, as stated, in the algorithm.As can be understood from the graphs, in the case of both force optimization and displacement optimization, it can be seen that derivatives approach towards zero and convergence occurs. If the nonlinearity of the spring optimization problem is considered, each added spring directly affects frequency.For the damping and the transfer function values, it is difficult to apply a gradient based method. Here it can be noted that convergence takes place, as can be seen from the changes in the analytically derived sensitivities. Comparing the results with GWO, which is a direct optimization method, and reaching the same values in some modes and acceptable levels in some other modes, the analitically derived sensitivity equations are even more valuable.

Fig. 9

Variation of first order sensitivities with respect to design variables according to design step number incase of different mode control

Fig. 10

Variation of first order derivative of transfer function with respect to design variables according to design step number incase of different mode control

Fig. 11

Variation of amplitude of the support shear force function according to excitation frequency incase of different mode control

Fig. 11 shows the frequency behavior of the amplitude of the support shear force function for the proposed model, without springs, with uniform distribution of springs and themodel presented in (Aydin 2014). The amplitude of the support force function is reduced for all modes. The location indicated by blue dot refers to the controlled resonant pointfor that mode.In Fig.11(a), the worst performance is in the uniform design, while the best performance shows the design according to the proposed method here.For the 2nd, 3rd, 5th and 6th modes except for 1st and 4th modes, the optimum designs according to both purpose functions show the same performance. Moreover, it is obvious that these optimal designs show better performance than designs of both uniform designs andwithout springs.In terms of uniform designs, high amplitudes are observed in case of both without spring and uniform spring design.Moreover, the frequency considered is shifted to the larger values according to the uniform increase in stiffness.

The optimal design is investigated in the frequency domain and the time behaviour of the support force of the optimum designs found is also examined. The optimum design for each mode is compared to the results achieved in the model without springs, with uniform distribution of springs and in the model presented in (Aydin 2014).In the case of resonance, thebehaviour of the beam is checked by using time history analyses. Thus, the vertical support acceleration of excitation is chosen as ${\ddot{u}}_g=\mathit{\sin}\left({\omega}_nt\right)$n = 1,..,6. As a result of the time history analyses, the changes in the support shear force of the design for each mode are plotted in Fig. 12. The graphics in Fig. 12 clearly show that the optimum designs found with the investigated method can reduce the support shear force to a stable level. In the case of separate control of each mode, when a harmonic load corresponding to that mode is applied, the variation of the support shear force according to the two optimal designs shows that the optimum designs give very close results. Uniform designs create greater force values than optimum designs.In addition, the time behaviour of the tip displacement of the cantilever beam at harmonic forces is plotted in Fig. 13. It can be seen that the optimal designs improve the behaviour of the beam in terms of displacement.As can be seen from Fig. 13, optimum designs perform better for each mode than both uniform designs and without spring cases.

Fig. 12

Support shear force time histories incase of optimal spring designs for different mode control

Fig. 13

Tip deflection time histories incase of optimal spring designs for different mode control

Beams are important structural elements in many different engineering designs. In some engineering problems, the first mode is dominant, whilethe other mode can be a priority in the other designs. In this proposed method, whichever mode is focused, it tries to reduce the value of the resonance case in that mode. It has been shown that the supporting shear force defined by the i^th frequency is reduced to a minimal value when it is compared with üniform design and without springcase. It is important to reduce displacements by adding springs which was presented in many previous researches. If the support shear force is considered to be decreased by supported springs in a force-based design, the support forces cannot reach to its yielding limits.Depending on which frequency the designers chooses,theycan seek for an optimum control over that frequency.

4.1 The effects of structural damping and the mesh sensitivity

The field of damping matrix identification is one which still holds quite a bit of intrigue in the engineering community. This is because the modelling of damping is very complex and is still considered somewhat of an unknown or grey area. The effects of damping are clear, but the characterization of damping is a puzzle waiting to be solved. The damping properties of structures are often assumed to beina modal form. They are introduced as damping coefficients in the modal equations. This is done not only for the sake of analytical simplicity, but also because it is the most convenient way to measure or estimate it. This is the way, for example, to estimate the material damping in the finite-element analysis of large flexible structures, where the modal analysis is executed, the low-frequency modesareretained, and modal damping for these modes isassumed. The resulting damping is a proportional one. In another approach, a damping matrix proportional either to the mass or to the stiffness matrix, or to both, is introduced. This technique produces proportional damping as well. A proportional damping is used in terms of a single mode here because it is considered on the individual vibration control of each mode to find the optimum distribution of the springs. It is chosen aseither a mass proportional or stiffness proportional damping matrix because only the effect of the single mode is considered. Both matrices have diagonal orthogonality characteristics. These are the classic damping matrices. Stiffness proportional damping appeals to intuition because it can be interpreted to model energy dissipation arising from the deformations. In contrast, mass proportional damping is difficult to justify physically. Mass proportional damping may represent the energy loss associated with a momentumandis termed as themomentum damping. Physically, this is incorporated by assigning a viscous damper between each degree of freedom and its fixed reference, with the damping constant proportional to the mass. Neither of two damping models is appropriate for practical applications. Rayleigh damping can also be selected in proportion to both rigidity and mass, but the frequency and damping ratios of the two modes should be used to calculate the proportion coefficients. In this study, Rayleigh damping is not selected since each mode is consideredto be single.

In this study, mass proportional damping, which can be calculated according to a single mode, is chosen. In addition, optimum designs are found in each mode for different damping ratios of the beam. Fig. 14 illustrate the changes of the objective functions according to five different structural damping ratios. From the graphs it can be seen that the changes in the structural damping ratio for the first six modes decrease the objective function values as expected. Furthermore, as can be seen from the Table 3 below, the change in the damping ratio from 0,01 to 0,05 in the first mode does not generally change the optimum designs.In case of damping ratio of 0,07 and 0,10, it can be seen that besides 4^thand 5^thnode, a small spring is added to node 4.

Fig. 14

The effects of structural damping ratio on the transfer function amplitude of support shear force

Table 3 Optimal spring coefficients in the case of different structural damping ratio

When the designs for different damping ratios are examined in Table 3 according to the second mode, while the damping ratio isinbetween 0,01 −0,02, the optimum designs are the same while the increase in the damping ratio (such as 0,05 0,07 and 0,1) changes the optimum designsat least. While the total stiffness coefficient for the first two damping ratios is focused on sixth node, the optimum designs for the last three damping ratios are distributed to the first node together with the sixth node. It could be seen that different designs emerged if the third mode are examined according to different damping ratios and the optimum designs arecalculated as shown in Table 3. While the increase in damping ratio causes the total amount of rigidity to be generally distributed to more nodes, there are some exceptions to which this increase is added on fewer nodes. In case of increasing damping ratio by 0,05 and subsequent damping ratio, a small spring is added to node 3 as well as node 4.When the effect of the increase in damping ratio in the control of the fourth mode on the optimal design is examined, the increase in damping ratio causes a small spring to be added to the fifth node as well as the nodes 3 and 6, except when the damping ratio is 0,05.In the control of the fifth mode, the design does not change at all damping ratio except for the 0,10 damping ratio, whereas in the case of damping ratio of 0,01, a little spring is placed on node 2 as well as node 5.All designs are the same when the sixth mode is controlled.As a result, the structural damping is aneffectiveparameter in optimum spring design. It is important that the designer selects the structural damping parameter in a realistic way.

In order to examine the mesh sensitivity, the 6-element sample is reanalysed by dividing the beam into 60 elements. For each mode, the frequencies, optimum designs and transfer function amplitudes are calculated in both the 6-element and 60-element beam and are shown in Table 4. In both designs, the locations of the springs and the total spring coefficient are kept constant to compare the optimal design. When the change of the first six natural frequencies is examined, it canbe seen that especially the high frequencies fall as expected in the 60-element model. This has led to changes in optimum designs in some higher modes. The total stiffness coefficient is distributed mainly in the fourth and fifth node in case of 6-element model. In the 60-element model, this is the same. Although there is no effect of mesh sensitivity in the designs for the second, third and fifth modes, the results for the fourth and sixth mode are different. The optimum design of the elastic springs supporting the cantilever beams requires a sufficient number of elements divided by the number of elements to be used to model the beam.

Table 4 The effects of mesh sensitivity on the optimal springs

5 Conclusions

Beams are structural elements that are important in many engineering problems. Timoshenko cantilever beam resting on springs are investigated, the best supporting conditions are studied and compared to the results obtained in the model without springs, with uniform distribution of springs and tothe optimal design model presented in literature.New approach of optimization algorithm is developed.The beamis modelled with finite elements and springs which are optimally designed andplaced at node points. The equation of motion of the cantilever beam in the time domain is transformed into frequency domain equation by Fourier Transform. In the frequency domain, a new transfer function is defined for the support shear force of the beam and the optimization problem is madeto minimize it. Sensitivity equations required for optimization problem are analytically derived and a solution algorithm is proposed to find the optimal spring locations and its stiffness coefficients. The proposed method is tested with the numerical example. As a result of the analyses, the following results can be summarized:

• The support conditions of the beams, which are important for engineering works, seriously affect the force behaviour of the beam,

• Changing of the spring supports influences on vibrations of the beam in different modes,

• Spring distributions are found to minimize the support shear force for different modes, and the optimal spring designs are shown to improve behaviour in both time domain and frequency domain,

• The springs supporting the beam can also increase the forces as well as change the dynamic properties. An increase of internal force may cause the yielding of the material. From this point of view, the design of the elastic supports that minimizes the support force for any modescan be useful for many engineering applications,

• Different support conditions for different modes arise. In this case, it is necessary to show how the beam is subjected to a dynamic load,

• The results of the proposed gradient based method are proved to be accurate by comparing the results with a metaheuristic optimization method (GWO) and the same or acceptable results for many modes.

• The analysis showed that the total stiffness chosen by the designer, the structural damping ratio, the number of finite elements selected and the mode number of consideration are important parameters that affect the optimum design of the springs supporting the beam.

• The proposed method is effective to decrease the support shear force by optimal springs. In addition, the presented method gives designers an idea abouthow to support vibrating beams in different modes.

The method shown in this paper is characterized by high efficiency of reducing the shear force on the support and is a helpful tool in the design of beams under dynamic loads.

6 Replication of results

In this study the new approach of optimization algorithm with use of gradient based method is developed for the purpose of the minimization of the shear force support. Due to objective function, for finding the optimal location and amount of springs, the new algorithm takes into consideration the situation when the direction of the internal forces changes in different modes and this direction change is calculated by taking into account the positive or negative signs in the calculation of the support shear force.

The methodology consists of the following steps:assuming the stiffness coefficients of all springs supporting the beam to be k_j=0 where j=1,...,n, selecting vibration mode number of beam, finding the eigenvalue and eigenvectors, assuming the increment of the stiffness, computing the transfer function amplitude (V) and the first order sensitivities, finding an index ‘z’ satisfying$\mathit{\operatorname{Max}}\left(\frac{\partial V}{\partial {k}_j}\right)-\frac{\partial V}{\partial {k}_z}=0$ if the sign of objective function is the negative. If the sign of objective function is the positive, we find an index ‘z’ satisfying$\mathit{\operatorname{Min}}\left(\frac{\partial V}{\partial {k}_j}\right)-\frac{\partial V}{\partial {k}_z}=0$, and thenwe updateV. If the function V meets the criterion, it is assumed to be the solution, otherwise the steps of the algorithm are repeated. Detailed steps of the algorithm are presented in the paper.

APPENDIX

1.1 CANTILEVER BEAM MODEL WITH TWO ELEMENTS

For a better understanding of the problem, let us do a numerical analysis and show a step on a cantilever beam model with 2 elements and 4 degrees of freedom as shown in Fig. 15. The cantilever beam (length is 6 m) is modelled as a Timoshenko beam by dividing it into 3 m finite elements and assuming vertical displacements and rotations at each node. Two vertical and rotational displacements at each node are considered and a total of 4 degrees of freedom are defined in the system. The shear modulus is G= 7,94 10¹⁰ N/m², the correction factor κ=5/6, the cross-sectional area A=0,05 m², the moment of inertia I= 2,08 10⁻⁴ m⁴, density of material ρ= 7,8 10³ kg/m³, the modulus of elasticity E= 2,06 10¹¹ N/m². A mass of 100 kg is also added to the end of the beam. Structural damping matrix is selected as mass proportional and structural damping ratio is assumed as 0,02. The total stiffness is assumed to be $\overline{K}=9x{10}^6N/m$ and the amount of additional stiffness in each step is calculated as $\Delta K=\frac{9x{10}^6}{300}=30000\ N/m$ where design step number (d) is selected as 300.

Using element stiffness and mass matrices, the global stiffness and mass matrices of the 4 degree of freedom beam are found as follows

$$ K=\left[\begin{array}{ccc}3,74406\kern0.5em 0,00000& -1,87203& 2,80804\\ {}\begin{array}{cc}0,00000& 11,2807\end{array}& -2,80804& 2,78380\\ {}\begin{array}{cc}\begin{array}{c}-1,87203\\ {}2,80804\end{array}& \begin{array}{c}-2,80804\\ {}2,78380\end{array}\end{array}& \begin{array}{c}1,87203\\ {}-2,80804\end{array}& \begin{array}{c}-2,80804\\ {}5,64033\end{array}\end{array}\right]\ast {10}^7 $$

(43)

$$ M=\left[\begin{array}{ccc}\mathrm{868,698}\kern0.5em \mathrm{0,000}& \mathrm{150,651}& -\mathrm{109,277}\\ {}\begin{array}{cc}\mathrm{0,000}& \kern0.5em \mathrm{201,01}\end{array}& \mathrm{109,277}& -75,8064\\ {}\begin{array}{cc}\begin{array}{c}\mathrm{150,651}\\ {}-\mathrm{109,277}\end{array}& \begin{array}{c}\mathrm{109,277}\\ {}-\mathrm{75,806}\end{array}\end{array}& \begin{array}{c}\mathrm{534,349}\\ {}-\mathrm{183,223}\end{array}& \begin{array}{c}-\mathrm{183,223}\\ {}\mathrm{100,505}\end{array}\end{array}\right] $$

(44)

In the first step, the system’s natural circular frequencies are calculated as ω_i ={29,8,881,189,4,946,366,731,694,69}rad/s from the eigenvalue-eigenvector analysis. The first eigenvector normalized to the tip degree of freedom of the system is found as ∅₁ ={0,3,357,330,192,635 100,000 0,232,286}. The damping matrix of the beam model can be calculated in proportion to the mass as follows.

$$ C=2\upzeta {\upomega}_1M=2\ast 0,02\ast 29,8881\ast \left[\begin{array}{ccc}\mathrm{868,698}\kern0.5em \mathrm{0,000}& \mathrm{150,651}& -\mathrm{109,277}\\ {}\begin{array}{cc}\mathrm{0,000}& \kern0.5em \mathrm{201,01}\end{array}& \mathrm{109,277}& -75,8064\\ {}\begin{array}{cc}\begin{array}{c}\mathrm{150,651}\\ {}-\mathrm{109,277}\end{array}& \begin{array}{c}\mathrm{109,277}\\ {}-\mathrm{75,806}\end{array}\end{array}& \begin{array}{c}\mathrm{534,349}\\ {}-\mathrm{183,223}\end{array}& \begin{array}{c}-\mathrm{183,223}\\ {}\mathrm{100,505}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{cc}1590,92& \mathrm{0,000}\end{array}& \mathrm{275,901}& -\mathrm{200,13}\\ {}\begin{array}{cc}\mathrm{0,000}& \kern0.5em \mathrm{368,127}\end{array}& \mathrm{200,130}& -\mathrm{138,831}\\ {}\begin{array}{cc}\begin{array}{c}\mathrm{275,901}\\ {}-\mathrm{200,13}\end{array}& \begin{array}{c}\mathrm{200,13}\\ {}-\mathrm{138,831}\end{array}\end{array}& \begin{array}{c}\mathrm{978,601}\\ {}-\mathrm{335,552}\end{array}& \begin{array}{c}-\mathrm{335,552}\\ {}\mathrm{184,063}\end{array}\end{array}\right] $$

(45)

The stiffness matrix of the springs added and its partial derivations with respect to k₁ and k₂ are given below

$$ {\boldsymbol{K}}_{\boldsymbol{S}}=\left[\begin{array}{ccc}{k}_1\kern0.5em 0& 0& 0\\ {}\begin{array}{cc}0& \kern0.5em 0\end{array}& 0& 0\\ {}\begin{array}{cc}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}& \begin{array}{c}{k}_2\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}\right]\frac{\partial {\boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_1}=\left[\begin{array}{ccc}\begin{array}{cc}1& 0\end{array}& 0& 0\\ {}\begin{array}{cc}0& 0\end{array}& 0& 0\\ {}\begin{array}{cc}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}& \begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}\right]\frac{\partial {\boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_2}=\left[\begin{array}{ccc}\begin{array}{cc}0& 0\end{array}& 0& 0\\ {}\begin{array}{cc}0& 0\end{array}& 0& 0\\ {}\begin{array}{cc}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}& \begin{array}{c}1\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}\right] $$

(46)

The calculation of matrix A given in Eq. (9) is as follows

$$ \boldsymbol{A}=\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right)+i{\omega}_1\boldsymbol{C}-{\omega}_1^2\boldsymbol{M}=\left[\begin{array}{ccc}3,74406\kern0.5em 0,00000& -1,87203& 2,80804\\ {}\begin{array}{cc}0,00000& 11,2807\end{array}& -2,80804& 2,78380\\ {}\begin{array}{cc}\begin{array}{c}-1,87203\\ {}2,80804\end{array}& \begin{array}{c}-2,80804\\ {}2,78380\end{array}\end{array}& \begin{array}{c}1,87203\\ {}-2,80804\end{array}& \begin{array}{c}-2,80804\\ {}5,64033\end{array}\end{array}\right]\ast {10}^7+\left[\begin{array}{ccc}\begin{array}{cc}{k}_1& 0\end{array}& 0& 0\\ {}\begin{array}{cc}0& \kern0.5em 0\end{array}& 0& 0\\ {}\begin{array}{cc}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}& \begin{array}{c}{k}_2\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}\right]+i\ast 29,8881\ast \left[\begin{array}{ccc}\begin{array}{cc}1590,92& \mathrm{0,000}\end{array}& \mathrm{275,901}& -\mathrm{200,13}\\ {}\begin{array}{cc}\mathrm{0,000}& \kern0.5em \mathrm{368,127}\end{array}& \mathrm{200,13}& -\mathrm{138,831}\\ {}\begin{array}{cc}\begin{array}{c}\mathrm{275,901}\\ {}-\mathrm{200,13}\end{array}& \begin{array}{c}\mathrm{200,13}\\ {}-\mathrm{138,831}\end{array}\end{array}& \begin{array}{c}\mathrm{978,601}\\ {}-\mathrm{335,552}\end{array}& \begin{array}{c}-\mathrm{335,552}\\ {}\mathrm{184,063}\end{array}\end{array}\right]-29,{8881}^2\ast \left[\begin{array}{ccc}\begin{array}{cc}\mathrm{868,698}& \mathrm{0,000}\end{array}& \mathrm{150,651}& -\mathrm{109,277}\\ {}\begin{array}{cc}\mathrm{0,000}& \kern0.5em \mathrm{201,01}\end{array}& \mathrm{109,277}& -75,8064\\ {}\begin{array}{cc}\begin{array}{c}\mathrm{150,651}\\ {}-\mathrm{109,277}\end{array}& \begin{array}{c}\mathrm{109,277}\\ {}-\mathrm{75,806}\end{array}\end{array}& \begin{array}{c}\mathrm{534,349}\\ {}-\mathrm{183,223}\end{array}& \begin{array}{c}-\mathrm{183,223}\\ {}\mathrm{100,505}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{cc}3,66646\ast {10}^7+31040,3\ast i& 0,0000000+0,0000000\ast i\end{array}& -1,88549\ast {10}^7+5383,06\ast i& 2,8178\ast {10}^7-3904,7\ast i\\ {}\begin{array}{cc}0,0000000+0,000000\ast i\kern1.25em & \kern0.5em 1,12627\ast {10}^8+7182,47\ast i\end{array}& -2,8178\ast {10}^7+3904,7\ast i& 2,79057\ast {10}^7-2708,71\ast i\\ {}\begin{array}{cc}\begin{array}{c}-1,88549\ast {10}^7+5383,06\ast i\\ {}2,8178\ast {10}^7-3904,7\ast i\end{array}& \begin{array}{c}-2,8178\ast {10}^7+3904,7\ast i\\ {}2,79057\ast {10}^7-2708,71\ast i\end{array}\end{array}& \begin{array}{c}1,82429\ast {10}^7+19093,3\ast i\\ {}-2,79167\ast {10}^7-6546,9\ast i\end{array}& \begin{array}{c}-2,79167\ast {10}^7-6546,9\ast i\\ {}5,63135\ast {10}^7+3591,24\ast i\end{array}\end{array}\right] $$

(47)

Initial values of design variables (k₁and k₂) are assumed to be zero, The modal mass for 1st mode and the partial derivative of first eigenvalue with respect to k₁ and k₂ are obtained as

$$ {\overline{m}}_1={\boldsymbol{\varPhi}}_{\mathbf{1}}^{\boldsymbol{T}}\boldsymbol{M}{\boldsymbol{\varPhi}}_{\mathbf{1}}=\left\{\begin{array}{c}0,335733\ \\ {}0,192635\\ {}\ 1,00000\\ {}\ 0,232286\end{array}\right\}\left[\begin{array}{ccc}\mathrm{868,698}\kern0.5em \mathrm{0,000}& \mathrm{150,651}& -\mathrm{109,277}\\ {}\begin{array}{cc}\mathrm{0,000}& \kern0.5em \mathrm{201,01}\end{array}& \mathrm{109,277}& -75,8064\\ {}\begin{array}{cc}\begin{array}{c}\mathrm{150,651}\\ {}-\mathrm{109,277}\end{array}& \begin{array}{c}\mathrm{109,277}\\ {}-\mathrm{75,806}\end{array}\end{array}& \begin{array}{c}\mathrm{534,349}\\ {}-\mathrm{183,223}\end{array}& \begin{array}{c}-\mathrm{183,223}\\ {}\mathrm{100,505}\end{array}\end{array}\right]\left\{0,335733\kern0.75em 0,192635\kern1em 1,00000\kern1em 0,232286\right\}=\mathrm{679,458} $$

(48)

$$ \frac{\partial {\varOmega}_1}{\partial {k}_1}=\frac{1}{{\overline{m}}_1}\frac{\partial {\overline{k}}_1}{\partial {k}_1}=\frac{1}{\mathrm{679,458}}\left\{\begin{array}{c}0,335733\ \\ {}0,192635\\ {}\ 1,00000\\ {}\ 0,232286\end{array}\right\}\left[\begin{array}{ccc}1\kern0.5em 0& 0& 0\\ {}\begin{array}{cc}0& 0\end{array}& 0& 0\\ {}\begin{array}{cc}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}& \begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}\right]\left\{0,335733\kern1em 0,192635\kern1em 1,00000\kern0.75em 0,232286\right\}=0,000165892 $$

(49)

$$ \frac{\partial {\varOmega}_1}{\partial {k}_2}=\frac{1}{{\overline{m}}_1}\frac{\partial {\overline{k}}_1}{\partial {k}_2}=\frac{1}{\mathrm{679,458}}\left\{\begin{array}{c}0,335733\ \\ {}0,192635\\ {}\ 1,00000\\ {}\ 0,232286\end{array}\right\}\left[\begin{array}{ccc}0\kern0.5em 0& 0& 0\\ {}\begin{array}{cc}0& 0\end{array}& 0& 0\\ {}\begin{array}{cc}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}& \begin{array}{c}1\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}\right]\left\{0,335733\kern1em 0,192635\kern0.75em 1,00000\kern0.75em 0,232286\right\}=0,00147176 $$

(50)

The transfer function vector is calculated as

$$ \overset{\sim }{\boldsymbol{U}}\left({\omega}_1\right)=-{\boldsymbol{A}}^{-1}\boldsymbol{Mr}=\left\{\begin{array}{c}-0,0000142032+0,0135566i\\ {}0,00000110433+0,00777842i\\ {}\begin{array}{c}0,0000155147+0,040379i\\ {}0,0000140347+0,00937945i\end{array}\end{array}\right\} $$

(51)

The transfer function vector of elastic forces are obtained as follows

$$ \boldsymbol{F}\left({\omega}_1\right)=\left(\boldsymbol{K}+{\boldsymbol{K}}_{\boldsymbol{s}}\right)\overset{\sim }{\boldsymbol{U}}\left({\omega}_1\right)=\left\{\begin{array}{c}-\mathrm{428,114}+15038,9i\\ {}79,6148+4703,22i\\ {}\begin{array}{c}\mathrm{131,217}+20322,7i\\ {}-12,1448-7616,93i\end{array}\end{array}\right\} $$

(52)

where the elements of K_s are zero in the first step. The absolute value of the F(ω_n) are given as

$$ \left|\boldsymbol{F}\left({\omega}_1\right)\right|=\left\{\begin{array}{c}15045,00\\ {}4703,89\\ {}\begin{array}{c}20323,10\\ {}7616,94\end{array}\end{array}\right\} $$

(53)

The transfer function amplitude of the support shear force is found as

$$ V\left({\omega}_n\right)=\sum \limits_{s=1}^2\mathit{\operatorname{sign}}\left({\varnothing}_{is}\right)\left|{F}_s\left({\omega}_1\right)\right|=\mathit{\operatorname{sign}}\left({\varnothing}_{11}\right)\left|{F}_1\left({\omega}_1\right)\right|+\mathit{\operatorname{sign}}\left({\varnothing}_{13}\right)\left|{F}_2\left({\omega}_1\right)\right|=\mathit{\operatorname{sign}}\left(0,335733\right)15045,00+\mathit{\operatorname{sign}}\left(1,00000\right)20323,10=\left(+\right)15045,00+\left(+\right)20323,10=35362,8 $$

(54)

where s is defined as the number of degree of freedom corresponding to the translational modes. The first order sensitivity with respect to the k₁ and k₂are given as

$$ \frac{\partial \boldsymbol{F}}{\partial {k}_1}=\left(\frac{\partial {\boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_1}-{\boldsymbol{K}}_{\boldsymbol{s}}{\boldsymbol{A}}^{-\mathbf{1}}\frac{\partial \boldsymbol{A}}{\partial {k}_1}\right)\overset{\sim }{\boldsymbol{U}}=\left\{\begin{array}{c}-1,50914\ast {10}^{-5}-3,26491\ast {10}^{-4}i\\ {}-5,72376\ast {10}^{-8}-4,40133\ast {10}^{-6}i\\ {}\begin{array}{c}-1,70528\ast {10}^{-7}-\mathrm{1,745}\ast {10}^{-5}i\\ {}1,54417\ast {10}^{-6}+3,74729\ast {10}^{-5}i\end{array}\end{array}\right\} $$

(55)

$$ \frac{\partial \boldsymbol{F}}{\partial {k}_2}=\left(\frac{\partial {\boldsymbol{K}}_{\boldsymbol{s}}}{\partial {k}_2}-{\boldsymbol{K}}_{\boldsymbol{s}}{\boldsymbol{A}}^{-\mathbf{1}}\frac{\partial \boldsymbol{A}}{\partial {k}_2}\right)\overset{\sim }{\boldsymbol{U}}=\left\{\begin{array}{c}2,67383\ast {10}^{-5}+1,06866\ast {10}^{-3}i\\ {}3,53174\ast {10}^{-6}+5,56696\ast {10}^{-5}i\\ {}\begin{array}{c}7,5875\ast {10}^{-6}+5,10216\ast {10}^{-5}i\\ {}-5,71166\ast {10}^{-6}-1,40692\ast {10}^{-4}i\end{array}\end{array}\right\} $$

(56)

The absolute values of first order sensitivities of the elastic force in two nodes are calculated as

$$ \frac{\partial \left|{F}_1\right|}{\partial {k}_1}=\frac{1}{\left|{F}_1\right|}\left\{\mathit{\operatorname{Re}}\left[{F}_1\right]\left(\mathit{\operatorname{Re}}\left[\frac{\partial {F}_1}{\partial {k}_1}\right]\right)+\mathit{\operatorname{Im}}\left[{F}_1\right]\left(\mathit{\operatorname{Im}}\left[\frac{\partial {F}_1}{\partial {k}_1}\right]\right)\right\}=\frac{1}{15045,00}\left\{\left(-\mathrm{428,114}\right)\ast \left(-1,50914\ast {10}^{-5}\right)+\left(15038,9\right)\ast \left(-3,26491\ast {10}^{-4}\right)\right\}=-0,000325929 $$

(57)

$$ \frac{\partial \left|{F}_1\right|}{\partial {k}_2}=\frac{1}{\left|{F}_1\right|}\left\{\mathit{\operatorname{Re}}\left[{F}_1\right]\left(\mathit{\operatorname{Re}}\left[\frac{\partial {F}_1}{\partial {k}_2}\right]\right)+\mathit{\operatorname{Im}}\left[{F}_1\right]\left(\mathit{\operatorname{Im}}\left[\frac{\partial {F}_1}{\partial {k}_2}\right]\right)\right\}=\frac{1}{15045,00}\left\{\left(-\mathrm{428,114}\right)\ast \left(2,67383\ast {10}^{-5}\right)+\left(15038,9\right)\ast \left(1,06866\ast {10}^{-3}\right)\right\}=0,00106747 $$

(58)

$$ \frac{\partial \left|{F}_2\right|}{\partial {k}_1}=\frac{1}{\left|{F}_2\right|}\left\{\mathit{\operatorname{Re}}\left[{F}_2\right]\left(\mathit{\operatorname{Re}}\left[\frac{\partial {F}_2}{\partial {k}_1}\right]\right)+\mathit{\operatorname{Im}}\left[{F}_2\right]\left(\mathit{\operatorname{Im}}\left[\frac{\partial {F}_2}{\partial {k}_1}\right]\right)\right\}=\frac{1}{20323,10}\left\{\left(\mathrm{131,217}\right)\ast \left(-1,70528\ast {10}^{-7}\right)+\left(20322,7\right)\ast \left(-\mathrm{1,745}\ast {10}^{-5}\right)\right\}=-0,0000174508 $$

(59)

$$ \frac{\partial \left|{F}_2\right|}{\partial {k}_2}=\frac{1}{\left|{F}_2\right|}\left\{\mathit{\operatorname{Re}}\left[{F}_2\right]\left(\mathit{\operatorname{Re}}\left[\frac{\partial {F}_2}{\partial {k}_2}\right]\right)+\mathit{\operatorname{Im}}\left[{F}_2\right]\left(\mathit{\operatorname{Im}}\left[\frac{\partial {F}_2}{\partial {k}_2}\right]\right)\right\}=\frac{1}{20323,10}\left\{\left(\mathrm{131,217}\right)\ast \left(7,5875\ast {10}^{-6}\right)+\left(20322,7\right)\ast \left(5,10216\ast {10}^{-5}\right)\right\}=0,0000510695 $$

(60)

The first order sensitivities of transfer function amplitude of the support force with respect to design variables (k₁and k₂) are obtained as follows

$$ \frac{\partial V}{\partial {k}_1}=\mathit{\operatorname{sign}}\left({\varnothing}_{11}\right)\left(-0,000325929\right)+\mathit{\operatorname{sign}}\left({\varnothing}_{13}\right)\left(-0,0000174508\right)=-0,00034338 $$

(61)

$$ \frac{\partial V}{\partial {k}_2}=\mathit{\operatorname{sign}}\left({\varnothing}_{11}\right)\left(0,00106747\right)+\mathit{\operatorname{sign}}\left({\varnothing}_{13}\right)\left(0,0000510695\right)=0,00111854 $$

(62)

$$ \frac{\partial V}{\partial k}=\left\{-0,00034338\kern1.25em 0,00111854\right\} $$

(63)

$$ \mathit{\operatorname{Max}}\left(\frac{\partial V}{\partial k}\right)-\frac{\partial V}{\partial {k}_1}=0,00111854-0,00034338\ne 0 $$

(64)

$$ \mathit{\operatorname{Max}}\left(\frac{\partial V}{\partial k}\right)-\frac{\partial V}{\partial {k}_2}=0,00111854-0,00111854=0 $$

(65)

In Eq. (65), there is a z=2 index which satisfies the optimality condition. All spring stiffness coefficients are updated as follows

$$ {k}_1=0\kern1.25em {k}_2=0+\Delta K=30000\ N/m $$

(66)

According to this value, the cycle continues until the total stiffness coefficient ($\overline{K}$) is reached in the end of step 300. In each step, all calculations are updated such as eigenvalue, eigenvectors, objective function and sensitivities. Some basic calculations in each step are summarized briefly where the objective function is minimized.

Fig. 15

Cantilever beam with 2 elements