1 INTRODUCTION

Elastic bodies are widely applied in engineering so no wonder a considerable number of studies deal with their optimization using diverse criteria. Reducing production costs to lower prices and improve sustainability of production processes imposes a task of mass reduction. Thus, mass minimization of elastic bodies is a frequently used optimization criterion. For example, [1] presents mass minimization of a cantilever beam with mass concentration at its end, in axial vibrations, by applying variational calculus. In [2] mass minimization of a cantilever beam is also performed, however, change in the cross-section is carried out in a different manner. Optimization criterion of the fundamental frequency of Euler–Bernoulli beams in bending vibrations by changing the cross-section is applied in [3]. In [4], optimization of the fundamental frequency of a cantilever beam with mass concentration at its end is performed using the variational calculus. The gradient projection algorithm is applied for optimization of cantilever beams in [5]. Reference [6] features the application of simultaneous mass minimization and strain energy maximization, which represent the so-called multiobjective optimization problems. In [7], mass minimization is conducted by applying biologically inspired algorithms—firefly algorithm, bat algorithm. Mass minimization of a beam is conducted in [8] with respect to the prescribed fundamental frequency of coupled axial and bending vibrations of a circular homogeneous Euler–Bernoulli beam by using Pontryagin’s maximum principle. The modified Pontryagin’s maximum principle is implemented in [9] for the optimization of Euller–Bernoulli beams with periodically varying cross-sectional profile. The importance of imposing the proper constraints of the optimization problem of Timoshenko beams is emphasized in [10].

The application of functionally graded materials has begun in Japan [11] in the space industry. These materials have been used increasingly as constitutive material in elastic structural elements due to the possibility to design a material of requested characteristics. For the comprehensive analysis of elasticity and continuum mechanics authors may refer to [12, 13]. In general, literature differs two types of functionally graded beams, namely sandwich and axially functionally graded beams, the thorough review being presented in [14]. The analysis of vibrations and stability of the elastic beams made of axially functionally graded (AFG) materials can be found, for example, in [15–17]. Regarding discrete systems, one may refer to [18] where the influence of dissipative forces upon stability of nonconservative systems is analyzed. The modified Andronov–Pontryagin method is applied in the analysis of nonconservative mechanical system with two degrees of freedom in [19]. Optimization of natural frequencies of the beams made of functionally graded (FG) materials is available in [8, 20, 21]. The reference [20] deploys a real-coded genetic algorithm, whereas in [21] optimization is based on using differential evolution, while in [8] Pontryagin’s maximum principle is applied. By applying differential evolution in [22], optimizing the frequencies of elastic beams, and optimizing the mass of clamped arch is performed. Mass minimization and maximization of the plate vibrations frequency is presented in [23] by applying FAIPA algorithm. Optimization of beams of the FG materials using differential evolution method aided by artificial neural networks is implemented in [24], where frequency is maximized in one example and in another the beam mass is minimized. In [25] maximization of the fundamental oscillation frequency of the beam is conducted using the firefly algorithm. The particle swarm algorithm [26] is employed to demonstrate mass optimization of the plate of an FG material. The same algorithm is utilized in [27] to maximize bending stiffness of the beam without change in its mass. The structural-acoustic optimization of functionally graded beams is studied in [28]. Authors apply the transfer matrix method in structural and acoustic analysis, while hybrid particle swarm optimization and cell mapping method is applied to search Pareto optimal solutions. Reference [29] describes optimization of critical bending load of an FG plate by varying its thickness. In [30], authors perform shape optimization of a beam with respect to lateral buckling. A variational formulation of two-parametric optimization problem is presented, and an optimal shape is obtained. The Rayleigh–Ritz method is applied. References [31–34] indicate multiobjective optimization problems in elastic bodies, where one of the criteria in all references is mass optimization. It is also noteworthy to refer to [35] which considers multiobjective optimization of the micro-beam. The multiobjective shape optimization of funcitionally graded microbeams is performed in [36]. Modeling of flexibility in contact area of brake shoe with a wheel is accomplished in [37]. In [38] optimization of the natural frequencies is obtained by changing the beam profile, which remains constant along the longitudinal axis. In the present paper, optimization of the beam mass is performed by changing the cross-section along the longitudinal axis and, at the same time, the results are compared for several cross-sectional shapes, whereby it is shown which cross-section yields the highest percent saving of the mass.

The application of Pontryagin’s maximum principle is most closely related to the problems of optimal control [39–41]. As for its application in elastic bodies, to the best of authors’ knowledge, it has been used for optimization of the columns shape against buckling load [42–44], the column in an elastic medium with respect to buckling and fundamental frequency [45], and to the mass minimization of a homogeneous Euler–Bernoulli beam of a circular cross-section, [8]. In this paper, the application of Pontryagin’s maximum principle in elastic bodies is extended to optimization of the shape of an AFG Euler–Bernoulli beam with coupled axial and bending vibrations by means of mass minimization.

In [46], the shape of flexible manipulators is optimized. The manipulator is modeled as an Euler–Bernoulli beam. The extremum of objective functions is obtained using sequential quadratic programming. A procedure to conduct structural analysis optimization tasks using standard available finite element solvers is given in [47]. Firstly, the maximization of the first natural frequency with a volume constraint is conducted and then the optimality criterion is extended to volume minimization problem with multiple natural frequency constraints. Maximization of the natural frequency of coupled bending and torsion vibrations by changing the cross-section is conducted in [48]. In [49], optimization of the intermediate axis is performed by minimization of the frequency of coupled torsion and bending vibrations to prevent resonance. The coupling of mode shapes can occur due to the specific shape of a cross-section, where in cross-sections with one axis of symmetry there is a coupling of the torsion and bending vibrations, whereas in cross-sections with two axes of symmetry and previous buckling along the longitudinal axis there is a coupling of the bending vibrations along both axes of symmetry [50]. Coupling of the axial and bending vibrations can occur due to complex boundary conditions [51], and it is this type of coupling that is considered in the presented paper as the continuation of the research published in paper [8]. Based on the available literature, to the authors’ best knowledge, the problem of mass minimization of AFG Euler–Bernoulli beams with coupled bending and axial vibrations at prescribed fundamental frequency has not been considered so far. Based on the information provided, it becomes evident that the topic of minimizing the mass of beams, particularly when modes (axial, bending, torsion) are coupled, has received limited attention. Therefore, further research in this field holds significant potential for significant results in the future.

2 PROBLEM STATEMENT

Partial differential equations of an AFG Euler–Bernoulli beam, length L, with coupled bending and axial vibrations can be written in the following manner [50–52], respectively:

$$\frac{\partial }{{\partial z}}\left[ {{{F}_{t}}\left( {z,t} \right)} \right] - \rho (z)A\left( z \right)\frac{{{{\partial }^{2}}{v}\left( {z,t} \right)}}{{\partial {{t}^{2}}}} = 0,\quad \frac{\partial }{{\partial z}}\left[ {{{F}_{a}}\left( {z,t} \right)} \right] - \rho (z)A\left( z \right)\frac{{{{\partial }^{2}}w\left( {z,t} \right)}}{{\partial {{t}^{2}}}} = 0,$$
(1)

where \({v}\left( {z,t} \right)\) and \(w\left( {z,t} \right)\) are transverse and axial displacements, \(\rho \left( z \right)\) is a beam density that changes along axis z, \({{F}_{a}}\left( {z,t} \right)\) and \({{F}_{t}}\left( {z,t} \right)\) are axial and transverse forces, \(A\left( z \right) = {{k}_{A}}d{{\left( z \right)}^{2}}\) is a cross-sectional area, where kA is the coefficient of cross-sectional area, and d(z) is a variable generalized dimension of the beam cross-section (it can be a diameter, cross-sectional width or height). The paper considers the cases of a circular, square and rectangular cross-section, and Table 1 gives values of the coefficient’s kA for the corresponding type of a cross-section. It is noteworthy that the rectangular cross-section has two axes of symmetry and in order that the infinite number of solutions is avoided, even at constant cross-section for prescribed fundamental frequency, the constraint between cross-sectional height and width must be prescribed (the same frequency can be obtained for various ratios of height and width). Two examples of the rectangular cross-section with different ratios of height and width are presented. Axial and transverse force can be written, respectively, as follows:

$${{F}_{a}}\left( {z,t} \right) = E(z)A\left( z \right)\frac{{\partial w(z,t)}}{{\partial z}},\quad {{F}_{t}}\left( {z,t} \right) = \frac{{\partial {{M}_{f}}(z,t)}}{{\partial z}},$$
(2)

where E(z) is Young’s modulus of elasticity, which changes along the beam axis z, Mf is the bending moment which can be written as:

$${{M}_{f}}\left( {z,t} \right) = - E(z){{I}_{x}}\left( z \right)\frac{{{{\partial }^{2}}{v}(z,t)}}{{\partial {{z}^{2}}}},$$
(3)

where \({{I}_{x}}\left( z \right) = {{k}_{I}}d{{\left( z \right)}^{4}}\) is the cross-sectional area axial moment of inertia and where kI represents the coefficient of the axial moment of inertia. Its values for different types of cross-sections are given in Table 1.

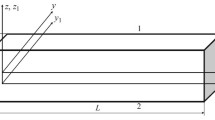
Table 1. Values of coefficients kA and kI
Full size table

Figure 1 shows an AFG beam of length L with complex boundary conditions. The beam elements can move in axial and transverse direction with respect to the longitudinal axis of the beam relative to the stationary Cartesian inertial system Oxyz placed at the left end of the beam, w(z, t) and \({v}\)(z, t) stand for axial and transverse displacements of the beam elements. The beam is supported by one rotational and two translational springs at each end. The beam supports are modeled, in a general case, by two mutually orthogonal translational springs, one rotational spring, and an eccentrically displaced rigid body at each end of the beam. Stiffnesses of springs at the left and right end are respectively c1l, c2l, cl, c1r c2r, and cr. Two rigid bodies are supposed to have masses ml and mr and centroidal mass moments of inertia JCl and JCr. Axial and transverse eccentricities of mass centers of rigid bodies left and right to the beam’s ends are given as el, dl, er and dr.

Fig. 1.
figure 1

General shape of the beam with eccentrically positioned rigid bodies at both ends, which is made of axially functionally graded material.

Full size image

It is noticeable that differential equations (1) are not mutually coupled, but there is a connection between quantities that correspond to axial and bending vibrations at the beam ends. Boundary conditions are derived from the laws of classical mechanics applied to the free body at each of the beam ends. The rotational motion equation is written for the mass center of each body. Namely, for the case of a beam shown in Fig. 1, the coupled boundary conditions for the left (z = 0) and right (z = L) can be written analogously to [53] as follows:

$$ - {{\omega }^{2}}{{J}_{{{{C}_{l}}}}}{\bar {v}}'(0) = - {{c}_{l}}{\bar {v}}'(0) - {{\bar {M}}_{f}}(0) - {{\bar {F}}_{a}}(0){{d}_{l}} + {{\bar {F}}_{t}}(0){{e}_{l}} + {{d}_{l}}{{c}_{{2l}}}\bar {w}(0) - {{e}_{l}}{{c}_{{1l}}}{\bar {v}}(0),$$
(4)
$$ - {{m}_{l}}{{\omega }^{2}}\left[ {\bar {w}(0) + {\bar {v}}'(0){{d}_{l}}} \right] = {{\bar {F}}_{a}}(0) - {{c}_{{2l}}}\bar {w}(0),$$
(5)
$$ - {{m}_{l}}{{\omega }^{2}}\left[ {{\bar {v}}(0) - {\bar {v}}'(0){{e}_{l}}} \right] = {{\bar {F}}_{t}}(0) - {{c}_{{1l}}}{\bar {v}}(0),$$
(6)
$$ - {{\omega }^{2}}{{J}_{{{{C}_{r}}}}}{\bar {v}}'(L) = - {{c}_{r}}{\bar {v}}'(L) + {{\bar {M}}_{f}}(L) + {{\bar {F}}_{a}}(L){{d}_{r}} + {{\bar {F}}_{t}}(L){{e}_{l}} + {{d}_{r}}{{c}_{{2r}}}\bar {w}(L) + {{e}_{r}}{{c}_{{1r}}}{\bar {v}}(L),$$
(7)
$$ - {{m}_{r}}{{\omega }^{2}}\left[ {\bar {w}(L) + {\bar {v}}'(L){{d}_{r}}} \right] = - {{\bar {F}}_{a}}(L) - {{c}_{{2r}}}\bar {w}(L),$$
(8)
$$ - {{m}_{l}}{{\omega }^{2}}\left[ {{\bar {v}}(L) + {\bar {v}}'(L){{e}_{r}}} \right] = - {{\bar {F}}_{t}}(L) - {{c}_{{1r}}}{\bar {v}}(L).$$
(9)

Differential equations (1) are linear, so they can be solved by the method of the separation of variables [50–52]:

$${v}(z,t) = {\bar {v}}\left( z \right)T(t),\quad w(z,t) = \bar {w}\left( z \right)T(t).$$
(10)

where the function of time T(t), on account of coupled axial and bending vibrations due to boundary conditions, is the same for both types of vibrations. This way, variables can be also separated in the expressions for transverse and axial forces and bending moment:

$${{F}_{t}}\left( {z,t} \right) = {{\bar {F}}_{t}}\left( z \right)T\left( t \right),\quad {{F}_{a}}\left( {z,t} \right) = {{\bar {F}}_{a}}\left( z \right)T\left( t \right),\quad {{M}_{f}}\left( {z,t} \right) = {{\bar {M}}_{f}}\left( z \right)T\left( t \right)$$
(11)

Based on [50–52], the function of time T(t) has the following property:

$$\frac{{{{\partial }^{2}}T(t)}}{{\partial {{t}^{2}}}} = - {{\left( {2f\pi } \right)}^{2}}T(t),$$
(12)

where f is the frequency of the corresponding form of vibrations. In this paper, it is assumed that the fundamental (first) frequency is prescribed.

Now, if dimensionless variables are inserted:

$$\begin{gathered} R = \frac{\rho }{{{{\rho }_{0}}}},\quad \overline E = \frac{E}{{{{E}_{0}}}},\quad Z = \frac{z}{L},\quad D = \frac{d}{L},\quad W = \frac{{\bar {w}}}{L},\quad V = \frac{{{\bar {v}}}}{L}, \\ {{F}_{T}} = \frac{{{{{\bar {F}}}_{t}}}}{{{{E}_{0}}{{L}^{2}}}},\quad {{F}_{A}} = \frac{{{{{\bar {F}}}_{a}}}}{{{{E}_{0}}{{L}^{2}}}},\quad {{M}_{F}} = \frac{{{{{\bar {M}}}_{f}}}}{{{{E}_{0}}{{L}^{3}}}}, \\ \end{gathered} $$
(13)

where ρ0 and E0 are reference values for density and Young’s modulus of elasticity, the following differential equations are obtained:

$$\begin{gathered} V' = {{V}_{P}},\quad V_{P}^{'} = - \frac{{{{M}_{F}}}}{{\overline E {{k}_{I}}{{D}^{4}}}},\quad M_{F}^{'} = {{F}_{T}}, \\ F_{T}^{'} = - {{p}^{2}}R{{k}_{A}}{{D}^{2}}V,\quad W' = \frac{{{{F}_{A}}}}{{\overline E {{k}_{A}}{{D}^{2}}}},\quad F_{A}^{'} = - {{p}^{2}}R{{k}_{A}}{{D}^{2}}W, \\ \end{gathered} $$
(14)

where p is a dimensionless frequency, which depends on the beam length, fundamental frequency, density and modulus of elasticity of the material:

$$p = 2f\pi L\sqrt {\frac{{{{\rho }_{0}}}}{{{{E}_{0}}}}} .$$
(15)

Note that in Eqs. (14) the differentiation over the dimensionless independent variable Z is presented using ()'. Considering (13), boundary conditions (4)–(9) can be also written in the dimensionless form (see [53]).

The optimization problem can be formulated in such a way that for a prescribed value of parameter p the function D = D(Z) should be determined to satisfy differential equations (14) and corresponding dimensionless boundary conditions from [53], so that the mass of the considered beam is minimal. Based on this formulation, the minimizing functional has the form:

$$J = \int\limits_0^1 {R{{k}_{A}}{{D}^{2}}dZ} .$$
(16)

Separate sections will consider the case of a limited diameter and beam length, respectively:

$${{C}_{2}} \leqslant D \leqslant {{C}_{1}},\quad {{C}_{1}} \in {{\mathbb{R}}^{ + }},\quad {{C}_{2}} \in {{\mathbb{R}}^{ + }},$$
(17)

which makes sense in terms of the Euler–Bernoulli theory, and the set of all positive real numbers is denoted by R+. In other words, if the diameter or width were not limited, the optimal shape of the beam, for selected certain system parameters, would not be within the limits of the recommendation of the validity of Euler–Beornulli theory, because the ratio of diameter or width and length of the beam would exceed 1 : 10 [50]. Additionally, for smaller dimensions the question is posed concerning the strength of a beam, and therefore it is sometimes necessary to limit cross-sectional dimension by the lower boundary value.

The procedure of the shape optimization is presented using an example of a cantilever beam, length L = 1 m, with eccentrically positioned rigid body at its free end, as shown in Fig. 2. The rigid body has mass mr and moment of inertia JCr. Axial and bending eccentricities of the rigid body, er and dr, are shown in Fig. 2. In the selected AFG material the laws of change in density and modulus of elasticity are taken like in [54, 55]:

$$\begin{gathered} \rho (z) = {{\rho }_{0}}(1 - 0.8\cos (\pi z)),\quad {{\rho }_{0}} = 7850\,\frac{{{\text{kg}}}}{{{{{\text{m}}}^{{\text{3}}}}}}, \\ E(z) = {{E}_{0}}(1 - 0.2\cos (\pi z)),\quad {{E}_{0}} = 2.068 \times {{10}^{{11}}}\,\frac{{\text{N}}}{{{{{\text{m}}}^{{\text{2}}}}}}. \\ \end{gathered} $$
(18)
Fig. 2.
figure 2

Cantilever beam with eccentrically positioned rigid body at its free end.

Full size image

Value of the fundamental frequency is taken to be f = 10 Hz. Boundary conditions for this example can be obtained from general conditions (4)–(9) as follows:

$$V\left( 0 \right) = 0,\quad {{V}_{P}}\left( 0 \right) = 0,\quad W\left( 0 \right) = 0,$$
(19)
$$\begin{gathered} {{M}_{F}}(1) + {{F}_{A}}(1){{D}_{R}} + {{F}_{T}}(1){{E}_{R}} + {{p}^{2}}{{J}_{{CR}}}{{V}_{P}}(1) = 0, \\ {{F}_{A}}(1) - {{p}^{2}}{{M}_{R}}W(1) - {{p}^{2}}{{M}_{R}}{{D}_{R}}{{V}_{P}}(1) = 0, \\ {{F}_{T}}(1) - {{p}^{2}}{{M}_{R}}V(1) - {{p}^{2}}{{M}_{R}}{{E}_{R}}{{V}_{P}}(1) = 0. \\ \end{gathered} $$
(20)

where the following dimensionless parameters were used:

$${{M}_{R}} = \frac{{{{m}_{r}}}}{{{{\rho }_{0}}{{L}^{3}}}},\quad {{J}_{{CR}}} = \frac{{{{J}_{{Cr}}}}}{{{{\rho }_{0}}{{L}^{5}}}},\quad {{D}_{R}} = \frac{{{{d}_{r}}}}{L},\quad {{E}_{R}} = \frac{{{{e}_{r}}}}{L}.$$
(21)

3 DETERMINING THE DIAMETER OF A CANTILEVER BEAM WITH CONSTANT CROSS-SECTION BY A PRESCRIBED FUNDAMENTAL FREQUENCY

The next chapter considers a cantilever beam with constant cross-sectional width and diameter DC, respectively. A numerical procedure is presented using the example of a circular cross-section and is identical for all other shapes of the cross-section. Considering the linearity of the system of differential equations (14), as well as the fact that symbolic-numeric method of the initial parameters can be applied [53, 56], the influence of the diameter DC on its natural frequency can be analyzed. Applying the parametric solving of the system of linear differential equations, using the ParametricNDSolve[] program package Wolfram Mathematica [57], the solution can be written as the function of natural frequency and diameter DC:

$$\begin{gathered} {\mathbf{X}}\left( {Z,p,{{D}_{C}}} \right) = \\ {{\left[ {V\left( {Z,p,{{D}_{C}}} \right),{{V}_{P}}\left( {Z,p,{{D}_{C}}} \right),{{M}_{F}}\left( {Z,p,{{D}_{C}}} \right),{{F}_{T}}\left( {Z,p,{{D}_{C}}} \right),W\left( {Z,p,{{D}_{C}}} \right),{{F}_{A}}\left( {Z,p,{{D}_{C}}} \right)} \right]}^{T}} \\ = {{A}_{1}}{{{\mathbf{X}}}_{1}}\left( {Z,p,{{D}_{C}}} \right) + {{A}_{2}}{{{\mathbf{X}}}_{2}}\left( {Z,p,{{D}_{C}}} \right) + {{A}_{3}}{{{\mathbf{X}}}_{3}}\left( {Z,p,{{D}_{C}}} \right), \\ \end{gathered} $$
(22)

where A1, A2 and A3 represent unknown constants of integration, and vectors of particular solutions are of the form as follows:

$$\begin{gathered} {{{\mathbf{X}}}_{j}}\left( {Z,p,{{D}_{C}}} \right) \\ = {{\left[ {{{V}_{j}}\left( {Z,p,{{D}_{C}}} \right),{{V}_{P}}_{j}\left( {Z,p,{{D}_{C}}} \right),{{M}_{F}}_{j}\left( {Z,p,{{D}_{C}}} \right),{{F}_{T}}_{j}\left( {Z,p,{{D}_{C}}} \right),{{W}_{j}}\left( {Z,p,{{D}_{C}}} \right),{{F}_{A}}_{j}\left( {Z,p,{{D}_{C}}} \right)} \right]}^{T}} \\ j = 1,2,3. \\ \end{gathered} $$
(23)

These particular solutions must satisfy boundary conditions (19) on the left side, which can be written as follows:

$$\begin{gathered} {{{\mathbf{X}}}_{1}}\left( {0,p,{{D}_{C}}} \right) = {{\left[ {0\,\,\,\,0\,\,\,\,0\,\,\,\,0\,\,\,\,0\,\,\,\,1} \right]}^{T}}, \\ {{{\mathbf{X}}}_{2}}\left( {0,p,{{D}_{C}}} \right) = {{\left[ {0\,\,\,\,0\,\,\,\,0\,\,\,\,1\,\,\,\,0\,\,\,\,0} \right]}^{T}}, \\ {{{\mathbf{X}}}_{3}}\left( {0,p,{{D}_{C}}} \right) = {{\left[ {0\,\,\,\,0\,\,\,\,1\,\,\,\,0\,\,\,\,0\,\,\,\,0} \right]}^{T}}. \\ \end{gathered} $$
(24)

Constants A1, A2 and A3 can be determined from the condition that solution (22) satisfies boundary conditions (20). For that reason, based on (20), the following expressions can be written:

$${{e}_{{1j}}}\left( {p,{{D}_{C}}} \right) = - {{F}_{A}}_{j}\left( {1,p,{{D}_{C}}} \right) + {{M}_{R}}\,{{p}^{2}}\left( {{{W}_{j}}\left( {1,p,{{D}_{C}}} \right) + {{V}_{P}}_{j}\left( {1,p,{{D}_{C}}} \right){{D}_{R}}} \right),$$
(25)
$${{e}_{{2j}}}\left( {p,{{D}_{C}}} \right) = - {{F}_{T}}_{j}\left( {1,p,{{D}_{C}}} \right) + {{M}_{R}}\,{{p}^{2}}\left( {{{V}_{j}}\left( {1,p,{{D}_{C}}} \right) + {{V}_{P}}_{j}\left( {1,p,{{D}_{C}}} \right){{E}_{R}}} \right),$$
(26)
$$\begin{gathered} {{e}_{{3j}}}\left( {p,{{D}_{C}}} \right) = {{M}_{F}}\left( {1,p,{{D}_{C}}} \right) + {{F}_{A}}\left( {1,p,{{D}_{C}}} \right){{D}_{R}} \\ \, + {{F}_{T}}\left( {1,p,{{D}_{C}}} \right){{E}_{R}} + {{p}^{2}}{{J}_{{CR}}}{{V}_{P}}\left( {1,p,{{D}_{C}}} \right), \\ \end{gathered} $$
(27)

which represent the functions of dimensionless natural frequency \(p\) and the diameter DC. Now, the following system of equations can be developed:

$$\left[ \begin{gathered} {{e}_{{11}}}\left( {p,{{D}_{C}}} \right)\,\,\,\,\,{{e}_{{12}}}\left( {p,{{D}_{C}}} \right)\,\,\,\,\,{{e}_{{13}}}\left( {p,{{D}_{C}}} \right) \\ {{e}_{{21}}}\left( {p,{{D}_{C}}} \right)\,\,\,\,\,{{e}_{{22}}}\left( {p,{{D}_{C}}} \right)\,\,\,\,\,{{e}_{{23}}}\left( {p,{{D}_{C}}} \right) \\ {{e}_{{31}}}\left( {p,{{D}_{C}}} \right)\,\,\,\,\,{{e}_{{32}}}\left( {p,{{D}_{C}}} \right)\,\,\,\,\,{{e}_{{33}}}\left( {p,{{D}_{C}}} \right) \\ \end{gathered} \right]\left[ \begin{gathered} {{A}_{1}} \\ {{A}_{2}} \\ {{A}_{3}} \\ \end{gathered} \right] = 0.$$
(28)

In order that this system has nontrivial solutions, the determinant of a system must equal zero:

$$g\left( {p,D{}_{C}} \right) \equiv \left| \begin{gathered} {{e}_{{11}}}\left( {p,D{}_{C}} \right)\,\,\,\,\,{{e}_{{12}}}\left( {p,D{}_{C}} \right)\,\,\,\,\,{{e}_{{13}}}\left( {p,D{}_{C}} \right) \\ {{e}_{{21}}}\left( {p,D{}_{C}} \right)\,\,\,\,\,{{e}_{{22}}}\left( {p,D{}_{C}} \right)\,\,\,\,\,{{e}_{{23}}}\left( {p,D{}_{C}} \right) \\ {{e}_{{31}}}\left( {p,D{}_{C}} \right)\,\,\,\,\,{{e}_{{32}}}\left( {p,D{}_{C}} \right)\,\,\,\,\,{{e}_{{33}}}\left( {p,D{}_{C}} \right) \\ \end{gathered} \right| = 0.$$
(29)

This determinant represents the frequency equation of coupled axial and bending vibrations of an AFG Euler–Bernoulli beam [53] and is given as the function of natural frequency \(p\) and diameter DC. This way, we have the function of two symbolic variables, and using the ContourPlot[] command of Wolfram Mathematica program package [57] dependency of the frequency on the diameter can be shown.

Figure 3 gives graphical correlation between a dimensionless diameter DC and the first and second dimensionless frequency p of a cantilever beam, from where it is seen for which values of DC the frequency f = 10 Hz, fundamental or second, is prescribed. Since it is necessary in further work to ensure for that frequency to be fundamental, and not any of the higher ones, by substituting this value in Eqs. (15) and (29), the zeros of Eq. (29) are numerically determined. The fundamental frequency is matched by the greatest solution of the Eq. (29).

Fig. 3.
figure 3

The graphical correlation between a dimensionless diameter DC and the first and second dimensionless frequency p of a cantilever beam.

Full size image

Table 2 gives corresponding values of the cross-sections obtained by this method. The problem is solved for the following selected values of the parameters:

$${{M}_{R}} = 0.00125,\quad {{J}_{{CR}}} = 0.0003125,\quad {{D}_{R}} = 0.5,\quad {{E}_{R}} = 0.5,$$
(30)
$${{M}_{R}} = 0.01,\quad {{J}_{{CR}}} = 0.0025,\quad {{D}_{R}} = 0.5,\quad {{E}_{R}} = 0.5,$$
(31)

where parameters (30) and (31) are utilized for the cantilever beams of the circular, square and two rectangular cross-sections.

Table 2. Values of the cross-sectional sizes at prescribed value of the fundamental frequency f = 10 Hz
Full size table

4 OPTIMIZATION OF THE CANTILEVER BEAM WITHOUT LIMITED DIAMETER OR WIDTH OF THE CROSS-SECTION APPLYING PONTRYAGIN’S MAXIMUM PRINCIPLE

In order to apply Pontryagin’s maximum principle, by formulating the optimal control problem, it is needed to introduce state quantities V, VP, W, MF, FA, FT, \(\overline Z \) so that one more equation is adjoined to differential equations (14), and therefore the equations of state are of the form:

$$\begin{gathered} V{\kern 1pt} ' = {{V}_{P}},\quad V_{P}^{'} = - \frac{{{{M}_{F}}}}{{\overline E {{k}_{I}}{{D}^{4}}}},\quad M_{F}^{'} = {{F}_{T}},\quad F_{T}^{'} = - {{p}^{2}}R{{k}_{A}}{{D}^{2}}V, \\ W{\kern 1pt} ' = \frac{{{{F}_{A}}}}{{\overline E {{k}_{A}}{{D}^{2}}}},\quad F_{A}^{'} = - {{p}^{2}}R{{k}_{A}}{{D}^{2}}W,\quad \overline Z {\kern 1pt} ' = 1 \\ \end{gathered} $$
(32)

The \(\overline Z \) is so-called rheonomic coordinate which has the same properties like coordinate Z and will be used instead of it in density and modulus of elasticity of the material, due to the specifity of Pontryagin’s maximum principle. Generalized dimension of the cantilever beam cross-section (diameter and width, respectively) is taken for the function of scalar control. The problem of shape optimization is reduced to determining the control piecewise continuous function D = D(Z) so that solutions of the equations of state (32) satisfy initial (19) and final conditions (20), whereby the functional (16) has a minimum value [58].

It is necessary to develop the Hamiltonian of the Hamilton–Pontryagin form [58–60]:

$$\begin{gathered} H = - R{{k}_{A}}{{D}^{2}} + {{\lambda }_{V}}{{V}_{P}} - {{\lambda }_{{{{V}_{P}}}}}\frac{{{{M}_{F}}}}{{\overline E {{k}_{I}}{{D}^{4}}}} + {{\lambda }_{{{{M}_{F}}}}}{{F}_{T}} - {{\lambda }_{{{{F}_{T}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}}V \\ \, + {{\lambda }_{W}}\frac{{{{F}_{A}}}}{{\overline E {{k}_{A}}{{D}^{2}}}} - {{\lambda }_{{{{F}_{A}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}}W + {{\lambda }_{{\overline Z }}}, \\ \end{gathered} $$
(33)

where quantities \({{\lambda }_{V}},\,{{\lambda }_{{{{V}_{P}}}}},{{\lambda }_{{{{M}_{F}}}}},{{\lambda }_{{{{F}_{T}}}}},{{\lambda }_{W}},{{\lambda }_{{{{F}_{A}}}}},{{\lambda }_{{\overline Z }}}\) are constant variables, with the corresponding costate system of equations which has the form:

$$\begin{gathered} \lambda _{V}^{'} = - \frac{{\partial H}}{{\partial V}} = {{\lambda }_{{{{F}_{T}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}},\quad \lambda _{{{{V}_{P}}}}^{'} = - \frac{{\partial H}}{{\partial {{V}_{P}}}} = - {{\lambda }_{V}},\quad \lambda _{{{{M}_{F}}}}^{'} = - \frac{{\partial H}}{{\partial {{M}_{F}}}} = {{\lambda }_{{{{V}_{P}}}}}\frac{1}{{\overline E {{k}_{I}}{{D}^{4}}}}, \\ \lambda _{{{{F}_{T}}}}^{'} = - \frac{{\partial H}}{{\partial {{F}_{T}}}} = - {{\lambda }_{{{{M}_{F}}}}},\quad \lambda _{W}^{'} = - \frac{{\partial H}}{{\partial W}} = {{\lambda }_{{{{F}_{A}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}},\quad \lambda _{{{{F}_{A}}}}^{'} = - \frac{{\partial H}}{{\partial {{F}_{A}}}} = - {{\lambda }_{W}}\frac{1}{{\overline E {{k}_{A}}{{D}^{2}}}}, \\ \lambda _{{\overline Z }}^{'} = - \frac{{\partial H}}{{\partial \overline Z }} = \frac{{\partial R}}{{\partial \overline Z }}{{k}_{A}}{{D}^{2}} + {{\lambda }_{{{{V}_{P}}}}}\frac{{{{M}_{F}}}}{{{{k}_{I}}{{D}^{4}}}}\frac{{\partial ({{{\bar {E}}}^{{ - 1}}})}}{{\partial \overline Z }} + {{\lambda }_{{{{F}_{T}}}}}\frac{{\partial R}}{{\partial \overline Z }}{{p}^{2}}{{k}_{A}}{{D}^{2}}V \\ \, - {{\lambda }_{W}}\frac{{{{F}_{A}}}}{{{{k}_{A}}{{D}^{2}}}}\frac{{\partial ({{{\bar {E}}}^{{ - 1}}})}}{{\partial \overline Z }} + {{\lambda }_{{{{F}_{A}}}}}\frac{{\partial R}}{{\partial \overline Z }}{{p}^{2}}{{k}_{A}}{{D}^{2}}W. \\ \end{gathered} $$
(34)

By applying Pontryagin’s maximum principle in optimization problems, it is possible, analogously to [42–44], to express costate variables by the state quantities:

$${{\lambda }_{V}} = k{{F}_{T}},\quad {{\lambda }_{{{{V}_{P}}}}} = - k{{M}_{F}},\quad {{\lambda }_{{{{M}_{F}}}}} = k{{V}_{P}},\quad {{\lambda }_{{{{F}_{T}}}}} = - kV,\quad {{\lambda }_{W}} = k{{F}_{A}},\quad {{\lambda }_{{{{F}_{A}}}}} = - kW,$$
(35)

where k is an arbitrary real constant. In the cited references, the authors observed that, in the problems they considered, if all coupled variables are expressed through a single arbitrary constant, the costate system and transversality conditions can be completely eliminated from further considerations. Now, using (35) the first six equations of the costate system (34) are reduced to the first six state Eqs. (32).

Transversality conditions can be represented in the form as follows:

$$\left. {\left( {{{\lambda }_{V}}\delta V + {{\lambda }_{{{{V}_{P}}}}}\delta {{V}_{P}} + {{\lambda }_{{{{M}_{F}}}}}\delta {{M}_{F}} + {{\lambda }_{{{{F}_{T}}}}}\delta {{F}_{T}} + {{\lambda }_{W}}\delta W + {{\lambda }_{{{{F}_{A}}}}}\delta {{F}_{A}} + {{\lambda }_{{\overline Z }}}\delta \overline Z } \right)} \right|_{0}^{{{{t}_{f}}}} = 0,$$
(36)

where \(\delta \left( \cdot \right)\) represents asynchronous variation [61] of quantity \(\left( \cdot \right)\). After varying the boundary conditions (19) and (20) and substituting in (36), the following expressions are obtained, and thereby transversality conditions are fulfilled:

$$\begin{gathered} ~{{\lambda }_{{{{F}_{T}}}}}\left( 0 \right) = 0,\quad {{\lambda }_{{{{F}_{A}}}}}\left( 0 \right) = 0,\quad {{\lambda }_{{{{M}_{F}}}}}\left( 0 \right) = 0, \\ - {{D}_{R}}{{\lambda }_{{{{M}_{F}}}}}\left( 1 \right) + {{\lambda }_{{{{F}_{A}}}}}\left( 1 \right) + \frac{1}{{{{M}_{R}}{{p}^{2}}}}{{\lambda }_{W}}\left( 1 \right) = 0,\quad {{\lambda }_{{\overline Z }}}\left( 1 \right) = 0 \\ - {{E}_{R}}{{\lambda }_{{{{M}_{F}}}}}\left( 1 \right) + {{\lambda }_{{{{F}_{T}}}}}\left( 1 \right) + \frac{1}{{{{M}_{R}}{{p}^{2}}}}{{\lambda }_{V}}\left( 1 \right) = 0, \\ - {{p}^{2}}{{J}_{{CR}}}{{\lambda }_{{{{M}_{F}}}}}\left( 1 \right) + {{\lambda }_{{{{V}_{P}}}}}\left( 1 \right) - {{E}_{R}}{{\lambda }_{V}}\left( 1 \right) - {{D}_{{R\,}}}{{\lambda }_{W}}\left( 1 \right) = 0. \\ \end{gathered} $$
(37)

If expressions (35) are substituted in (37), mentioned transversality conditions become identically satisfied when boundary conditions (19) and (20) are fulfilled. This largely facilitates solving the two-point-boundary value problem (TPBVP), obtained by applying Pontryagin’s maximum principle, because the number of differential equations is reduced, and in the shooting method, which will be applied, avoiding a very demanding assessment of a range of initial values for costate variables is enabled. Note that this also holds for a general case of boundary conditions, so the procedure of determining the optimal form is identical for any other example.

The necessary optimality condition of Pontryagin’s maximum principle, using (35), is of the form [58]:

$$\frac{{\partial H}}{{\partial D}} = - \frac{{2({{k}_{I}}k{{D}^{2}}F_{A}^{2} + 2{{k}_{A}}kM_{F}^{2} + k_{A}^{2}{{k}_{I}}{{D}^{6}}\bar {E}R(1 - {{p}^{2}}k{{V}^{2}} - {{p}^{2}}k{{W}^{2}}))}}{{{{k}_{A}}{{k}_{I}}{{D}^{5}}\bar {E}}} = 0.$$
(38)

In order that the condition for a maximum of the function H is satisfied, considering (35) and (38), it is necessary:

$$\frac{{{{\partial }^{2}}H}}{{\partial {{D}^{2}}}} = \frac{{8k({{k}_{I}}{{D}^{2}}F_{A}^{2} + 3{{k}_{A}}M_{F}^{2})}}{{{{k}_{A}}{{k}_{I}}{{D}^{6}}\bar {E}}} < 0,$$
(39)

from where it follows k = –q2 < 0 where q is a real constant. In order to eliminate this parameter, the following shifts can be inserted:

$$\bar {V} = qV,\quad {{\bar {V}}_{P}} = q{{V}_{P}},\quad {{\bar {M}}_{F}} = q{{M}_{F}},\quad {{\bar {F}}_{T}} = q{{F}_{T}},\quad \bar {W} = qW,\quad {{\bar {F}}_{A}} = q{{F}_{A}}.$$
(40)

By inserting these shifts, differential equations (32) are reduced to the form as follows:

$$\begin{gathered} \bar {V}' = \overline {{{V}_{P}}} ,\quad \bar {V}_{P}^{'} = - \frac{{\overline {{{M}_{F}}} }}{{\overline E {{k}_{I}}{{D}^{4}}}},\quad \bar {M}_{F}^{'} = {{F}_{T}}, \\ \bar {F}_{T}^{'} = - {{p}^{2}}R{{k}_{A}}{{D}^{2}}\bar {V},\quad \overline W ' = \frac{{\overline {{{F}_{A}}} }}{{\overline E {{k}_{A}}{{D}^{2}}}},\quad \bar {F}_{A}^{'} = - {{p}^{2}}R{{k}_{A}}{{D}^{2}}\bar {W},\quad \overline Z ' = 1. \\ \end{gathered} $$
(41)

The relation of the necessary optimality condition should be adjoined to them (38). Identically, the initial and final conditions are written:

$$\bar {V}\left( 0 \right) = 0,\quad {{\bar {V}}_{{\bar {P}}}}\left( 0 \right) = 0,\quad \bar {W}\left( 0 \right) = 0,\quad \overline Z \left( 0 \right) = 0,$$
(42)
$$\begin{gathered} \overline {{{M}_{F}}} (1) + \overline {{{F}_{A}}} (1){{D}_{R}} + \overline {{{F}_{T}}} (1){{E}_{R}} + {{p}^{2}}{{J}_{{CR\,}}}\overline {{{V}_{P}}} (1) = 0, \\ \overline {{{F}_{A}}} (1) - {{p}^{2}}{{M}_{R}}\bar {W}(1) - {{p}^{2}}{{M}_{R}}{{D}_{R}}\overline {{{V}_{P}}} (1) = 0, \\ \overline {{{F}_{T}}} (1) - {{p}^{2}}{{M}_{R}}\bar {V}(1) - {{p}^{2}}{{M}_{R}}{{E}_{R}}\overline {{{V}_{P}}} (1) = 0. \\ \end{gathered} $$
(43)

Numerical solution of TPBVP, which consists of Eqs. (41)–(43) and Eq. (38), by applying the shooting method, is reduced to selecting the appropriate values of the missing initial conditions \(\overline {{{M}_{F}}} (0),\overline {{{F}_{A}}} (0)\) and \(\overline {{{F}_{T}}} (0)\) which satisfy conditions (43). Determination of unknown initial values is carried out using the program package Wolfram Mathematica [57] and command NDSolve[] in such a way that numeric relations are written, containing each quantity of state \(\overline {{{M}_{F}}} (1),\overline {{{F}_{A}}} (1),\overline {{{F}_{T}}} (1),\overline {{{V}_{P}}} (1),\bar {W}(1)\) and \(\bar {V}(1)\) expressed depending on three missing initial conditions \(\overline {{{M}_{F}}} (0),\overline {{{F}_{A}}} (0)\) and \(\overline {{{F}_{T}}} (0)\), and then they are defined from three final conditions (43). For a detailed procedure of solving this problem the reader can refer to [39]. It should be emphasized that in preparing the command NDSolve[] it is not necessary to explicitly express D(Z) from Eq. (38), because it allows simultaneous solving of differential and ordinary equations.

Figure 4 displays the radius values for the cantilevers of a circular cross-section, as well as the half widths for the cantilevers of square and two rectangular cross-sections for the ratio of sides 1.5 and 2 for the parameters’ values (30) (Fig. 4a) and (31) (Fig. 4b). Table 3 gives numerical solutions of the missing initial conditions. It is noticeable that the maximum value of the diameter and width of the beam cross-section in a beam clamp, respectively, for the cantilevers with parameters (31), goes beyond the limits of the validity of the Euler–Bernoulli theory, and the corresponding cantilevers of a constant cross-section fulfilled that condition. For this reason, the next chapter presents the procedure for the shape optimization of a cantilever with limited values of the maximum cross section from relations (17).

Fig. 4.
figure 4

Diagrams of radii (solid line), half side of a square (dashed line), half width of a rectangle for the ratio of height and width 1.5 (dash-dot-dash) and ratio 2 (dotted); solutions of the parameter’s values for (30) are given in (a), and for (31) in (b).

Full size image
Table 3. Values of the missing boundary values for infinite cases and relative percent saving of the cantilever beam mass against the cantiver beam of a constant cross-section
Full size table

Also, Table 3 gives values of the relative percent saving of cantilevers masses against the cantilevers of a constant cross-section, whose values are presented in Chapter 3. For any cross-section, this value is obtained from the following formula:

$$\Delta = \frac{{\left( {\int\limits_0^1 {RD_{C}^{2}dZ} - \int\limits_0^1 {RD{{{\left( Z \right)}}^{2}}dZ} } \right)}}{{\int\limits_0^1 {RD_{C}^{2}dZ} }} \times 100\% ,$$
(44)

where numerical integration of the corresponding solution of the D(Z) system was carried out (41), and DC is the value of the constant generalized dimension from chapter 3 of this paper. It can be inferred that the highest relative percent saving is achieved for a circular cross-section, and the higher the ratio of height and width of a rectangular cross-section, the lower relative percent saving of the material.

5 SHAPE OPTIMIZATION OF THE CANTILEVER BEAM OF A LIMITED MAXIMUM CROSS-SECTIONAL DIAMETER OR WIDTH BY APPLYING PONTRYAGIN’S MAXIMUM PRINCIPLE

In the optimization of the cantilever with a limited maximum cross-section it is necessary to insert an additional term in the Hamilton–Pontryagin function, so it can be written in the manner as follows [58–60]:

$$\begin{gathered} {{H}_{1}} = H + {{\mu }_{1}}({{D}^{2}} - C_{1}^{2}) = - R{{k}_{A}}{{D}^{2}} + {{\lambda }_{V}}{{V}_{P}} - {{\lambda }_{{{{V}_{P}}}}}\frac{{{{M}_{F}}}}{{\overline E {{k}_{I}}{{D}^{4}}}} + {{\lambda }_{{{{M}_{F}}}}}{{F}_{T}} - {{\lambda }_{{{{F}_{T}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}}V \\ \, + {{\lambda }_{W}}\frac{{{{F}_{A}}}}{{\overline E {{k}_{A}}{{D}^{2}}}} - {{\lambda }_{{{{F}_{A}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}}W + {{\lambda }_{{\overline Z }}} + {{\mu }_{1}}({{D}^{2}} - C_{1}^{2}), \\ \end{gathered} $$
(45)

where \({{\mu }_{1}}\) is an indefinite multiplier, which, after the shifts (35), k = –q2 < 0 and (40), can be determined from necessary optimality conditions of Pontryagin’s principle [58]:

$$\frac{{\partial {{H}_{1}}}}{{\partial D}} = 0 \Rightarrow {{\mu }_{1}}{\text{ = }} - \frac{{\overline {F_{A}^{2}} }}{{{{k}_{A}}{{D}^{4}}\overline E }} - \frac{{2\overline {M_{F}^{2}} }}{{{{k}_{I}}{{D}^{6}}\overline E }} + {{k}_{A}}R(1 + {{p}^{2}}{{\bar {V}}^{2}} + {{p}^{2}}{{\bar {W}}^{2}}).$$
(46)

If the corresponding maximum dimension of the cross-section is limited by (17) along the cantilever axis, it can reach that value at certain locations but at others it can’t. At locations where it does not reach the limit, it can be determined, like in the case without a limit, from (38). Accordingly, from Pontryagin’s maximum principle the control quantity has the following values:

$$D = \left\{ \begin{gathered} {{C}_{1}},\quad {{\mu }_{1}} \ne 0, \\ f(\overline {{{M}_{F}}} ,\bar {V},\overline {{{F}_{A}}} ,\bar {W}),\quad {{\mu }_{1}} = 0, \\ \end{gathered} \right.$$
(47)

where \(D = f(\overline {{{M}_{F}}} ,\bar {V},\overline {{{F}_{A}}} ,\bar {W})\) is the solution of Eq. (38).

Checking the fulfillment of optimality conditions is identical to (39), where by inserting shifts \(k = - {{q}^{2}} < 0\), (40) and (46), it can be written:

$$\begin{gathered} {{\left. {\frac{{{{\partial }^{2}}{{H}_{1}}}}{{\partial {{D}^{2}}}}} \right|}_{{{{\mu }_{1}} = 0}}} = \frac{{ - 8({{k}_{I}}{{D}^{2}}\overline {F_{A}^{2}} + 3{{k}_{A}}\overline {M_{F}^{2}} )}}{{{{k}_{A}}{{k}_{I}}{{D}^{6}}\overline E }} < 0, \\ {{\left. {\frac{{{{\partial }^{2}}{{H}_{1}}}}{{\partial {{D}^{2}}}}} \right|}_{{{{\mu }_{1}} \ne 0}}} = \frac{{ - 8({{k}_{I}}C_{1}^{2}\overline {F_{A}^{2}} + 3{{k}_{A}}\overline {M_{F}^{2}} )}}{{{{k}_{A}}{{k}_{I}}C_{1}^{6}\overline E }} < 0. \\ \end{gathered} $$
(48)

So, differential equations (41) are used, with identical initial and final conditions (42) and (43), however if the multiplier \({{\mu }_{1}}\) is different from zero, the corresponding dimension of a cross section reaches the limit, so this value is used in equations. If it equals zero, the control quantity is computed from the equation (38). The problem is solved first for the case when there is no maximum limit from (17), and then the largest value of control quantity is analyzed. In those segments where maximum value from (17) is disrupted it can be assumed that control is at the limit. Then we have intervals of limited and unlimited cross-sections.

This procedure is viewed through the example of a cross-section with the parameters’ values (31). Solution without limit is given in the previous section in Fig. 4, and, as explained, the ratio of beam diameter and length in a clamp is larger than 1:10 so that Euler–Bernoulli theory cannot produce sufficiently accurate results. After limits are inserted (17), the structure of limited and unlimited diameter occurs where:

$$D = \left\{ \begin{gathered} {{C}_{1}},\quad 0 \leqslant Z \leqslant {{Z}_{1}}, \\ f\left( {{{{\bar {M}}}_{F}},\bar {V},{{{\bar {F}}}_{A}},\bar {W}} \right),\quad {{Z}_{1}} \leqslant Z \leqslant 1. \\ \end{gathered} \right.$$
(49)

Now, solving TPBVP is considerably more complex. The system (41) is solved two times, for the limited case, and then for the unlimited, where in transition to the unlimited case the condition must be satisfied:

$${{\left. {\frac{{\partial {{H}_{1}}}}{{\partial D}}} \right|}_{{{{Z}_{1}},D = {{C}_{1}}}}} = \frac{{\overline {F_{A}^{2}} ({{Z}_{1}})}}{{{{k}_{A}}C_{1}^{3}\overline E ({{Z}_{1}})}} + \frac{{2\overline {M_{F}^{2}} ({{Z}_{1}})}}{{{{k}_{I}}C_{1}^{5}\overline E ({{Z}_{1}})}} - {{k}_{A}}{{C}_{1}}R({{Z}_{1}})(1 + {{p}^{2}}{{\bar {V}}^{2}}({{Z}_{1}}) + {{p}^{2}}{{\bar {W}}^{2}}({{Z}_{1}})) = 0.$$
(50)

Now, we obtain four-parameter shooting, where \({{\bar {M}}_{F}}(0),{{\bar {F}}_{A}}(0),{{\bar {F}}_{T}}(0)\) and Z1 are selected so that the conditions (43) and (50) are satisified.

Table 4 gives numerical solutions of the missing values, as well as relative percent saving of the cantilevers mass against the cantilevers of a constant cross-section. Figure 5 presents diagrams of the corresponding cross-sectional dimensions after this TPBVP is solved. It is noteworthy that due to taking the same limit by the cross-sectional larger dimension, percent saving of the circular cross-section mass is now the least. This can be explained by the fact that in this cross-section its diameter constant value is larger than constant values of other cross-sectional dimensions. This way, a square cross-section has the best saving of mass if cross-sectional limit is needed.

Table 4. Values of the missing boundary values for limited cases and relative percent saving of the cantilever beam mass against the cantilever beam of a constant cross-section
Full size table
Fig. 5.
figure 5

Diagrams of a limited radius (solid line), half side of a square (dashed line), half width of a rectangle for the ratio of height and width 1.5 (dash-dot-dash) and ratio 2 (dotted).

Full size image

6 SHAPE OPTIMIZATION OF THE CANTILEVER BEAM OF A LIMITED MAXIMUM AND MINIMUM DIAMETER BY APPLYING PONTRYAGIN’S MAXIMUM PRINCIPLE

It is evident from Fig. 5 that the diameter value on the cantilever right side can be quite small. In that case, the cantilever strength can be disrupted, therefore, apart from maximum limitation, it is needed to perform limitation of the cantilever minimum diameter, as shown by relation (17). At the same time, the expanded Hamilton-Pontryagin function is of the form as follows [58–60]:

$$\begin{gathered} {{H}_{2}} = - R{{k}_{A}}{{D}^{2}} + {{\lambda }_{V}}V - {{\lambda }_{{{{V}_{P}}}}}\frac{{{{M}_{F}}}}{{\overline E {{k}_{I}}{{D}^{4}}}} + {{\lambda }_{{{{M}_{F}}}}}{{F}_{T}} - {{\lambda }_{{{{F}_{T}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}}V \\ \, + {{\lambda }_{W}}\frac{{{{F}_{A}}}}{{\overline E {{k}_{A}}{{D}^{2}}}} - {{\lambda }_{{{{F}_{A}}}}}{{p}^{2}}R{{k}_{A}}{{D}^{2}}W + {{\lambda }_{{\overline Z }}} + {{\mu }_{1}}({{D}^{2}} - C_{1}^{2}) + {{\mu }_{2}}( - {{D}^{2}} + C_{2}^{2}), \\ \end{gathered} $$
(51)

where \({{\mu }_{1}}\) and \({{\mu }_{2}}\) are indefinite multipliers. So, the diameter can have a maximum limited value, a minimum limited value or the value between these two extremes:

$$D = \left\{ \begin{gathered} {{C}_{1}},\quad {{\mu }_{1}} \ne 0,\quad {{\mu }_{2}} = 0, \\ f({{{\bar {M}}}_{F}},\bar {V},{{{\bar {F}}}_{A}},\bar {W}),\quad {{\mu }_{1}} = 0,\quad {{\mu }_{2}} = 0, \\ {{C}_{2}},\quad {{\mu }_{1}} = 0,\quad {{\mu }_{2}} \ne 0. \\ \end{gathered} \right.$$
(52)

Based on this, indefinite multipliers can be determined as:

$$\begin{gathered} {{\left. {\frac{{\partial {{H}_{2}}}}{{\partial D}}} \right|}_{{{{\mu }_{2}} = 0}}} = 0 \Rightarrow {{\mu }_{1}}\,{\text{ = }} - {\kern 1pt} \frac{{\overline {F_{A}^{2}} }}{{{{k}_{A}}{{D}^{4}}\overline E }} - \frac{{2\overline {M_{F}^{2}} }}{{{{k}_{I}}{{D}^{6}}\overline E }} + {{k}_{A}}R(1 + {{p}^{2}}{{{\bar {V}}}^{2}} + {{p}^{2}}{{{\bar {W}}}^{2}}), \\ {{\left. {\frac{{\partial {{H}_{2}}}}{{\partial D}}} \right|}_{{{{\mu }_{1}} = 0}}} = 0 \Rightarrow {{\mu }_{{2\,}}}{\text{ = }}\,\frac{{{{k}_{I}}{{D}^{2}}\overline {F_{A}^{2}} + 2{{k}_{A}}\overline {M_{F}^{2}} - k_{A}^{2}{{k}_{I}}{{D}^{6}}\overline E R(1 + {{p}^{2}}{{{\bar {V}}}^{2}} + {{p}^{2}}{{{\bar {W}}}^{2}})}}{{{{k}_{A}}{{k}_{I}}{{D}^{6}}\overline E }}. \\ \end{gathered} $$
(53)

Optimality conditions are also fulfilled over all subintervals:

$$\begin{gathered} {{\left. {\frac{{{{\partial }^{2}}{{H}_{2}}}}{{\partial {{D}^{2}}}}} \right|}_{{{{\mu }_{1}} = 0,\,{{\mu }_{2}} = 0}}} = \frac{{ - 8({{k}_{I}}{{D}^{2}}\overline {F_{A}^{2}} + 3{{k}_{A}}\overline {M_{F}^{2}} )}}{{{{k}_{A}}{{k}_{I}}{{D}^{6}}\overline E }} < 0, \\ {{\left. {\frac{{{{\partial }^{2}}{{H}_{2}}}}{{\partial {{D}^{2}}}}} \right|}_{{{{\mu }_{1}} \ne 0,\,{{\mu }_{2}} = 0}}} = \frac{{ - 8({{k}_{I}}C_{1}^{2}\overline {F_{A}^{2}} + 3{{k}_{A}}\overline {M_{F}^{2}} )}}{{{{k}_{A}}{{k}_{I}}C_{1}^{6}\overline E }} < 0, \\ {{\left. {\frac{{{{\partial }^{2}}{{H}_{2}}}}{{\partial {{D}^{2}}}}} \right|}_{{{{\mu }_{1}} = 0,\,{{\mu }_{2}} \ne 0}}} = \frac{{ - 8({{k}_{I}}C_{2}^{2}\overline {F_{A}^{2}} + 3{{k}_{A}}\overline {M_{F}^{2}} )}}{{{{k}_{A}}{{k}_{I}}C_{2}^{6}\overline E }} < 0. \\ \end{gathered} $$
(54)

The control structure is of the form as follows:

$$D = \left\{ \begin{gathered} {{C}_{1}},\quad 0 \leqslant Z \leqslant {{Z}_{1}}, \\ f\left( {{{{\bar {M}}}_{F}},\bar {V},{{{\bar {F}}}_{A}},\bar {W}} \right),\quad {{Z}_{1}} \leqslant Z \leqslant {{Z}_{2}}. \\ {{C}_{2}},\quad {{Z}_{2}} \leqslant Z \leqslant 1 \\ \end{gathered} \right.$$
(55)

Now, the system (41) is solved three times, the first time, for \({{\mu }_{1}} \ne 0\) when we have a maximum limited diameter C1, the second time, for \({{\mu }_{1}} = 0\) and \({{\mu }_{2}} = 0\) when the diameter is obtained from (38), and the third time, for \({{\mu }_{2}} \ne 0\) when we have a minimum limited diameter C2. In transition from one structure to another it is necessary to have the following conditions satisfied:

$$\begin{gathered} {{\left. {\frac{{\partial {{H}_{2}}}}{{\partial D}}} \right|}_{{{{Z}_{1}},D = {{C}_{1}}}}} = \frac{{\overline {F_{A}^{2}} ({{Z}_{1}})}}{{{{k}_{A}}C_{1}^{3}\overline E ({{Z}_{1}})}} + \frac{{2\overline {M_{F}^{2}} ({{Z}_{1}})}}{{{{k}_{I}}C_{1}^{5}\overline E ({{Z}_{1}})}} - {{k}_{A}}{{C}_{1}}R({{Z}_{1}})(1 + {{p}^{2}}{{{\bar {V}}}^{2}}({{Z}_{1}}) + {{p}^{2}}{{{\bar {W}}}^{2}}({{Z}_{1}})) = 0, \\ {{\left. {\frac{{\partial {{H}_{2}}}}{{\partial D}}} \right|}_{{{{Z}_{2}},D = {{C}_{2}}}}} = \frac{{\overline {F_{A}^{2}} ({{Z}_{2}})}}{{{{k}_{A}}C_{2}^{3}\overline E ({{Z}_{2}})}} + \frac{{2\overline {M_{F}^{2}} ({{Z}_{2}})}}{{{{k}_{I}}C_{2}^{5}\overline E ({{Z}_{2}})}} - {{k}_{A}}{{C}_{2}}R({{Z}_{2}})(1 + {{p}^{2}}{{{\bar {V}}}^{2}}({{Z}_{2}}) + {{p}^{2}}{{{\bar {W}}}^{2}}({{Z}_{2}})) = 0. \\ \end{gathered} $$
(56)

Now, we have a five-parameter shooting, where \({{\bar {M}}_{F}}(0),{{\bar {F}}_{A}}(0){{\bar {F}}_{T}}(0)\), Z1 and Z2 are selected so as to satisfy conditions (43) and (56). To solve this problem, parameters (30) are used, with the missing boundary values: \({{\bar {M}}_{F}}(0) = 438.440 \times {{10}^{{ - 11}}},\) \({{\bar {F}}_{T}}(0) = - 242.949 \times {{10}^{{ - 11}}},\) \({{\bar {F}}_{A}}(0) = - 106.894 \times {{10}^{{ - 11}}},\) Z1 = 0.269349, Z2 = 0.811487. Relative percent saving of the mass amounts to Δ = 21.902%. The values of diameter limitations are C1 = 0.06 and C2 = 0.04. Fig. 6 presents the diagram of a limited radius of a circular cross-section and the case of unlimited radius that corresponds to the first column from Table 3. It can be noted that the implementation of boundaries reduces the percentage of mass savings that was Δ = 23.4975%.

Fig. 6.
figure 6

Diagram of a limited and unlimited radius of a circular cross section.

Full size image

7 CONCLUSIONS

This paper presents an extension of a previously conducted research of mass minimization of a homogeneous elastic beam. Shape optimization of an AFG Euler–Bernoulli cantilever beam of a circular, square and rectangular cross-section with coupled bending and axial vibrations is performed. Coupling of mode shapes is a consequence of eccentricities of mass center of rigid bodies and it is included in the presented model. Cantilever beam mass is minimized at a prescribed fundamental frequency as a prerequest. In solving this optimization problem, the Pontryagin’s maximum principle is applied. By this application, authors proposed a tool for optimization of functionally graded beams in terms of mass minimization. Pontryagin’s maximum principle has been mainly used for solving optimization problems in buckling and mass optimization of homogeneous simply-supported elastic beam. Mass minimization of a cantilever beam is accomplished by taking the cross-sectional diameter and width, respectively, for control quantities. In order to ensure the validity of Euler-Bernoulli beam theory, the limitation of the control quantity maximum value is introduced. Also, to ensure the corresponding strength of a cantilever beam, limitation of the control quantity minimum value is introduced. Furthermore, this study shows a percentage saving in beam mass using the optimal variable cross-section relative to the corresponding beam with a constant cross-section. The presented optimization procedure can be also applied to examples where the coupling of axial and bending vibrations occurred due to complex boundary conditions, whereby it is necessary to apply the appropriate boundary conditions corresponding to a concrete structural element.