1 Introduction

The bearing plays an indispensable role in the mechanical industry. As a key component of mechanical equipment, its reliability has a great impact on the overall mechanical system (Wang et al. 2017). Lubrication can improve reliability of bearings, because the failure modes of bearing such as abrasion and scuffing are related to lubrication (Qu et al. 1999). The lubricating film can reduce friction of rolling elements. The roller and roller table directly contact when the oil film is too thin. Moreover, with the sharp rise of local temperature, the bearing will be scuffed, which greatly affects the service life of bearings (Peng et al. 2015). The two surfaces may come in solid contact, this is the regime of boundary lubrication (Persson 1993). In practice, due to the randomness of load and speed, the oil film thickness changes continuously. Oil film rupture may occur during bearing operation.

In order to judge the state of bearing lubrication, the thickness of bearing lubricating film must be obtained firstly. Linear contact elastohydrodynamic lubrication theory was used to calculate the thickness of bearing lubrication film. The theoretical basis of elastohydrodynamic lubrication is the Hertz contact theory and Reynolds (Wen 2007). As early as 1916, Martin applied the Reynolds theory to analyze the problem of linear contact lubrication (Martin 1916). Then, Dowson and Higginson obtained the complete numerical solution of the linear contact elastohydrodynamic lubrication and proposed a formula for calculating the minimum film thickness (Dowson et al. 1978).

However, the above studies were assumed to be the contact problems with infinite line, which had some limitations in practical problems. Later, researchers proposed the elastohydrodynamic lubrication theory with finite line. Now, bearing lubrication analysis has received extensive attention, including roughness, temperature, positioning error, and randomness (Venner and Hooke 2006). Gentle used the minimum film thickness formula to predict the central film thickness of rolling bearings, the calculated results are close to the experimental results (Gentle and Cameron 1973). Koye verified Dowson-Higginson’s formula through many experiments, and the result was 30% larger on average (Koye 1981). Steinführer applied Dowson-Higginson’s formula to calculate oil film thickness of heavy duty roller at different speeds (Steinführer 1980). Dowson-Higginson’s formula is widely used in engineering because it is simple to calculate and the result is credible.

As the working conditions are random, the reliability of bearing needs to be analyzed. Reliability can be defined as the probability that a product or system performs specified functions at specified times and under specified conditions (Choi et al. 2007). The bearing fatigue strength is used as failure criterion in traditional bearing reliability analysis. Jin et al. used artificial neural network to establish the probabilistic reliability analysis model (Jin et al. 2018). The performance degradation was considered as the failure criterion. Qin analyzed the vibration acceleration of the bearing and obtained the reliability with different time (Qin et al. 2017). There are few studies on the reliability of lubrication. It is necessary to propose a new reliability estimation method considering the thickness film.

For the bearing lubrication, reliability refers to the probability that boundary lubrication does not occur during the bearing operation. The lubricating reliability is a time-dependent problem because of the wear of bearing.

For the research on time-dependent reliability, Rice first proposed the transcendental formula in 1944 (Rice 1944). Coleman proposed a formula for calculating the first transcendence probability based on Poisson process (Coleman 1959). Zhang and Du proposed a time-dependent reliability method based on the random variables that obey Gaussian distribution (Zhang et al. 2011). Sudret put forward a new analytic expression of the outcrossing rate and applies this method to evaluate the reliability of steel girder under random load in midspan (Sudret 2008). Hu and Du raised an analytical method of joint crossing rate, and based on this method, a fault probability estimation method was developed and applied to the reliability analysis of beams and mechanisms (Hu and Du 2013). Geng and Wang brought forward a time-dependent reliability analysis method based on interval mathematics and the first crossing theory, and verified the effectiveness of the method with four-bar linkage (Geng et al. 2016). Based on the mixed uncertainty and the first crossing theory, Wang and Xiong posed a time-dependent reliability evaluation method for closed-loop control problems (Wang et al. 2018). There are many researches on solving time-dependent reliability problems by using the first crossing method. However, there are few researches on complex engineering problems such as lubrication; the main reason is that the failure criteria of such problems are not easy to obtain.

In this paper, the analytical method of lubrication reliability was proposed, the model of lubrication reliability was presented. The main content in this paper included presenting a method to analyze the time-dependent reliability of bearing lubrication, establishing the time-dependent reliability analysis model of Dawson and Higginson’s formula, substituting it into numerical examples for solution, and using Monte Carlo simulation to verify its accuracy and efficiency.

2 The minimum oil film thickness

This article studied the lubrication reliability of cylindrical roller bearings. The contact between roller and raceway of cylindrical roller bearing is linear, so Dowson-Higginson’s formula can be used to calculate the film thickness. Dowson-Higginson’s formula is shown as (Steinführer 1980):

$$ {h}_{min}=2.65.\frac{\alpha^{0.54}\times {\left({\eta}_0\times u\right)}^{0.7}\times {r}^{0.43}}{E^{0.03}\times {W}^{0.13}} $$
(1)

where hmin is the minimum film thickness on the contact surface, r is the equivalent radius, E is the equivalent elastic modulus of the metal surfaces, α is the (isothermal) pressure exponent of viscosity, η0 is the dynamic viscosity of lubrication, u is the entrainment velocity, and W is road per unit contact length:

$$ \left\{\begin{array}{c}W={Q}_{max}/L\ \\ {}{Q}_{max}=4.6.{F}_r/Z\end{array}\kern0.75em \right. $$
(2)

where Qmax is the maximum load of roller, L is the effective contact length between the roller and the raceway, Fr is the radial road, and Z is the number of rollers.

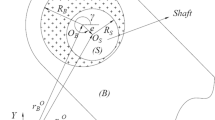
Figure 1 shows some parameters of the cylindrical roller bearing, r1 and u1 are roller parameters, r2 and u2 are groove parameters.

Fig. 1
figure 1

The equivalent radius and the entrainment velocity

Full size image

The equivalent radius r and the entrainment velocity u are calculated by:

$$ \left\{\begin{array}{c}r=\frac{1}{\frac{1}{r_1}+\frac{1}{r_2}\ }\ \\ {}u=\frac{u_1+{u}_2}{2\ }\end{array}.\right. $$
(3)

In this paper, it is assumed that r1 increases with time and r2 decreases with time. Since r1 is much smaller than r2, the trend of r is the same as r1. Therefore, it can be obtained that r decreases with time. The velocity u and loads Fr are assumed to be random variables.

3 Film thickness ratio

In Dowson-Higginson’s formula, the minimum film thickness is based on an assumption that surfaces are smooth. However, in reality, surfaces of bearing have some degree of roughness. The effect of roughness on film thickness is very complex (Nahm and Bamberger 1980). The empirical formula film thickness ratio was used to evaluate the effect of roughness on lubrication. The film thickness ratio λ is

$$ \uplambda =\frac{h_{min}}{\sqrt{{\sigma_u}^2+{\sigma_l}^2}} $$
(4)

where hmin is the minimum film thickness, σu is the roughness of upper surface, and σl is the roughness of the lower surface.

The relationship between film formation rate and film thickness ratio summarized by other scholars is shown in Fig. 2 (Tian et al. 2018).

Fig. 2
figure 2

The relationship between film formation rate and film thickness ratio

Full size image

The abscissa of Fig. 2 is the film thickness ratio, the ordinate is the film formation rate. As shown in the graph, there is no oil film formation in region A (λ < 0.7). Meanwhile, there is boundary lubrication between the raceway and the roller, and the contact surface will soon be damaged. In region B (0.7 < λ < 1.5), film formation rate is less than 50%, it is in the state of mixed friction; the surface damage of the mechanism is accelerated, and the service life is reduced. While the film formation rate is greater than 50% in region C (1.5 < λ < 3), the contact area also in the state of mixed friction and the contact surface is barely damaged. While λ is greater than 3, the contact surface is completely separated by a continuous lubricating film. It is in the state of fluid lubrication. The service life of mechanism will even increase, but it is difficult to achieve.

4 Derivation of lubrication reliability formula

4.1 Derivation of formulas

In the lubrication process of cylindrical roller bearing, once the contact surface is under the boundary lubrication state, the bearing life will be sharply reduced. Therefore, the lubrication reliability of the bearing is defined as the probability that the boundary lubrication state does not occur under given condition, or the probability that the film thickness ratio is not less than 0.7.

It is assumed that the bearing lubrication time interval is [t0, t1]. For the entire service life of the bearing, the allowable minimum film thickness is greater than ε, then time-dependent reliability is expressed as:

$$ R\left({t}_0,{t}_1\right)=\Pr \left\{g\left(X,t\right)={h}_{min}\ge \upvarepsilon, t\in \left({t}_0,{t}_1\right)\right\} $$
(5)

where ε is the film thickness of boundary lubrication, X = ( u, W).

The failure probability Pf is expressed by:

$$ {P}_f\left({\mathrm{t}}_0,{\mathrm{t}}_1\right)=\Pr \left\{g\left(X,t\right)={h}_{min}<\upvarepsilon, t\in \left({t}_0,{t}_1\right)\right\} $$
(6)

First passage method (FPM) is adopted for time-dependent reliability calculation (Zhang et al. 2011). Figure 3 depicts the upcrossing event and downcrossing event in FPM. Lubrication failure occurs when the function g(X, t) exceeds the allowable upper limit at +ε (upcrossing event) or is below the allowable lower limit at −ε (downcrossing event). Introduction the upcrossing rate v+ and downcrossing rate v−, the time-dependent reliability can be written as:

$$ R\left({t}_0,{t}_1\right)=R\left({t}_0\right)\mathit{\exp}\left\{-{\int}_{t_0}^{t_1}\left[{\mathrm{v}}^{+}(t)+{\mathrm{v}}^{-}(t)\right]. dt\right\}. $$
(7)
Fig. 3
figure 3

Upcrossing event and downcrossing event

Full size image

For bearing lubrication, only a lower limit is allowed because the lubrication failure will occur when the film thickness is less than a certain value. The formula is deformed into:

$$ R\left({t}_0,{t}_1\right)=R\left({t}_0\right)\mathit{\exp}\left\{-{\int}_{t_0}^{t_1}{\mathrm{v}}^{-}(t). dt\right\} $$
(8)

where R(t0) is the point reliability:

$$ R\left({t}_0\right)=\Pr \left\{g\left(X,{t}_0\Big)\right)={h}_{min}\ge \upvarepsilon \right\}. $$
(9)

Point reliability is solved by the first-order reliability method (FORM) (Zhang et al. 2012). The basic idea of the FORM is to linearize the function, then use the first and second moments of the variables to calculate the first and second moments of the function, and then obtain the reliability of the function. Point reliability can be expressed as:

$$ R=1-\Phi \left(\frac{-\varepsilon -{\mu}_g}{\sigma_g}\right). $$
(10)

According to the film thickness ratio theory mentioned above, while the film thickness ratio (λ) is less than 0.7, no oil film is formed between the contact surfaces. Therefore, it is assumed that the lubrication is failure when the film thickness ratio (λ) is less than 0.7. ε can be expressed as:

$$ \upvarepsilon =0.7\times \sqrt{{\sigma_u}^2+{\sigma_l}^2}. $$
(11)

To facilitate calculation, the performance function is:

$$ {\upvarepsilon}_1=\upvarepsilon -V $$
(12)

where V is a parameter to derive the crossing rate. Its value depends on the thickness of the minimum film, V = hmin(μX).

To facilitate calculation, the limit state equation is simplified as:

$$ g\left(X,t\right)={h}_{min}-V=2.65.\frac{\alpha^{0.54}\times {\left({\eta}_0\times u\right)}^{0.7}\times {r}^{0.43}}{E^{0.03}\times {W}^{0.13}}-V $$
(13)

where X = (u, W), t ∊ (t0, t1). Taylor expansion of the function at the mean value:

$$ g\left(X,t\right)\approx \hat{g}\left(X,t\right)=g\left({\mu}_X,t\right)+\sum \limits_{i=1}^2\frac{\mathrm{\partial g}\left(X,\mathrm{t}\right)}{\partial {X}_i}.\left({X}_i-{\mu}_i\right). $$
(14)

To simplify the formula further, since the variable X is normally distributed, X can be transformed into Xi = μi + σi ∙ Ui, where Ui~N(0, 1).

The linear function \( \hat{g}\left(X,\mathrm{t}\right) \) becomes:

$$ \hat{g}\left(U,t\right)={b}_0(t)+\sum \limits_{i=1}^2{b}_i(t){U}_i $$
(15)

where U = (U1, U2), b0(t) = g(μX, t),

$$ {b}_i(t)={\left.\frac{\partial g\left(X,t\right)}{\partial {X}_i}\right|}_{\mu_X}.{\sigma}_i $$
(16)
$$ g\left({\mu}_X,t\right)={\left[{h}_{min}-V\right]}_{\mu_X}. $$
(17)

The mean and standard deviation of the linear function \( \hat{g}\left(X,t\right) \) are

$$ {\mu}_g(t)={b}_0(t) $$
(18)
$$ {\sigma}_g={\left[\sum \limits_{i=1}^2{b_i}^2(t)\right]}^{1/2} $$
(19)

so,

$$ {\mu}_g(t)={b}_0(t)={\left[{h}_{min}-\mathrm{A}\right]}_{\mu_X}=2.65\times \frac{\alpha^{0.54}\times {\left({\eta}_0\times {\mu}_u\right)}^{0.7}\times {r}^{0.43}}{E^{0.03}\times {\mu_W}^{0.13}}-V $$
(20)
$$ {\sigma}_g(t)={\left[{b_1}^2(t)+{b_2}^2(t)\right]}^{1/2} $$
(21)

where

$$ {b}_1(t)={\left.\frac{\partial g\left(X,t\right)}{\partial u}\right|}_{\mu_X}\times {\sigma}_1=2.65\times \frac{\alpha^{0.54}\times {\eta_0}^{0.7}\times {r}^{0.43}}{E^{0.03}\times {\mu_W}^{0.13}}\times 0.7\times {\mu_u}^{-0.3}\times {\sigma}_1 $$
(22)
$$ {b}_2(t)=\frac{\partial g\left(X,t\right)}{\partial W}\times {\sigma}_2=2.65\frac{\alpha^{0.54}{\left({\eta}_0{\mu}_u\right)}^{0.7}{r}^{0.43}}{E^{0.03}}\times \left(-0.13\right)\times {\mu_W}^{-1.13}\times {\sigma}_2. $$
(23)

The next step is to find the crossing rate. The down crossing rate is defined as:

$$ {\mathrm{v}}^{-}(t)=\underset{\Delta t\to 0}{\lim}\frac{{\mathrm{w}}^{-}\left(t,\Delta t\right)}{\Delta t} $$
(24)

where w−(t, ∆t) is given by:

$$ {\mathrm{w}}^{-}\left(t,\Delta t\right)=\Pr \left\{g\left(X,t\right)>-\upvarepsilon \cap g\left(X,t+\Delta t\right)<-\upvarepsilon \right\}. $$
(25)

According to the above formula, w−contains the events g(X, t) >  − ε and g(X, t + ∆t) <  − ε. Through the linear equation \( \hat{g}\left(X,t\right) \):

$$ {\mathrm{w}}^{-}\left(t,\Delta t\right)\approx \Pr \left\{\hat{g}\left(X,t\right)>-\upvarepsilon \cap \hat{g}\left(X,t+\Delta t\right)<-\upvarepsilon \right\}=\Pr \left\{-\hat{g}\left(X,t\right)<\upvarepsilon \cap \hat{g}\left(X,t+\Delta t\right)<-\upvarepsilon \right\}. $$
(26)

To simplify the process, the \( -\hat{g}\left(X,t\right) \) and\( \hat{g}\left(X,t+\Delta t\right) \) are substituted into standard normal distribution random variables Ug(t) and Ug(t + ∆t):

$$ {U}_g(t)=\frac{-g\left(X,\mathrm{t}\right)-\left[-{\mu}_g(t)\right]}{\sigma_g(t)} $$
(27)
$$ {U}_g\left(t+\Delta t\right)=\frac{g\left(X,t+\Delta t\right)-\left[{\mu}_g\left(t+\Delta t\right)\right]}{\sigma_g\left(t+\Delta t\right)}. $$
(28)

According to (18, 19), the formula can be obtained:

$$ {U}_g(t)=\frac{\sum \limits_{i=1}^2{b}_i(t){U}_i}{{\left[\sum \limits_{i=1}^2{b_i}^2(t)\right]}^{1/2}}=-c(t)\times U $$
(29)
$$ c(t)=\frac{b(t)}{\left\Vert b(t)\right\Vert } $$
(30)

||·|| represents the value of the matrix, b(t) = (b1(t), b2(t)):

$$ {U}_g\left(t+\Delta t\right)=\frac{\sum \limits_{i=1}^2{b}_i\left(t+\Delta t\right){U}_i}{{\left[\sum \limits_{i=1}^2{b_i}^2\left(t+\Delta t\right)\right]}^{1/2}}=c\left(t+\Delta t\right).U $$
(31)
$$ c\left(t+\Delta t\right)=\frac{b\left(t+\Delta t\right)}{\left\Vert b\left(t+\Delta t\right)\right\Vert } $$
(32)

where b(t + ∆t) = (b1(t + ∆t), b2(t + ∆t)).

Transform the downcrossing event by Eq. (26), (27) and (29):

$$ {\mathrm{w}}^{-}\left(t,\Delta t\right)=\Pr \left\{-{\mu}_g(t)+{\sigma}_g(t){U}_g(t)<\upvarepsilon \cap {\mu}_g\left(t+\Delta t\right)+{\sigma}_g\left(t+\Delta t\right){U}_g\left(t+\Delta t\right)<-\upvarepsilon \right\}=\Pr \left\{{U}_g(t)<{\upbeta}_{-}(t)\cap {U}_g\left(t+\Delta t\right)<-{\upbeta}_{-}\left(t+\Delta t\right)\right\} $$
(33)

where \( {\upbeta}_{-}(t)=\frac{\upvarepsilon +{\mu}_g(t)}{\sigma_g(t)} \), \( {\upbeta}_{-}\left(t+\Delta t\right)=\frac{\upvarepsilon +{\mu}_g\left(t+\Delta t\right)}{\sigma_g\left(t+\Delta t\right)} \).

As Ug(t) and Ug(t + ∆t) are bivariate joint normal distribution, the downcrossing rate can be obtained by the bivariate cumulative distribution function:

$$ {\mathrm{w}}^{-}\left(t,\Delta t\right)={\Phi}_2\left[{\upbeta}_{-}(t),-{\upbeta}_{-}\left(t+\Delta t\right),\rho \left(t,t+\Delta t\right)\right] $$
(34)

where Φ2 is the normal cumulative distribution function; its probability density function ϕ2 is:

$$ {\phi}_2\left(x,y,\rho \right)=\frac{1}{2\pi \sqrt{1-{\rho}^2}}\exp \left[-\frac{1}{2}\frac{x^2-2\rho xy+{y}^2}{1-{\rho}^2}\right] $$
(35)

ρ is the correlation coefficients:

$$ \rho \left(t,t+\Delta t\right)=-c(t).c\left(t+\Delta t\right) $$
(36)

because w−(t, 0) = 0:

$$ {\left.{\mathrm{v}}^{-}(t)=\underset{\Delta t\to 0}{\lim}\frac{{\mathrm{w}}^{-}\left(t,\Delta t\right)-{\mathrm{w}}^{-}\left(t,0\right)}{\Delta t}=\frac{\partial {\mathrm{w}}^{-}\left(t,\Delta t\right)}{\mathrm{\partial \Delta }t}\right|}_{\Delta t=0}. $$
(37)

To solve the partial derivative, the following two equations are introduced:

$$ \frac{\partial {\Phi}_2\left(x,y,\rho \right)}{\partial y}=\phi (y)\Phi \left(\frac{x-\rho y}{\sqrt{1-{\rho}^2}}\right) $$
(38)
$$ \frac{\partial {\Phi}_2\left(x,y,\rho \right)}{\partial \rho }={\phi}_2\left(x,y,\rho \right). $$
(39)

Substitute these into equations:

$$ \frac{\partial {\mathrm{w}}^{-}\left(t,\Delta t\right)}{\mathrm{\partial \Delta }t}={I}_1\left(t,\Delta t\right)+{I}_2\left(t,\Delta t\right) $$
(40)
$$ {I}_1\left(t,\Delta t\right)=\frac{\partial {\Phi}_2\left[{\upbeta}_{-}(t),-{\upbeta}_{-}\left(t+\Delta t\right),\rho \left(t,t+\Delta t\right)\right]}{\partial \left[{\upbeta}_{-}\left(t+\Delta t\right)\right]}=-\phi \left[{\upbeta}_{-}\left(t+\Delta t\right)\right]\Phi \left(\mathrm{A}\right){\beta}_{-}^{\prime}\left(t+\Delta t\right) $$
(41)
$$ {I}_2\left(t,\Delta t\right)=\frac{\partial {\Phi}_2\left[{\upbeta}_{-}(t),-{\upbeta}_{-}\left(t+\Delta t\right),\rho \left(t,t+\Delta t\right)\right]}{\partial \left[\rho \left(t,t+\Delta t\right)\right]}=-{\phi}_2\left[{\upbeta}_{-}(t),-{\upbeta}_{-}\left(t+\Delta t\right),\rho \left(t,t+\Delta t\right)\right]{\rho}^{\prime}\left(t,t+\Delta t\right) $$
(42)

where

$$ \mathrm{A}=\frac{\upbeta_{-}(t)+\rho \left(t,t+\Delta t\right){\upbeta}_{-}\left(t+\Delta t\right)}{\sqrt{1-{\rho}^2\left(t,t+\Delta t\right)}}. $$
(43)

Then, the downcrossing rate is:

$$ {\left.{\mathrm{v}}^{-}(t)=\frac{\partial {\mathrm{w}}^{-}\left(t,\Delta t\right)}{\mathrm{\partial \Delta }t}\right|}_{\Delta t=0}=\underset{\Delta t\to 0}{\lim}\left[{I}_1\left(t,\Delta t\right)+{I}_2\left(t,\Delta t\right)\right]. $$
(44)

To find the limits of I1 and I2, the following derivation is performed:

$$ c(t)=\frac{b(t)}{\left\Vert b(t)\right\Vert } $$
(45)

c(t) is the unit vectory, so c(t) ∙ c′(t) = 0.

Derivative again:

$$ c(t).{c}^{\prime \prime }(t)=-{\left[{c}^{\prime }(t)\right]}^2=-{\left\Vert {c}^{\prime }(t)\right\Vert}^2 $$
(46)

on the correlation coefficient, ρ do the following operation:

$$ \underset{\Delta t\to 0}{\lim }{\rho}^{\prime}\left(t,t+\Delta t\right)=-c(t).{c}^{\prime }(t)=0 $$
(47)
$$ \underset{\Delta t\to 0}{\lim }{\rho}^{\prime \prime}\left(t,t+\Delta t\right)=-c(t).{c}^{\prime \prime }(t)={\left\Vert {c}^{\prime }(t)\right\Vert}^2. $$
(48)

M is defined as:

$$ M=\underset{\Delta t\to 0}{\lim}\left[-\frac{\sqrt{1-{\rho}^2\left(t,t+\Delta t\right)}}{\rho^{\prime}\left(t,t+\Delta t\right)}\right]. $$
(49)

Using L’Hospital’s rule:

$$ M=\underset{\Delta t\to 0}{\lim}\left[-\frac{\sqrt{1-{\rho}^2\left(t,t+\Delta t\right)}}{\rho^{\prime}\left(t,t+\Delta t\right)}\right]=\frac{\left[c(t).c(t)\right]}{\left[c(t).{c}^{\prime \prime }(t)\right]}\underset{\Delta t\to 0}{\lim}\left[\frac{\left[c(t).{c}^{\prime}\left(t+\Delta t\right)\right]}{\sqrt{1-{\left[-c(t).c\left(t+\Delta t\right)\right]}^2}}\right]=\frac{1}{{\left\Vert {c}^{\prime }(t)\right\Vert}^2}\frac{1}{M} $$
(50)

so \( M=\frac{1}{\left\Vert {c}^{\prime }(t)\right\Vert } \)

$$ \underset{\Delta t\to 0}{\lim }A=\underset{\Delta t\to 0}{\lim}\frac{\upbeta_{-}(t)+\rho \left(t,t+\Delta t\right){\upbeta}_{-}\left(t+\Delta t\right)}{\sqrt{1-{\rho}^2\left(t,t+\Delta t\right)}}={\beta}_{-}^{\prime }(t)M=\frac{\beta_{-}^{\prime }(t)}{\left\Vert {\boldsymbol{c}}^{\prime }(t)\right\Vert }. $$
(51)

Then,

$$ \underset{\Delta t\to 0}{\lim }{I}_1\left(t,\Delta t\right)=\underset{\Delta t\to 0}{\lim }-\phi \left[{\upbeta}_{-}\left(t+\Delta t\right)\right]\Phi \left(\mathrm{A}\right){\beta}_{-}^{\prime}\left(t+\Delta t\right)=-{\beta}_{-}^{\prime }(t)\phi \left[{\upbeta}_{-}(t)\right]\Phi \left[\frac{\beta_{-}^{\prime }(t)}{\left\Vert {\boldsymbol{c}}^{\prime }(t)\right\Vert}\right]. $$
(52)

Then, derive the value of I2(t, ∆t) as ∆t → 0:

$$ {I}_2\left(t,\Delta t\right)=\frac{\rho^{\prime}\left(t,t+\Delta t\right)}{\sqrt{1-{\rho}^2\left(t,t+\Delta t\right)}}\frac{1}{2\pi}\exp (B) $$
(53)
$$ B=-\frac{1}{2}\frac{\upbeta_{-}^2(t)+2\rho \left(t,t+\Delta t\right){\upbeta}_{-}(t){\upbeta}_{-}\left(t+\Delta t\right)+{\upbeta}_{-}^2\left(t+\Delta t\right)}{1-{\rho}^2\left(t,t+\Delta t\right)} $$
(54)

and

$$ \underset{\Delta t\to 0}{\lim }B=\underset{\Delta t\to 0}{\lim }-\frac{1}{2}\frac{\upbeta_{-}^2(t)+2\rho \left(t,t+\Delta t\right){\upbeta}_{-}(t){\upbeta}_{-}\left(t+\Delta t\right)+{\upbeta}_{-}^2\left(t+\Delta t\right)}{1-{\rho}^2\left(t,t+\Delta t\right)}=-\frac{1}{2}\left[{\beta}_{-}^2(t)+\frac{\beta_{-}^{\prime 2}(t)}{{\left\Vert {\boldsymbol{c}}^{\prime }(t)\right\Vert}^2}\right]. $$
(55)

So, the limit of I2(t, ∆t) is shown:

$$ \underset{\Delta t\to 0}{\lim }{I}_2\left(t,\Delta t\right)=\frac{1}{M}\underset{\Delta t\to 0}{\lim}\frac{1}{2\pi}\exp (B)=\left\Vert {c}^{\prime }(t)\right\Vert \phi \left[{\upbeta}_{-}(t)\right]\phi \left[\frac{\beta_{-}^{\prime }(t)}{\left\Vert {c}^{\prime }(t)\right\Vert}\right]. $$
(56)

According to the limit of I1(t, ∆t) and I2(t, ∆t), the downcrossing rate is shown:

$$ {\mathrm{v}}^{-}(t)=\underset{\Delta t\to 0}{\lim }{I}_1\left(t,\Delta t\right)+\underset{\Delta t\to 0}{\lim }{I}_2\left(t,\Delta t\right)=\left\Vert {c}^{\prime }(t)\right\Vert \phi \left[{\upbeta}_{-}(t)\right]\Psi \left[\frac{\beta_{-}^{\prime }(t)}{\left\Vert {c}^{\prime }(t)\right\Vert}\right] $$
(57)

where Ψ(x) = ϕ(x) − xΦ(x).

The basic parameter of the downcrossing rate is derived:

$$ {c}^{\prime }(t)=\left[\frac{b(t)}{\left\Vert b(t)\right\Vert}\right]=\frac{\sigma_g(t){b}^{\prime }(t)+b(t){\sigma}_g^{\prime }(t)}{\sigma_g^2(t)} $$
(58)

where

$$ {\sigma}_g^{\prime }(t)=\frac{b(t).{b}^{\prime }(t)}{\sigma_g(t)} $$
(59)
$$ {\beta}_{-}^{\prime }(t)=\frac{\sigma_g(t){\mu}_g^{\prime }(t)-\left[\boldsymbol{\varepsilon} +{\mu}_g(t)\right]{\sigma}_g^{\prime }(t)}{\sigma_g^2(t)} $$
(60)
$$ {\left.{\mu}_g^{\prime }(t)=\frac{\mathrm{\partial g}\left(\mathbf{X},\mathrm{t}\right)}{\partial t}\right|}_{\mu_X}. $$
(61)

4.2 Procedure

The steps to solve the lubrication reliability are given as follows:

  1. 1.

    Input basic parameters, including time-dependent parameter (radius), viscosity, the equivalent elastic modulus, the (isothermal) pressure exponent of viscosity, and mean and standard deviation of velocity and load.

  2. 2.

    Linearize the equation of minimum film thickness, b is solved by (15), (16), (23), the derivative of b is b′, c is solved by (45), the derivative c′ using (58), μg and σg using (18), (21), the derivative\( {\mu}_g^{\prime }\ {\sigma}_g^{\prime } \) using (59), (61).

  3. 3.

    Substitute this result into (33), (60) to solve β− and \( {\beta}_{-}^{\prime } \), then use (57) to solve for v−.

  4. 4.

    Calculate the initial reliability R(t0) using (10).

  5. 5.

    Calculate the time-dependent reliability R using (8).

Fig. 4 is the program flow chart.

Fig. 4
figure 4

The program flow

Full size image

5 Numerical example and analysis

Cylindrical roller bearing was adopted in this paper, the viscosity of grease and other parameters were referred to Yang’s article (Yang 2009). Specific parameters of load, speed, and bearing are shown in Table 1.

Table 1 The basic parameters
Full size table

The radius of the roller and raceway changes gradually with the wear. Several articles have pointed out that the wear depth increased linearly with the time within limits. Guo and Chen have conducted groups of the wear experiments, and they found that the relation of the wear depth and time was linear (Guo and Chen 2008). Jeon and Lee draw a conclusion that the degree of wear changed linearly with the test duration (Jeon and Lee 2013). Roller radius decreased with time; raceway radius increased with time. With other’s results, the author assumed that they wore 0.0023 mm every 5000 revolutions, so the equivalent radius changed 0.0012 mm per unit time T (the unit time T represents 5000 revolutions). Fig. 5 shows the trend of r(T).

$$ r(T)=0.022875-\frac{0.0012}{1000}\times T $$
(62)
Fig. 5
figure 5

The trend of r(T).

Full size image

Firstly, the minimum film thickness was solved by substituting each parameter into the equation of minimum film thickness. As shown in Fig. 6, it can be seen that due to the randomness of velocity and load, the minimum film thickness also varies randomly.

Fig. 6
figure 6

The minimum film thickness

Full size image

The time-dependent reliability was calculated with the above parameters, including the raceway surface roughness of 0.63 μm, the roller surface roughness of 0.16 μm, and the ultimate minimum film thickness of \( 0.7\times \sqrt{{\sigma_u}^2+{\sigma_l}^2} \). The reliability curve is shown in Fig. 7. Generally, while the surface roughness is large, the reliability of the bearing in service is low. The main reason is that the probability of direct contact between the two contact surfaces increases with the roughness increase. Then, the bearing is easy to enter into the boundary lubrication state. Table 2 shows the calculation results of the two methods with different error limits, and the maximum relative error is 5.769%, the average error is 3.39%. However, the sample points of FPM are 462, and the sample points of Monte Carlo Simulation (MCS) are 1,050,000. (In FPM, each ε has 22 points. In MCS, each ε has 50,000 points.) FPM’s sample points are far less than that of MCS. Plainly, both the solving efficiency and the solving accuracy of the proposed method for reliability analysis of lubrication are very high.

Fig. 7
figure 7

The reliability curve with different ε

Full size image
Table 2 The relative error and reliability with different ε
Full size table

Figure 8 shows the reliability curves at different time. The wear rate is 0.0012 mm per unit time T. It can be seen that reliability of lubrication decreases gradually with the increase of time. The main reason is that with the increase of wear, the minimum film thickness decreases, the reliability of lubrication within the time interval decreases. Table 3 shows the calculation results and relative errors of the two methods at different times. It can be seen from the table that the maximum error is 2.222%, the average error is 0.19%. Moreover, the sample points of FPM are 493, and the sample points of MCS are 2,400,000. FPM’s sample points are far less than that of MCS. Therefore, the proposed method may be adopted in time-dependent reliability analysis of lubrication.

Fig. 8
figure 8

The reliability curve with different times

Full size image
Table 3 The relative error and reliability with different time
Full size table

Figure 9 shows the reliability with different velocity standard deviations. The red, green, and blue color lines represent the three reliabilities with gradually increasing standard deviation. As can be seen from the figure, when the change of the velocity increases, the reliability decreases. The main reason is that the probability of crossing increases with the more unstable velocity.

Fig. 9
figure 9

The reliability curve with different velocity standard deviations

Full size image

6 Conclusion

Due to the uncertainty of factors such as load and speed, the thickness of lubricating oil film changes over time, which may lead to lubrication failure. In this paper, a time-dependent reliability analytical method was proposed based on Dowson-Higginson’s formula and the crossing method. The model of lubrication reliability was presented.

The time-dependent reliability under given conditions was calculated, and the accuracy of the results was verified by MCS. The results showed that, the larger the surface roughness was, the smaller the lubrication reliability would be. Due to the randomness of the velocity load, the time-dependent reliability decreased over time. With the unstable change of the velocity, the lubrication reliability decreased with time. When the time-dependent reliability was calculated by FPM, the results were close to that of MCS, but the computational efficiency of FPM is higher than MCS.

This method can improve the computational efficiency of complex engineering problems and can provide guidance for the time-dependent reliability analysis of complex problems. By this method, the application range of FPM was extended, and the application of reliability theory in engineering was developed.