1 Introduction

Heat conduction is a dominant mode of heat transfer in many engineering systems. This physics phenomenon can be used purposefully to heat and cool matter through the designed use of a heat spreading device. The research presented here focuses on the design of heat spreading devices using topology optimization methodologies (Bendsøe and Kikuchi 1988). Topology optimization has been used successfully to design heat spreaders for various applications. One similarity between the design of these heat spreaders is the use of a structural mechanics analog objective, thermal compliance. This objective is favorable from a numerical optimization solution performance perspective, but may not represent the true goal of a heat spreader. The investigations presented here will focus on reformulating the topology optimization problem for various different heat spreader design tasks.

Researchers in topology optimization have investigated several problem formulations for heat spreader design. Gersborg-Hansen et al. (2006) presented a well-known example where a thermal compliance-based heat conduction problem was solved using the finite volume method. Burger et al. (2013) solved a 3D thermal compliance problem to evaluate the performance of optimized structures for a variety of finite fixed-temperature boundary conditions. Asymmetric optimal structures were obtained when dividing and segregating the Dirichlet boundary. In an recent study, Yan et al. (2018) investigated the optimality of dendritic structures for compliance and maximum temperature minimization problems. It was concluded that lamellar needle-like topologies outperform the typically reported dendritic structures. Given the local nature of gradient-based optimization, careful consideration should be given to the initial design vector value to support convergence towards better-performing optimized structures. One strategy for selecting a good initial design vector is to perform optimization using a reduced-dimension design representation, such as a generative algorithm (Lohan 2016). This strategy was shown to improve design performance consistently when compared with topology optimization with a homogeneous initial material distribution.

More complex formulations that involve elements beyond a simple compliance objective and volume constraints have been investigated. For example, Marck et al. (2012) investigated the tradeoff between mean temperature and temperature variance to formulate a more realistic design problem. The authors used the method of weighted sums to produce a Pareto front by calculating both combined objectives and derivatives. The optimized topological structures have clear differences when comparing mean temperature solutions to variance-optimized solutions. In another example, Dirker and Meyer (2013) investigated several objectives in a problem formulation with design-dependent volumetric heat generation. Their objectives included the maximum domain temperature, the average domain temperature, and a summation of the temperature across volumetric heat generating elements. The authors observed dendritic patterns in the optimized structures for all objective functions. Utilizing more realistic objectives may improve the practical applicability of topology optimization; however, the functional role of a heat spreader may depend on additional practical constraints. For example, Zhuang and Xiong (2015) solved a minimum compliance design problem incorporating point and local area temperature constraints. The fundamental structure of the optimized topology changed when considering the area temperature constraints.

As a logical extension to heat conduction problems that are commonly solved, design-dependent loading has been investigated in applications with convection. Two strategies for parameterizing convection in a conduction framework have been proposed by Bruns (2007) and Iga et al. (2009). These approaches have been extended recently to 3D problems. Consider the work of Zhou et al. (2016), where a static conduction-based convection topology optimization was performed and compared with a benchmark heat sink design. The authors observed a 20 ∘C decrease in temperature when comparing the optimized design with the reference design using thermo-fluidic simulations. Another example is in the work of Dede et al. (2015), where conduction-based convection optimization was performed to design a heat sink for a circular air jet. The authors fabricated the optimized topology and experimentally compared performance with standard heat sink topologies. The optimized heat sink showed comparable performance with conventionally designed heat sinks.

Fully coupled thermo-fluidic analysis has also been solved for in many cooling design applications. For forced air convection, a 3D to 2D model reduction was used to design fin topology, Haertel and Nellis (2017), using COMSOL Multiphysics. The lower-order model results agreed with 3D simulation, and a decrease in thermal resistance of 13% was achieved through optimization. A full 3D thermo-fluid topology optimization including buoyancy effects was performed by Alexandersen et al. (2016). It was shown that complex geometries can improve cooling performance when compared with straight fin heat sinks. In a recent paper, Dbouk (2017) asserted that topology optimization methodologies are not yet robust enough to be used in industrial applications. Though this is true for some formulations, there are many applications where industry-relevant problems can be solved well using topology optimization methods. Take for example this heat conduction dominant system where topology optimization has been practically used to achieve a large reduction in domain temperature (Dede et al. 2018). In the research presented here, we investigate a similar application: power electronic systems.

In electronic systems, heat sinks are often selected based on commercially available products. Recent work has demonstrated the interesting opportunity of employing heat sinks tailored using optimization to further improve performance for specific applications. Consider the work of Christen et al. (2016) where a thermal resistor network was used to model heat sinks for natural convection. Using optimization, the authors reduced the heat sink size 50% and experimentally verified performance. As another example, a radial heat sink was designed for an LED by Yu et al. (2011) solving the Navier-Stokes equation. Different styles of radial heat sinks were optimized using evolutionary algorithms to explore the effects of fundamental design changes. Moving towards a more flexible formulation, Ramphueiphad and Bureerat (2018) optimized both fin cross-section and height for a 3D heat sink using a multi-objective evolutionary algorithm. This study revealed that non-uniform fin cross-sections and fin heights are superior to pin fin designs with a constant fin height. In our research, we utilize topology optimization to provide maximal design freedom, motivated by the positive correlation between design flexibility and system performance observed in the literature across multiple application domains.

The heat conduction topology optimization problems as previously discussed translate to electronics applications where heat generating devices also must satisfy strict temperature constraints. In this work, two different sets of topology optimization problems are investigated. First, an investigation of optimization objective functions is presented on a benchmark heat transfer topology optimization problem. The findings are applied to several practical problem formulations for power electronics on a domain with discrete heat sources. The following sections will describe the topology optimization methodology and present numerical results for all problem formulations.

2 Topology optimization methodology

To address the topological design of heat spreaders, a density-based topology optimization approach is used. The design domain is discretized into finite elements to match the analysis domain. The analysis problem is solved using a standard Galerkin finite element procedure with linear shape functions. A design variable, xi, is assigned to each finite element and is used to scale the material density of the element. In this study, the solid isotropic micro-structure with penalization (SIMP) method is used to bias the elements towards solid (1) or void (0) material properties. Using this method, the thermal conductivity of element, i, κi, depends on the associated design variable xi in the following manner:

$$ {\kappa_{i} = \kappa_{\min} + \alpha(x_{i}) \kappa_{0}, \quad \alpha(x_{i}) = {x_{i}^{P}},} $$
(1)

where α(⋅) is a penalty function and P is a penalty parameter, which is increased at intervals to improve optimization convergence. The elemental thermal conductivity is allowed to vary between \(\kappa _{\min }~=~1\)W/mK and κ0 = 400 W/mK. The method of moving asymptotes (MMA) algorithm is used to optimize the nonlinear design optimization problem until a convergence tolerance of 0.01 on design variable changes, or a maximum of 100 outer loop MMA iterations is reached.

A custom finite element analysis code was written in Matlab to analyze thermal properties on the domain using four node elements with linear shape functions. A regular mesh of 300 × 300 elements was chosen for both design and analysis as it produced < 0.1% error in the maximum temperature when compared with a benchmark COMSOL analysis. A density filter is used where appropriate to enforce length-scale control on the domain and the adjoint method is used to obtain gradient information for the objective and constraint functions. These definitions are consistent across all presented case studies unless otherwise noted.

2.1 Adjoint differentiation

The derivative of the objective function is obtained using the adjoint method. A discretize-then-optimize approach is used to obtain the gradient of the objective function. Consider an objective function, Θ, which can be represented by some function, π(⋅):

$$ {\Theta} (\textbf{x}) = {\Pi} (\mathbf{U}(\mathbf{x}), \mathbf{P}(\mathbf{x}), \textbf{x}), $$
(2)

that depends on the thermal load, P, temperature, U, and the design variable vector, x. The residual of the finite element analysis is multiplied by an adjoint variable λ and is added to this objective:

$$ \begin{array}{@{}rcl@{}} {\Theta} (\mathbf{x}) &= &{\Pi} (\mathbf{\mathbf{U}}(\mathbf{\mathbf{x}}), \mathbf{\mathbf{P}}(\mathbf{\mathbf{x}}), \mathbf{\mathbf{x}}) \\ &&+ {\lambda}^{T} \left[\mathbf{K}(\mathbf{x})\mathbf{U}(\mathbf{x}) - \mathbf{P}(\mathbf{x}) \right]. \end{array} $$
(3)

Note that K(x) is the stiffness matrix for the finite element analysis. The gradient of this expression can be obtained using the chain rule:

$$ \begin{array}{@{}rcl@{}} d{\Theta} (\mathbf{x}) &=& \frac{\partial \Pi}{\partial \mathbf{U}(\mathbf{x})} \frac{\partial \mathbf{U}(\mathbf{x})}{\partial \mathbf{x}} + \frac{\partial \Pi}{\partial \mathbf{P}(\mathbf{x})} \frac{\partial \mathbf{P}(\mathbf{x})}{\partial \mathbf{x}} + \frac{\partial \Pi}{\partial \mathbf{x}} \\ &&+ {\lambda}^{T} \left[ \mathbf{K}(\mathbf{x}) \frac{\partial \mathbf{U}(\mathbf{x})}{\partial \mathbf{x}} + \frac{\partial \mathbf{K}(\mathbf{x})}{\partial \mathbf{x}} \mathbf{U}(\mathbf{x}) - \frac{\partial \mathbf{P}(\mathbf{x})}{\partial \mathbf{x}} \right]. \end{array} $$
(4)

These terms can be rearranged to suggest useful choices for the adjoint vector:

$$ \begin{array}{@{}rcl@{}} d{\Theta}(\mathbf{x}) = \left( \frac{\partial \Pi}{\partial \mathbf{U}(\mathbf{x})} {+} {\lambda}^{T} \mathbf{K}(\mathbf{x}) \right)\frac{\partial \mathbf{U}(\mathbf{x})}{\partial \mathbf{x}} \end{array} $$
(5a)
$$ \begin{array}{@{}rcl@{}} + \left( \frac{\partial \Pi}{\partial \mathbf{P}(\mathbf{x})} - {\lambda}^{T} \right) \frac{\partial \mathbf{P}(\mathbf{x})}{\partial \mathbf{x}} \end{array} $$
(5b)
$$ \begin{array}{@{}rcl@{}} + \frac{\partial \Pi}{\partial \mathbf{x}} + {\lambda}^{T} \frac{\partial \mathbf{K}(\mathbf{x})}{\partial \mathbf{x}} \mathbf{U}(x). \end{array} $$
(5c)

Based on the problem formulation, the adjoint vector, λ, can be chosen such that expensive gradient calculations are avoided. For example, if the problem does not have design-dependent loading, Eq. (5b) drops out. Simplifications such as this become apparent when considering the boundary conditions in the problem formulation.

2.2 Density filtering

To enforce the minimum length-scale requirements, a linear density filter is used.

$$ \tilde{\rho} = \sum\limits_{j} w_{ij} \rho_{j}, $$
(6)

where the weighting function, w, is defined based on the centroid distances of neighboring elements:

$$ w_{i,j} = \left\{\begin{array}{ll} \frac{R-d(i,j)}{\sum (R-d(i,k))} & \quad j \in N_{i}\\ 0 & \quad j \notin N_{i}. \end{array}\right. $$
(7)

The filter weight, wi,j, is scaled based on the difference between a prescribed minimum radius, R, and the distance between element centers d(i,j), and a summation of neighboring element distances, d(i,k). This simple filter is effective at biasing the designs to satisfy the minimum radius constraint. There are many other filtering strategies that can be used to influence design representation; refer to Svanberg and Svärd (2013) for a helpful study of filters.

2.3 Boundary definiteness

Using a filter effectively biases the design towards satisfying the minimum radius constraint and makes the design solution independent of the analysis mesh size. However, using a filter also results in a design with an ill-defined solid/void interface. This interface is defined by elements with partial density. A strategy to measure the boundary definiteness was proposed by Dirker and Meyer (2013) and is presented in the following equation:

$$ {\epsilon = 1 - \frac{ \text{mean}(x^{2} - x)}{V^{2}_{\max} - V_{\max}},} $$
(8)

where the boundary definiteness, 𝜖, is measured as the difference between 1 and a function of the partially defined material. This function compares the fraction of elements which are partially defined to the fraction of elements which are conductive, \(V_{\max \nolimits }\). This measure of boundary definiteness will be used in the following sections to compare the boundary quality of the heat spreading structures.

3 Objective function investigations

This first set of studies involves designing a heat sink using three sets of boundary conditions for a 1 × 1 m homogeneously heated domain (Fig. 1). This analysis problem was chosen to showcase the effect of objective function selection for a design problem that is commonly solved in the literature. This design domain can serve as an abstraction for a system with some distribution of heat on the domain; solving for discrete sources, as are common in power electronic systems, is a simple extension of this, as will be demonstrated in the next section.

Fig. 1
figure 1

Three insulated homogeneously heated domains with fixed temperature boundaries. A fully fixed boundary (left), a partially fixed boundary (center), and a point-fixed boundary (right) are shown

Full size image

The design domain, Ω, is homogeneously heated, the Neumann boundary (left, right, and top boundaries), ΓN, is adiabatic, and the Dirichlet boundary (bottom boundary, or point), ΓD, has fixed temperature. These properties can be expressed as:

$$ \begin{array}{@{}rcl@{}} \nabla \cdot (\kappa \nabla T ) + f & = 0 \text{ on } \Omega, \end{array} $$
(9)
$$ \begin{array}{@{}rcl@{}} T & = 0 \text{ on } {\Gamma}_{D}, \end{array} $$
(10)
$$ \begin{array}{@{}rcl@{}} (\kappa \nabla T) \cdot \textbf{n} & = 0 \text{ on } {\Gamma}_{N}. \end{array} $$
(11)

In this design problem, a constant power of 1,000 W is applied uniformly to the design domain, independent of the design parameters. A conductive heat spreader is optimized to extract heat from this domain through the fixed temperature boundary. In application, a secondary heat exchanger may be present to maintain the lower boundary at a fixed temperature. In all of the following examples, this boundary temperature is fixed at 0 ∘C.

To achieve the goal of reducing the temperature on the domain, consider this commonly used topology optimization design problem formulation presented in (P1):

$$ \begin{array}{@{}rcl@{}} &&\underset{\textbf{x}}{\min} \quad{\Theta} (\textbf{x}) \\ &&\text{s. t.} \quad V(\textbf{x}) \leq V_{\max} \\ &&\quad\quad R(\textbf{x}) \geq R_{\min} \\ &&\quad\quad {0 \leq \textbf{x} \leq 1}, \end{array} $$
(P1)

where some objective, Θ, is minimized subject to a volume constraint. The volume, V, is constrained by a maximum value, \(V_{\max \nolimits }\), and a minimum radius constraint is imposed where the radius of design features, R, must be greater than a prescribed value, \(R_{\min }\). For 2-dimensional examples, the volume constraint translates to an upper limit on area, constraining the amount of conductive material used. For this problem formulation, conductive material is restricted to 30% of the domain area. The minimum radius constraint is implicitly satisfied via the density filter described in the previous section; the filtering radius is set to 0.04 m. This formulation (P1) works particularly well for structural topology optimization, where a volume constraint may represent a cost requirement and the minimum feature size of a structure may be restricted by manufacturing technology (Patterson et al. 2019). Furthermore, the formulation is straightforward to implement and fairly numerically stable when using a SIMP topology optimization approach with the MMA algorithm. It is important to note that the actual numerical optimization problem, the MMA algorithm solves, does not include the radius constraint, as this is implicitly satisfied using the density filter.

3.1 Candidate objective functions

The first objective of interest is thermal compliance. This objective is defined as the product of the heat flux, q, and temperature gradient, ∇T:

$$ {\Theta} (\textbf{x}) = {\int}_{\Omega} q \nabla T d {\Omega} \to {\Theta} (\textbf{x}) = \textbf{U}^{T} \textbf{P}. \\ $$
(12)

The compliance metric may be represented simply by the dot product of the thermal load, P, and the nodal temperature vector, U. This is a popular objective function because the adjoint variable can be defined directly using a known quantity, U, eliminating the need to solve an additional linear system for the adjoint variable.

A mean temperature objective is an alternative to the compliance objective that may align better with the goal of reducing the domain temperature. The thermal compliance objective biases the performance of the structure in areas where there is input heat flux. A mean temperature objective does not explicitly account for the influence of the loading conditions:

$$ {\Theta} (\textbf{x}) = \frac{1}{n}{\int}_{\Omega} T d{\Omega} \to {\Theta} (\textbf{x}) = \frac{\textbf{L}^{T} \textbf{U}}{n}. \\ $$
(13)

In discrete form, the mean temperature objective can be represented—in terms of finite element model quantities—as the product of a vectors of ones, L, and the nodal temperature vector, U, divided by the number of finite element nodes n.

Often, the goal of a heat spreader is to help reduce the maximum temperature on the domain. If point-wise hot spots are a primary concern, then minimizing maximum temperature may be a more appropriate objective than thermal compliance or mean temperature. The max function, however, is not differentiable. As an approximation to the max function, a p-norm approximation is used here:

$$ {\Theta} (\textbf{x}) = ||T||_{p} \to {\Theta} (\textbf{x}) = \left( \textbf{L}^{T} \textbf{U}^{p} \right)^{1/p}. $$
(14)

The p-norm approximates the maximum temperature by applying a root to the power p on the summation of temperature to the power p. The accuracy of this approximation increases with the magnitude of p, and as \(p\to \infty \), the norm converges to the max function. The discrete problem can be described similarly, where the summation is replaced with the product of a ones vector, L, and the nodal temperature vector, U, raised to the power p. To maintain a smooth approximation function with well-defined derivatives, p = 10 is chosen. This will not result in an accurate measure of the maximum temperature on the entire domain, but the gradient of which should direct the topology towards a “lower” temperature solution.

While minimizing temperature is an important goal of heat spreader design, some situations involving electronics may favor temperature uniformity, where large temperature gradients adversely affect performance. While the max or mean temperatures provide some useful information about the temperature distribution on the domain, these single parameters do not capture more global information. One way to quantify temperature homogeneity across the domain is to use temperature variance as an objective:

$$ \begin{array}{@{}rcl@{}} {\Theta} (\textbf{x}) &=& \frac{1}{n}{\int}_{\Omega} \left( T-T_{\text{av}} \right)^{2} d{\Omega}\\ \to {\Theta} (\textbf{x}) &=& \frac{1}{n} \left( \textbf{U} - \frac{\textbf{L}^{T} \textbf{U}}{n} \right)^{T} \left( \textbf{U} - \frac{\textbf{L}^{T} \textbf{U}}{n} \right), \end{array} $$
(15)

where the temperature variance is given by the average of the squared difference of an element temperature, T, and the average temperature, Tav. This can be represented in discrete form in terms of the ones vector, L, and the temperature vector U.

3.2 Optimization results

The optimized designs for the homogeneous heating design problem considering all optimization objectives and boundary conditions are presented in Table 1. The optimizer converged to the best solution for the given objective. The computational expense using these objective functions in optimization is comparable since they share the same problem formulation and an equal number of operations are required to numerically obtain the derivatives. All four of the objective functions reached the maximum iteration limit without reaching any MMA inner-loop iteration limits. When optimizing for a particular objective, performance improvements in the range of 1–112% were observed between solutions. The potential performance improvement dwarfs any variations in computational expense that are experienced from the use of the MMA algorithm. As such, the use of proxy objective functions in an effort to reduce computational expense is not recommended.

Table 1 Topology optimization solutions for various objective functions. Solutions share a common color scale for each boundary condition
Full size table

The compliance and mean temperature optimization routines converged to nearly identical optimized topologies for all three boundary condition variations. Investigating the mathematical formulation of these objectives reveals that they are linearly proportional. The mean temperature objective is a summation of temperature values divided by a constant. For the homogeneously heated domain design problem, compliance is also the summation of temperature, but multiplied by a constant (thermal load). For this specific design problem where the load is uniformly distributed, the thermal compliance derivatives point in the same direction as the mean temperature derivatives during optimization. For general non-uniformly distributed thermal loading, the mean temperature objective should provide an alternate topology. Furthermore, it can be concluded that the compliance objective function for this problem formulation should be used in place of the average temperature objective for computational efficiency if minimum average temperature is the preferred objective.

When using an approximate maximum temperature objective function, temperature reductions of 13–30% were observed when compared with topologies optimized by other objectives. The reduction in domain temperature may justify the use of this objective, even though the single global approximation function loses accuracy for large mesh sizes as observed by Lohan and Allison (2017). Furthermore, the inaccuracy of the p-norm approximation will propagate to the derivatives. However, the p-norm function will overestimate the value maximum temperature and is monotonic for values greater than zero. These characteristics of the approximation function will point the derivatives towards a “lower” temperature solution, which may not represent the “lowest” temperature design, directly. An accurate maximum temperature value may be calculated directly using the maximum function after the optimization solution is obtained.

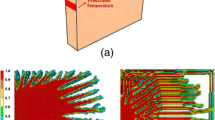
The optimized structures when using the variance objective tended to be more dendritic. Conductive material is allocated such that the non-conductive white space is more evenly distributed on the domain. Furthermore, in all three cases, the contact surface to the fixed temperature boundary seems to be smaller than those for solutions obtained when using the other objective functions. To analyze these effects, a normalized gradient is superimposed on the compliance and variance-optimized topologies for the first boundary condition in Fig. 2.

Fig. 2
figure 2

Temperature gradient comparison between compliance (left) and variance (right) minimization solutions. Normalized gradients share a color scale. Variance-optimized solution moves largest variance gradients towards heat sink

Full size image

Notice how the compliance solution (left) has higher gradient concentrations, denoted by the lighter contours, near the black structure. These are located at the end points of the conductive structure. The variance-optimized solution does not feature the same magnitude of gradients at the endpoints of the structure, and its highest gradients are located near the heat sink. This may be due to the reduced presence of conductive material (i.e., inverse taper) near the fixed temperature boundary. Though this objective function can be successfully used to minimize the variance of the temperature on the domain, it does not minimize the average temperature about which the variance is calculated. In some cases, the temperature rose significantly, 30%, in order to produce a solution with a minimized variance. To use this objective function more effectively for electronics, it should be paired with some form of temperature constraint. An example formulation is presented in the next section.

4 Practical formulations for power electronic systems

With a practical understanding obtained from analyzing different objective function results in the previous section, findings are applied to case studies relevant to power electronics applications. Consider the 10 x 10 cm design domain consisting of 8 discrete 5 mm × 2.5 mm heat sources, illustrated in Fig. 3. The heat sources centers are spaced evenly such that a = 2.5 cm and b = 2 cm. One application that would produce such a domain is an electronics circuit board where heat is generated by electronic devices (Dede et al. 2018). This type of system has additional design considerations, including devices with distinct properties (different temperature limits, etc.). A variety of problem formulations to address this design problem class are investigated in the following sections.

Fig. 3
figure 3

Simplified 2-D printed circuit board (PCB) domain with 8 heat generating devices

Full size image

The governing equations of this system involve heat generation prescribed in specific regions, Ω1,...,8. In these regions, the heat generating components are assumed to be thermally conductive. The design domain, Ω0, does not generate heat, and thermally conductive material distribution will be designed via the optimization process to extract heat. The governing equations of this system follow:

$$ \begin{array}{@{}rcl@{}} \nabla \cdot (\kappa \nabla T ) & = &0 \text{ on } {\Omega}_{0}, \end{array} $$
(16)
$$ \begin{array}{@{}rcl@{}} \nabla \cdot (\kappa \nabla T ) + f & =& 0 \text{ on } {\Omega}_{1 ,...,8}, \end{array} $$
(17)
$$ \begin{array}{@{}rcl@{}} T & =& 0 \text{ on } {\Gamma}_{D}, \end{array} $$
(18)
$$ \begin{array}{@{}rcl@{}} (\kappa \nabla T) \cdot \textbf{n} & =& 0 \text{ on } {\Gamma}_{N}. \end{array} $$
(19)

For these studies, an input power, f = 1.25 W, is applied to each of the eight rectangular devices on the domain, for a total of 10 W of loss within the domain. The Dirichlet boundary (bottom boundary) remains fixed at 0 ∘C, and the Neumann boundary (remaining boundaries) restrict heat flux out of the domain. Using a fixed temperature boundary, where the device and heat sink will be connected by a conductive bridge, small temperature variations between device and sink are expected, and were observed for all case studies. Though this accurately represents some electronics systems, it is not true for all electronics systems. For all subsequent studies, the Dirichlet boundary is retained and constraints are modified to account for this boundary condition for demonstration purposes.

4.1 Maximum temperature minimization

With the recent advances in wide-band gap devices, the temperature difference between heat source and sink may vary by 100’s of degrees Celsius during steady state operation. The accuracy of the p-norm approximation is dependent on the magnitude of the norm value, and for large temperature variations on the domain numerical issues can be experienced. A similar situation is well studied in structural mechanics, were stress is an important parameter. In many cases, stress is enforced in a normalized constraint to avoid these numerical issues (Le et al. 2010). In this research, we adapt this concept in a novel way to perform a normalized temperature minimization. One strategy to normalize the temperature measurements is to optimize the maximum temperature constraint value on the domain while enforcing a temperature constraint. The problem formulation (P2) is:

$$ \begin{array}{@{}rcl@{}} &&\underset{\textbf{d}}{\min} \quad d_{1}\\ &&\text{s. t.} \quad V(\textbf{x}) \leq V_{\max} \\ &&\quad\quad R(\textbf{x}) \geq R_{\min} \\ &&\quad\quad {\left( \textbf{L}_{1,...,8}^{T} \frac{\textbf{U}}{d_1}^{p} \right)^{1/p} - 1\leq 0}\\ &&\quad\quad {0 \leq \textbf{d} \leq 1}, \end{array} $$
(P2)

with the design vector defined as:

$$ \mathbf{d} = \left[T_{\max}, \textbf{x} \right]^{T} = \left[ T_{\max}, x_{1}, ... , x_{n} \right]^{\mathrm{T}}. $$
(20)

Here, the maximum temperature constraint value, d1, is minimized, subject to volume (≤ 30%), radius (≥ 0.4 cm), and a single normalized p-norm temperature constraint. To prevent numerical oscillations resulting from the temperature constraint switching between active and inactive, a move limit of 0.01 is applied to the maximum temperature design variable. Device locations are fixed and the global temperature constraint is only applied to device nodes, assuming that other materials in the system are less sensitive to temperature. If instead all points across the domain were constrained to be less than \(T_{\max \nolimits }\), instead of just the devices, this problem would be mathematically equivalent to the formulation presented in Section 3 that minimized an approximated maximum temperature. The topology optimization solution for this problem is presented in Fig. 4.

Fig. 4
figure 4

Max temperature optimization solution results in a ladder-like structure

Full size image

The MMA algorithm found a “ladder-like” topology to reduce the maximum device temperatures. The maximum temperature of the devices are symmetric across the central axis and are presented in order by device number: [0.037 0.030 0.022 0.012 0.037 0.030 0.022 0.012] ∘C. Minimizing maximum device temperatures may make sense for electronic heat spreader design and similar problems where device lifetime and temperature are correlated.

In addition to the adaptive normalization benefits, this formulation presents increased design flexibility. For example, consider the following objective function:

$$ {\Theta} (d) = T_{\max 1}(1-{d_{1}^{p}}) + T_{\max 2}{d_{1}^{P}}, $$
(21)

where optimization may select an appropriate temperature constraint based on the heat spreader design task. The value for \(T_{{\max \nolimits } 1}\) is set to 0.02, which is beyond the capability of the optimal heat spreading structure, and \(T_{{\max \nolimits } 2}\) is set to 0.04, which is above the maximum temperature of the optimal heat spreading structure. This objective may serve as an abstraction of a component selection task while considering heat spreading capability. It was observed that the optimizer first tried to minimize the maximum temperature on the domain. As the optimizer could not satisfy the temperature constraint, the constraint limit was increased. The optimizer successfully pushed d1 to a value of 1 to select the components with a higher temperature constraint. This resulted in the same topology as illustrated in Fig. 4.

4.2 Average temperature matching optimization

In some electronics applications, the circuit performance may be improved by matching the temperature of specific sensitive devices. Furthermore, the optimization of electronic layouts may result in asymmetric device layout. To emulate this, this next case study was formulated where the devices nearest and furthest from the heat sink were required to have identical temperatures, while satisfying maximum temperature constraints on all eight devices. Consider the case where devices 4 and 5 (as labeled in Fig. 3) must operate at the same temperature for ideal performance. This formulation is appropriate for photonics systems, where device behavior is highly sensitive to temperature changes, and maintaining similar temperatures on multiple devices is required for desired performance. One approach to achieve this is to minimize a square of the difference between the average temperature of nodes corresponding to these two devices:

$$ \begin{array}{@{}rcl@{}} &&\underset{\textbf{x}}{\text{min.}} \quad \left( \frac{\textbf{L}_4^{T} \textbf{U}}{n} - \frac{\textbf{L}_5^{T} \textbf{U}}{n} \right)^2\\ &&\text{s. t.} \quad V(\textbf{x}) \leq V_{\max}\\ &&\quad\quad R(\textbf{x}) \geq R_{\min}\\ &&\quad\quad {\left( \textbf{L}_{1,...,8}^{T} \left( \frac{\textbf{U}}{T_{\max}} \right)^{p} \right)^{1/p} -1 \leq 0 }\\ &&\quad\quad {0 \leq \textbf{x} \leq 1.} \end{array} $$
(P3)

The elements of the selection vector Li that correspond to nodes within device i are 1, and all other elements are zero. In addition to matching the temperature between devices 4 and 5, a general maximum temperature constraint across all eight devices must be satisfied. The maximum temperature constraint for each device is once again formulated as a p-norm applied to device node temperatures. Since the previous optimization found a minimum max temperature of 0.04 ∘C, this formulation relaxes the requirement to a known feasible \(T_{\max \nolimits }~=~0.06~^{\circ }\)C to demonstrate the capability of the procedure. This design problem is again subject to a volume constraint, where \(V_{\max \nolimits }~=~0.3\), and a constraint on the minimum feature size, \(R_{\min }~=~0.4\) cm. The design variables are once again solely a function of material density parameters: \(\mathbf {x}~=~\left [\rho _{1}, ... , \rho _{n} \right ]^{\mathrm {T}}\). This topology optimization problem can be solved to result in the structure presented in Fig. 5.

Fig. 5
figure 5

Temperature matching optimization solution produces asymmetric structure to satisfy maximum temperature constraint

Full size image

The temperature of the devices are given in order as [0.525 0.474 0.042 0.059 0.510 0.038 0.262 0.157] ∘C. To match the temperature of a device near the temperature boundary and a device away from the temperature boundary, the optimizer allowed device 4 to heat up to match the temperature of device 5 (still satisfying the temperature constraint). The result is an asymmetric topology where device 5 is connected to the boundary with conductive material, and device 4 is minimally connected with thermally conductive material.

4.3 Average temperature maximization

In this study, we demonstrate a practical use of an average temperature optimization for an energy harvesting application subject to localized temperature constraints. This may be important for circuits with thermo-electric devices that can harvest energy (Dede et al. 2016), or for circuits placed near energy storage devices that require higher temperatures to operate efficiently. One example of this type of design problem can be formulated as:

$$ \begin{array}{@{}rcl@{}} &&\underset{\textbf{x}}{\min} \quad - \frac{1}{n}\left( \textbf{L}_2^{T} \textbf{U} + \textbf{L}_6^{T} \textbf{U} \right) \\ &&\text{s. t.} \quad V(\textbf{x}) \leq V_{\max} \\ &&\quad\quad R(\textbf{x}) \geq R_{\min} \\ &&\quad\quad {\left( \textbf{L}_{1,...,8}^{T} \left( \frac{\textbf{U}}{T_{\max}} \right)^{p} \right)^{1/p} \leq 1 }\\ &&\quad\quad {\frac{1}{n} \left( \textbf{L}_2^{T} \textbf{U} - \textbf{L}_6^{T} \textbf{U} \right)^2 \leq 0.01} \\ &&\quad\quad {0 \leq \textbf{x} \leq 1}. \end{array} $$
(P4)

The objective now is to minimize the negative sum of the average temperatures on devices 2 and 6. A p-norm temperature constraint is enforced on the elements of the remaining devices to prevent failure. The temperature constraint is further relaxed here to 0.08∘ to demonstrate the variation in topology. In addition to these constraints, an additional temperature constraint is placed on devices 2 and 6 to ensure they operate at the same temperature. The same constraint values for volume and radius are prescribed: \(V_{\max \nolimits }~=~0.3\) and \(R_{\min }~=~0.4\) cm, respectively. The results of this topology optimization are presented in Fig. 6.

Fig. 6
figure 6

Constrained max temperature optimization solution produces a heat spreading structure that avoids specific devices

Full size image

As expected, the heat spreader design avoids devices 2 and 6 while connecting the heat sink directly to the remaining devices. The maximum temperature on devices 2 and 6 was 0.15 ∘C, and the maximum temperature on the remaining devices was 0.8 ∘C. The optimizer was able to nearly double the maximum temperature on the domain while maintaining the temperature constraint on the remaining devices. Due to layout and boundary conditions symmetry, the fourth constraint is somewhat redundant.

4.4 Temperature variance optimization

In Section 3, it was observed that the temperature variance objective may increase the maximum temperature on the domain to minimize the variance of the temperature on the domain. In this study, we demonstrate a practical use of temperature variance minimization subject to a localized temperature constraint. Consider the following problem formulation:

$$ \begin{array}{@{}rcl@{}} &&{\underset{\textbf{x}}{\min}} \quad {\left[ \frac{1}{n} \left( \textbf{U} - \frac{\textbf{L}^{T} \textbf{U}}{n} \right)^{T} \left( \textbf{U} - \frac{\textbf{L}^{T} \textbf{U}}{n} \right) \right]_{1,...,8}}\\ &&{\text{s. t.}} \quad {V(\textbf{x}) \leq V_{\max}} \\ &&\quad\quad {R(\textbf{x}) \geq R_{\min}} \\ &&\quad\quad {\left( \textbf{L}_{1,...,8}^{T} \left( \frac{\textbf{U}}{T_{\max}} \right)^{p} \right)^{1/p} -1 \leq 0 }\\ &&\quad\quad {0 \leq \textbf{x} \leq 1,} \end{array} $$
(P5)

where the variance in temperature across all devices is minimized, subject to a volume, minimum radius, and a single temperature constraint across all device nodes. The maximum allowable temperature here is relaxed to 0.06 ∘C to allow room for the optimizer to rearrange material. The same constraint values for volume and radius are prescribed as \(V_{\max \nolimits }~=~0.3\) and \(R_{\min }~=~0.4\) cm. The optimized structure is presented in Fig. 7.

Fig. 7
figure 7

Variance-optimized solution subject to a global temperature constraint. Optimized structure maintains 0.1 ∘C temperature constraint

Full size image

The optimization algorithm converged to a solution which connected most of the devices together to minimize the variance while satisfying the temperature constraint. The conductive structure formed a partial-density connection to the components closest to the fixed temperature boundary to maintain the temperature constraint. This may be achieved practically by selecting a different material, with lower thermal conductivity, to interface the devices.

5 Conclusion

Though there are some technical limitations for topology optimization as described by Dbouk (2017), topology optimization may be used creatively to achieve many design tasks. Furthermore, these studies motivate a concept of designing a temperature distribution for electronics applications. This can be imposed with several objective and/or constraints, instead of optimizing a single global parameter that describes performance.

In this research, several objective functions relevant to power electronics applications have been investigated. It was shown that thermal compliance and mean temperature optimized structures are nearly identical for a homogeneously heated design domain. This is due to the mathematical similarity between objective functions. Using a p-norm approximation of the maximum function can be used to consistently produce “lower-” temperature solutions, despite the inaccuracies in the gradient calculation. The variation-optimized solutions produced more dendritic structures with relatively small connections to the fixed temperature boundary. These solution were observed to raise the maximum temperature on the domain to enable minimization of the variance in temperature on the domain.

These findings were used to design several practical formulations for power electronics systems. The second design problem considered a discrete heating domain, corresponding to systems such as an electronics-printed circuit board. For this design problem, several temperature constraints where introduced to capture realistic requirements for PCB applications. Formulations including design-dependent constraints, asymmetric loading, and temperature maximizations were considered. In utilizing various combinations of objectives and constraints, a temperature distribution on the domain was designed. Framing the optimization problem as designing a specific temperature map instead of a minimizing temperature may lead to improved system-level performance in power-dense applications.

One of the key advantages of topology optimization is the ability to represent various topologies and solve for their performance on a finite element mesh without remeshing. The design variables do not have to be restricted to material density scalars, as was demonstrated in this study (P2), to make further use of the advantage. Integrating additional system-level characteristics into this gradient based optimization routine is left as a topic of future work.

6 Replication of results

To facilitate the replication of the results in this paper, Matlab® code for the objective and constraint derivatives has been provided in Appendices 1 and 2. These have been modified to interface directly with the 88-line or 99-line Matlab® codes (Andreassen et al. 2011; Sigmund 2001). The 99-line matlab code contains instructions to modify the code for heat transfer. The MMA algorithm in Matlab® may be purchased to allow for exact replication of these results (Svanberg 1987). If the MMA algorithm is not available, Matlab®fmincon() may be used to optimize the design problems as well.