1 Introduction

Reliability has been utilized to measure the safety of the system in the presence of various uncertainties that can be classified as inherent variability (i.e., aleatory uncertainty) and reducible uncertainty due to a lack of knowledge (i.e., epistemic uncertainty). These two uncertainties are propagated to the uncertainty of the system performances that may lead to unexpected failure of the system, so that accurate reliability analysis with exhaustive representation and quantification of the uncertainties is indispensable for design optimization.

There have been numerous researches on reliability-based design optimization (RBDO) to obtain a reliable optimum design employing probabilistic quantification of uncertain performance. It can be typically categorized into sampling approaches (Dubourg et al. 2011; Lee et al. 2011a; Zhao et al. 2013; Wang and Wang 2014) and most probable point (MPP)-based approaches (Tu et al. 1999; Youn et al. 2003; Li et al. 2015; Choi et al. 2018). These extensive RBDO researches have generally assumed that statistical information of input random variables is fully accessible. However, obtaining true input statistical information from a set of finite samples is difficult due to the limitation of resource for testing samples to quantify the variability. Therefore, inaccurate input model is a much practical condition in real engineering problems. Epistemic uncertainty in simulation-based design optimization can be comprehensively defined including simulation model uncertainty due to the uncertainty of model parameters and model bias (Der Kiureghian and Ditlevsen 2009; Liang and Mahadevan 2011; Nannapaneni and Mahadevan 2016; Moon et al. 2017; Peng et al. 2017; Bae et al. 2017, 2018); hence, the uncertainty of input statistical models will be mainly treated in this paper.

There have been a few researches to quantify the uncertainty of input random variables induced by insufficient input dataset. In the early stage, possibility-based approaches (Du et al. 2006a, b; Lee et al. 2013) and interval uncertainty approaches (Rao and Cao 2002; Sankararaman and Mahadevan 2011; Yoo and Lee 2014; Muscolino et al. 2016) have been adopted, but the Bayesian approach is a more direct and intuitive way to use insufficient input data statistically. Gunawan and Papalambros (2006) assumed that the variability of reliability could be exhibited as the beta distribution and performed RBDO while maximizing the confidence of reliability. Youn and Wang (2008) proposed a similar approach focusing on the extreme case of the beta distribution to make a sufficiency, in which Bayesian reliability has to be smaller than exact reliability. On the other hand, the uncertainty of the input random variable can be handled by adjusting the standard deviation and correlation coefficient (Noh et al. 2011a, b). In addition, likelihood-based approaches have been proposed that the distribution of the parameters can be quantified through the maximum likelihood estimation (MLE) and Gaussian process interpolation (Sankararaman and Mahadevan 2011, 2013a, b). Instead of Bayes’ theorem, the researches utilizing the bootstrap method without the assumption that data follow certain distribution have been proposed (Picheny et al. 2010; Noh et al. 2011b). Ito et al. (2018) propose a conservative reliability index (CRI) decomposed into the aleatory part and the epistemic part for Gaussian input distribution. Meng et al. (2015b) and Hao et al. (2017) developed non-probabilistic RBDO to treat lack of input data by employing a convex model to describe uncertain-but-bounded parameters rather than the stochastic model. Recently, Cho et al. (2016a) and Moon et al. (2018) proposed conservative RBDO (CRBDO) to fully model the probability of reliability in the presence of the uncertainty of input distribution types and parameters. Employing Bayes’ theorem and Monte Carlo simulation (MCS) (Rubinstein and Kroese 2016), accurate confidence of reliability under given dataset can be obtained. However, estimating a cumulative distribution function (CDF) of reliability is very computationally demanding.

Therefore, the motivation of our research is to reduce the excessive amount of function evaluations to obtain the confidence of reliability. It is noted that the confidence of reliability has to be assessed for design optimization rather than the whole CDF of reliability. In this paper, we propose a reliability measure approach (RMA) and confidence-based design optimization (CBDO) which have constraints for the confidence of reliability. The reliability will be treated as a function of input distribution types and parameters. Due to the discreteness of input distribution type, it is divided into two approaches depending on prior knowledge of input distribution types, and kernel density estimation (KDE) (Silverman 2018) is used to quantify the variability of a random variable when its distribution type is totally unknown. Once the input distribution types are given or identified through any model identification method (Kang et al. 2016), the probabilistic domain that consists of input distribution parameters can be defined. The process has been inspired from performance measure approach (PMA) (Tu et al. 1999), but random design variables, performance functions, and reliability are replaced with input distribution parameters, reliability, and confidence of reliability, respectively. In other words, the input distribution parameter space is regarded as the upper-level space of input random variables where RMA is performed. The proposed method handles the confidence of reliability by searching MPP in the probabilistic space denoted as P-space transformed from input distribution parameter space. Consequently, the double-loop MCS can be reduced to a nested RMA-MCS loop leading to a significant reduction of function evaluations for MCS. Moreover, sensitivity analysis in P-space is derived through the first-order score functions that are an essential concept to facilitate stochastic sensitivity analysis in sampling-based RBDO (Lee et al. 2011b) and explicit expression of uncertainties.

The paper is organized as follows. PMA for RBDO and confidence of reliability in CRBDO are explained in Section 2. In Section 3, general RMA for CBDO and stochastic sensitivity analysis is formulated, and two approaches depending on the prior knowledge of input distribution types are given in Section 4. Then, the feasibility and effectiveness of the developed sensitivity analysis, RMA, and CBDO are verified in Section 5. The conclusion and future research will be given in Section 6.

2 Overview of reliability analysis and confidence of reliability

2.1 Performance measure approach for reliability-based design optimization

Reliability analysis is to obtain the probability of failure which is the probability that a performance function is larger than zero since G(X) > 0 means failure in this paper. The probability of failure is in general computed through the multi-dimensional integration as

$$ {P}_F\equiv \Pr \left[G\left(\mathbf{X}\right)>0\right]={\int}_{G\left(\mathbf{X}\right)>0}{f}_{\mathbf{X}}\left(\mathbf{x}\right)d\mathbf{x} $$
(1)

where G(X) is the performance function, and X is the vector of random design variables following the joint probability density function (PDF) of fX(x).

Reliability-based design optimization (RBDO) with probabilistic constraints is formulated to

$$ {\displaystyle \begin{array}{l}\underset{\mathbf{d}}{\operatorname{minimize}\;}\kern0.48em \mathrm{cost}\left(\mathbf{d}\right)\\ {}\mathrm{subject}\ \mathrm{to}\kern0.48em \Pr \left[{G}_i\left(\mathbf{X}\right)>0\right]\le {P}_{F_i}^{\mathrm{Target}},\kern0.6em i=1,..., nc\\ {}\kern3.119999em {\mathbf{d}}^L\le \mathbf{d}\le {\mathbf{d}}^U\end{array}} $$
(2)

where X is the vector of random variables, d is the design vector defined as the mean of X, \( {P}_{F_i}^{\mathrm{Target}} \) is the target probability of failure for the ith constraint, and nc is the number of probabilistic constraints. Exact estimation of the probabilistic constraints in (2) defined by (1) is very difficult since it requires a large number of simulations. Therefore, performance measure approach (PMA) using MPP has been proposed (Tu et al. 1999; Youn et al. 2003, 2005; Yang and Yi 2009; Meng et al. 2015a; Keshtegar and Lee 2016). In PMA for RBDO, the MPP has the largest performance function value on the hypersphere with a radius of the given target reliability index βt. If the performance function value at MPP is smaller than zero, the probabilistic constraint of PMA is satisfied. Thus, MPP in PMA can be obtained by solving the following optimization as

$$ {\displaystyle \begin{array}{l}\underset{\mathbf{u}}{\operatorname{maximize}}\kern0.75em G\left(\mathbf{x}\left(\mathbf{u}\right)\right)\\ {}\;\mathrm{subject}\ \mathrm{to}\kern0.74em \left\Vert \mathbf{u}\right\Vert ={\beta}_t\\ {}\kern1.08em \mathrm{where}\kern0.73em \mathbf{u}={\Phi}^{-1}\left({F}_{\mathbf{X}}\left(\mathbf{x}\right)\right)\end{array}} $$
(3)

where u is the random variable vector following the standard normal distribution transformed from original X-space by the Rosenblatt transformation (Rosenblatt 1952) where cumulative distribution function (CDF) of X is FX(x). MPP, the optimum of (3), is denoted as u∗. Hence, the probabilistic constraint in (2) can be rewritten using PMA as

$$ g\left({\mathbf{u}}^{\ast}\right)\le 0 $$
(4)

which is identical with G(x(u∗)) ≤ 0 as a function at MPP in the original domain.

2.2 Confidence of reliability with insufficient input data

Confidence of reliability is defined as the probability that given target reliability is satisfied at a design point. Uncertainty of reliability is originated from input model uncertainty, distinguished from input variability, which means that insufficient input data induce uncertain input statistical models such as distribution types and parameters. Using Bayes’ theorem, joint PDF of the reliability under given dataset ∗x can be obtained as (Cho et al. 2016a; Moon et al. 2018)

$$ f\left(\operatorname{Re},\boldsymbol{\upzeta}, \boldsymbol{\uppsi} |\ast \mathbf{x}\right)=f\left(\operatorname{Re}|\boldsymbol{\upzeta}, \boldsymbol{\uppsi}, \ast \mathbf{x}\right)P\left(\boldsymbol{\upzeta} |\boldsymbol{\uppsi}, \ast \mathbf{x}\right)f\left(\boldsymbol{\uppsi} |\ast \mathbf{x}\right) $$
(5)

where ζ and ψ are input distribution types and parameters, respectively. Since the distribution types are not continuous variables, the probability mass function (PMF) obtained from Bayes’ theorem is used in (5). Therefore, the confidence level of the given target reliability is obtained using CDF of the reliability as (Cho et al. 2016a)

$$ \mathrm{CL}\left(\operatorname{Re}|\ast \mathbf{x}\right)\equiv 1-{F}_{\mathrm{Re}}\left(\operatorname{Re}|\ast \mathbf{x}\right)=1-{\int}_0^{\mathrm{Re}}{\int}_{\varOmega_{\boldsymbol{\upzeta}}}{\int}_{\varOmega_{\boldsymbol{\Psi}}}f\left(\phi, \boldsymbol{\upzeta}, \boldsymbol{\uppsi} |\ast \mathbf{x}\right)d\boldsymbol{\uppsi} d\boldsymbol{\upzeta} d\phi $$
(6)

where ϕ is a variable for reliability bounded from 0 to 1.

The main difficulty to evaluate (6) is its large computational demands since double-loop MCS with a large number of samples has to be used: inner-loop MCS for reliability estimation and outer-loop MCS for estimation of confidence of reliability caused by the uncertainty of input distribution types and parameters. Using the double-loop MCS, CDF of the reliability in (6) is expressed as (Cho et al. 2016a)

$$ {F}_{\mathrm{Re}}\left(\operatorname{Re}|\ast \mathbf{x}\right)\cong \frac{1}{NMC{S}_{\mathbf{Z}} NMC{S}_{\boldsymbol{\Psi}}}\sum \limits_{n=1}^{NMC{S}_{\boldsymbol{\Psi}}}\sum \limits_{m=1}^{NMC{S}_{\mathbf{Z}}}{I}_{\left[0,\operatorname{Re}\right]}\left(\operatorname{Re}\left({\zeta}^{(m)},{\psi}^{(n)}\right)\right) $$
(7)

where I[0, Re](ϕ) is an indicator function in which the value is 1 if ϕ is between 0 and Re, and 0 otherwise. It should be noted that the number of samples for the double-loop MCS is NMCSRe × NMCSΖ × NMCSΨ where NMCSRe, NMCSΖ, and NMCSΨ are the number of samples for estimation of Re(ζ(m), ψ(n)), input distribution types, and input distribution parameters, respectively. Reliability is a function of input distribution types and parameters using indicator function due to the insufficient input dataset. So, the reliability is estimated through the sampling method as (Rubinstein and Kroese 2016)

$$ \operatorname{Re}\left(\boldsymbol{\upzeta}, \boldsymbol{\uppsi} \right)={\int}_{{\mathbb{R}}^N}I\left(G\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x};\boldsymbol{\uppsi}, \boldsymbol{\upzeta} \right)d\mathbf{x} $$
(8)

where ψ is the input distribution parameter vector, ζ is the input distribution types, and I(G(x)) is the indicator function defined as

$$ I\left(G\left(\mathbf{x}\right)\right)=\Big\{{\displaystyle \begin{array}{l}\;1,\kern1.44em G\left(\mathbf{x}\right)\le 0\\ {}\;0,\kern1.32em \mathrm{otherwise}\end{array}} $$
(9)

2.3 Conservative reliability-based design optimization

General formulation of CRBDO considering the confidence of reliability as constraints can be formulated as

$$ {\displaystyle \begin{array}{l}\kern0.96em \mathrm{given}\kern0.36em \ast \mathbf{x}\\ {}\underset{\mathbf{d}}{\operatorname{minimize}}\kern0.36em \mathrm{cost}\left(\mathbf{d}\right)\\ {}\mathrm{subject}\ \mathrm{to}\kern0.36em \Pr \left[\Pr \left[{G}_i\left(\mathbf{X}\right)\le 0\right]\ge {\operatorname{Re}}_i^{\mathrm{Target}}\right]\ge {\mathrm{CL}}_i^{\mathrm{Target}}\kern0.36em \mathrm{for}\kern0.24em i=1,2,..., nc\end{array}} $$
(10)

which uses (7) to estimate the confidence of reliability at a design point under given dataset x. As can be seen from (10), CRBDO yields an optimum considering epistemic uncertainty caused by insufficient input data but requires a huge amount of function evaluations. Uncertainty quantification of input distribution parameters and types used to evaluate the confidence of reliability in (10) will be explained in the next section.

3 Confidence-based design optimization using a reliability measure approach

In this section, confidence-based design optimization (CBDO) using a reliability measure approach (RMA) is proposed to resolve the efficiency issue of CRBDO. Decomposition of input dataset can be referred to Section 2.2 of the literature (Cho et al. 2016a). An underlying condition in CBDO is that there are random variables in which statistical information is not given and should be estimated using only a few samples. Accordingly, the confidence of reliability will be mainly treated as a probabilistic constraint instead of reliability used in conventional RBDO since the reliability of a system has also uncertainty propagated from the uncertainty on the input statistical model.

There are two sources of uncertainty in the statistical model of input random variable: input distribution types and parameters. Since the input distribution type is not a continuous random variable, the proposed method takes variability of input distribution parameters into consideration in the probabilistic domain to obtain confidence of reliability under two circumstances: 1) input distribution types are known, but input distribution parameters are unknown and 2) both input distribution types and parameters are unknown. In this study, uncertainties of input distribution parameters are quantified based on the normality condition, and unknown distribution types are described by kernel density estimation (KDE).

Under the aforementioned configurations, the confidence of reliability defined as a probability that the reliability of a performance function is larger than the user-specified target reliability needs to be computed in CBDO. However, it is very difficult to be calculated even if a surrogate model is used because double-loop MCS is necessary for repetitive reliability computations with respect to uncertain parameters. Therefore, RMA is proposed to efficiently estimate the confidence of reliability in parameter space by utilizing the framework of PMA. Reliability and input distribution parameters correspond to a performance function and random variables in PMA, respectively. Therefore, RMA finds MPP for the reliability with the target confidence in the input distribution parameter space and thus requires several MCSs only for searching MPP, unlike CRBDO. After finding the MPP, the confidence of reliability is obtained using a linear approximation of the reliability function in parameter space. Consequently, RMA can significantly reduce the computational burden in CRBDO since it estimates the confidence of reliability in an analytic way rather than sampling methods.

The uncertainty quantification of input distribution model is presented in Section 3.1. The formulation of the proposed RMA in P-space and stochastic sensitivity analysis for reliability based on uncertainty quantifications of input distribution parameters are explained in Section 3.2. Two cases for known and unknown input distribution types are discussed in Section 4.

3.1 Uncertainty of input distribution model

Variabilities of input distribution parameters that arise due to insufficient input data have to be explicitly quantified to define probabilistic space for reliability estimation. Under the normality assumption described in the literature (Gelman et al. 2013; Cho et al. 2016a), variabilities of mean and variance are expressed as normal and inverse-gamma distributions, respectively. The normality assumption does not mean that the true distribution type is a normal distribution, but it is the intermediate assumption for uncertainty quantifications of input distribution parameters without causing a significant error. Uncertainties of variance and mean of the ith random variable can be described as

$$ {\sigma}_i^2\mid \ast {\mathbf{x}}_i\sim \mathrm{IG}\left(\frac{ND-1}{2},\frac{\left( ND-1\right){s}_i^2}{2}\right) $$
(11)

and

$$ {\mu}_i\mid {\sigma}_i,{{}^{\ast }{}_{\mathbf{x}}{}^{\ast}\mathbf{x}}_i\sim N\left(\ast {\overline {\mathbf{x}}}_i,\sqrt{\frac{\sigma_i^2}{ND}}\right), $$
(12)

respectively, where ∗xi is given input data for the ith random variable; ND is the number of input data; \( {s}_i^2 \) is the sample variance of the ith random variable; and \( \ast {\overline {\mathbf{x}}}_i \) is the sample mean of the ith random variable. It is noted that the normal distribution of the mean in (12) is conditional to the variance in (11). The sample mean in (12) will change during design optimization since it is used as a design vector d in (10). In other words, the dataset is used to identify the initial design and sample variance which is assumed to be constant during the optimization, and design movement can be achieved by shifting the data. Obviously, the sample mean of random parameter is invariant during the optimization

The PDF of reliability under given input distribution parameters and types becomes a Dirac delta function expressed by

$$ f\left(\operatorname{Re}|\boldsymbol{\uppsi}, \boldsymbol{\upzeta}, \ast \mathbf{x}\right)=\delta \left(\operatorname{Re}-\operatorname{Re}\left(\boldsymbol{\uppsi}, \boldsymbol{\upzeta} \right)\right) $$
(13)

where ψ is the input distribution parameters, and ζ is the input distribution types that can be either specific parametric distribution or nonparametric KDE depending on prior knowledge as will be explained in Section 4. Consequently, when ψ and ζ are given, the reliability is considered as a deterministic value obtained from MCS, so that PDF of reliability has an infinity value only at the deterministic reliability, Re(ψ, ζ).

3.2 Reliability measure approach

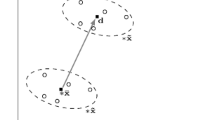
In this section, RMA to explore MPP in the standard normal parameter space (P-space) transformed from input distribution parameter space is explained. In RMA, MPP search is performed in P-space to find the smallest reliability on the given hypersphere with a radius βCL derived from the target confidence level, CLTarget. Note that the smallest reliability should be explored unlike the maximization problem in (3). Figure 1 illustrates the concept of RMA in P-space and design history for searching MPP where N is the number of random variables with insufficient samples. The initial point is set to origin in the standard normal P-space in general, and optimizer finds the next MPP candidate point based on the gradient of reliability in P-space which can be obtained from sensitivity analysis of reliability with respect to each parameter employing the first-order score functions. Once the MPP is identified as black filled circle in Fig. 1, the reliability at the MPP calculated from transformed input distribution parameters denoted as ψ including mean and variance is used to judge the violation of the confidence constraint. In Fig. 1, the reliability at the MPP is estimated as 0.87 that has to be larger than the target reliability. If the target confidence is set to 0.87, RMA for CBDO will decide that the current design point satisfies the confidence constraint even though the yellow region is the true unconfident region where reliability is less than the target reliability. Details of formulation and sensitivity analysis will be explained in Sections 3.2.1, 3.2.2, and 3.2.3.

Fig. 1
figure 1

Concept of RMA in P-space

Full size image

3.2.1 Formulation of RMA

The optimization to find MPP in P-space can be formulated to

$$ {\displaystyle \begin{array}{l}\underset{\mathbf{p}}{\operatorname{minimize}}\kern0.62em \operatorname{Re}\left(G\left(\mathbf{X}\right)|\boldsymbol{\upmu}, {\boldsymbol{\upsigma}}^2\right)\\ {}\;\mathrm{subject}\ \mathrm{to}\kern0.5em \left\Vert \mathbf{p}\right\Vert ={\Phi}^{-1}\left({\mathrm{CL}}_{\mathrm{Target}}\right)\\ {}\kern1.08em \mathrm{where}\kern0.49em \operatorname{Re}\left(G\left(\mathbf{X}\right)|\boldsymbol{\upmu}, {\boldsymbol{\upsigma}}^2\right)=\int {I}_{\varOmega_R}\left(G\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x};\boldsymbol{\upmu}, {\boldsymbol{\upsigma}}^2\right)d\mathbf{x}\cong \frac{1}{N_{MCS}}\sum \limits_{j=1}^{N_{MCS}}{I}_{\varOmega_R}\left(G\left({\mathbf{x}}^{(j)}\right)\right)\\ {}\kern3.119999em {I}_{\varOmega_R}\left(G\left(\mathbf{x}\right)\right)=\Big\{\begin{array}{l}1,\kern0.96em G\left(\mathbf{x}\right)\le 0\\ {}0,\kern0.84em \mathrm{otherwise}\end{array}\kern2.879999em \\ {}\kern3.239999em \Phi \left({p}_{2i-1}\right)={F}_{\sigma_i^2}\left({\sigma}_i^2|\ast {\mathbf{x}}_i\right)\\ {}\kern3.239999em \Phi \left({p}_{2i}\right)={F}_{\mu_i}\left({\mu}_i|{\sigma}_i^2,\ast {\mathbf{x}}_i\right)\kern0.84em for\kern0.24em i=1,2,...N\;\end{array}} $$
(14)

In Eq. (14) Re(G(X)| μ, σ2) is reliability for the given performance function G(X) and realizations of input distribution parameters. It means that uncertainty of performance function propagated from a random vector X is conditional to input distribution parameters. CLTarget is the target confidence level to be satisfied in CBDO. The indicator function for a reliable domain, \( {I}_{\varOmega_R}\left(G\left({\mathbf{x}}^{(j)}\right)\right) \), is to judge whether the jth sampling point is in the reliable region or not. NMCS means the number of samples for reliability estimation, and N is the number of random variables which are assumed to be independent in this study. It can be seen that two input distribution parameters for the ith random variable following \( {F}_{\mu_i}\left({\mu}_i|{\sigma}_i^2,\ast {\mathbf{x}}_i\right) \) and \( {F}_{\sigma_i^2}\left({\sigma}_i^2|\ast {\mathbf{x}}_i\right) \) are transformed to P-space following the standard normal distribution. The MPP that has minimal reliability as a function of input distribution parameters in P-space would be explored, and the number of random variables in P-space becomes 2N since a two-parameter distribution is assumed for the input random variables.

3.2.2 Stochastic sensitivity analysis in RMA

Sensitivity analysis of reliability with respect to mean and variance is essential for efficient and accurate gradient-based optimization. The stochastic sensitivity analysis has been discussed in the previous studies to develop the sampling-based RBDO (Lee et al. 2011a, b; Cho et al. 2016b). The sensitivity analysis with respect to the ith mean can be described using the first-order score function and chain rule as

$$ \frac{\partial \operatorname{Re}}{\partial {P}_{\mu_i}}=\frac{\partial \operatorname{Re}}{\partial {\mu}_i}\frac{\partial {\mu}_i}{\partial {P}_{\mu_i}}=\int {I}_{\varOmega_R}\left(G\left(\mathbf{x}\right)\right)\frac{\partial \ln {f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)}{\partial {\mu}_i}{f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)d\mathbf{x}\times \frac{\partial {\mu}_i}{\partial {P}_{\mu_i}} $$
(15)

where the PDF of mean is given in (12). The derivative of mean with respect to a corresponding \( {P}_{\mu_i} \) can be obtained through the following relationship as

$$ \frac{\partial {\mu}_i}{\partial {P}_{\mu_i}}=\frac{\mathrm{\partial \Phi}\left({P}_{\mu_i}\right)}{\partial {P}_{\mu_i}}/\frac{\partial {F}_{\mu_i}\left({\mu}_i\right)}{\partial {\mu}_i}=\frac{\phi \left({P}_{\mu_i}\right)}{f_{\mu_i}\left({\mu}_i\right)} $$
(16)

where \( {F}_{\mu_i}\left({\mu}_i\right)=\Phi \left({P}_{\mu_i}\right) \) and \( {P}_{\mu_i} \) is a random variable following the standard normal distribution transformed from the mean of i-th random variable denoted as μi. ϕ and Φ are PDF and CDF of the standard normal distribution, respectively. On the other hand, the sensitivity analysis with respect to the variance of i-th random variable, which seems to be more complicated since the mean is conditional to the variance, is derived as

$$ {\displaystyle \begin{array}{l}\frac{\partial \operatorname{Re}}{\partial {P}_{\sigma_i^2}}=\frac{\partial \operatorname{Re}}{\partial {\sigma}_i^2}\frac{\partial {\sigma}_i^2}{\partial {P}_{\sigma_i^2}}=\int {I}_{\varOmega_R}\left(G\left(\mathbf{x}\right)\right)\frac{d\ln {f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)}{d{\sigma}_i^2}{f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)d\mathbf{x}\times \frac{\partial {\sigma}_i^2}{\partial {P}_{\sigma_i^2}}\\ {}\\ {}\kern5.039997em =\int {I}_{\varOmega_R}\left(G\left(\mathbf{x}\right)\right)\left(\frac{\partial \ln {f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)}{\partial {\sigma}_i^2}+\frac{\partial \ln {f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)}{\partial {\mu}_i}\frac{d{\mu}_i}{d{\sigma}_i^2}\right){f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)d\mathbf{x}\times \frac{\phi \left({P}_{\sigma_i^2}\right)}{f_{\sigma_i^2}\left({\sigma}_i^2\right)}\end{array}} $$
(17)

where \( {P}_{\sigma_i^2} \) is a random variable following the standard normal distribution corresponding to \( {\sigma}_i^2 \). The PDF of variance is given in (11). The derivatives of the random variable with respect to distribution parameters can be shown in the literature using the relationship of the Rosenblatt transformation written as (Cho et al. 2017)

$$ \frac{d{x}_i}{d{p}_i}=-\frac{1}{f_{X_i}\left({x}_i;{a}_i,{b}_i\right)}\frac{\partial }{\partial {p}_i}{F}_{X_i}\left({x}_i;{a}_i,{b}_i\right) $$
(18)

where pi corresponds to either mean or variance of i-th random variable, and ai and bi are general distribution parameters as functions of mean and variance. Therefore, the derivative of mean with respect to variance in (17) can be derived as

$$ {\displaystyle \begin{array}{l}\frac{d{\mu}_i}{d{\sigma}_i^2}=-\frac{1}{f_{\mu_i}\left({\mu}_i;{{}^{\ast}\overline{x}}_i,\sqrt{\sigma_i^2/ ND}\right)}\times \frac{-\left({\mu}_i-{{}^{\ast}\overline{x}}_i\right)}{2{\sigma}_i^3/\sqrt{ND}}\times \phi \left(\frac{\mu_i-{{}^{\ast}\overline{x}}_i}{\sqrt{\sigma_i^2/ ND}}\right)\\ {}\kern1.44em =\frac{\mu_i-{{}^{\ast}\overline{x}}_i}{2{\sigma}_i^2}\end{array}} $$
(19)

where \( {{}^{\ast}\overline{x}}_i \) is the sample mean of data which equivalent to design point of ith random variable. In addition, the first-order score functions of various parametric distribution, \( \frac{\partial \ln {f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)}{\partial {\mu}_i} \) and \( \frac{\partial \ln {f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)}{\partial {\sigma}_i^2} \) used in (15–17), are derived analytically in the literature (Lee et al. 2011a, b; Cho et al. 2016b).

Searching MPP with any algorithms of PMA demands the gradient vector at the current point, and thus the gradient vector of reliability with respect to input distribution parameters is necessary. Employing developed sensitivity analysis in this section, searching MPP in P-space can be performed without any additional MCSs to obtain the gradient vector. Therefore, only one MCS can provide the gradient vector to any optimizer in searching MPP.

3.2.3 Sensitivity analysis in CBDO

Like conventional PMA, sensitivity analysis with respect to a design variable vector—mean vector of random variables—in CBDO can be described as (Lee et al. 2010)

$$ \frac{\partial \operatorname{Re}}{\partial {d}_i}{\left|{}_{\mathbf{p}={\mathbf{p}}^{\ast }}=\frac{\partial \operatorname{Re}}{\partial {\mu}_i}\right|}_{\mathbf{p}={\mathbf{p}}^{\ast }}=\int {I}_{\varOmega_R}\left(G\left(\mathbf{x}\right)\right)\frac{\partial \ln {f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)}{\partial {\mu}_i}{f}_{\mathbf{x}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right)d\mathbf{x} $$
(20)

Equation (20) can be easily obtained since \( \frac{\partial \ln {f}_{\mathbf{x}}\left(\mathbf{x};\boldsymbol{\uppsi} \right)}{\partial {\mu}_i} \) is already used in (15) and (17). Unlike sensitivity analysis in searching MPP described in Section 3.2.2, sensitivity analysis of reliability with respect to mean vector is used to find the optimal design point rather than MPP. In other words, CBDO has a double-loop algorithm composed of MPP search as an inner loop and optimal design search as an outer loop. Sensitivity analyses in Sections 3.2.2 and 3.2.3 are for the inner loop and outer loop, respectively. Note that (20) is equivalent to (15), except that the probabilistic space has to be transformed to P-space.

Using RMA, MPP in P-space is obtained, and reliability at the MPP is used as an index of violation under the given confidence of a reliability constraint. Since the function approximation method is the same as the conventional MPP-based reliability analysis, the second-order reliability method (SORM) (Lee et al. 2012; Park and Lee 2018), and MPP-based dimension reduction method (DRM) (Rahman and Xu 2004; Jung et al. 2019) can be utilized for more accurate confidence estimation.

4 Two approaches for input distribution type uncertainty

As mentioned earlier, there are two sources of uncertainties in input statistical models: input distribution parameters and distribution types. In Section 3, only uncertainties of input distribution parameters are treated for RMA and their sensitivity analysis. In this section, two approaches for input distribution type uncertainties—known input distribution type and unknown input distribution type—are explained for estimation of reliability and its sensitivity for CBDO.

4.1 Known input distribution type

Knowing input distribution types means that a designer has set the distribution types based on any prior knowledge or has figured out the most likely distribution type. For instance, model selection methods can determine the best distribution for the given data among multiple candidate distributions, and acceptance or rejection of the hypothesis with respect to the adequacy of given distribution type can be determined through goodness-of-fit (GOF) tests. Thus, the designer is able to use the model identification methods before the proposed CBDO as a preprocessing if there is no particular clue about the distribution type. Since the identification of a distribution type is beyond the purpose of this research, readers can refer to recent research on distribution type identification (Kang et al. 2016). The reason for separating uncertainty of a distribution type and its parameters is that it is difficult to include discrete variables for MPP-based approaches, and even if it is possible, it requires additional assumption and can become too complicated since two uncertainties are correlated.

When input distribution types are known as parametric distributions, the input joint PDF can be expressed as

$$ {f}_{\mathbf{X}}\left(\mathbf{x};\boldsymbol{\uppsi} \right)=\prod \limits_{i=1}^N{f}_{X_i}\left({x}_i;\boldsymbol{\uppsi} \right) $$
(21)

Since input random variables are assumed to be independent in this study. The PDF of the ith random variable can be described as (Cho et al. 2016b)

$$ {f}_{X_i}\left({x}_i;\boldsymbol{\uppsi} \right)={f}_{X_i}\left({x}_i;{\mu}_i,{\sigma}_i^2\right) $$
(22)

Assuming that the PDF is a two-parameter distribution with parameters of μi(ai, bi) and σi(ai, bi) as a function of two general distribution parameters. Under this configuration, RMA and its sensitivity analysis can share the sampling-based RBDO framework, and the relationship between mean and variance and general distribution parameters can be found in the literature (Lee et al. 2011a, b; Cho et al. 2016b). Note that any two-distribution parameters need to be expressed as mean and variance and vice versa to utilize the framework of RMA. Furthermore, the first-order score functions with respect to mean and variance for various parametric distributions can be found.

Once input distribution types are decided, epistemic uncertainty induced by an insufficient number of data is merely quantified as uncertainties of input distribution parameters. The reliability of target performance is a function of input distribution parameters so that the proposed MPP-search in P-space is available. The sensitivity analysis of reliability in (15) and (17) can be performed since \( {f}_{\mathbf{X}}\left(\mathbf{x};{\mu}_i,{\sigma}_i^2\right) \) is given as an explicit function of mean and variance. However, when input distribution types are still unknown, PDFs should be defined using KDE prior to RMA, which will be presented in the next section.

4.2 Unknown input distribution type

4.2.1 Uncertainty quantification using kernel density estimation

When input distribution types are unknown, it is necessary to describe fX(x; ψ) without using any parametric distribution. In this research, kernel density estimation (KDE) is implemented for the purpose. KDE under given input data is described as (Silverman 2018)

$$ \hat{f}(x)=\frac{1}{nh}\sum \limits_{i=1}^nk\left(\frac{X_i-x}{h}\right) $$
(23)

where n is the number of samples; X1, X2, ..., Xn are independent and identically distributed random samples; k(u) is a kernel function satisfying \( {\int}_{-\infty}^{\infty }k(u) du=1 \); h is a smoothing parameter of KDE. In this paper, the standard normal density function is employed for the kernel function.

It should be noted that the shape of the KDE expression in (23) does not change during design optimization. Only mean, which is the sample mean initially, changes in the optimization process. Thus, during the design optimization, a shifted KDE of the independent jth random design variable with n samples is used as an input distribution given by

$$ {\overset{\wedge }{f}}_{X_j}\left(x;{{}^{\ast}\mathbf{x}}_j,{\mu}_j\right)=\frac{1}{n{h}_j}\sum \limits_{i=1}^nk\left(\frac{s_i\left({{}^{\ast}\mathbf{x}}_j,{\mu}_j\right)-x}{h_j}\right) $$
(24)

where \( {s}_i\left({{}^{\ast}\mathbf{x}}_j,{\mu}_j\right)={{}^{\ast }x}_{j,i}-{{}^{\ast}\overline{x}}_j+{\mu}_j \) is the ith shifted sample of the jth random variable, and μj is the given mean of the jth random variable. On the other hand, the uncertainty of variance cannot be directly reflected in (24) since the variance of KDE is always larger than the sample variance (Hansen 2009). Therefore, using the same normality condition used in Section 3.1, the bandwidth in (24) can be determined using the normal reference rule as (Silverman 2018)

$$ {h}_j={\left(\frac{4{\sigma_j}^5}{3n}\right)}^{\frac{1}{5}}\approx 1.06{\sigma}_j{n}^{-\frac{1}{5}} $$
(25)

where \( {\sigma}_j^2 \) is the given variance of the jth random variable. The bandwidth of normal reference rule is to choose the optimal bandwidth that minimizes the mean integrated squared error when underlying density function is a normal distribution. Despite the normality assumption, (24) can express a plausible PDF for any input distribution. Through (24) and (25), KDE can reflect the given mean and variance to compute the reliability in P-space. Note that given mean and variance as μj and \( {\sigma}_j^2 \) indicate the input distribution parameters to specify the uncertain input distribution since mean and variance are changed during MPP search in P-space, and KDE has to reflect to difference mean and variance following the current MPP candidate.

4.2.2 Stochastic sensitivity analysis for kernel density estimation

To utilize the stochastic sensitivity analysis in Section 3.2.2 for unknown input distribution cases, the first-order score function for KDE needs to be obtained. Using (24) and (25), the first-order score function with respect to mean for KDE of the jth independent random variable is derived as

$$ {\displaystyle \begin{array}{l}\frac{\partial \ln {\overset{\wedge }{f}}_{X_j}\left(x;h\right)}{\partial {\mu}_j}\kern0.36em =\frac{\partial \ln {\overset{\wedge }{f}}_{X_j}}{\partial^{\ast }{x}_{j,1}}\frac{\partial^{\ast }{x}_{j,1}}{\partial {\mu}_j}+...+\frac{\partial \ln {\overset{\wedge }{f}}_{X_j}}{\partial^{\ast }{x}_{j,n}}\frac{\partial^{\ast }{x}_{j,n}}{\partial {\mu}_j}\\ {}\kern3.839998em =\sum \limits_{i=1}^n\frac{x-{{}^{\ast }x}_{j,i}}{\sqrt{2\pi }n{h}_j^3{\overset{\wedge }{f}}_{X_j}(x)}{e}^{-\frac{1}{2}{\left(\frac{x-{{}^{\ast }x}_{j,i}}{h_j}\right)}^2}\end{array}} $$
(26)

where ∗xj, i is ith sample of jth random variable, \( {\overset{\wedge }{f}}_{X_j}(x)=\frac{1}{n{h}_j}\sum \limits_{i=1}^n\phi \left(\frac{x{-}^{\ast }{x}_{j,i}}{h_j}\right) \), and \( \phi (z)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{z^2}{2}} \)which is the standard normal density function. Similarly, the first-order score function with respect to the variance for KDE of the jth independent random variable is derived as

$$ {\displaystyle \begin{array}{l}\frac{\partial \ln {\overset{\wedge }{f}}_{X_j}\left(x;h\right)}{\partial {\sigma}_j^2}=\frac{\partial \ln {\overset{\wedge }{f}}_{X_j}}{\partial {h}_j}\frac{\partial {h}_j}{\partial {\sigma}_j^2}\\ {}\kern3.839998em =-\frac{1}{h_j}+\frac{\sum \limits_{i=1}^n{\left(x-{{}^{\ast }x}_{j,i}\right)}^2\phi \left(\frac{x-{{}^{\ast }x}_{j,i}}{h_j}\right)}{h_j^3\sum \limits_{i=1}^n\phi \left(\frac{x-{{}^{\ast }x}_{j,i}}{h_j}\right)}\frac{{\left(1.06{n}^{-1/5}\right)}^2}{2{h}_j}\end{array}} $$
(27)

Hence, (26) and (27) are substituted in (15–17) and (20) for the stochastic sensitivity analysis for CBDO when there is no prior knowledge on input distribution types.

4.3 Flowchart and practical issues

Figure 2 shows the flowchart of the proposed CBDO with RMA. Starting at the initial design point, variabilities of mean and variance are quantified as a normal and inverse-gamma distribution using the given input dataset. Before MPP search, input distribution types have to be specified according to which method is used. If the distribution types are parametrically identified, the parametric distributions are directly used for random sampling with respect to realizations of mean and variance. Otherwise, KDE is used to describe input distributions based on the given input dataset. To check violation of confidence constraints, uncertain input distribution parameters are transformed to P-space to find MPP using the stochastic sensitivity analysis for reliability. After finding the MPP, the current design point is moved to the next point using any nonlinear optimizer (e.g., sequential quadratic programming).

Fig. 2
figure 2

Flowchart for the proposed CBDO with RMA

Full size image

There are two remarks compared to common MPP searches used in PMA. Firstly, since reliability is always bounded between 0 and 1, sensitivity may become zero in case of totally violated or safe constraints. Therefore, it is recommended to check reliability values before MPP search in P-space to prevent numerical instability due to zero sensitivity. Secondly, characteristics of reliability with respect to mean and variance may result in multiple MPPs. This happens when a performance function has multiple failure regions in the probabilistic domain. It can occur in conventional reliability analysis as well, but may be more frequent in RMA since reliability is a much more complex function with respect to input distribution parameters. The issue in the second remark will be discussed in further works.

5 Numerical examples

Two mathematical examples and one engineering example are introduced in this section for demonstration of the proposed CBDO with RMA. The proposed sensitivity analysis with respect to each input distribution parameter is validated, and MPP search in P-space is visualized to show its feasibility by checking contours of reliability functions for the 1-D mathematical function. In the 2-D mathematical example, the results of proposed CBDO under various circumstances and its effectiveness have been analyzed. Finally, the 11-D side impact example is used to test the applicability of the proposed CBDO to practical and complex engineering problems.

5.1 One-dimensional mathematical function for RMA

To demonstrate the proposed RMA and its sensitivity analysis, 1-D mathematical performance function given by

$$ G(X)=-0.35+X\sin (X)-0.5{X}^2 $$
(28)

is introduced. Even though the performance function has only one random design variable, its probabilistic space of input distribution parameters is expressed in 2-D space since a two-parameter distribution will be used for the random variable X. There are 10 input data for X randomly drawn from normal, lognormal, Weibull, and Gumbel distributions where the true variance is set to 0.52, respectively.

5.1.1 Verification of sensitivity analysis in RMA

The proposed stochastic sensitivity analysis with respect to mean and variance in P-space is verified in this section by comparing with the finite difference method (FDM). Although FDM could be used for sensitivity analysis, it requires additional function evaluations, and proper perturbation is unknown in general due to truncation and round-off error in computation. Therefore, analytical sensitivity analysis is critical in design optimization in terms of both efficiency and accuracy. The FDM results are merely used as a reference to validate the derivation on analytical sensitivity analysis. For the test, a design point of p∗ = {1.1897, 1.1357}T which is the MPP in P-space with given dataset drawn from the normal distribution is utilized. Sensitivities of reliability with respect to distribution parameters for parametric distributions and nonparametric distribution given in (15) and (17) and FDM sensitivities with 0.5% perturbation are listed in Tables 1 and 2. Agreements between the proposed and FDM sensitivities are shown in the parenthesis. From the tables, it is shown that accurate sensitivities in P-space are obtained even when a distribution of a random variable is expressed using KDE.

Table 1 Sensitivity analysis results using known parametric distribution
Full size table
Table 2 Sensitivity analysis results using KDE
Full size table

5.1.2 Results of RMA

In this section, the proposed RMA is explained using the same 1-D performance function. Figure 3 shows the contours of reliability and hyperspheres for 95% target confidence in P-space assuming input distributions are known. Figure 3 also shows MPP search history which is obtained by hybrid mean value method (HMV) (Youn et al. 2003), and all the reliability values at converged points are the smallest on the target confidence circle. Hence, it can be seen that the MPP search has been successfully performed based on accurate sensitivity information. Each axis in Fig. 3 represents input distribution parameters transformed to P-space.

Fig. 3
figure 3

Contour of reliability and MPP-search history in P-space with samples drawn from normal (a), lognormal (b), Weibull (c), and Gumbel distribution (d)

Full size image

In case of no prior knowledge on input distribution types, contours of reliability are shown in Fig. 4 where the dataset of the previous case is reused for KDE. Even though the same dataset is used, the variability of random design variables changes resulting in different reliability contours. This is because only 10 samples are used for input statistical modeling.

Fig. 4
figure 4

Contour of reliability and MPP-search history using KDE in P-space with samples drawn from normal (a), lognormal (b), Weibull (c), and Gumbel distribution (d)

Full size image

Results of the proposed RMA for 95% target confidence level are listed in Table 3. For validation, MCS using original parametric distributions is performed at MPP obtained using RMA and agreements between two results are written in the parentheses. Table 3 shows that RMA is more accurate when input distributions are known and KDE shows slightly higher error especially in non-normal cases. It can be seen from Fig. 3 that limit-state reliability functions near MPP seem to be linear so that the RMA results using parametric distributions are accurate. On the other hand, in case of unknown distribution as shown in Fig. 4, it should be addressed that KDE cannot accurately approximate the original input distribution of the random variable with 10 samples only. Therefore, the larger errors in KDE are mainly caused by inexact estimations of the original PDF.

Table 3 MCS results at MPP obtained using RMA with a 95% confidence level using 10 data
Full size table

Table 4 shows RMA results when the number of input data is 30. Accuracy is generally improved using more data in two ways. First, increasing the number of data will reduce the variability of each input distribution parameter. Therefore, the limit-state reliability function near MPP in P-space becomes more linear, thereby reducing error due to the linearization. Second, when input distribution types are unknown, increasing the number of data can reduce error due to inaccurate estimation of input distributions by KDE as well. Therefore, increasing the number of data improves the accuracy of RMA with KDE more as shown in Table 4.

Table 4 MCS results at MPP obtained using RMA with a 95% confidence level using 30 data
Full size table

5.2 Two-dimensional confidence-based design optimization

Efficiency and accuracy of the proposed CBDO with RMA are verified through a 2-D mathematical example formulated as

$$ {\displaystyle \begin{array}{l}\kern0.48em \min \kern0.96em -\frac{{\left({d}_1+{d}_2-10\right)}^2}{30}-\frac{{\left({d}_1-{d}_2+10\right)}^2}{120}\\ {}\kern0.96em \mathrm{s}.\mathrm{t}\kern1.08em \Pr \left[\Pr \left[{G}_j\left(\mathbf{X}\left(\mathbf{d}\right)\right)\le 0\right]\ge 0.9772\right]\ge 0.9000,j=1,2,3\\ {}\kern2.639999em 0\le {d}_i\le 10,i=1,2\\ {}\mathrm{where}\kern0.96em {G}_1\left(\mathbf{X}\right)=1-\frac{X_1^2{X}_2}{20},\\ {}\kern2.639999em {G}_2\left(\mathbf{X}\right)=-1+{\left(0.9063{X}_1+0.4226{X}_2-6\right)}^2+{\left(0.9063{X}_1+0.4226{X}_2-6\right)}^3\\ {}\kern4.679997em -0.6{\left(0.9063{X}_1+0.4226{X}_2-6\right)}^4-\left(-0.4226{X}_1+0.9063{X}_2\right),\\ {}\kern2.639999em {G}_3\left(\mathbf{X}\right)=1-\frac{80}{X_1^2+8{X}_2+5}\end{array}} $$
(29)

where the target reliability and target confidence of reliability are set to 97.72% and 90.00%, respectively. In other words, the optimization in Eq. (29) explores a conservative optimum satisfying the confidence constraints with 90.00 % target confidence and 97.79 % target reliability. The number of MCS samples for reliability computation is 106, and the number of MCS samples for input distribution parameters in double-loop CRBDO is 104.

The design history of CBDO is illustrated in Fig. 5 when 10 input data are given. For efficiency, the sampling-based RBDO is performed from the initial point, and then CBDO is carried out from the RBDO optimum which is supposed to be near the CBDO optimum compared to arbitrary initial points. It is reasonable that the CBDO optimum is farther from each limit-state function than the RBDO optimum to compensate the input uncertainties. Note that the sampling-based RBDO is performed only with the inherent randomness of input variables using sample mean and variance.

Fig. 5
figure 5

Design history of the proposed CBDO with 10 input data

Full size image

Tables 5, 6, and 7 show design optimization results obtained using the proposed CBDO for known and unknown input distribution cases and conventional double-loop CRBDO. The confidence in each table means exact confidence for each constraint obtained using MCS with true input distributions. When input distribution types are known, the CBDO optimum gradually approaches the double-loop CRBDO optimum as the number of data increases. On the other hand, in case of unknown input distribution type, the CBDO optimum becomes conservative especially for the second constraint as the number of data increases. This is because the reliability for the second constraint obtained using KDE is overestimated due to its nonlinearity and inaccurate density estimation. The number of MCSs in the last columns of Tables 5, 6, and 7 means the number of reliability calculations using MCS. Since the third constraint is perfectly safe during the design optimization, only one MCS is required to check feasibility in each iteration of CBDO. However, in the case of CRBDO, MCS with 104 samples for input distribution parameters is performed for a constraint in each iteration. Thus, the total number of MCSs in CRBDO becomes the number of design iterations × the number of constraints × the number of MCS samples for input distribution parameters. As a result, the total number of MCSs is reduced from 180,000 in CRBDO to 44 and 36 in CBDO for a case of 100 input samples meaning that efficiency of CBDO is significantly improved maintaining the acceptable level of accuracy compared to CRBDO. Notably, confidence at the optimum is slightly overestimated or underestimated because the proposed method is an MPP-based approximation method inducing approximation error. In this paper, we cannot estimate nonlinearity of reliability with respect to input distribution parameters, but the accuracy will be definitely improved using higher-order MPP-based approximation methods.

Table 5 Results of CBDO when input distribution types are known
Full size table
Table 6 Results of CBDO when input distribution types are KDE
Full size table
Table 7 Results of double-loop CRBDO
Full size table

On the other hand, true reliability, reliability at mean value (i.e., sample variance), and reliability at the target confidence level can be compared to see how much uncertainty should be allowed in Table 8. The differences between reliabilities can be indices to quantify the impact of epistemic uncertainty. In Table 8, all results are taken from the CBDO optimum when distribution types are known. Certainly, reliability at MPP has to be the same with the target reliability of 97.72% for the first and second constraints which are active. Reliability at mean value indicates the reliability when variances of random variables are set to sample variances. It should be gradually closer to the true reliability in which the exact variances of random variables are known. Unlike overall tendency of results, it seems that the reliability at mean value is very similar to the true reliability when the number of input data is 10 since the sample variance of drawn data from a population is coincidently very close to the true variance.

Table 8 Reliability under various input distribution parameters with known distribution types
Full size table

5.3 Eleven-dimensional side impact problem

In this section, the proposed CBDO is applied to the vehicle side impact crashworthiness problem with nine random variables and two random parameters (Youn et al. 2004). It is assumed that statistical information of nine random variables is fully known and two random parameters have uncertainty induced by insufficient input with various numbers of data. Design optimization for the vehicle side impact problem is formulated as

$$ {\displaystyle \begin{array}{l}\kern0.48em \min \kern0.72em \mathrm{cost}\left(\mathbf{d}\right)=1.98+4.9{d}_1+6.67{d}_2+6.98{d}_3+4.01{d}_4+1.78{d}_5+2.73{d}_7\\ {}\kern0.96em \mathrm{s}.\mathrm{t}\kern0.72em \Pr \left[\Pr \left[{G}_j\left(\mathbf{X}\left(\mathbf{d}\right)\right)\le 0\right]\ge 0.95\right]\ge 0.95,j=1,2,3\\ {}\kern2.28em {\mathbf{d}}^L\le \mathbf{d}\le {\mathbf{d}}^U\\ {}\mathrm{where}\kern0.6em {G}_1\left(\mathbf{X}\right)=14.36-9.9{X}_2-12.9{X}_1{X}_8+0.1107{X}_3{X}_{10}\\ {}\kern2.28em {G}_2\left(\mathbf{X}\right)=0.72-0.5{X}_4-0.19{X}_2{X}_3-0.0122{X}_4{X}_{10}\\ {}\kern4.799997em +0.009325{X}_6{X}_{10}+0.000191{X}_{11}^2\\ {}\kern2.28em {G}_3\left(\mathbf{X}\right)=1.35-0.489{X}_3{X}_7-0.843{X}_5{X}_6+0.0432{X}_9{X}_{10}\\ {}\kern4.799997em -0.0556{X}_9{X}_{11}-0.000786{X}_{11}^2\end{array}} $$
(30)

where the objective is the vehicle weight, both the target confidence of reliability and target reliability are set to 95%, and the statistical information of random variables is listed in Table 9. The original side impact problem contains 10 constraints among which only three are active, and they are included in (30). Note that X10 and X11 are random parameters which are invariant during the optimization, and samples are randomly drawn from the normal distribution as shown in Table 9.

Table 9 Properties of random input (9 variables and 2 parameters) for side impact crashworthiness problem
Full size table

CBDO results with various numbers of input data are listed in Tables 10 and 11. In addition, CBDO results using KDE are listed in Tables 12 and 13. Overall results show that as the number of data increases, the CBDO optimum gradually approaches the RBDO optimum where true input distributions of two parameters are used. It is natural that an insufficient number of samples may provide large uncertainty in distribution parameters, and thus the optima become more conservative to compensate for the lack of knowledge on input statistical models. As discussed in the previous example, the accuracy of KDE is slightly worse than known distribution cases due to inaccurate input distribution estimation and propagation of variance to the smoothing parameter in KDE.

Table 10 Optima under various numbers of data when input distribution types are known
Full size table
Table 11 Confidences at optima when input distribution types are known
Full size table
Table 12 Optima under various numbers of data when input distribution types are KDE
Full size table
Table 13 Confidences at optima when input distribution types are KDE
Full size table

6 Conclusion

This paper proposes RMA of CBDO that can be defined as an MPP-based approximation method in P-space to eliminate outer-loop MCS of CRBDO to efficiently obtain the confidence of reliability. RMA to deal with the uncertainty of input distributions searches MPP in P-space and approximates the reliability based on MPP, resulting in significant improvement in efficiency with an acceptable level of accuracy. For the MPP search in P-space, two approaches using input distribution parameters quantified through the normality assumption are proposed according to the uncertainty of input distribution types. In addition, stochastic sensitivity analysis for reliability with respect to input distribution parameters is derived employing the first-order score function to reduce the number of MCSs and provides accurate search direction to an optimizer. Finally, CBDO with RMA accounting for the confidence of reliability is proposed adopting the framework of RBDO using PMA when the uncertainty of input statistical models exists. As a result, a conservative optimum in the presence of the uncertainty of input statistical models can be obtained using much-reduced computations compared to the previous CRBDO. Moreover, other existing MPP-based approximation methods can be directly combined with the proposed CBDO for more accurate results.

In future work, reweighting samples of MCS to estimate the reliability will be investigated to further reduce the number of MCSs. Samples to compute the reliability at a design point in P-space can be reused in the next point during MPP search using the scheme of the importance sampling. It can be effective in RMA in CBDO because input distribution parameters vary locally in P-space. In addition, the cost to add input samples will be treated as development cost to find the balanced optimum between system cost and development cost satisfying confidence constraints.

7 Replication of Results

Matlab codes for the mathematical examples in Section 5 are uploaded on https://github.com/Yongsu-Jung/SMO_CBDO.git. Overall concepts and algorithms can be validated through the mathematical example.