1 Introduction

In these days, performances of engineering designs are evaluated using computer simulations instead of physical testing to save cost and time for design development. As the simulation models become more complex, their computational cost has soared significantly. For the reason, surrogate modeling has been utilized to replace the time-consuming simulation models. However, for high-dimensional problems, building a surrogate model itself is a computationally expensive task since the number of samples for surrogate modeling highly depends on the dimensionality (Jin et al. 2002). The dimensionality issue can be effectively relieved by selecting and using essential variables that have great influence on the output response when we create surrogate models (Shan and Wang 2010). Therefore, for high-dimensional problems, variable selection is necessary to create an accurate surrogate model with given computational resources.

Many variable selection methods use samples produced by experimental design methods to identify the degree of relationship between variables and the output responses. More accurate and efficient variable selection is possible when the sample has high quality, i.e., orthogonality and space-filling property. To find effective sample location, experimental design has been extensively studied: input-domain-based criterion (Jin et al. 2003; Joseph et al. 2015; Joseph and Hung 2008; Pronzato and Walter 1988; Stein 1987), information-based criterion (Beck and Guillas 2016; Ko et al. 1995), and uncertainty-based criterion of posterior variance of the Gaussian process regression (GPR) model (Gorodetsky and Marzouk 2016). Some variable selection methods are paired with a specific experimental design to maximize their performance. For example, analysis of variance (ANOVA) that is the most classical variable selection method is mostly utilized in combination with the design of experiment (DOE) (Hayter 2012). Moon et al. introduced a two-stage variable selection method in combination with their own sampling technique based on Gram-Schmidt orthogonalization (Moon et al. 2012). Once the sample location is determined, output response at each sample is computed, and relevance between variables and output responses is measured. As a measure of the relevance, influence diagnostic scores such as information gain, Akaike information criterion (AIC), Bayesian information criterion (BIC), and linear/nonlinear coefficients (Qi and Zhang 2001; Helton et al. 2006) have been used. In addition, Sobol’ indices, which is a global sensitivity analysis method, was developed to measure the influence of mutually interacting input variables on the output in highly nonlinear problems (Homma and Saltelli 1996; Sobol 2001). A better index compared with Sobol’ indices when applied in strong interaction properties is also developed (Saltelli et al. 2009). To consider random variables, statistical sensitivity has been developed by several studies (Lee et al. 2011; Cho et al. 2014; Cho et al. 2016). After the relevance or influence measure is evaluated, essential variables can be determined according to the measure.

Especially, the number of samples used in variable selection—the efficiency of variable selection—is an important factor that should be carefully taken care in high-dimensional problems. Researchers (Székely et al. 2007, Cook 2000, Zhao et al. 2013) developed new influence diagnostic scores for efficient variable selection using a small number of samples. To ensure more stable result even with a few samples, there have been researches using the model-based method. Welch et al. utilized the likelihood of GPR as the criteria for variable screening (Welch et al. 1992). In the method, essential variables are detected by adding candidate variables one by one to the GPR model, and the variable which causes the highest improvement of the likelihood is selected. It was successfully applied to a 20-dimensional problem with less than 50 samples. Gaussian process (GP) classification (Rasmussen, 2006) calculates posterior using prior and given pre-labeled samples and makes small posterior smaller and large posterior larger. Hence, GP classification classifies relevant and irrelevant variables more distinctively. Recently, Wu et al. developed partial metamodel-based optimization utilizing radial basis function model with sensitive variables, which finally aims to obtain the optimal point with a reduced number of function evaluations (Wu et al. 2018). The method enhances the efficiency of the interwoven process of metamodeling and optimization by decomposing the space and focuses on the search area near the optimal point.

Throughout the literature survey, several aspects are found to be improved. First, several variable selection methods require well-positioned samples using delicate experimental design (Jin et al. 2003; Joseph et al. 2015; Joseph and Hung 2008; Pronzato and Walter 1988; Stein 1987; Beck and Guillas 2016; Ko et al. 1995; Gorodetsky and Marzouk 2016), or are coupled with specific experimental design methods (Hayter 2012; Moon et al. 2012). However, we may encounter samples that are not well-located. Second, the relevance measure that cannot identify the effect of interaction terms of variables on output response (Qi and Zhang 2001) could cause faulty variable selection in highly nonlinear problems. To capture the interaction term using Sobol’ indices, enormously large number of samples (e.g., millions) could be required (Homma and Saltelli 1996; Sobol 2001). Statistical sensitivity method has the same drawback of requiring too many samples (Cho et al. 2014; Cho et al. 2016; Lee et al. 2011). Third, variable selection through influence diagnostic scores could produce a different selection of variables due to the fluctuation of influence diagnostics scores depending on the number of samples or locations of samples (Székely et al. 2007; Cook 2000; Zhao et al. 2013). Fourth, GP classification (Rasmussen, 2006) requires pre-labeled samples—the predetermined data to which group they belong in classification (Guyon and Elisseeff 2003; Li et al. 2017; Chandrashekar and Sahin 2014). Finally, some modeling methods sacrifice the model accuracy, and the sensitivity analysis is performed with the intermediate metamodel to boost the optimization efficiency (Wu et al. 2018).

Therefore, this paper proposes an integrated variable selection and surrogate modeling algorithm that can cope with aforementioned difficulties—high dimensionality and nonlinearity, insufficient samples, arbitrary sample quality, the existence of interaction terms, and unlabeled data. The proposed method carries out the variable selection and surrogate modeling simultaneously without sensitivity analysis using as less number of samples as possible. In the proposed method, GPR is adopted for the surrogate modeling method, and variable subsets are evaluated with conservative multi-criteria. Variables that result in distinctly superior model performance are selected as the essential model inputs. Sequential adaptive sampling is carried out to avoid sample overuse. A conservative stopping criterion is developed to prevent premature stop of variable selection loop. For variable selection, two kinds of machine learning techniques are utilized for the proposed algorithm, clustering (Jain et al. 1999; Bouguettaya et al. 2015) and the Wrapper method (Kohavi and John 1997) since there is a functional similarity between data-driven modeling and physics-based modeling framework (Sun and Sun 2015; Solomatine and Ostfeld 2008; Bessa et al. 2017). Clustering is adopted to avoid ambiguous selection criteria because it can bisect data into distinctly different groups without a label. Especially agglomerative hierarchical clustering is adopted for the problem characteristic (Bouguettaya et al. 2015). The Wrapper method is also utilized due to its fitness for a variable selection in high uncertainty circumstances caused by a small number of samples. The Wrapper method determines the influence of a certain variable by the model performance formulated with the variable.

The organization of remaining parts of this paper is as follows. Section 2 reviews previous related researches. In Section 3, the proposed method is described in detail with an illustrative example. Section 4 presents two test examples to verify the performance of the proposed method. All results are summarized in Section 5.

2 Technological background

In this section, Sobol’ indices and GPR model are briefly revisited. Sobol’ indices and GPR are utilized as a benchmark to check variable selection accuracy and as surrogate modeling method, respectively, in this study. Specifically, the GPR model performances—marginal loglikelihood and integrated posterior variance—are core indices for variable selection criterion in the proposed method, and integrated posterior variance is also used for the experimental design criteria.

2.1 Sobol’ indices

Sobol’ indices is a global sensitivity index based on variance decomposition with Monte Carlo simulation. If the number of samples is enough, Sobol’ indices can identify the accurate influence of input on output response for any type of functions such as highly nonlinear and high-dimensional problems with interaction terms. The basic concept of Sobol’ indices is to decompose total variance to each variance caused by individual input and combinations of inputs (Homma and Saltelli 1996; Sobol 2001). When I is the unit interval [0, 1], In is the n-dimensional unit hypercube, and let us consider a function f(x) with x = [x1, x2, ⋯, xn] ∈ In which can be formulated as

$$ f\left(\mathbf{x}\right)=f\left({x}_1,{x}_2,\cdots, {x}_n\right)={f}_0+\sum \limits_{i=1}^n{f}_i\left({x}_i\right)+\sum \limits_{i<j}^n{f}_{ij}\left({x}_i,{x}_j\right)+\cdots +{f}_{12\cdots n}\left({x}_1,{x}_2,\cdots, {x}_n\right) $$
(1)

where n is the input dimension. Equation (1) is called ANOVA representation of f(x) if

$$ {\int}_0^1{f}_{ij...h}\left({x}_i,{x}_j,\cdots, {x}_h\right)d{x}_id{x}_j\cdots d{x}_h=0\ \mathrm{for}\ 1\le i<j<\cdots <h\le n. $$
(2)

Equation (2) satisfies

$$ {f}_0=\int f\left(\mathbf{x}\right)d\mathbf{x}, $$
(3a)
$$ {f}_i\left({x}_i\right)=\int f\left(\mathbf{x}\right)\prod \limits_{a\ne i}d{x}_a-{f}_0, $$
(3b)
$$ {f}_{ij}\left({x}_i,{x}_j\right)=\int f\left(\mathbf{x}\right)\prod \limits_{a\ne i,j}d{x}_a-{f}_0-{f}_i\left({x}_i\right)-{f}_j\left({x}_j\right), $$
(3c)

and so on. The total variance of f is defined as

$$ D=\int {f}^2\left(\mathbf{x}\right)d\mathbf{x}-{f_0}^2 $$
(4)

which can be calculated as the sum of partial variances as

$$ D=\sum \limits_i^n{D}_i+\sum \limits_{i<j}^n{D}_{ij}+\cdots +{D}_{12\cdots n} $$
(5)

where the partial variance is calculated as

$$ {D}_{ij\cdots h}=\int {f}_{ij\cdots h}^2d{x}_id{x}_j\cdots d{x}_h\ \mathrm{for}\ 1\le i<j<\cdots <h\le n $$
(6)

Using (5) and (6), Sobol’ indices is defined as

$$ {S}_{ij\cdots h}=\frac{D_{ij\cdots h}}{D}\ \mathrm{for}\ 1\le i<j<\cdots <h\le n $$
(7)

2.2 Gaussian process regression

GPR is one of the most commonly used methods for data-driven modeling (Sun and Sun 2015). Although neural network (NN) is more widely used in data-driven modeling framework, GPR is better suited for computationally expensive cases that cannot provide a large number of samples. There are more reasons why GPR is chosen as a modeling method in this study. The first reason is that GPR is a well-formulated regression method that can cope with noise that results from the effect of removed variables on the original function value. Since the proposed algorithm uses a selective variable subset, the modeling method should be able to handle the noise. The second reason is that the marginal loglikelihood and posterior variance of GPR can be utilized as the variable selection measure.

GPR formulas are constructed as following procedure (Quiñonero-Candela and Rasmussen 2005; Rasmussen 2006; Bastos and O’Hagan 2009; Oakley and O’Hagan 2004). Random function f(x) with zero mean and covariance function k with a hyperparameter set θ in a specified point x is expressed as

$$ f\left(\mathbf{x}\right)\sim GP\left(0,k\left(\mathbf{x},{\mathbf{x}}^{\prime };\boldsymbol{\uptheta} \right)\right). $$
(8)

Assume that there are given m training data, that is, X = [x1, x2, ⋯, xm]T ∈ ℝm × n is a set of training inputs of m observations where each xi ∈ ℝn is the ith training input. Training output y is a noisy version of f(X) defined by y = f(X) + ε where f(X) is the latent function values of Gaussian process since the true noisy-free function value cannot be known, and ε(i) is an independent and identically distributed Gaussian noise. When the signal noise variance is σ2, the joint distribution of y and posterior prediction f∗ on new input X∗ follows multivariate normal distribution as

$$ \left[\begin{array}{c}\mathbf{y}\\ {}{\mathbf{f}}_{\ast}\end{array}\right]\sim N\left(\mathbf{0},\left[\begin{array}{cc}K\left(\mathbf{X},\mathbf{X}\right)+{\sigma}^2\mathbf{I}& K\left(\mathbf{X},{\mathbf{X}}_{\ast}\right)\\ {}K\left({\mathbf{X}}_{\ast },\mathbf{X}\right)& K\left({\mathbf{X}}_{\ast },{\mathbf{X}}_{\ast}\right)\end{array}\right]\right) $$
(9)

where I is the identity matrix and K is defined with \( \mathbf{X}={\left\{{\mathbf{x}}_i\right\}}_{i=1}^v \) and \( \mathbf{XX}={\left\{\mathbf{x}{\mathbf{x}}_j\right\}}_{j=1}^w \) as

$$ K\left(\mathbf{X},\mathbf{XX}\right)=\left[\begin{array}{ccc}k\left({\mathbf{x}}_1,\mathbf{x}{\mathbf{x}}_1\right)& \cdots & k\left({\mathbf{x}}_1,\mathbf{x}{\mathbf{x}}_w\right)\\ {}\vdots & \ddots & \vdots \\ {}k\left({\mathbf{x}}_v,\mathbf{x}{\mathbf{x}}_1\right)& \cdots & k\left({\mathbf{x}}_v,\mathbf{x}{\mathbf{x}}_w\right)\end{array}\right]. $$
(10)

Based on Bayesian approach, the posterior prediction output f∗ on the new input points X∗ can be obtained with conditioning given training data as

$$ {\mathbf{f}}_{\ast}\mid \mathbf{X},\mathbf{y},{\mathbf{X}}_{\ast}\sim N\left({\overline{\mathbf{f}}}_{\ast },\operatorname{cov}\left({\mathbf{f}}_{\ast}\right)\right) $$
(11)

with the posterior mean as

$$ {\overline{\mathbf{f}}}_{\ast }=E\left({\mathbf{f}}_{\ast }|{\mathbf{X}}_{\ast },\mathbf{X},\mathbf{y}\right)=K\left({\mathbf{X}}_{\ast },\mathbf{X}\right){\left[K\left({\mathbf{X}}_{\ast },\mathbf{X}\right)+{\sigma}^2\mathbf{I}\right]}^{-1}\mathbf{y} $$
(12a)

and posterior covariance as

$$ \operatorname{cov}\left({\mathbf{f}}_{\ast}\right)=K\left({\mathbf{X}}_{\ast },{\mathbf{X}}_{\ast}\right)-K\left({\mathbf{X}}_{\ast },\mathbf{X}\right){\left[K\left(\mathbf{X},\mathbf{X}\right)+{\sigma}^2\mathbf{I}\right]}^{-1}K\left(\mathbf{X},{\mathbf{X}}_{\ast}\right). $$
(12b)

Next, a function g(x) of nonzero mean which incorporates f(x) with polynomial function h(x)Tβ is considered as

$$ g\left(\mathbf{x}\right)=h{\left(\mathbf{x}\right)}^{\mathrm{T}}\boldsymbol{\upbeta} +f\left(\mathbf{x}\right) $$
(13)

where h(x)∈Rp×1 is a basis function consisting of p polynomial basis such as 1, x1, x2,..., xn, x12, x22,..., xn2. We obtain the posterior output on the new input X∗ conditioning training data as

$$ {\mathbf{g}}_{\ast}\mid \mathbf{X},\mathbf{y},{\mathbf{X}}_{\ast}\sim N\left({\overline{\mathbf{g}}}_{\ast },\operatorname{cov}\left({\mathbf{g}}_{\ast}\right)\right) $$
(14)

where the posterior mean is

$$ {\displaystyle \begin{array}{l}{\overline{\mathbf{g}}}_{\ast }={{\mathbf{H}}_{\ast}}^{\mathrm{T}}\widehat{\boldsymbol{\upbeta}}+{{\mathbf{K}}_{\ast}}^T{\left[\mathbf{K}+{\sigma}^2\mathbf{I}\right]}^{-1}\left(\mathbf{y}-{\mathbf{H}}^{\mathrm{T}}\widehat{\boldsymbol{\upbeta}}\right),\\ {}\end{array}} $$
(15a)

and posterior covariance is

$$ \mathit{\operatorname{cov}}\left({\mathbf{g}}_{\ast}\right)=\operatorname{cov}\left({\mathbf{f}}_{\ast}\right)+{\left({\mathbf{H}}_{\ast }-\mathbf{H}{\left[\mathbf{K}+{\sigma}^2\mathbf{I}\right]}^{-1}{\mathbf{K}}_{\ast}\right)}^{\mathrm{T}}{\left(\mathbf{H}{\left[\mathbf{K}+{\sigma}^2\mathbf{I}\right]}^{-1}{\mathbf{H}}^T\right)}^{-1}\left({\mathbf{H}}_{\ast }-\mathbf{H}{\left[\mathbf{K}+{\sigma}^2\mathbf{I}\right]}^{-1}{\mathbf{K}}_{\ast}\right) $$
(15b)

where H = [h(x1), h(x2), ⋯]T, H∗ = [h(x1∗), h(x2∗), ⋯]T, K∗ = K(X∗, X),  and K = K(X, X) with cov(f∗) in (12b).

For the parameter estimation, β can be estimated with σ2 and θ as

$$ \widehat{\boldsymbol{\upbeta}}\left(\boldsymbol{\uptheta}, {\sigma}^2\right)={\left({\mathbf{H}}^{\mathrm{T}}{\left[\mathbf{K}+{\sigma}^2\mathbf{I}\right]}^{-1}\mathbf{H}\right)}^{-1}{\mathbf{H}}^{\mathrm{T}}{\left[\mathbf{K}+{\sigma}^2\mathbf{I}\right]}^{-1}\mathbf{y} $$
(16)

where σ2 is the noise variance and θ is a hyperparameter vector of covariance function. The marginal likelihood is the integral of the likelihood times prior over the function values as

$$ p\left(\mathbf{y}|\mathbf{X}\right)=\int p\left(\mathbf{y}|\mathbf{f},\mathbf{X}\right)p\left(\mathbf{f}|\mathbf{X}\right)d\mathbf{f}. $$
(17a)

Since solving (17a) is intractable, plausible analytic solutions to solve (17a) have been suggested (Quiñonero-Candela and Rasmussen 2005; Rasmussen 2006; Bastos and O’Hagan 2009). In this study, we propose to use optimization to obtain the marginal likelihood with hyperparameters as

$$ \left\{\widehat{\boldsymbol{\uptheta}},{\widehat{\sigma}}^2\right\}=\arg \underset{\boldsymbol{\uptheta}, {\sigma}^2}{\max }p\left(\mathbf{y}|\mathbf{X}\right) $$
(17b)

where the loglikelihood with m observations can be approximated as (Rasmussen 2006)

$$ \log p\left(\mathbf{y}|\mathbf{X}\right)=-\frac{1}{2}{\left(\mathbf{y}-\mathbf{H}\widehat{\boldsymbol{\upbeta}}\right)}^{\mathrm{T}}{\left(\mathbf{K}+{\sigma}^2\mathbf{I}\right)}^{-1}\left(\mathbf{y}-\mathbf{H}\widehat{\boldsymbol{\upbeta}}\right)-\frac{m}{2}\log 2\pi -\frac{1}{2}\log \mid \mathbf{K}+{\sigma}^2\mathbf{I}\mid . $$
(17c)

Hence, (17b) can be solved using (16) and (17c).

Predictive posterior variance c(x| X) is the same as cov(g∗) in (15b) except for replacing X∗ with specified single design input x∗. Then, the integrated posterior variance can be calculated as

$$ IVAR=\underset{{\mathbf{x}}_{\ast}\in \chi }{\int }c\left({\mathbf{x}}_{\ast }|\mathbf{X}\right) d\mu $$
(18)

where μ is the PDF of x in space χ. This indicates μ-weighted integration over the design space χ. Through this process, two model performance indices for variable selection, marginal loglikelihood in (17c) and integrated posterior variance in (18), are obtained.

3 Proposed method

The main concept of the proposed method is that the marginal likelihood and integrated posterior variance are used as variable selection criteria. As mentioned in Introduction, the marginal likelihood was used as a variable screening criterion by Welch et al. (Welch et al. 1992), and the integrated posterior variance was reported as the model uncertainty measure by Gorodetsky et al. (Gorodetsky and Marzouk 2016). Hence, the marginal likelihood and the integrated posterior variance can be good measures to check the importance of input variables. Moreover, the integrated posterior variance is utilized for the sequential experimental design criteria at the same time. The following sections explain the proposed algorithm. Section 3.1 shows the basic concept of the proposed method and Sections from 3.2 to 3.5 explain the proposed algorithm in detail. Section 3.6 summarizes the proposed algorithm with a flowchart and Section 3.7 illustrates the proposed process with a simple mathematical example.

3.1 Basic concept of the proposed algorithm

The proposed algorithm distinguishes between essential and unnecessary variables using the Wrapper method (Kohavi and John 1997). The Wrapper method actually creates a surrogate model with a selected variable subset and determines the importance of variables based on the model performance of the surrogate model. When the performance of a GPR model with a certain variable set is clearly superior to models with other variable sets, variables in the set are significantly relevant to the output response and selected as essential variables. The model performance is quantified with (17c) and (18) after the GPR model is built.

Figure 1 visualizes the main concept of the proposed algorithm. Since the functional change almost depends on x1 and x2 has little effect as shown in Fig. 1a, x2 is dispensable for the function. Figure 1b, c shows the function f when it is projected on x2-y and x1-y plane, respectively. The deviation of the GPR model with x2 in Fig. 1b is much larger than the one in Fig. 1c. Hence, it can be seen that f is a function of mainly x1, not x2.

Fig. 1
figure 1

a–c The concept of GPR and essential variable selection

Full size image

The intuitive concept of the proposed algorithm can be more comprehensively explained using (17c) given in the form of normal distribution. The first term of (17c) explains the L2-norm which is a discrepancy between true observation y and Hβ. The last term of (17c) is the log-determinant of the GPR model that means how much data is scattered from the regression. Because Hβ is formulated with low-order polynomials, it is not enough to explain highly nonlinear and noisy response. Therefore, the covariance function handles the remaining elaborate scatter of data. If the data is largely scattered from the prediction, the marginal likelihood becomes small, and the variance becomes large. This is why the marginal likelihood and the integrated variance can be indicators that show whether the data can be well described with essential variables. These two indicators with various variable subsets can be divided distinctly into superior and inferior groups. The validity of two GPR model performances for the variable selection will be demonstrated in Section 3.7 in more detail using an illustrative mathematical example.

3.2 Variable selection algorithm

The subset selection process of the proposed method consists of three core methods: (1) the Wrapper method, (2) agglomerative hierarchical clustering, and (3) forward greedy search. As mentioned in Section 3.1, the Wrapper method is used to measure the importance of variable sets. For the clustering method, agglomerative hierarchical clustering (Bouguettaya et al. 2015) is used to detect essential variables as shown in Fig. 2.

Fig. 2
figure 2

a–d The concept of agglomerative hierarchical clustering

Full size image

In this study, the number of the final clusters is set to two for data bisection, and Euclidean distance and single linkage are adopted as the distance metric and for linkage criterion, respectively. Single linkage criterion is the metric between two groups of A and B expressed as

$$ \mathrm{Linkage}=\min \left(\mathrm{dist}\left(\mathbf{a},\mathbf{b}\right):\mathbf{a}\in \mathbf{A},\mathbf{b}\in \mathbf{B} \right) $$
(19)

where dist(a,b) is Euclidian distance between a and b. Agglomerative hierarchical clustering links the closest data or clusters sequentially based on the linkage metric in (19) until the number of the clusters becomes 2.

Forward greedy search is a subset selection algorithm based on exhaustive search, which means that it finds the best subset by selecting variables one by one sequentially. Figure 3 shows the concept of the proposed variable selection algorithm combining three methods using a 20-dimensional example. As shown in Fig. 3a, forward greedy search is utilized to generate candidate variable sets in each iteration. For each variable, the Wrapper method is used to score the subset importance based on GPR model performances as shown in Fig. 3b, and agglomerative hierarchical clustering is used to distinguish the outstanding variable set which is x12 in Fig. 3b. In the second iteration, the forward greedy search is again applied to test all the combinations of two-variable sets with the selected x12. In this way, the variable selection process continues until the GPR model obtained with selected variables only satisfies predefined accuracy.

Fig. 3
figure 3

a–c The concept of the proposed variable selection algorithm with a 20-dimensional example

Full size image

Different from general greedy forward search that identifies the best subset using optimization, the proposed algorithm utilizes clustering as shown in Fig. 3b, c. Clustering can bisect data into definitely two different clusters. If there exists only one subset in the best cluster, it is classified as an important variable set. In addition, two model performance measures are utilized in the proposed method so that the important variable set which has the maximum of marginal loglikelihood and minimum of integrated posterior variance at the same time is selected. This conservativeness reduces the possibility of faulty variable selection.

Last but not least, the proposed algorithm utilizes two-variable addition when a definitely outstanding variable set does not exist due to strong interaction terms as shown in Fig. 4. This two-variable addition is necessary for two reasons: (1) there are some variables that have high sensitivities when combined with other variables such as interaction terms, and (2) there can be two variables with similar sensitivities, and one variable cannot be distinguished from the other as an outstanding one. After performing two-variable addition, if there exists an outstanding set such as x12 ∪ [x1, x5] as shown in Fig. 4a, the variables in the set are classified into the important variable set. However, if there is no outstanding combination of two variables as shown in Fig. 4b even after two-variable addition, appearances of all the variables that belong to the best cluster (the box of Fig. 4b) are counted. If a variable repeatedly appears in the subsets of the best cluster as shown in Fig. 4c, it is classified as an essential one (x20 in Fig. 4b, c). If there is still no outstanding variable set even after clustering using two-variable addition, the algorithm performs sequential sampling to increase the accuracy of GPR model. Even if two-variable addition method can be easily extended to three or n-variable addition method, the number of variables to be added is restricted to 2 since the computational cost exponentially increases as the number increases.

Fig. 4
figure 4

a–c Two-variable addition method for variable selection

Full size image

Since the proposed method starts with a relatively small number of initial samples, it is possible that the wrong variables could be selected. In other words, a lack of samples or sample quality makes GPR model performance indices unstable which leads to fluctuation of variable importance ranking. Therefore, to avoid possible erratic results, a definitely outstanding variable must be selected that will be performed after outlier detection of the model performance in the proposed method.

3.3 Outlier detection

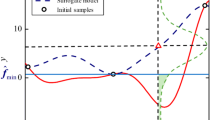
High deviation in the scatter plot of marginal loglikelihood and integrated variance means that the input sample quality or amount is not enough to select an outstanding variable. As shown in Fig. 5, if there exist outliers, one model performance index is improved while the other becomes worse at the outlier points. These outliers can be estimated using deviation from the regression line to the candidate outlier point, and if the deviation is larger than a target number, the point is identified as an outlier. In this study, the target number is set to 0.15 from the 2nd order regression in the normalized space as shown in Fig. 5. Outliers are detected when a GPR model is not accurate enough to be used for variable selection. Hence, once outliers are encountered, a sequential sampling that will be explained in the next section needs to be performed to increase the accuracy of the model.

Fig. 5
figure 5

Outlier detection in the normalized space of GPR model performances

Full size image

3.4 Sequential sampling criterion for GPR model

In the proposed method, Latin hypercube sampling (LHS) that is a moderate level of sampling is utilized for initial sample generation in GPR modeling. However, there are two cases where the proposed algorithm performs sequential sampling in addition to the initial samples: (1) when an outlier exists in the model performances and (2) when accuracy of the model built with the current subset does not meet the target value, which means all of the important variables are not selected yet. For sequential sampling criterion, the method of a previous research (Gorodetsky and Marzouk 2016) that minimizes integrated posterior variance (IVAR) for GPR sampling is adopted in this study. In their research, it was explained that the IVAR criterion is equivalent to an expected integrated mean squared error (IMSE) of the posterior mean. The integrated posterior variance can be calculated using (18). According to the IVAR criterion, a new point xa for sequential sampling can be obtained as

$$ {\mathbf{x}}_a=\underset{\mathbf{x}\in \mathbf{U}}{\mathrm{argmin}}\int c\left(\mathbf{x}|\mathbf{X}\right) d\mu \approx \underset{\mathbf{x}\in \mathbf{U}}{\mathrm{argmin}}\frac{1}{N}\sum \limits_{i=1}^Nc\left(\mathbf{x}|\mathbf{X}\right) $$
(20)

where U is the feasible design space and N is the number of Monte Carlo samples. If the integration in (20) is computationally expensive, xb can be used to find a new sample point instead of (20) as

$$ {\mathbf{x}}_b=\underset{\mathbf{x}\in \mathbf{U}}{\mathrm{argmax}}c\left(\mathbf{x}|\mathbf{X}\right) $$
(21)

which searches for a point of the highest posterior variance.

3.5 GPR model accuracy measure

To build a GPR model with reduced dimension as explained in Section 2.2, X, an n × m matrix of current input samples where n denotes the number of sample and m denotes the dimension, is reduced to selected columns as X = X(:, subset) where subset denotes the selected variables. At the end of each iteration, the accuracy of the GPR model built with the subset is calculated using cross validation error (CVE) with the normalized root mean squared error (n–rmsecve) that is expressed as

$$ n- rms{e}_{\mathrm{cve}}=\frac{1}{\left({y}_{\mathrm{max}}-{y}_{\mathrm{min}}\right)}\sqrt{\frac{1}{N_{\mathrm{samp}}}\sum \limits_{i=1}^{N_{\mathrm{samp}}}{e_i}^2},{e}_i={y}_i-{\widehat{f}}_{\sim i}\left({\mathbf{x}}_i\right) $$
(22)

where ymax and ymin are the maximum and minimum output of the true training output, respectively, Nsamp is the number of training samples, \( {\widehat{f}}_{\sim i} \) is the response from the surrogate model built without the ith sample, and yi is the true output evaluated at the ith sample. As a stop criterion of the algorithm, n–rmsecve in (22) is utilized. However, to avoid premature convergence, two more samples are sequentially added to build additional GPR models once the GPR model satisfies the accuracy condition (n–rmsecve < 0.05). Then, if all three GPR models satisfy the target accuracy, the algorithm stops.

When additional test samples are available, (22) is modified as

$$ n- rmse=\frac{1}{\left({y}_{\mathrm{max}}-{y}_{\mathrm{min}}\right)}\sqrt{\frac{1}{N_{\mathrm{samp}}}\sum \limits_{i=1}^{N_{\mathrm{samp}}}{e_i}^2},{e}_i={y}_i-\widehat{f}\left({x}_i\right) $$
(23)

where \( \widehat{f} \) is the response from the surrogate model built with all samples. Note that different from (22), ymax and ymin represent the maximum and minimum of the test output, respectively, and Nsamp is the number of test samples in this case.

3.6 Overall algorithm

The overall process and pseudocode in Matlab form of the proposed algorithm explained in Sections 3.2~3.5 are presented in this section, and its flowchart is shown in Fig. 6.

  • Step 1: Generate (2n + 1) initial samples using LHS where n is the problem dimension.

  • Step 2: Construct candidate variable subsets using forward greedy search. In the initial iteration, the candidate variable subsets are (x1), (x2),...(xn). Continue to construct candidate variable subsets including selected variables.

  • Step 3: Using the constructed subsets in Step 2 and given samples, build GPR models and evaluate their model performances using the Wrapper method.

  • Step 4: Carry out outlier detection using the model performances obtained in Step 3. If outliers are detected, perform sequential sampling and return to Step 2.

  • Step 5: Perform clustering in the normalized space of two GPR model performances using the agglomerative hierarchical clustering.

  • Step 6: If there is no outstanding variable set identified after the clustering, perform two-variable addition in Step 2. If there is no outstanding variable set even after the two-variable addition, perform sequential sampling and return to Step 2.

  • Step 7: Evaluate the accuracy of the GPR model built with the selected variables and check the stopping criterion by Section 3.5.

  • Step 8: If the model satisfies the stopping criterion, then stop. Otherwise, repeat Steps 2 to 7 until the model accuracy is satisfied.

Fig. 6
figure 6

Flowchart of the proposed algorithm

Full size image
figure a

3.7 An illustrative mathematical example for the proposed algorithm

For a better understanding of the proposed method and validity check of GPR model performances for variable selection, an illustrative example is utilized in this section given by

$$ f\left(\mathbf{x}\right)=200{x_1}^2+250{x}_2{x}_3+90{x_4}^2+60{x_5}^2+10{x}_6,{x}_i\in \left[0,1\right]\ \mathrm{for}\ \mathrm{all}\ i=1,...,6. $$
(24)

This example includes an interaction term of x2x3 for which the two-variable addition explained in Section 3.5 is required. The number of initial samples is 600, which is 100 times the problem dimension, to remove the necessity of sequential sampling.

A previous research (Campolongo et al. 2007) developed a new sensitivity index and compared it with Sobol’ indices. Similarly, we will show that there exists a monotonic relationship between GPR model performances and Sobol’ indices using the illustrative example. As shown in Fig. 7a, b, there are monotonic relationships between the Sobol’ indices and loglikelihood and Sobol’ indices and integrated variance, respectively. This validates that two GPR model performances can replace Sobol’ indices, which is very computationally expensive to obtain for variable selection.

Fig. 7
figure 7

a and b A monotonic relationship between two GPR model performances and Sobol’ indices

Full size image

Clustering results of successive iterations are shown in Fig. 8. It can be easily seen in Fig. 8a that x1 is selected as an essential variable in the 1st iteration. In the 2nd iteration as shown in Fig. 8b, no one outstanding variable set exists due to the strong interaction between x2 and x3. Therefore, two-variable addition is performed, and x2 and x3 are included in the important variable set as shown in Fig. 8c. In the 3rd iteration, x4 is added to the important variable set as shown in Fig. 8d. This variable selection process is summarized in Fig. 9. At the end of the 3rd iteration, the GPR model built with the subset (x1,x2,x3,x4) satisfies the target accuracy, that is, n-rsmecve < 0.05, and thus the algorithm stops. Since the influence of x5 and x6 is ignorable as shown in Fig. 10, the GPR model with only four variables can replace the original 6-dimensional model without loss of accuracy.

Fig. 8
figure 8

a–d Variable selection process for illustrative example in (24)

Full size image
Fig. 9
figure 9

Variable selection process and model accuracy in each iteration

Full size image
Fig. 10
figure 10

Sobol’ indices of illustrative example in (24)

Full size image

This example intentionally eliminates the possibility of sequential sampling by using a sufficiently large number of initial samples which means there will be no outlier detected during the process. To test the proposed algorithm in the case of a small number of initial samples, 13(= 2n + 1) initial samples by uniform random sampling and LHS are generated in 6-dimensional space as shown in Fig. 11a, b, respectively. From Fig. 11, it can be seen that LHS shows better space-filling capability compared with uniform random sampling meaning that sample quality by LHS is better than the one by uniform random sampling.

Fig. 11
figure 11

Experimental design of a uniform random sampling and b LHS

Full size image

Figure 12a–c is the results generated from uniform random sampling and Fig. 12d is the result generated from LHS. Figure 12a shows there exists an outlier due to the poor sample quality whereas there is no outlier in Fig. 12c with the same sampling method since sufficient samples are used. It can be seen that sequential sampling reduces the deviation in Fig. 12a as shown in Fig. 12b and thus removes the outlier. This means that sequential sampling can alleviate instability of model performances caused by poor sample quality. This test also verifies the importance of initial sampling which is the reason why LHS is used in this study. As shown in Fig. 12d, there is no outlier in the GPR model generated using 13 samples with LHS.

Fig. 12
figure 12

Normalized GPR performances generated by a uniform random 13 samples, b uniform random 13 samples + 1 sequential sample, c uniform random 600 samples, and d Latin hypercube 13 samples

Full size image

4 Numerical examples

The usefulness of the proposed algorithm can be quantified by the accuracy of variable selection, final model accuracy, and the number of final samples used. The proposed algorithm is tested with two examples that have different properties. These examples verify the excellent performance of the proposed algorithm with high model accuracy and with a small number of samples.

4.1 Mathematical example

Welch et al. performed variable screening for a 20-dimensional and highly nonlinear mathematical example given by (Welch et al. 1992)

$$ f\left(\mathbf{x}\right)=\frac{5{x}_{20}}{1+{x}_1}+5{\left({x}_4+{x}_{20}\right)}^2+{x}_5+40{x_{19}}^3-5{x}_{19}+0.05{x}_2+0.08{x}_3-0.03{x}_6+0.03{x}_7-0.09{x}_9-0.01{x}_{10}-0.07{x}_{11}+0.25{x_{13}}^2-0.04{x}_{14}+0.06{x}_{15}-0.01{x}_{17}-0.03{x}_{18},{x}_i\in \left[-\mathrm{0.5,0.5}\right]\ \mathrm{for}\ \mathrm{all}\ i=1,\dots, 20. $$
(25)

from which it can be seen that there exist interaction terms as well as nonlinear terms. The Sobol’ indices of variables of this example obtained using one million samples are shown in Fig. 13. As shown in Fig. 13, x12 is the most important variable, and x12, x4, x20, x19, x1, and x5 could be selected as essential variables.

Fig. 13
figure 13

Sobol’ indices of the example in (25)

Full size image

The result of the proposed algorithm is summarized in Fig. 14 and Table 1. From the figure, it is shown that x12, x20, x19, x4, x5, and x1 are sequentially selected which is identical with the result of the Sobol’ indices. It can also be seen that the variables with low Sobol’ indices such as (x1, x5) are identified later than the ones with high indices such as (x4, x12, x19, x20). n–rmsecve of the GPR model built with the selected variables is lower than 0.05 with 54 samples; however, 55th and 56th samples are used to avoid premature convergence of model accuracy. Hence, total samples used are 56, which is only 0.0058% of those of the Sobol’ indices, while the variable selection results are identical verifying that the proposed method selects essential variables accurately and efficiently.

Fig. 14
figure 14

Sequential variable selection process of (25)

Full size image
Table 1 Variable selection results of (25)
Full size table

It should be noted that the GPR model generated using the proposed method is much more accurate than the surrogate model of full dimensions especially when the number of samples used is small as shown in Fig. 15. The full-dimension surrogate model requires more than 150 maximin LHS samples to satisfy the model accuracy criterion while the proposed method requires only 56 LHS samples. n–rmse in Fig. 15 is calculated with additionally generated 100 test samples. In conclusion, the more accurate surrogate model is generated in this example using the proposed algorithm with less number of samples by removing unnecessary variables.

Fig. 15
figure 15

Comparison of model accuracy between conventional and proposed methods of (25)

Full size image

4.2 Engineering example

Cho et al. carried out statistical variable screening using 11 functions with 44 variables which are nine vehicle safety performances and two noise, vibration, and harshness (NVH) performances as listed in Table 2 (Cho et al. 2016). Six variables (x1~x5 and x8) are common variables for all 11 functions, and two variables (x6 and x7) are for safety only, and the other 36 variables are for NVH. All the 44 input variables correspond to the steel plate thickness of each part of the vehicle NVH model. As shown in Fig. 16, many variables in G11 have very similar and low Sobol’ indices meaning that the indices are not easily distinguishable. For the reason, G11 is selected among 11 functions to validate the proposed algorithm.

Table 2 Function definition
Full size table
Fig. 16
figure 16

Sobol’ indices for G11 of engineering example

Full size image

The result of the proposed method is summarized in Table 3. In 13 iterations, 13 variables among 44 are selected as essential variables. This result is identical with variable selection by the Sobol’ indices as shown in Table 4. The total number of samples used is 105 which is very efficient considering that conventional surrogate models with full dimension would use at least 132 samples (3n) as the initial sample.

Table 3 Variable selection results of the engineering example
Full size table
Table 4 Rank of Sobol’ indices and variable selection results of engineering example
Full size table

The accuracy of the GPR model built with the selected variables is compared with the full-dimensional model in Fig. 17. Since the variables are not highly correlated and the original model is very accurate with only 100 samples in this example, the accuracy of the full-dimensional model is similar to the one of the reduced GPR model. However, since users do not know how many samples are required for the model in advance, the proposed method can be regarded as a meaningful preprocess for general-purpose-use.

Fig. 17
figure 17

Model accuracy comparison between the conventional and proposed model of the engineering example

Full size image

5 Conclusion

In this paper, we present an efficient variable selection methodology to overcome the curse of dimensionality in surrogate modeling. GPR is used for the surrogate modeling, and marginal loglikelihood and integrated posterior variance are used as measures to select essential variables according to the Wrapper method. Variables that induce high marginal loglikelihood and low integrated posterior variance in surrogate modeling are selected as essential variables. To find essential variables systematically, the greedy forward search has been modified and utilized. Agglomerative hierarchical clustering is adopted to distinguish essential variables and the others clearly. When essential variables cannot be identified clearly due to a limited number of samples in each algorithm loop, adaptive samples are sequentially added to increase the accuracy of GPR models. Major contribution of the proposed algorithm is that it effectively reduces required number of samples for surrogate modeling when the fraction of dispensable variables is high since the number of samples depends only on essential variables in the proposed method. Another advantage is that the algorithm is less dependent on the initial sample quality since sequential sampling is utilized. In addition, it can carry out both variable selection and surrogate modeling simultaneously. The proposed algorithm was verified with two numerical examples with high dimensions and challenging properties. A numerical study shows that with a much smaller number of samples variable selection accuracy is almost the same with the Sobol’ indices, and the GPR model shows similar or better accuracy than the conventional full-dimension model.