An efficient method for statistical moments and reliability assessment of structures

Abstract

The probability density function (PDF) of a performance function can be constructed from the perspective of first four statistical moments, and the failure probability can be evaluated accordingly. Since the shifted generalized lognormal distribution (SGLD) model will be fitted to recover the PDF based on the first four statistical moments, the evaluation of statistical moments of the performance function is of critical significance for the structural reliability analysis. This paper presents a new method for statistical moments and reliability assessment of structures with efficiency and accuracy, especially when large variabilities in the input random vector and nonlinearities are considered . First, a numerical method is established based on rotating the points in the quasi-symmetric point method (Q-SPM), which is very efficient for evaluating the statistical moments. This numerical method is called the rotational quasi-symmetric point method (RQ-SPM). The optimal angles of rotation in RQ-SPM can be determined via an optimization problem, where the objective function is adopted as minimizing the differences between the marginal moments of input random variables estimated by the points after rotation and their exact values. By doing so, the information of marginal distributions and their tail distributions could be better reproduced, which is of paramount importance to the statistical moments assessment of the performance function, especially for the high-order moments. Once the statistical moments are available, the PDF of the performance function can be recovered by the SGLD model. Finally, the failure probability can be evaluated by a simple integral over the PDF of the performance function. Several numerical examples are given to demonstrate the efficacy of the proposed method. Comparisons of the new method, the original Q-SPM, the univariate dimension reduction method (UDRM) and the bivariate dimension reduction method (BDRM) are also made on the statistical moments assessment. The results manifest the accuracy and efficiency of the proposed method for both the statistical moments and reliability assessment of structures.

1 Introduction

Probabilistic and non-probabilistic reliability problems (Wang et al. 2011, 2016, 2017; Qiu and Wang 2016) are always concerned in practical engineering. In probabilistic reliability assessment, recovering the probability density function (PDF) of the performance function of uncertain structural systems is essential (Franko and Nagode 2015), which arises in a diverse field of engineering practices. There are usually two kinds of methods to deal with this problem. The first is the probability density evolution method (PDEM), which straightforwardly derives the PDF of a performance function via a partial differential equation (Li and Chen 2009; Chenn and Yuan 2014a, 2014b; Chen et al. 2016; Xu and Li 2016; Xu et al. 2016). The other is the indirect method from a finite number of statistical moments such as the Edgeworth series (Wallace 1958), the orthogonal expansion method (Winterstein 1988; Winterstein and Kashef 2000; Choi and Sweetman 2010), and the maximum entropy method (Zhang and Pandey 2013, 2014; Xu 2016; Xu et al. 2016, 2017; Xu and Wang 2017; Xu and Kong 2018), etc.. It is well-known that the first four central moments, i.e. the mean, standard deviation, skewness and kurtosis are widely employed in the indirect methods because they embody the bulk of the probabilistic information. However, each of these indirect methods has its own peculiarities. For example, the Edgeworth series has the weakness of being positive definite and stable only under certain conditions. The orthogonal expansion method is a monotonic transformation of the normal distribution, however, the monotonic transformation does not hold for certain combinations of skewness and kurtosis. The maximum entropy method with four integer-order statistical moments as constraints may not be able to provide accurate tail distribution. Recently, a new distribution model, named as shifted generalized lognormal distribution (SGLD) has been developed for fitting the first four central moments (Low 2013). This distribution almost encompasses the entire skewness-kurtosis region permissible for uni-modal densities. In this regard, this distribution model has high flexibility in shape and is able to model several well known distributions as well as actual datasets. Particularly, the distribution tail can be reproduced by SGLD model with favorable accuracy, which is closely related to the evaluation of failure probability, especially when the small failure probability is concerned. In the present paper, the SGLD model is employed to reconstruct the PDF of the performance function by fitting the first four central moments for structural reliability analysis. Then, the efficient estimation of statistical moments of the performance function plays an important role in this method.

The estimation of statistical moments, especially for the high-order moments is always a challenging task. This is because the high-order moments are invariably to analyze, and they exhibit greater variability when sampled. Several methods have been developed for evaluating the statistical moments. The first is the Taylor expansion method (Ibrahim 1987; Singh and Lee 1993), which requires the computation of derivatives of the performance function. Since the derivatives of the implicit performance function are difficult to obtain, this method could not be applicable to general cases. Instead, the point estimate method (PEM) (Hong 1998; Zhao and Ono 2000), which is a derivative free approach, is employed to evaluate the statistical moments based on a weighted summation of the performance function at a finite number of points. However, it is quite difficult to keep the tradeoff of accuracy and efficiency by using the PEM for general purpose. For example, the number of points grows exponentially if the PEM developed by Rosenblueth is applied (Rosenblueth 1975); low accuracy could be encountered if the PEM developed by Zhao and Ono (2000) is employed for strongly nonlinear problems. The third is the dimension reduction method (DRM), which decomposes a multivariate function into several low-dimensional functions (Xu and Rahman 2004; Rahman and Wei 2006; Li and Zhang 2011). In this regard, the statistical moments can be evaluated by several low-dimensional numerical integrations. The most commonly used DRMs are the univariate dimension reduction method (UDRM) and the bivariate dimension reduction method (BDRM). Since the high-order terms are included in the residue error, the UDRM may not be able to accurately capture the statistical moments of the performance function involving multiple random variables. Although the BDRM is much more accurate, the computational effort could be prohibitively large when the number of random variables increases (Fan et al. 2016). The fourth is the multi-dimensional numerical integration method, where the tensor product method (Isaacson and Keller 1994; Xu et al. 2012) and the sparse grid method (Xiong et al. 2009) could be widely found. Despite achieving good accuracy, these methods may still consume large computational effort for estimating the statistical moments. Alternatively, some efficient cubature formulas with fixed algebraic accuracy (Xu and Lu 2017) and unscented transformation (Xiao and Lu 2016, 2017) have been well developed and investigated for statistical moments assessment. Unfortunately, when the variabilities of basic random variables are large and strong nonlinearities are involved in the performance function, these methods may not be able to achieve the tradeoff of efficiency and accuracy to estimate the statistical moments, especially for the skewness and kurtosis. The errors in estimating the high-order moments could further induce the incorrect reliability results when these moments are substituted into the SGLD model. In some circumstances, the accuracy of using the first two moments, which are easy to be accurately and efficiently obtained, for moments based reliability analysis, e.g. FORM, SORM, may be even better. Nevertheless, for general purposes, the method, which can evaluate the first four central moments with the tradeoff of efficiency and accuracy, still needs to be developed.

The objective of the present paper is to develop a new method for statistical moments and reliability assessment of structures with efficiency and accuracy, especially when large variabilities in the input random vector and nonlinearities are addressed. This paper is organized as follows. In Section 2, the formulation of the statistical moments based on a family of quasi-symmetric point method (Q-SPM) is introduced. Then, in Section 3, a new rotational quasi-symmetric point method (RQ-SPM) is proposed to evaluate the statistical moments of the performance function with accuracy and efficiency. Section 4 devotes to introducing the SGLD model to reconstruct the PDF of the performance function based on the statistical moments for structural reliability analysis. Several numerical examples are investigated to validate the proposed method in Section 5. The final section contains some concluding remarks.

2 Statistical moments assessment based on quasi-symmetric point method

Without loss of generality, the performance function of a random structural system is denoted as

$$ Z = G\left( {\mathbf{X}} \right)\ $$

(1)

where Z is the performance function of concern, G is a deterministic operator and ${\mathbf {X}}=[X_{1},X_{2},X_{3}...,X_{d}]^{T}$ is a d-dimensional random vector involved in the random system, whose joint PDF is known as $p_{\mathbf {X}}(\textbf {x})$. Since correlated non-normal random variables can be transformed to be independent standard normal random variables, which are denoted as ${\mathbf {U}}=[U_{1},U_{2},U_{3}...,U_{d}]^{T}$, (1) can be written as

$$ Z = G\left( {\mathbf{X}} \right) = G\left( {{T^{- 1}}\left( {\mathbf{U}} \right)} \right)\ $$

(2)

where $T^{-1}$ represents the inverse Nataf transformation (Li et al. 2008).

Then, the statistical moments, here denoted as the first four central moments, of Z can be approximated by a weighted summation of a set of deterministic function evaluations at a finite number of integration points such that (Cools 2003; Xu et al. 2012; Xu and Lu 2017)

$$ {\mu_{Z}}{{ = E}}\left[ Z \right] = {\int}_{- \infty }^{+ \infty } {G\left( {{T^{- 1}}({\mathbf{u}})} \right){p_{\mathbf{U}}}\left( {\mathbf{u}} \right)} d{\mathbf{u}} = \sum\limits_{j = 1}^{N} {{a_{j}}} G\left[ {{T^{- 1}}\left( {{{\mathbf{u}}_{j}}} \right)} \right]\ $$

(3)

$$ \begin{array}{l} {\sigma_{Z}^{2}} = {\int}_{- \infty }^{+ \infty } {{{\left( {Z - {\mu_{Z}}} \right)}^{2}}{f_{Z}}\left( z \right)} dz\\ = E\left[ {{Z^{2}}} \right] - {\left( {E\left[ Z \right]} \right)^{2}}\\ = {\int}_{- \infty }^{+ \infty } {{G^{2}}\left( {{T^{- 1}}({\mathbf{u}})} \right){p_{\mathbf{U}}}\left( {\mathbf{u}} \right)} d{\mathbf{u}} - {\mu_{Z}}^{2}\\ = \sum\limits_{j = 1}^{N} {{a_{j}}} {G^{2}}\left[ {{T^{- 1}}\left( {{{\mathbf{u}}_{j}}} \right)} \right] - {\mu_{Z}}^{2} \end{array}\ $$

(4)

$$ \begin{array}{l} \begin{array}{l} {\alpha_{3Z}} = \left\{ {{\int}_{- \infty }^{+ \infty } {{{\left( {Z - {\mu_{Z}}} \right)}^{3}}{f_{Z}}\left( z \right)} dz} \right\}/{\sigma_{Z}^{3}}\\ = \left\{ {E\left[ {{Z^{3}}} \right] - 3E\left[ {{Z^{2}}} \right]{\mu_{Z}} + 2{\mu_{Z}}^{3}} \right\}/{\sigma_{Z}^{3}}\\ = \left\{ {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{3}}\left[ {{T^{- 1}}\left( {{{\mathbf{u}}_{j}}} \right)} \right] - 3\left\{ {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{2}}\left[ {{T^{- 1}}\left( {{{\mathbf{u}}_{j}}} \right)} \right]} \right\}{\mu_{Z}} + 2{\mu_{Z}}^{3}} \right\}/{\sigma_{Z}^{3}} \end{array}\ \end{array}\ $$

(5)

$$ \begin{array}{*{20}{l}} {{\alpha_{4Z}} = \left\{ {{\int}_{- \infty }^{+ \infty } {{{\left( {Z - {\mu_{Z}}} \right)}^{4}}{f_{Z}}\left( z \right)} dz} \right\}/{\sigma_{Z}^{4}}}\\ { = \left\{ {E\left[ {{Z^{4}}} \right] - 4E\left[ {{Z^{3}}} \right]{\mu_{Z}} + 6E\left[ {{Z^{2}}} \right]{\mu_{Z}}^{2} - 3{\mu_{Z}}^{4}} \right\}/{\sigma_{Z}^{4}}}\\ { = \left\{ \begin{array}{l} \sum\limits_{j = 1}^{N} {{a_{j}}} {G^{4}}\left[ {{T^{- 1}}\left( {{{\mathbf{u}}_{j}}} \right)} \right] - 4\left\{ {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{3}}\left[ {{T^{- 1}}\left( {{{\mathbf{u}}_{j}}} \right)} \right]} \right\}{\mu_{Z}}\\ + 6\left\{ {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{2}}\left[ {{T^{- 1}}\left( {{{\mathbf{u}}_{j}}} \right)} \right]} \right\}{\mu_{Z}}^{2} - 3{\mu_{Z}}^{4} \end{array} \right\}/{\sigma_{Z}^{4}}} \end{array}\ $$

(6)

where $\mu _{Z}$, $\sigma _{Z}$, $\alpha _{3Z}$ and $\alpha _{4Z}$ are the mean, standard deviation, skewness and kurtosis of Z, respectively; ${p_{\textbf {U }}}\left ({\mathbf {u}} \right ) = \prod \limits _{i = 1}^{d} {{p_{{U_{^{i}}}}}\left ({{u_{^{i}}}} \right )} = \frac {1}{{{{\left ({\sqrt {2\pi } } \right )}^{d}}}}\exp \left ({ - \frac {{{{\mathbf {u}}^{T}}{\mathbf {u}}}}{2}} \right )$ is the joint PDF of random vector $\mathbf {U}$; $a_{j}$s are the constant weights and ${\mathbf {u}}_{j}$s are the integration points in the d-dimensional infinite random-variate space.

Then, the determination of the constant weights and the integration points is of paramount importance to the tradeoff of efficiency and accuracy for evaluating the statistical moments. It is noted that Gaussian weighted multi-dimensional integrals are actually involved in (3)–(6). In this regard, the numerical methods suitable for the Gaussian weighted multi-dimensional integral, i.e.

$$ I\left[ f \right] = {\int}_{- \infty }^{+ \infty } {\frac{1}{{{{\left( {\sqrt {2\pi } } \right)}^{d}}}}} \exp \left( { - \frac{{{{\mathbf{u}}^{T}}{\mathbf{u}}}}{2}} \right)f\left( {\mathbf{u}} \right)d{\mathbf{u}} = \sum\limits_{j = 1}^{N} {{a_{j}}} f\left( {{{\mathbf{u}}_{j}}} \right)\ $$

(7)

could be applied to evaluate the moments, where f is an arbitrary integrand. Besides, the methods, which can give satisfactory accuracy with a small number of deterministic evaluations, are highly desirable.

Recently, a family of quasi-symmetric point method (Q-SPM) has been developed by Victoir based on the orthogonal arrays and invariant theory (Victoir 2004; Xu et al. 2012) for the Gaussian weighted numerical integration. This method is also referred to as the thinned cubature (Bernardo 2015). The following will give the points and weights in Q-SPM for integrations over the entire space $\mathbb {R}_{d}$ with weight function p_U (u). The index “Perm” designates a set of fully symmetric points, generated by permutation of coordinates and their sign. For example, $(r,0,0)_{Perm}$ represents the six points $(\pm r,0,0)$, $(0,\pm r,0)$ and $(0,0,\pm r)$.

When $d \geq 3$, the two symmetric point sets ${\mathbf {P}}_{0}$ and ${\mathbf {P}}_{1}$ together with respective weights $A_{0}$ and $A_{1}$ involved in the Q-SPM are given as

$$ {{\mathbf{P}}_{0}} = {\left( {r,0,...,0} \right)_{Perm}}\begin{array}{*{20}{c}} {}&{{A_{0}}} \end{array}\ $$

(8)

$$ {{\mathbf{P}}_{1}} = {\left( {s,s,...,s} \right)_{Perm}}\begin{array}{*{20}{c}} {}&{{A_{1}}} \end{array}\ $$

(9)

where the parameters are

$$ r = \sqrt {\frac{{d + 2}}{2}} ,\begin{array}{*{20}{c}} {}&{s = } \end{array}\sqrt {\frac{{d + 2}}{{d - 2}}} \ $$

(10)

and

$$ {A_{0}} = \frac{{8d}}{{{{\left( {d + 2} \right)}^{2}}}}\begin{array}{*{20}{c}} {}&{{A_{1}} = } \end{array}\frac{{{{\left( {d - 2} \right)}^{2}}}}{{{{\left( {d + 2} \right)}^{2}}}}\ $$

(11)

where $A_{0}+A_{1}= 1$.

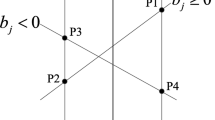
It is noted that a total of $2d + 2^{d}$ points are involved in these two fully symmetric point sets, where the set of $2^{d}$ points in ${\mathbf {P}}_{1}$ have a product structure and the same weight. By using the point sets and weights above in the numerical integration, the 5-th degree of algebraic(polynomial) accuracy could be achieved. However, the number of points grows exponentially with the dimension in ${\mathbf {P}}_{1}$, which may results in prohibitively large computational efforts. Based on the orthogonal arrays and invariant theory, the number of points in ${\mathbf {P}}_{1}$ can be reduced, where the 5-th degree of algebraic accuracy is still ensured. That means a subset of points in ${\mathbf {P}}_{1}$, which is called the quasi-symmetric point set, is actually adequate for the numerical integration (see Fig. 1 for a two-dimensional illustration). In this regard, this method for the numerical integration is called the quasi-symmetric point method (Q-SPM). The number of points in quasi-symmetric point set is $2^{k}$ with $k\leq d$ and the total number of points in Q-SPM is $2d + 2^{k}$. For practical applications, the exponent k is given in Table 1 when 3 ≤ d ≤ 24.

Fig. 1

Quasi-symmetric points in two-dimensional space

Table 1 Exponent k as a function of dimension d

Then, the integration points in Q-SPM can be given as

$$ {{\mathbf{u}}_{j}} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {r,0,...,0} \right)}_{Perm}},\begin{array}{*{20}{c}} {}&{j = 1,2..,2d} \end{array}}\\ {{{\left( {s,s,...,s} \right)}_{Perm}},\begin{array}{*{20}{c}} {}&{j = 2d + 1,2d + 2..,2d + {2^{k}}} \end{array}} \end{array}} \right.\ $$

(12)

For example, if $d = 6$ is considered, the integration points are u₁ = (2,0,...,0), u₂ = (0,2,...,0), ...u₆ = (0,0,...,2), u₇ = (− 2,0,...,0), ...u₁₂ = (0,0,...,− 2), u₁₃ = (2,2,...,2), u₁₄ = (2,− 2,...,2), ...u₄₈ = (− 2,− 2,...,− 2).

Correspondingly, the weight for each integration point could be expressed as

$$ {a_{j}} = \left\{ {\begin{array}{*{20}{c}} {4/{{(d + 2)}^{2}},\begin{array}{*{20}{c}} {}&{j = 1,2..,2d} \end{array}}\\ {\begin{array}{*{20}{c}} {{{(d - 2)}^{2}}/\left[ {{2^{k}}{{(d + 2)}^{2}}} \right],}&{j = 2d + 1,2d + 2..,2d + {2^{k}}} \end{array}} \end{array}} \right.\ $$

(13)

where $a_{j}>0$ and ∑ a_j = A₀ + A₁ = 1.

In this regard, the integration points together with their weights in Q-SPM can be employed to numerically evaluate the statistical moments in (3)–(6). It can be found that when $d \leq 7$, only tens of integration points are required; when $8 \leq d\leq 20$, hundreds of points are adequate for the numerical integration; and when 21 ≤ d ≤ 24, only one thousand of integration points are generated to obtain the moments. This feature demonstrates the high efficiency of Q-SPM. Nevertheless, it was still found in Ref. Chen and Zhang (2013) that the Q-SPM may not be accurate enough even for estimating the standard deviation of response. That may be because the quasi-symmetry and sparseness of this method leads to the marginal PDF, especially the tail distribution, cannot be sufficiently captured (Chen and Zhang 2013). To resolve this problem, several rotational quasi-symmetric point methods (RQ-SPM) have been developed, e.g. GF-discrepancy based RQ-SPM (Chen and Zhang 2013) and fractional moments based RQ-SPM (Xu et al. 2017). Unfortunately, these RQ-SPMs may not be applicable to accurately evaluate the high-order moments (α_3Z and $\alpha _{4Z}$) although they perform quite well to obtain the mean and standard deviation and fractional moments of response (Chen and Zhang 2013). The reason is that the integrands for the high-order moments (5) and (6) could be oscillatory functions, which are much more complicated than those for the low-order moments. In this regard, a new RQ-SPM will be explored for estimating the statistical moments of the performance function, especially for the high-order moments.

3 Marginal moments based rotational quasi-symmetric point method

As is mentioned, the marginal PDFs and their tails of input random vector could be better reproduced by rotating the integration points in Q-SPM, which is of paramount importance to the accurate numerical evaluation of the statistical moments of the performance function. The Givens transform is actually employed to rotate these points in multi-dimensional random-variate space. If the point u_j = (u_1,j,u_1,j,...u_d,j) in Q-SPM is counterclockwise rotated in the two-dimensional $(k,l)$ plane by an angle $\theta$ (in rad), then the point after rotation is (Chen and Zhang 2013)

$$ {{\tilde{\mathbf{ u }}}_{j}} = {{\mathbf{W}}_{kl}}\left( \theta \right){{\mathbf{u}}_{j}}\ $$

(14)

where ${{\tilde {\mathbf { u }}}_{j}}$ denotes the point after rotation and ${\mathbf {W}}_{kl}$ is the rotational matrix in the $(k,l)$ plane, given by (Chen and Zhang 2013)

$$ \begin{array}{l} {{\mathbf{W}}_{kl}}\left( \theta \right) = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1\\ \vdots \end{array}}\\ 0\\ \vdots \end{array}}\\ 0\\ {\vdots} \\ 0\end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {...}\\ \ddots \end{array}}\\ {...}\\ {} \end{array}}\\ {...}\\ {}\\ {...} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0\\ \vdots \end{array}}\\ {\cos \theta }\\ \vdots \end{array}}\\ {\sin \theta }\\ {\vdots} \\ 0\end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {...}\\ {} \end{array}}\\ {...}\\ \ddots \end{array}}\\ {...}\\ {}\\ {...} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0\\ \vdots \end{array}}\\ { - \sin \theta }\\ \vdots \end{array}}\\ {\cos \theta }\\ {\vdots} \\ 0\end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {...}\\ {} \end{array}}\\ {...}\\ {} \end{array}}\\ {...}\\ {\ddots} \\ {...} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0\\ \vdots \end{array}}\\ 0\\ \vdots \end{array}}\\ 0\\ {\vdots} \\ 1\end{array}} \right]\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}\\ {} \end{array}}\\ {{k-_{}}t{h_{}}~row}\\ {} \end{array}}\\ {{l-_{}}t{h_{}}~row}\\ {}\\ {} \end{array}\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{}&{{~~~~~~~~~~~~~~~~~~~k-_{}}t{h_{}}~column} \end{array}}&{{~~~~~~~~l-_{}}t{h_{}}~column}&{}&{} \end{array}}&{}&{}&{} \end{array} \end{array}\ $$

(15)

Then, the rotation of the point in the entire space can be expressed as

$$ {{\tilde{\mathbf{ u }}}_{j}}\left( {\boldsymbol{\theta }} \right) = \prod\limits_{k = 1}^{d} {\prod\limits_{l = i + 1}^{d} {{{\mathbf{W}}_{kl}}\left( {{\theta_{k,l}}} \right){{\mathbf{u}}_{j}}} } = {\mathbf{R}}\left( {\boldsymbol{\theta }} \right){{\mathbf{u}}_{j}}\ $$

(16)

where R (𝜃) = ∏ k= 1d∏ l = k+ 1dW_kl (𝜃_k,l) is the rotational matrix in the entire space. It is seen that a total of $d\times (d-1)/2$ times plane rotations are implemented and the rotational angles, denoted as 𝜃 = {𝜃_1,2,𝜃_1,3,...𝜃_d− 1,d} determine the points after rotation. It should be noted that the weights associated with the points after rotation are still the same with those in Q-SPM. In this regard, the angle vector ${\boldsymbol {\theta }}$ should be optimally specified to achieve the best results. The points after rotation is called the rotational quasi-symmetric points. Figure 2 illustrates the rotation of points in a two-dimensional case. Clearly, by doing the rotation, the projection ratio of points is increased and the tail distribution information may be captured sufficiently by the points after the rotation.

Fig. 2

Rotation of points in two-dimensional space

To optimally determine the angle vector ${\boldsymbol {\theta }}$, an appropriate objective function needs to formulated, which is of great significance for accurate estimating the statistical moments of the performance function. Besides, the objective function should be calculated efficiently even in high dimensions. The basic idea of establishing the objective function is that the objective function can be estimated based on the points after rotation together with their weights without conducting deterministic analysis of systems. Further, the objective function may take the same formulation with respect to input random variables with those of statistical moments of the performance function. In this regard, the more accurate the objective function is, the more accurate the statistical moments of the performance function would be.

In the present paper, a marginal moments based objective function is proposed. The estimated marginal moments of input random variables can be expressed as

$$ {\mu_{{X_{i}}}}(\boldsymbol{\theta}) = \sum\limits_{j = 1}^{N} {{a_{j}}} {T^{- 1}}\left( {{\tilde{u}_{i,j}}}(\boldsymbol{\theta}) \right){,_{}}~~i = 1,2,...,d\ $$

(17)

$$ \sigma_{{X_{i}}}^{2}(\boldsymbol{\theta}) = \sum\limits_{j = 1}^{N} {{a_{j}}} {G^{2}}\left[ {{T^{- 1}}\left( {{\tilde{u}_{i,j}}} (\boldsymbol{\theta})\right)} \right] - {\mu_{{X_{i}}}}^{2}(\boldsymbol{\theta}),\begin{array}{*{20}{c}} {}&{i = 1,2,...,d} \end{array}\ $$

(18)

$$ {\alpha_{3{X_{i}}}}({\boldsymbol{\theta }}) = \left\{ \begin{array}{l} \sum\limits_{j = 1}^{N} {{a_{j}}} {G^{3}}\left[ {{T^{- 1}}\left( {{\tilde{u}_{i,j}}({\boldsymbol{\theta }})} \right)} \right] - \\ 3\left\{ {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{2}}\left[ {{T^{- 1}}\left( {{\tilde{u}_{i,j}}({\boldsymbol{\theta }})} \right)} \right]} \right\}{\mu_{{X_{i}}}}({\boldsymbol{\theta }}) + 2{\mu_{{X_{i}}}}^{3} \end{array} \right\}/\sigma_{{X_{i}}}^{3}({\boldsymbol{\theta }})\begin{array}{*{20}{c}} {}&{i = 1,2,...,d} \end{array}\ $$

(19)

$$ \begin{array}{l} {\alpha_{4{X_{i}}}}({\boldsymbol{\theta }}) = \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{4}}\left[ {{T^{- 1}}\left( {{\tilde{u}_{i,j}}({\boldsymbol{\theta }})} \right)} \right] - 4\left\{ {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{3}}\left[ {{T^{- 1}}\left( {{\tilde{u}_{i,j}}({\boldsymbol{\theta }})} \right)} \right]} \right\}{\mu_{{X_{i}}}}({\boldsymbol{\theta }})}\\ { + 6\left\{ {\sum\limits_{j = 1}^{N} {{a_{j}}} {G^{2}}\left[ {{T^{- 1}}\left( {{\tilde{u}_{i,j}}({\boldsymbol{\theta }})} \right)} \right]} \right\}{\mu_{{X_{i}}}}^{2} - 3{\mu_{{X_{i}}}}^{4}({\boldsymbol{\theta }})} \end{array}} \right\}/\sigma_{{X_{i}}}^{4}({\boldsymbol{\theta }})\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{}&{} \end{array}}&{}&{}&{} \end{array}}&{}&{}&{} \end{array}}&{}&{}&{} \end{array}}&{}&{}&{} \end{array}}&{}&{}&{} \end{array}}&{}&{}&{i = 1,2,...,d} \end{array} \end{array} $$

(20)

where $\tilde {u}_{i,j}$ represents the i-th coordinate of the point $\tilde {\mathbf { u }}_{j}$.

On the other hand, the exact values of marginal moments of input random variables can be evaluated easily by direct integrations, which are denoted as ${{\bar \mu }_{{X_{i}}}}$, ${{\bar \sigma }_{{X_{i}}}}$, ${{\bar \alpha _{3{X_{i}}}}}$ and ${{\bar \alpha _{4{X_{i}}}}}$, respectively. It is seen that the estimated marginal moments of input random variables (17)–(20) have the sameformulations with those in statistical moments of the performance function(3)–(6), indicating the points after rotation and their weights may have the same performance in both the marginal moments of input random variables and the statistical moments of the performance function. In this regard, if the estimated marginal moments of input random variables is close to their exact values, it is expected that the differences between the estimated statistical moments of the performance function and their underlying true values will be small. Thus, the objective function can be defined as the maximum relative error between the estimated marginal moments of input random variables and their exact values such that

$$ J\left( {\boldsymbol{\theta }} \right) = {e_{\max }}\left( {\boldsymbol{\theta }} \right) = \mathop {\max }\limits_{} \left[ {\mathop {\max }\limits_{1 \le i \le d} \left\{ {{e_{\mu ,i}}({\boldsymbol{\theta }}),{e_{\sigma ,i}}({\boldsymbol{\theta }}),{e_{{\alpha_{3}},i}}({\boldsymbol{\theta }}),{e_{{\alpha_{4}},i}}}({\boldsymbol{\theta }})\right\}} \right]\ $$

(21)

where

$$ {e_{\mu ,i}}({\boldsymbol{\theta }}) = \frac{{\left| {{\mu_{X_{i}}}({\boldsymbol{\theta }}) - {{\bar \mu }_{X_{i}}}} \right|}}{{\left| {{{\bar \mu }_{X_{i}}}} \right|}}\begin{array}{*{20}{c}} \end{array}\ $$

(22)

$$ {e_{\sigma ,i}}({\boldsymbol{\theta }}) = \frac{{\left| {{\sigma_{X_{i}}}({\boldsymbol{\theta }}) - {{\bar \sigma }_{X_{i}}}} \right|}}{{\left| {{{\bar \sigma }_{X_{i}}}} \right|}}\begin{array}{*{20}{c}} \end{array}\ $$

(23)

$$ {e_{{\alpha_{3,i}}}}({\boldsymbol{\theta }}) = \frac{{\left| {{\alpha_{3X_{i}}}({\boldsymbol{\theta }}) - {{\bar \alpha }_{3X_{i}}}} \right|}}{{\left| {{{\bar \alpha }_{3X_{i}}}} \right|}}\begin{array}{*{20}{c}} \end{array}\ $$

(24)

$$ {e_{{\alpha_{4,i}}}}({\boldsymbol{\theta }}) = \frac{{\left| {{\alpha_{4X_{i}}}({\boldsymbol{\theta }}) - {{\bar \alpha }_{4X_{i}}}} \right|}}{{\left| {{{\bar \alpha }_{4X_{i}}}} \right|}}\begin{array}{*{20}{c}} \end{array}\ $$

(25)

It is noted that the smaller the objective function J (𝜃) is, the more accurate the estimated values of marginal moments by RQ-SPM are. Therefore, the accuracy of the statistical moments of the performance function will be improved due to the similarities in the formulations (see (3)–(6) and (17)–(20)) (Xu and Lu 2017). Then, the task changes to minimize the objective function J (𝜃). Since the mean and standard deviation can be always captured accurately, which indicates e_μ,i and e_σ,i, $i = 1,2,...,d$ are quite small if the points in Q-SPM are rotated (Chen and Zhang 2013). Then, the objective function is equivalent to

$$ J\left( {\boldsymbol{\theta }} \right) = {e_{\max }}\left( {\boldsymbol{\theta }} \right) = \mathop {\max }\limits_{} \left[ {\mathop {\max }\limits_{1 \le i \le d} \left\{ {{e_{{\alpha_{3}},i}}\left( {\boldsymbol{\theta }} \right),{e_{{\alpha_{4}},i}}\left( {\boldsymbol{\theta }} \right)} \right\}} \right]\ $$

(26)

Further, the objective function can be written as

$$ J\left( {\boldsymbol{\theta }} \right) = {e_{\max }}\left( {\boldsymbol{\theta }} \right) = \mathop {\max }\limits_{} \left[ {\mathop {\max }\limits_{1 \le i \le d} \left\{ {{e_{{M_{3,i}}}}\left( {\boldsymbol{\theta }} \right),{e_{{M_{4,i}}}}\left( {\boldsymbol{\theta }} \right)} \right\}} \right]\ $$

(27)

where

$$ {e_{{M_{3,i}}}}({\boldsymbol{\theta }}) = \frac{{\left| {{M_{3X_{i}}}({\boldsymbol{\theta }}) - {{\bar M}_{3X_{i}}}} \right|}}{{\left| {{{\bar \alpha }_{3X_{i}}}} \right|}}\begin{array}{*{20}{c}} \end{array}\ $$

(28)

$$ {e_{{M_{4,i}}}}({\boldsymbol{\theta }}) = \frac{{\left| {{M_{4X_{i}}}({\boldsymbol{\theta }}) - {{\bar M}_{4X_{i}}}} \right|}}{{\left| {{{\bar \alpha }_{4X_{i}}}} \right|}}\begin{array}{*{20}{c}} \end{array}\ $$

(29)

where ${{M_{3X_{i}}}}$ and ${{M_{4X_{i}}}}$ denotes the estimated values of the $3rd$ and $4th$ raw moments, which are evaluated by

$$ {M_{3X_{i}}}({\boldsymbol{\theta }}) = \sum\limits_{j = 1}^{N} {{a_{j}}} {G^{3}}\left[ {{T^{- 1}}\left( {{u_{i,j}}({\boldsymbol{\theta }})} \right)} \right]\ $$

(30)

$$ {M_{4X_{i}}}({\boldsymbol{\theta }}) = \sum\limits_{j = 1}^{N} {{a_{j}}} {G^{4}}\left[ {{T^{- 1}}\left( {{u_{i,j}}({\boldsymbol{\theta }})} \right)} \right]\ $$

(31)

and ${{{\bar M}_{3X_{i}}}}$ and ${{{\bar M}_{4X_{i}}}}$ are the corresponding exact values, which can be evaluated easily by

$$ {{\bar M}_{3{X_{i}}}} = {\int}_{- \infty }^{+ \infty } {{X_{i}}^{3}{f_{{X_{i}}}}\left( {{x_{i}}} \right)d{x_{i}}} \ $$

(32)

$$ {{\bar M}_{4{X_{i}}}} = {\int}_{- \infty }^{+ \infty } {{X_{i}}^{4}{f_{{X_{i}}}}\left( {{x_{i}}} \right)d{x_{i}}} \ $$

(33)

Then, the following optimization problem needs to be tackled to determine the optimal angle vector in RQ-SPM such that

$$ \begin{array}{l} \text{find}\begin{array}{*{20}{c}} {}&{\boldsymbol{\theta }} \end{array}\\ \text{objective}\begin{array}{*{20}{c}} {}&{\min \left[ {J\left( {\boldsymbol{\theta }} \right)} \right]} \end{array}\\ \text{s.t.}\begin{array}{*{20}{c}} {}&{{\theta_{kl}}} \end{array} \in \left[ {0,2\pi } \right],\begin{array}{*{20}{c}} {}&{\forall {\theta_{kl}} \in } \end{array}{\boldsymbol{\theta }} \end{array}\ $$

(34)

Obviously, the global optimization method such as the genetic algorithm and the particle swarm algorithm can be employed to find the optimal angle vector $\boldsymbol {\theta }$. Then, the points after rotation $\tilde {\mathbf { u }}_{j}$s with their weights $a_{j}$s (j = 1,2,...,N) can be applied for the numerical integration. Although solving the optimization problem above requires a certain amount of computational time, the computational effort for statistical moments assessment mainly depends on the repeated deterministic analysis of the performance function. For example, if a total of 30 repeated deterministic analysis are required to evaluate the moments and each deterministic analysis involves the time-consuming finite element analysis, e.g. 30 min, the computational time of the optimization problem (34), which may cost 5 min, could be negligible compared to the total effort of performing repeated deterministic analysis of the performance function, which is 900 min. It should be also mentioned that the rotation will not reduce the algebraic degree of accuracy compared with that of the original Q-SPM (Chen and Zhang 2013; Xu et al. 2017). Besides, the information of marginal PDFs and the tail distributions of input random variables could be characterized more clearly by the points after rotation. In this regard, the accuracy of numerical evaluation of the high-order moments of the performance function could be significantly improved by using the points after rotation. Since the rotation is performed based on the Q-SPM and the objective function is the marginal moments of input random variables, this method is called the marginal moments based rotational quasi-symmetric point method (RQ-SPM). Substituting ${\mathbf {u}}_{j}$ in (3)–(6) as $\tilde {\mathbf { u }}_{j}$, the statistical moments of the performance function can be evaluated by RQ-SPM without inducing extra difficulty.

Actually, the rotation of the points is performed in the standard normal random-variate space, which increases the projection ratio of the points on the tail and may improve the accuracy for high-order moments calculations. It should be pointed out that the rotation does not induce correlations between the input random variables. This could be found from the covariance matrix ${C_{\tilde {\mathbf {U}}\tilde {\mathbf {U}}}}$, i.e.

$$ C_{\tilde{\mathbf{ U}}\tilde{\mathbf{U}}} = \sum\limits_{j = 1}^{N} {{a_{j}}\left( {{{\tilde{\mathbf{ u}}}_{j}} - {{\mathbf{m}}_{\tilde{\mathbf{ U}}}}} \right)} {\left( {{{\tilde{\mathbf{ u}}}_{j}} - {{\mathbf{m}}_{\tilde{\mathbf{ U}}}}} \right)^{T}}\ $$

(35)

where $\tilde {\mathbf {U}}$ is the random vector after the rotation and m_U~ is the mean vector. Since the rotation does not change the mean vector in the standard normal random variate space, which is still m_U~ = [0,0,....,0]^T, the covariance matrix above can be further expressed as

$$ \begin{array}{l} C_{\tilde{\mathbf{ U}}\tilde{\mathbf{U}}} = \sum\limits_{j = 1}^{N} {{a_{j}}\left( {{{\tilde{\mathbf{ u}}}_{j}}} \right)} {\left( {{{\tilde{\mathbf{ u}}}_{j}}} \right)^{T}}\\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sum\limits_{j = 1}^{N} {{a_{j}}\left( {R\left( {\boldsymbol{\theta }} \right){{\mathbf{u}}_{j}}} \right)} {\left( {R\left( {\boldsymbol{\theta }} \right){{\mathbf{u}}_{j}}} \right)^{T}}\\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sum\limits_{j = 1}^{N} {R\left( {\boldsymbol{\theta }} \right){R^{T}}\left( {\boldsymbol{\theta }} \right){a_{j}}{{\mathbf{u}}_{j}}{{\mathbf{u}}_{j}}^{T}} \end{array}\ $$

(36)

It can be easily proved that R (𝜃)R^T (𝜃) = I = diag (1,1,....,1) (Chen and Zhang 2013). In this regard, we have

$$ {C_{\tilde{\mathbf{ U}}\tilde{\mathbf{U}}} = \sum\limits_{j = 1}^{N} {{a_{j}}{{\mathbf{u}}_{j}}{{\mathbf{u}}_{j}}^{T} = {C_{{\mathbf{UU}}}} = {\mathbf{I}}} }\ $$

(37)

It is noted that the covariance matrix is C_U~U~ = I, which is the same with that before the rotation, which means the random variables after the rotation are still independent with each other. Thus, the rotation of points does not induce correlations among the input random variables.

Further, the proposed marginal moments based RQ-SPM is different from the fractional moments based one in Ref. (Xu et al. 2017). The differences lie in: (1). The fractional moments based RQ-SPM is performed over the normal random variables, whereas the proposed RQ-SPM is directly developed on the basis of original input random variables; (2). The objective function in Ref. Xu et al. (2017) is formulated based on minimizing the differences between the fractional moments of normal random variables in an interval of fractional orders, which are the raw moments in essence. However, the objective function in the proposed method is established based on minimizing the differences of integer central moments of original input random variables. It is known that the small errors in raw moments could be accumulated and still result in quite large errors in central moments. Although the fractional moments based RQ-SPM works particularly well for fractional moments assessment, it may be imprudent to use the fractional moments based RQ-SPM to evaluate the integer central moments, especially for the high-order central moments. The similar problem also exists in the GF discrepancy based RQ-SPM in Ref. (Chen and Zhang 2013). In this regard, it is of great necessity to develop the new RQ-SPM particularly applicable for this kind of problems due to its high efficiency.

4 PDF evaluation and reliability assessment based on SGLD model

Once the first four statistical moments of the performance function are available, the construction of the PDF of the performance function from the moments will be investigated for structural reliability analysis. In the present paper, the shifted generalized lognormal distribution (SGLD) model (Low 2013) is fitted to obtain the PDF based on the first four statistical moments. This distribution model actually combines the three-parameter lognormal distribution (Cohen and Whitten 1980), which is asymmetrical distribution and encompasses the entire range of skewness, and the exponential power distribution (Nadarajah 2005), which is a symmetrical distribution and encompasses the entire range of kurtosis. In this regard, the SGLD model, which synthesizes the features of these distributions above, has a high flexibility in the shape and encompasses the entire skewness-kurtosis region permissible for unimodal densities (He and Gong 2016). It should be pointed out that the SGLD model is only effective when the skewness of the random variable Z is positive. If negative skewness is involved, one can simply define a variable $Z^{\prime }=-Z$ and obtain the PDF of $Z^{\prime }$ for structural reliability analysis.

The PDF of Z, represented by the SGLD model can be expressed as (Low 2013)

$$ {p_{Z}}\left( z \right) = \frac{\alpha }{{z - b}}\exp \left( { - \frac{1}{{r{\lambda^{r}}}}{{\left| {\ln \frac{{z - b}}{\kappa }} \right|}^{r}}} \right),\begin{array}{*{20}{c}} {}&{b < z < \infty } \end{array}\ $$

(38)

where b is the location parameter; $\kappa$ is the scale parameter; $\lambda >0$ and $r>0$ are the shape parameters and the coefficient $\alpha$ is defined as

$$ \alpha = \frac{1}{{\left[ {2{r^{1/r}}\lambda {\Gamma} \left( {1 + 1/r} \right)} \right]}}\ $$

(39)

where ${\Gamma }(.)$ is the Gamma function, which is Γ(x) = ∫ 0∞t^x− 1e^−tdt.

It can be observed that the SGLD model is a four-parameter distribution, where $\lambda , r, b, \kappa$ need to be specified. Moreover, for each fixed pair (λ,r), the location and scale parameters $(b, \kappa )$ can be determined via (Low 2013)

$$ \kappa = {\sigma_{Z}}/{\sigma_{Y}},\begin{array}{*{20}{c}} {}&{b = } \end{array}{\mu_{Z}} - \kappa {\mu_{Y}}\ $$

(40)

where $\mu _{Y}$ and $\sigma _{Y}$ are the mean and standard deviation of a reduced variable $Y=(Z-b)/\kappa$, which can be evaluated from the following raw moments (Low 2013)

$$ E\left[ {{Y^{k}}} \right] = \frac{1}{{{\Gamma} \left( {1/r} \right)}}\sum\limits_{n = 0}^{\infty} {\frac{{{{\left( {k\lambda } \right)}^{2n}}}}{{\left( {2n} \right)!}}} {r^{2n/r}}{\Gamma} \left( {\frac{{2n + 1}}{r}} \right)\ $$

(41)

for each fixed pair (λ,r).

Then, only two parameters, i.e. $\lambda$ and r, need to be determined. Define v = [λ,r]^T, it is known that the skewness and kurtosis of Z are actually the function of $\mathbf {v}$, which are denoted as $\alpha _{3Z}(\mathbf {v})$ and $\alpha _{4Z}(\mathbf {v})$. Then, the following moment equations hold

$$ {\mathbf{H}}\left( {\mathbf{v}} \right) = \left[ {\begin{array}{*{20}{c}} {{\alpha_{3Z}}\left( {\mathbf{v}} \right) - {\alpha_{3Z}}}\\ {{\alpha_{4Z}}\left( {\mathbf{v}} \right) - {\alpha_{4Z}}} \end{array}} \right] = 0\ $$

(42)

where the vector $\mathbf {v}$ can be solved by using the Newton’s iteration method. The iterative scheme can be formulated such that

$$ {{\mathbf{v}}_{l + 1}} = {{\mathbf{v}}_{l}} - {{\mathbf{J}}^{- 1}}\left( {{{\mathbf{v}}_{l}}} \right){\mathbf{H}}\left( {{{\mathbf{v}}_{l}}} \right)\ $$

(43)

where the Jacobian is

$$ {\mathbf{J}}\left( {{{\mathbf{v}}_{l}}} \right) = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\alpha_{3Z}}}}{{\partial \lambda }}}&{\frac{{\partial {\alpha_{3Z}}}}{{\partial r}}}\\ {\frac{{\partial {\alpha_{4Z}}}}{{\partial \lambda }}}&{\frac{{\partial {\alpha_{4Z}}}}{{\partial r}}} \end{array}} \right]\ $$

(44)

which is numerically evaluated at ${\mathbf {v}}_{l}$

Finally, the PDF of Z can be reconstructed, and the failure probability can be conveniently evaluated by

$$ {p_{f}} = {\int}_{- \infty }^{0} {{p_{Z}}\left( z \right)dz} $$

(45)

and the reliability is $R = 1-p_{f}$.

Figure 3 shows the PDFs represented by SGLD with different moments. It is clear that the SGLD model is highly flexible in shape.

Fig. 3

The SGLD with different moments (μ_Z = 0,σ_Z = 1)

To summarize, the proposed method for structural reliability analysis involves the following steps:

• Step 1. Employ the original Q-SPM to generate the basic point set for the dimension d.

• Step 2. Rotate the basic point set according to the marginal moments of input random vector (16). In this step, the optimal angles for the rotation need to be specified by (34).

• Step 3. Evaluate the statistical moments of the performance function based on the point set after the rotation.

• Step 4. Substitute the statistical moments into the SGLD model to derive the entire range of the PDF of the performance function.

• Step 5. Perform a simple integral over the PDF of the performance function to obtain the failure probability/reliability.

5 Numerical examples

Four examples are presented to validate the proposed method for statistical moments and reliability assessment in this section. In each example, Monte Carlo simulation method is carried out to produce the “exact” solutions for comparisons. Besides, the performance of the proposed method is examined through comparisons with the original Q-SPM, the widely-used univariate dimension reduction method (UDRM) (Rahman and Wei 2006) and the bivariate dimension reduction (BDRM) (Xu and Rahman 2004), respectively.

5.1 Example 1

The first example considers a rigid-plastic portal frame subjected to a horizontal load F and a vertical load $F_{G}$, which is shown in Fig. 4. The performance function is given by (Nie and Ellingwood 2000)

$$ Z = G\left( {\mathbf{X}} \right) = \min \left\{ {{G_{1}}\left( {\mathbf{X}} \right),{G_{2}}\left( {\mathbf{X}} \right),{G_{3}}\left( {\mathbf{X}} \right)} \right\}\ $$

(46)

where

$$ {G_{1}}\left( {\mathbf{X}} \right) = {X_{2}} + 2{X_{3}} + {X_{4}} - F_{G}b\ $$

(47)

$$ {G_{2}}\left( {\mathbf{X}} \right) = {X_{1}} + {X_{2}} + {X_{4}} + {X_{5}} - Fa\ $$

(48)

$$ {G_{3}}\left( {\mathbf{X}} \right) = {X_{1}} + 2{X_{3}} + 2{X_{4}} + {X_{5}} - Fa - {F_{G}}b\ $$

(49)

in which $X_{1}$-X₅ are the plastic bending capacities at the joints, which are independent lognormal random variables with means 1 and coefficients of variation (C.O.V.) 0.20; F is the horizontal load, which is also a lognormal random variable with a mean 2.4 and a C.O.V. 0.3; $F_{G}$ is the vertical load, which is a deterministic value as 1.15; and the distances $a=b = 1$ are considered in this case. It is seen that the large variability is involved in the input random vector, which consists of 6 independent random variables.

Fig. 4

Rigid-plastic portal frame

Table 2 lists the statistical moments of the performance function by RQ-SPM, Q-SPM, UDRM and BDRM, respectively. Simultaneously, the results by MCS (10⁷ runs) are taken as the “exact” values for comparisons. The relative errors between the results obtained by different methods and those of MCS are also shown in Table 2. It is noted that all these methods can result in very accurate means and standard deviations. Besides, the RQ-SPM and the original Q-SPM only use 44 deterministic evaluations to obtain the moments of the performance function, which is almost comparable with that of UDRM (26 deterministic runs). However, the original Q-SPM gives the kurtosis $\alpha _{4Z}$ with less accuracy, where the relative error is as large as $18.37 \%$. The skewness $\alpha _{3Z}$ and the kurtosis $\alpha _{4Z}$ given by the UDRM severely deviate from the results by MCS. Further, although the BDRM can produce the results with relatively fair accuracy, the computational time is far larger than that of UDRM and the original Q-SPM. Remarkably, the proposed RQ-SPM is still able to give very accurate moments of the performance function with a few number of deterministic evaluations, where the maximum relative error is less than $4.2 \%$. In this regard, it is demonstrated that the proposed RQ-SPM can achieve very good tradeoff of accuracy and efficiency for evaluating the statistical moments of the performance function.

Table 2 Statistical moments and failure probabilities of Example 1

Further, the reliability is evaluated based on the SGLD model. It is noted that the skewness of the performance function is smaller than zero and the SGLD model is effective for positive skewness. In this regard, we define $Z^{\prime }=g({\mathbf {X}})=-G(\mathbf {X})$ and the failure probability is ${p_{f}} = {\int }_{0}^{\infty } {{p_{Z^{\prime }}}\left (z \right )dz}$. Figure 5a shows the PDF of $Z^{\prime }$ obtained from the proposed method, where the histogram by MCS is also pictured for comparison. It is seen that the result by the proposed method accord very well with the histogram. Besides, the probability of exceedance (POE) curves in logarithmic scale are compared in Fig. 5b, where the close agreement can be noticed again. As far as the failure probability is concerned, the proposed method gives 0.0388, where the failure probability by MCS is 0.0387. It should be emphasized that this high accuracy is achieved just with 44 deterministic evaluations of the performance function. These computational results demonstrate the accuracy and efficiency of the proposed method for structural reliability analysis.

Fig. 5

PDF and POE comparisons (Example 1)

If the UDRM and the original Q-SPM is applied to evaluate the statistical moments in the SGLD model, the results are shown in Fig. 6. Obviously, it can be noted that the PDFs and POE curves by using UDRM and Q-SPM in the SGLD model deviate seriously with the results obtained from MCS. The comparisons of failure probabilities are also listed in Table 2. Again, it is noted that the relative errors of failure probabilities evaluated by the SGLD with UDRM and Q-SPM are obviously much larger than that by the proposed method. Besides, the proposed method can achieve the comparable accuracy for failure probability assessment with that by BDRM but cost much less computational effort. In summary, the proposed method still gives the most accurate failure probability with minimum number of samples.

Fig. 6

PDF and POE comparisons using UDRM and Q-SPM (Example 1)

It is also noted that the relative error of kurtosis by the proposed method is relatively large, say $>4\%$, which actually affects the accuracy of the far-end of the tail distribution. Since the failure probability above is relatively large, which is related to the near-end of the tail distribution, this moment error does not induce quite large error in assessing the failure probability. Further, when $Z=G({\mathbf {X}})+ 4$ is considered for reliability analysis, only the mean is changed and other statistical moments are still the same with those above, where the large relative error of kurtosis still exists. The POE in logarithmic scale of $Z^{\prime }=-G({\mathbf {X}})-4$ is shown in Fig. 7. Clearly, slight deviation between the results by the proposed method and MCS could be observed at the far-end of the tail distribution. The failure probabilities given by the proposed method and MCS are $1.04 \times 10^{-5}$ and $1.67 \times 10^{-5}$, respectively. Although the relative error becomes much larger for small failure probability problems, the accuracy could be still acceptable for most of engineering problems.

Fig. 7

POE with small failure probability

5.2 Example 2

The second example involves the ultimate bending moment of resistance of a reinforced concrete, where the performance function is given by (Breitung and Faravelli 1994; Zhou and Nowak 1988; Zhang and Pandey 2013)

$$ Z=G({\mathbf{X}}) = \left[ {{X_{1}}{X_{2}}{X_{3}} - \frac{{{X_{1}^{2}}{X_{2}^{2}}X_{4}}}{{X_{5}X_{6}}}} \right]-M_{B}\ $$

(50)

where the involved random variables and their descriptions are listed in Table 3. It is noted that a nonlinear performance function with large C.O.V.s of random variables are actually considered in this case.

Table 3 Random variables in Example 2

The computational results are shown and compared in Table 4. It can be found that the UDRM produces the spurious results of the high-order moments, i.e. $\alpha _{3Z}$ and α_4Z although it consumes the smallest computational time. Besides, even the relative error of standard deviation $\sigma _{Z}$ is larger, say $1.19 \%$ than the counterparts of other methods. The accuracy of $\alpha _{3Z}$ and $\alpha _{4Z}$ is not satisfactory by Q-SPM, where the relative error of $\alpha _{4Z}$ goes up to $10.89 \%$. Again, the results by the proposed RQ-SPM accord very well with those by MCS, where the maximum relative error in this case is less than $3 \%$. Besides, this high accuracy of RQ-SPM is only based on 78 deterministic analyses of the performance function. It is noted that the results by the proposed RQ-SPM are quite close to those of BDRM in this example. However, the BDRM requires 533 times deterministic analyses of the performance function. In this regard, the computational efficiency of the proposed RQ-SPM is much better than that of BDRM.

Table 4 Statistical moments and failure probabilities of Example 2

It is noted that the skewness in this example is positive, and the PDF and CDF in logarithmic scale of the performance function can be obtained by the proposed method, which are shown in Fig. 8. Again, it is seen the results by the proposed method still accord very well with those of MCS. The failure probabilities are also listed in Table 4. It is seen that the proposed method still gives the most accurate failure probability with the lowest computational burden. Therefore, the efficacy of the proposed method for structural reliability is validated again.

Fig. 8

PDF and CDF comparisons (Example 2)

5.3 Example 3

The third example considers a nine-bar planar truss structure under vertical loads, which is shown in Fig. 9 (Xu et al. 2017). The young’s modulus E, the cross sectional area of each bar A, and the external loads $F_{1}$ and $F_{2}$ are all lognormal random variables with means $2.0 \times 10^{5} MPa$, $2.5 \times 10^{-3} m^{2}$, 500kN, $400 kN$ and C.O.V.s 0.1, 0.05, 0.3, 0.3, respectively. Note that a closed-form expression for the nodal deflection is not available and it has to be computed by linear finite-element analysis. The implicit performance function is defined as (Xu et al. 2017)

$$ Z = G\left( {\mathbf{X}} \right) = {U_{b}} - \mathop {\max }\limits_{1 \le i \le 6} \left\{ {\sqrt {U_{{X_{i}}}^{2} + U_{{Y_{i}}}^{2}} } \right\}\ $$

(51)

where $U_{X_{i}}$ and $U_{Y_{i}}$ denote the horizontal and the vertical deflection at the i-th node and $U_{b}$ is the deterministic threshold.

Fig. 9

Nine bar truss structure

Actually, if we define $Z^{\prime }= \mathop {\max }\limits _{1 \le i \le 6} \left \{ {\sqrt {U_{{X_{i}}}^{2} + U_{{Y_{i}}}^{2}} } \right \}$, then the failure probability goes to ${p_{f}} = {\int }_{{U_{b}}}^{\infty } {{p_{Z^{\prime }}}\left (z \right )dz}$. In this regard, the statistical moments and the entire distribution of $Z^{\prime }$ is of great concern.

Table 5 compares the results of statistical moments by the proposed RQ-SPM, the original Q-SPM, UDRM and BDRM, respectively. The “exact” results are also provided by $10^{6}$ direct MCS. Similarly, it is seen that the UDRM is still not able to give accurate results of the high-order moments, whereas the BDRM cannot achieve the balance of accuracy and efficiency. The means and standard deviations by RQ-SPM and Q-SPM are the same, however, the proposed RQ-SPM can significantly improve the accuracy of the high-order moments. In this example, the maximum relative error of moments by RQ-SPM is only $1.19\%$. It should be emphasized that only 24 deterministic evaluations are performed in RQ-SPM. Thus, the RQ-SPM is indeed of accuracy and efficiency for statistical moments assessment of the performance function (Table 5).

Table 5 Statistical moments and failure probabilities of Example 3 (U_b = 0.15m)

Since positive skewness is involved herein, the SGLD model with the RQ-SPM is employed to derive the entire distribution of $Z^{\prime }$. Similarly, the PDF and POE curve in logarithmic scale of $Z^{\prime }$ are pictured in Fig. 10, where the results by MCS are provided for comparisons. The failure probabilities evaluated by different methods are also shown in Table 5 when $u_{b}= 0.15m$. Remarkably, the proposed method is still able to reproduce the entire distribution range and provides the failure probability with high accuracy and efficiency. Table 6 lists the comparisons of failure probabilities by the proposed method when the threshold $U_{b}$ is assigned different values. Again, it is noted that the proposed method can even accurately and efficiently obtain the very small failure probabilities (order of $10^{-4}-10^{-6}$).

Fig. 10

PDF and POE comparisons (Example 3)

Table 6 Failure probabilities of Example 3

Further, in this example, the GF discrepancy based RQ-SPM (Chen and Zhang 2013) and fractional moments based RQ-SPM (Xu et al. 2017) are employed to evaluate the statistical moments and reliability. The results are shown in Table 7 and Fig. 11. Obviously, although the efficiency of these RQ-SPMs is the same, the accuracy of the proposed RQ-SPM is much better than other ones for both the statistical moments and reliability assessment.

Table 7 Statistical moments and failure probabilities of Example 3 (2) (U_b = 0.15m)

Fig. 11

POE comparisons with other RQ-SPMs

5.4 Example 4

The last example considers a three-bay eight-storey planar frame structure subjected to lateral loads, which is pictured in Fig. 12. The structural parameters are given as follows: Young’s modulus $E = 210 Gpa$; cross sectional area of beam $A_{B}= 73.303 cm^{2}$; cross sectional area of column $A_{B}= 120.4 cm^{2}$; moment of inertial of beam I_B = 11400cm⁴ and moment of inertial of column $I_{C}= 20500 cm^{4}$. The lateral loads $F_{1}$-F₈ are lognormal random variables with means 10kN, 11.5kN, 12kN, 12kN, 12kN, 10kN, 11kN and 13kN and C.O.V.s all being 0.3. Likewise, the finite-element analysis of the structure is carried out and the implicit performance function is

$$ Z = G\left( {\mathbf{X}} \right) = {u_{b}} - {\max_{1 \le i \le 8;1 \le j \le 4}}\left| {{u_{ij}}\left( {\textbf{x}} \right)} \right|\ $$

(52)

where u_ij (x) represents the inter-storey-drift at the j-th joint on the i-th storey, and $u_{b}$ is the deterministic allowable drift.

Fig. 12

Three-bay eight-storey frame structure

Like Example 3, the reliability can be evaluated by ${p_{f}} = {\int }_{{u_{b}}}^{\infty } {{p_{Z^{\prime }}}\left (z \right )dz}$, where $Z^{\prime }={\max _{1 \le i \le 8;1 \le j \le 4}}\left | {{u_{ij}}\left ({\textbf {x}} \right )} \right |$. Then, the statistical moments and entire distribution of $Z^{\prime }$ is of interest.

The results of statistical moments of $Z^{\prime }$ are shown in Table 8. Again, it can be observed that the results by UDRM and the original Q-SPM are not close to the “exact” results by MCS. The accuracy of RQ-SPM with only 144 samples is comparable with that of BDRM with 705 samples. However, the proposed RQ-SPM is much more efficient than BDRM. This example also demonstrates the efficiency and accuracy of the proposed RQ-SPM for statistical moments assessment of the performance function.

Table 8 Statistical moments and failure probabilities of Example 4 (u_b = h/250m)

The PDF and POE curve in logarithmic scale are shown in Fig. 13, which are compared with the results by MCS. For example, if the allowable drift is adopted as $u_{b}=h/250$, the failure probabilities given by different method are also listed in Table 8. Again, very good accordance between the results by the proposed method and MCS can be observed, which validates the effectiveness of the proposed method for structural reliability analysis.

Fig. 13

PDF and POE comparisons (Example 4)

6 Concluding remarks

A new method, named the rotational quasi-symmetric point method (RQ-SPM), has been developed for statistical moments assessment of the performance function. This method has been established based on rotating the points in the quasi-symmetric point method (Q-SPM), where the optimal angles need to be found. The marginal moments of input random variables has been employed to formulate the objective function. The new method can better reproduce the marginal probabilistic information of input random variables, especially for the tail distributions. In this regard, it can efficiently evaluate the statistical moments of the performance function, particulary for the high-order moments with high accuracy. Then, this method has been combined with the shifted generalized lognormal distribution (SGLD) to obtain the entire range of the PDF of the performance function for structural reliability assessment.

Four numerical examples involving both explicit and implicit performance functions have been analyzed to demonstrate the efficiency and accuracy of the proposed method. In all examples, Monte Carlo simulations have been carried out to provide the results for comparisons. It has been observed that the proposed method is much more accurate than the original Q-SPM, univariate dimension reduction method. Besides, it has been also found that this method is much more efficient than the bivariate dimension reduction method.

It is noted that the proposed method is applicable for problems with 3-24 random variables. For high-dimensional reliability problems, further investigations are needed.