1 Introduction

Reliability and local reliability sensitivity (LRS) analysis are very important to ensure the reliability of structures, and there are many developments of the methods to analyze them in recent years. Reliability refers to the probability that the structure can complete the specified function within the specified time, while failure probability (FP) refers to the probability that the structure cannot complete the specified function. LRS analysis aims at studying the effect of random input distribution parameters on the FP, and it can provide gradient information for reliability-based design optimization (RBDO) (Torii et al. 2017; Dubourg et al. 2011).

In practical engineering problem, the random uncertainty is definitely unavoidable due to the uncontrolled occasional factor in geometric size, material properties, applied load and working environment, etc.. Thus, it is necessary to consider the random uncertainty in the design optimization, and RBDO by taking the random uncertainty into consideration is developed for optimizing the structure performance under ensuring the reliability. In RBDO model, the failure probability is generally embedded as a constraint in the design parameter optimization. The LRS, which is defined as the partial differential of the failure probability with respect to the design parameter (usually the distribution parameter of random input), can help provide an optimal direction for searching the optimal design parameter. Thus, researching efficient method to solve the LRS is necessary to improve the efficiency of solving RBDO by the gradient-based RBDO optimization strategy, and this work devotes to the efficient solution of the LRS.

At present, most of methods for LRS analysis are developed on the basis of reliability analysis methods, mainly including moment method (Zhao and Ono 1999; Xiao and Lu 2018; Zhao and Lu 2007), numerical simulation method (Li et al. 2012; Au and Beck 1999; Alvarez et al. 2018) and surrogate model method (Cadini et al. 2014; Zhai et al. 2016; Fan et al. 2018). In engineering applications, the moment method is more suitable for estimating the reliability and LRS of the structure due to its high computational efficiency.

The basic idea of the moment method for estimating reliability is to approximate the probability density function (PDF) of the performance function by computing the first few moments, and then estimate FP by the PDF of the performance function. The methods for estimating moments of performance function mainly include Taylor expansion (Hasofer and Lind 1974; Hohenbichler et al. 1987; Huang et al. 2018) and point estimation (Rosenblueth 1981; Seo and Kwak 2002; Zhao and Ono 2001, 2000). The method based on the first and second order Taylor expansion of performance function needs to compute the gradient of performance function, which is difficult to get accurately for implicit nonlinear performance function. The point estimation-based method uses numerical integration to estimate the first few moments of the performance function (Zhou and Nowak 1988), such methods mainly include two-point estimation (Rosenblueth 1981) and three-point estimation (Seo and Kwak 2002), etc. Since point estimation only requires the performance function evaluations at the integral grid nodes to estimate the performance function moments, it has a wider range of application than the Taylor expansion where the gradient is required. After the first few moments of the performance function are obtained, the FP of the structure can be estimated. At present, the main methods to estimate the FP based on the first few moments of performance function are second-moment method (Zhao and Ono 1999; Wong 1985), third-moment method (Hong et al. 1999) and fourth-moment method (Xiao and Lu 2018; Zhao and Lu 2007; Zhao and Ono 2004). With the increase of the order of the employed moment, the statistical information of the performance function increases gradually, and the computational accuracy of the FP is improved as a result. However, the increase of the moment order needs to compute the integral of the performance function with a higher order, and it means a higher degree of nonlinearity integral needs to be completed. It is well-known that the higher the degree of nonlinearity is, the more difficult the estimation of the integral is accurately completed by the finite integral nodes. Balancing the computational difficulty of performance function moment and the inclusion degree of statistical information of the performance function by moments, 4 is usually taken as the highest order of performance function moment to estimate FP.

The methods for LRS analysis developed on the moment method for reliability mainly include the second-moment (Karamchandani and Cornell 1992; Zhang et al. 2011a)-based first-order Taylor expansion and the fourth-moment-based point estimation (Lu et al. 2010). In these two kinds of method, the sensitivity of FP with respect to distribution parameter can be obtained by the chain rule. However, the numerical approximation expression of FP cannot guarantee the approximate accuracy of derivative function of the FP. Therefore, these methods are not rigorous in theory even if the numerical examples do not find a large computational error. In addition, it is worth pointing out that the computational cost of the fourth-moment (Lu et al. 2010)-based three-point estimation increases exponentially with the dimension of random input, thus it is only suitable for problems with a lower dimension of random input.

In view of the lack of theoretical rigor and dimensionality disaster in estimating the LRS by the existing fourth-moment-based methods, a new moment method is proposed for LRS analysis in this paper. The proposed method starts from the integral definition of the LRS, and it equivalently derives the LRS by integral transformation as the weighted sum of the FP and extended FPs, in which these derived FPs possess the same performance function but different PDFs. No assumption is introduced in the whole derivation, which ensures the theoretical rigor. These derived FPs have the same performance function, and their PDFs have the explicit relationship. By taking advantage of these characteristics, a strategy of sharing integral nodes is elaborately designed on the multiplicative dimensional reduction (Zhang and Pandey 2013), on which it can simultaneously compute the first four moments of the performance function required by the derived FPs. In the designed strategy, the multivariate integral for estimating the moments of performance function is transformed into the product of univariate integrals, thus it avoids dimensionality disaster in the existing three-point estimation method. Compared with the existing moment method for LRS, the advantages of the proposed method mainly lie in two aspects. The first is no assumption is introduced in derivation from LRS to the FP and extended FPs, and it is theoretically rigorous. The second is the computational cost of the proposed method increases linearly with the dimension of random input due to the designed strategy of sharing integral nodes on multiplicative dimensional reduction.

The structure of this paper is as follows. Firstly, Sect. 2 introduces the definition of LRS and the idea for computing LRS by fourth moment-based three-point estimation. In Sect. 3, by use of integral transformation, the LRS is equivalently derived to the weighted sum of original FP and extended FPs, on which the multiplicative dimensional reduction-based strategy of sharing integral nodes is designed for estimating the derived FPs efficiently. Numerical examples and engineering examples are used to verify the superiority of the proposed method in Sect. 4, and the conclusions are drawn in Sect. 5.

2 The definition of LRS and its estimation through the existing fourth moment-based method

2.1 Definition of LRS

Let \(g = g({\varvec{X}})\) denote the structure performance function with n-dimensional random input \(\user2{X = }\left[ {X_{1} ,X_{2} , \ldots ,X_{n} } \right]^{T}\), then the corresponding FP denoted by \(P_{f}\) can be defined by Eq. (1),

$$\begin{gathered} P_{f} = P\left\{ F \right\} = P\left\{ {g({\varvec{x}}) \le 0} \right\} \hfill \\ { = }\int_{F} {f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}} = \int_{{{\varvec{g}}\left( {\varvec{x}} \right) \le 0}} {f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}} \hfill \\ \end{gathered},$$
(1)

where \(F = \left\{ {{\varvec{x}}\left| {g({\varvec{x}}) \le 0} \right.} \right\}\) represents the failure domain, \(P\left\{ \cdot \right\}\) represents the probability operator, \(f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )\) is the joint PDF of the random input \({\varvec{X}}\), and \({\varvec{\theta}}_{{\varvec{X}}}\) represents the distribution parameter vector of \({\varvec{X}}\). Let \(l_{i}\) be defined as the number of distribution parameters for the \(i{\text{th}}\) random variable \(X_{i}\) \((i = 1,2, \cdot \cdot \cdot ,n)\).

It can be seen from Eq. (1) that \(P_{f}\) changes with the distribution parameter \({\varvec{\theta}}_{{\varvec{X}}}\) of the random input \({\varvec{X}}\), and the effect of \({\varvec{\theta}}_{{\varvec{X}}}\) on \(P_{f}\) can be quantified by LRS. The LRS is defined as the partial differential of \(P_{f}\) with respect to \(\theta_{{X_{i} }}^{(k)}\)\((i = 1,2, \cdot \cdot \cdot ,n;k = 1,2, \cdot \cdot \cdot ,l_{i} )\), i.e., \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \theta_{{X_{i} }}^{(k)} }}} \right. \kern-0pt} {\partial \theta_{{X_{i} }}^{(k)} }}\), where \(\theta_{{X_{i} }}^{(k)}\) represents the kth distribution parameter of \(X_{i}\). By substituting Eq. (1) into the definition of LRS, the following Eq. (2) can be obtained for estimating LRS.

$$\frac{{\partial P_{f} }}{{\partial \theta_{{X_{i} }}^{(k)} }} = \frac{{\partial \left[ {\int_{F} {f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}}} \right]}}{{\partial \theta_{{X_{i} }}^{(k)} }}{ = }\int_{F} {\frac{{\partial f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}{{\partial \theta_{{X_{i} }}^{(k)} }}d{\varvec{x}}}$$
(2)

2.2 Existing fourth moment-based method for LRS

The existing fourth moment-based method (Lu et al. 2010) for estimating LRS is established on three-point estimation, in which \(P_{f}\) is approximated by Eq. (3) numerically (Xiao and Lu 2018; Zhao and Lu 2007; Zhao and Ono 2004) and the LRS is derived on this numerical approximation of \(P_{f}\) by chain rule.

$$\begin{gathered} P_{f} \approx \Phi ( - \beta_{4M} ){ = }\Phi \left( { - \frac{{3(\alpha_{4g}^{{P_{f} }} - 1)\beta_{2M} + \alpha_{3g}^{{P_{f} }} (\beta_{2M}^{2} - 1)}}{{\sqrt {(5(\alpha_{3g}^{{P_{f} }} )^{2} - 9\alpha_{4g}^{{P_{f} }} + 9)(1 - \alpha_{4g}^{{P_{f} }} )} }}} \right) \hfill \\ \quad \quad \quad \quad \quad \;\;{ = }\Phi \left( { - \frac{{3(\alpha_{4g}^{{P_{f} }} - 1)({{\alpha_{1g}^{{P_{f} }} } \mathord{\left/ {\vphantom {{\alpha_{1g}^{{P_{f} }} } {\alpha_{2g}^{{P_{f} }} }}} \right. \kern-0pt} {\alpha_{2g}^{{P_{f} }} }}) + \alpha_{3g}^{{P_{f} }} (({{\alpha_{1g}^{{P_{f} }} } \mathord{\left/ {\vphantom {{\alpha_{1g}^{{P_{f} }} } {\alpha_{2g}^{{P_{f} }} }}} \right. \kern-0pt} {\alpha_{2g}^{{P_{f} }} }})^{2} - 1)}}{{\sqrt {(5(\alpha_{3g}^{{P_{f} }} )^{2} - 9\alpha_{4g}^{{P_{f} }} + 9)(1 - \alpha_{4g}^{{P_{f} }} )} }}} \right) \hfill \\ \end{gathered}$$
(3)

In Eq. (3), the \(m{\text{th}}\) moment \(\alpha_{mg}^{{P_{f} }} (m = 1,2,3,4)\) of the performance function is approximately estimated by three-point estimation integral procedure. \(\Phi ( \cdot )\) represents the cumulative distribution function of the standard normal variable, \(\beta_{4M} = \frac{{3(\alpha_{4g}^{{P_{f} }} - 1)\beta_{2M} + \alpha_{3g}^{{P_{f} }} (\beta_{2M}^{2} - 1)}}{{\sqrt {(5(\alpha_{3g}^{{P_{f} }} )^{2} - 9\alpha_{4g}^{{P_{f} }} + 9)(1 - \alpha_{4g}^{{P_{f} }} )} }}\) is the fourth moment reliability index, and \(\beta_{2M} = {{\alpha_{1g}^{{P_{f} }} } \mathord{\left/ {\vphantom {{\alpha_{1g}^{{P_{f} }} } {\alpha_{2g}^{{P_{f} }} }}} \right. \kern-0pt} {\alpha_{2g}^{{P_{f} }} }}\) is the second moment reliability index.

Based on the numerically approximate expression of \(P_{f}\) in Eq. (3), the LRS \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \theta_{{X_{i} }}^{(k)} }}} \right. \kern-0pt} {\partial \theta_{{X_{i} }}^{(k)} }}\) is derived by the differential chain rule in Ref. (Lu et al. 2010) in Eq. (4).

$$\begin{gathered} \frac{{\partial P_{f} }}{{\partial \theta_{{X_{i} }}^{(k)} }} \approx \frac{{\partial P_{f} }}{{\partial \beta_{4M} }}\frac{{\partial \beta_{4M} }}{{\partial \theta_{{X_{i} }}^{(k)} }} \hfill \\ \, = \frac{{\partial P_{f} }}{{\partial \beta_{4M} }}\left[ {\frac{{\partial \beta_{4M} }}{{\partial \beta_{2M} }}\left( {\frac{{\partial \beta_{2M} }}{{\partial \alpha_{1g}^{{P_{f} }} }}\frac{{\partial \alpha_{1g}^{{P_{f} }} }}{{\partial \theta_{{X_{i} }}^{(k)} }} + \frac{{\partial \beta_{2M} }}{{\partial \alpha_{2g}^{{P_{f} }} }}\frac{{\partial \alpha_{2g}^{{P_{f} }} }}{{\partial \theta_{{X_{i} }}^{(k)} }}} \right) + \frac{{\partial \beta_{4M} }}{{\partial \alpha_{3g}^{{P_{f} }} }}\frac{{\partial \alpha_{3g}^{{P_{f} }} }}{{\partial \theta_{{X_{i} }}^{(k)} }} + \frac{{\partial \beta_{4M} }}{{\partial \alpha_{4g}^{{P_{f} }} }}\frac{{\partial \alpha_{4g}^{{P_{f} }} }}{{\partial \theta_{{X_{i} }}^{(k)} }}} \right] \hfill \\ \end{gathered},$$
(4)

where the partial differentials required in Eq. (4) can be obtained analytically except for \({{\partial \alpha_{mg}^{{P_{f} }} } \mathord{\left/ {\vphantom {{\partial \alpha_{mg}^{{P_{f} }} } {\partial \theta_{{X_{i} }}^{\left( k \right)} }}} \right. \kern-0pt} {\partial \theta_{{X_{i} }}^{\left( k \right)} }}(m = 1,2,3,4)\), and \({{\partial \alpha_{mg}^{{P_{f} }} } \mathord{\left/ {\vphantom {{\partial \alpha_{mg}^{{P_{f} }} } {\partial \theta_{{X_{i} }}^{\left( k \right)} }}} \right. \kern-0pt} {\partial \theta_{{X_{i} }}^{\left( k \right)} }}\) can also be obtained by the three-point estimation integral procedure after the transformation (Lu et al. 2010).

It can be observed from Eq. (4) that the existing fourth moment-based method for LRS is derived by the chain rule and the numerical approximation of \(P_{f}\). However, the numerical approximation function of \(P_{f}\) may not be applicable to its derivative function, thus this derivation is not rigorous in theory and may lead to the error of LRS. In addition, the computational cost of estimating \(\alpha_{mg}^{{P_{f} }}\) and \({{\partial \alpha_{mg}^{{P_{f} }} } \mathord{\left/ {\vphantom {{\partial \alpha_{mg}^{{P_{f} }} } {\partial \theta_{{X_{i} }}^{\left( k \right)} }}} \right. \kern-0pt} {\partial \theta_{{X_{i} }}^{\left( k \right)} }}\)\((m = 1,2,3,4;i = 1,2, \cdot \cdot \cdot ,n;k = 1,2, \cdot \cdot \cdot ,l_{i} )\) increases exponentially with the dimension of random input due to the three-point estimation is employed in the existing method.

3 The proposed method for LRS

In order to avoid the limitations of the existing fourth moment method for LRS, a new and efficient method is proposed for estimating the LRS in this paper. The basic idea of the proposed method includes equivalent derivation of LRS to the weighted sum of a series of FPs and design of multiplicative dimensional reduction-based sharing integral node for estimating the derived FPs.

3.1 Equivalent derivation of LRS

According to the definition of LRS in Eq. (2), the equivalent expression in Eq. (5) can be obtained by integral transformation,

$$\frac{{\partial P_{f} }}{{\partial \theta_{{X_{i} }}^{(k)} }} = \int_{F} {\frac{{\partial f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}{{\partial \theta_{{X_{i} }}^{(k)} }}d{\varvec{x}}} { = }\int_{F} {\omega_{{\theta_{{X_{i} }}^{(k)} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}}$$
(5)

in which \(\omega_{{\theta_{{X_{i} }}^{\left( k \right)} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} ){ = }\frac{1}{{f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}\frac{{\partial f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}{{\partial \theta_{{X_{i} }}^{(k)} }}\).

When the random input is non-normal, the transformation proposed by Rackwitz et al. can be used to obtain the equivalent normal variable corresponding to the non-normal random one (Rackwitz and Flessler 1978; Hohenbichler and Rackwitz 1981). Assuming that the non-normal variable \(X\) follows a distribution with cumulative distribution function (CDF) \(F_{X} (x)\) and PDF \(f_{X} (x)\). The equivalent normal variable corresponding to non-normal variable \(X\) is denoted as \(X^{\prime} \sim N\left( {\mu^{\prime}_{X} ,\sigma^{\prime}_{{X^{2} }} } \right)\), and its two distribution parameters \(\mu^{\prime}_{X}\) and \(\sigma^{\prime}_{X}\) can be determined by the following equivalent transformation established by Refs. (Rackwitz and Flessler 1978; Hohenbichler and Rackwitz 1981).

$$F_{X} \left( {x^{ * } } \right) = \Phi_{{X^{\prime}}} \left( {x^{ * } } \right) = \Phi \left( {\frac{{x^{ * } - \mu^{\prime}_{X} }}{{\sigma^{\prime}_{X} }}} \right)$$
(6)
$$f_{X} \left( {x^{ * } } \right) = \Phi^{\prime}_{{X^{\prime}}} \left( {x^{ * } } \right) = \Phi^{\prime}\left( {\frac{{x^{ * } - \mu^{\prime}_{X} }}{{\sigma^{\prime}_{X} }}} \right) = \frac{1}{{\sigma^{\prime}_{X} }}\varphi \left( {\frac{{x^{ * } - \mu^{\prime}_{X} }}{{\sigma^{\prime}_{X} }}} \right)$$
(7)

where \({\varvec{x}}^{ * }\) is the most probable failure point (MPP), \(\Phi ( \cdot )\) and \(\varphi ( \cdot )\) are the CDF and PDF of standard normal variable, respectively, and \(\Phi^{\prime}( \cdot )\) is the derivative function of standard normal CDF.

Equations (6) and (7) establish the numerical relationship among the distribution parameters of the equivalent normal variable and those of the non-normal variable, and based on this numerical relationship, the local reliability sensitivity with respect to the distribution parameter of equivalent normal variable can be numerically transformed to that with respect to the distribution parameter of non-normal variable. Since this transformation has no analytical solution generally, the error is inevitable.

When the random input variables are dependent variables, the dependent random variables can also be transformed into independent normal ones (Rosenblatt 1952; Lu et al. 2020). In this paper, the input variables following independently normal distribution are concerned. When \(X_{i} \, (i = 1,2, \ldots ,n)\) follows normal distribution with the mean of \(\mu_{{X_{i} }}\) and standard deviation of \(\sigma_{{X_{i} }}\), denoted by \(\theta_{{X_{i} }}^{(1)} { = }\mu_{{X_{i} }}\) and \(\theta_{{X_{i} }}^{(2)} { = }\sigma_{{X_{i} }},\) respectively, \(\omega_{{\theta_{{X_{i} }}^{\left( k \right)} }} ({\varvec{x}}, \, {\varvec{\theta}}_{{\varvec{X}}} ){\kern 1pt} {\kern 1pt} (k = 1,2)\) can be derived as Eqs. (8) and (9).

$$\omega_{{\theta_{{X_{i} }}^{\left( 1 \right)} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} ) = \omega_{{\mu_{{X_{i} }} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} ) = \frac{1}{{f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}\frac{{\partial f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}{{\partial \mu_{{X_{i} }} }} = \frac{{x_{i} - \mu_{{X_{i} }} }}{{\sigma_{{X_{i} }}^{2} }}$$
(8)
$$\omega_{{\theta_{{X_{i} }}^{\left( 2 \right)} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} ){ = }\omega_{{\sigma_{{X_{i} }} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} ){ = }\frac{1}{{f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}\frac{{\partial f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )}}{{\partial \sigma_{{X_{i} }} }} = \frac{1}{{\sigma_{{X_{i} }} }}\left( {\frac{{(x_{i} - \mu_{{X_{i} }} )^{2} }}{{\sigma_{{X_{i} }}^{2} }} - 1} \right)$$
(9)

By substituting Eqs. (8) and (9) into Eq. (5), the LRS with respect to mean and standard deviation can be obtained in Eqs. (10) and (11), respectively.

$$\begin{gathered} \frac{{\partial P_{f} }}{{\partial \theta_{{X_{i} }}^{\left( 1 \right)} }}{ = }\frac{{\partial P_{f} }}{{\partial \mu_{{X_{i} }} }}{ = }\int_{F} {\omega_{{\mu_{{X_{i} }} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}} \\ { = }\int_{F} {\frac{{x_{i} - \mu_{{X_{i} }} }}{{\sigma_{{X_{i} }}^{2} }}f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}}\quad \quad \quad \quad \quad (i = 1,2, \ldots ,n) \\ { = }\frac{1}{{\sigma_{{X_{i} }}^{2} }}\int_{F} {x_{i} f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}} - \frac{{\mu_{{X_{i} }} }}{{\sigma_{{X_{i} }}^{2} }}P_{f} \\ { = }\frac{1}{{\sigma_{{X_{i} }}^{2} }}\varphi_{{\mu_{{X_{i} }} }} - \frac{{\mu_{{X_{i} }} }}{{\sigma_{{X_{i} }}^{2} }}P_{f} \\ \end{gathered}$$
(10)
$$\begin{gathered} \frac{{\partial P_{f} }}{{\partial \theta_{{X_{i} }}^{\left( 2 \right)} }}{ = }\frac{{\partial P_{f} }}{{\partial \sigma_{{X_{i} }} }}{ = }\int_{F} {\omega_{{\sigma_{{X_{i} }} }} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}} \\ { = }\int_{F} {\frac{1}{{\sigma_{{X_{i} }} }}\left( {\frac{{(x_{i} - \mu_{{X_{i} }} )^{2} }}{{\sigma_{{X_{i} }}^{2} }} - 1} \right)f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}}\quad \quad \quad \quad \quad (i = 1,2, \ldots ,n) \\ { = }\frac{1}{{\sigma_{{X_{i} }}^{3} }}\int_{F} {(x_{i} - \mu_{{X_{i} }} )^{2} f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}} - \frac{1}{{\sigma_{{X_{i} }} }}P_{f} \\ { = }\frac{1}{{\sigma_{{X_{i} }}^{3} }}\varphi_{{\sigma_{{X_{i} }} }} - \frac{1}{{\sigma_{{X_{i} }} }}P_{f} \\ \end{gathered}$$
(11)

where \(\varphi_{{\mu_{{X_{i} }} }} = \int_{F} {x_{i} f_{{\varvec{X}}} \left( {{\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} } \right) \, } d{\varvec{x}}\), \(\varphi_{{\sigma_{{X_{i} }} }} = \int_{F} {\left( {x_{i} - \mu_{{X_{i} }} } \right)^{2} f_{{\varvec{X}}} \left( {{\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} } \right) \, } d{\varvec{x}}\).

It can be observed from Eqs. (10) and (11) that, through the equivalent integral transformation, the LRS is derived as the estimation of \(P_{f}\), \(\varphi_{{\mu_{{X_{i} }} }}\) and \(\varphi_{{\sigma_{{X_{i} }} }}\)\((i = 1,2, \ldots ,n)\), while the integral domains in the integral of estimating \(\varphi_{{\mu_{{X_{i} }} }}\) and \(\varphi_{{\sigma_{{X_{i} }} }}\) are same as the failure domain of estimating \(P_{f}\) defined by the original performance function, and the integrand functions of estimating \(\varphi_{{\mu_{{X_{i} }} }}\) and \(\varphi_{{\sigma_{{X_{i} }} }}\) are related to \(x_{i}\) and the original PDF \(f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )\). By converting equivalently the integrand functions of estimating \(\varphi_{{\mu_{{X_{i} }} }}\) and \(\varphi_{{\sigma_{{X_{i} }} }}\) into the extended PDFs, \(\varphi_{{\mu_{{X_{i} }} }}\) and \(\varphi_{{\sigma_{{X_{i} }} }}\) can be derived as the estimations of the extended FPs, in which the performance functions are still \(g({\varvec{x}})\) but the PDFs are the extended PDFs.

3.2 Reconstruction of extended PDFs for estimating \(\varphi_{{\mu_{{X_{i} }} }}\) and \(\varphi_{{\sigma_{{X_{i} }} }}\)

Since the integrand function \((x_{i} - \mu_{{X_{i} }} )^{2} f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )\) in \(\varphi_{{\sigma_{{X_{i} }} }} = \int_{F} {(x_{i} - \mu_{{X_{i} }} )^{2} f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )} d{\varvec{x}}\) is always greater than or equal to zero, it is easy to reconstruct its extended PDF, and it is demonstrated as follows.

It is well-known that the PDF \(f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )\) of independent random inputs can be expressed as the form in Eq. (12), thus \(\varphi_{{\sigma_{{X_{i} }} }}\) can be derived as the form in Eq. (13) equivalently.

$$f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} ){ = }f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )$$
(12)
$$\begin{gathered} \varphi_{{\sigma_{{X_{i} }} }} = \int_{F} {(x_{i} - \mu_{{X_{i} }} )^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )} d{\varvec{x}} \\ { = }\int_{F} {\frac{{\int_{{x_{i} }} {(x_{i} - \mu_{{X_{i} }} )^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )dx_{i} } }}{{\int_{{x_{i} }} {(x_{i} - \mu_{{X_{i} }} )^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )dx_{i} } }}(x_{i} - \mu_{{X_{i} }} )^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )} d{\varvec{x}} \\ { = }\sigma_{{X_{i} }}^{2} \int_{F} {f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )d{\varvec{x}}} \\ \end{gathered}$$
(13)

where \({\varvec{X}}_{ - i} = \left[ {X_{1} , \ldots ,X_{i - 1} ,X_{i + 1} , \ldots ,X_{n} } \right]^{T}\), \({\varvec{\theta}}_{{X_{i} }}\) and \({\varvec{\theta}}_{{{\varvec{X}}_{ - i} }}\) represent the distribution parameter vectors of \(X_{i}\) and \({\varvec{X}}_{ - i},\) respectively. \(f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} ){ = }\frac{{(x_{i} - \mu_{{X_{i} }} )^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )}}{{\int_{{x_{i} }} {(x_{i} - \mu_{{X_{i} }} )^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )dx_{i} } }}{ = }\frac{{(x_{i} - \mu_{{X_{i} }} )^{2} }}{{\sigma_{{X_{i} }}^{2} }}f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )\) is the extended PDF of random variable \(X_{i}\) in estimating \(\varphi_{{\sigma_{{X_{i} }} }}\), and \({\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)}\) is the distribution parameter vector of extended PDF \(f_{{X_{i} }}^{\left( 1 \right)} ( \, \cdot \, , \, \cdot \, )\). Obviously, the reconstructed \(f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )\) satisfies the basic properties of PDF.

By the derivation of Eq. (13), \(\varphi_{{\sigma_{{X_{i} }} }}\)\((i = 1,2, \ldots ,n)\) is transformed into the extended FP with the performance function \(g({\varvec{x}})\) and the extended joint PDF \(f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )\). In this paper, estimating \(\varphi_{{\sigma_{{X_{i} }} }}\) is completed by the fourth moment method based on the multiplicative dimensional reduction integral. Since the performance functions of \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(P_{f}\) are same, and there is an explicit relation between the extended PDF \(f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )\) of \(X_{i}\) and the original PDF \(f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )\) of \(X_{i}\), on which the next subsection will design the same set of multiplicative dimensional reduction integral nodes to estimate \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(P_{f}\) simultaneously. Then, the LRS \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \sigma_{{X_{i} }} }}} \right. \kern-0pt} {\partial \sigma_{{X_{i} }} }}\) with respect to standard deviation can be obtained by Eq. (11).

Similarly, the following part shows the procedure for reconstructing the extended PDF of estimating \(\varphi_{{\mu_{{X_{i} }} }}\). For reconstructing extended PDF of estimating \(\varphi_{{\mu_{{X_{i} }} }}\), \(\varphi_{{\mu_{{X_{i} }} }}\) is transformed as follows,

$$\begin{gathered} \varphi_{{\mu_{{X_{i} }} }} { = }\int_{F} {x_{i} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )} d{\varvec{x}} \hfill \\ { = }\int_{F} {\frac{{x_{i}^{2} + \mu_{{X_{i} }}^{2} - (x_{i} - \mu_{{X_{i} }} )^{2} }}{{2\mu_{{X_{i} }} }}f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )} d{\varvec{x}} \hfill \\ { = }\frac{1}{{2\mu_{{X_{i} }} }}\int_{F} {x_{i}^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )} d{\varvec{x}} - \frac{1}{{2\mu_{{X_{i} }} }}\int_{F} {(x_{i} - \mu_{{X_{i} }} )^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )} d{\varvec{x}}{ + }\frac{{\mu_{{X_{i} }} }}{2}P_{f} \hfill \\ { = }\frac{1}{{2\mu_{{X_{i} }} }}\varphi_{{x_{i}^{2} }} - \frac{1}{{2\mu_{{X_{i} }} }}\varphi_{{\sigma_{{X_{i} }} }} { + }\frac{{\mu_{{X_{i} }} }}{2}P_{f} \hfill \\ \end{gathered}$$
(14)

in which \(\varphi_{{x_{i}^{2} }} { = }\int_{F} {x_{i}^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )} d{\varvec{x}}\), i.e., \(\varphi_{{x_{i}^{2} }}\) is also the integral over the failure domain defined by the performance function \(g({\varvec{x}})\).

By reconstructing the integrand function of estimating \(\varphi_{{x_{i}^{2} }}\) as an extended PDF, \(\varphi_{{x_{i}^{2} }}\) can also be derived equivalently as the extended FP. Thus, the following equivalent transformation is executed for \(\varphi_{{x_{i}^{2} }}\),

$$ \begin{gathered} \varphi_{{x_{i}^{2} }} { = }\int_{F} {x_{i}^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )d{\varvec{x}}} \\\quad \quad{ = }\int_{F} {\frac{{\int_{{x_{i} }} {x_{i}^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )dx_{i} } }}{{\int_{{x_{i} }} {x_{i}^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )dx_{i} } }}x_{i}^{2} f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )d{\varvec{x}}} \\ { = }(\sigma_{{X_{i} }}^{2} + \mu_{{X_{i} }}^{2} )\int_{F} {f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )d{\varvec{x}}} \\ \end{gathered} $$
(15)

where \(f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} ){ = }\frac{{x_{i}^{2} }}{{\sigma_{{X_{i} }}^{2} + \mu_{{X_{i} }}^{2} }}f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )\) is the extended PDF of \(X_{i}\) in estimating \(\varphi_{{x_{i}^{2} }}\), and \({\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)}\) is the distribution parameter vector of the extended PDF \(f_{{X_{i} }}^{\left( 2 \right)} ( \, \cdot \, , \, \cdot \, )\).

Similar to the estimation of \(\varphi_{{\sigma_{{X_{i} }} }}\)\((i = 1,2, \cdot \cdot \cdot ,n)\), \(\varphi_{{x_{i}^{2} }}\)\((i = 1,2, \cdot \cdot \cdot ,n)\) can also be estimated by the fourth moment method based on the multiplicative dimensional reduction integral. Since the performance function for estimating \(\varphi_{{x_{i}^{2} }}\) is same as that for estimating \(P_{f}\), and the extended PDF \(f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )\) about \(X_{i}\) in estimating \(\varphi_{{x_{i}^{2} }}\) has an explicit relation with the PDF \(f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )\) about \(X_{i}\) in estimating \(P_{f}\), the same set of multiplicative dimensional reduction integral nodes can be used to estimate \(\varphi_{{x_{i}^{2} }}\) and \(P_{f}\) simultaneously.

It can be known from above derivations that \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \sigma_{{X_{i} }} }}} \right. \kern-0pt} {\partial \sigma_{{X_{i} }} }}\)\((i = 1,2, \cdot \cdot \cdot ,n)\) can be obtained by substituting the extended FP \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(P_{f}\), which are estimated by the same set of the multiplicative dimensional reduction integral nodes, into Eq. (11), and \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \mu_{{X_{i} }} }}} \right. \kern-0pt} {\partial \mu_{{X_{i} }} }}\)\((i = 1,2, \cdot \cdot \cdot ,n)\) can be obtained by substituting \(\varphi_{{\mu_{{X_{i} }} }}\), which is estimated in Eq. (14) through \(\varphi_{{x_{i}^{2} }}\), \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(P_{f}\) estimations by the same set of the multiplicative dimensional reduction integral nodes, and \(P_{f}\) into Eq. (10). In the next section, the strategy of multiplicative dimensional reduction-based sharing integral nodes is designed for simultaneously estimating the first four moments required by \(P_{f}\), \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\).

3.3 Fourth moment method for estimating \(P_{f}\), \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) by multiplicative dimensional reduction integral

In this paper, the fourth moment method based on multiplicative dimensional reduction integral is employed to estimate the FP \(P_{f}\) and the extended FPs \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\). According to the fact that \(P_{f}\) and the extended FPs \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) have the same performance function \(g({\varvec{x}})\), and there are explicit relations between the extended PDFs \(f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )\), \(f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )\) and the PDF \(f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )\) about \(X_{i}\) in estimating \(\varphi_{{\sigma_{{X_{i} }} }}\), \(\varphi_{{x_{i}^{2} }}\) and \(P_{f},\) respectively, the strategy of sharing integral nodes is designed to estimate the required first four moments by \(P_{f}\), \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\), i.e., through the same set of Gaussian integral nodes, the first four moments required by \(P_{f}\), \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) are estimated simultaneously, and then \(P_{f}\), \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) can be obtained by the fourth moment method.

3.3.1 Moments estimation of performance function based on multiplicative dimensional reduction integral

On the basis of the first-order expansion and equivalent logarithmic transformation of the high-dimensional model in Ref. (Zhang and Pandey 2013), the performance function \(g = g({\varvec{X}})\) can be approximately expressed as the product of multiple univariate functions in Eq. (16),

$$g({\varvec{X}}) \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{1 - n} \prod\limits_{k = 1}^{n} {g(\mu_{{X_{1} }} , \cdot \cdot \cdot ,\mu_{{X_{k - 1} }} ,X_{k} ,\mu_{{X_{k + 1} }} , \cdot \cdot \cdot ,\mu_{{X_{n} }} )}$$
(16)

in which \(\mu_{X} = \left[ {\mu_{{X_{1} }} ,\mu_{{X_{2} }} , \ldots ,\mu_{{X_{n} }} } \right]^{T}\) is the mean vector of the random input vector \({\varvec{X}}\).

By use of Eq. (16), the \(n{\text{ - dimensional}}\) integral for the \(m{\text{th}}\) origin moment \(M_{mg}\) of the performance function \(g = g({\varvec{X}})\) can be transformed into the product of \(n\) univariate integrals in Eq. (17).

$$\begin{gathered} M_{mg} = \int_{{R^{n} }} {\left[ {g({\varvec{X}})} \right]}^{m} f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )d{\varvec{x}} \\ \, \approx \int_{{R^{n} }} {\left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} } \prod\limits_{k = 1}^{n} {\left[ {g(x_{k} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} )} \right]^{m} } f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )d{\varvec{x}} \\ \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} \prod\limits_{k = 1}^{n} {\int_{{x_{k} }} {\left[ {g(x_{k} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} )} \right]^{m} f_{{X_{k} }} (x_{k} ,{\varvec{\theta}}_{{X_{k} }} )dx_{k} } } \\ \end{gathered}$$
(17)

Each univariate integral \(\int_{{x_{k} }} {\left[ {g(x_{k} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} )} \right]^{m} f_{{X_{k} }} (x_{k} ,{\varvec{\theta}}_{{X_{k} }} )dx_{k} } \, k = (1,2, \cdot \cdot \cdot ,n)\) in Eq. (17) can be estimated by Gaussian integral (Zhou and Nowak 1988; Zhang and Pandey 2013) in Eq. (18),

$$\begin{gathered} M_{mg} \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} \prod\limits_{k = 1}^{n} {\int_{{x_{k} }} {\left[ {g(x_{k} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} )} \right]^{m} f_{{X_{k} }} (x_{k} ,{\varvec{\theta}}_{{X_{k} }} )dx_{k} } } \hfill \\ \, \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} \prod\limits_{k = 1}^{n} {\left\{ {\sum\limits_{j = 1}^{{N_{k} }} {w_{k}^{(j)} \left[ {g(x_{{_{k} }}^{(j)} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} )} \right]^{m} } } \right\}} \hfill \\ \end{gathered},$$
(18)

where \(x_{k}^{(j)}\) and \(w_{k}^{(j)}\)\((j = 1,2, \cdot \cdot \cdot ,N_{k} )\) respectively represent the \(j{\text{th}}\) Gaussian integral node and the corresponding Gaussian integral weight of \(x_{k}\), and \(N_{k}\) represents the number of Gaussian integral node. \({\varvec{\mu}}_{{{\varvec{X}}_{ - k} }}\) is the vector composed of the mean values of the remaining variables except \(\mu_{{X_{k} }}\) of \(x_{k}\), i.e., \({\varvec{\mu}}_{{X_{ - k} }} = \left[ {\mu_{{X_{1} }} , \ldots ,\mu_{{X_{k - 1} }} ,\mu_{{X_{k + 1} }} , \ldots ,\mu_{{X_{n} }} } \right]^{T}\). In this paper, the input variables in Eq. (18) are following independently normal distribution, for non-normal random input variables, they should be transformed into equivalent normal variable first. Then it can refer Appendix A for Gaussian integral formulas, five-point Gaussian integral nodes and corresponding weights.

3.3.2 The strategy of sharing integral node for the first four moments required by \(P_{f}\), \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\)

According to the definition of the origin moment of \(g({\varvec{x}})\), the first four origin moments \(M_{mg}^{{P_{f} }}\)\((m = 1,2,3,4)\) required by \(P_{f}\) can be obtained using the multiplicative dimensional reduction integral in Eqs. (17) and (18), i.e., \(M_{mg}^{{P_{f} }} = M_{mg}\).

Refer to Appendix B for the transformation relation between the origin moment and the central moment of the performance function, the first four central moments \(\alpha_{mg}^{{P_{f} }}\) \((m = 1,2,3,4)\) of \(g({\varvec{x}})\) required by \(P_{f}\) can be obtained, on which the FP \(P_{f}\) can be estimated by Eq. (3) of the fourth moment method.

Similarly, the first four origin moments \(M_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }}\) and \(M_{mg}^{{\varphi_{{x_{i}^{2} }} }}\)\((m = 1,2,3,4)\) required by \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) can be, respectively, obtained in Eqs. (19) and (20) using the multiplicative dimensional reduction integral method shown in Eqs. (17) and (18).

$$\begin{gathered} M_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }} = \int_{{R^{n} }} {(g({\varvec{x}}))^{m} f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )d{\varvec{x}}} \hfill \\ \, \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} \prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{n} {\left[ {\int_{{x_{k} }} {(g(x_{k} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} ))^{m} f_{{X_{k} }} (x_{k} ,{\varvec{\theta}}_{{X_{k} }} )dx_{k} } } \right]} \cdot \int_{{x_{i} }} {(g(x_{i} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )} dx_{i} \hfill \\ \, \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} \prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{n} {\left[ {\sum\limits_{j = 1}^{{N_{k} }} {w_{k}^{(j)} (g(x_{k}^{(j)} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} ))^{m} } } \right]} \cdot \left\{ {\sum\limits_{j = 1}^{{N_{i} }} {w_{i}^{(j)} \left[ {(g(x_{i}^{(j)} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} \frac{{(x_{i}^{(j)} - \mu_{{X_{i} }} )^{2} }}{{\sigma_{{X_{i} }}^{2} }}} \right]} } \right\},(i = 1,2, \cdot \cdot \cdot ,n) \hfill \\ \end{gathered}$$
(19)
$$\begin{gathered} M_{mg}^{{\varphi_{{x_{i}^{2} }} }} = \int_{{R^{n} }} {(g({\varvec{x}}))^{m} f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )d{\varvec{x}}} \hfill \\ \, \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} \prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{n} {\left[ {\int_{{x_{k} }} {(g(x_{k} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} ))^{m} f_{{X_{k} }} (x_{k} ,{\varvec{\theta}}_{{X_{k} }} )dx_{k} } } \right]} \cdot \int_{{x_{i} }} {(g(x_{i} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )} dx_{i} \hfill \\ \, \approx \left[ {g({\varvec{\mu}}_{{\varvec{X}}} )} \right]^{m(1 - n)} \prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{n} {\left[ {\sum\limits_{j = 1}^{{N_{k} }} {w_{k}^{(j)} (g(x_{k}^{(j)} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - k} }} ))^{m} } } \right]} \cdot \left\{ {\sum\limits_{j = 1}^{{N_{i} }} {w_{i}^{(j)} \left[ {(g(x_{i}^{(j)} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} \frac{{(x_{i}^{(j)} )^{2} }}{{\sigma_{{X_{i} }}^{2} + \mu_{{X_{i} }}^{2} }}} \right]} } \right\},(i = 1,2, \cdot \cdot \cdot ,n) \hfill \\ \end{gathered}$$
(20)

The following Eqs. (21) and (22), respectively, extract the univariate integral about \(x_{i}\) in Eqs. (19) and (20),

$$\int_{{x_{i} }} {(g(x_{i} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )} dx_{i} { = }\int_{{x_{i} }} {(g(x_{i} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} \frac{{(x_{i} - \mu_{{X_{i} }} )^{2} }}{{\sigma_{{X_{i} }}^{2} }}f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )} dx_{i}$$
(21)
$$\int_{{x_{i} }} {(g(x_{i} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )} dx_{i} { = }\int_{{x_{i} }} {(g(x_{i} ,{\varvec{\mu}}_{{{\varvec{X}}_{ - i} }} ))^{m} \frac{{x_{i}^{2} }}{{\sigma_{{X_{i} }}^{2} + \mu_{{X_{i} }}^{2} }}f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )} dx_{i}$$
(22)

in above equations, \(f_{{X_{i} }} (x_{i} ,{\varvec{\theta}}_{{X_{i} }} )\) can be used as the PDF to select the Gaussian integral nodes of \(x_{i}\), so that the integral nodes for \(M_{mg}^{{P_{f} }}\) can be reused to estimate \(M_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }}\) and \(M_{mg}^{{\varphi_{{x_{i}^{2} }} }}\)\((m = 1,2,3,4)\) simultaneously, which realizes using the same set of integral nodes to simultaneously estimate the first four origin moments of the performance function \(g({\varvec{x}})\) under the original PDF \(f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )\) as well as extended PDFs \(f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )\) and \(f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )\), respectively.

Refer to Appendix B for the transformation relation between the origin moment and the central moment of the performance function, the required first four central moments \(\alpha_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }}\) and \(\alpha_{mg}^{{\varphi_{{x_{i}^{2} }} }}\)\((m = 1,2,3,4;i = 1,2, \cdot \cdot \cdot ,n)\) can be obtained from the first four origin moments \(M_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }}\) and \(M_{mg}^{{\varphi_{{x_{i}^{2} }} }}\) of \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }},\) respectively, and then the extended FPs \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) can be, respectively, estimated by Eq. (3) of the fourth moment method.

So far, the FP \(P_{f}\) as well as the extended FPs \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) can be estimated, on which \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \sigma_{{X_{i} }} }}} \right. \kern-0pt} {\partial \sigma_{{X_{i} }} }}\) and \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \mu_{{X_{i} }} }}} \right. \kern-0pt} {\partial \mu_{{X_{i} }} }}\)\((i = 1,2, \cdot \cdot \cdot ,n)\) can be obtained by Eq. (11) and (10), respectively.

3.4 The detailed steps of the proposed method for estimating LRS

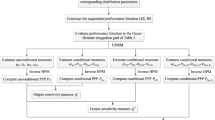
Based on the above theoretical derivation and the strategy of sharing integral node, the flow chart of the proposed method for estimating LRS is shown in Fig. 1, and the detailed steps are listed as follows.

Fig. 1
figure 1

Flow chart of the proposed method for estimating LRS

Full size image

Step 1 The input variables following independently normal distribution are concerned, for the case with non-normal input variables, the non-normal input variables can be transformed into normal ones at first (Rackwitz and Flessler 1978; Hohenbichler and Rackwitz 1981). So it corresponds to “Normal Gauss-Hermite” in the Tables of Appendix A, then select the corresponding Gaussian integral formulas, and record \(N_{k}\) selected Gaussian integral nodes and corresponding weights of each integration variable \(x_{k}\) as \((x_{k}^{\left( j \right)} ,w_{k}^{\left( j \right)} )\)\((j = 1,2, \cdot \cdot \cdot ,N_{k} ;\)\(k = 1,2, \cdot \cdot \cdot ,n)\).

Step 2 Estimate the first four origin moments \(M_{mg}^{{P_{f} }}\)\((m = 1,2,3,4)\) of \(g({\varvec{x}})\) with PDF \(f_{{\varvec{X}}} ({\varvec{x}},{\varvec{\theta}}_{{\varvec{X}}} )\) by Eq. (18). Then estimate the first four center moments \(\alpha_{mg}^{{P_{f} }}\) \((m = 1,2,3,4)\) corresponding to \(M_{mg}^{{P_{f} }}\) by the conversion relation between the origin moment and the central moment. Finally, estimate the failure probability \(P_{f}\) by the fourth moment method in Eq. (3).

Step 3 By the strategy of multiplicative dimensional reduction-based sharing integral node, estimate the first four origin moments \(M_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }}\) and \(M_{mg}^{{\varphi_{{x_{i}^{2} }} }}\) \((m = 1,2,3,4;i = 1,2, \cdot \cdot \cdot ,n),\) respectively, by Eqs. (19) and (20), corresponding to the extended PDFs \(f_{{X_{i} }}^{\left( 1 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 1 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )\) and \(f_{{X_{i} }}^{\left( 2 \right)} (x_{i} ,{\varvec{\theta}}_{{X_{i} }}^{\left( 2 \right)} )f_{{{\varvec{X}}_{ - i} }} ({\varvec{x}}_{ - i} ,{\varvec{\theta}}_{{{\varvec{X}}_{ - i} }} )\). Then transform \(M_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }}\) and \(M_{mg}^{{\varphi_{{x_{i}^{2} }} }}\) into the first four central moments \(\alpha_{mg}^{{\varphi_{{\sigma_{{X_{i} }} }} }}\) and \(\alpha_{mg}^{{\varphi_{{x_{i}^{2} }} }}\)\((m = 1,2,3,4;i = 1,2, \cdot \cdot \cdot ,n),\) respectively, by the conversion relation of the origin moment and the central moment, on which the extended FPs \(\varphi_{{\sigma_{{X_{i} }} }}\) and \(\varphi_{{x_{i}^{2} }}\) can be, respectively, estimated by the fourth moment method in Eq. (3).

Step 4 Estimate \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \sigma_{{X_{i} }} }}} \right. \kern-0pt} {\partial \sigma_{{X_{i} }} }}\) and \({{\partial P_{f} } \mathord{\left/ {\vphantom {{\partial P_{f} } {\partial \mu_{{X_{i} }} }}} \right. \kern-0pt} {\partial \mu_{{X_{i} }} }}\)\((i = 1,2, \cdot \cdot \cdot ,n),\) respectively, by Eqs. (11) and (10).

3.5 Computational cost discussion of the proposed method

For estimating LRS with \(n{\text{ - dimensional}}\) random input, the computational cost of the proposed method in Ref. (Lu et al. 2010) is 3n, and it increases exponentially with the dimension of the random input. For the problem with medium and high dimension input variables, this existing method will face dimensionality disaster. The method proposed in this paper employs the multiplicative dimensional reduction integral to transform the n-dimensional integral of estimating the performance function moments into the product of n univariate integrals. For each univariate integral, it can be approximated with an acceptable precision only by estimating the performance function at a finite number of integral nodes. The computational cost of the proposed method is \(\sum\nolimits_{k = 1}^{n} {N_{k} } + 1\) in this paper, where \(N_{k}\) represents the number of integral nodes required for each univariate integral. The five-point Gaussian integral is employed in this paper, i.e., \(N_{k} = 5\)\((k = 1,2, \cdot \cdot \cdot ,n)\), thus the computational cost is 5n + 1 for n-dimensional random input, which increases linearly with the dimension of the random input. Thus, the proposed method in this paper is applicable for medium and high dimension problems.

4 Examples

Four examples are presented. The first one is a numerical example with exponential limit state performance function, which verifies the applicability of the proposed method. The second example considers a high dimensional numerical example with non-normal random variable, demonstrating the efficiency of the proposed method to the high dimension problems and the applicability to the problems with non-normal random variable. In the third example, a finite element example is presented to illustrate the applicability of the proposed method to implicit limit state performance function problems. Finally, an example of a system with multiple failure modes is presented to illustrate the limitation of the proposed method.

4.1 Numerical example with exponential limit state function

In order to illustrate the applicability and superiority of the proposed method, a numerical example in the form of an exponential limit state performance function with a high degree of nonlinear is presented, and its performance function is as follows,

$$g({\varvec{X}}) = \frac{{1.2X_{4} X_{5}^{2} X_{6}^{3} }}{{e^{{1.5X_{1} X_{2} - X_{3} }} }} - 1,$$
(23)

where \(X_{i}\)\((i = 1,2, \cdot \cdot \cdot ,6)\) are assumed as independent normal random inputs, \({\varvec{\mu}}_{{\varvec{X}}} = \left[ {1.5, \, 1, \, 1.5, \, 1.2, \, 1.2, \, 1.2} \right]^{{\text{T}}}\) and \({\varvec{Cov}}_{{\varvec{X}}} = \left[ {0.05, \, 0.06, \, 0.05, \, 0.05, \, 0.05, \, 0.05} \right]^{{\text{T}}}\) are their mean vector and variation coefficient vector, respectively.

The solutions of FP estimated by different methods are shown in Table 1. The solutions of LRS with respect to mean and standard deviation estimated by different methods are shown in Figs. 2 and 3, respectively. Among them, the Monte-Carlo method is denoted as MC, the method in Ref. (Lu et al. 2010) is denoted as Moment-4, the method proposed in this paper is denoted as PM. N is the number of evaluating the performance function. The solutions obtained by the MC can be regarded as the reference.

Table 1 The solutions of FP in 4.1
Full size table
Fig. 2
figure 2

LRS with respect to mean in 4.1

Full size image
Fig. 3
figure 3

LRS with respect to standard deviation in 4.1

Full size image

From Table 1, one can see that the results of the FP estimated by the Moment-4 and PM are close to that of the MC, however, the PM is obviously superior to the Moment-4 in terms of computational efficiency. From Figs. 2 and 3, one can see that the LRS solutions of the PM method are generally closer to those of the MC than those of the Moment-4 method. Therefore, the efficiency and applicability of the PM are verified by this numerical example.

4.2 High dimensional numerical example

In order to illustrate the advantages of the PM in computing efficiency, this example considers a numerical example with 18-dimensional random inputs, and the performance function can be expressed as

$$g({\varvec{X}}) = \frac{{\prod\nolimits_{i = 1}^{18} {X_{i} } }}{16} - 1,$$
(24)

where \(X_{i} (i = 1,2, \ldots ,18)\) are random inputs, the distribution parameters are listed in Table 2. In this example, the Weibull distribution of input \(X_{i} (i = 9,10, \ldots ,18)\) should be transformed into normal distribution (Rosenblatt 1952; Lu et al. 2020) first. Then based on the transformed normal distribution, the PM can be employed. The solutions of FP estimated by different methods are shown in Table 3. The solutions of LRS with respect to mean and standard deviation estimated by different methods are shown in Figs. 4 and 5, respectively.

Table 2 Distribution parameters of input variables in 4.2
Full size table
Table 3 The solutions of FP in 4.2
Full size table
Fig. 4
figure 4

LRS with respect to mean in 4.2

Full size image
Fig. 5
figure 5

LRS with respect to standard deviation in 4.2

Full size image

As can be seen from Table 3, the results of FP estimated by the moment-4 and PM are consistent, but the computational cost of the PM is far less than that of the Moment-4, and the computational cost of the Moment-4 is even 19 times more than that of the MC. With the increase of the dimension of the random inputs, the computational cost of the Moment-4 increases exponentially, which will face dimensionality disaster. On the contrary, the computational cost of the PM just increases linearly, it can also keep a small computational cost in the high dimensional problems. In this example, when the computational cost of the Moment-4 reaches \(3^{18}\), the computational cost of the PM is only 91, which reflects the significant advantage of the PM in computational efficiency. Figures 4 and 5 show the results of LRS with respect to mean and standard deviation of the three comparison methods. It can be seen that the results of the Moment-4 and PM are roughly consistent with those of the MC.

4.3 Simplified wing box structure

During flight, the wing box structure bears most of the vertical load from the wing, and the displacement of its free end may be relatively large. The simplified wing box model is shown in Fig. 6. Large displacement may cause rod deformation and lead to rod or plate damage, which is not allowed during flight, so it is necessary to calculate the displacement of wing box structure. The wing box structure consists of 64 rods and 42 plates. The 64 rods are divided into 3 groups according to their direction, and the lengths of the rods in the direction of \(x\), \(y\) and \(z\) are \(2L\), \(L\) and \(3L,\) respectively. The cross-sectional area of all rods is A, the thickness of all plates is TH, E and P are the elastic modulus and external load of all plates and rods, respectively, and Poisson's ratio is 0.3. Assuming that the input variables are independent normal variables, their distribution parameters are shown in Table 4.

Fig. 6
figure 6

Simplified wing box model

Full size image
Table 4 Distribution parameters of input variables of the wing box structure
Full size table

In this paper, the maximum displacement \(D_{\max }\) of the free end of the wing box structure can be expressed as

$$D_{\max } = D(L,A,E,P,TH),$$
(25)

where \(D(L,A,E,P,TH)\) is the implicit function about the input variable, which is determined by finite element analysis. Figure 7 shows the finite element model of the wing box structure constructed in ABAQUS 6.41, in which the input variables are fixed at their mean values. In addition, the deformation of the wing box structure is shown in Fig. 8. The failure is defined as that the value of \(D_{\max }\) exceeds \(6.6 \times 10^{ - 3}\)(m). Then the limit state performance function of the wing box structure can be expressed as \(g({\varvec{X}}) = 6.6 \times 10^{{{ - }3}} - D_{\max }\). The solutions of FP estimated by different methods are shown in Table 5. The solutions of LRS with respect to mean and standard deviation estimated by different methods are shown in Figs. 9 and 10, respectively.

Fig. 7
figure 7

Finite element model of wing box structure

Full size image
Fig. 8
figure 8

Deformation of wing box structure

Full size image
Table 5 The solutions of FP in 4.3
Full size table
Fig. 9
figure 9

LRS with respect to mean in 4.3

Full size image
Fig. 10
figure 10

LRS with respect to standard deviation in 4.3

Full size image

From Table 5, one can see that the results of FP for the moment-4 and PM are consistent with that for the MC, but the computational cost required by the PM is significantly lower than that of the Moment-4. Figures 9 and 10 show the LRS with respect to mean and standard deviation of the three comparison methods, respectively. It can be seen that the results of the Moment-4 and PM are very close to those of the MC. However, the computational cost of the PM is significantly lower than that of Moment-4, which shows the efficiency of the PM and the applicability of the PM to the problem with implicit limit state performance function.

In addition, the dimensionless LRS results are listed in Table 6. From Table 6, it can be seen that the increase of means of L and P will increase the FP, and the impact on FP of \(P\) mean is more than that of L mean on FP. While the increase of means of A, E and TH will decrease the FP, and the impact on FP of E mean is most. Contrarily, the increase of the standard deviation of all inputs will increase the FP, and the impact on FP of \(E\) standard deviation is most, while the impact on FP of \(A\) standard deviation is least. The above quantitative conclusions drawn from LRS analysis can provide gradient information for the failure probability concerned uncertainty design optimization.

Table 6 The values after non-dimensional treatment for LRS in 4.3
Full size table

4.4 One-bay elastoplastic frame

The accuracy of the proposed method is high and matches the accuracy of the existing method in Ref. (Lu et al. 2010) in the above three examples, but it should be pointed out that there are some limitations of the proposed method. That is, when the proposed method is applied to the problem with multiple failure modes or the problem with a small FP, the computational error may be large.

For addressing the limitation of proposed method in detail, the derivation of the proposed method is reviewed as follows. Firstly, the proposed method analytically derives the LRS as a weighted sum of FP and some extended FPs, and no error is introduced in this stage of the proposed method in case of normal input. Secondly, the proposed method dexterously designs a strategy of sharing integral nodes to estimate the first four moments for simultaneously obtaining the FP and extended FPs, and this stage of the proposed method may produce some errors due to the multiplicative dimensional reduction and Gaussian quadrature for the univariate integral are employed. The multiplicative dimensional reduction method transforms the \(n\)-dimensional multivariate integral into the product of \(n\) univariate integrals for estimating the first four moments of performance function, and this transformation is based on that the logarithm of performance function can be approximated by a polynomial of univariate function sum. For the case that the logarithm of performance function can be approximated with a high precision by the polynomial of univariate function sum, and the Gaussian integral nodes are enough to accurately estimate the univariate integral, then the precision of the proposed method is high. Namely, in case that the logarithm of performance function can be approximated accurately by the polynomial of univariate function sum, and the Gaussian integral nodes are enough to accurately estimate the univariate integral, then the proposed method can be reliably applied. Otherwise, the error of the proposed method may be large.

From the above explanation, it can be seen that the limitation of the proposed method is caused by the fact that the multiplicative dimensional reduction method is employed to estimate the statistical moments and the fourth moment method is employed to estimate the FP and extended FPs. However, if some efficient and accurate numerical methods, which can be applied to estimate simultaneously the original FP and extended FPs with high accuracy, can be found to replace the multiplicative dimensional reduction method and moment method, the limitation of the proposed method can be effectively avoided.

In order to illustrate the limitation of the proposed method more intuitively, an example of a system with multiple failure modes is presented. Considering a one-bay elastoplastic frame in Fig. 11. Four potential failure modes of structure system can be readily identified and their performance functions are defined as follows,

$$\begin{array}{*{20}l} {g_{1} = 2M_{1} + 2M_{3} - 4.5S} \hfill \\ {g_{2} = 2M_{1} + M_{2} + M_{3} - 4.5S} \hfill \\ {g_{3} = M_{1} + M_{2} + 2M_{3} - 4.5S} \hfill \\ {g_{4} = M_{1} { + }2M_{2} + M_{3} - 4.5S} \hfill \\ \end{array}$$
(26)
Fig. 11
figure 11

One-bay elastoplastic frame

Full size image

Since this is a series system, the performance function denoted as \(g\) of the structure system can be defined as the minimum of the above four performance functions, i.e., \(g = \min \left\{ {g_{1} ,g_{2} ,g_{3} ,g_{4} } \right\}\). In this example, \(M_{i} (i = 1,2,3)\) and \(S\) are independent normal inputs with means and standard deviations of \(\mu_{{M_{i} }} = 2(i = 1,2,3)\), \(\mu_{S} = 1\), \(\sigma_{{M_{i} }} = 0.2(i = 1,2,3)\) and \(\sigma_{S} = 0.25,\) respectively. The LRS results estimated by different methods are, respectively, listed in Table 7.

Table 7 The solutions of LRS
Full size table

From the results in Table 7, it is shown that the accuracy of the PM is much less than that of the Moment-4 method in Ref. (Lu et al. 2010) for the LRS of the system with multiple failure modes. The reason is that the logarithmic performance function of the system with multiple failure modes cannot be accurately approximated by the polynomial of the univariate function sum, and the integral node number of the multiplicative dimensional reduction integral quadrature is less than that of the three-point estimation. This example shows that the PM is not suitable for analyzing the LRS of the system with multiple failure modes.

5 Conclusions

In this paper, an efficient method for local reliability sensitivity (LRS) is proposed by use of moment method. Firstly, the proposed method uses a series of integral transformation to derive equivalently the LRS into the weighted sum of failure probability (FP) and several extended FPs, and these derived FPs have the same performance function but different probability density functions (PDFs), including original PDF and extended PDFs. No approximation is introduced in the derivation for normal variable, which ensures the theoretical rigor of the LRS. Then, on the basis of the fact that derived FPs have the same performance function and there are the explicit relations between the PDF and the extended PDFs, the strategy of multiplicative dimensional reduction-based sharing integral node is designed dexterously to estimate the statistical moments of the performance function required by the original FP and extended FPs. In the proposed method, the multiplicative dimensional reduction integral is employed to transform the multivariate integral of the performance function moments into the product of a series of univariate integrals, on which the first four moments of the performance function corresponding to the derived FPs can be estimated simultaneously by the same set of multiplicative dimensional reduction integral nodes. By the designed strategy of multiplicative dimensional reduction-based sharing integral node and the rigor derivation of the LRS, the computational cost of the proposed method increases linearly with the dimension of the random input, which is superior to the existing moment method for LRS.

Because the proposed method adopts the multiplicative dimensional reduction method to estimate the statistical moments of the performance function, and the fourth moment method to estimate the FP and extended FPs, it is hard to avoid the limitations of the multiplicative dimensional reduction method and the moment method, i.e., for a small FP or the multiple failure modes, the computational error may be large. However, the proposed method has good expansibility, by choosing the numerical simulation method (Au and Beck 1999; Alvarez et al. 2018) that can estimate simultaneously the original FP and extended FPs with high accuracy by sharing the sample information, the limitations of the multiplicative dimensional reduction method and the moment method can be avoided and the calculational accuracy of LRS can be improved.