Global kriging surrogate modeling for general time-variant reliability-based design optimization problems

Abstract

While design optimization under uncertainty has been widely studied in the last decades, time-variant reliability-based design optimization (t-RBDO) is still an ongoing research field. The sequential and mono-level approaches show a high numerical efficiency. However, this might be to the detriment of accuracy especially in case of nonlinear performance functions and non-unique time-variant most probable failure point (MPP). A better accuracy can be obtained with the coupled approach, but this is in general computationally prohibitive. This work proposes a new t-RBDO method that overcomes the aforementioned limitations. The main idea consists in performing the time-variant reliability analysis on global kriging models that approximate the time-dependent limit state functions. These surrogates are built in an artificial augmented reliability space and an efficient adaptive enrichment strategy is developed that allows calibrating the models simultaneously. The kriging models are consequently only refined in regions that may potentially be visited by the optimizer. It is also proposed to use the same surrogates to find the deterministic design point with no extra computational cost. Using this point to launch the t-RBDO guarantees a fast convergence of the optimization algorithm. The proposed method is demonstrated on problems involving nonlinear limit state functions and non-stationary stochastic processes.

1 Introduction

The goal of engineering design is to conceive structures that meet the requirements for performance and safety with the minimum lifecycle cost. The design process is challenging because of inherent uncertainties in the material properties, geometry and loadings. In the last three decades, design optimization under uncertainty has been widely studied and various methods for reliability-based design optimization (RBDO) were developed (Aoues & Chateauneuf, 2010). The RBDO verifies the reliability of structures under static loads and thus does not consider the aging process. However, civil engineering structures have often fixed design capacities and long service lives. They may be subjected to environmental dynamic loads (e.g. winds, waves, earthquake, traffic loads) and may lose strength over time due to material degradation (e.g. corrosion, fatigue, creep, wear). Therefore, and in spite of the conceptual and numerical complexity introduced by the time-variability, it is necessary to perform a time-variant reliability-based design optimization (t-RBDO) in order to ensure the safety level throughout the service life of the structure (Singh et al., 2010). The general problem of t-RBDO can be formulated as follows:

$$ {\displaystyle \begin{array}{ll}\operatorname{Minimize}& C\left(\mathbf{d},{\boldsymbol{\uptheta}}_{{\mathrm{x}}_{\mathrm{d}}}\right)\\ {}\mathrm{Subject}\kern0.17em \mathrm{to}& \left\{\begin{array}{ll}\mathrm{Prob}\left\{{G}_i\left(\mathbf{d},{\mathbf{X}}_{\mathrm{d}},{\mathbf{X}}_{\mathrm{c}},\mathbf{Y}(t),t\right)<0\right\}\le {p}_i^{\ast }&, j=1,\dots, {n}_{pc}\\ {}{H}_j\left(\mathbf{d},{\boldsymbol{\uptheta}}_{{\mathrm{x}}_{\mathrm{d}}}\right)\le 0&, j=1,\dots, {n}_{dc}\end{array}\right.\end{array}} $$

(1)

and the optimal design is denoted by . In the above equation, C is the cost function (also called objective function) to be minimized with respect to the design parameters that might be either deterministic d, or statistical moments ${\boldsymbol{\uptheta}}_{{\mathbf{X}}_{\mathrm{d}}}$ (i.e. mean value ${\boldsymbol{\upmu}}_{{\mathbf{X}}_{\mathrm{d}}}$ or standard deviation ${\boldsymbol{\upsigma}}_{{\mathbf{X}}_{\mathrm{d}}}$) of the design random variables X_d. X_c is the vector of classical random variables whose parameters are predefined. Y(t) is the vector of stochastic processes and t ∈ [0, T] is the parameter time that varies between zero and the prescribed service life T of the structure. The optimal design should verify the n_pc probabilistic constraints and the n_dc deterministic constraints. G_i (i = 1, …, n_pc) represents the i^th time-dependent performance function where ${p}_i^{\ast }$ is the maximum allowable probability of failure. H_j (j = 1, …, n_dc) is the j^th deterministic soft constraint that usually allows to bound the admissible design space and is inexpensive to evaluate.

So far, few methods have been developed in the literature for t-RBDO (Kuschel & Rackwitz, 2000; Jensen et al., 2012; Wang & Wang, 2012; Hu & Du, 2016). The progress has been hampered by the inclusion of time-variant loads and degradation phenomena. In particular, the problem of design optimization under non-stationary loadings is still not appropriately addressed. For instance, the sequential optimization and reliability analysis (SORA) method (Du & Chen, 2004) is expanded in (Hu & Du, 2016) to consider stationary stochastic processes by introducing the new concept of equivalent most probable point (MPP). In (Aoues et al., 2013), a sequential optimization and system reliability analysis method, also inspired from SORA is proposed. It was extended to t-RBDO problems (Aoues, 2008) by combining it with the PHI2 method (Andrieu-Renaud et al., 2004) given that PHI2 relies on a parallel system reliability analysis. The sequential approach was also extended to non-probabilistic RBDO in (Meng et al., 2016). In (Kuschel & Rackwitz, 2000), a mono-level t-RBDO method that uses the out-crossing approach for the time-variant reliability analysis is developed for only non-intermitted stationary stochastic processes. Another method is proposed in (Jensen et al., 2012) for high dimensional problems, based on a nonlinear interior point algorithm and a line search strategy. In (Rathod et al., 2012) the probabilistic behavior of degradation phenomena is modeled and incorporated into RBDO. An optimal preventive maintenance methodology is proposed in (Li et al., 2012) to optimize the lifecycle cost while considering degradation phenomena. These methods are developed to be numerically efficient, but sometimes to the detriment of accuracy. For instance, sequential and mono-level approaches may not be provably convergent and may have some accuracy issues, yielding spurious optimal designs (Agarwal, 2004). More reliable results can be obtained by adopting a straightforward double-loop (i.e. coupled) optimization procedure that consists in embedding the time-variant reliability analysis in an optimization algorithm. The coupled t-RBDO usually incurs a prohibitive computational cost. This is mainly due to the iterative nature of the optimization procedure that requires performing repetitive time-variant reliability analyses of complex structures, knowing that a single analysis can be itself computationally expensive.

Developing efficient and accurate time-variant reliability approaches is still a very active research field. In the literature, some methods (Andrieu-Renaud et al., 2004; Hu & Du, 2013) are proposed based on the out-crossing approach, first introduced by Rice (Rice, 1944). Even though computationally efficient, these methods may yield erroneous results in case of nonlinear Limit State Functions (LSF). To overcome this issue, a time-variant reliability analysis method based on stochastic process discretization (Jiang et al., 2014) was proposed that avoids the calculation of the out-crossing rates. As well, a response surface method was developed in (Zhang et al., 2017) with an iterative procedure for generating the sample points using the Bucher strategy and a gradient projection technique. Another class of methods focuses on the extreme response search and define the cumulative probability of failure as the probability that the extreme value exceeds a given threshold (Wang & Wang, 2013; Hu & Du, 2015; Wang & Chen, 2017). In this context, a nested extreme response surface (NERS) method is proposed in (Wang & Wang, 2013). It uses, first, an efficient global optimization (EGO) technique (Jones et al., 1998) to extract samples of the extreme response. Then, it uses the kriging technique to build a nested time prediction model that allows to predict the time at which the extreme response occurs. Thus, any time-independent reliability method (MCS, FORM, etc) can be performed considering only the extreme response. This method was also extended to t-RBDO by embedding it in a double-loop procedure (Wang & Wang, 2012). However, it is noted that for time-dependent problems involving stochastic processes, the structural response often presents several peaks over the time dimension. This dramatically increases the computational demand on the global optimization that may not converge and get stuck at local extrema. In addition, the discretization of the stochastic processes using techniques such as Expansion Optimal Linear Estimation (EOLE) (Li & Der Kiureghian, 1993), Orthogonal Series Expansion (OSE) (Sudret & Der Kiureghian, 2000) and Karhunen-Loève (KL) expansion (Huang et al., 2001) increases the dimension of the surrogate modeling problem (i.e. the total number of input random variables). This makes it difficult to use kriging that is known to be numerically impractical in case of high dimensional problems. To overcome these issues, a SIngle-Loop Kriging-based (SILK) approach is developed in (Hu & Mahadevan, 2016a; Hu & Mahadevan, 2016b). This method considers the time parameter as an input random variable uniformly distributed over [0,T]. Therefore at a given sampled instant, a stochastic process can be represented by a single random variable. SILK is based on the idea that the reliability assessment does not necessarily require an accurate approximation of the extreme response value, but rather a classification of the response trajectories between safe or failing according to the sign of the time-dependent response.

In this work, we propose a kriging-based t-RBDO method in a coupled framework. The aim is to develop an accurate and affordable numerical tool that can handle general time-variant problems, even when non-stationary stochastic processes are involved. First, the computational efficiency of the coupled approach is considerably improved by replacing the time-dependent performance functions with global kriging surrogate models that are built and refined in an artificial augmented reliability space (Taflanidis & Beck, 2009). This allows to cover all the design space while also accounting for the uncertainty of the input variables. These models can then be repeatedly used throughout the optimization algorithm for a fast assessment of the time-variant reliability regardless of the position of the design point. Second, for the construction of these kriging surrogates, a classification technique inspired from SILK is proposed. It is worth noting here that SILK was originally developed for component reliability analysis, whereas in the context of t-RBDO we are likely to have multiple time-dependent probabilistic constraints that should be satisfied together. This can be viewed as a series system reliability problem. Therefore and in contrast to most methods in the literature where the surrogate models are refined independently and sequentially, we propose an enrichment scheme that allows the refinement of the kriging surrogates of the several time-dependent performance functions simultaneously. Accordingly, the kriging model of a probabilistic constraint does not need to be refined in the regions where at least one other constraint is surely violated. The computational cost related to the construction of the global surrogate models is therefore reduced.

Furthermore, once the surrogate models are defined, they are used throughout a gradient-based optimization algorithm (in particular, Polak-He (Polak, 1997)) along with the score function (Wu, 1994) for a fast stochastic reliability analysis. In this work, we also propose to use these same surrogate models to firstly find the time-dependent Deterministic Design Point (DDP) previous to the optimization procedure. Due to the global feature of the surrogates, the deterministic optimization problem can be performed without any additional computational cost. Using the DDP as initial design point for the Polak-He algorithm guarantees a fast convergence of the optimization and thus further contributes to reduce the overall computational effort of the t-RBDO.

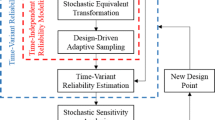
The herein proposed t-RBDO method will be referred to as TROSK (Time-variant Reliability-based design Optimization using Simultaneously refined Kriging models) in the sequel. This paper is organized as follows: In Section 2, the method for building the global kriging surrogate models simultaneously in the augmented reliability space is presented. Then, the search for the deterministic design point for launching the coupled t-RBDO is detailed in Section 3. In Section 4, two case studies are selected to compare TROSK with some recent t-RBDO approaches and to demonstrate its effectiveness for problems involving non-stationary stochastic processes. Finally, a concluding summary is given in Section 5.

2 Kriging surrogate modeling for stochastic time-dependent performance functions

2.1 Augmented reliability space

In RBDO problems, it is common to use the structural weight as the objective function to be optimized with respect to various geometry parameters. These design parameters are often considered as deterministic variables or mean values of the distribution functions of random variables, knowing the standard deviation or the coefficient of variation. In the latter case, the probability density functions (PDF) of the design random variables vary over the design space, as shown in Fig. 1. Therefore, approximating each time-dependent performance function with a different surrogate model after each update of the values of the design variables would be quite ponderous. To circumvent this issue, a unique surrogate model can be built in an augmented reliability space (Taflanidis & Beck, 2009). This consists in defining an augmented PDF that allows to account simultaneously for instrumental (related to the value of the design variable) and aleatory (related to the aleatory character of the random variable) uncertainties of the design random variables. Examples of augmented PDF for two types of probability distributions (normal and lognormal) are depicted in Fig. 1 by thick red lines. These functions are obtained by artificially considering that the design parameters (θ) are uncertain with a uniform distribution π(θ) over the admissible design space D_θ. Thus, for each design random variable following a PDF f_X(x), corresponds an (artificial) augmented PDF h_X(x), expressed as follows:

$$ {h}_X(x)={\int}_{{\mathrm{D}}_{\uptheta}}{f}_X\left(x|\theta \right)\pi \left(\theta \right)\mathrm{d}\theta $$

(2)

Fig. 1

Example of augmented PDF of a lognormal and b normal design random variables

In this work, we propose to perform the time-variant reliability analysis on global kriging surrogate models that are built and refined in the augmented space. In order for these models to be accurate for the evaluation of the probabilistic constraints regardless the position of the design point, the input sampling should uniformly span a sufficiently large confidence region of the augmented PDF. To this end, a lower and upper quantiles (resp. ${q}_{X_i}^{-}$ and ${q}_{X_i}^{+}$) are defined to bound the confidence interval of each design random variable X_i, ensuring a minimum reliability level β_{0, i}. ${q}_{X_i}^{-}$ and ${q}_{X_i}^{+}$ are determined as follows (Dubourg et al., 2011):

$$ \left\{\begin{array}{c}{q}_{X_i}^{-}={}_{\boldsymbol{\uptheta} \in {\mathrm{D}}_{\boldsymbol{\uptheta}}}{}^{\mathit{\min}\kern0.5em }\ {F}_{X_i}^{-1}\left(\Phi \left(-{\beta}_{0,i}\right)|\boldsymbol{\uptheta} \right)\\ {}{q}_{X_i}^{+}={}_{\boldsymbol{\uptheta} \in {\mathrm{D}}_{\boldsymbol{\uptheta}}}{}^{\mathit{\max}\kern0.5em }\ {F}_{X_i}^{-1}\left(\Phi \left(+{\beta}_{0,i}\right)|\boldsymbol{\uptheta} \right)\end{array}\right. $$

(3)

where ${F}_{X_i}^{-1}$ is the quantile function of the margin of X_i, and Φ is the cumulative distribution function of the standard normal distribution. In practice, the choice of β_{0, i} depends on the order of magnitude of the target probability of failure (${\beta}_{0,i}\ge {\Phi}^{-1}\left(1-{p}_i^{\ast}\kern0.50em \right)$). The lower is ${p}_i^{\ast }$, the higher β_{0, i} should be in order to cover the low probable values of X_i.

2.2 Simultaneous refinement of the global kriging models

A major advantage of kriging is that it provides a local error measure. This allows the use of active learning techniques to adaptively refine the surrogate model under construction. Many RBDO methods are proposed based on kriging. They usually consist in approximating independently each performance function with a kriging surrogate model. However, this incurs unnecessary evaluations of the performance functions that are, in general, described with complex and heavy models. Once the surrogate model of a performance function is built and refined, it can be used to determine the failure zone associated to this function. Subsequently, it would be particularly inefficient to refine the surrogate model of another function over this zone. This requires the enrichment of the associated Experimental Design (ED) in regions we know will never be visited by the optimizer.

To circumvent this issue, we develop in this paper a strategy to build and refine the surrogate models simultaneously. First, an initial reduced experimental design ED₀ is used to build kriging models of the performance functions. At this step, the experimental design of the i^th performance function ED_i ≡ ED₀, i = 1, …, n_pc. Then at each iteration of the refinement process, the proposed algorithm determines which LSF should be enriched next and detects the best next point to be added to the corresponding ED. This algorithm is explained in what follows.

2.2.1 Construction of the initial kriging surrogate models

For the sake of clarity, let us introduce the vector X = {d, X_d, X_c} that groups the three types of variables so as the performance functions can be expressed as G_i(X, Y(t), t), i = 1, …, n_pc. First, the time interval of study [0, T] is discretized into N_t equidistant time nodes. Then, N_mcs samples of X and N_mcs trajectories of Y(t) are generated over the predefined augmented space. This serves as a validation set for the refinement of the global kriging models under construction. This step requires the discretization of the input stochastic processes. In this work, we adopt the KL expansion (Huang et al., 2001) as being both efficient and easy to implement and because it allows to discretize general stochastic processes (i.e. stationary and non-stationary, Gaussian and non-Gaussian) (Phoon et al., 2005; Hawchar et al., 2017). However, other discretization techniques might also be used (e.g. OSE, EOLE). Let Y(t) be a stochastic process defined by its mean function μ_Y(t), standard deviation σ_Y(t) and autocorrelation function ρ_Y(t_i, t_j). The KL expansion consists in approximating Y(t) as follows:

$$ Y(t)={\mu}_Y(t)+\sum \limits_{q=1}^M\sqrt{\lambda_q}{\xi}_q{f}_q(t) $$

(4)

where M is the truncation order and {ξ_q, q = 1, …M} is a set of uncorrelated zero-mean random variables of the same distribution function as Y(t). λ_q and f_q(t) are respectively the eigenvalues and eigenfunctions of the autocovariance function defined as C_{i, j}(t_i, t_j) = σ_Y(t_i)σ_Y(t_j)ρ_Y(t_i, t_j) with t_i, t_j ∈ [0, T]. This discretization allows to represent a stochastic process with a vector ξ of M independent random variables.

For the construction of the initial experimental design, N₀ samples (N₀ ≪ N_mcs) of X, ξ and t are generated using a space filling technique such as the Latin Hypercube Sampling (LHS) over the augmented reliability space. By replacing ξ and t in (4), we obtain N₀ values of Y(t). The training points of ED₀ are denoted by P^(m, n) = [X^(m), Y^(m)(t_n), t_n] with m = 1, …, N₀ and n ∊ [1, N_t]. For each point, the exact responses G_i(P^(m, n)), i = 1, …, n_pc are computed by evaluating the original models describing the time-dependent performance functions. Then, an initial kriging metamodel is built for each function using the corresponding ED defined by ED₀ = {P, G_i}. In this case, the dimension of the surrogate modeling problem is equal to N_X + N_Y + 1 where N_X and N_Y are respectively the sizes of X and Y, and the additional dimension corresponds to the time variable. Note here that the discretization of the input stochastic processes does not affect the dimensionality of the metamodeling problem. According to the classical kriging method, the evaluation of the surrogate model at a new trial point (X^∗, Y^∗(τ), τ), τ ∊ [0, T] yields a normal random variable whose mean value ${\mu}_{\widehat{G}}\left({\mathbf{X}}^{\ast },{\mathbf{Y}}^{\ast}\left(\tau \right),\tau \right)$ represents the surrogate model approximation, and whose variance ${\sigma}_{\widehat{G}}^2\left({\mathbf{X}}^{\ast },{\mathbf{Y}}^{\ast}\left(\tau \right),\tau \right)$ measures the local uncertainty of the prediction (Jones et al., 1998; Echard et al., 2011). The kriging method is briefly reviewed in the appendix.

When the initial surrogate models are defined, they can be used to predict the N_mcs trajectories of the n_pc time-dependent performance functions. In what follows, we define the global safe zone ${\mathcal{S}}_g$ regarding the t-RBDO problem as the intersection of the safe zones ${\mathcal{S}}_i,i=1,\dots, {n}_{pc}+{n}_{dc}$ of all the constraint functions $\left({\mathcal{S}}_g={\bigcap}_{i=1}^{n_{pc}+{n}_{dc}}{\mathcal{S}}_i\right)$. Consequently, the global failure zone ${\mathcal{F}}_g$ is defined as the union of the failure zones ${\mathcal{F}}_i,i=1,\dots, {n}_{pc}+{n}_{dc}$ $\left({\mathcal{F}}_g={\bigcup}_{i=1}^{n_{pc}+{n}_{dc}}{\mathcal{F}}_i\right)$. Note that ${\mathcal{S}}_g\bigcap {\mathcal{F}}_g=\varnothing$ and ${\mathcal{S}}_g\bigcup {\mathcal{F}}_g$ returns the predefined augmented space. The global LSF is then delimited by the interface between these two regions. In the proposed TROSK approach, we only focus on the estimation of this interface and thus no particular effort is made to accurately estimate the values of the performance functions over ${\mathcal{S}}_g$ or ${\mathcal{F}}_g$. Therefore, we aim to classify the samples [X^(m), ξ^(m)], m = 1, …, N_mcs of input random variables into three categories: surely belongs to ${\mathcal{S}}_g$, surely belongs to ${\mathcal{F}}_g$ and unsure otherwise. For this purpose, the learning function U, first introduced by (Echard et al., 2011), is here used. It is defined as follows:

$$ {U}_i\left({\mathbf{X}}^{(m)},{\mathbf{Y}}^{(m)}\left({t}_n\right),{t}_n\right)=\frac{{\mu_{\widehat{G}}}_i\left({\mathbf{X}}^{(m)},{\mathbf{Y}}^{(m)}\left({t}_n\right),{t}_n\right)}{{\sigma_{\widehat{G}}}_i\left({\mathbf{X}}^{(m)},{\mathbf{Y}}^{(m)}\left({t}_n\right),{t}_n\right)},i=1,\dots, {n}_{pc} $$

(5)

In practice, if |U| ≥ 2, then the estimator ${\mu}_{\widehat{G}}$ is supposed to be accurate (this corresponds to an error of 0.023). For each input sample point of the validation set [X^(m), ξ^(m)], m = 1, …, N_mcs, the learning function is evaluated for the n_pc kriging surrogates and at the N_t time nodes. These points can then be classified as follows:

• surely belongs to ${\mathcal{S}}_g$: if $\forall n\in \left[1,{N}_t\right],\forall i\in \left[1,{n}_{pc}\right]:{\mu}_{{\widehat{G}}_i}\left({\mathbf{X}}^{(m)},{\mathbf{Y}}^{(m)}\left({t}_n\right),{t}_n\right)\ge 0$ and U(X^(m), Y^(m)(t_n), t_n) ≥ 2. Their number is denoted by ${N}_{\mathcal{S}}$.

• surely belongs to ${\mathcal{F}}_g$: if $\exists n\in \left[1,{N}_t\right],\exists i\in \left[1,{n}_{pc}\right]:{\mu}_{{\widehat{G}}_i}\left({\mathbf{X}}^{(m)},{\mathbf{Y}}^{(m)}\left({t}_n\right),{t}_n\right)<0$ and U(X^(m), Y^(m)(t_n), t_n) ≤  − 2. Their number is denoted by ${N}_{\mathcal{F}}$.

• unsure: otherwise. Their number is denoted by ${N}^{\ast }={N}_{mcs}-\left({N}_{\mathcal{S}}+{N}_{\mathcal{F}}\right)$ and from which ${N}_{\mathcal{F}}^{\ast }$ points falls potentially in the failure zone ($0\le {N}_{\mathcal{F}}^{\ast}\le {N}^{\ast }$). For such a point, $\exists n\in \left[1,{N}_t\right],\exists i\in \left[1,{n}_{pc}\right]:{\mu}_{{\widehat{G}}_i}\left({\mathbf{X}}^{(m)},{\mathbf{Y}}^{(m)}\left({t}_n\right),{t}_n\right)<0$.

The cumulative probability of failure over [0, T] can then be approximated as follows:

$$ {\widehat{P}}_{f,c}\left(0,T\right)=\frac{N_{\mathcal{F}}+{N}_{\mathcal{F}}^{\ast }}{N_{mcs}} $$

(6)

and its maximum percentage error is computed by (Hu & Mahadevan, 2016a):

$$ {\varepsilon}^{max}=\frac{\mathit{\max}}{n_{\mathcal{F}}^{\ast}\in \left[0,{N}^{\ast}\right]}\ \left\{\frac{\left|{N}_{\mathcal{F}}^{\ast }-{n}_{\mathcal{F}}^{\ast}\right|}{N_{\mathcal{F}}+{N}_{\mathcal{F}}^{\ast }} \times 100\%\right\} $$

(7)

All surrogate models are considered well trained when ε^max becomes lower than a preset target error rate (e.g ${\varepsilon}_{tgt}^{max}=0.1\%$). Otherwise, the kriging surrogates need to be refined.

2.2.2 Refinement of the kriging surrogate models

The herein proposed refinement strategy consists in adding one point per iteration. The new training point ${P}^{\left({m}_{new},{n}_{new}\right)}=\left[{\mathbf{X}}^{\left({m}_{new}\right)},{\mathbf{Y}}^{\left({m}_{new}\right)}\left({t}_{n_{new}}\right),{t}_{n_{new}}\right]$ is selected among the « unsure » points of the third category as the one yielding the lowest value of the learning function, denoted by U_MIN. This results in the best improvement of the approximation. This point is identified as follows:

$$ {m}_{new}=\underset{m\in \left[1,{N}_{mcs}\right]}{\arg\ \min }\ \left\{\underset{\begin{array}{c}n=1,\dots, {N}_t\\ {}i=1,\dots, {n}_{pc}\end{array}}{\min}\left|{U}_i\left({\mathbf{X}}^{(m)},{\mathbf{Y}}^{(m)}\left({t}_n\right),{t}_n\right)\right|\right\} $$

(8)

and

$$ {n}_{new}=\underset{n\in \left[1,{N}_t\right]}{\arg\ \min}\left\{\underset{i=1,\dots, {n}_{pc}}{\min}\left|{U}_i\left({\mathbf{X}}^{\left({m}_{new}\right)},{\mathbf{Y}}^{\left({m}_{new}\right)}\left({t}_n\right),{t}_n\right)\right|\right\} $$

(9)

${P}^{\left({m}_{new},{n}_{new}\right)}$ is then used to enrich the ED of the probabilistic constraint corresponding to this minimum value U_MIN. The index $i$ of the ED is identified as follows:

$$ i=\underset{i\in \left[1,{n}_{pc}\right]}{\arg\ \min }\ \left|{U}_i\left({\mathbf{X}}^{\left({m}_{new}\right)},{\mathbf{Y}}^{\left({m}_{new}\right)}\left({t}_{n_{new}}\right),{t}_{n_{new}}\right)\right| $$

(10)

Furthermore, and in order to avoid the clustering issue, the correlation between the new training point and the current $E{D}_i$ is evaluated. This allows to discard points that are highly correlated with $E{D}_i$, since adding such points only increase the computational demand, without necessarily improving the representativeness of the sample (Hu & Mahadevan, 2016a). Therefore, ${P}^{\left({m}_{new},{n}_{new}\right)}$ should also verify the following condition:

$$ \underset{P_i\in E{D}_i}{\max}\left\{\rho \left({P}^{\left({m}_{new},{n}_{new}\right)},{P}_i\right)\right\}<{\rho}_{max} $$

(11)

where ${P}_i$ denotes the set of points of the $E{D}_i$ at the current iteration. ρ_max is the maximum value of correlation above which ${P}^{\left({m}_{new},{n}_{new}\right)}$ is considered highly correlated with $E{D}_i$ (e.g. ρ_max = 0.95).

Once $E{D}_i$ is enriched with ${P}^{\left({m}_{new},{n}_{new}\right)}$, the corresponding kriging surrogate model ${\widehat{G}}_i$ is updated while the others remain unchanged. This step allows to refine the approximation of the ${i}^{th}$ LSF and consequently ${\mathcal{S}}_g$ and ${\mathcal{F}}_g$. The global refinement strategy converges when ${\varepsilon}^{max}<{\varepsilon}_{tgt}^{max}$. At convergence, the final sizes of ED_i, i = 1, …, n_pc are not necessarily equal. They are automatically determined throughout this enrichment algorithm.

The final kriging models provide an accurate approximation of the sign of the performance functions over the time space and the augmented reliability space. They can thus be used for the assessment of the reliability throughout a time-variant reliability-based design optimization. It is noted however, that the local accuracy of the kriging surrogates is systematically checked throughout the TROSK algorithm for each new position of the design point and further refinement can be made if needed.

3 Reliability-based design optimization

3.1 Gradient-based optimization procedure

By substituting the complex performance functions with the kriging surrogates, it is made numerically affordable to solve (1) using a coupled approach. In this work, the Polak-He algorithm (Polak, 1997) is retained for the optimization procedure. It was first developed to efficiently solve deterministic optimization problems with inequality constraints by penalizing the most violated constraint. Providing an initial design point , each iteration (k = 1, 2, …) consists in finding the descent direction δ^(k) and the correspondent step size s^(k) so that . Determining δ^(k) and s^(k) requires the calculation of the gradients of the cost function, is the gradient operator with respect to the design parameters) and also of the failure probabilities, via a stochastic sensitivity analysis. The latter is, in general, a source of computational burden. However, the use of the so-called score function (Dubourg et al., 2011) allows to estimate with the same N_mcs evaluations of the metamodel that had been beforehand used to estimate P_{f, c}(0, T). This considerably reduces the numerical effort of the stochastic sensitivity analysis. The r^th coordinate of is approximated as follows:

(12)

where is the score function that can be analytically obtained as follows:In this optimization algorithm, only the safe region is investigated (i.e. all the design points throughout the optimization algorithm belong to ${\mathcal{S}}_g$ such that all constraints are met). Hence, convergence occurs when the relative variation of the cost function with respect to the previous iteration becomes lower than a given threshold (e.g. ${\varepsilon}_{cost}^{tgt}={10}^{-3}$).

3.2 Selection of the initial design point

The effectiveness of the optimization method highly depends on the topology of the design space and the choice of the initial design point. Therefore, in some cases the gradient-based optimization algorithm risks getting stuck in local optima (minima). Hence, it would be of great utility to use the DDP as initial design point in RBDO. However, finding this point is in itself an optimization problem that requires additional evaluations of the original models. For this reason, the starting point is often chosen arbitrary or at the centre of the design intervals (Wang & Wang, 2012; Dubourg et al., 2011).

In this work, we propose to find the DDP using the predefined surrogate models with no extra computational cost. This is made possible due to the construction of the kriging surrogate models in the augmented reliability space. In time-variant problems, finding the DDP () consists in solving the following optimization problem:

$$ {\displaystyle \begin{array}{ll}\operatorname{Minimize}& \mathrm{C}\left(\mathbf{d},{\boldsymbol{x}}_{\mathbf{d}}\right)\\ {}\mathrm{Subject}\kern0.17em \mathrm{to}& \left\{\begin{array}{ll}{\widehat{G}}_i\left(\mathbf{d},{\boldsymbol{x}}_{\mathbf{d}},{\boldsymbol{x}}_{\mathbf{c}},\tilde{\mathbf{Y}}(t),t\right)\ge 0&, j=1,\dots, {n}_{pc}\\ {}{H}_j\left(\mathbf{d},{\boldsymbol{x}}_{\mathbf{d}}\right)\le 0&, j=1,\dots, {n}_{dc}\end{array}\right.\end{array}} $$

(14)

The deterministic problem is formulated by replacing in (1) the random variables x by deterministic values x. Assuming that all random variables are independent, each variable is replaced by its median x, given that the median is a value for which $\mathrm{Prob}\left(X\le x\right)=\mathrm{Prob}\left(X\ge x\right)=0.5$. As well, a stochastic process is replaced by a representative trajectory $\overset{\sim }{\mathbf{Y}}(t)$ around its median value. When the LSFs are time-dependent, the feasible zone is defined by the set of points $\left\{\mathrm{d},{x}_{\mathrm{d}}\right\}$ for which $\forall \tau \in \left[0,T\right],\forall i\in \left[1,{n}_{pc}\right],\forall j\in \left[1,{n}_{dc}\right]:{\widehat{G}}_i\left(\mathbf{d},{\boldsymbol{x}}_{\mathbf{d}},{\boldsymbol{x}}_{\mathbf{c}},\overset{\sim }{\mathbf{Y}}\left(\tau \right),\tau \right)\ge 0$ and ${H}_j\left(\mathbf{d},{\boldsymbol{x}}_{\mathbf{d}}\right)\ge 0$. Equation (14) can be solved using any numerical discretization method.

The optimum solution of TROSK is expected to be located not far from , inside the feasible region $\left({\mathcal{S}}_g\right)$ so that the prescribed reliability level is attained. Given that is a point on the contour of ${\mathcal{S}}_g$ having the lowest cost, then at the first iteration the cost can only decreases . Therefore, the Polak-He algorithm is slightly modified so as the search for exclusively is conducted only in the direction of . For the next iterations, is determined by considering both gradient vectors and .

The proposed initial design point and the privilege given to in the first iteration lead to a fast convergence of the optimization algorithm toward the reliability-based optimal design after only few iterations. Finally, it is worth to be noted that the determination of the DDP does not necessarily need to be highly accurate. The aim here is to approach the cheapest zone inside ${\mathcal{S}}_g$ in order to launch the reliability-based optimal design search. The TROSK approach is summarized in the flowchart of Fig. 2.

Fig. 2

Flowchart of the TROSK approach

Illustration on a numerical example

In this paragraph, the influence of the choice of the initial design point as explained previously is highlighted. However, and for the sake of clarity of the illustration, static LSFs are considered as we focus here on the gradient-based optimization procedure. The following numerical example has been also studied in (Lee & Jung, 2008; Dubourg, 2011). The optimization problem is defined as follows:

$$ {\displaystyle \begin{array}{ll}\operatorname{Minimize}& \mathrm{C}\left({\mu}_{x_1},{\mu}_{x_1}\right)={\left({\mu}_{x_1}-3.7\right)}^2+{\left({\mu}_{x_2}-4\right)}^2\\ {}\mathrm{Subject}\kern0.17em \mathrm{to}& \mathrm{Prob}\left({G}_i\left(\mathbf{X}\right)\le 0\right)\le \Phi \left(-2\right),\kern0.5em i=i,2\end{array}} $$

(15)

where X = {X₁, X₂} is the vector of two normal random variables: ${X}_1\sim \mathcal{N}\left({\mu}_{X_1},0.1\right)$ and ${X}_2\sim \mathcal{N}\left({\mu}_{X_2},0.1\right)$, with ${\mu}_{X_1}\in \left[\mathrm{0,3.7}\right]$ and ${\mu}_{X_2}\in \left[0,4\right]$. The two performance functions are defined as follows:

$$ {G}_1\left(\mathbf{X}\right)=-{X}_1\mathit{\sin}\left(4{X}_1\right)-1.1{X}_2\mathit{\sin}\left(2{X}_2\right) $$

(16)

$$ {G}_2\left(\mathbf{X}\right)={X}_1+{X}_2-3 $$

(17)

Figure 3 depicts the real LSFs as well as their kriging approximates. An initial experimental design of size N₀ = 5 is used. It is represented by the black dots. LSF₁ is highly nonlinear and is denoted by purple dashed line, whereas LSF₂ is linear and is denoted by blue dashed line. The construction of the two surrogate models in the augmented reliability space using the global refinement strategy presented in Section 2.2 requires the enrichment of ED₁ with 26 new sample points, represented by the red diamonds. The final experimental design procures a very accurate approximation of the global LSF and thus of ${\mathcal{S}}_g$, represented by the white area. Note that LSF₁ is not accurate over all the design space, in particular over ${\mathcal{F}}_2$. This is a particularity of the herein proposed strategy of simultaneous enrichment of the EDs that avoids the refinement of the global kriging models in regions that will never be visited by the optimizer.

Fig. 3

Comparison between the real limit state functions and their kriging surrogates

The initial design point is determined by applying a numerical discretization algorithm, resulting in the convergence toward as shown in Fig. 4. The contours of the quadratic objective function are denoted by grey solid lines that decrease up and to the right. In order to guarantee the convergence toward the optimal point, more than one discretization scheme may be performed considering, for example, different discretization steps or interpolation techniques.

Fig. 4

Search for the deterministic optimal design point using numerical discretization

In (Dubourg, 2017), the Polak-He algorithm was also used to solve this RBDO problem, but it was launched with an arbitrary initial design point . Fig. 5 shows that in both cases, the optimization algorithm converges toward the optimal design point around [2.8230,3.2491]. However starting from requires 11 iterations, whereas considering the proposed initial design point allows convergence after only 3 iterations. It is noted as well that for different arbitrary starting points, the algorithm may converge even more slowly or gets stuck in a local optimum.

Fig. 5

Convergence of the optimization algorithm considering different initial design points

4 Application examples

In this section, two case studies are used to demonstrate the accuracy and high performance of TROSK, in particular in case of (1) nonlinear LSF and (2) non-stationary stochastic loads.

The first case study involves three nonlinear LSFs and has been already used in (Wang & Wang, 2012). It consists in a two-dimensional benchmark problem, allowing graphical representations of the results. The second case study consists of a two bar frame structure (Hu & Du, 2016) subject to a stationary Gaussian stochastic load. It is then extended to consider a non-stationary and non gaussian stochastic process to highlight the applicability of the herein proposed method to such a problem.

In order to demonstrate the numerical efficiency of TROSK, we provide the total number of calls to the deterministic model (N_func) and the relative error of the failure probabilities. This error is only significant for violated constraints and is defined as follows:

$$ {\varepsilon}_{\%}^{(i)}=\frac{\left|{P}_{f,c}^{MCS}{\left(0,T\right)}^{(i)}-{p}_i^{\ast}\right|}{P_{f,c}^{MCS}{\left(0,T\right)}^{(i)}}\times 100\% $$

(18)

where i is the index of the violated constraint. ${P}_{f,c}^{MCS}\left(0,T\right)$ is the cumulative probability of failure computed with the classical Monte-Carlo simulation method performed at the optimal design point.

4.1 Case study 1: numerical example

The first case study consists in a mathematical problem that involves two normal random variables: ${X}_1\sim \mathcal{N}\left({\mu}_1,0.6\right)$ and ${X}_2\sim \mathcal{N}\left({\mu}_2,0.6\right)$. The design vector is $d=\left\{{\mu}_1,{\mu}_2\right\}$. The study is carried out over the time interval [0, 5] and the optimization problem is formulated as follows:

$$ {\displaystyle \begin{array}{ll}\operatorname{Minimize}& \mathrm{C}\left({\mu}_1,{\mu}_2\right)={\mu}_1+{\mu}_2\\ {}\mathrm{Subject}\kern0.17em \mathrm{to}& \left\{\begin{array}{ll}\mathrm{Prob}\left\{{G}_i\left({X}_1,{X}_2,t\right)<0\right\}\le {p}_i^{\ast }&, i=1,2,3\\ {}0\le {\mu}_j\le 10&, j=1,2\end{array}\right.\end{array}} $$

(19)

where ${p}_i^{\ast }=0.1\ \left(i=1,2,3\right)$. Figure 6 depicts the three time-dependent LSFs that are given by:

$$ \left\{\begin{array}{c}{G}_1\left({X}_1,{X}_2,t\right)={X}_1^2{X}_2-5{X}_1t+\left({X}_2+1\right){t}^2-20\\ {}{G}_2\left({X}_1,{X}_2,t\right)=\frac{{\left({X}_1+{X}_2-0.1t-5\right)}^2}{30}+\frac{{\left({X}_1-{X}_2+0.2t-12\right)}^2}{120}-1\\ {}{G}_3\left({X}_1,{X}_2,t\right)=\frac{90}{\left({\left({X}_1+0.05t\right)}^2+8\left({X}_2+0.1t\right)-\mathit{\sin}(t)+5\right)}-1\end{array}\right. $$

(20)

Fig. 6

Evolution in time of the limit state functions

In order to perform TROSK, first the augmented PDF of X₁ and X₂ are defined. The three global kriging surrogate models are built from an initial ED₀ of size N₀ = 10 and then are simultaneously refined using the algorithm presented in Section 2.2 until the target accuracy ${\varepsilon}_{tgt}^{max}=5\%$ is reached. This requires adding 14, 8 and 20 data points to ED₁, ED₂ and ED₃, respectively. This procures, as shown in Fig. 7, a very good approximation of the global LSF without necessarily accurately estimating the performance functions all over the time dimension and the augmented space. Fig. 8 depicts the initial experimental design (ED₀) as well as the enriched EDs of each time-dependent performance function (ED₁, ED₂ and ED₃). This figure shows that the data points are indeed generated around the global LSF.

Fig. 7

Approximated time-dependent limit state functions

Fig. 8

Enriched experimental designs of the three performance functions

The initial design point is found to be as shown in Fig. 9. The grey solid lines represent the contours of the objective function that decreases down and to the left. Table 1 compares the results of TROSK to those obtained using NERS (Wang & Wang, 2012). Fig. 10 depicts the various positions of the design point throughout the optimization algorithm for both methods, and Fig. 11 gives the evolution of the cumulative probabilities of failure. These numerical and graphical results show that when applying NERS, the first LSF is violated and the allowable probability of failure is exceeded with an error ${\varepsilon}_{\%}^{(1)}=12.16\%$. Whereas, with TROSK, the algorithm converges to the optimal design point at which both LSF₁ and LSF₂ are violated with errors ${\varepsilon}_{\%}^{(1)}$ and ${\varepsilon}_{\%}^{(2)}$ lower than 3%. Note as well that TROSK requires 72 function evaluations compared to 336 using NERS. This represents a gain in the computational cost of 76%.

Fig. 9

Search for the deterministic design point

Table 1 Comparative results of NERS and TROSK

Fig. 10

Convergence of the optimization algorithm using NERS and TROSK

Fig. 11

Evolution of the three probabilities of failure throughout the optimization algorithm

4.2 Case study 2: two-bar frame structure

Let us consider the two-bar frame sketched in Fig. 12, already studied in (Hu & Du, 2016). The frame is subjected to a stochastic load F(t), and its bars have random lengths (L₁ and L₂), diameters (D₁ and D₂) and yield strengths (S₁ and S₂). The distribution parameters of the input random variables are given in Table 2.

Table 2 Random parameters of the two-bar frame structure

Let X = {D₁, D₂, L₁, L₂, S₁, S₂} denotes the vector of random variables. The reliability of the structure is verified over 10 years, and the t-RBDO problem is defined as follows:

$$ {\displaystyle \begin{array}{ll}\operatorname{Minimize}& C\left({\mu}_{D_1},{\mu}_{D_2}\right)=\frac{{\pi \mu}_{L_1}{\mu}_{D_1}^2}{4}+\frac{\pi \sqrt{\mu_{L_1}^2+{\mu}_{L_2}^2{\mu}_{D_2}^2}}{4}\\ {}\mathrm{Subject}\kern0.17em \mathrm{to}& \left\{\begin{array}{ll}\mathrm{Prob}\left\{{G}_i\left({\mathbf{X}}_1,F(t),t\right)<0\right\}\le {p}_i^{\ast }&, i=1,2,3\\ {}0.07\le {\mu}_{D_j}\le 0.25&, j=1,2\end{array}\right.\end{array}} $$

(21)

where ${p}_1^{\ast }=0.01$, ${p}_2^{\ast }=0.001$. The time-dependent performance functions are expressed by:

$$ \left\{\begin{array}{c}{G}_1\left(\mathbf{X},t\right)=\frac{\pi }{4}{D}_1^2{S}_1-\frac{\sqrt{L_1^2+{L}_2^2\ }}{L_2}F(t)\\ {}{G}_2\left(\mathbf{X},t\right)=\frac{\pi }{4}{D}_2^2{S}_2-\frac{L_1}{L_2}F(t)\kern3.75em \end{array}\right. $$

(22)

In the sequel, two assumptions are made regarding the behavior of F(t).

4.2.1 Case of a stationary gaussian stochastic load

We first consider the case where F(t) is modeled with a stationary Gaussian stochastic process with an exponential square autocorrelation function given by (23). Its mean value and standard deviation are, respectively, μ_F = 2.2 × 10⁶ N and σ_F = 2 × 10⁵ N.

$$ {\rho}_F\left({t}_i,{t}_j\right)=\exp \left(-{\left(\frac{t_j-{t}_i}{0.1}\right)}^2\ \right) $$

(23)

In order to perform TROSK, F(t) is discretized over 10 intervals of one year using the KL expansion technique. An initial experimental design (ED₀) of size N₀ = 50 is used to build the initial kriging metamodels, then 167 and 180 samples are added to refine ${\widehat{G}}_1$ and ${\widehat{G}}_2$, respectively. ED₀ as well as the final experimental designs (ED₁ and ED₂) are depicted in Fig. 13 where the shaded green area represents the global failure zone ${\mathcal{F}}_g$.

Fig. 12

A two-bar frame under a stochastic load

Fig. 13

Enriched experimental designs of the two performance functions (case of a stationary Gaussian stochastic load)

The initial design point is found to be as shown in Fig. 14. The grey solid lines represent the quadratic contours of the objective function that decreases down and to the left. The various positions of the design point throughout the optimization algorithm are also presented in this figure. The results of TROSK and t-SORA are summarized in Table 3 where the exact optimal design is also given. These results show that TROSK procures a very accurate solution of the t-RBDO problem involving a stochastic process. Its efficiency is proven by the low number of function calls required by the surrogate modeling technique (38% less than t-SORA), and as well, by the low number of iterations required by the optimization algorithm.

Fig. 14

Convergence of the optimization algorithm using TROSK (case of a stationary Gaussian stochastic load)

Table 3 Convergence of TROSK and comparison with t-SORA (case of a stationary Gaussian stochastic load)

4.2.2 Case of a non-stationary Gumbel stochastic load

We now model F(t) as a non-stationary Gumbel (i.e. type I extreme value distribution) stochastic process with the following autocorrelation function:

$$ {\rho}_F\left({t}_i,{t}_j\right)=\exp \left(0.2{\left|{t}_j-{t}_i\right|}^2\ \right) $$

(24)

The time-dependent mean value and standard deviation are expressed as follows:

$$ {\mu}_F(t)=2.2\times {10}^6\exp \left(t/20\ \right) $$

(25)

$$ {\sigma}_F(t)=2\times {10}^5\exp \left(t/20\ \right) $$

(26)

In this case, and due to the non-stationary behavior of the stochastic process, the feasible region of this problem shrinks. As the optimal design is supposed to be higher than the previous case, the admissible design space is enlarged and thus $0.10\le {\mu}_{D_j}\le 0.40,j=1,2$. The same target reliability levels are considered. The proposed method is performed with N₀ = 50, then 117 and 113 samples are adaptively added to improve the accuracy of LSF₁ and LSF₂, respectively. These points are depicted in Fig. 15. The gradient green color representing the failure zone shows how the two LSFs evolve in time.

Fig. 15

Enriched experimental designs of the two performance functions (case of a non-stationary Gumbel stochastic load)

The initial design point is found to be and is represented with a red dot in Fig. 16. The convergence of the design point towards its optimal position is also depicted. The numerical results of TROSK are given in Table 4, as well as the real optimal solution. It is noted here that t-SORA could not be applied as it is not applicable to problems involving non-stationary stochastic processes. It is observed that the results obtained with TROSK after only 3 iterations are very close to the analytical solution (${\varepsilon}_{\%}^{(1)}=2\%$ and ${\varepsilon}_{\%}^{(2)}$ is nul), with a total number of 330 function calls.

Fig. 16

Convergence of the optimization algorithm using TROSK (case of a non-stationary Gumbel stochastic load)

Table 4 Convergence of TROSK (case of a non-stationary Gumbel stochastic load)

5 Conclusion

This paper presents an efficient method for time-variant reliability based-design optimization, referred to as TROSK. The efficiency of this method is mainly due to: (1) performing a classification-based adaptive kriging technique in an augmented reliability space; (2) refining the surrogate models of the several time-dependent limit state functions simultaneously; and (3) finding the deterministic design point with no extra computational cost and using it as initial design point for the t-RBDO algorithm. The effectiveness of the proposed method is demonstrated on benchmark problems of which one involves stationary and non-stationary stochastic loads. The obtained results show that TROSK outperforms some recent methods from the literature.

However, it is noted that TROSK being based on kriging, it inherits the drawbacks of this technique. Indeed and for high dimensional problems (10–100 inputs), the method is very likely to require large experimental designs. In such case, the covariance matrix of the kriging model dramatically increases in size and its inversion becomes computationally expensive. The improvement of this aspect as well as the application of the proposed method to a complex civil engineering problem is currently under investigation.

Appendix: Kriging technique

The kriging technique consists in approximating a function G(x) that depends on a vector of input variables x = {x₁, x₂, …, x_m} as a sum of a regression model and a Gaussian stochastic process. This can be expressed as follows:

$$ \widehat{G}\left(\mathbf{x}\right)=\mathbf{f}{\left(\mathbf{x}\right)}^t\boldsymbol{\upbeta} +{\upsigma}_{\mathrm{Z}}^2Z\left(\mathbf{x}\right) $$

(27)

where f(x) = {f₁(x), f₂(x), …, f_p(x)}^t is a vector of regression functions, β is a vector of unknown coefficients and f(x)^tβ is the mean value of the Gaussian process, also known as the trend. ${\upsigma}_{\mathrm{Z}}^2$ is the Gaussian process variance and Z(x) is a stationary Gaussian process with zero mean and unit variance. Z(x) is completely described by its user-defined autocorrelation function R(x⁽ⁱ⁾, x^(j), θ) where θ = {θ₁, θ₂, …, θ_d} represents the vector of unknown correlation parameters to be determined.

Given an experimental design {x⁽ⁱ⁾, G(x⁽ⁱ⁾)}, i = 1, …, n, β and ${\upsigma}_{\mathrm{Z}}^2$ can be approximated as follows (Jones et al., 1998):

$$ \widehat{\boldsymbol{\upbeta}}\left(\boldsymbol{\uptheta} \right)={\left({\mathbf{F}}^t{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}{\mathbf{F}}^t{\mathbf{R}}^{-1}\mathbf{G} $$

(28)

and

$$ {\widehat{\upsigma}}_{\mathrm{Z}}^2\left(\boldsymbol{\uptheta} \right)=\frac{1}{n}{\left(\mathbf{G}-\mathbf{F}\boldsymbol{\upbeta } \right)}^t{\mathbf{R}}^{-1}\left(\mathbf{G}-\mathbf{F}\boldsymbol{\upbeta } \right) $$

(29)

where F is a matrix of size n × p and of general term F_ij = f_j(x⁽ⁱ⁾). And G = {G(x⁽¹⁾), G(x⁽²⁾), …, G(x⁽ⁿ⁾)}^t is the response vector.

Note that β and ${\upsigma}_{\mathrm{Z}}^2$ both depend on the correlation parameters θ_i. The optimal values of θ can be determined by maximum likelihood estimation (Marrel et al., 2008):

$$ {\boldsymbol{\uptheta}}^{opt}=\underset{\boldsymbol{\uptheta}}{\mathit{\arg}\;\mathit{\min}}\left(\widehat{\sigma}2{\left(\det \mathbf{R}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}\right) $$

(30)

Once the kriging parameters are determined, they can be used to predict the model response at a new trial point x^∗ as a Gaussian random variable of mean ${\mu}_{\widehat{G}}\left({\mathbf{x}}^{\ast}\right)$ and variance ${\sigma}_{\widehat{G}}^2\left({\mathbf{x}}^{\ast}\right)$ (Jones et al., 1998) defined as follows:

$$ {\mu}_{\widehat{G}}\left({\mathbf{x}}^{\ast}\right)=\mathbf{f}{\left({\mathbf{x}}^{\ast}\right)}^t\boldsymbol{\upbeta} +\mathbf{r}{\left({\mathbf{x}}^{\ast}\right)}^t{\mathbf{R}}^{-1}\left(\mathbf{G}-\mathbf{F}\boldsymbol{\upbeta } \right) $$

(31)

and

$$ {\sigma}_{\widehat{G}}^2\left({\mathbf{x}}^{\ast}\right)={\upsigma}_{\mathrm{Z}}^2\left(1-\left[\mathbf{f}{\left({\mathbf{x}}^{\ast}\right)}^t\kern0.75em \mathbf{r}{\left({\mathbf{x}}^{\ast}\right)}^t\right]\left[\begin{array}{cc}\mathbf{0}& {\mathbf{F}}^t\\ {}\mathbf{F}& \mathbf{R}\end{array}\right]\left[\begin{array}{c}\mathbf{f}\left({\mathbf{x}}^{\ast}\right)\\ {}\mathbf{r}\left({\mathbf{x}}^{\ast}\right)\end{array}\right]\right) $$

(32)

where r(x^∗) is the correlation vector between x^∗ and the inputs of the experimental design: r_i(x^∗) = R(x⁽ⁱ⁾, x^∗, θ^opt).