Optimum parameters and performance of negative stiffness and inerter based dampers for base-isolated structures

Abstract

Novel combinations of true negative stiffness dampers (NSDs) and inerter devices are used concurrently as supplemental dampers for response control of base-isolated structures. The combination of the inerter and NSD is denoted as negative stiffness inerter damper (NSID). Classical H∞ optimisation based on a well-known fixed-point theory of tuned mass dampers is used to derive optimal parameters for NSD and three configurations of NSIDs. Optimal NSIDs and NSD are supplemented to the base-isolated structure as passive control devices. The closed-form expressions for optimal parameters are derived, which will be useful for the initial design process of these devices for isolated structures. A numerical searching technique is used to verify the derived closed-form expressions for the optimal parameters of NSIDs. A comparative analysis is also run by utilising three configurations of NSIDs and a true NSD as supplemental control devices to the flexible base-isolated structure. The governing equations of motion are written in state-space form, and the performance of the proposed supplemental dampers for the base-isolated structure is investigated under real earthquake records. Time history analysis shows that the optimal NSIDs and NSD effectively control the objective variables of base displacement, inter-storey drift, and top storey acceleration. Especially under near-fault, which may bring isolation systems to critical working conditions, the proposed supplemental dampers cushion against failure by improving energy dissipation capacity compared to conventional passive dampers. Optimal NSID parameters are lower in magnitude than NSD parameters, resulting in a smaller damper size, which is desirable from a practical design standpoint.

1 Introduction

Structural control engineering has received considerable attention during the past decades. Seismic base-isolation is a well-established structural control passive technique to reduce the dynamic response of structures subjected to strong ground motions (Kelly 1986; Buckle and Mayes 1990; Jangid and Datta 1995). The core idea of seismic base isolation is to decouple the superstructure from the earthquake ground motion by introducing a flexible interface between the base and foundation of a structure. Although base-isolated structures have proven to be very protective against far-field (FF) earthquakes, large isolator displacement is a big concern, especially under near-fault (NF) excitations. Forward site directivity produces NF motion, having large velocity pulses, and can bring seismic isolation devices to a critical working condition (Jangid and Kelly 2001; Rao and Jangid 2001; Jadhav and Jangid 2006; Providakis 2008). The NF zone is assumed to be within 20 km of the ruptured fault (Rong 2020). Significant displacement demand of isolators in the NF area impacts the service lines passing through the base isolator slabs. Therefore, there is a strong need to control base isolator displacement demand in NF zones. Conventional practice to address extensive base isolator demand under NF excitations is to supplement the base isolation with passive dampers (PD) such as viscous dampers (VD) and visco-elastic dampers (VED). However, there is a problem associated with supplemental PDs; it activates the higher modes of the isolated structure and defeats the purpose of base isolation. A high value of damping requirement for NF motion becomes exceptionally high for FF motion (Providakis 2008; Lee and Kelly 2019). Hence, supplemental damping to reduce isolator displacement demand seems attractive for base isolation under NF motion but may show adverse effects for FF motion (Zelleke et al. 2015).

Recently, negative stiffness dampers (NSDs) have been widely studied for seismic response mitigation characteristics. Geometrically, NSD consists of a compressed spring (working on the force assisting motion, also referred to as true negative stiffness) and a PD configuration. The true negative stiffness (TNS) concept is presented by Pasala et al. (2013), which utilises TNS to shift yielding away from the main structure to TNS device (called apparent yielding), resulting in reduced base shear. However, due to apparent yielding, the structural deformation increased. The addition of a PD reduces these displacements considerably with a slight increase in base shear. This assembly, referred to as an adaptive negative stiffness system (ANSS), shows promising results as a control device. Analytical modelling and experimental evaluation are presented in work by (Sarlis et al. 2013), and it has been demonstrated dynamic inertia can be neglected for most practical cases. Experimental investigation for ANSS as a controlled device has shown that displacement, acceleration and base shear are reduced considerably (Pasala et al. 2014). Shake table testing of an isolated 3-storey building supplemented with ANSS has substantially reduced base displacement, base shear, floor acceleration, and inter-storey drifts (Sarlis et al. 2016). ANSS devices have been supplemented to scaled-down isolated bridges models (Attary et al. 2015a, b). Analytical studies for optimal placement and the number of the ANSS devices required for efficient seismic control of the multi-degree of freedom (MDOF) shear model have been carried out (Mathew and Jangid 2018). A passive NSD proposed by (Wang et al. 2019b) called negative stiffness amplifying damper (NSAD) uses a TNS system combined with a flexibly supported VD (represented by classical Maxwell damping element). The overall assembly consists of a negative stiffness spring in parallel combination with VD, a series connected with a positive spring. It has been shown that single degree of freedom (SDOF) system with NSAD achieves a magnified damping effect (called damping magnification) and is effective in seismic control under both FF and NF type excitations. The application of NSAD to an MDOF system and modal optimisation of NSAD parameters have been investigated (Wang et al. 2019a).

Recently, inerter based vibration absorbers (IVAs) have created widespread excitement in control engineering as these are considered potential future passive control devices. Inerter is a two-terminal mechanical analogue to an electrical capacitor with the property that the force developed is proportional to the relative acceleration between its two terminals (Smith 2002; Baker 2007; Chen et al. 2009). The constant ratio between force developed and corresponding relative acceleration between terminals is called inertance measured in mass unit. From the initial use of inerters in Formula-One suspension systems as J-dampers (Chen et al. 2009), inerters are widely used as vibration control devices for civil engineering structures (Baker 2007; Marian and Giaralis 2014; Brzeski et al. 2015; Chen et al. 2021). The unique characteristic of the inerter system is that large inertance or equivalent mass can easily be achieved using a small physical mass (Chen and Hu 2019) which is an advantage for vibration isolation. IVAs can be categorised into the following groups: inerter based energy dissipators (ED), inerter based dynamic vibration absorbers (DVA) and inerter based vibration isolators. It has been demonstrated that increased inertance results in reducing natural frequency (Chen et al. 2014). Inerter based ED uses various inerter-spring-damper configurations, called inertial mass dampers (IMD), against traditional spring-damper arrangements, and hence an extra degree of freedom ensures better performance. It also provides better energy dissipation capacity than an identical spring-damper setup called the damping enhancement effect (Zhang et al. 2020; Ma et al. 2021). For various IMDs developed, refer to the studies by (Makris and Kampas 2016; Basili et al. 2017; Gao et al. 2021; Wang et al. 2021b). The effectiveness of conventional DVAs depends on the high mass ratio between secondary and host structures. In this regard, inerters have been used to upgrade conventional DVA by utilising the property of mass amplification. Some inerter based DVAs are listed: tuned mass inerter damper (TMDI) (Marian and Giaralis 2014), tuned inerter damper (TID) (Baker 2007), tuned liquid inerter system (TLIS) (Zhao et al. 2019) and shape memory alloy tuned mass damper system (SMA-TMDI) (Tiwari et al. 2021). Closed-form expressions for the optimal design of various inerter based DVAs have been developed for effective structural control (Nishihara and Asami 2002; Barredo et al. 2018). Inerter based isolators are very common in suspensions of automobiles (Smith and Wang 2004; Hu et al. 2017). The working mechanism of automotive suspensions and vibration isolators is almost the same. Hu et al. (2015) presented the analysis and optimisation of five configurations of inerter based isolators. The effectiveness of inerter based isolators can be attributed to the fact inerters results in reduction of natural frequency of system. On similar principles, (Ma et al. 2020) developed an isolator named an inerter based isolation system to counter heave motion due to sea waves for semi-submersible platforms. Moreover, an inerter based isolator was used to reduce the sloshing effect of cylindrical tanks subjected to ground excitations, and optimal design parameters were also derived (Luo et al. 2016; Jiang et al. 2020).

As mentioned, NF motions introduce significant displacement demand for base-isolated structures. Supplemental dampers in the form of inerter based ED systems have been used to counter this drawback. IMD in the form of gyro mass inertial damper (Saitoh 2012) and angular mass inertial damper (Pradono et al. 2008a effectively reduced lateral displacement demand for the isolated structure. However, increased acceleration response was seen under some earthquakes due to their large force at higher frequencies. Another approach for base displacement control involving inerters is using inerter based DVAs. A base-isolated structure with supplemental TMDI has been proposed by De Domenico and Ricciardi (2018), and the numerical investigation showed that optimal TMDI reduces the base displacement demand. TID was used as a supplemental damper to a base-isolated structure (Jangid 2021). Optimal parameters were derived using the numerical searching technique, and optimally designed TID was more efficient under soft soil conditions than firm soils. The performance of an inerter-based passive device is assessed experimentally to address the deficiency of a vibration isolator in the lower frequency band (Siami et al. 2018). The use of a grounded inerter in TMDs to reduce the lateral displacement of base-isolated systems without considerably raising accelerations is examined by De Angelis et al. (2019). TID was used to improve the seismic performance of dual isolated structures by an optimization design technique represented as a restricted multi-objective optimization design problem (Nyangi and Ye 2021). According to numerical and experimental shake table results, the optimised base-isolated TMDI system could result in performance gains in terms of the lateral displacement of the isolated structure and the seismic responses of the isolated host structures by adding a limited physical mass (Pietrosanti et al. 2021). Analytical and numerical results demonstrate that the electromagnetic IMDs consisting of an inerter element and a damping element can significantly enhance the seismic performance of a base-isolated structure (Wang et al. 2021b). The ideal design and efficacy of three control methods, tuned viscous mass damper (TVMD), TID, and TMD, minimising base-isolated structures’ seismic responses, were thoroughly investigated (Li et al. 2021). Analytical and numerical research is undertaken to determine the performance of the inertial amplifier coupled base isolator in the frequency domain, incorporating harmonic and random vibration excitations (Chowdhury et al. 2021). Negative stiffness and inerter dampers were used in a comparison study of vibration isolation performance (Shi and Zhu 2019). The fixed point theory is used to derive optimal parameters for the SDOF system equipped with the combination of inerter and NSD for seismic protection (Wang et al. 2021a, b). A unified study of multimode damping effects of negative stiffness and inerter mechanisms is performed when paired with a viscous damper for cable vibration control (Chen et al. 2021).

Here-in, inerter and NSD are combined and used concurrently as a supplemental damping device for base displacement control in an isolated shear building. Hereafter, the combination of inerter and NSD are referred to as negative stiffness inerter dampers (NSIDs). Objectives of this study include: (1) presenting the three configurations of novel NSIDs as passive control devices and developing the corresponding mathematical model, (2) investigating the optimal parameters for NSIDs and NSD based on the classical H∞ optimisation (Den Hartog 1985), (3) validating the optimal parameters derived using the numerical search technique, (4) presenting the enhanced energy dissipation capacity of proposed devices, and (5) studying comparative performance of NSD and three NSIDs as supplemental damping devices for an isolated shear building under NF and FF motions.

2 SDOF structure with supplemental dampers

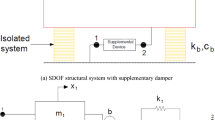
A single bay single storey frame of structural mass $m$, stiffness $k$ and inherent damping $c$ are considered; it can be modelled into an SDOF system as shown in Fig. 1. This dynamic system is supplemented with a damper for vibration control. Schematic representation and geometry of supplemental dampers are shown in Fig. 2. Let $k_{ns}$, $k_{p}$, $c_{d}$ and $b$ represent negative stiffness, positive stiffness, dashpot damping and inertance of supplemental dampers, respectively. Terminal 1 of the supplemental damper is connected to the mass of SDOF system, while terminal 2 is connected to the ground. For the system under consideration, the following system parameters are defined as

$$ \omega_{n} = \sqrt {{\raise0.7ex\hbox{$k$} \!\mathord{\left/ {\vphantom {k m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \quad and \quad \xi = {\raise0.7ex\hbox{$c$} \!\mathord{\left/ {\vphantom {c {2m\omega_{n} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2m\omega_{n} }$}} $$

(1)

$$ \alpha = {\raise0.7ex\hbox{${k_{ns} }$} \!\mathord{\left/ {\vphantom {{k_{ns} } {k_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${k_{p} }$}};\,\beta = {\raise0.7ex\hbox{${k_{p} }$} \!\mathord{\left/ {\vphantom {{k_{p} } k}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$k$}};\,\gamma = {\raise0.7ex\hbox{${c_{d} }$} \!\mathord{\left/ {\vphantom {{c_{d} } c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}};\, \xi_{d} = {\raise0.7ex\hbox{${c_{d} }$} \!\mathord{\left/ {\vphantom {{c_{d} } {2m\omega_{n} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2m\omega_{n} }$}} \;and\;\, \mu = {\raise0.7ex\hbox{$b$} \!\mathord{\left/ {\vphantom {b m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}} $$

(2)

where $\alpha$, $\beta$ and $\mu$ are the negative stiffness ratio, positive stiffness ratio, inertance to mass ratio, respectively; and $\xi$ and $\xi_{d}$ are the inherent damping ratio and supplemental damping ratio, respectively.

Fig. 1

Analytical model of the SDOF structure with supplemental damper

Fig. 2

Schematic representation of supplemental dampers: a NSD, b NSID-1, c NSID-2, d NSID-3

The dynamic equation of motion for the SDOF system with supplemental damper subjected to earthquake excitation is given as

$$ m\ddot{x} + c\dot{x} + kx + f_{d} = - m\ddot{x}_{g} $$

(3)

where $x$ is the displacement of SDOF system relative to the ground; $f_{{\text{d}}}$ is the control force generated across the terminals 1–2 of the supplemental damper; and $\ddot{x}_{g}$ is the earthquake acceleration.

2.1 SDOF structure with NSD

NSDs are passive devices that utilise compressed spring and damper configuration. NSD, based on the principle of NSAD proposed by Wang et al. (2019a, b), is investigated as a supplemental damper. From now onwards, NSD and NSAD will be used synonymously. Geometrically NSD consists of a negative stiffness spring in parallel combination with VD, series connected with a positive spring. Schematic representation of NSD is given in Fig. 2a. The damping force generated by NSD is given by

$$ f_{d} = k_{ns} y + c_{d} \dot{y} = k_{p} \left( {x - y} \right) $$

(4)

where $y$ is the relative displacement across terminals 3–2 of NSD.

Assuming such a harmonic earthquake acceleration as $\ddot{x}_{g} = e^{i\omega t}$, where ω is the circular frequency and $i = \sqrt { - 1}$, the steady-state displacement response is expressed as

$$ x = H\left( {i\omega } \right)\;e^{i\omega t} $$

(5)

where $H\left( {i\omega } \right)$ is the frequency response function (FRF) or transfer function of the displacement x. Defining frequency ratio as $\lambda = {\raise0.7ex\hbox{$\omega $} \!\mathord{\left/ {\vphantom {\omega {\omega_{n} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\omega_{n} }$}}$, the FRF of displacement is expressed by

$$ H\left( {i\omega } \right)\omega_{n}^{2} = \frac{{\left( {\beta + \alpha \beta } \right) + i\left( {2\xi_{d} \lambda } \right)}}{{\left\{ {\left( {1 - \lambda^{2} } \right)\left( {\beta + \alpha \beta } \right) - 4\xi \xi_{d} \lambda^{2} + \alpha \beta^{2} } \right\} + i2\lambda \left\{ {\xi_{d} \left( {1 - \lambda^{2} } \right) + \xi \left( {\alpha + \alpha \beta } \right) + \beta \xi_{d} } \right\}}} $$

(6)

The magnitude of complex FRF can be expressed in the following form

$$ \left| {R_{1} \left( \lambda \right)} \right| = \left| {H\left( {i\omega } \right)\omega_{n}^{2} } \right| = \sqrt {\frac{{A^{2} + B^{2} }}{{C^{2} + D^{2} }}} $$

(7)

where $A = \beta + \alpha \beta$, $B = 2\xi_{d} \lambda$, $C = \left( {1 - \lambda^{2} } \right)\left( {\beta + \alpha \beta } \right) - 4\xi \xi_{d} \lambda^{2} + \alpha \beta^{2}$ and $D = 2\lambda \left\{ {\xi_{d} \left( {1 - \lambda^{2} } \right) + \xi \left( {\alpha + \alpha \beta } \right) + \beta \xi_{d} } \right\}$.

2.2 SDOF structure with NSID-1

A schematic representation of NSID-1 is given in Fig. 2b. Proposed NSID-1 consists of an inerter parallel to a positive spring in the otherwise NSD configuration. Control force $f_{d}$ developed in NSID-1 is given by

$$ f_{d} = k_{ns} y + c_{d} y = k_{p} \left( {x - y} \right) + b\left( {\ddot{x} - \ddot{y}} \right) $$

(8)

where ${ }y$ is the relative displacement across terminals 1–3 of NSID-1.

The corresponding FRF magnitude denoted by $R_{2} \left( \lambda \right)$ can be expressed by Eq. (7) with the values of the constants as $A = \left( {\alpha \beta + \beta - \mu \lambda^{2} } \right)$, $B = 2\xi_{d} \lambda$ $C = \left( {1 - \lambda^{2} } \right)\left( {\alpha \beta + \beta - \mu \lambda^{2} } \right) - 4\xi \xi_{d} \lambda^{2} + \alpha \beta \left( {\alpha - \mu \lambda^{2} } \right)$ and $D = \left( {2\lambda } \right)\left\{ {\xi \left( {\alpha \beta + \beta - \mu \lambda^{2} } \right) + \xi_{d} \left( {1 - \lambda^{2} } \right) + \xi_{d} \left( {\beta - \mu \lambda^{2} } \right)} \right\}$.

2.3 SDOF structure with NSID-2

A schematic representation of NSID-2 is given in Fig. 2c. Here, the role of the inerter is reversed with the dashpot element in the otherwise NSID-1 configuration. Control force $f_{d}$ developed in NSID-2 is given by

$$ f_{d} = k_{ns} y + b\ddot{y} = k_{p} \left( {x - y} \right) + c_{d} \left( {\dot{x} - \dot{y}} \right) $$

(9)

where $y$ is the relative displacement across negative spring terminals 1–3.

The corresponding FRF magnitude of displacement, x, denoted by $R_{3} \left( \lambda \right)$ can be expressed by Eq. (7) with the values of the constants as $A = \left( {\alpha \beta + \beta - \mu \lambda^{2} } \right)$, $B = 2\xi_{d} \lambda$, $C = \left( {1 - \lambda^{2} } \right)\left( {\alpha \beta + \beta - \mu \lambda^{2} } \right) - 4\xi \xi_{d} \lambda^{2} + \alpha \beta \left( {\alpha \beta - \mu \lambda^{2} } \right)$ and $D = \left( {2\lambda } \right)\left\{ {\xi \left( {\alpha \beta + \beta - \mu \lambda^{2} } \right) + \xi_{d} \left( {1 - \lambda^{2} } \right) + \xi_{d} \left( {\alpha \beta - \mu \lambda^{2} } \right)} \right\}$.

2.4 SDOF structure with NSID-3

A schematic representation of NSID-3 is given in Fig. 2d. The NSID-3 setup is the modification of NSD where dashpot and inerter are placed parallel to negative spring. The corresponding control force is by

$$ \left\{ {\begin{array}{*{20}l} {f_{d} = k_{ns} y + b\ddot{z} = k_{p} \left( {x - y} \right)} \hfill \\ {b\ddot{z} = c_{d} \left( {\dot{y} - \dot{z}} \right)} \hfill \\ \end{array} } \right. $$

(10)

where $y$ is the relative displacement across the terminals 3–2; and $z$ is the displacement across terminals 4–2 of NSID-3.

The corresponding FRF of displacement, x, denoted by $R_{4} \left( \lambda \right)$ can be expressed by Eq. (7) with the values of the constants as $A = - \left( {{\upalpha }\beta + {\upbeta }} \right)\mu \lambda^{2}$, $B = \left( {2\xi_{d} \lambda } \right)\left( {\alpha \beta + \beta - \mu \lambda^{2} } \right)$, $C = - \left( {\alpha \beta + \beta } \right)\left( {1 - \lambda^{2} + \beta \lambda^{2} } \right)\mu \lambda^{2} + 4\xi \xi_{d}^{2} \lambda^{2} \left( {\alpha \beta + \beta - \mu \lambda^{2} } \right) + \beta^{2} \mu \lambda^{2}$ and $D = \left( {2\lambda } \right)\left\{ {\left( {1 - \lambda^{2} + \beta \lambda^{2} } \right)\left( {\alpha + \alpha \beta - \mu \lambda^{2} } \right)\xi_{d} - \beta^{2} \xi_{d} - \left( {\alpha \beta + \beta } \right)\left( {\mu \lambda^{2} } \right)\xi } \right\}$.

2.5 Stability of system

Introducing the negative stiffness in the system can cause stability problems (Shi and Zhu 2019). The Routh-Hurwitz stability criteria and static stiffness stability (at $\lambda$ = 0) criteria are used to identify the range of negative stiffness to ensure the system’s stability. For all the supplemental damping systems considered in the study, maximum achievable $\alpha$ for a given value of $\beta$ is limited to

$$ \alpha > - \frac{1}{1 + \beta } $$

(11)

All the optimal values for α are calculated considering the limit prescribed by Eq. (11).

3 H∞ optimisation

H∞ optimisation aims to minimise the maximum response (resonant amplitude) in the frequency domain. This optimisation criterion has been used for deriving optimal parameters for TMDs (Den Hartog 1985; Ren 2001; Cheung and Wong 2011). Optimal parameters for the best possible response are evaluated using the same principles. It has been observed that fixed points or invariant points independent of damping exist for the proposed NSD and NSIDs when attached to an SDOF system.

Plots between the magnitude of the transfer function and frequency ratio for the SDOF system with various supplemental dampers are given in Fig. 3. An exciting feature in Fig. 3 is the presence of fixed points (P, Q and R), which are independent of the damping $\xi_{d}$. Primary assumption in these transfer function amplitude plots is neglecting the inherent damping of the SDOF system $\xi$. For the optimisation, there exists four parameters ($\alpha ,\beta ,\mu ,\xi_{d}$) for NSIDs and three for NSD ($\alpha ,\beta ,\xi_{d}$). The objective of optimal design is to find optimal curve of the transfer function for which horizontal tangent passes through the highest of fixed points. The parameters of the optimal curve of the transfer function will define optimal parameters for various supplemental dampers. For the optimisation process, inherent damping $\xi$ of system is neglected for simplicity.

Fig. 3

Transfer function amplitudes of SDOF system with proposed supplemental dampers: a NSD (β = 0.6 and α = − 0.3), b NSID-1 (μ = 0.25, β = 0.6 and α = − 0.3), c NSID-2 (μ = 0.125, β = 0.7 and α = −0.3), d NSID-3 (μ = 0.25, β = 0.3 and α = − 0.3)

3.1 Optimal NSD

The general optimisation process is summarised as.

• 1. For a given positive stiffness ratio $\beta$, find the invariant or fixed-point P.

• 2. Calculate the value of negative stiffness ratio $\alpha$ such ordinate of the transfer function at P and static response of the system are equal i.e. $R_{1} \left( {\lambda_{P} } \right) = R_{1} \left( 0 \right)$.

• 3. Obtain the damping ratio $\xi_{P}$ such that transfer function curves pass horizontally through P.

The transfer expression by neglecting the inherent damping $\xi$ is given as

$$ R_{1}^{2} \left( \lambda \right) = \frac{{\left( {\beta + \alpha \beta } \right)^{2} + \left( {2\xi_{d} \lambda } \right)^{2} }}{{\left\{ {\left( {1 - \lambda^{2} } \right)\left( {\beta + \alpha \beta } \right) + \alpha \beta^{2} } \right\}^{2} + \left( {2\xi_{d} \lambda } \right)^{2} \left( {1 - \lambda^{2} + \beta } \right)^{2} }} = \frac{{A^{2} + B^{2} }}{{C^{2} + D^{2} }} $$

(12)

For an invariant point to exist, Eq. (12) should satisfy the following equality $\frac{{A^{2} }}{{C^{2} }} = \frac{{B^{2} }}{{D^{2} }}$. On simplification the location of fixed-point P is given as

$$ \lambda_{P}^{2} = \frac{\beta + 2\alpha \beta + 2\alpha + 2}{{2\left( {1 + \alpha } \right)}} $$

(13)

For the optimal value of negative stiffness ratio, $\alpha$ ordinate of the transfer function at P and static response of the system are equated i.e. $R_{1} \left( {\lambda_{P} } \right) = R_{1} \left( 0 \right)$. Since the fixed point, P, is independent of damping, the transfer function curve for the case of damping value $\xi_{d} = \infty$ is utilised for evaluating $R_{1} \left( {\lambda_{P} } \right)$.

$$ \left| {R_{1} \left( {\lambda_{P} } \right)} \right|\left( {\xi_{d} = \infty } \right) = \left| {\frac{\alpha \beta + \beta }{{\left( {1 - \lambda_{P}^{2} } \right)\left( {\alpha \beta + \beta } \right) + \alpha \beta^{2} }}} \right| $$

(14)

The magnitude of the transfer function at $\lambda = 0$ is given as

$$ \left| {R_{1} \left( 0 \right)} \right| = \left| {\frac{\alpha + 1}{{\alpha + 1 + \alpha \beta }}} \right| $$

(15)

From the Eqs. 13–15, the optimal value of $\alpha$ is given as

$$ \alpha_{opt} = \frac{\beta - 2}{{2\left( {\beta + 1} \right)}} $$

(16)

The optimal damping ratio is evaluated such that the peak (global maximum) of the transfer function passes through the invariant point P. To make fixed point P the maximum point on the transfer function curve, a horizontal tangent is made to pass through it. For simplicity, the square of the transfer function is differentiated instead of the transfer function itself

$$ \frac{{\partial \left| {R_{3}^{2} \left( \lambda \right)} \right|}}{{\partial \lambda^{2} }} = 0, \,\,at points\, \lambda^{2} = \lambda_{ P }^{2} $$

(17)

Simplifying Eq. (17) given optimal damping ratio

$$ \xi_{d,opt} = \frac{{\beta \left( {\alpha + 1} \right)}}{{2\sqrt {\lambda_{P} } }} $$

(18)

3.2 Optimal NSID-1

The general optimisation process is summarised as.

• 1. For a given inertance to mass ratio $\mu$, find the invariant or fixed points (P, Q, R) and denote the fixed points such that $\lambda_{P} < \lambda_{Q} < \lambda_{R}$.

• 2. Find the value of the positive stiffness ratio $\beta$ such that ordinates of the transfer function at P and Q are equal i.e. $R_{2} \left( {\lambda_{P} } \right) = R_{2} \left( {\lambda_{Q} } \right)$.

• 3. Calculate the value of negative stiffness ratio $\alpha$ such that ordinate of the transfer function at R and static response of the system are equal i.e. $R_{2} \left( {\lambda_{R} } \right) = R_{2} \left( 0 \right)$.

• 4. Obtain the damping ratio $\xi_{P}$ and $\xi_{Q}$ such that transfer function curves pass horizontally through P and Q, respectively.

• 5. Obtain the optimal damping ratio as $\sqrt {\frac{{\xi_{P}^{2} + \xi_{Q}^{2} }}{2}}$

Following the above procedure gives the following optimal parameters:

$$ \beta_{opt} = \frac{\mu }{{\alpha \mu^{2} + 2\alpha \mu + \alpha + 1}} $$

(19)

$$ \alpha_{opt} = \frac{{ - \left\{ {2\mu + 3 - \sqrt {4\mu^{2} + 12\mu + 1} } \right\}}}{{4\left( {\mu + 1} \right)}} $$

(20)

3.3 Optimal NSID-2

The general optimisation process is summarised as.

• 1. For a given inertance to mass ratio $\mu$, find the invariant or fixed points (P, Q, R) and denote the fixed points such that $\lambda_{P} < \lambda_{Q} < \lambda_{R}$.

• 2. Find the value of the positive stiffness ratio $\beta$ such that ordinates of the transfer function at P and Q are equal i.e. $R_{3} \left( {\lambda_{P} } \right) = R_{3} \left( {\lambda_{Q} } \right)$.

• 3. Calculate the value of negative stiffness ratio $\alpha$ such that all three invariant points (P, Q and R) exist.

• 4. Obtain the damping ratio $\xi_{P}$ and $\xi_{Q}$ such that transfer function curves pass horizontally through P and Q, respectively.

• 5. Obtain the optimal damping ratio as $\sqrt {\frac{{\xi_{P}^{2} + \xi_{Q}^{2} }}{2}}$

Following the above procedure gives the following optimal parameters:

$$ \beta_{opt} = \frac{2\mu }{{2\alpha + 3\mu + \alpha \mu^{2} + \mu^{2} + \alpha \mu + 2}} $$

(21)

$$ \alpha_{opt} = - \frac{\mu }{{4\left( {\mu + 2} \right)}} $$

(22)

3.4 Optimal NSID-3

The general optimisation process is summarised as.

• 1. For a given positive stiffness ratio $\beta$, find the invariant or fixed points P and Q.

• 2. Calculate the value of inertance to mass ratio $\mu$ such ordinate of the transfer function at P and Q of the system are equal i.e. $R_{4} \left( {\lambda_{P } } \right) = R_{4} \left( {\lambda_{Q} } \right)$.

• 3. Calculate the value of negative stiffness ratio $\alpha$ such that the overall system remains stable.

• 4. Obtain the damping ratio $\xi_{P}$ or $\xi_{Q}$ such that transfer function curves pass horizontally through P or Q.

• 5. Obtain the optimal damping ratio as $\sqrt {\frac{{\xi_{P}^{2} + \xi_{Q}^{2} }}{2}}$

Following the above procedure gives the following optimal parameters:

$$ \mu_{opt} = \frac{{2\beta \left( {1 - \beta } \right)\left( {\alpha + 1} \right)^{2} }}{2\alpha - 3\beta + 2} $$

(23)

$$ \alpha_{opt} = \frac{1}{2}\left( {{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\beta - 1} \right) $$

(24)

The optimum parameters for proposed supplemental dampers are tabulated in Table 1. For proper comparison, it becomes necessary to look for one common parameter for an adequate comparison study. So, β = 0.25 is selected as a common parameter, and the rest are derived from formulae given in preceding sections. The table shows that the negative stiffness ratio required for NSD is comparatively on the higher side. By using the inerter mechanism the negative stiffness ratio requirement decreases. Also, optimal damping values are minimal when compared with standard supplemental VDs and VEDs. Optimal transfer curves based on are plotted in Fig. 4. The figure shows that the uncontrolled SDOF structure has considerable resonant amplitude. However, the resonant amplitude is controlled efficiently in the SDOF system with optimal supplemental dampers. Among the four supplemental dampers, NSD and NSID-3 show a better reduction in resonant amplitude.

Table 1 Optimum parameters of the NSD and NSIDs

Fig. 4

Optimal transfer function curves for various supplemental dampers

4 Validation of optimal parameters of NSD and NSIDs

4.1 Effect of neglecting inherent damping

When the primary system’s intrinsic structural damping is taken into account, obtaining explicit mathematical formulations that correspond to the optimum parameters of NSIDs and NSDs becomes difficult to evaluate. In addition, the presence of fixed or invariant points is also lost. The optimisation procedure for getting optimal parameters is based on rigorous mathematical optimisation techniques. As a result, the system’s intrinsic damping is ignored for simplicity, and optimal parameters are obtained, as described in the previous section. However, a numerical searching approach is used to determine the effect of neglecting inherent damping. Tables 2, 3, 4 shows the numerical search results corresponding to 5% and zero intrinsic structural damping ratio. The numerical search scheme reveals that the inaccuracy in predicting NSID-1’s optimum parameters is relatively small. The fixed-point technique accurately predicts the ideal negative stiffness ratio and damping ratio. When inherent damping is taken into account, the transfer function values are smaller, as expected. The fixed-point technique predicts lower damping ratios and higher transfer function values for NSID-2. Similarly, for NSID-3, the fixed-point method slightly over-predicts damping ratios. Thus, parameters of NSIDs obtained from the fixed-point method can be used for the initial design process without introducing much error in the analysis.

Table 2 Optimal NSID-1 parameters (damped vs undamped)

Table 3 Optimal NSID-2 parameters (damped vs undamped)

Table 4 Optimal NSID-3 parameters (damped vs undamped)

4.2 Energy dissipation by NSIDs and NSD

This section demonstrates the energy dissipation capacity of optimal supplemental dampers in contrast with intrinsic structural damping. Optimal parameters for supplemental dampers are based on the closed-form expressions derived from fixed-point theory.

The seismic input energy is dissipated for elastic systems via inherent damping and supplemental damping systems installed. Energy dissipation by intrinsic damping mechanisms is given by the following

$$ E_{in} = \mathop \int \nolimits_{0}^{T} c\dot{x}^{2} dt $$

(25)

where $T$ is the duration of seismic excitation.

The energy dissipated by the supplemental damping device is given as

$$ E_{su} = \mathop \int \nolimits_{0}^{T} F_{d} \dot{x}dt $$

(26)

The total energy dissipated is given by the following expression

$$ E_{total} = E_{in} + E_{su} $$

(27)

The time history of normalised energy dissipation by supplemental dampers (NSIDs and NSD) throughout seismic activity for the Imperial Valley earthquake (1940, El Centro) is shown in Fig. 5. Table 1 describes the optimum parameters for various supplemental dampers, and the inherent damping of the system is 0.02. As shown in figure Fig. 5, the normalised energy dissipation of NSD is 0.917, while for the inherent dissipation, it is about 0.083. Similarly, for NSID-1, NSID-2 and NSID-3 the normalised energy dissipation value is about 0.775, 0.833 and 0.887, respectively. Thus, the energy dissipation of supplemental dampers proposed is significantly higher than the inherent energy dissipation capacity of the SDOF system. This efficient energy dissipation capacity indicates that proposed dampers can dissipate most seismic input and structure protection. To quantitatively measure the efficiency of energy dissipation, the energy dissipation ratio is defined as

$$ E_{DP} = {\raise0.7ex\hbox{${E_{su} }$} \!\mathord{\left/ {\vphantom {{E_{su} } {E_{in} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${E_{in} }$}} $$

(28)

Fig. 5

Dissipation energy of SDOF system for supplemental dampers subjected to El Centro (1940) earthquake

For, NSD $E_{DP}$ is equal to 11.048, implying that the enhancement of energy dissipation by a factor of 11.048. Similarly, for NSID-1, NSID-2 and NSID-3, energy dissipation is improved by 3.44, 4.98 and 7.13, respectively.

5 Base isolated shear building with supplemental dampers

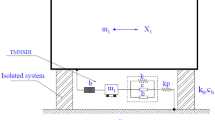
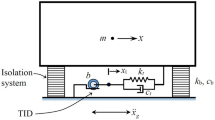
The fundamental mode of vibration for base-isolated structures is the dominant vibration mode (Kulkarni and Jangid 2003). Utilising this fact, classical H∞ optimisation described is used for the base-isolated structure. Seismic base isolation will synonymously mean base isolation using rubber. The following sections present an analytical analysis of base displacement control using proposed supplemental dampers. A five-storey shear building has been isolated with a linear isolator to study the performance of proposed supplemental dampers. For modelling and analysing the structure, some simplifying assumptions are made: (1) structure is linear and stories are rigid, (2) no torsional effect on stories, (3) soil-structure interaction is neglected, and (4) a linear spring and linear viscous model of isolation system is assumed.

Schematic representation of the base-isolated (BI) shear model with supplemental damper is shown in figure Fig. 6. Mass and stiffness are assumed to be uniformly distributed throughout the building, i.e., all lumped masses are equal, and each storey stiffness is the same. The mass associated with each DOF is 5000 kg, and the stiffness of each storey is 1.5228 × 10⁷ N/m. The fundamental time period (T_n) for the fixed base (FB) model is chosen as 0.5 s. The damping ratio for the first two modes is assumed as 0.02, and the rest modes are calculated using Rayleigh damping. The equivalent stiffness and damping of isolation are represented by $k_{b}$ and $c_{b}$. The base isolation system considered can be characterized by the two parameters, namely, isolation period and damping ratio defined as

$$ T_{b} = {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } {\omega_{b} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\omega_{b} }$}}, \omega_{b} = \sqrt {{\raise0.7ex\hbox{${k_{b} }$} \!\mathord{\left/ {\vphantom {{k_{b} } {m_{t} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${m_{t} }$}}} \,{\text{and}}\,\zeta_{b} = {\raise0.7ex\hbox{${c_{b} }$} \!\mathord{\left/ {\vphantom {{c_{b} } {2m_{t} \omega_{b} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2m_{t} \omega_{b} }$}} $$

(29)

where $m_{t}$ total storey mass including base slab.

Fig. 6

Schematic representation of BI shear building model with supplemental damper

For present study, properties of the base isolator (linear) are: damping ratio ζ_b = 0.1; isolating time period T_b = 1.75 secs and mass m_b = 5000 kgs. Two sets of real earthquake records, NF and FF, are used to demonstrate the effectiveness of dampers.

5.1 Base-isolated structure

Dynamic equation of motion of base-isolated (BI) structure subjected to seismic excitation is given as (Kelly 1993)

$$ \left[ {\begin{array}{*{20}c} {m_{t} } & {r^{T} \left[ m \right]} \\ {\left[ m \right]\left\{ r \right\}} & {\left[ m \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{x}_{b} } \\ {\ddot{x}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {c_{b} } & 0 \\ 0 & {\left[ c \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{x}_{b} } \\ {\dot{\user2{x}}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{b} } & 0 \\ 0 & {\left[ k \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {x_{b} } \\ {\varvec{x}} \\ \end{array} } \right\} = - \left\{ {\begin{array}{*{20}c} {m_{t} } \\ {\left[ m \right]\left\{ r \right\}} \\ \end{array} } \right\}\ddot{x}_{g} $$

(30)

where $m_{t}$ is the total storey mass including base slab; $\left[ m \right]$, $\left[ c \right]$ and $\left[ k \right]$ are the mass, damping and stiffness matrix of the 5-DOF FB structure, respectively; $x_{b}$ is the base isolator displacement; ${\varvec{x}}$ is a vector of 5 × 1 dimension representing relative displacements with respect to base isolator of five storeys above base-isolator given by $\left\{ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } \\ \end{array} \begin{array}{*{20}c} {x_{4} } & {x_{5} } \\ \end{array} } \right\}^{T}$; and $r$ is the influence coefficient vector of 5 × 1 order.

5.2 Base isolated with NSD and NSIDs

For the BI model with the proposed supplemental dampers, the general equation of motion is given in the following manner

$$ \left[ {\begin{array}{*{20}c} {m_{t} } & {r^{T} m} \\ {\left[ m \right]\left\{ r \right\}} & {\left[ m \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{x}_{b} } \\ {\ddot{x}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {c_{b} } & 0 \\ 0 & {\left[ c \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{x}_{b} } \\ {\dot{\user2{x}}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{b} } & 0 \\ 0 & {\left[ k \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {x_{b} } \\ {\varvec{x}} \\ \end{array} } \right\} + \left\{ \lambda \right\}f_{d} = - \left\{ {\begin{array}{*{20}c} {m_{t} } \\ {\left[ m \right]\left\{ r \right\}} \\ \end{array} } \right\}\ddot{x}_{g } $$

(31)

where λ is the vector of 6 × 1 dimension is defined as $\left\{ {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} \begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right\}^{T}$; and $f_{d}$ is the control force generated by the supplemental dampers.

The corresponding control force, $f_{d}$ for the NSD, NSID-1, NSID-2 and NSID-3 are given by Eqs. (4), 8–10, respectively. A nomenclature for BI structure with the supplemental NSD, NSID-1, NSID-2 and NSID-3 is given as BINSID, BINSID-1, BINSID-2 and BINSID-3, respectively. The Eq. (31) is converted to a state-space model by invoking the command ‘ss’ command in MatLab. The numerical solution of the state-space model subjected to ground acceleration is evaluated by fetching the model to the command ‘lsim’ in MatLab.

6 Analysis under real earthquake records

Two sets of real earthquake records, NF and FF, are selected to evaluate the effectiveness of NSD and NSIDs as potential supplemental dampers to BI structure. Ground motions used in response history analysis are described in Tables 5 and 6. Base displacement, storey shear and top storey acceleration are three response parameters to define the effectiveness of supplemental dampers. Table 1 describes the optimum parameters for various dampers selected for the study. Since objective parameters are not mutually exclusive, the effectiveness of proposed dampers will depend on the combined performance of objective parameters. The conventional practice focuses on the base displacement parameter to counter the NF effects of an earthquake. However, ignoring other parameters can prove critical for the proper working of base isolation.

Table 5 A suite of FF ground motions

Table 6 A suite of NF ground motions

6.1 Performance evaluation

Time history plots for base displacement are given in Fig. 7 under Imperial Valley-02 El Centro (FF) and Northridge-01 Sylmar Olive (NF). Both plots showcase the base displacement control of proposed supplemental dampers. Base displacement for NF motion is higher than FF. Peak values of base displacements for each case are marked in the plots. Similarly, the time history for top storey acceleration is given in Fig. 8 under Northridge-01 Sylmar Olive (NF) and Imperial Valley-02 El Centro (FF). These plots show top storey acceleration is controlled effectively and is not amplified. Plots show higher acceleration values for NF motion compared to FF motion. Peak accelerations values are marked in the plots. The first storey drifts time history under Northridge-01 Sylmar Olive (NF) and Imperial Valley-02 El Centro (FF) is given in Fig. 9. It becomes clear that the proposed supplemental dampers achieve satisfactory seismic reduction performance concerning all three objective parameters (base displacement, storey shear/drift and top storey acceleration).

Fig. 7

Base displacement time history for BI structure with supplemental dampers: a NF motion (Northridge), b FF motion (El Centro)

Fig. 8

Top storey acceleration time history for BI structure with various supplemental dampers: a NF motion (Northridge), b FF motion (El Centro)

Fig. 9

First storey drift time history for BI structure with various supplemental dampers: a NF motion (Northridge), b FF motion (El Centro)

Mean envelopes of peak storey drift for the five cases discussed are given in Fig. 10. Maximum base displacement values are tabulated in Table 7. These plots and tabulated values show that base displacements for FF ground motion are substantially less than the NF motions. Thus, for the case of FF motions, base displacement control is not essential. However, providing the supplemental dampers reduces the base displacement demand. For instance, mean base displacement reduces from 85.9 to 63.6 mm, 78.9 mm, 61 mm and 62.3 mm for BINSD, BINSID-1, BINSID-2 and BINSID-3, respectively. The damping requirement for base displacement control for NF motion is high because of the considerable base displacement demand. The optimal NSD and NSIDs show promising results as supplemental dampers for base displacement control for NF motions. NSID-3 outperforms others in the base displacement control variable among the various proposed devices. However, as previously discussed, base displacement control is not the lone efficiency parameter. While using supplemental dampers for base displacement control, storey accelerations may increase. The reason is the introduction of rigidity to an otherwise flexible system resulting in activation of higher modes. Figure 11 shows the mean envelopes of peak storey acceleration for the set of NF and FF motions. Maximum top storey acceleration values are tabulated in Table 7. It becomes clear not only has base displacement controlled but at the same time storey acceleration parameter is also checked. Among the various proposed control devices, NSD outperforms others in acceleration control. Another parameter for evaluating the efficiency of supplements PDs is storey shear. The storey shear variation for five cases is given in Fig. 12. Compared to uncontrolled BI structures, proposed dampers substantially reduce the inter-storey shear and acceleration for under NF and FF excitations.

Fig. 10

Mean envelopes of peak storey drift for the BI structure with various supplemental dampers under FF and NF motion

Table 7 Maximum mean response for NF and FF motions

Fig. 11

Mean envelopes of peak storey acceleration for the BI structure with various supplemental dampers under FF and NF motion

Fig. 12

Mean envelopes of peak storey shear for the BI structure with various supplemental dampers under FF and NF motion

6.2 Discussion

Thus, the optimised supplemental dampers (NSD and NSIDs) simultaneously reduce all objective parameters to the desired working level. The combination of inerter and negative stiffness allows minimal use of dashpot damping with maximum output result. The dynamic magnification effect (Wang et al. 2019a) due to negative stiffness is further enhanced due to the inerter element. This allows base displacement control under NF motions and simultaneously reduces acceleration response. From Table 1, the optimum damping ratios obtained are 0.0392, 0.0203, 0.0314 and 0.1024 for NSD, NSID-1, NSID-2 and NSID-3 respectively. The inherent first mode damping of the isolation system is 0.1, i.e., NSD, NSID-1, NSID-2 and NSID-3 damping ratios are only 0.392, 0.203, 0.314 and 1.024 times the inherent damping, respectively. These values are lower than the standard supplemental damping provided (usually VDs or VEDs). The increase in VD and VED’s damping ratio excites higher modes and accelerates higher storey. The fundamental assumption is that only the first mode dominates, for the base-isolated structures are violated for conventional VED and VD dampers. Due to the negative stiffness element present in proposed dampers, structural vibrations due to higher modes is controlled, and hence, only the first mode dominates. This means the optimal damping procedure prescribed for SDOF systems will be the initial optimal design for the MDOF base-isolated structure.

From the response history analysis and comparison between proposed supplemental damping devices, NSIDs shows better base displacement control than NSD. This aspect is seen especially under NF motion, where base displacement reduction is 15 mm only using NSD. Base displacement control is enhanced by the incorporation of the inerter mechanism along with NSD. However, numerical results show increased peak top storey acceleration. Thus, numerical results reveal that the proposed NSIDs outperform NSD for reducing the base displacement; however, the NSD achieves better performance for the superstructure. This is because the inertial force of the inerter is dominant at high frequencies, potentially amplifying the system’s high-frequency responses. Due to the injection of high-frequency earthquake excitation, the inerter devices increase storey acceleration. Similar detrimental effects of optimally designed TMDs and TMDIs to the structural acceleration of the BI structure have also been reported in the past (Taniguchi et al. 2008; Pradono et al. 2008; Petti et al. 2010; De Domenico and Ricciardi 2018; De Angelis et al. 2019; Pietrosanti et al. 2021). However, for NSIDs, acceleration response is well below the benchmark of uncontrolled structure.

Furthermore, the optimum negative stiffness ratio for the same positive stiffness ratio is lower for NSIDs. This results in the advantage of a lower payload for maintaining the negative stiffness of the system. Among the three NSIDs, NSID-3 outperforms the other two in terms of objective parameters defined. However, the optimal damping requirement is on the higher side for the same positive stiffness ratio. Inerter and negative stiffness based supplemental dampers have been proposed as potential alternatives to conventional VEDs and VDs. The optimal parameters have been derived by reducing the H∞ norm of the SDOF system. Same optimal parameters have been used for supplemental dampers in an MDOF isolated shear structure based on the premise that only the fundamental mode is the dominant mode of the system. The drawback of exciting higher modes in classical VDs and VEDs (Lee and Kelly 2019) when using higher damping can be effectively reduced by using minimal damping coefficient of dashpot.

7 Conclusion

This paper presented a study on supplemental dampers in the form of pure NSD and NSIDs. The initial part of the study focused on developing optimal parameters of the supplemental dampers. The optimisation is based on lowering the maximum response (resonating amplitude) of the SDOF system. Also, a numerical search scheme has been employed to validate the optimal parameters. The second part of the study evaluates the seismic performance of the MDOF base-isolated structure with proposed dampers as supplemental dampers. The same parameters derived for the SDOF system have been employed to MDOF structure based on the argument that fundamental mode dominates the response. The essential findings of the study are summarised as:

• 1. An undamped SDOF system with NSD and NSIDs provide the non-static invariant points in the transfer function plots of the system. Such non-static invariant points allow derivation of closed-form expressions for the optimal NSD and NSIDs parameters using the classical fixed-point method.

• 2. The optimal value of negative stiffness required for NSIDs is lower in magnitude for the same positive stiffness ratio ($\beta$) than pure NSD. However, this is considered efficient from a design perspective because it requires a lower payload to maintain compression in spring.

• 3. Increasing the inertance to mass ratio results in lowering the resonant amplitude. Increasing the inertance to mass ratio is deemed technically easier than increasing negative stiffness as only apparent mass needs to be added.

• 4. Based on the numerical search technique, a comparison of optimum parameters with the damped and undamped system has shown negligible error in the proposed closed-form expressions. Hence these closed-form expressions are helpful for the effective design of the base-isolated structure with supplemental NSIDs.

• 5. Introducing negative stiffness and inerter mechanisms to dashpot improves its dissipation capacity without the need for a higher damping value. Introducing such a mechanism that enhances dissipation capacity is ideal for base displacement control of isolated structures.

• 6. Dynamic analysis shows that optimally designed BI structures with NSD and NSIDs effectively deal with NF and FF seismic motions. The three response parameters, i.e., base-displacement demand, top storey acceleration, and storey shears, are effectively checked and minimised to the desired working level.

• 7. While designing for NF motion, arbitrarily increasing damping value has a negative impact on acceleration response. Therefore, the effectiveness of base isolation is upheld with NSD and NSIDs as supplemental dampers compared to conventional passive dampers as minimum dashpot coefficient is utilised.