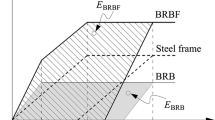
Abstract
In this paper, an optimum design method for buckling restrained brace frames subjected to seismic loading is presented. The multi-objective charged system search is developed to optimize costs and damages caused by the earthquake for steel frames. Minimum structural weight and minimum seismic energy which including seismic input energy divided by maximum hysteretic energy of fuse members are selected as two objective functions to find a Pareto solutions that copes with considered preferences. Also, main design constraints containing allowable amount of the inter-story drift and plastic rotation of beam, column members and plastic displacement of buckling restrained braces are controlled. The results of optimum design for three different frames are obtained and investigated by the developed method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the last two decades, with rapid population growth and dynamic economic developments, the demand for residential, mixed use and commercial buildings has been increasing significantly all around the world. Due to the excessive increase in height of buildings in this era, there is a significant impact on the methods of analysis and design as well as using appropriate resistant systems and materials for buildings. On the other hand, with increasing height, seismic loads increase exponentially proportional to the structure’s height. So, the seismic design of these buildings in the high seismic zones becomes very important. Due to increasing the number of degrees of freedom in buildings, advanced methods of analysis should be employed in order to predict the actual behavior of these structures. These advanced analysis methods should cover all key factors such as geometric nonlinearities (p-delta effects), inelastic material, imperfection geometry, etc. So, a non-linear analysis is required to consider above factors for structural designs. In general, two types of nonlinear analysis approaches for building frameworks are categorized based on the method of modeling the plastification of members as: the distributed or lumped plasticity. The distributed plasticity method, also called the plastic-zone method, discretizes the structural members into many line segments, and further subdivides the cross-section of each segment into a number of finite elements (Chen and Toma 1994; Chen et al. 1996; Ziemian and McGuire 2002). The lumped plasticity method, also widely known as the plastic-hinge method, assumes that plasticity is concentrated at a zero-length plastic hinge section at the ends of the elements. Other regions in the frame elements are assumed to behave elastically (Spacone et al. 1996; Alemdar and White 2005; Hjelmstad and Taciroglu 2005).
Until now, very limited researches have been performed on the second-order finite-element plasticity analysis of steel frame structures under earthquake excitations. Foley and Vinnakota (1997, 1999a, b) developed a nonlinear finite element program for the second-order distributed plasticity analysis of multi-story planar steel frames under static loadings. After that, in order to improve computational performance, Foley (2001) proposed parallel processing and vectorization in which the main structure is separated into several sub-structures for reducing the number of unknown system equations. Teh and Clarke (1999) presents a co-rotational formulation of a spatial beam element for the purpose of 3D plastic-zone analysis of steel frames composed of compact tubular and open sections with no significant torsional warping. Alemdar and White (2005) shows several beam–column finite element formulations for full nonlinear distributed plasticity analysis of planar frame structures. Scott et al. (2008) proposed a framework for simulating the response of frame members with material and geometric nonlinearities by using the equations of beam mechanics. They also proposed a new method for computing the sensitivity of the responses of force-based beam–column elements when the displacement field is not specified (Scott et al. 2004). Chiorean (2009) introduced another efficient computer-based method for analyzing inelastic space steel frames with non-linear flexible joint connections and large deflections. He used the most refined type of second order inelastic analysis, the plastic zone analysis. Then, Thai and Kim (2011a, b) presents a fiber beam–column element which considers both geometric and material nonlinearities for steel frames. At their work, the geometric nonlinearities are captured using stability functions obtained from the exact stability solution of a beam–column subjected to axial force and bending moments. Then, a beam–column element formulation and solution procedure for nonlinear inelastic analysis of planar steel frame structures under dynamic loadings is presented by Nguyen and Kim (2014) and Nguyen et al. (2014), which the spread of plasticity is considered by tracing the uniaxial stress–strain relationship of each fiber on the cross section of sub-elements.
In addition to the utilized analysis method in the design of structures, more attentions should be paid to constructional costs of buildings. So, the use of appropriate tools to optimize the structures is very affordable. In this regard, Degertekin (2008) developed harmony search algorithm for optimum design of steel frames. The objective is to obtain minimum weight of frames by selecting suitable sections from a standard set of steel sections such as American Institute of Steel Construction (AISC) wide-flange (W) shapes. Degertekin and Hayalioglu (2010) developed a harmony search-based algorithm to determine the minimum cost design of steel frames with semi-rigid connections and column bases under displacement, strength and size constraints. Daloglu et al. (2016) investigated the effect of soil-structure interaction on the optimum design of steel space frames using some meta-heuristic algorithms. Truong and Kim (2017) proposed an effective numerical procedure for reliability-based design optimization (RBDO) of nonlinear inelastic steel frames by integrating a harmony search technique (HS) for optimization and a robust method for failure probability analysis. Kaveh and BolandGerami (2017) utilized an enhanced colliding bodies algorithm for optimal design of large-scale space steel frames. Then, Kaveh et al. (2017) indicated optimum seismic design of 3D steel moment frames with different types of lateral resisting systems according to the AISC-LRFD design criteria. These frames are analyzed by Response Spectrum Analysis (RSA), and optimization process is performed using nine different well-established meta-heuristic algorithms.
This paper presents the Charged System Search algorithm (CSS) approach (Kaveh and Talatahari 2010a, b, c; 2012 as the optimization tool for finding nonlinear seismic optimum design of steel frames with buckling restrained braces (BRBs). In the CSS, each possible solution is considered as a Charged Particle (CP), where each CP is treated as a charged sphere that can exert an electrical force to other agents (CPs). The quantity of the resulting electric force exerted to each agent is calculated by the laws of Coulomb and Gauss from electrostatics. The CSS also uses the governing laws of motion from the Newtonian mechanics to determine the position of CPs. Application of these laws provides a good balance between the exploration and the exploitation of the algorithm (Kaveh and Talatahari 2010a). Since the defined problem contains different objectives, a Multi-objective Charged System Search algorithms (MoCSS) is utilized, here. The rest of the paper is as follows: in Section 2, the nonlinear finite element beam-column formulation is presented. The formulation of the optimization problem is presented in Section 3. Sections 4 and 5 describe the single objective (standard) and multi-objective CSS algorithms, respectively. An overview of multi-criteria decision making method is described in section 6. Then, the numerical investigation is presented in Section 7. Finally, Section 8 concludes the paper.
2 Nonlinear finite element beam-column formulation
The nonlinear time history analysis is the best tool currently available for predicting building responses at different intensity levels of the ground motion. Various aspects of nonlinear analysis such as acceptance criteria, element discretization and assumptions on modeling of energy dissipation through viscous damping are required to use specific features of the analytical model of the system with various behavioral effects which captured in the nonlinear component models. So, identification of the nonlinear finite element modeling in this analysis is crucial. Structural nonlinearities can be specified as:
-
1.
Geometrical nonlinearities: The effect of large displacements on the overall geometric configuration of structures.
-
2.
Material nonlinearities: The yielding effects of structural members are simulated in accordance with the stress-strain relations of materials.
-
3.
Boundary nonlinearities, (displacement dependent boundary conditions): The most frequent boundary nonlinearities are encountered in contact problems.
Among these, geometric and material nonlinearities are two major concerns in the nonlinear analysis of steel structures. The nonlinearity properties of structural members can generally be represented by using advanced analytical finite element models. Meanwhile, the structural responses, such as displacements and internal forces, are approximated for each element step by step according to nonlinear time-history analysis procedure. To simulate material nonlinear property of a structural member, either “concentrated plasticity with elastic interior” or “distributed plasticity” models can be used through various approaches. A concentrated plasticity analysis is often an approximate method where it separates axial force-moment interaction from the member behavior, while for reaching a real behavior of the element, the integration of the sectional response contribution along the element length is required. On the other hand, the gradual spread of yielding can be accurately captured by a distributed plasticity analysis method since the stress state is being updated with respect to responses of the integrated member sections. Therefore, this research utilizes a distributed plasticity model for modeling nonlinear beam-column elements.
The distributed plasticity model of a beam-column member can be simulated either by displacement-or force-based formulations. Following the standard displacement-based approach, the transverse and axial displacements of a beam-column member are expressed as appropriate interpolation functions of the nodal displacements. To approximate the nonlinear displacement field in the displacement-based formulation, several elements are required along the length of a frame member to represent the distributed plastic behavior if the axial force becomes large. On the other hand, the force-based beam-column element employs section forces interpolation functions to formulate element flexibility matrix with respect to the element nodal forces. So, in the force-based elements with using just one force-based element to simulate the nonlinear behavior of a frame member is enough to maintain equilibrium along the element (even in the range of nonlinear response) (Neuenhofer and Filippou 1997). In this paper, we utilized force-based distributed plasticity nonlinear beam-Column elements to simulate the nonlinear behavior of the frame members.
According to the co-rotational formulation (Crisfield 1991), each element is modeled in the basic system without rigid body modes and the specific transformation is employed to transform the basic variables to the global system. The basic (rotating) and global coordinate systems of a beam-column element are shown in Fig.1. The material nonlinearity within the basic system is represented by a discrete number of cross sections (which are located at the control points of the numerical integration algorithm along the length of the element). Moreover, these sections (i.e., 5 cross sections as shown in Fig.1) can be further subdivided into fibers such that the nonlinear sectional response can be obtained through the integration of the fiber responses with respect to the given material constitutive relationship rather than a directly defined force-deformation relationship curve. For the two-dimensional elements, Wand V are the element force and deformation vectors respectively; and S and D are the corresponding sectional force and deformation vectors, respectively.
Basic (rotating) and global coordinate system, (Neuenhofer and Filippou 1997)
In the force-based method, the force interpolation functions are employed to approximate the force field within a segment of the element. The relation between the nodal force vector and internal section force vector is described as:
where a(x) contains the force interpolation functions. Those interpolation functions can be readily obtained from the equilibrium of axial forces and bending moments within the element:
The compatibility relationship between the section and element deformations can be determined by employing the principle of virtual force, as:
The linearization of (3) with respect to the basic forces gives the element flexibility matrix:
While the control sections are subdivided, the strain distribution in a section x of the element can be determined based on the assumption that the plane section remains plane and normal to the longitudinal axis. Then the corresponding stresses and tangent modulus with respect to the strain values at each fiber are computed according to the material constitutive relation. Subsequently, the section stiffness, k s (x), and resisting force, S(x), are evaluated through numerical integration schemes. The section stiffness is then inverted to obtain the flexibility matrix, f s (x). Then, the element flexibility matrix, F, is computed from (4). So, the relation between the element deformation, V, and the section deformation, D, can be numerically expressed as:
where ξ and ω are locations and associated weights of the N p integration points over the element length [0, L], respectively. Gauss–Lobatto quadrature is used in force-based elements because it places integration points at the element ends, where the bending moments are largest in the absence of member loads. A graphical representation of the five-point (N P = 5) Gauss–Lobatto quadrature rule applied to (5) is shown in Fig. 2, (Scott and Fenves 2006).
Evaluation of force-based element compatibility relation, (Scott and Fenves 2006)
3 Design problem formulation
The general formmulti-objectives of energy-based BRB frames design contains the cost, seismic input energy and seismic dissipated energy. Also, we considered plastic hinge rotations and plastic displacements of members and inter-story drifts as constraints. The following subsections presents the mathematical relations regarding these matters.
3.1 Objective functions
In this study, two objective functions concerning structural cost and seismic energy (seismic input energy / seismic dissipated energy) under earthquake loads are defined. The first objective function can be formulated as follows:
where, A k is the design cross-sectional area variable for member k; L k is the total length of design group k; n e and n BRB are the number of design variables for frames and bracing, respectively; and ρ e and ρ BRB are the material mass density for beams and columns as well as bracing systems, respectively.
The second objective contains the earthquake energy which is based on the earthquake input energy to minimize and the absorbed seismic energy by fuse members to maximize and it can be defined as follows:
where \( {\widehat{\mathrm{E}}}_{\mathrm{i}} \) is the total input energy to the structure floors;
in which, n m is the number of the degree-of-freedom. Earthquake input energy not only depends on the type of seismicity but also depends on the type of structural design. Thus by choosing the appropriate design of structures, work or earthquake input energy can be optimized and structural stability under seismic loads will be increased. In the above equation, the absorbed seismic energy by fuse members, \( \widehat{\beta} \), is selected to be maximize by energy dissipating in BRBs than other structural members. Therefore, we use it in the denominator of (7). Here, \( \widehat{\upbeta} \) is equal to \( \widehat{\upbeta}={\mathrm{E}}_{\mathrm{h}\mathrm{f}}/{\mathrm{E}}_{\mathrm{h}} \), in which E hf is the total hysteretic energyof fuse members (BRBs) and E h is the total hysteretic energy.
3.2 Design constraints
Constraints on the design are intended as performance and side constraints. In this paper performance limitations are classified into two forms: plastic hinge rotations and plastic displacements of members and inter-story drifts, as:
where, φq and ∆r are the member-end plastic rotations and displacements, respectively; φ0 and ∆0 are the allowable values of members end plastic rotations and displacements, respectively; δ s is the values of the s-th inter-story drift and δ 0 is its allowable values. n B & C and n s are the number of total beam-column elements and total stories of the structure, respectively.
On the other hand, the side constraints which are considered in selected sections are related to factors such as: availability, febricity, physical limitations, etc. The beams and columns section are allowed to be standard AISC sections while the braces are selected from cruciate sections defined by the authors:
where C l and D m are the set of discrete sections available for beams-columns and BRBs, respectively and A l and B m are the element section of beams-columns and BRBs members for variable l and m, respectively.
4 Standard charged system search
The charged system search is based on electrostatic and Newtonian mechanics laws. The Coulomb and Gauss laws provide the magnitude of the electric field at a point inside and outside a charged insulating solid sphere, respectively, as follows (Halliday et al. 2008):
where k e is a constant known as the Coulomb constant; r ij is the separation of the center of sphere and the selected point; q i is the magnitude of the charge; and a is the radius of the charged sphere. Using the principle of superposition, the resulting electric force due to N charged spheres is equal to (Halliday et al. 2008):
Also, according to Newtonian mechanics, we have (Halliday et al. 2008):
where r old and r new are the initial and final position of a particle, respectively; v is the velocity of the particle; and a is the acceleration of the particle. Combining the above equations andusing Newton’s second law, the displacement of any object as a function of time is obtained as:
Inspired by the above electrostatic and Newtonian mechanics laws, the CSS algorithm was presented as (Kaveh and Talatahari 2010a):
First, an array of charged particles (CPs) with random positions and zero velocities are initialized. Then based on the values of the fitness function for the CPs, a number of the best CPs are stored in the charged memory (CM). For generating the new CPs as candidates of solutions, the attracting force vector for each CP is calculated as follows:
where F j is the resultant force affecting the jth CP.
By moving the CPs toward their new positions, the new results are obtained:
where rand j1 and rand j2 are two random numbers uniformly distributed in the range (0, 1). k a is the acceleration coefficient; k v is the velocity coefficient to control the influence of the previous velocity. If each new CP exits from the allowable search space, its position should be corrected using the HS-based handling approach (Kaveh and Talatahari 2009a, b). Finally, if some new CP vectors are better than the worst ones in the CM, in terms of their objective function values, they will be included in the CM and the worst ones will be excluded from the CM. The above mentioned process is repeated until a terminating criterion is satisfied.
5 Multi-objective charged system search
Multi-objective optimization problems consist of several objectives that are necessary to be handled simultaneously. In many problems there are two or more, sometimes competing or incommensurable objective functions have to be minimized concurrently. In contrast to the single-objective optimization case, multi-objective problems are characterized by trade-offs and, thus, there is a multitude of Pareto optimal solutions, which correspond to different settings of the investigated multi-objective problem. So, some changes and some additional steps are considered in the pure charged system search algorithm for change into multi-objective optimization procedure. Similar to all other multi-objective optimization algorithm, the MoCSS can be used for any problem defined as multi-objective one. However in this paper we applied this method for energy based design of BRB frames. Unlike other current proposals to extend evolutionary algorithms to solve multi-objective optimization problems, our algorithm uses a secondary (i.e., external) repository of charged particles that is later used by other particles to determine their own positions and velocities.
This algorithm consists of the following steps:
-
Level 1: Initialization
-
Step 1. Initialization. Initialize the parameters of the CSS algorithm. Initialize an array of charged particles (CPs) with random positions. The initial velocities of the CPs are taken as zero. Each CP has a charge of magnitude (q i ) defined considering the quality of its solution as:
$$ {\mathrm{q}}_{\mathrm{i}}={\prod}_{k=1}^{N_{Obj}}\frac{{\mathrm{fit}}_k\left(\mathrm{i}\right)-{\mathrm{fit}}_k\left(\mathrm{worst}\right)}{{\mathrm{fit}}_k\left(\mathrm{best}\right)-{\mathrm{fit}}_k\left(\mathrm{worst}\right)},\kern0.5em \mathrm{i}=1,2,\dots, \mathrm{N}\kern0.75em $$(22)where N Obj is the number of objective function, fit k (best) and fit k (worst) are the best and the worst fitness value of kth function; fit k (i) represents the fitness value of agent i.
-
Step 2. CP ranking. Sort the CPs according to Pareto optimal solutions.
-
Step 3. CM creation. Store the CPs which is on the first front Pareto curve as shown in Fig.3.
-
-
Level 2: Search
-
Step 1. Force determination. Determine the probability of moving each CP toward the others considering the following probability function:
$$ {\mathrm{P}}_{\mathrm{ij}}=\left\{\begin{array}{l}1\kern1.5em \operatorname{rank}\left(\mathrm{i}\right)>\mathit{\operatorname{rank}}\left(\mathrm{j}\right)\hfill \\ {}0\kern7em \mathrm{else}\hfill \end{array}\right. $$(23)and calculate the attracting force vector for each CP as follows:
$$ {\boldsymbol{F}}_j={q}_j{\sum}_{i,i\ne j}\left(\frac{q_i}{{\boldsymbol{a}}^3}{\boldsymbol{r}}_{ij}.{i}_1+\frac{q_i}{{\boldsymbol{r}}_{ij}^2}.{i}_2\right){p}_{ij}\left({\boldsymbol{X}}_i-{\boldsymbol{X}}_j\right),\left\{\begin{array}{c}\hfill j=1,2,\dots, N\hfill \\ {}\hfill {i}_1=1,{i}_2=0\leftrightarrow {\boldsymbol{r}}_{ij}<a\hfill \\ {}\hfill {i}_1=0,{i}_2=1\leftrightarrow {\boldsymbol{r}}_{ij}\ge a\hfill \end{array}\right. $$(24)where F j is the resultant force affecting the jth CP.
-
Step 2. Solution construction. Move each CP to the new position and find its velocity using the following equations:
$$ {\boldsymbol{X}}_{j, new}={rand}_{j1}.{k}_a.{\boldsymbol{F}}_j+{rand}_{j2}.{k}_v.{\boldsymbol{V}}_{j. old}+{\boldsymbol{X}}_{j, old} $$(25)$$ {\boldsymbol{V}}_{j, new}={\boldsymbol{X}}_{j, new}-{\boldsymbol{X}}_{j, old} $$(26)where rand j1 and rand j2 are two random numbers uniformly distributed in the range (0, 1).
-
Step 3. CP position correction. Similar to the standard CSS, the positions of violated CPs are corrected by using the HS-based handling approach by applying one of the following rules for the violated component of the CP:
-
a)
selecting a new value for the violated CP from CM,or
-
b)
choosing a value from neighboring of the best CP,
-
c)
using a random value.
-
a)
-
Step 4. CP ranking. Evaluate the objective values of the new CPs and determine the rank of them. The comparison of solutions is done in three ways (either in tournament selection, or dominance concept):
-
1.
Two feasible solutions, choose the one with the best objective function(s). It means that X A is said to dominate another X B , if:
$$ \left\{\begin{array}{l}{fit}_k\left({X}_A\right)\le {fit}_k\left({X}_B\right)\to \kern3.25em for\ all\ indices\ k\in \left\{1,2,\dots, {N}_{obj}\right\}\hfill \\ {}\kern0.5em {fit}_l\left({X}_A\right)<{fit}_l\left({X}_B\right)\to for\ atleast\ one\ index\ l\in \left\{1,2,\dots, {N}_{obj}\right\}\hfill \end{array}\right. $$(27) -
2.
An infeasible and a feasible solution, choose the feasible one.
-
3.
Two infeasible solutions, choose the one with the lowest sum of normalized constraint violations.
-
1.
-
Step 5. CM updating. For CM updating, the following steps are performed:
-
5–1) Pool creating: All new generated CPs in the current iteration as well as all stored ones in the CM accumulated to a pool as shown in Fig. 4, then the first Pareto solution of these solutions are selected as new CM.
-
5–2) Remove close CPs: Find the distance between all non-dominated solutions at CM as follows:
$$ {d}_{ij}=\sqrt{\sum_{k=1}^{N_{obj}}{\left({u}_k\left({fit}_k(i)-{fit}_k(j)\right)\right)}^2} $$(28)where uk is a constant and chosen to make all uk(fitk) close to each other, then remove some near non-dominated solutions from the CM.
-
-
Level 3: Controlling the terminating criterion
Repeat the search level steps until a terminating criterion is satisfied.
6 Overview onMulti-criteria decision making method
The multi-criteria decision making (MCDM) is a branch of a general class of operations research models which deal with decision problems under the presence of a number of decision criteria. Whether in our daily lives or in professional settings, there are typically multiple conflicting criteria that need to be evaluated in making decisions. Cost or price is usually one of the main criteria, although some measure of quality is typically another criterion that is in conflict with the cost. So, the MCDM is further divided into multi-objective decision making (MODM) and multi-attribute decision making (MADM) (Climaco 1997). There are several methods in each of above categories that share common characteristics of conflict among criteria, incomparable units and difficulties in selection of alternatives. In multiple objective decisions making a set of objective functions is optimized subject to a set of constraints and alternatives are not predetermined. The most satisfactory and efficient solution is sought and is not possible to improve the performance of any objective without degrading the performance of at least one other objective. In multiple attribute decision making, a small number of alternatives are to be evaluated against a set of attributes which are often hard to quantify. The best alternative is usually selected by making comparisons between alternatives with respect to each attribute.
Many different approaches can be used for the MCDM process (Fishburn 1970). A simple method is the multi-criteria tournament decision making method (MTDM) (Parreiras et al. 2005). According to the preferences of a human decision maker, this method provides the ranking of alternatives from best to worst. So, it has another positive aspect, involving few input parameters, just the importance weight of each criterion. This method introduces a function, R, capable of reflecting the MCDM global interests. First, each possible solution is compared to the others with considering only the kth-criterion in order to find this function. The pairwise comparisons are performed through the tournament function, Tk(a, A), which counts the ratio of times alternative a wins the tournament against each other b solution from A. So, with considering that a is a non-dominated point in the objective space, Tk(a, A) can be stated as:
where:
The tournament functionassigns a score to each solution in the Pareto front. The assigned score as a performance measure provides a distinct ordering of the elements of A for each criterion. In order to generate the global ranking, taking into account all criteria and their respective weights, w i (priority factors), the scores are aggregated into the global ranking function, R. The weighted geometric mean is considered as the aggregation function in this paper, therefore:
where N obj is the number of objective functions. In accordance with the following conditions, the priority weights must be specified by the MCDM, namely:
The ranking index, R(a), gives an idea of how much each alternative is preferred to the others. In other words: if R(a) > R(b), then, a is preferred to b, and when R(a) = R(b), then a is indifferent to b.
7 Numerical examples
7.1 Problem description
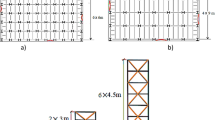
Three building frameworks are considered for numerical investigation of energy based optimum seismic design using the developed MoCSS algorithm. These structures are in California/Nevada at latitude 36.9° N and longitude 120° W. The structural layout is symmetric in each direction and seismic lateral loads are resisted by a pair of 3-bay concentrically braced frames located at the primate of the building. Each bay has 6.35 m wide center-to-center and all stories are 3.81 m high. The structures have 6, 12 and 18 stories, respectively. For reducing the search space and analysis time, we grouping the design variables of frames into 6, 16 and 24 groups for these examples, respectively as illustrated in Fig. 5. For each frame, the seismic weights of floors, and the roof are 790 KN, 604 KN, and the linear distributed loads of floors and roof are equal to 13.83 KN/m and 10.5 KN/m, respectively.
The steel material used for beam and column members is ASTM A992 (Fy = 50 ksi), while ASTM A36 or SN 400B (Fy = 42 ksi) is considered for the BRBs core material. Also, all columns and beams are selected from 297 W shape sections (AISC 2010) and all of BRBs sections are selected from 150 predetermined cruciate sections as presented in Table 1. The detailed properties of the different W-shaped sections are available in the manual of the American Institute of Steel Construction (AISC 2010). The plastic rotation limit φ0 for all beam and columns and the plastic displacement limits ∆0 for braces are given in Table 2. The inter-story drift limit δ0 is taken as 2.0% of story height (i.e., δ0 =3810 × 0.025 = 76.2 mm, Fishburn 1970).
As mentioned earlier, the nonlinear time history analysis is an analysis tool for optimum energy based design of RBRFs. Since the selection of an appropriate record of ground motions has a large impact on the results of the nonlinear time history analysis, the average results of 7 earthquake records or the maximum results of 3 earthquake records should be selected according to FEMA-450 recommendation for non-linear time history analysis. Since the developed optimization method is an iterative process, so we use 3 records of earthquake for mitigating calculation burden. These three earthquake records are selected and scaled according to the maximum considered earthquake (MCE) spectral response acceleration as presented Table 3, (Climaco 1997). It is assumed that the site is Class D or stiff soil. The response spectra of selected ground motions and design spectra (with probability of 2% in 50 years) are shown in Fig. 6.
7.2 Parameter setting
It is known that there is no universal optimization method applicable to an arbitrary problem. Our method follows this point as well. However for the defined structural problem in this paper, the MoCSS method works better than the others. Some reasons are that the MoCSS utilizes all CPs while other methods use just some selected agents. Also, the MoCSS utilizes the controlling rules for moving the CPs; while the MoPSO, as an example, just can detect the direction of the movement and the amount of it is selected randomly. Besides, MoCSS has a memory for saving the so far best solutions and it uses an advanced constraint handling approach (HS-Based method) as described in Step 3 of the algorithm. These all raise the power of the algorithm. This means that the influence of the parameters of the algorithm is less for this method than other ones. As a result in this paper, the parameters of k a and k v are simply set to unit. However, since these parameters control the exploitation and exploration of the algorithm (Kaveh and Talatahari 2010a), one can reach better results by adjusting suitable amounts for them. Considering the complexity of the presented problem in this paper, it seems that these simple values are applicable. The number of agents is taken as 100, the maximum number of iterations is set to 200 and a = 1 and k t = 0.75. In addition to the MoCSS, we utilized a real coded NSGA-II (Deb et al. 2002) with a population size of 100, a crossover probability of 0.9 (p c = 0.9), tournament selection, a mutation rate of 1/Nvar (where Nvar is the number of decision variables), and distribution indexes for crossover and mutation operators are taken as η c = 20 and η m = 20, respectively (as recommended in Deb et al. 2002). Also, the MOPSO (Coello and Lechuga 2002) is used with a population of 100 particles, an archive size of 100 particles, a mutation rate of 0.5, and30 divisions for the adaptive grid (Coello and Lechuga 2002). For all examples presented in this paper, the number of fitness function evaluations (structural analysis) in the multi-objective optimization phase is restricted to 20,000.
7.3 Results
Table 4 presents the extreme values obtained by the MoCSS, MoPSO and NSGA-II for the three examples. It should be noted that the maximum allowable values for the objectives are considered as reported in the tables. According to Table 4 for 6-story example and those points which fit 2 is more important than fit 1, the MoCSS yields 25% and 20% better than the MoPSO and NSGA-II, respectively. These values are 10% and 16.8% for the second example. Also, for the 18-story frame MoCSS can find 14.22 for the second objective while the final result of the MoPSO and NSGA-II are 15.19 and 15.49, respectively.
When the weight (fit 1) is considered as the main objective, for the first example the results of MoCSS are16% and 21.5% better than those of the MoPSO and NSGA-II, respectively. For the 12 story frame, the best weight obtained by the MoCSS, MoPSO and NSGA-II are 138.3, 159.31 and 175.13 tons, respectively. Also for the 18-story frame, MoCSS can find 284.90 tons while the final result of the MoPSo and NSGA-II are 312.46 and 318.63 tons, respectively. Clearly, the best results are obtained by the MoCSS. The Pareto fronts of three methods for the first example are presented in Fig. 7. Also, Figs. 8 and 9 showthe Pareto fronts for the second and third examples, respectively. According to these figures, the results of the MoCSS are obviously better than the two other methods.
To clarify the values of design constraints, we normalized and plotted the values of constraints for the best results (with the smallest weight) obtained by the MoCSS as shown in Fig. 10 for the last frame as an example. Since the conditions of the structures vary in every time step of the earthquake for each node, to obtain a single number for comparison we chose the maximum value of the time history. It is obvious that if maximum value becomes acceptable, rest values will be satisfied. Therefore, the final reported designs are feasible. This figure represents the maximum values of rotation and axial deformations for all beams, columns and BRBs, regardless of their grouping. As shown in Fig. 10, the BRB members as energy absorbent members (fuse members), have a controlling role in the amount of deformations constraints. There is also another constraint such as inter-story drift in the problem that controlled the dimension of non-fuse members (beams, columns).
For the process of decision making, five different scenarios are considered. Table 5 presents the solutions obtained via the MoCSS and two other methods corresponding to each considered scenario for the examples. As it can be seen, the all good results are found by the MoCSS for all three examples. It should be noted that these scenarios become important when some different designs are necessary.
8 Conclusion
This study proposes a multi-objective optimal seismic design method for the buckling restrained braced frames. The proposed optimal seismic design method considers two objective functions (i.e., minimization of structural cost, minimum earthquake energy) to optimize the economic feasibility and seismic performance of a structure, simultaneously. Also, this paper uses discrete structural optimization so called the multi-objective charged system search algorithm which is based on some basic laws of physics and mechanics.
In this paper several designs with improved weight or seismic performance (Controlled energy absorption) were obtained. Because the suggested optimal design method optimizes two objective functions simultaneously, it can suggest different designs to engineers, who can choose the final design based on such alternatives.
The results obtained amply demonstrate that the presented approach is efficient in converging to the true Pareto fronts and in finding a diverse set of solutions along the Pareto front. Considering results, it is obvious that the Pareto front obtained by the MoCSS is more diverse and better than other methods for BRB frames. After computing the Pareto front, the engineers involved in making design decisions, express their preferences about different criteria (objectives or other independent criteria). By aggregating different ideas, the final solution is selected by an algorithm called MTDM.
References
AISC (2010). Specification for structural steel buildings (ANSI/AISC 360-10). Chicago, IL: American Institute of Steel Construction
Alemdar BN, White DW (2005) Displacement, flexibility, and mixed beam-column finite element formulations for distributed plasticity analysis. J Struct Eng 131(12):1811–1819
Chen WF, Toma S (1994) Advanced analysis of steel frames, theory, software, and applications. CRC Press, Boca Raton. isbn:0-8493-8281-5
Chen WF, Goto Y, Liew JYR (1996) Stability Design of Semi-Rigid Frames. Wiley, New York. isbn:0-471-07670-8
Chiorean CG (2009) A computer method for nonlinear inelastic analysis of 3D semi-rigid steel frameworks. Eng Struct 31(12):3016–3033
Climaco J (1997) Multicriteria analysis. Springer-Verlag, New York
Coello CA, Lechuga MS (2002) MOPSO: A proposal for multiple objective particle swarm optimization. Proc Cong Evol Comput 1:1051–1056
Crisfield MA (1991) Non-linear finite element analysis of solids and structures. Wiley, Chichester
Daloglu AT, Artar M, Özgan K, Karakas A (2016) Optimum design of steel space frames including soil-structure interaction. Struct Multidiscip Optim 54(1):117–131
Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multi objective genetic algorithm:NSGA-II. IEEE Trans Evol Comput 6:182–197
Degertekin SO (2008) Optimum design of steel frames using harmony search algorithm. Struct Multidiscip Optim 36(4):393–401
Degertekin SO, Hayalioglu MS (2010) Harmony search algorithm for minimum cost design of steel frames with semi-rigid connections and column bases. Struct Multidiscip Optim 42(5):755–768
Fishburn PC (1970) Utility theory for decision making. Wiley, New York
Foley CM (2001) Advanced analysis of steel frames using parallel processing and vectorization. Comput Aided Civ Infrastruct Eng 16:305–325
Foley CM, Vinnakota S (1997) Inelastic analysis of partially restrained un-braced steel frames. Eng Struct 19:891–902
Foley CM, Vinnakota S (1999a) Inelastic behavior of multistory partially restrained steel frames. Part I J Struct Eng 125:854–861
Foley CM, Vinnakota S (1999b) Inelastic behavior of multistory partially restrained steel frames. Part II J Struct Eng 125:862–869
Halliday D, Resnick R, Walker J (2008) Fundamentals of physics, 8th edn. Wiley
Hjelmstad KD, Taciroglu E (2005) Variational basis of nonlinear flexibility methods for structural analysis of frames. J Eng Mech 131(11):157–1169
Kaveh A, BolandGerami A (2017) Optimal design of large-scale space steel frames using cascade enhanced colliding body optimization. Struct Multidiscip Optim 55(1):237–256
Kaveh A, Talatahari S (2009a) Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures. Comput Struct 87(5–6):267–283
Kaveh A, Talatahari S (2009b) A particle swarm ant colony optimization algorithm for truss structures with discrete variables. J Constr Steel Res 65(8–9):1558–1568
Kaveh A, Talatahari S (2010a) A novel heuristic optimization method: charged system search. Acta Mech 213(3–4):267–289
Kaveh A, Talatahari S (2010b) Optimal design of skeletal structures via the charged system search algorithm. Struct Multidiscip Optim 37(6):893–911
Kaveh A, Talatahari S (2010c) A charged system search with a fly to boundary method for discrete optimum design of truss structures. Asian J Civ Eng 11(3):277–293
Kaveh A, Talatahari S (2012) Charged system search for optimal design of frame structures. Appl Soft Comput 12(1):82–93
Kaveh A, Ghafari MH, Gholipour Y (2017) Optimal seismic design of 3D steel moment frames: different ductility types. Struct Multidiscip Optim:1–16
Neuenhofer A, Filippou FC (1997) Evaluation of nonlinear frame finite-element models. J Struct Eng 123(7):958–966
Nguyen PC, Kim SE (2014) Distributed plasticity approach for time-history analysis of steel frames including nonlinear connections. J Constr Steel Res 100:36–49
Nguyen PC, Doan NTN, Ngo-Huu C, Kim SE (2014) Nonlinear inelastic response history analysis of steel frame structures using plastic-zone method. Thin-Walled Struct 85:20–233
Parreiras RO, Maciel JHRD, Vasconcelos JA (2005) Decision making in multi-objective optimization problems. New York: Nova Science. ISE Book Series on Real Word Multi-Objective System Engineering, pp 1–20
Scott M, Fenves G (2006) Plastic hinge integration methods for force-based beam-column elements. J Struct Eng 132(2):244–252
Scott M, Franchin P, Fenves G, Filippou F (2004) Response sensitivity for nonlinear beam–column elements. J Struct Eng 130(9):1281–1288
Scott M, Fenves G, McKenna F, Filippou F (2008) Software patterns for nonlinear beam-column models. J Struct Eng 134(4):562–571
Spacone E, Ciampi V, Filippou FC (1996) Mixed formulation of nonlinear beam finite element. Comput Struct 58(1):71–83
Teh LH, Clarke MJ (1999) Plastic-zone analysis of 3D steel frames using beam elements. J Struct Eng 125:1328–1337
Thai HT, Kim SE (2011a) Second-order inelastic dynamic analysis of steel frames using fiber hinge method. J Constr Steel Res 67(10):1485–1494
Thai HT, Kim SE (2011b) Nonlinear inelastic analysis of space frames. J Constr Steel Res 67(4):585–592
Truong VH, Kim S-E (2017) An efficient method for reliability-based design optimization of nonlinear inelastic steel space frames. Struct Multidiscip Optim 56(2):331–351
Ziemian RD, McGuire W (2002) Modified tangent modulus approach: a contribution to plastic hinge analysis. J Struct Eng 128(10):1301–1307
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rezazadeh, F., Mirghaderi, R., Hosseini, A. et al. Optimum energy-based design of BRB frames using nonlinear response history analysis. Struct Multidisc Optim 57, 1005–1019 (2018). https://doi.org/10.1007/s00158-017-1791-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-017-1791-4