Keywords

1 Introduction

Optimization is an important and decisive activity in design of structures. Designers will only be able to design better models if they use optimization methods to save time and design expenses. Many optimization problems in engineering are naturally more complex and difficult than they could be solved by conventional optimization methods, such as linear programming methods and the like. One of the solutions to deal with such problems is the use of evolutionary algorithms. In addition, the goal of optimization is to find the best acceptable solution with regard to the limitations of the problem. There may be different solutions for a problem, and in order to compare them and select the optimal solution, a function called the objective function is defined.

Currently, in order to waste earthquake energy, the use of energy dampers in structures has been considered. Conventional braces normally dissipate energy while they are loaded in tension. In compression, the occurrence of buckling phenomenon before yielding results in less energy dissipation, reduced lateral stiffness of the frame, reduced closed area of the hysteresis loops, and instability in one story or the whole structure (Ali Razavi 2011; Uang et al. 2003; Clark et al. 1999).

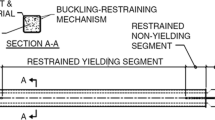
BRBs are a relatively new and improved type of concentric braced frames, whose performance is almost identical both in tension and compression (Fig. 7.1). In these braces, the axial stresses are tolerated by a steel core. The buckling resistance of the brace is provided by an external encasing made of concrete, steel, or any other combination of steel concrete material. While the encasing prohibits the brace from global buckling, the steel core only withstands uniform axial strains both in compression and tension (Lopez and Sabelli 2004). The aim of this research is therefore to achieve an optimal design for the cross section and length of BRBs at the height of the structure while providing the desired constraints. This aim has been accomplished using the genetic algorithm and the multi-objective algorithm.

Fig. 7.1
A schematic diagram and a graph. The diagram of B R B displays a structural frame with sleeve enclosing the core in the middle. Graph plots P versus delta. A rectangular loop starts at origin in the first quadrant, passes through fourth and third quadrants, and remains open in the second quadrant.

Schematic behavior of BRB (Lopez and Sabelli 2004)

Full size image

Genetic algorithm is an optimization method inspired by the living nature (living organisms) that can be considered as an evolutionary algorithm in the classification of optimization methods from among a set of randomly guided search algorithms. This is an iteration-based algorithm, and its basic principles are adopted from genetics. Genetics is the scientific study of how biological traits are inherited and passed from one generation to the next. Chromosomes and genes are the main factors in the transfer of biological traits in living organisms, and the way they work is such that eventually the superior and stronger genes and chromosomes survive and the weaker ones are destroyed. In other words, the result of the interaction of genes and chromosomes is the survival of the fittest. The genetic algorithm likewise finds the best optimization solution accordingly. In addition, in this research, multi-objective algorithms such as NSGA_II, MOPSO, MOEA_D, PESA_II, SPEA2 have been used.

Since the cost-controlling factor in BRB depends on their core’s cross section and their length, the main purpose of this study is to optimize the core’s cross section of these braces and their length in the height of 2D frames. One of the constraints is that in all stories, the story drift satisfies the allowable limit. Three objective functions are defined including bracing weight, total weight of the structure (without bracing weight), and deviation from the uniform drift over the height of the structure. In the optimization process, another constraint was controlled which addresses the low-cycle fatigue to ensure that the braces do not rupture during seismic event.

In order to achieve the optimal distribution, meta-heuristic algorithms were applied in MATLAB and a nonlinear analysis was conducted under seven ground motions using OpenSees software. At a part of research implementation, a bilateral connection was established between OpenSees and MATLAB software.

2 Multi-objective Optimization

In the single-objective optimization, the algorithm ends by optimizing the objective function. However, in multi-objective problems, optimizing several objective functions at the same time is complicated and time-consuming. Furthermore, in most of the problems, a number of acceptable solutions are obtained based on unfavorable criteria. Thus, the final solution is in the form of a set of solutions that is indicative of a balanced representation of the various objective functions of the problem. Finally, one of the solutions is selected as the reference solution by the decision maker. A general multi-objective optimization problem can be defined as Eq. (7.1):

$$\begin{array}{*{20}l} {f\left( x \right) = \left[ {f_{1} \left( x \right),f_{2} \left( x \right), \ldots ,f_{Q} \left( x \right)} \right]} \hfill \\ {{\text{Subject}}:x \in X} \hfill \\ \end{array} ,$$
(7.1)

where \(X \subseteq R^{Q}\) is the problem-solving space and \(x = \left\{ {x_{1} ,x_{2} , \ldots ,x_{p} } \right\}\) is the set of decision variables in the next p-space. Among this set of finite solutions, the appropriate solution will be the answers that have acceptable performance with regard to all goals. Solving multi-objective problems using the beam approach is among more complex problems. This is because there is usually no specific optimal solution for these methods (Deb 2001).

To make appropriate comparisons in multi-objective optimization, the concept of dominance is used, assuming that F is the total space of the problem and \(x_{1} ,x_{2} \in F\) are two answers of this problem. \(x_{1}\) dominates \(x_{2}\) (or \(x_{2}\) is defeated by \(x_{1}\)) if and only, \(x_{1}\) is not worse than \(x_{2}\) in neither of the objectives \(\left( {f_{i} \left( {x_{1} } \right) \le f_{i} \left( {x_{2} } \right)\forall i \in \left\{ {1,2, \ldots ,m} \right\}} \right)\) and \(x_{1}\) is definitely better than \(x_{2}\) in at least one of the objectives \(\left( {f_{i} \left( {x_{1} } \right) < f_{i} \left( {x_{2} } \right)} \right)\). In other words, unresolved solutions are solutions that cover other solutions, but are not themselves covered by other solutions. Now, according to this concept, two operators have been added to single-objective algorithms and are known as multi-objective algorithms. These two operators are fast non-dominated sorting (FNDS) and crowding distance (CD) (Deb 2001).

2.1 Structural Geometry

The structure presented by Hosseini Hashemi et al. (2016) is considered as a benchmark. The aforementioned structure is located in Tehran with soil type II. The structure is seismically designed using the Iranian seismic regulations according to Standard 2800 (BHRC 2014). Figure 7.2 shows the A-axis frame which is used for nonlinear modeling and optimization of the braces. The optimization of the two structures, a 6-story building and a 10-story building, will be performed in two dimensions. The elevations of these structures are shown in Fig. 7.3a and b, respectively. Table 7.1 shows the seismic load-resisting system parameters.

Fig. 7.2
A design of the braced frame plan. It consists of columns A to F and floors 1 to 6. The bays are connected in the form of a grid with the help of beams. It highlights the first column. A compass with North pointing up is beside the plan.

Braced frame plan (Hosseini Hashemi et al. 2016)

Full size image
Fig. 7.3
2 illustrations a and b present the frame elevation of 10 and 6 floors, respectively. The columns are distanced at 5 meters and floors are distanced at 3 meters in both a and b. The columns are diagonally braced alternatively in both structures.

Frame elevation of 6 and 10 floors

Full size image
Table 7.1 Seismic load-resisting system parameters
Full size table

2.2 Nonlinear Structural Modeling

OpenSees, which is an open-source software, was used for modeling and nonlinear analysis of the structure. The braces are modeled using a nonlinear beam–column element and a fiber-based cross section. In this method, the desired cross-sectional area is divided into small elements, and by assigning the desired material to each of the elements, instead of assuming the process of plasticization in certain parts of the structure (such as assuming a plastic hinge in the middle or two ends of the beam), plasticization can be considered as distributed along the entire length of the element, which increases the accuracy of the modeling process (Tauer et al. 1991).

As explained in the previous sections, the columns and beams of the BRBs frame must be strong enough to remain elastic during the earthquake and not to enter the inelastic region. Therefore, assigning the elastic beam–column element to the columns and beams does suffice and the speed of nonlinear analysis is reduced. However, in order to control the behavior of these elements and to know whether they have entered the nonlinear region or not, the nonlinear beam–column element has been used. In both structures, the A-axis frame is considered for nonlinear 2D analysis and optimization.

The stress–strain material model of steel sections is simulated using Steel02 materials in OpenSees software. These materials approximate the cyclic behavior well and consider the strain stiffness kinematically.

The parameters required to determine the behavior of Steel02 materials are as follows: Fy is yield stress, E is initial elastic stiffness, b is strain stiffness ratio, and R is the degree of curvature at the intersection of the two lines of the diagram. The yield stresses of the steel core of the BRBs and the columns and beams are 2620 and 2400 kg/cm2, respectively. Steel02 was calibrated according to the test data obtained from Ali Razavi et al. (2018).

As a means to estimate the of low-cycle fatigue status of BRBs modeled in OpenSees, fatigue material has been used in order to control the damage criterion. This material is defined by Uriz (2005), which considers the effect of low-cycle fatigue on the model. Based on the cumulative damage of Miner (1945) and the Coffin-Manson equation (Stephens et al. 2000), this material determines the damage criterion in the braces that are allocated to Steel02 material. The parameters required to define this material are the yield stress of the cross-sectional steel as well as the two values m and E0, which indicate the slope of the Coffin-Manson curve in the logarithmic space and the amount of strain in the loops leading to rupture, respectively.

2.3 Time History Analysis

Nonlinear dynamic analysis was performed on the frame in 6- and 10-story structures. According to scaling guidelines of Standard No. 2800, the selected ground motions should preferably reflect the actual motion of the ground at the construction site during an earthquake. To reach this goal, at least seven pairs of horizontal ground motions are required. Therefore, seven pairs of accelerograms have been used in this research in order to use the average of their responses in the optimization process.

2.4 Ground Motion Records

In order to perform nonlinear dynamic analyses, seven records including Nahanni, Loma Prieta, Cape Mendecino, Northrukidge, Chichi, Irpinia, and Loma Prieta were used to calculate the responses, so that their average responses could be used. Records were selected from the set of records provided by PEER. Table 7.2 shows the specifications of the selected records, and Fig. 7.4 shows the chart of time history of the acceleration of the selected records.

Table 7.2 Specifications of earthquake records (http://peer.berkeley.edu/nga)
Full size table
Fig. 7.4
A line graph plots response spectra of acceleration versus time. The fluctuating lines for Nahanni, Lomap Bran, Cape mend, North H R, Chichi, Italy, Lomap Saratoga, and average have declining trend and reach between 0 to 0.25 at 3.81 seconds. Lomap Bran has the highest value at 0.41 seconds.

Average of the response spectrum of the acceleration records

Full size image

Figure 7.5 shows the average of acceleration response spectrum of the selected records.

Fig. 7.5
A line graph plots response spectra of acceleration versus period in seconds. The fluctuating lines for type 2 2800, 1.4 type 2 2800, scaled average, and average have declining trend and reach between 0 to 0.5 at 5 seconds. Average has the highest acceleration value.

Scaling the average response spectrum of earthquakes with the soil response spectrum II

Full size image

3 Optimization Process

The purpose of optimization in this study is to minimize the length and cross-sectional area of the BRBs by observing the defined constraints. To calculate and control the constraints, the average of the results obtained from the nonlinear analysis of frames under seven earthquakes by OpenSees software in the optimization algorithm coded in MATLAB has been used. For this purpose, it was necessary to establish a connection between OpenSees and MATLAB software, so that the results of nonlinear analysis in OpenSees could be used as the input of the optimization algorithm and vice versa. In other words, the sections generated by the optimization algorithm could be used in OpenSees. The process is presented in the following section.

3.1 Formulation of the Optimization Problem

Optimization searches for the optimal values of design variables, so that the best output could be given to the objective function and could meet the criteria of the regulations and the designer’s objective (constraints). The optimal value can be the minimum or maximum value of the desired function. In this research, the minimum value of the objective function is the answer to the optimization problem.

In order to use the multi-objective algorithms such as NSGA_II MOPSO, MOEA_D, PESA_II, SPEA2 in the optimization process, the parameters required in this algorithm are shown in Table 7.3.

Table 7.3 Parameters used in the algorithm for optimization
Full size table

3.2 Design Variables

During a seismic event, the BRBs effectively dissipate the input energy both in tension and compression. Changes in the cross-sectional area, length and characteristics of the material used in the bracing core, and its installation location in the structure affect the yield of the bracing core. The total weight of the braces, the total weight of the structure excluding the weight of the braces, and the drift uniformity are selected as the target functions. The thickness of the brace sections is considered constant value of 30 mm and the design variable; i.e., the width of the sections and the length of the brace are considered for optimization (Formulas (7.2) and (7.3)) (Ali et al. 2014).

$$X = \left( {b_{1} ,b_{2} ,b_{3} , \ldots ,b_{n} } \right)$$
(7.2)
$$L = \left( {l_{1} ,l_{2} ,l_{3} , \ldots ,l_{n} } \right)$$
(7.3)

where n is the number of the stories and \(l_{i}\) is the width of the section and \(b_{i}\) is the length of the i brace. It should be noted that a common brace is considered for each floor.

3.3 Design Constraints

In structural design, variables cannot have any value and must be limited by a series of requirements and constraints called design constraints. The most important necessity in BRBFs after the earthquake is to minimize the residual deformations in the structure and the amount of damage to it. In this research, providing such a requirement is accomplished by satisfying the criteria of limiting the lateral displacement of the story to the allowable amount, i.e., Formula (7.4). In order to control the residual displacement of the structure, the amount addressed in Eq. (7.5), is considered as the upper permissible limit.

$${\text{Allowable Drift}} = 0.02$$
(7.4)
$${\text{Residual Displacement}} = 0.005 H,$$
(7.5)

where H is the height of the structure. In the above equations, allowable drift is the relative displacement of the floor, and residual displacement is the amount of residual displacement allowed. The amount of relative lateral displacement of the floors shall be limited to 2% according to ASCE 7–16 (American Society of Civil Engineers 2016).

The maximum brace strain is not the only criterion for the proper performance of BRB up to the end of loading, since according to the cumulative damage criterion, a set of low-cycle fatigue losses in different cycles should be considered in order to guarantee the BRB stable performance. Accordingly, the end of the performance of BRBs during seismic loads is the rupture due to low-cycle fatigue. It is noteworthy that the probability of this rupture is increased by reduction in the length of the braces. According to the explanations provided, a constraint has been considered to control the criterion of damage due to low-cycle fatigue. The criterion of damage for each brace is calculated during a chronological analysis. The criterion of fatigue damage (FDI index) of all braces during each of the seven chronological analyses must be less than one.

In addition, other lateral constraints such as the minimum and maximum amount for the width of the braces core section are equal to 1 cm and 20 cm, respectively. The minimum length of the BRB length is considered 35 cm both the six-story and ten-story frame.

Furthermore, since the number of analyses in optimizations is high and each of them is important, there is a limit to the adequacy of shear, flexural, and axial forces for beams and columns, meaning that in each analysis, individual beams and columns are examined. And their appropriate cross section will be selected from the list of prepared cross sections.

3.4 Objective Functions

The objective function, commonly known as a cost or performance criterion, is defined based on design variables and decision motivation. In optimal design, the best value of the objective function (minimum or maximum) is obtained, so that all constraints will be met. It is, therefore, important to select an appropriate objective function. In this research, a multi-objective optimization problem is solved using the objective function related to cost under seismic loads. The aim is to minimize the cross section and length of BRBs by three objective functions. The first objective function is to minimize the weight of BRBs (7.6), the other is to minimize the weight of the whole structure without BRBs (7.7), and the last is the uniform relative displacement (Drift) in the structure, Eq. (7.8).

$${\text{ Minimize }}F_{1} \left( x \right) = S_{f} \left( { \rho \sum\limits_{i = 1}^{n} {\frac{{f_{p} }}{{f_{d} }}\left\{ {L_{i} \cdot A_{i} } \right\}} + \rho \sum\limits_{i = 1}^{n} {\frac{{f_{d} }}{{f_{p} }}\left\{ {L_{i} \cdot A_{i} } \right\}} } \right),$$
(7.6)

where n is the number of braces, A is the core area of the brace, i and L are the length of the brace, and i and ρ are the specific gravity of the steel used for beams and columns. \(S_{f}\) is a coefficient to control low-cycle fatigue. If any of the braces buckle due to low-cycle fatigue, this coefficient sets the whole function of the BRB weight (\(F_{1} \left( x \right)\)) equal to a maximum value to prevent it from being percent in later generations. Only one of the terms of Eq. (7.6) will be calculated depending on which of the applied force or the axial strength of the brace is greater. This is because somehow less or more effect than the required cross-sectional capacity of the brace can be seen in optimization algorithms. Here \(S_{f}\), \(f_{p}\), and \(f_{d}\) play the role of the penalty function. In order to consider the effect of the constraints in determining the best population (minimum value for the objective function), a penalty function proportional to the distance of the constraints from the permissible space of the problem’s decision is defined, which is then applied to the objective function. As the value of the target function of a population increases, the probability of selecting that population as the best solution decreases.

$${\text{ Minimize }}F_{2} \left( x \right) = \rho \sum\limits_{j = 1}^{n} {\left\{ {L_{j} \cdot A_{j} } \right\},}$$
(7.7)

where n is the number of beams and columns and A is the cross-sectional area of the beam and column i, and L is the length of the beam and column, i and ρ are the specific gravity of the beams and columns.

In Eq. (7.8), the first part of the equation is related to the objective function of uniform relative displacement itself, and the second and third parts are the functions of relative displacement penalty and residual displacement of the permissible values, respectively. This function is such that the less its value is, the better will be the uniformity of drift in the structure.

$$\begin{aligned} {\text{ Minimize }}F_{3} \left( x \right) & = \sum\limits_{j = 1}^{n} {\left| {{\text{Avg}}_{{{\text{Drift}}}} - {\text{story}}_{{{\text{Drift}}}} } \right|} + W_{{{\text{Drift}}}} \left( {\sum\limits_{j = 1}^{n} {\left| {{\text{Drift}}_{{{\text{story}}}} - 0.02} \right|} } \right) \\ & \quad + W_{{{\text{Disp}}}} \left( { \sum\limits_{j = 1}^{n} {\left| {{\text{Disp}}_{{{\text{story}}}} - 0.005H} \right|} } \right) \\ \end{aligned}$$
(7.8)

where \({\text{ Avg}}_{{{\text{Drift}}}}\) is the average relative displacement (Drift) of the whole structure, \({\text{ story}}_{{{\text{Drift}}}}\) and \({\text{ Drift}}_{{{\text{story}}}}\) is the relative displacement (Drift) of each floor, \({\text{Disp}}_{{\text{story }}}\) is the residual displacement in each floor, H is the height of the structure and \(W_{{{\text{Drift}}}}\) and \(W_{{{\text{Disp}}}}\) are the reduction coefficients that will be multiplied by the constraints, so that the values of the constraint terms do not dominate the objective function.

Obtaining the values of the objective function requires going through several steps, which include checking the shear flexural adequacy and axial force of the beams and columns. Moreover, the adequacy of the relative displacement in the height of the structure is examined. The steps are shown in Fig. 7.6. Most of the algorithms used in this research support the Pareto system, meaning that in addition to the response values, the response space is also examined. Consequently, infinite and empty answers are not acceptable and interfere with the optimization process. In case of the occurrence of changes in generations, unacceptable numbers in the form of structural geometry are not entered in the OpenSees program. These constraints are considered in the program to obtain acceptable and logical answers.

Fig. 7.6
A flowchart. If the brace dimensions are acceptable then, perform nonlinear analysis and check are the beams and columns are sufficient else, set maximum values. If sufficient for drift, then use open sees application, analyze, and show results.

Different steps of obtaining objective functions and the effect of some constraints in OpenSees

Full size image

3.5 Evaluation of Optimization Results

The optimization will be done using NSGA_II, MOPSO, MOEA_D, PESA_II, SPEA2 multi-objective optimization algorithms, and the results will be shown by three-dimensional diagrams, each axis of which symbolizes one of the objective functions. The goal is considered simultaneously.

The general process for all optimization algorithms is that by creating an initial population and examining it and using the formulas and methods in each of the algorithms, the best solutions are selected. Then, the features and characteristics in each of the populations are used in the next generations to create the best new populations, and in all these cases, all the target functions are examined. The results shown in the diagrams represent the selected populations in the latest generations or the best solutions in all generations depending on the performance of the algorithm.

Optimization will be done for two 6- and 10-story structures. First, the results of the 6-story structure, then the results of the 10-story structure, and then the performance of both 6- and 10-story structures will be shown in a diagram for each of the algorithms. Finally, the optimization results for all algorithms will be shown simultaneously in a three-dimensional diagram for each of the 6- and 10-story structures.

4 Results of Optimization Algorithms for 6-Story Structures

The optimization results for the 6-story structure under different algorithms are shown below. These algorithms have fine convergence that the values of drift uniformity increase with the increase in the weight of the structure. Furthermore, with the increase in the weight of the BRB, the amount of weight of the structure and the amount of drift uniformity decrease. Moreover, it has been attempted to find a variety of objective functions to achieve the necessary coherence and convergence in the solutions. Similar to a catalog, the obtained solutions are selected from the best solutions obtained in the thousands of analyses performed by the algorithm, and the respondent can choose and use one of the solutions depending on his needs and the values required for the objective functions. Although the range of solutions is different from each other, the algorithm has attempted to select the whole desired range and the best possible solutions and to show the best results in the end, as well as to create the necessary consistency between the solutions.

Figures 7.7, 7.8, 7.9, 7.10, 7.11 and 7.12 show the optimization results for the 6-story structure. It should be noted that the values of the objective functions are adjusted in such a way that lower values will be better solutions. However, given the fact that there are three objective functions and a change in one of the objective functions will cause a change in the others, the algorithm selects a set of solutions at different intervals so that the best solutions could be selected. Meanwhile, the solutions have even better values compared to the results obtained from the algorithm itself, and they are selected and superior solutions.

Fig. 7.7
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. The dots are plotted for M O E A D 6 story, M O P S O 6 story, N S G A 2 6 story, P I S A 2 6 story, and S P E A 2 6 story. As structure weight increases, the B R B weight and drift uniformity decrease.

Comparison of the results of all multi-objective optimization algorithms for 6-story structures

Full size image
Fig. 7.8
A 3-D scatterplot plots drift uniformly versus structure weight versus B R B weight. As the structure weight increases the B R B weight decreases. The drift uniformity is more for low B R B weight and high structure weight.

Results of SPEA2 algorithm optimization for 6-story structures

Full size image
Fig. 7.9
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the structure weight increases the B R B weight decreases. The drift uniformity is high for lower B R B weight and high structure weight values.

Results of MOPSO algorithm optimization for 6-story structures

Full size image
Fig. 7.10
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the structure weight increases the B R B weight decreases. The drift uniformity is high for lower B R B weight and high structure weight values. Most of the dots are scattered along x-y axis.

Results of PESA2 algorithm optimization for 6-story structures

Full size image
Fig. 7.11
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the structure weight increases the B R B weight decreases. The drift uniformity is high for lower B R B weight and high structure weight values. Most of the dots are scattered along high values of x and y-axis.

Results of MOEA-D algorithm optimization for 6-story structures

Full size image
Fig. 7.12
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the structure weight increases the B R B weight decreases. The drift uniformity is high for lower B R B weight and high structure weight values.

Results of NSGA II algorithm optimization for 6-story structures

Full size image

Considering the results of the diagrams, it can be inferred that with an increase in the weight of the structure, the values of the weight function of the BRB decrease. The population is at the lowest level for the weight of the brace.

These results indicate the accuracy of the solutions obtained from different algorithms relative to each other; and the obtained solutions are in a significant range for the weight function of the BRB, which decreases with the increase in the values of the structure weight function and the relative displacement uniformity according to the diagram.

5 Results of Optimization Algorithms for 10-Story Structures

The solutions are scattered and the algorithm has attempted to achieve the necessary convergence by finding different solutions in different intervals. By decreasing the values of the weight function of the BRB, the values of the weight function of the structure increase. By decreasing the weight of the BRB, the values of the relative displacement uniformity function also increase. Figures 7.13, 7.14, 7.15, 7.16, 7.17 and 7.18 show the optimization results for the 10-story structure.

Fig. 7.13
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the B R B weight decreases the structure weight and drift uniformity increase. Most of the dots are scattered along the x-y plane.

Comparison of the results of all multi-objective optimization algorithms for 10-story structures

Full size image
Fig. 7.14
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the B R B weight decreases the structure weight and drift uniformity increase.

Results of NSGA II algorithm optimization for 10-story structures

Full size image
Fig. 7.15
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the B R B weight decreases the structure weight and drift uniformity increase.

Results of SPEA2 algorithm optimization for 10-story structures

Full size image
Fig. 7.16
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the B R B weight decreases the structure weight and drift uniformity increase.

Results of MOEA-D algorithm optimization for 10-story structures

Full size image
Fig. 7.17
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the B R B weight decreases the structure weight and drift uniformity increase. Most of the dots are scattered along the x-y plane.

Results of PESA2 algorithm optimization for 10-story structures

Full size image
Fig. 7.18
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. As the B R B weight decreases the structure weight and drift uniformity increase.

Results of MOPSO algorithm optimization for 10-story structures

Full size image

Figure 7.13 shows the optimization results for a 10-story structure under all the algorithms used in this research. The results obtained from this diagram also reveal that the results of different algorithms are consistent with each other, indicating that the obtained solutions are in the acceptable range. Regarding the analysis of the diagram itself, it can be stated that with the decrease in the weight of the brace, the values of the structure weight, and the relative displacement of the floors increase, which is common for all the used algorithms. In addition to confirming the solutions obtained by other algorithms, it also shows the trend of the movement of the value of the objective function. Furthermore, the range of changing the solutions for the objective functions was relatively the same in different algorithms, which indicates the agreement of the solutions in different algorithms.

6 Comparison of the Results of Optimization Algorithms for 6- and 10-Story Structures

Figures 7.19, 7.20, 7.21, 7.22 and 7.23 show the comparison between the optimization of 6-story and 10-story structures. The value of the response intervals for the objective function of the weight of the brace in the 10-story structure is higher than in the 6-story structure, which is due to its higher number of floors. Moreover, the structure weight in a 10-story structure is more than that of a 6-story structure. However, the values of the uniform relative displacement function in a 10-story structure change between numbers two and zero and in a 6-story structure between zero and eight. This indicates that the algorithm in the 10-story structure could better solution the objective of drift uniformity. Also, in the 6-story structure this value is several times greater than that of the 10-story structure, both of which are less than the amount of static analysis results that will be compared in the following sections.

Fig. 7.19
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. The dots for M O E A D 6 story and `10 story are plotted for lower B R B weight values. The drift uniformity for 6 story is between 0 and 8, for 10 story between 0 and 2.

Optimization results of MOEA-D algorithm for 6- and 10-story structures

Full size image
Fig. 7.20
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. The dots for S P E A 2 6 story and `10 story are plotted. The drift uniformity for 6 story is between 0 and 10, and for 10 story between 0 and 5. The structure weight of 6 story is less than 10 story.

Optimization results of SPEA2 algorithm for 6- and 10-story structures

Full size image
Fig. 7.21
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. The dots for P I S A 2 6 story and `10 story are plotted. The drift uniformity for 6 story is between 0 and 10, and for 10 story between 0 and 5. The structure weight of 6 story is less than 10 story.

Optimization results of PISA II algorithm for 6- and 10-story structures

Full size image
Fig. 7.22
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. The dots for N S G A 2 6 story and `10 story are plotted. The drift uniformity for 6 story is between 0 and 8, and for 10 story between 0 and 5. The structure weight of 6 story is less than 10 story.

Optimization results of NSGA II algorithm for 6- and 10-story structures

Full size image
Fig. 7.23
A 3-D scatterplot plots drift uniformity versus structure weight versus B R B weight. The dots for M O P S O 6 story and `10 story are plotted. The drift uniformity for 6 story is between 0 and 8, and for 10 story between 0 and 2. The structure weight of 6 story is less than 10 story.

Optimization results of MOPSO algorithm for 6- and 10-story structures

Full size image

The value of the BRB weight function is in relatively similar ranges, and it is because of the performance of this brace that the selected range in which the brace could move has been analyzed by every range. Therefore, the range of solutions obtained for it is greater than other algorithms. However, the results of the uniform relative displacement function are much better for a 10-story structure than for a 6-story structure, which is similar to other algorithms and performs better in a 10-story structure.

7 Comparison of the Results of All Multi-objective Optimization of 6- and 10-Story Structures with the Results of Static Linear Analysis

Due to the nature of the solutions in the multi-objective optimization algorithm, a set of solutions is obtained, each of which shows better performance in one of the objective functions or in several objective functions. Thus, it will not be possible to compare it with one of the results. Therefore, the performance of all algorithms as well as the range of solutions obtained shall be compared. The value of the three objective functions for the 6-story and 10-story structures under static linear analysis is shown in Tables 7.4 and 7.5.

Table 7.4 Values of objective functions for 6-story structures under static analysis
Full size table
Table 7.5 Values of objective functions for 10-story structures under static analysis
Full size table

Figures 7.7 and 7.13 show the optimization results of 6- and 10-story structures resulted from optimization algorithms. According to the solution range in 6-story structure for the BRB weight function, the majority of optimization results are less than 50% that of the linear elastic analysis. Moreover, all the solutions obtained from the optimization algorithms are less than the static linear analysis in terms of structure weight. The majority of the results are less than the values corresponding to that of static linear analysis in terms of drift uniformity function.

Considering the range of solutions in the 10-story structure for the BRB weight function, it is shown that the majority of the solutions are in the range of 2000–7000, which is less than those of the 6-story structure for the BRB weight function, as well as all the solutions obtained in the section. The weight of the structure is less than the weight of the structure in linear static analysis. Also, the points obtained for the uniform drift function are all less than the amount of the linear static, indicating better optimization performance for the 10-story structure in the drift uniformity function.

The comparison of the objective functions with the results obtained in the linear static analysis shows that the optimization has been able to show quite significant percentages of reduction of values for each of the objective functions, which shows the importance and efficiency of optimization in the designs. Also, due to the presence of control coefficients in the values of the objective functions, a specific unit cannot be considered for the objective functions, including the results of the linear static analysis.

8 Conclusion

In the present research, meta-heuristic algorithms such as NSGA_II, MOPSO, MOEA_D, PESA_II SPEA2 were used in MATLAB software to search for the best solution in a set of possible solutions for BRB cross sections and lengths. Moreover, in order to consider the actual behavior of the structures and to use the maximum capacity of the braces, the structures were analyzed under seven earthquake records in OpenSees software using nonlinear dynamic procedure.

By applying constraints to the optimization problem, a set of possible solutions was generated, and during several optimization steps, an attempt was made to select the solution that results in the least value for the three objective functions of BRB weight, total weight of the structure without a brace and drift uniformity. The constraints considered in this study were the allowable amount of lateral displacement (Drift) in all stories, control of residual displacement, control of flexural and shear forces of beams and columns, and control of failure of the BRB cores due to low-cycle fatigue. Based on the extent each of the constraints were exceeded, a penalty function was defined for each individual in the population, which correspondingly reduced or increased the likelihood of that member being selected.

The frames were modeled in OpenSees software. After creating the length and cross-sectional area using optimization algorithm, the braces entered the OpenSees environment. After examining the structure for satisfying code criteria, the results of nonlinear time history analysis were used to get the output to obtain the values of the objective functions.

Since the use of optimization algorithm and nonlinear analysis are all effective in reducing the cross section and length of BRB, their effect was investigated separately by the three objective functions, i.e., BRB weight, total weight of bracing structure and relative displacement uniformity in structure height. Using the optimization algorithm, the solutions were directed so that the minimum solutions were selected for the objective functions, while the interaction of these three objective functions is reflected in the generated diagrams.

According to the results of the performed algorithms, it can be concluded that reducing the value of the weight function of the BRB increases the total weight of the structure and increases the value of the drift uniformity function.

Moreover, by comparing the optimization results with the results of linear static analysis, it was found that the values obtained in optimization process reduce the values of bracing weight, structure weight and drift uniformity with quite significant percentages. This further shows the importance of optimization in designs.

These diagrams generated in this research act as a catalog showing the effect of each of the objective functions on each other. One can select this structure from the diagram and take the length of the brace and area of the core to gain an optimum design.