1 Introduction

Presence of initial cracks due to material imperfections in engineering structures is inevitable and they may become extremely dangerous and result in catastrophic structural failures. In parallel to many studies on various causes of crack nucleation, increasing structural strength in the presence of cracks has also gained considerable interest in recent years. Up to now, there are broadly two types of strategies to address this issue: the first one is the patch repair (Davis and Bond 1999) or hole drilling techniques (Thomas et al. 2000), which can be adopted during the structural service; another type of strategy is structural optimization at the design stage. In the latter category, effective size and shape optimization techniques to improve the fracture strength of brittle materials (Eschenauer and Kobelev 1992; Lund 1998; Papila and Haftka 2003; Peng and Jones 2008) or fatigue life (Serra 2000; Banichuk et al. 2006; Edke and Chang 2011) have been developed. In most of these studies, fracture strength is measured by the stress intensity factor, and the fatigue life can be also related to the stress intensity factor under certain assumptions. Prior to the size or shape optimization, a crack needs to be prescribed and then the fracture mechanics behavior of the cracked body can be optimized with various methods, e.g., gradient-based mathematical programing methods (Lund 1998) and Genetic Algorithm (GA) (Peng and Jones 2008). Compared with the patch repair or hole drilling techniques, these approaches offer a rational design tool that allows the structure itself to suppress cracking or to sustain a required fatigue life in presence of cracks. However, it is still highly desired to develop a systematic method to seek the least crack insensitive structural layout in the conceptual design stage. On the other hand, in some particular applications, such as the transfer printing process in MEMS fabrication (Carlson et al. 2012) as shown in Fig. 1 and the demold process of resin transfer molding in composite manufacture (Potter 2012), it is desirable to make detachment of the structure along a given material interface easier. This just raises the problem of designing a force transmission path allowing easy crack opening, or in other words, being sensitive to cracks at specified location of the interface. To the authors’ knowledge, there has been little work addressing this topic.

Fig. 1
figure 1

Illustration of transfer printing process in MEMS fabrication

Full size image

Continuum topology optimization provides a more efficient tool than the size or shape optimization in that it can simultaneously change the boundary shape as well as the layout of a structure. This technique has seen a rapid development over the last two decades since the seminal study on the homogenization method (Bendsøe and Kikuchi 1988). Nowadays, three topology optimization methods have become popular, which are the SIMP approach (Bendsøe 1989; Rozvany et al. 1992; Bendsøe and Sigmund 1999), the evolutionary structural optimization (ESO) method (Xie and Steven 1993) and the level set method (Wang et al. 2003; Allaire et al. 2004). The first two methods are based on the material distribution concept and the third one on implicit boundary description. Due to ease of numerical implementation, the SIMP method has been widely applied in various fields. Recently, a new review paper on developments and applications of topology optimization over the last decade has also been published (Deaton and Grandhi 2014).

Strength-related continuum topology optimization has been extensively studied. Duysinx and Bendsøe (1998) proposed a stress criterion for the SIMP model at the intermediate densities. A pq-relaxation approach is proposed by Bruggi (2008) for avoiding singularity of local stress constraint (Cheng 1995). To handle the large number of stress constraints, aggregate functions have been used by Le et al. (2010) as global/regional stress measures. Luo et al. (2013) proposed an enhanced aggregation method which can alleviate the numerical difficulties encountered in the conventional K-S function and more efficiently tackle large-scale stress-constrained problems. Luo and Kang (2012) and Bruggi and Duysinx (2012) first discussed incorporating Drucker-Prager failure criteria in topology optimization. The level set method has also been employed by Allaire and Jouve (2008) and Guo et al. (2011) in stress-constrained topology optimization. There have also been some studies on topology optimization considering damage behaviors. For instance, Bendsøe and Díaz (1998) studied optimal reinforcement of an damaged structure by including a constraint on the amount of damage. Desmorat and Desmorat (2008) maximized the lifetime of a structure with topology optimization by considering damage-governed low cycle fatigue. Optimal placement of reinforcement bars considering damage in concrete structures was treated by Amir and Sigmund (2013) and Amir (2013). Recently, James and Waisman (2013) proposed a constraint on the maximum local damage intensity in topology optimization problems to achieve failure mitigation. A fail-safe design model aiming at generating structural topologies that can still be operated in a damaged state considering local failure is studied by Jansen et al. (2014).

Despite of many studies on abovementioned stress-related formulations, topology optimization considering fracture behaviors has been seldom addressed. One study on this topic was done by Challis et al. (2008), who applied the virtual crack extension technique to maximize the fracture resistance characterized by the elastic energy released during crack propagating.

Similarly as in the stress-constrained and damage-related problems, one needs to define a proper constraint in the local area of interest in topology optimization for fracture mechanics behaviors. With this consideration, we propose a topology optimization framework to incorporate fracture mechanics criteria at certain locations to generate designs that are crack insensitive in specified region of interest. As known, once a macro-crack forms, the near-tip stress field is assumed to be singular in the linear elastic fracture mechanic theory. Therefore the J integral (Rice 1968) as an energy measurement is used to characterize the fracture strength in this study. More specifically, we first set one or more cracks to introduce stress singularity in the region of interest specified by the designer, in which the most critical crack locations can be identified with engineering experience, or determined by a finite element analysis of the current product design, and then optimize the load path connecting to this region.

In analysis of the cracked body, we consider linear elasticity and brittle fracture behavior in the framework of linear elastic fracture mechanics (LEFM). LEFM is applicable when the size of the fracture process zone is much smaller than the crack length. To model singularity of the stress field around the crack tip more accurately, we use the singularity element technique in the finite element analysis. These singularity elements are transformed from the eight-node plane element by changing the mid-side node’s positions (Henshell and Shaw 1975) and thus the shape functions of these singularity elements are able to reflect the r − 1/2 singularity of the stress field near the crack tip. The topology optimization problem is parameterized with the SIMP model, in which the design variables are element-wise constant densities. The J integral is widely used in fracture mechanics as an indicator to assess whether fracture may occur or not. In the considered optimization problem, it is included into the objective function to be minimized (or maximized as shown in the last numerical example) to make cracking difficult (or easy) to happen under certain load conditions. To guarantee stiffness of the structure, mean compliance is also employed here as another objective and the two objectives are weighted as a scalar one by two constant coefficients. The sensitivity of the J integral is derived in a discrete form based on adjoint method. The design optimization problem is solved by a gradient based algorithm, namely the MMA (the Method of Moving Asymptotes) method (Svanberg 1987).

The rest of this paper is organized as follows. Basic concepts of LEFM and J integral, as well as singularity elements, are introduced in Section 2. Section 3 is devoted to the topology optimization formulation and the sensitivity analysis. In Section 4, several numerical examples are presented to show the validity of the present method. Finally, conclusions are drawn in Section 5. In Appendix A, the derivation of discrete form of the J integral is given, which is the base of finite element implementation and sensitivity analysis.

2 Fracture mechanics analysis

As a prerequisite, fundamental concepts of LEFM are briefly introduced in this section.

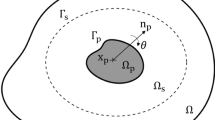
LEFM is a well-established branch of fracture mechanics. It is applicable to brittle fracture of materials exhibiting linear elastic global behaviors. Even when the material exhibits small-scale plasticity at the crack tip, LEFM is still effective with some corrections (Anderson and Anderson 2005). It is also the basis of other branches in fracture mechanics. In the present work, we restrict our models in the context of LEFM under small deformation assumption. The considered design domain with prescribed initial cracks is schematically illustrated in Fig. 2.

Fig. 2
figure 2

Design domain with an initial crack at specified location

Full size image

2.1 J integral

In fracture mechanics, the J integral (Rice 1968) is used as a crack growth criterion: if the value of J integral at a given loading condition is larger than the critical value J C, which is a material dependent parameter, the crack will grow. It is equivalent to the energy release rate G and proportional to the stress intensity factor K in LEFM.

The J integral is a contour integral around the crack tip (see Fig. 3) and has the expression

Fig. 3
figure 3

Schematic illustration of the contour integral around the crack tip

Full size image
$$ J={\displaystyle {\int}_{\varGamma}\left(w\mathrm{d}y-{T}_i\frac{\partial {u}_i}{\partial x}\mathrm{d}s\right)}, $$
(1)

where \( w={\displaystyle {\int}_0^{\varepsilon_{ij}}{\sigma}_{ij}\mathrm{d}{\varepsilon}_{ij}} \) is the strain energy density, T i  = σ ij n j is the traction on the contour with n j being the outward unit normal vector of Γ, and u i is the displacement.

The J integral is a path independent integral. As a more general measurement of energy release rate, it can be used as an important criterion to predict fracture in LEFM, as well as in nonlinear fracture mechanics.

2.2 Finite element modeling and singularity element

In this study, eight-node planar isoparametric elements are used to discretize the structure. Singularity elements are adopted at the crack tip for modeling the r − 1/2 stress singularity in the context of LEFM. As schematically illustrated in Fig. 4, the singularity element is transformed from a standard eight-node isoparametric element by changing a mid-side node from its usual position at the center of each side to the 1/4 position (nodes \( \mathtt{A}-\mathtt{E} \)), and thus the singularity of order r − 1/2 of the stress field is automatically recovered at the crack tip (node \( \mathtt{O} \)) (Henshell and Shaw 1975).

Fig. 4
figure 4

Singularity elements at the crack tip

Full size image

In a discrete form, the J integral is expressed in matrix form as

$$ J={\mathbf{d}}^{\mathrm{T}}\left({\mathbf{K}}_{\mathrm{I}}-{\mathbf{K}}_{\mathrm{I}\mathrm{I}}\right)\mathbf{d} $$
(2)

where d is the nodal displacement vector, K I is a symmetric matrix and K II is an asymmetric matrix, and the details of the derivation are given in Appendix A.

3 Topology optimization considering presence of initial cracks

Generally, nucleation and development of cracks are closely related to high values of the maximum principal stress during structural service. Therefore, if cracks always appear at the same locations for a given batch of engineering products, it usually indicates an improperly designed force transmission path. With this consideration, we first assume that an initial crack exists at the most critical stress concentration region, and then employ the topology optimization technique to seek a well-defined force transmission path that is able to suppress further crack development at this particular location.

3.1 Objective function

In the present topology optimization model, the J integral is introduced into the objective function to control growing of the predefined cracks. From a physical point of view, minimizing the J integral typically leads to reductions of the stress level near the crack tip.

Besides the J integral, the mean compliance C = d T Kd/2 is also considered as another design criterion in the optimization model to ensure overall stiffness of the structure. Therefore the design objective can be generally written as

$$ \min .\kern0.5em \left\{J,\kern0.5em C\right\} $$
(3)

In this bi-criteria optimization problem, the two design criteria usually conflict with each other. Therefore, a trade-off must be made between them. In order to obtain a Pareto optimum, it is common to transform the bi-criteria optimization problem into one with a scalarized objective function. In this study, a scalar objective function is defined as the weighted sum of the above two objectives as

$$ \varPhi =\alpha J+\left(1-\alpha \right)C. $$
(4)

Here, 0 ≤ α ≤ 1 is the weighting factor. One can change the weighting factor to explore the competitive relationship between J and C, and to obtain a set of Pareto optimal solutions.

It should be pointed out here the J integral is evaluated in a non-design area around the assumed crack tip. This means that it can better capture the energy release rate associated with crack opening during the optimization process when the topology changes. Though the predicted J integral value is still affected by displacement inaccuracy caused by gray elements in other parts of the design domain, it provides an acceptable energy criterion of linear fracture mechanics.

Equation 4 can be further expressed in a discrete matrix form as

$$ \varPhi \left(\boldsymbol{\uprho}, \mathbf{d}\right)=\alpha {\mathbf{d}}^{\mathrm{T}}\left({\mathbf{K}}_{\mathrm{I}}-{\mathbf{K}}_{\mathrm{I}\mathrm{I}}\right)\mathbf{d}+\frac{1}{2}\left(1-\alpha \right){\mathbf{d}}^{\mathrm{T}}\mathbf{K}\mathbf{d}, $$
(5)

Derivation of design sensitivity of the objective function in a discrete form will be shown later.

3.2 Formulation of the optimization problem

The task of topology optimization is to find the optimal structural layout in a given design domain. In the material distribution concept-based framework, this can be cast into a discrete 0–1 optimization problem, in which the structural topology is described by a function

$$ \chi \left(\mathbf{x}\right)=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill \forall \mathbf{x}\in {\varOmega}_{\mathrm{s}},\kern1.5em \hfill \\ {}\hfill 0\hfill & \hfill \forall \mathbf{x}\in \varOmega \backslash {\varOmega}_{\mathrm{s}},\hfill \end{array}\right. $$
(6)

where Ω denotes the design domain and Ω s is the region occupied by solid material.

Thus the considered topology optimization problem is stated as

$$ \begin{array}{l}\mathrm{Find}\kern1em \chi \left(\mathbf{x}\right)\in {L}^{\infty}\left(\varOmega \right),\kern0.5em \mathbf{u}\left(\mathbf{x}\right)\in {H}^1\left(\varOmega \right)\\ {} \min .\kern0.5em \varPhi \left(\chi, \mathbf{u}\right)=\alpha J+\left(1-\alpha \right)C\\ {}\mathrm{s}.\mathrm{t}.\kern1em a\left(\mathbf{u},\mathbf{v}\right)=l\left(\mathbf{v}\right),\kern0.75em \forall\ \mathbf{v}\in {U}_{\mathrm{a}},\\ {}\kern2.25em {\displaystyle {\int}_{\varOmega}\chi \left(\mathbf{x}\right)\mathrm{d}\varOmega}\le {f}_{\mathrm{v}}{V}_0\kern0.5em ,\\ {}\kern2.25em \chi \left(\mathbf{x}\right)=\left\{0,\kern0.5em 1\right\}\kern0.5em \end{array} $$
(7)

where a(u, v) and l(v) are the energy bilinear form and the load linear form, respectively; u and v are the continuous displacement field and the virtual displacement field, respectively, U a is the space of kinematically admissible displacement fields, V 0 is the volume of the design domain and f v is the specified material volume fraction.

The SIMP model is used to convert the originally discrete optimization problem (7) to a continuous one. Here, the design variables are the relative densities, which are element-wise constant in discrete form. The Young’s modulus of each element is penalized to the pth power (p equals 3 here) of its density to suppress intermediate density values. Without loss of generality, we assume the first N d elements are designable elements. Thus the formulation of the considered optimization problem is now expressed as

$$ \begin{array}{l}\mathrm{Find}\kern0.75em \boldsymbol{\uprho} ={\left\{{\rho}_1,\kern0.5em {\rho}_2,\kern0.5em \dots, \kern0.5em {\rho}_{N_{\mathrm{d}}}\right\}}^{\mathrm{T}}\\ {} \min .\kern0.5em \varPhi \left(\boldsymbol{\uprho}, \mathbf{d}\right)=\alpha J+\left(1-\alpha \right)C\\ {}\mathrm{s}.\mathrm{t}.\kern1.25em \mathbf{K}\mathbf{d}=\mathbf{p},\\ {}\kern2.5em {\displaystyle \sum_{i=1}^N{\rho}_i{V}_i}\le {f}_{\mathrm{v}}{V}_0,\ \\ {}\kern2.5em 0<{\rho}_{\min}\le {\rho}_i\le 1,\kern0.75em i=1, \dots,\ {N}_{\mathrm{d}}.\kern1em \end{array} $$
(8)

where ρ i and V i denote the density and volume of element i, respectively; ρ min < < 1 is the lower bound limit for the density design variables.

3.3 Sensitivity analysis

In this subsection we derive the sensitivity of the objective function with respect to the design variables in the framework of the adjoint variable method. By introducing the Lagrangian multiplier λ (the adjoint vector), we express the Lagrangian function of the objective function Φ(ρ, d) as

$$ L=\varPhi \left(\boldsymbol{\uprho}, \mathbf{d}\right)+{\boldsymbol{\uplambda}}^{\mathrm{T}}\left(\mathbf{K}\mathbf{d}-\mathbf{p}\right). $$
(9)

The derivative of L with respect to ρ i is

$$ \frac{\mathrm{d}L}{\mathrm{d}{\rho}_i}=\frac{\partial \varPhi \left(\boldsymbol{\uprho}, \mathbf{d}\right)}{\partial {\rho}_i}+\frac{\partial \varPhi \left(\boldsymbol{\uprho}, \mathbf{d}\right)}{\partial \mathbf{d}}\frac{\partial \mathbf{d}}{\partial {\rho}_i}+{\boldsymbol{\uplambda}}^{\mathrm{T}}\left(\frac{\partial \mathbf{K}}{\partial {\rho}_i}\mathbf{d}+\mathbf{K}\frac{\partial \mathbf{d}}{\partial {\rho}_i}\right). $$
(10)

By substituting Equations 5 into 10, Equation 10 can be further written as

$$ \begin{array}{l}\frac{\mathrm{d}L}{\mathrm{d}{\rho}_i}=\alpha {\mathbf{d}}^{\mathrm{T}}\frac{\partial \left({\mathbf{K}}_{\mathrm{I}}-{\mathbf{K}}_{\mathrm{I}\mathrm{I}}\right)}{\partial {\rho}_i}\mathbf{d}+\frac{1}{2}\left(1-\alpha \right){\mathbf{d}}^{\mathrm{T}}\frac{\partial \mathbf{K}}{\partial {\rho}_i}\mathbf{d}+{\boldsymbol{\uplambda}}^{\mathrm{T}}\frac{\partial \mathbf{K}}{\partial {\rho}_i}\mathbf{d}\\ {}\kern2.5em +\left(\alpha {\mathbf{d}}^{\mathrm{T}}\left(2{\mathbf{K}}_{\mathrm{I}}-{\mathbf{K}}_{\mathrm{I}\mathrm{I}}-{{\mathbf{K}}_{\mathrm{I}\mathrm{I}}}^{\mathrm{T}}\right)+\left(1-\alpha \right){\mathbf{d}}^{\mathrm{T}}\mathbf{K}+{\boldsymbol{\uplambda}}^{\mathrm{T}}\mathbf{K}\right)\frac{\partial \mathbf{d}}{\partial {\rho}_i}.\end{array} $$
(11)

We let the adjoint vector λ satisfy the following adjoint equation

$$ \mathbf{K}\boldsymbol{\uplambda } =-\alpha \left(2{\mathbf{K}}_{\mathrm{I}}-{\mathbf{K}}_{\mathrm{I}\mathrm{I}}-{{\mathbf{K}}_{\mathrm{I}\mathrm{I}}}^{\mathrm{T}}\right)\mathbf{d}-\left(1-\alpha \right)\mathbf{K}\mathbf{d}. $$
(12)

After solving Equation 12, the sensitivity of the objective function can be obtained by substituting λ into the third term of Equation 11 as

$$ \frac{\partial \varPhi }{\partial {\rho}_i}=\frac{\mathrm{d}L}{\mathrm{d}{\rho}_i}=\alpha {\mathbf{d}}^{\mathrm{T}}\frac{\partial \left({\mathbf{K}}_{\mathrm{I}}-{\mathbf{K}}_{\mathrm{I}\mathrm{I}}\right)}{\partial {\rho}_i}\mathbf{d}+\frac{1}{2}\left(1-\alpha \right){\mathbf{d}}^{\mathrm{T}}\frac{\partial \mathbf{K}}{\partial {\rho}_i}\mathbf{d}+{\boldsymbol{\uplambda}}^{\mathrm{T}}\frac{\partial \mathbf{K}}{\partial {\rho}_i}\mathbf{d}, $$
(13)

in which the derivative of the matrices K, K I and K II with respect to ρ i can be easily calculated at elemental levels. For instance, the derivative of the stiffness matrix in the third term can be explicitly expressed as

$$ \frac{\partial \mathbf{K}}{\partial {\rho}_i}=p{\rho_i}^{p-1}{{\mathbf{G}}_i}^{\mathrm{T}}\left({\displaystyle {\int}_{\varOmega_i}{{\mathbf{B}}_i}^{\mathrm{T}}{\mathbf{D}}_i{\mathbf{B}}_i\mathrm{d}\varOmega}\right){\mathbf{G}}_i, $$
(14)

where B i is the displacement–strain matrix; D i is the material elasticity matrix; G i is the mapping matrix between the local DOFs of element i and global DOFs. Since the J integral is evaluated within the non-design domain, the first term on the right-hand side of Equation 13 vanishes.

In our study, the design sensitivities calculated with Equation 13 have been verified by the finite difference method.

4 Numerical examples

In all the numerical examples, initial cracks are positioned at the location where the maximum principal stress occurs according to the finite element analysis results of the crack-free structure. The main part of the design domain is discretized with standard eight-node planar elements, and singularity elements are positioned around the crack tip to capture the stress singularity. Unless otherwise stated, the Young’s modulus and Poisson’s ratio of the material are 1.0 and 0.3, respectively. The initial values of the design variables are set to be the volume fraction f V in all the examples. The sensitivity filter (Sigmund 2001) is adopted to suppress checkerboard patterns. The optimization problem is solved with the MMA algorithm. The obtained crack insensitive or easily detachable designs are compared with conventional minimum compliance designs.

4.1 Topology optimization of a portal frame

We first consider the design of a portal frame structure, as depicted in Fig. 5. Here, we aim to optimize the structural layout so as to reduce the intensity of stress singularity in the presence of a crack with a length 0.42 at the specified location, while still providing the maximum stiffness as possible. The radius of sensitivity filter is set to be 1.05, which is about 1.5 times the average element size.

Fig. 5
figure 5

The portal frame design problem

Full size image

The gray region in Fig. 5 is defined as the design domain. The J integral is calculated within the green domain, where the material distribution is not to be changed during optimization. We treat the blue region also as a non-design domain; otherwise this local part would be disconnected from the main structure after optimization, yielding a meaningless trivial solution.

For the weighting factor α = 0.5 and the volume fraction ratio f v = 0.3, the optimization process converged after 90 iterations. The obtained optimal solution (referred to as the crack insensitive design) is shown in Fig. 6. For comparison, the conventional minimum compliance design (obtained without predefined cracks) is also given in the figure. Clearly, the overall topology of the crack insensitive design is basically similar to that of the minimum compliance design, implying that its searching direction is largely guided by the second objective function, i.e., the structural compliance. On the other hand, as can be seen from the figures, the crack insensitive design still exhibits some notable differences in the force transmission path owing to introduction of the J integral into the objective function. Compared with the minimum compliance solution, the two beams connecting the crack area from above have a curved shape and the two thin beams on both sides of the crack area are vertically oriented. As a consequence, the local crack area sustains a much smaller stretching force than in the case of minimum compliance design. This greatly reduces the tensile stress level near the crack tip and is thus beneficial for avoiding further crack propagation.

Fig. 6
figure 6

Optimal solutions (a) crack insensitive design (α = 0.5) (b) minimum compliance design

Full size image

This can be also confirmed by the stress distribution contour shown in Fig. 7, where the first principal stresses around the crack tip have been greatly reduced (each element is divided into 3 × 3 sub-elements for the stress contour plotting). In the figures, the loading area is shown in gray color to hide the stress concentration area at the loading point. When plotting the stresses, we use the same interpolation scheme of Young’s moduli used in computing the elemental stiffness matrices.

Fig. 7
figure 7

First principal stress distribution of (a) crack insensitive design (α = 0.5) (b) minimum compliance design

Full size image

In Fig. 7a, the stress in the area above the crack tip is slightly increased, though it is still much less than the maximum stress of the minimum compliance design (0.68 v.s. 1.17). The increase of stress in other parts of the structure is natural since we only take into account the fracture behavior at the specified crack. However, our numerical experiences show that the increase of stress level in other parts of the structure can be controlled to some extent by reducing the weight of the J integral objective.

The scaled deformed shapes (computed with the penalized stiffness) of both optimized structures are also depicted in Fig. 8 to show the local stretch state near the crack.

Fig. 8
figure 8

Scaled deformed and undeformed configurations of (a) crack insensitive design (α = 0.5) (b) minimum compliance design

Full size image

From our experience, if an unreasonably large radius of sensitivity filter is applied, it may lead to increase of gray elements and loss of topology/shape details in the optimized design.

The objective function values for both optimal solutions are listed in Table 1. Compared with the minimum compliance design, the crack insensitive design achieves a remarkably lower J integral value (0.0868 v.s. 0.5349) without significantly increasing the mean compliance (12.9505 v.s. 12.6097). Here, the objective function values for the minimum compliance design are reanalysis results considering the predefined crack.

Table 1 Objective function values of crack insensitive designs (α = 0.5), minimum compliance design and initial design
Full size table

To explore the effects of the initial crack size, four different crack sizes are considered, and the optimized topologies are shown in Fig. 9. It is observed that the optimal designs have no distinct differences when the crack size varies within a reasonable range (from half to twice of the size we initially adopted (0.42)). This demonstrates the robustness of the present method. However, when the initial crack size is assumed to be so large as being comparable to the member size scale, the optimal topology may differ from these results. This is because that the large initial crack itself changes the load transmission path. Such a scenario is not a major focus of this study.

Fig. 9
figure 9

Optimized topologies obtained for different initial crack lengths. (a) 0.21; (b) 0.42; (c) 0.63; (d) 0.84

Full size image

To further study the effect of the weighting factor of the objective function, we obtained a set of Pareto optima with 9 different weighting factors ranging from α = 0.3 to α = 0.7, as depicted in Fig. 10. In these solutions, the J integral value drops from 0.1674 (α = 0.3) to 0.0262 (α = 0.7) as α increases, while the mean compliance changes slightly from 12.7583 (α = 0.3) to 13.3596 (α = 0.7). This indicates that the J integral and the structural global stiffness are two conflicting objectives in this particular design problem, and therefore one has to make a compromise between them. As can be observed from the insets, as the weighting factor α increases, the optimized structure has a tendency to alleviate the local stretching at the crack area.

Fig. 10
figure 10

Pareto optima obtained with different weighting factors

Full size image

The iteration histories of the two objective functions for weighting factor α = 0.5 are given in Fig. 11, which shows a dramatic decrease of both objective functions during the first optimization steps and then a steady convergence. The volume fraction constraint is active for the optimal designs in all the cases. For instance, the iteration history of the volume fraction for the weighting factor α = 0.5 is shown in Fig. 12.

Fig. 11
figure 11

Iteration history of the objective functions for the crack insensitive design problem

Full size image
Fig. 12
figure 12

Iteration history of the volume fraction for the crack insensitive design problem

Full size image

4.2 Topology optimization of an L-bracket

The optimal design of a planar L-bracket is studied now. The design domain and loading condition are shown in Fig. 13. An initial crack of 0.71 in length is positioned at the reentrant corner along the direction of 45 degrees. The upper bound limit of the volume fraction is set as f v = 40%. Uniformly sized square elements are used in the finite element discretization, with the element size being 1. The radius of sensitivity filter is set to be 1.5.

Fig. 13
figure 13

The L-bracket design problem

Full size image

The obtained crack insensitive design is compared with the minimum compliance design in Fig. 14, where distinct differences can be seen in the joint region at the corner. In the former design, the stiffness of this joint region is notably weakened so that the tension and shear forces around the crack are reduced, making potential cracks at the corner more difficult to further develop.

Fig. 14
figure 14

Optimal solutions (a) crack insensitive design (α = 0.4) (b) minimum compliance design

Full size image

To verify the optimal designs, the first principal stress contours of both designs are plotted in Fig. 15 (stress concentration at the loading point is hidden with gray color). As can be seen, in the crack insensitive design, the first principal stress at the crack tip is much lower compared with that in the minimum compliance design. In Table 2, the objective function values for both designs are summarized, which reflect that the J integral value is significantly reduced at the cost of an only slightly increased compliance in the crack insensitive design. For a deeper insight of the local stretch state of the optimal designs, the deformed configurations are shown in Fig. 16, which shows clearly the effect of different joint stiffness.

Fig. 15
figure 15

First principal stress distribution of (a) crack insensitive design (α = 0.4) (b) minimum compliance design

Full size image
Table 2 Objective function values of crack insensitive designs (α = 0.4), minimum compliance design and initial design
Full size table
Fig. 16
figure 16

Deformed and undeformed configuration of (a) crack insensitive design (α = 0.4) (b) minimum compliance design

Full size image

To further explore the competitive relationship between the two weighted objectives, a series of Pareto optimal solutions are obtained with different weighting factors, as depicted in Fig. 17. This figure shows that the weighing factor has an obvious influence on local material layout near the crack. However, a too large weighting factor for the J integral may slightly worsen the overall structural stiffness. Again, the volume constraint is active in all the optimal solutions.

Fig. 17
figure 17

Pareto optima obtained with different weighting factors

Full size image

We also compare the optimal design obtained with the present method with that of the stress-constrained compliance-minimization problem in Fig. 18. In the latter problem, the maximum allowable von Mises stress is 0.5, and the p-q relaxation (Bruggi 2008) (p = 3 and q = 8/3) and P-norm (Le et al. 2010) (P = 6) are used to handle the stress constraint. This stress-constrained optimization problem exhibited convergence difficulties, and it was stopped after the specified maximum number of iteration steps 300 was reached. In Fig. 18, the two designs have obviously different layouts. For a fair comparison, we reanalyze the optimal design obtained with the present method with a mesh without the presumed crack. The contours of the first principal stress and von Mises stress are plotted in Figs. 19 and 20. Though the p-norm constraint was satisfied, the maximum von Mises stress still exceeded the prescribed upper limit, as shown Fig. 20. It is interesting that the crack insensitive design results in a lower stress level at the reentrant corner than the stress-constrained design, even without considering explicit stress constraints.

Fig. 18
figure 18

Comparison of optimal solutions of (a) crack insensitive design (α = 0.4) (b) stress-constrained design

Full size image
Fig. 19
figure 19

Comparison of first principal stress distribution of (a) crack insensitive design (α = 0.4) (b) stress-constrained design

Full size image
Fig. 20
figure 20

Comparison of von Mises stress distribution of (a) crack insensitive design (α = 0.4) (b) stress-constrained design

Full size image

4.3 Topology optimization of MBB beam problem

In this example, we apply the present method to the well-known MBB beam and show the influence of predefined crack locations. The problem setting and three different cases of crack locations to be considered are shown in Fig. 21. The length of the predefined crack is 0.50 and the volume constraint is given as f v = 50%. The design domain is discretized with uniform square elements of side length of 0.5, and the radius for sensitivity filter is 0.75.

Fig. 21
figure 21

MBB problem (five assumed crack locations evenly spaced along the bottom edge)

Full size image

The optimized topologies are shown in Fig. 22 and compared with the corresponding minimum compliance solution, while the objective function values are given in Table 3. Again, the volume constraint is active in all the cases. It can be seen from these results that the crack insensitive design considering each case of crack locations differs from each other. This is not surprise since the optimal force transmission path should reduce the tensile stresses at each individual specified crack location.

Fig. 22
figure 22

Optimal solutions (a–c) crack insensitive designs for predefined crack location cases 1–3 (d) minimum compliance design

Full size image
Table 3 Objective function values of crack insensitive designs (α = 0.5) considering initial cracks at three different locations and minimum compliance design
Full size table

Such a tendency can also be observed from the first principal stress contours plotted in Figs. 23, 24, and 25. From these figures and the J integral values in Table 3, we find that including the J integral into the objective function achieves substantial reduction of tensile stress at different specified crack locations as compared with the conventional minimum compliance design in the presence of initial cracks. As can be seen in Table 3, the predefined crack location has little impact on the mean compliance values of the optimized topologies, since they mainly reflect the overall stiffness of the structure rather than local features.

Fig. 23
figure 23

First principal stress distribution of the (a) crack insensitive design and (b) minimum compliance design for a predefined crack at location 1

Full size image
Fig. 24
figure 24

First principal stress distribution of the (a) crack insensitive design and (b) minimum compliance design for a predefined cracks at location 2

Full size image
Fig. 25
figure 25

First principal stress distribution of the (a) crack insensitive design and (b) minimum compliance design for a predefined cracks at location 3

Full size image

4.4 Topology optimization of cantilever beam with a rectangular reserved functionality region

In this example, we consider topology optimization of a cantilever beam, in which a rectangular-shaped region (non-design domain in Fig. 26) is reserved for supporting certain functional devices. In order to achieve a design that is insensitive to possible cracks along the boundary of the reserved region, we here consider 20 possible crack locations, as shown in Fig. 26. Here, we assume the crack length is 2. In each iteration of the optimization process, the J integral of each individual potential crack location is separately computed based on the finite element analysis of the current design, and then the most dangerous crack location (the one with the largest J integral value) is determined and the corresponding sensitivities of the current design are evaluated. That means the most critical crack position changes with the evolving structural topology.

Fig. 26
figure 26

The cantilever beam design problem with a rectangular reserved functionality region

Full size image

In this example, the filter radius is 1.5 times the average mesh size. The volume fraction of given material is 45%. The weighting factor α of the J integral in the objective is set to be 0.1.

The obtained crack insensitive optimal design is shown is Fig. 27a. For comparison, the minimum compliance design is also given in Fig 27b. The two optimal topologies are obviously different, which indicates that the J integral has a significant effect on the material distribution. The mean compliance of the designs in Fig. 27a and b are 42.5406 and 40.3499, respectively, while the J integral values are 0.0023 and 0.1203 (the J integral of the minimum compliance design is re-computed for the most dangerous crack location identified for this design), respectively. Clearly, the J integral value of the most dangerous crack in the crack insensitive design is much lower than that of the minimum compliance design.

Fig. 27
figure 27

Optimal designs (a) crack insensitive design (b) minimum compliance design

Full size image

To further verify the optimal designs, we plot the first principal stress distribution and the most dangerous crack locations of both designs in Fig. 28 (the stress of the minimum compliance design is re-computed with its most dangerous crack). It is seen that in the crack insensitive design the region of interest (non-design domain) mainly undergoes compression, while in the minimum compliance design it is subjected to relatively high tensile stress. From these results one can see that the present method can generate an intuitively reasonable load path making the region of interest crack insensitive.

Fig. 28
figure 28

First principal stress distribution of (a) crack insensitive design (b) minimum compliance design

Full size image

4.5 Force transmission path design in transfer printing

The versatility of the proposed formulation is shown in this numerical example, which aims to provide an easily detachable design by maximizing the J integral in the design of stamps used in transfer printing. Transfer printing (Carlson et al. 2012) is a technique widely used in the fabrication and assembly of micro- and nano-devices. While operating, the ‘ink’ is picked up by a ‘stamp’ from the substrate and then printed to the ‘receiver’.

In the simulation of the detaching process of transfer printing, we place an initial crack at the edge of the interface between the stamp and the receiver in order to analyze the detaching behavior. We assume that the two parts start to separate if the J integral is larger than the stamp/receiver bonding strength when a given pulling force is applied. The problem setting is depicted in Fig. 29. The length of the predefined crack is 2. The stamp has a Young’s modulus of 1.8 and Poisson’s ratio of 0.48; while the receiver has a Young’s modulus of 13 and Poisson’s ratio of 0.27. The material volume fraction in the design domain is set as 30%. The objective function is stated as Φ(ρ, d) = α(−J) + (1 − α)C, where the weighting factor α is set to be 0.5 in this optimization problem. The radius for sensitivity filter is set to be 5.4, which is about 2.2 times of the maximum mesh size.

Fig. 29
figure 29

Design problem of easily detachable structure in transfer printing

Full size image

The optimal solution of easily detachable design obtained with the present optimization model is shown in Figure 30. For comparison purpose, optimal structural topology with minimum compliance is also given. The volume constraint is active in both solutions. Distinct differences between the two designs can be observed in Fig. 30. Obviously, the local features of the former design are able to increase tension and shear forces transmitted to the stamp edges. This is also reflected by the first principal stress contour shown in Fig. 31. Therein, it is seen that the maximum first principal stress at the stamp/receiver interface of the easily detachable design is 132% higher than that of the minimum compliance design.

Fig. 30
figure 30

Optimal solutions (a) easily detachable structure; (b) minimum compliance structure

Full size image
Fig. 31
figure 31

First principal stress distribution (a) easily detachable structure (b) minimum compliance structure

Full size image

The final objective function values for both designs are summarized in Table 4. In fact, the J integral value of the easily detachable design is 6.25 times of that of the minimum compliance design.

Table 4 Objective function values for easily detachable design (α = 0.5), minimum compliance design and initial design
Full size table

5 Concluding remarks

For engineering structures, without properly designed force transmission paths, fractures may occur and develop at particular locations, e.g., high tensile stress areas. In some other problems, it is desired to make a material interface to be easily detached. To address these problems, we propose a topology optimization method considering fracture mechanics behaviors at specified locations by including the J integral around a predefined crack as an objective function to be minimized/maximized. The resulting multi-criteria optimization problem is treated with the weighted sum approach. The adjoint-variable sensitivity analysis of the J integral with respect to the design variables is derived, which enables the optimization problem to be efficiently solved with gradient-based mathematical programing algorithms.

The validity and applicability of the proposed topology optimization formulation are illustrated with four numerical examples. The first three examples show that the proposed method is effective to generate optimized structures that are insensitive to cracks at specified locations. Compared with the corresponding minimum compliance designs, the obtained crack insensitive designs exhibit certain differences, particularly at the local regions near the assumed crack locations. This indicates that introducing the J integral into the design objective results in changes of the local force transmission path. As shown in the last numerical example, the proposed method can also be used to generate a design with easily detachable material interface.

The major differences between the present method and the stress-constrained topology optimization are summarized in Table 5.

Table 5 Major differences between the present method and stress-constrained topology optimization methods
Full size table

In the proposed formulation, it would be very expensive or impossible to take into account all the possible lengths, directions and locations of the initial cracks. It is therefore more realistic to set up cracks at the most fracture-critical positions in the region of interest, which can be predefined by the designer according to engineering experience or stress analysis of current designs. These critical positions may also be updated after reanalysis of the intermediate designs when necessary. Even so, this method still has limitations since it relies on predefined crack locations and thus cannot consider all the possible crack locations. Also, the regions immediately around the assumed crack tips are set as non-design domains and only the load path in other parts of the design domain is optimized.

For the considered bi-criteria optimization problem, if the Pareto set is not convex in the objective function space, the weighted sum approach cannot ensure the Pareto front be tracked by simply changing the weighting factor. However, this would not cause any difficulties in practical applications, since our goal is to seek an acceptable trade-off between the fracture sensitivity and the global structural stiffness.