Abstract
An algorithm for risk-based optimization (RO) of engineering systems is proposed, which couples the Cross-entropy (CE) optimization method with the Line Sampling (LS) reliability method. The CE-LS algorithm relies on the CE method to optimize the total cost of a system that is composed of the design and operation cost (e.g., production cost) and the expected failure cost (i.e., failure risk). Guided by the random search of the CE method, the algorithm proceeds iteratively to update a set of random search distributions such that the optimal or near-optimal solution is likely to occur. The LS-based failure probability estimates are required to evaluate the failure risk. Throughout the optimization process, the coupling relies on a local weighted average approximation of the probability of failure to reduce the computational demands associated with RO. As the CE-LS algorithm proceeds to locate a region of design parameters with near-optimal solutions, the local weighted average approximation of the probability of failure is refined. The adaptive refinement procedure is repeatedly applied until convergence criteria with respect to both the optimization and the approximation of the failure probability are satisfied. The performance of the proposed optimization heuristic is examined empirically on several RO problems, including the design of a monopile foundation for offshore wind turbines.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Problem definition
The design of an engineering system aims at producing an economical structure and minimizing risk. Risk is a measure of potential adverse consequences for the owner, society and environment. The objectives of structural cost and risk minimization are often contradictory and an optimal trade-off must be identified, which is the goal of the Risk Optimization (RO) framework (e.g., Beck et al. 2015; Rackwitz 2000; Rosenblueth and Mendoza 1971). RO minimizes the total costs of a system, which is composed of the design cost of a system (e.g., production cost) and the expected cost of failure (i.e., failure risk). The set of design parameters that minimizes the total cost is found within a set of feasible or admissible designs, which is determined by a series of deterministic (e.g., geometry limitations) and probabilistic constraints. In ROs of engineering systems, the probabilistic constraints are often reliability constraints (i.e. upper bounds on the failure probabilities). Alternative design optimization frameworks include Deterministic Design Optimization (DDO) (e.g., Beck and de Santana Gomes 2012) and Reliability-Based Design Optimization (RBDO) (e.g., Beck and de Santana Gomes 2012; Valdebenito and Schuëller 2010), which aim at optimizing the design cost of a structure with respect to a series of constraints, while not accounting for the failure risk on the objective function. In the DDO framework the constraints are defined by a series of deterministic constraints (e.g., allowable stress), while in the RBDO framework the set of constraints is expanded to include reliability constraints.
In this study, the RO problem is defined as follows:
subject to
where the total cost, C(t), is a function of design variables t=[t 1,t 2,...,t n ]T ∈Ω t , C D (t) specifies the design cost of a structure or an engineering system to account for the cost of production, operation, inspection, maintenance, and disposal, C F k (t) is the cost of the kth failure event, and P F k (t) is the corresponding failure probability. h i (t) defines the ith deterministic constraint, while \(P_{Fk}^{\lim }\) specifies the kth reliability constraint. The upper and lower bounds for t are t l and t u.
For a given t, P F k (t) is defined as an m-dimensional integral:
where u=[u 1,u 2,...,u m ]T∈Ω u is a realization of a vector of independent standard normal random variables, U=[U 1,U 2,...,U m ]T, with zero-mean and unit standard deviation; g k (u,t) is the performance function corresponding to the kth failure criterion, which has a positive value, g k (u,t)>0, in the safe domain (i.e., safe state of a structure), and a nonpositive value, g k (u,t)≤0, in the failure domain of the outcome space; ϕ m (u) is an m-dimensional joint probability density function composed of m independent standard normal marginal distributions. In the general case, where g k is a function of dependent non-normal random variables, X, it is assumed that suitable probability preserving transformations exist, u=Θ x,u (x) and x=Θ u,x (u) (e.g., Nataf (Liu and Der Kiureghian 1986) and Rosenblatt 1952).
1.2 Short literature review
Due to the similarity between the RO and RBDO formulations, the following section provides a short literature review of RO and RBDO algorithms. Although the RO and RBDO formulations are relatively similar, the implementations of the two formulations are different in case one relies on sampling-based failure probability estimates (e.g., Beck and de Santana Gomes 2012; de Santana Gomes and Beck 2013). The corresponding RO implementations are often characterized by noisy objective functions due to the numerical noise associated with sampling-based failure probability estimates. Consequently, the solution to the RO problem often relies on the implementation of a global optimization algorithm (e.g., Genetic Algorithm (Spall 2005), Cross-entropy (Botev et al. 2013)), while the solution to the RBDO problem can be found through numerically more efficient nonlinear programming algorithms (e.g., Royset et al. 2006).
A relatively straightforward solution to RO and RBDO problems is obtained by nesting a reliability algorithm within an optimization algorithm in a so-called ‘double-loop’ formulation. The implementations of the double-loop formulation are often associated with high computational cost due to the nature of optimization and reliability algorithms, which commonly require numerous evaluations of complex structural models (e.g., finite element models). To avoid the high computational cost associated with the double-loop formulations, a relatively large number of advanced formulations and simplifications have been proposed in the literature. However, the majority of these formulations examine the RBDO problem (e.g., Valdebenito and Schuëller 2010; Cheng et al. 2006; Royset et al. 2001; Aoues and Chateauneuf2010; Yang and Gu2004), while the number of proposed formulations for the RO problem is relatively limited (e.g., Kuschel and Rackwitz1997; Gomes and Beck2016; de Santana Gomes and Beck2013; Taflanidis and Beck2008; Jensen et al. 2009).
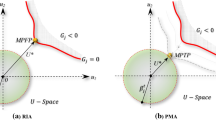
Depending on the type of reliability methods employed in the evaluation of RBDO or RO problems, the RBDO and RO algorithms can be classified into algorithms that apply sampling reliability methods (e.g., Monte Carlo, Importance Sampling, Subset Simulation) and algorithms that apply approximate reliability methods (e.g., FORM, SORM). As suggested by (Valdebenito and Schuëller 2010), the RBDO and RO algorithms that apply approximate reliability methods can be further divided into double-loop, single-loop, and decoupling approaches. The two most commonly implemented double-loop formulations are known as the Reliability Index Approach (RIA) (e.g., Nikolaidis and Burdisso1988; Enevoldsen and Sørensen 1994) and the Performance Measure Approach (PMA) (e.g., Der Kiureghian et al. 1994). The application of the RIA formulation to both RBDO and RO problems was examined in Enevoldsen and Sørensen (1994). The failure probabilities in the objective function of the RO problem in Enevoldsen and Sørensen (1994) are approximated with FORM estimates. The performance of the PMA formulation on RBDO and RO problems was examined, respectively, in Royset et al. (2001) and Royset et al. (2006), where the failure probabilities in the objective function of the RO problem are approximated with auxiliary variables. Single-loop algorithms transform the double loop into a single loop by replacing reliability constraints with approximate deterministic constraints (e.g., Chen et al. 1997) or utilizing the Karush-Kuhn-Tacker optimality conditions (e.g., Kuschel and Rackwitz1997). The application of the single loop algorithm to the RO formulation in (Kuschel and Rackwitz 1997) relies on the FORM approximation of the failure probability in the objective function. In the decoupling approaches, the RBDO problem is transformed into a sequence of deterministic optimizations, with periodic reliability analyses conducted to update the set of admissible designs. The Sequential Optimization and Reliability Assessment (SORA) method is a decoupling approach that evaluates the RBDO problem through a sequence of deterministic and reliability analyses (Du and Chen 2004). The reliability analyses are conducted after the deterministic optimization to ensure constraint feasibility (Du and Chen 2004). The Sequential Approximate Programming (SAP) is an alternative decoupling method that transforms the RBDO problem into a series of approximate subproblems with approximate objective function and constraints (Cheng et al. 2006). The SAP method provides a solution to the RBDO problem by sequentially improving the optimal design and the approximation of the FORM estimate of the failure probability (Cheng et al. 2006). Although the decoupling approaches are mainly applied to the RBDO formulations, the SAP method was evaluated on an RO formulation in Cheng et al. (2006) with an approximation of the FORM estimates of the failure probability in the objective function.
Applications of RO and RBDO algorithms with approximate reliability methods rely on the adequacy of the reliability estimates. In the case of significant nonlinearities in the reliability problems, the approximations can lead to over- or under-estimates of the failure probabilities. This can significantly affect the ability of the corresponding RO and RBDO algorithms in locating the minimizer and satisfying the reliability constraints. In such conditions one usually resorts to RBDO and RO algorithms that implement sampling-based reliability methods. As suggested in Valdebenito and Schuëller (2010), the RBDO and RO algorithms implementing sampling-based reliability methods can be organized into three groups; applications of metamodels, decoupling approaches, and enhanced reliability approaches. A metamodel is commonly a regression or a classification model constructed as an approximation of the performance function (e.g., Depina et al. 2016). A metamodel is applied within RO or RBDO algorithms to reduce the computational demands resulting from computationally complex models of engineering structures. Some of the commonly considered metamodels in structural reliability literature include: polynomial response surfaces (e.g., Bucher and Bourgund1990), Kriging (e.g., Dubourg et al. 2011; Chen et al. 2014; Lee et al. 2011), Artificial Neural Networks (e.g., de Santana Gomes and Beck2013) and Support Vector Machines (e.g., Basudhar et al. 2008). The majority of the proposed metamodel-based algorithms consider the RBDO formulation (e.g., Chen et al. 2014; Lee et al. 2011), while several approaches examine the RO formulation (e.g., Dubourg et al. 2011; de Santana Gomes and Beck2013). Similar to the decoupling approaches with approximate reliability methods, the decoupling approaches for RBDO problems with sampling-based reliability methods attempt to approximate the probability of failure throughout the optimization process. For example, in Jensen and Catalan (2007), Jensen (2005), and Valdebenito and Schuëller (2011), the probability of failure is approximated by an exponential function of design parameters, while in Au (2005) and Ching and Hsieh (2007) the Bayesian theorem is applied to approximate the reliability problem based on samples from the failure domain. Applications of decoupling approaches to the RO formulation include the Design Space Root Finding (DSRF) method, which aims to approximate the failure probabilities over the design space by calculating the roots of the limit state function (Gomes and Beck 2016).
Direct integration of simulation techniques with optimization methods is implemented in several enhanced reliability methods (e.g., Royset and Polak2004; Taflanidis and Beck2008). For example, the RBDO algorithm in Royset and Polak (2004) utilizes the sample average approximation to supply gradients of the probabilities to an optimization algorithm. An alternative simulation based approach, known as the Stochastic Subset Optimization (SSO) (Taflanidis and Beck 2008), seeks to locate a region of the design space where the failure probability is minimized. The SSO method operates on a set of samples in a so-called augmented reliability space where the design parameters are artificially considered as uniformly distributed random variables. The SSO algorithm proceeds iteratively to locate a subset of the design space likely to contain the optimal solution, which can be found by a more detailed local search.
1.3 Scope and outline
This paper proposes a decoupling RO algorithm based on sampling reliability methods, referred to as CE-LS. The proposed RO algorithm combines the Line Sampling (LS) (e.g., Pradlwarter et al. 2007) reliability method and the Cross-entropy (CE) (e.g., De Boer et al. 2005) global optimization method. The CE-LS coupling is considered as advantageous within the context of the RO problem due to the robustness of the CE global optimization algorithm and the fact that the LS reliability method provides efficient and unbiased failure probability estimates in both low- and high-dimensional reliability problems. Driven by the random search of the CE algorithm, the CE-LS method proceeds iteratively to update a set of random search distributions in the design space such that the optimal or near-optimal solution of the RO problem is likely to occur. To avoid potentially high computational demands associated with this double-loop implementation, a local weighted average (LWA) approximation of the probability of failure is iteratively refined as the optimization algorithm proceeds. The adaptive refinement procedure of the CE-LS algorithm is repeatedly applied until convergence criteria with respect to both the optimization and the probability of failure estimates are satisfied. The proposed optimization heuristic is examined on several RO problems and an RBDO problem.
The paper is organized to provide a basic overview of the LS method in Section 2 and the CE method for optimization in Section 3. The formulation of the proposed CE-LS algorithm is introduced in Section 4 with a discussion of the implementation, convergence criteria and constraint modeling. The proposed algorithm is examined in Section 5 on several RO problems and a RBDO problem. A discussion on the performance of the CE-LS algorithm is provided in Section 6, followed by a short summary with conclusions in Section 7.
2 Line sampling
LS formulates a reliability problem as a number of conditional one-dimensional reliability problems in the outcome space Ω u (e.g., Hohenbichler and Rackwitz1988; Koutsourelakis et al. 2004). The one-dimensional reliability problems are defined parallel to the important direction, α. α is a unit vector pointing to the region of the failure domain nearest to the origin of Ω u , as illustrated in Fig. 1. A general approach for determining α is based on a unit vector pointing to the average of a set of samples generated with the Markov Chain Monte Carlo (MCMC) method from the distribution of the random variables conditioned on the failure event (Koutsourelakis et al. 2004). In case of moderately nonlinear performance functions, α can be closely approximated by a unit vector pointing to the most likely point in the failure domain, also known as the design point. Some of the additional approximate approaches for determining α include a normalized gradient vector of g(u) pointing to the direction of the steepest descent, or a unit vector based on engineering judgment. In this paper, α is selected as the direction of the design point or approximations thereof.
Sampling is performed on the hyperplane orthogonal to α. For each sample, the contribution to the P F is calculated as a one-dimensional reliability integral along α. Given α, the failure domain, F, can be expressed as:
where u α is a standard normal random variable defined along α, \(\textbf {u}^{\perp } \in \mathbb {R}^{m-1}\) is a vector of random variables orthogonal to α, while F α is a function representing the failure domain along α, defined on \(\mathbb {R}^{m-1}\) (Pradlwarter et al. 2007). P F can be expressed as follows:
where I F (u) is an indicator function, such that I F (u)=1 if u∈F and I F (u)=0 otherwise.
In the case that F α (u ⊥) is bounded by [β(u ⊥),∞), the conditional one-dimensional reliability problem can be evaluated as Φ(F α (u ⊥))=Φ(−β(u ⊥)), where β(u ⊥) is the distance from the hyperplane u ⊥=0 along α to the limit state surface, g(u)=0, as indicated in Fig. 1. In the case that F α (u ⊥) is composed of several discontinuous intervals this formulation is extended analogously, for example (−∞,β 1(u ⊥)]∪[β 2(u ⊥),∞), where β 2(u ⊥)≥β 1(u ⊥), leads to Φ(F α (u ⊥))=Φ(β 1(u ⊥))+Φ(−β 2(u ⊥)).
If F α (u ⊥) is bounded by [β(u ⊥),∞), an unbiased estimate of P F is calculated as:
where \(\left \lbrace \textbf {u}_{i}^{\perp } \sim \phi _{m-1}(\textbf {u}^{\perp }): i=1,...,N \right \rbrace \) is a set of samples from the (m−1)-dimensional hyperplane orthogonal to α. It is important to observe from (4) that even a single line search along the important direction provides an estimate of P F . This property of the LS method will be one of the main building elements of the proposed CE-LS method in the following sections. The variance of the estimator \(\hat {P}_{F}\) can be evaluated as:
The coefficient of variation of \(\hat {P}_{F}\), estimated as \(\hat {\text {CoV}}(\hat {P}_{F})=\) \(\sqrt {\hat {\text {Var}}\left \lbrack \hat {P}_{F}\right \rbrack } \) \(/\hat {P}_{F}\), is commonly used to asses the accuracy of \(\hat {P}_{F}\).
3 Cross-entropy method for optimization
The CE method is a heuristic approach for estimating rare events and solving optimizations problems (De Boer et al. 2005; Botev et al. 2013). The method was initially developed as an adaptive importance sampling method for the estimation of rare-event probabilities by minimizing the cross-entropy or Kullback-Liebler divergence as a measure of distance between two distributions. Given that the probability of locating the optimal or a near-optimal solution using naive random search is usually a rare-event probability, the CE method can be applied as a randomized algorithm for optimization (De Boer et al. 2005). The CE method adaptively updates a series of sampling distributions of the random search such that the optimal or near-optimal solution is more likely to occur. The sampling distributions are adaptively updated to converge to a distribution with high probability mass in the region of near-optimal solutions (Botev et al. 2013). The method is selected for an application to RO problems as it features a robust global optimization algorithm and requires the choice of only a relatively low number of parameters.
Consider a function S(t) over a search space Ω t with a single minimizer, \(\textbf {t}^{*}=\left \lbrack t_{1}^{*},...,t_{n}^{*} \right \rbrack ^{T} \in {\Omega }_{\textbf {t}}\), and the corresponding minimum, γ ∗:
The CE importance sampling formulation for rare-event estimation is adapted to solve the optimization problem in (6) by considering the probability P(S(t)≤γ), where t is associated with a probability density function f(t;𝜃) on Ω t , and 𝜃 are distribution parameters, while γ is close to the unknown minimum γ ∗. The CE algorithm adaptively updates γ and 𝜃 to provide an importance sampling distribution that concentrates its probability mass in the neighborhood of t ∗, as illustrated in Fig. 2 a to b. Random sampling from such a distribution is more likely to provide the optimal or near-optimal solution (Botev et al. 2013) for the problem in (6).
This study implements the CE algorithm for optimization with normal updating as specified in Algorithm 1. The CE algorithm with normal updating employs a set of independent normal distributions to generate design states separately for each of the components of the parameter vector t=[t 1,...,t n ]T∈Ω t . In the CE algorithm with normal updating, f(t;𝜃) is a multivariate normal distribution with independent components specified by 𝜃=(μ,σ 2), where μ=[μ 1,...,μ n ]T is a vector of means and \(\boldsymbol {\sigma }^{2}=\left \lbrack {\sigma _{1}^{2}},...,{\sigma _{n}^{2}} \right \rbrack ^{T}\) is a vector of variances.

The CE algorithm proceeds iteratively to update 𝜃 and γ until a convergence criterion is satisfied. In the implementation of the CE algorithm with normal updating in Botev et al. (2013), the convergence criterion is expressed in terms of the maximum value of the standard deviation in the ith iteration among the design components, such that \(\max _{r} \sigma _{ir} < \epsilon _{\lim }; r=1,...,n\), where \(\epsilon _{\lim }\) is a tolerance limit. Once convergence is achieved, it is common to select the mean value of the random search distributions as the minimizer (e.g., Botev et al. 2013).
Although global optimization algorithms are relatively efficient in locating the region of near-optimal solutions, considerable computational expenses are often required to locate the true optimum within the region of near-optimal solutions (e.g., Beck and de Santana Gomes2012). Different techniques can be implemented in such conditions, as for example hybrid optimization algorithms that combine global optimization and nonlinear programming algorithms (e.g., Beck and de Santana Gomes2012). In the context of the CE method it is common to implement the dynamic smoothing (e.g., Kroese et al. 2006) or the injection (e.g., Botev and Kroese2004) techniques. The dynamic smoothing introduces a set of coefficients which impede the updating of the parameters of the random search distributions. The coefficients of the dynamic smoothing are selected to prevent the parameters of the random search distribution from converging too quickly to a sub-optimal solution. The injection extension prevents the optimization process from converging to a sub-optimal solution by increasing the variance of the random search distribution periodically throughout the optimization process.
Deterministic (1b) and reliability constraints (1c) can be incorporated in the CE method by implementing the acceptance-rejection or the penalty method (Kroese et al. 2006). Given a random search state of the CE algorithm, the acceptance-rejection method enforces constraints by accepting the state if the constraints are satisfied. Otherwise, the considered state is rejected and the random search proceeds to generate another state. The acceptance-rejection procedure is repeated until the specified number of random search states are accepted. The efficiency of the acceptance-rejection method depends on the ratio of accepted over the total number of proposed design states, known as the acceptance rate. In situations with low acceptance rates and/or computationally demanding numerical models, used to evaluate constraints, the acceptance-rejection method can result in high computational costs.
The penalty method is an alternative to the acceptance-rejection method in situations with low acceptance rates and/or computationally demanding constraints. The penalty method modifies the objective function to penalize the constraint violation. For example, in the case of a deterministic constraint as in (1b), the penalty function can take the following form:
where P k (t) are penalty functions. The penalty function is usually defined to penalize the constraint violation proportionally:
where S P k >0 is selected according to the importance of the kth constraint violation.
4 CE-LS method
4.1 Introduction
A straightforward coupling of the CE optimization and the LS reliability method in a double-loop RO algorithm is associated with high computational costs. An alternative CE-LS coupling is formulated in this study in which an LWA approximation of the probability of failure in the design space is constructed and refined throughout the optimization process. The LWA approximation of the probability of failure enables the CE-LS coupling to avoid repeated nested estimations of the reliability problem within the optimization algorithm.
The motivation for the coupling between the CE optimization and the LS reliability methods is rooted in several important features of the two methods. The CE method is a robust global optimization algorithm well-suited for noisy objective functions. The LS method is a robust and highly efficient reliability method that provides unbiased reliability estimates for a wide range of problems, including nonlinear and high-dimensional reliability problems (e.g., Schuëller et al. 2004). One relevant feature of the LS method is that a single sample (i.e., line search) provides an estimate of the failure probability. This property is utilized within the LWA approximation of the reliability estimates to integrate the CE and LS methods, as shown later in this Section. The LWA is selected because it provides a nonparametric local regression model with a reasonable trade-off between accuracy and computational efficiency. The LWA model is compatible with the CE method, as the CE algorithm requires only local estimates of the objective function at each design state. The compatibility also extends to the LS method, where the failure probability estimate is defined as an average estimator, which allows for a straightforward implementation of the LWA estimator.
4.2 Formulation
Consider a set of N S design states generated in the ith step of the CE algorithm with normal updating:
where t j =[t j1,...,t j n ]T, while μ i =[μ i1,...,μ i n ]T and \(\boldsymbol {\sigma }_{i}^{2}=\left \lbrack \sigma _{i1}^{2},...,\sigma _{in}^{2} \right \rbrack ^{T}\) are the parameters of the normal random search distribution in the ith step. In order to evaluate the total cost and the reliability constraints, as defined in (1a–1d), estimates of the probability of failure are required for the set of design states generated by the random search in (9). In contrast to the double-loop algorithm, which requires highly accurate estimates of the probability of failure for the design states in (9), the CE-LS algorithm relies on an LWA approximation of the failure probability. The LWA approximation of the probability of failure in the design space is constructed with the Nadaraya-Watson nonparametric regression model (Nadaraya 1964; Watson 1964), presented in Appendix A.
The LWA approximation is constructed under the assumption that the limit state surface of the reliability problem is smooth in the vicinity of a design state, such that the reliability estimates at the neighboring design states can be employed collectively to provide an accurate approximation of the probability of failure. An approximation of the probability of failure at a design state can be obtained with smaller sample size relative to the corresponding double-loop algorithm due to the reliance of the LWA model on the collective of reliability estimates at neighboring design states.
The LWA approximation of the reliability problem is expected to provide sufficient guidance to the random search of the CE-LS algorithm as it requires information on the relative optimality of samples within a population, and not highly accurate estimates of the absolute optimality at the intermediate sampling steps of the optimization process. The updating mechanism of the CE algorithm is based on the identification of the relative difference in the optimality of the samples within a population at each intermediate sampling step. This means that although the averaging of the LWA model results in a certain bias in the total cost estimates, the optimization process is not expected to be significantly affected as long as the relative differences in optimality between the samples can be correctly identified. Moreover, as the LWA estimate is refined throughout the optimization process, this bias is expected to decrease at later sampling steps.
The accuracy of the LWA approximation of the failure probability estimate at a design state can be controlled by the sample size at the considered design state and the number of design states in its neighborhood. To simplify the implementation of the CE-LS method in this study, the accuracy of the approximation is here controlled only by the number of design states. The sample size per design state in (9) is fixed to a single line search along the important direction, as defined in the LS method.
Consider that a single line search is evaluated for each of the design states in (9) for the kth reliability problem, as presented in Fig. 3:
Line searches are conducted along the important directions, α k ;k=1,...,n r , for each of the design states. In general α k is dependent on the design parameters, but often a single α k provides a reasonable approximation of the important direction across the design space.
Based on the set of line searches in (10), the estimator in (4) is transformed into an LWA estimator as follows:
where w k s ;s=1,...,N S is a set of weights:
with kernel function K H (v):
where K(v) is a function defined to provide higher weights to the design states closer to v=0, while H is a n×n nonsingular positive definite bandwidth matrix. In this study, K(v) is the Gaussian kernel, while H is selected to be a diagonal matrix with entries proportional to the variances of the normal random search distributions, \(H=h\cdot \text {diag} ({\sigma _{1}^{2}},...,{\sigma _{n}^{2}})\), where h is a bandwidth parameter. Proper selection of h is important as it affects the variance and the bias of the estimate. Larger values of h reduce the variance of the estimate as more values have a significant effect on the estimate. However, as h increases the estimator is averaged across a broader range of design states, which can lead to a larger bias. The value of h is determined to balance the effects of variance and bias of the estimators by minimizing the leave-one-out cross validation score, following Appendix A (42).
An estimate of the variance of the weighted estimator in (11) is calculated as (Wasserman 2006):
where \(\hat {\sigma }_{k}^{2}(\textbf {t}_{j})\) is the estimate of the residual variance for the kth reliability problem, calculated as discussed in Appendix A.
An LWA approximation of the total cost is constructed at the design states in (9) as follows:
The total cost estimate is a biased estimator due to the bias in the estimates of the failure probabilities. The variance of the total cost is estimated as:
An estimate of the coefficient of variation for the local average estimate of the total cost is calculated as:
The estimates of the total cost in (15) and the reliability problem in (11) are used to evaluate the constraints and update the parameters of the random search distributions, as defined in Algorithm 1. The constraints can be included by the acceptance-rejection or the penalty method, as discussed in Section 3.
The parameters of the random search distributions are updated based on the set of N e samples with the lowest estimated total cost according to Algorithm 1. With the parameters of the random search distribution updated, the procedure in (9) to (17) is reiterated to provide another set of design states and reliability estimates in the region of the design space previously identified to minimize the total cost. Since the CE-LS algorithm requires information on the regions of the design space minimizing the total cost, and not necessarily highly accurate estimates of the total cost, it is expected that the bias in the total cost estimates will not significantly affect the performance of the algorithm. It is important to note that the design states generated in the previous iterations of the algorithm are not discarded, but are used to construct the LWA approximation in the current iteration. As the CE-LS method localizes the region of the design space with near-optimal solutions, the LWA approximation of the failure probability is adaptively refined with additional design states, thus improving the accuracy of the approximation. Consequently, due to a decreased extent of averaging, the bias in the LWA approximation of the probability of failure is reduced.
4.3 Convergence criteria
The CE-LS algorithm proceeds iteratively until certain convergence criteria are satisfied with respect to the random search in the design space and the convergence of the total cost estimate. The convergence of the random search is monitored with respect to the maximum value of the standard deviation scaled by the interval between the upper and lower bound of the corresponding design parameter in the ith iteration of the algorithm:
where \({t_{r}^{u}}\) and \({t_{r}^{l}}\) are, respectively, finite upper and lower bounds for the rth design parameter, while \(\epsilon _{\lim }\) is a tolerance limit.
Convergence of the total cost estimate can be monitored by the value of the coefficient of variation in (17). The average value of the coefficient of variation of the total cost estimate, among the design states in an iteration step, is utilized as a convergence criterion:
where \(\text {CoV}_{\lim }\) is the limiting value.
Once convergence is achieved, it is common to select the mean value of the random search distributions as the minimizer (e.g., Botev et al. 2013). Alternatively, the solution to the RO problem can be further refined by conducting a local search based on the parameters of the random search distribution obtained in the last iteration step of the algorithm. A local search can be conducted with the corresponding double-loop or any alternative optimization algorithm in the region of the design space localized in the last iteration of the CE-LS algorithm.
4.4 Implementation
The implementation of the CE-LS method for an unconstrained RO problem is summarized in Algorithm 2. The total cost is specified with C D (t) and C F , while the bounds of the feasible design space are specified with t l and t u. The CE-LS algorithm requires the specification of the maximum number of iteration steps, N O , the number of design states per iteration, N S , the number of elite samples, N e , the initial parameters of the random search distributions, μ 0 and σ 0, and the convergence limits, \(\epsilon _{\lim }\) and \(\text {CoV}_{\lim }\). Although the selection of the parameters of the CE-LS algorithm is problem dependent, efficient performance of the CE algorithm is achieved in Kroese et al. (2006) with N e =10 for n<50 and N e =20 for 50≤n≤100. Provided that common values of ρ are between 0.01 and 0.1, the values of 100<N S <1000 for n<50 and 1000<N S <2000 for 50<n<100 can serve as an initial guidance.

The initial parameters of the random search distribution, μ 0 and σ 0, should be selected such that a set of random states covers the design space relatively uniformly between t l and t u. The selection of N O , \(\epsilon _{\lim }\), and \(\text {CoV}_{\lim }\) primarily depends on the available computational resources. In general, larger values of N O allow for lower values of \(\epsilon _{\lim }\) and \(\text {CoV}_{\lim }\) to be achieved. Low values of \(\epsilon _{\lim }\) will lead to finer estimates of the region of the design space with near-optimal solutions, while low values of \(\text {CoV}_{\lim }\) lead to higher accuracy in the total cost estimates.
4.5 Constraints
The implementation of the CE-LS method to an unconstrained RO problem in Algorithm 2 can be extended to optimization problems with deterministic and probabilistic constraints by implementing the acceptance-rejection and/or the penalty method. As discussed in Section 3, the acceptance-rejection is commonly applied in RO problems with computationally inexpensive constraints and relatively large acceptance rates. These criteria are commonly satisfied by deterministic constraints, specified by closed form expressions. Reliability constraints are commonly computationally expensive to evaluate in structural ROs due to the application of computationally demanding reliability methods and/or complex structural models (e.g., finite element model). To avoid potentially low acceptance rates and the corresponding computational costs, the reliability constraints are modeled by the penalty method. The penalty method modifies the objective function to penalize the reliability constraint violations. The following formulation of the penalty function is adopted in this study:
where C P >0 measures the importance of constraint violation, while \(P_{Fk}^{\lim }\) is the kth constraint limitation. The value of C P should be selected large enough to prevent the samples violating the constraints from updating the parameters of the random search distributions in the following iteration of the CE-LS algorithm.
5 Numerical examples
5.1 Risk optimization problem
The CE-LS method is applied to an RO problem taken from Gomes and Beck (2016) to investigate the effects of noise in the objective function on the optimization process. The RO problem is specified with an n-dimensional vector of design parameters t=[t 1,...,t n ]T, and a vector of three independent normally distributed random variables, X=[X 1,X 2,X 3]T, where X 1,X 2,X 2∼N(1,0.2). The RO problem is defined as follows:
where
and C F =20.
As observed from (21a), the objective function incorporates a risk term to account for the expected failure cost, defined as a product of the failure cost and the corresponding failure probability. The application of sampling reliability methods for the estimation of the failure probability produces estimates that are subject to a certain degree of numerical noise. Consequently, the noise is transferred to the values of the objective function, as illustrated in Fig. 4. Figure 4 presents a realization of the objective function where the failure probability estimates were calculated with the LS method and \(\text {CoV}(\hat {P}_{F}) \le 0.01 \). From Fig. 4 it can be observed that the presence of noise in the failure probability estimates leads to a noisy objective function. The CE-LS method is developed to address this type of problems as is relies on the CE global optimization algorithm.
A realization of the cost function in (21a). The grayscale plot shows the logC(t) values
The CE-LS algorithm is applied to the RO problem in (21a–21d) with the following parameters; N O =20, N S =102, ρ=0.1, \(\epsilon _{\lim }=0.01\). The important directions are selected to point in the direction of the design point. The design points are located numerically for each design state. The results are presented in Table 1 for a range of dimensions of the optimization problem, n={2,10,20}, in terms of the estimate of the average value of the design components at the minimizer, \(\hat {\bar {t}}_{\min }=1/n {\sum }_{r=1}^{n} \hat {t}_{\min ,r}\), estimate of the minimum, \(\hat {C}_{\min }\), estimate of P F at the minimizer, \(\hat {P}_{F}(\hat {\textbf {t}}_{\min })\), the total number of objective function calls, N o , and the total number of performance function calls, N g . The results in Table 1 correspond to the average values among ten runs of the algorithm. The results are presented with the corresponding coefficients of variation, CoV, to examine the variability in the estimates among the ten runs of the algorithm. The CoV values are calculated empirically as a ratio of the standard deviation of an estimate over its average value.
The performance of the CE-LS method is compared to the corresponding double-loop algorithm, obtained by coupling the CE optimization and the LS reliability methods. The double-loop algorithm is implemented with the same convergence criteria as the CE-LS algorithm. The reliability estimates are calculated with a convergence criterion of \(\text {CoV}_{\lim }=0.05\). The double-loop results in Table 1 correspond to the average values among ten runs of the algorithm.
Additionally, the numerical performance of the CE-LS approach is compared to the DSRF method in Gomes and Beck (2016). The DSRF method evaluates the failure probabilities over the design space by calculating the roots of the limit state function. The RO problem in (21a–21d) was examined with the DSRF method in Gomes and Beck (2016) with the primary goal of examining the numerical efficiency of the approach. Although the estimates of the minimizer, minimum, and failure probability are illustrated for some numerical examples in Gomes and Beck (2016), they are not explicitly presented. For that reason, Table 1 presents only the computational performance of the DSRF approach in terms of the number of performance function evaluations, N g , as these results were explicitly provided in Gomes and Beck (2016).
A reference estimate of the minimizer for the RO problem in (21a–21d) is obtained by coupling the Genetic Algorithm global optimization algorithm with the Monte Carlo method (GA-MC). The Genetic Algorithm is implemented with 15 generations, a population size of 50 per generation, and 5 % elite population. The Monte Carlo estimates of the failure probability are calculated with the convergence criteria defined by the coefficient of variation of the total cost of \(\text {CoV}(\hat {C}) \le 0.001\) or the maximum number of samples of 107. Given that the cost function is symmetric with respect to the diagonal between t l=[0,...,0]T and t l=[1,...,1]T and that the minimum is found at the diagonal, as shown in Fig. 4, the application of the GA-MC algorithm is simplified by considering a one-dimensional optimization problem along the diagonal. Due to the simplification of the optimization problem, the GA-MC results in Table 1 are not directly comparable with the results of the CE-LS and the double-loop algorithms in terms of accuracy and computational efficiency. The main purpose of the GA-MC estimates is to provide reference results to the CE-LS and the double-loop algorithms.
The comparison of the results in Table 1 reveals that the CE-LS method located the minimizer and the minumum in the region of near-optimal solutions, comparable to the results from the double-loop and the GA-MC algorithms. The variabilities in the estimates between the CE-LS and the double-loop algorithms are comparable and increase from ≈2 % for n=2 to ≈10 % for n=20. The results demonstrate that the CE-LS method can be efficiently applied to RO problems characterized by noise in the objective function introduced by sampling-based failure probability estimates. The comparison between the number of objective and performance function evaluations reveals that the majority of computational expenses are associated with the performance function evaluations. The number of objective function evaluations increases with n, with no significant difference between the CE-LS and the double-loop algorithm. The differences in the number of performance function evaluations reveal that the CE-LS algorithm can provide significant reductions in computational expenses when compared to the double-loop and the DSRF algorithms.
5.2 Nonlinear RBDO problem
The CE-LS method is applied to an RBDO problem studied in Chen et al. (2014), which features a deterministic objective function with deterministic and reliability constraints. The problem is selected to investigate the performance of the CE-LS algorithm on a classic RBDO problem and the implementation of deterministic and reliability constraints. The RBDO problem is specified with two design parameters t=[t 1,t 2]T, two independent normally distributed random variables, X=[X 1,X 2]T, and three probabilistic constraints, defined by respective performance functions g 1(X), g 2(X), and g 3(X). The RBDO problem is defined as follows:
subject to
where
The RBDO problem in (22a–22i) can be examined graphically in Fig. 5. The reliability constraints in Fig. 5 are constructed based on Monte Carlo estimates of probabilities in (22b) with 107 samples of the random parameters X. The graphical solution (GS) to the RBDO problem is found at t=[3.312,2.886]T with the corresponding objective function value C(t)=6.198. The values of the performance functions and the reliability constraints corresponding to the GS minimum estimate are presented in Table 2.
In addition to the GS, Table 2 contains the estimates obtained with the CE-LS algorithm, the corresponding double-loop algorithm, and a series of RBDO algorithms that apply approximate reliability methods, which include RIA, PMA, SORA and SAP. The results corresponding to the PMA, SORA and SAP methods are obtained from benchmark tests in Aoues and Chateauneuf (2010).
The CE-LS algorithm is applied to search for the minimum value of the objective function with the following parameters; N O =10, N S =102, ρ=0.1, \(\epsilon _{\lim }=0.05\). In order to accelerate the convergence of the CE-LS algorithm to the minimizer at the intersection of two reliability constraints, the injection technique (Botev and Kroese 2004) was applied to Algorithm 2. After initially satisfying the convergence criterion defined by \(\epsilon _{\lim }\), the injection technique increases the variance of the random search distributions to prevent the search process from converging to a sub-optimal solution. In this example, the injection technique is applied once within a search to set the variance of the random search distributions equal to the variance in the second iteration of the CE-LS algorithm.
Since the optimal solution is found on the boundary of reliability constraints corresponding to P F1 and P F2, the CE-LS estimate of the minimizer is calculated by conducting a local search based on the near-optimal design states in the last step of the CE-LS algorithm. To ensure that the CE-LS estimate of the minimizer satisfies the reliability constraints, relatively accurate estimates of the failure probabilities in (22b) are calculated with the LS method for the design states in the last step of the CE-LS algorithm. The estimates of the failure probabilities are calculated with a target \(\text {CoV}_{\lim }=0.1\).
The important directions are selected to point in the direction of the design point. The design points are located numerically for each design state. The reliability constraints in (22b) are enforced in the CE-LS algorithm with the penalty method. The objective function is reformulated as:
where C p >0 is the penalty cost. The value of C p is iteratively increased from 102 in the first iteration step up to 105 at N O =10 to prevent severe violations of the reliability constraint as the CE-LS algorithm proceeds to locate the region of the design space with near-optimal solution.
The performance and stability of the CE-LS algorithm are examined on ten evaluations of the RBDO problem in (22a–22i). The CE-LS results in Table 2 correspond to the average values among the ten runs of the algorithm. The results are presented with the corresponding coefficients of variation, CoV, to examine the variability in the estimates among the ten runs of the algorithm. The CoV values are calculated empirically as a ratio of the standard deviation of an estimate over its average value.
The double-loop algorithm is performed with the same convergence criteria as the CE-LS algorithm. The reliability estimates are calculated with a target \(\text {CoV}_{\lim }=0.05\) for all the reliability problems. The reliability constraints are enforced by the acceptance-rejection algorithm.
The comparison of results in Table 2 reveals that the CE-LS method located the region of the design space with near-optimal solutions, comparable to the results of the alternative approaches. The comparison of the minimum estimates indicates that the CE-LS and the double-loop algorithm provide slightly higher estimates than the GS. This is considered to be primarily a consequence of the low efficiency of global optimization algorithms is approaching local optima (e.g., Beck and de Santana Gomes2012). The minimum estimates provided by RBDO algorithms that employ approximate reliability methods are slightly lower than the GS solution. This is a consequence of the FORM approximation that results in under-estimates of P F1 and violations of the corresponding reliability constraint. These results demonstrate that the CE-LS algorithm is capable of incorporating both the deterministic constraints via the acceptance-rejection method and the reliability constraints via the penalty method.
The comparison of computational expenses in terms of N o and N g shows that CE-LS method can significantly reduce the computational expenses when compared to the corresponding double-loop algorithm. However, the computational expenses of RBDO algorithms with approximate reliability methods are lower as compared to ones of the CE-LS method. These results indicate that the CE-LS method is not expected to perform more efficiently than the existing RBDO algorithms on problems with convex objective functions and where FORM approximations of the reliability estimates do not lead to constraint violations. The CE-LS method is expected to perform efficiently on problems with noisy objective functions and nonlinear reliability problems.
5.3 High-dimensional RO problems
In the following section, a parametric study is conducted on an RO problem to evaluate the effect of the number of design parameters and the number of random variables on the performance of the CE-LS algorithm. The effect of nonlinearity of a reliability problem on the CE-LS algorithm is examined by comparing a linear with a parabolic failure limit. Given that a reliability problem with a linear performance function requires a single line search along a known important direction to be evaluated, the application of the CE-LS algorithm to the RO problem with a linear reliability problem is intended primarily to investigate the effect of the number of design parameters on the performance of the algorithm. The implementation of the reliability problem with a parabolic failure limit serves to investigate the combined effects of the number of design parameters and the number of random variables on the performance of the CE-LS algorithm.
5.3.1 Linear failure limit
The RO problem is defined as follows:
subject to
where
while C(t) is the total cost as a function of a set of design parameters t=[t 1,...,t n ]T, U=[U 1,...,U m ]T is a vector of independent standard, normally distributed random variables with zero-mean and unit standard deviation, C i ,i=1,...,n are the design cost parameters, C F is the cost of failure, \(P_{F}^{\lim }=10^{-4}\) is the failure probability limit. Due to a relatively simple formulation of the RO problem in (24a–24d), the minimizer can be found analytically as shown in Appendix B.
The RO problem in (24a–24d) is studied for a range of n (number of design parameters) and m (number of random variables). The location of the minimizer in (47) is defined by m and the desired reliability index of β min=4 at the minimum. The design cost parameter C i is defined according to (49) in Appendix B by specifying C F =1010. The CE-LS method is implemented with the following parameter values; N O =100, N S =103, ρ=0.1, \(\text {CoV}_{\lim }=0.1\), and \(\epsilon _{\lim }=0.001\) for n=2, while \(\epsilon _{\lim }=0.01\) for n=10 and n=100. Higher values of \(\epsilon _{\lim }\) for n=10 and n=100 are selected due to higher computational costs of the CE-LS algorithm in these cases. In the initial step of the CE-LS algorithm, the design states are generated uniformly within the bounds of the design space. Given the linear performance function, the important direction of the LS method can be determined analytically to be \(\boldsymbol {\alpha }=1/\sqrt {m} \cdot \left \lbrack 1,...,1 \right \rbrack ^{T}\). The reliability constraint in (24b) is implemented with the penalty method by modifying the objective function:
where C p is the penalty cost. The value of C p is iteratively increased from zero at the first iteration of the algorithm to 1010 at N O =100.
The performance of the CE-LS algorithm is examined based on ten evaluations of the RO problem in (24a–24d). The CE-LS results in Table 3 correspond to the average values among the ten runs of the algorithm. The variability in the estimates among the ten runs of the algorithm is examined with the corresponding coefficients of variation, CoV.
The CE-LS estimates are compared to the corresponding analytical solutions for a range of dimensions of the optimization and the reliability problem. The mean value of the normal random search distribution is selected as the estimate of the minimizer. Since the analytical solution specifies that all the design components have the same value at the minimum in (46), the results are compared with respect to the average value of the design components at the minimizer \(\bar {t}_{\min }=1/n {\sum }_{r=1}^{n} t_{\min ,r}\). \(\hat {\bar {t}}_{\min }\) denotes the CE-LS estimate of the minimizer, and \(\bar {t}_{\min }\) denotes that of the analytical solution. The CE-LS estimates and the analytical solution agree well. The examination of CoV values reveals relatively low variation in the estimates of the minimizer, usually below 10 %. The convergence of the minimizer is examined by plotting the mean values of the random search distribution, μ i r ;r=1,...,n, for different iterations steps, i, in Fig. 6 (n=10 and m=2). Figure 6 shows that the mean values converge relatively uniformly to the value of \(\hat {\bar {t}}_{\min }=0.562\).
From the results in Table 3, a good agreement is observed between the CE-LS estimates of the total cost, \(\hat {C}_{\min }\), and the analytical values of the minimum total cost, C min. The variation in \(\hat {C}_{\min }\) is relatively low with CoV’s lower than 5 %. The estimates of the total cost are associated with very low coefficients of variation, \(\hat {\text {CoV}} \left \lbrack \hat {C}_{\min } \right \rbrack \), due to accurate estimates of the probability of failure at the minimizer. Additionally, the estimated value of P F at \(\hat {\textbf {t}}_{\min }\), \(\hat {P}_{F}(\hat {\textbf {t}}_{\min })\), is compared to the analytical solution, P F (t min), to investigate the accuracy of the local average approximation of the probability of failure. The comparison between the CE-LS estimates and the analytical values of P F in Table 3 reveals good agreement. A slightly higher variation in the \(\hat {P}_{F}\) values is expected to be a consequence of the variation in the minimizer values. The computational demands of the CE-LS algorithm can be examined with the number of objective function evaluations, N o , and the number of performance function evaluations, N g . The value of N g corresponds to three performance evaluations per design state for the evaluation of the line search along α. An increase in the computational costs is observed with an increase in the number of design parameters in Table 3 with a variation up to 21 %. Since the values of \(\hat {\text {CoV}} \left \lbrack \hat {C}_{\min } \right \rbrack \) are relatively low, the convergence of the CE-LS algorithm is governed by the value of 𝜖.
5.3.2 Parabolic failure limit
The effects of n and m on the efficiency of the CE-LS algorithm are evaluated by a performance function with a parabolic failure limit for the RO problem in (24a–24d):
where a is a constant.
The performance of the CE-LS algorithm is evaluated for a range of n and m as presented in Tables 4, 5 and 6. The parameters of the random variables and the design cost, C i and C F , are specified in Section 5.3.1, while −5≤t i ≤5;i=1,...,n. The penalty method is implemented to enforce the reliability constraint with the parameters specified in Section 5.3.1. To adapt to the performance function in (26), the important direction of the LS method is selected to point in the direction of the design point, along the axis of the standard normal space corresponding to u 1. The constant of the performance function is selected to be a=1 for m=2 and m=10, and a=0.1 for m=100 in order to obtain the failure probability at the optimum in the range between 10−5 and 10−12.
The results of the CE-LS algorithm are validated numerically with a double-loop algorithm, where the optimization problem is solved with the CE method, while the reliability problem is solved with the LS method. The CE algorithm is applied with the convergence limit \(\epsilon _{\lim }=0.01\). The convergence limit for the LS estimate of the failure probability is specified by \(\text {CoV}\left \lbrack \hat {P}_{F} \right \rbrack \le 0.1\).
Additionally, the performance of the CE-LS method is compared to the RO algorithms that implement approximate reliability methods with the implementation of the RIA algorithm. The RIA algorithm is implemented with the MATLAB TM implementation of the Sequential Quadratic Programming (SQP) optimization algorithm for the minimization of the cost function and the determination of the design point for FORM-based reliability estimates.
The performance and numerical stability of the CE-LS algorithm are examined by evaluating the RO problem ten times. The CE-LS results in Tables 4, 5 and 6 correspond to the average values among the runs of the algorithm. The variability in the estimates is examined with the corresponding CoV values. The CoV values are calculated empirically as a ratio of the standard deviation of an estimate over its average value. The average value among the components of the CE-LS estimate of the minimizer is denoted by \(\hat {\bar {t}}_{\min }\). The comparison of the results in Tables 4, 5 and 6 reveals a good agreement between the estimates of the minimizer with the CE-LS and the double-loop algorithms. A large relative variation (often relatively low in absolute terms) in certain CE-LS estimates of the minimizer can be attributed to the highly nonlinear optimization problem and averages that approach near-zero values. The comparison between the CE-LS and RIA estimates shows a significant disagreement. This is considered to be an outcome of the inadequacy of the FORM approximation of the reliability problem defined by the parabolic performance function in (26). The adequacy of the FORM reliability estimates is examined by comparing them with the corresponding LS reliability estimates in Tables 4, 5 and 6. The comparison of reliability estimates often reveals a difference of several orders of magnitude, which can significantly affect the ability of an RO algorithm implementing approximate reliability estimates in locating the minimizer and satisfying the reliability constraints.
Figure 7 presents the mean values of the random search distribution, μ i r ;r=1,...,n (n=10 and m=2) with the iterations of the CE-LS algorithm, i, to illustrate the convergence of the minimizer. It can be observed that the CE-LS algorithm locates the area in the proximity of the minimizer within eleven iteration steps, but continues to iterate until satisfying the convergence criteria. Figure 8 displays the convergence of the mean values of the random search distribution with the iterations of the the double-loop algorithm (n=10 and m=2). The convergence criteria in (18) is satisfied after ten iterations of the algorithm. The comparison between the results of the CE-LS and the double-loop algorithm for n=10 and m=2 in Table 5 and in Figs. 7 and 8 reveals that both algorithms estimate the minimizer in a similar region of the design space.
The comparison of the CE-LS and the double-loop estimates of the minimal total cost, \(\hat {C}_{\min }\), in Tables 4, 5 and 6 shows a good agreement. The divergence between the RIA and the CE-LS estimates of C min is caused by the inadequacy of the FORM approximation of the reliability problem defined by the performance function in (26). Similar to the estimates of the minimizer, a relatively large relative variation of \(\hat {C}_{\min }\) in certain conditions can be partially attributed to the highly nonlinear optimization problem and averages that approach near-zero values. The values of the coefficient of variation for the CE-LS total cost estimates, \(\text {CoV} \left \lbrack \hat {C}_{\min } \right \rbrack \), in Tables 4, 5 and 6 indicate a relatively accurate approximation of the total cost based on the LWA model of the reliability problem. The accuracy of the LWA model can be also examined by comparing the CE-LS and the corresponding double-loop estimate of P F at the minimizer, \(\hat {P}_{F}(\hat {\textbf {t}}_{\min })\), in Tables 4, 5 and 6. The variation in the values of \(\hat {P}_{F}(\hat {\textbf {t}}_{\min })\) increases as the effect of the risk term on the total cost reduces.
The computational costs of different approaches are examined in terms of the total number of objective function evaluations, N o , and the total number of performance function evaluations, N g . The CE-LS algorithm was executed with a single line search per design state, which required three performance function evaluations. The double-loop algorithm required significantly larger number of line searches per design state to satisfy the target \(\text {CoV}_{\lim }=0.1\), ranging approximately from 3⋅103 for m=2 to 1.1⋅105 for m=10. The computational expenses of the RIA algorithm increase with the dimensionality of the optimization problem in terms of both N o and N g . As the dimensionality of the optimization problem increases, the computational expenses of the RIA algorithm become comparable or surpass the expenses of the CE-LS algorithm.
5.4 RO of a monopile foundation
An RO of a monopile foundation for offshore wind turbines is conducted to examine the performance of the CE-LS algorithm on a design of an engineering structure. The goal of the RO is to guide the selection of the monopile design parameters such that the total cost is minimized, while satisfying safety criteria specified by a reliability constraint. The response of a monopile is simulated by a finite element pile-soil model, and it is subject to uncertainties in lateral load and soil properties.
5.4.1 Numerical pile-soil model
The response of a pile to lateral load is commonly simulated by a finite element model, known as the p-y model (Matlock 1970). The p-y model is based on Winkler’s beam on elastic foundation, where the response of soil is simulated by a series of elastic springs. The p-y formulation extends the Winkler model by incorporating nonlinearities in the soil response. The nonlinearities are modeled by p-y curves, where p is the soil reaction per unit length of a pile, and y is the lateral displacement of a pile. The p-y curves were developed by backcalculating a series of field test on laterally loaded piles in different soil types (e.g., Matlock1970).
The monopile, in this study, is a hollow tube specified by length L P , diameter D, and a constant pile wall thickness w. Basic elements of the monopile model are presented in Fig. 9. The pile material is steel with Young’s modulus of E S =2.1⋅105 MPa, Poisson’s ratio of ν S =0.3, and density ρ S =7850 kg/m 3. The material behavior of the pile is assumed to be linear elastic. On the other hand, the material behavior of soil is nonlinear, defined by the p-y curves for medium stiff clay. The monopile is laterally loaded with a random load, consisting of H and M = H⋅30 m applied at the sea bed level. H is assumed to be distributed according to the Gumbel distribution, H∼f H (μ H ,μ H ⋅CoV(H)), where μ H =2500 kN is the mean and CoV(H)=0.2 is the selected coefficient of variation.
5.4.2 Soil Variability
A parameter of the p-y curves for medium stiff clay, known as the undrained shear strength, s u , is considered as uncertain to account for variability of soil properties. Other parameters of the p-y curves are assumed to be deterministic with the following values; unit weight γ=18.0 kN/m 3, empirical model parameter J=0.25, strain corresponding to one half of the maximum principal stress difference y 50=0.005.
The variability of s u is expected to significantly influence the pile-soil response due to the formulation of the p-y curves for clay, where s u is directly related to the peak value of soil resistance (Matlock 1970). The variability of s u is modeled by means of a one-dimensional random field:
where G is the studied soil domain, d is soil depth or the reference variable {d∈G:0≤d≤L P }, while \(f_{s_{u}}(s_{u})\) is the lognormal marginal pdf of s u (d). The mean function of s u (d) is:
with parameters \(\alpha _{s_{u}}=50\) kPa and \(\beta _{s_{u}}=3\) kPa/m. The covariance structure of the logarithm of the random field is determined by a given coefficient of variation CoV(s u )=0.4, and the Markov correlation function:
where {(d ′,d ″)∈G}, and 𝜃 d is the correlation length of lns u =2 m, as in Fenton and Griffiths (2008).
Realizations of the random field in (27) are generated with the midpoint method (e.g., Sudret and Der Kiureghian2000) by discretizing the domain {d∈G:0≤d≤L P } in P=40 equal intervals, with interval length of d L = L P /P. The derived random variables are denoted with \(\textbf {X}_{s_{u}}\). The intervals are selected to correspond to the discretization of the finite element mesh of the numerical pile-soil model.
5.4.3 Reliability analysis
The ultimate limit state is defined by the monopile steel yield stress, \(\sigma _{\lim }=235\) MPa, being exceeded. A transformation of random variables \(\textbf {X}=\left \lbrack \textbf {X}_{s_{u}},H\right \rbrack ^{T}\) to a set of independent standard normally distributed random variables, U, is applied to implement the LS method. For a given realization of random parameters u and a combination of design parameters t, which are introduced in the following section, the performance function is defined as:
where σ(u,t) is the maximal stress along the monopile for a given u and t.
5.4.4 RO problem
The RO is performed to optimize the monopile total cost, C(t), with respect to the design parameters t=[D,w,L P ]T∈Ω t . The total cost is composed of the design cost, C D (t), and the failure cost, C F . The design cost approximates the cost of production, transportation, and installation of a monopile with an expense of C d =2 €/kg of the monopile weight.The cost of failure is C F =107 €.
The RO is employed to guide the selection of the design parameters such that the total cost is minimized while satisfying certain safety criteria, specified by a limiting failure probability, \(P_{F}^{\lim }=10^{-4}\). The value of \(P_{F}^{\lim }=10^{-4}\) is selected based on the analysis of the consequences associated with failures of offshore wind turbines in Sørensen and Tarp-Johansen (2005). The RO problem is defined as follows:
where
subject to
The CE-LS algorithm is applied to the RO problem in (31a–31d) with the following parameter values; N O =20, N S =500, ρ=0.1, \(\epsilon _{\lim }=0.01\) and \(\text {CoV}_{\lim }=0.1\). Due to a dominant influence of H on the monopile response, the important direction of the LS method is selected to point approximately in the direction of the design point, parallel to the axis assigned to H in the standard normal space. The reliability constraint in (31c) is approximated by a penalty function which modifies the total cost as follows:
where C P >0 is a term penalizing the reliability constraint violation. The value of C P is selected to increase iteratively from C P =0 € at the first iteration up to C P =1020 € at N O =20.
To evaluate the performance and numerical stability of the CE-LS method, the RO problem in (31a–31d) is evaluated ten times with the CE-LS algorithm. The CE-LS results in Table 7 correspond to the average values among the ten runs of the algorithm. The variability in the estimates is examined with the corresponding empirical CoVs. The results in Table 7 indicate that the region of the design space with near-optimal total costs is found in the proximity of the parameter values \(\hat {t}_{\min }=\left \lbrack 5.528,0.051,33.575 \right \rbrack ^{T}\) m with a cost of \(\hat {C}_{\min }=4.616 \cdot 10^{5}\) €. A relatively low variability in the CE-LS estimates with CoV values of ≈1%.
The results of the CE-LS algorithm are validated with a double-loop algorithm, where the optimization problem is solved with the CE method, while the reliability problem is solved with the LS method. Due to the computationally demanding finite element pile-soil model, the CE algorithm is implemented with N S =100 design states per iteration and the same convergence criteria as the optimization component of the CE-LS algorithm. The convergence criteria for the LS estimate of the failure probability is defined by the coefficient of variation \(\text {CoV} \left \lbrack \hat {P}_{F} \right \rbrack =0.1\). The comparison of the results in Table 7 shows similar estimate of the minimum total cost between the two approaches.
Although the double-loop algorithm was implemented with fewer design states per iteration step, N S =100 compared to the CE-LS algorithm with N S =500, the CE-LS algorithm was able to provide reductions in computational efforts. An evaluation of the CE-LS algorithm required on average 27136 simulations of the finite element pile-soil model, while an evaluation the double-loop algorithm required 95145 finite element simulations.
6 Discussion
A coupling between the CE optimization and the LS reliability method for RO of engineering structures is developed in this study. In contrast to the straightforward double-loop coupling of the two methods, the CE-LS coupling relies on an LWA approximation of the probability of failure to avoid repeated evaluations of the reliability problem throughout the optimization process. The LWA approximation of the probability of failure is constructed with the Nadaraya-Watson nonparametric regression model and adaptively refined throughout the optimization process to provide information on the regions of the design space minimizing the objective function. Due to the LWA approximation of the probability of failure, the reliability and the total cost estimates are biased. However, as the algorithm localizes the region of the design space with near-optimal solutions, the extent of averaging is reduced, thus limiting the bias in the reliability and the total cost estimates. It is expected that the bias in the estimates will not affect the performance of the algorithm significantly since the CE-LS algorithm requires information on the relative optimality of samples within the population at each intermediate sampling step, and not highly accurate estimates of the absolute optimality. The updating mechanism of the CE algorithm is based on the identification of the relative difference in the optimality of the samples at each sampling step. This means that although the averaging of the LWA model results in a certain bias in the total cost estimates, the optimization process is not expected to be significantly affected as long as the relative differences in optimality between the samples can be correctly identified.
The CE-LS algorithm was validated on several RO problems including a monopile foundation design for offshore wind turbines. The algorithm demonstrated efficient performance with good agreement between the estimates of the minimizer and the validation results for a range of numbers of design parameters and random variables. Only a slight decrease in the accuracy of the CE-LS estimates of the minimum is observed with increasing number of design parameters. The decrease in the accuracy is likely to be attributed to the reduced convergence of the Nadaraya-Watson model with the increase in the dimensionality of the model (Wasserman 2006). The Nadaraya-Watson model was found to provide satisfying approximation of the reliability problem, with the CE-LS estimates of failure probabilities usually found within one order of magnitude of the validation results for the studied range of dimensions of the optimization and reliability problems.
More advanced local weighted approximation models (e.g., local polynomial regression, penalized regression, splines (Wasserman 2006)) are not considered here. The implementation of such models is expected to further improve the approximation of the probability of failure (e.g., local polynomial regression reduces bias on the boundary), but also increase the computational demands of the CE-LS algorithm. In reliability problems where the important direction is unknown, the approximation of the probability of failure furthermore depends on the selection of the important direction for the LS method. This is a consequence of the convergence rate of the LS method being dependent on the accuracy of the approximation of the important direction (e.g., Koutsourelakis et al. 2004). The approximation of the reliability problem, in situations where the important direction is unknown, might be improved by implementing the Advanced Line Sampling method (De Angelis et al. 2015). The Advanced Line Sampling method provides improved convergence when compared to the LS method by adaptively refining the approximation of the important direction throughout the analysis.
The acceptance-rejection algorithm was applied to enforce deterministic constraints, commonly defined with computationally inexpensive functions. The reliability constraints were modeled by the penalty method, which prevented severe constraint violations and guided the optimization algorithm in locating a region of the design space with near-optimal solutions in problems where the optimum is located on the boundary of reliability constraints. In situations where the optimal solution is found at the constraint boundary, a detailed local search is advised at the final iteration step to locate the minimizer. Otherwise, the mean value of the random search distribution can be selected as the estimate of the minimizer.
7 Conclusion
A coupling between the CE optimization method and the LS reliability method for RO of engineering structures or systems, referred to as CE-LS, is proposed in this study. The CE-LS coupling relies on an LWA approximation of the probability of failure to avoid repeated evaluations of the reliability problem throughout the optimization process, associated with the corresponding double-loop coupling of the methods. The LWA approximation of the probability of failure is refined throughout the optimization process to guide the optimization process to the region of the design space with near-optimal solutions and provide total cost estimates with relatively low bias and variance.
The CE-LS algorithm was validated on several analytical ROs and on a practical RO of a monopile foundation for offshore wind turbines. The algorithm demonstrated efficient performance with accurate estimation of the minimizer for a range of dimensions of the optimization and reliability problems.
Based on the demonstrated performance, it is expected that the CE-LS method has a considerable application potential for ROs of engineering structures. The method performs optimally in ROs with moderately nonlinear reliability problems and medium dimensional (n<100) design parameter spaces.
References
Aoues Y, Chateauneuf A (2010) Benchmark study of numerical methods for reliability-based design optimization. Struct Multidiscip Optim 41(2):277–294
Au S (2005) Reliability-based design sensitivity by efficient simulation. Comput Struct 83(14):1048–1061
Basudhar A, Missoum S, Sanchez AH (2008) Limit state function identification using support vector machines for discontinuous responses and disjoint failure domains. Probab Eng Mech 23(1):1–11
Beck AT, Gomes WJ, Lopez RH, Miguel LF (2015) A comparison between robust and risk-based optimization under uncertainty. Struct Multidiscip Optim 52(3):479–492
Beck AT, de Santana Gomes WJ (2012) A comparison of deterministic, reliability-based and risk-based structural optimization under uncertainty. Probab Eng Mech 28:18–29
Botev Z, Kroese DP (2004) Global likelihood optimization via the cross-entropy method with an application to mixture models. In: Proceedings of the 36th conference on winter simulation. Winter simulation conference, pp 529–535
Botev ZI, Kroese DP, Rubinstein RY, LEcuyer P, et al. (2013) The cross-entropy method for optimization. In: Govindaraju V, Rao CR (eds) Machine learning: theory and applications, vol 31. Elsevier BV, Chennai, pp 35–59
Bucher C, Bourgund U (1990) A fast and efficient response surface approach for structural reliability problems. Struct Saf 7(1):57–66
Chen X, Hasselman TK, Neill DJ, et al. (1997) Reliability based structural design optimization for practical applications. In: Proceedings of the 38th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and materials conference, pp 2724–2732
Chen Z, Qiu H, Gao L, Li X, Li P (2014) A local adaptive sampling method for reliability-based design optimization using kriging model. Struct Multidiscip Optim 49(3):401–416
Cheng G, Xu L, Jiang L (2006) A sequential approximate programming strategy for reliability-based structural optimization. Comput Struct 84(21):1353–1367
Ching J, Hsieh YH (2007) Local estimation of failure probability function and its confidence interval with maximum entropy principle. Probab Eng Mech 22(1):39–49
De Angelis M, Patelli E, Beer M (2015) Advanced line sampling for efficient robust reliability analysis. Struct Saf 52:170–182
De Boer PT, Kroese DP, Mannor S, Rubinstein RY (2005) A tutorial on the cross-entropy method. Ann Oper Res 134(1):19–67
Depina I, Le TMH, Fenton G, Eiksund G (2016) Reliability analysis with metamodel line sampling. Struct Saf 60:1–15
Der Kiureghian A, Zhang Y, Li CC (1994) Inverse reliability problem. J Eng Mech 120(5):1154–1159
Du X, Chen W (2004) Sequential optimization and reliability assessment method for efficient probabilistic design. J Mech Des 126(2):225–233
Dubourg V, Sudret B, Bourinet JM (2011) Reliability-based design optimization using kriging surrogates and subset simulation. Struct Multidiscip Optim 44(5):673–690
Enevoldsen I, Sørensen JD (1994) Reliability-based optimization in structural engineering. Struct Saf 15 (3):169–196
Fenton GA, Griffiths DV (2008) Risk assessment in geotechnical engineering. Wiley
Gomes WJ, Beck AT (2016) The design space root finding method for efficient risk optimization by simulation. Probab Eng Mech 44:99–110
Hohenbichler M, Rackwitz R (1988) Improvement of second-order reliability estimates by importance sampling. J Eng Mech 114(12):2195–2199
Jensen H, Valdebenito M, Schuëller G., Kusanovic D (2009) Reliability-based optimization of stochastic systems using line search. Comput Methods Appl Mech Eng 198(49):3915–3924
Jensen HA (2005) Design and sensitivity analysis of dynamical systems subjected to stochastic loading. Comput Struct 83(14):1062–1075
Jensen HA, Catalan MA (2007) On the effects of non-linear elements in the reliability-based optimal design of stochastic dynamical systems. Int J Non Linear Mech 42(5):802–816
Koutsourelakis P, Pradlwarter H, Schuëller G. (2004) Reliability of structures in high dimensions, part i: algorithms and applications. Probab Eng Mech 19(4):409–417
Kroese DP, Porotsky S, Rubinstein RY (2006) The cross-entropy method for continuous multi-extremal optimization. Methodol Comput Appl Probab 8(3):383–407
Kuschel N, Rackwitz R (1997) Two basic problems in reliability-based structural optimization. Math Meth Oper Res 46(3):309–333
Lee I, Choi K, Zhao L (2011) Sampling-based rbdo using the stochastic sensitivity analysis and dynamic kriging method. Struct Multidiscip Optim 44(3):299–317
Liu PL, Der Kiureghian A (1986) Multivariate distribution models with prescribed marginals and covariances. Probab Eng Mech 1(2):105–112
Matlock H (1970) Correlations for design of laterally loaded piles in soft clay. Offshore Technology in Civil Engineering Hall of Fame Papers from the Early Years:77–94
Nadaraya EA (1964) On estimating regression. Theory of Probability & Its Applications 9(1):141–142
Nikolaidis E, Burdisso R (1988) Reliability based optimization: a safety index approach. Comput Struct 28(6):781–788
Pradlwarter H, Schueller G, Koutsourelakis P, Charmpis D (2007) Application of line sampling simulation method to reliability benchmark problems. Struct Saf 29(3):208–221
Rackwitz R (2000) Optimization-the basis of code-making and reliability verification. Struct Saf 22(1):27–60
Rosenblatt M (1952) Remarks on a multivariate transformation. Ann Math Stat:470–472
Rosenblueth E, Mendoza E (1971) Reliability optimization in isostatic structures. J Eng Mech Div 97 (6):1625–1642
Royset J, Kiureghian AD, Polak E (2001) Reliability-based optimal design of series structural systems. J Eng Mech 127(6):607– 614
Royset J, Polak E (2004) Reliability-based optimal design using sample average approximations. Probab Eng Mech 19(4):331– 343
Royset JO, Der Kiureghian A, Polak E (2006) Optimal design with probabilistic objective and constraints. J Eng Mech 132(1):107–118
de Santana Gomes WJ, Beck AT (2013) Global structural optimization considering expected consequences of failure and using ann surrogates. Comput Struct 126:56–68
Schuëller G, Pradlwarter H, Koutsourelakis P (2004) A critical appraisal of reliability estimation procedures for high dimensions. Probab Eng Mech 19(4):463–474
Sørensen JD, Tarp-Johansen NJ (2005) Reliability-based optimization and optimal reliability level of offshore wind turbines. Int J Offshore Polar Eng 15(02)
Spall JC (2005) Introduction to stochastic search and optimization: estimation, simulation, and control, vol 65. Wiley
Sudret B, Der Kiureghian A (2000) Stochastic finite element methods and reliability: a state-of-the-art report. Department of Civil and Environmental Engineering University of California
Taflanidis A, Beck J (2008) Stochastic subset optimization for optimal reliability problems. Probab Eng Mech 23(2):324– 338
Valdebenito M, Schuëller G (2011) Efficient strategies for reliability-based optimization involving non-linear, dynamical structures. Comput Struct 89(19):1797–1811
Valdebenito MA, Schuëller G. I. (2010) A survey on approaches for reliability-based optimization. Struct Multidiscip Optim 42(5):645–663
Wasserman L (2006) All of nonparametric statistics. Springer Science & Business Media
Watson GS (1964) Smooth regression analysis. Sankhyā: The Indian Journal of Statistics, Series A:359–372
Yang R, Gu L (2004) Experience with approximate reliability-based optimization methods. Struct Multidiscip Optim 26(1-2):152– 159
Acknowledgments
The authors gratefully acknowledge the financial support by the Research Council of Norway and several partners through the research Centres SAMCoT and Klima 2050.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix: A: Nadaraya-Watson kernel estimator
The Nadaraya-Watson kernel estimator (Nadaraya 1964; Watson 1964; Wasserman 2006) is constructed on N pairs of observations (t 1,Y 1),...,(t N ,Y N ), where a response variable Y is related to the covariate t=[t 1,...,t n ]T with the following model:
such that r is the regression function, while σ(t i )κ i is the residual with location dependent variance, σ 2(t i ).
The Nadaraya-Watson kernel estimator of r(t) is defined by:
where w i (t) is a weight:
with kernel function:
K is a function defined to provide higher weights to observations closer to v=0, while H is a nonsingular positive definite bandwith matrix. Often the covariates are scaled so that a one-dimensional kernel with bandwidth, h>0, can be employed:
The variance of the estimator in (34) is (Wasserman 2006):
An estimate of σ 2(t) is evaluated based on a vector of fitted values, \( \hat {\textbf {r}}_{N}=\left \lbrack \hat {r}_{N}(\textbf {t}_{1}),...,\hat {r}_{N}(\textbf {t}_{N}) \right \rbrack ^{T} \), which is calculated as:
where Y=[Y 1,...,Y N ]T is the vector of observed response variables, while W is a N×N ’hat’ or ’smoothing’ matrix with entries W i j = w j (t i ). Starting from the expression in (33), a second regression model is introduced to estimate σ 2(t) (Wasserman 2006):
From (40) it can be observed that an estimate of ln(σ 2(t)) can be obtained by regressing Z i ’s on t i ’s. For example, a non-parametric regression model can be employed to obtain an estimate \(\hat {\nu }(\textbf {t})\) of logσ 2(t). The estimate of the variance then becomes:
A value of h for the kernel function in (37) is commonly selected by minimizing the leave-one-out cross-validation score (e.g., Wasserman2006):
where W i i = w i (t i ) is the ith diagonal element of the smoothing matrix.
Appendix: B: Analytical solution to the linear optimization problem
The RO problem in (24a–24d) can be solved analytically, based on the fact that g(u,t) is a linear combination of independent standard normally distributed random variables. Consequently, this leads to g(u,t) being a normally distributed random variable with mean, μ g , and standard deviation, σ g . The mean and the standard deviation are calculated to be, respectively, \( \mu _{g}=\sum \limits _{i=1}^{n}t_{i}\) and \(\sigma _{g}=\sqrt {m}\). The failure probability is calculated as:
where Φ is the standard normal cumulative density function. With the analytical solution of the reliability problem in (43), the total cost is formulated as:
The minimum of the total cost is located by differentiating the cost function with respect to the design parameters, setting it equal to zero, and solving for the design parameters. The derivative of the cost function with respect to t i is:
where ϕ is the standard normal probability density function. After setting the derivative equal to zero, the following expression is obtained:
Since (46) contains t i on both sides, the ith component of the minimizer is defined by specifying a desired reliability index, β min at the minimizer.
where all the design parameters have the same value at the minimum, t min. From (47) it follows:
In order for (46) to be consistent, the values of the design cost parameters, C i , are defined based on the values of β min, t min, and C F :
An additional requirement for the results in (47) to (49) is that \({\Phi }(-\beta _{\min }) \le P_{F}^{\lim } \). Otherwise, the minimum is found at the reliability constraint.
Rights and permissions
About this article
Cite this article
Depina, I., Papaioannou, I., Straub, D. et al. Coupling the cross-entropy with the line sampling method for risk-based design optimization. Struct Multidisc Optim 55, 1589–1612 (2017). https://doi.org/10.1007/s00158-016-1596-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-016-1596-x