1 Introduction

In engineering applications, many optimization problems face a common challenge: the high cost of evaluating candidate solutions, which may require a significant amount of computational resources, time, experimental equipment, or labor costs. It directly leads to expensive costs in the engineering design process [1]. These problems may lack explicit mathematical expressions and fall into the category of expensive optimization problems. This kind of problem span various domains in engineering. For example, in aerospace engineering, designing the shape of an aircraft requires extensive aerodynamic simulations and structural analyses [2]. In architectural engineering, designing the structure of buildings involves complex finite element analysis and earthquake simulations [3]. In chemical engineering, optimizing the design of chemical reactors requires intricate reaction kinetics simulations and fluid dynamics analyses [4]. In power system scheduling optimization, many power flow simulations and optimization calculations are needed to achieve stable operation and economy for the power grid [5]. These evaluation processes demand significant computational resources and time and may entail expensive experimental equipment and labor costs.

Specifically, expensive optimization problems cover a variety of types, including single/multi-objective expensive optimization problems [6, 7], multimodal expensive optimization problems [8, 9], high-dimensional expensive optimization problems [10, 11], constrained expensive optimization problems [12, 13], dynamic optimization problems [14, 15], etc. Some researchers employ evolutionary algorithms to tackle such problems. Evolutionary algorithms simulate the process of natural selection and genetic mechanisms in biological evolution. Through operations like crossover and mutation among individuals in the population, they iteratively optimize the solutions within the search space. However, since the real evaluation of the objective function is required in each iteration, a considerable amount of computational resources and time are needed to find the optimal solution. Additionally, Bayesian optimization methods are utilized in some related studies. These methods based on Bayesian inference, guide the search process by constructing the posterior distribution of the objective function, aiming to find the optimal solution with as few evaluations as possible. Due to the high computational costs of expensive optimization problems, traditional optimization algorithms consume substantial computational resources and exhibit low efficiency when solving such problems. Therefore, specialized optimization strategies and algorithms are needed to accelerate the solving process and enhance optimization efficiency.

Researchers have recently proposed surrogate-assisted evolutionary algorithms to solve expensive optimization problems [16]. Figure 1 shows the number of relevant research papers in the past two decades, which is counted by Web of Science. The number of papers in this study is approximately increasing year by year. Surrogate models, also known as approximation models, represent a data-driven approximation model. By collecting a large number of actual samples to train the model, surrogate models establish approximate mappings between variables and objective values to replace the original simulation, effectively serving as a model of the model [5]. Many machine learning models can serve as surrogate models, such as Gaussian process model (GP) [17], Kriging model (KRG) [18], radial basis function model (RBF) [19], polynomial regression model (also known as response surface model) (PRS) [20], artificial neural networks (ANNs) [7], support vector machines (SVM) [21], or combinations of multiple surrogate models [22]. Different surrogate models exhibit different advantages in dealing with specific expensive problems [23]. Evolutionary algorithms possess strong global search capabilities and robustness, enabling them to efficiently search for global optimal or near-optimal solutions in complex spaces. They have been widely applied across multiple domains with significant effectiveness. Common evolutionary algorithms include the genetic algorithm (GA) [24], particle swarm optimization algorithm (PSO) [25], differential evolution algorithm (DE) [26], ant colony optimization (ACO) [27], bee colony optimization algorithm (BCO) [28], etc. Their common characteristic is utilizing collective search behavior to solve problems, with the difference in the variations of their population evolution mechanisms.

Fig. 1
figure 1

The number of research papers on surrogate-assisted evolutionary algorithms

Full size image

Based on the different functions of surrogate models, surrogate-assisted evolutionary algorithms can be divided into regression-based algorithms and classification-based algorithms. The fundamental idea of the former is to use surrogate models to predict objective function values in place of expensive real evaluations, thereby reducing computational resource consumption during the optimization process. The basic procedure involves initially constructing a surrogate model to approximate the objective function. Subsequently, the constructed surrogate model is used to evaluate the performance of candidate solutions. Finally, based on the evaluations from the surrogate model, an evolutionary algorithm is employed to optimize until a satisfactory solution is found. Unlike regression-based surrogate models, classification-based surrogate models do not directly predict the objective function values of candidate solutions. Instead, they classify candidate solutions into different categories, such as identifying whether a candidate solution is dominated or non-dominated. This classification model can assist in evaluating the quality of candidate solutions, thereby quickly identifying potential high-quality solutions and reducing the reliance on expensive real objective function evaluations. These algorithms are typically used for complex optimization problems and multi-objective optimization problems. In summary, surrogate-assisted evolutionary algorithms transform the optimization of the original problem into the optimization of the model [29]. This can significantly reduce the number of real evaluations required, enabling the discovery of high-quality solutions within limited computational resources [30]. Such algorithms can accelerate the optimization process and improve optimization efficiency, and they remain a research hotspot in the field of engineering optimization.

Existing studies have shown that approximation errors of surrogate models are inevitable in the case of limited training data, which may mislead evolutionary search. Therefore, it is important to make full use of the limited data to build accurate models in SAEA. Data resources can be roughly divided into direct data and indirect data [31]. The former refers to data collected directly from computer simulations or physical experiments, which consists of decision variables and corresponding objective function values, and can be directly used to train surrogate models to approximate the objective function [32]. The latter are not displayed as concrete values, but they can be used to calculate the value of the objective function, which is then used to train the surrogate model. Typically, the data collected is primarily used to build and update the surrogate model to drive evolutionary operations. In the process of evolution, whether to actively generate new data is the main difference between off-line optimization and online optimization [33]. Online optimization uses a small number of expensive real evaluations and can run simulation programs or physical experiments to generate new data to update surrogate models. No new data is provided in off-line optimization, and only a limited historical data management models is used [34].

The accuracy of the model depends on the quality, quantity and diversity of the sample data. High-quality sample data can provide more accurate model training signals and help the surrogate model to better generalize to new environments. If there is noise, error, or bias in the sample data, the performance of the model may be degraded. Sufficient sample data can provide more information to guide the optimization process of the model. Too little sample data may cause the evolutionary algorithm to lack sufficient information in the optimization process, thus affecting the accuracy of the model [35]. The diverse sample data can help the evolutionary algorithm to better explore the search space and avoid falling into the local optimal solution. To maximize the utilization of sample data, it is necessary to select a reasonable sampling strategy to ensure that the evolutionary algorithm can make full use of the information of the sample data and avoid relying too much or too little on some samples. It is important to pre-process the sample data before using it to ensure that it meets the input requirements of the model and to extract the relevant feature information. Pre-processing includes data cleaning, noise removal, feature extraction, feature selection, and so on. In addition, data enhancement techniques can increase the diversity and quantity of data by transforming, expanding, or synthesizing sample data. It helps to improve the search efficiency of the algorithm and the generalization ability of the model [36]. On the other hand, in the process of algorithm optimization, it is very important to evaluate the performance of the model on the test set. It can help detect overfitting or performance degradation problems of the model early and adjust optimization strategies in time.

The remainder of this paper is organized as follows. Section 2 introduces the relevant knowledge of expensive optimization problems and evolutionary computation methods. Section 3 focuses on the framework of SAEA and representative expensive optimization algorithms. Section 4 discusses methods for model management strategy, analyzes the characteristics of different methods and summarizes relevant literature. Section 5 presents the challenges and future directions of this research, hoping to provide reference for researchers in this field.

2 Background

This section briefly introduces the relevant knowledge of expensive single-objective, expensive multi-objective, expensive constrained optimization problems and evolutionary computation methods.

2.1 Expensive single-objective optimization problems

In single-objective optimization problems, there is only one optimization objective or objective function that needs to be optimized. In the minimization problem, optimization algorithms aim to find solutions that minimize the objective function. Single-objective optimization problems are typically represented in the following form:

$$\begin{aligned} \left\{ \begin{aligned}&\!\min f\left( x \right) ; \\&\!\!\!\!\!\!\quad x_{\text {min}} \le \!\!\!\! \quad x_i\le \!\!\!\! \quad x_{\text {max}}, \end{aligned} \right. \end{aligned}$$
(1)

where x denotes the variables of the optimization problem, also referred to as decision variables or optimization parameters; \(x=\left( x_1,x_2,\ldots ,x_n \right)\) belongs to variable space \(\left[ x_{\text {min}}, x_{\text {max}} \right] \in R^n\); f(x) represents the objective function to be optimized. The objective of single-objective optimization problems is to find a set of values for x such that f(x) achieves the minimum value. Expensive single-objective optimization problems refer to cases where the evaluation of the objective function f(x) is costly.

2.2 Expensive multi-objective optimization problems

Many optimization problems involve more than one, but two or more objectives being optimized, where improving one objective may lead to deterioration in other objectives. These problems are referred to as multi-objective optimization problems. The definition of a multi-objective optimization problem aimed at minimizing objectives is as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\!\min f(x) = [f_1(x), f_2(x), \ldots , f_m(x)]; \\&\!\!\!\!\!\!\quad x_{\text {min}} \le \!\!\!\! \quad x_i\le \!\!\!\! \quad x_{\text {max}}, \end{aligned} \right. \end{aligned}$$
(2)

where \(x=\left( x_1,x_2,\ldots ,x_n \right)\) denotes the n-dimensional decision variables; m represents the number of objectives to be optimized; the objective function f(x) contains m conflicting subobjectives.

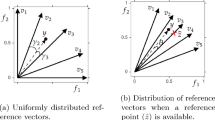
In general, it is not possible to find the optimal value for all targets simultaneously. A common approach for solving multi-objective optimization problems is to identify the set of optimal trade-off solutions among different objectives. While a single-objective optimization problem has a single optimal solution, the solutions of multi-objective optimization problems form a set of balanced points. These points are mutually non-dominated and are referred to as the Pareto optimal set (PS). The mapping of the Pareto optimal set in the objective space is termed the Pareto front (PF). In the case of a two-objective optimization problem, the relationship between PS and PF is illustrated in Fig. 2. The black points in the decision space represent the PS of the multi-objective optimization problem, while the black points in the objective space represent the PF of the problem.

Fig. 2
figure 2

PS and PF diagram of multi-objective optimization problem

Full size image

Definition 1

(Pareto domination) For a minimization multi-objective optimization problem with two solutions \(x_1=\left( x_{\text {11}},x_{\text {12}},\ldots ,x_{\text {1n}} \right)\) and \(x_2=\left( x_{\text {21}},x_{\text {22}},\ldots ,x_{\text {2n}} \right)\), if the objective values of \(x_1\) are less than or equal to those of \(x_2\) in all objectives, and at least one objective value of \(x_1\) is strictly less than that of \(x_2\). The formula is as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\forall i\in \left\{ 1,2,\ldots ,m \right\} ,\,f_i\left( x_1 \right) \leqslant f_i\left( x_2 \right) ; \\&\exists j\in \left\{ 1,2,\ldots ,m \right\} ,f_j\left( x_1 \right) <f_j\left( x_2 \right) . \end{aligned} \right. \end{aligned}$$
(3)

Then \(x_1\) Pareto dominates \(x_2\), denoted as \(x_1\prec x_2\).

Definition 2

(Pareto optimal set) Given a set \(\varGamma \in R^n\), if \(x \in \varGamma\), and there exists no other element \(x^{\prime } \in \varGamma\) in set \(\varGamma\) such that \(x^{\prime } \prec x\) holds, then x is considered the optimal solution with respect to set \(\varGamma\). For a minimization multi-objective optimization problem, if \(x^*\) is an optimal solution in the feasible domain \(\varOmega\), then \(x^*\) is referred to as the Pareto optimal solution of the problem, and PS is the set of Pareto optimal solutions:

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{PS}=\left\{ x^*\in \varOmega |\lnot \exists x\in \varOmega ,x\prec x^* \right\} . \end{aligned} \right. \end{aligned}$$
(4)

Definition 3

(Pareto front) The mapping of Pareto optimal set in the target space is called Pareto front:

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{PF}=\left\{ f\left( x \right) =\left[ f_1\left( x \right) ,f_2\left( x \right) ,\ldots ,f_m\left( x \right) \right] |x\in \textrm{PS} \right\} . \end{aligned} \right. \end{aligned}$$
(5)

Expensive multi-objective optimization problems refer to those where the evaluation of one or more objective functions in f(x) is computationally expensive. In surrogate-assisted multi-objective optimization algorithms, surrogate models often approximate the Pareto front or predict optimal solutions [37]. In surrogate-assisted single-objective optimization algorithms, multiple variables correspond to a single objective value, representing a many-to-one mapping relationship, allowing a single model to perform prediction tasks. However, in surrogate-assisted multi-objective optimization algorithms, where multiple variables correspond to two, three, or even more objectives, representing a many-to-many mapping relationship, a common approach is to construct a separate model for each objective function.

2.3 Expensive constrained optimization problems

In practical applications, some problems need to meet a series of constraints in addition to optimizing the objective function during optimization. These problems belong to the class of constrained optimization problems, which are typically represented in the following form:

$$\begin{aligned} \left\{ \begin{array}{lll} &\min \quad F\left( x \right) ;\\ &\mathrm{s.t.}\quad g_j(x) \leqslant 0, \!\!\!\quad j = 1,2,\ldots ,k; \\ &x_{\text {min}} \le \!\!\!\! \quad x_i\le \!\!\!\! \quad x_{\text {max}} \end{array}\right. \end{aligned}$$
(6)

where x denotes decision variable; F(x) represents the objective function to be optimized; \(g_j(x)\) corresponds to jth constraint.

Expensive constrained optimization problems refer to those where the evaluation of the objective function or the constraint function is expensive. In other words, the evaluation for the objective or constraints are not readily available, and the fitness evaluations rely on time-consuming simulations or expensive physical experiments. Additionally, not all objectives or constraints in expensive constrained optimization problems are costly. Expensive constrained single-objective optimization problems contain one objective and at least one constraint. While expensive constrained multi-objective optimization problems need to optimize multiple objective functions \(F(x) = [f_1(x), f_2(x), \ldots , f_m(x)]\). Expensive constrained optimization problems widely exist in science and engineering field, such as aerospace and automotive design [38], computational electromagnetics [39] and structure design [40]. To solve these problems, it is necessary to design specific optimization algorithms and strategies, and select appropriate methods to find the optimal solution satisfying the constraint conditions within the limited computing resources.

2.4 Evolutionary computation methods

Evolutionary computation methods are a class of optimization and search techniques based on biological evolution, swarm intelligence, and other natural phenomena. It simulates the evolution process in nature. The optimal solution or approximate optimal solution in the solution space is searched through the operation of heredity, variation and selection. The main idea is to start from an initial population and through simulating mechanisms observed in biological evolution, iteratively evolve individuals that better adapt to the environment, thereby gradually optimizing the value of the objective function. In general, the flowchart of evolutionary computation methods can be presented as Fig. 3, which includes initialization, fitness evaluation, solution evolution with evolution operators, and selection. Moreover, the solution evolution and selection will be iteratively performed to generate and select better solutions from the previous generation to the next generation, so as to obtain the optimal or satisfactory solution [41]. Evolutionary computation methods typically possess strong global search capabilities, and can find good solutions in complex solution spaces. Additionally, these methods are suitable for various types of optimization problems, including single-objective, multi-objective, and constrained optimization, demonstrating better generality.

Fig. 3
figure 3

General flowchart of evolutionary computation methods

Full size image

3 Surrogate-assisted evolutionary algorithms

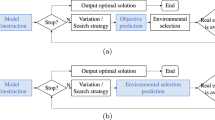
In surrogate-assisted evolutionary algorithms, surrogate models are utilized to replace expensive real evaluations, thereby reducing the number of evaluations of the true objective function, lowering computational costs, and speeding up the optimization process. The evolutionary algorithm is primarily responsible for driving the entire optimization process, providing feedback to the surrogate model, and ultimately obtaining an approximate optimal solution for expensive optimization problems. Figure 4 illustrates the basic flowchart of SAEA. Initially, an initial population is generated, and their objective function values are computed using the real objective function. Then, samples with real evaluations are selected to construct the surrogate model. Subsequently, the evolutionary algorithm updates the population, and the surrogate model is utilized to evaluate the fitness values of offspring individuals. Next, a subset of high-quality individuals is selected as filling samples for real evaluations. This process is repeated until the termination condition is met, and the optimal solution is outputted. The main difference between surrogate-assisted evolutionary algorithms and general evolutionary algorithms lies in evaluating fitness values for offspring individuals: in SAEAs, surrogate models are utilized to replace expensive real evaluations. It dramatically reduces the number of evaluations of the true objective function and the associated resource consumption.

Fig. 4
figure 4

The basic flowchart of SAEAs

Full size image

As shown in Fig. 5, the SAEA framework mainly consists of three parts: surrogate model construction, model management, and evolutionary algorithm. The surrogate model construction module utilizes data science knowledge and machine learning techniques to construct high-quality surrogate models. Firstly, it is necessary to select a surrogate model, and then use existing sample data to train the model to approximate the actual objective function. Additionally, the accuracy and reliability of the surrogate model need to be validated. The model management module is primarily responsible for the information exchange between the surrogate model and the evolutionary algorithm, dynamically managing and utilizing the surrogate model during the iteration process. The evolutionary algorithm module focuses on driving the entire optimization process. These three modules complement each other and are indispensable.

In recent years, researchers have begun to explore combining different optimization algorithms with surrogate model techniques to seek efficient solutions for expensive optimization problems. The following will introduce the surrogate model and the current research status on surrogate-assisted single-objective and multi-objective optimization algorithms.

3.1 Surrogate model

In surrogate-assisted evolutionary algorithms, the number of surrogate models can significantly affect the performance of the algorithm. Depending on the number of surrogate models used, surrogate-assisted evolutionary algorithms can be divided into single surrogate-assisted evolutionary algorithms and multiple surrogate-assisted evolutionary algorithms. These two types of algorithms are introduced in Sects. 3.1.1 and 3.1.2, summarizing related work and analyzing their characteristics.

3.1.1 Single surrogate model

In addressing expensive optimization problems, the single surrogate-assisted evolutionary algorithms use only one surrogate model. According to the functionality of the surrogate model, it can be categorized into global surrogate-assisted evolutionary algorithms and local surrogate-assisted evolutionary algorithms.

Fig. 5
figure 5

The main components of surrogate-assisted evolutionary algorithms

Full size image

Global surrogate-assisted evolutionary algorithms utilize information from the entire search space to construct optimization model commonly employed in the early search stages. They aid in exploring the search space comprehensively, thereby avoiding getting trapped in local optima. In recent years, significant research has been done on global surrogate-assisted evolutionary algorithms. Ratle [42] proposed to use the Kriging interpolation as a function approximation model to replace the real function evaluation. An RBF network was proposed in [43] to assist an evolutionary algorithm for computationally expensive multiobjective problems by prescreening the most promising individuals to be exactly evaluated. Liu et al. [44] proposed a GP surrogate model to assist differential evolution to solve computationally expensive optimization problems. To further address high-dimensional expensive optimization problems, a global surrogate-assisted cooperative differential evolution algorithm was introduced. It exploits promising information in good individuals and potential information hidden in flawed individuals to generate multiple promising mutant solutions. Then, a surrogate is used to determine the most promising subpopulation solutions [12]. Li et al. [11] used a surrogate-assisted multi-group optimization algorithm (SAMSO) to solve high-dimensional expensive problems. This method divides the population into two subgroups, proposes a scheme for dynamically adjusting the group size to control the evolutionary process, and uses a global RBF surrogate model instead of expensive real evaluations. Song et al. [45] proposed a global Kriging model-assisted dual-archive evolutionary algorithm (KTA2) for solving expensive multi-objective optimization problems. Jie et al. [46] proposed a surrogate-assisted multi-objective particle swarm optimization algorithm (KMOPSO). This method adaptively constructs Kriging models for each objective function. Then, it utilizes the non-dominated solutions of the models to guide the particle swarm update. Han et al. [47] introduced a new filling point criterion (EIR2), which combines the Kriging model, optimal Latin hypercube sampling, and particle swarm optimization to develop an algorithm for solving expensive multi-objective optimization problems. Jin et al. [48] adopted a neural network to be a global surrogate model to assist a covariance matrix adaptation evolution strategy and investigated the effectiveness of the individual-based and generation-based model management strategies. Praveen et al. [49] developed a surrogate-assisted particle swarm optimization by employing the radial-basis-function model to construct a global surrogate for prescreening the promising solutions. However, the main drawback of these current global surrogate-assisted methods is that the modeling process becomes very time-consuming when the number of training data is large, or the dimensionality of decision variables is high.

To alleviate the issues above, researchers employ local surrogate-assisted evolutionary algorithms to address expensive optimization problems, which can reduce computational costs. Unlike the global surrogate model, the local surrogate model utilizes only a portion of the search space real data to establish local surrogate model. By accurately modeling the local search space, they can provide more precise predictions of the objective function, better adapting to the problem’s local structure and characteristics, thus enhancing the algorithm’s adaptability and robustness. Ong et al. [38] employed a trust region method in local search to alternate between precise models of the objective function and constrained functions and an inexpensive RBF surrogate model. Martinize and Coello [50] proposed a surrogate-assisted local search algorithm to accelerate the convergence of multi-objective evolutionary algorithms. Chugh et al. [35] constructed a local Kriging model for each objective function, reducing the computation time for solving expensive multi-objective optimization problems by considering the relationship between training samples and reference vectors. Yu et al. [51] established local surrogates around the current best point and used the optimal individuals predicted by the local surrogate model in the local region to accelerate PSO algorithm convergence. Yang et al. [52] pre-screened offspring generated by three different strategies using dimensionality reduction techniques processed by the GP model. Moreover, it comprehensively explores promising regions using a local GP-assisted local search strategy. Wang et al. [53] utilized a RBF-based interior point local search method to assist differential evolution algorithms in solving expensive constraint problems. Sun et al. [54] proposed the fitness estimation strategy (FES) for particle swarm optimization algorithm, which approximates the fitness of particles from their parents, ancestors, and siblings.

3.1.2 Multiple surrogate models

Multiple surrogate-assisted evolutionary algorithms use multiple surrogate models in the optimization process rather than a single model. Multiple surrogate models includes using multiple global surrogate models, multiple local surrogate models, and integrated models comprising global and local surrogate models. Different accuracies and types of surrogate models may lead to different optimization results [55]. Through the competitive selection among multiple models, adverse effects caused by inaccurate models on algorithm convergence performance can be effectively mitigated, thus accelerating algorithm convergence. Parallel computing based on multiple surrogate models not only reduces the time cost of the optimization process, but also enhances the convergence and robustness of the algorithm. In most cases, the performance of multiple surrogate models surpasses that of a single surrogate model, showing promising prospects for solving expensive optimization problems.

Multiple global surrogate models can be constructed using all samples in the variable space. Evolutionary algorithms assisted by global surrogate models first construct different types of surrogate models using the same dataset and then perform surrogate-based optimization separately in the entire variable space. Chaudhuri et al. [56] assisted the NSGA-II algorithm in solving expensive multi-objective optimization problems by constructing multiple SVR models with different parameter configurations, and experimental results showed a significant improvement in algorithm performance. Viana et al. [57] proposed a PSO algorithm based on a hybrid surrogate model of RBF and PRS, effectively enhancing its global approximation accuracy by combining two types of surrogate models. Tang et al. [58] introduced a multi-surrogate model technique based on GP and PRS and a PSO algorithm with multiple sampling strategies based on EI and PoI, performing parallel optimization. Given that Kriging surrogate models can provide uncertain information about candidate solutions, various surrogate models were combined with Kriging surrogate models for batch sampling [22]. Mueller et al. [59] proposed and deeply analyzed a mixed surrogate model based on Dempster–Shafer theory. In engineering applications, Glaz et al. [60] applied surrogate-assisted algorithms to design and optimize helicopter rotor blades, demonstrating that the prediction accuracy and robustness of multiple surrogate models exceeded those of single surrogate models. Zerpa et al. [61] constructed multiple surrogate models into an ensemble model using an adaptive weighting method and applied it to optimize oil extraction processes. Habib et al. [62] proposed a multi-objective evolutionary algorithm called hybrid surrogate model-assisted evolutionary algorithm (HSMEA) to solve computationally expensive problems, effectively approximating the objective function using multiple surrogate models. Espinosa [63] proposed a multi-surrogate assisted multi-objective evolutionary algorithm for feature selection, specially designed to improve generalization error. Yu et al. [64] introduced an adaptive surrogate model selection technique, combining elemental surrogate models into multiple integrated surrogate models and adaptively selecting the most promising model from the model library based on the root mean square error (RMSE). Moreover, they integrated this technique with two evolutionary algorithms to solve antenna structure optimization problems. Li [65] proposed a surrogate-assisted particle swarm optimization algorithm (EAPSO). The algorithm generates multiple trial positions for each particle in the population. To accelerate convergence and avoid erroneous global guidance by the model, both RBF and PRS models are utilized to guide evolution. Husain and Kim [66] utilized Kriging, RSM, and RBF models, while Montano et al. [67] employed RBF models with different basis functions as multiple surrogate models.

Multiple local surrogate models can be constructed using a subset of samples from the variable space. While global surrogate models can approximately reflect the overall trend of response surfaces in the variable space, they may not accurately describe local characteristics. When the population concentrates on exploring local regions, the role of local surrogate models becomes more significant. Therefore, by partitioning the variable space to construct multiple local surrogate models and executing surrogate-assisted evolutionary algorithms in each subspace, the problem of high modeling cost of global surrogate models can be effectively avoided, but also the local search capability of the algorithm can be enhanced [52]. Li et al. [13] proposed an algorithm called multiple penalization and multiple local surrogates (MPMLS) to solve expensive constrained optimization problems. This algorithm defines multiple sub-problems and constructs a local surrogate model for each sub-problem to reduce the overall computational burden of the algorithm. Li et al. [68] proposed a global parallel optimization method based on a spatial decomposition strategy, which constructs multiple surrogate models and implements distributed parallel computation using a multi-point sampling strategy. In [69], a new method utilizing Kriging, RBF, Multi-Layer Perceptron, and RSM is proposed, which adaptively constructs spatially distributed surrogate models based on the accuracy of specific surrogate models in the design neighborhood. Although constructing multiple local surrogate models can improve the local search capability of the algorithm, research on the management strategy of local surrogate models is relatively limited. Blindly executing local search may lead to problems such as waste of computational resources and reduction of optimization efficiency.

Local surrogate models are more likely to provide accurate fitness estimates than global surrogate models. However, the local surrogate model may fail to help the evolutionary algorithm escape local optima, thus losing a significant potential benefit of surrogates [70]. Studies have shown that integrated surrogate models composed of local and global surrogates generally outperform single surrogate models. In most existing surrogate-assisted evolutionary algorithms using multiple surrogate models, the global surrogate model typically aims to smoothen out the local optima, while the local ones aim to capture the local details of the fitness function around the neighborhood of the current individuals [51]. Georgopoulou and Giannakoglou [71] proposed using an RBF network for low-cost pre-evaluation of candidate solutions in global search and gradient-based refinement of promising solutions in local search. In [72], a global surrogate model was proposed for better pre-selection bias, while a local surrogate model was used to approximate fitness in local search. Cai et al. [73] also introduced a surrogate model-assisted differential evolution algorithm (S-JADE), which combines the optimal values predicted by both global and local RBF surrogates with the mutation operator to guide the mutation direction of the differential evolution algorithm. To leverage the advantages of both global and local surrogate models, Tenne and Armfield [74] proposed a meme algorithm framework based on variable global surrogate models and local surrogate models. Zhou et al. [75] proposed a hierarchical surrogate-assisted evolutionary algorithm, employing GP as the global surrogate for pre-screening promising individuals. Moreover, using RBF networks as local surrogate models to assist in trust-region gradient search demonstrates accelerated algorithm convergence. Mueller et al. [76] constructed multiple SVR models with different kernels and then combined them using an adaptive weighting method, with experimental results demonstrating the superior performance of the ensemble model over individual models. Lin and Wu [77] proposed an ensemble surrogate-based framework to address high-dimensional expensive optimization problems. Train global surrogate models across the entire search space to explore global regions and train multiple sub-surrogate models in different search subspaces to exploit sub-regions, thereby enhancing prediction accuracy and reliability. In [78], a decision space partition based surrogate-assisted evolutionary algorithm (DSP-SAEA) is proposed. A two-stage search strategy is introduced, where the global search and the local search are seamlessly integrated. The decision space can be partitioned into several regions based on the clusters. Furthermore, the surrogate model is constructed in each region. Zhai [79] proposed a composite surrogate-assisted evolutionary algorithm for expensive many-objective optimization. The method constructs two types of models: a global model, constructed based on all costly real evaluations, and local models construct using partial samples.

3.2 Surrogate-assisted single-objective algorithms

There are various algorithms for solving expensive single-objective optimization problems. This section introduces some relevant algorithms to summarize the current research status of expensive single-objective optimization algorithms.

For instance, Yang et al. [12] proposed the surrogate-assisted classification-based cooperative differential evolution algorithm (SAC-CDE). This algorithm divides the current population into two subpopulations based on specific feasibility rules and introduces a classification-based cooperative mutation operation. Then, a surrogate model is utilized to identify the most promising subpopulation solutions to accelerate convergence. To address the optimization of expensive antenna structures, Liu et al. [80] developed a parallel surrogate modeling-based differential evolution algorithm. Yu et al. [81] suggested a brand-new model management strategy based on multi-RBF parallel modeling technology. The proposed strategy aims to adaptively select a high-fidelity surrogate from a pre-specified set of RBF modeling techniques during the optimization process. Liu introduces an efficient surrogate-assisted bi-swarm evolutionary algorithm (SABEA) [82]. The evolutionary swarm is randomly partitioned into two sub-swarms, one sub-swarm evolves using the differential evolution (DE) and the other one evolves using teaching–learning-based optimization (TLBO). Yi et al. [83] introduced an online variable-fidelity surrogate-assisted harmony search algorithm with a multi-level screening strategy to solve the optimal design problem of elongated cylindrical gas pressure vessels. Building upon the hierarchical learning swarm optimizer and gradient-boosting decision tree classifier, Wei et al. [84] proposed a classifier-assisted hierarchical learning swarm optimizer to enhance the robustness and scalability of SAEA. Yu et al. [85] introduced an optimal restart strategy for a surrogate-assisted social learning particle swarm optimization (SL-PSO) based on a generated surrogate model. This algorithm periodically restarts within the global RBF model and reinitializes the population using the best sample points from the database at each restart. Additionally, a global search framework is introduced, which adaptively adjusts the classification-based cooperative mutation operation based on iterative information to achieve an effective global search. Li et al. [86] proposed a rapid surrogate-assisted particle swarm optimization algorithm (FSAPSO) to address moderately sized problems with high computational costs by employing a limited number of function evaluations. It selects candidate individuals for expensive real evaluations simultaneously using two pre-screening criteria. To improve the search performance of population, Li and Zhang [87] proposed a three-layer radial basis function SAEA by designing strategies such as global exploration, subregion search and local exploitation. Yu [34] proposed a twofold infill criterion-driven heterogeneous ensemble surrogate-assisted neighborhood field optimization algorithm (HESNFO). The proposed algorithm takes into account both the diversity and accuracy of surrogates to speed up the optimization process. Jia et al. [88] proposed hybrid surrogate modeling (HSM) approach and particle swarm optimization (PSO) algorithm for efficient optimization. In addition, the multi-parameter optimization of electromagnetic acoustic transducer is conducted with the proposed algorithm. Chen developed a surrogate-assisted evolutionary algorithm with hierarchical surrogate technique and adaptive infill strategy (SAEA-HAS) [89]. This algorithm uses a novel hierarchical surrogate technique and proposes an adaptive infill strategy. Gong [90] presented a novel two-stage progressive search approach with unsupervised feature learning and Q-learning (TSLL) to enhance surrogate-assisted evolutionary optimization for medium-scale expensive problems. Chu et al. [91] proposed a surrogate-assisted social learning particle swarm optimization (SASLPSO) to handle expensive optimization problems. An adaptive local surrogate (ALS) strategy introduced in SASLPSO is introduced to accurately fit the landscape near the global optimum.

To address high-dimensional expensive optimization problems, Chu et al. [92] proposed a fuzzy hierarchical surrogate-assisted probabilistic particle swarm optimization algorithm. This algorithm first fits fitness evaluation functions using fuzzy surrogate-assisted models, including local and global surrogate models. Then, it utilizes a probabilistic particle swarm optimization algorithm to predict and update samples based on the trained models. Dong et al. [10] introduced an RBF-assisted wolf optimization algorithm with a strategy of global search and multiple restarts of local search to tackle high-dimensional expensive black-box optimization problems. Gu et al. [93] proposed a surrogate-assisted differential evolution algorithm with adaptive multi-subspace search (SADE-AMSS) to solve large-scale expensive optimization problems. This algorithm constructs multiple subspaces based on principal component analysis and random decision variable selection and employs three search strategies for adaptive search within the constructed subspaces. In [94], a surrogate-assisted differential evolution with fitness-independent parameter adaptation (SADE-FI) is proposed in the paper. The SADE-FI algorithm consists of a global surrogate-assisted prescreening strategy (GSA-PS) and a local surrogate-assisted DE with fitness-independent parameter adaptation (LSA-FIDE). Additionally, researchers employ various multi-population cooperative evolution mechanisms to improve the performance of expensive optimization algorithms during the evolutionary process. For example, Li [11] introduces a surrogate-assisted multi-group optimization algorithm (SAMSO) for high-dimensional computational cost problems. The proposed algorithm divides the population into two subgroups and proposes a scheme for dynamically adjusting population size to control evolution. Sun et al. [95] use a surrogate-assisted particle swarm optimization algorithm and a social learning-based PSO algorithm to search for the global optimum jointly. They share promising solutions that are evaluated by the real fitness function. Tian et al. [96] proposed a new method to solve high-dimensional expensive optimization problems, in which the population will firstly be granulated into two subsets, coarse-grained individuals and fine-grained ones, then different approximation methods are proposed for each category. Ren and Guo [97] proposed a new hierarchical SAEA. This algorithm first randomly projects training samples onto a set of low-dimensional subspaces, then trains a surrogate model in each subspace, and finally achieves evaluations of candidate solutions by averaging the resulting models. The combination of global and local search strategies is also a common approach to deal with high-dimensional expensive problems. For example, Chu et al. [92] used a fuzzy clustering technology to cluster high-dimensional variables, and established a local surrogate model based on the clustering results. Wang [98] proposed an evolutionary sampling-assisted optimization method (ESAO) that combines global exploration and local exploitation capabilities. This kind of method can handle high-dimensional problems well, but its robustness is relatively low because the construction of the global surrogate has a great influence on the selection of the subsequent optimal solution. Although the above algorithms show great performance in solving high-dimensional expensive problems, training and predicting with surrogate models in high-dimensional spaces become more challenging, and the accuracy and efficiency of the models may degrade. It remains a worthwhile research question.

3.3 Surrogate-assisted multi-objective algorithms

In expensive multi-objective optimization algorithms, surrogate models are often used to approximate the Pareto front or predict the Pareto optimal solutions. This section introduces various types of expensive multi-objective optimization algorithms, summarizes the related work, and analyzes their characteristics.

According to different solution approaches of multi-objective optimization algorithms, surrogate-assisted multi-objective optimization algorithms can be classified into three categories: dominance-based, decomposition-based, and indicator-based surrogate-assisted multi-objective optimization algorithms. In the first category, algorithms rank and filter the solution set by comparing the dominance relationships among candidate solutions. The algorithms construct a nondominated solution set based on dominance relationships and select the optimal solution as the final Pareto solution set. Examples include NSGA-II-GP [99], CSEA [7], CPS-MOEA [100], and KMOPSO [46], among others. The second algorithms transform the multi-objective optimization problem into a series of single-objective optimization problems. Examples include K-RVEA [35], ParEGO [101], HSMEA [62], and MOEA/D-EGO [102], GCS-MOE [103], among others. Indicator-based surrogate-assisted multi-objective optimization algorithms evaluate and rank the solution set by introducing a set of evaluation indicators. These indicators can measure the performance of the solution set on different objective functions, such as solution diversity and convergence [104].

In surrogate-assisted multi-objective evolutionary algorithms, surrogate models are utilized to approximate the objective functions and other functions to expedite the evolutionary process. Based on the functionalities of surrogate models, existing SAEAs can be roughly categorized into two different classes. In the first category, one or multiple models can approximate the fitness function. And the fitness function can be a single objective function, an aggregation function of all objective functions, or even a performance indicator. For instance, ParEGO constructs a single Kriging model to approximate the aggregation function at each iteration, where the aggregation function is constructed from randomly selected weight vectors from a set of uniformly distributed weight vectors [101]. In SMS-EGO, individual fitness is defined as the contribution of the individual to the overall HV score, and a Kriging model is built to approximate the HV function [104]. Similarly, the K-RVEA algorithm uses separate models to approximate multiple objective functions, while the MOEA/D-EGO algorithm builds a Kriging model for each objective function of each subproblem [99]. In the second class of surrogate-assisted multi-objective optimization algorithms, surrogate models are used as classifiers to partition candidate solutions into good or bad, dominated or non-dominated solutions [105]. For example, the classification and pareto sorting-based multi-objective evolutionary algorithm (CPS-MOEA) [100] and the decomposition and preselection-based multi-objective evolutionary algorithm (MOEA/DP) [106]. Then, a classification and regression tree method is used to predict the category of newly generated offspring to reduce the number of real function evaluations [107]. Lu et al. [108] proposed a classification and regression-assisted differential evolution algorithm called CRADE. Pan et al. [7] introduced a classifier-assisted evolutionary algorithm (CSEA) for solving multi-objective optimization problems, using a surrogate model to predict the dominant relationship between candidate solutions and reference solutions. Tian proposed a novel surrogate-assisted evolutionary algorithm [109], which employs a surrogate model to conduct pairwise comparisons between candidate solutions, rather than directly predicting fitness values.

In addition, there are a lot of related work for solving expensive multi-objective optimization problems. For example, a two-stage adaptive multi-fidelity surrogate-assisted MOGA (AMFS-MOGA) is developed to relieve computational burden [110]. It shows great potential in solving engineering design problems. Lv et al. [111] proposed a surrogate-assisted PSO with Pareto active learning. At the same time, to enhance the quality of candidate solutions, a hybrid mutation sampling method based on the simulated evolution is used. Li proposed incorporating the surrogate-assisted multi-offspring method and surrogate-based infill points into a multi-objective evolutionary algorithm to solve high-dimensional computationally expensive problems [112]. A hierarchical pre-screening criterion is used to select the surviving offspring and exactly evaluated offspring. Oliveira proposed a framework that uses an inverse modeling approach coupled with an MOEA [113]. The inverse surrogate modeling is used to sample solutions that are combined with the evolutionary search of the MOEA. Shen [114] proposed a decomposition-based local learning strategy to accelerate convergence in the high-dimensional search space. Specifically, an individual is updated by learning from one of the best solutions of its corresponding local area based on the multi-objective decomposition approach. Li et al. [115] proposed an SAEA framework named explanation operator based surrogate-assisted evolutionary algorithm (EXO-SAEA). It divides the current population into two populations according to the a priori knowledge from the surrogate model. Li [116] proposed a novel framework for expensive multi-objective optimization called RM-SAEA, which utilizes a regularity model (RM) operator to generate offspring more effectively. Mazumdar [117] proposed a hybrid multi-objective policy optimization approach for solving multi-objective reinforcement learning (MORL) problems with continuous actions. It combines the faster convergence of multi-objective policy gradient (MOPG) and a surrogate assisted multi-objective evolutionary algorithm (MOEA) to produce a dense set of Pareto optimal policies. Pan [118] proposed a two-phase SAEA (TP-SAEA), which follows the idea of convergence first and diversity second, for solving high-dimensional expensive multi-objective optimization problems. Li [119] proposed an inverse distance weighting (IDW) and RBF-based surrogate assisted evolutionary algorithm (IR-SAEA). In this algorithm, an RBF–IDW model is developed to provide both the predicted objective values and the uncertainty of the predictions. Gu [120] developed a large-scale multi-objective evolutionary algorithm guided by low-dimensional surrogate models of scalarization functions. The proposed algorithm (LDS-AF) reduces the dimension of the original decision space based on principal component analysis. Wu [121] proposed a fast SAEA using sparse GPs for medium-scale expensive multi-objective optimization problems. These algorithms provide great insights for solving expensive multi-objective optimization problems and reduce the management cost of surrogate models, but they still have the following shortcomings. Firstly, how to balance the diversity and convergence of the algorithms remains a topic that needs further research. Secondly, some existing algorithms do not sufficiently exploit the estimated solution quality information from the surrogate models during offspring generation. Moreover, how to apply existing common high-dimensional processing methods to high-dimensional expensive multi-objective problems is still challenging.

4 Model management strategy

Model management is primarily responsible for maintaining the interaction between surrogate models and evolutionary algorithms, managing the constructed surrogate models, and leveraging the available information provided by algorithms to enhance the predictive performance of models. Model management strategy allow adjustments and updates to surrogate models based on feedback information and data provided by the optimization algorithm. Model management strategy mainly involves managing surrogate models during the optimization process based on feedback information and data provided by the algorithm. Depending on whether real fitness evaluations can be performed during the optimization process, surrogate-assisted evolutionary algorithms can be categorized as online SAEA and off-line SAEA [122]. As is shown in Fig. 6, the main difference between them lies in their ability to perform real fitness evaluations on population individuals: online SAEA can perform real fitness evaluations on population individuals, and then model management strategy use the real available information the algorithm provides to help construct more accurate surrogate models. Online SAEA is suitable for scenarios where a small number of fitness evaluations can be obtained from physical experiments or expensive computations during the optimization process, while off-line SAEA is designed for cases where real fitness evaluations are too expensive or difficult to implement. Although there are differences between the two, their main idea is to use surrogate models to reduce the number of real evaluations and save computational resources to accelerate the optimization process.

Fig. 6
figure 6

The framework of the off-line SAEA and online SAEA

Full size image

4.1 Off-line SAEA

Off-line SAEA cannot obtain new data through real fitness evaluations during optimization; it can only use limited historical data to construct surrogate models. This approach is suitable for problems with large datasets where obtaining real data is difficult. There are many real-world off-line optimization problems, such as trauma system design, magnesium furnace performance optimization, and ore processing operation indicators [123].

In off-line surrogate-assisted evolutionary algorithms, the model management strategy heavily relies on the quality and quantity of available data. Since new data cannot be generated, the surrogate model can only be constructed using limited data, posing significant challenges to model management. Therefore, there are currently few studies on off-line SAEA. To alleviate the current challenges, Wang et al. [33] proposed an advanced DDEA-SE algorithm using a selective ensemble surrogate method. This algorithm exhibits excellent optimization efficiency for off-line data-driven optimization problems. The DDEA-SE algorithm constructs many surrogate models by resampling from off-line data. It adaptively selects built surrogate models to approximate fitness functions at different evolutionary stages to reduce prediction errors. To address the issues of insufficient available data and accurate surrogate construction, an algorithm consisting of novel boosting strategies and local data generation strategies has been proposed [124]. The boosting strategy iteratively constructs and combines surrogate models to obtain the optimal model for different problems. The local data generation strategy generates new data within the neighborhood of evaluated data to increase the available data volume, indirectly improving the quality of constructed surrogate models. Building upon this, Li et al. [125] proposed a data perturbation-based ensemble surrogate-assisted evolutionary algorithm framework incorporating multi-faceted surrogate generation and selective ensemble methods. Guo et al. [99] simultaneously constructed low-order PR and GP models using limited small datasets. The low-order PR model serves as the true fitness function to generate new data during the optimization program search process, while the GP model acts as a surrogate to assist in evolutionary search. To address the problem of designing surrogate models using only limited off-line data capable of correctly guiding the search, Yang et al. [126] proposed an off-line data-driven multi-objective evolutionary algorithm based on knowledge transfer between surrogate models.

Since no new data is available during the optimization process, the algorithm can only utilize existing data to build surrogate models for exploring the search space. Studies have found that the quality of data samples used to construct surrogate models significantly affects the performance of the algorithm. Therefore, many data preprocessing methods are used to eliminate the influence of poor-quality data on the models. For instance, in multi-objective blast furnace optimization problems, Chugh et al. [127] employed a local regression approach to reduce noise in the off-line dataset, followed by establishing the Kriging model to enhance the evolutionary algorithm guided by reference vectors. For large and redundant datasets, data mining and related methods can be utilized to reduce redundancy and lengthy computation times. For example, in trauma system design problems, Wang et al. [122] applied clustering methods within multi-objective algorithms to identify valuable data patterns for constructing models, ultimately saving approximately ninety percent of algorithm runtime. In cases where the given dataset is too small to build accurate surrogate models, generating additional data may be a promising solution [31]. For instance, in multi-objective magnesium furnace optimization problems, Guo et al. utilized low-order polynomial models to generate synthetic data and predict their fitness values [99].

The above algorithms proved to be very efficient, but there are still some challenges. One serious challenge is the unavailability of new data during the optimization. Without creating new data for model management during the optimization process, the search ability can be limited since surrogate models are built barely based on the data generated off-line. What’s more, no new data is available to assess the quality of surrogate models, making it very challenging to ensure the reliability.

4.2 Online SAEA

Compared to off-line SAEA, online SAEA can provide more real data for model management, and incremental data can be reused during optimization. In the iterative optimization process of evolutionary algorithms, a portion of generated individuals are subjected to real evaluation and used for updating surrogate models, which helps improve the predictive accuracy of the models. The frequency of generating new data samples and how to use these new data samples also affect model updates, which are also worthy of research attention.

Online SAEA can utilize the data evaluated in real-time for model testing, allowing the model management strategy to select better-performing models for fitness prediction adaptively. Current model management strategy mainly involves generation-based or individual-based selection methods. In online SAEA, generation-based strategies adjust the frequency of sampling new data generation by generation, while individual-based strategies select a subset of individuals for sampling in each iteration [123]. Individual-based strategies are more flexible compared to generation-based individual selection strategies. Surrogate models can help select individuals for real evaluation by using pre-screening criteria, which are crucial for SAEA. Firstly, not all fitness values are equally important during the iterative process, and evaluating only a subset of individuals can save computational resources. Secondly, pre-screening criteria determine which individuals can be calculated through accurate evaluation. It significantly impacts the balance between exploration and exploitation of the algorithm, indirectly affecting the convergence rate of the algorithm. Pre-screening criteria typically fall into three categories: performance-based criteria, uncertainty-based criteria, and a combination of both [30].

In performance-based criteria, individuals with promising prospects are typically selected. Promising samples are usually located near the optimal values of the surrogate model, and sampling promising individuals can enhance the predictive accuracy of the surrogate model in the promising region [48]. Real evaluations of such individuals contribute to improving the reliability of the model [128]. For instance, Regis [129] designed multiple trial positions for each particle and then used an RBF model to select positions with the minimum predicted fitness values. Sun et al. [8] utilized a global and local surrogate-assisted PSO algorithm (SAPSO) to address computationally expensive problems, precisely evaluating particles with predicted fitness values lower than their personal best values. The lower confidence bound (LCB) criterion of GP model was employed to select promising offspring [44]. Tang [58] proposed a surrogate-assisted particle swarm optimization algorithm, where the surrogate model guides particles toward better directions by solving for the global optimum predicted by the model. A comparison between the global optimum predicted by the model and the global best particle is made to select a better leader. Yu et al. [64] introduced an adaptive surrogate model selection technique to adaptively select a promising model from constructed multiple models and perform real evaluations on individuals with predicted values lower than the current global best. Mallipeddi and Lee [130] used surrogate models to generate competitive offspring among trial offspring points. Gong utilized a cost-effective density function model to select the most promising candidate offspring from a set of candidate offspring generated by multiple breeding operators [131]. Cai et al. [73] proposed a surrogate model-assisted Differential Evolution algorithm, selecting individuals with the minimum predicted model values for accurate evaluation. Jie [46] proposed a Kriging metamodel assisted multi-objective particle swarm optimization method. Calculating the generalized expected improvement (GEI) to get a general judgment of the improvement on objective value of each particle. Then, a limited number of particles with highest GEI are selected to perform actual simulation. To reduce expensive evaluations, a prescreening criterion is put forward to choose promising individuals for exact evaluations, which uses nondominated ranks and distance information [132]. In [77], a new infill sampling criterion is designed based on a set of reference vectors to select promising samples for training the models.

Samples with high uncertainty often reside in unexplored regions of the search space. Enhancing the collection of uncertain samples can further assist evolutionary algorithms in exploring unknown regions and effectively improve the diversity of surrogate models. Real evaluations of such individuals are beneficial for discovering potential locations of the best solution [133]. Liu and Wu [134]took the uncertainty as a criterion and proposed a surrogate-assisted evolutionary criterion based on uncertain grouping infill. Many methods for predicting fitness uncertainty have been proposed. The Kriging model can provide confidence levels based on predictions, making them the preferred choice when model management requires uncertain information [35]. In addition to Kriging model, Wang and Guo [135] attempted to use the predicted variance of the surrogate model as a measure of individual uncertainty. The distance from samples to training data is also commonly used to measure uncertainty [136]. Li and Dong [137] selected excellent individuals far from the existing sample points and proposed a distance-based infill strategy. Furthermore, the predicted variance output by ensemble models based on machine learning can also serve as an uncertainty indicator for predicting fitness [138].

To better leverage the strengths of each strategy and balance the exploration and exploitation capabilities of algorithms, a combination strategy based on both performance and uncertainty can be employed. This combined strategy evaluates both promising individuals and uncertain individuals. In the individual-based selection approach, the combination strategy balances promising samples and uncertain samples by adopting multiple selection criteria, which in Bayesian optimization is also referred to as acquisition functions or infill sampling criteria [139], such as expected improvement (EI) [140], probability of improvement (PoI) [141], and lower confidence bound (LCB) [70]. Given the dual advantages of combination strategies, Tian et al. [142] proposed a multi-objective infill criterion-driven GP-assisted social learning PSO for solving high-dimensional expensive optimization problems. The multi-objective infill criterion simultaneously optimizes fitness and minimizes uncertainty. Ding et al. [123] introduced a multi-objective infill criterion that considers predicted fitness and estimated fitness variance as two optimization objectives. This criterion selects the first and last individuals of the Pareto front as new infill samples, which shows significant effectiveness for high-dimensional optimization problems. Li et al. [86] simultaneously consider both promising individual-based selection strategies and uncertainty-based individual selection strategies to balance the exploratory and exploitative performance of the algorithm. A surrogate-assisted particle swarm optimization algorithm is employed to generate multiple trial positions for each particle in the population, and promising positions are selected based on both performance and uncertainty criteria [65]. In [79], optimization is classified into three requirements: convergence, diversity, and uncertainty. The authors consider all three aspects when selecting individual solutions for actual fitness evaluation. Song et al. [45] proposed an adaptive infill criterion that identifies the most important requirement on convergence, diversity, or uncertainty to determine an appropriate sampling strategy for re-evaluations using the expensive objective functions. Song [143] proposed a generic framework with a Pareto-based bi-indicator infill sampling criterion. It calculates their corresponding potential improvement of convergence and diversity. Then, the non-dominated sorting approach is applied to screen the solution in the first front. The screened solutions are evaluated through expensive functions. Zheng et al. [144] proposed a noise-resistant surrogate-assisted multi-objective evolutionary algorithm. It uses a noise-resistant infill sampling criterion considers convergence, diversity, and model uncertainty to select the most potential individual from candidates for re-evaluation.

In online SAEA, the main goals are to enhance the accuracy of the surrogate models and balance the convergence and diversity. Thus, model management is critical. In an ideal scenario, any evolutionary algorithm can be used in online SAEA. However, in reality, the evolutionary algorithms and the surrogates should be integrated seamlessly to ensure the success of the surrogate-assisted optimization algorithms [31]. Therefore, how to choose appropriate evolutionary algorithms and surrogate models is a significant issue to consider. How to select the training data is another challenge. In online SAEA, surrogates need to be continuously updated to enhance their accuracy and to improve the exploration of the evolutionary algorithms as well.

5 Challenges and future research

Many studies have successfully implemented surrogate-assisted evolutionary algorithms to efficiently solve expensive optimization problems. However, we found that research in this area is still not systematic enough, and there are still some problems that need to be solved. Therefore, this section summarizes the existing problems in the above research status and the future research direction from the following aspects. It is hoped that the further extensive and in-depth study of this subject can be inspired.

Selection of sample data: When training a surrogate model, choosing the right sample data is critical to the model’s accuracy and generalization ability. How to select high quality training data is a current challenge. The accuracy of the model depends on the quality, quantity and diversity of the sample data. In online SAEA, the surrogate model needs to be constantly updated to improve its accuracy and the exploration performance of evolutionary algorithms. Therefore, the diversity and convergence of the surrogate model should be considered when selecting training samples. In addition, the size of the sample data also affects the algorithm effect, which is often overlooked in many online optimization algorithms. Using a large number of training samples may increase the complexity of model construction and even cause overfitting. Too little training data will easily lead to underfitting and reduce the prediction accuracy of the model. Therefore, how to select the appropriate scale of training data is also worthy of attention.

Model construction and management: How to choose the right surrogate model is an urgent problem. It is found that different models have different performance in different optimization problems. In many cases, the surrogate model is chosen based on the user’s experience. There are few reports on the theoretical guidance or research literature on the selection of surrogate models. In the face of surrogate models with many types and great performance differences, it is more significant to design a suitable model selection method. The next key problem after determining the models is how to use them in evolutionary algorithms. For instance, using surrogate models to approximate the objective function, classifying individuals based on their fitness, predicting individual ranks [145] or hypervolumes [146], transforming multi-objective optimization problems into single-objective problems to approximate scalar functions [147], and approximating the Pareto front [148] are all issues that researchers must consider and address when designing algorithms. To better manage models, researchers have proposed several popular sampling criteria for selecting candidate solutions. However, these sampling techniques and model management strategies have their advantages and limitations and must be tailored to specific optimization problems and combined with the evolutionary algorithms used.

Selection of evolutionary algorithm: In the surrogate-assisted evolutionary algorithms, it is also crucial to choose the appropriate evolutionary algorithm. However, in the current research, there are not many studies on how to choose evolutionary algorithms [31]. In reality, different evolutionary algorithms have different advantages and limitations and should be used according to the nature of the problem to be solved. For example, using dominance-based evolutionary algorithms for optimization problems with three or more objectives may not be feasible [149]. Although some studies have used transfer learning techniques to build surrogate models between related objectives, research on expensive multi-objective optimization problems with different delays between objective functions still needs to be improved.

In addition, designing appropriate termination criteria and performance metrics is crucial. Especially for expensive optimization problems, if the quality of the solutions does not improve, continuing to run the algorithm may result in resource waste. Metrics such as inverted generational distance (IGD) or hypervolume (HV) contribution are often used as performance indicators for multi-objective algorithms to measure the algorithm’s solving ability. However, the calculation of IGD is influenced by the reference set size, and these metrics may not provide accurate measurement results. As Ishibuchi et al. [150] pointed out, we need to consider not only the impact of parameters on algorithm performance metrics and termination criteria but also the impact of the accuracy and uncertainty of surrogate models on them.