Can a ban on child labour be self-enforcing, and would it be efficient?

Abstract

Existing literature shows that a ban on child labour may be self-enforcing under the extreme assumption that, above the subsistence level, no amount of consumption can compensate parents for the disutility of child labour. The present paper shows that a partial ban may be self-enforcing also in a more general model where education is an alternative to work, and the disutility of child labour can be compensated by higher present consumption or future income, but a total ban may not. It also shows that, in the absence of informational asymmetries, child labour can be eliminated and a first best achieved if the ban is combined with a credit-backed policy including a subsidy to parents, and a tax on skilled adults. A first best is out of reach if the use children make of their time when they are neither at school, nor working in the labour market is private information, because the policy maker then faces an incentive-compatibility constraint. The second-best policy reduces child labour, but not to zero.

1 Introduction

Basu and Van (1998) show that, if the economy admits a multiplicity of equilibria, some with and some without child labour, a ban on the latter may be self-enforcing in the sense that, once an equilibrium without child labour is established, parents have no incentive to depart from it.¹ That is a valuable result, because it implies that a major obstacle to human and economic development can be eradicated without coercion. However, the assumptions under which this result is obtained are rather extreme. One is that there are no opportunities for increasing a child’s future earnings by investing in the child’s education. Another is that, at or above the subsistence level, parents would rather see their children do nothing and consume the subsistence minimum, than work even only a little and consume more than the minimum. The present paper asks four questions. First, under which conditions does the result hold? Second, does the result hold not only under Basu-Van assumptions, but also under the more usual assumption that education is an alternative to work, and that the disutility of child labour can be compensated by the expected utility of future income? Third, if a ban is self-enforcing under these, more usual, assumptions, will it increase or decrease efficiency? The answer is not straightforward, because there are at least three obstacles to an efficient allocation.

Baland and Robinson (2000) demonstrate that education may be inefficiently low, and child labour inefficiently high, because children cannot commit to pay back a loan. As pointed out in Cigno and Rosati (2005), this implies not only that parents will not lend to their children (they can only make them presents), but also that parents cannot borrow on their children’s behalf. As pointed out by Ranjan (2001), only the children of sufficiently rich and generous parents will then receive the efficient amount of education. For his part, Pouliot (2006) demonstrates that child labour could be inefficiently high even if parents were sufficiently rich not to be credit rationed, because education may be a safe investment from society’s point of view (if individual risks are uncorrelated), but it is a risky investment where parents are concerned. Realistically assuming that insurance in general and educational insurance in particular is not available in a developing country, even rich and generous parents will then give their children less than the efficient amount of education (they will give their children conventional assets). From a different angle, Dessy and Pallage (2001) argue that the reason why child labour may be inefficiently high is lack of coordination between parents investing in their children’s education and firms investing in skill-intensive technology. Removing only one or some of these obstacles would not bring education to its efficient level.

The present paper shows that, in the absence of informational asymmetries, the government can remove all three obstacles at once by announcing in advance that it will (i) ban child labour, (ii) borrow from the international credit market, (iii) use the loan to subsidize parents, and (iv) tax skilled workers in order to pay the loan back with interests. The policy achieves a first-best social optimum. If the allocation of the children’s time is private information, however, the government’s choice of policy is subject to an incentive-compatibility constraint that puts a first best out of reach. The outcome is then a second-best social optimum, where children work less than they would without the policy, but still work.

2 The original model

I shall start by outlining the basic model in Basu and Van (1998), with some minimal and uninfluential changes that will make it easier to extend. There is a large number of identical firms demanding labour and an equally large number of identical families supplying it. This allows us to reason in terms of a representative family and a representative firm. Firm owners are neither workers nor parents of potential workers, so their profits do not end up in the workers’ pockets.

Adult labour, denoted by $L_{a}$, and child labour, denoted by $L_{c}$, are perfect substitutes in the production of the numeraire good at the constant rate $\gamma$. We may thus conduct the analysis in terms of a single market for adult-equivalent labour,

$$ L=L_{a}+\gamma L_{c}\text {, }0<\gamma <1\text {,} $$

instead of two interrelated ones. The representative firm maximizes its profit

$$\begin{aligned} P=F\left( L_{a}+\gamma L_{c}\right) -wL_{a}-w_{c}L_{c}, \end{aligned}$$

(1)

where w is the adult wage rate, $w_{c}$ the child wage rate, and F(.) the production function, increasing and strictly concave. From the first-order conditions for an interior solution, we find that

$$\begin{aligned} F^{\prime }(L)=w \end{aligned}$$

(2)

and

$$ w_{c}=\gamma w. $$

A family consists of the parental couple and n school-age children. Each adult is endowed with one unit of time, and each child with $\gamma$ units of adult-equivalent time. There are two critical values of w. One, denoted by $\overline{w}$, is the minimum wage rate that would allow the entire family to survive if the parents worked full time, and the children did not work at all. The other, denoted by $\underline{w}$,² is the minimum wage rate that would allow the entire family to survive if everybody worked full time. Clearly, $2\overline{w}=\left( 2+\gamma n\right) \underline{w}$ is the subsistence level of family consumption. Decisions are taken by parents. Their preferences are such that the family will supply $L=2$ units of adult labour if w is at least equal to $\overline{w}$, or $L=2+\gamma n$ units of adult-equivalent labour if w is less than $\overline{w}$. It is thus implicitly assumed that, at or above $\overline{w}$, no amount of the numeraire good can compensate the parents for even a very small amount of the child labour bad (preferences are lexicographic). If the wage rate falls below $\overline{w}$, child labour ceases to be a bad. Given such preferences, it is not possible to draw indifference curves, and no utility function exists.

Fig. 1

Child labour

Figure 1 illustrates the possible equilibria.³ The (inverse) labour supply function is represented by the broken SS curve. Below $\underline{w}$, there is no labour supply, because there are no workers. The (inverse) demand for labour function is represented by the DD line. The labour market has two possible equilibria, one at point A, where $w>\overline{w}$ and $L=2$, the other at point C, where $\underline{w}<w<$ $\overline{w}$ and $L=2+\gamma n$. If the equilibrium is initially C, and child labour is banned, the only possible equilibrium left is A. At that equilibrium, firms have an interest in offering to employ children at a wage rate lower than $\gamma w^{A}$, but parents would reject such an offer because they abhor child labour. The Basu-Van result thus applies.

Notice however that, if the DD line did not cut the SS line at or above the point where children do not work, a ban on child labour would not be self-enforcing. If it cuts the SS line only at that point, a ban would be pointless. For the result of interest to apply, it must then be true that

$$\begin{aligned} \underline{w}\le F^{\prime }\left( 2+\gamma n\right) <\overline{w}\le F^{\prime }\left( 2\right) . \end{aligned}$$

(3)

Assuming that $F^{\prime }(.)$ satisfies the conditions for the existence of a demand for labour function, (3) implies that this function must be sufficiently elastic for the equilibrium wage rate to jump from below to above $\overline{w}$ as children are banned from the labour market.⁴ If the demand is more than unit-elastic as pictured, family income and thus family consumption decrease as child labour is reduced.

3 An alternative formulation

Let us now consider a more conventional setting, where children have access to education, and education raises a child’s expected future wage rate. For simplicity, I make the common “equivalence-scale” assumption that the children’s consumption is proportional to the parents’. There are two dates, indexed $t=1,2$. At $t=1$, a family consists of the parental couple and n school-age children as in the last section. Here, however, the parents take decisions that affect not only the entire family’s current consumption, but also their children’s future incomes. At $t=2$, the parents will be dead, and their children will be adults. Firms still maximize (1). For comparability, I shall assume that the demand for labour function exists and is more than unit-elastic as in the last section.

At $t=1$, all workers are unskilled. The wage rate, denoted by $w_{1}$, is known with certainty. At $t=2$, an adult’s wage rate, denoted by $w_{2}$, is equal to $w^{S}$ with probability $\pi \left( e\right)$, or $w^{U}<w^{S}$ with probability $1-\pi \left( e\right)$, where e is the amount of adult-equivalent time that the present adult spent in education at date 1, when he or she was a child. This amount is defined to include not only school attendance, but also rest and homework, because the probability of a favourable educational outcome is positively affected by those too.⁵ The function $\pi \left( .\right)$ is increasing and strictly concave. Assuming $\pi \left( 0\right) =0$, so that $w_{2}=w^{U}$ for $e=0$, I shall refer to $w^{U}$ as the unskilled and $w^{S}$ as the skilled wage rate.

An adult is endowed with one unit of time, and a child with $\gamma$ units of adult-equivalent time. At date 1, the parents supply the labour market with 2 units of time. The children supply a nonnegative amount of adult-equivalent time,

$$\begin{aligned} \left( \gamma -e\right) n\ge 0. \end{aligned}$$

(4)

A child’s education has an opportunity-cost $w_{1}e$, proportional to e, and a fixed out-of-pocket cost p, which includes the tuition fee and the cost of the essential didactic material. Given this fixed cost, there may be equilibria where children are not enrolled at school.

Let s denote the amount that the parents save at date 1 for each of their n children. Let r be the interest factor, so that a a child’s future income is

$$\begin{aligned} y=w_{2}+rs. \end{aligned}$$

(5)

Given that the parents will not be around at date 2 to pay back a debt incurred at date 1, and cannot commit their children to do so on their behalf for the already mentioned Baland-Robinson argument, parents cannot borrow

$$\begin{aligned} ns\ge 0. \end{aligned}$$

(6)

Using (5), I represent parental preferences by the expected utility function

$$\begin{aligned} EU=u_{1}\left( c\right) +n\left\{ \pi \left( e\right) u_{2}\left( w^{S}+rs\right) +\left[ 1-\pi \left( e\right) \right] u_{2}\left( w^{U}+rs\right) \right\} , \end{aligned}$$

(7)

where c denotes current consumption. The $u_{t}\left( .\right)$ functions are increasing and strictly concave,⁶ implying risk aversion. I assume that $u_{t}^{\prime }\left( c\right)$ tends to infinity as c approaches the subsistence level. For $e=0$, Eq. (7) reduces to

$$\begin{aligned} U=u_{1}\left( c\right) +nu_{2}\left( w^{U}+rs\right) . \end{aligned}$$

(8)

If $\left( p,r,w_{1},w^{S},w^{U}\right)$ is such that children are enrolled at school, the parents’ choice of $\left( c,e,s\right)$ maximizes (7) subject to the (4) and (6) nonnegativity constraints,⁷ and to the budget constraint

$$\begin{aligned} c+n\left( p+s\right) =w_{1}\left[ 2+n\left( \gamma -e\right) \right] . \end{aligned}$$

(9)

For the Kuhn-Tucker theorem, either (6) is not binding, and the Marginal Rate of Substitution of c for y,

$$\begin{aligned} MRS:=\frac{u_{1}^{\prime }\left( w_{1}\left[ 2+\left( \gamma -e\right) n\right] -\left( p+s\right) n\right) }{\pi \left( e\right) u_{2}^{\prime }\left( w^{S}+rs\right) +\left[ 1-\pi \left( e\right) \right] u_{2}^{\prime }\left( w^{U}+rs\right) }, \end{aligned}$$

(10)

is then equated to r, or it is binding, and MRS is higher than r. Similarly, either (4) is not binding, and the expected Marginal Return to Education,

$$\begin{aligned} MRE:=\frac{\pi ^{\prime }\left( e\right) \left[ u_{2}\left( w^{S}+rs\right) -u_{2}\left( w^{U}+rs\right) \right] }{u_{1}^{\prime }\left( w_{1}\left[ 2+\left( \gamma -e\right) n\right] -\left( p+s\right) n\right) }, \end{aligned}$$

(11)

is then equated to $w_{1}$, or it is binding, and MRE is greater than $w_{1}$. I show in Appendix that MRE is a decreasing function of e and s. Assuming diminishing Absolute Risk Aversion, these effects become larger as c decreases.

Otherwise, if $\left( p,r,w_{1},w^{S},w^{U}\right)$ is such that children are not enrolled at school, the parents’ choice of $\left( c,s\right)$ maximizes (8) subject to (6) and to (9) with $e=p=0$. Once again, either (6) is not binding, and the Marginal Rate of Substitution of c for y, now given by

$$\begin{aligned} MRS:=\frac{u_{1}^{\prime }\left( w_{1}\left( 2+\gamma n\right) -\left( p+s\right) n\right) }{u_{2}^{\prime }\left( w^{U}+rs\right) }, \end{aligned}$$

(12)

is equated to r, or (6) is binding, and MRS is then greater than r.

Fig. 2

Education and child labour

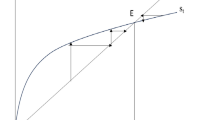
In Fig. 2, the vertical axis measures $w_{1}$ and MRE. The horizontal axis measures L from left to right, and en from right to left. The (inverse) demand for L is still represented by the DD line tracing (2). The MR curve traces the MRE schedule under the assumption that (6) is binding, and s consequently zero. In other words, I assume that the couple are too poor to save and make bequests to their children. As shown in Appendix, if (6) were relaxed, the MR curve would shift upwards. In other words, the marginal return to a child’s education would be higher if this form of investment could be paid for by borrowing against the child’s expected future earnings. The labour market has two possible equilibria. One is at point C, where the wage rate is $w_{1}^{C}$, and children work full time ($L=2+\gamma n$). The other is at point B, where the wage rate is $w_{1}^{B}$, higher than $w_{1}^{C}$, and children divide their time between work and study ($2<L^{B}<2+\gamma n$). Given this equilibrium, a share $\pi \left( e^{B}\right)$ of the date-2 population will earn $w^{S}$, and the rest $w^{U}$. Suppose that the equilibrium is initially at C. The equilibrium can be nudged towards point B, where children work less and study more than at C, by imposing a ceiling on child labour equal to $L^{B}-2$ (or, equivalently, by making education compulsory up to $e^{B}$). Once the new equilibrium is established, there is no further need for a ceiling. A partial ban would thus be self-enforcing. A total ban would not, because A is not an equilibrium.

Dessy and Pallage (2001) demonstrate that, if the ban were announced sufficiently in advance, employers would be led to expect an increase in the share of skilled workers in the date-2 adult workforce and parents to expect an increase in the date-2 skilled wage rate. Firms would consequently invest more in skill-intensive technology,⁸ and families in skill-enhancing education. The coordination problem would then go away. Would A become an equilibrium as a result? Other things being equal, if $w^{S}$ increases relative to $w^{U}$, the numerator of MRE rises. Given, however, that parents are risk-averse, and realistically assuming that insurance in general, and educational insurance in particular, is hard to come by in developing countries, we still have the Pouliot problem that educational investment is inefficiently high. Indeed, if we assume diminishing Absolute Risk Aversion (see Appendix), and the demand for labour function is more than unit-elastic as assumed, the ban will make parents more risk-averse because it will reduce their current income. The denominator of MRE also rises. Given that parents are credit-constrained for the Baland-Robinson argument, the reduction in current family income caused by the ban will in fact translate into lower consumption and thus in higher marginal utility of the same. Indeed, given that $u_{1}^{\prime }\left( c\right)$ tends to infinity as c falls towards its subsistence level, MRE will tend to zero as $w_{1}$ rises towards $\overline{w}$. If children are banned from the labour market, the MR curve may thus shift upwards (the numerator of MRE may rise more than the denominator), but not enough to cut the DD line at or above point A. Consequently, the policy announcement may well solve the Dessy-Pallage coordination problem. As the Baland-Robinson and Pouliot problems are still in place, however, the incentive for parents to invest in their children’s education will be stifled by the rise in the marginal utility of current consumption and aversion to take risks. Simply announcing that a ban will be imposed is not sufficient to make the ban self-enforcing.

Provided that the policy maker has full information about the use children make of their time, the ban will be self-enforcing if it is supplemented by other policy measures. Let $w_{2}=\omega \left( e^{*}\right)$, where $e^{*}$ denotes the equilibrium value of e, and $\omega \left( .\right)$ is an increasing function of e taking value 1 for $e=0$, and value greater than 1 for $e>0$. Let full-time education be efficient in the sense that, at the internationally determined risk-free interest factor, normalized to unity, the expected wage increase is at least as large as the full cost of giving children a full-time education,

$$\begin{aligned} \pi \left( \gamma \right) \left[ \omega \left( \gamma \right) -1\right] \ge p+\gamma F^{\prime }\left( 2\right) . \end{aligned}$$

(13)

Let the government announce in advance that it will borrow from the international credit market the amount

$$\begin{aligned} \sigma =p+\gamma F^{\prime }\left( 2\right) \end{aligned}$$

(14)

per school-age child, use the loan to subsidize parents at the rate $\sigma$ per school-age child at date 1, and levy a tax

$$\begin{aligned} \tau =\omega \left( \gamma \right) -1 \end{aligned}$$

(15)

on every skilled worker at date 2. In light of (13), the tax revenue will then be sufficient for the government to pay its international creditors back with interests. The government can thus do what the parents cannot, namely borrow on the children’s behalf.

The credit-backed policy just outlined removes the Dessy-Pallage problem, because it aligns employers and parents’ expectations. It solves the Baland-Robinson problem, because it relaxes the parents’ credit constraint. It solves also the Pouliot problem, because it fully insures parents against the risk of an educationally unfavourable outcome. In so doing, it takes away the incentive for parents to invest in education, because their children’s after-tax wage rate will then be the same irrespective of education, but that does not matter, because the ban leaves parents with no say over e. Children benefit nonetheless, because they receive a positive s (instead of zero as they would in the absence of policy). With the policy, the marginal return to education is given by

$$\begin{aligned} MRE:=\frac{u_{2}\left( 1+rs\right) }{u_{1}^{\prime }\left( 2w_{1}+\left( \sigma -s\right) n\right) }, \end{aligned}$$

(16)

and it is thus certain. In Fig. 2, (16) is represented by the dashed MR’ curve, higher than MR. The equilibrium is at point $A^{\prime }$, higher than A. I show in the Appendix that, at point $A^{\prime }$, MRE is greater than $w_{1}$, and MRS equal to r. With the policy, the equilibrium is thus efficient. The policy yields a First Best.

4 Asymmetric information

Throughout the developing world, a large part of the work children do is private information, because it occurs in the family farm or family business, or within the home carrying out household chores, rather than in the labour market.⁹ Having defined e to include rest and homework as well as school attendance, education also is private information. Therefore, school attendance is common knowledge, but what happens outside school hours is not. Consequently, the government can ban children from the labour market, or oblige them to attend school,¹⁰, but it cannot prescribe e as it would in the absence of informational asymmetry. The issue is analyzed by Cigno (2012) in a context where the demand for labour is infinitely elastic, and families are heterogeneous. Given that the wage rate does not respond to changes in labour supply, the focus there is on the equity-efficiency tradeoff. Here, the wage rate responds to changes in labour supply, and the focus is on the effects of banning the observable component of the children’s work.

Let d (for “domestic”) denote the amount of adult-equivalent time that a child spends working in the family ambit, so that the amount worked in the labour market is now $\gamma -d-e$. The latter is observable by the government, but the former is not. Let $G\left( nd\right)$ be the income produced by n children, each working d units of time within the family, and $G\left( .\right)$ is another production function, increasing and strictly concave like $F\left( .\right)$. If children are enrolled at school, the parents’ choice of $\left( d,e,s\right)$ maximizes (7) subject to the nonnegativity constraints

$$\begin{aligned} nd\ge 0, \end{aligned}$$

(17)

$$\begin{aligned} \left( \gamma -d-e\right) n\ge 0 \end{aligned}$$

(18)

and (6),¹¹ and to the budget constraint

$$\begin{aligned} c_{1}+\left( p+s\right) n=w_{1}\left[ 2+n\left( \gamma -d-e\right) \right] +G\left( nd\right) . \end{aligned}$$

(19)

If children are not enrolled at school, the parents’ choice of $\left( d,s\right)$ maximizes (8) subject to (18) and (19) with $e=p=0$.

As shown in Appendix, if (6) is not binding, the Marginal Rate of Substitution of c for y, now given by

$$\begin{aligned} MRS:=\frac{u_{1}^{\prime }\left( \left[ 2+\left( \gamma -d-e\right) n\right] w_{1}+G\left( nd\right) -\left( p+s\right) n\right) }{\pi \left( e\right) u_{2}^{\prime }\left( w^{S}+rs\right) +\left[ 1-\pi \left( e\right) \right] u_{2}^{\prime }\left( w^{U}+rs\right) }, \end{aligned}$$

(20)

is again equated to r. Otherwise, it is greater than r. If children are enrolled at school, and (18) is not binding, the expected Marginal Return to Education, now given by

$$\begin{aligned} MRE:=\frac{\pi ^{\prime }\left( e\right) \left[ u_{2}\left( w^{S}+rs\right) -u_{2}\left( w^{U}+rs\right) \right] }{u_{1}^{\prime }\left( w_{1}\left[ 2+n\left( \gamma -d-e\right) \right] +G\left( dn\right) -n\left( p+s\right) \right) }, \end{aligned}$$

(21)

is equated to the higher of $w_{1}$ and $G^{\prime }\left( nd\right)$. Otherwise, it is greater than either of them. I continue to assume that $w^{S}=\omega \left( e^{*}\right)$ and $w^{U}=1$, where $e^{*}$ denotes the equilibrium value of e (exogenous where parents are concerned).

Fig. 3

Education and child labour with asymmetric information

The introduction of a second form of child work multiplies the number of equilibrium types. In Fig. 3, the horizontal axis measures the two forms of work from left to right, and education from right to left. The vertical axis measures the marginal returns to the different uses of time. The MRE schedule is again represented by the MR curve, and $F^{\prime }\left( L\right)$ by the DD line. The $G^{\prime }\left( nd\right)$ schedule is represented by the MP line. In the case illustrated, there are again two possible equilibria. One is at point $B^{\prime }$, where children divide their time between education and work within the family. As only adults work in the labour market, the equilibrium wage rate is $w_{1}^{A}$. The other equilibrium is at point C, where children work full-time in the labour market, and the equilibrium wage rate is $w_{1}^{C}$. If the equilibrium is initially at C, banning children from the labour market would leave $B^{\prime }$ as the only alternative. Paradoxically, asymmetric information may thus make a total ban on labour market work self-enforcing. The paradox is only apparent, however, because child work does not disappear, it only goes underground. The ban reduces child work nonetheless, because it makes $G^{\prime }\left( nd^{B^{\prime }}\right)$, lower than $w_{1}^{A}$, the opportunity cost of e.

Once again, a ban can be usefully complemented by a credit-backed combination of subsidies for parents and taxes on skilled workers. Given that information is asymmetric, however, the government cannot tax and subsidize as much as it otherwise would, because it must satisfy the incentive-compatibility constraint represented by the first-order condition on the parents’ choice of d. Geometrically, the equilibrium is then restricted to be a point on the MP line. I show in the Appendix that, without the policy, $G^{\prime }\left( nd\right)$ could be higher than, equal to, or lower than $w_{1}$. With the policy, $G^{\prime }\left( nd\right)$ can be at most equal to $w_{1}$. Banning children from the labour market, subsidizing current adults, and taxing educationally successful future adults, will then cause the equilibrium point to slide up the MP line, but only as far as point $A^{\prime }$, where $G^{\prime }\left( nd\right)$ is equal to $w_{1}^{A}$. At that point, children work less than at $B^{\prime }$, but they still work, because the subsidy is not large enough to cover the cost of full-time education, and the tax is not large enough to equalize future after-tax wage rates. Therefore, the subsidy relaxes the credit constraint, but not as much as would be necessary to induce full-time education. The tax provides some insurance, but not full insurance. The policy yields a Second Best.

The analysis so far has taken the number of children to be exogenously given as in the original Basu-Van article. If that is not true, a policy that aims to raise e must take into account not only the direct effect, but also the indirect one via n. Given that an increase in the number of children tightens the parents’ budget constraint, if it so happens that a policy aimed at raising e raises also n, the indirect effect will tend to offset the direct one. The net effect will then be smaller than it otherwise would and may even have the wrong sign. Cigno et al. (2003) model policy design as a principal-agent problem, with the government in the role of principal, and parents in that of agents, in an endogenous fertility setting where child labour is not explicitly mentioned. As in the simpler model sketched out in the present section, the second-best policy insures parents and children against the risk of an adverse educational outcome,¹² but does not go as far as it would if all parental actions were observable by the government.

Due to the policy maker’s limited administrative capacity, the policies actually implemented in developing countries fall rather short of Second Best standard. They typically rely on only one instrument at a time when several would be called for. It is thus little wonder if actual policies show disappointingly modest results, or are even counterproductive. Where the effect of a partial or total ban on child labour is concerned, Piza and Souza (2017) find that the 1998 change in the Brazilian constitution, which raised the minimum legal working age from 14 to 16, reduced the labour force participation of boys, but not of girls. Bargain and Boutin (2017) find that the same legislative change had no effect on child labour. Studying the effects of India’s 1986 Child Labour Act, which prohibited work under the age of 14 in some but not all sectors, Bharadwaj et al. (2019) find that child labour participation actually rose and that it rose more in sectors where the prohibition applied than in sectors where the prohibition did not apply. Self-reported school attendance fell.

5 Discussion

The present paper set out to investigate whether the celebrated proposition in Basu and Van (1998), that a ban on child labour may be self-enforcing, holds not only under those authors’ extreme assumptions, but also under the more usual ones that education is available and that the disutility of child labour may be compensated by the utility of present consumption or expected future income. There are at least three reasons why education may be inefficiently low and child labour inefficiently high. The first, pointed out by Baland and Robinson (2000), is that children cannot commit to pay back a loan. As noted by Ranjan (2001), and Cigno and Rosati (2005), this implies not only that parents will not lend to their children (they can only make them presents), but also that parents cannot borrow on their children’s behalf. The second, pointed out by Pouliot (2006), is that education may be a safe investment where society is concerned, but it is a risky one from the parents’ point of view. Without insurance, risk-averse parents would then invest less than the efficient amount even if they were not credit-constrained. The third reason, pointed out by Dessy and Pallage (2001), is that the expected return to education may be inefficiently low because of lack of coordination between firms investing in skill-intensive technology and parents investing in skill-enhancing education. Parents may not invest enough in education because the expected return is low. Firms may not invest enough in technology because the expected number of skilled workers is small.

I have shown that, depending on the properties of the demand for labour function, a partial ban may be self-enforcing even under conventional assumptions, but a total ban may not. In the absence of informational asymmetries, if full-time education is efficient, child labour can be eliminated by the government announcing in advance that it will borrow from the international credit market, use the loan to subsidize parents, and tax future skilled workers to pay back the international creditors. This policy solves at once the Baland-Robinson, the Pouliot, and the Dessy-Pallage problems, because it relaxes the credit constraint, fully insures families against the risk of an unfavourable educational outcome, and aligns the expectations of the firms with those of the parents.¹³ The resulting equilibrium is a first best. Could the same result be obtained if parents did not die when their children become adults as assumed in the present paper, and a family rule obliged the latter to support the former in old age? Not quite. Cigno (1993, 2006) demonstrates that such a rule is self-enforcing and renegotiation-proof under rather weak conditions.¹⁴ If it is, it gets around the problem that parents cannot lend to their children, but not the one that parents cannot borrow on their children’s behalf, because any credits parents might acquire towards their children by fulfilling their family obligations cannot be legally passed on to a third party. The government does not face this restriction, because it can claw back any subsidy it gives parents by taxing their children’s future wages. It can thus do what parents cannot, namely borrow on the children’s behalf.¹⁵

In reality, however, information is asymmetric. The work that children do in the labour market is observable by the government, but the work they do in the family farm or family business, and performing household chores, is not. Similarly, school attendance is observable by the government, but a child’s educational results depend also on time spent resting and carrying out school assignments outside school hours, which is private information. Therefore, the government can ban children from the labour market and oblige them to attend school, but it cannot stop them working within the family ambit or oblige them to leave enough time for rest and homework. Consequently, a ban on children’s work may be only apparently self-enforcing, and education only apparently compulsory. It may still reduce the total amount of work a child does, however, because the opportunity cost of education is then the marginal product of the unobservable component of the child’s work, which in equilibrium cannot be higher and may be lower than the wage rate. Therefore, a ban can still play a useful role, but the government cannot tax and subsidize as much as it would without the informational asymmetry, because it must satisfy an incentive-compatibility constraint. The policy will consequently raise education and reduce child labour, but not to the efficient level. The resulting equilibrium is a second best.

Epstein and Kahana (2008) examine another possible remedy for high child labour and low education, namely emigration and migrants’ remittances. The effects are similar to those of the credit-backed policy examined in the present paper. As the authors themselves point out, however, not enough adults may emigrate, and their remittances may not be large enough, for the education of the children back home to reach the efficient level. To this, it may be added that the cost of emigration is not negligible as Epstein and Kahana implicitly assume, because the destination countries are increasingly reluctant to take in more migrants. This prompts the consideration that unwanted immigration may be prevented or reduced more humanely and possibly at a lower cost to the destination country, if instead of causing people to drown or freeze to death trying to get in illegally, and locking them up or repatriating them if they succeed in getting in, the destination countries subsidized the countries of origin that committed to carry out the policy outlined in the present paper. That would make unnecessary for the countries of origin to borrow from the international credit market in order to carry out the policy.