Household Self-Employment Eliminates Child Labour

Abstract

This paper shows that if a minimal proportion of poor households is empowered with self-employment opportunities, child labour will not arise in equilibrium. The economy will have a unique ‘good’ equilibrium generating a sufficiently high wage to support full child schooling.

1 Introduction

In a seminal paper, Basu and Van (1998) (henceforth BV) offered an explanation of child labour, in which a downward sloping household labour supply curve intersects a standard labour demand curve several times generating multiple equilibria. One of these is low-wage equilibrium where children will have to work along with their parents to meet the family’s subsistence consumption. Despite several other explanations, such as negative externality (Baland and Robinson 2000), parental selfishness and external bargaining (Gupta 2000) and credit constraints (Ranjan 2001; Jafarey and Lahiri 2002), the BV model has remained an inspiration for empirical investigations in this literature [see for instance, Bhalotra and Heady (2003) and Basu et al. (2010)].

An implicit assumption crucial to the multiple equilibria of BV is that there is no lower bound on the parent’s income. Certain policies work by putting such lower bounds, such as minimum wage legislation (Basu 2000) or a ban on child labour (Basu and Van 1998). However, it is well known that enforcement of a ban or minimum wage is not easy and they might cause unemployment (Basu 2000).

In this paper, we study intervention in the form of providing self-employment opportunities. The intervention is self-enforcing and easy to implement, but surprisingly it has not received sufficient attention in the child labour literature. We show that if only a fraction of the poor households are endowed with such opportunity, the child labour equilibrium will be eliminated.

The idea is that self-employment puts a natural lower bound on income allowing parents to switch to self-employment at low wages and protect their children’s education. Their withdrawal from wage employment moves the labour supply curve inward creating excess demand (at low wages) and in turn eliminating the child labour equilibrium. The fraction of the households switching to self-employment should be just enough to cause the necessary displacement of the labour supply curve, crucial for this outcome.

This insight adds a twist to the recommendation of the microfinance literature for the extensive spread of self-employment (Morduch 1999). We argue that it suffices to help only a critical proportion of the households be self-employed, as the labour market will then correct itself.

The literature on child labour is largely concentrated on wage workers or farming households [see Bhalotra and Heady (2003) and Basu et al. (2010)]. There is also significant interest in the effect of economic liberalization or trade reform on child labour (Swaminathan 1998). However, the evidence of parental occupations on the child’s likelihood of being out of school is somewhat limited. From a socio-economic point of view, self-employed households running small shops or informal businesses are considered to be better off than the wage worker households. This is so because self-employment provides a minimum assured income, which also justifies microfinance. If so, then the possibility of multiple equilibria in the labour market as argued by Basu and Van (1998) diminishes. This paper investigates this possibility.

Having said that, there is also an issue that the self-employed households may have a perverse incentive to employ their own children, cutting short their education. This particular aspect is being explored in Pal and Saha (2019), where they find that if own children could be employed, then they will be used more when the market wage rises (as a substitute for the market labour), and less when the market wage falls. In equilibrium, the child labour patterns would be different between the wage worker households and self-employed households. The existing literature has not studied how self-employment affects child labour. This paper looks at one of the two above-mentioned implications of self-employment. In their preliminary empirical analysis, Pal and Saha (2019) do find statistically significant and positive relationship between parental self-employment status and child’s work hours. This is similar to the findings on the child labour impact of microfinance, such as Hazarika and Sarangi (2008) for rural Malawi and Islam and Choe (2013) for rural Bangladesh. But we need to be aware that these results vary across countries; for example, Karlan and Zinman (2009) found the opposite relationship in Manila.¹ Clearly, the theoretical connections between parental self-employment and child labour are intriguing, and there is a need for more empirical investigations.

The rest of the paper is organized as follows. Section 2 presents the main model and the results, followed by some concluding remarks in Sect. 3.

2 The Model

We consider the same set-up as in BV with N households, each of which consists of one parent and one child, each having 1 unit of labour to supply. One unit of child labour is equivalent to $\gamma (<1)$ unit of adult labour.² Households are identical except in one respect: $\alpha$ proportion of them have self-employment (SE) opportunity, and $(1-\alpha )$ proportion is entirely dependent on wage employment (WE). In both households, the child’s time is divided between outside work e and schooling $(1-e)$. The child wage is denoted as $\omega$. The WE parents inelastically supply their labour to earn w each. The SE parents, on the other hand, split their time between wage employment (l) and self-employment ($1-l$). The income from self-employment is given by R(x) with $R'(x)>0$ and $R''(x)<0$, where $x=1-l$. Thus, the total income of an SE parent is $y(w)=wl+ R(x) = wl +R(1-l)$.

An important assumption is that the self-employed parents do not engage any other labour input either from home or outside. If other labour inputs were permitted, they could use their own children, and the model would have different implications. This case is being studied in Pal and Saha (2019).³

A set of competitive firms employ both child and adult labour as substitutes (the substitution axiom of BV) and their aggregate labour demand (expressed in adult unit) is given by $L^D=L^D(w, \omega )$ which is declining in both $(w,\omega )$. For both types of labour to be used, the relation $\omega = \gamma w$ must hold (the ridge-line equilibrium condition of BV).

Parents must meet a subsistence consumption $\underline{c}$ before they value education (the luxury axiom of BV). Thus, for both groups the objective function is same:

$$\begin{aligned} U= & {} (c- \underline{c})(1-e)\,\,\,\,\, {\text {if}} \,\,\, c \ge s \\= & {} (c-\underline{c}) \,\,\,\,\,\,\,\,\,\, {\text {if}} \,\,\, c < \underline{c}, \nonumber \end{aligned}$$

(1)

where c is parent’s consumption, and $\beta c$ is child’s consumption ( $\beta <1$).

The budget constraint for the WE and the SE parents, respectively, is

$$\begin{aligned} w+ e \gamma w\ge & {} c(1+\beta ), \end{aligned}$$

(2)

$$\begin{aligned} wl+ R(1-l)+ e \gamma w\ge & {} c(1+\beta ). \end{aligned}$$

(3)

Parents maximize (1) with respect to (e, c) or (e, c, l) (depending on being WE or SE) subject to their respective constraint (2) or (3).

The wage-employed household. A typical WE household’s optimal child labour supply is given by

$$\begin{aligned} e_{W}= & {} 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, {\text {for}}\,\,\,\,\ w > \frac{\sigma }{1- \gamma }, \nonumber \\= & {} \frac{1}{2} + \frac{\sigma -w}{2 \gamma w},\,\,\,\,\,\,\,\,\,\,\, {\text {for}}\,\,\,\,\ w \in [ \frac{\sigma }{1+ \gamma }, \frac{\sigma }{1- \gamma }],\\= & {} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, {\text {for}}\,\,\,\,\ w < \frac{ \sigma }{1+ \gamma }, \nonumber \end{aligned}$$

(4)

where $\sigma =\underline{c}(1+ \beta )$. If the adult wage exceeds (falls below) a high (low) wage level, child studies (works) full-time. At moderate wages, he works part-time, and it is easy to check that $e_{W}'(w)<0$. The household’s combined labour supply (in adult unit) is $z_{W} = 1+ \gamma e_{W}(w)$, which is also downward sloping at all $w \in (\frac{\sigma }{1+ \gamma }, \frac{\sigma }{1-\gamma })$.

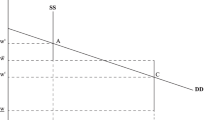
Now consider a special case, where all households are wage-employed. The economy’s aggregate labour supply curve (expressed in adult labour unit) is $L^S(w) = N[1+ \gamma e_{W}(w)]$. Suppose $L^D(w)$ ($\equiv L(w, \gamma w)$) intersects $L^S(w)$ at three places as shown in Fig. 1. Two stable equilibria⁴ occur at points G and B called ‘good’ and ‘bad’ equilibria, respectively. At G, the wage is high and no child works. At B, the wage is low and no child goes to school; they work instead. This is the BV model. Note that for both equilibria to coexist, labour supply must exceed labour demand between $w_U$ and $w_B$.

Fig. 1

Multiple equilibria

The self-employed household. We show that with a self-employment option, the excess labour supply between $w_U$ and $w_B$ can be eliminated. Consider an SE household’s labour supply decision $(l, e_S)$, given by (5)–(6):

$$\begin{aligned} - R'(1-l) + w= & {} 0, \end{aligned}$$

(5)

$$\begin{aligned} \sigma + \gamma w - y(l(w),\, w) - 2 \gamma w e= & {} 0. \end{aligned}$$

(6)

The adult labour supply for wage employment l(w) given by (5) is increasing in w (i.e. $l'(w) = -\frac{1}{ R''(.)}>0$), and for simplification assume $R'(1)=0$ allowing us to set $l(0)=0$.

We can now write $y(l(w), w) \equiv y(w) = wl(w) + R(1-l(w))$. By differentiating y(.) with respect to w, we obtain

$$\begin{aligned} y'(w) =&[\underbrace{l + wl'(w)}] - \underbrace{R'(1-l) l'(w)}\\&\qquad \,>0 \qquad \qquad >0\\ \end{aligned}$$

As both terms are positive, as such the sign of $y'(w)$ is ambiguous. However, intuitive reasoning would help us conclude that y(w) would be monotonically increasing as demonstrated in Fig. 2, or at least be flat at R(1).

Fig. 2

Shape of y(w)

To understand why y(w) would be non-decreasing, we first note that l(w) maximizes the parent’s total income $y(l(w), \,w) = wl+R(1-l(w))$ with respect to l. Hence, his total income must be at least w or R(1) because he can work full-time either outside or at self-employment and guarantee himself of w or R(1), whichever is maximum. So given any w, say $w_0$, if he finds splitting his time between self-employment (say, $1-l$ unit of time) and outside (l unit of time) a better option than being fully self-employed or being fully wage-employed, it must be that $y(l(w_0), w_0) > \max [R(1), w_0]$.

Now, starting from $w_0$ if w rises further, the parent can at least maintain the same allocation of time and earn more from wage employment. If indeed l(w) is continuous and strictly increasing, then extra earning from wage employment will more than compensate for the loss in self-employment. Therefore, y(w) must be increasing or will be just a flat line R(1) at all w. In Fig. 2, we demonstrate the increasing case.

Observation 1

(i) The self-employed parent’s income will have the following lower bound: $y(l(w),w) \ge \max [ w, \, R(1)]$. (ii) The self-employed parent’s total income must be either increasing in w or at least be non-decreasing in w.

A second implication of the self-employment option is that if R(1)—the minimum he can earn under any circumstances—is large enough to support the subsistence consumption $\sigma$, the child will not have to be sent to work. Of course, self-employment technology needs to be sufficiently productive. To consider a non-trivial case, assume $\sigma > R(1)$ so that providing schooling still depends on the equilibrium wage.

Now, consider Eq. (6). There are two critical wages. Set $e=0$ and let $\bar{w}$ implicitly solve $\sigma + \gamma w - y(w)=0$. At any wage above $\bar{w}$, child labour supply is zero. If the parent’s total income covers the subsistence consumption and the foregone child income ($\gamma w$), the child is kept at school full-time. On the other hand, if $e=1$ and $\underline{w}$ implicitly solves $\sigma - \gamma w -y(w)=0$, then we can say that at all wage below $\underline{w}$, the child will work full-time. Here, the combined income of the child and the parent hardly covers the subsistence consumption. More formally, the child labour supply of an SE household is

$$\begin{aligned} e_S= & {} 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, {\text {for}}\,\,\,\,\ w > \bar{w} \nonumber \\= & {} \frac{1}{2} + \frac{\sigma -y(l(w), \, w)}{2 \gamma w} \,\,\,\,\,\,\,\,\,\,\, {\text {for}} \,\,\,\,\ w \in [\underline{w}, \bar{w}]\\= & {} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, {\text {for}}\,\,\,\,\ w < \underline{w}. \nonumber \end{aligned}$$

(7)

Child labour is non-increasing in w. In particular at $w \in [\underline{w}, \bar{w}]$,

$$\begin{aligned} \frac{\partial e_S}{\partial w} = \frac{1}{2 \gamma w^2}\left[ - \frac{\partial y(.)}{\partial l} l'(w) w - \{ \sigma - R(1-l) \} \right] = - \frac{\sigma - R(1)}{2 \gamma w^2}<0. \end{aligned}$$

(8)

This is due to our assumption that $\sigma > R(1)$ and the fact that y(.) is maximized by l. The combined labour supply curve of the SE household is $z_S =l(w)+\gamma e_S$. At $w \in [\underline{w}, \, \bar{w}]$, $z_S'(w) = l'(w) + e_S'(w)$ which is ambiguous in sign. But at $w > \bar{w}$ and $w< \underline{w}$, clearly $z_S'(w) = l'(w)>0$. Then at all w that are close to, but still less than, $\bar{w}$ the curve must bend backward to turn upward sloping again. Figure 3a shows the household supply curve being backward bending. Figure 3b shows that if all households were SE, then we can have a unique market equilibrium where the adult wage is sufficiently high to support full child schooling.

Fig. 3

Equilibrium with only self-employed parents

For Fig. 3b to be valid, we must have that the SE households supply less labour than the WE households. The following observation confirms this.

Observation 2

(i) An SE child switches to full schooling earlier and drops out of school later than a WE child. (ii ) The total labour supply of an SE household is less, or no greater, than that of a WE household.

Part (i) of the above observation requires proving that $\bar{w}< \frac{\sigma }{1-\gamma }$ and $\underline{w} < \frac{\sigma }{1+\gamma }$ [refer to Eq. (4)]. To see this let us consider Eq. (7). At $w=\bar{w}$, we have $\sigma + \gamma \bar{w} - y(\bar{w})=0$, or $\sigma + \gamma \bar{w} + \bar{w} - \bar{w} - y(\bar{w})=0$, which yields

$$\begin{aligned}&\sigma - [y(\bar{w}) - \bar{w}] = \bar{w} (1- \gamma ),\\ \text{ or }&\bar{w} = \frac{\sigma - [y(\bar{w}) - \bar{w}]}{1- \gamma } \,\,\, \le \, \frac{\sigma }{1- \gamma }. \end{aligned}$$

This is because y(w) must be no less than w or R(1) whichever is maximum. Similarly, consider $\underline{w}$ at which we have $\sigma - \gamma \underline{w} - y(\underline{w})=0$, obtain

$$\begin{aligned}&\sigma - [y(\underline{w}) - \underline{w}] = \underline{w} (1+ \gamma ),\\ \text{ or }&\underline{w} = \frac{\sigma - [y(\underline{w}) - \underline{w}]}{1 + \gamma } \,\,\, \le \, \frac{\sigma }{1+\gamma }. \end{aligned}$$

For part (ii) of the observation, compare Eq. (4) with Eq. (7) for $w \in [ \frac{\sigma }{1+\gamma }, \, \bar{w}]$. Since $w \le y(w)$, we have $e_W \ge e_S$. The SE parent’s labour supply is $l(w) \le 1$. Hence, the SE household’s labour supply never exceeds that of the WE household. In particular, $z_S < z_W$ at $w \le \frac{\sigma }{1- \gamma }$.

Elimination of the bad equilibrium. Now, consider the aggregate labour supply with mixed households: $L^S(w; \alpha ) = N [\alpha z_S(w) + (1- \alpha ) z_W(w)]$. In Fig. 1, we have $\alpha =0$, and by construction, there are three equilibria; in Fig. 2b, we have $\alpha =1$, and by construction, there is only one equilibrium. Then for $L^S(w; \alpha )$, we may have one or three equilibria depending on the magnitude of $\alpha$. $L^S(.)$ is a declining function of $\alpha$.

Let us consider all $w \in [0, \frac{\sigma }{1- \gamma }]$ and define an excess labour demand function $\phi (w; \alpha )= L^D(w) - L^S(w; \alpha )$. By construction, for $\alpha =0$ there exists an interval of w such that $\phi (w)<0$ over the entire interval, and for $\alpha =1$ at all w ($\le \frac{\sigma }{1- \gamma })$, $\phi (w)>0$. Since $\phi (.)$ is a continuous and increasing function of $\alpha$, by the intermediate value theorem there must exist a critical $\alpha$, say $\hat{\alpha }$, such that $\phi (w; \hat{\alpha }) = 0$ at some w and strictly positive at all other $w \le \frac{\sigma }{1- \gamma }$ .

Figure 4 shows this critical $\alpha$ at which the labour supply curve swings back sufficiently to be just tangent to the labour demand curve at some wage between $w_U$ and $w_B$ where previously there was an excess supply. The result is that there is only one equilibrium which not only supports full schooling for all children but also improves the equilibrium wage to $w^*$, as the new equilibrium point $G'$ is to the north-west of the old equilibrium point G.

Proposition 1

If the self-employment opportunity R(.) is made available to the $\hat{\alpha }$ fraction (or more) households, then the economy will have only the good equilibrium with child labour eliminated.

Fig. 4

Elimination of the bad equilibrium

3 Concluding Remarks

The policy implication of the result of this paper is dramatic. To eliminate child labour, all households need not be targeted for intervention. All we need is to intervene up to a critical proportion. A related question is how productive self-employment should be to have the required impact. Our model suggests that if $R(1) \ge w_B$ (i.e. the bad equilibrium wage), SE parents will withdraw from the market, which in turn would push the wage upward. From the literature on microfinance, it is seen that extensive provision of small loans can have a significant impact on household welfare including child schooling (see Morduch 1999) and access to microfinance makes self-employment sustainable (see Crepon et al. 2014). We argue that from the child labour perspective, a minimal intervention might just be sufficient.

There is also a caveat in order. A number of studies, such as Islam and Choe (2013) for Malawi and Hazarika and Sarangi (2008) for Bangladesh, and also the ongoing work of Pal and Saha (2019) for India have shown that children from the self-employed households are also more likely to work as child labour (and receive less education) primarily because of a substitution between home labour and outside labour triggered by an outside wage increase. This substitution has not been allowed in the present paper, which is clearly a limitation; but in reality, that possibility has to be taken into account. Therefore, our model has more relevance to those contexts where the self-employment activity is not scalable, i.e. it cannot be expanded by hiring additional labour, especially child labour. For example, a child is unsuitable to man a family-run shop, or cook in a family-run eatery. Our model is also applicable to where the microfinance intervention augments mainly the human capital of the beneficiary and the business is predominantly his/her skill based. It is in these contexts, credit interventions will likely have a positive effect of the kind that we established.