1 Introduction

“Economics is all about how people make choices; sociology is all about how they don’t have any choices to make.” (Duesenberry 1960)

Intergenerational relations within the family are a case in point. Both the “unitary” and the “collective” economic models of the family assume individual optimization subject only to the law of the land. The sociology of the family, by contrast, stresses social constraints on individual behavior. Reality lies somewhere in between these extremes. We do make individual choices about all kinds of things, including fundamental ones such as whether to maintain a relationship with our parents and whether to marry and have children. But if we do not cut our inherited links or if we forge new ones, we implicitly make commitments that impose constraints on the allocation of our time and on the use of our money. The tools of modern economic analysis allow us to simultaneously model the determination of family rules and the choice of individual behavior given those rules. The constitutional branch of modern political economy does, in fact, tell us that it may be in the interest of all members of a community to agree first on a constitution, allowing them to safely renounce the dominant strategy in a prisoner’s dilemma type of situation and then to optimize individually subject to that constitution.

Although originally conceived with reference to city or nation states, the constitution concept can be applied also to smaller groupings, such as extended families. Building on Shubick’s (1981) notion of a threat equilibrium, Cigno (1993) puts forward the idea of a “family constitution” and establishes conditions under which this is self-enforcing in the sense that it supports a subgame-perfect Nash equilibrium. This approach is very different from that of Guttman (2001) and others, who start from the hypothesis that parents can somehow make their children altruistic towards them. Both approaches aim to explain why some adults support their elderly parents; but one takes preferences as given, the other assumes that preferences can be manipulated.

Rosati (1996) adds uncertainty to the basic model. Cigno and Rosati (2000) introduce personal services without a perfect market substitute. Anderberg and Balestrino (2003) introduce education. The present paper extends the analysis in three directions. First, it identifies circumstances in which a family constitution is renegotiation-proof. That is important because a constitution worth its name cannot be changed at will. Second, it explores the implications of introducing the intuitively appealing notion that parents are altruistic towards their children. Third, it shows how the model’s behavioral implications differ from those of more conventional theories. In particular, it shows how the existence of family constitutions affects individual responses to policy.

The following assumptions and conventions will be used throughout the paper. The life cycle consists of three periods, labelled \(t=0,1,2\). A person is said to be young in period \(0\), an adult in period \(1\), and old in period \(2\). An adult can make money and have children. The young and the old can do neither. The young and the old are credit rationed, the former because they are not allowed to enter into legally binding contracts, the latter because they will not be around to pay back their debt, and will not allowed to leave a negative estate. To simplify matters, we shall reason as if reproduction occurred by parthenogenesis (hence, the feminine gender) and suppose that, up to some physiological maximum, a woman can have as many children as she wants by bearing a fixed cost \(p\) for every birth. This constant will include the child’s subsistence consumption over the first period of life as well as all the unavoidable costs associated with childbirth. We further assume that, given the parameters of the decision problem, the physiological maximum is never binding. These widely used assumptions are clearly unrealistic but do not affect the points at issue in the present paper.

At any given date, a family consists of individuals at different points of the life cycle. These age differences are important because they provide an opportunity for cooperation between members of the same family. Such an opportunity could arise also from differences of sex and other personal characteristics, but we assume those away to focus on intergenerational cooperation. In the simple case where the economic environment is known with certainty and constant over time, we define a family constitution as a set of unwritten, typically unspoken rules dictating (1) the minimum amount of money or personal services yielding the same utility, \(z\), that an adult must transfer to each of her children (in addition to the subsistence consumption included in \(p\)), if she has any, and (2) the minimum amount of money or personal services yielding the same utility, \(x\), that the same adult must transfer to her parent, conditional on the latter having obeyed the rules. The conditionality attached to (2) makes it in every adult’s interest to punish transgressors. That is important because only an adult can punish another adult. Neither the young nor the old have the means to do so. When we introduce personal services (“attention”) without a perfect market substitute, we shall relax (1) and (2) by saying that the agent must give his children and parent money and attention yielding at least the same utility as, respectively, \(z\) and \(x\).

The existence of a family constitution gives each adult a choice of two strategies. One is to go it alone in the market (defect). The other is to comply with the constitution (cooperate). Let \(m_{0}\) be the amount of money (or the sum of the money and of the money equivalent of the utility of the attention) that the agent gives each of her \(n\) children when they are young and \(m_{1}\) the net amount that she gives each of them when they become adults.Footnote 1 A complier then faces the constraints

$$ nm_{0}\geq nz \label{z_constraint} $$
(1)

and

$$ nm_{1}\geq -nx, \label{min_m2} $$
(2)

The first says that the complier cannot give a young child less than \(z\). The second says that she cannot take from a grown-up child more than \(x\).

2 The model with selfish agents

In the present section, we make the standard economist’s assumption (to be relaxed in the section “The model with altruistic agents”) that individuals are selfish. To begin with, we further assume that individuals derive utility only from market goods. Both of these simplifying assumptions will be relaxed towards the end of the section.

A person’s lifetime utility is given by

$$ U=u_{0}\left( c_{0}\right) +u_{1}\left( c_{1}\right) +u_{2}\left( c_{2}\right) , $$
(3)

where \(c_{t}\) is consumption in period \(t\), and the functions \(u_{i}\left( .\right) \) are increasing and concave, with \(u_{i}^{\prime }\left( 0\right) =\infty \).

2.1 Go-it-aloners

Will a selfish go-it-aloner have children? As births are costly and any children the agent might have would give her nothing when she gets old, she will have no children. For an adult with income \(y\), the pay-off of going it alone is then

$$\eqalign{ v(r,y)=\max_{s}u_{1}\left( y-s\right) +u_{2}\left( rs\right) , }$$

where \(r\) denotes the interest factor and \(s\) is the money saved. As saving is the only means of providing for old-age consumption, \(s\) will never be negative.

As in standard life cycle theory, go-it-aloners will then equate the marginal rate of substitution of present for future consumption to the interest factor,

$$ \dfrac{u_{1}^{\prime }\left( y-s\right) }{u_{2}^{\prime }\left( rs\right) }% =r $$
(4)

The effects of small changes in \(\left( r,y\right) \) on the pay-off of the strategy are

$$ v_{r}(r,y)=su_{2}^{\prime }\left( rs\right) ,\rm{ }v_{y}(r,y)=u_{1}^{ \prime }\left( y-s\right) , $$
(5)

both positive.

2.2 Compliers

Compliers will have children, or there would be no point in complying. As they confidently expect to get filial support in old age, compliers may want to borrow from the market. That, however, they are not allowed to do because an entitlement arising from an informal arrangement like a family constitution is not legally transferable and cannot, thus, be used as collateral.Footnote 2 Therefore,

$$ s\geq 0, \label{credit ration}$$
(6)

On the other hand, for reasons that will become apparent in a moment, selfish compliers have no interest in lending. Therefore, (6) will hold as an equation. As selfish compliers do not make presents any more than selfish go-it-aloners do, (1) and (2) will hold as equations, too.

If the children also comply, the pay-off for an agent with income \(y\) of complying with a constitution that prescribes \(\left( x,z\right) \) is

$$v^{\ast }(p,x,y,z)=\max_{n}u_{1}\left( y-x-\left( p+z\right) n\right) +u_{2}\left( nx\right)$$

The agent’s choice of \(n\) satisfies

$$ \dfrac{u_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) }{u_{2}^{\prime }\left( nx\right) }=\dfrac{x}{p+z}. $$
(7)

Notice that the agent’s marginal rate of substitution is equated to the marginal return of money spent on children, not to the market interest factor as in the go-it-aloner’s case.

The effects of small changes in \(\left( p,x,y,z\right) \) on the pay-off of complying are

$$v_{x}^{\ast }(p,x,y,z)=-u_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) +nu_{2}^{\prime }\left( nx\right) , \label{v*} $$
(8)
$$v_{y}^{\ast }(p,x,y,z)=u_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) , \label{v*y} $$
(9)
$$v_{z}^{\ast }(p,x,y,z)=-nu_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) , \label{v*z} $$
(10)
$$v_{p}^{\ast }(p,x,y,z)=-nu_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) . \label{v*p}$$
(11)

Those of \(p\) and \(z\) are clearly negative. That of \(y\) is clearly positive. That of \(x\) may be negative or positive depending on whether the marginal rate of marginal substitution is higher or lower than \(n\).

2.3 Self-enforcing family constitutions

Suppose that all (present and future) members of the same family are identical. Provided that

$$ v^{\ast }(p,x,y,z)\geq v(r,y), $$
(12)

complying with a family constitution that prescribes \((x,z)\) is then the best response to every other member of the family doing the same. The set of “comply” strategies (one for each member of the family) is, thus, a Nash equilibrium. As complying implies threatening one’s own parent of punishment if she does not comply too, and as the threat is credible because carrying it out is in the interest of the person making it, the equilibrium is sub-game perfect. In equilibrium, the threat is never carried out because everybody complies.

For a complier, having a child is a form of investment, costing \(\left( p+z\right) \) now and yielding (in equilibrium) \(x\) when she gets old. As a complier must satisfy (2) irrespective of how many children she chooses to have, a necessary condition for (12) to be true is that

$$ \dfrac{x}{p+z}>r. \label{enforceability}$$
(13)

Otherwise, there would be no way to recover the fixed cost of complying. That is indeed why a complier has no interest in saving. In view of (7), a complier’s marginal rate of substitution is higher than the interest factor.

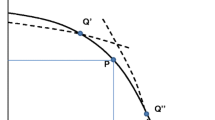
Figure 1 illustrates the properties of the set of constitutions that can be supported by a sub-game perfect Nash equilibrium. The set consists of all the \((x,z)\) pairs that satisfy (12). As young children cannot make transfers, \(z\) cannot be negative. It can be zero, however, because adults would be happy to subscribe to a constitution that did not oblige them to spend more than \(p\) for each of their children. On the other hand, adults would not countenance a constitution that did not entitle them to receive transfers from the same children in the next period. Therefore, all points of the set satisfy

$$z\geq 0,\rm{ }x>0.$$
Fig. 1
figure 1

The Nash-frontier and the renegotiation-proof family constitution

Full size image

The slope of the line segment joining \(\left( -p,0\right) \) to any point in the set is the marginal return to children implicit in the constitution represented by that point. The constitution with the highest marginal return is the one represented by point \(\left( 0,x^{m}\right) \).

The boundary of the set (the heavy line in Fig. 1) is the locus of the \( \left( x,z\right) \) pairs that satisfy (12) as an equation. In view of (8–10), the slope of this boundary is given by

$$ \dfrac{dz}{dx}=\frac{u_{2}^{\prime }\left( xn\right) }{u_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) }-\dfrac{1}{n}. \label{Nash trade-off}$$
(14)

As

$$ \dfrac{d^{2}z}{d\left( x\right) ^{2}}=\dfrac{nu_{1}^{\prime }u_{2}^{\prime \prime }+u_{1}^{\prime \prime }u_{2}^{\prime }}{\left( u_{1}^{\prime }\right) ^{2}} \label{convex xz}$$
(15)

is clearly negative, \(z\) is then maximized at the point \(\left( z^{\ast },x^{\ast }\right) \), where (14) is equal to zero. In view of (7), this implies

$$ n=\dfrac{x}{p+z}. \label{max z}$$
(16)

Although \(v_{y}\) and \(v_{y}^{\ast }\) are both positive in view of (5) and (9), a rise in \(y\) would shift the boundary outwards because the marginal rate of substitution is higher for compliers than for go-it-aloners in view of (4), (7), and (13). By contrast, a rise in \(p\) or \(r\) would shift the boundary inwards because \(v_{p}^{\ast }\) is negative in view of (11) and \(v_{r}\) positive in view of (5). The probability of complying is, thus, increasing in \(y\) and decreasing in \(p\) and \(r\).

2.4 Renegotiation-proof family constitutions

We have seen that a constitution satisfying (12) is self-enforcing in the limited sense that it is in every family member’s interest to obey it and have it obeyed. Given, however, that an infinite number of constitutions may have that property, what is there to stop a generation re-writing the rules to its own advantage? A constitution worth its name must not be amendable unless unforeseen circumstances make it unviable. In this section, we adapt the renegotiation-proofness concept developed by Bernheim and Ray (1989) and Maskin and Farrell (1989). In those papers, the players are always the same, and the arrangement is, thus, to do with the way an individual behaves towards his contemporaries. By contrast, the players here change at each round, and the arrangement concerns the way present adults behave towards their predecessors and descendants.

Any generation can propose a new constitution. Will subsequent ones take any notice? Not if the old constitution (1) satisfies (12) and (2) is not Pareto-dominated by any other constitution also satisfying (12). If the existing constitution is undominated, the only way a person can offer her children a better deal and not loose in the bargain is, in fact, to pay her parent less than the existing constitution requires—in other words, to default on the existing constitution. But that makes her liable to punishment at the hands of her own children, who will be better-off upholding the existing constitution, which entitles them to pay nothing to her, than acquiescing to the proposed new one. Once established, a constitution satisfying the double requirement of being a sub-game perfect Nash equilibrium and undominated by any other constitution that is itself a sub-game perfect Nash equilibrium is, thus, unamendable. Let us look at its properties.

Selfish adults are interested only in their own adult and old-age consumption. As their children are interested in their entire lifetime consumption stream, however, a family constitution is renegotiation-proof if it maximizes

$$V\left( n,x,z\right) \equiv u_{0}\left( z\right) +u_{1}\left( y-x-\left( p+z\right) n\right) +u_{2}\left( xn\right)$$

subject to (12). The first-order conditions are (16) and

$$ \dfrac{u_{0}^{\prime }}{u_{1}^{\prime }}=\left( 1+\lambda \right) n=\left( 1+\lambda \right) \dfrac{u_{1}^{\prime }}{u_{2}^{\prime }}, \label{constr_renegproof1}$$
(17)

where \(\lambda \) is the Lagrange multiplier of (12).

If (12) is not binding (\(\lambda =0\)), the parent equates her marginal rate of substitution of adult for old-age consumption to her children’s marginal rate of substitution of childhood for adult consumption. The common value of these marginal rates is equal to the number of children, hence, to the marginal return of money spent on them. If (12) is binding (\(\lambda >0\)), the parent’s marginal rate of substitution will still be set equal to the number of children and, thus, to the marginal return of money spent on them, but lower than the children’s marginal rate of substitution. In the first case, the renegotiation-proof constitution could be anywhere inside the Nash frontier. In the second, it can only be at \(\left( x^{\ast },z^{\ast }\right) \) because that is the only point of the frontier satisfying (16). The only renegotiation-proof constitution is then the one that maximizes parental support for young children.

In Fig. 1, the broken curves, with slope \(\left( u_{0}^{\prime }-u_{1}^{\prime }n\right) /\left( -u_{1}^{\prime }+u_{2}^{\prime }n\right) \), are the contours of \(V\left( .\right) \). The picture is drawn under the assumption that this function happens to reach a maximum just inside the Nash frontier, close to \(\left( z^{\ast },x^{\ast }\right) \). There is obviously no special reason why this should be the case. As the Nash frontier shifts inwards as the interest rate rises, however, the probability that the solution is at or close to \(\left( z^{\ast },x^{\ast }\right) \) increases with \(r\). Notice that the constitution which maximizes the marginal return to children, \(\left( 0,x^{m}\right) \), can never be renegotiation-proof.Footnote 3

2.5 Extensions: uncertainty and personal attention

By allowing exchange across states of nature as well as across dates, uncertainty extends the scope for cooperation within the family from the field of credit to that of mutual insurance (Di Tella and MacCullogh 2002). There remains, however, the problem that informal intra-family contracts, whether of the credit or of the insurance type, are not enforceable though the courts. Therefore, cooperative behavior is still dependent on the existence of a self-enforcing and renegotiation-proof family constitution. Were it possible to make constitutional prescriptions fully contingent, uncertainty would make no difference of substance to our story. However, realistically assuming that doing this would be prohibitively costly and that the constitutional prescriptions will be of the kind that an adult is excused paying his parent \(x\) if his own income falls below a certain level, investing in children will be risky.Footnote 4 But, investment in conventional assets may be risky too. Assuming that the two kinds of risk are not positively correlated, a risk-averse complier may then find it optimal to save and have children (Rosati 1996). Apart from that, the predictions of the non-altruistic model remain unaltered.

The other extension consists in allowing utility to depend not only on the consumption of market goods (“money”) but also on the personal services (“attention”) without perfect market substitutes that the agent receives from her parent when she is young, and from her children when she is old. The variable \(c_{t}\) is now to be interpreted as the money equivalent of goods consumed and attention received in period \(t\). Constraint 1 is similarly to be interpreted as saying that a young person is entitled to receive from her parent a combination of money and attention yielding at least the same utility as \(z\) and (2) as saying that an old person is entitled to receive from each of her children a combination of money and attention yielding at least the same utility as \(x\). As compliers will then give their elderly parent and young children the cost-minimizing combination of money and attention, the enforceability condition (13) is easier to satisfy (Cigno and Rosati 2000).

Introducing attention in the utility function has, thus, the effect of relaxing the Nash constraint and raising the probability that an agent will comply. Intuitively, that is not only because the opportunity of substituting attention for money makes complying less costly but also because the only way to get attention from one’s own grown-up children is to comply. If giving attention reduces \(y\), another effect of this extension is that a wage rate rise need not shift the Nash frontier uniformly outwards as in the basic model. The frontier associated with a higher wage rate may now cross the one associated with a lower wage rate. The effect of a wage rate change may, thus, depend on where the existing renegotiation-proof constitution is located.

3 The model with altruistic agents

Introspection and casual observation suggest that parents may be altruistic towards their children. But, does altruism make a difference to the way people actually behave in the presence of self-enforcing family constitutions? If the answer were no, we could not tell whether a person observed making a transfer to her mother or children is doing that out of her own good heart or because it is in her own interest to do so. If the answer were yes, would it still make sense to talk of self-enforcing family constitutions? To answer these questions, we introduce descending altruism as in Becker and Barro (1988). Like those authors and many others after them, we, thus, assume that altruism flows from parents to children, not the other way round. This may seem rather extreme, but nothing of substance changes if we assume, instead, that people are more altruistic towards their children than towards their parents.

For simplicity of exposition, we revert to assuming that the state of nature is certain and that there are perfect market substitutes for parental and filial attention. A person’s lifetime utility is now given by

$$ U=u_{0}\left( c_{0}\right) +u_{1}\left( c_{1}\right) +u_{2}\left( c_{2}\right) +\beta U^{\ast }\left( m_{0},m_{1}\right) n,\rm{ }0<\beta<1, $$
(18)

where \(U^{\ast }\left( m_{0},m_{1}\right) \) stands for a child’s lifetime utility maximized subject to the transfers \(\left( m_{0},m_{1}\right) \) that she received from her parent. The function \(U^{\ast }\left( .\right) \) is increasing and concave. The parameter \(\beta \) is a measure of parental altruism.

3.1 Altruistic go-it-aloners

Unlike a selfish go-it-aloner, an altruistic one may choose to have children and make transfers to them. As the children will not reciprocate when they become adults, however, and cannot be forced to accept a negative bequest, a go-it-aloner’s choice of \(m_{1}\) must satisfy

$$ nm_{1}\geq 0. \label{nonnegative m2}$$
(19)

As the agent cannot rely on her children for old-age support, her \(s\) will still be positive as in the non-altruistic model. It, thus, remains true that a go-it-aloner cannot be credit rationed.

The pay-off of going it alone is now

$$v{\left( {p,r,y} \right)} = {\mathop {\max }\limits_{{\left( {m_{0} ,m_{1} ,n,s} \right)}} }u_{1} {\left( {y + m_{{ - 1}} - s - {\left( {p + m_{0} } \right)}n} \right)} + u_{2} {\left( {sr - nm_{1} } \right)} + \beta U*{\left( {m_{0} ,m_{1} } \right)}n,s.t.{\left( {19} \right)},$$

where \(m_{-1}\) is the amount (nonnegative like \(m_{1}\)) that the agent inherited from her own parent.

The choice of \(\left( m_{0},m_{1},n,s\right) \) associated with this strategy satisfies

$$ \dfrac{u_{1}^{\prime }\left( y+m_{-1}-s-\left( p+m_{0}\right) n\right) }{ u_{2}^{\prime }\left( sr-nm_{1}\right) }=r=\frac{\beta U_{0}^{\ast }}{\beta U_{1}^{\ast }+\upsilon } \label{FOCs_altr.}$$
(20)

and

$$\frac{\beta U^{\ast }\left( m_{0},m_{1}\right) }{u_{1}^{\prime }\left( y+m_{-1}-s-\left( p+m_{0}\right) n\right) }=p+m_{0}+\left( 1-\frac{\upsilon }{u_{2}^{\prime }\left( sr-nm_{1}\right) }\right) \frac{m_{1}}{r}, $$
(21)

where \(\upsilon \) is the Lagrange multiplier of (19).

Condition 20 says that, if the agent is rich or altruistic enough (\(y+m_{-1}\) or \(\beta \) high enough) for (19) to be slack (\(\upsilon =0\)), the parent’s and children’s marginal rates of substitution of present for future consumption will be equalized, and the common value of these two marginal rates set equal to the interest factor. If \(m_{1}\) is at a corner (\(\upsilon >0\)), the parent’s marginal rate of substitution will still be equated to the interest factor, but the children’s will be higher. Condition 21 tells us that, if (19) is slack, she will have children to the point where the marginal benefit, \(\frac{\beta U^{\ast }}{u_{1}^{\prime }}\), equals to the marginal cost, \(\left( p+m_{0}+ \frac{m_{1}}{r}\right) \). Otherwise, she will have more.

The effects of small changes in \(\left( p,r,y\right) \) on the pay-off of going it alone are now

$$ v_{p}(p,r,y)=-nu_{1}^{\prime }\left( y+m_{-1}-s-\left( p+m_{0}\right) n\right) , \label{vp_altr.}$$
(22)
$$ v_{r}(p,r,y)=su_{2}^{\prime }\left( sr-nm_{1}\right) \label{vr_altr.}$$
(23)

and

$$ v_{y}(p,r,y)=u_{1}^{\prime }\left( y+m_{-1}-s-\left( p+m_{0}\right) n\right) .\rm{ } \label{vw_altr.}$$
(24)

That of \(p\) is clearly negative. Those of \(r\) and \(y\) are positive as in the non-altruistic model.

3.2 Altruistic compliers

Unlike a selfish complier, an altruistic one may choose to give each of her children more than \(z\) when they are young and accept less than \(x\) from each of them when they become adults. An altruistic complier may indeed choose to bequeath each child a sum larger than \(x\), thus making \(m_{1}\) positive. Therefore, (1) need not hold as an equation as in the non-altruistic model. The same applies, in principle, also to (2). If that were the case, however, the element of threat that makes a constitution sustainable as a sub-game perfect Nash equilibrium would be missing. For the constitution to be an effective restriction on behavior, (2) must, thus, hold as an equation.

It remains true that a complier cannot borrow against the transfers she expects to receive from her children when she gets old. It is no longer true, however, that she is not interested in saving. We will show in a moment that \(s\) may be positive. Therefore, it is not necessarily true that (6) will always hold as an equation as in the model without altruism. For an altruistic agent, the pay-off of complying is

$$v*{\left( {p,r,x,y,z} \right)} = {\mathop {\max }\limits_{{\left( {m_{0} ,n,s} \right)}} }u_{1} {\left( {y + m_{{ - 1}} - s - x - {\left( {p + m_{0} } \right)}n} \right)} + u_{2} {\left( {sr - nx} \right)} + \beta U*{\left( {m_{0} - x} \right)}n,s.t.{\left( 1 \right)},{\left( 6 \right)}.$$

The altruistic complier’s choice of \(\left( m_{0},n,s\right) \) satisfies

$$ u_{1}^{\prime }\left( y-x-s-\left( p+m_{0}\right) n\right) =\beta U_{0}^{\ast }\left( m_{0},-x\right) +\zeta \label{FOCm_compalt.}$$
(25)
$$ \dfrac{u_{1}^{\prime }\left( y-x-s-\left( p+m_{0}\right) n\right) -\sigma }{ u_{2}^{\prime }\left( sr+nx\right) }=r, \label{FOCs_compalt}$$
(26)

and

$$ \frac{\beta U^{\ast }\left( m_{0},-x\right) }{u_{1}^{\prime }\left( y-x-s-\left( p+m_{0}\right) n\right) }=p+m_{0}-\frac{u_{2}^{\prime }\left( sr+nx\right) }{u_{1}^{\prime }\left( y-x-s-\left( p+m_{0}\right) n\right) }x, $$
(27)

where \(\zeta \) and \(\sigma \) are the Lagrange multipliers of, respectively, (1) and (6).

According to (25), if \(m_{0}\) is not at a corner (\(\zeta =0\)), the agent will reduce the amount transferred to each young child to the point where the marginal utility that she altruistically derives from the child’s current consumption equals the marginal utility that she selfishly derives from her own current consumption. Otherwise (\( \zeta >0\)), she will give each young child exactly \(z\). In view of (26), if \(s\) is not at a corner (\(\sigma =0\)), the agent will reduce her saving to the point where her marginal rate of substitution of present for future consumption equals the interest factor. Otherwise (\(\sigma >0\)), she will save nothing. Whichever is the case, there is nothing, at this stage, to ensure that marginal rates of substitution of parent and children will be equalized. In view of (27), the agent will again have children to the point where the marginal benefit equals the marginal cost. As the right-hand side of (27) is lower than that of (21), however, the agent will have more children if she complies than if she goes it alone.Footnote 5

The effects of small changes in \(\left( p,x,y,z\right) \) on the pay-off of complying are now

$$ v_{p}^{\ast }(p,r,x,y,z)=-nu_{1}^{\prime }\left( y+m_{-1}-s-x-\left( p+m_{0}\right) n\right) , \label{v*p_alt}$$
(28)
$$ v_{r}^{\ast }(p,r,x,y,z)=su_{2}^{\prime }\left( sr+nx\right) , \label{v*r_alt}$$
(29)
$$v^{*}_{x} {\left( {p,r,x,y,z} \right)} = u^{\prime }_{1} {\left( {y + m_{{ - 1}} - s - x - {\left( {p + m_{0} } \right)}n} \right)} + nu^{\prime }_{2} {\left( {sr + nx} \right)} - n\beta U^{*}_{1} {\left( {m_{0} , - x} \right)},$$
(30)
$$ v_{y}^{\ast }(p,r,x,y,z)=u_{1}^{\prime }\left( y+m_{-1}-s-x-\left( p+m_{0}\right) n\right) \label{v*y_alt}$$
(31)

and

$$ v_{z}^{\ast }(p,r,x,y,z)=-n\zeta . \label{v*z_alt}$$
(32)

That of \(p\) is clearly negative. Those of \(r\) and \(y\) are clearly positive. That of \(x\) is negative if the agents’s marginal rate of substitution is not lower than \(n\). Otherwise, it may be positive.Footnote 6 That of \(z\) is negative if \(m_{0}\) is at a corner, zero otherwise (in the model without altruism, \( m_{0} \) is always at a corner).

3.3 Self-enforcement and renegotiation-proofness under altruism

A constitution prescribing \((x,z)\) is now a subgame-perfect Nash equilibrium if and only if

$$ v^{\ast }(p,r,x,y,z)\geq v(p,r,y). \label{altr. Nash}$$
(33)

In contrast with (12), this does not imply (13) because the return for an altruistic agent of investing in children is higher than \(\frac{x}{p+m_{0}}\). We can, in fact, see from (26) and (27) that

$$ \frac{x}{p+m_{0}}=\left( r+\frac{\sigma }{u_{2}^{\prime }\left( sr+nx\right) }\right) \left( 1-\frac{\beta U^{\ast }\left( m_{0},-x\right) }{\left( p+m_{0}\right) u_{1}^{\prime }\left( y+m_{-1}-s-x-\left( p+m_{0}\right) n\right) }\right) . $$
(34)

Therefore, an agent may comply even if \(\frac{x}{p+m_{0}}\) is not greater than \(r\). If a complier is not effectively credit rationed (\(\sigma =0\)), \(\frac{x}{p+m_{0}}\) is indeed definitely lower than \(r\).

The slope of the Nash boundary is now given by

$$ \dfrac{dz}{dx}=-\frac{u_{1}^{\prime }\left( y+m_{-1}-s-x-\left( p+m_{0}\right) n\right) -nu_{2}^{\prime }\left( sr+nx\right) +n\beta U_{1}^{\ast }\left( m_{0},-x\right) }{n\zeta }. \label{altr. Nash trade-off}$$
(35)

If (1) is not binding (\(\zeta =0\)), the boundary is, thus, a straight line, perpendicular to the \(x\) axis. There is then no trade-off between \(z\) and \(x\). If (1) is binding (\(\zeta >0\)), the boundary has the same shape as in the non-altruistic model (see Fig. 1), but \(z\) is now maximized where

$$ \frac{u_{1}^{\prime }\left( y+m_{-1}-s-x-\left( p+m_{0}\right) n\right) }{ u_{2}^{\prime }\left( sr+nx\right) }=\left( 1-\frac{\beta U_{1}^{\ast }\left( m_{0},-x\right) }{u_{2}^{\prime }\left( sr+nx\right) }\right) n. \label{altr_maxz}$$
(36)

In view of (26), it is then clear that, in the case where \(m_{0}\) is at a corner, \(z\) reaches a maximum at a point of the Nash frontier where \(n\) is higher than \(r\) as in the model without altruism. In view of (20), (22), (24), (26), (28), (29), and (31), the effects of \(p\), \( r \) and \(y\) on the probability of complying are qualitatively the same as in the non-altruistic model. It, thus, remains true that a rise in \(p\) or \(r\) reduces the probability that a self-enforcing family constitution exists, while a rise in \(y\) will increase it.

Assuming that \(\beta \) is small enough for \(\beta n\) to be less than unity,Footnote 7 otherwise the optimization would be unbounded, a renegotiation-proof constitution maximizes

$$\eqalign{ W\left( n,x,z\right) \equiv \frac{u_{0}\left( m_{0}\right) +u_{1}\left( y-x-s-\left( p+m_{0}\right) n\right) +u_{2}\left( sr+nx\right) }{1-\beta n}, }$$

subject to (1), (6), and (33).

The solution then satisfies (26), (27),

$$ \frac{u_{0}^{\prime }\left( z\right) }{u_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) }=\left( 1-\mu \left( 1-\beta n\right) \frac{v_{z}^{\ast }}{u_{1}^{\prime }\left( y-x-\left( p+z\right) n\right) }\right) n \label{z_z bind} $$
(37)

and

$$ \frac{u_{1}^{\prime }\left( y+m_{-1}-s-x-\left( p+z\right) n\right) }{ u_{2}^{\prime }\left( sr+nx\right) }=n+\mu \left( 1-\beta n\right) \frac{ v_{x}^{\ast }(p,r,x,y,z)}{u_{2}^{\prime }\left( sr+nx\right) }. \label{x_z bind} $$
(38)

As in the non-altruistic model, a renegotiation-proof constitution will, thus, equate the marginal rates of substitution of parent and children to \(n\) and, to each other, if and only if the Nash constraint is not binding (\(\mu =0\)). If credit is not effectively rationed (\(\sigma =0\)), \(n\) will be set equal to \(r\). Otherwise (\(\sigma >0\)), \(n\) will be greater than \(r\) as in the non-altruistic model (where, recall, compliers are always credit rationed). In the case where the Nash constraint is binding (\(\mu >0\)), the parent’s marginal rate of substitution will be lower than the children’s. The only difference of substance altruism makes is, thus, that the fertility rate and the common value of the marginal rates of substitution of present for future consumption of parent and children may now be equated to the interest factor. The intuitive explanation is that an agent may now save to make bequests rather than because it earns a higher return than investing in children.

4 Efficiency

We shall now inquire whether individual choice, with or without family constitutions, brings about an efficient allocation. But, what does efficient mean in an endogenous fertility context? The Pareto criterion allows us to compare different allocations of goods to the same collection of individuals. It cannot, thus, be applied in a context like the present one, where the existence of future adults depends on decisions taken by the present ones. We can use, however, the quasi-Pareto criterion proposed by Baland and Robinson (2002).

According to those authors, an allocation \(\mathbf{A}\) is deemed Pareto-preferred to an allocation \(\mathbf{B}\) if both the utility of the parent and the average utility of the children are higher in \( \mathbf{A}\) than in \(\mathbf{B}\). The reference to an average level of utility leaves the door open for the possibility that the number of children associated with \(\mathbf{A}\) is different from the one associated with \(\mathbf{B}\). Assuming that children are (a) born sequentially and (b) equally treated by their parents, this allows us to step into the middle of an agent’s reproductive career and ask if there exists a contract between her and the children born up to that moment that would induce the former to curtail her fertility plans.

In the non-altruistic version of the model, only compliers have children. If the Nash constraint is slack, the parent’s and the children’s marginal rates of substitution are equalized. Otherwise, the parent values her current consumption, at the margin, less than her children value theirs. The situation is illustrated in Fig. 2, where the convex-to-the-origin curves describe a child’s intertemporal preferences. If the constitution is effectively constrained by (12), the children’s marginal rate of substitution is equal to \(\delta \). That of the parent is equal to \(\gamma \), lower than \(\delta \). The parent’s utility maximizing plan is to have \(\gamma \) children and to allocate the resources under her command so that each child consumes \(c_{0}^{B}\) now and \(c_{1}^{B}\) in adult life.

Fig. 2
figure 2

The effect of a binding Nash constraint

Full size image

Suppose that a number of children lower than \(\gamma \) is already born. It is clear that any of these children would be happy to trade \(\left( c_{1}^{B}-c_{1}^{A}\right) \) units of future, for \(\left( c_{0}^{A}-c_{0}^{B}\right) \) of present consumption. If such a contract were enforceable, the parent would be better-off accepting the deal, than having an extra child. This makes the original plan inefficient in the Baland–Robinson sense. As a child cannot credibly commit to pay a parent more than \(x\), however, the deal will not go through. The parent can then do no better than carry out the original plan. Fertility will consequently be inefficiently high.Footnote 8

The necessary and sufficient condition for the allocation brought about by a renegotiation-proof family constitution to be efficient is, thus, that it lies inside the Nash frontier (in other words, that it makes the adults of the day strictly better-off complying, than going it alone in the market). The intuitive explanation is that, as the agents are adults who will become old but will not be young again, the requirement that an agent must not be worse-off complying than going it alone conflicts, if binding, with the one that the lifetime utility of each individual must be at a maximum given everyone else’s.

Altruism does not change this conclusion in any way but allows for the possibility that fertility will equal the interest factor (if the complier is not credit rationed) and, thus, that the system will be efficient also in a dynamic sense. In the presence of altruism, however, go-it-aloners also may have children. Will they behave efficiently? If a go-it-aloner is rich and altruistic enough for (19) to be slack, she sets her marginal rate of substitution equal to her children’s. Otherwise, she sets it lower and has an inefficiently high number of children. The necessary and sufficient condition for an altruistic go-it-aloner to behave efficiently is, thus, that \(m_{1}\) is not at a corner.

The first to remark that “operative bequests” are necessary for altruistic agents optimizing subject only to the law of the land to behave efficiently were Becker and Murphy (1988). But, those authors had in mind the standard Pareto criterion that cannot be applied in an endogenous fertility context. The purpose of Baland and Robinson (2002) was essentially to show that the proposition remains true even if one applies their extended Pareto criterion. They also show that “operative bequests” are not enough to ensure efficiency. It must also be true that the agents are not credit rationed. But, both pairs of authors are talking of agents unfettered by family constitutions (in our language, altruistic go-it-aloners), and we have argued that such agents will never be credit rationed because they need to save for old age (all the more if they propose to make bequests). Where altruistic compliers are concerned, we have also shown that \(s\) not at a corner is necessary for dynamic efficiency, not for efficiency in the Baland–Robinson sense. For efficiency in that limited sense, it is sufficient that the Nash constraint does not effectively restrict the selection of the renegotiation-proof constitution.

5 Behavioral and policy implications

Granted that self-enforcing and renegotiation-proof family constitutions may exist, what difference does it make to the way individuals respond to a change in the economic environment?Footnote 9 Recall that an agent may respond by either adjusting what variables she can under the present strategy or by switching strategies. In this section, we examine the effects of two environmental changes with a direct bearing on intergenerational transfers, the introduction of a mandatory pension system and a tightening of the credit ration. We shall assume throughout that agents differ only in their income. As an increase in current income raises the pay-off of complying more than the pay-off of going it alone, we can then find a threshold level of income, \(y^{m}\), such that an agent will comply if and only if she is at or above the threshold. A small rise in \(y^{m}\) will cause agents at the threshold to switch from comply to go-it-alone. A small reduction will cause agents just below the threshold to switch the other way. We shall call an agent who switches strategies a marginal player.

5.1 Pensions

Consider the effects of introducing or expanding a pension system that requires each adult to pay \(\tau \) and entitles each old person to receive \( \pi \). To isolate the effects of compulsory old-age insurance from those of any implicit pension tax or subsidy,Footnote 10 we assume that the scheme is actuarially fair. In our certainty framework, this simply means

$$ \pi =r\tau . \label{pie} $$
(39)

We further assume that \(\tau \) is no higher than the amount that go-it-aloners would save without the policy. This implies that only compliers can be credit rationed. In view of (39), the wealth position of go-it-aloners is, thus, unaffected by the policy. By contrast, the policy leaves non-altruistic compliers worse-off because it forces them to pay more into a public scheme that, in view of (13), yields a lower marginal return than the family one. In view of (34), the same is not necessarily true of altruistic compliers. If these agents are not credit rationed, their wealth position is unaffected.

We start by assuming that agents are not altruistic. The pay-off of the go-it-alone strategy is now

$$ \eqalign{ v\left( r,y,\tau \right) =\max_{s}\left[ u_{1}\left( y-\tau -s\right) +u_{2}\left( \left( \tau +s\right) r\right) \right] . }$$

As the policy does not alter their wealth position, inframarginal go-it-aloners have no reason to change their life plans. As it lowers their demand for old-age consumption, however, it induces them to reduce their saving by the amount of the extra pension contribution,

$$ \frac{ds}{d\tau }=-1. \label{ds/dtau_tau} $$
(40)

Their fertility and transfers remain zero.

The effect of \(y\) on the pay-off of going it alone,

$$ v_{y}\left( r,y,\tau \right) =u_{1}^{\prime }\left( y-\tau -s\right) , \label{dv/dy_tau} $$
(41)

remains positive. That of \(\tau \),

$$ v_{\tau }\left( r,y,\tau \right) =-u_{1}\left( y-\tau -s\right) +ru_{2}\left( \left( \tau +s\right) r\right) , \label{dv/dtau_tau} $$
(42)

is zero in view of (4).

The pay-off of the comply strategy is now

$$ \eqalign{ v^{\ast }(p,x,y,z,\tau )=\max_{n}\left[ u_{1}\left( y-\tau -x-\left( p+z\right) n\right) +u_{2}\left( nx+r\tau \right) \right] . }$$

Although the policy reduces their demand for old-age consumption, inframarginal compliers cannot respond by saving less because their saving is already zero. As their transfer behavior is prescribed by the constitution and their fertility is fixed by (16), all that will change is then their utility. Using (16), the effect of \(y\) on the pay-off of the strategy,

$$ v_{y}^{\ast }(p,x,y,z,\tau )=u_{1}^{\prime }\left( y-\tau -2x\right) , \label{dv*/dy_tau} $$
(43)

remains positive. That of \(\tau \),

$$v_{\tau }^{\ast }(p,x,y,z,\tau )=-u_{1}^{\prime }\left( y-\tau -2x\right) +\left( r-\frac{x}{p+z}\right) u_{2}^{\prime }\left( \frac{x^{2}}{p+z}+r\tau \right) , $$
(44)

is negative in view of (13).

The threshold level of income below which agents go it alone solves

$$ \eqalign{ v^{\ast }(p,x,y,z,\tau )=v\left( r,y,\tau \right) . }$$

As \(v_{y}^{\ast }(p,x^{m},y^{m},z^{m},\tau )\) is larger than \(v_{y}\left( r,y^{m},\tau \right) \) in view of (4), (7), and (13) and having established that (44) is negative,

$$ \frac{dy^{m}}{d\tau }=-\frac{v_{\tau }^{\ast }(p,x^{m},y^{m},z^{m},\tau )}{ v_{y}^{\ast }(p,x^{m},y^{m},z^{m},\tau )-v_{y}\left( r,y^{m},\tau \right) } \label{dym/dtau} $$
(45)

will be positive. The policy, raises the threshold, thereby inducing marginal players to switch from the comply to the go-it-alone strategy. These agents will stop having children and making transfers and will start saving.

It is, thus, clear that, in a selfish world, the policy has non-positive effects on the fertility and private transfers of all inframarginal players and has negative ones on those of marginal players. Aggregate fertility will consequently fall, and some of the old will be left without filial support. The effect on saving is non-positive where inframarginal players are concerned, positive where marginal ones are. If there are enough of the latter, the policy will then raise aggregate saving. This is in sharp contrast with the prediction of standard life cycle theory.

Let us now introduce altruism. As not only compliers but also go-it-aloners may now have children, make transfers, and save, the pay-off of going it alone becomes

$$\eqalign{ v(p,r,y,\tau ) =\max_{\left( m_{0},m_{1},n,s\right) }u_{1}\left( y-\tau +m_{-1}-s-\left( p+m_{0}\right) n\right) +u_{2}\left( \left( s+\tau \right) r-nm_{1}\right) \cr+\beta U^{\ast }\left( m_{0},m_{1}\right) n\rm{, s.t. }\left(19\right) . }$$

As in the non-altruistic model, inframarginal go-it-aloners will not change their consumption, fertility and transfer plans in response to the policy. They will just save less. The effect of \(y\) on the pay-off of the strategy,

$$ v_{y}(p,r,y,\tau )=u_{1}^{\prime }\left( y-\tau +m_{-1}-s-\left( p+m_{0}\right) n\right) , \label{dv/dy_alt_tau} $$
(46)

is again positive. That of \(\tau \),

$$v_{\tau }(p,r,y,\tau )=-u_{1}^{\prime }\left( y-\tau +m_{-1}-s-\left( p+m_{0}\right) n\right) +ru_{2}^{\prime }\left( \left( s+\tau \right) r-nm_{1}\right) , $$
(47)

is zero in view of (20).

The pay-off of the comply strategy is

$$\eqalign{ v^{\ast }(p,r,x,y,z) =\max_{\left( m_{0},n\right) }u_{1}\left( y-\tau +m_{-1}-s-x-\left( p+m_{0}\right) n\right) +u_{2}\left( \left( s+\tau \right) r+nx\right) \cr+\beta U^{\ast }\left( m_{0},-x\right) n\rm{, s.t. }\left(1\right), \left(6\right) . }$$

If the credit ration is not binding, inframarginal compliers will respond to the policy like inframarginal go-it-aloners. They will save less. If (6) is binding, however, their saving is already zero. The policy will then make them poorer, and there will, be income effects. Compliers will, in that case, reduce \(n\) and, if it is not effectively constrained by (1), \(m_{0}\). If they cannot reduce \(m_{0}\) because (1) is binding, they will reduce \(n\) even more. The effect of \(y\) on the pay-off of the policy,

$$ v_{y}^{\ast }(p,r,x,y,z,\tau )=u_{1}^{\prime }\left( y-\tau +m_{-1}-s-x-\left( p+m_{0}\right) n\right) , \label{dv*/dy_alt_tau} $$
(48)

is positive as usual. In view of (26), the effect of \(\tau \),

$$v_{\tau }^{\ast }(p,r,x,y,z,\tau )=-u_{1}^{\prime }\left( y-\tau +m_{-1}-s-x-\left( p+m_{0}\right) n\right) +ru_{2}\left( \left( s+\tau \right) r+nx\right) , $$
(49)

is zero if credit is not effectively rationed, negative otherwise.

In the presence of altruism, \(y^{m}\) satisfies

$$ \eqalign{ v^{\ast }(p,r,x^{m},y^{m},z^{m},\tau )\equiv v\left( p,r,y^{m},\tau \right) . }$$

The effect of the policy on the threshold level of income,

$$ \frac{dy^{m}}{d\tau }=-\frac{v_{\tau }^{\ast }(p,r,x^{m},y^{m},z^{m},\tau )}{ v_{y}^{\ast }(p,r,x^{m},y^{m},z^{m},\tau )-v_{y}(p,r,y^{m},\tau )}, \label{dym/dtau_alt} $$
(50)

is positive or zero depending on whether marginal players would or would not be credit rationed if they complied. In the first case, the policy would induce marginal players to switch from the comply to the go-it-alone strategy. The behavioral implications would then be qualitatively the same as in the model without altruism. Some of the old would loose their children’s support, aggregate fertility would definitely fall and aggregate saving could go either way. In the second case, nobody would change strategy. Aggregate fertility would again fall, but so would aggregate saving, and no old person would lose her children’s support because of the policy.

Altruism, therefore, does not alter the proposition that an expansion in (actuarially fair) pension coverage reduces aggregate fertility and may raise aggregate saving. This proposition is in sharp contrast with the predictions of the Becker–Barro model that the policy will induce agents to save less and will have no effect on their fertility and transfer behavior (because it does not entail an intergenerational transfer). There is evidence that, controlling for the intergenerational transfer implied by a deficit or surplus in the pension fund budget, pension coverage does indeed have a nonnegative effect on aggregate household saving and a negative effect on aggregate fertility.Footnote 11 This appears to reject the hypothesis that all agents optimize subject only to the law of the land (as in life cycle theory and in altruistic models a la Becker–Barro), but not the alternative hypothesis that a substantial number of agents optimizes subject to a family constitution.

5.2 Credit rationing

We now turn to the implications of a reduction in the credit ration. To do that, we must allow the ration to be positive in the first place, rather than zero as we have assumed so far. For example, in the presence of a public pension scheme like the one considered in the last subsection, we might assume that agents are allowed to borrow up to some fraction of \(\tau \). We shall then re-write the credit rationing constraint as

$$ s\geq -b, \label{b_ration} $$
(51)

where \(b\) is a nonnegative number.

Let us again start with the assumption that agents are not altruistic. The pay-off of the go-it-alone strategy is now

$$ \eqalign{ v\left( b,r,y_{1},y_{2}\right) =\max_{s}\left[ u_{1}\left( y_{1}-s\right) +u_{2}\left( y_{2}+rs\right) \right] \rm{, s.t. }\left(51\right) , }$$

where \(y_{t}\) denotes income in period \(t\) (\(t=1,2\)). If \(y_{2}\) is sufficiently high, the agent may want to borrow. If (51) is binding, a reduction in the credit ration will then reduce the amount borrowed and, consequently, the agent’s utility. The effect on the pay-off of going it alone is given by

$$ v_{b}\left( b,r,y_{1},y_{2}\right) =\xi , $$
(52)

where \(\xi \) is the Lagrange multiplier of (51), positive and equal to \(u_{1}^{\prime }\left( y_{1}-s\right) \) if that constraint is binding, zero otherwise. That of a small change in current income,

$$ v_{y_{1}}(b,r,y_{1},y_{2})=u_{1}^{\prime }\left( y_{1}-s\right) , $$
(53)

is positive as usual.

As a non-altruistic complier is always credit rationed, the pay-off of the comply strategy is

$$ \eqalign{ v^{\ast }(b,p,r,x,y_{1},y_{2},z)=\max_{n}\left[ u_{1}\left( y_{1}+b-x-\left( p+z\right) n\right) +u_{2}\left( y_{2}-br+nx\right) \right] . }$$

A reduction in the credit ration will always reduce both the amount borrowed and the utility of inframarginal compliers. Their fertility and transfer behavior will remain the same. The effect on the pay-off of the strategy,

$$ v_{b}^{\ast }(b,p,r,x,y_{1},y_{2},z)=u_{1}^{\prime }\left( y_{1}+b-x-\left( p+z\right) n\right) -ru_{2}^{\prime }\left( y_{2}-br+nx\right) , \label{dv*/db_b} $$
(54)

is positive for the usual reason that the marginal rate of substitution is equated to \(n\), greater than \(r\). That of a small change in current income,

$$ v_{y_{1}}^{\ast }(b,p,r,x,y_{1},y_{2},z)=u_{1}^{\prime }\left( y_{1}+b-x-\left( p+z\right) n\right) , $$
(55)

is positive as usual.

The threshold level of current income, \(y_{1}^{m}\), is now defined by

$$\eqalign{ v^{\ast }(b,p,r,x,y_{1}^{m},y_{2},z)=v\left( b,r,y_{1}^{m},y_{2}\right) . }$$

The effect of \(b\) on \(y^{m}\) is given by

$$ \frac{dy^{m}}{db}=-\frac{v_{b}^{\ast }(b,p,r,x,y_{1}^{m},y_{2},z)-v_{b}(b,r,y_{1}^{m},y_{2})}{v_{y_{1}}^{\ast }(b,p,r,x,y_{1}^{m},y_{2},z)-v_{y_{1}}\left( b,r,y_{1}^{m},y_{2}\right) }. \label{dym/db} $$
(56)

There are two possibilities. One is that (51) is binding only if the agent complies, in which case (56) is definitely negative. The other is that (51) is binding whichever the strategy, in which case (56) may take either sign. A reduction in \(b\) may, thus, induce agents just below the income threshold to switch from going it alone to complying. These agents will start having children and making transfers. In the presence of altruism, the first proposition remains true, the second one becomes that agents just below the threshold may have more children and make more transfers.

The constitution model, thus, predicts that tighter credit may induce some agents to make more transfers despite the fact that they have become poorer. If altruism is absent or low, agents either above or sufficiently below the threshold will not change their transfer behavior. Controlling for possible endogeneity of the credit ration, Cigno et al. (2007) find survey data evidence that the probability of making a transfer does indeed increase if the agent is credit rationed. As that cannot be explained by conventional models of either the altruistic or the exchange variety, the finding rejects the hypothesis that transfer behavior is the outcome of unfettered individual optimization. Consistent with the constitution story, that paper also finds that the probability of making a transfer shows very low elasticity to the giver’s income and assets.

6 Discussion

Portraying the family as a society governed by a constitution, rather than as a purely affective relationship, enriches the economic analysis of fertility, saving and transfer behavior. It also narrows the gap between the sociologist’s stance, that individual actions are socially determined, and the economist’s approach, which assumes unfettered individual choice. But, we do not just assume that there are exogenously determined constraints on individual behavior. We derive conditions for the existence of a self-enforcing, renegotiation-proof family constitution prescribing that an adult must give at least a certain amount of money (or money and personal services yielding the same utility) to her parent and to each of her children if she has any.

For a constitution to be self-enforcing, adults must be at least as well-off complying with it, as going it alone in the market. For a constitution to be renegotiation-proof, the adults of the day must have no interest in amending it. Parental altruism makes it more likely that a constitution with these characteristics exists. But, if an agent is so rich and altruistic that she wants to give her children (not only while they are young but also when they grow up) more than the constitution prescribes, the constitution is obviously irrelevant.

A renegotiation-proof family constitution generates an efficient allocation of resources if and only if it makes the adults of the day strictly better-off complying, than going it alone. The intuitive explanation is that, as the agents are adults who will become old but will not be young again, the requirement that an agent must not be worse-off complying than going it alone would conflict, if binding, with the one that the lifetime utility of each individual must be at a maximum given everyone else’s. If the first requirement is binding, the agent will have too many children. Parental altruism makes no difference to that.

If an agent is so rich and altruistic that the constitution does not impose any effective restriction on her behavior, she will not necessarily behave efficiently. As already pointed out by Baland and Robinson in relation to the Becker–Barro model (where all agents are, in effect, altruistic go-it-aloners), the allocation will, in that case, be efficient if and only if neither the credit rationing nor the nonnegative bequests constraint is binding. As the second of these constraints is more restrictive than the constitutional prescription that an old person cannot take more than a certain amount from each of her grown-up children, the possible irrelevance of the family constitution does not make efficiency any more likely.

Exogenous changes in the economic environment may affect individual behavior in two ways: (a) by changing the choice of strategy and (b) by changing the behavior associated with each strategy. The former applies only to agents with income close to the threshold below which, in the absence of policy, it is optimal to go-it-alone. The latter applies to all agents. This may make the predictions of the model quite different from those of conventional economic models, where agents are assumed to optimize subject only to the law of the land. We looked at the effects of two environmental changes, the introduction or expansion of an actuarially fair pension scheme and a tightening of credit conditions. Those examples were chosen advisedly because the sign of (a) is or may be different from that of (b).

In the absence of parental altruism, the pension policy has non-positive effects on the fertility and private transfers of inframarginal compliers, those with income sufficiently higher than the threshold, and negative effects on those of marginal compliers. Some old people will consequently lose their children’s support. The effect on individual saving is negative where inframarginal go-it-aloners are concerned, positive where marginal compliers are concerned, zero where inframarginal compliers are. The effect on aggregate fertility is, thus, definitely negative, but the effect on aggregate saving may be positive or negative. This is in sharp contrast with the prediction of life cycle theory that the pension contribution would displace saving on a one-for-one basis. Parental altruism makes some difference in other respects but does not change the proposition that the policy may raise aggregate saving. This is in sharp contrast with the prediction of Becker–Barro that an actuarially fair pension system will cause a reduction in life-cycle saving but will have no effect on fertility and transfer behavior because it does not imply a forced transfer to or from the next generation.

Whether the agents are altruistic towards their children or not, a reduction in the amount they are allowed to borrow may induce some of them to have more children and to make larger transfers. This prediction contrasts with those of conventional models of either the altruistic or exchange variety. These results may come as a surprise to anyone who is used to thinking in terms of infinitesimal adjustments of the decision variables to infinitesimal changes in the exogenous ones. In a model where the first and most important decision is about which strategy to follow, however, it is possible that the discreet changes associated with a strategy switch will dominate the infinitesimal ones associated with optimization within a given strategy.