1 Introduction

Considering climate change and the increasing demand for living space, wood as a sustainable and renewable raw material offers good perspectives in the construction industry (Zhang et al. 2022). However, the material can only be used if the material behavior is sufficiently known, and strength values are available for the calculation of the components used. It is generally accepted that the properties of wood can be expressed by an equivalent homogeneous anisotropic continuum (de Borst et al. 2013).

Over the years, static methods, but especially dynamic methods, have achieved accurate results in testing the elastic modulus, shear modulus and Poisson’s ratio (Wang et al. 2014, 2015, 2018, 2022; Su et al. 2021; Zhou et al. 2021; Dauletbek et al. 2022; Chen et al. 2022). Many researchers used probabilistic methods to study mechanical properties of materials (Wang and Ghanem 2021, 2022; Peng et al. 2018). The shear modulus is often tested by the static square-plate torsional test using the shear strain at the center of the square plate face (plate theory) to calculate the shear modulus (Yoshihara 2009) or the four-point bending test under asymmetrical loading (Yoshihara and Sawamura 2006). Here, the calculation is based on the relationship between the maximum shear stress and shear strain occurring at the center line of the rectangular cross-section (beam theory). The shear modulus is calculated by testing the shear strain at the center point on the neutral axis of the beam cross-section (Wang et al. 2019b).

Common static methods to test the elastic modulus and Poisson's ratio of the material are the axial tensile test and the four-point bending test under symmetrical loading. For example, the four-point bending test was applied by Wang and Cao (Wang et al. 2017; Cao et al. 2017) to test the longitudinal and transverse elastic modulus and Poisson's ratio of OSB as well as MDF. The test is also widely used to investigate the mechanical properties of wood components (Ponzo et al. 2021; Zhou et al. 2021; Li et al. 2022). Although the four-point bending test is a well-developed test method for testing the elastic modulus, Poisson's ratio, and shear modulus of wood, there is still little research on the theory and test accuracy.

In this paper, the applicability of the symmetrical four-point bending test to testing the longitudinal elastic modulus and Poisson's ratio and the asymmetrical four-point bending test to testing the longitudinal shear modulus is investigated mathematically and experimentally. The focus is placed on the development of methods to improve the accuracy of the test parameters. In this context, the extent to which the measurement of the lateral deformation (strain) of the wood depends on the wood grain on the surface of the specimen and on the type of loading (tensile or compressive) is examined.

A method for improving the accuracy of the Poisson's ratio of the tested wood is also presented. Specifically, strain gauges with half bridges are used in two sets of the four-point bending test. After the first set is completed, the specimen must be rotated 180° around its central axis for the second set. The average value \(-{\varepsilon }_{y}/{\varepsilon }_{x}\) of the two groups is used as the test value for the Poisson’s ratio of the specimen and verified by the axial tensile method.

The methods for dynamic testing of the shear modulus of wood include free-member torsional vibration method, free-plate torsional vibration method, cantilevered-member torsional vibration method, cantilevered-plate torsional vibration method, and Timoshenko beam iteration method (JIS A1127-2001 2001; Wang et al. 2012, 2019a; Wang et al. 2016). The method for dynamic and static Poisson’s ratio testing of wood is also the method for the transverse stress equal to zero of the cantilever plate, which is based on the stress and strain analysis of the first bending mode and the static bending of the cantilever slab.

Although the position of the strain gauge is different for dynamic and static Poisson's ratio testing, the same results can be measured for Poisson’s ratio (Yin 1996; Wang et al. 2021).

In this paper, the axial tensile test (static), the static square-plate torsional test and the torsional vibration method for free bars (dynamic) are used to verify the four-point bending test as a test method to determine the elastic modulus, Poisson’s ratio and shear modulus in the principal directions. Finally, the four-point bending test is evaluated in comparison with the axial tension method for testing the Poisson’s ratio of wood. Particular attention is paid to wood grain and whether the stress is tensile or compressive, as this has a major effect on the transverse strain of the wood.

2 Materials and methods

The static analysis of the four-point bending test includes the analysis of the test under symmetrical loads (referred to as the symmetrical four-point bending) and under asymmetrical loads (referred to as asymmetric four-point bending).

2.1 FE calculations

2.1.1 Numerical analysis: materials and methods

Three different types of wood (spruce, Scots pine and beech) were tested in longitudinal (L), radial (R), and transversal (T) direction. The test specimen size of each beam was l × b × h = 240 mm × 20 mm × 20 mm. The coordinate system was selected as shown in Fig. 1. The x-axis runs along the length of the beam, the y-axis along the width and the z-axis along the height.

Fig. 1
figure 1

Definition of beam specimen and its coordinate system

Full size image

The static calculation in ANSYS 19 with a mesh size of 72 × 6 × 6 is performed using 3D solid-shell elements with finite strain. A load of 240N was evenly applied along the tangential and radial directions of the beam, and a load of 24N in longitudinal direction along the beam. The input parameters in longitudinal, radial and transversal direction of the different wood species for the static structural analysis are shown in Table 1. In Fig. 1, the indices x, y, z of the material constants used in Table 1 are assigned according to the principal directions (L, R, T) of the wood: tangential plane LT (x → L, y → T, z → R); radial plane LR (x → L, y → R, z → T); longitudinal plane RT (x → R, y → T, z → L). xy plane is defined as the principal plane (top/bottom plane) (Fig. 2).

Table 1 Input parameters for the static structural analysis ANSYS 19.0 for spruce, Scots pine and beech (Yin 1996)
Full size table
Fig. 2
figure 2

Schematic diagram of principal direction L, T and R of beam corresponding to x, y and z

Full size image

2.1.2 Stresses and strains for symmetrical four-point bending

The mechanical model for the static analysis of the symmetrical four-point bending beam is shown in Fig. 3. The center span is subjected to pure bending with a bending moment of Pl/6. The stress and strain output of ANSYS static analysis contains not only the stress or strain distribution along the x direction and y direction, but also z direction. As far as the elastic modulus and Poisson’s ratio of the symmetrical four-point bending test are concerned, it is only related to the stress or strain distribution along the x direction and y direction, so only the x, y stress and strain components are involved in the following Table 2 and Fig. 4. The results of the static analysis with ANSYS show that there are no points where the transverse stress is zero at the bottom and top of the beam in this section.

Fig. 3
figure 3

Loading schematic diagram of symmetrical four-point bending test

Full size image
Table 2 Calculated values of shear stress \({\tau }_{xz}\) and shear strain \({\gamma }_{xz}\) at the midspan of the beam of asymmetric four-point bending spruce, Scots pine and beech beams (x → L, y → T, z → R) (Yin 1996)
Full size table
Fig. 4
figure 4

Curvilinear expression on the centerline of pure bending of spruce radial beams across the surface

Full size image

The stresses and strains at the center of the top and bottom surfaces of the beam are calculated by ANSYS from the symmetrical four-point bending test for longitudinal, radial and tangential beams.

Figure 4a shows the \(E-x/l\) curve of a spruce radial beam along its surface centerline in a state of pure bending. From this curve, it can be seen that the \({\sigma }_{x}/{\varepsilon }_{x}\) ratio of the beam is equal to the input value of the elastic modulus \((E=11.6\) GPa). Figure 4b and c show the \({\sigma }_{y}/{\sigma }_{x}-x/l\) and the \(-{\varepsilon }_{y}/{\varepsilon }_{x}-x/l\) -curve of the same beam. It can be seen that the \({\sigma }_{R}/{\sigma }_{L}\) ratio in the middle region is approximately zero. In this region, the ratio of \(-{\varepsilon }_{R}/{\varepsilon }_{L}\) corresponds to the spruce’s radial Poisson’s ratio (\({\mu }_{LR}=0.37\)). At no point on the surface centerline, it is lower than this value.

2.1.3 Static calculation for asymmetrical four-point bending

The test setup for testing the shear modulus of wood using the asymmetrical four-point bending test is shown in Fig. 5. When the line of action of the load P acting perpendicularly on the auxiliary beam passes through the center of the beam specimen and the geometric restraint conditions of the auxiliary beam and the beam specimen are met as shown in Fig. 5a, only shear force acts on the midspan section of the beam specimen, whose value is equal to P/2. The bending moment is equal to zero, as shown in Fig. 5b.

Fig. 5
figure 5

Schematic diagram and force diagram of experimental setup for asymmetrically loaded four-point bending beam

Full size image

The output data of the ANSYS static structural analysis are shown in Table 2. The shear stress and shear strain at the center of the beam and the ratio of shear stress to shear strain are listed. This agrees with the reference value of the main shear modulus from the static calculation of ANSYS.

2.2 Experimental design

The experiments in this paper were conducted at equilibrium under constant temperature and humidity. The objective of these experiments is to improve the implementation and accuracy of the symmetrical four-point bending test to improve the determination of the longitudinal elastic modulus, Poisson’s ratio of wood. In addition, the patch scheme and full bridge method to improve the accuracy of testing wood principal shear modulus by asymmetrical four-point bending beam method are studied.

The parameters of the beam and plate specimens in the radial and tangential directions of larch and the beam and plate specimens in the transverse direction of Sitka spruce are shown in Table 3.

Table 3 Parameters of larch radial, larch tangential, and Sitka spruce longitudinal specimens
Full size table

The beam specimens were subjected to symmetrical four-point bending and asymmetrical four-point bending loading tests with a span of 240 mm. The shear modulus of the plate specimens was tested by the free bar torsional vibration method and the square plate static torsional strain method (Wang et al. 2019c) to verify the validity of the four-point bending beam method.

2.3 Installation scheme of strain gauges

2.3.1 Symmetrical four-point bending test

To verify the test values of wood elastic modulus, Poisson’s ratio and shear modulus are related to the stress state and wood grain distribution characteristics of the specimens. Especially, the stress state of the specimen and the distribution characteristics of wood grain have a significant impact on the test value of Poisson's ratio. In the symmetrical four-point bending test, a four-channel 1/4 bridge is designed to simultaneously test the \(0^\circ\) strain and \(90^\circ\) strain of the center of the top and bottom surfaces of the specimen and calculate the elastic modulus and the \(-{\varepsilon }_{90^\circ }/{\varepsilon }_{0^\circ }\) ratio, respectively.

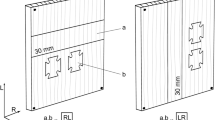
Strain gauges are attached longitudinally (0°) and transversely (90°) to the midpoints of the top and bottom of the specimen (one of the principal faces of the wood, LT, LR or RT), as shown in Fig. 6. The radial and tangential planes are perpendicular to each other, and the patch is shown in Fig. 7. A symmetrical load is applied to the beam specified in Fig. 3, and the longitudinal and transverse strains at the midpoint c are measured. The longitudinal and transverse strain measurements each occupy one channel of the strain gauge and a half-bridge circuit is used for connection. The tests are carried out with strain gauges of BX-120 type, which have a grid pattern of 5 mm × 3 mm.

Fig. 6
figure 6

Transverse and longitudinal strain gauges pasted at the center point of the beam surface (principal plane)

Full size image
Fig. 7
figure 7

Schematic diagram of pasting strain gauges at the center point of beam surface both radially and tangentially

Full size image

2.3.2 Asymmetrical four-point bending test

With the asymmetrical four-point bending test, the principal shear modulus is tested as follows: Two strain gauges are attached symmetrically at \(\pm 4{5}^{\mathrm{o}}\) relative to the center on the centerline of a side surface (wood main plane) of the specimen. Strain gauges are placed on both sides on the sample. To improve the accuracy, the test of the four strain gauges was carried out using the full bridge method to determine the principal shear modulus of the wood.

Strain gauges are attached at \(\pm\) 45° angles to the midpoints of the test plane of the beam specimen (to one of the principal faces of the wood, LT, LR or RT) as shown in Fig. 8. The beam is loaded asymmetrically as shown in Fig. 4 and the shear strain at the center point C is measured. The strain gauges on the front and back of the beam occupy one channel of the strain gauge and a full-bridge circuit is used for connection. They were used to measure average strain of both side surfaces in a channel directly.

Fig. 8
figure 8

Strain gauge pasted at the center point of the side (principal plane) of the beam surface

Full size image

2.4 Calculation

2.4.1 Elastic modulus

In the middle section, a region of pure bending occurs in the beam during the symmetrical four-point bending test. The normal stress (\(\sigma )\) on the top and bottom of the beam can be calculated as follows:

$$\sigma =\frac{Pl}{b{h}^{2}}$$
(1)

where P is the load in N, l is the beam length in mm, b is the beam width in mm and h is the beam height in mm. When the longitudinal strain of the midpoint of the top and bottom of the beam is \({\varepsilon }_{x}\), the elastic modulus can be expressed by Hooke's law as shown in Eq. (2), written incrementally for ease of testing:

$$E=\frac{\Delta Pl}{b{h}^{2}{\Delta \varepsilon }_{x}}$$
(2)

where E is the elastic modulus in MPa, \(\Delta P\) is the load increment in N and \(\Delta {\varepsilon }_{x}\) is the longitudinal strain increment in \(\mathrm{\mu m}/\mathrm{m}\).

2.4.2 Poisson's ratio

In the area of pure bending, the Poisson's ratio (\(\mu\)) for the symmetrical four-point bending beam can be expressed by the ratio of the transverse strain (\({\varepsilon }_{y})\) and the longitudinal strain (\({\varepsilon }_{x})\) at the midpoint of the top and bottom faces of the beam, as seen in Eq. (3).

$$\mu =-\frac{{\Delta \varepsilon }_{y}}{{\Delta \varepsilon }_{x}}$$
(3)

2.4.3 Shear modulus

The shear modulus (G) describes the relationship between the shear stress (\(\tau )\) and the engineering shear strain (\(\gamma )\). The maximum shear stress is located at the neutral axis of the beam and is calculated for a rectangular cross-section as shown in Eq. (4).

$$\tau =\frac{3P}{4bh}$$
(4)

The shear strain is calculated as \(\gamma ={\varepsilon }_{-4{5^\circ }}-{\varepsilon }_{4{5^\circ }}\) using the strains measured in the negative 45° and positive 45° directions in the asymmetrical four-point bending test at the center of the average of both side faces of the beam. From this, the shear modulus of wood can be calculated using Hooke's shear law. To simplify the calculation, the equation is written in incremental form:

$$G=\frac{3\Delta P}{4bh\left|{\Delta \varepsilon }_{-45^\circ }-{\Delta \varepsilon }_{45^\circ }\right|}$$
(5)

If a full bridge circuit is used, the strain increment measurement (\({\Delta \varepsilon }_{swot})\) can be inserted in Eq. (5) to calculate the shear modulus by the asymmetrical four-point bending test.

$$G=\frac{3\Delta P}{8bh{\Delta \varepsilon }_{swot}}$$
(6)

When the top and bottom surfaces of the beam are defined as one of the principal planes (LT, LR, RT), the principal elastic moduli EL, ER, ET are tested according to Eq. (2) and Poisson's ratios \({\mu }_{LT},{\mu }_{LR},{\mu }_{RT}\) are tested according to Eq. (3). If the front and back surfaces are defined as the principal planes of the wood, the principal shear moduli GLT, GLR and GRT are tested according to Eq. (5).

2.5 Implementation of the symmetrical four-point bending test with half-bridges

The LR and LT tests are both on (actually the same) specimens with beams in longitudinal direction. There are 3 such specimens. Their size is 260 mm × 20 mm × 20 mm. They were recorded as Larch 1–3. The total of 8 strain gauges are pasted at the center of each specimen as shown in Fig. 7 and Fig. 9. When determining E and \(\mu\) using the symmetrical four-point bending test, the wood grain should be considered. As in Fig. 9, when the LT surface is the top and bottom surfaces, one of the top and bottom surfaces is artificially defined as the A surface, then the other side is defined as the B surface. This definition method is also applicable to the case where the LR surface is the top and bottom surfaces. During the bending test, a compressive stress is generated on the upper face of the beam and a tensile stress on the lower face. Table 4 shows the values for each of the four placing options of the beam in the testing machine. Thus, the transversal side with the wood grain type A is first on top (compressive stress) and then on the bottom (tensile stress) by rotating 180° around the center axis. This is done identically for the side B. The words upward and downward indicate the compressive stress on the upper surface and the tensile stress on the lower surface, respectively.

Fig. 9
figure 9

Test specimen (larch) for four-point bending: Definition of fiber direction and wood grain

Full size image
Table 4 Elastic modulus (E), shear modulus (G) and Poisson's ratio (μ) tested by four-point bending, the axial tensile method, the torsional vibration method for free bars and the static square-plate torsional test (COV %)
Full size table

2.6 Validation tests

The axial stretching method (Gere and Goodno 2012) is used to demonstrate the validity of the symmetric four-point bending beam method for measuring E and \(\mu\).

The square plate static torsional strain method and the free rod torsional vibration method (Wang et al. 2019c) are used to demonstrate the validity of the asymmetric four-point bending beam method for G.

3 Results and discussion

3.1 Validation of test results

Symmetrical four-point bending tests for measuring the elastic modulus and the Poisson’s ratio and asymmetrical four-point bending tests for measuring the shear modulus were validated by axial tension (Yamasaki and Sasaki 2003), static square-plate torsional tests and the torsional vibration method (Wang et al. 2019c) for free bars. Table 4 shows the comparison of the longitudinal and radial constants (E, G, µ) of larch and the transverse constants (E, G, µ) of Sitka spruce determined with the different test methods.

It can be seen that the Poisson's ratio tested by four-point bending agrees with the Poisson's ratio tested by the axial tensile method. However, ER tested by four-point bending is about 11% higher and EL is 24% higher than the elastic modulus tested by the axial tensile method. The shear modulus tested by four-point bending agrees with the shear modulus tested by static square-plate torsional tests and the torsional vibration method for free bars. Furthermore, it was checked whether the beam length influences the test results (E, µ) in the symmetrical four-point bending tests. It was found that the measured values in the area of pure bending for a 300 mm long larch beam were almost identical to those of the 240 mm long beam.

3.2 Feasibility analysis of the symmetrical four-point bending test for measuring E

The data in Tables 2, 3, and 5 show that the ratio of longitudinal stress to longitudinal strain at the center point of the top and bottom beam surfaces is basically equal to the value of the principal elastic modulus. Figure 4 also shows that the ratio of longitudinal stress to longitudinal strain at any point on the centerline of the beam surface along the pure bending section is equal to the value of the principal elastic modulus EL of the spruce beam. This shows that it is possible to measure the elastic modulus using the symmetric four-point bending beam method.

Table 5 Influence of the wood grain on the modulus of elasticity (E) and Poisson's ratio (-εy/εx) in longitudinal and radial direction on the top and bottom of the specimen
Full size table

If the experimental values (P = 240N, l = 240 mm, b = 20 mm, h = 20 mm) are used in Eq. (1) to calculate the longitudinal stress, the calculated stress of 7.2 MPa is almost 4.5% higher than the longitudinal stress calculated by ANSYS for the beam at the midpoint of the top and bottom surfaces. It is about 4.7% larger, but the measured results may have a higher percentage (Table 4).

3.3 Feasibility analysis of the asymmetrical four-point bending test for measuring G

The values of shear stress and shear strain on the neutral axis of the central cross-section calculated with ANSYS as well as the ratio \({\tau }_{xz}/{\gamma }_{xz}\) (Table 5) agree well with the measured values for the principal shear moduli (\({G}_{LR}\), \({G}_{LT}\) and \({G}_{RT})\) in the asymmetrical four-point bending test. The \({\tau }_{xz}\) value of the longitudinal center point calculated by ANSYS is also in good agreement with the calculated value of Eq. (4) (0.45 MPa in the longitudinal and radial directions and 0.045 MPa in the transverse direction). Therefore, the asymmetrical four-point bending test can be used to calculate the principal shear modulus of wood by measuring the shear strain on the neutral axis of the mid span cross-section and calculating the shear modulus according to Eq. (5).

3.4 Error analysis of the symmetrical four-point bending test for measuring μ

It is assumed that the middle section of the beam in the symmetrical four-point bending test is in a plane stress state, i.e., that the transverse stress in this area is zero. In reality, however, there are no points where the transverse stress is zero. This inevitably leads to an error in the ratio of transverse to longitudinal strain and the Poisson’s ratio. In general, the stress–strain relationship in the tangential direction of wood can be calculated as follows:

$${\varepsilon }_{L}=\frac{{\sigma }_{L}}{{E}_{L}}-{\mu }_{TL}\frac{{\sigma }_{T}}{{E}_{T}}$$
(7)
$${\varepsilon }_{T}=\frac{{\sigma }_{T}}{{E}_{T}}-{\mu }_{LT}\frac{{\sigma }_{L}}{{E}_{L}}$$
(8)

From Eqs. (7) and (8) and the relationship of \({E}_{L}{\mu }_{TL}={E}_{T}{\mu }_{LT}\), the formula for calculating Poisson's ratio considering transverse stress can be derived:

$${\mu }_{LT}=\left(-\frac{{\varepsilon }_{L}}{{\varepsilon }_{L}}+\frac{{\sigma }_{T}}{{\sigma }_{L}}\bullet \frac{{E}_{L}}{{E}_{T}}\right)/\left(1-\frac{{\varepsilon }_{T}}{{\varepsilon }_{L}}\frac{{\sigma }_{T}}{{\sigma }_{L}}\right)$$
(9)

A Scots pine beam in longitudinal direction is studied as an example. It is assumed that there is a numerical relationship between the calculated longitudinal and transverse strains and the Poisson's ratio from the four-point bending test of the principal direction of the material at the center of the top and bottom faces of the beam.

Since \({\sigma }_{T}/{\sigma }_{L}\) for Scots pine is only about 0.0004, the Poisson's ratio can be calculated sufficiently accurately using the four-point bending test with the equation \(-{\varepsilon }_{T}/{\varepsilon }_{L}\) for the midpoint on the top and bottom sides of the beam. The magnitude of the inaccuracy is only 1.4%.

3.5 The influence of the wood grain on the modulus of elasticity and Poisson's ratio in longitudinal and radial direction on the top and bottom of the specimen

As shown in Fig. 8, the upper and lower surfaces are LT surfaces, where the modulus and Poisson's ratio of larch (LT) can be tested, and the strain gauges are attached to the upper and lower surfaces. To test the modulus and Poisson's ratio of larch (LR), the specimen is rotated \(90^\circ\) around the x-axis so that the radial surface LR is located on the upper and lower surfaces of the specimen (the so-called upper and lower surfaces and front and rear sides of the specimen are relative to the specimen placed on the support of the four-point bending test rig) as shown in Table 5.

From the test data in Table 5, it can be seen that the stress state and wood grain distribution characteristics on the top and bottom of the specimen stress has little effect on the modulus of elasticity, or longitudinal strain.

The radial and tangential elastic modulus and Poisson’s ratio of larch 1 and larch 2 tested by 1/4 bridge and half bridge method are shown in Table 5. Two sets of the symmetrical four-point bending half-bridge method tests were performed to ensure the accuracy of the elastic modulus and Poisson’s ratio of the wood. After completing one group of tests, the specimen was rotated 180° about its central axis (Fig. 9) and placed on the test stand. Then another group was measured. Each group of half-bridges was measured three times, and the average value of the last two sets was determined. Take the average value as the final test result, as shown in Table 5. The test values of elastic modulus and Poisson's ratio of two groups of half bridge wood of Larch 3 are also listed in Table 5, and the law is the same as that of Larch 1 and 2.

3.6 Comparison of the four-point bending test and the axial tensile test for measuring E and μ

The axial tensile method is suitable for both isotropic and anisotropic materials for measuring longitudinal and transverse strain and thus for calculating the elastic modulus and Poisson’s ratio. The formula for deriving the elastic modulus or the Poisson’s ratio is independent of the material type, making the axial tensile method a classic method for measuring the elastic modulus and the Poisson’s ratio of a material. In the four-point bending test, in addition to the elastic modulus and the Poisson's ratio of the material, the shear modulus of the material can also be tested, which is the advantage of the four-point bending test.

For Poisson’s ratio testing of wood, both the axial tensile method and the four-point bending test determine Poisson’s ratio from the ratio of transverse strain to longitudinal strain, but it should be clear that there are differences between the two methods. Considering the need to eliminate the bending strain that may occur due to the misalignment of the load during axial stretching and the different distribution characteristics of the wood grains on the two surfaces of the specimen, in the axial tension method, strain gauges in the longitudinal and transverse directions are pasted to both surfaces of the specimen, and then each connected in series and joined by a 1/4 bridge. The tensile specimen is subjected to a uniform tensile stress, so the axial tensile method does not take into account the different signs of the stresses on the two surfaces of the specimen. When testing Poisson’s ratio according to the four-point bending test, strain gauges are also applied to both surfaces of the specimen in the longitudinal and transverse directions. They take into account not only the different distribution characteristics of the wood grain on the two surfaces of the specimen, but also the different signs of the stresses occurring on the two surfaces, i.e., one surface of the specimen is subjected to tensile stress while the other surface must be subjected to compressive stress. From this point of view, the four bending test better reflects the mechanical behavior of wood than the axial tensile method when testing material parameters.

4 Conclusion

The present work aimed to explore the factors affecting the accuracy of wood elastic modulus, Poisson's ratio and shear modulus tested by four-point bending beam method, and to provide methods to improve the test accuracy. Based on the results of this study, the following conclusions can be drawn:

  • Under symmetrical loading, the longitudinal strain of the beam in the four-point bending test is uniformly distributed at each point of the centerline on the top and bottom surfaces in the pure bending section. From the ratio of longitudinal stress to longitudinal strain of beams’ center, the principal elastic modulus of wood can be calculated. The transverse strain is uniformly distributed only in a small area in the middle of the beam (x/l = 0.45–0.55), so that the principal Poisson's ratio of wood can be calculated there using the ratio of transverse strain to longitudinal strain.

  • For asymmetrical loading in the four-point bending test, the ratio between shear stress and shear strain at the center of the beam side is exactly equal to the shear modulus of the top plane.

  • In the symmetrical four-point bending test, the test values for the longitudinal strain of each point on the centerline of the top and bottom of the beam in the section of pure bending are basically independent of the different characteristics of the wood grain and the stress properties of the top and bottom of the beam. However, the test values for the transverse strain are quite sensitive to the characteristics of the wood grain and the stress properties of the top and bottom of the beam, so the test value for the Poisson’s ratio has a large variation

  • The dispersiveness of the Poisson’s ratio test values in the symmetrical four-point bending test can be reduced by conducting two sets of the symmetrical four-point bending half-bridge method tests, while the second time, the specimens were rotated180°. Furthermore, the results can be verified by the tensile method.

  • The asymmetrical four-point bending test with the application of one strain gauge each in a positive and negative 45° angle with a full-bridge configuration can effectively obtain the exact shear modulus of wood.

  • The suitability and its accuracy of the four-point bending test for testing the principal elastic modulus, Poisson's ratio and shear modulus were verified by the axial tensile method, static square-plate torsional tests and the torsional vibration method for free bars