1 Introduction

Wood is an orthotropic material that has many uses in daily life. In structural design and load-bearing applications, some important parameters of wood, such as its shear elasticity (GLT and GLR) and true longitudinal elasticity (EL), are relatively difficult to measure. These parameters are required in engineering simulation software or theoretical models for predicting the behavior of wood. It is difficult to obtain true E values through general three-point bending test methods owing to the shear effects under bending according to Timoshenko’s beam theory (Timoshenko and Young 1962). The elastic modulus calculated based on deflection is also underestimated (Kollmann and Côte 1968; Bodig and Jayne 1982). Further, the exact G value cannot be obtained.

Many studies have been conducted to measure these two parameters. For example, the shear elasticity has been determined through a twisting test (Yoshihara 1993) or a 45° off-axis compression test or test involving various grain angles (Wilczyński and Kociszewski 2011; Aira et al. 2014); EL could be obtained by three-point bending with various span/depth ratios or by four-point loading (Dong et al. 1994; Bostrom 1999; Brancheriau et al. 2002; Nocetti et al. 2013). Some of these approaches can only be applied to small and clear specimens rather than standard specimens, and they have extremely stringent requirements related to grain distribution and orientation. Furthermore, some standard approaches cannot deal with EL and G at the same time (ASTM D143-14  2014; BS EN 408 2012; ISO 3133 1975; JIS Z 2101 2009).

The four-point bending is one of the most common approaches to evaluate the modulus without shear effect, in which the deflection is not influenced by loading head indentation (Brancheriau et al. 2002). However, the quality of the material in the shear-free section may affect the overall deflection of the specimens. In addition, the four-point bending test is usually applied to large size specimens. The higher material size requirements are also a limitation of the four-point bending method in practice for small specimens. Moreover, the four-point bending test is also subject to some error due to the initial twist of specimens and the little deflection scale (Nocetti et al. 2013). More details about the difference between a three-point bending and a four-point bending are described in previous studies (Brancheriau et al. 2002; Babiak et al. 2018).

Kass (1975) used levers and suspended heavy objects to create constant bending moment conditions. However, these methods cannot ensure that the material is subjected to only pure bending. Samson and Sotomayor-Castellanos (2007) used edge bending to obtain the E of structural materials; however, their measurement setup was complicated and was suitable only for edge bending. By contrast, many researchers have used dynamic methods such as ultrasonic wave, plate vibration, or stress wave to determine E (Nakao et al. 1985; Sobue 1986; Gonçalves et al. 2011; Yang et al. 2015; Wang et al. 2018). However, these indirect methods cannot easily obtain the true E value under bending. Although these methods offer fast operation, they require relatively complicated and expensive equipment. Further, the shear effect of the beam during bending changes with the span/depth ratio; as an alternative, an equation describing the relationship among the shear elasticity, apparent bending elasticity, and true bending elasticity was applied by measuring the apparent elasticity under various span/depth ratios, and then, the shear elasticity and true bending elasticity were estimated by regression (Yoshihara et al. 1998; Bradtmueller et al. 1998). However, according to the current analyses in this study, this method is affected by the local stress concentration effect induced by the loading head, and thus, the E /G ratio would vary with the span range used for regression.

A strain gauge is a common and cheap strain measuring tool. Yoshihara and Tsunematsu (2006) used a strain gauge to determine the elastic modulus of spruce. Bending elasticities were calculated by measuring the deflections at the middle and quarter-point of the span using center loading. The effects of shear deflection and stress concentration at the loading point on the measured elasticities were compared. Further, the true elasticity was estimated through a regression analysis; however, the shear elasticity was not considered.

The aim of the present study was to develop a new method to directly measure the true E and G values by using a strain gauge and a dial gauge simultaneously. To evaluate the validity of the presented approach, E and E /G estimated through the regression method using the apparent EL under various span/depth ratios were used. Further, four-point loading with shear-free surface strain was measured and applied to determine the true E for comparison. The four-point bending tests were also conducted for verification. The proposed approach could be applied to various settings to easily obtain true E and G values.

2 Theory

According to Timoshenko’s beam theory, when a beam is subjected to center loading, the shear stress induces additional deflection. The total deflection at the midspan (δt) of the beam is the sum of deflections caused by the bending moment (δb) and shear stress (δs), and it can be expressed as follows:

$${\delta }_{t}={\delta }_{b}+{\delta }_{s}$$
(1)

The total deflection is expressed as

$${\delta }_{t}=\frac{P{l}^{3}}{48{E}_{a}I}$$
(2)

where P is the central load below the proportional limit, I, is the moment of inertia of the cross section, l, is the span, and Ea, the apparent bending elasticity.

The deflection induced by the bending moment is expressed as

$${\delta }_{b}=\frac{P{l}^{3}}{48EI}$$
(3)

where E is the true bending elasticity.

The deflection caused by shear is calculated by shear strain analyses and is expressed as

$${\delta }_{s}=\frac{0.3Pl}{GA}$$
(4)

where A is the cross-sectional area and G is the shear elasticity. Using deflection and strain, E can be expressed as

$$E=\frac{P{l}^{3}}{48{\delta }_{b}I}= \frac{Plh}{8\epsilon I}$$
(5)

where ε is the axial bending strain on the lower side of the beam at the midspan and h is the thickness of the beam.

Equation (5) is rearranged to obtain the following relation between δb and ε:

$${\delta }_{b}=\epsilon \left(\frac{{l}^{2}}{6 h}\right)$$
(6)

Further, Eqs. (1)–(4) using rectangular cross-section are rearranged to obtain a general equation of G and E associated with span/depth ratio.

$$\frac{1}{{E}_{a}}=\frac{1}{E}+\frac{1.2}{G}\frac{{h}^{2}}{{l}^{2}}$$
(7)

where 1.2 is Timoshenko’s shear factor. G here represents GLT or GLR, depending on loading directions and configurations.

3 Materials and methods

3.1 Materials

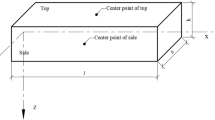
In this study, red oak (Quercus rubra) and Japanese cedar (Cryptomeria japonica) were selected to represent hardwood and softwood, respectively. Representative specimens from the hardwood and softwood were selected to demonstrate the operating method presented in this study, and the feasibility of this method was verified by experimental data. These specimens were conditioned at approximately 25°C and 65% relative humidity for at least 1 year before the tests. Two clear specimens for each species with dimensions of 1000 mm (longitudinal), 20 mm (width), and 20 mm (depth) were cut and processed carefully to ensure that the annual rings were distributed orthogonally on the cross section and the grain was parallel to the longitudinal direction. GLT and GLR can be obtained through loading on the radial and tangential surfaces of the specimen, respectively, as shown in Fig. 1. Table 1 lists the basic properties of the materials, including the equilibrium moisture content (EMC), ring width, and bulk density.

Table 1 Basic properties of specimens
Full size table

3.2 Center loading bending test

Experiments were conducted using universal testing machine (Model 43, MTS Inc., USA) with a 2.5 kN loadcell. All experiments in this study were conducted according to ASTM D 143-14. Strain gauges (FLA-3-11-5 L, Tokyo Measuring Instruments Lab., Tokyo, Japan) were attached to the center point of the radial (R) and tangential (T) surfaces of the same specimen, respectively, along the neutral axis then through loading on the backside (Fig. 1). In other words, the strain gauge was attached to the tension side of the beam to make conventional approach more efficient. At the same time, the deflection of the whole specimen was measured using a digital dial gauge (543-791B, Mitutoyo Corp., Tokyo, Japan.), and the displacement of the vertical movement of the crosshead was recorded. The span was varied from 780 mm (span/depth ratio = 39) to 160 mm (span/depth ratio = 8), and the pitch was gradually reduced in steps of 40 mm. To obtain a more representative Ea/E curve, according to Bodig and Jayne (1982), for a span shorter than 300 mm, the interval was reduced to 20 mm. Under each span, bending tests were performed three times at a load speed of 2 mm/min.

By rearranging Eq. (5), E can be calculated using Eq. (8). The strain ε is measured using the strain gauge at the corresponding P. This E is considered the true E because the strain ε measured using the strain gauge is only the axial strain.

$$\it {E}=\frac{3Pl}{2\epsilon b{h}^{2}}$$
(8)

where b is the width of the beam specimen.

The apparent bending elasticity Ea can be calculated using Eq. (9), where δt is the dial gauge reading, representing the total deflection.

$${E}_{a}=\frac{P{l}^{3}}{4{\delta }_{t}b{h}^{3}}$$
(9)

Moreover, Eq. (10) is obtained by rearranging Eqs. (1), (2), (4), and (6); therefore, G can be calculated by directly measuring δt and ε simultaneously at load P. Figure 1 shows the setup of the test.

$$G=\frac{0.3Pl}{\left({\delta }_{t}-\epsilon \left(\frac{{l}^{2}}{6 h}\right)\right)A}$$
(10)

Equation (7) is derived from the deflection relationship of the center-loading bending as Eq. (1), where Ea can only be measured from the δt that is obtained from the dial gauge within the proportional limit during the test. Therefore, it is traditionally necessary to use regression method to calculate true E and G values (Yoshihara and Tsunematsu 2006). This study used strain gauge to measure E, and Eq. (6) to convert strain to δb. Then, the strain measured using strain gauge and δt using dial gauge in the center-loading bending test were substituted into Eq. (10) to directly determine G. This is a valuable novel approach to measure and determine true E and G values simultaneously by isolating the Timoshenko’s shear effect. Strain from the surface was not affected by beam shear, and the shear modulus could thus be derived from the difference between \({\delta }_{t}\) and \(\epsilon\).

3.3 Estimation of E L and E/G

Equation (7) describes the relationship among E, Ea, and G. In a conventional bending test, only the apparent Ea can be obtained by measuring the total deflection δt. In this study, by using Ea obtained at various span-depth ratios, E and E/G can be estimated by linear regression. By plotting Ea (h/l)2 on the X-axis and Ea on the Y-axis, the slope of the regression line is obtained as 1.2 E/G, and the intercept at the Y-axis is E. This regression equation is reorganized based on Eq. (7), in order to indicate a clear physical meaning directly. As the span approaches infinity, (h/l)2 will approach to zero. Since the effect of shear is eliminated, Ea will be equivalent to E, which is exactly equal to the intercept of the regression line on the Y-axis.

3.4 Four-point loading bending test

A four-point bending test was conducted using the same machine as that mentioned previously and at the same loading speed. The total span was 675 mm; this is three times the inner span. Equation (11) can be used for calculating E under pure bending, where ε is measured at the lower side of the inner midspan. The E value was determined from strain gauge on the surfaces of the specimen rather than the load-deflection diagram obtained from the four-point bending test.

$$E=\frac{Pl}{\epsilon b{h}^{2}}$$
(11)

4 Results and discussion

4.1 Measurement of elasticity

Figure 2 shows plots of E versus l/h (span/depth ratio) obtained using different methods. First, the elasticity values obtained using various methods differed significantly under different span-to-depth ratios. For small spans, the E values obtained through different approaches gradually diverged from each other. The E values measured using a strain gauge did not change with span/depth ratio for the two species and two loading surfaces but increased slightly when the span was reduced (Fig. 2). Theoretically, the true E does not change with the span/depth ratio because it is independent of the effect of shear. However, the force distribution of the three-point load is not an ideal “point force” but is affected by the radius of the loading head, resulting in a local indentation effect due to high stress concentration. When the span/depth ratio is small, the force required to create a certain strain is increased greatly. Therefore, the position originally approximated as the “point load” becomes the locally distributed load, and the effective bending moment in the bending test decreases slightly. In turn, the actual strain is underestimated, causing E to increase slightly; this is consistent with the results of Yoshihara and Tsunematsu (2006) regarding local indentation. The solid lines in Fig. 2 indicate E obtained using the representative regression method, which can be used to verify the strain gauge method investigated in this study. E measured by the two methods was similar, especially for a large span/depth ratio. This means that the proposed method has high applicability and can be used to estimate the actual E value. Because the strain measured using a strain gauge only reflects the tensile strain, which is only distributed on the specimen surface, the shear effect does not influence the results.

Many studies have confirmed that red oak has higher stiffness than Japanese cedar (Kollmann and Côte 1968). The radial surface usually possesses higher stiffness owing to the structure of the earlywood and the latewood arrangement. The three E in Fig. 2 all show the same relative relationship. However, the level of deviation between the regression method and the strain gauge method E differs slightly between species. In this study, the hardwood had higher stiffness and surface hardness, and therefore, it may have exhibited a smaller effect of local depression compared with the softwood.

As mentioned previously, the effect of shear became considerable when the span/depth ratio decreased; the Ea/E ratio curve plotted in Fig. 3 can be used to describe this phenomenon. Ea and E are remarkably similar at large spans, and the values of the curve are also close to 1. However, as the span decreased, the Ea/E ratio also decreased gradually. Notably, the gap between the two curves in Fig. 3 increased when the span decreased, and the Ea/E curve obtained using the strain gauge was lower than that obtained using the regression approach; this, too, can be attributed to local depression. In the regression approach, the range used for the regression was maintained within 780–260 mm to avoid the influence of local depression data to a certain extent. The Ea/E ratio calculated accordingly should more accurately reflect the gradual elaboration of the shear effect with a decrease in span. This reaffirms that the problems caused by local depressions cannot be ignored.

Finally, theoretically, a pure bending moment area without shear effect can be created by conducting a four-point bending test, to obtain a realistic E value by using a strain gauge to measure the surface strain. Table 2 lists the results and elastic constants obtained using different approaches. It shows that the E value is similar to the regression results within 780–260 mm, and it is similar to the E value obtained using the strain gauge with standard ASTM specimens (l/h = 14). This reconfirms that the reliability of the E value measured using the strain gauge was quite high. However, the load point of the four-point load also has a curvature; therefore, E was still overestimated due to local depression. Samson and Sotomayor-Castellanos (2007) found that the four-point bending test has more noticeable size effects than the three-point test, which is a limitation of the ASTM test.

Table.2 Overall comparison of results
Full size table

4.2 Regression approach

The regression approach was used for verification in this study. A depth/span ratio approaching 0 indicates that the span is infinite. When the effect of the shear force can be ignored completely, Ea coincides completely with E, and therefore, the Y-axis intercept of the regression line is E. The slope represents the relative effect between the bending elasticity and the shear force as the span changes. Therefore, E/G can be obtained by dividing the slope by the shear factor. Figure 4 shows the representative regression results and regression equation.

However, owing to the aforementioned effects, the Ea variation under different span/depth ratios changes the regression results. E calculated using different regression ranges is listed in the supplementary information (Table S1). Table 2 shows the calculated regression results within 780–260 mm considering the largest R2 value. Under the full range regression, R2 is significantly lower. As the E/G ratio increases gradually with a decrease in regression range, once the points with a small span/depth ratio are included, the slope of the regression line gradually becomes smaller. The difference in the regression ranges leads to different calculation results that have not been mentioned in previous studies (Yoshihara and Tsunematsu 2006); the most reasonable explanation for this phenomenon may be local indentation. As shown in Table 2, the best fit was within the 780–260 mm range according to the highest R2; these results were chosen for representing the regression approach in this study. Table 2 also lists the average values of E, GLT and GLR, which were similar to the regression results. Furthermore, compared with the results measured using the strain gauge for a span/depth ratio of 14, the results were practically credible. The relative trend of species and the load surfaces of specimens were quite consistent with common knowledge (Kollmann and Côte 1968). In Fig. 4, the radial surface for both softwood and hardwood shows higher R2 values. This can be attributed to the more homogeneous microstructure on the radial surface under the bending test.

4.3 Shear elasticity G and E/G ratio

The G value can also be obtained using the strain gauge and regression. The detailed results are presented in the supplementary information (Fig. S1). Table 2 also lists the values for a span/depth of = 14 for the standard test span, and Fig. 5 shows plots of E/G at different spans. Dashed lines in Fig. 5 represent the values of E/GLT and E/GLR obtained through the regression method. The regressed G values depend on the combination of Ea for regression, and therefore, the local indentation effect induced in Ea is also reflected in the calculated G values. The inclusion of small span/depth ratios caused overestimated G values. Although good elastic constant measurement results were obtained using the strain gauge results, the G values were more discrete than E, particularly at large span/depth ratios. Nonetheless, overall, the representative regression G ran through data points obtained using the strain gauge provided a valuable reference. The deviation may arise because (1) the gauge factor of the strain gauge has an error range of ±1%, resulting in an error in the measured strain; (2) Ea used for regression was affected by the load point effect and excluding the affected range made the G values decrease gradually; or (3) the strain gauge used for measurements was in a small range below the linear-elastic limit, resulting in a serious deviation of the strain values under a large span when Ea and E were close. Verification was performed by increasing the strain level close to the linear limit; the corresponding results are presented in the supplementary information (Fig. S2). The aforementioned results indicate the feasibility of using strain gauges to measure the G value of wood.

In addition, E/G has been used in other studies to determine the magnitude of the shear effect relative to the bending moment effect. For example, Yoshihara et al. (1998) measured the E/G values of many tree species and reported values of 10–50. However, in this study, the E/G value obtained using either the strain gauge or the standard regression was closer to 16, the average value of wood, and these results had less variations (Fig. 5; Bodig and Jayne 1982). These results indicated that the value measured using the strain gauge can be used as a reference value; further, the single range regression used in other studies was insufficient. As detailed in Fig. 5, E/G values obtained using the strain gauge decreased slightly with increasing span/depth because the G values were overestimated slightly owing to the similarity of E and Ea. The credibility of the E/G value can be checked from the Ea/E value in Fig. 3. Red oak wood contains well-developed wood rays, and a larger G value decreases the shear strain. This indicates that the amount of deflection amplified by the shear strain effect is less, and therefore, the Ea/E of hardwood is higher than that of softwood with the same span/depth ratio (Kubojima et al. 2006). The orthotropy may also be affected by the internal structure of the wood and may influence the shear characteristics.

5 Conclusion

This study proposed a simple, inexpensive, and highly applicable approach for directly measuring the true elastic constant E and shear modulus G of wood under bending with a strain gauge and verified these values through regression using apparent elasticity and four-point flexural tests. The results confirmed that measuring E using a strain gauge on the tension side is a highly accurate and feasible approach when applied to the standard test. The only concern is that when the span/depth ratio is small, the local indentation effect may result in a slight overestimation of the E value. Although the G values were slightly inaccurate, the relative trend can still be used as a reference. Further studies are required to reduce the test error when measuring the G value caused by local indentation and unsteady strain gauge value.

The present experiments revealed some shortcomings of previous experimental methods. For example, calculating E based on the amount of deflection of the specimen provides inaccurate results because the effect of the shear force may result in E being underestimated. When using regression to determine the elastic constants, the data from a single range of small spans should not be adopted because of the nonnegligible local indentation effect induced by the loading head. Finally, the various methods considered in this study suitably reflected the differences in the species and load surfaces of wood and could therefore serve as a valuable reference for similar studies in the future. The summaries of value of the current approach proposed: (1) Measure and determine true E and G values simultaneously. (2) Compatible with conventional specimen requirements and test setup. (3) Sufficient accuracy and reliability of the measured elasticity compared to other existing approaches.

Fig. 1
figure 1

Setup of three-point bending test and measurement

Full size image
Fig. 2
figure 2

E values obtained using different approaches: a oak radial surface, b oak tangential surface, c cedar radial surface, and d cedar tangential surface. The solid line represents E value from regression methods

Full size image
Fig. 3
figure 3

Ea / E ratio of the a oak radial surface, b oak tangential surface, c cedar radial surface, and d cedar tangential surface

Full size image
Fig. 4
figure 4

Ea regression within 780–260 mm: a oak radial surface, b oak tangential surface, c cedar radial surface, and d cedar tangential surface

Full size image
Fig. 5
figure 5

E /G ratio obtained using a strain gauge with various span/depth ratios: a oak radial surface, b oak tangential surface, c cedar radial surface, and d cedar tangential surface. The dashed line represents E /GLT or E /GLR values from the regression method

Full size image