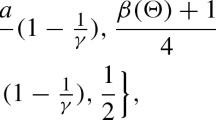A Note on Non-tangential Convergence for Schrödinger Operators

Abstract

The goal of this note is to establish non-tangential convergence results for Schrödinger operators along restricted curves. We consider the relationship between the dimension of this kind of approach region and the regularity for the initial data which implies convergence. As a consequence, we obtain an upper bound for p such that the Schrödinger maximal function is bounded from $H^{s}(\mathbb {R}^{n})$ to $L^{p}(\mathbb {R}^{n})$ for any $s > \frac{n}{2(n+1)}$.

1 Introduction

The solution to the Schrödinger equation

$$\begin{aligned} i{u_t} - \Delta u = 0, (x,t) \in {\mathbb {R}^n} \times \mathbb {R}^{+}, \end{aligned}$$

(1.1)

with initial datum $u\left( {x,0} \right) = f,$ is formally written as

$$\begin{aligned} {e^{it\Delta }}f\left( x \right) : = \int _{{\mathbb {R}^n}} {{e^{i\left( {x \cdot \xi + t{{\left| \xi \right| }^2}} \right) }}\widehat{f}} \left( \xi \right) d\xi . \end{aligned}$$

The problem about finding optimal s for which

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow 0^{+}} {e^{it\Delta }}f\left( x \right) = f(x) a.e. \end{aligned}$$

(1.2)

whenever $f \in {H^s}\left( {{\mathbb {R}^n}} \right) ,$ was first considered by Carleson [4], and extensively studied by Sjölin [20] and Vega [21], who proved independently the convergence for $s > 1/2$ in all dimensions. Dahlberg–Kenig [8] showed that the convergence does not hold for $s < 1/4$ in any dimension. In 2016, Bourgain [3] gave a counterexample showing that convergence can fail if $s<\frac{n}{2(n+1)}$. Very recently, Du–Guth–Li [9] and Du–Zhang [11] obtained the sharp results by the polynomial partitioning and decoupling method.

It is very interesting to consider whether a.e. convergence results mentioned above still hold true if we replace the vertical line by a wider approach region, such as non-tangential convergence to the initial data. In fact, Sjölin-Sjögren [19] constructed a function $f \in H^{\frac{n}{2}}(\mathbb {R}^{n})$ such that

$$\begin{aligned} \limsup _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ |x-y| < \gamma (t), t >0 \end{array}}|e^{it\Delta }f(y)| =\infty , \end{aligned}$$

for all $x \in \mathbb {R}^{n}$, where $\gamma$ is strictly increasing and $\gamma (0)=0$. This indicates the failure of non-tangential convergence for $s \le n/2$. Comparing the previous results along vertical line, one can observe that to guarantee a.e. existence of the non-tangential limit, it is necessary to require more regularity on the initial data. Therefore, in [6], the authors tried to seek the relationship between the approach region and the required Sobolev regularity of the initial data. More concretely, let $\Gamma _{x,t}=\{x+t\theta :$ $\theta \in \Theta \}$, where $t\in [-1,1]$, $\Theta$ is a given compact set in $\mathbb {R}^{1}$. In [6], they proved that the corresponding non-tangential convergence result holds for $s>\frac{\beta (\Theta )+1}{4}$, here $\beta (\Theta )$ denotes the upper Minkowski dimension of $\Theta$. This result in [6] was established by the $TT^{\star }$ method and a time localizing lemma. Recently, by getting around the key localizing lemma in [6], Shiraki [18] generalized this result to a wider class of equations which includes the fractional Schrödinger equation.

However, the above question remains open in $\mathbb {R}^n$ ($n\ge 2$) until recently. In this article, we consider the non-tangential convergence problem along the set of points in $\mathbb {R}^{n} \times \mathbb {R}$ given by $\{(y,t): y \in \Gamma _{x,t}\}$ for each $t\in [0,1]$, where

$$\begin{aligned} \Gamma _{x,t}=\{\gamma (x,t,\theta ): \theta \in \Theta \} \end{aligned}$$

for a given compact set $\Theta$ in $\mathbb {R}^{n}$. $\gamma$ is a map from $\mathbb {R}^{n} \times [0,1] \times \Theta$ to $\mathbb {R}^{n}$, which satisfies $\gamma (x,0,\theta ) =x$ for all $x \in \mathbb {R}^{n}$, $\theta \in \Theta$, and the following (C1)–(C3) hold:

(C1) For fixed $t \in [0,1]$, $\theta \in \Theta$, $\gamma$ has at least $C^{1}$ regularity in x, and there exists a constant $C_{1} \ge 1$ such that for each $x, x^{\prime } \in \mathbb {R}^{n}$, $\theta \in \Theta$, $t \in [0,1]$,

$$\begin{aligned} C_{1}^{-1}|x- x^{\prime }| \le |\gamma (x,t, \theta )-\gamma (x^{\prime },t, \theta )| \le C_{1}|x- x^{\prime }|; \end{aligned}$$

(1.3)

(C2) There exists a constant $C_{2} >0$ such that for each $x \in \mathbb {R}^{n}$, $\theta \in \Theta$, $t,t^{\prime } \in [0,1]$,

$$\begin{aligned} |\gamma (x,t, \theta )-\gamma (x,t^{\prime }, \theta )| \le C_{2}|t- t^{\prime }|; \end{aligned}$$

(1.4)

(C3) There exists a constant $C_{3} >0$ such that for each $x \in \mathbb {R}^{n}$, $t \in [0,1]$, $\theta , \theta ^{\prime } \in \Theta$,

$$\begin{aligned} |\gamma (x,t, \theta )-\gamma (x,t, \theta ^{\prime })| \le C_{3}|\theta - \theta ^{\prime }|. \end{aligned}$$

(1.5)

We consider the relationship between the dimension of $\Theta$ and the optimal s for which

$$\begin{aligned} \lim _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}}e^{it\Delta }f(y) = f(x) a.e. \end{aligned}$$

(1.6)

whenever $f \in {H^s}\left( {{\mathbb {R}^n}} \right)$.

We first give two examples for $\Gamma _{x,t}$. It is not hard to check that all the conditions mentioned above can be satisfied if we take (E1): $\gamma (x,t,\theta ) = x + t\theta$, where $\Theta$ is a compact subset of the unit ball in $\mathbb {R}^{n}$. When $n=1,$ this is just the problem considered in [6]. Another example is (E2): $\gamma (x,t,\theta ) = x + t^{\theta }$, where $t^{\theta } =(t^{\theta _{1}}, t^{\theta _{2}}, \cdot \cdot \cdot , t^{\theta _{n}} )$ for $\theta =(\theta _1,\theta _2,\cdots ,\theta _n) \in \Theta$. Here, $\Theta$ is a compact subset in the first quadrant away from the axis of $\mathbb {R}^{n}$. For this example, it is worth to mention that when $\theta$ is fixed, Lee–Rogers [14] have obtained that the convergence along the curve $(\gamma _{\theta }(x,t),t)$ is equivalent to the convergence along the vertical line.

Fig. 1

$\Theta =\{2,5/2,\cdots ,3-1/k,\cdots ,3:k=1,2,\cdots \}$

Fig. 2

$\bigcup _{t\in [0,1/2]}\{(y,t):y\in \Gamma _{x,t}\}$ consists of all black points where $\Gamma _{x,t}=\{x+t^{\theta }, \theta \in \Theta \}$. For every layer $t=t_0$, there are countable black points corresponding to $\Theta$. We try to seek the optimal s for which $e^{it\Delta }f(y)\rightarrow f(x)$ along different green-paths whose points are from $\bigcup _{t\in [0,1/2]}\{(y,t):y\in \Gamma _{x,t}\}$ whenever $f\in H^s$

In order to characterize the size of $\Theta$, we introduce the so called logarithmic density or upper Minkowski dimension of $\Theta$,

$$\begin{aligned} \beta (\Theta )= \limsup _{\delta \rightarrow 0^{+}} \frac{logN(\delta )}{-log\delta }, \end{aligned}$$

where $N(\delta )$ is the minimum number of closed balls of diameter $\delta$ to cover $\Theta$. It is not hard to see that when $\Theta$ is a single point, $\beta (\Theta ) =0$; when $\Theta$ is a compact subset of $\mathbb {R}^{n}$ with positive Lebesgue measure, $\beta (\Theta ) =n$.

By standard arguments, in order to obtain the convergence result, it is sufficient to establish the bounded estimates for the maximal operator defined by

$$\begin{aligned} \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }f(\gamma (x,t,\theta ))|. \end{aligned}$$

Our main results are as follows. Firstly, we show the following main result in general dimensional case.

Theorem 1.1

Let $n \ge 1$. Suppose that there exists $p \ge 2$ such that for any $s> \frac{n}{2(n+1)}$,

$$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{0<t<1}|e^{it\Delta }f(x)|\biggl \Vert _{L^p(B(0,1))} \le C_s\Vert f\Vert _{H^s(\mathbb {R}^n)} \end{aligned}$$

(1.7)

whenever $f \in H^{s}(\mathbb {R}^{n})$. If $\gamma$ satisfies (C1)-(C3), then for a given $B(x_{0},R) \subset \mathbb {R}^{n}$ and any $s> \frac{\beta (\Theta )}{p} + \frac{n}{2(n+1)}$, it holds that

$$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }f(\gamma (x,t,\theta ))|\biggl \Vert _{L^{p}(B(x_{0},R))} \le C\Vert f\Vert _{H^s(\mathbb {R}^n)} \end{aligned}$$

(1.8)

whenever $f\in H^s(\mathbb {R}^n)$. Here, the constant C depends on s, $C_{1}$, $C_{2}$, $C_{3}$, and the choice of $B(x_{0}, R)$, but does not depend on f.

Theorem 1.1 implies that if (1.7) holds for some $p \ge 2$ whenever $f \in H^{s}(\mathbb {R}^{n})$ for any $s> \frac{n}{2(n+1)}$, then for any $s> \frac{\beta (\Theta )}{p} + \frac{n}{2(n+1)}$,

$$\begin{aligned} \lim _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}}e^{it\Delta }f(y) = f(x) a.e. \end{aligned}$$

(1.9)

whenever $f \in H^{s}(\mathbb {R}^{n})$. We briefly sketch the proof of Theorem 1.1, and leave the details to Sect. 2. We decompose $\Theta$ into small subsets $\{\Theta _{k}\}$ with bounded overlap, where the size of each $\Theta _{k}$ is small enough so that our problem can be reduced to estimate the maximal function for Schrödinger operator along certain curves, i.e. the maximal operator defined by

$$\begin{aligned} \mathop {\mathrm{sup}}\limits _{t \in (0,1)} |e^{it\Delta }f(\gamma (x,t,\theta _{k}^{0})| \end{aligned}$$

(1.10)

for some $\theta _{k}^{0} \in \Theta _{k}$. The number of $\Theta _{k}$ is determined by $\beta (\Theta )$. In order to get the bounded estimate for maximal function defined by (1.10), we need inequality (1.7). The idea to establish the bounded estimate for maximal function defined by (1.10) using inequality (1.7) comes from the method adopted by Lee–Rogers [14] to show equivalence between convergence result for Schrödinger operators along smooth curves and vertical lines. However, we should be more careful since we need an estimate uniformly in k. In our case, this can be realized since $\Theta$ is compact.

When $n=2$, Du–Guth–Li [9] proved that for any $s>1/3$, inequality (1.7) holds for any function $f\in H^s(\mathbb {R}^2)$ with $p=3$. Therefore, combining with Theorem 1.1, we obtain the following theorem.

Theorem 1.2

When $n=2$ and $\gamma$ satisfies (C1)–(C3),

• (1) for a given $B(x_{0},R) \subset \mathbb {R}^{2}$, it follows that for any $s> \frac{\beta (\Theta )+1}{3}$,

  $$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }f(\gamma (x,t,\theta ))|\biggl \Vert _{L^{3}(B(x_{0},R))} \le C\Vert f\Vert _{H^s(\mathbb {R}^2)} \end{aligned}$$

  (1.11)

  whenever $f\in H^s(\mathbb {R}^2)$, where the constant C depends on s, $C_{1}$, $C_{2}$, $C_{3}$, and the choice of $B(x_{0}, R)$, but does not depend on f;

• (2) as a consequence of (1), we have

  $$\begin{aligned} \lim _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}}e^{it\Delta }f(y) = f(x) a.e. \end{aligned}$$

  (1.12)

  whenever $f\in H^s(\mathbb {R}^2)$ for each $s> \frac{\beta (\Theta )+1}{3}$.

We notice that the convergence result obtained in Theorem 1.2 is sharp when $\beta (\Theta ) = 0$ ( [9] and [3]) or $\beta (\Theta ) = 2$ ( [19]). It is quite interesting to seek whether (1.12) is sharp when $0< \beta (\Theta ) <2$.

When $n \ge 3$, then it comes to the question about what is the largest possible value for p such that (1.7) holds for any $s> \frac{n}{2(n+1)}$. This question is still open to our best knowledge, but combining with the counterexample given by Sjölin-Sjögren [19], we get an upper bound for p.

Theorem 1.3

For general positive integer n, if there exists $p \ge 2$ such that for any $s> \frac{n}{2(n+1)}$, (1.7) holds whenever $f \in H^{s}(\mathbb {R}^{n})$, then $p \le \frac{2(n+1)}{n}$.

The upper bound given by Theorem 1.3 is sharp for $n=1$ ( [4]) and $n=2$ ( [9]). In [11], it was proved that (1.7) holds for $p=2$ when $n \ge 3$. There is a gap between 2 and $\frac{2(n+1)}{n}$, then there may still be margin to improve for $n \ge 3$. Also, combining the result of [11] with Theorem 1.1, we have the following theorem.

Theorem 1.4

When $n \ge 3$, if $s> \frac{\beta (\Theta )}{2} + \frac{n}{2(n+1)}$, then

$$\begin{aligned} \lim _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}}e^{it\Delta }f(y) = f(x) a.e. \end{aligned}$$

whenever $f\in H^s(\mathbb {R}^n)$.

What’s more, by parabolic rescaling and time localizing lemma, inequality (1.7) is equivalent to

$$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{0<t<\lambda }|e^{it\Delta }f(x)|\biggl \Vert _{L^p(B(0,\lambda ))} \le C_\epsilon \lambda ^{n(\frac{1}{p}-\frac{n}{2(n+1)}) + \epsilon } \Vert f\Vert _{L^2(\mathbb {R}^n)} \end{aligned}$$

(1.13)

whenever supp$\hat{f} \subset \{\xi \in \mathbb {R}^{n}: |\xi | \sim 1\}$, where $\lambda \gg 1$. The range of p has been discussed in Du–Kim–Wang–Zhang [10], but the optimal range of p is still unknown.

Conventions Throughout this article, we shall use the well known notation $A\gg B$, which means if there is a sufficiently large constant G, which does not depend on the relevant parameters arising in the context in which the quantities A and B appear, such that $A\ge GB$. We write $A\sim B$, and mean that A and B are comparable. By $A\lesssim B$ we mean that $A \le CB$ for some constant C independent of the parameters related to A and B. Given $\mathbb {R}^{n}$, we write B(0, 1) instead of the unit ball $B^{n}(0,1)$ in $\mathbb {R}^{n}$ centered at the origin for short, and the same notation is valid for $B(x_{0},R)$.

2 Proofs of Theorem 1.1 and Theorem 1.2

Proof of Theorem 1.1 In order to prove Theorem 1.1, using Littlewood-Paley decomposition, we only need to show that for f with supp$\hat{f} \subset \{\xi \in \mathbb {R}^{n}: |\xi | \sim \lambda \}$, $\lambda \gg 1$,

$$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }f(\gamma (x,t,\theta ))|\biggl \Vert _{L^{p}(B(x_{0},R))} \le C\lambda ^{s_{0}+\epsilon } \Vert f\Vert _{L^{2}}, \,\ \forall \epsilon >0, \end{aligned}$$

(2.1)

where $s_{0}=\frac{\beta (\Theta )}{p} + \frac{n}{2(n+1)}$.

We decompose $\Theta$ into small subsets $\{\Theta _{k}\}$ such that $\Theta = \cup _{k}\Theta _{k}$ with bounded overlap, where each $\Theta _{k}$ is contained in a closed ball with diameter $\lambda ^{-1}$. Then we have

$$\begin{aligned} 1 \le k \le \lambda ^{\beta (\Theta ) + \epsilon }. \end{aligned}$$

(2.2)

Under the assumption of Theorem 1.1, we claim that for each k,

$$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta _{k}} |e^{it\Delta }f(\gamma (x,t,\theta ))|\biggl \Vert _{L^{p}(B(x_{0},R))} \le C\lambda ^{\frac{n}{2(n+1)}+\frac{(p-1)\epsilon }{p}} \Vert f\Vert _{L^{2}}. \end{aligned}$$

(2.3)

Then we have

$$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }f(\gamma (x,t,\theta ))|\biggl \Vert _{L^{p}(B(x_{0},R))}&\le \biggl (\sum _{k} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta _{k}} |e^{it\Delta }f(\gamma (x,t,\theta ))|\biggl \Vert _{L^{p}(B(x_{0},R))}^{p} \biggl )^{1/p} \\&\le C\biggl (\sum _{k} \lambda ^{\frac{np}{2(n+1)}+(p-1)\epsilon } \Vert f\Vert _{L^{2}}^{p} \biggl )^{1/p} \\&\le C\lambda ^{\frac{\beta {(\Theta )}}{p} +\frac{n}{2(n+1)} +\epsilon } \Vert f\Vert _{L^{2}}, \end{aligned}$$

which implies inequality (2.1).

Now we are left to prove inequality (2.3). For this goal, we first show the following Lemma 2.1. The original idea comes from Lemma 2.2 in [14].

Lemma 2.1

Assume that g is a Schwartz function whose Fourier transform is supported in $\{\xi \in \mathbb {R}^{n}: |\xi | \sim \lambda \}$. If

$$\begin{aligned} |\theta - \theta ^{\prime }| \le \lambda ^{-1},\end{aligned}$$

then for each $x \in B(x_{0},R)$ and $t \in (0, 1)$,

$$\begin{aligned} |e^{it\Delta }g(\gamma (x,t,\theta ))| \le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl |\int _{\mathbb {R}^{n}}{e^{i[\gamma (x,t,\theta ^{\prime })+ \frac{\mathfrak {l}}{\lambda }]\cdot \xi +it|\xi |^{2}}\hat{g}}(\xi )d\xi \biggl |}, \end{aligned}$$

(2.4)

where the constant C depends on n and $C_{3}$ in inequality (1.5).

Proof

We introduce a cut-off function $\phi$ which is smooth and equal to 1 on B(0, 2) and supported on $(-\pi , \pi )^{n}$. After scaling we have

$$\begin{aligned} e^{it\Delta }g(\gamma (x,t,\theta ))&= \lambda ^{n} \int _{\mathbb {R}^{n}}{e^{i\lambda \gamma (x,t,\theta )\cdot \eta + it|\lambda \eta |^{2}} \phi (\eta )\hat{g}(\lambda \eta ) d\eta } \nonumber \\&= \lambda ^{n} \int _{\mathbb {R}^{n}}{e^{i\lambda \gamma (x,t, \theta )\cdot \eta -i\lambda \gamma (x,t,\theta ^{\prime }) \cdot \eta +i\lambda \gamma (x,t,\theta ^{\prime }) \cdot \eta + it|\lambda \eta |^{2}} \phi (\eta )\hat{g}(\lambda \eta ) d\eta }. \end{aligned}$$

(2.5)

Since it follows by inequality (1.5),

$$\begin{aligned} \lambda |\gamma (x,t,\theta )-\gamma (x,t,\theta ^{\prime })| \le C_{3},\end{aligned}$$

then by the Fourier expansion,

$$\begin{aligned} \phi (\eta )e^{i\lambda [\gamma (x,t,\theta )-\gamma (x,t,\theta ^{\prime })] \cdot \eta } = \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{c_{\mathfrak {l}}(x,t,\theta , \theta ^{\prime })e^{i\mathfrak {l}\cdot \eta }},\end{aligned}$$

where

$$\begin{aligned} |c_{\mathfrak {l}}(x,t,\theta , \theta ^{\prime })| \le \frac{C}{(1+|\mathfrak {l}|)^{n+1}}\end{aligned}$$

uniformly for each $\mathfrak {l} \in \mathbb {Z}^{n}$, $x \in B(x_{0},R)$ and $t \in (0, 1)$. Then we have

$$\begin{aligned} |e^{it\Delta }g(\gamma (x,t,\theta ))|&\le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{\frac{C\lambda ^{n}}{(1+|\mathfrak {l}|)^{n+1}}\biggl |\int _{\mathbb {R}^{n}}{e^{i \mathfrak {l} \cdot \eta +i\lambda \gamma (x,t,\theta ^{\prime }) \cdot \eta + it|\lambda \eta |^{2}} \hat{g}(\lambda \eta ) d\eta } \biggl |} \\&= \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl |\int _{\mathbb {R}^{n}}{e^{i \frac{\mathfrak {l}}{\lambda } \cdot \xi +i \gamma (x,t,\theta ^{\prime }) \cdot \xi + it|\xi |^{2}} \hat{g}(\xi ) d\xi } \biggl |}, \end{aligned}$$

then we arrive at (2.4). $\square$

By the similar argument, we can prove the following lemma.

Lemma 2.2

Assume that g is a Schwartz function whose Fourier transform is supported in $\{\xi \in \mathbb {R}^{n}: |\xi | \sim \lambda \}$. If

$$\begin{aligned} |t - t^{\prime }| \le \lambda ^{-1},\end{aligned}$$

then for each $x \in B(x_{0},R)$ and $\theta \in \Theta$,

$$\begin{aligned}&|e^{it\Delta }g(\gamma (x,t,\theta ))| \nonumber \\&\quad \le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}} {\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl |\int _{\mathbb {R}^{n}}{e^{i[\gamma (x,t^{\prime },\theta )+ \frac{\mathfrak {l}}{\lambda }]\cdot \xi +it|\xi |^{2}}\hat{g}}(\xi )d\xi \biggl |}, \end{aligned}$$

(2.6)

where the constant C depends on n and $C_{2}$ in inequality (1.4).

We now prove inequality (2.3). For fixed k, by the construction of $\Theta _{k}$, there is a $\theta _{k}^{0} \in \Theta _{k}$ such that

$$\begin{aligned} |\theta - \theta _{k}^{0}| \le \lambda ^{-1}\end{aligned}$$

holds for each $\theta \in \Theta _{k}$. Then according to Lemma 2.1, for each $x \in B(x_{0},R)$, $t \in (0, 1)$ and $\theta \in \Theta _{k}$, we have

$$\begin{aligned} |e^{it\Delta }f(\gamma (x,t,\theta ))|&\le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl |\int _{\mathbb {R}^{n}}{e^{i \gamma (x,t,\theta _{k}^{0}) \cdot \xi +it|\xi |^{2}} e^{i\frac{\mathfrak {l}}{\lambda } \cdot \xi }\hat{f}}(\xi )d\xi \biggl |} \nonumber \\&= \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl |\int _{\mathbb {R}^{n}}{e^{i \gamma (x,t,\theta _{k}^{0}) \cdot \xi +it|\xi |^{2}} \hat{f_{\lambda }^{\mathfrak {l}}}}(\xi )d\xi \biggl |} \nonumber \\&= \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl | e^{it\Delta } f_{\lambda }^{\mathfrak {l}} (\gamma (x,t,\theta _{k}^{0})) \biggl |}, \end{aligned}$$

(2.7)

where

$$\begin{aligned} \hat{f_{\lambda }^{\mathfrak {l}}} (\xi )=e^{i\frac{\mathfrak {l}}{\lambda } \cdot \xi }\hat{f}(\xi ). \end{aligned}$$

It follows that

$$\begin{aligned}&\biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta _{k}} |e^{it\Delta }f(\gamma (x,t,\theta ))|\biggl \Vert _{L^{p}(B(x_{0},R))} \nonumber \\&\quad \le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}} \frac{C}{(1+|\mathfrak {l}|)^{n+1}} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta _{k}} |e^{it\Delta }f_{\lambda }^{\mathfrak {l}}(\gamma (x,t,\theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))} \nonumber \\&\quad = \sum _{\mathfrak {l} \in \mathbb {Z}^{n}} \frac{C}{(1+|\mathfrak {l}|)^{n+1}} \biggl \Vert \mathop {\mathrm{sup}}\limits _{t \in (0,1)} |e^{it\Delta }f_{\lambda }^{\mathfrak {l}}(\gamma (x,t,\theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))} \nonumber \\&\quad \le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}} \frac{C}{(1+|\mathfrak {l}|)^{n+1}} \lambda ^{\frac{n}{2(n+1)}+ \frac{(p-1)\epsilon }{p}} \Vert f_{\lambda }^{\mathfrak {l}}\Vert _{L^{2}} \nonumber \\&\quad \le \lambda ^{\frac{n}{2(n+1)}+ \frac{(p-1)\epsilon }{p}} \Vert f\Vert _{L^{2}}, \end{aligned}$$

(2.8)

provided that we have proved the following lemma.

Lemma 2.3

Under the assumption of Theorem 1.1, if g is a Schwartz function whose Fourier transform is supported in the annulus $\{\xi \in \mathbb {R}^{n}: |\xi | \sim \lambda \}$. Then for each k,

$$\begin{aligned} \biggl \Vert \mathop {\mathrm{sup}}\limits _{t \in (0,1)} |e^{it\Delta }g(\gamma (x,t,\theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))} \le C \lambda ^{\frac{n}{2(n+1)}+ \frac{(p-1)\epsilon }{p}} \Vert g\Vert _{L^{2}}, \end{aligned}$$

(2.9)

where the constant C is independent of k.

Now let’s turn to prove Lemma 2.3. The following theorem is required.

Theorem 2.1

( [14]) Let $\rho : \mathbb {R}^{n+1} \rightarrow \mathbb {R}^{n}$, $q, r \in [2, +\infty ]$, $\lambda \ge 1$, supp $\nu \subset [-2,2]$, $\lambda \ge \Vert 1\Vert _{L_{\mu }^{q}L_{\nu }^{r}}^{1/n}$, and suppose that

$$\begin{aligned} \mathop {\mathrm{sup}}\limits _{x \in supp(\mu ), t \in supp(\nu )}|\rho (x,t)| \le M, \end{aligned}$$

where $M >1$. Suppose that for a collection of boundedly overlapping intervals I of length $\lambda ^{-1}$, there exists a constant $C_{0} >1$ such that

$$\begin{aligned} \Vert e^{it\Delta }f(\rho (x,t))\Vert _{L_{\mu }^{q}L_{\nu }^{r}(I)} \le C_0\Vert f\Vert _{L^2(\mathbb {R}^n)} \end{aligned}$$

whenever $\hat{f}$ is supported in $\{\xi \in \mathbb {R}^{n}: |\xi | \sim \lambda \}$. Then there is a constant $C_{n} >1$ such that

$$\begin{aligned} \Vert e^{it\Delta }f(\rho (x,t))\Vert _{L_{\mu }^{q}L_{\nu }^{r}(\cup I)} \le C_{n} M^{1/2} C_0\Vert f\Vert _{L^2(\mathbb {R}^n)} \end{aligned}$$

whenever $\hat{f}$ is supported in $\{\xi \in \mathbb {R}^{n}: |\xi | \sim \lambda \}$.

Notice that in our case, for each k, we have

$$\begin{aligned}&\mathop {\mathrm{sup}}\limits _{(x,t) \in B(x_{0},R) \times (0,1)}|\gamma (x,t,\theta _{k}^{0})| \\&\quad \le \mathop {\mathrm{sup}}\limits _{(x,t,\theta ) \in B(x_{0},R) \times (0,1) \times \Theta }|\gamma (x,t,\theta )|. \end{aligned}$$

By inequality (1.4), for each $(x,t,\theta ) \in B(x_{0},R) \times (0,1) \times \Theta$,

$$\begin{aligned}|\gamma (x,t,\theta ) - \gamma (x,0,\theta )| \le C_{2},\end{aligned}$$

then $|\gamma (x,t,\theta )|$ is uniformly bounded for $(x,t,\theta ) \in B(x_{0},R) \times (0,1) \times \Theta$, and the upper bound is determined by $C_{2}$ and the choice of $B(x_{0},R)$, but independent of k.

Therefore, according to Theorem 2.1, in order to prove Lemma 2.3, we only need to show that for each interval $I \subset (0,1)$ of length $\lambda ^{-1}$, and any function g such that $\hat{g}$ is supported in $\{\xi \in \mathbb {R}^{n}: |\xi | \sim \lambda \}$, we have

$$\begin{aligned}&\biggl \Vert \mathop {\mathrm{sup}}\limits _{t \in I} |e^{it\Delta }g(\gamma (x,t,\theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))}\nonumber \\&\quad \le C \lambda ^{\frac{n}{2(n+1)}+ \frac{(p-1)\epsilon }{p}} \Vert g\Vert _{L^{2}}. \end{aligned}$$

(2.10)

Since I is an interval of length $\lambda ^{-1}$, there exists $t_{I}^{0} \in I$ such that for each $t \in I$,

$$\begin{aligned} |t - t_{I}^{0}| \le \lambda ^{-1}.\end{aligned}$$

Then by Lemma 2.2, for each $x \in B(x_{0},R)$, $t \in I$, we have

$$\begin{aligned}&|e^{it\Delta }g(\gamma (x,t,\theta _{k}^{0}))| \nonumber \\&\quad \le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}} {\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl |\int _{\mathbb {R}^{n}}{e^{i \gamma (x,t_{I}^{0},\theta _{k}^{0}) \cdot \xi +it|\xi |^{2}} e^{i\frac{\mathfrak {l}}{\lambda } \cdot \xi }\hat{g}}(\xi )d\xi \biggl |} \nonumber \\&\quad = \sum _{\mathfrak {l} \in \mathbb {Z}^{n}}{\frac{C}{(1+|\mathfrak {l}|)^{n+1}}\biggl | e^{it\Delta } g_{\lambda }^{\mathfrak {l}} (\gamma (x,t_{I}^{0},\theta _{k}^{0})) \biggl |},\nonumber \\ \end{aligned}$$

(2.11)

where

$$\begin{aligned} \widehat{g_{\lambda }^{\mathfrak {l}}} (\xi )=e^{i\frac{\mathfrak {l}}{\lambda } \cdot \xi }\hat{g}(\xi ). \end{aligned}$$

It follows that

$$\begin{aligned}&\biggl \Vert \mathop {\mathrm{sup}}\limits _{t \in I} |e^{it\Delta }g(\gamma (x,t,\theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))} \nonumber \\&\quad \le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}} \frac{C}{(1+|\mathfrak {l}|)^{n+1}} \biggl \Vert \mathop {\mathrm{sup}}\limits _{t \in I} |e^{it\Delta }g_{\lambda }^{\mathfrak {l}}(\gamma (x,t_{I}^{0},\theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))}. \end{aligned}$$

(2.12)

For each $t_{I}^{0}$, $\theta _{k}^{0}$, $\gamma _{t_{I}^{0}, \theta _{k}^{0}}$ is at least $C^{1}$ from $\mathbb {R}^{n}$ to $\mathbb {R}^{n}$. By inequality (1.3), for each $x \in \mathbb {R}^{n}$,

$$\begin{aligned}C_{1}^{-1} \le |\nabla _{x}\gamma (x,t_{I}^{0},\theta _{k}^{0})| \le C_{1}.\end{aligned}$$

By the same reason, for each $x \in B(x_{0},R)$,

$$\begin{aligned}|\gamma (x,t_{I}^{0},\theta _{k}^{0}) - \gamma (x_{0},t_{I}^{0},\theta _{k}^{0})| \le C_{1}R,\end{aligned}$$

which implies $\gamma _{t_{I}^{0}, \theta _{k}^{0}}(B(x_{0},R)) \subset B( \gamma (x_{0},t_{I}^{0},\theta _{k}^{0}),C_{1}R)$. Therefore, changes of variables and inequality (1.7) imply that

$$\begin{aligned}&\biggl \Vert \mathop {\mathrm{sup}}\limits _{t \in I} |e^{it\Delta }g_{\lambda }^{\mathfrak {l}}(\gamma (x,t_{I}^{0}, \theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))}\nonumber \\&\quad \le C \lambda ^{\frac{n}{2(n+1)} + \frac{(p-1)\epsilon }{p}} \Vert g_{\lambda }^{\mathfrak {l}}\Vert _{L^{2}}. \end{aligned}$$

(2.13)

Combining inequality (2.12) with inequality (2.13), we have

$$\begin{aligned}&\biggl \Vert \mathop {\mathrm{sup}}\limits _{t \in I} |e^{it\Delta }g(\gamma (x,t,\theta _{k}^{0}))|\biggl \Vert _{L^{p}(B(x_{0},R))} \nonumber \\&\quad \le \sum _{\mathfrak {l} \in \mathbb {Z}^{n}} \frac{C}{(1+|\mathfrak {l}|)^{n+1}} \lambda ^{\frac{n}{2(n+1)}+ \frac{(p-1)\epsilon }{p}} \Vert g_{\lambda }^{\mathfrak {l}}\Vert _{L^{2}} \nonumber \\&\quad \le C\lambda ^{\frac{n}{2(n+1)}+ \frac{(p-1)\epsilon }{p}} \Vert g\Vert _{L^{2}}. \end{aligned}$$

(2.14)

This completes the proof of Lemma 2.3.

Proof of Theorem 1.2

We only need to prove that (1) implies (2). The proof is quite standard. We write the details for completeness. Let $s> \frac{\beta (\Theta )+1}{3}$, and $f \in H^{s}(\mathbb {R}^{2})$. For a fixed $\lambda >0$, choose $g \in C_{c}^{\infty }(\mathbb {R}^{2})$ such that

$$\begin{aligned}\Vert f-g\Vert _{H^{s}(\mathbb {R}^{2})} \le \frac{\lambda \epsilon ^{1/3}}{2C},\end{aligned}$$

where the constant C is the constant in inequality (1.11), which follows

$$\begin{aligned}&\biggl |\biggl \{ x \in B(x_{0},R): \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }(f-g)(\gamma (x,t,\theta ))| > \frac{\lambda }{2}\biggl \}\biggl | \nonumber \\&\quad \le \frac{2^{3}}{\lambda ^{3}} \biggl \Vert \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }(f-g)(\gamma (x,t,\theta ))|\biggl \Vert _{L^{3}(B(x_{0},R))}^{3} \nonumber \\&\quad \le \frac{2^{3}C^{3}}{\lambda ^{3}}\Vert f-g\Vert _{H^{s}(\mathbb {R}^{2})}^{3} \nonumber \\&\quad \le \epsilon . \end{aligned}$$

(2.15)

Moreover,

$$\begin{aligned} \lim _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}} e^{it\Delta }g(y) =g(x) \end{aligned}$$

(2.16)

uniformly for $x \in B(x_{0},R)$. Indeed, for each $x \in B(x_{0},R)$,

$$\begin{aligned} \limsup _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}} |e^{it\Delta }g(y) - g(x)|&\le \limsup _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}} |e^{it\Delta }g(y) - e^{it\Delta }g(x)| + \limsup _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}} |e^{it\Delta }g(x) - g(x)| \nonumber \\&= \limsup _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}} |e^{it\Delta }g(y) - e^{it\Delta }g(x)| + \limsup _{t \rightarrow 0^{+}} |e^{it\Delta }g(x) - g(x)|. \end{aligned}$$

(2.17)

By mean value theorem and inequality (1.4), we have

$$\begin{aligned} | e^{it\Delta }(g)(\gamma (x,t,\theta ))-e^{it\Delta }g(x)| \le t\int _{\mathbb {R}^{2}}{|\xi ||\hat{g}(\xi )|d\xi }, \end{aligned}$$

(2.18)

and

$$\begin{aligned} |e^{it\Delta }g(x) -g(x)| \le t\int _{\mathbb {R}^{2}}{|\xi |^{2}|\hat{g}(\xi )|d\xi }. \end{aligned}$$

(2.19)

Inequalities (2.17) - (2.19) imply (2.16).

By (2.15) and (2.16) we have

$$\begin{aligned}&\biggl |\biggl \{{ x \in B(x_{0},R): \limsup _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}} |e^{it\Delta }(f)(y)-f(x)|}> \lambda \biggl \}\biggl | \nonumber \\&\quad \le \biggl |\biggl \{{ x \in B(x_{0},R): \limsup _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ y\in \Gamma _{x,t} \end{array}} |e^{it\Delta }(f-g)(y)|}> \frac{ \lambda }{2}\biggl \}\biggl | \nonumber \\&\qquad +\biggl |\biggl \{{ x \in B(x_{0},R): |f(x)-g(x)|}> \frac{ \lambda }{2}\biggl \}\biggl | \nonumber \\&\quad \le \biggl |\biggl \{ x \in B(x_{0},R): \mathop {\mathrm{sup}}\limits _{(t,\theta ) \in (0,1) \times \Theta } |e^{it\Delta }(f-g)(\gamma (x,t,\theta ))|> \frac{\lambda }{2}\biggl \}\biggl | \nonumber \\&\qquad +\biggl |\biggl \{{ x \in B(x_{0},R): |f(x)-g(x)|} > \frac{ \lambda }{2}\biggl \}\biggl | \nonumber \\&\quad \lesssim \epsilon + \frac{2^{2}}{\lambda ^{2}}\Vert f-g\Vert _{H^{s}(\mathbb {R}^{2})}^{2} \nonumber \\&\quad \le \epsilon +\frac{\epsilon ^{\frac{2}{3}}}{C^{2}} \nonumber \\&\quad \le \epsilon +\epsilon ^{\frac{2}{3}}, \end{aligned}$$

(2.20)

since we can always assume that $C \ge 1$, which implies convergence for $f \in H^{s}(\mathbb {R}^{2})$ and almost every $x \in B(x_{0}, R)$. By the arbitrariness of $B(x_{0}, R)$, in fact we can get convergence for almost every $x \in \mathbb {R}^{2}$. This completes the proof of Theorem 1.2. $\square$

3 Proof of Theorem 1.3

Proof of Theorem 1.3 We take $\gamma (x,t,\theta ) = x + t\theta$, where $\Theta$ is the interior of the unit ball in $\mathbb {R}^{n}$. Then we have

$$\begin{aligned} \beta (\Theta ) = n, \end{aligned}$$

(3.1)

and for $t \in [0,1]$, choose

$$\begin{aligned} \Gamma _{x,t} = \{\gamma (x,t,\theta ): \theta \in \Theta \} =\{y: |y-x| < t \}. \end{aligned}$$

(3.2)

Assuming that (1.7) holds, then it follows from Theorem 1.1 and the choice of $\Gamma _{x,t}$ that for any $s > \frac{\beta (\Theta )}{p} + \frac{n}{2(n+1)}$,

$$\begin{aligned} \lim _{\begin{array}{c} (y,t) \rightarrow (x,0) \\ |x-y| < t \end{array}} e^{it\Delta }f(y) = f(x) a.e. \end{aligned}$$

(3.3)

whenever $f\in H^s(\mathbb {R}^n)$. But according to Theorem 3 in [19], this result fails for any $s \le \frac{n}{2}$. Therefore, we get

$$\begin{aligned} \frac{\beta (\Theta )}{p} + \frac{n}{2(n+1)} \ge \frac{n}{2}. \end{aligned}$$

(3.4)

Then inequality (3.4) and equality (3.1) imply Theorem 1.3. $\square$