On Pointwise Convergence for Schrödinger Operator in a Convex Domain

Abstract

In this paper, we prove that the maximal inequality

$$\begin{aligned} \big \Vert \sup _{|t|<1}|e^{it\Delta _D}f(x,y)|\big \Vert _{L^2_{\mathrm{loc}}(\Omega )}\le C\Vert f\Vert _{H^s_D(\Omega )},\quad \forall ~f\in H^s_D(\Omega ) \end{aligned}$$

holds for any $s>\tfrac{1}{2}$ with $\Omega =\{(x,y)\in \mathbb {R}^2\mid x>0\}$ and $\Delta _D=\partial _x^2+(1+x)\partial _y^2$. As a direct application, we obtain the pointwise convergence for the free Schrödinger equation $i\partial _tu+\Delta _D u=0$ with initial data $u(0)=f$ inside strictly convex domain.

1 Introduction

Let $\Omega$ be the upper right plane $\{(x,y)\in \mathbb {R}^2\mid x>0\}$. Define the Laplacian on $\Omega$ to be $\Delta _D=\partial _x^2+(1+x)\partial _y^2$, together with Dirichlet boundary conditions on $\partial \Omega :$ one may easily see that $\Omega$, with the metric inherited from $\Delta _D$, is a strictly convex domain, we refer the reader to [17, 18] about the dispersive estimate and Strichartz estimates for wave equation in such convex domain. In this paper, we study the following local maximal inequality

$$\begin{aligned} \big \Vert \sup _{|t|<1}|S(t)f(x,y)|\big \Vert _{L^2_{\mathrm{loc}}(\Omega )}\le C\Vert f\Vert _{H^s_D(\Omega )},\quad \forall ~f\in H^s_D(\Omega ), \end{aligned}$$

(1.1)

where $u(t,x,y):=S(t)f(x,y)$ solves

$$\begin{aligned} {\left\{ \begin{array}{ll} i\partial _tu+\Delta _Du=0,\quad (t,x,y)\in \mathbb {R}\times \Omega \\ u(t,x,y)=0,\quad (x,y)\in \partial \Omega ,\\ u(0,x,y)=f(x,y), \end{array}\right. } \end{aligned}$$

(1.2)

and we define $H_D^s(\Omega )$ as the completion of $C^\infty _c(\Omega )$ equipped with norm

$$\begin{aligned} \Vert f\Vert _{H_D^s(\Omega )}^2:=\Vert f\Vert _{L^2(\Omega )}^2+\big \Vert (-\Delta _D)^\frac{s}{2}f\big \Vert _{L^2(\Omega )}^2. \end{aligned}$$

(1.3)

Using the standard process of approximation (see Corollary 1.2 below), we obtain the point-wise convergence by (1.1)

$$\begin{aligned} \lim _{t\rightarrow 0}S(t)f(x,y)=f(x,y),~\text {a.e.}~(x,y)\in \Omega ,\quad \forall ~f\in H^s_D(\Omega ), \end{aligned}$$

(1.4)

We easily check that (1.1) is valid for $s>1$ by Sobolev embedding [1]: $H^s_D(\Omega )\hookrightarrow L^\infty (\Omega )$. In this paper, we want to look for the minimal s to ensure (1.1). The impetus to consider this problem stems from a series of recent works of the dispersive operators, including the Schrödinger operator and the wave operator in the flat space $\mathbb {R}^d$, since Carleson [8] on the Schrödinger operator. We also refer to [4,5,6, 8,9,10,11, 19, 23,24,25, 27,28,34].

To be more precise, let us recall the results for maximal operators associated to the Schrödinger equation in the flat space $\mathbb {R}^d$

$$\begin{aligned} \big \Vert \sup _{|t|<1}|e^{-it\Delta }f(x)|\big \Vert _{L^2(B(0,1))}\le C\Vert f(x)\Vert _{H^s(\mathbb {R}^d)}, \end{aligned}$$

(1.5)

where $B(0,1)\subset \mathbb {R}^d$ is the unit ball centered at zero. Carleson first raised such problem in [8], where he answered the $d=1$ case with $s\ge \frac{1}{4}$. This result was shown to be optimal by Dahlberg and Kenig [11]. In dimension $d\ge 2$, Sjölin [29] and Vega [33] established (1.5) with $s>\tfrac{1}{2}$ independently. In particular, the result can be strengthened to $s=\tfrac{1}{2}$ by Sjölin [29] when $d=2$. Meanwhile, Vega [33] gave a counterexample to show that (1.5) fails if $s<\tfrac{1}{4}$.

The maximal inequality (1.5) for dimension two is closely related to the development of the Fourier restriction theory. The first breakthrough for $s<\tfrac{1}{2}$ was achieved by Bourgain [4, 5], where he proved that there exists $s<\tfrac{1}{2}$ such that (1.5) holds true. Thereafter, Moyua–Vargas–Vega [25] further developed Tomas-Stein $X_{p,4}$-space to obtain that (1.5) holds if $s>s_0$ for some $s_0\in \left( \tfrac{20}{41},\tfrac{40}{81}\right)$. By making use of the bilinear Restriction estimate for paraboloid, Tao–Vargas [32] and Tao [31] improved the result to $s>\frac{15}{32}$ and $s>\frac{2}{5}$ respectively. Recently, observing the localization properties of Schrödinger waves, Lee [19] obtained the result for $s>\tfrac{3}{8}$. Shao [30] gave an alternative proof by using the method of stationary phase and wave packet decomposition. In [7], Bourgain gave a counterexample to show that $s\ge \frac{1}{3}$ is necessary for (1.5) with $d=2$. By using polynomial partitioning and decoupling method [16], Du–Guth–Li [13] got the result for $s>\frac{1}{3}$, which is sharp up to the endpoint $s=\frac{1}{3}$.

Previous to [6], the results about $d\ge 3$ remained $s>\frac{1}{2}$, and $s\ge \frac{1}{4}$ was still believed to be the correct condition for (1.5) in every dimension. The study on this problem stagnated for several years until the recent work [6], where the $\frac{1}{2}-$barrier was broken for all dimensions. More precisely, Bourgain [6] proved that (1.5) holds if $s>\tfrac{1}{2}-\tfrac{1}{4d}$. More surprisingly, Bourgain also discovered some counterexamples to disprove the widely believed assertion on the $\frac{1}{4}-$threshold. Specifically, he showed that $s\ge \frac{1}{2}-\frac{1}{d}$ is necessary for (1.5) if $d\ge 5$. These examples originated essentially from an observation on arithmetical progressions. Recently, R. Luca and M. Rogers [20] showed that $s\ge \frac{1}{2}-\frac{1}{d+2}$ is necessary for (1.5) if $d\ge 3$. More recently, Bourgain [7] gave a counterexample to see that $s<\frac{1}{2}-\frac{1}{d+2}$ is necessary for $d\ge 3$. Up to the endpoint, Du–Zhang [14] proved the sharp result for (1.5) in higher dimensions $d\ge 3.$ We remark that their result [14] also gives improved results on the size of divergence set of Schrödinger solutions, the Falconer distance set problem and the spherical average Fourier decay rates of fractal measures.

Pointwise convergence

			Counterexample
$d=1$	$s\ge \frac{1}{4}$	Carleson [8]	Dahlberg–Kenig [11]$s<\frac{1}{4}$
$d=2$	$s=\frac{3}{8}+$	Bouragin [7], Lee [19], Shao [30]
	$s>\frac{1}{3}$	Du–Guth–Li [13]	Bourgain [7]$s<\frac{1}{3}$
$d\ge 3$	$s>\frac{1}{2}$	Sjölin [29], Vega [33]
	$s>\frac{1}{2}-\frac{1}{4d}$	Bourgain [6]	$s<\frac{1}{2}-\frac{1}{d}$, $d\ge 5$
		Luca-Rogers [20, 21], Demeter–Guo [12]	$s<\frac{1}{2}-\frac{1}{d+2}$, $d\ge 3$
		Bourgain [7]	$s<\frac{1}{2}-\frac{1}{2(d+1)}$
	$s>\frac{1}{2}-\frac{1}{2(d+1)}$	Du–Zhang [14]
$d\ge 1$	$s\ge \frac{1}{4}$	Gigante–Soria [15]	Radial initial data

Now, we list our main results.

Theorem 1.1

Let $s>\frac{1}{2}$. There holds

$$\begin{aligned} \big \Vert \sup _{|t|<1}|S(t)f|\big \Vert _{L^2(B((x_0,y_0),1)\cap \Omega )}\le C\Vert f\Vert _{H^s_D(\Omega )},\quad \forall ~f\in H^s_D(\Omega ) \end{aligned}$$

(1.6)

for any $(x_0,y_0)\in \Omega$, where $B((x_0,y_0),1)$ is the unit ball centered at $(x_0,y_0)$, with the metric inherited from $\Delta _D$.

As a consequence of Theorem 1.1, we obtain the point-wise convergence result.

Corollary 1.2

Let $s>\frac{1}{2}$. Then, we have

$$\begin{aligned} \lim _{t\rightarrow 0}S(t)f(x,y)=f(x,y),~\text {a.e.}~(x,y)\in \Omega , \end{aligned}$$

(1.7)

for any function $f\in H^s_D(\Omega )$.

Theorem 1.3

The convergence property (1.4) requires $s\ge \frac{1}{4}$.

Remark 1.4

As I know, this is the first result to consider the point-wise convergence result in convex domain. In the future, we will try to utilize the polynomial partitioning and decoupling method to improve the result in Theorem 1.1, and describe the size of divergence set of Schrödinger solutions in convex domain.

We conclude this section by giving some notations which will be used throughout this paper. To simplify the expression of our inequalities, we introduce some symbols $\lesssim , \thicksim$. If X, Y are nonnegative quantities, we use $X\lesssim Y$ or $X=O(Y)$ to denote the estimate $X\le CY$ for some absolute constant C, and $X \thicksim Y$ to denote the estimate $X\lesssim Y\lesssim X$.

2 Preliminaries

2.1 Airy Function

First, we recall a few well-known facts about Airy functions. For $z\in \mathbb {C}$, $\mathrm{Ai}(z)$ is defined by

$$\begin{aligned} \mathrm{Ai}(z):=\tfrac{1}{2\pi }\int _{\mathbb {R}}e^{i(s^3/3-sz)}\;ds=\tfrac{1}{2\pi }\int _{\mathbb {R}}\cos \big (\tfrac{s^3}{3}-sz\big )\;ds. \end{aligned}$$

(2.1)

This integral is not absolutely convergent, but is well-defined as the Fourier transform of a temperate distribution. And it is easy to see that $\mathrm{Ai}(z)$ satisfies the Airy equation

$$\begin{aligned} \mathrm{Ai}''(z)-z\mathrm{Ai}(z)=0. \end{aligned}$$

(2.2)

For positive $z>0$, as $z\rightarrow \infty$, we have $\mathrm{Ai}(z)=O(z^{-\infty })$, while for negative values

$$\begin{aligned} \mathrm{Ai}(-z)=e^{-i\frac{\pi }{3}}\mathrm{Ai}(e^{-i\frac{\pi }{3}}z)+e^{i\frac{\pi }{3}}\mathrm{Ai}(e^{i\frac{\pi }{3}}z)=:A_+(z)+A_-(z). \end{aligned}$$

Notice that $A_-(z)=\overline{A_+({\bar{z}})}$. We also have asymptotic expansion (e.g. [26])

$$\begin{aligned} A_-(z)=\frac{1}{2\sqrt{\pi }z^\frac{1}{4}}e^{i\frac{\pi }{4}}e^{-\frac{2}{3}iz^\frac{3}{2}}e^{\Upsilon (z^\frac{3}{2})}=z^{-\frac{1}{4}}e^{i\frac{\pi }{4}}e^{-\frac{2}{3}iz^\frac{3}{2}} \Psi _-(z), \end{aligned}$$

(2.3)

with $e^{\Upsilon (z^\frac{3}{2})}\sim \big (1+\sum \limits _{k\ge 1}c_kz^{-\frac{3k}{2}}\big )\sim 2\sqrt{\pi }\Psi _-(z)$ as $z\rightarrow +\infty$, and the corresponding expansion for $A_+$, where we define $\Psi _+(z):=\overline{\Psi _-({\bar{z}})}.$

Next, we recall some basic properties of Ai(z).

Proposition 2.1

[22] All the zeros of $\mathrm{Ai}(z)$ are real and negative, say

$$\begin{aligned} \mathrm{Ai}(-w_k)=0,\quad -1>-w_1>-w_2>\cdots \rightarrow -\infty . \end{aligned}$$

(2.4)

Moreover,

$$\begin{aligned} w_k=\Big (\tfrac{3}{2}\big (k-\tfrac{1}{4}\big )\pi \Big )^\frac{2}{3}\simeq k^\frac{2}{3},\quad \forall ~k\ge 1. \end{aligned}$$

(2.5)

Lemma 2.2

[17] There exists $C_0$ such that for $L\ge 1$, the following holds true:

$$\begin{aligned} \sup _{b\in \mathbb {R}}\Bigg (\sum _{1\le k\le L}k^{-\frac{1}{3}}|\mathrm{Ai}(b-w_k)|^2\Bigg )\le C_0L^\frac{1}{3}. \end{aligned}$$

(2.6)

2.2 Eigenfunctions and Sobolev Spaces

In this subsection, we recall some basic properties of Sobolev spaces in the Friedlander model case as in [17, 18]. Let $\Omega :=\{(x,y)\in \mathbb {R}^2\mid x>0,~y\in \mathbb {R}\}$ denote the half-space $\mathbb {R}_+^2:=\mathbb {R}^+\times \mathbb {R}$ with the Laplacian given by $\Delta _D=\partial _x^2+(1+x)\partial _y^2$ with Dirichlet boundary condition on $\partial \Omega$. Taking the Fourier transformation in the $y-$variable gives

$$\begin{aligned} -\Delta _{D,\eta }=-\partial _x^2+(1+x)\eta ^2. \end{aligned}$$

For $\eta \ne 0,~-\Delta _{D,\eta }$ is a self-adjoint, positive operator on $L^2([0,\infty ))$ with compact resolvent. In fact, the potential $V(x,\eta )=(1+x)\eta ^2$ is bounded from below, it is continuous and $\lim \limits _{x\rightarrow \infty }V(x,\eta )=\infty$. Thus, we can consider the form associated with $-\partial _x^2+V(x,\eta ),$

$$\begin{aligned} \begin{aligned} Q(v)=&\int _{0}^\infty \big (|\partial _xv|^2+V(x,\eta )|v|^2\big )dx,\\ D(Q)=&H_0^1(\mathbb {R}_+)\cap \big \{v\in L^2(\mathbb {R}_+), (1+x)^{1/2}v\in L^2(\mathbb {R}_+)\big \}, \end{aligned} \end{aligned}$$

which is clearly symmetric, closed and bounded from below by a positive constant c. If $c\gg 1$ is chosen such that $-\Delta _{D,\eta }+c$ is invertible, then $(-\Delta _{D,\eta }+c)^{-1}$ sends $L^2([0,\infty ))$ in D(Q) and we deduce that $(-\Delta _{D,\eta }+c)^{-1}$ is also a self-adjoint and compact operator. The last assertion follows from the compact inclusion

$$\begin{aligned} D(Q)=\big \{v|~\partial _xv,~(1+x)^{1/2}v\in L^2([0,\infty )),v(0)=0\big \}\hookrightarrow ~L^2([0,\infty )). \end{aligned}$$

Thus, we derive from classical spectral theory that there exists a base of eigenfunctions $v_k$ of $-\Delta _{D,\eta }$ associated to a sequence of eigenvalues $\lambda _k(\eta )\rightarrow \infty$. From $-\Delta _{D,\eta }v=\lambda v$, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _x^2v=(\eta ^2-\lambda +x\eta ^2)v,\\ v(0,\eta )=0. \end{array}\right. } \end{aligned}$$

and after a suitable change of variables, we find that an orthonormal basis of $L^2([0,+\infty ))$ is given by eigenfunctions

$$\begin{aligned} e_k(x,\eta )=f_k\frac{\eta ^{1/3}}{k^{1/6}}\mathrm{Ai}(\eta ^\frac{2}{3}x-w_k) \end{aligned}$$

(2.7)

where $f_k$ are constants so that

$$\begin{aligned} \Vert e_k(\cdot ,\eta )\Vert _{L^2((0,\infty ))}=1, \end{aligned}$$

and $e_k$ satisfies

$$\begin{aligned} -\Delta _{D,\eta }e_k(x,\eta )=\lambda _k(\eta )e_k(x,\eta ),\quad \lambda _k(\eta )=\eta ^2+w_k\eta ^\frac{4}{3}, \end{aligned}$$

(2.8)

with $\{w_k\}_k$ being the zeros of Airy’s function in decreasing order, see (2.5).

Remark 2.3

• (1) As Remark 3.1 in [17], if we denote $\delta _{x=a}$ to be the Dirac distribution on $\mathbb {R}^+,~a>0$, then it reads as follows

  $$\begin{aligned} \delta _{x=a}=\sum _{k\ge 1}e_k(x,\eta )e_k(a,\eta ). \end{aligned}$$

  (2.9)

• (2) $f_k$ as in (2.7) has uniform upper bound and lower bound with respect to k. Indeed, we get by $\Vert e_k(x,\eta )\Vert _{L_x^2(R^+)}^2=1$

  $$\begin{aligned} f_k^2\frac{\eta ^{2/3}}{k^{1/3}}\int _0^\infty |\mathrm{Ai}(\eta ^\frac{2}{3}x-w_k)|^2dx=1. \end{aligned}$$

  By scaling, we have

  $$\begin{aligned} \frac{f_k^2}{k^{1/3}}\int _0^\infty |\mathrm{Ai}(x-w_k)|^2dx=1. \end{aligned}$$

  Hence,

  $$\begin{aligned} f_k^2=k^\frac{1}{3}\Big (\int _0^\infty |\mathrm{Ai}(x-w_k)|^2dx\Big )^{-1}. \end{aligned}$$

  We are reduced to show that there exist constants $C_1$ and $C_2$ such that

  $$\begin{aligned} C_1k^\frac{1}{3}\le \int _0^\infty |\mathrm{Ai}(x-w_k)|^2\;dx\le C_2k^\frac{1}{3}. \end{aligned}$$

  (2.10)

  Using the asymptotic behavior of Airy function: $\mathrm{Ai}(-z)=O(z^{-\frac{1}{4}})$ as $z\rightarrow +\infty$, and $w_k\simeq k^\frac{2}{3}$, we obtain for k sufficiently large

  $$\begin{aligned} \int _0^{w_k-w_k^\frac{1}{3}} |\mathrm{Ai}(x-w_k)|^2\;dx\simeq&\int _0^{w_k-w_k^\frac{1}{3}} (w_k-x)^{-\frac{1}{2}}dx \\ \simeq&2\sqrt{w_k}-2 \simeq \sqrt{w_k}\simeq k^\frac{1}{3}, \end{aligned}$$

  By $|\mathrm{Ai}(z)|\le C(1+|z|)^{-\frac{1}{4}}$, we estimate

  $$\begin{aligned} \int _{w_k-w_k^\frac{1}{3}}^{w_k+w_k^\frac{1}{3}}|\mathrm{Ai}(x-w_k)|^2\;dx\lesssim w_k^\frac{1}{3}\lesssim k^\frac{2}{9}. \end{aligned}$$

  On the other hand, by the asymptotic behavior of Airy function: $\mathrm{Ai}(z)=O(z^{-\infty })$ as $z\rightarrow +\infty$, we get

  $$\begin{aligned} \int _{w_k+w_k^\frac{1}{3}}^\infty |\mathrm{Ai}(x-w_k)|^2\;dx\lesssim&\int _{w_k^\frac{1}{3}}^\infty x^{-6}\;dx\lesssim 1. \end{aligned}$$

  And so (2.10) follows.

• (3) We have by (2.6)

  $$\begin{aligned} \sup _{x\in \mathbb {R}^+}\Big (\sum _{1\le k\le L}|e_k(x,\eta )|^2\Big )\le C_0\eta ^\frac{2}{3}L^{\frac{1}{3}}. \end{aligned}$$

  (2.11)

For each function $f(x,y)\in L^2(\Omega )$, taking the Fourier transformation in the y-variable, and using the fact that $\{e_k(x,\eta )\}_{k\ge 1}$ forms an orthonormal basis of $L^2([0,+\infty ))$, we have the expansion formula

$$\begin{aligned} \hat{f}(x,\eta )=\sum _{k=1}^\infty \hat{f}_k(\eta )e_k(x,\eta ),\quad \hat{f}_k(\eta )=\int _{0}^\infty \hat{f}(x,\eta )e_k(x,\eta )\;dx. \end{aligned}$$

By orthogonality, it gives

$$\begin{aligned} \Vert \hat{f}(x,\eta )\Vert _{L^2_x(\mathbb {R}^+)}=\Big (\sum _{k=1}^\infty |\hat{f}_k(\eta )|^2\Big )^\frac{1}{2}. \end{aligned}$$

Therefore, we have by Plancherel theorem

$$\begin{aligned} \Vert f(x,y)\Vert _{L^2(\Omega )}=\Vert \hat{f}(x,\eta )\Vert _{L^2(\mathbb {R}^+\times \mathbb {R})}=\Big (\sum _{k=1}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(\mathbb {R})}^2\Big )^\frac{1}{2}. \end{aligned}$$

(2.12)

Similarly,

$$\begin{aligned} \Vert f(x,y)\Vert _{\dot{H}^s_D(\Omega )}=\Big (\sum _{k=1}^\infty \big \Vert \lambda _k(\eta )^\frac{s}{2}\hat{f}_k(\eta )\big \Vert _{L^2(\mathbb {R})}^2\Big )^\frac{1}{2}. \end{aligned}$$

(2.13)

3 Proof of Main Theorem

3.1 Proof of Theorem 1.1

First, we recall the dyadic partition of unity, see Proposition 2.10 in Bahouri-Chemin-Danchin [3].

Proposition 3.1

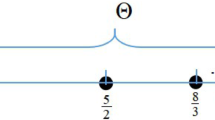
(Dyadic partition of unity, [3]) Let $\mathcal {C}$ be the annulus $\big \{\xi \in \mathbb {R}:\;\tfrac{3}{4}\le |\xi |\le \tfrac{8}{3}\big \}$. There exist even functions $\varphi$ and $\psi$, valued in the interval [0, 1], and $\mathrm{supp}\varphi \subset B(0,4/3),\;\mathrm{supp}\psi \subset \mathcal {C}$, and such that

$$\begin{aligned} \varphi (\xi )+\sum _{j\ge 0}\psi (2^{-j}\xi )=1,\qquad \forall \;\xi \in \mathbb {R}. \end{aligned}$$

(3.1)

Applying the dyadic partition of unity (3.1), we estimate

$$\begin{aligned}&\Big \Vert \sup _{|t|<1}|S(t)f|\Big \Vert _{L^2(B((x_0,y_0),1)\bigcap \Omega )}\nonumber \\&\quad \le \Big \Vert \sup _{|t|<1}|S(t)\varphi (\sqrt{-\Delta _D}) f|\Big \Vert _{L^2(B((x_0,y_0),1)\bigcap \Omega )}\nonumber \\&\quad +\sum _{j=0}^\infty \Big \Vert \sup _{|t|<1}|S(t)\psi (2^{-j}\sqrt{-\Delta _D})f|\Big \Vert _{L^2(B((x_0,y_0),1)\bigcap \Omega )}. \end{aligned}$$

(3.2)

Then, we are reduced to show

$$\begin{aligned} \Vert S(t)\varphi (\sqrt{-\Delta _D}) f\Vert _{L_{t,x,y}^\infty }\le&C\Vert f\Vert _{L^2(\Omega )}, \end{aligned}$$

(3.3)

$$\begin{aligned} \Big \Vert \sup _{|t|<1}|S(t)\psi (2^{-j}\sqrt{-\Delta _D})f|\Big \Vert _{L^2(B((x_0,y_0),1)\bigcap \Omega )}\le&C2^{\frac{j}{2}}\big \Vert \psi (2^{-j}\sqrt{-\Delta _D})f\big \Vert _{L^2(\Omega )}. \end{aligned}$$

(3.4)

Indeed, plugging (3.3) and (3.4) into (3.2), and using the Cauchy–Schwartz inequality, we obtain for any $s>\tfrac{1}{2}$

$$\begin{aligned}&\Big \Vert \sup _{|t|<1}|S(t)f|\Big \Vert _{L^2(B((x_0,y_0),1)\bigcap \Omega )}\\&\quad \lesssim \Vert f\Vert _{L^2(\Omega )}+\Big (\sum _{j=0}^\infty 2^{j}\big \Vert \psi (2^{-j}\sqrt{-\Delta _D})f\big \Vert _{L^2(\Omega )}^2\Big )^\frac{1}{2}\\&\quad \lesssim \Vert f\Vert _{L^2(\Omega )}+\Big (\sum _{j=0}^\infty 2^{j}\sum _{k=1}^\infty \big \Vert \psi \big (2^{-j}\sqrt{\lambda _k(\eta )}\big )\hat{f}_k(\eta )\big \Vert _{L^2(\mathbb {R})}^2\Big )^\frac{1}{2}\\&\quad \lesssim \Vert f\Vert _{L^2(\Omega )}+\Big (\sum _{k=1}^\infty \big \Vert \lambda _k(\eta )^\frac{s}{2}\hat{f}_k(\eta )\big \Vert _{L^2(\mathbb {R})}^2\Big )^\frac{1}{2}\\&\quad \lesssim \Vert f\Vert _{H^s_D(\Omega )}. \end{aligned}$$

First, we consider the contribution from the lower frequency term, i.e. (3.3). Taking the Fourier transformation in the y-variable, we have

$$\begin{aligned} \varphi (\sqrt{-\Delta _{D,\eta }})\hat{f}(x,\eta )=\sum _{k=1}^\infty \varphi \big (\sqrt{\lambda _k(\eta )}\big )\hat{f}_k(\eta )e_k(x,\eta ). \end{aligned}$$

By the support property of $\varphi$, we know that $|\eta |\lesssim 1.$ Then, we obtain by Bernstein’s inequality in y-variable and (2.11) with $L\sim |\eta |^{-2}$

$$\begin{aligned} \Vert S(t)\varphi (\sqrt{-\Delta _D}) f\Vert _{L_y^\infty (\mathbb {R})}\lesssim&\Vert S(t)\varphi (\sqrt{-\Delta _D}) f\Vert _{L_y^2(\mathbb {R})}\\ \lesssim&\big \Vert e^{it\Delta _{D,\eta }}\varphi \big (\sqrt{-\Delta _{D,\eta }}\big )\hat{f}(x,\eta )\big \Vert _{L^2_\eta (\mathbb {R})}\\ \lesssim&\Big \Vert \sum _{k=1}^\infty e^{-it\lambda _k(\eta )}\varphi \big (\sqrt{\lambda _k(\eta )}\big )\hat{f}_k(\eta )e_k(x,\eta )\Big \Vert _{L^2_\eta (\mathbb {R})}\\ \lesssim&\Big \Vert \Big (\sum _{k=1}^\infty |\hat{f}_k(\eta )|^2\Big )^\frac{1}{2} \Big (\sum _{k=1}^{|\eta |^{-2}}|e_k(x,\eta )|^2\Big )^\frac{1}{2}\Big \Vert _{L^2_\eta (\mathbb {R})}\\ \lesssim&\Big (\sum _{k=1}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(\mathbb {R})}^2\Big )^\frac{1}{2}\\ \lesssim&\Vert f\Vert _{L^2(\Omega )}. \end{aligned}$$

And so (3.3) follows.

Next, we turn to prove (3.4). Notice that

$$\begin{aligned}&S(t)\psi (2^{-j}\sqrt{-\Delta _D})f(x,y)\\&\quad =\int _{\mathbb {R}}e^{iy\eta }e^{it\Delta _{D,\eta }}\psi \big (2^{-j}\sqrt{-\Delta _{D,\eta }}\big )\hat{f}(x,\eta )\;d\eta \\&\quad =\int _{\mathbb {R}}e^{iy\eta }\sum _{k=1}^\infty e^{-it\lambda _k(\eta )}\psi (2^{-j}\sqrt{\lambda _k(\eta )})\hat{f}_k(\eta )e_k(x,\eta )\;d\eta \\&\quad =2\int _{0}^\infty \cos (y\rho )\sum _{k=1}^\infty e^{-it\lambda _k(\rho )}\psi (2^{-j}\sqrt{\lambda _k(\rho )})\hat{f}_k(\rho )e_k(x,\rho )\;d\rho \\&\quad = \int _{0}^\infty e^{-it\tau }\Big [2\sum _{k=1}^\infty \cos \big (y\rho (\tau ,k)\big )\psi (2^{-j}\sqrt{\tau })\hat{f}_k\big (\rho (\tau ,k)\big )\frac{\partial \rho (\tau ,k)}{\partial \tau }e_k\big (x,\rho (\tau ,k)\big )\Big ]\;d\tau \\&\quad =\mathcal {F}^{-1}_{t\mapsto \tau }\bigg [2\chi _{[0,\infty )}(\tau )\sum _{k=1}^\infty \cos \big (y\rho (\tau ,k)\big )\psi (2^{-j}\sqrt{\tau })\hat{f}_k\big (\rho (\tau ,k)\big )\frac{\partial \rho (\tau ,k)}{\partial \tau }e_k\big (x,\rho (\tau ,k)\big )\bigg ](t), \end{aligned}$$

where we use a change of variables: $\tau =\lambda _k(\rho )=\rho ^2+w_k\rho ^\frac{4}{3}\sim 2^{2j}$. We utilize Bernstein’s inequality and Plancherel theorem in time t to get

$$\begin{aligned}&\sup _{|t|<1}\big |S(t)\psi (2^{-j}\sqrt{-\Delta _D})f(x,y)\big |^2\\&\quad \le 2^{2j}\Vert S(t)\psi (2^{-j}\sqrt{-\Delta _D})f(x,y)\Vert _{L_t^2(\mathbb {R})}^2\\&\quad \le 2^{2j+1}\int _0^\infty \Big |\sum _{k=1}^\infty \cos \big (y\rho (\tau ,k)\big ) \psi (2^{-j}\sqrt{\tau })\hat{f}_k\big (\rho (\tau ,k)\big )\frac{\partial \rho (\tau ,k)}{\partial \tau }e_k\big (x,\rho (\tau ,k)\big )\Big |^2\;d\tau . \end{aligned}$$

By orthogonality, it gives

$$\begin{aligned}&\Big \Vert \sup _{|t|<1}\big |S(t)\psi (2^{-j}\sqrt{-\Delta _D})f(x,y)\big |\Big \Vert _{L_x^2(\mathbb {R}^+)}^2\\&\quad \le 2^{2j+1}\int _0^\infty \int _0^\infty \Big |\sum _{k=1}^\infty \cos \big (y\rho (\tau ,k)\big ) \psi (2^{-j}\sqrt{\tau })\hat{f}_k\big (\rho (\tau ,k)\big )\\&\quad \quad \times \frac{\partial \rho (\tau ,k)}{\partial \tau } e_k\big (x,\rho (\tau ,k)\big )\Big |^2\;dx\;d\tau \\&\quad \lesssim 2^{2j}\sum _{k=1}^\infty \int _0^\infty |\psi (2^{-j}\sqrt{\tau })|^2\big |\hat{f}_k\big (\rho (\tau ,k)\big )\big |^2\Big |\frac{\partial \rho (\tau ,k)}{\partial \tau }\Big |^2\;d\tau \\&\quad \lesssim 2^{2j}\sum _{k=1}^\infty \int _{\rho }|\psi (2^{-j}\sqrt{\lambda _k(\rho )} )|^2\big |\hat{f}_k\big (\rho \big )\big |^2\Big |\frac{\partial \rho (\tau ,k)}{\partial \tau }\Big |\;d\rho \\&\quad \lesssim 2^{2j}\sum _{k=1}^\infty \int _{\rho }|\psi (2^{-j}\sqrt{\lambda _k(\rho )} )|^2\big |\hat{f}_k\big (\rho \big )\big |^2\frac{1}{2\rho +\frac{4}{3}w_k\rho ^\frac{1}{3}}\;d\rho \\&\quad \lesssim 2^{j}\sum _{k=1}^\infty \big \Vert \psi (2^{-j}\sqrt{\lambda _k(\eta )} )\hat{f}_k(\eta )\big \Vert _{L^2(\mathbb {R})}^2\\&\quad \lesssim 2^{j}\big \Vert \psi (2^{-j}\sqrt{-\Delta _D})f\big \Vert _{L^2(\Omega )}^2, \end{aligned}$$

where we use the changing variable $\tau =\lambda _k(\rho )=\rho ^2+w_k\rho ^\frac{4}{3}$ and

$$\begin{aligned} \frac{1}{2\rho +\frac{4}{3}w_k\rho ^\frac{1}{3}}\lesssim \frac{\rho }{\lambda _k(\rho )}\lesssim 2^{-j}. \end{aligned}$$

Thus, using Hölder’s inequality, we obtain

$$\begin{aligned}&\Big \Vert \sup _{|t|<1}|S(t)\psi (2^{-j}\sqrt{-\Delta _D})f|\Big \Vert _{L^2(B((x_0,y_0),1)\bigcap \Omega )}\\&\quad \lesssim \sup _{y\in \mathbb {R}} \Big \Vert \sup _{|t|<1}|S(t)\psi (2^{-j}\sqrt{-\Delta _D})f|\Big \Vert _{L^2_x(\mathbb {R}^+)}\\&\quad \lesssim 2^{\frac{j}{2}}\big \Vert \psi (2^{-j}\sqrt{-\Delta _D})f\big \Vert _{L^2(\Omega )}. \end{aligned}$$

This implies (3.4).

Therefore, we complete the proof of Theorem 1.1.

3.2 Proof of Corollary 1.2

Fixed $f(x,y)\in H^s_D(\Omega )$, we define

$$\begin{aligned} \Omega _*f(x,y):=\varlimsup _{t\rightarrow 0}S(t)f(x,y)-\varliminf _{t\rightarrow 0}S(t)f(x,y)\quad {and}\quad \Omega ^*f(x,y):=\sup _{|t|<1}\big |S(t)f\big |. \end{aligned}$$

Then, $|\Omega _*f(x,y)|\le 2\Omega ^*f(x,y)$. By the density, we get for each $f(x,y)\in H^s_D(\Omega )$,

$$\begin{aligned} \forall ~\varepsilon >0,~\exists ~ g\in C_c^\infty (\Omega ),~s.t.~\Vert f-g\Vert _{H^s_D(\Omega )}<\frac{\varepsilon }{3}. \end{aligned}$$

(3.5)

Observing that

$$\begin{aligned} \Vert S(t)g-g\Vert _{L^\infty (\Omega )}\lesssim \Vert S(t)g-g\Vert _{H^{\frac{3}{2}}_D(\Omega )}\rightarrow 0,\quad \text {as}\quad t\rightarrow 0, \end{aligned}$$

we obtain $\Omega _*g(x)\equiv 0,~\forall ~g\in C_c^\infty (\Omega ).$ Hence,

$$\begin{aligned} \Omega _*f=\Omega _*(f-g),~\big |\Omega _*f\big |=\big |\Omega _*(f-g)\big |\le 2\Omega ^*(f-g). \end{aligned}$$

This together with (1.6) and (3.5) yields that

$$\begin{aligned} \big \Vert \Omega _*f\big \Vert _{L^2_\mathrm{loc}(\Omega )}\le 2\big \Vert \Omega ^*(f-g)\big \Vert _{L^2_\mathrm{loc}(\Omega )}\lesssim \Vert f-g\Vert _{H^s_D(\Omega )}<\varepsilon . \end{aligned}$$

(3.6)

We obtain $\Omega _*f=0,~a.e.~(x,y)\in \Omega$, since $\varepsilon$ is arbitrary. And so the limits $\lim \limits _{t\rightarrow 0}S(t)f$ exists almost everywhere. On the other hand, by the orthonormal basis of $L^2([0,\infty ))$, we have

$$\begin{aligned} \hat{f}(x,\eta )=\sum _{k=1}^\infty \hat{f}_k(\eta )e_k(x,\eta ),\quad \hat{f}_k(\eta )=\int _{0}^\infty \hat{f}(x,\eta )e_k(x,\eta )\;dx, \end{aligned}$$

and

$$\begin{aligned} \Vert f\Vert _{H^s_D(\Omega )}^2=&\Vert \hat{f}(x,\eta )\Vert _{L^2(\mathbb {R}^+\times \mathbb {R})}^2+\big \Vert (-\Delta _{D,\eta })^\frac{s}{2}\hat{f}(x,\eta )\big \Vert _{L^2(\mathbb {R}^+\times \mathbb {R})}^2\\ =&\sum _{k=1}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(\mathbb {R})}^2+\sum _{k=1}^\infty \big \Vert \lambda _k(\eta )^\frac{s}{2}\hat{f}_k(\eta )\big \Vert _{L^2(\mathbb {R})}^2, \end{aligned}$$

with $e_k(x,\eta ),~\lambda _k(\eta )$ and $\Delta _{D,\eta }$ defined in Sect. 2. Thus, for any $\varepsilon >0$, there exists $N>0$ and $R>0$ such that

$$\begin{aligned} \sum _{k=N}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(\mathbb {R})}^2+\sum _{k=1}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(|\eta |>R)}^2<\frac{\varepsilon }{2}. \end{aligned}$$

Then, for $|t|<\frac{c\varepsilon }{\Vert f\Vert _{L^2(\Omega )}^2(R^2+N^\frac{2}{3}R^\frac{4}{3})}$, we estimate

$$\begin{aligned} \big \Vert S(t)f-f\big \Vert _{L^2(\Omega )}^2=&\big \Vert e^{it\Delta _{D,\eta }}\hat{f}(x,\eta )-\hat{f}(x,\eta )\big \Vert _{L^2(\mathbb {R}^+\times \mathbb {R})}^2\\ =&\sum _{k=1}^\infty \big \Vert \big (e^{it\lambda _k(\eta )}-1\big )\hat{f}_k(\eta )\big \Vert _{L^2(\mathbb {R})}^2\\ \le&\sum _{k=1}^N\big \Vert \big (e^{it\lambda _k(\eta )}-1\big )\hat{f}_k(\eta )\big \Vert _{L^2(\mathbb {R})}^2+\sum _{k=N}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(\mathbb {R})}^2\\ \le&\sum _{k=1}^N\big \Vert \big (e^{it\lambda _k(\eta )}-1\big )\hat{f}_k(\eta )\big \Vert _{L^2(|\eta |\le R)}^2+\sum _{k=1}^N\big \Vert \hat{f}_k(\eta )\big \Vert _{L^2(|\eta |> R)}^2\\&+\sum _{k=N}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(\mathbb {R})}^2 <\varepsilon , \end{aligned}$$

where we use the fact that

$$\begin{aligned} \sum _{k=1}^N\big \Vert \big (e^{it\lambda _k(\eta )}-1\big )\hat{f}_k(\eta )\big \Vert _{L^2(|\eta |\le R)}^2\le&\sup _{\begin{array}{c} 1\le k\le N\\ |\eta |\le R \end{array}}\big |e^{it\lambda _k(\eta )}-1\big |\sum _{k=1}^\infty \Vert \hat{f}_k(\eta )\Vert _{L^2(\mathbb {R})}^2<\varepsilon \end{aligned}$$

in the last inequality. This implies

$$\begin{aligned} \lim _{t\rightarrow 0}\big \Vert S(t)f-f\big \Vert _{L^2}=0. \end{aligned}$$

Therefore, (1.7) follows by the fact that the limit $\lim \limits _{t\rightarrow 0}S(t)f$ exists almost everywhere.

3.3 Proof of Theorem 1.3

Let $\phi _k\in C_c^\infty ([2^k,2^k+2^{\frac{k}{2}}]),~k=1,2,\ldots ,$ and

$$\begin{aligned} 0\le \phi _k\le 1,~\Big |\frac{d^i}{dx^i}\phi _k(x)\Big |\le C2^{-\frac{k}{2}i}. \end{aligned}$$

Taking

$$\begin{aligned} g_k(x,y)=\mathcal {F}^{-1}\big (\phi _k(\eta )e_{2^{k+2}}(x,\eta )\big ), \end{aligned}$$

then, we have

$$\begin{aligned} e^{it\Delta _D}g_k(x,y)=&\int _{\mathbb {R}} e^{i(y\eta -t\lambda _{2^{k+2}}(\eta ))}\phi _k(\eta )e_{2^{k+2}}(x,\eta )\;d\eta . \end{aligned}$$

Writing $\Phi (\eta ):=y\eta -t\lambda _{2^{k+2}}(\eta )-\tfrac{2}{3}z(\eta ,x)^\frac{3}{2}$ with $z(\eta ,x)=w_{2^{k+2}}-\eta ^\frac{2}{3}x$, then $\Phi '(\eta )=y-t\big (2\eta +\tfrac{4}{3}w_{2^{k+2}}\eta ^\frac{1}{3}\big )+\tfrac{2}{3}z(\eta ,x)^\frac{1}{2}\eta ^{-\frac{1}{3}}x$. For $\tfrac{1}{2}\le x,y\le 1,$ taking

$$\begin{aligned} t(x,y)=\frac{y+\tfrac{2}{3}z(\eta _0,x)^\frac{1}{2}\eta _0^{-\frac{1}{3}}x}{2\eta _0+\frac{4}{3}w_{2^{k+2}}\eta _0^\frac{1}{3}},~\eta _0=2^k+2^{\frac{k}{2}-1}, \end{aligned}$$

we get $\Phi '(\eta _0)=0$ and

$$\begin{aligned} \big |\Phi (\eta )-\Phi (\eta _0)\big |\le \sup _{\bar{\eta }}|\Phi '(\bar{\eta })|\cdot |\eta -\eta _0|\le \tfrac{1}{2},\quad \forall ~\eta \in [2^k,2^k+2^{\frac{k}{2}}]. \end{aligned}$$

(3.7)

By (2.7), (2.3) and Remark 2.3, we get for all $\eta \in [2^k,2^k+2^{\frac{k}{2}}]$ and $|x|\le 1$

$$\begin{aligned} z:=&w_{2^{k+2}}-\eta ^\frac{2}{3}x\simeq 2^{\frac{2}{3}k},~ e_{2^{k+2}}(x,\eta )=f_{2^{k+2}}\frac{\eta ^\frac{1}{3}}{2^\frac{k+2}{6}}\mathrm{Ai}(-z),\\ \mathrm{Ai}(-z)=&A_-(z)+A_+(z),~A_+(z)=\overline{A_-(z)},\\ A_-(z)=&z^{-\frac{1}{4}}e^{i\frac{\pi }{4}}e^{-\frac{2}{3}iz^\frac{3}{2}} \Psi _-(z),~ 2\sqrt{\pi }\Psi _-(z)\sim \left( 1+\sum \limits _{k\ge 1}c_kz^{-\frac{3k}{2}}\right) \end{aligned}$$

Thus,

$$\begin{aligned}&e^{it(y)\Delta _D}g_k(x,y)\\&\quad =\int _{\mathbb {R}} e^{i(y\eta -t\lambda _{2^{k+2}}(\eta ))}\phi _k(\eta )f_{2^{k+2}}\frac{\eta ^\frac{1}{3}}{2^\frac{k+2}{6}}\big [A_++A_-\big ](z(\eta ,x))\;d\eta \\&\quad =e^{i\frac{\pi }{4}}e^{i\Phi (\eta _0)}\int _{\mathbb {R}}e^{i[\Phi (\eta )-\Phi (\eta _0)]}\phi _k(\eta )f_{2^{k+2}} \frac{\eta ^\frac{1}{3}}{2^\frac{k+2}{3}}\Psi _-(z(\eta ,x))\;d\eta \\&\quad \quad +e^{-i\frac{\pi }{4}}\int _{\mathbb {R}}e^{i(y\eta -t\lambda _{2^{k+2}}(\eta )+\frac{2}{3}z(\eta ,x)^\frac{3}{2})}f_{2^{k+2}} \phi _k(\eta )\frac{\eta ^\frac{1}{3}}{2^\frac{k+2}{3}}\Psi _+(z(\eta ,x))\;d\eta \\&\quad :=I_1+I_2. \end{aligned}$$

From (3.7), we know that

$$\begin{aligned} |I_1|=\Big |\int _{\mathbb {R}}e^{i[\Phi (\eta )-\Phi (\eta _0)]}\phi _k(\eta )f_{2^{k+2}}\frac{\eta ^\frac{1}{3}}{2^\frac{k+2}{6}}z(\eta ,x)^{-\frac{1}{4}} \Psi _-(z(\eta ,x))\;d\eta \Big |\gtrsim 2^\frac{k}{2}. \end{aligned}$$

Since $|\partial _\eta [y\eta -t\lambda _{2^{k+2}}(\eta )+\frac{2}{3}z(\eta ,x)^\frac{3}{2}]|\ge c_0>0$, and $|\partial _\eta ^2[y\eta -t\lambda _{2^{k+2}}(\eta )+\frac{2}{3}z(\eta ,x)^\frac{3}{2}]|\le C2^{-k},$ and

$$\begin{aligned} \Big |\partial _\eta \Big [f_{2^{k+2}} \phi _k(\eta )\frac{\eta ^\frac{1}{3}}{2^\frac{k+2}{3}}\Psi _+(z(\eta ,x))\Big ]\Big |\le C2^{-k}, \end{aligned}$$

we estimate by integrating by parts

$$\begin{aligned} |I_2|=\Big |\int _{\mathbb {R}}e^{i(y\eta -t\lambda _{2^{k+2}}(\eta )+\frac{2}{3}z(\eta ,x)^\frac{3}{2})} f_{2^{k+2}} \phi _k(\eta )\frac{\eta ^\frac{1}{3}}{2^\frac{k+2}{3}}\Psi _+(z(\eta ,x))\;d\eta \Big |\lesssim 2^{-\frac{k}{2}}. \end{aligned}$$

Hence,

$$\begin{aligned} \big |e^{it(y)\Delta _D}g_k(x,y)\big |\ge |I_1|-|I_2| \gtrsim&2^\frac{k}{2},\quad \forall ~ \tfrac{1}{2}\le x,y\le 1. \end{aligned}$$

(3.8)

On the other hand,

$$\begin{aligned} \Vert g_k(x,y)\Vert _{H^s_D(\Omega )}\lesssim 2^{k(s+\frac{1}{4})}. \end{aligned}$$

(3.9)

Now, we argue by contradiction. We assume that the convergence property (1.4) holds for any function $f\in H^s_D(\Omega )$ with $s<\tfrac{1}{4}$. Then, by the same argument as in [2, Lemma C.1], we have

$$\begin{aligned} \Big |\big \{(x,y)\in \Omega :~\tfrac{1}{2}\le y\le 1,~|x|\le 1,~\sup _{0<t<1}|e^{it\Delta _D}f(x,y)|>\lambda \big \}\Big |\le C\Big (\frac{\Vert f\Vert _{H^s_D(\Omega )}}{\lambda }\Big )^2. \end{aligned}$$

This together with (3.8) and (3.9) implies for $\lambda =2^\frac{k}{2}$

$$\begin{aligned} \frac{1}{2}\le&\Big |\big \{(x,y)\in \Omega :~\tfrac{1}{2}\le y\le 1,~|x|\le 1,~\sup _{0<t<1}|e^{it\Delta _D}g_k(x,y)|>2^\frac{k}{2}\big \}\Big |\\ \le&C\Big (\frac{\Vert g_k\Vert _{H^s_D(\Omega )}}{2^\frac{k}{2}}\Big )^2\\ \le&C2^{2k(s-\frac{1}{4})}, \end{aligned}$$

which is a contradiction as $k\rightarrow +\infty$, as long as $s<\tfrac{1}{4}$. Therefore, we conclude Theorem 1.3.